Integrating Stereo Images and Laser Altimetry Points Derived from the Same Satellite for High-Accuracy Stereo Mapping
Abstract
:1. Introduction
2. Related Works
3. Materials and Methods
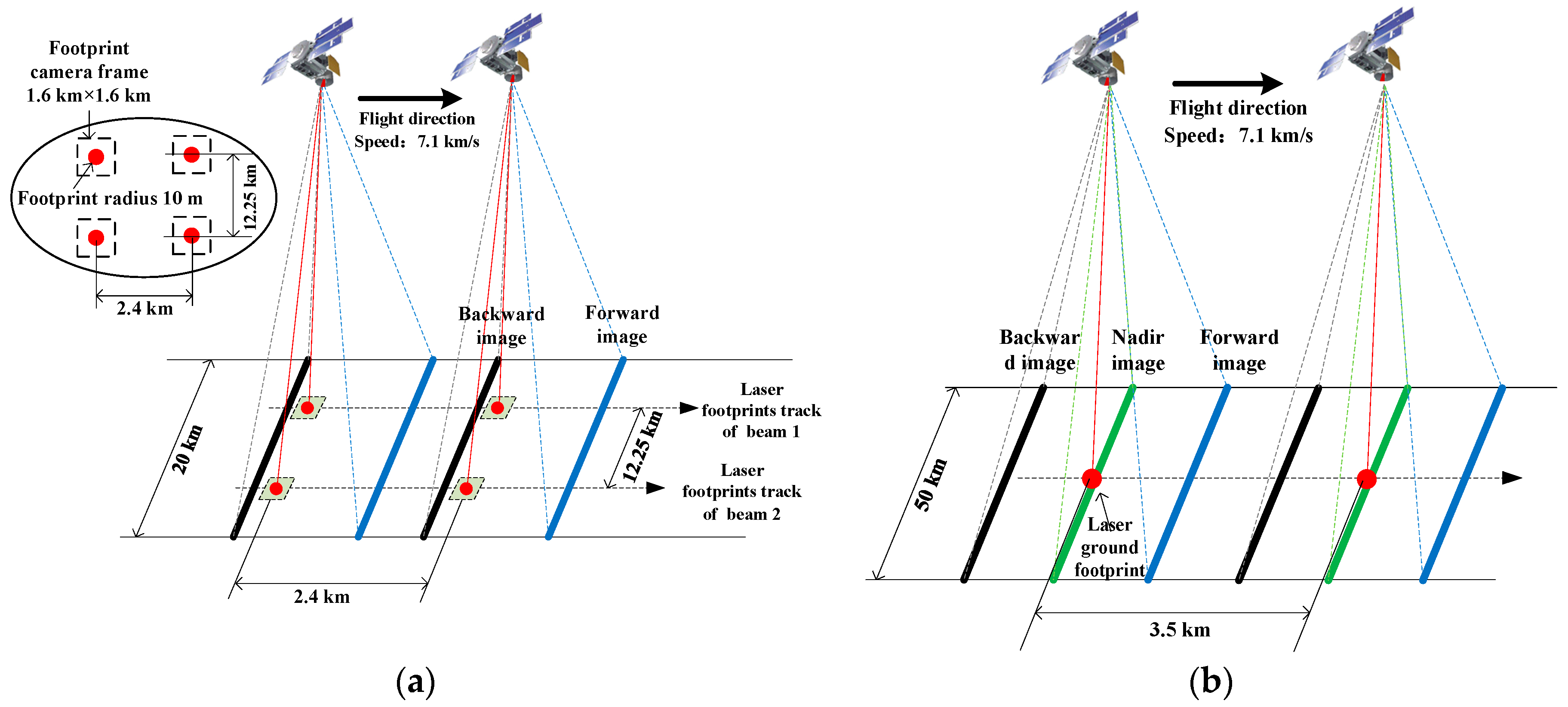
3.1. Working Mechanism for Obtaining LAPs and Images from the Same Satellite
3.1.1. Data Acquisition from the GF7 and ZY3-03 Satellites
3.1.2. GF7 and ZY3-03 Data Processing
3.1.3. Feasibility of using LAPs to Improve Image Geometric Accuracy
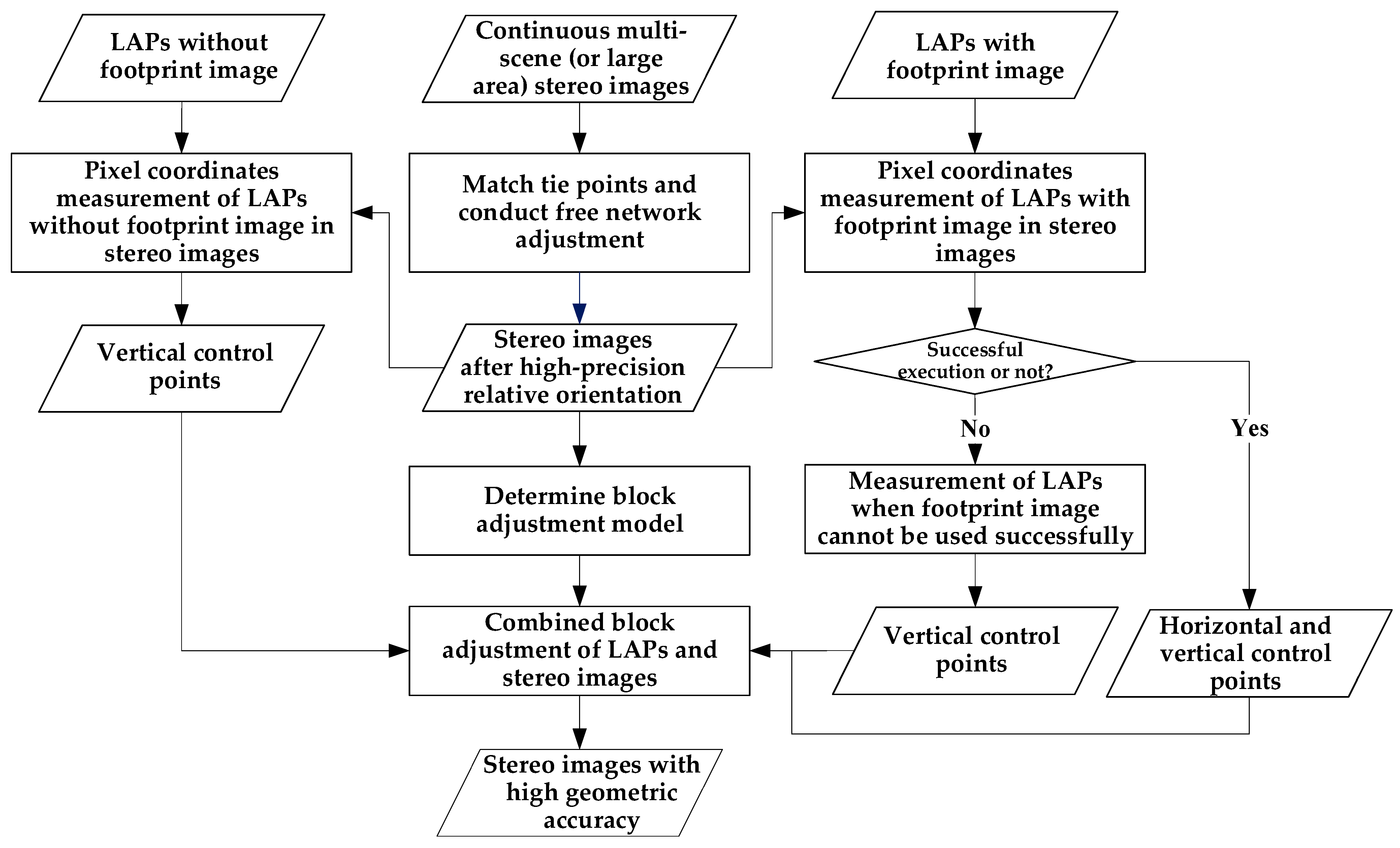
3.2. Integrated Processing Steps
- Stereo images from continuous multi-scenes or large areas were selected. The dense tie points within each stereo image were automatically matched, after which an appropriate number of common tie points in the overlapping region among the adjacent stereo images were automatically matched. Thereafter, the free network adjustment of the stereo images was performed. Stereo images resulting from the high-precision relative orientation were then used for the subsequent steps.
- For LAPs with footprint images, high-precision matching was performed between the laser footprint image and the stereo images using the method described in Section 3.3.1 to obtain the correct pixel coordinates of the LAPs in the stereo images. The LAPs were also used as vertical or horizontal control points for block adjustment. For LAPs that could not use the above method, the method described in Section 3.3.2 was used to obtain tie points within the range of the laser footprint on the stereo images, and a tie point closest to the footprint center was used as the vertical control point.
- For LAPs without footprint images, the method described in Section 3.4 was used to calculate the pixel coordinates of the LAPs in the image with the smallest imaging tilt angle in the synchronously obtained stereo image. Image matching was then performed between the image with the smallest imaging tilt angle and the other constituent images of the stereo image to obtain the correct pixel coordinates of the LAPs in the stereo images. The LAPs were then used as the vertical control points.
- The block adjustment model described in Section 3.5 was used to conduct a combined block adjustment of the stereo images and LAPs to effectively improve the vertical accuracy of the stereo images. Finally, the RFM of the stereo image was updated according to the block adjustment results.
3.3. Pixel Coordinate Measurement of LAPs with Footprint Images in Stereo Images
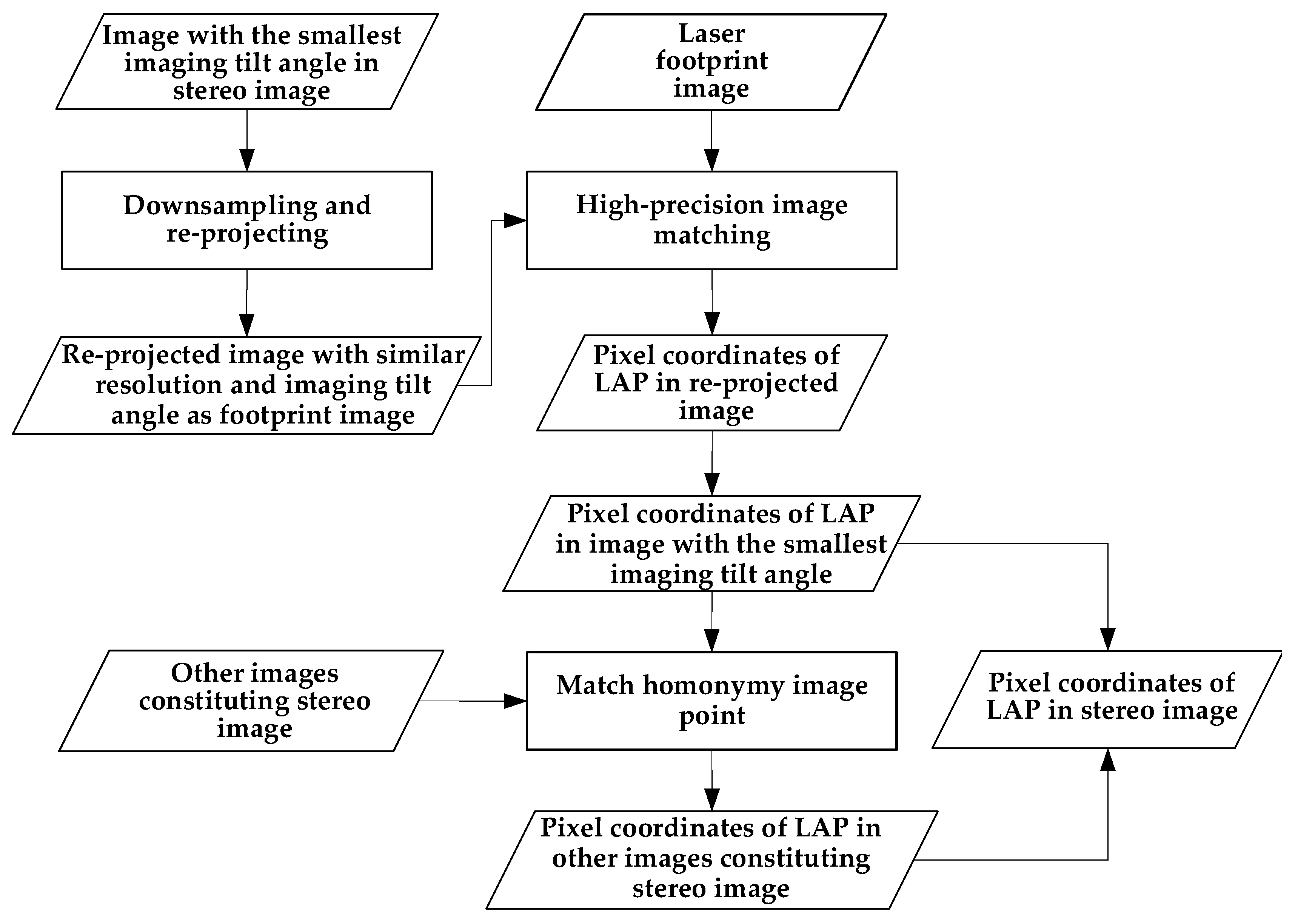
3.3.1. Measurement of LAPs when Successfully Using Footprint Image
- According to the spatial resolution and imaging tilt angle of the laser footprint camera, the image with the smallest imaging tilt angle in the stereo image was down-sampled and re-projected to generate a re-projected image with a similar spatial resolution and imaging tilt angle as the footprint image. This improves the image matching success rate between the footprint and the stereo images.
- Using a combination of scale-invariant feature transform (SIFT) matching [42] and least squares matching [43], image matching was performed between the re-projected image and the laser footprint image to obtain the homonymy image point on the re-projected image that corresponds to the laser image point on the footprint image. According to the corresponding relationship between the re-projected image and the original image before projection, the homonymy image point on the image with smallest imaging tilt angle that corresponds to the laser image point on the footprint image was calculated.
- Using a combination of SIFT matching and least squares matching, image matching was performed between the image with the smallest imaging tilt angle and the other images constituting the stereo image to obtain the homonymy image points on the other images comprising the stereo image, corresponding to the image point of the LAP on the image with the smallest imaging tilt angle. The pixel coordinates of the homonymy image points in the stereo images are actually the pixel coordinates of the LAPs in the stereo images.
3.3.2. Measurement of LAPs when Footprint Image Cannot Be Used Successfully
- 1.
- Equation (1) is used to obtain the horizontal relative error corrections and in the longitude and latitude directions between the processing LAP and the image with smallest imaging tilt angle.where and are the horizontal relative errors in the longitude and latitude directions, respectively, between the previous processed LAP acquired on the same orbit and the image with the smallest imaging tilt angle. and are the horizontal relative errors in the longitude and latitude directions between the latter processed LAP acquired on the same orbit and the image with the smallest imaging tilt angle. These are obtained by subtracting the longitude and latitude coordinates of the processed LAP from the ground longitude and latitude coordinates that were calculated using the pixel coordinates of the processed LAP in the image with the smallest imaging tilt angle to perform the spatial forward intersection. N is the theoretical number of LAPs between the previous and the latter processed LAPs acquired on the same orbit and by the same beam. n is the theoretical number of LAPs between the processing LAP and the previous processed LAP acquired on the same orbit and by the same beam. If the previous processed LAP does not exist, then . If the latter processed LAP does not exist, then .
- 2.
- Using the longitude and latitude coordinates and the elevation values of the processing LAPs, the pixel coordinates of the processing LAPs in the image with the smallest imaging tilt angle are calculated using the imaging geometric model of the image. The pixel coordinates are also corrected using the and obtained in the previous step. According to the laser footprint radius, the pixel range of the ground footprint of the processing LAP on the image with the smallest imaging tilt angle can be obtained.
- 3.
- The image matching between the image with the smallest imaging tilt angle and other constituent images of the stereo image is used to obtain multiple tie points. After eliminating the incorrect tie points, the tie point that is closest to the center point of the laser footprint and distributed within the range of the laser footprint on the image with the smallest imaging tilt angle is selected as the vertical control point, and its elevation is used as the elevation of the LAP.
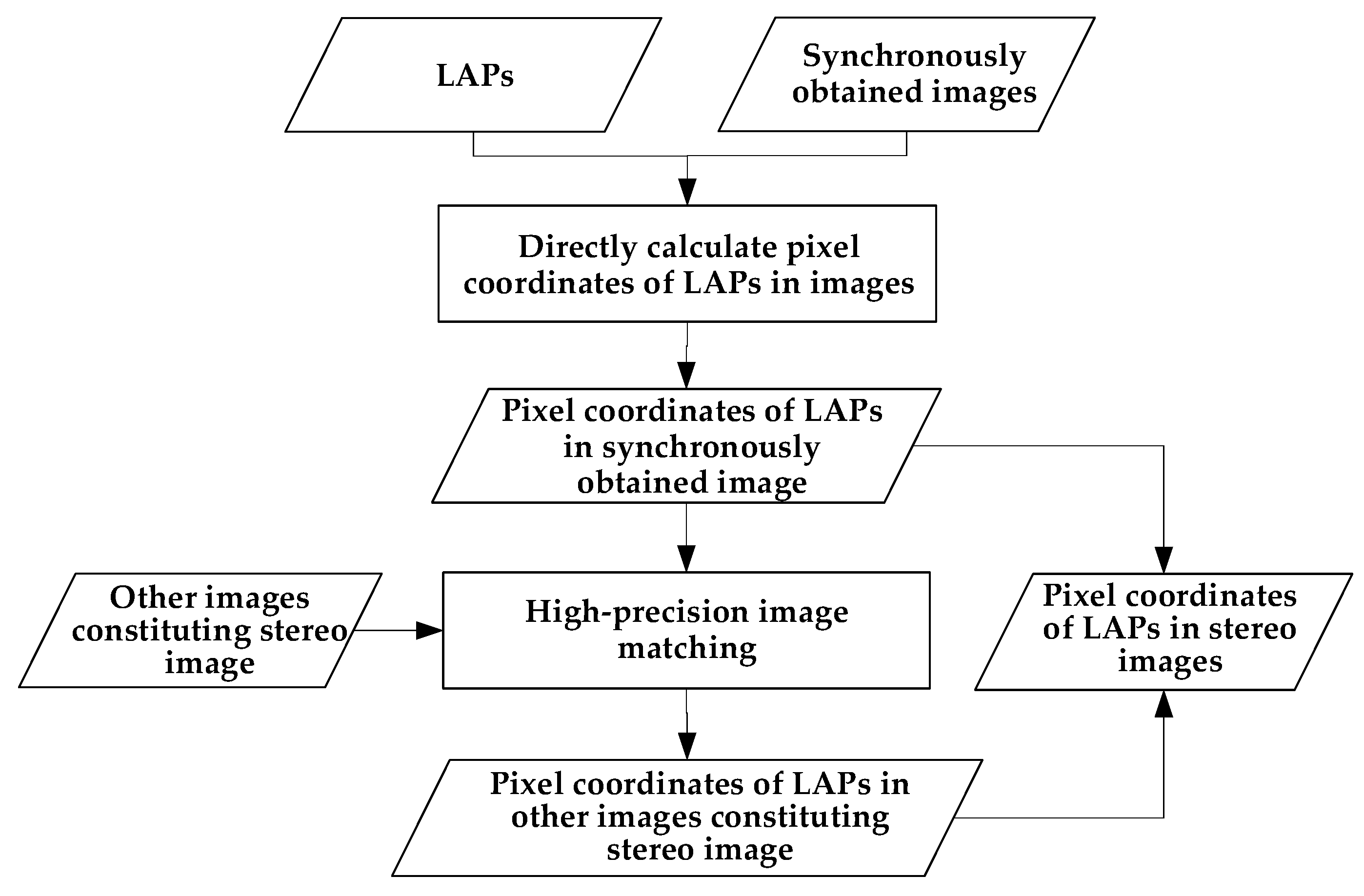
3.4. Pixel Coordinate Measurement of LAPs without Footprint Image on Stereo Images
- According to the longitude and latitude coordinates and the elevations of the LAPs, the pixel coordinates of the LAP on the synchronously obtained image can be calculated directly using the RFM of the image.
- A combination of SIFT feature matching and least squares matching is used to perform high-precision image matching of the stereo images. On the other constituent images of the stereo image, the homonymy points of the pixel coordinates of the LAPs in the synchronously obtained image were obtained, i.e., the accurate pixel coordinates of the LAPs in the stereo image were obtained.
3.5. Combined Block Adjustment Model
4. Results and Discussion
4.1. Experimental Regions and Data
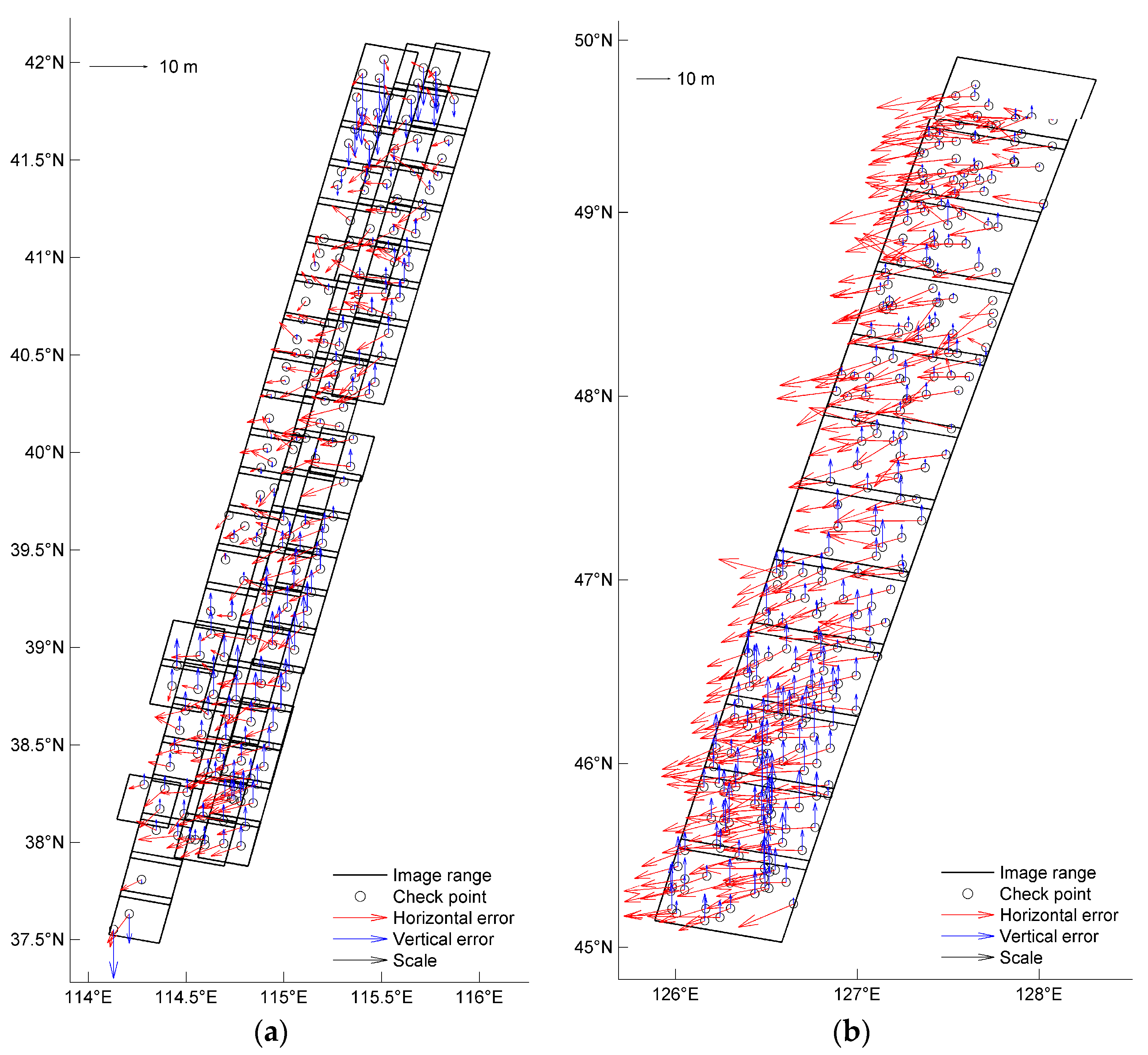
4.2. Initial Stereo Images and LAPs Accuracy Verification
4.2.1. Initial Image Geometric Accuracy Verification
4.2.2. Initial LAP Geometric Accuracy Verification
4.3. Integrated Processing Accuracy Verification
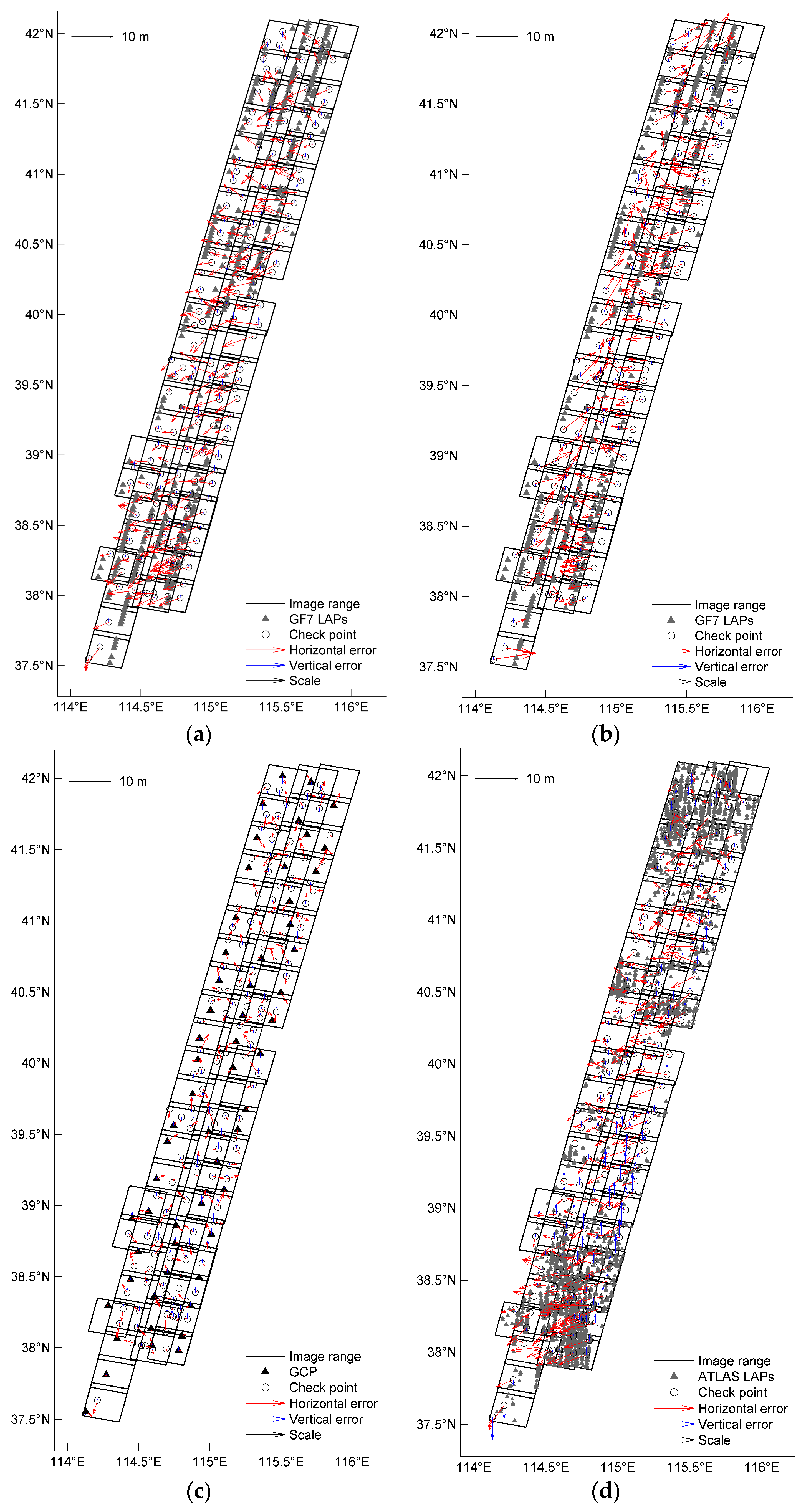
- The GF7 LAPs were measured on the GF7 stereo images using the method described in Section 3.3 and were utilized as vertical control points. All GPS points were used as check points, and block adjustment was performed using the block adjustment model described in Section 3.5. This group of experiments was used to verify whether the GF7 LAPs effectively improved the vertical accuracy of the stereo images.
- The GF7 LAPs were measured on the GF7 stereo images using the method described in Section 3.3.1 and were utilized as horizontal and vertical control points. All GPS points were used as check points and block adjustment was performed using the block adjustment model described in Section 3.5. This group of experiments was used to verify whether the GF7 LAPs effectively improved the horizontal and vertical accuracies of the stereo images simultaneously.
- Fifty-seven GPS points were selected as horizontal and vertical control points, and the remaining GPS points were used as check points to perform block adjustment of the GF7 stereo images. This group of experiments was used to reflect the accuracy level that can be achieved for stereo images when high-precision ground control points are available.
- The pixel coordinates of all ATLAS LAPs in the GF7 stereo images were measured, and the ATLAS LAPs were used as vertical control points. All GPS points were taken as checkpoints and the combined block adjustment model described in Section 3.5 was used to conduct block adjustment of stereo images. This group of experiments was used to verify the accuracy level of integrated processing using LAPs and stereo images obtained from different satellites, which reflects the actual effect of using the traditional integration method. The measurement method of the pixel coordinates of LAPs in this group of experiments is as follows. First, the pixel coordinates of the ATLAS LAPs in the GF7 backward image were calculated through the longitude, latitude, and elevation parameters of the LAPs. Then, through high-precision image matching between the GF7 forward image and backward image, the corresponding pixel coordinates of the ATLAS LAPs in the forward image were obtained.
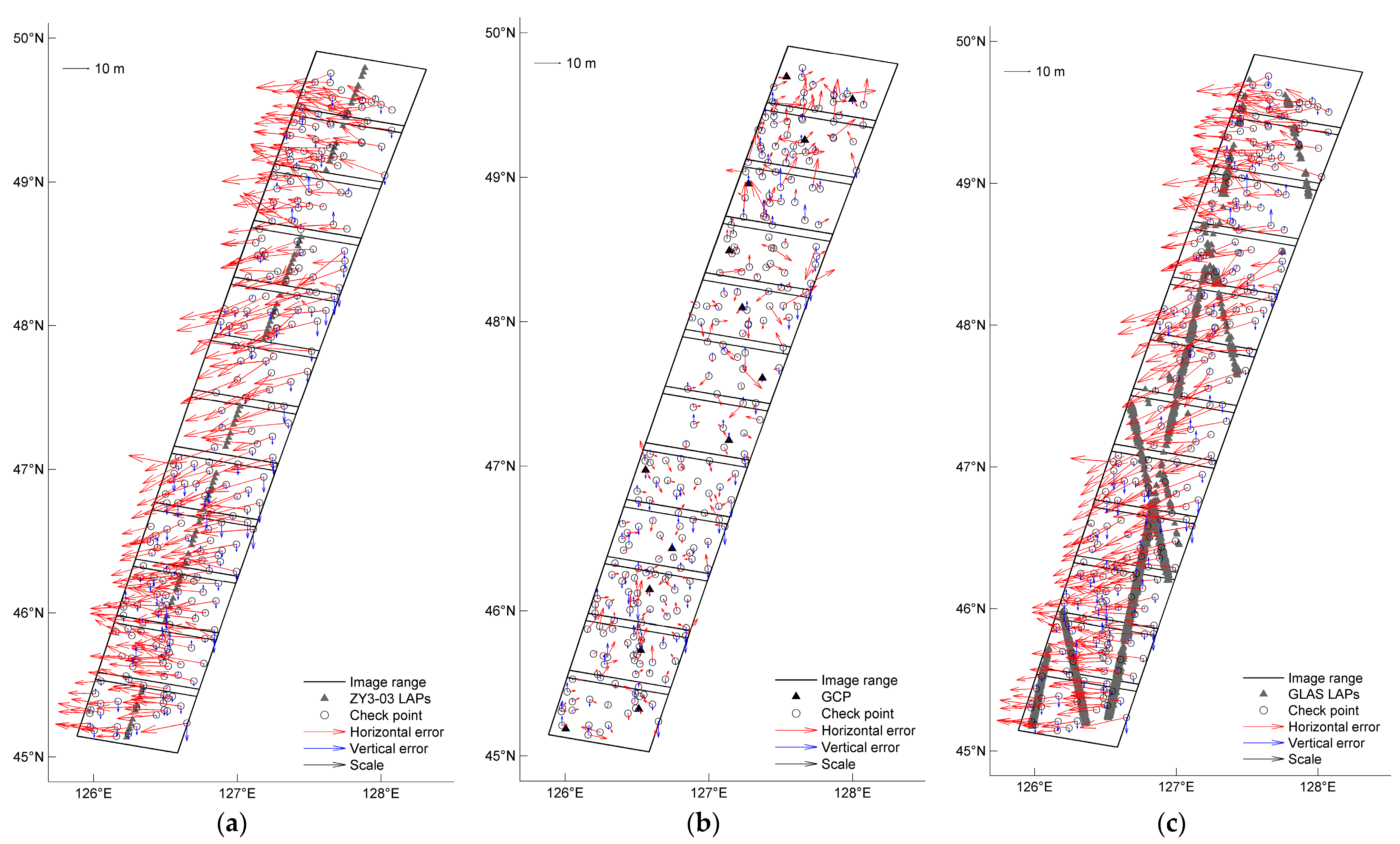
- The ZY3-03 LAPs were measured on the ZY3-03 stereo images using the method described in Section 3.4 and were used as vertical control points. All GPS points were used as check points, and the block adjustment model described in Section 3.5 was applied to perform block adjustment.
- Fourteen GPS points were selected as horizontal and vertical control points, and the remaining GPS points were used as check points to perform block adjustment of the ZY3-03 stereo images.
- The pixel coordinates of all the GLAS LAPs in the ZY3-03 stereo image were measured and used as vertical control points. Taking all GPS points as check points, the block adjustment of stereo images was conducted using the combined block adjustment model described in Section 3.5. The measurement method of the pixel coordinates of LAPs in this group of experiments is as follows. First, the pixel coordinates of the GLAS LAPs in the ZY3-03 Nadir image were calculated through the longitude, latitude, and elevation parameters of the LAPs. Then, through high-precision image matching between the ZY3-03 forward image and the Nadir image, and between the backward image and the Nadir image, the corresponding pixel coordinates of the LAPs in the forward image and the backward image were obtained.
5. Conclusions
- Using the LAPs as vertical control points in the integrated processing method proposed herein, the vertical RMSEs of the GF7 images in flat, hilly, mountainous, and high-mountainous terrain and throughout the region were reduced to 0.35 m, 0.66 m, 0.74 m, 0.91 m, and 0.68 m, respectively, which meet the accuracy requirements for 1:10,000 (even 1:5000) scale stereo mapping in China. The vertical accuracy was even better than the results of block adjustment using an appropriate number of GPS points as control points. Moreover, the vertical RMSEs of the ZY3-03 images in flat and hilly terrain and throughout the region were reduced to 2.78 m, 2.24 m, and 2.58 m, respectively, which meet the accuracy requirements for 1:50,000 scale stereo mapping in China. These results indicate that the integrated processing method proposed herein can improve the vertical accuracy of stereo images in a variety of terrain types.
- In the integrated processing of the GF7 data, LAPs were used as both horizontal and vertical control points. Although the vertical accuracy of experimental images improved, the horizontal accuracy did not change substantially. This indicates that using LAPs cannot ensure improvements in the horizontal accuracy of stereo images.
- The ATLAS LAPs were used to replace the GF7 LAPs, and the combined block adjustment experiment was conducted with GF7 experiment images. The GLAS LAPs were used to replace the ZY3-03 LAPs, and the combined block adjustment experiment was conducted with the ZY3-03 experiment images. The two groups of experiments reflect the effect that can be achieved by using the traditional method to conduct the integrated processing of LAPs and stereo images obtained from different satellites. Although the number and vertical accuracy of ATLAS and GLAS LAPs in the experiments are far better than those of GF7 and ZY3-03 LAPs, the final experiment results are worse than those obtained using our method. This shows that the method of acquiring stereo images and LAPs on the same platform at the same time has great advantages, and the technical method proposed in our study based on these advantages has been proven to be effective and advanced.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spudis, P.D.; Gillis, J.J.; Reisse, R.A. Ancient Multiring Basins on the Moon Revealed by Clementine Laser Altimetry. Science 1994, 266, 1848–1851. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Jackson, G.B.; Cavanaugh, J.F.; Neumann, G.A.; Riris, H.; Sun, X.; Zellar, R.S.; Coltharp, C.; Connelly, J.; et al. The Lunar Orbiter Laser Altimeter Investigation on the Lunar Reconnaissance Orbiter Mission. Space Sci. Rev. 2009, 150, 209–241. [Google Scholar] [CrossRef]
- Cavanaugh, J.F.; Smith, J.C.; Sun, X.; Bartels, A.E.; Ramos-Izquierdo, L.; Krebs, D.J.; McGarry, J.F.; Trunzo, R.; Novo-Gradac, A.M.; Britt, J.L.; et al. The Mercury Laser Altimeter Instrument for the MESSENGER Mission. Space Sci. Rev. 2007, 131, 451–479. [Google Scholar] [CrossRef]
- Li, C.; Ren, X.; Liu, J.; Zou, X.; Mu, L.; Wang, J.; Shu, R.; Zou, Y.; Zhang, H.; Lu, C.; et al. Laser altimetry data of Chang’E-1 and the global lunar DEM model. Sci. China Earth Sci. 2010, 53, 1582–1593. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite—2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Xie, J.; Liu, R.; Huang, G.; Zhao, C.; Zhen, Y.; Tang, H.; Dou, X. Overview of the GF-7 Laser Altimeter System Mission. Earth Space Sci. 2020, 7, e2019EA000777. [Google Scholar] [CrossRef]
- Zhou, P.; Tang, X.; Li, D.; Wang, X. Combined Block Adjustment of Stereo Imagery and Laser Altimetry Points of the ZY3-03 Satellite. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Xie, J.; Tang, X.; Mo, F.; Tang, H.; Wang, Z.; Wang, X.; Liu, Y.; Tian, S.; Liu, R.; Xia, X. In-orbit geometric calibration and experimental verification of the ZY3-02 laser altimeter. Photogramm. Rec. 2018, 33, 341–362. [Google Scholar] [CrossRef]
- Spiegel, M.; Baumgartner, A.; Ebner, H. Orientation of Mars Express/HRSC imagery using laser altimeter data as control information. In Proceedings of the ISPRS Workshop High Resolution Mapping from Space 2003, Hannover, Germany, 6–8 October 2003. [Google Scholar]
- Yoon, J.-S.; Shan, J. Combined Adjustment of MOC Stereo Imagery and MOLA Altimetry Data. Photogramm. Eng. Remote Sens. 2005, 71, 1179–1186. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.-Y.; Muller, J.-P.; Mills, J.P.; Miller, P.E. An assessment of surface matching for the automated co-registration of MOLA, HRSC and HiRISE DTMs. Earth Planet. Sci. Lett. 2010, 294, 520–533. [Google Scholar] [CrossRef]
- Di, K.; Yue, Z.; Peng, M.; Liu, Z. Co-registration of CHANG’E-1 stereo images and laser altimeter data for 3D mapping of lunar surface. In Proceedings of the ASPRS/CaGIS 2010 Specialty Conference, Orlando, FL, USA, 15–19 December 2010. [Google Scholar]
- Di, K.; Hu, W.; Liu, Y.; Peng, M. Co-registration of Chang’E-1 stereo images and laser altimeter data with crossover adjustment and image sensor model refinement. Adv. Space Res. 2012, 50, 1615–1628. [Google Scholar] [CrossRef]
- Ye, J.; Qiang, Y.; Zhang, R.; Liu, X.; Deng, Y.; Zhang, J. High-Precision Digital Surface Model Extraction from Satellite Stereo Images Fused with ICESat-2 Data. Remote Sens. 2021, 14, 142. [Google Scholar] [CrossRef]
- Howat, I.M.; Porter, C.; Smith, B.E.; Noh, M.-J.; Morin, P. The Reference Elevation Model of Antarctica. Cryosphere 2019, 13, 665–674. [Google Scholar] [CrossRef]
- Magruder, L.; Neuenschwander, A.; Klotz, B. Digital terrain model elevation corrections using space-based imagery and ICESat-2 laser altimetry. Remote Sens. Environ. 2021, 264, 112621. [Google Scholar] [CrossRef]
- Dongchen, E.; Shen, Q.; Xu, Y.; Chen, G. High-accuracy topographical information extraction based on fusion of ASTER stereo-data and ICESat/GLAS data in Antarctica. Sci. China Ser. D Earth Sci. 2009, 52, 714–722. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T.; Tsutsui, K. Algorithm development of high resolution global DSM generation by ALOS prism. In Proceedings of the IGARSS 2014–2014 IEEE International Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Li, G.; Tang, X.; Gao, X.; Wang, H.; Wang, Y. ZY-3 Block adjustment supported by GLAS laser altimetry data. Photogramm. Rec. 2016, 31, 88–107. [Google Scholar] [CrossRef]
- Zhou, P.; Tang, X.; Wang, Z.; Cao, N.; Wang, X. Vertical Accuracy Effect Verification for Satellite Imagery with Different GCPs. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1268–1272. [Google Scholar] [CrossRef]
- Cao, N.; Zhou, P.; Wang, X.; Tang, X.M.; Li, G.Y. Refined processing of satellite imaging geometric model assisted by laser altimetry data. J. Remote Sens. 2018, 22, 599–610. [Google Scholar] [CrossRef]
- Li, G.; Tang, X.; Gao, X.; Wang, X.; Fan, W.; Chen, J.; Mo, F. Integration of ZY3-02 satellite laser altimetry data and stereo images for high-precise surveying and mapping. Photogramm. Eng. Remote Sens. 2018, 84, 569–578. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, K.; Jia, P.; Hao, X.; Li, D. Integrating Stereo Images and Laser Altimeter Data of the ZY3-02 Satellite for Improved Earth Topographic Modeling. Remote Sens. 2019, 11, 2453. [Google Scholar] [CrossRef]
- Zhang, G.; Jiang, B.; Wang, T.; Ye, Y.; Li, X. Combined Block Adjustment for Optical Satellite Stereo Imagery Assisted by Spaceborne SAR and Laser Altimetry Data. Remote Sens. 2021, 13, 3062. [Google Scholar] [CrossRef]
- Chen, J.; Tang, X.; Xue, Y.; Li, G.; Zhou, X.; Hu, L.; Zhang, S. Registration and Combined Adjustment for the Laser Altimetry Data and High-Resolution Optical Stereo Images of the GF-7 Satellite. Remote Sens. 2022, 14, 1666. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, G.; Zhu, X.; Pan, H.; Jiang, Y.; Zhou, P.; Wang, X. Triple linear-array image geometry model of ZiYuan-3 surveying satellite and its validation. Int. J. Image Data Fusion 2013, 4, 33–51. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, G.; Tang, X.; Li, D.; Zhu, X.; Zhou, P.; Jiang, Y. Basic Products of the ZiYuan-3 Satellite and Accuracy Evaluation. Photogramm. Eng. Remote Sens. 2013, 79, 1131–1145. [Google Scholar] [CrossRef]
- Xie, J.; Huang, G.; Liu, R.; Zhao, C.; Dai, J.; Jin, T.; Mo, F.; Zhen, Y.; Xi, S.; Tang, H.; et al. Design and Data Processing of China’s First Spaceborne Laser Altimeter System for Earth Observation: GaoFen-7. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1034–1044. [Google Scholar] [CrossRef]
- Li, G.; Tang, X.; Chen, J.; Yao, J.; Liu, Z.; Gao, X.; Zuo, Z.; Zhou, X. Processing and preliminary accuracy validation of the GF-7 satellite laser altimetry data. Acta Geod. Cartogr. Sin. 2021, 50, 1338–1348. [Google Scholar] [CrossRef]
- NASA Goddard Space Flight Center. The GLAS Algorithm Theoretical Basis Document for Laser Footprint Location (Geolocation) and Surface Profiles. 1 July 2014. Available online: https://ntrs.nasa.gov/citations/20140017859 (accessed on 21 November 2022.).
- Li, G.; Guo, J.; Tang, X.; Ye, F.; Zuo, Z.; Liu, Z.; Chen, J.; Xue, Y. Preliminary quality analysis of GF-7 satellite laser altimeter full waveform data. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B1-2, 129–134. [Google Scholar] [CrossRef]
- Zhou, P.; Tang, X. Geometric Accuracy Verification of GF-7 Satellite Stereo Imagery Without GCPs. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6509105. [Google Scholar] [CrossRef]
- Tang, X.; Xie, J.; Mo, F.; Dou, X.; Li, X.; Li, S.; Li, S.; Huang, G.; Fu, X.; Liu, R.; et al. GF-7 dual-beam laser altimeter on-orbit geometric calibration and test verification. Acta Geod. Cartogr. Sin. 2021, 50, 384–395. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, M.; Xiong, J.; Lu, Y.; Xiong, X. On-Orbit Geometric Calibration of ZY-3 Three-Line Array Imagery With Multistrip Data Sets. IEEE Trans. Geosci. Remote Sens. 2013, 52, 224–234. [Google Scholar] [CrossRef]
- Tang, X.; Zhou, P.; Zhang, G.; Wang, X.; Pan, H. Geometric Accuracy Analysis Model of the Ziyuan-3 Satellite without GCPs. Photogramm. Eng. Remote Sens. 2015, 81, 927–934. [Google Scholar] [CrossRef]
- Zhou, P.; Tang, X.; Wang, X.; Liu, C.; Wang, Z. Geometric accuracy evaluation model of domestic push-broom mapping satellite image. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 1628–1634. [Google Scholar] [CrossRef]
- Xie, J.; Ren, C.; Jiao, H.; Pan, J. In-orbit geometric calibration approach and positioning accuracy analysis for the Gaofen-7 laser footprint camera. IET Image Process. 2021, 15, 3130–3141. [Google Scholar] [CrossRef]
- NASA Goddard Space Flight Center. The Algorithm Theoretical Basis Document for the Atmospheric Delay Correction to GLAS Laser Altimeter Ranges. 1 October 2012. Available online: https://ntrs.nasa.gov/search.jsp?R=20130001652 (accessed on 21 November 2022.).
- NASA Goddard Space Flight Center. The algorithm theoretical basis document for tidal corrections. 1 December 2012. Available online: https://ntrs.nasa.gov/search.jsp?R=20130013632 (accessed on 21 November 2022.).
- Li, G.; Tang, X.; Zhou, P.; Chen, J.; Liu, Z.; Dou, X.; Zhou, X.; Wang, X. Laser altimetry data processing and combined surveying application of ZY3-03 satellite. Infrared Laser Eng. 2022, 51, 20210356. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Gruen, A. Adaptive least squares correlation: A powerful image matching technique. S. Afr. J. Photogramm. Remote Sens. Cartogr. 1985, 14, 175–187. [Google Scholar]
- Fraser, C.S.; Hanley, H.B. Bias-compensated RPCs for Sensor Orientation of High-resolution Satellite Imagery. Photogramm. Eng. Remote Sens. 2005, 71, 909–915. [Google Scholar] [CrossRef]
- Fraser, C.; Yamakawa, T. Insights into the affine model for high-resolution satellite sensor orientation. ISPRS J. Photogramm. Remote Sens. 2004, 58, 275–288. [Google Scholar] [CrossRef]
- Li, B.; Xie, H.; Liu, S.; Tong, X.; Tang, H.; Wang, X. A Method of Extracting High-Accuracy Elevation Control Points from ICESat-2 Altimetry Data. Photogramm. Eng. Remote Sens. 2021, 87, 821–830. [Google Scholar] [CrossRef]
- Krieger, G.; Fiedler, H.; Zink, M.; Hajnsek, I.; Younis, M.; Huber, S.; Bachmann, M.; Gonzalez, J.H.; Werner, M.; Moreira, A. The TanDEM-X mission: A satellite formation for high-resolution SAR interferometry. In Proceedings of the Radar Conference, EuRAD 2007, Munich, Germany, 10–12 October 2007. [Google Scholar]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J.-P. Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1529–1558. [Google Scholar] [CrossRef] [Green Version]
- CH/T 9009.1-2013; Digital Products of Fundamental Geographic Information—1:5000 1:10,000 1:25,000 1:50,000 1:100,000—Part 1:Digital Line Graphs. Surveying and Mapping Press: Beijing, China, 2013.


| Data Type | Covering Terrain | Stereo Images | LAPs | Number of GPS Points | |||
|---|---|---|---|---|---|---|---|
| Covering Area (km2) | Number | Image Orbit | Number | Data Orbit | |||
| GF7 Satellite data | Flat | 3500 | 70 | 2449, 3267, 5806, 5880, 5962 | 134 | 3267, 6786, 6868, 7679, 8652 | 40 |
| Hilly | 4200 | 84 | 26 | ||||
| Mountainous | 17,300 | 244 | 124 | ||||
| High mountainous | 2000 | 1 | 11 | ||||
| All regions | 27,000 | 463 | 201 | ||||
| ZY3-03 Satellite data | Flat | 16,000 | 12 | 1552 | 56 | 1552 | 167 |
| Hilly | 14,000 | 25 | 103 | ||||
| All regions | 30,000 | 81 | 270 | ||||
| Data Type | Terrain Type | Number of Check Points | Horizontal Accuracy (m) | Vertical Accuracy (m) | ||
|---|---|---|---|---|---|---|
| RMSE | Max. Error | RMSE | Max. Error | |||
| GF7 satellite data | Flat | 40 | 5.00 | 9.26 | 3.07 | −6.72 |
| Hilly | 26 | 3.81 | 6.40 | 4.68 | −7.14 | |
| Mountainous | 124 | 4.32 | 8.12 | 2.86 | −7.17 | |
| High mountainous | 11 | 6.36 | 8.89 | 2.48 | 6.23 | |
| All regions | 201 | 4.93 | 9.26 | 3.19 | −7.17 | |
| ZY3-03 satellite data | Flat | 167 | 15.20 | 21.61 | 5.38 | 10.29 |
| Hilly | 103 | 15.36 | 25.02 | 5.09 | 7.61 | |
| All regions | 270 | 15.26 | 25.02 | 5.27 | 10.29 | |
| Scale | Horizontal RMSE (m) | Vertical RMSE (m) | ||||
|---|---|---|---|---|---|---|
| Flat and Hilly | Mountainous and High Mountainous | Flat | Hilly | Mountainous | High Mountainous | |
| 1:50,000 | 25 | 37.5 | 3 | 5 | 8 | 14 |
| 1:10,000 | 5 | 7.5 | 0.5 | 1.2 | 2.5 | 5 |
| Experimental Region | Terrain Type | Number of Laser Points | Vertical Accuracy (m) | |
|---|---|---|---|---|
| RMSE | Max. Error | |||
| GF7 experimental region | Flat | 129 | 2.96 | −6.33 |
| Hilly | 75 | 4.76 | −8.06 | |
| Mountainous | 216 | 2.95 | −8.22 | |
| High mountainous | 1 | 2.41 | 2.41 | |
| All regions | 421 | 3.32 | −8.22 | |
| ZY3-03 experimental region | Flat | 56 | 5.90 | −12.08 |
| Hilly | 25 | 5.62 | −8.97 | |
| All regions | 81 | 5.79 | −12.08 | |
| Terrain Type | Number of LAPs | Horizontal Accuracy (m) | |
|---|---|---|---|
| RMSE | Max. Error | ||
| Flat | 30 | 0.40 | 0.46 |
| Hilly | 4 | 0.33 | 0.39 |
| Mountainous | 31 | 0.29 | 0.40 |
| High mountainous | 1 | 0.35 | 0.35 |
| All regions | 66 | 0.35 | 0.46 |
| Terrain | GPS Check Points | GF7 Laser Vertical Control Points | ||||||
|---|---|---|---|---|---|---|---|---|
| Number | Horizontal Accuracy | Vertical Accuracy | Number | Vertical Residual | ||||
| RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | |||
| Flat | 40 | 4.99 | 8.39 | 0.35 | −0.72 | 134 | 0.33 | −0.84 |
| Hilly | 26 | 3.52 | 6.72 | 0.66 | −1.40 | 84 | 0.57 | 1.33 |
| Mountainous | 124 | 4.42 | 7.54 | 0.74 | 2.07 | 244 | 0.69 | 1.61 |
| High mountainous | 11 | 5.99 | 8.08 | 0.91 | 1.80 | 1 | 0.82 | 1.00 |
| All regions | 201 | 4.82 | 8.39 | 0.68 | 2.07 | 463 | 0.60 | 1.61 |
| Terrain | GPS Check Points | GF7 Laser Horizontal and Vertical Control Points | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number | Horizontal Accuracy | Vertical Accuracy | Number | Horizontal Residual | Vertical Residual | |||||
| RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | |||
| Flat | 40 | 4.94 | 8.83 | 0.35 | −0.77 | 129 | 4.55 | 8.45 | 0.34 | −0.87 |
| Hilly | 26 | 3.12 | 6.48 | 0.62 | −1.44 | 75 | 3.01 | 5.99 | 0.56 | 1.28 |
| Mountainous | 124 | 5.28 | 10.85 | 0.73 | 1.92 | 216 | 4.97 | 8.77 | 0.70 | 1.56 |
| High mountainous | 11 | 5.68 | 9.11 | 0.90 | 1.78 | 1 | 6.13 | 6.13 | 0.80 | 0.98 |
| All regions | 201 | 5.00 | 10.85 | 0.67 | 1.92 | 421 | 4.55 | 8.77 | 0.59 | 1.56 |
| Terrain | GPS Check Points | GPS Horizontal and Vertical Control Points | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number | Horizontal Accuracy | Vertical Accuracy | Number | Horizontal Residual | Vertical Residual | |||||
| RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | |||
| Flat | 29 | 1.64 | 3.25 | 0.92 | 1.33 | 11 | 1.63 | 2.89 | 0.77 | 1.54 |
| Hilly | 17 | 2.40 | 3.60 | 0.95 | 1.86 | 9 | 2.31 | 3.33 | 0.84 | −1.75 |
| Mountainous | 91 | 2.34 | 4.16 | 0.88 | 2.21 | 33 | 2.05 | 3.85 | 0.88 | 2.09 |
| High mountainous | 7 | 2.51 | 3.86 | 0.94 | −1.53 | 4 | 1.67 | 2.41 | 0.83 | −1.28 |
| All regions | 144 | 2.23 | 4.16 | 0.90 | 2.21 | 57 | 1.99 | 3.84 | 0.85 | 2.09 |
| Terrain | GPS Check Points | ATLAS Laser Vertical Control Points | ||||||
|---|---|---|---|---|---|---|---|---|
| Number | Horizontal Accuracy | Vertical Accuracy | Number | Vertical Residual | ||||
| RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | |||
| Flat | 40 | 4.99 | 8.43 | 1.33 | 4.29 | 3038 | 1.28 | −6.46 |
| Hilly | 26 | 3.53 | 6.36 | 1.21 | −2.48 | 3248 | 1.24 | 9.53 |
| Mountainous | 124 | 4.29 | 7.65 | 2.01 | 5.59 | 2493 | 1.68 | 5.69 |
| High mountainous | 11 | 6.02 | 8.22 | 1.74 | 2.55 | 45 | 0.99 | 1.94 |
| All regions | 201 | 4.79 | 8.43 | 1.78 | 5.59 | 8824 | 1.39 | 9.53 |
| Terrain | GPS Check Points | ZY3-03 Laser Vertical Control Points | ||||||
|---|---|---|---|---|---|---|---|---|
| Number | Horizontal Accuracy | Vertical Accuracy | Number | Vertical Residual | ||||
| RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | |||
| Flat | 167 | 15.41 | 25.24 | 2.78 | −7.63 | 56 | 1.51 | −3.93 |
| Hilly | 103 | 14.94 | 24.85 | 2.24 | −7.07 | 25 | 1.77 | −3.90 |
| All regions | 270 | 15.35 | 25.69 | 2.58 | −7.63 | 81 | 1.56 | −3.93 |
| Terrain | GPS Check Points | GPS Horizontal and Vertical Control Points | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number | Horizontal Accuracy | Vertical Accuracy | Number | Horizontal Residual | Vertical Residual | |||||
| RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | |||
| Flat | 157 | 4.15 | 10.60 | 2.53 | −7.03 | 10 | 2.95 | 5.35 | 2.61 | 3.81 |
| Hilly | 99 | 6.12 | 18.54 | 2.41 | −7.25 | 4 | 4.24 | 6.84 | 1.98 | 3.88 |
| All regions | 256 | 4.99 | 18.56 | 2.41 | −7.25 | 14 | 3.37 | 6.84 | 2.45 | 3.88 |
| Terrain | GPS Check Points | GLAS Laser Vertical Control Points | ||||||
|---|---|---|---|---|---|---|---|---|
| Number | Horizontal Accuracy | Vertical Accuracy | Number | Vertical Residual | ||||
| RMSE | Max. Error | RMSE | Max. Error | RMSE | Max. Error | |||
| Flat | 167 | 15.53 | 25.32 | 2.43 | 7.05 | 7647 | 2.05 | 14.93 |
| Hilly | 103 | 14.99 | 24.99 | 2.75 | 7.47 | 881 | 2.26 | −8.43 |
| All regions | 270 | 15.32 | 25.33 | 2.55 | 7.47 | 8528 | 2.07 | 14.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Zhou, P.; Guo, L.; Pan, H. Integrating Stereo Images and Laser Altimetry Points Derived from the Same Satellite for High-Accuracy Stereo Mapping. Remote Sens. 2023, 15, 869. https://doi.org/10.3390/rs15040869
Tang X, Zhou P, Guo L, Pan H. Integrating Stereo Images and Laser Altimetry Points Derived from the Same Satellite for High-Accuracy Stereo Mapping. Remote Sensing. 2023; 15(4):869. https://doi.org/10.3390/rs15040869
Chicago/Turabian StyleTang, Xinming, Ping Zhou, Li Guo, and Hongbo Pan. 2023. "Integrating Stereo Images and Laser Altimetry Points Derived from the Same Satellite for High-Accuracy Stereo Mapping" Remote Sensing 15, no. 4: 869. https://doi.org/10.3390/rs15040869
APA StyleTang, X., Zhou, P., Guo, L., & Pan, H. (2023). Integrating Stereo Images and Laser Altimetry Points Derived from the Same Satellite for High-Accuracy Stereo Mapping. Remote Sensing, 15(4), 869. https://doi.org/10.3390/rs15040869







