Backscattering Statistics of Indoor Full-Polarization Scatterometric and Synthetic Aperture Radar Measurements of a Rice Field

Abstract

The backscattering coefficient ${\sigma }^0$ of a rice field is closely related to the amplitude, power, and phase of its radar backscattered signals. An investigation of the statistics of indoor full-polarization scatterometric and synthetic aperture radar (SAR) measurements on rice fields in the Laboratory of Target Microwave Properties (LAMP) is implemented in terms of the amplitude, power, and phase difference of backscattered signals. The validity and accuracy of LAMP measured data are studied and confirmed for the first time. The Rayleigh fading model and phase difference statistical model are both validated by the experimental data. Continuous microwave spectrum is obtained after spatial and frequency averaging over N independent scatterometric samples and full-polarization images are generated by applying a focusing algorithm to the SAR data. Comparisons between scatterometric results and SAR images with three resolutions of rice field scene are conducted with respect to amplitude and co-pol phase difference (CPD) statistics, as well as backscattering coefficients. The results show that the measured statistics of a rice field scene are in good agreement with those calculated by theoretical formulas. Spatial and frequency averaging of scatterometric data can increase N and thus improve the estimation accuracy of the backscattering coefficients. SAR images show a shift to the near range due to the intrinsic height of the rice plants and the probable existence of the double bounce scattering between vertical rice stems and the water surface considering the measurement geometry. The measured amplitude statistics of the SAR images approach a Rayleigh distribution with reduction of the resolution cell size while the size has little effect on the CPD statistics. The differences between backscattering coefficients extracted from the scatterometric data and SAR images confirm a 1-dB calibration accuracy in power of the LAMP measurement system.

1. Introduction

Rice is an important staple crop and provides food for about 50% of the world’s population [1,2,3]. It was reported that approximately 193 million people in 53 countries/territories were faced with serious food crises in 2021 due to persistent conflicts, pre-existing and COVID-19-related economic shocks, and weather extremes [4]. Therefore, rice monitoring and yield estimation are essential for farmers and governments in decision-making and policy formulation. According to the National Bureau of Statistics of China (NBSC), China is the largest producer of rice with an output of 211.86 million tons in 2020 [5]. It is well known that most rice grows in tropical and subtropical regions with frequently cloudy and rainy weather conditions. It is usually difficult to acquire optical remote sensing images with good quality in such regions. Synthetic aperture radar (SAR) plays an important role in rice monitoring and yield estimation because of its inherent all-weather and all-day working capacities [6,7].

In general, there are two primary ways to monitor rice by virtue of radar. One approach is monitoring rice in fields with spaceborne radar sensors or ground-based scatterometers [8,9,10,11,12,13,14], in order to explore the scattering characteristics of rice fields. The other approach is retrieving rice growth parameters or biophysical variables using microwave scattering models [15,16,17,18,19], as well as probing into the interactions between electromagnetic wave and rice plants. In an anechoic chamber experiment, the estimate for the backscattering coefficient ${\sigma }^0$, geometrical and biophysical parameter data of rice plants can be easily obtained, in this sense the indoor measurements are complementary to the rice monitoring in the field.

Previous research on microwave measurements in an anechoic chamber were mainly presented based on the European Microwave Signature Laboratory (EMSL) at Ispra, Italy [20,21]. Depending on the measurement mode, their measurements can be divided into two basic patterns: scatterometric (SCT) and SAR imaging. The type of targets measured at the EMSL includes metallic spheres [22,23], soils of different moisture content [24], various surfaces with different roughness [25,26,27], rice plants [28,29,30], maize samples [28,31], and fir trees [23,32], which validate the application potential of anechoic chamber measurements for crops or vegetation.

The advantages of indoor measurements in an anechoic chamber are manifested in the controllability of measurement modes and parameters, repeatability of experimental operations and procedures, and stability of experimental samples and environment, and the experimental conditions are more operable and easier to be satisfied in an anechoic chamber. For these reasons, an anechoic chamber can provide more detailed and reliable data sets for research on scattering characteristics of rice fields and is a very important data source for traditional rice monitoring and microwave remote sensing [33].

The Laboratory of Target Microwave Properties (LAMP) was built in July 2018 at Deqing county of Zhejiang province in China. The LAMP is a unique and large experimental facility with advanced and highly integrated performance. After a system test and performance assessment, the operational phase has begun at the start of 2019. To date, a mass of scatterometric and SAR imaging data concerning natural targets (such as rice fields, maize plants, grasses, trees, reeds, soils, water, etc.) and manmade objects (such as metallic spheres, calibrators, unmanned aerial vehicles, cars, roads, buildings, etc.) has been acquired by the LAMP, and these results are very valuable and significant for investigating characteristics of different targets and their interactions with radar signals. Furthermore, better understanding and recognition of SAR images measured in the LAMP could optimize SAR imaging algorithms and effectively broaden the application domains of SAR data. However, the validity and measurement accuracy of the LAMP data have not been studied or verified for distributed targets, for example rice fields, which is the original motivation of this paper.

The backscattering coefficient ${\sigma }^0$ of a distributed target is closely related to the amplitude, power, and phase of its radar backscattered signals. The Rayleigh fading model provides an effective method to describe radar backscattering features in terms of amplitude, power, and phase difference for statistically distributed terrains. Terrain targets that satisfying the Rayleigh assumptions include agriculture fields, dense forest canopies, and bare and snow-covered ground surfaces, backscattering statistical data for soil and rock surfaces, trees, grasses, shrubs, short vegetation, road surfaces, urban areas, and dry/wet snow were given in [34,35,36], but there are not enough backscattering statistical data for rice fields. Different from artificial targets, rice fields can be seen as an ensemble of independent and randomly distributed scatterers with comparable scattering strengths. The different locations, orientations, and geometries of each scatterer lead to different scattering features. In each direction, the total scattering field is a vector sum of many scattering field phasors scattered by single scatterer, which includes random phase delays due to different locations of scatterers with respect to the center of the illuminated rice field. Thus, this scattering echo shows fluctuations in the backscattering direction. Generally, a Rayleigh distribution is a better choice to describe the backscattering statistics of rice fields.

The main objective of this paper is to present a comparison of the backscattering statistics between LAMP’s scatterometric and SAR measurement data of rice fields. To be specific, the current study has the following basic objectives and potential advantages:

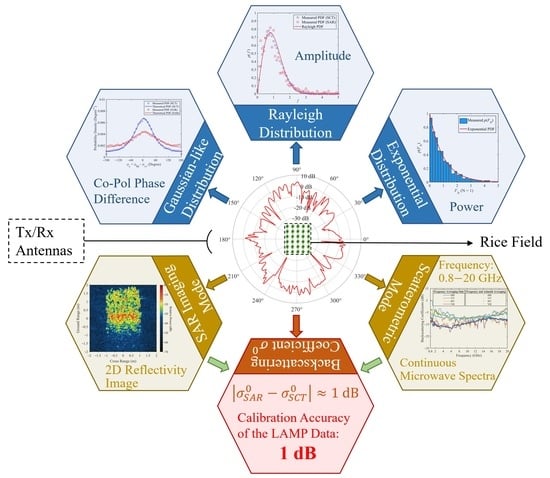
• To provide more data sets with multifrequency, multi-angular, and full-polarization sensor configurations for research on rice field scattering characteristics and mechanisms.
• To illustrate the theoretical basis for processing methods of LAMP’s indoor scatterometric and SAR measurement data, particularly the methods to reduce backscattered signal fluctuations.
• To verify the applicability of the Rayleigh fading model and phase difference statistical model in rice fields.
• To verify the validity and accuracy of the LAMP’s measured data for distributed targets (rice fields) from both theoretical and experimental points of view.
• To elucidate the strengths and weaknesses of the data measured in the LAMP.
• To provide theoretical basis and contrast to potential applications for rice microwave scattering models and radar system designs through analysis of the measured data.

The remainder of this article is organized as follows. Section 2 introduces the overall system configurations and basic setup of rice field scene measurements in the LAMP. Section 3 describes the Rayleigh fading model, phase difference statistical model, and data processing methods. Section 4 presents the results of the measured rice field scene data. Finally, conclusions are included in Section 5.

2. Measurement Setup

2.1. Overall System Configuration

As shown in Figure 1, the LAMP experimental platform is set up inside a 24 m (length) × 24 m (width) × 17 m (height) box-like space where the Full-Factors Microwave Properties Measurement System (FFMPMS) operates in a 20-m-diameter quarter sphere covered with pyramidal absorbers (Figure 2) inside the surface to shield undesired electromagnetic waves. The FFMPMS can measure a continuous microwave spectrum of targets with a frequency range of 0.8–20 GHz, incident angle of 0–90°, azimuth angle of 0–360°, and full-polarization (HH/VV/HV/VH). The positioning accuracy of Sled 1/2 is 0.01° while the linear displacement accuracy along the slide track is 0.1 mm [37].

Measurements taken by the FFMPMS are performed by transmitting frequency-stepped signals with two kinds of quad ridge horn antennas (QR800 and QR6000), which are used for measuring low (0.8–6 GHz) and high (6–18 GHz) frequencies, respectively. The QR800 and QR6000 antennas are installed in the sleds at a small distance, so the FFMPMS can be seen as a quasi-monostatic radar when measuring in the backscattering direction. The dynamic range and sensitivity of the RF system are better than 100 dB and −60 dBsm. The calibration accuracy of the measurement system is better than 1 dB in power and 5° in phase with cross polar discrimination better than 30 dB.

2.2. Rice Field Scene Layout

In contrast to traditional experiments on rice paddies in a field, measurements in an anechoic chamber overcome the influence of external environment factors and guarantee reliable and quality data as well as enhanced controllability and flexibility of experimental implementation.

Rice plant samples were obtained from the surrounding town of Deqing county in the Zhejiang province (30°34′29.0″N, 120°11′35.5″E) and two experiments were carried out in LAMP with the same rice growth stage (milky stage) in September 2019 (Scene 1, as shown in Figure 3a) and September 2021 (Scene 2, as shown in Figure 3b). The parameters of the two rice field scenes are presented in

Table 1. Layout parameters of two rice field scenes.

Rice Field Scene Parameters	Scene 1	Scene 2
Rice Growth Stage	Milky Stage	Milky Stage
Rice Filed Scene Size (length × width, unit: m)	1.8 × 1.6	1.6 × 1.2
Container Size/Number (length × width × height, unit: m)	0.6 × 0.4 × 0.3; 12 Small Containers Assemble Together	1.6 × 1.2 × 0.3; One Single Large Container
Water Depth (cm)	2	Underlying Surface of Moist Soil
Average Height of Rice Plants (cm)	103.7	95.7
Cluster Size (length × width)	9 × 8	8 × 6
Average Number of Rice Plants	15	13.5
Row Space (cm)	26.5	23.7
Column Space (cm)	23.5	22.3

. Before measurements began, rice plants were transplanted into rectangular boxes, which kept the rice samples in the same growing status as in their natural environment. There were some differences between the two rice filed scenes measured in 2019 and 2021, including the scene size, container size/number, underlying surface type, average height of rice plants, cluster size, etc. It should be noted that the average height difference of rice plants may come from different growing conditions or rice varieties. However, it seems that all of the above differences have little effect on the comparison of the backscattering coefficient results for the two rice field scenes, which will be shown in Section 4.4.

As shown in Figure 4 and Figure 5, the tested rice field scenes were placed at the center of a rectangular turntable supported by a cylinder target support. The turntable could rotate about its z axis according to the measurement requirements. The dimension of the turntable is 4 m × 3 m, it is 3.5 m above the chamber floor and 0.5 m below the dome center (focal point), the distance between the Tx/Rx antennas and the dome center is 9.3 m. Based on antenna theory [35], the half-power beamwidth of the Tx/Rx antennas can be obtained and the 3 dB footprint is always larger than the size of the rice field scenes within the frequency ranges for the LAMP measurements.

2.3. Measurement Setup

The FFMPMS has two measurement modes. In the scatterometric mode, the turntable can be rotated in steps about the z axis to acquire independent observations in the azimuthal direction. While in SAR imaging mode, the turntable can be moved linearly from −2.4 m to 2.4 m along the x axis to simulate a strip-map SAR or rotated about the z axis for spotlight SAR or ISAR image formation. Accordingly, the measurement setups of the two modes are shown in Figure 5.

Table 2. Measurement parameters of the two rice field scenes.

Measurement Mode	Parameter	Scene 1	Scene 2
Scatterometric Mode	Tx/Rx Mode	Quasi-Monostatic	Quasi-Monostatic
	Polarization	HH/VV/HV/VH	HH/VV/HV/VH
	Incident Angle Range/Step (°)	10–60/5	10–60/10
	Azimuth Angle Range/Step (°)	0–360/45	0–360/5
	Frequency Range/Step (GHz)	0.8–18/0.025	0.8–20/0.01
SAR Imaging Mode	Tx/Rx Mode	Quasi-Monostatic	Quasi-Monostatic
	Polarization	HH/VV/HV/VH	HH/VV/HV/VH
	Incident Angle Range/Step (°)	10–60/10	10–60/10
	Azimuth Angle Range/Step (°)	0–360/45	0–360/45
	Frequency Range/Step (GHz)	0.8–1.7/0.025, 9–16/0.025	0.8–20/0.04
	Band	L, X, Ku	L, S, C, X, Ku
	Linear Displacement Range (m)	−2.4–2.4	−2.28–2.28

presents detailed measurement parameter settings of the two rice field scenes in both scatterometric and SAR imaging modes. For the SAR imaging mode, the desired spatial resolution in ground and cross range can be obtained by applying different frequency bandwidths and linear displacement extents (synthetic aperture length) of the raw data in the SAR image formation process [38].

3. Methodology

In LAMP, the scattered field vector of the rice field scene, $E^s$, illuminated by two antennas with orthogonal polarizations $v$ and $h,$ can be related to the incident field vector $E^i$ by the scattering matrix $S$, which is expressed as

$$E^s=\frac{e^{jkr}}{r}S{E}^i=\frac{e^{jkr}}{r}\left[\begin{array}{cc}{S}_{vv}& S_{vh}\\ S_{hv}& S_{hh}\end{array}\right]E^i,$$

(1)

where $r$ denotes the distance from the radar to the center of the rice field scene, $k$ is the wavenumber, and $S_{pq}\left(p,q=v \mathrm{or} h\right)$ is the element of the scattering matrix. Considering the reciprocity in the backscattering case, $S_{vh}=S_{hv}$, the total scattered field for the rice field scene measurement is the vector superposition of the fields scattered by all the scatterers inside the scene, thus the scattering matrix can be represented as

$$S_{pq}=\left|S_{pq}\right|e^{j{\varphi }_{pq}}={\displaystyle \sum }_{n=1}^N\left|S_{pq}^n\right|e^{j{\varphi }_{pq}^n}=X_{pq}+Y_{pq}j.$$

(2)

In Equation (2), $\left|S_{pq}^n\right|$ and ${\varphi }_{pq}^n$ are the scattering amplitude and phase of the n-th scatterer, $X_{pq}$ and $Y_{pq}$ are the real and imaginary parts, respectively, that are zero-mean, Gaussian random variables with the same standard deviation, and $N$ is the number of scatterers. It is demonstrated that $\left|S_{pq}\right|$ and ${\varphi }_{pq}$ are Rayleigh and uniform independent random variables, respectively [35,39].

3.1. Rayleigh Fading Model

The measured backscattering coefficient, ${\sigma }^0$, of the rice field scene in 2021 as functions of frequency (at a fixed azimuth angle 0°) and azimuth angle (at a fixed frequency 5.3 GHz) are shown in Figure 6. The incident angles in Figure 6a,b are both 40° relative to the normal incidence. In Figure 6a, apparent changes in measured backscattering coefficient are observed with the maximum difference reaching 25.6 dB at VV polarization. Analogously, significant variations of the backscattering coefficient, by an order of magnitude of 10 dB, can be observed when the azimuthal angle varies slightly (5°) in Figure 6b, with the largest difference reaching 30.5 dB at HV polarization.

With the given measurement setups, the measured backscattering coefficient of the rice field scene exhibits large fluctuations. These fluctuations are caused by random phase delays of scatterers at different locations. Fluctuations or fading variations show a speckled appearance at the pixel-to-pixel scale for SAR images of distributed targets such as rice fields. The terms fluctuation, fading, and scintillation have all been used interchangeably to describe the random-like intensity variations in backscattered signals. The Rayleigh fading model is used to characterize the fluctuation statistics of the backscattered signals of the rice field scene in this paper, of which the underlying assumptions are presented in [34,35,36]. The distributions satisfied by amplitude $E_s$ and phase $\varphi$ of the backscattered field are the Rayleigh and uniform distributions, respectively, which are expressed as

$$p\left(E_s\right)=\frac{E_s}{s^2}\exp \left(-\frac{E_s^2}{2s^2}\right),E_s\ge 0,$$

(3)

$$p\left(\varphi \right)=\frac{1}{2\pi },-\pi \le \varphi \le \pi ,$$

(4)

where $p\left(E_s\right)$ and $p\left(\varphi \right)$ are the probability density functions (PDFs) of $E_s$ and $\varphi$, and $s$ is the scale parameter of the distribution. It should be pointed out that $E_s$ denotes the total backscattered field intensity before detection by the receiver. For most receivers, linear and square-law detection are the two frequently used means to convert input signal into an output voltage.

3.1.1. Linear Detection

If the linear detector is used by the receiver, output voltage $V$ is directly proportional to the input electric field $E_s$. We define the normalized fading random variable $f$ as the ratio of the output voltage to its ensemble average, $\overline{V}$, which is expressed as

$$f=V/\overline{V}=E_s/\overline{E_s},$$

(5)

where $f$ denotes the variations of different observations (for the scatterometric mode) or image pixels (for the SAR imaging mode) and $\overline{E_s}$ is the mean value of $E_s$. For linear detection, the normalized fading random variable $f$ also follows the Rayleigh distribution considering the linear relation between $V$ and $E_s$, it can be represented as

$$p\left(f\right)=\frac{\pi f}{2}\exp \left(-\frac{\pi f^2}{4}\right), f\ge 0.$$

(6)

The mean value $\overline{f}$ and standard deviation (STD) $s_f$ in Equation (6) are $\overline{f}=1$ and $s_f=s_V/\overline{V}={\left(4/\pi -1\right)}^{1/2},$ and the corresponding cumulative distribution density (CDF) is

$$p\left(f\le f^{\prime }\right)=1-\exp \left(-\pi {f^{\prime }}^2/4\right), f^{\prime }\ge 0.$$

(7)

3.1.2. Square-Law Detection

Output voltage $V$ of the receiver with a square-law detector is directly proportional to power $P$ of the input signal. Similarly, the normalized fading random variable, $F$, can be defined as $F=V/\overline{V}=P/\overline{P}=E_s^2/\overline{E_s^2}$ and the distribution of $F$ is characterized by the exponential distribution expressed as

$$p\left(F\right)=e^{-F}.$$

(8)

The mean value, $\overline{F}$, and standard deviation, $s_F$, are both equal to one, and the CDF it follows is indicated as

$$p\left(F\le F^{\prime }\right)=1-e^{-F^{\prime }}.$$

(9)

For measurements of the rice field scenes, the backscattering coefficient, ${\sigma }^0$, is directly proportional to $\overline{E_s^2}$, which means that the output voltage of the receiver is also in proportion to ${\left({\sigma }^0\right)}^n$, with $n=1/2$ for linear detection and $n=1$ for square-law detection.

3.2. Phase Difference Statistical Model

As mentioned earlier, ${\varphi }_{pq}$ is uniformly distributed between $-\pi$ and $\pi$ and thus contains no information about the geometrical and dielectric properties of the distributed targets. In fact, the cross-pol phase difference (XPD), ${\varphi }_x={\varphi }_{hv}-{\varphi }_{vv}$, is also uniformly distributed between $-\pi$ and $\pi$, while the distribution satisfied by the co-pol phase difference (CPD), ${\varphi }_c={\varphi }_{hh}-{\varphi }_{vv}$, is approximately Gaussian in shape [40] and can be characterized by

$$p\left({\varphi }_c\right)=\frac{1-{\beta }^2}{2\pi \left[1-{\beta }^2{\cos }^2\left({\varphi }_c-{\varphi }_0\right)\right]}\left\{1+\frac{\beta \cos \left({\varphi }_c-{\varphi }_0\right)}{\sqrt{1-{\beta }^2{\cos }^2\left({\varphi }_c-{\varphi }_0\right)}}\left[\frac{\pi }{2}+{\tan }^{-1}\frac{\beta \cos \left({\varphi }_c-{\varphi }_0\right)}{\sqrt{1-{\beta }^2{\cos }^2\left({\varphi }_c-{\varphi }_0\right)}}\right]\right\}.$$

(10)

In Equation (10), ${\varphi }_0$ and $\beta$ are referred to as the polarized phase difference and degree of correlation corresponding to the mean and variance of the Gaussian distribution, respectively. $\beta$ and ${\varphi }_0$ can be derived from the ensemble-averaged Muller matrix $\langle M\rangle$ and are represented as

$$\beta =\frac{1}{2}\sqrt{\frac{{\left(M_{33}+M_{44}\right)}^2+{\left(M_{34}-M_{43}\right)}^2}{M_{11}{M}_{22}}}, 0<\beta <1,$$

(11)

$${\varphi }_0={\tan }^{-1}\frac{M_{34}-M_{43}}{M_{33}+M_{44}},-\pi <{\varphi }_0<\pi .$$

(12)

where $\langle M\rangle$ is given as

$$\langle M\rangle =\left[\begin{array}{cc}\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}{M}_{33}& M_{34}\\ M_{43}& M_{44}\end{array}\end{array}\right].$$

(13)

The elements of $\langle M\rangle$ in Equation (13) are as follows:

$$\left\{\begin{array}{l}\begin{array}{l}{M}_{11}=\langle {\left|S_{vv}\right|}^2\rangle \hfill \\ M_{22}=\langle {\left|S_{hh}\right|}^2\rangle \hfill \\ M_{12}=M_{21}=\langle {\left|S_{hv}\right|}^2\rangle =\langle {\left|S_{vh}\right|}^2\rangle \hfill \end{array}\hfill \\ \begin{array}{l}{M}_{33}=\langle \mathrm{Re}\left(S_{vv}{S}_{hh}^{*}+S_{vh}{S}_{hv}^{*}\right)\rangle \hfill \\ M_{34}=-M_{43}=\langle -\mathrm{Im}\left(S_{vv}{S}_{hh}^{*}-S_{vh}{S}_{hv}^{*}\right)\rangle \hfill \\ M_{44}=\langle \mathrm{Re}\left(S_{vv}{S}_{hh}^{*}-S_{vh}{S}_{hv}^{*}\right)\rangle \hfill \end{array}\hfill \end{array}.\right.$$

(14)

The theoretical mean value and standard deviation of the CPD can be obtained by integrating with respect to PDF $p\left({\varphi }_c\right)$ over $\left[-\pi ,\pi \right]$, which are expressed as

$$\overline{{\varphi }_c}={{\displaystyle \int }}_{-\pi }^{\pi }{\varphi }_{c}p\left({\varphi }_c\right)d{\varphi }_c,$$

(15)

$$s_{{\varphi }_c}={\left[{{\displaystyle \int }}_{-\pi }^{\pi }{\left[{\varphi }_c-\overline{{\varphi }_c}\right]}^{2}p\left({\varphi }_c\right)d{\varphi }_c\right]}^{1/2}.$$

(16)

3.3. Signal Fluctuation Reduction by Spatial Averaging

Considering the large fluctuations of ${\sigma }^0$ of the measured rice field scene in Figure 6, the estimate accuracy of the measured value of ${\sigma }^0$ can be improved by increasing the number of spatially independent observations or samples, N, and averaging among them. This amounts to trading spatial resolution for improved radiometric resolution. One way to increase N in an anechoic chamber is to rotate the rice field scene in the azimuthal direction. Studies have shown that a step of 5° is sufficient to obtain independent samples [26,38], and thus reduce the uncertainty of measured backscattering results.

3.3.1. Linear Detection

For N randomly selected or independent samples, the average value of output voltage $V_i$ characterized by the Rayleigh distribution is expressed as $V_N=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{V}_i$. Thus, the fading random variable, $f_N$, for the average output voltage of N independent samples is defined as

$$f_N=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{f}_i,$$

(17)

whose PDF can be obtained by N-successive convolutions of Equation (6), mean value $\overline{f_N}=1$, and standard deviation is inversely proportional to $\sqrt{N}$ and $s_{f_N}={\left[\left(4/\pi -1\right)/N\right]}^{1/2}$. Furthermore, CDF $p\left(f_N\le f_N^{\prime }\right)$ can be calculated by integrating the corresponding PDF in the interval $\left[0, f_N^{\prime }\right]$.

3.3.2. Square-Law Detection

For square-law detection, we define the fading random variable, $F_N$, corresponding to the average output of $N$ independent samples as $F_N=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{F}_i$. The PDF is represented as

$$p\left(F_N\right)=\frac{F_N^{N-1}{N}^N{e}^{-N{F}_N}}{\left(N-1\right)!}, F_N\ge 0,$$

(18)

which is a chi-square distribution with 2N degrees of freedom, and the mean value and standard deviation are $\overline{F_N}=1$ and $s_{F_N}=1/\sqrt{N}$. Likewise, CDF $p\left(F_N\le F_N^{\prime }\right)$ can be also obtained by integrating Equation (9) in the interval $\left[0, F_N^{\prime }\right]$.

3.4. Signal Scintillation Reduction by Frequency Averaging

In order to further reduce the impact of signal scintillation on the measurement of ${\sigma }^0$, another way to increase the number of independent samples is averaging over a certain frequency range in backscattered power. For any scatterer in the rice field scene illuminated by radar antennas at two different frequencies, $f_1$ and $f_2$, the decorrelation between the two backscattered signals is due to the difference in instantaneous phase. For square-law detection, the autocorrelation function is defined by

$$R\left(f_1,f_2\right)=\overline{P\left(f_1\right)P\left(f_2\right)}.$$

(19)

For randomly distributed targets, the process is stationary and $R\left(f_1,f_2\right)=R\left(\Delta f\right)$, thus the autocovariance function is given by

$$R_f\left(\Delta f\right)=R\left(\Delta f\right)-\overline{P^2}=\overline{P^2}{\left[\frac{\sin \left(\alpha \Delta f\right)}{\alpha \Delta f}\right]}^2,$$

(20)

where $\overline{P}$ is the mean value of the input power, $\Delta f=f_2-f_1$, $\alpha =2\pi D/c=2\pi r_g\sin \theta /c$, $r_g$ denotes the width of the rice field scene in ground range, $D$ is the projection length of $r_g$ in the slant range, and $c$ is the speed of light. Therefore, the correlation coefficient between the two backscattered signals is defined as the normalized autocovariance function

$$\rho \left(\Delta f\right)=\frac{R_f\left(\Delta f\right)}{R_f\left(0\right)}={\left[\frac{\sin \left(\alpha \Delta f\right)}{\alpha \Delta f}\right]}^2.$$

(21)

We assume that the two signals are statistically uncorrelated when $\rho \left(\Delta f\right)$ is smaller than a specific value, such as 0.5. If $\Delta f$ is located at the first zero of $\rho \left(\Delta f\right)$, the two signals are totally uncorrelated. In this case, it is referred to as the critical frequency change or decorrelation bandwidth, $\Delta f_c$, which is given by

$$\Delta f_c=\frac{\pi }{\alpha }=\frac{c}{2D}\cong \frac{150}{D}.$$

(22)

As mentioned previously, the rice field scenes can be regarded as randomly distributed terrain targets. Among N observations of the rice field scene at different frequencies in the LAMP, they are mutually uncorrelated or independent if the difference between any pair of frequencies is not below the decorrelation bandwidth. In other words, the mean value of the N measurements is statistically equivalent to that of N spatially independent observations. From this point of view, frequency averaging has the same effect on reducing signal scintillation as spatial averaging.

For a frequency bandwidth, B, ranging from $f_1$ to $f_2$, the mean power is

$$\overline{P}=P\left(B\right)={{\displaystyle \int }}_{f_1}^{f_2}P\left(f\right)df,$$

(23)

and the standard deviation is the square root of Equation (24) and represented as

$$s_P^2=\frac{2}{B}{{\displaystyle \int }}_0^B\left(1-\frac{v}{B}\right)R_f\left(v\right)dv=\frac{2\overline{P^2}}{B}{{\displaystyle \int }}_0^B\left(1-\frac{v}{B}\right){\left[\frac{\sin \left(\alpha v\right)}{\alpha v}\right]}^{2}dv,$$

(24)

where $v$ denotes the frequency separation. Sequentially, the effective number of independent samples, N, associated with frequency averaging is defined by

$$N={\left(\frac{\overline{P}}{s_P}\right)}^2=\frac{B}{2}{\left[{{\displaystyle \int }}_0^B\left(1-\frac{v}{B}\right){\left[\frac{\sin \left(\alpha v\right)}{\alpha v}\right]}^{2}dv\right]}^{-1}.$$

(25)

3.5. Scatterometric and SAR Imaging Data Processing

For simplicity, scatterometric and SAR imaging measurements in the LAMP were confined to the backscattering case. Before further investigating the measured data, some preprocessing steps were followed. First, a simple empty room subtraction in the frequency domain was applied to the raw measured data. Then, range gating in the time domain was followed to isolate the desired response of the rice field scene under test from spurious reflections from the chamber. In the end, a full polarimetric calibration algorithm was used to acquire the absolute amplitude and phase of the response of the rice field scene [41].

In addition, azimuthal averaging and frequency averaging are required for improved radiometric accuracy for scatterometric data. Taking the scatterometric data measured in 2021 as an example, the maximum extent of the rice field scene is equal to 2 m, thus the decorrelation bandwidth at an incidence angle of 40° is about 117 MHz calculated by Equation (22). As a result, an average in backscattered power with a frequency band of 500 MHz and over 72 azimuth angles was performed for the calibrated data.

As far as the SAR imaging data is concerned, a focusing operation is necessary before the SAR imaging procedure. For the distributed rice plants, the scene size is large with respect to the range between the scene center and antennas, in contrast to the calibrators, so near-field phase distortion has to be considered in SAR imaging of electrically large targets [42,43]. In the case of the SAR imaging geometry in Figure 5, a reconstructed two-dimensional (2-D) reflectivity image on the horizontal plane at height $h$ is given by

$$I\left(x,y\right)=\frac{4}{c^2}{{\displaystyle \int }}_{x_1}^{x_2}{{\displaystyle \int }}_{f_1}^{f_2}{E}_s\left(f,x_a\right)\Psi \left(f,x_a,x,y\right)dfd{x}_a,$$

(26)

where $f$ is the frequency, ranging from $f_1$ to $f_2$, $x_a$ is the location of the rice field scene in the x axis direction, which ranges from $x_1$ to $x_2$, $E_s\left(f,x_a\right)$ denotes the measured backscattered field, and $\Psi \left(f,x_a,x,y\right)$ represents the near-field focusing operator and is expressed as

$$\Psi \left(f,x_a,x,y\right)=\frac{y_a}{x_a^2+y_a^2}\frac{1}{\sqrt{G\left(f,x_a,x,y\right)}}{\left(\frac{R}{R_0}\right)}^{2}f{e}^{j2k\left(R-R_0\right)}.$$

(27)

In Equation (27), $G\left(f,x_a,x,y\right)$ is the Tx/Rx antenna pattern and we assume that it is a constant in the measurement. Therefore, the term $1/\sqrt{G\left(f,x_a,x,y\right)}$ can be neglected. $k$ is the wavenumber, $y_a$ is the ground range coordinate of the antennas, $R_0=9.3 \mathrm{m}$ is the distance between the dome center and antennas, and $R$ denotes the slant range between the pixel at coordinates $\left(x,y\right)$ and the antennas and is expressed by

$$R=\sqrt{{\left(x-x_a\right)}^2+{\left(y-y_a\right)}^2+{\left(h-R_0\cos \theta \right)}^2}.$$

(28)

In Equation (28), $\theta$ is the incident angle, and $h=0$.

4. Results and Discussion

This section first shows the LAMP backscattering statistical results for the rice field scene corresponding to linear and square-law detection types. For the measured data, the measured and theoretical statistics are compared in terms of the amplitude, power, and co-pol and cross-pol phase differences of the backscattered field, as well as the real and imaginary parts of the scattering matrix. Then, contrasts before and after spatial and frequency averaging are carried out in order to acquire more accurate estimates of the backscattering coefficient, ${\sigma }^0$, and the effects of backscattered signal fluctuation reduction are verified. In addition, we also present the angular dependences or variations of both ${\sigma }^0$ and the CPD. Finally, the results obtained from the scatterometric measurements and SAR images are compared.

4.1. Statistical Results of Indoor Rice Field Scene Measurement Data

4.1.1. Real and Imaginary Part Statistics

As introduced in Section 3, Figure 7 shows that the real and imaginary parts of the scattering matrix follow a zero-mean Gaussian distribution and the standard deviations are approximately the same within the measuring error ranges.

4.1.2. Amplitude and Power Statistics

The theoretical PDFs of $f_N$ and $F_N$ corresponding to linear detection (for the amplitude of the backscattered field) and square-law detection (for the power of the backscattered field) for different N values are shown in Figure 8a,b with red lines. The PDFs become more peaked and narrower with N increasing from 1 to 10, and the mean values $\overline{f_N}$ and $\overline{F_N}$ are approaching 1 (0 dB). The regions between the blue lines denotes the 90% confidence intervals of the fading random variables $f_N$ and $F_N$ while N is increased from 1 to 100. The dashed lines are the 5% levels and the solid lines represent the 95% levels of the corresponding CDFs. In particular, the magenta line segments denote the lengths of the 90% confidence intervals when $N$ is equal to 1, 2, 4, and 10, respectively. It should be noted that $f_N$ and $F_N$ in Figure 8 are expressed in dB while they are indicated as the normalized dimensionless quantity in Figure 9 and Figure 10.

In Figure 9 and Figure 10, comparisons between measured and theoretical PDFs, $p\left(f_N\right)$ and $p\left(F_N\right)$, are presented. As expected in Section 3.1, the distributions of $f_N$ and $F_N$ are characterized by Rayleigh and exponential PDFs separately when $N=1$. As N increases, the statistical distributions of the measured rice field scene with full-polarization are all in good agreement with the theoretical results.

Considering the 90% confidence intervals when $N=1$, the ranges between the 5% level and 95% level are approximately 17.7 dB for both $p\left(f_N\right)$ and $p\left(F_N\right)$. This corresponds to the fading ranges of the backscattered signal. The fading ranges are so large that if we take only one measurement of the rice field scene, the result will fall into the 17.7 dB range randomly with a 90% chance and the measured ${\sigma }^0$ will be less likely to approach the optimal estimation. Moreover, we can find in

Table 3. Statistical results of the backscatter from rice field scene 2 when N = 1, 2, 4, and 10, for linear and square-law detection.

Detection Method	$\mathit{N}$	$\overline{{\mathit{f}}_{\mathit{N}}}$ or $\overline{{\mathit{F}}_{\mathit{N}}}$		${\mathit{s}}_{{\mathit{f}}_{\mathit{N}}}$ or ${\mathit{s}}_{{\mathit{F}}_{\mathit{N}}}$					90% Confidence Interval	90% Interval Ratio (Percent)
		Theo.	Meas.	Theo.	Meas.				Theo.	Meas.
					HH	VV	HV	VH		HH	VV	HV	VH
Linear Detection	1	1.0	1.0	0.523	0.520	0.539	0.471	0.515	[−11.90, 5.80]	90.03	88.70	93.02	90.37
	2			0.370	0.394	0.338	0.336	0.381	[−7.08, 4.41]	89.03	92.52	91.77	88.78
	4			0.261	0.276	0.275	0.236	0.290	[−4.52, 3.29]	90.44	87.32	92.52	85.86
	10			0.165	0.190	0.184	0.177	0.192	[−2.65, 2.19]	87.28	88.03	87.03	86.03
Square-law Detection	1	1.0	1.0	1.000	0.980	0.958	1.001	1.036	[−12.92, 4.75]	86.89	90.26	89.51	89.51
	2			0.707	0.716	0.687	0.670	0.758	[−7.52, 3.74]	88.24	89.69	89.05	90.18
	4			0.500	0.503	0.522	0.467	0.569	[−4.68, 2.87]	92.13	89.50	93.44	85.30
	10			0.316	0.298	0.333	0.313	0.311	[−2.66, 1.95]	90.34	87.54	91.28	90.65

that the 90% confidence interval becomes smaller with the increasing N, which explains that increasing independent samples exactly reduces the signal fluctuations and improves the estimate accuracy of ${\sigma }^0$.

From another point of view, the standard deviations of $f_N$ and $F_N$ are both inversely proportional to $\sqrt{N}$ and are indicated as narrower PDFs with mean values approaching 1 in Figure 8. For $N$ values of 1, 2, 4, and 10, the calculated mean values, standard deviations, and 90% interval ratios of the measured rice field scene are in Table 3, where the 90% interval ratio is the ratio of the measured $f_N$ or $F_N$ falling into the theoretical 90% confidence interval. The results show that the measured mean values, standard deviations, and 90% interval ratios all coincide well with the theoretical results, which proves again from the other side that the key to promoting measurement accuracy of ${\sigma }^0$ is to increase N as far as possible.

4.1.3. Phase Statistics

The statistical results of the measured SAR and scatterometric data of rice field Scene 2 in terms of CPD and XPD are presented in Figure 11 at the Ku band (center frequency: 15 GHz) and at a 10° incidence angle. The measured PDFs of the CPD are found to be consistent with Equation (10) and the measured PDFs of the XPD are shown to follow a uniform distribution between $-\pi$ and $\pi$. For the CPD and XPD of the two types of data, the measured standard deviations are very close to the theoretical values, which are in accordance with the calibration accuracy of 5° in phase of the LAMP measurement system. The same results can be seen in Figure 12 for different incidence angles.

Furthermore, Figure 12 shows the variations of the mean and standard deviation of the CPD as functions of the frequency band and incidence angle. Overall, the mean and standard deviation both increase slightly with the increase of incidence the angle, from 10° to 60°, for all five frequency bands. The mean values of the CPD are all located at about 0°, except for the L band with a mean value of about −10°. For the standard deviation, the values gradually decrease in the order of L, S, C, X, and Ku bands. Specifically, the standard deviations at the L band are much higher than those in other frequency bands, which is probably due to the lower calibration accuracy of the LAMP measurement system at the L band.

4.2. Experimental Results of the Rice Field Scene by Spatial and Frequency Averaging

As can be seen in Figure 6a, the backscattering coefficients of the rice field scene change continuously with frequency variation, which implies high correlation between adjacent frequency points. The theoretical correlation coefficient between two backscattered signals is plotted in Figure 13 with the first null corresponding to the frequency decorrelation of 117 MHz at a 40° incident angle. For the 72 independent samples measured in azimuth angles ranging from 0° to 360° with a step 5°, the average correlation coefficient can be calculated by

$$\overline{\rho }\left(\Delta f\right)=\frac{1}{72}{\displaystyle \sum }_{i=1}^{72}{\rho }_i\left(\Delta f\right),$$

(29)

where ${\rho }_i\left(\Delta f\right)$ corresponds to the correlation coefficient of the i-th azimuth angle. It can also be easily observed in Figure 13 that the calculated full-polarized $\overline{\rho }\left(\Delta f\right)$ of the measured backscatter from rice field Scene 2 decrease a little faster than the theoretical curve with increasing of the frequency separation, $\Delta f$, but they are generally in good agreement with the theoretical result.

A comparison of the measured backscattering coefficient result between the single azimuth ($\phi$ = 0°) and 72 azimuthal average is shown in Figure 14a. The backscattered signal fluctuations are reduced after implementing azimuthal averaging at the C band. The comparison of the measured backscattering coefficient result between the single frequency (5 GHz) and frequency average over 2 GHz (4–6 GHz) bandwidth in Figure 14b also verifies the effect of reducing signal fluctuations by frequency averaging.

In Section 3.3, we easily derived the normalized standard deviations (NSTDs) of $f_N$ and $F_N$ as the ratio of the standard deviation to the mean for linear and square-law detection, which are $s_{f_N}/\overline{f_N}={\left[\left(4/\pi -1\right)/N\right]}^{1/2}$ and $s_{F_N}/\overline{F_N}=1/\sqrt{N}$, respectively, and are presented in Figure 15a. The measured results are also given by averaging the backscattered signals among N different azimuth angles. According to Equation (25), we can define the NSTD associated with frequency averaging as

$$\frac{s_P\left(B\right)}{\overline{P}}={\left[\frac{2}{B}{{\displaystyle \int }}_0^B\left(1-\frac{v}{B}\right)\rho \left(v\right)dv\right]}^{\frac{1}{2}}=\frac{1}{\sqrt{N}}.$$

(30)

In Equation (30), the NSTD $s_P/\overline{P}$ is inversely proportional to $\sqrt{N}$. Figure 15b shows the theoretical and measured NSTDs of $P$ as a function of the frequency averaging bandwidth at the same time. As shown previously in Figure 13, the effective number of independent samples, N, is almost directly proportional to the bandwidth, B, and the slope is approximately 1 when the ratio $B/\Delta f_c\ge 2$.

Overall, the NSTDs calculated from the experimental data are all in good agreement with the theoretical results, whether for spatial or frequency averaging. This also suggests that fluctuations or fading of backscattered signals from distributed targets can be effectively reduced by spatial and frequency averaging, which is equivalent to increasing the number of independent samples, N. Considering the issue from another perspective, we can see in Figure 8 that the 90% confidence intervals become narrower as the N value increases, which indicates improvement of the estimate accuracy of the measured backscattering coefficient results for the rice field scene.

4.3. Experimental Results of LAMP Scatterometric and SAR Measurements

As explained in Section 3.5, the preprocessing procedures including the empty room subtraction, time gating, and full polarimetric calibration, are the same for both measured scatterometric and SAR LAMP data of rice field scenes. For the scatterometric data, an average in backscattered power with a frequency bandwidth of 500 MHz and over 72 azimuth angles was performed for data calibration in order to reduce fluctuations of the backscattered signals. In Figure 16, the measured backscattering coefficient results extracted from the scatterometric data of rice field Scene 2 are provided, the lines denote the results obtained by frequency averaging only and the dotted lines represent the results after both frequency and azimuthal averaging processes. The experimental results show that better backscattering coefficient estimates can be obtained by both frequency and azimuth averaging than only frequency averaging. The backscattering coefficients first decrease at low frequencies (L, S, and C bands) and then increase at higher frequencies (X and Ku bands) with continuous frequency change. It has been demonstrated that attenuation loss of a rice canopy for incident waves increases with decreasing wavelength in low frequencies [31]. Additionally, the rice ear layer is becoming an important contributor to the total volume scattering from the rice canopy at higher frequencies [15]. Both of these findings lead to the aforementioned changes of ${\sigma }^0$.

For the SAR data, Figure 17 shows the full-polarization 2-D reflectivity images of the rice field scene at the Ku band (center frequency: 12.5 GHz) and an incidence angle of 40° reconstructed at the horizontal plane, $h=0$. We can observe that the rice field scene in Figure 17 presents an obvious shift toward the top of the images (near range). The width in the ground range is about 2.5 m and larger than the actual scene width (1.6 m: −0.8 m–0.8 m), which is caused by the heights of the rice plants and shows the elevation distortions in the SAR images [35]. For the top of the rice plants, the propagation distance of the incident wave is shorter than the distance for the bottom, so it appears closer than does the bottom in the SAR images. The brighter spots correspond to the bottom surface (water substrate), which induces double bounce scattering between the vertical rice stems and the water surface, which can also be demonstrated by the CPD of the SAR images at an incidence angle 40° in Section 4.5, where ${\varphi }_c$ is approaching $\pm \pi$. Below the brighter spots, the backscattering power of the rice canopy is gradually decreasing because of the enhanced attenuation effect of the rice plants in the farther slant range. One example to quantitatively determine the scattering mechanisms inside the rice canopy is presented in [29], but it still requires further analysis of the SAR data in this paper. For the width in cross range, it remains the same as the actual scene extent (1.8 m: −0.9 m–0.9 m). Furthermore, a comparison of scatterometric and SAR data is presented in Section 4.5.

4.4. Angular Variations of the Mean Backscattering Coefficient

Table 4. Statistical results of the measured backscattering coefficient of rice field scene 1 at the C band.

Incident Angle (°)	Polarization
	HH				VV				HV				VH
	Mean (dB)	STD (dB)	5% Level (dB)	95% Level (dB)	Mean (dB)	STD (dB)	5% Level (dB)	95% Level (dB)	Mean (dB)	STD (dB)	5% Level (dB)	95% Level (dB)	Mean (dB)	STD (dB)	5% Level (dB)	95% Level (dB)
10	−6.6	0.9	−7.6	−4.4	−8.5	0.6	−9.3	−7.1	−16.6	1.1	−18.2	−14.4	−16.5	1.2	−17.9	−14.3
15	−6.5	0.9	−7.9	−5.0	−9.5	1.3	−11.5	−7.3	−16.6	1.1	−18.1	−14.9	−16.6	1.3	−18.3	−14.7
20	−8.6	1.2	−11.4	−7.4	−10.2	1.3	−12.2	−8.2	−16.2	1.6	−18.9	−14.2	−16.5	1.6	−18.6	−13.8
25	−9.1	1.0	−10.6	−7.6	−10.9	1.7	−12.9	−8.3	−16.6	1.7	−18.6	−14.1	−16.5	1.8	−18.9	−13.7
30	−9.3	1.7	−11.7	−6.7	−9.9	2.4	−12.6	−6.2	−15.9	2.2	−18.2	−11.8	−14.5	3.9	−18.7	−8.1
35	−10.3	1.8	−12.8	−7.3	−10.6	2.7	−13.5	−6.7	−16.1	2.6	−18.7	−11.3	−15.2	4.6	−20.4	−7.9
40	−11.1	1.2	−12.7	−8.8	−11.7	1.6	−14.1	−9.3	−18.0	1.6	−19.9	−15.5	−18.0	1.9	−20.0	−14.4
45	−11.2	1.0	−12.7	−9.8	−12.1	1.3	−14.0	−9.9	−18.5	1.7	−20.5	−15.0	−18.4	1.7	−20.4	−15.3
50	−11.9	1.5	−13.6	−9.6	−12.4	1.5	−14.4	−9.8	−18.8	2.0	−21.1	−15.3	−19.0	2.4	−21.5	−14.8
55	−11.4	1.8	−13.3	−7.9	−12.2	0.6	−13.3	−11.2	−18.9	1.6	−21.0	−16.4	−18.9	1.5	−20.8	−16.4
60	−8.1	2.9	−11.6	−3.1	−9.7	1.9	−12.2	−6.4	−19.4	1.7	−21.9	−16.8	−19.2	2.0	−21.9	−15.8

shows the statistical mean values, standard deviations, 5% levels, and 95% levels of the measured backscattering coefficients calculated from the scatterometric data of rice field Scene 1 at the C band. The incidence angle ranges from 10° to 60° with a step of 5°, the 5% and 95% levels denote the limits of the 90% confidence intervals of ${\sigma }^0$, and ${\sigma }^0$ is obtained by spatial averaging over 8 azimuth angles and frequency averaging over a 500 MHz bandwidth. The unit of ${\sigma }^0$ is expressed in dB.

In a given polarization, the mean of the backscattering coefficient as a function of incidence angle $\theta$ can be generated by least squares nonlinear fitting. We assume the fitting function as

$$\overline{{\sigma }^0}=g\left(\theta \right)=G_1+G_2\exp \left(-G_3\theta \right)+G_4\cos \left(G_5\theta +G_6\right),$$

(31)

where $G$ denotes the undetermined coefficients. In most incidence angles, satisfactory convergence of the iteration is assumed when the residual errors are lower than 1 dB.

With the same measurement environment and setups, we assume the mean of ${\sigma }^0$ follows a Gaussian distribution and the standard deviations vary with incidence angle. Analogously, the standard deviation as a function of the incidence angle can also be obtained by least squares nonlinear fitting and defined as

$$s\left(\theta \right)=s_1+s_2\exp \left(-s_3\theta \right),$$

(32)

from which the 5% and 95% levels can be calculated as

$$\left\{\begin{array}{l}{\sigma }_{5\%}^0=g\left(\theta \right)-1.645s\left(\theta \right)\hfill \\ {\sigma }_{95\%}^0=g\left(\theta \right)+1.645s\left(\theta \right)\hfill \end{array}\right. .$$

(33)

Figure 18 is the fitting results of the mean backscattering coefficient as a function of the incidence angle at the C band. In the figure, the fitting mean, 5% and 95% levels, and 90% confidence intervals of the backscattering coefficient ${\sigma }^0$ are compared with the measured results. The values are all in good agreement with the results calculated from the measured data, except for the 90% confidence intervals at incidence angles of 30°, 35°, and 60°, which may come from measurement errors. This can be further confirmed by the slightly larger standard deviations for the three angles in Table 4. In addition, the measured mean values, $\overline{{\sigma }^0}$, of rice field Scene 2 are given as well to prove the fitting process. It should be pointed out that the fitting results are vulnerable to the selection of initial values. In other words, the fitting results may not be the global optimum solutions. The fitting method and process can also be applied to other frequency bands in the same way.

4.5. Comparison between Scatterometric and SAR Data

In this section, we compare scatterometric and SAR data of rice field Scene 2 at the Ku band (center frequency: 15 GHz) measured in 2021 in terms of statistical distributions of the amplitude and CPD, as well as the extracted backscattering coefficients. For the SAR data, the comparison is implemented with LAMP constructed 2-D reflectivity images, which have the format of a single look complex. The statistics of multi-look polarimetric images were conducted in [44]. Due to the extent of the rice field scene being relatively large with respect to the distance between the antennas and the focal point, the local incidence angles vary within certain ranges for different locations of the scene with respect to the nominal incidence angle [26,38]. However, the measured rice field scene is the same for scatterometric and SAR measurements, so it is reasonable to assume that the effect of the local incidence angle is negligible for comparison.

4.5.1. Amplitude Statistics

For the scatterometric data, the amplitude statistics with full-polarization for linear detection are presented in Figure 9(a1–a4). For the SAR data, better agreement of amplitude statistics with the Rayleigh PDF require that the size of the resolution cells is large enough to contain more scatterers. Figure 19 presents comparisons between measured and Rayleigh PDFs of SAR images with different resolutions at HH polarization and 30° incidence angle. SAR images with different spatial resolutions were generated by applying different frequency bandwidths and linear displacement extents of the raw data to the imaging process. As can be expected, the measured normalized fading variable, $f$, for the amplitude becomes more Rayleigh distributed with the increase of resolution size from 0.03 m to 0.07 m. In Figure 20, we make a comparison of PDFs in terms of normalized fading variable between measured scatterometric and SAR data (Resolut. = 0.07 m), the Rayleigh PDF is also given as a reference. Consequently, good agreement is observed between the two kinds of data, and similar results apply equally to comparisons for other bands and incidence angles.

4.5.2. Co-Pol Phase Difference Statistics

The comparison of the CPD statistics between scatterometric and SAR data (Resolut. = 0.03 m) was implemented at the same incidence angle of 30°, as illustrated in Figure 21. We can see that the measured PDFs correspond with the theoretical PDFs. Thus, in Figure 22 we only present the theoretical PDFs of other incidence angles, which are calculated by the Muller matrix. At a specific incidence angle, the theoretical PDFs of the CPD for images with three different resolutions are compared with that of the scatterometric data. This comparison shows that the size of the resolution cells has little effect on the CPD statistics. For the comparison among different incidence angles in Figure 22, the degree of correlation, which corresponds to the variance of the Gaussian distribution, first decreases and subsequently increases with the increase of incidence angle for both scatterometric and SAR data. This means that the standard deviation of the CPD changes in the same manner, which previously was given in Figure 12b, and it also shows the same trend in other bands. [45] has demonstrated that the CPD of double bounce scattering is $\pm \pi$ and it will lead to broadening of the CPD PDFs and an increase of corresponding standard deviations. This implies the existence of double bounce scattering in the rice field scene when considering the measurement geometry. Specifically, the maximum value of the standard deviation occurs at an incidence angle of 40° for the SAR data, while the maximum standard deviation for the scatterometric data appears at a 50° incidence angle, which may indicate the location of the maximum of double bounce scattering in the rice field scene measurement.

4.5.3. Backscattering Coefficients

As one of the distributed targets, the area of rice field Scene 2 is A = 1.2 m × 1.6 m, the backscattering coefficients of the scatterometric data can be calculated by

$${\sigma }_{pq}^0=\frac{\langle {\sigma }_{pq}\rangle }{A} , \left(p,q=v \mathrm{or} h\right),$$

(34)

where $\langle {\sigma }_{pq}\rangle$ is the ensemble average of the radar cross section obtained from multiple independent measurements, and spatial and frequency averaging are both applied to reduce the signal fluctuations and improve estimate accuracy of the backscattering coefficients. For the SAR images, which can be seen as an indirect way to acquire the backscattering coefficients of the measured scene, we can express the process as

$${\sigma }_{pq}^0=\frac{4\pi }{AN}{\displaystyle \sum }_{i=1}^N{\left|S_{pq}^i\right|}^2=\frac{4\pi }{A}\langle {\left|S_{pq}\right|}^2\rangle , \left(p,q=v \mathrm{or} h\right).$$

(35)

In Equation (35), N is the number of resolution cells, A is the area of the resolution cells, and $S_{pq}^i$ represents the corresponding i-th scattering amplitude.

Table 5. Comparison of backscattering coefficients between scatterometric measurements and SAR images with azimuth angles ranging from 0° to 360° at the Ku band and an incidence angle of 40°.

Incidence Angle (°)	Azimuth Angle (°)	SCT (dB)				SAR (dB)
		HH	VV	HV	VH	HH	VV	HV	VH
40	0	−6.7	−7.5	−12.0	−11.5	−5.7	−7.2	−10.8	−10.9
	45	−11.0	−11.0	−12.1	−12.4	−7.5	−8.5	−10.1	−10.0
	90	−10.5	−10.7	−12.5	−12.2	−5.9	−8.0	−9.0	−9.2
	135	−10.8	−10.4	−12.5	−12.9	−7.0	−8.1	−9.2	−9.2
	−180	−2.2	−1.5	−10.7	−11.3	−4.1	−6.1	−10.0	−10.3
	−135	−8.1	−7.0	−10.1	−9.0	−7.8	−9.7	−10.4	−10.6
	−90	−6.4	−6.3	−10.2	−10.4	−6.6	−9.4	−11.1	−11.2
	−45	−7.8	−8.2	−10.2	−9.5	−7.5	−9.1	−11.4	−11.3
Average		−7.9	−7.8	−11.3	−11.1	−6.5	−8.3	−10.3	−10.3

presents the comparisons of backscattering coefficients of eight azimuth angles between scatterometric measurements and SAR images at 40° incidence angle. It is obvious that large discrepancies exist between scatterometric and SAR results at azimuth angles of 45°, 90°, and 135° with the maximum difference approaching 4.6 dB at −180° for VV polarization. However, the maximum average difference is only 1.4 dB at HH polarization, which suggests that the results at a specific azimuth angle are not representative for the contrast. In general, the value of the measured ${\sigma }^0$ falls into a relatively large range (90% confidence interval) due to the nature of signal fading, so it makes little sense to compare ${\sigma }^0$ obtained from a single measurement. As illustrated in Table 3, the increase of N will contribute to the contraction of the 90% confidence intervals and the promotion of the estimate accuracy of ${\sigma }^0$. Therefore, the operation of spatial and frequency averaging before comparison between scatterometric measurements and SAR images is of great significance, both in theory and practice.

Table 6. Comparison of backscattering coefficients between scatterometric measurements and SAR images at the Ku band with incidence angles ranging from 10° to 60°.

Incidence Angle (°)	SCT (dB)				SAR (dB)
	HH	VV	HV	VH	HH	VV	HV	VH
10	−6.8	−6.7	−10.2	−10.2	−6.1	−5.7	−10.1	−9.8
20	−8.1	−9.2	−11.0	−10.9	−8.8	−9.1	−9.6	−9.6
30	−7.8	−9.0	−11.0	−11.0	−9.3	−10.3	−10.3	−10.4
40	−7.9	−7.8	−11.3	−11.1	−6.5	−8.3	−10.3	−10.3
50	−10.0	−10.1	−11.8	−11.6	−8.2	−10.2	−12.0	−12.1
60	−8.3	−8.5	−12.4	−12.2	−7.5	−9.6	−12.3	−12.3

displays comparisons of backscattering coefficients obtained from scatterometric and SAR measurements at incidence angles ranging from 10° to 60°, almost all differences of ${\sigma }^0$ for the same polarization are within 1 dB, which are in good agreement with the calibration accuracy of 1 dB in power of the LAMP measurement system.

5. Conclusions

This paper presented backscattering statistics of indoor full-polarization scatterometric and SAR measurements of rice fields in terms of amplitude, power, and phase difference of the backscattered signals, and verified the validity and accuracy of the LAMP measured data for the first time. As a representative distributed target, the measured statistics are all in good agreement with those calculated using the theoretical formulas, which validated the applicability of the Rayleigh fading model and phase difference statistical model. For the scatterometric data, we illustrated the results of spatial and frequency averaging among N independent samples in theory and in practice. Continuous microwave spectra of ${\sigma }^0$ with improved estimate accuracy, as well as angular variations of the mean backscattering coefficients with increasing of incidence angle, were obtained using the least squares of nonlinear fitting. For the SAR data, full-polarization images were generated with the help of a focusing algorithm. Considering the measurement geometry and the intrinsic height of rice plants, the generated SAR images have distinct characteristics that show a shift to the near range and the probable existence of double bounce scattering between vertical rice stems and the water surface. Quantitative examination of the SAR images still requires further analysis in the future. A comparison between the measured scatterometric and SAR data of the rice field scene were implemented in terms of the statistical distributions of the amplitude and CPD, as well as the backscattering coefficients. The results showed good agreement between the two types of data.