Monitoring Displacements and Damage Detection through Satellite MT-InSAR Techniques: A New Methodology and Application to a Case Study in Rome (Italy)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sources
2.2. Methodology
2.2.1. Background Information
- a brief history of Palazzo Primoli and its major constructive phases;
- geometric survey and drawings;
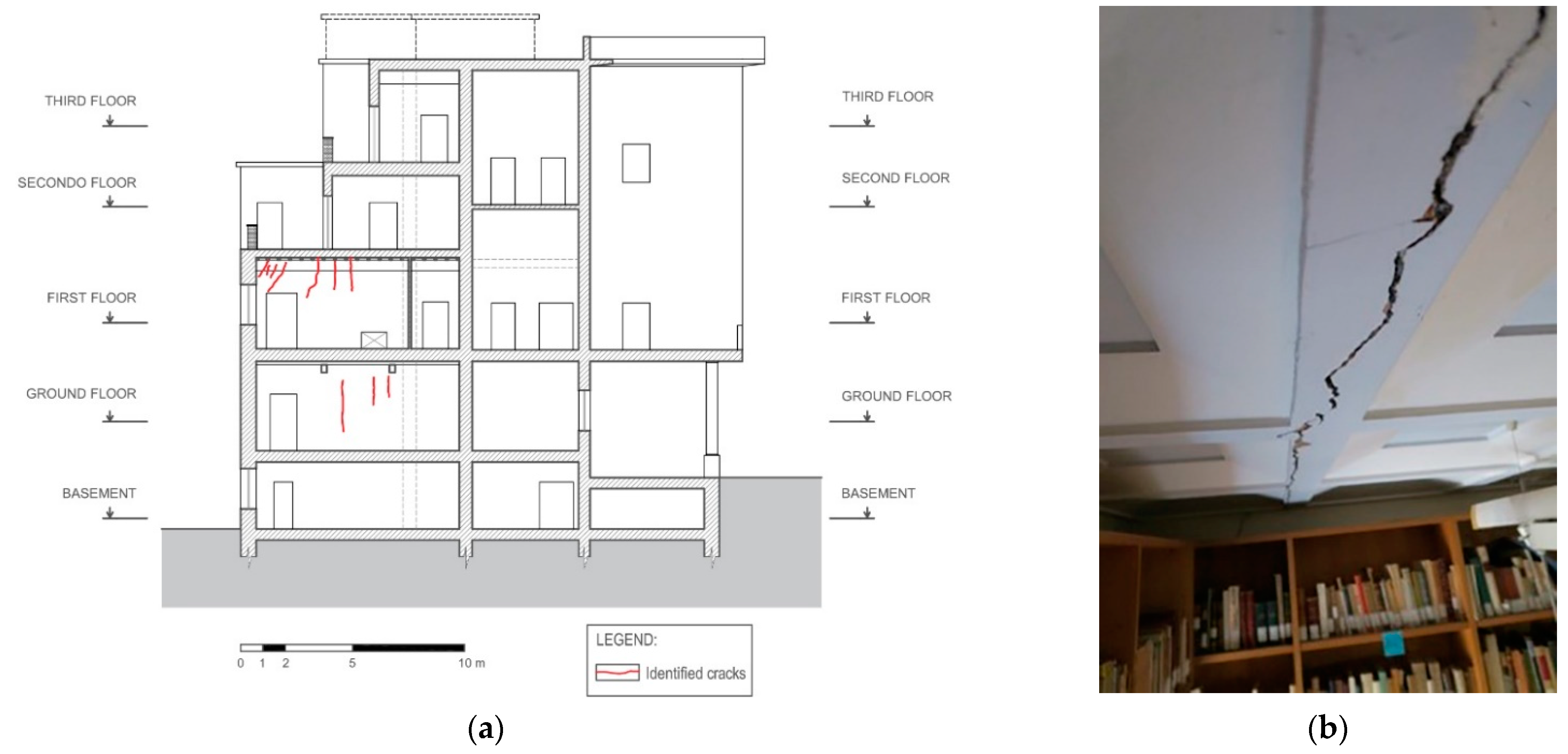
- critical evaluation of the building, including damage and crack patterns.
2.2.2. Pre-Processing
2.2.3. Back Analysis
- qualitative analysis of displacement time series: observation of time series and their relationship aims to identify a similar deformation evolution.
- quantitative comparison of displacement time series through two correlation coefficients, such as:
- proximity analysis of MPs: evaluation of planimetric and elevation location of each MP. Every MP inside a cluster must be within:
- a 2 m radius neighborhood from the center in planimetry of the cluster.
- a 2 m radius neighborhood from the center in elevation of the cluster.
- The goodness of fit (GOF) [75], evaluated by means of the absolute error index of the Normalized Root Mean Squared Error (NRMSE):
- 2.
- Loss function λ0 [76]:
- 3.
- Final prediction error (FPE) [77]:
2.3. The Case Study Application: Palazzo Primoli, Rome
3. Results
3.1. Background Information
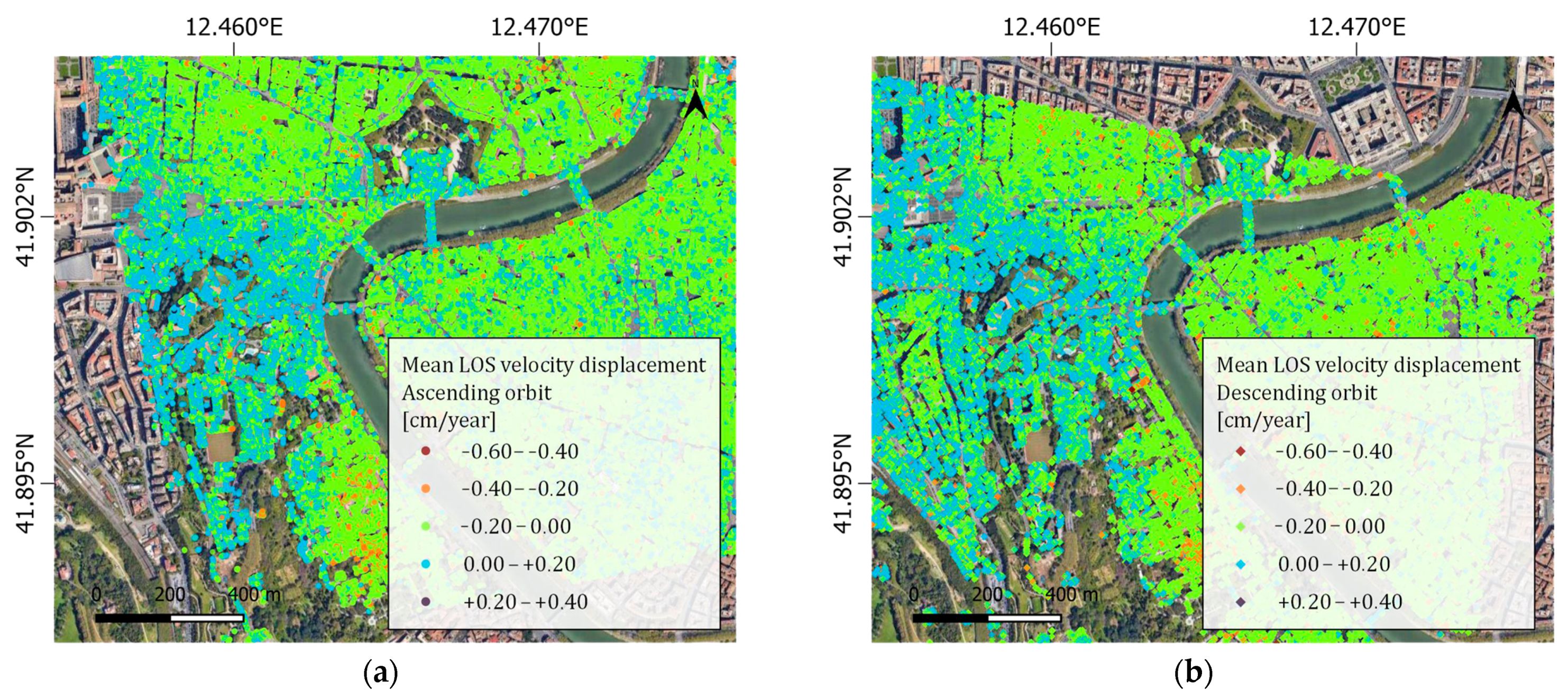
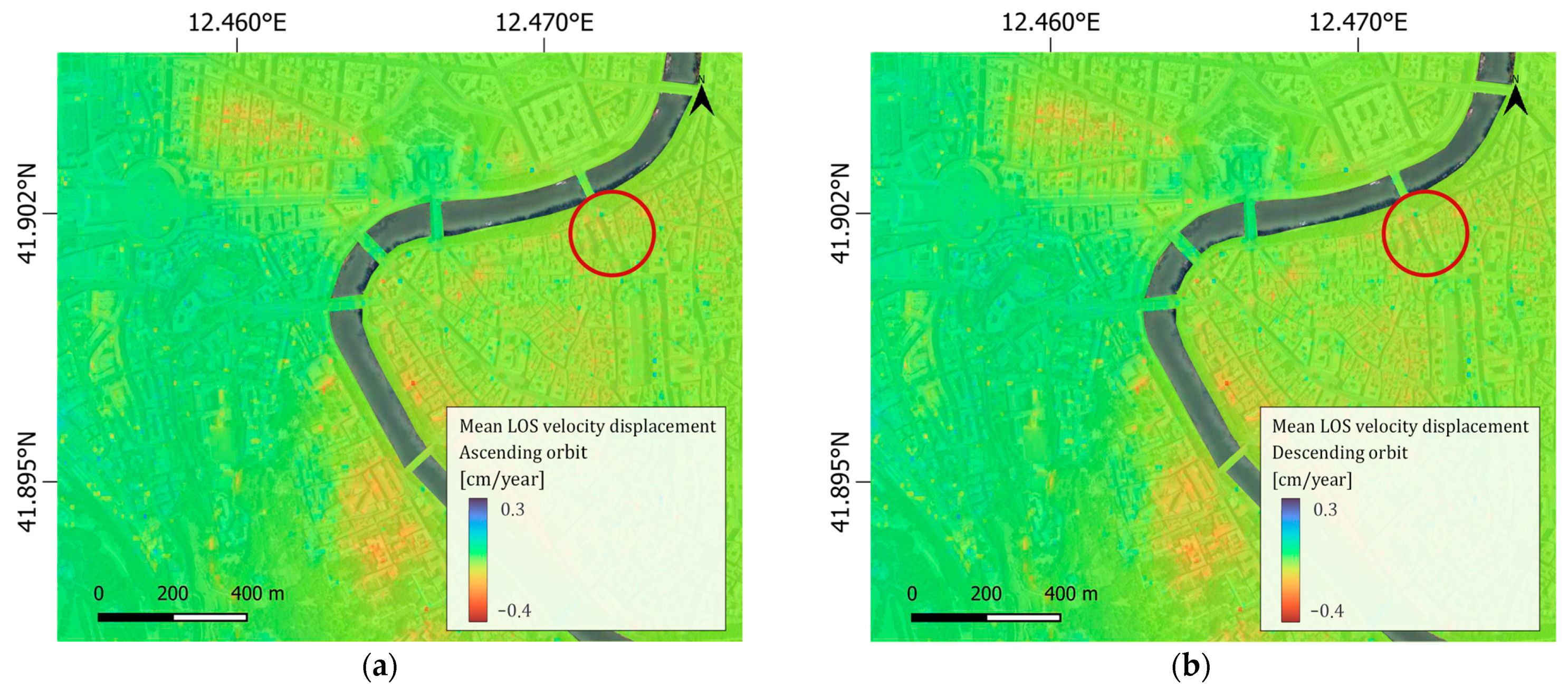
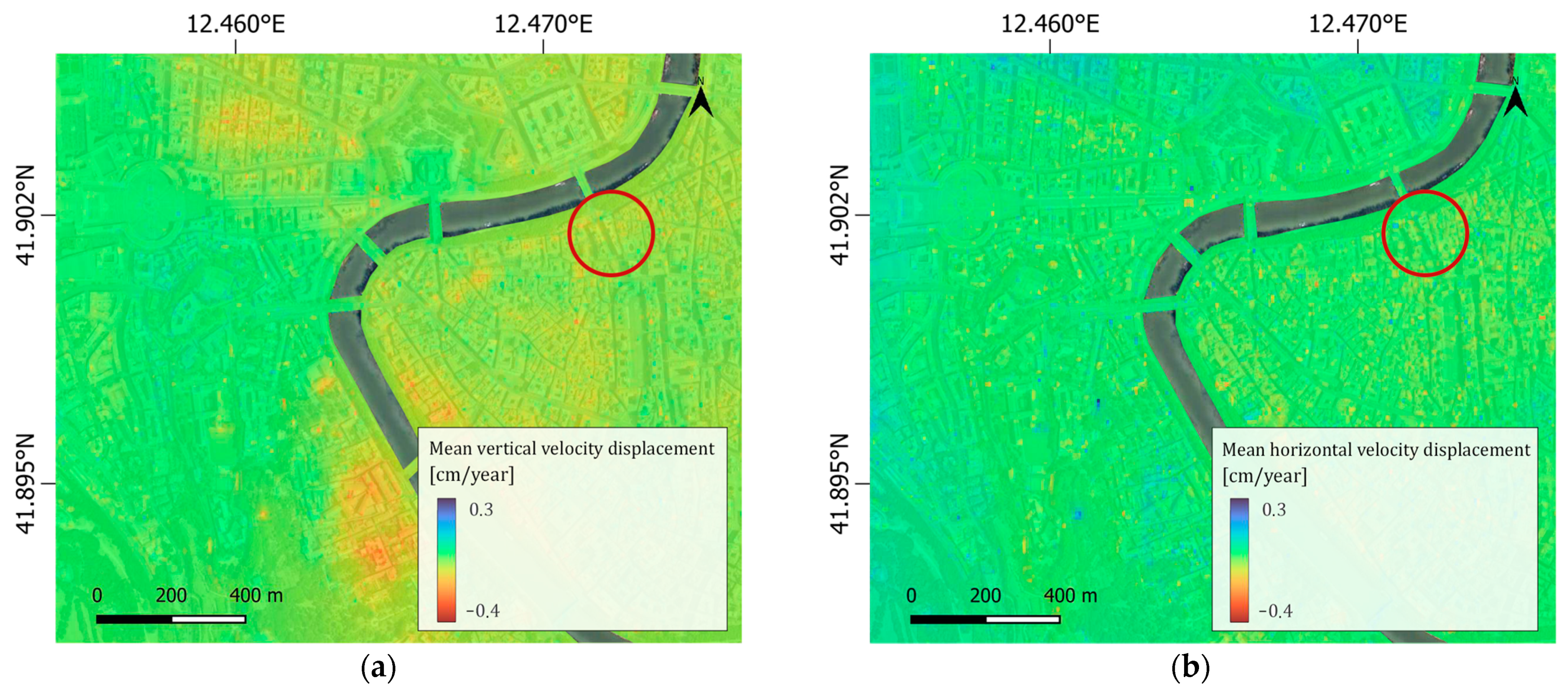
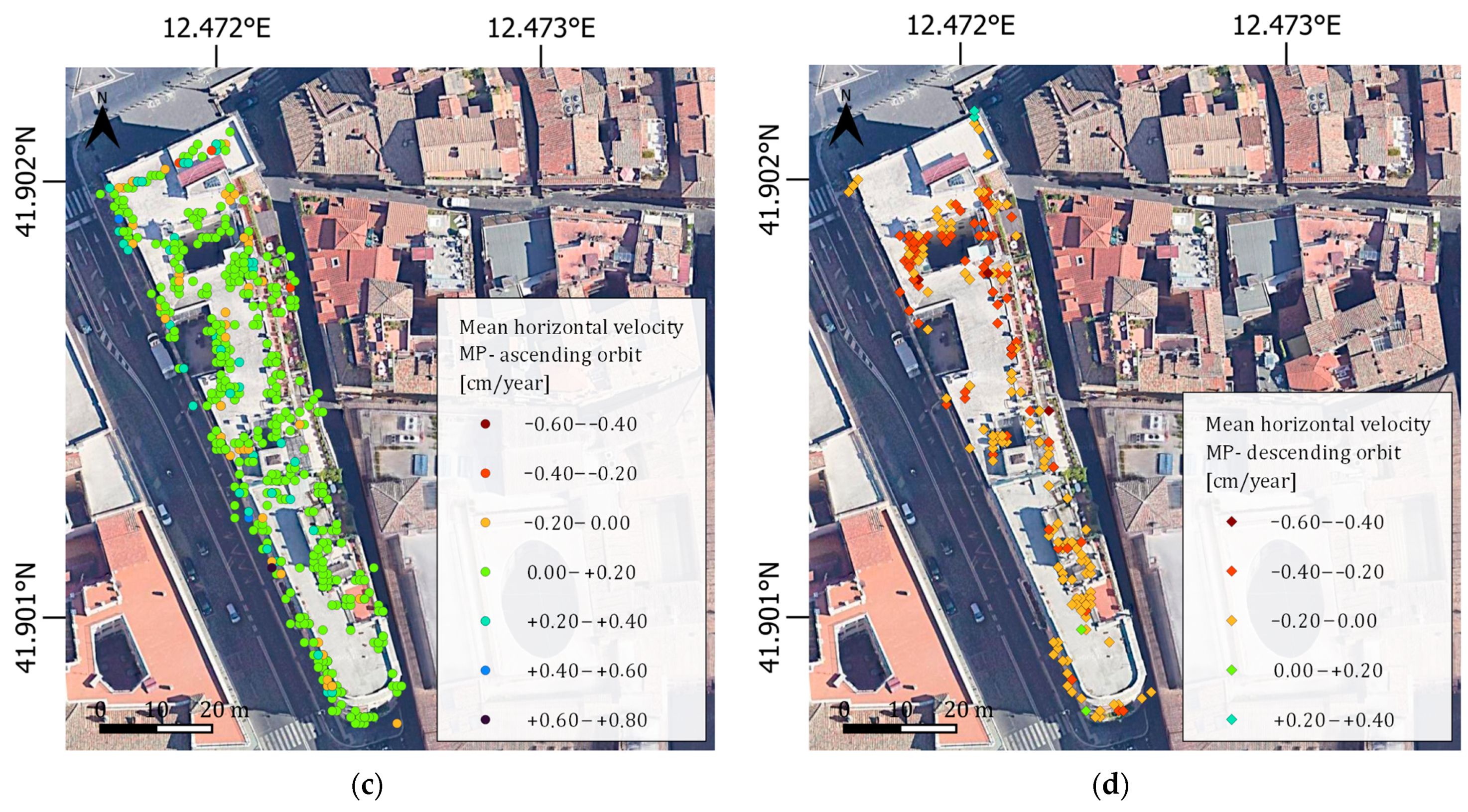
3.2. Pre-Processing
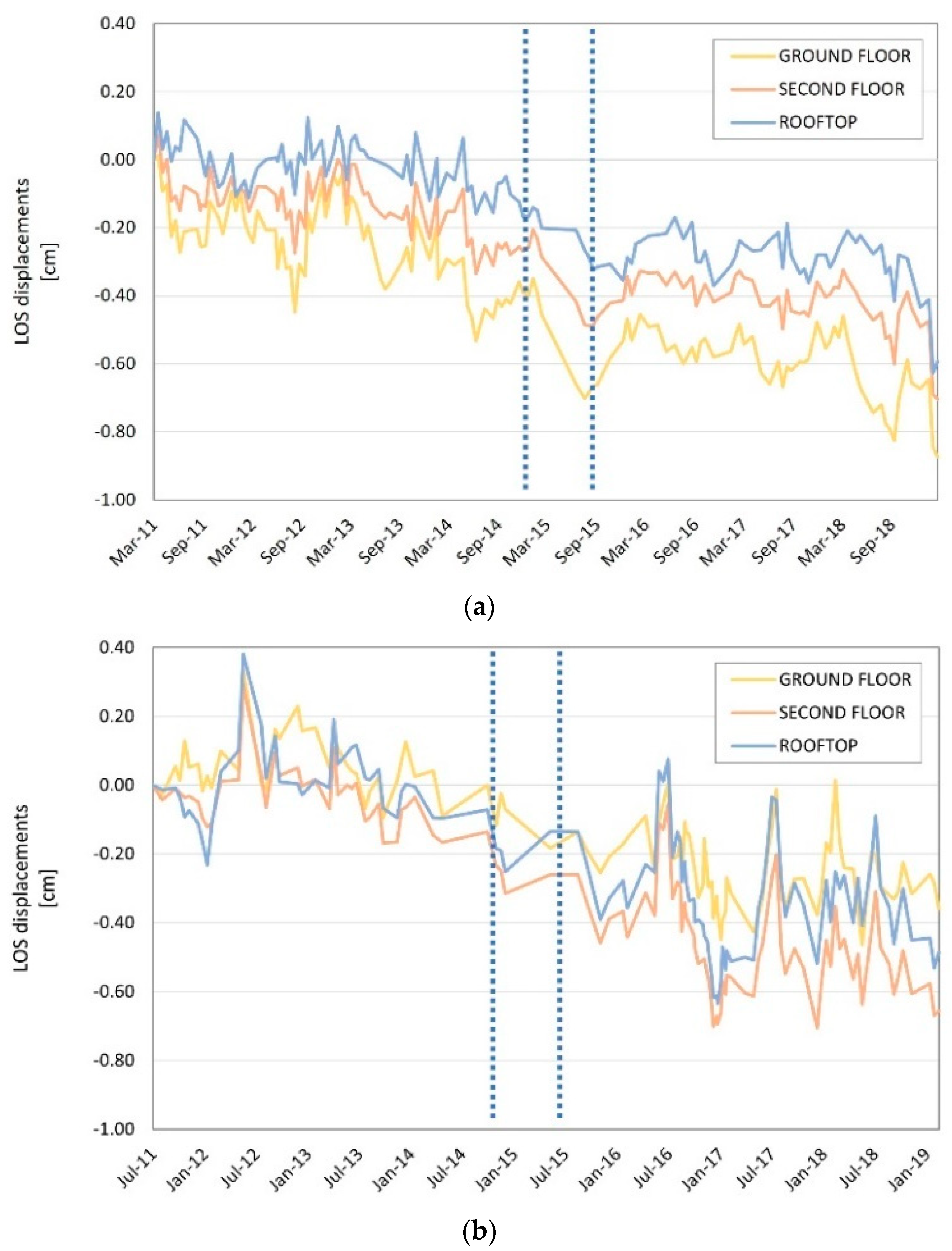
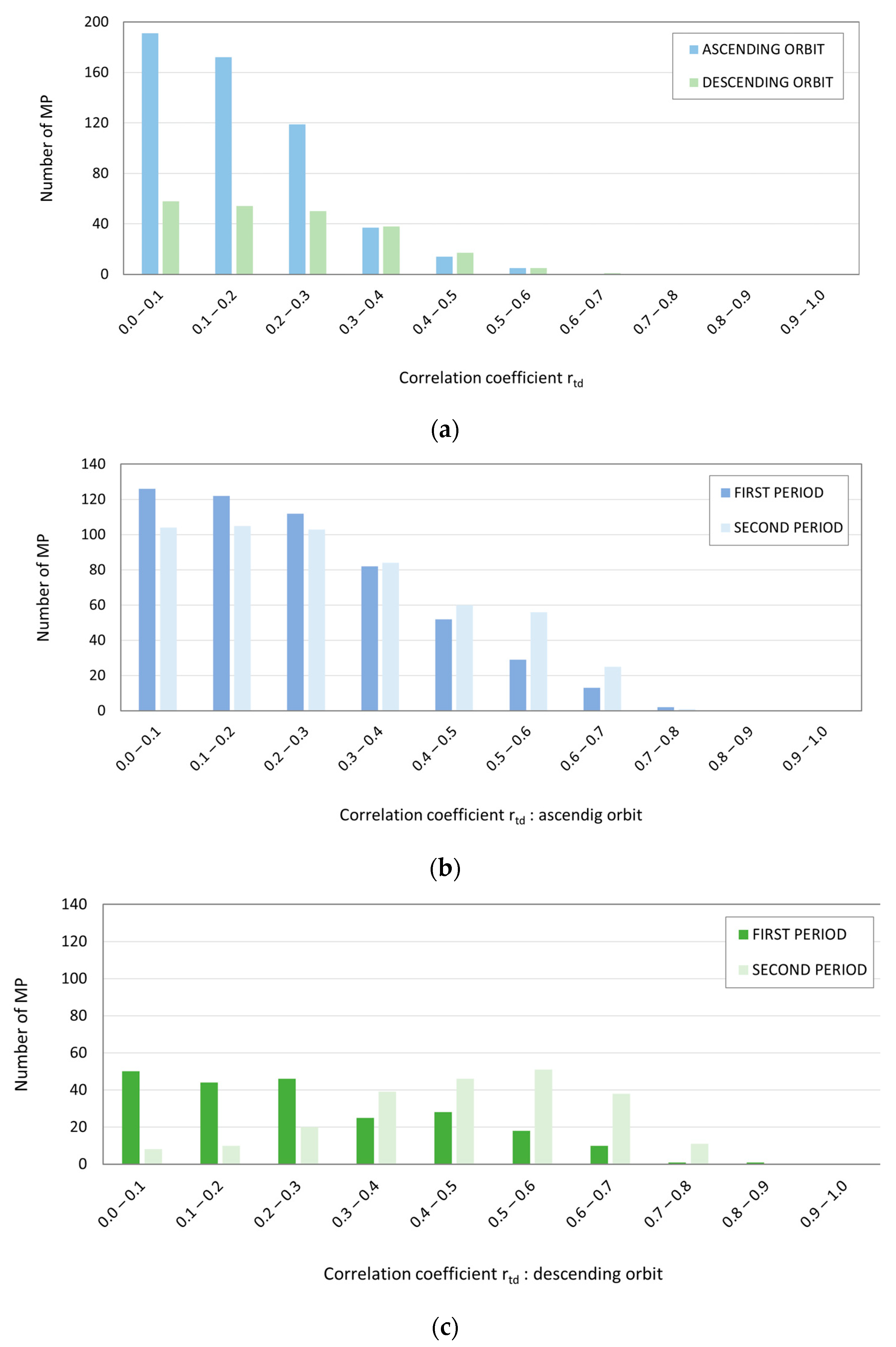
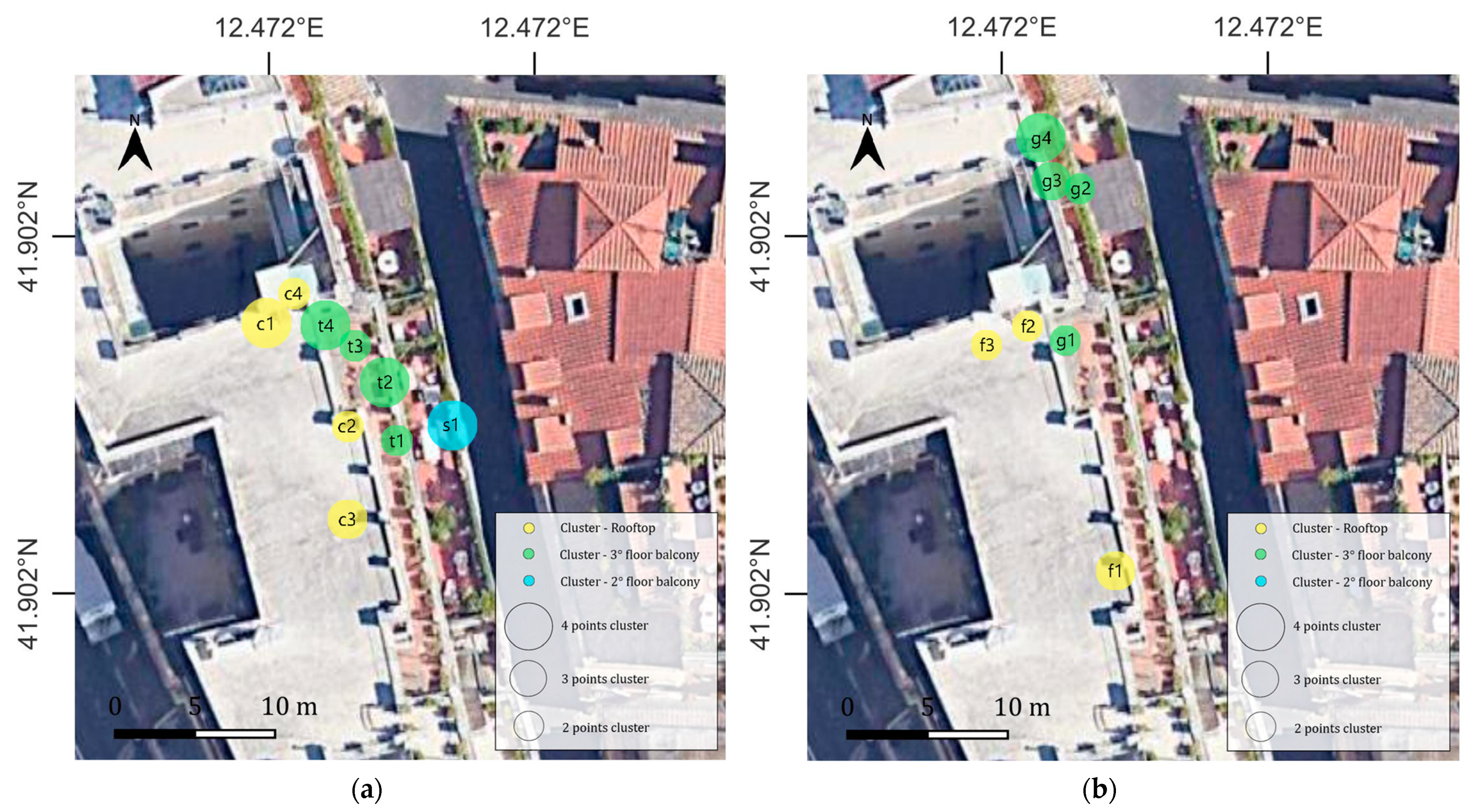
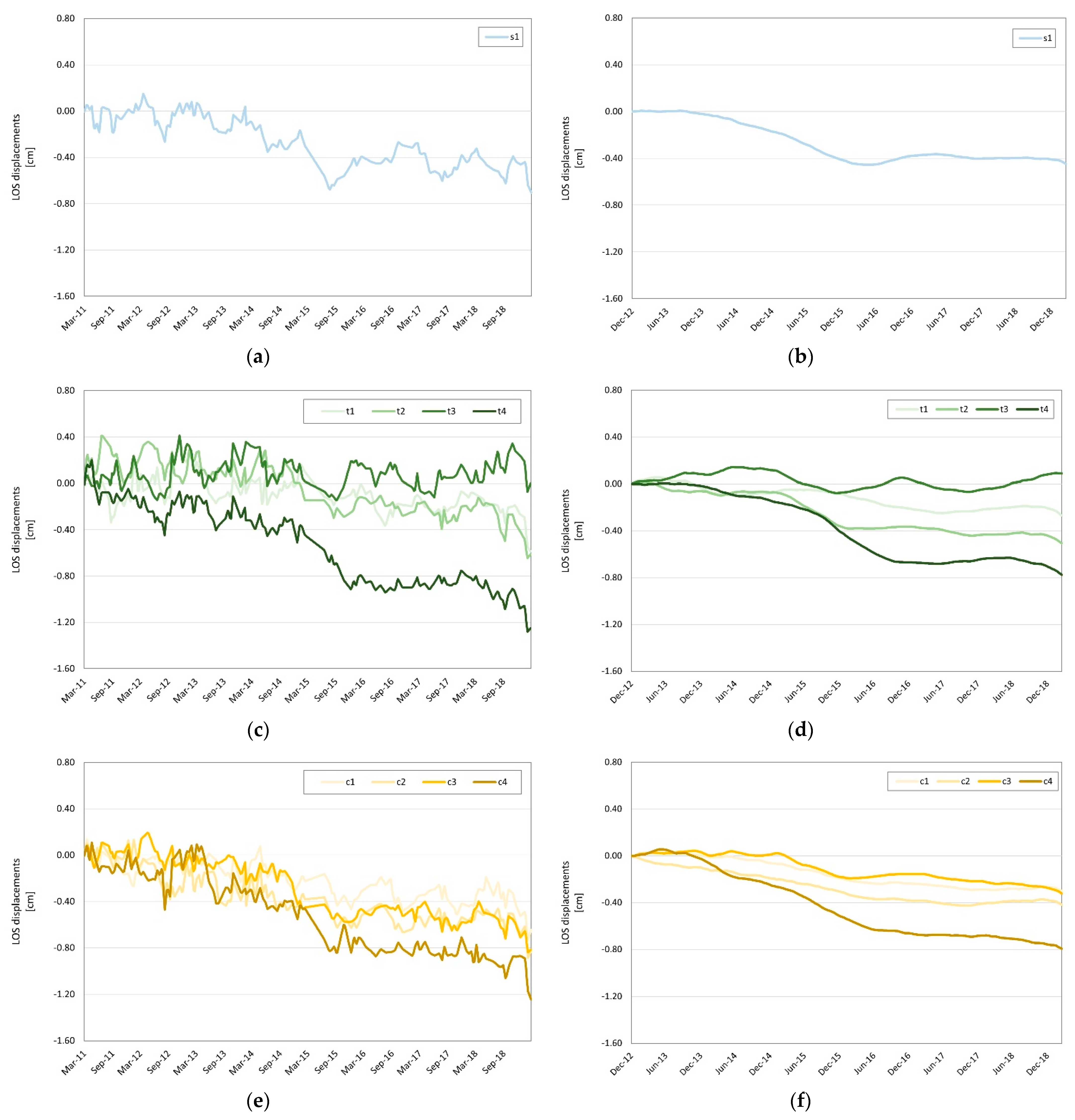
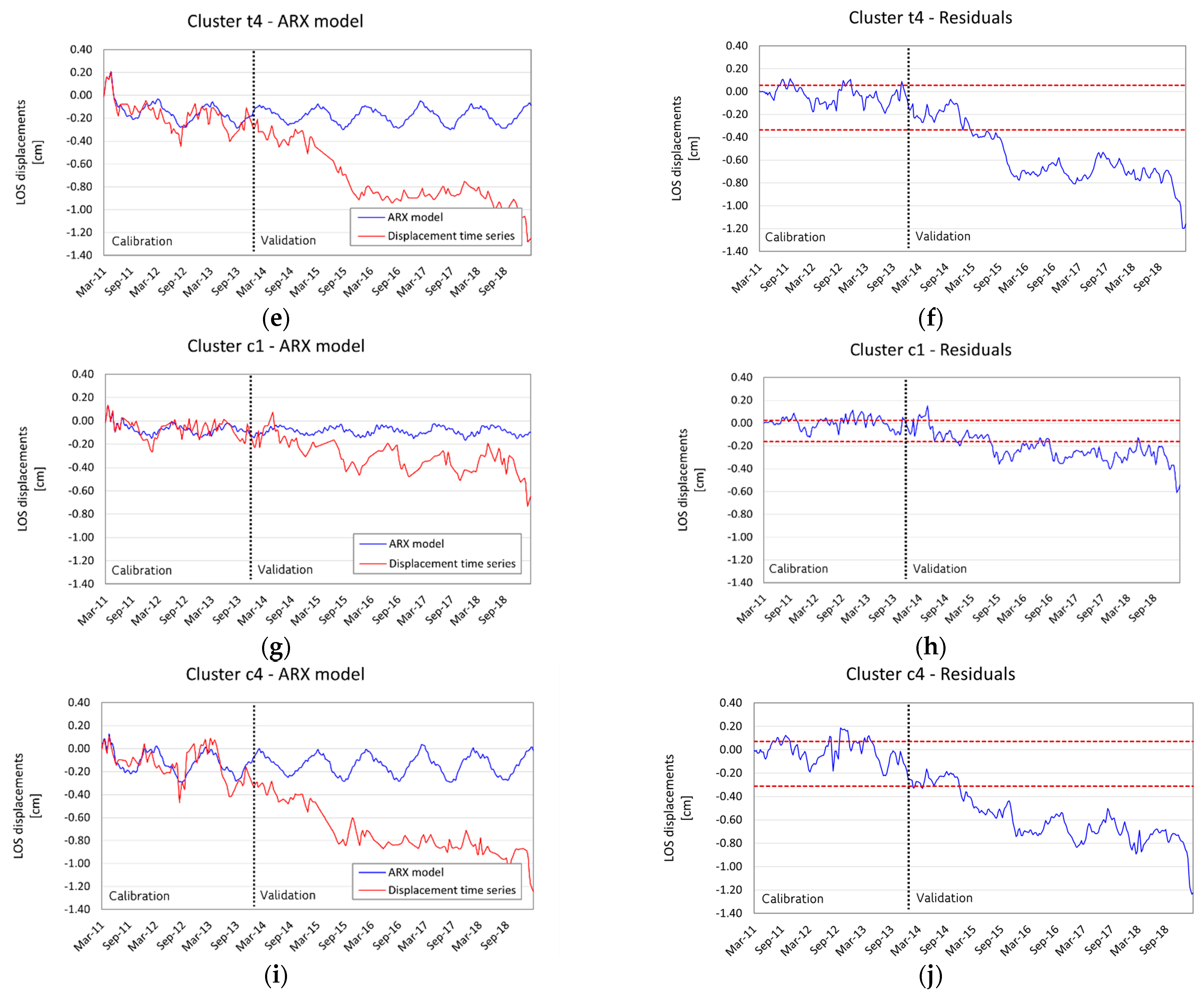
3.3. Back Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeni, G.; Bonano, M.; Casu, F.; Manunta, M.; Manzo, M.; Marsella, M.; Pepe, A.; Lanari, R. Long-Term Deformation Analysis of Historical Buildings through the Advanced SBAS-DInSAR Technique: The Case Study of the City of Rome, Italy. J. Geophys. Eng. 2011, 8, S1–S12. [Google Scholar] [CrossRef]
- Ferretti, A.; Monti-Guarnieri, A.; Prati, C.; Rocca, F.; Massonet, D. InSAR Principles: Guidelines for SAR Interferometry: Processing and Interpretation; ESA TM; ESA publications: Noordwijk, The Netherlands, 2007; ISBN 978-92-9092-233-9. [Google Scholar]
- Massonnet, D.; Feigl, K.L. Radar Interferometry and Its Application to Changes in the Earth’s Surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic Aperture Radar Interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Chen, F.; Lasaponara, R.; Masini, N. An Overview of Satellite Synthetic Aperture Radar Remote Sensing in Archaeology: From Site Detection to Monitoring. J. Cult. Herit. 2017, 23, 5–11. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lanari, R. Synthetic Aperture Radar Processing; Electronic Engineering Systems Series; CRC Press: Boca Raton, FL, USA, 1999; ISBN 978-0-8493-7899-7. [Google Scholar]
- Negula, I.D.; Sofronie, R.; Virsta, A.; Badea, A. Earth Observation for the World Cultural and Natural Heritage. Agric. Agric. Sci. Procedia 2015, 6, 438–445. [Google Scholar] [CrossRef] [Green Version]
- Tapete, D.; Fanti, R.; Cecchi, R.; Petrangeli, P.; Casagli, N. Satellite Radar Interferometry for Monitoring and Early-Stage Warning of Structural Instability in Archaeological Sites. J. Geophys. Eng. 2012, 9, S10–S25. [Google Scholar] [CrossRef]
- Tapete, D.; Cigna, F. Site-Specific Analysis of Deformation Patterns on Archaeological Heritage by Satellite Radar Interferometry. MRS Proc. 2012, 1374, 283–295. [Google Scholar] [CrossRef] [Green Version]
- Luo, L.; Wang, X.; Guo, H.; Lasaponara, R.; Zong, X.; Masini, N.; Wang, G.; Shi, P.; Khatteli, H.; Chen, F.; et al. Airborne and Spaceborne Remote Sensing for Archaeological and Cultural Heritage Applications: A Review of the Century (1907–2017). Remote Sens. Environ. 2019, 232, 111280. [Google Scholar] [CrossRef]
- Macchiarulo, V.; Giardina, G.; Milillo, P.; González Martí, J.; Sánchez, J.; DeJong, M.J. Settlement-Induced Building Damage Assessment Using MT-Insar Data for the Crossrail Case Study in London. In International Conference on Smart Infrastructure and Construction 2019 (ICSIC); ICE Publishing: Cambridge, UK, 2019; pp. 721–727. [Google Scholar]
- Tang, P.; Chen, F.; Zhu, X.; Zhou, W. Monitoring Cultural Heritage Sites with Advanced Multi-Temporal InSAR Technique: The Case Study of the Summer Palace. Remote Sens. 2016, 8, 432. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Chen, F.; Guo, H. Differential Radar Interferometry for Structural and Ground Deformation Monitoring: A New Tool for the Conservation and Sustainability of Cultural Heritage Sites. Sustainability 2015, 7, 1712–1729. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A Small-Baseline Approach for Investigating Deformations on Full-Resolution Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Agapiou, A.; Lysandrou, V. Detecting Displacements Within Archaeological Sites in Cyprus After a 5.6 Magnitude Scale Earthquake Event Through the Hybrid Pluggable Processing Pipeline (HyP3) Cloud-Based System and Sentinel-1 Interferometric Synthetic Aperture Radar (InSAR) Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6115–6123. [Google Scholar] [CrossRef]
- Alani, A.M.; Tosti, F.; Ciampoli, L.B.; Gagliardi, V.; Benedetto, A. An Integrated Investigative Approach in Health Monitoring of Masonry Arch Bridges Using GPR and InSAR Technologies. NDT E Int. 2020, 115, 102288. [Google Scholar] [CrossRef]
- Alberti, S.; Ferretti, A.; Leoni, G.; Margottini, C.; Spizzichino, D. Surface Deformation Data in the Archaeological Site of Petra from Medium-Resolution Satellite Radar Images and SqueeSARTM Algorithm. J. Cult. Herit. 2017, 25, 10–20. [Google Scholar] [CrossRef]
- Aslan, G.; Cakir, Z.; Lasserre, C.; Renard, F. Investigating Subsidence in the Bursa Plain, Turkey, Using Ascending and Descending Sentinel-1 Satellite Data. Remote Sens. 2019, 11, 85. [Google Scholar] [CrossRef] [Green Version]
- Cascini, L.; Ferlisi, S.; Fornaro, G.; Lanari, R.; Peduto, D.; Zeni, G. Subsidence Monitoring in Sarno Urban Area via Multi-temporal DInSAR Technique. Int. J. Remote Sens. 2006, 27, 1709–1716. [Google Scholar] [CrossRef]
- Cavalagli, N.; Kita, A.; Falco, S.; Trillo, F.; Costantini, M.; Ubertini, F. Satellite Radar Interferometry and In-Situ Measurements for Static Monitoring of Historical Monuments: The Case of Gubbio, Italy. Remote Sens. Environ. 2019, 235, 111453. [Google Scholar] [CrossRef]
- Cigna, F.; Del Ventisette, C.; Liguori, V.; Casagli, N. Advanced Radar-Interpretation of InSAR Time Series for Mapping and Characterization of Geological Processes. Nat. Hazards Earth Syst. Sci. 2011, 11, 865–881. [Google Scholar] [CrossRef]
- Farneti, E.; Cavalagli, N.; Costantini, M.; Trillo, F.; Minati, F.; Venanzi, I.; Ubertini, F. A Method for Structural Monitoring of Multispan Bridges Using Satellite InSAR Data with Uncertainty Quantification and Its Pre-Collapse Application to the Albiano-Magra Bridge in Italy. Struct. Health Monit. 2023, 22, 353–371. [Google Scholar] [CrossRef]
- Fiaschi, S.; Holohan, E.; Sheehy, M.; Floris, M. PS-InSAR Analysis of Sentinel-1 Data for Detecting Ground Motion in Temperate Oceanic Climate Zones: A Case Study in the Republic of Ireland. Remote Sens. 2019, 11, 348. [Google Scholar] [CrossRef] [Green Version]
- Lasaponara, R.; Masini, N. Satellite Synthetic Aperture Radar in Archaeology and Cultural Landscape: An Overview: Editorial. Archaeol. Prospect. 2013, 20, 71–78. [Google Scholar] [CrossRef]
- Luo, S.; Feng, G.; Xiong, Z.; Wang, H.; Zhao, Y.; Li, K.; Deng, K.; Wang, Y. An Improved Method for Automatic Identification and Assessment of Potential Geohazards Based on MT-InSAR Measurements. Remote Sens. 2021, 13, 3490. [Google Scholar] [CrossRef]
- Macchiarulo, V.; Milillo, P.; Blenkinsopp, C.; Giardina, G. Monitoring Deformations of Infrastructure Networks: A Fully Automated GIS Integration and Analysis of InSAR Time-Series. Struct. Health Monit. 2022, 21, 1849–1878. [Google Scholar] [CrossRef]
- Moise, C.; Dana Negula, I.; Mihalache, C.E.; Lazar, A.M.; Dedulescu, A.L.; Rustoiu, G.T.; Inel, I.C.; Badea, A. Remote Sensing for Cultural Heritage Assessment and Monitoring: The Case Study of Alba Iulia. Sustainability 2021, 13, 1406. [Google Scholar] [CrossRef]
- Necula, N.; Niculiță, M.; Fiaschi, S.; Genevois, R.; Riccardi, P.; Floris, M. Assessing Urban Landslide Dynamics through Multi-Temporal InSAR Techniques and Slope Numerical Modeling. Remote Sens. 2021, 13, 3862. [Google Scholar] [CrossRef]
- Pepe, A.; Sansosti, E.; Berardino, P.; Lanari, R. On the Generation of ERS/ENVISAT DInSAR Time-Series Via the SBAS Technique. IEEE Geosci. Remote Sens. Lett. 2005, 2, 265–269. [Google Scholar] [CrossRef]
- Selvakumaran, S.; Plank, S.; Geiß, C.; Rossi, C.; Middleton, C. Remote Monitoring to Predict Bridge Scour Failure Using Interferometric Synthetic Aperture Radar (InSAR) Stacking Techniques. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 463–470. [Google Scholar] [CrossRef]
- Urrego, L.E.B.; Verstrynge, E.; Balen, K.V.; Wuyts, V.; Declercq, P.-Y. Settlement-Induced Damage Monitoring of a Historical Building Located in a Coal Mining Area Using PS-InSAR. In 6th Workshop on Civil Structural Health Monitoring; Queen’s University: Belfast, UK, 2016; pp. 1–8. [Google Scholar]
- Xiong, S.; Wang, C.; Qin, X.; Zhang, B.; Li, Q. Time-Series Analysis on Persistent Scatter-Interferometric Synthetic Aperture Radar (PS-InSAR) Derived Displacements of the Hong Kong–Zhuhai–Macao Bridge (HZMB) from Sentinel-1A Observations. Remote Sens. 2021, 13, 546. [Google Scholar] [CrossRef]
- Arangio, S.; Calò, F.; Di Mauro, M.; Bonano, M.; Marsella, M.; Manunta, M. An Application of the SBAS-DInSAR Technique for the Assessment of Structural Damage in the City of Rome. Struct. Infrastruct. Eng. 2014, 10, 1469–1483. [Google Scholar] [CrossRef]
- Zhu, M.; Wan, X.; Fei, B.; Qiao, Z.; Ge, C.; Minati, F.; Vecchioli, F.; Li, J.; Costantini, M. Detection of Building and Infrastructure Instabilities by Automatic Spatiotemporal Analysis of Satellite SAR Interferometry Measurements. Remote Sens. 2018, 10, 1816. [Google Scholar] [CrossRef] [Green Version]
- Ardizzone, F.; Bonano, M.; Giocoli, A.; Lanari, R.; Marsella, M.; Pepe, A.; Perrone, A.; Piscitelli, S.; Scifoni, S.; Scutti, M.; et al. Analysis of Ground Deformation Using SBAS-DInSAR Technique Applied to COSMO-SkyMed Images, the Test Case of Roma Urban Area. In Proceedings of the SPIE 8536, SAR Image Analysis, Modeling, and Techniques XII, Edinburgh, UK, 21 November 2011; Volume 85360D. [Google Scholar]
- Bozzano, F.; Esposito, C.; Mazzanti, P.; Patti, M.; Scancella, S. Imaging Multi-Age Construction Settlement Behaviour by Advanced SAR Interferometry. Remote Sens. 2018, 10, 1137. [Google Scholar] [CrossRef] [Green Version]
- Cigna, F.; Lasaponara, R.; Masini, N.; Milillo, P.; Tapete, D. Persistent Scatterer Interferometry Processing of COSMO-SkyMed StripMap HIMAGE Time Series to Depict Deformation of the Historic Centre of Rome, Italy. Remote Sens. 2014, 6, 12593–12618. [Google Scholar] [CrossRef] [Green Version]
- Pepe, A.; Lanari, R. On the Extension of the Minimum Cost Flow Algorithm for Phase Unwrapping of Multitemporal Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Falabella, F.; Serio, C.; Masiello, G.; Zhao, Q.; Pepe, A. A Multigrid InSAR Technique for Joint Analyses at Single-Look and Multi-Look Scales. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ojha, C.; Manunta, M.; Lanari, R.; Pepe, A. The Constrained-Network Propagation (C-NetP) Technique to Improve SBAS-DInSAR Deformation Time Series Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4910–4921. [Google Scholar] [CrossRef]
- Bonano, M.; Manunta, M.; Marsella, M.; Lanari, R. Long-Term ERS/ENVISAT Deformation Time-Series Generation at Full Spatial Resolution via the Extended SBAS Technique. Int. J. Remote Sens. 2012, 33, 4756–4783. [Google Scholar] [CrossRef]
- Di Carlo, F.; Miano, A.; Giannetti, I.; Mele, A.; Bonano, M.; Lanari, R.; Meda, A.; Prota, A. On the Integration of Multi-Temporal Synthetic Aperture Radar Interferometry Products and Historical Surveys Data for Buildings Structural Monitoring. J. Civ. Struct. Health Monit. 2021, 11, 1429–1447. [Google Scholar] [CrossRef]
- Casu, F.; Manzo, M.; Lanari, R. A Quantitative Assessment of the SBAS Algorithm Performance for Surface Deformation Retrieval from DInSAR Data. Remote Sens. Environ. 2006, 102, 195–210. [Google Scholar] [CrossRef]
- Bonano, M.; Manunta, M.; Pepe, A.; Paglia, L.; Lanari, R. From Previous C-Band to New X-Band SAR Systems: Assessment of the DInSAR Mapping Improvement for Deformation Time-Series Retrieval in Urban Areas. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1973–1984. [Google Scholar] [CrossRef]
- Talledo, D.A.; Miano, A.; Bonano, M.; Di Carlo, F.; Lanari, R.; Manunta, M.; Meda, A.; Mele, A.; Prota, A.; Saetta, A.; et al. Satellite Radar Interferometry: Potential and Limitations for Structural Assessment and Monitoring. J. Build. Eng. 2022, 46, 103756. [Google Scholar] [CrossRef]
- Manunta, M.; De Luca, M.; Zinno, I.; Casu, F.; Manzo, M.; Bonano, M.; Fusco, A.; Pepe, A.; Onorato, G.; Berardino, P.; et al. The Parallel SBAS Approach for Sentinel-1 Interferometric Wide Swath Deformation Time-Series Generation: Algorithm Description and Products Quality Assessment. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6259–6281. [Google Scholar] [CrossRef]
- Shepard, D. A Two-Dimensional Interpolation Function for Irregularly-Spaced Data. In Proceedings of the 1968 23rd ACM National Conference; Association for Computing Machinery: New York, NY, USA, 1968; pp. 517–524. [Google Scholar]
- Floris, M.; Fontana, A.; Tessari, G.; Mulè, M. Subsidence Zonation Through Satellite Interferometry in Coastal Plain Environments of NE Italy: A Possible Tool for Geological and Geomorphological Mapping in Urban Areas. Remote Sens. 2019, 11, 165. [Google Scholar] [CrossRef] [Green Version]
- Lu, G.Y.; Wong, D.W. An Adaptive Inverse-Distance Weighting Spatial Interpolation Technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Matano, F.; Sacchi, M.; Vigliotti, M.; Ruberti, D. Subsidence Trends of Volturno River Coastal Plain (Northern Campania, Southern Italy) Inferred by SAR Interferometry Data. Geosciences 2018, 8, 8. [Google Scholar] [CrossRef] [Green Version]
- Raspini, F.; Cigna, F.; Moretti, S. Multi-Temporal Mapping of Land Subsidence at Basin Scale Exploiting Persistent Scatterer Interferometry: Case Study of Gioia Tauro Plain (Italy). J. Maps 2012, 8, 514–524. [Google Scholar] [CrossRef] [Green Version]
- Vilardo, G.; Ventura, G.; Terranova, C.; Matano, F.; Nardò, S. Ground Deformation Due to Tectonic, Hydrothermal, Gravity, Hydrogeological, and Anthropic Processes in the Campania Region (Southern Italy) from Permanent Scatterers Synthetic Aperture Radar Interferometry. Remote Sens. Environ. 2009, 113, 197–212. [Google Scholar] [CrossRef]
- QGIS.org QGIS User Guide—QGIS Documentation. Available online: https://docs.qgis.org/3.22/en/docs/user_manual/index.html (accessed on 14 January 2022).
- Google Earth User Guide Documentation. Available online: https://earth.google.com/intl/ar/userguide/v4/index.htm (accessed on 23 January 2022).
- Di Traglia, F.; De Luca, C.; Manzo, M.; Nolesini, T.; Casagli, N.; Lanari, R.; Casu, F. Joint Exploitation of Space-Borne and Ground-Based Multitemporal InSAR Measurements for Volcano Monitoring: The Stromboli Volcano Case Study. Remote Sens. Environ. 2021, 260, 112441. [Google Scholar] [CrossRef]
- Coccimiglio, S.; Coletta, G.; Lenticchia, E.; Miraglia, G.; Ceravolo, R. Combining Satellite Geophysical Data with Continuous On-Site Measurements for Monitoring the Dynamic Parameters of Civil Structures. Sci. Rep. 2022, 12, 2275. [Google Scholar] [CrossRef]
- Lorenzoni, F.; Caldon, M.; da Porto, F.; Modena, C.; Aoki, T. Post-Earthquake Controls and Damage Detection through Structural Health Monitoring: Applications in l’Aquila. J. Civ. Struct. Health Monit. 2018, 8, 217–236. [Google Scholar] [CrossRef]
- Clima Roma/Urbe—Dati Climatici. Available online: https://it.tutiempo.net/clima/ws-162350.html (accessed on 7 January 2022).
- Lee Rodgers, J.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E.; Tatham, R.L. Multivariate Data Analysis, 7th ed.; Pearson Education Limited: Harlow, UK, 2014; ISBN 978-1-292-02190-4. [Google Scholar]
- Swinscow, T.D.V.; Campbell, M.J. Statistics at Square One, 10th ed.; BMJ: London, UK, 2002; ISBN 1-280-19790-0. [Google Scholar]
- Johnston, F.R.; Boyland, J.E.; Meadows, M.; Shale, E. Some Properties of a Simple Moving Average When Applied to Forecasting a Time Series. J. Oper. Res. Soc. 1999, 50, 1267. [Google Scholar] [CrossRef]
- Hansun, S. A Novel Research of New Moving Average Method in Time Series Analysis. Int. J. New Media Technol. IJNMT 2014, 1, 22. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Heathmont, Australia, 2018; ISBN 978-0-9875071-1-2. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice-Hall Information and System Sciences Series; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999; ISBN 0-13-656695-2. [Google Scholar]
- He, X. Vibration-Based Damage Identification and Health Monitoring of Civil Structures. Ph.D. Thesis, University of California San Diego, La Jolla, CA, USA, 2008. [Google Scholar]
- Lorenzoni, F. Integrated Methodologies Based on Structural Health Monitoring for the Protection of Cultural Heritage Buildings. Ph.D. Thesis, Univerità degli Studi di Trento, Trento, Italy, 2013. [Google Scholar]
- Peeters, B.; De Roeck, G. One Year Monitoring of The Z24-Bridge: Environmental Influences Versus Damage Events. Proc. SPIE Int. Soc. Opt. Eng. 2001, 30, 149–171. [Google Scholar]
- Ramos, L. Damage Identification on Masonry Structures Based on Vibration Signatures. Ph.D. Thesis, University of Minho, Braga, Portugal, 2007. [Google Scholar]
- Modena, C.; Lorenzoni, F.; Caldon, M.; da Porto, F. Structural Health Monitoring: A Tool for Managing Risks in Sub-Standard Conditions. J. Civ. Struct. Health Monit. 2016, 6, 365–375. [Google Scholar] [CrossRef]
- Lorenzoni, F.; Casarin, F.; Caldon, M.; Islami, K.; Modena, C. Uncertainty Quantification in Structural Health Monitoring: Applications on Cultural Heritage Buildings. Mech. Syst. Signal Process. 2016, 66–67, 268–281. [Google Scholar] [CrossRef]
- Ljung, L. System Identification ToolboxTM—User’s Guide; The Mathworks, Inc.: Natick, MA, USA, 2022. [Google Scholar]
- Huber-Carol, C.; Balakrishnan, N.; Nikulin, M.S.; Mesbah, M. Goodness-of-Fit Tests and Model Validity; Birkhäuser: Boston, MA, USA, 2002; ISBN 978-1-4612-6613-6. [Google Scholar]
- Wald, A. Statistical Decision Functions. Nature 1951, 167, 1044. [Google Scholar] [CrossRef]
- Akaike, H. Fitting Autoregressive Models for Prediction. Ann. Inst. Stat. Math. 1969, 21, 243–247. [Google Scholar] [CrossRef]
- Floridi, G. Il Palazzo Romano Filonardi Già Gottifredi, Poi Primoli in Piazza Dell’Orso. Strenna dei Romanisti 2004, LXV, 279–286. [Google Scholar]
- Pietrangeli, C. Il Palazzo Primoli All’Orso. Strenna Dei Rom. 1965, XXVI, 341–344. [Google Scholar]
- Tapete, D.; Cigna, F. Rapid Mapping and Deformation Analysis over Cultural Heritage and Rural Sites Based on Persistent Scatterer Interferometry. Int. J. Geophys. 2012, 2012, 618609. [Google Scholar] [CrossRef] [Green Version]
- Wasowski, J.; Bovenga, F. Investigating Landslides and Unstable Slopes with Satellite Multi Temporal Interferometry: Current Issues and Future Perspectives. Eng. Geol. 2014, 174, 103–138. [Google Scholar] [CrossRef]



| Satellite | Acquisition Mode | Sensor Type | Resolution | Revisiting Time | Orbit | Incidence Angle |
|---|---|---|---|---|---|---|
| COSMO-SkyMed | Stripmap HIMAGE | X band HH polarization | 3 m | 16 days | Ascending | 34.12° |
| Descending | 28.76° |
| Orbit | Frame Number | Monitoring Period | Satellite Images | Reference Date | Reference Point | MP Density |
|---|---|---|---|---|---|---|
| Ascending | H4-05 | 21 March 2011–11 March 2019 | 129 | 21/03/2011 | 41.89928°; 12.50264° | 73513 MP/km2 |
| Descending | H4-03 | 29 July 2011–13 March 2019 | 103 | 29/07/2011 | 41.88835°; 12.49818° | 38918 MP/km2 |
| Phase | Period | Samples Number | Data | Data Type |
|---|---|---|---|---|
| Estimation phase | 21 March 2011– 29 December 2013 | 146 | Input | Temperature |
| Output | LOS displacements | |||
| Validation phase | 5 January 2014– 17 March 2019 | 272 | Input | Temperature |
| Output | LOS displacements |
| Orbit | VLOS [cm/Year] | |
|---|---|---|
| VLOS ≥ 0.00 | VLOS < 0.00 | |
| Ascending MPs | 18.2% | 81.8% |
| Descending MPs | 31.0% | 69.0% |
| Orbit | VLOS [cm/Year] | ||
|---|---|---|---|
| VLOS > +0.15 | +0.15 ≥ VLOS ≥ −0.15 | VLOS < −0.15 | |
| Ascending MPs | 0.3% | 93.0% | 6.7% |
| Descending MPs | 0.5% | 95.3% | 4.2% |
| Orbit | G (Ground Floor) | S (Second Floor) | R (Rooftop) |
|---|---|---|---|
| Ascending MPs | 18% | 24% | 58% |
| Descending MPs | 9% | 48% | 43% |
| Orbit | VLOS [cm/Year] | |
|---|---|---|
| VLOS ≥ 0.00 | VLOS < 0.00 | |
| Ascending MPs | 8.7% | 91.3% |
| Descending MPs | 2.2% | 97.8% |
| Orbit | VLOS [cm/Year] | ||
|---|---|---|---|
| VLOS > +0.15 | +0.15 ≥ VLOS ≥ −0.15 | VLOS < −0.15 | |
| Ascending MPs | 0.5% | 96.0% | 3.5% |
| Descending MPs | 0.5% | 93.5% | 6.0% |
| Cluster | na | nb | nk | λ0 | FPE | Goodness of Fit |
|---|---|---|---|---|---|---|
| s1 | 10 | 10 | 4 | 0.0004 | 0.0004 | 76.5% |
| t1 | 10 | 10 | 2 | 0.0007 | 0.0011 | 80.3% |
| t4 | 10 | 10 | 4 | 0.0004 | 0.0006 | 82.8% |
| c1 | 10 | 10 | 8 | 0.0002 | 0.0004 | 76.3% |
| c4 | 10 | 10 | 4 | 0.0006 | 0.0009 | 81.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonaldo, G.; Caprino, A.; Lorenzoni, F.; da Porto, F. Monitoring Displacements and Damage Detection through Satellite MT-InSAR Techniques: A New Methodology and Application to a Case Study in Rome (Italy). Remote Sens. 2023, 15, 1177. https://doi.org/10.3390/rs15051177
Bonaldo G, Caprino A, Lorenzoni F, da Porto F. Monitoring Displacements and Damage Detection through Satellite MT-InSAR Techniques: A New Methodology and Application to a Case Study in Rome (Italy). Remote Sensing. 2023; 15(5):1177. https://doi.org/10.3390/rs15051177
Chicago/Turabian StyleBonaldo, Gianmarco, Amedeo Caprino, Filippo Lorenzoni, and Francesca da Porto. 2023. "Monitoring Displacements and Damage Detection through Satellite MT-InSAR Techniques: A New Methodology and Application to a Case Study in Rome (Italy)" Remote Sensing 15, no. 5: 1177. https://doi.org/10.3390/rs15051177
APA StyleBonaldo, G., Caprino, A., Lorenzoni, F., & da Porto, F. (2023). Monitoring Displacements and Damage Detection through Satellite MT-InSAR Techniques: A New Methodology and Application to a Case Study in Rome (Italy). Remote Sensing, 15(5), 1177. https://doi.org/10.3390/rs15051177







