Intelligent Fusion Structure for Wi-Fi/BLE/QR/MEMS Sensor-Based Indoor Localization

Abstract

Due to the complexity of urban environments, localizing pedestrians indoors using mobile terminals is an urgent task in many emerging areas. Multi-source fusion-based localization is considered to be an effective way to provide location-based services in large-scale indoor areas. This paper presents an intelligent 3D indoor localization framework that uses the integration of Wi-Fi, Bluetooth Low Energy (BLE), quick response (QR) code, and micro-electro-mechanical system sensors (the 3D-WBQM framework). An enhanced inertial odometry was developed for accurate pedestrian localization and trajectory optimization in indoor spaces containing magnetic interference and external acceleration, and Wi-Fi fine time Measurement stations, BLE nodes, and QR codes were applied for landmark detection to provide an absolute reference for trajectory optimization and crowdsourced navigation database construction. In addition, the robust unscented Kalman filter (RUKF) was applied as a generic integrated model to combine the estimated location results from inertial odometry, BLE, QR, Wi-Fi FTM, and the crowdsourced Wi-Fi fingerprinting for large-scale indoor positioning. The experimental results indicated that the proposed 3D-WBQM framework was verified to realize autonomous and accurate positioning performance in large-scale indoor areas using different location sources, and meter-level positioning accuracy can be acquired in Wi-Fi FTM supported areas.

1. Introduction

Precise indoor positioning plays an important role in the field of urban navigation by providing continuous location-based services (LBS) in urban areas covered by global navigation satellite systems (GNSS). A range of indoor positioning technologies, such as Wi-Fi [1], fifth-generation mobile communication technology (5G) [2], ultra-wideband (UWB) [3], acoustic sources [4], light sources [5], Bluetooth Low Energy (BLE) [6], and smartphone integrated sensors [7], have been developed to achieve the realization of positioning performance with different levels of accuracy.

Wi-Fi-based indoor localization is more feasible for the indoor positioning of wide-area targets due to its low cost, easy maintenance and wide coverage. Normally, a Wi-Fi positioning system (WPS) contains two main approaches: ranging [8] and fingerprinting [9]. IEEE 802.11-2016 improves the positioning ability of WPS by proposing the Wi-Fi fine time measurement (FTM) protocol, which is estimated to achieve meter-level Wi-Fi distance-measurement precision between different smart terminals and corresponding wireless stations [10]. At this stage, only a fraction of Wi-Fi access points (APs) or mobile terminals are updated with the FTM protocol; thus, the fingerprinting-based approach is still important for providing location ability in large-scale indoor areas. Traditional Wi-Fi fingerprinting typically involves a point-to-point collection method, which is labor-consuming and inefficient [11]. The crowdsourcing-based Wi-Fi fingerprinting collection approach is developed using public daily-life trajectories, and the accuracy of the generated navigation database is subject to the performance of raw collected trajectories [12], the number of reference points [13], and the bias of different devices [14].

Micro-electro-mechanical system (MEMS) sensors can determine an accurate short-term localization performance of pedestrians, while the positioning error can accumulate over time. In addition, artificial interference can affect the performance of MEMS sensor-based heading estimations and final location updates [15,16]. Wi-Fi FTM and fingerprinting approaches can realize more consistent long-term accuracy, but they are susceptible to inaccuracy in complex indoor scenes, including multipath propagation and non-line-of-sight (NLOS). Therefore, to improve the precision of indoor pedestrian tracking, a multi-source fusion approach is usually adopted to combine the superiorities of existing location sources to achieve precision-controllable indoor localization performance through the organic combination of different positioning sources [17,18,19].

To conquer the above challenges, this paper proposes an intelligent 3D indoor positioning framework based on the combination of Wi-Fi, BLE, QR code, and MEMS sensors (the 3D-WBQM framework), which enables autonomous and precisely controlled indoor positioning performance in large-scale indoor spaces. The contributions of this work are summarized below:

(1)

To enhance the performance of MEMS sensor-based dead reckoning, an enhanced inertial odometry was developed that combines the inertial navigation system (INS) mechanization with multiple-sensors-originated observations and can significantly eliminate the effects of magnetic interference and external accelerations.

(2)

Three different location sources (Wi-Fi FTM, BLE, and QR) were selected as the landmark points that can provide an absolute reference for inertial odometry in large-scale indoor environments, and a dynamic time-warping (DTW) method was developed to further improve the performance of landmark detection and fingerprinting database generation.

(3)

An enhanced multilayer perceptron network (MLP) was proposed to perform an autonomous error evaluation of crowdsourced trajectories by extracting the spatiotemporal features of the collected trajectories, which can effectively improve the efficiency of the final Wi-Fi fingerprinting database construction and enhance the performance of database matching.

(4)

Based on the results of inertial odometry, Wi-Fi FTM, crowdsourced fingerprinting, and landmark recognition, the 3D-WBQM framework was proposed. A robust unscented Kalman filter (RUKF) was adopted to integrate all the location sources and eliminate the effects of outliers. The combination of different integration models provides a continuous and accuracy-controllable positioning performance in large-scale and multiple-scene contained indoor environment.

The general structure of this work is as follows. Section 2 presents related works. Section 3 describes the MEMS sensor-based localization and optimization framework and the MLP-based crowdsourced trajectories evaluation criteria. Section 4 presents the RUKF-based 3D-WBQM framework. Section 5 introduces the evaluation performance of the proposed 3D-WBQM framework. Section 6 summarizes this article.

2. Related Works

In this section, a comprehensive review of previous literature on MEMS sensors, wireless signals, and multi-source fusion-based positioning solutions is presented and the challenges faced by each kind of the localization approach are discussed.

2.1. MEMS Sensor-Based Positioning Solution

There are two main MEMS sensor-based localization methods targeting pedestrians: INS and pedestrian dead-reckoning (PDR) structures. Both INS and PDR can obtain real-time position, velocity, and attitude (PVA) information about the user for localization purposes. Normal PDR mechanization typically consists of four essential stages: gait recognition [20], step-length update [21], heading calculation [22], and location update [23]. Typically, PDR mechanization is the most widely used solution for pedestrian navigation, although the performance of PDR is limited by the cumulative errors of low-cost sensors, complex handheld and motion patterns, and indoor magnetic disturbance [24,25]. An alternative approach to pedestrian navigation is the strap-down inertial navigation system (SINS), through which real-time 3D attitude and location can be obtained; however, the accuracy of SINS is also constrained by sensor errors and SINS cannot be applied for a long period of time [26].

To limit the cumulative and drifting errors of SINS, various methods have been applied. The first applications of zero-velocity update technology (ZUPT) and zero-angular rate update (ZARU) were in the foot-mounted positioning system (FPS), which can significantly improve the accuracy of FPS. The performance of ZUPT and ZARU degrades when applied to mobile terminals, due to variation in handheld and walking styles of pedestrians, so other constraints are required in this case.

Wang et al. [27] analyzed the influencing factors of ZUPT performance and designed corresponding simulations and experimental analyses, with final experimental results demonstrating that the rate random walk of the gyroscope contributed most to the detection performance. Zhao et al. [28] proposed a novel zero-velocity cycle detection algorithm, which achieved ZUPT detection accuracy by extracting and removing pseudo-zero velocity cycles and pseudo-motion periods of 87.24%.

The accuracy of the traditional PDR approach in the real world is usually constrained by low accuracy with respect to walking speed, cumulative errors and heading deviations due to magnetic disturbance, and changeable handheld modes. Previous researchers have developed and carried out integrated experiments to reduce errors in the various components.

Tong et al. [22] developed a novel two-step traceless Kalman filter that performed attitude error correction in two steps by estimating the magnetic vector and gravity vectors. In addition, the hidden Markov model (HMM) was applied to enhance the identification accuracy of ZUPT cycles and realize more accurate heading estimation and dead-reckoning performance.

Klein et al. [29] used a machine learning (ML) approach to classify changeable handheld modes of mobile terminals and to increase the precision of PDR by selecting appropriate gain values. Zheng et al. [30] focused on the pocket mode and swing mode of smartphones and analyzed the relationship between rotational motion, walking states, and heading information. An enhanced rotation method and a single-point algorithm were developed for heading estimation in pocket mode and swing mode, respectively, which effectively improved the final performance.

Guo et al. [31] proposed a novel algorithm for pedestrian walking-speed estimation by considering four different handheld modes of smartphones. Feature vectors were extracted from the collected motion data provided by the integrated sensors, and then the classified handheld modes were tightly integrated using an adaptive gait-recognition approach. The final experimental results proved that the presented framework realized a classification precision of 98.85% and that speed-estimation error was less than 0.061 m/s.

2.2. Wireless-Signals-Based Positioning Solution

Wi-Fi and BLE localization systems, which usually contain approaches based on wireless ranging and fingerprinting, are regarded as effective and practical approaches for wireless positioning.

For BLE-assisted localization methods, additional BLE nodes are usually required to be deployed due to the limited number of local stations. In addition, traditional BLE RSSI-based ranging methods have degrading localization performance in large-scale indoor spaces due to signal transmission power, and most mobile terminals do not support combined methods such as the angle of arrival (AOA) and the angle of departure (AOD), or the interface is not open. As a result, the BLE proximity detection approaches and the fingerprinting approach are commonly applied as the positioning solutions in large-scale indoor environments.

You et al. [32] analyzed the effect of pedestrian swing arms on PDR performance and used an RSSI-based multipoint localization algorithm to decrease cumulative errors. Luo et al. [33] proposed an integrated Wi-Fi and BLE positioning framework by using an influential BLE layout plan and hierarchical topological fingerprinting (HTF), which enabled the proposed deployment strategy and HTF based on optimal localization performance.

Dinh et al. [34] developed a pedestrian-targeted indoor localization solution that used BLE beacons and smartphone integrated sensors. A trilateration approach of improved RSSI analysis provided the accurate initial location of PDR, and a light-weight fingerprinting approach was proposed to decrease the orbital drift of the PDR. Yu et al. [6] presented a 3D indoor localization framework based on the integration of BLE nodes and low-cost sensors, which incorporates INS and PDR mechanization as well as quasi-static magnetic-field recognition. A DTW-based BLE landmark recognition algorithm was applied to enhance the detection performance, and the adaptive unscented Kalman filter was finally applied to realize the meter-level positioning performance in selected experimental sites.

For Wi-Fi based localization methods, the crowdsourced fingerprinting approach is considered to be an efficient way to autonomously construct a navigation database in large-scale indoor areas; the performance of the generated crowdsourced navigation database depends on the quality of the collected daily-life motion traces. Currently, the new Wi-Fi FTM protocol is supported by a variety of mobile devices and wireless stations, and has proven to be applicable to be a meter-level location source for large-scale indoor areas. The combination of Wi-Fi fingerprinting and Wi-Fi FTM provides an autonomous and precisely controllable solution for large-scale indoor localization.

Sun et al. [35] proposed a secure crowdsourced indoor-positioning scheme that incorporated an adversarial sample discriminator, BERT-AD, and an indoor positioning model, BERT-LOC, to detect fake fingerprinting results and malicious beacons during the online positioning phase.

Yu et al. [36] compared the major characteristics affecting the performance of Wi-Fi ranging and designed the NLOS recognition model to decrease the influence of NLOS transmission, and they further combined Wi-Fi FTM with multiple-motion-modes integrated PDR mechanization and realized high accuracy in NLOS/LOS mixed indoor environments [37]. In addition, they extended the 2D scene to a 3D positioning scene and used a traceless partial filter to combine the distance-estimation and landmark-detection results. The final experimental results indicated that the meter-level localization performance was stably acquired by the proposed 3D integrated framework [10].

In general, the traditional fingerprinting-based approaches require the off-line phase of database generation, which is labor-consuming; the crowdsourcing-based algorithm can provide a more efficient method of database construction, while the effective evaluation and integration of crowdsourced trajectories is essential. The AOA and time-measurement-based approaches can realize more automatic localization performance and higher accuracy, thereby avoiding the time period required to build the navigation database; however, additional local facilities and consumer terminals are needed to support the AOA or time-measurement functions. Thus, to provide a more universal indoor-positioning function, different positioning methods need to be adaptively integrated.

2.3. Multi-Source-Fusion-Based Positioning Solution

Integrated navigation techniques have become increasingly popular in complex indoor environments, due to their improved robustness and precision, compared with single-location sources. Existing integration approaches, such as the Kalman filter (KF), the extended Kalman filter (EKF), and the particle filter (PF), are applied as typical integration methods for multi-source integrated navigation and localization.

For large-scale indoor positioning based on wireless signals and MEMS sensors, it is a challenge to efficiently design integration models for different positioning sources according to local environments. Furthermore, controlling the quality of each positioning source and adaptively adjusting the fusion weights in the integration model are a problems to be faced.

Li et al. [17] developed a robust dead-reckoning (DR)/Wi-Fi fingerprinting/magnetic matching (MM) fusion framework using a three-step quality-control strategy to enhance the localization performance from the signal-source level. The estimated experimental results showed that the proposed approach significantly reduced the root mean square (RMS) of the localization error by percentages between 13.3% and 55.2% in the tested environments and motion modes.

Wu et al. [38] used a combination of a mobile-generated Wi-Fi navigation database and a corner-based geomagnetic matching approach to improve localization precision. Gauss–Newton algorithms were developed for trajectory optimization, and DTW and the Pearson correlation coefficient (PCC) were proposed for corner-matching algorithms. Finally, the proposed algorithm framework was evaluated on two open datasets, with good performance.

Xu et al. [39] proposed a large-scale acoustic indoor localization system that applied the integration of BLE nodes, acoustic modules, and MEMS sensors. They applied an integrated acoustic propagation framework combining frequency-division multiple access, time-division multiple access, and space-division multiple access, respectively, for acoustic signal enhancement, and the information from BLE and the floor plan was further fused by the enhanced PF.

Shi et al. [40] improved the performance of conventional PF by applying the optimal estimation results in particle swarm to provide a particle selection reference for state-vector estimation. In addition, an adaptive optimization firefly approach was presented to avoid the local-optimum problem. The experimental results could realize an average positioning error within 0.5 m.

Based on the current literature, multi-source fusion is regarded as an effective way to implement LBS function in large-scale indoor areas, and existing multi-source-fusion-based positioning systems suffer from the following limitations that need to be addressed: (1) The MEMS sensor-based position and orientation system (POS) is affected by cumulative error and magnetic interference in complex indoor environments; (2) Traditional fingerprinting-based approaches require labor-consuming collection processes, while the performance of crowdsourcing-based approaches is limited by the uncontrollable accuracy of crowdsourced trajectories; (3) Effective and adaptive combinations of different location sources are needed to maintain positioning accuracy in complex and large-scale indoor spaces.

In our work, Wi-Fi FTM, Wi-Fi fingerprinting, BLE, QR codes, and MEMS sensors are intelligently integrated to provide a large-scale positioning solution aimed at complex and various indoor scenes. Wi-Fi FTM is more suitably applied in indoor open areas to avoid NLOS and multipath propagation, while the Wi-Fi fingerprinting approach is more suitable for applications in narrow indoor areas than in open indoor areas. Thus, in our work, the Wi-Fi fingerprinting database is autonomously generated using crowdsourced daily-life trajectories; BLE, Wi-Fi FTM station, and QR codes are applied as the landmark points to provide reference to crowdsourced daily-life trajectories; and MEMS sensors are applied as the link between different location sources for more continuous positioning performance.

3. Mems Sensor-Based Localization, Optimization, and Evaluation Framework

MEMS sensor-based localization solutions can provide accurate short-term positioning results by means of a heading projection method. In this section, an enhanced inertial odometry is presented which utilizes a combination of different sensors’ information and observations, and a global optimization algorithm is developed to increase the precision of the forward trajectory. Furthermore, the optimized trajectories are autonomously evaluated by the proposed MLP-based trajectory evaluation algorithm in order to eventually generate a crowdsourced navigation database.

3.1. Design of Inertial Odometry

Conventional MEMS sensor-based pedestrian tracking approaches typically incorporate PDR and INS mechanizations, which are susceptible to cumulative errors from built-in sensors, indoor artificial interference, and complex motion modes. In this section, a pre-integrated INS model is applied that takes into account the measurement biases of the inertial sensors, and it is further combined with multi-level observations to obtain higher trajectory-modeling precision.

(1) The measurement model for inertial sensors: Because of the low-cost nature of MEMS sensors, the estimated biases of accelerometers and gyroscopes need to be compensated in real time for error constraint. The modeled outputs for acceleration and angular rate are described as [23]:

$$\{\begin{array}{l}{a}^{-}(t)=a(t)+b_a(t)+R_w^{}(t)g^w+n_a\\ w_{}^{-}(t)=w(t)+b_w(t)+n_w\end{array}$$

(1)

where $a^{-}(t)$ and $w_{}^{-}(t)$ represent a modeled real-time measurement of acceleration and angular rate information; $a(t)$ and $w(t)$ represent ideal acceleration and angular rate data; $R_w^{}(t)$ indicates the attitude matrix with timestamp t; and $g^w$ indicates the local gravity value. $n_a$ and $n_w$ are the measurement noises that are the derivatives of $b_a(t)$ and $b_w(t)$, both following the Gaussian distribution. In this case, the biases of the accelerometer and the gyroscope are modeled as the random walk procedure:

$$\{\begin{array}{l}{\dot{b}}_a(t)=n_{b_a},n_{b_a}~N(0,{\sigma }_{b_a}^2)\\ {\dot{b}}_w(t)=n_{b_w},n_{b_w}~N(0,{\sigma }_{b_w}^2)\end{array}$$

(2)

(2) Pre-integration: For two adjacent sampling periods [t_u, t_u+1], the 3D location $P_{b_{u+1}}^{b_u}$, speed $V_{b_{u+1}}^{b_u}$, and attitude ${\varphi }_{b_{u+1}}^{b_u}$ information can be updated based on the last moment of motion information and estimated sensor bias:

$$\{\begin{array}{l}{P}_{b_{u+1}}^{b_u}=\int {\int }_{t\in [t_u,t_{u+1}]}{R}_t^{b_u}(a^{-}(t)-b_a(t))d{t}^2\\ V_{b_{u+1}}^{b_u}={\int }_{t\in [t_u,t_{u+1}]}{R}_t^{b_u}(a^{-}(t)-b_a(t))dt\\ {\varphi }_{b_{u+1}}^{b_u}={\int }_{t\in [t_u,t_{u+1}]}\frac{1}{2}\mathsf{\Omega }(w_{}^{-}(t)-b_w(t)){\varphi }_t^{b_u}dt\end{array}$$

(3)

where $R_t^{b_u}$ is the rotation matrix and $\mathsf{\Omega }$ is described as:

$$\mathsf{\Omega }(w)=\left[\begin{array}{cc}-\lfloor \mathit{w}\times \rfloor & \mathit{w}\\ -{\mathit{w}}^T& 0\end{array}\right],\lfloor w\times \rfloor =\left[\begin{array}{ccc}0& -w_z& w_y\\ w_z& 0& -w_x\\ -w_y& w_x& 0\end{array}\right]$$

(4)

where $\mathit{w}=\left[\begin{array}{ccc}{w}_x& w_y& w_z\end{array}\right]$ indicates the three-axis angular velocity vector.

(3) Error correction: Following the sensor-bias-estimation procedure, the updated bias is further applied to the model correction using first-order approximations:

$$\begin{array}{l}{P}_{b_{u+1}}^{b_u}\approx {\widehat{P}}_{b_{u+1}}^{b_u}+{\mathit{J}}_{b_a}^P\delta b_{a_u}+{\mathit{J}}_{b_w}^P\delta b_{w_u}\\ V_{b_{u+1}}^{b_u}\approx {\widehat{V}}_{b_{u+1}}^{b_u}+{\mathit{J}}_{b_a}^V\delta b_{a_u}+{\mathit{J}}_{b_w}^V\delta b_{w_u}\\ {\varphi }_{b_{u+1}}^{b_u}\approx {\widehat{\varphi }}_{b_{u+1}}^{b_u}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{\mathit{J}}_{b_w}^{\varphi }\delta b_{w_u}\end{array}\right]\end{array}$$

(5)

In the case of indoor artificial disturbances and complex motion modes, errors in the corrected motion information also cumulate, so additional observations are required to further minimize errors.

3.2. Observations and Trajectory Optimization

Limited by the cumulative errors from the built-in sensors of low-cost terminals, a single pre-integrated INS cannot realize accurate 3D indoor positioning by itself. In this section, multi-level observations are proposed to reduce the cumulative errors of pre-integrated INS systems by comprehensively considering environmental factors.

(1) Quasi-static magnetic field (QSMF) recognition: In indoor scenes containing complex artificial interference, detection of the disturbed local magnetic fields is required to improve heading-estimation performance [24]. The local magnetic fields of pedestrians during straight indoor travel are collected for QSMF detection:

$${\mathit{M}}_{\mathrm{refer}}^n={\mathit{C}}_{b,1}^n\cdot {\mathit{M}}_{k,1}^b$$

(6)

where ${\mathit{M}}_{k,1}^b$ denotes the first magnetic output epoch under the recognized QSMF period and ${\mathit{C}}_{b,1}^n$ indicates the attitude matrix at the current moment. ${\mathit{M}}_{\mathrm{refer}}^n$ denotes the calibrated local magnetic vector, applied as the reference magnetic field:

$$\delta {\mathit{z}}_M^n={\mathit{C}}_{b,k}^n\cdot {\mathit{M}}_k^b-{\mathit{M}}_{\mathrm{refer}}^n$$

(7)

where ${\mathit{M}}_k^b$ indicates the magnetometer collected at other epochs of the detected QSMF period and ${\mathit{C}}_{b,k}^n$ indicates the pose matrix at other QSMF moments.

(2) External acceleration observation: In the case of complex motion models of pedestrians, external acceleration can degrade the performance of roll- and pitch-angle estimation in the calculated attitude matrix [25]. In this section, external acceleration values are modeled as an observation equation:

$$\begin{array}{ll}\delta {\mathit{f}}^n& ={\mathit{f}}^n-{\widehat{\mathit{C}}}_b^n{\tilde{\mathit{f}}}^b\\ & \approx {\mathit{f}}^n-(\mathbf{I}-[\mathsf{\psi }\times ]){\mathit{C}}_b^n{\mathit{f}}^b+{\mathit{C}}_b^n{\mathit{n}}_a\\ & =[\mathsf{\psi }\times ]{\mathit{f}}^n+{\mathit{C}}_b^n{\mathit{n}}_a\\ & =[{\mathit{f}}^n\times ]\mathsf{\psi }+{\mathit{C}}_b^n{\mathit{n}}_a\end{array}$$

(8)

where ${\mathit{f}}^n$ represents the reference local gravity, ${\tilde{\mathit{f}}}^b$ represents the accelerometer output, and $\mathsf{\psi }\times$ indicates the skew-symmetric matrix derived from the error vector-attitude vector ${\varphi }_{b_{u+1}}^{b_u}$. The measurement noise n_a is adaptively adjusted to the context of the calculated external acceleration:

$${\mathit{n}}_a=\{\begin{array}{l}{\sigma }_a,\gamma \le {\varpi }_1\\ ({\gamma }^2/P){\sigma }_a,{\varpi }_1<\gamma \le {\varpi }_2\\ \infty ,\gamma >{\varpi }_2\end{array}$$

(9)

where $\gamma =\sqrt{\left|norm({\mathit{f}}^b)-\mathit{g}\right|}$ is the estimated external acceleration value, ${\sigma }_a$ is the bias stability of the accelerometer, and P is the covariance matrix in the RUKF. The parameter ${\varpi }_1$ is calculated by $\sqrt{{\sigma }_{a_x}^2+{\sigma }_{a_y}^2+{\sigma }_{a_z}^2}$, ${\sigma }_{a_x}^{}$, ${\sigma }_{a_y}^{}$, and ${\sigma }_{a_z}^{}$ represents the bias stability originated from the accelerometer. The parameter ${\varpi }_2$ is calculated by $s\cdot \left|\mathit{g}\right|$ and the scale parameter s needs to be turned according to the design requirement of the applications.

(3) The PDR mechanization can provide the relative step-length originated walking speed and the location increment to constrain the drift error of the pre-integrated INS solution:

$$\delta {\mathit{z}}_v^n={\mathit{v}}_{Step}^n-{\mathit{v}}_{{}_{INS}}^n$$

(10)

where ${\mathit{v}}_{Step}^n$ represents the calculated gait length value provided in [6] and ${\mathit{v}}_{{}_{INS}}^n$ is the velocity information provided by the pre-integrated INS solution. The observed residuals of two vectors are described as:

$$\delta {\mathit{z}}_p^n={\mathit{p}}_{Step}^n-{\mathit{p}}_{{}_{INS}}^n$$

(11)

where ${\mathit{p}}_{Step}^n$ represents the calculated 2D position results using PDR mechanization and ${\mathit{p}}_{{}_{INS}}^n$ indicates the inertial mechanization based on location estimation result.

The attitude-estimation performance using inertial mechanization will accumulate rapidly; thus, in this work, the barometer-originated observation is adopted for drift-error constraint of altitude estimation:

$$\delta {\mathit{z}}_h^n=h_B^n-h_{{}_{INS}}^n$$

(12)

where $h_B^n$ indicates the height of the barometer origin presented in [6] and $h_{{}_{INS}}^n$ is the z-axis location change estimated by inertial mechanization.

To further improve the accuracy of forward inertial odometry, a global optimization module was designed in this work, aiming to reduce the cumulative and drift errors originated by the smartphone integrated sensors and the dead-reckoning algorithm. Forward–backward smoothing filters were applied for location and attitude optimization, using the forward-navigation information [12]:

$${\widehat{\mathit{x}}}_{k-1|k}={\widehat{\mathit{x}}}_{k-1}+{\mathit{P}}_{k-1}{\mathit{\varphi }}_k^{\mathrm{T}}{({\mathit{P}}_{{}_{k-1}}^{-})}^{-1}({\widehat{\mathit{x}}}_k-{\widehat{\mathit{x}}}_k{}^{-})$$

(13)

$${\mathit{P}}_{k-1|k}={\mathit{P}}_{k-1}-({\mathit{P}}_{k-1}{\mathit{\varphi }}_k^{\mathrm{T}}{({\mathit{P}}_k{}^{-})}^{-1})({\mathit{P}}_k-{\mathit{P}}_k{}^{-})\cdot {({\mathit{P}}_{k-1}{\mathit{\varphi }}_k^{\mathrm{T}}{({\mathit{P}}_k{}^{-})}^{-1})}^{\mathrm{T}}$$

(14)

where ${\widehat{\mathit{x}}}_k$ and ${\widehat{\mathit{x}}}_k{}^{-}$ represent the updated state vectors recorded during forward inertial ranging and the recorded predicted state values. ${\mathit{P}}_{{}_{k-1}}^{-}$ is the predicted covariance matrix recorded during forward inertial odometry. ${\mathit{\varphi }}_k^{\mathrm{T}}$ is the state-update matrix for the current moment and ${\mathit{P}}_{k-1}$ is the recorded updated covariance matrix. ${\widehat{\mathit{x}}}_{k-1}$ and ${\widehat{\mathit{x}}}_{k-1|k}$ indicate the smoothed state vectors for the current and last moments and ${\mathit{P}}_{k-1|k}$ represents the corresponding smoothed covariance matrix.

3.3. MLP-Based Crowdsourced Trajectories Evaluation Algorithm

After the optimized trajectories were processed and collected, the trajectory error needed to be predicated for further trajectory selection and fusion. This section presents an MLP-based trajectory-error-prediction model that uses only motion features extracted from optimized trajectories to predict the accuracy of crowdsourced trajectories. 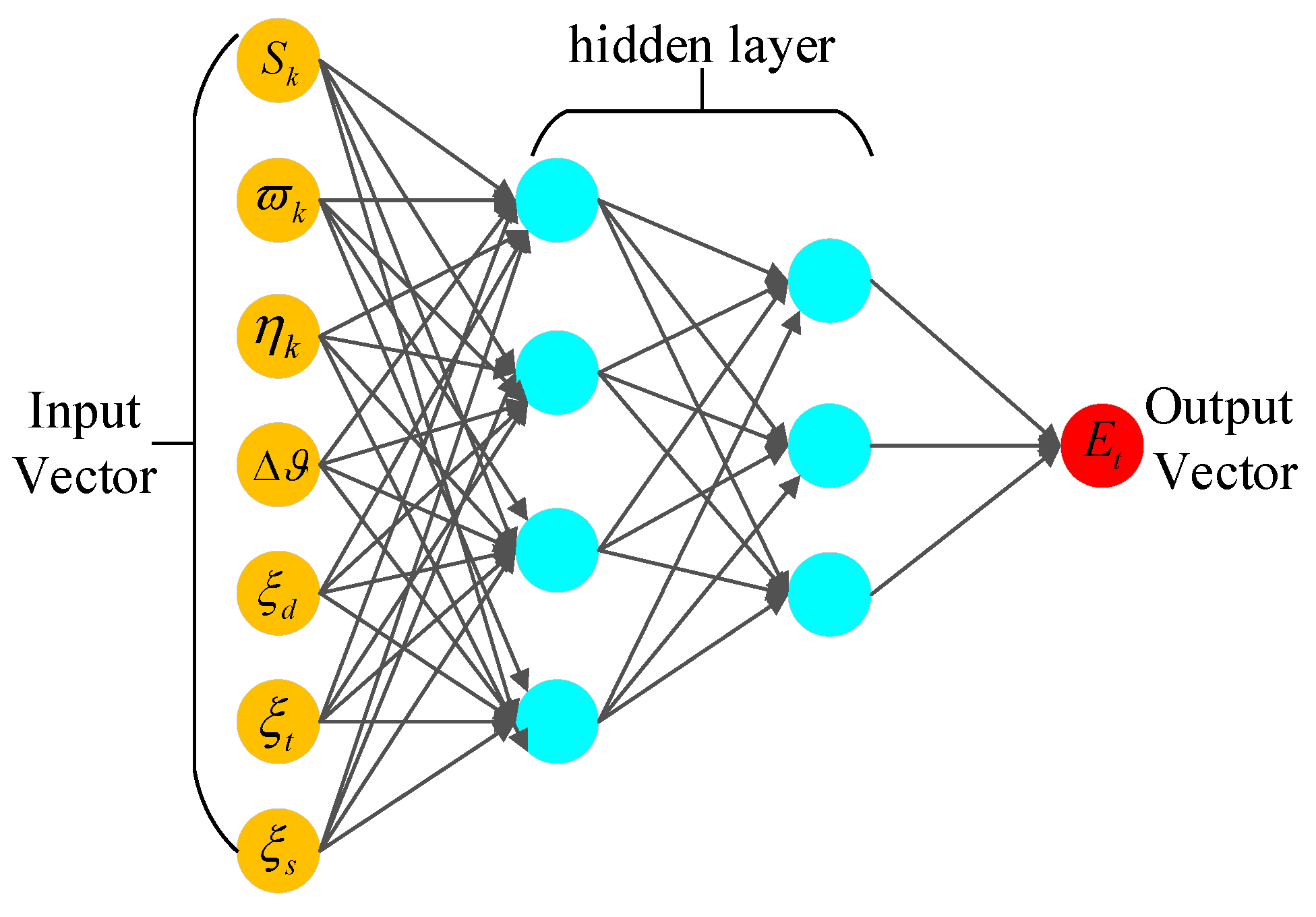Compared with other classical structures, such as long short-term memory (LSTM) [41] and the convolutional neural network (CNN) [42], MLP networks have a simpler structure and are more efficient to train. In addition, MLP networks can effectively learn and extract features from crowdsourced indoor trajectories and they are not limited by the length of the input vector. To improve the precision of the MLP-based error-evaluation model, different trajectory information features were extracted as input vectors in the MLP training phase, including:

(1) The step length calculated in real time during each gait;

(2) Estimated heading result ${\varpi }_k$ during each gait procedure;

(3) Cumulative numbers of steps ${\eta }_k$ from the first moment;

(4) Cumulative change in heading, which is calculated as follows:

$$\mathsf{\Delta }\vartheta (k)={\displaystyle \sum _{k=1}^n\sqrt{\left|{\varpi }_k{}^2-{\varpi }_{k-1}{}^2\right|}}$$

(15)

where $\mathsf{\Delta }\vartheta (k)$ indicates the cumulated heading difference and ${\varpi }_k$ is the real-time heading information;

(5) Ratio between used distance and total distance:

$${\xi }_d(k)=\frac{{\displaystyle \sum _{k=1}^{\beta }{L}_k}}{{\displaystyle \sum _{k=1}^n{L}_k}}$$

(16)

where n represents the recorded gait quantity of the specific trajectory and $\beta$ indicates the taken gaits;

(6) Ratio between used time and total time:

$${\xi }_t(k)=T(k)/T_{total}$$

(17)

where $T_{total}$ represents the overall time period of specific trajectory and $T(k)$ indicates the current time used;

(7) The ratio of the number of steps taken to the total number of steps:

$${\xi }_s(k)=step(k)/ste{p}_{total}$$

(18)

where $ste{p}_{total}$ represents the total gait detected under the selected route and $step(k)$ indicates the taken gait number at current moment.

The presented characteristics can adaptively simulate the accuracy of the selected crowdsourced trajectory from different perspectives, which will further be constructed as the input vector in the MLP model for training purposes; the input vector and output vector of the MLP network is described in Figure 1.

The loss function of the presented MLP is modeled as:

$$Loss(\mathit{\alpha },\mathit{\beta })=\frac{1}{2m}{{\displaystyle \sum _x\Vert g(\mathit{x})-\mathit{\eta }\Vert }}^2$$

(19)

where $\mathit{\alpha }$ and $\mathit{\beta }$ represent the weight and bias vectors, $g(\mathit{x})$ indicates the calculated result during each training phase, and $\mathit{\eta }$ indicates the reference output vector. The stochastic gradient descent (SGD) is adopted for model training, which is described as:

$$\{\begin{array}{l}{\alpha }_k\to {\alpha }_k={\alpha }_k-\frac{\nu }{m}{\displaystyle \sum _j\frac{\partial Los{s}_{x_j}}{\partial {\mathit{\alpha }}_k}}\\ {\beta }_l\to {\beta }_l={\beta }_l-\frac{\nu }{m}{\displaystyle \sum _j\frac{\partial Los{s}_{x_j}}{\partial {\mathit{\beta }}_l}}\end{array}$$

(20)

where $\nu$ represents the set learning rate during training phase and ${\alpha }_k$ and ${\beta }_l$ are the trained weight and bias parameters, respectively. The trained model of the MLP is further applied for the autonomous evaluation of crowdsourced trajectories.

4. Intelligent Integration Model of Wi-Fi/BLE/QR/Mems Sensors

This work provides an enhanced integration model of Wi-Fi/BLE/QR/MEMS sensor-based location sources. In the off-line phase, the original trajectory is optimized based on the Wi-Fi/BLE/QR-provided reference-points information, and the MLP-based trajectory evaluation framework is further employed to construct a crowdsourced fingerprinting database. In the online phase, the 3D attitude, speed, and location information provided by inertial odometry are further integrated with the wireless-signal-based observations, such as Wi-Fi RSSI- and FTM-based ranging results, Wi-Fi fingerprinting results, and landmark-detection results through RUKF, and the navigation error is corrected through a multi-source fusion procedure. The final 3D location, speed, and attitude are updated with the aim of providing accurate location-based information in large-scale indoor spaces. Figure 2 depicts the overall framework of the proposed 3D-WBQM algorithm.

4.1. Wi-Fi/BLE/QR-Based Landmark Detection and Uncertainty Measurement

To autonomously generate a crowdsourced Wi-Fi fingerprinting database indoors, reference to landmark points is required to provide absolute locations for the collected crowdsourced indoor trajectories in order to further optimize the crowdsourced trajectories. Based on the signal transmission characteristics of different localization sources, in order to cover different indoor scenarios, Wi-Fi FTM-supported sites, BLE nodes, and QR codes are mixed in this work in order to provide reliable landmark-detection information according to different indoor-localization scenarios. Among them, QR codes are usually deployed near the gate, BLE nodes are usually deployed at corridors or lifts, and Wi-Fi stations are more suitable for deployment in open areas to improve landmark-detection performance. The Wi-Fi/BLE/QR-based landmark detection is depicted in Figure 3.

Figure 3 shows that the measurements acquired from the local wireless stations demonstrate regular peaks during the passage of pedestrians. In this part, a universal wireless landmark-recognition approach is presented for the accurate detection of BLE- and Wi-Fi-based landmark points. For real-world scenes, the measured BLE RSS- or the Wi-Fi FTM-based range results are affected by the multipath propagation and NLOS effects, so that the range distribution collected in real time shows fluctuating results, with differences compared to the ideal range-result distribution.

In order to improve the performance of the ground-marker category and reduce the influence of environmental factors, this work developed DTW matching using the calculated distances acquired from the Wi-Fi ranging and BLE RSSI. The real-time ranging results from Wi-Fi ranging and BLE RSSI are described as:

$$L_{\mathrm{observed}}=L_{\mathrm{FTM}}+d_N+d_{\mathrm{random}}$$

(21)

where L_observed is regarded as a real-time modeled Wi-Fi distance measurement which contains NLOS erroe d_N and random error d_random, as well as the ground-truth value L_FTM.

The BLE RSSI can also be applied to distance measurements, and the conversion equation between the measured distance and the measured RSSI value is described as:

$$L_r(\varsigma )=L_0({\varsigma }_0)-10\mu \lg (\frac{\varsigma }{{\varsigma }_0})+\delta$$

(22)

where $L_r(\varsigma )$ indicates the measured BLE RSSI at the range $\varsigma$ between the pedestrian and BLE node, ${\varsigma }_0$ indicates the ground-truth distance, $L_0({\varsigma }_0)$ is the reference RSSI at the known distance d₀, $\mu$ indicates the path loss index, and $\delta$ represents the random error of measured RSSI.

In the procedure of the pedestrian walking past a local wireless landmark, normally the measured distance set between smartphone and landmarks would generate regular peaks. Normally, there exists an ideal distribution to describe this procedure, which is generated using the constant walking-speed information and the calculated distance between the pedestrian’s ideal position and the location of landmarks, as shown in Figure 3, while the collected distance set is affected by the real-world environments. To decrease the environmental effects, this paper proposed the DTW-assisted landmark recognition algorithm based on the calculated similarity results of the real-time collected measurement vector and the self-generated reference vector:

$$\begin{array}{l}DTW({\xi }_{\mathrm{refer}},{\xi }_k)\\ =Dist(e_n,f_m)+\min [D(e_n{}_{-1},f_m),D(e_n,f_{m-1}),D(e_{n-1},f_{m-1})]\end{array}$$

(23)

where $DTW({\xi }_{\mathrm{refer}},{\xi }_k)$ indicates the cumulated DTW indices of the real-time collected measurement vector and the generated reference vector, ${\xi }_{\mathrm{refer}}$ and ${\xi }_k$ represent the corresponding distributions that contain the ranging values $e_n$ and $f_m$. $D(e_n{}_{-1},f_m)$ denotes the calculated absolute value of the difference between the ranging values $e_n{}_{-1}$ and $f_m$.

4.2. Multi-Source Integration via Robust Unscented Kalman Filter

In this work, in order to cover a large-scale indoor space, hybrid measurements were used as the observation model, including the Wi-Fi FTM- and BLE-based ranging results, landmark-detection results, and MEMS sensor-based estimation results:

$$\delta z_d=\left[\begin{array}{c}\delta z_{1,ranging}\\ ⋮\\ \delta z_{m,ranging}\end{array}\right]=\left[\begin{array}{c}{\zeta }_{MEMS,1}-{\zeta }_{wifi/ble,1}\\ ⋮\\ {\zeta }_{MEMS,m}-{\zeta }_{wifi/ble,m}\end{array}\right]$$

(24)

where $\delta z_{m,ranging}$ indicates the calculated observation residuals between MEMS sensor-based distance-estimation results and the wireless-signal-based ranging results.

To provide a full range of observations, the landmark-detection results of Wi-Fi FTM stations can also be served as the observed location for the MEMS-sensor approach:

$$\delta {\mathit{z}}_r^n={\mathit{r}}_{wifi}^n-{\mathit{r}}_{{}_{MEMS}}^n=\delta \mathit{r}+n_{wifi}$$

(25)

where ${\mathit{r}}_{wifi}^n$ represents the location of the Wi-Fi FTM station obtained when the landmark is detected; in this case, the uncertainty error of detected Wi-Fi landmarks can be described as:

$$n_{wifi}\sim {\displaystyle \sum _{\tau =0}^{\partial }{\mathit{v}}_{{}_{RUKF}}^n(\tau )}d\tau$$

(26)

where ${\mathit{v}}_{{}_{RUKF}}^n(\tau )$ represents the RUKF-provided speed information in the landmark-detection procedure, $\tau$ indicates the recorded timestamp, and $\partial$ is the half-length of the DTW period.

BLE landmarks can also be identified when the DTW index meets a set threshold, and the absolute 3D position provided by the recognized BLE landmark is described as:

$$\delta {\mathit{z}}_p^n={\mathit{p}}_{BLE}^n-{\mathit{p}}_{{}_{INS}}^n=\delta \mathit{p}+n_{BLE}$$

(27)

where ${\mathit{p}}_{BLE}^n$ indicates the 3D position of the recognized BLE landmark; the measurement error of the detected BLE landmark is calculated as:

$$n_{BLE}\sim {\displaystyle \sum _{\tau =0}^{\partial }{\mathit{v}}_{{}_{INS}}^n(\tau )}d\tau$$

(28)

where ${\mathit{v}}_{{}_{INS}}^n(\tau )$ represents the travel speed of the inertial ranging provided within the time window applied, $\mathit{\tau }$ indicates the time epoch, and $\partial$ indicates the length-of-time window.

To improve the diversity of landmarks, the QR code is applied as a third kind of landmark point, which also provides absolute 3D location information:

$$\delta {\mathit{z}}_p^n={\mathit{p}}_{QR}^n-{\mathit{p}}_{{}_{INS}}^n=\delta \mathit{p}+n_{QR}$$

(29)

where ${\mathit{p}}_{QR}^n$ indicates the 3D positioning information of the scanned QR code; the measurement error of scanned QR code is calculated as:

$$n_{QR}\sim {\displaystyle \sum _{\tau =0}^{\partial }{\mathit{v}}_{{}_{INS}}^n(\tau )}d\tau$$

(30)

where ${\mathit{v}}_{{}_{INS}}^n(\tau )$ represents the inertial odometry-provided walking speed during the time period of camera scanning, $\tau$ indicates the time epoch, and $\partial$ indicates the recorded time period of the camera scanning.

To reduce the impact of gross errors in measurement-positioning sources, RUKF is used to achieve accurate and stable multi-source fusion based on the indoor positioning framework, as the ranging models based on Wi-Fi FTM and BLE RSSI are non-linear in the multi-source fusion process; hence, there is a need to use UKF for effective fusion, and the variance expansion parameter can effectively overcome the observed gross errors to improve the final positioning accuracy. In this context, we proposed the variance inflation parameter to adjust the weights of the measurement vectors accordingly:

$${\lambda }_{ii}=\{\begin{array}{l}1,\left|{\tilde{v}}_i\right|=\left|\frac{v_i}{{\sigma }_{v_i}}\right|\le c\\ \frac{\left|{\tilde{v}}_i\right|}{c},\left|{\tilde{v}}_i\right|>c\end{array}$$

(31)

where v_i represents the observed residuals of the corresponding location source and adaptively adjusts the weight according to the comparison ratio of the threshold c. In this case, the threshold c is set as a constant value, which is within the range 1 to 1.5 according to the real-world localization performance in corresponding indoor environments.

The other steps of proposed RUKF are as follows:

(1)

Calculate the residual of the state vector:

$$V_{{\overline{X}}_k}={\widehat{X}}_k-{\overline{X}}_k={\widehat{X}}_k-{\varphi }_{k,k-1}{\widehat{X}}_{k-1}$$

(32)

(2)

Calculate the observation residual at the current moment:

$$V_k=A_k{\widehat{X}}_k-{\mathit{L}}_k$$

(33)

(3)

Calculate the optimal state parameter that satisfies the minimum summation of the state prediction error and the observational residual error:

$${\Omega }_k=V_k^T{\overline{\mathit{P}}}_k{V}_k+{\alpha }_k{V}_{{\overline{X}}_k}^T{\overline{\mathit{P}}}_{{\overline{X}}_k}{V}_{{\overline{X}}_k}=\min$$

(34)

where ${\overline{\mathit{P}}}_k$ and ${\mathit{L}}_k$ indicate the robust equivalent weight matrix and ${\alpha }_k$ is the adaptive parameter.

(4)

Update the optimal state vector:

$$\{\begin{array}{l}{A}_k^T{\overline{\mathit{P}}}_k{V}_k+{\alpha }_k{\overline{\mathit{P}}}_{{\overline{X}}_k}{V}_{{\overline{X}}_k}=0\\ A_k^T{\overline{\mathit{P}}}_k(A_k{\widehat{X}}_k-{\mathit{L}}_k)+{\alpha }_k{\overline{\mathit{P}}}_{{\overline{X}}_k}({\widehat{X}}_k-{\overline{X}}_k)=0\\ (A_k^T{\overline{\mathit{P}}}_k{A}_k+{\alpha }_k{\overline{\mathit{P}}}_{{\overline{X}}_k}){\widehat{X}}_k=(A_k^T{\overline{\mathit{P}}}_k{\mathit{L}}_k+{\alpha }_k{\overline{\mathit{P}}}_{{\overline{X}}_k}{\overline{X}}_k)\\ {\widehat{X}}_k={(A_k^T{\overline{\mathit{P}}}_k{A}_k+{\alpha }_k{\overline{\mathit{P}}}_{{\overline{X}}_k})}^{-1}(A_k^T{\overline{\mathit{P}}}_k{\mathit{L}}_k+{\alpha }_k{\overline{\mathit{P}}}_{{\overline{X}}_k}{\overline{X}}_k)\end{array}$$

(35)

In which the related parameter ${\alpha }_k$ is adapted as:

$${\alpha }_k=\{\begin{array}{l}1,\left|\mathsf{\Delta }{\tilde{X}}_k\right|\le c\\ \frac{c}{\left|\mathsf{\Delta }{\tilde{X}}_k\right|},\left|\mathsf{\Delta }{\tilde{X}}_k\right|>c\end{array}$$

(36)

5. Experiment Results of the 3D-WBQM Algorithm

In this section, we describe a series of experiments that were designed to validate the performance of inertial odometry, landmark detection, an enhanced MLP-based trajectory evaluation framework, and the proposed 3D-WBQM algorithm. Two different indoor scenes were used as experimental sites, one containing a corridor-based scene and the other containing a 3D scene with two adjacent floors. Wi-Fi AP used Google Wi-Fi as the hardware and software platform and applied Google Pixel 1–4 to track the user; it supported Android 10-based Wi-Fi FTM and enabled real-time distance measurement between smartphones and surrounding Wi-Fi Aps. In addition, the sensors for the example accelerometer, the gyroscope, and the magnetometer were integrated. The BLE node used TI’s CC2640 chip, which supported the Bluetooth 5.0 protocol. The sampling rates of the MEMS sensors, Wi-Fi FTM, BLE, and Wi-Fi fingerprinting were 50 Hz, 5 Hz, 5 Hz, and 0.3 Hz, respectively. Under the offline phase, the crowdsourced trajectories provided by different users were evaluated and integrated together to autonomously generate the Wi-Fi fingerprinting database. Under the online phase, the real-time-collected FTM ranging results, the BLE RSSI, sensors data, and the Wi-Fi matching result were adaptively integrated in order to provide accurate and continuous positioning results under large-scale and multi-scenes contained indoor environments.

5.1. Accuracy Estimation of Inertial Odometry

The biggest problem with inertial odometry is the cumulative errors that occur when using for a long time period, especially under magnetic-interference contained indoor environments. In this work, to estimate the performance of the designed inertial odometry, an indoor scenario with a long corridor was used as the experimental scenario, as described in Figure 4. The tester began with point A, through to points B, C, D, E and F, and then returned to point A. For the long-term positioning accuracy evaluation, this walking route was repeated 12 times, and the total estimation period lasted more than 25 min. The collected magnetic environment in this scene is shown in Figure 5.

As can be seen in Figure 5, the selected experimental site contained serious magnetic interference that needed to be detected and eliminated. A comparison of the performance between the inertial odometry originated heading, the gyroscope originated heading, and the magnetic heading is shown in Figure 6.

Figure 6 shows that the magnetic heading can be seriously affected by indoor artificial interference and caused large fluctuations. The gyroscope heading showed cumulative error, with the heading error increasing over time. The odometry-provided heading maintains high accuracy and stability after long-term application and the estimated error was less than 2°.

The positioning performance of the proposed inertial odometry approach was compared with the improved step-length-based approach (ISL) proposed in [40]; to be fair, the same inertial odometry-originated heading was adopted in this case, and the final localization performance comparison is shown in Figure 7.

Figure 7 shows that the inertial odometry approach demonstrated better localization performance compared with the ISL approach; the cumulative positioning error maintained a slower divergence. The evaluated localization errors for the inertial odometry approach and ISL approach are compared in Figure 8.

Figure 8 shows that the estimated positioning error of the proposed inertial odometry method in this work provides better localization accuracy than the ISL approach, with an overall estimated positioning error during a time period of 25 min lower than 5.46 m in 75%, compared with the ISL approach with a positioning error of 9.08 m in 75%.

5.2. Accuracy Estimation of Landmark Detection and Trajectory Evaluation

This work employed three different landmark providers, including Wi-Fi FTM stations, BLE nodes, and QR codes, which could cover large-scale indoor environments containing different scenes. A DTW-based landmark-recognition approach was developed to implement a universal strategy for providing absolute location information to inertial odometry. The raw-collected RSSI or the RTT information was transferred as a ranging distance, which was modeled as the real-time distribution of the DTW algorithm, and the DTW algorithm compared the deviations of the reference distribution and the real-time distribution and found the nearest distance between the pedestrian and the landmarks. The results of the comparison between the reference and real-time distributions are shown in Figure 9 and the results of the DTW calculation are shown in Figure 10.

In addition, we conducted a comprehensive comparison of our proposed DTW approach with two different BLE- and Wi-Fi-based landmark-detection algorithms—the hybrid detection approach (HDA) [10] and critical point finding (CPF) approach [43]. The comparison results of Wi-Fi- and BLE-based landmark detection are described in Figure 11.

Figure 11 shows that the DTW-based landmark detection approach provided better recognition accuracy in the cases of both Wi-Fi- and BLE-detection. The overall detection errors for both Wi-Fi- and BLE-based landmarks were below 0.25 m in 75% and 0.52 m in 75%, respectively.

We have provided a brief summary of the three different landmark-detection approaches. The general performance comparison of three kinds of landmark-detection approaches is set out in

Table 1. Performance comparison of landmark detection approaches.

Landmarks	Accuracy	Time	Cost
Wi-Fi Station	0.25 m (75%)	Quick	High
BLE Node	0.52 m (75%)	Quick	Medium
QR Code	0.76 m (75%)	Slow	Low

.

Table 1 shows that the Wi-Fi station provided the best landmark-recognition accuracy due to the precise observation of Wi-Fi FTM. The BLE node had higher detection accuracy than the QR code-based method, and both Wi-Fi and BLE were more costly when deploying landmark points. The QR landmark-detection accuracy was estimated by calculating the distance between the positions of different people, scanning the QR codes and the real locations of the QR codes based on the statistical results collected from 105 different users. In addition, other factors would also affect the performance of landmark detection, such as the channel and the coherence time of the used bands and the signal-processing mode of equipment manufacturers. In this case, we also tested the Wi-Fi APs with 5 GHz and 2.4 GHz bandwidths, respectively, and the DTW matching algorithm was applied to realize landmark detection by using a period of collected data instead of instantaneous data, which would have decreased the effects of hardware difference; more effects of the channel and the coherence time of the used bands could be further explored to improve the landmark-detection algorithm.

In this work, the crowdsourced trajectories were autonomously evaluated by an enhanced trained MLP error-prediction structure. During the training phase, the data were collected from different indoor environments, inluding the office scene, the corridor scene, and the shopping mall scene. A total of 105 trajectories collected from different scenes were adopted as the training dataset, and after the training phase, the trained error-prediction model was applied to evaluate the localization error of each step period on the same trajectory. The final estimated accuracy of the error-prediction model was compared with the raw MLP model proposed in [8] on the same testing dataset, as described in Figure 12.

As can be seen in Figure 12, the enhanced MLP model provided better trajectory error-prediction performance, reaching 0.65 m in 75%. The overall trajectory error larger than the set threshold was not considered in the procedure of the final crowdsourced navigation database generation. To evaluate the accuracy of Wi-Fi fingerprinting based on the generated navigation database, the basic k-nearest-neighbors algorithm (KNN) and the support vector machine (SVM) were applied for Wi-Fi fingerprinting classification. In this case, we also compared the performance of two kinds of navigation database: the proposed MLP-enhanced database (CED) and quality-evaluation-aimed database (QED) [9]. A comparison of the final localization accuracy using KNN and SVM is shown in Figure 13.

Figure 13 shows that the proposed MLP-based database construction algorithm effectively improved the robustness of final generated database and obtained much better positioning performance than other algorithms; the estimated positioning error was within 5.22 m in 75% using different database matching algorithms.

5.3. Experiment Results of the 3D-WBQM Algorithm

In this section, two adjacent floors containing the open area and corridor area were adopted as the second experimental scenario, which is described in Figure 14. Three Wi-Fi APs were deployed at the gates and the elevator entrance of the fourth floor and the BLE nodes were deployed at the corridor scene; points L, O, R, W, Z, and the QR codes were deployed at gate points K and P. The crowdsourced trajectories were collected during a period of two days and an overall number of 46 trajectories provided by the different pedestrians were selected and generated as the final crowdsourced navigation database. For the accuracy evaluation of the 3D-WBQM framework, a cross-floor experiment was conducted; the tester began with point A, proceeded across point B–Z, and finally returned to point A. The specific route was A, B, C, D, E, F, G, A, D, E, H, I, F, G, J, K, L, M, N, O, N, M, L, K, P, Q, W, X, Y, Z, Y, X, W, Q, R, S, V, U, T, S, R, Q, P, F, G, A. The estimated 2D and 3D trajectories calculated by the inertial odometry- (IO) and RUKF-based multi-source fusion frameworks using the different combinations of location sources are shown in Figure 15a,b.

Figure 15 indicates that that there was a cumulative error in inertial ranging as usage time grew, especially when the pedestrians walked across floors. The proposed 3D-WBQM framework significantly reduced the cumulative errors in inertial odometry by fusing multi-source information using a universal fusion approach. A comparison of the CDF errors between the two methods is shown in Figure 16.

Figure 16 describes the significant improvement of 3D indoor-localization performances using the 3D-WBQM framework compared with a single inertial odometry approach. The overall estimated localization error was within 4.4 m in 75%, using the integration of IO, BLE, and QR; the overall estimated localization error was less than 3.55 m in 75% using the combination of IO, BLE, and QR and crowdsourced Wi-Fi fingerprinting; the overall estimated positioning error as within 1.66 m in 75% using the combination of IO, BLE, and QR, crowdsourced Wi-Fi fingerprinting, and Wi-Fi FTM, especially in the Wi-Fi FTM-supported indoor area, where the localization accuracy reached 1.08 m in 75%.

Finally, we performed a comprehensive comparison between the proposed 3D-WBQM framework and the state-of-the-art WFS-F solution [44], which contained hybrid fingerprinting of Wi-Fi FTM and RSSI. To be fair, the same constructed crowdsourced database was adopted, and the FTM database was generated using the same crowdsourced trajectories data. In addition, the same test routes were applied to the positioning-accuracy estimation. The result of the comparison of the two algorithms is shown in Figure 17.

It can be seen in Figure 17 that the presented 3D-WBQM structure achieved higher positioning precision than the WFS-F approach, with the overall positioning accuracy of the two algorithms reaching 1.66 m in 75% and 2.33 m in 75%, respectively. Therefore, the proposed 3D-WBQM framework realized an autonomous and highly adaptive 3D indoor-localization performance than those of other localization approaches, providing a comprehensive solution for large-scale indoor localization.

Furthermore, there are some other factors that affect the performance of the overall 3D-WBQM framework. First, the number of extracted features and the trained trajectories led to different performances of the final error-prediction model. The minimum amount of trajectories applied needed to fulfil the requirement of model convergence; the specific quantity depends on the structure of the deep-learning model and the training method under comprehensive experiments. In addition, the landmark-detection algorithm can provide reference locations for human motion; the farther the pedestrian is from landmarks, the worse the detection performance. Thus, in the range where the RSSI attenuation is small, normally not exceeding the effective distance of 1~3 m, the landmark-detection algorithm can maintain accuracy and the DTW matching method can also be applied to decrease the effects of the differences in indoor scenes.

6. Conclusions

To improve localization ability for large-scale indoor spaces, this paper proposed the 3D-WBQM framework, which mainly consists of four main sections:

(1)

MEMS sensor-based inertial odometry, which contains the multi-level observations and trajectory optimization modules;

(2)

MLP-based crowdsourced trajectories evaluation strategy, which can autonomously predict the error of each collected trajectory and improve the robustness of the final generated navigation database;

(3)

Three different kinds of landmark points and the DTW-based universal landmark-detection algorithm, which provide accurate absolute locations for the MEMS sensor-based approach; and

(4)

Multi-source fusion-based localization using RUKF.

A universal model was proposed that adaptively integrates the different location sources and adjusts the weight of each location source in real time.

The experimental results demonstrated that the presented 3D-WBQM framework is capable of achieving autonomous and highly adaptive 3D indoor-positioning accuracy for large-scale indoor areas, with a final evaluated positioning error lower than 1.66 m in 75% in complex and multi-floor contained indoor environments, and a final meter-level positioning accuracy in indoor areas supported by Wi-Fi FTM.

The advantages of the proposed 3D-WBQM framework are that daily-life trajectories are autonomously evaluated and integrated for crowdsourced Wi-Fi fingerprinting database generation using three different kinds of landmarks. In addition, the proposed multi-level-observation-assisted inertial odometry can maintain high precision after long-term use under magnetic interference in a contained large-scale indoor environment.

The proposed 3D-WBQM framework also has some disadvantages. First, the accuracy of crowdsourced trajectories is limited by the navigation time and by complex and changeable indoor scenes, and the positioning errors grow with time. Second, the performance of MLP-based positioning error evaluations can be further improved by considering and extracting more human motion and handheld-related features for a more intelligent fusion and construction of a crowdsourced navigation database.

In the future, with the development of the Internet of Things and artificial intelligence, mobile terminals will support more of the emerging positioning and perception technologies such as light fidelity, light detection and ranging (Lidar), and RIS-assisted mmWave networks, which will provide a more robust and accurate performance of indoor positioning, mapping, perception, and communication.