A Proposal for Modification of Plasmaspheric Electron Density Profiles Using Characteristics of Lightning Whistlers
Abstract
:1. Introduction
2. Fundamental Method
2.1. Ray Tracing
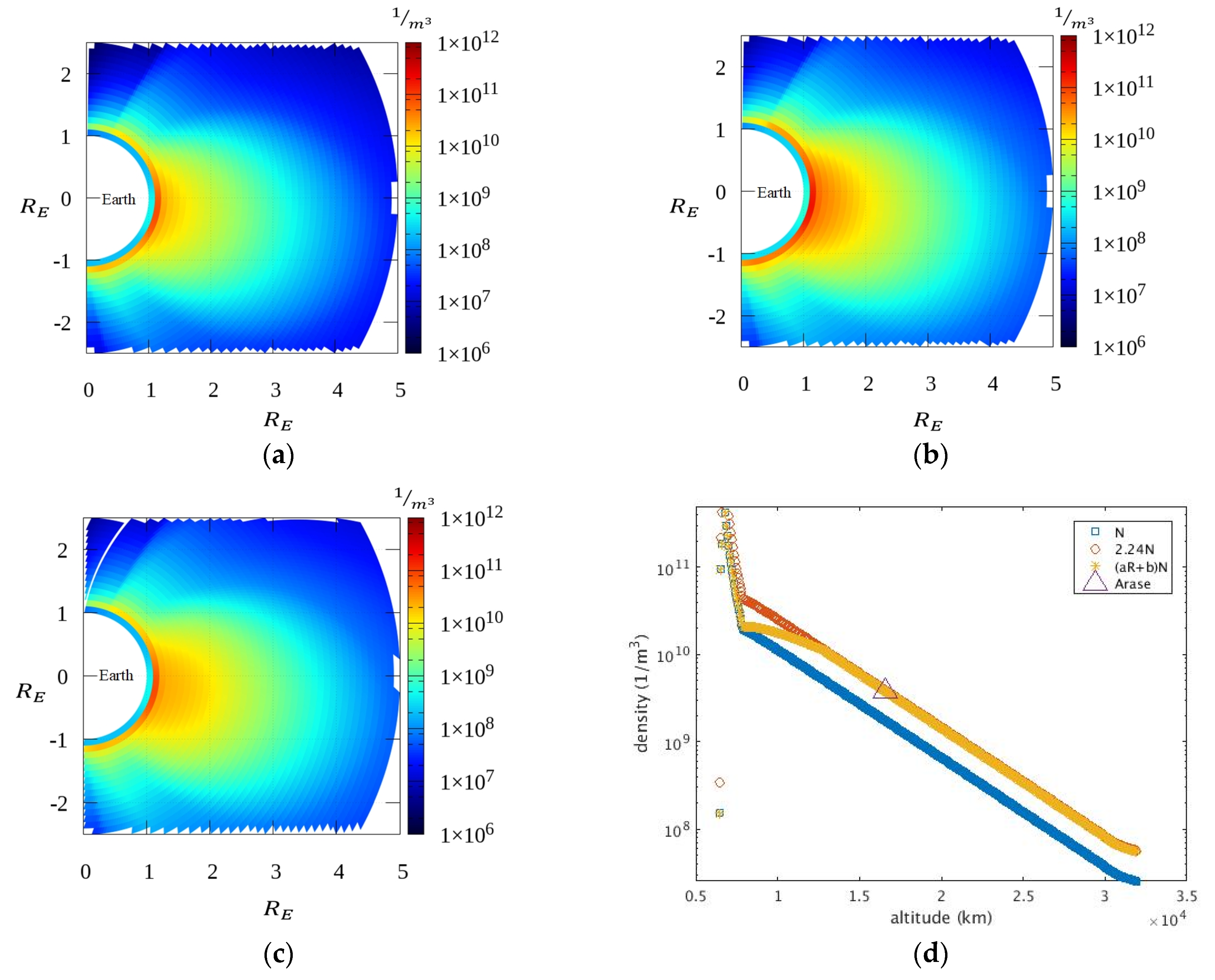
2.2. Magnetic Field and Electron Density Model
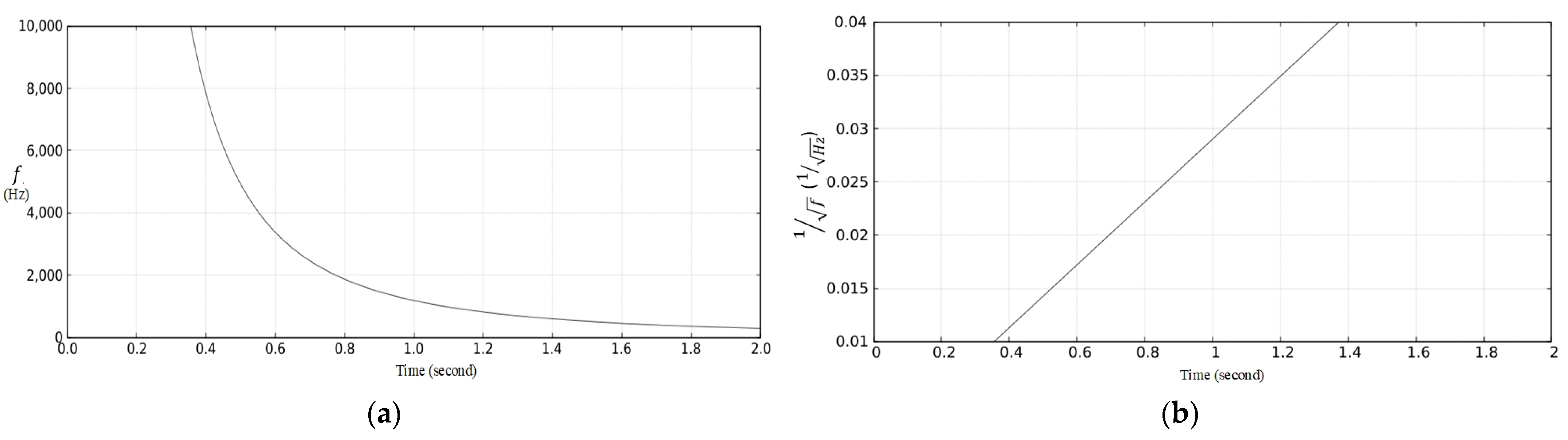
2.3. Dispersion of Lightning Whistlers
3. Proposed Method
3.1. Calculation Techniques
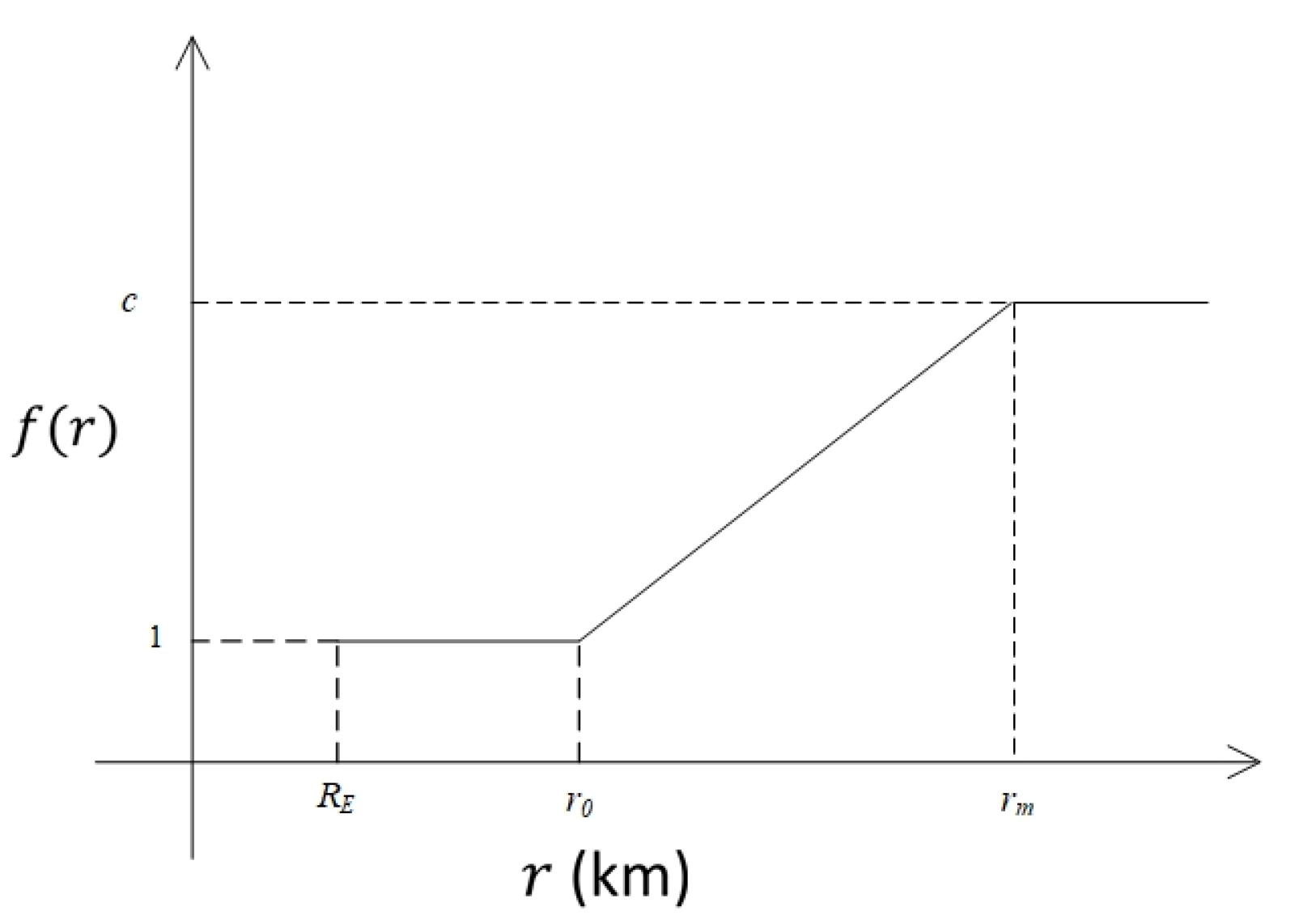
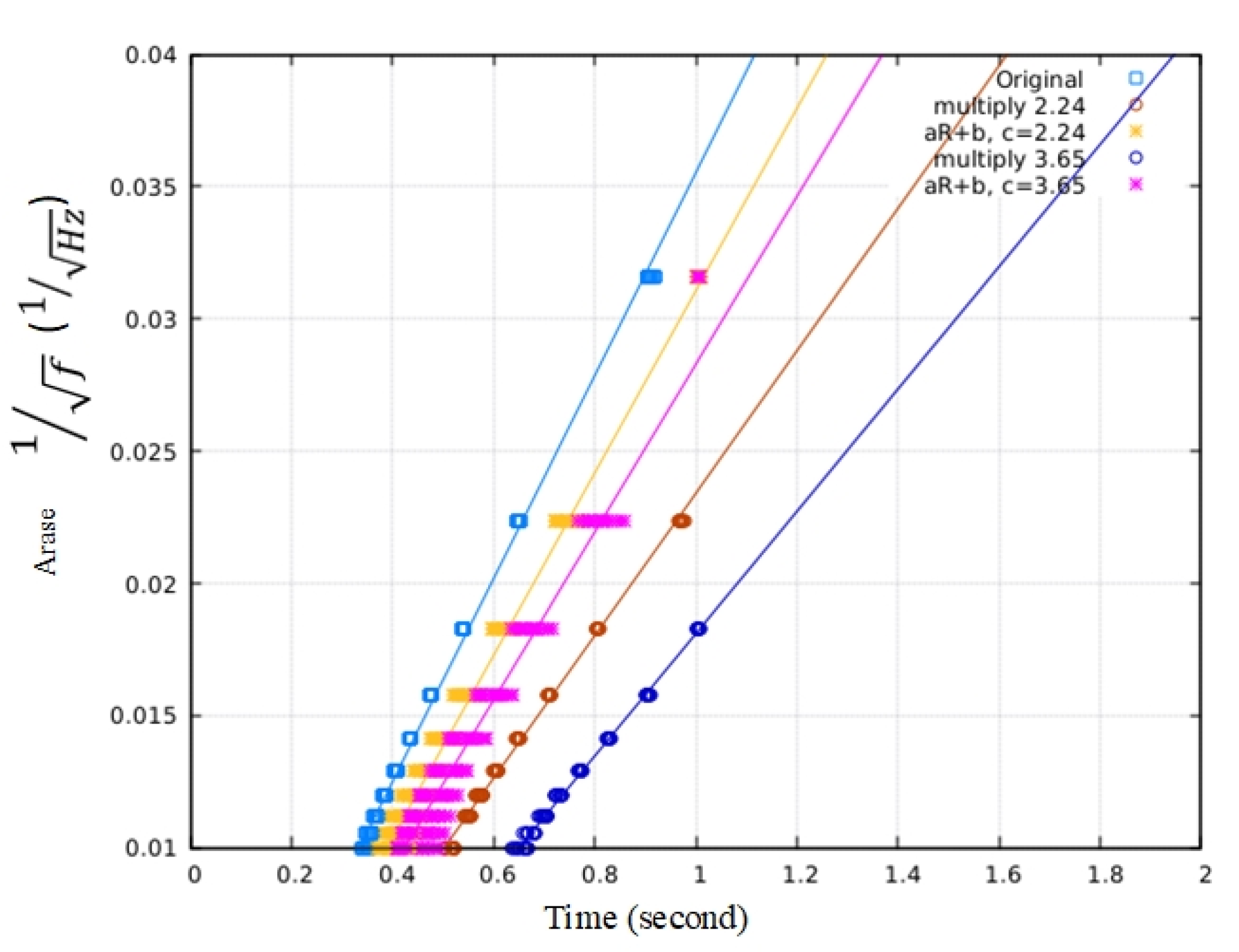
3.2. Proposed Modification Function
4. Implementation
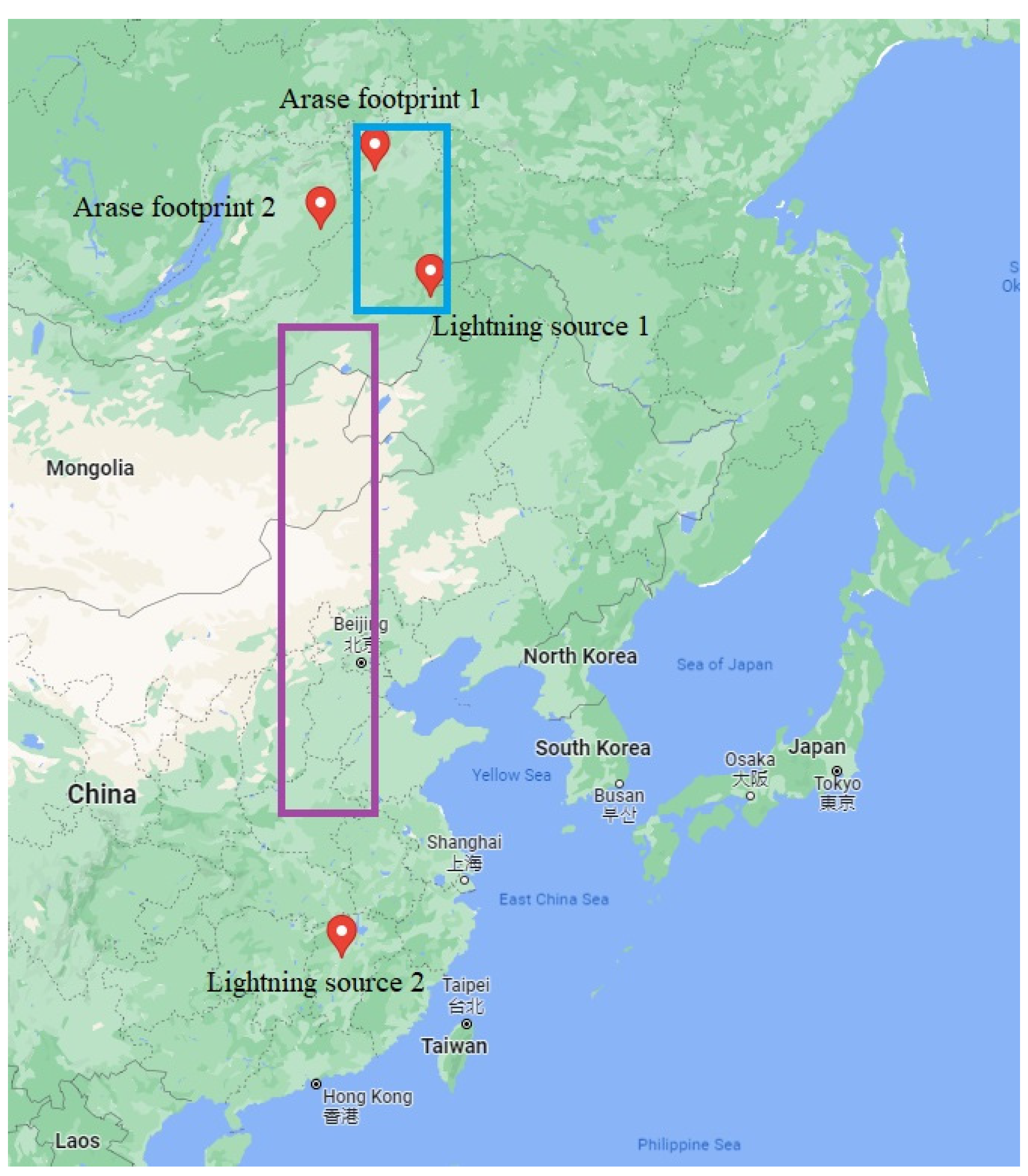
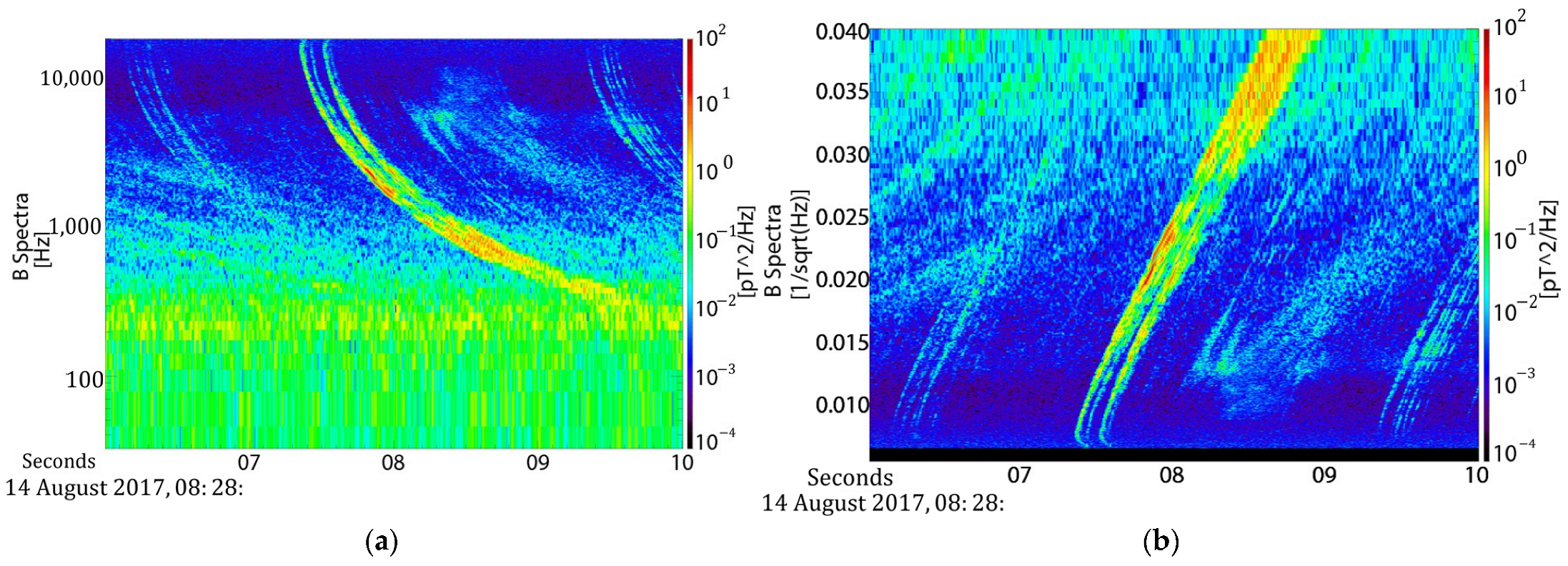
4.1. Observed Lightning Whistler
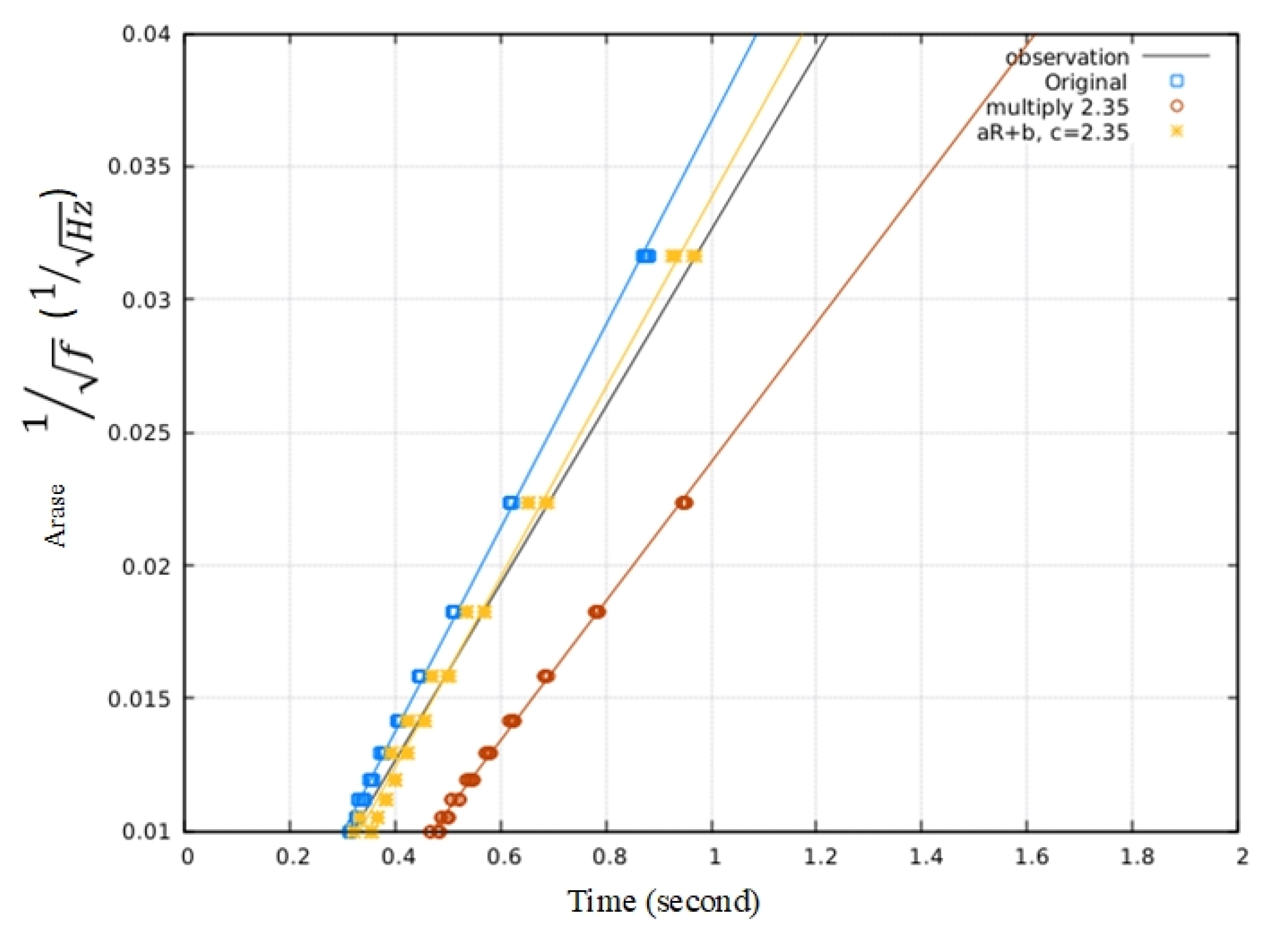
4.2. Result 1
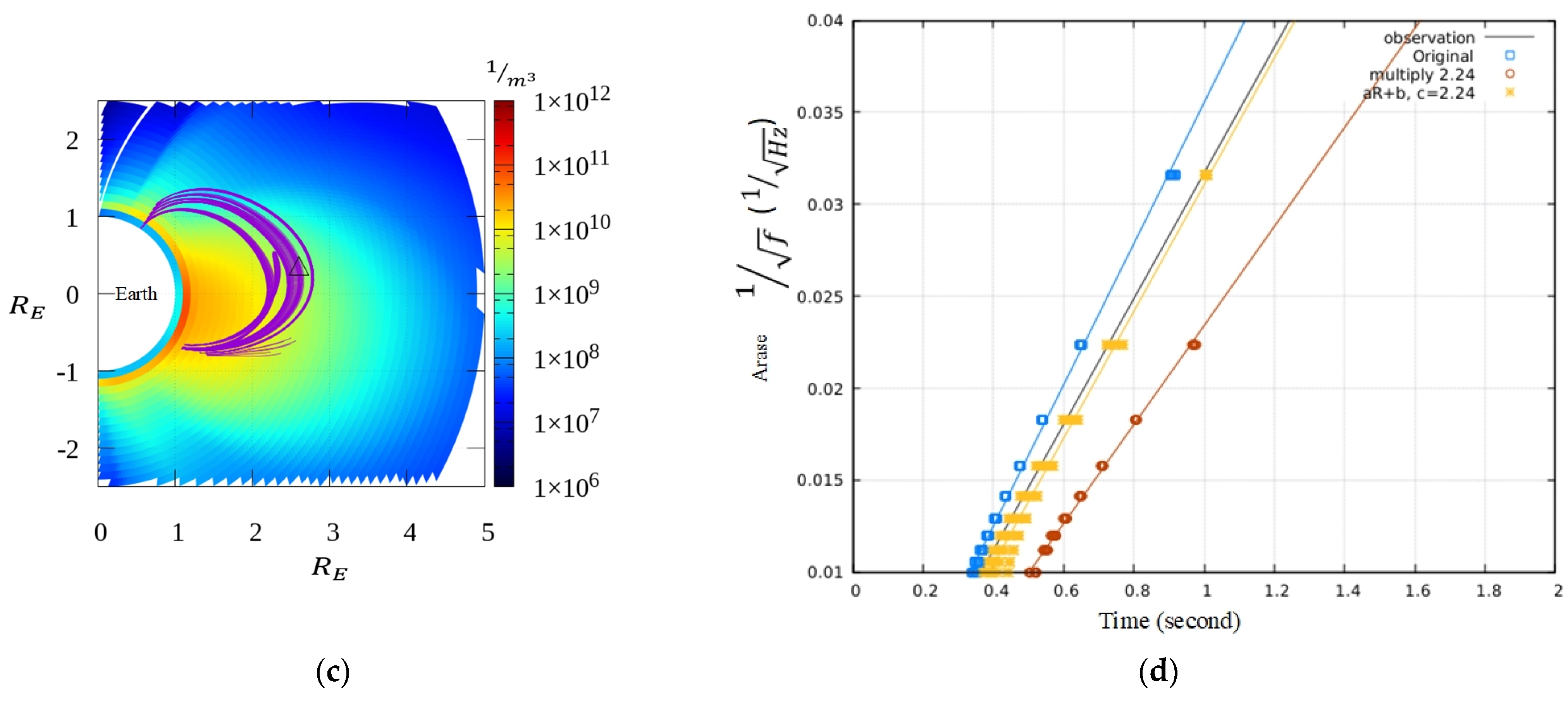
4.3. Result 2
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VLF | Very Low Frequency |
| TEC | Total Electron Content |
| GCPM | Global Core Plasma Model |
| IRI | International Reference Ionosphere |
| IGRF | International Geomagnetic Reference Filed |
References
- Forster, M.; Jakowski, N. The Nighttime Winter Anomaly (NWA) Effect in the American Sector as a Consequence of Interhemispheric Ionospheric Coupling. Pure Appl. Geophys. 1988, 127, Nos 2/3. [Google Scholar] [CrossRef]
- Chapman, J.; Warren, E.S. Topside Sounding of the Erath’s Ionosphere. Space Sci. Rev. 1968, 8, 846–865. [Google Scholar] [CrossRef]
- Otsuka, Y.; Ogawa, T.; Saito, A.; Tsugawa, T.; Fukao, S.; Miyazaki, S. A new technique for mapping of total electron content using GPS network in Japan. Earth Planets Space 2002, 54, 63–70. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geodesy 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Kurth, W.S.; De Pascuale, S.; Faden, J.B.; Kletzing, C.A.; Hospodarsky, G.B.; Thaller, S.; Wygant, J.R. Electron densities inferred from plasma wave spectra obtained by the Waves instrument on Van Allen Probes. J. Geophys. Res. Space Phys. 2015, 120, 904–914. [Google Scholar] [CrossRef] [Green Version]
- Reinisch, B.; Haines, D.; Bibl, K.; Cheney, G.; Galkin, I.; Huang, X.; Myers, S.; Sales, G.; Benson, R.; Fung, S.; et al. The Radio Plasma Imager investigation on the IMAGE spacecraft. Space Sci. Rev. 2000, 91, 319–359. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Huang, X.; Song, P.; Sales, G.S.; Fung, S.F.; Green, J.L.; Gallagher, D.L.; Vasyliunas, V.M. Plasma density distribution along the magnetospheric field: RPI observations from IMAGE. Geophys. Res. Lett. 2001, 28, 4521–4524. [Google Scholar] [CrossRef]
- Reiff, P.H.; Boyle, C.B.; Green, J.L.; Fung, S.F.; Benson, R.F.; Calvert, W.; Taylor, W.W. Radio Sounding of Multiscale Plasmas. Phys. Space Plasmas 1996, 14, 415–429. [Google Scholar]
- Goto, Y.; Kasahara, Y.; Sato, T. Determination of plasmapheric electron density profile by a stochastic approach. Radio Sci. 2003, 38, 1060. [Google Scholar] [CrossRef]
- Carpenter, D.L.T. Remote Sensing the Magnetospheric Plasma by Means of Whistler Mode Signals. Rev. Geophys. 1988, 263, 535–549. [Google Scholar] [CrossRef]
- Storey, L.R. An Investigations of Whistling Atmospherics. Phil. Trans. Roy. Soc. 1953, 246, 113–141. [Google Scholar]
- Oike, Y.; Kasahara, Y.; Goto, Y. Spatial distribution and temporal variations of occurrence frequency of lightning whistlers observed by VLF/WBA onboard Akebono. Radio Sci. 2014, 49, 753–764. [Google Scholar] [CrossRef]
- Ahmad, U.A.; Kasahara, Y.; Matsuda, S.; Ozaki, M.; Goto, Y. Automatic Detection of Lightning Whistlers Observed by the Plasma Wave Experiment Onboard the Arase Satellite Using the OpenCV Library. Remote Sens. 2019, 11, 1785. [Google Scholar] [CrossRef] [Green Version]
- Bayupati, I.P.; Kasahara, Y.; Goto, Y. Study of Dispersion of Lightning Whistler observed by Akebono Satellite in the Earth’s Plasmasphere. IEICE Trans. Commun 2012, E95–B, 3472–3479. [Google Scholar] [CrossRef] [Green Version]
- Santolík, O.; Miyoshi, Y.; Kolmašová, I.; Matsuda, S.; Hospodarsky, G.B.; Hartley, D.P.; Kasahara, Y.; Kojima, H.; Matsuoka, A.; Shinohara, I.; et al. Inter-Calibrated Measurements of Intense Whistlers by Arase and Van Allen Probes. J. Geophys. Res. Space Phys. 2021, 126, JA029700. [Google Scholar] [CrossRef]
- Haselgrove, C.B.; Haselgrove, J. Twisted Ray Paths in the Ionosphere. Proc. Phys. Soc. 1960, 75, 357–363. [Google Scholar] [CrossRef]
- Hines, C. Heavy-ion effects in audio-frequency radio propagation. J. Atmospheric Terr. Phys. 1957, 11, 36–42. [Google Scholar] [CrossRef]
- Thébault, E.; Finlay, C.C.; Beggan, C.D.; Alken, P. International Geomagnetic Reference Field: The 12th Generation. Earth Planets Space 2015, 67, 79. [Google Scholar] [CrossRef] [Green Version]
- Tsyganenko, N.A.; Sitnov, M.I. Modeling the dynamics of the inner magnetosphere during strong geomagnetic storms. J. Geophys. Res. 2005, 110, A03208. [Google Scholar] [CrossRef]
- Ray Tracing. Available online: http://waves.is.t.kanazawa-u.ac.jp/ (accessed on 1 June 2022).
- Gallagher, D.L.; Craven, P.D.; Comfort, R.H. Global core plasma model. J. Geophys. Res. Atmos. 2000, 105, 18819–18833. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather. 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Gurnett, D.A.; Kurth, W.S.; Cairns, I.H.; Granroth, L.J. Whistler in Neptune’s Magnetosphere: Evidence of Atmospheric Lightning. J. Geophys. Res. 1990, 95, 20967–20976.300. [Google Scholar] [CrossRef]
- Jacobson, A.R.; Holzworth, R.; Harlin, J.; Dowden, R.; Lay, E. Performance Assessment of the World Wide Lightning Location Network (WWLLN), Using the Los Alamos Sferic Array (LASA) as Ground Truth. J. Atmospheric Ocean. Technol. 2006, 23, 1082–1092. [Google Scholar] [CrossRef]
- Matsuda, S.; Kasahara, Y.; Kojima, H.; Kasaba, Y.; Yagitani, S.; Ozaki, M.; Imachi, T.; Ishisaka, K.; Kumamoto, A.; Tsuchiya, F.; et al. Onboard software of Plasma Wave Experiment aboard Arase: Instrument management and signal processing of Waveform Capture/Onboard Frequency Analyzer. Earth Planets Space 2018, 70, 75. [Google Scholar] [CrossRef]
- Kasahara, Y.; Kasaba, Y.; Kojima, H.; Yagitani, S.; Ishisaka, K.; Kumamoto, A.; Tsuchiya, F.; Ozaki, M.; Matsuda, S.; Imachi, T.; et al. The Plasma Wave Experiment (PWE) on board the Arase (ERG) satellite. Earth Planets Space 2018, 70, 86. [Google Scholar] [CrossRef] [Green Version]
- Miyoshi, Y.; Shinohara, I.; Takashima, T.; Asamura, K.; Higashio, N.; Mitani, T.; Kasahara, S.; Yokota, S.; Kazama, Y.; Wang, S.-Y.; et al. Geospace exploration project ERG. Earth Planets Space 2018, 70, 101. [Google Scholar] [CrossRef] [Green Version]
- Kasahara, Y.; Kojima, H.; Matsuda, S.; Ozaki, M.; Yagitani, S.; Shoji, M.; Nakamura, S.; Kitahara, M.; Miyoshi, Y.; Shinohara, I. The PWE/WFC instrument Level-2 magnetic field spectrum data of Exploration of energization and Radiation in Geospace (ERG) Arase satellite. Inst. Space-Earth Environ. Res. Nagoya Univ. 2020, 70, 101. [Google Scholar] [CrossRef]
- Nasa. Goddard Space Flight Center. Available online: https://sscweb.gsfc.nasa.gov/ (accessed on 1 June 2022).
- Jones, D. Schumann Resonances and e.l.f. propagation for inhomogeneous, isotropic ionosphere profiles. J. Atmospheric Terr. Phys. 1967, 29, 1037–1044. [Google Scholar] [CrossRef]
- Kumamoto, A.; Tsuchiya, F.; Kasahara, Y.; Kasaba, Y.; Kojima, H.; Yagitani, S.; Ishisaka, K.; Imachi, T.; Ozaki, M.; Matsuda, S.; et al. High Frequency Analyzer (HFA) of Plasma Wave Experiment (PWE) onboard the Arase spacecraft. Earth Planets Space 2018, 70, 82. [Google Scholar] [CrossRef] [Green Version]
- Kasahara, Y.; Kumamoto, A.; Tsuchiya, F.; Kojima, H.; Matsuda, S.; Matsuoka, A.; Teramoto, M.; Shoji, M.; Nakamura, S.; Kitahara, M.; et al. The PWE/HFA Instrument Level-3 Electron Density Data of Exploration of energization and Radiation in Geospace (ERG) Arase satellite. ERG Sci. Cent. 2021. [Google Scholar] [CrossRef]
- Matsuoka, A.; Teramoto, M.; Nomura, R.; Nosé, M.; Fujimoto, A.; Tanaka, Y.; Shinohara, M.; Nagatsuma, T.; Shiokawa, K.; Obana, Y.; et al. The ARASE (ERG) magnetic field investigation. Earth Planets Space 2018, 70, 43. [Google Scholar] [CrossRef] [Green Version]
- Miyoshi, Y.; Hori, T.; Shoji, M.; Teramoto, M.; Chang, T.F.; Segawa, T.; Umemura, N.; Matsuda, S.; Kurita, S.; Keika, K.; et al. The ERG Science Center. Earth Planets Space 2018, 70, 96. [Google Scholar] [CrossRef]




| Frequency(kHz) | |
| Altitude | |
| Longitude (degree) | |
| Latitude (degree) | |
| vector (degree) | |
| Frequency (kHz) | |
| Altitude R | |
| Longitude (degree) | |
| Latitude (degree) | |
| vector (degree) | |
| Parameter | |||||
|---|---|---|---|---|---|
| Event 1 | |||||
| Event 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Putri, D.P.S.; Kasahara, Y.; Ota, M.; Matsuda, S.; Tsuchiya, F.; Kumamoto, A.; Matsuoka, A.; Miyoshi, Y. A Proposal for Modification of Plasmaspheric Electron Density Profiles Using Characteristics of Lightning Whistlers. Remote Sens. 2023, 15, 1306. https://doi.org/10.3390/rs15051306
Putri DPS, Kasahara Y, Ota M, Matsuda S, Tsuchiya F, Kumamoto A, Matsuoka A, Miyoshi Y. A Proposal for Modification of Plasmaspheric Electron Density Profiles Using Characteristics of Lightning Whistlers. Remote Sensing. 2023; 15(5):1306. https://doi.org/10.3390/rs15051306
Chicago/Turabian StylePutri, Desy Purnami Singgih, Yoshiya Kasahara, Mamoru Ota, Shoya Matsuda, Fuminori Tsuchiya, Atsushi Kumamoto, Ayako Matsuoka, and Yoshizumi Miyoshi. 2023. "A Proposal for Modification of Plasmaspheric Electron Density Profiles Using Characteristics of Lightning Whistlers" Remote Sensing 15, no. 5: 1306. https://doi.org/10.3390/rs15051306
APA StylePutri, D. P. S., Kasahara, Y., Ota, M., Matsuda, S., Tsuchiya, F., Kumamoto, A., Matsuoka, A., & Miyoshi, Y. (2023). A Proposal for Modification of Plasmaspheric Electron Density Profiles Using Characteristics of Lightning Whistlers. Remote Sensing, 15(5), 1306. https://doi.org/10.3390/rs15051306






