Monitoring Structural Displacements on a Wall with Five-Constellation Precise Point Positioning: A Position-Constrained Method and the Performance Analyses
Abstract
:1. Introduction
2. Methodology
2.1. Classical PPP Model
2.2. PCPPP Model
2.3. Kalman Filter
2.4. Velocity Estimation for Structural Long-Term Displacements
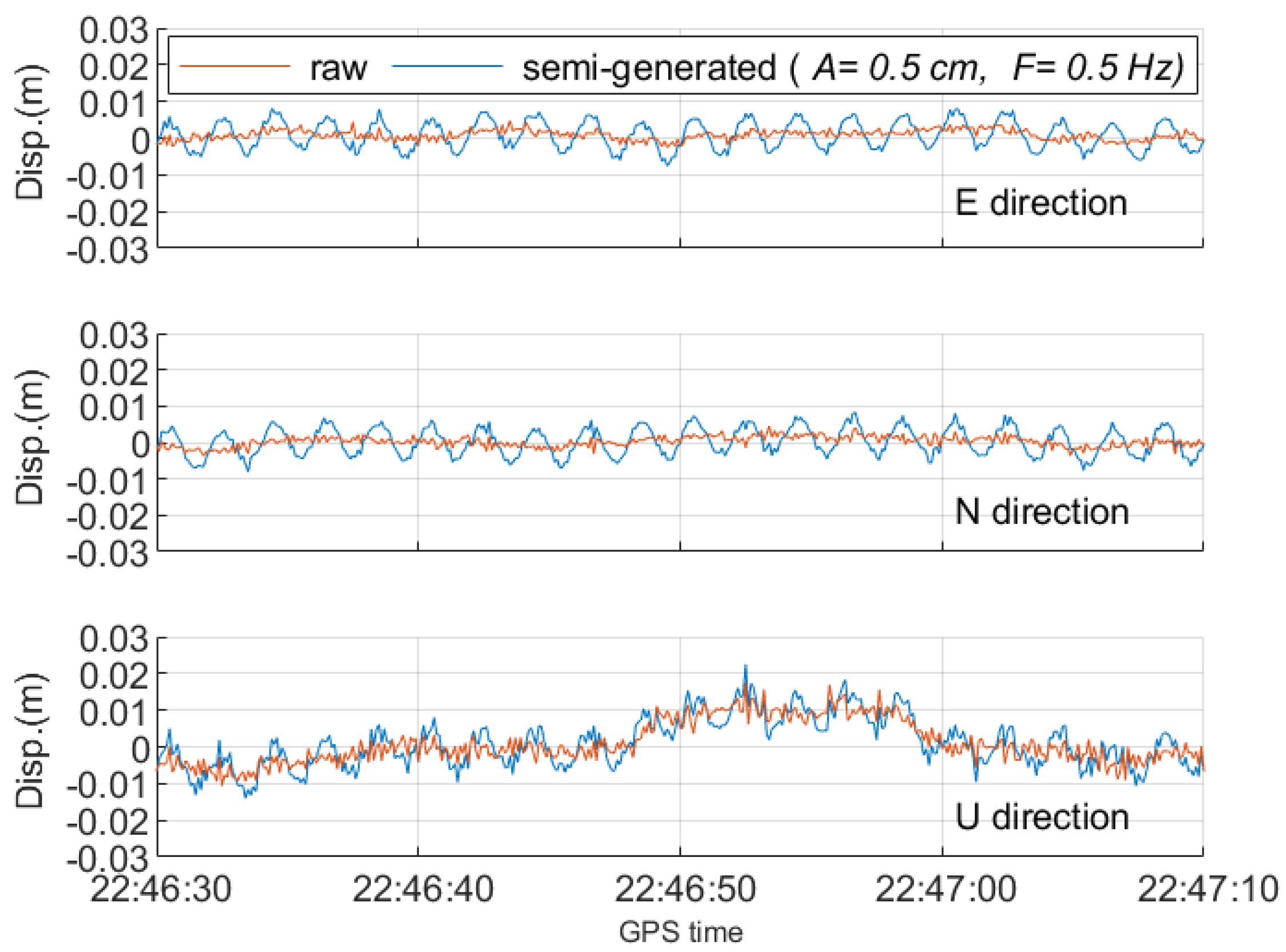
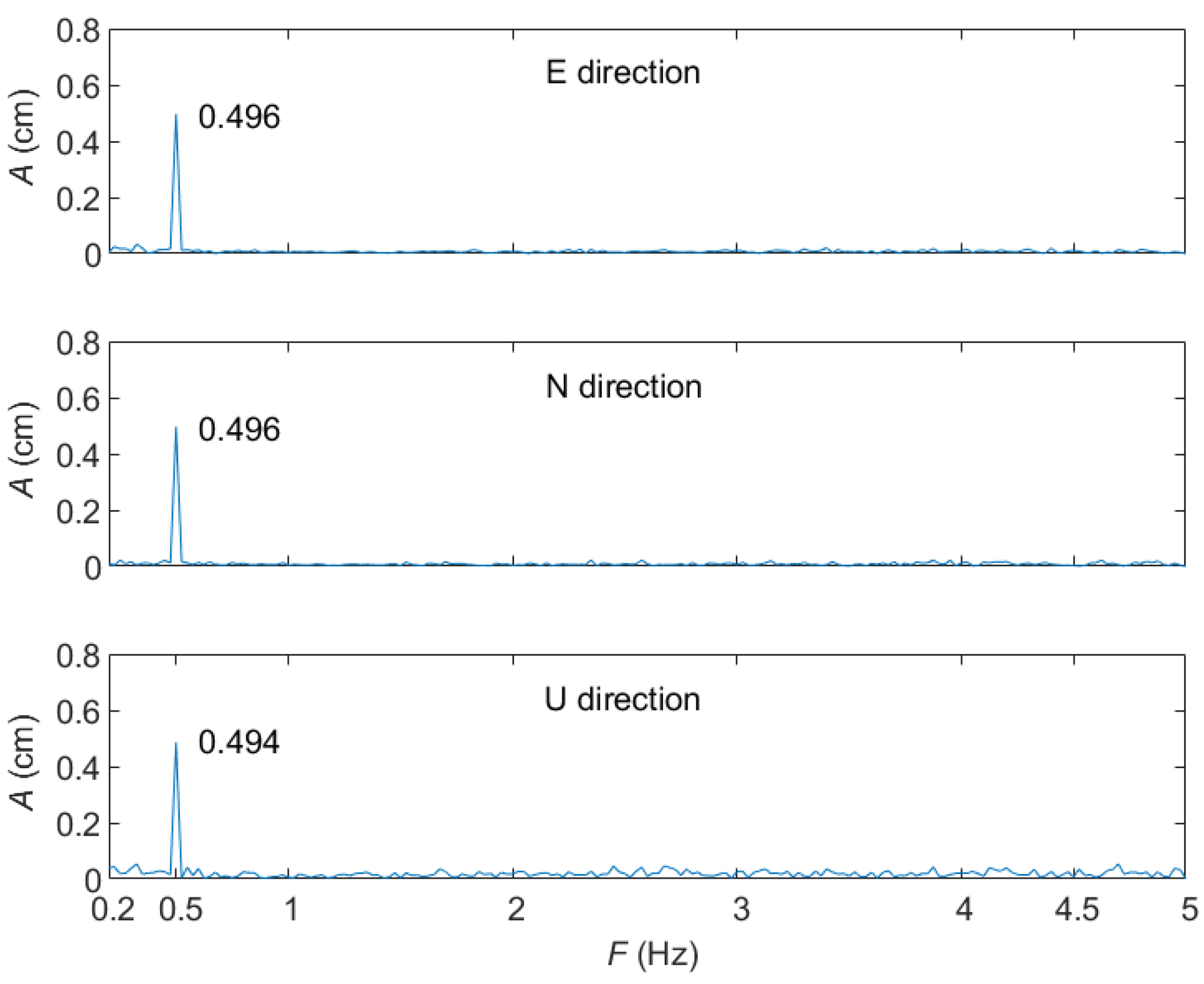
2.5. Semi-Generated GNSS Measurements
3. Monitoring SLDW
3.1. Velocity of Station NCCU
3.2. Performance Analysis
4. Monitoring SVDW
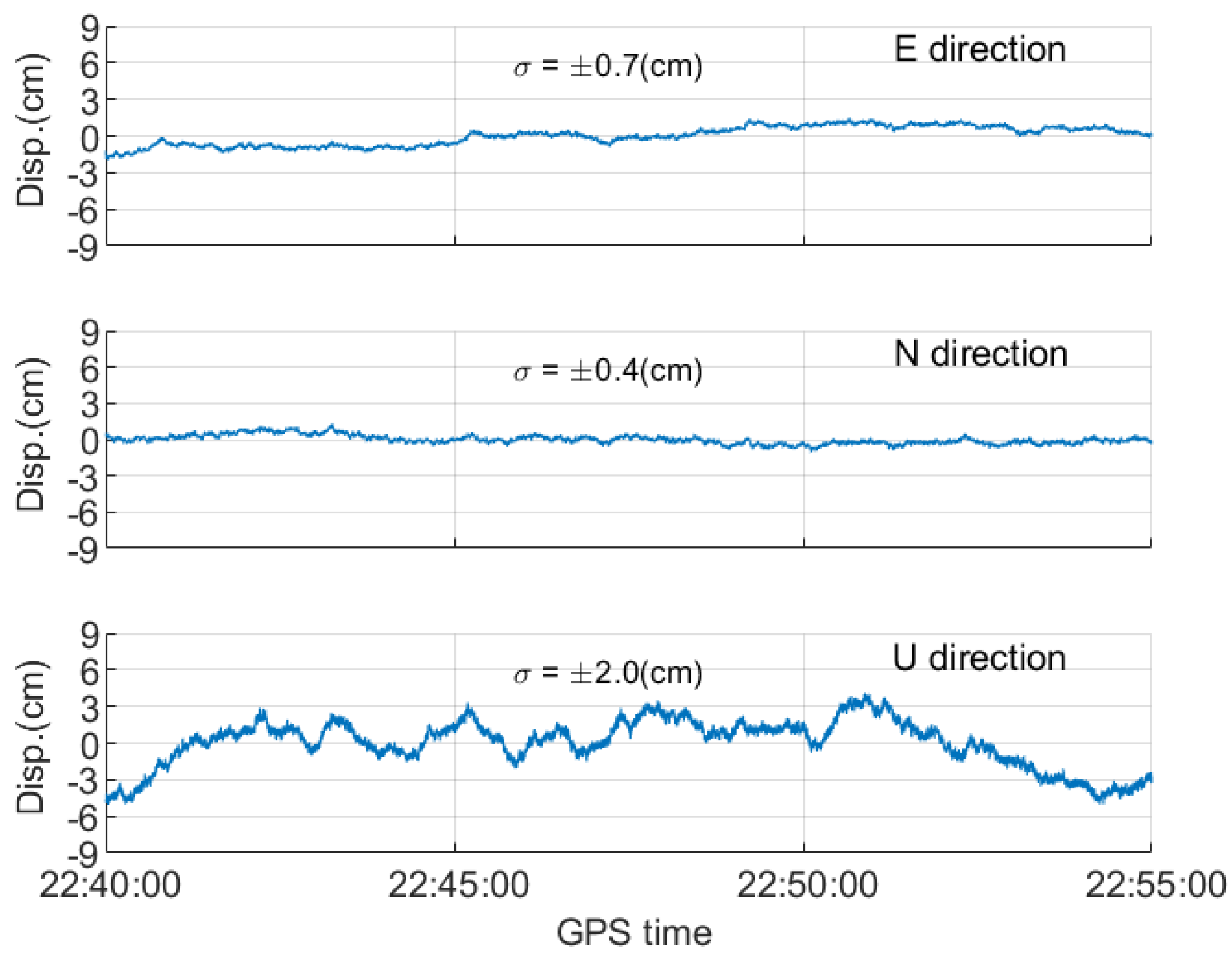
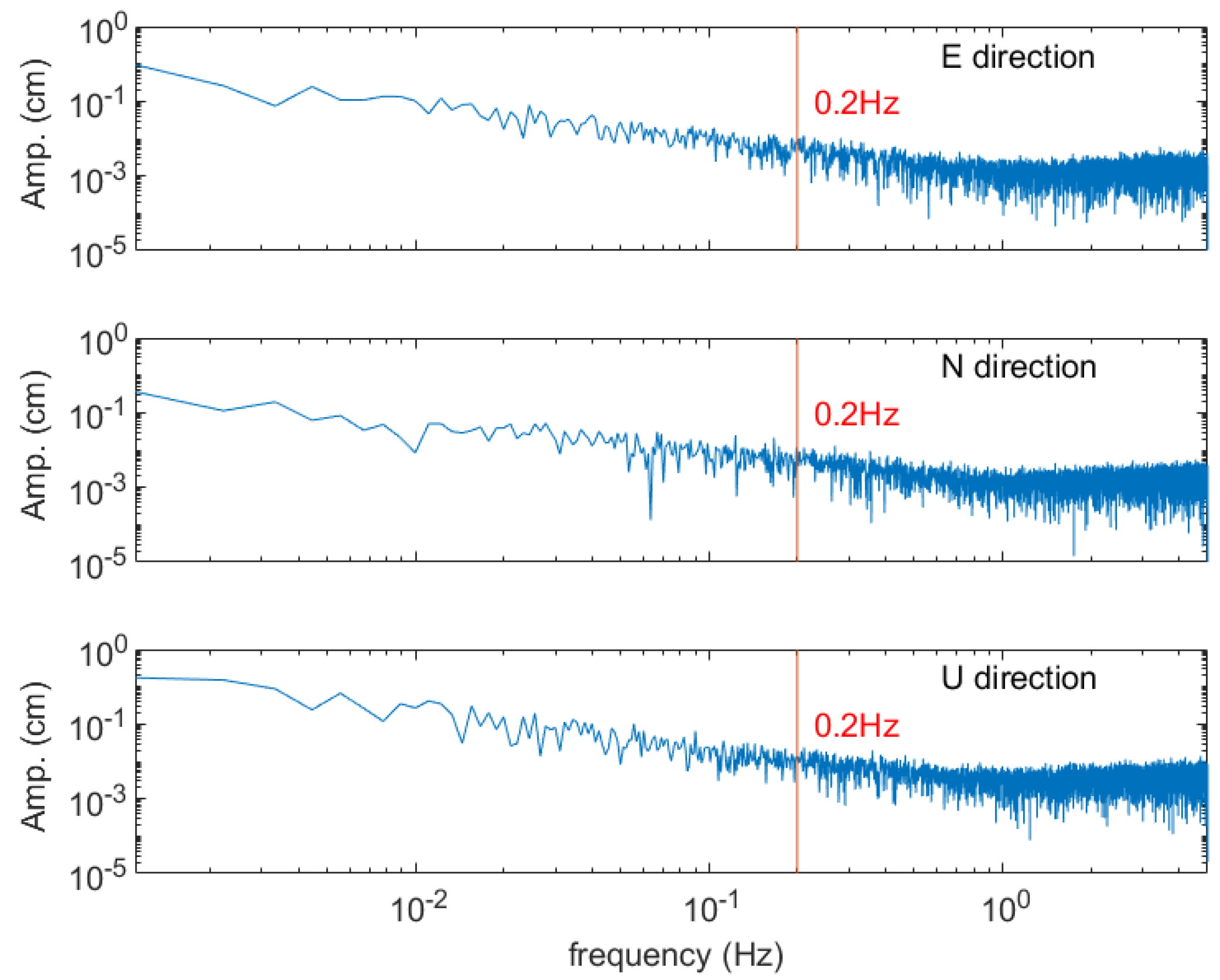
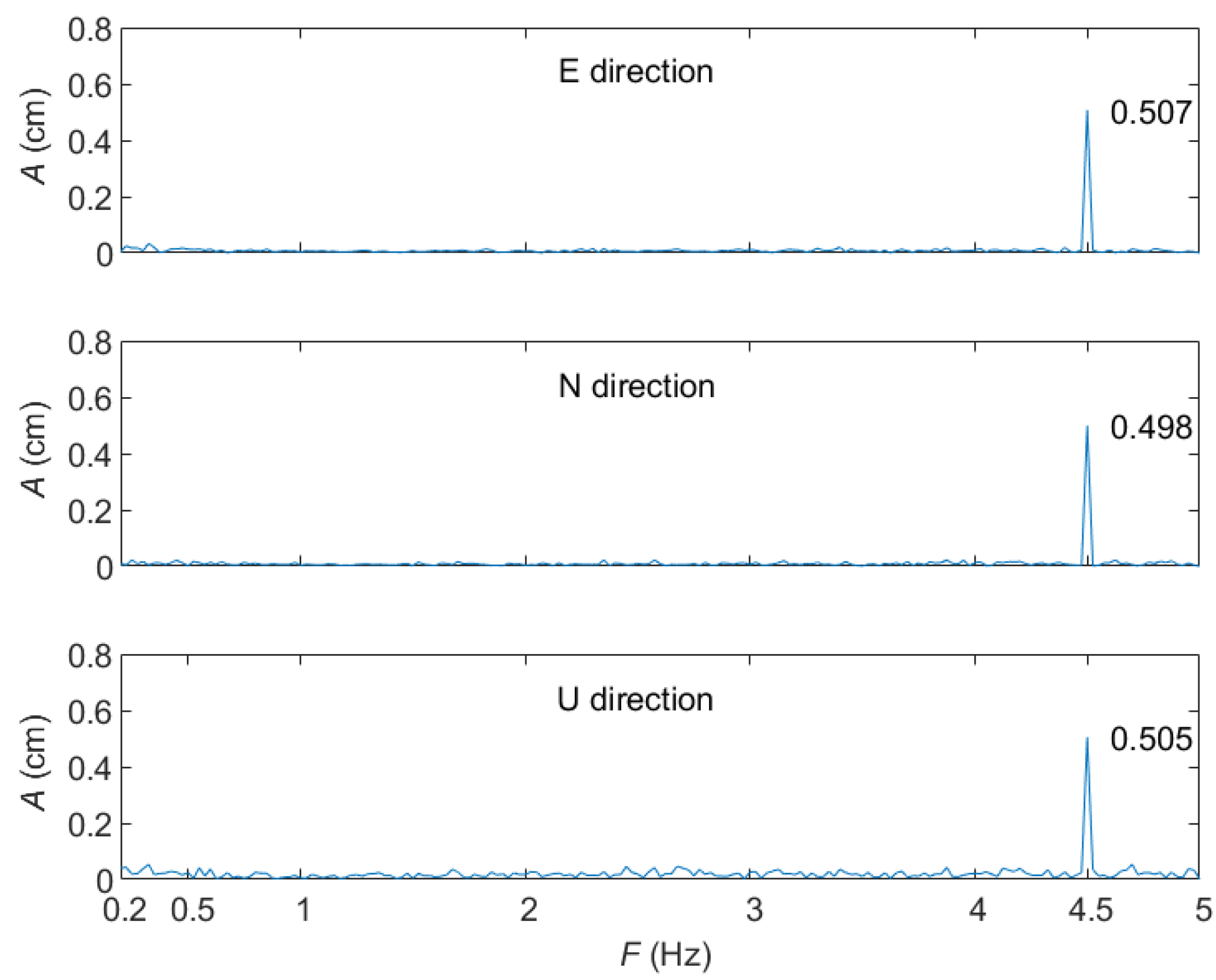
4.1. Vibrational Displacements of Station NCCU
4.2. Verifying the Semi-Generated GNSS Measurements
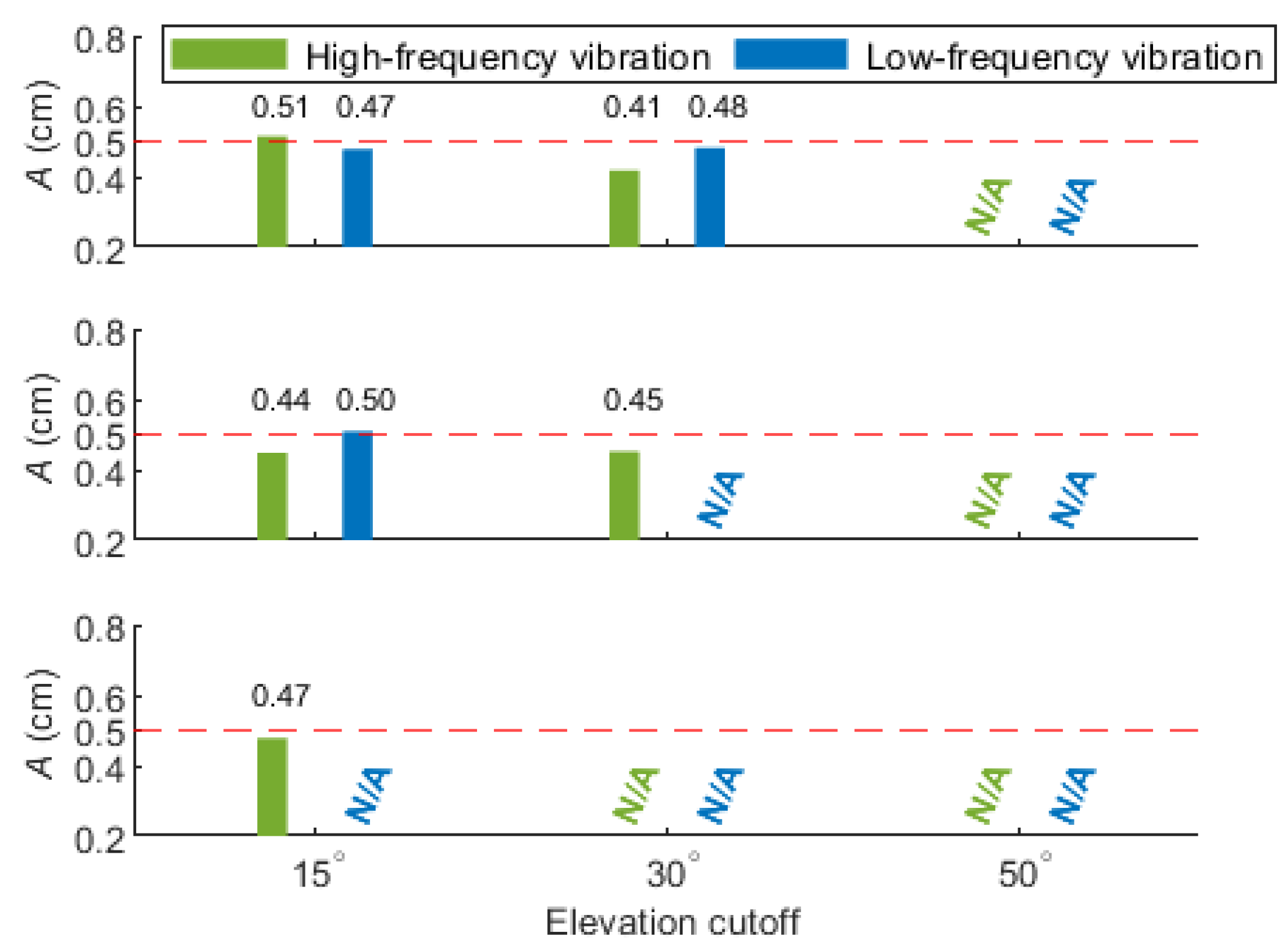
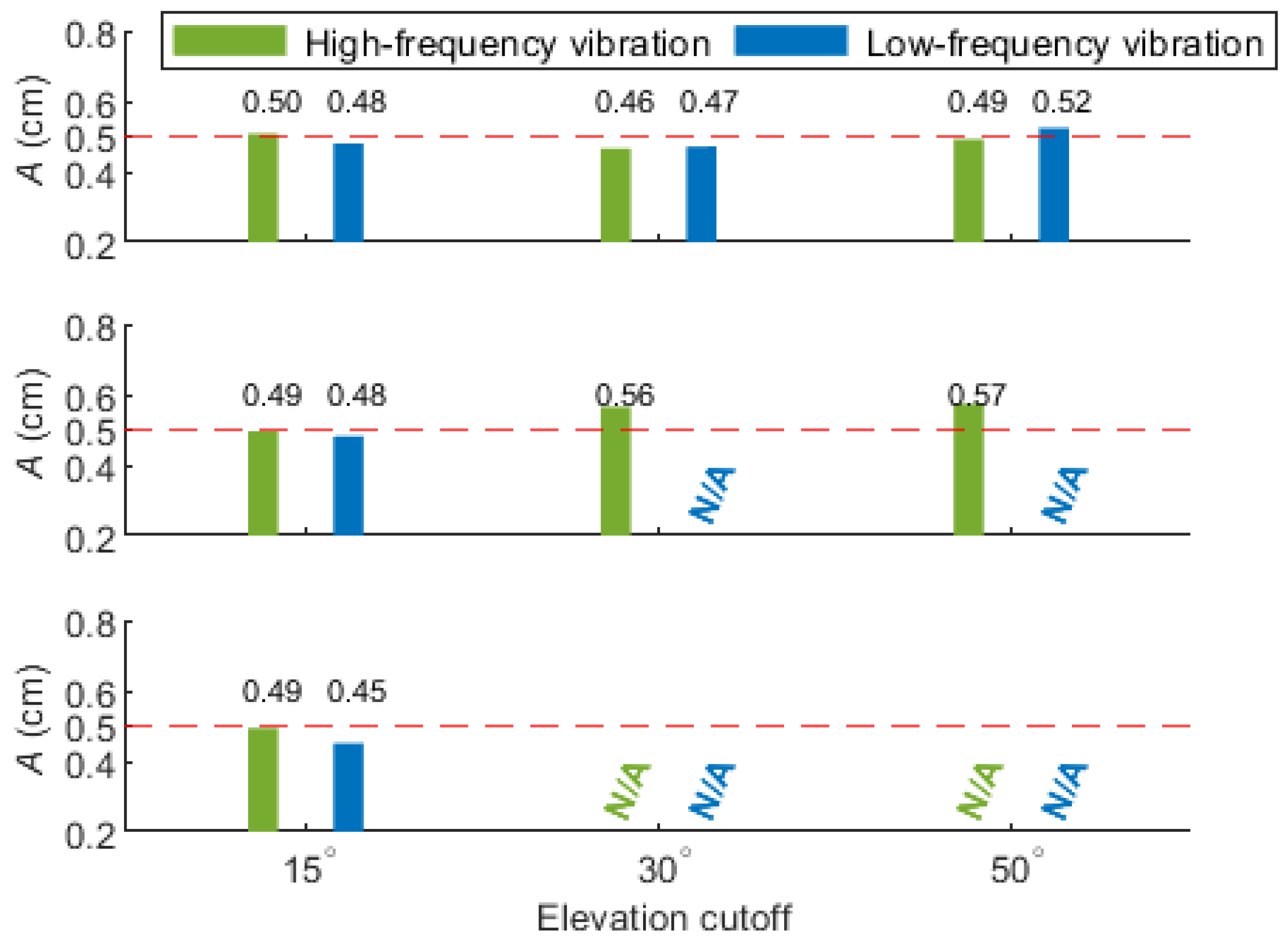
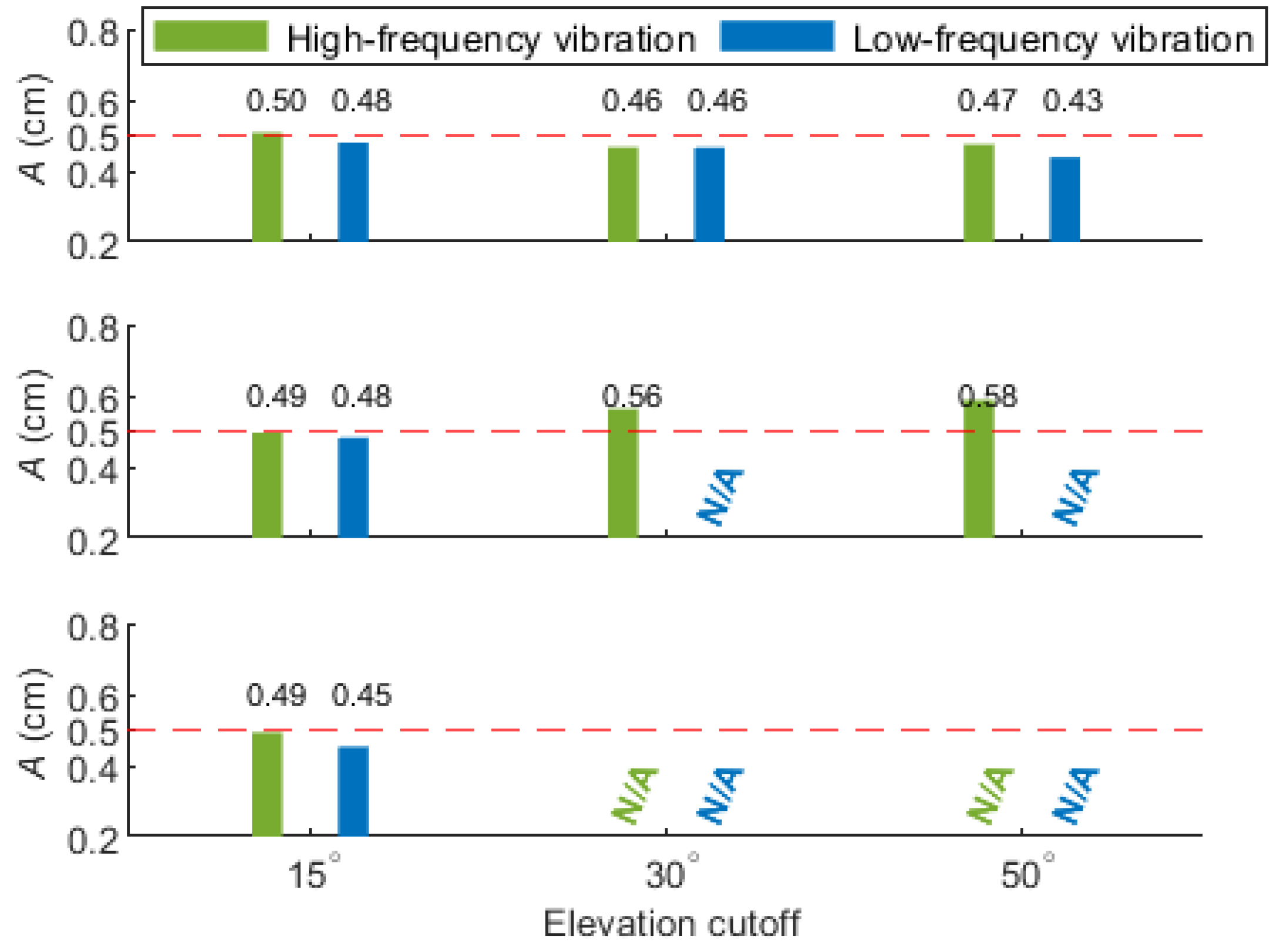
4.3. Performance Analysis with the Classical PPP and PCPPP Models
4.4. Availability Analysis for the Asia-Pacific Mid-Low-Latitude Regions
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.-N.; Li, D.-S.; Song, G.-B. Recent applications of fiber optic sensors to health monitoring in civil engineering. Eng. Struct. 2004, 26, 1647–1657. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, Z.; Xu, Y.; Ding, L.; Ding, H.; Yu, Q.; Su, Z. GNSS aided long-range 3D displacement sensing for high-rise structures with two non-overlapping cameras. Remote Sens. 2022, 14, 379. [Google Scholar] [CrossRef]
- Gokdemir, H.; Ozbasaran, M.; Dogan, M.; Unluoglu, E.; Albayrak, U. Effects of torsional irregularity to structures during earthquakes. Eng. Failure Anal. 2013, 35, 713–717. [Google Scholar] [CrossRef]
- Dat, B.T.; Traykov, A.; Traykova, M. Shear-lag effect and its effect on the design of high-rise buildings. E3S Web Conf. 2018, 33, 02001. [Google Scholar] [CrossRef] [Green Version]
- Kovacevic, I.; Dzidic, S. Lateral and accidental actions—Risk of progressive collapse in high-rise buildings. In Proceedings of the Contemporary Achievements in Civil Engineering 20, Subotica, Serbia, 20 April 2018. [Google Scholar]
- Franius, J.N.; Potts, D.M.; Addenbrooke, T.I.; Burland, J.B. The influence of building weight on tunneling-induced ground and building deformation. Soils Found. 2004, 44, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Eitzenberger, A. Train-Induced Vibrations in Tunnels—A review; Luleå University of Technology: Luleå, Sweden, 2008. [Google Scholar]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Phil. Trans. R. Soc. A 2007, 24, 303–315. [Google Scholar] [CrossRef]
- Ubertini, F.; Cavalagli, N.; Kita, A.; Comanducci, G. Assessment of a monumental masonry bell-tower after 2016 Central Italy seismic sequence by long-term SHM. Bull. Earthq. Eng. 2018, 16, 775–801. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Tanabashi, Y. Rheological parameter estimation for the prediction of long-term deformations in conventional tunnelling. Tunn. Undergr. Space Technol. 2009, 24, 250–259. [Google Scholar] [CrossRef] [Green Version]
- Gu, H.; Wang, T.; Zhu, Y.; Wang, C.; Yang, D.; Huang, L. A completion method for missing concrete dam deformation monitoring data pieces. Appl. Sci. 2021, 44, 463. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Liu, J.; Wang, L.; Tao, T.; Wu, D.; Chen, R. A Review of global navigation satellite system (GNSS)-based dynamic monitoring technologies for structural health monitoring. Remote Sens. 2019, 11, 1001. [Google Scholar] [CrossRef] [Green Version]
- Carpinteri, A.; Lacidogna, G. Damage monitoring of an historical masonry building by the acoustic emission technique. Mater. Struct. 2005, 39, 161–167. [Google Scholar] [CrossRef]
- Love, J.W.; Teskey, W.F.; Lachapelle, G.; Cannon, M.E. Dynamic deformation monitoring of tall structure using GPS technology. J. Surv. Eng. 1995, 121, 35–40. [Google Scholar] [CrossRef]
- Park, H.S.; Shon, H.G.; Kim, I.S.; Park, J.H. Monitoring of structural behavior of high-rise building using GPS. In Proceedings of the CTBUH 2004, Seoul, Korea, 10–13 October 2004. [Google Scholar]
- Xiong, C.; Niu, Y. Investigation of the dynamic behavior of a super high-rise structure using RTK-GNSS technique. KSCE J. Civ. Eng. 2019, 23, 654–665. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Li, B.; Qiu, G. GNSS-based verticality monitoring of super-tall buildings. Appl. Sci. 2018, 8, 991. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Yan, B.; Meng, X.; Shao, X.; Ye, H. Measurement of bridge dynamic responses using network-based real-time kinematic GNSS technique. J. Surv. Eng. 2016, 142, 04015013. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. Full-scale measurements of dynamic response of suspension bridge subjected to environmental loads using GPS technology. Sci. China Technol. Sci. 2010, 53, 469–479. [Google Scholar] [CrossRef]
- O’Keefe, K. Availability and reliability advantages of GPS/Galileo integration. In Proceedings of the ION GPS 2001, Salt Lake City, UT, USA, 11–14 September 2001. [Google Scholar]
- Chu, F.-Y.; Yang, M. GPS/Galileo long baseline computation: Method and performance analyses. GPS Solut. 2014, 18, 263–272. [Google Scholar] [CrossRef]
- Chu, F.-Y.; Yang, M.; Chen, Y.T. GEO-pivoted carrier ambiguity resolution: A method for instantaneous ambiguity resolution in mid-low-latitude regions. GPS Solut. 2019, 23, 107. [Google Scholar] [CrossRef]
- Kubo, N.; Tokura, H.; Pullen, S. Mixed GPS—BeiDou RTK with inter-systems bias estimation aided by CSAC. GPS Solut. 2019, 22, 5. [Google Scholar] [CrossRef]
- Takahashi, S.; Kubo, N.; Yamaguchi, N.; Yokoshima, T. Real-Time monitoring of structure movements using low-cost, wall-mounted, hand-held RTK-GNSS receivers. In Proceedings of the ION GNSS+ 2018, Miami, FL, USA, 24–28 September 2018. [Google Scholar]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Teunissen, P.J.G.; Montenbruck, O. Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland.
- Goad, C.; Yang, M. On Automatic Precision Airborne GPS Positioning. In Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation, Banff, AB, Canada, 30 August–2 September 1994. [Google Scholar]
- Watson, C.; Tregoning, P.; Coleman, R. Impact of solid Earth tide models on GPS coordinate and tropospheric time series. Geophys. Res. Lett. 2006, 33, L08306. [Google Scholar] [CrossRef] [Green Version]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. Geophys. Res. 1996, B2, 1978–2012. [Google Scholar] [CrossRef]
- Gelb, A. Applied Optimal Estimation; The M.I.T. Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Goad, C.; Yang, M. A new approach to precision airborne GPS positioning for photogrammetry. Photogramm. Eng. Remote Sens. 1997, 63, 1067–1077. [Google Scholar]
- Torge, W.; Müller, J. Geodesy, 4th ed.; Walter de Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Lee, J.; Lee, K.; Lee, S.; Lee, Y.; Sim, S. Long-term displacement measurement of bridges using a LiDAR system. Struct. Control Health Monit. 2019, 26, e2428. [Google Scholar] [CrossRef]
- Li, C.K.; Ching, K.E.; Chen, K.H. The ongoing modernization of the Taiwan semi-dynamic datum based on the surface horizontal deformation model using GNSS data from 2000 to 2016. J. Geod. 2019, 93, 1543–1558. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Noise characteristics of high-frequency, short-duration GPS records from analysis of identical, collocated instruments. Measurement 2013, 46, 1488–1506. [Google Scholar] [CrossRef]
- Nyquist, H. Thermal agitation of electric charge in conductors. Phys. Rev. 1928, 32, 110–113. [Google Scholar] [CrossRef]
- Kaartinen, E.; Dunphy, K.; Sadhu, A. LiDAR-based structural health monitoring: Applications in civil infrastructure systems. Sensors 2022, 22, 4610. [Google Scholar] [CrossRef]


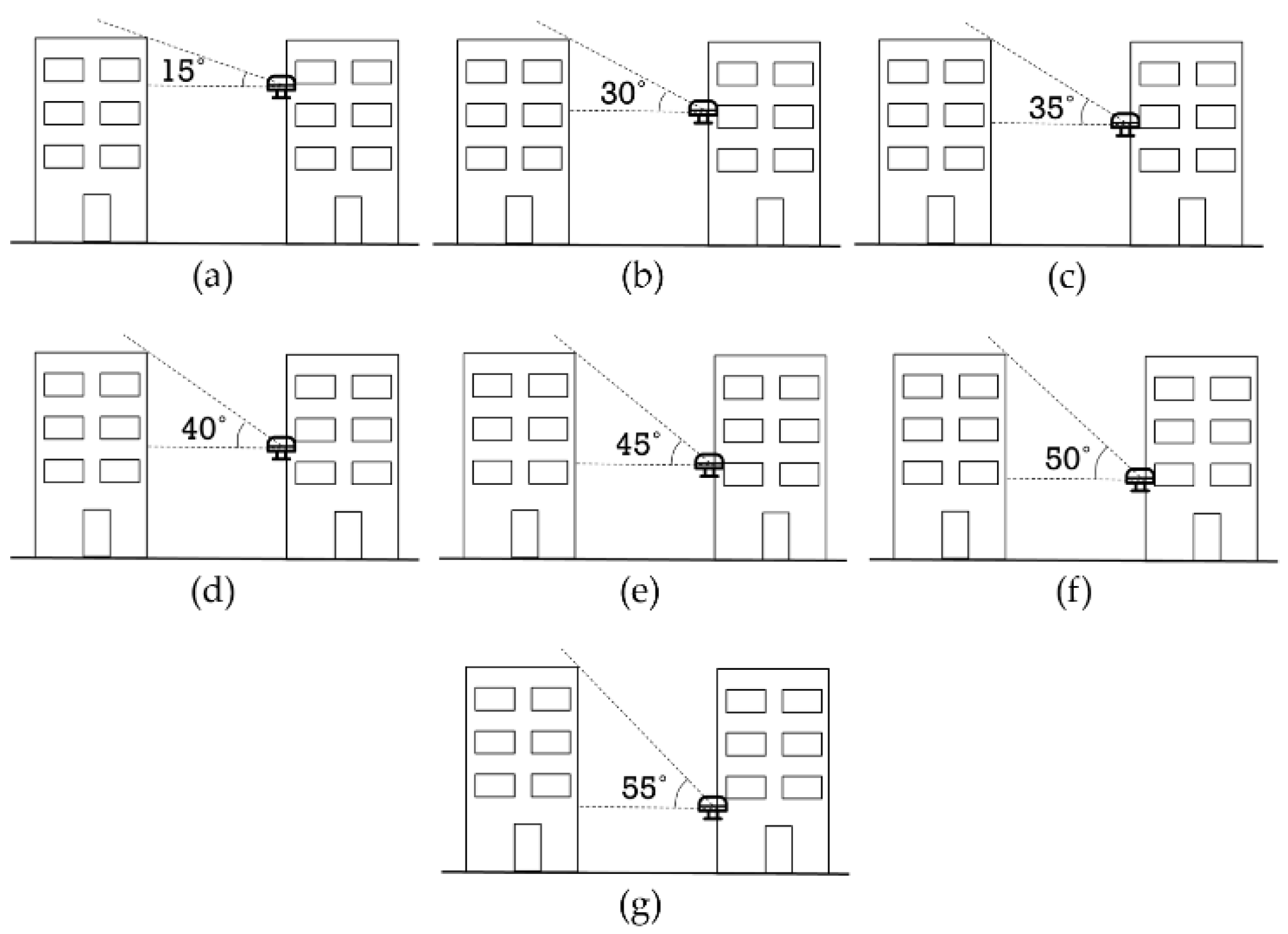


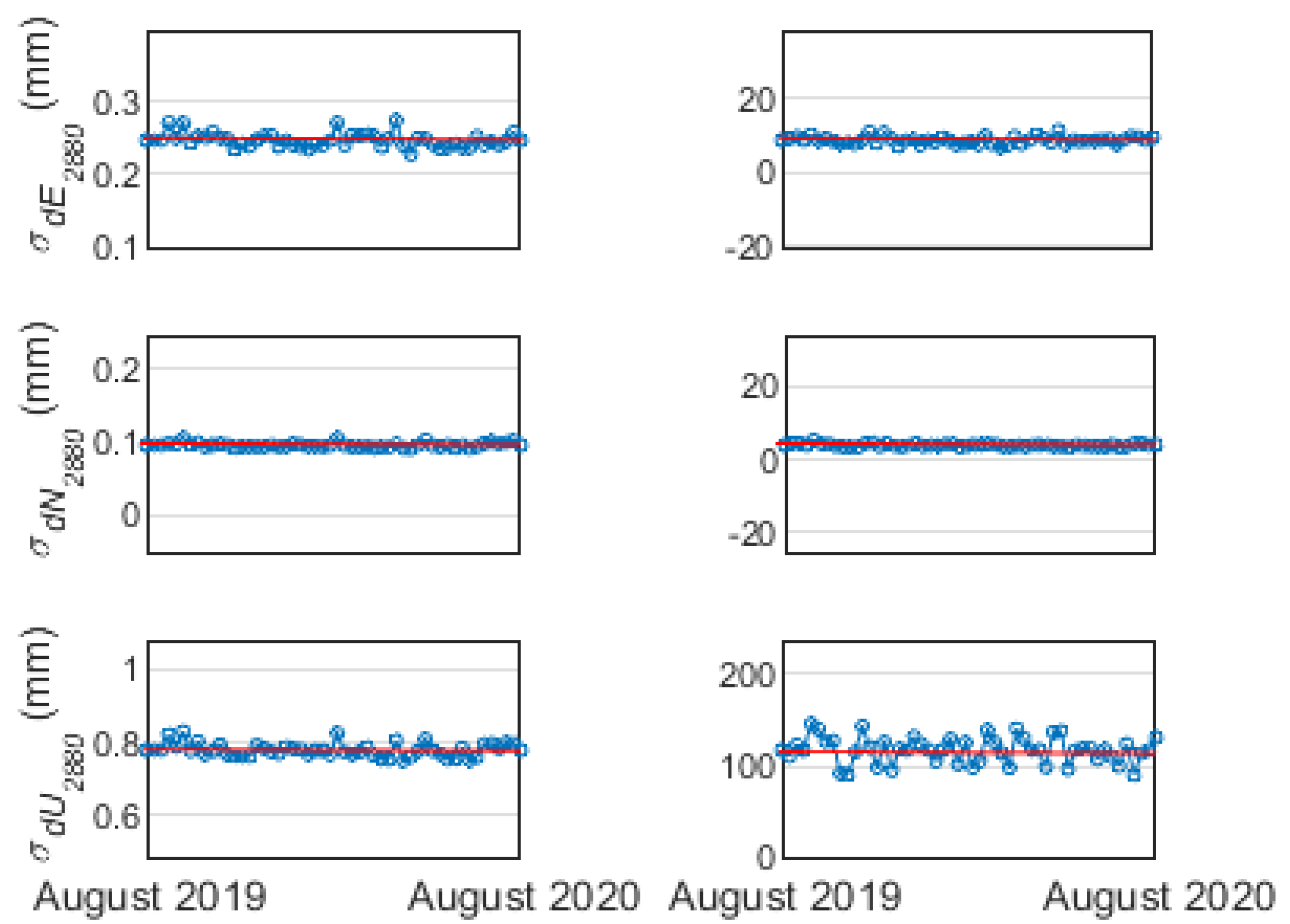
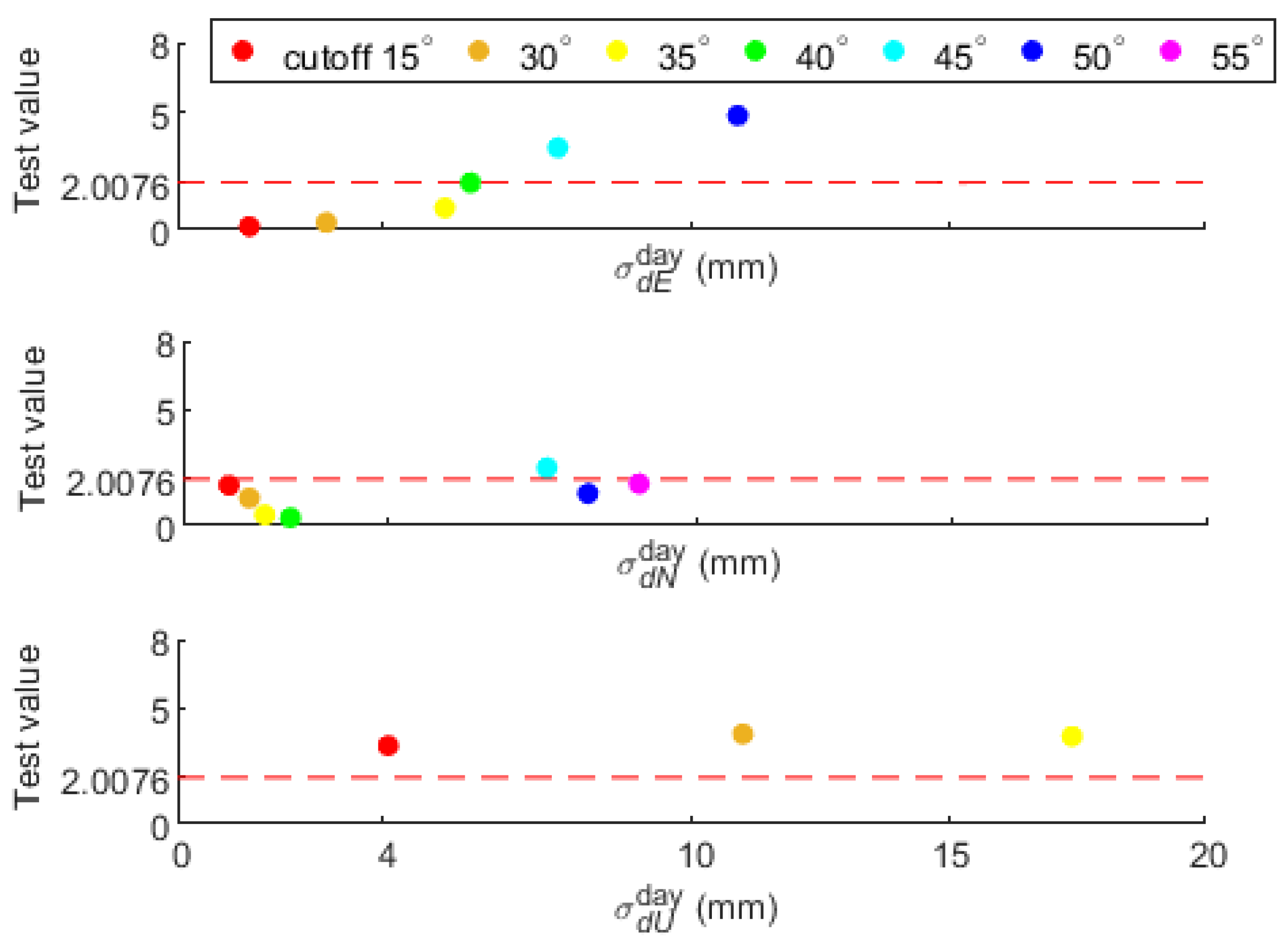
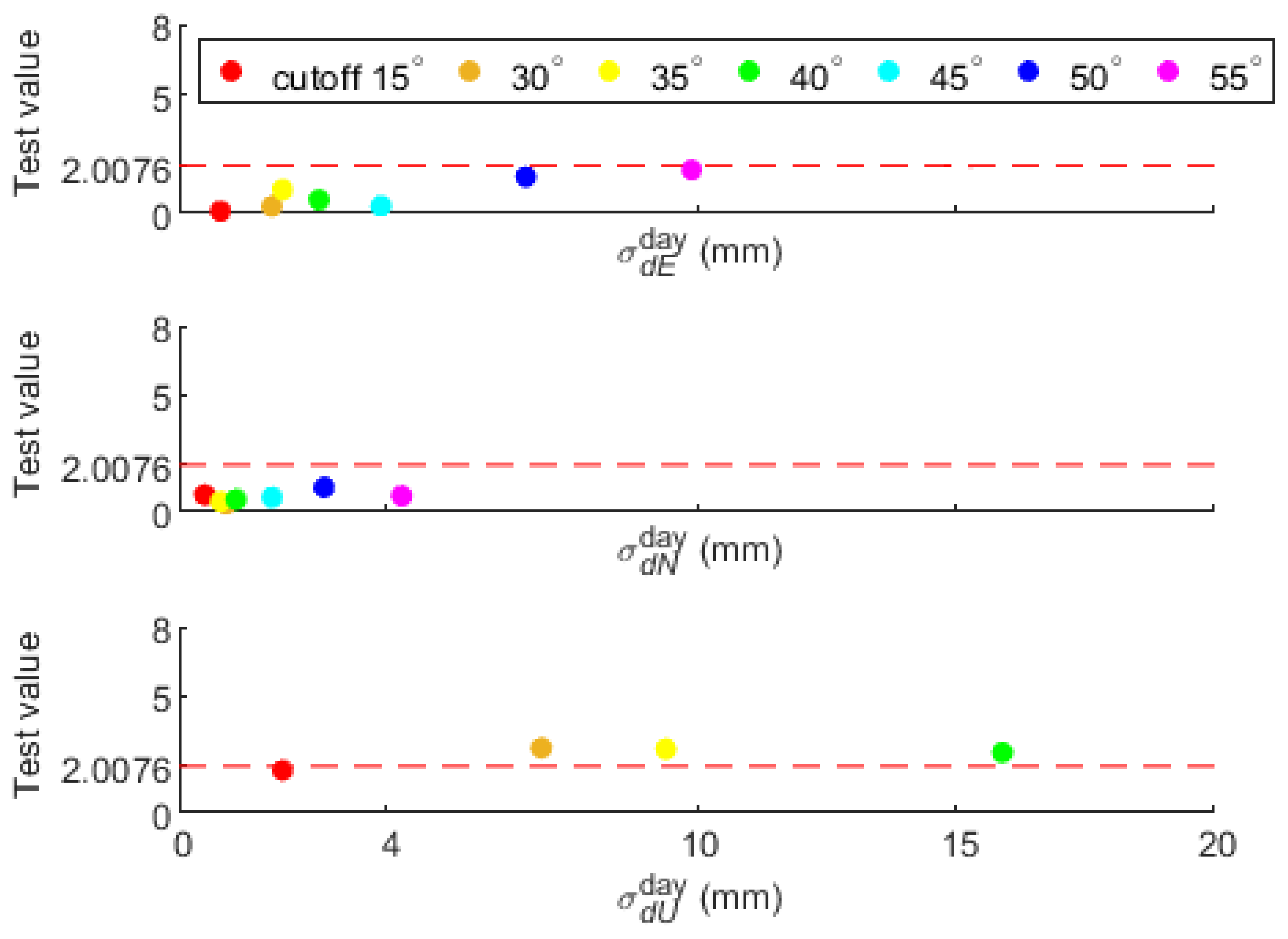



| Systematic Errors | Processing Strategies |
|---|---|
| Orbital errors | The final orbit products (SP3) of GeoForschungsZentrum (GFZ) is adopted. The orbital errors are assumed negligible. |
| Sat. clock errors | They are corrected with the high-rate clock products of GFZ. |
| Sat. and rec. phase-centre offsets | They are corrected with the International GNSS service (IGS) products (igsXXX.atx). |
| Phase windup | They are corrected with empirical methods with yaw-attitude modes [25]. |
| Relativistic effects | They are corrected with empirical methods [26]. |
| Tropospheric delays | Zenith hydrostatic delays are corrected with the modified Hopfield model [27], and the remaining delays are estimated with a parameter which stands for zenith troposphere delay. |
| Ionospheric delays | They are estimated with parameters. To achieve this, dual-frequency measurements are necessary. |
| Earth tide displacements | They are corrected with empirical methods [28]. |
| Sat. code biases | They are corrected with differential code biases (DCB) supported by the IGS. |
| Masking Conditions | (mm) | (mm) | (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Elevation Cutoff | Azimuth Cutoff | ||||||||
| 15° | N/A | 0.2 | 0.1 | 0.8 | 8 | 5 | 10 | 5 | 3 |
| 15° | 90–270° | 0.8 | 0.5 | 2.1 | 4 | 3 | 3 | 3 | 1 |
| 30° | 90–270° | 1.8 | 0.8 | 7.1 | 3 | 2 | 3 | 2 | 1 |
| 35° | 90–270° | 2.1 | 1.0 | 9.4 | 3 | 2 | 3 | 2 | 1 |
| 40° | 90–270° | 2.7 | 1.1 | 15.9 | 2 | 2 | 3 | 1 | 1 |
| 45° | 90–270° | 4.0 | 1.8 | 27.1 | 2 | 1 | 2 | 1 | 1 |
| 50° | 90–270° | 6.7 | 2.8 | 61.4 | 1 | 1 | 2 | 1 | 1 |
| 55° | 90–270° | 9.9 | 4.3 | 138.7 | 1 | 1 | 2 | 1 | 1 |
| Masking Conditions | Five-Constellation PPP | GPS PPP | |||||
|---|---|---|---|---|---|---|---|
| Elevation Cutoff | Azimuth Cutoff | E (cm) | N (cm) | U (cm) | E (cm) | N (cm) | U (cm) |
| 15° | 90–270° | 0.3 | 0.2 | 0.8 | 0.3 | 0.5 | 1.7 |
| 30° | 90–270° | 0.3 | 0.2 | 3.1 | 0.4 | 0.4 | 4.7 |
| 35° | 90–270° | 0.5 | 0.2 | 4.5 | 0.7 | 0.3 | 5.4 |
| 40° | 90–270° | 0.5 | 0.3 | 4.6 | 1.6 | 0.4 | 5.2 |
| 45° | 90–270° | 0.5 | 0.3 | 4.8 | 3.2 | 0.8 | 6.7 |
| 50° | 90–270° | 0.9 | 0.6 | 8.0 | 2.7 | 1.1 | 8.1 |
| 55° | 90–270° | 1.1 | 0.4 | 28.8 | 9.9 | 1.8 | 85.8 |
| Num. of Constellations () | One Epoch Is Processed | Two Epochs Are Processed | Three Epochs Are Processed |
|---|---|---|---|
| 1 | 5 | 3 | 3 |
| 2 | 6 | 4 | 4 |
| 3 | 7 | 6 | 6 |
| 4 | 8 | 8 | 8 |
| 5 | 10 | 10 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, F.-Y.; Chen, Y.-W. Monitoring Structural Displacements on a Wall with Five-Constellation Precise Point Positioning: A Position-Constrained Method and the Performance Analyses. Remote Sens. 2023, 15, 1314. https://doi.org/10.3390/rs15051314
Chu F-Y, Chen Y-W. Monitoring Structural Displacements on a Wall with Five-Constellation Precise Point Positioning: A Position-Constrained Method and the Performance Analyses. Remote Sensing. 2023; 15(5):1314. https://doi.org/10.3390/rs15051314
Chicago/Turabian StyleChu, Feng-Yu, and Yin-Wei Chen. 2023. "Monitoring Structural Displacements on a Wall with Five-Constellation Precise Point Positioning: A Position-Constrained Method and the Performance Analyses" Remote Sensing 15, no. 5: 1314. https://doi.org/10.3390/rs15051314
APA StyleChu, F.-Y., & Chen, Y.-W. (2023). Monitoring Structural Displacements on a Wall with Five-Constellation Precise Point Positioning: A Position-Constrained Method and the Performance Analyses. Remote Sensing, 15(5), 1314. https://doi.org/10.3390/rs15051314




