On the Interpretation of Synthetic Aperture Radar Images of Oceanic Phenomena: Past and Present
Abstract
1. Introduction
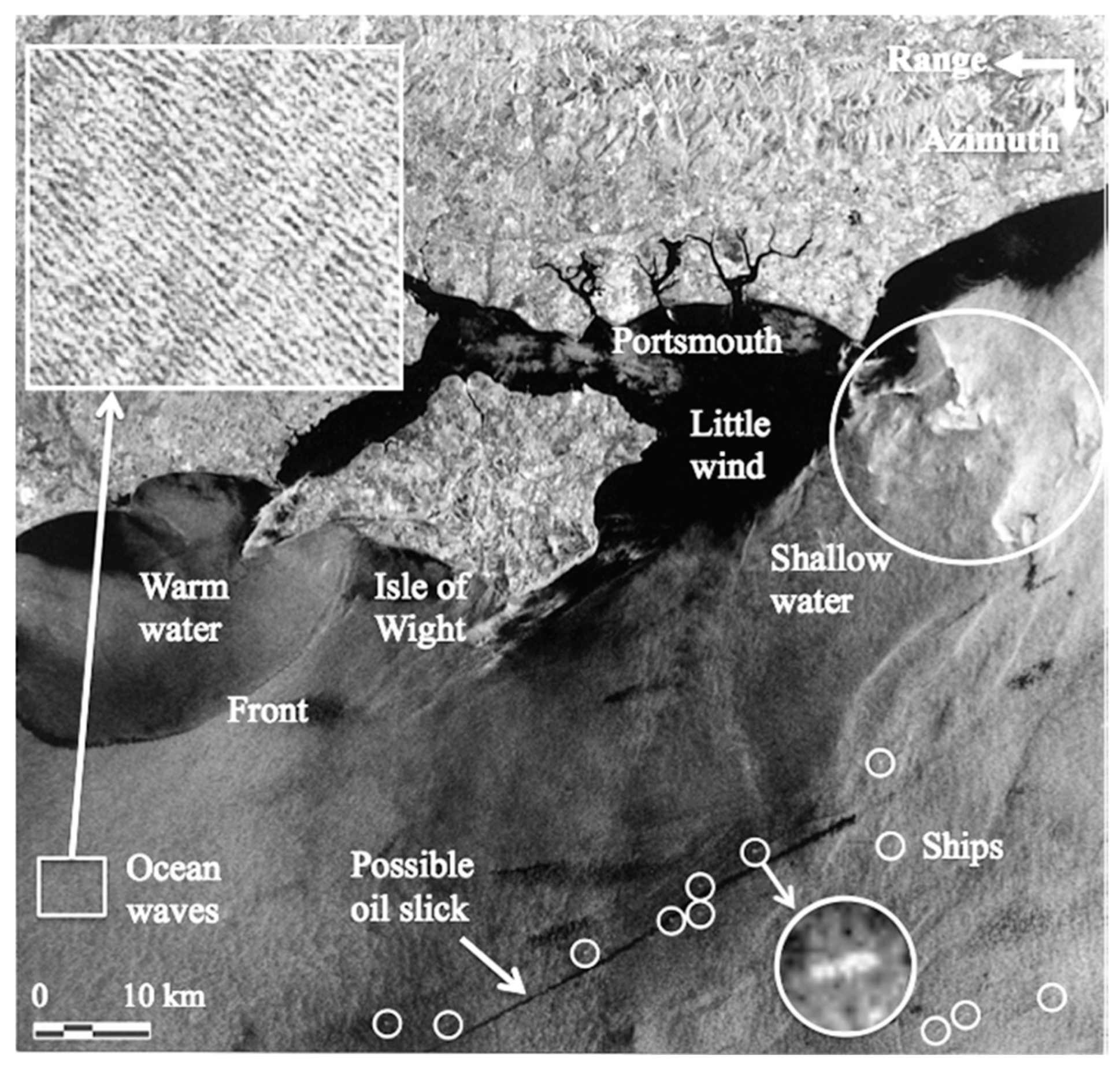
2. Ocean Surface Waves
2.1. Mirowave Backscatter from Sea Surface
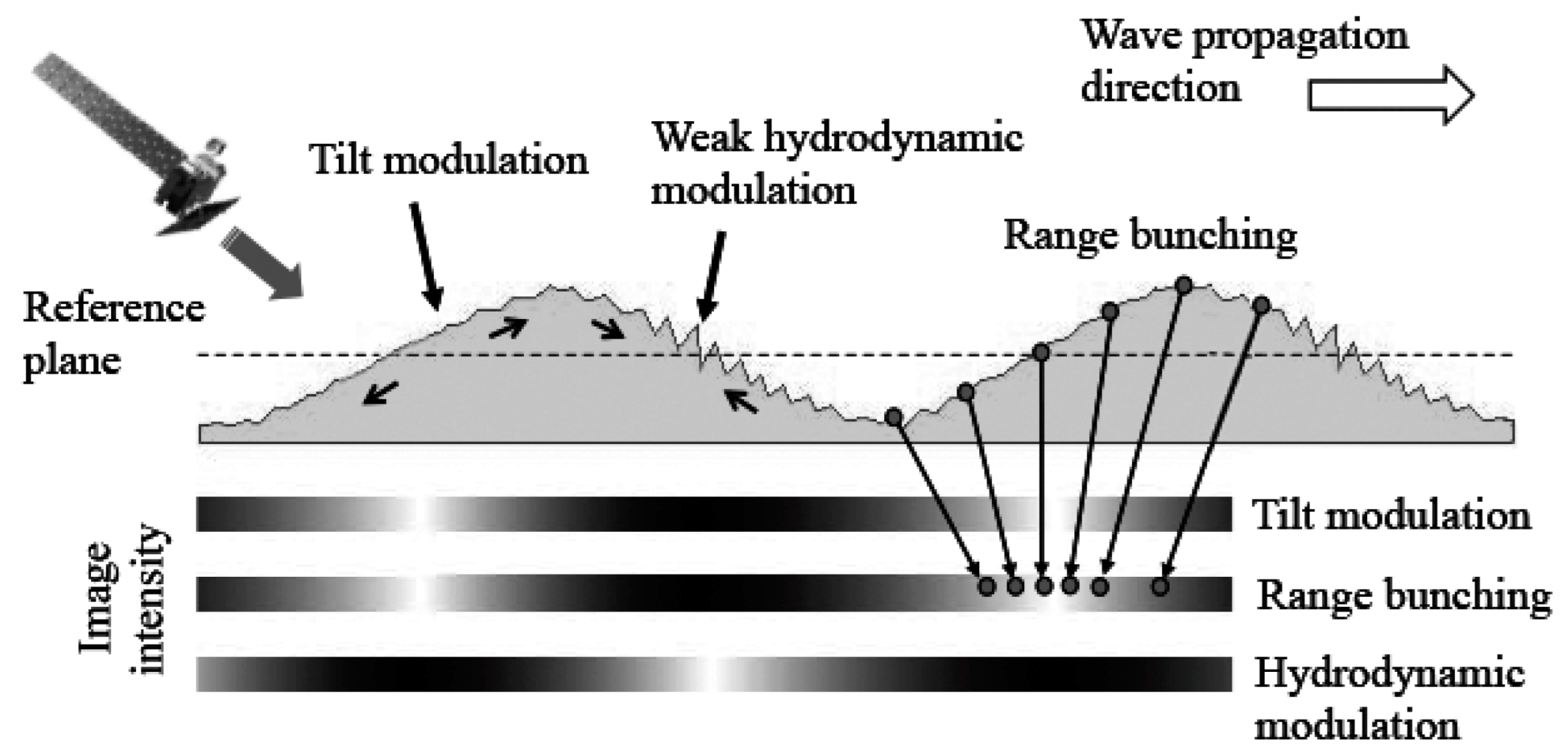
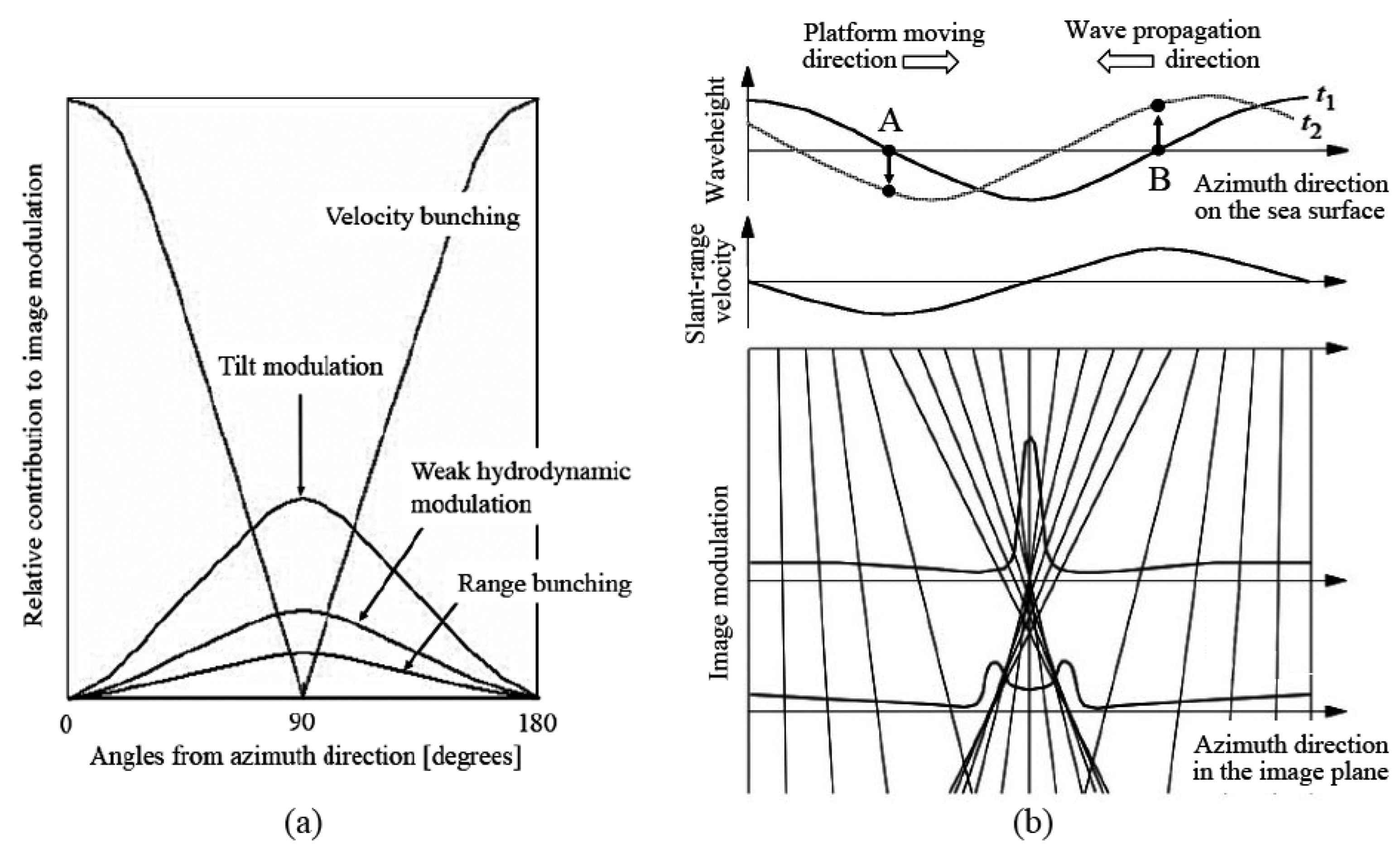
2.2. Imaging Process of Ocean Surface Waves
2.3. Directional Wave Spectrum
2.4. Waveheight
2.5. Breaking Waves
3. Oceanic Internal Waves
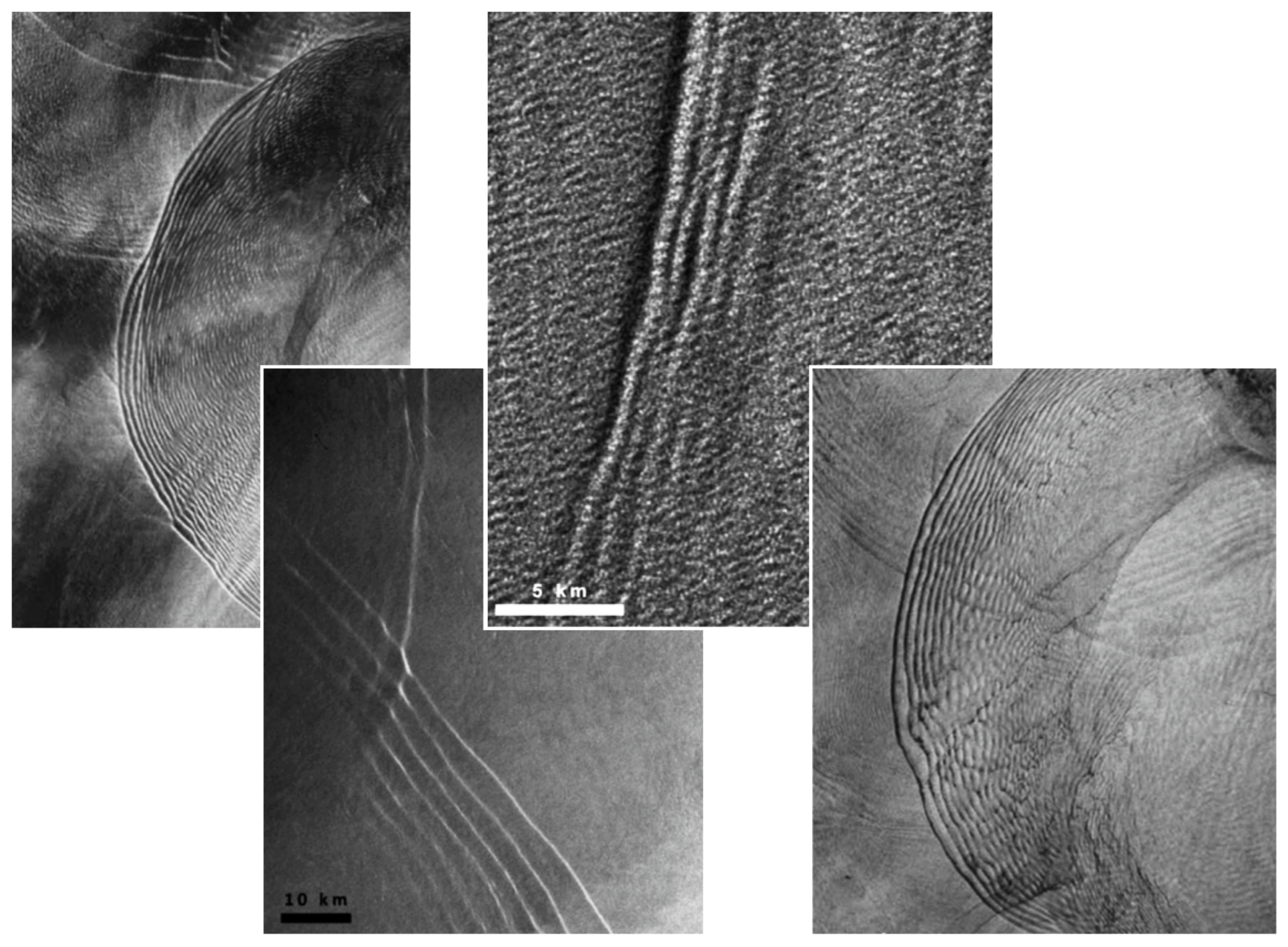
3.1. Observation and Impact
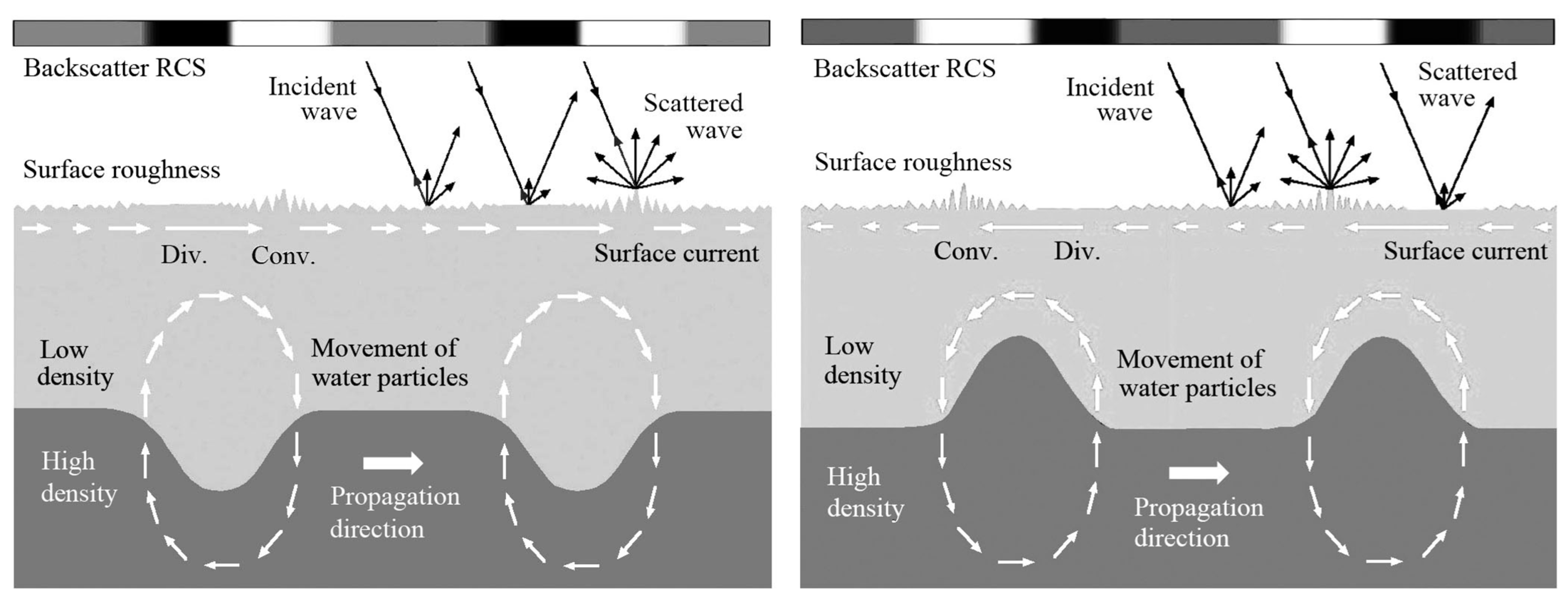
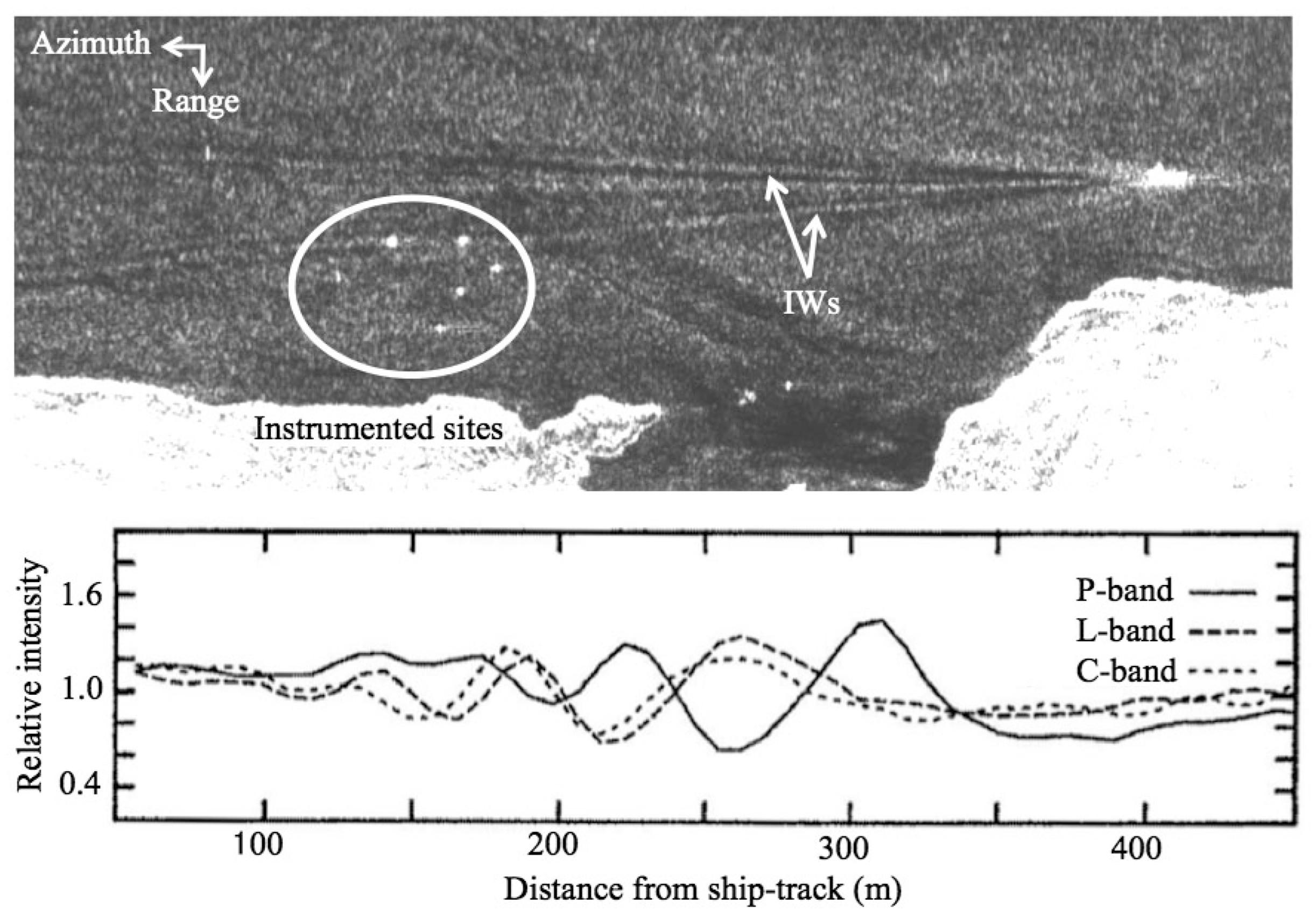
3.2. Imaging Process
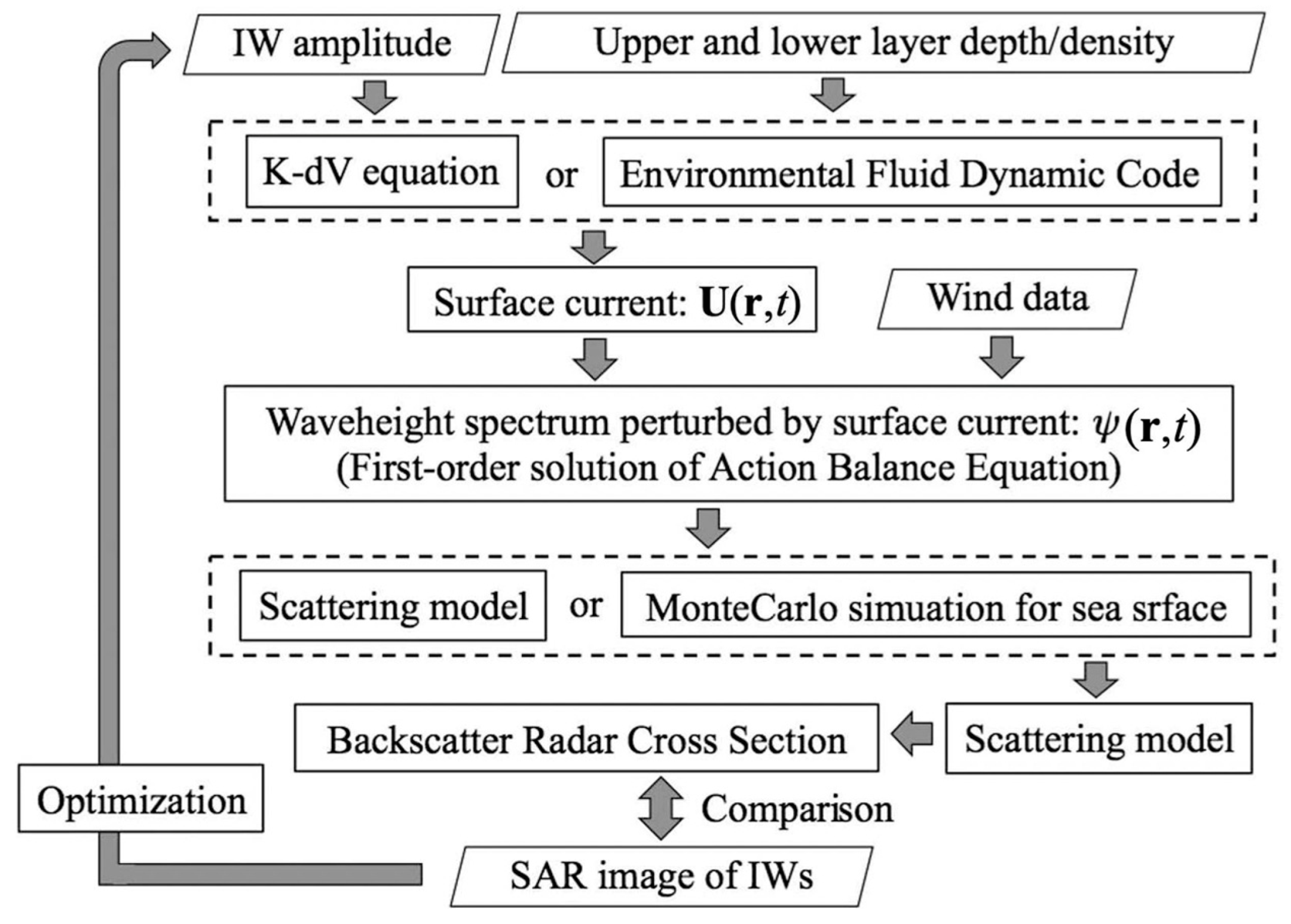
3.3. Estimation of Internal Wave Properties
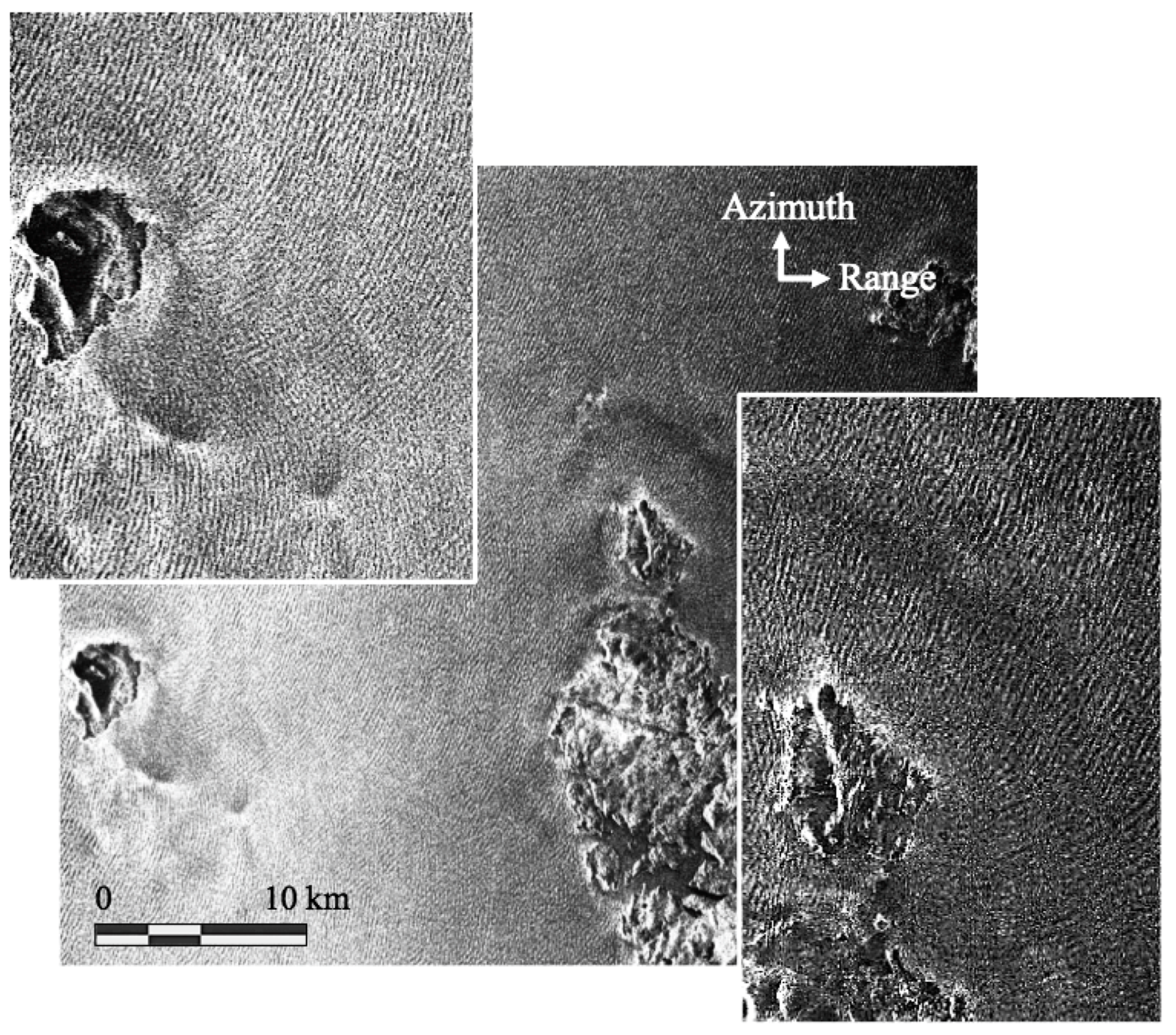
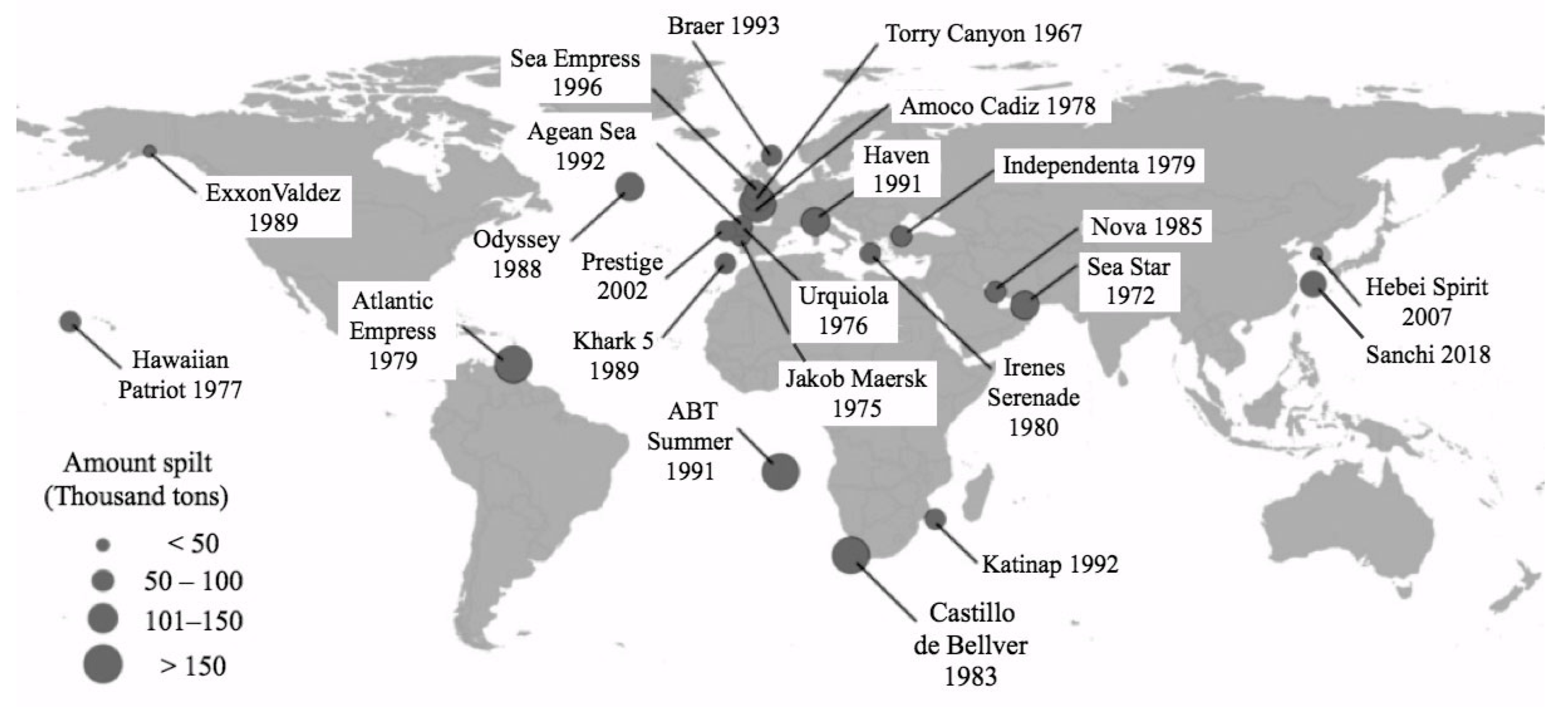
4. Oil Slicks
4.1. Background
4.2. Imaging Process
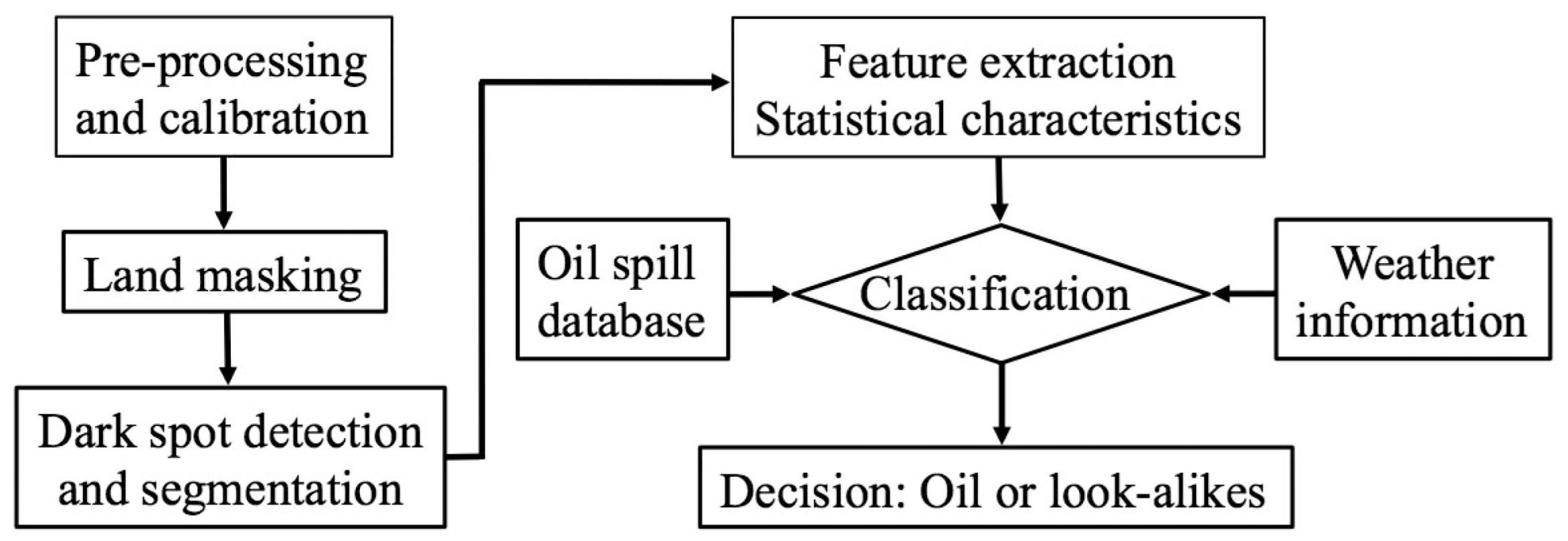
4.3. Detection and Classification
4.3.1. Manual Approach
4.3.2. Semi-Automatic/Automatic Approach
4.3.3. Polarimetric Analyses
4.3.4. Artificial Intelligence
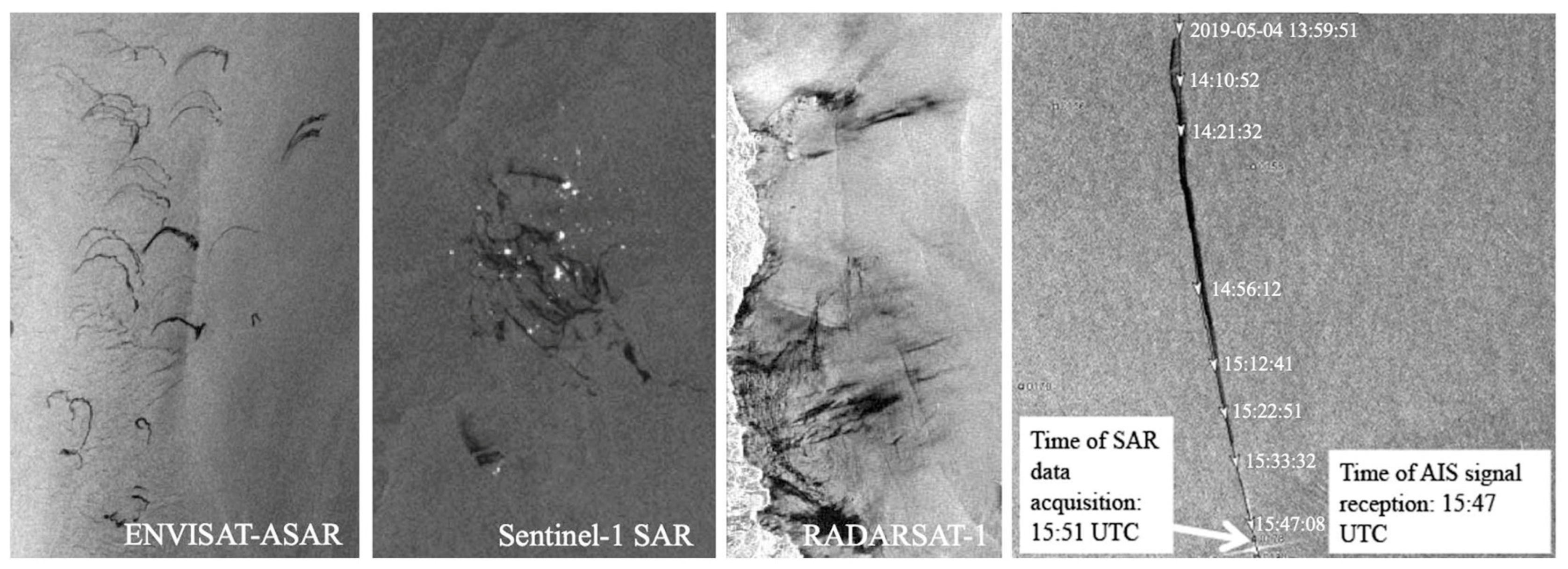
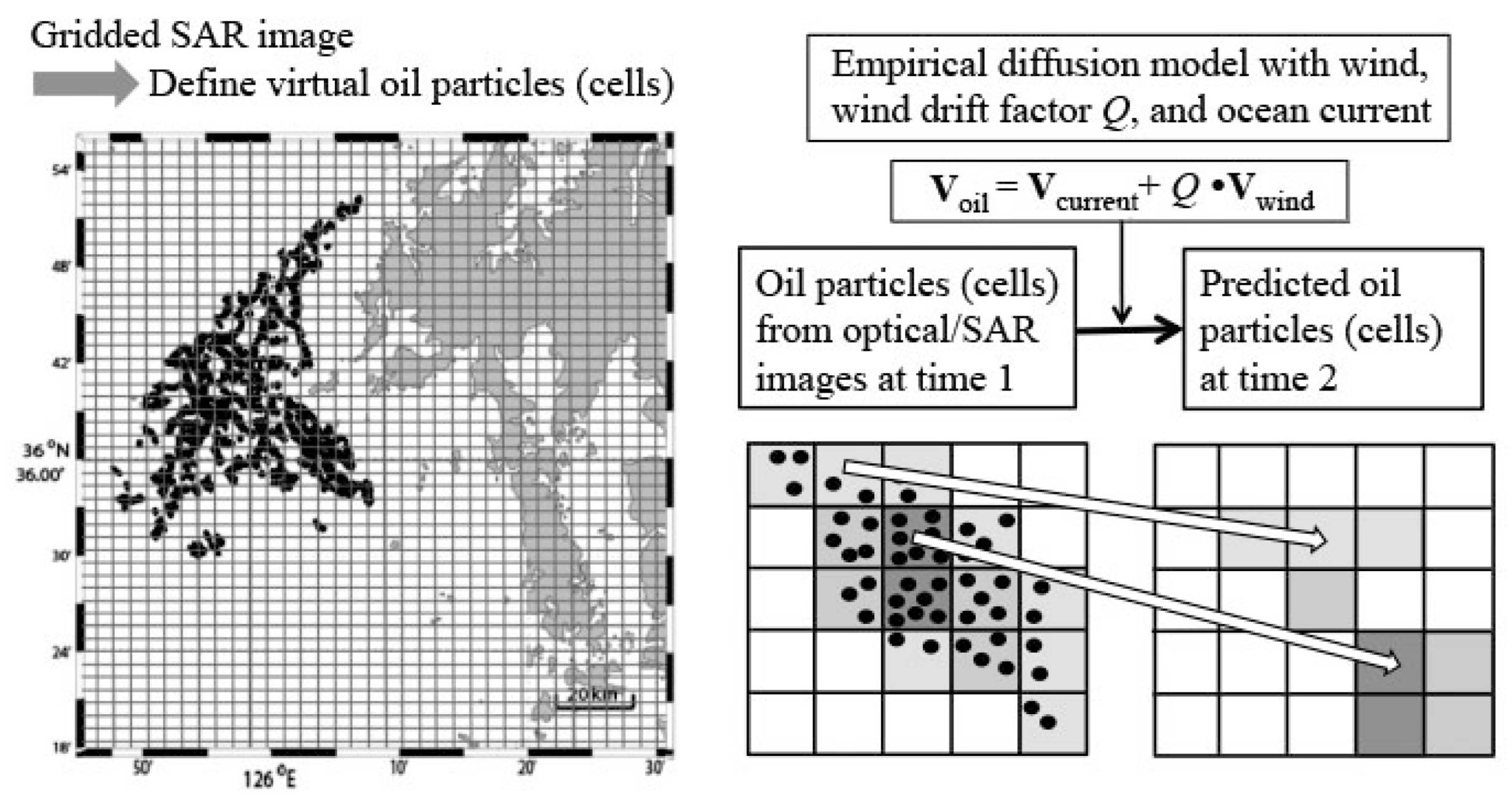
4.4. Tracking and Prediction
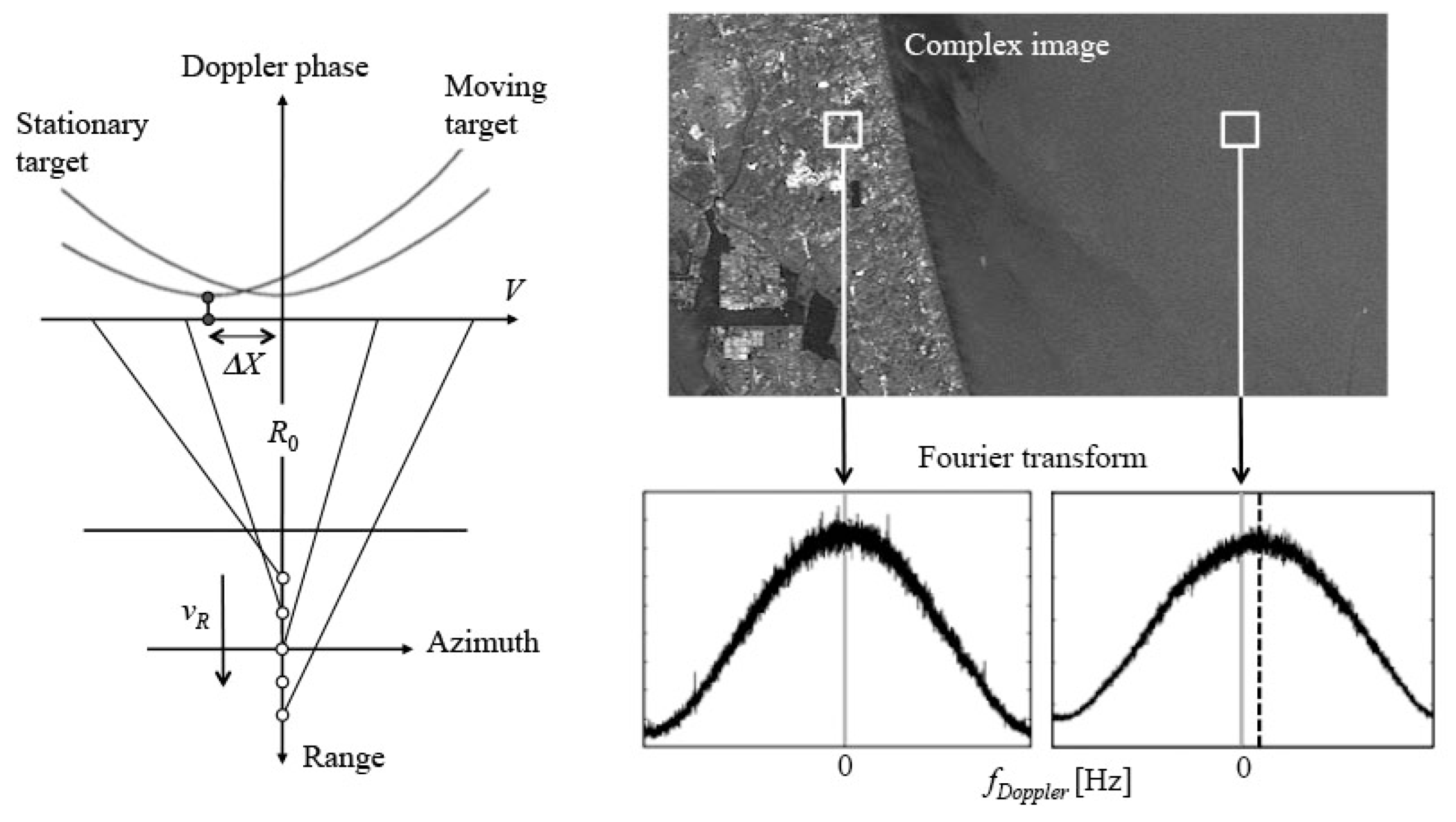
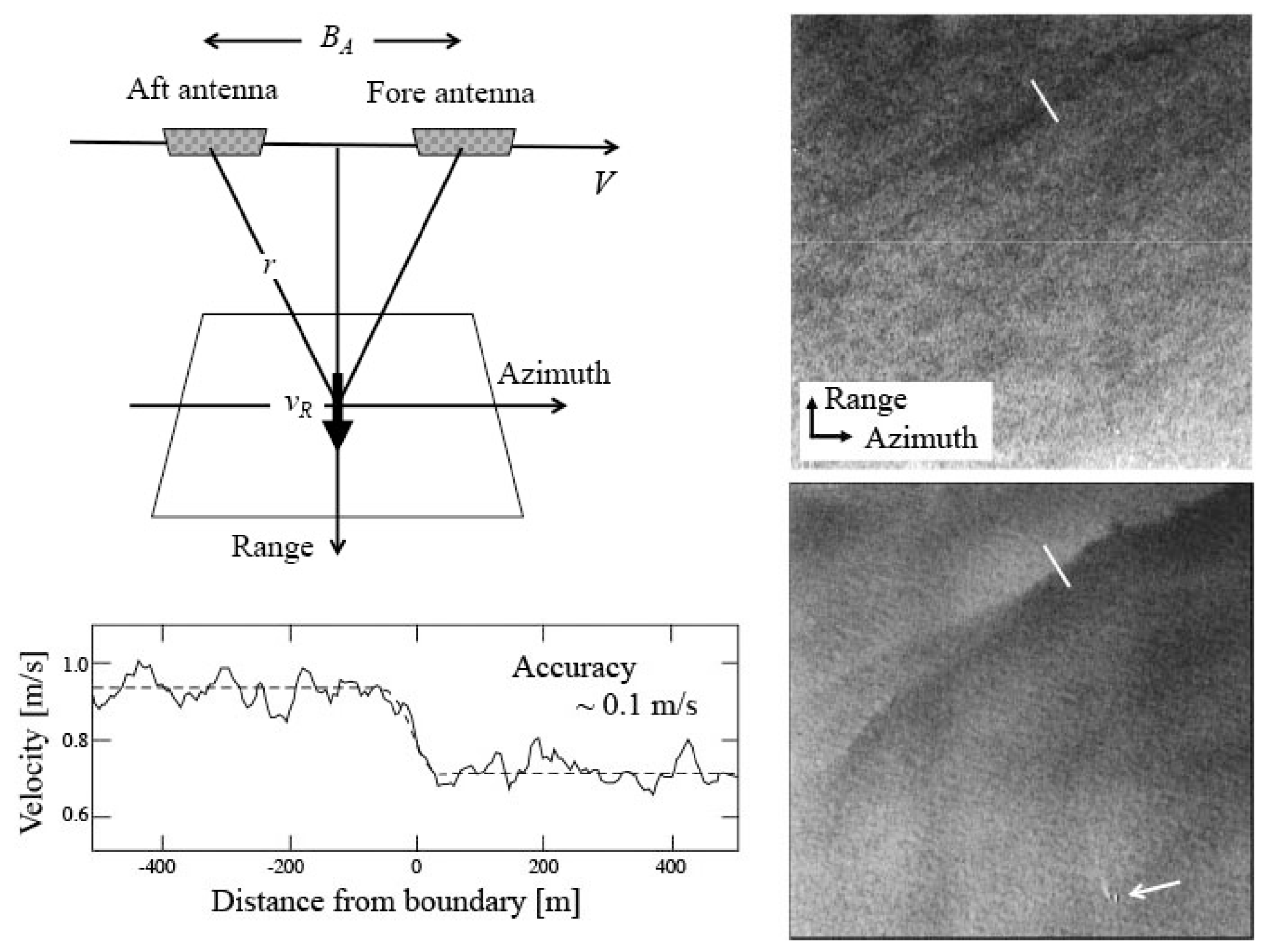
5. Ocean Current
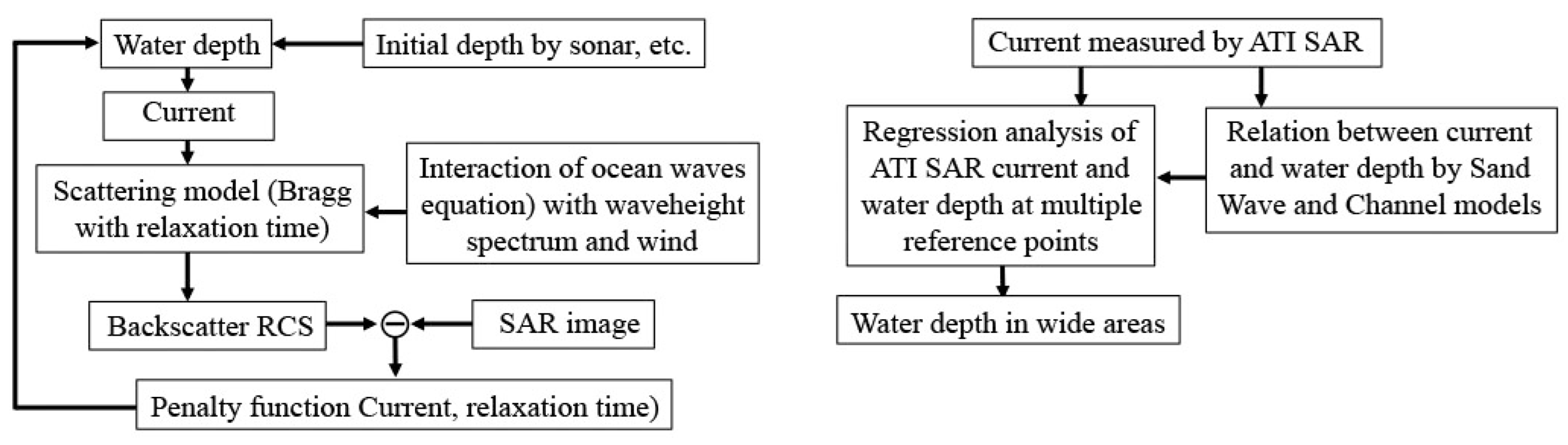
6. Bathymetry
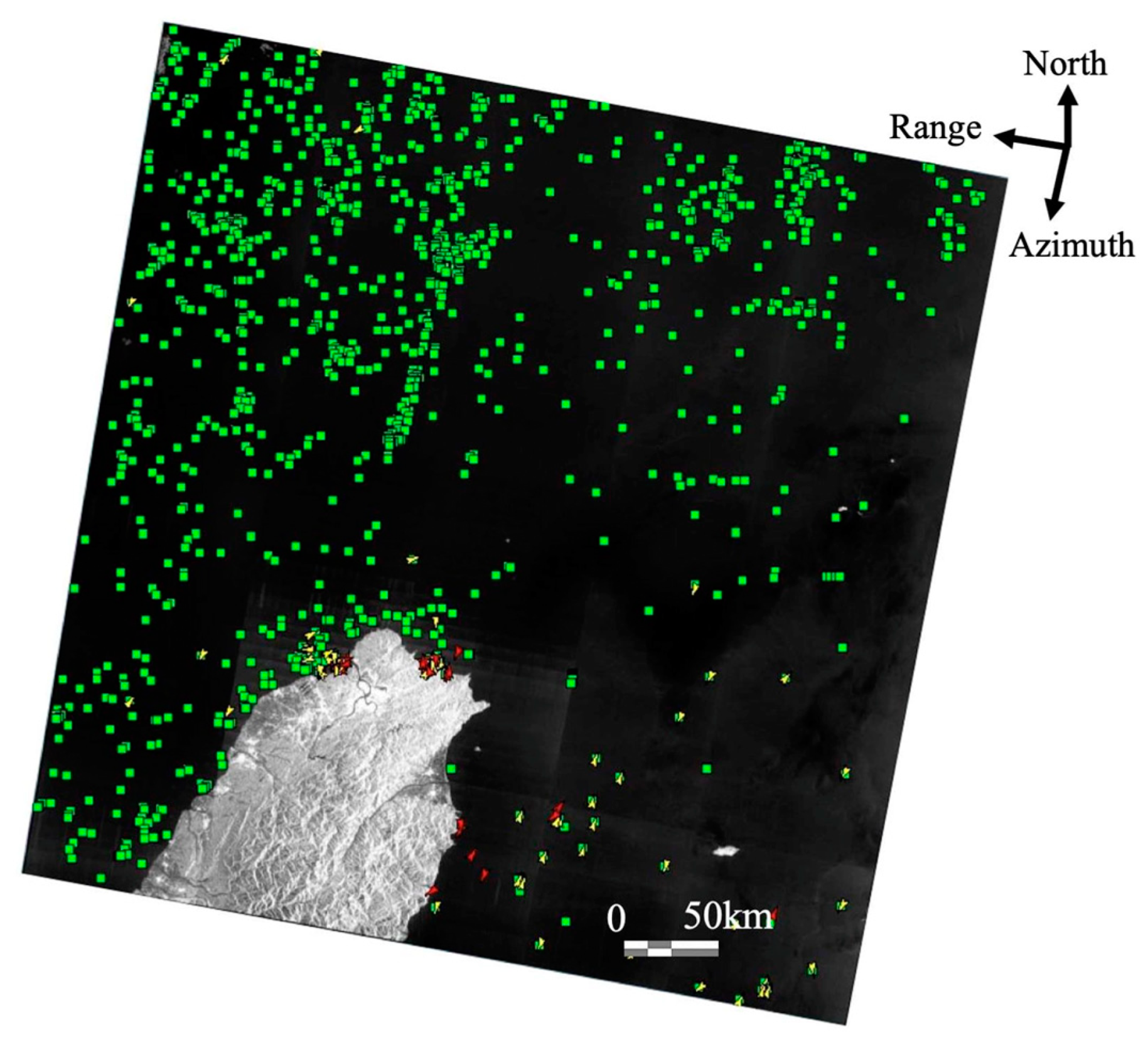
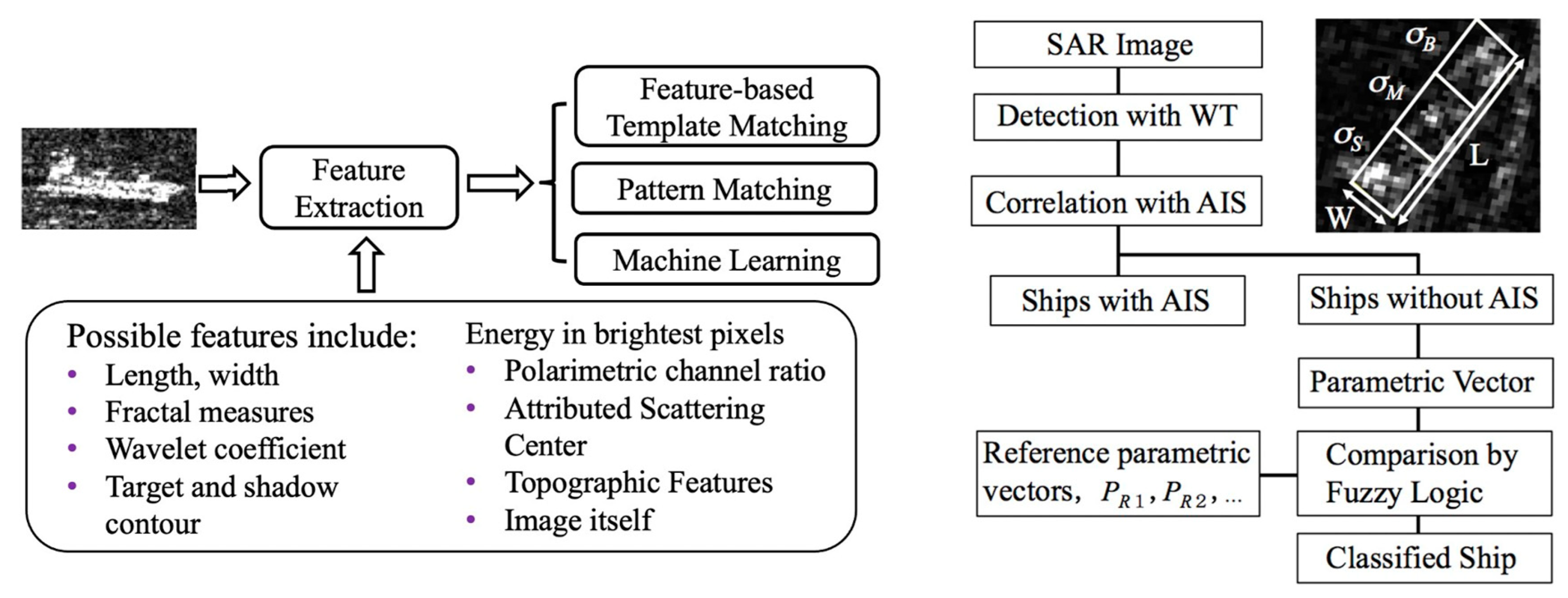
7. Ship Detection and Classification
7.1. Background
7.2. Ship Detection
7.2.1. Constant False Alarm Rate (CFAR)
7.2.2. Adaptive Threshold Method (ATM) [182,183]
7.2.3. Wavelet Transform [184,185]
7.2.4. Multi/Sub-Look-Based Methods [186,187,188,189,190]
7.2.5. Polarimetric Analyses [30,31,32]
7.2.6. Standard Deviation Filter (SDF) [192]
7.2.7. AI-Based Method
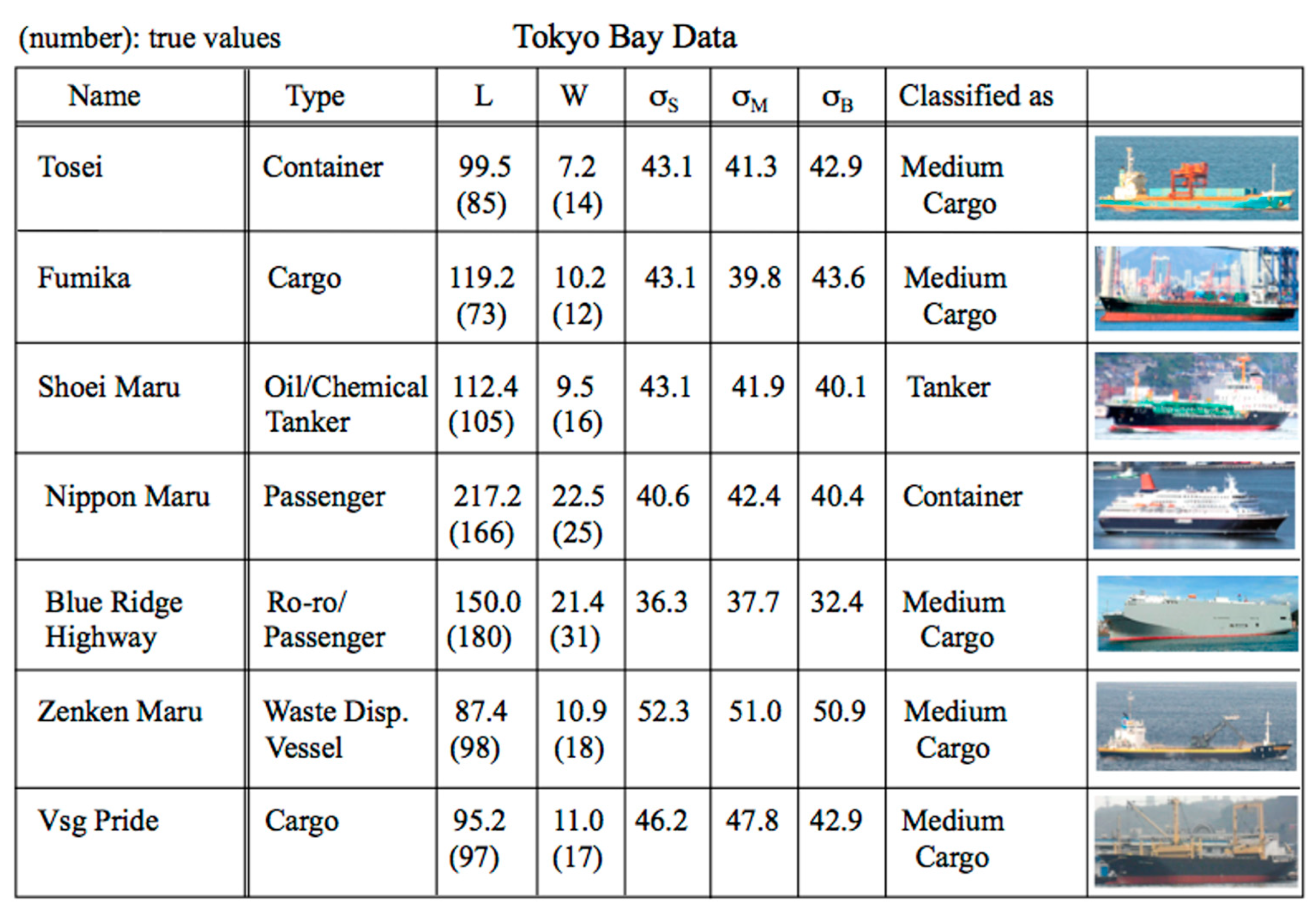
7.3. Ship Classification
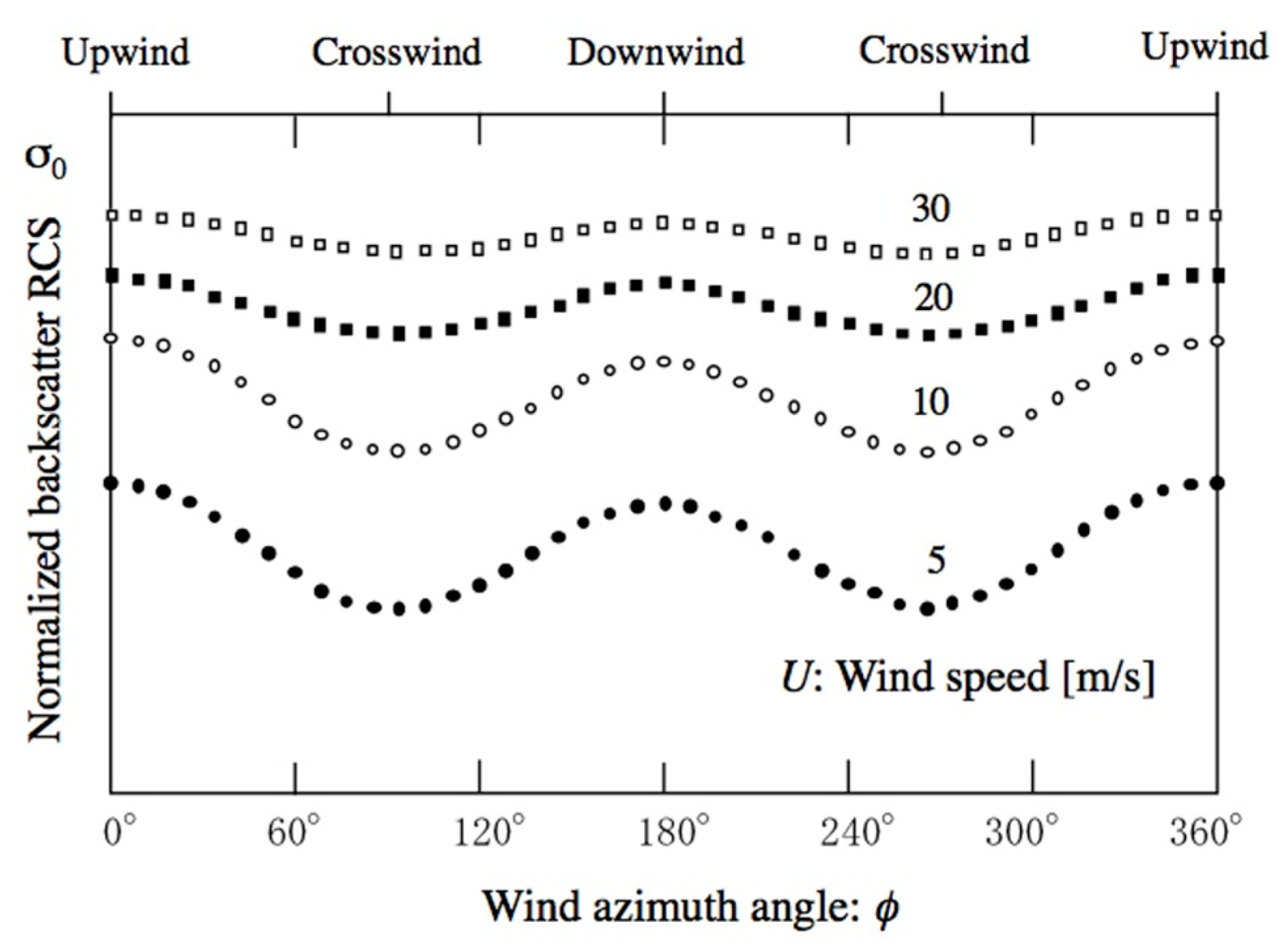
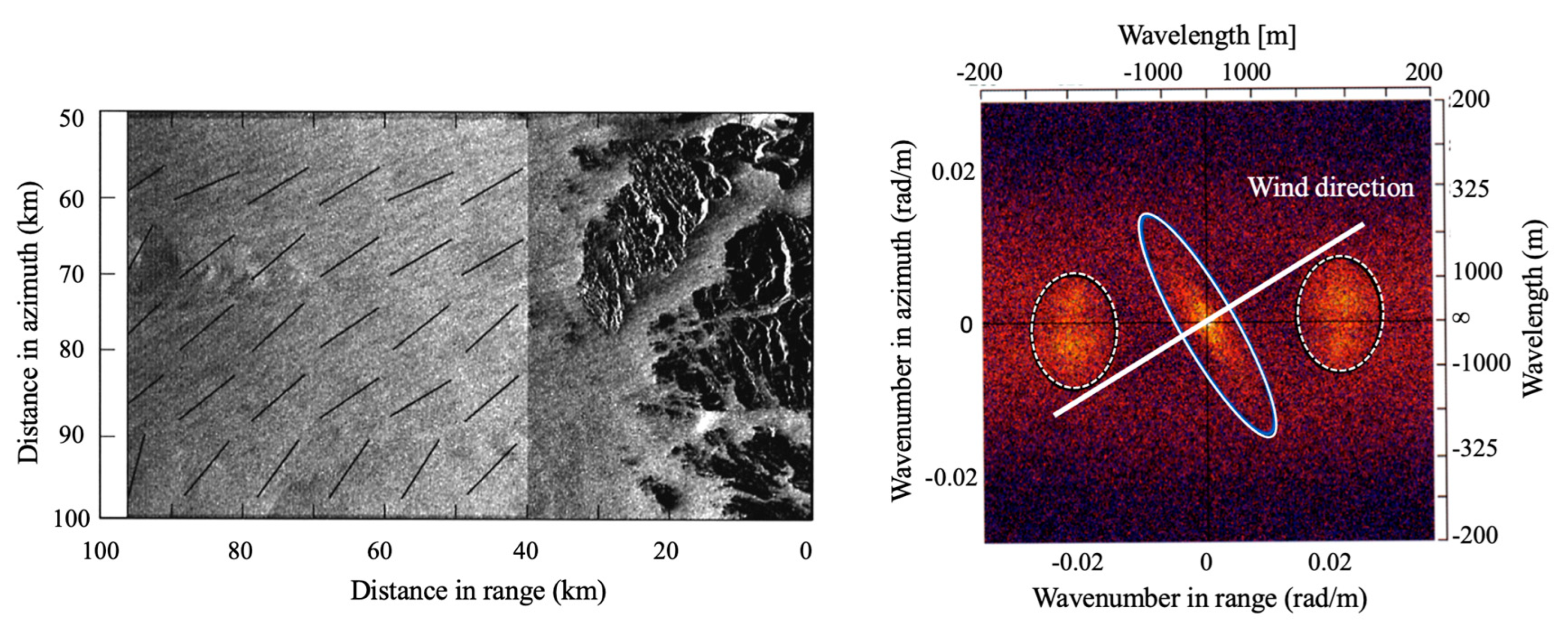
8. Wind
9. Other Oceanic Phenomena
9.1. Aquaculture
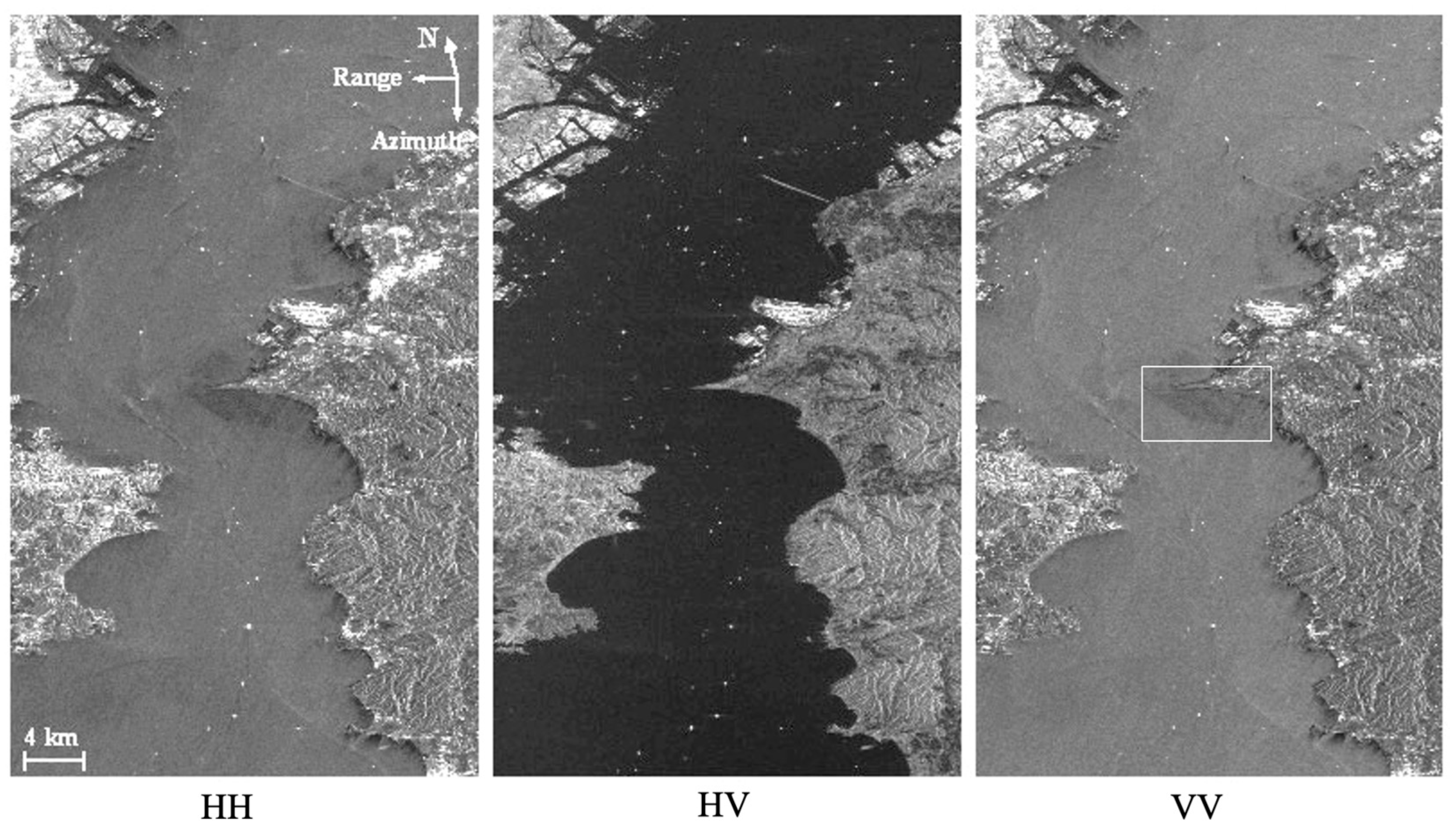
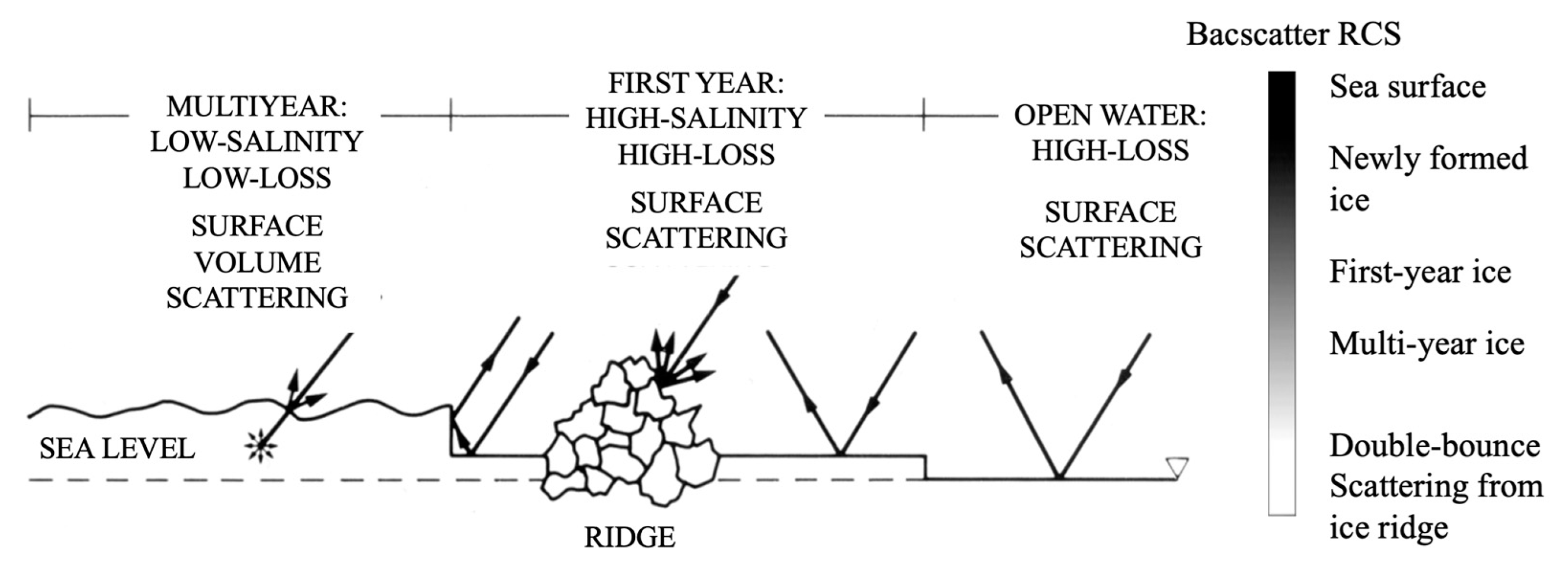
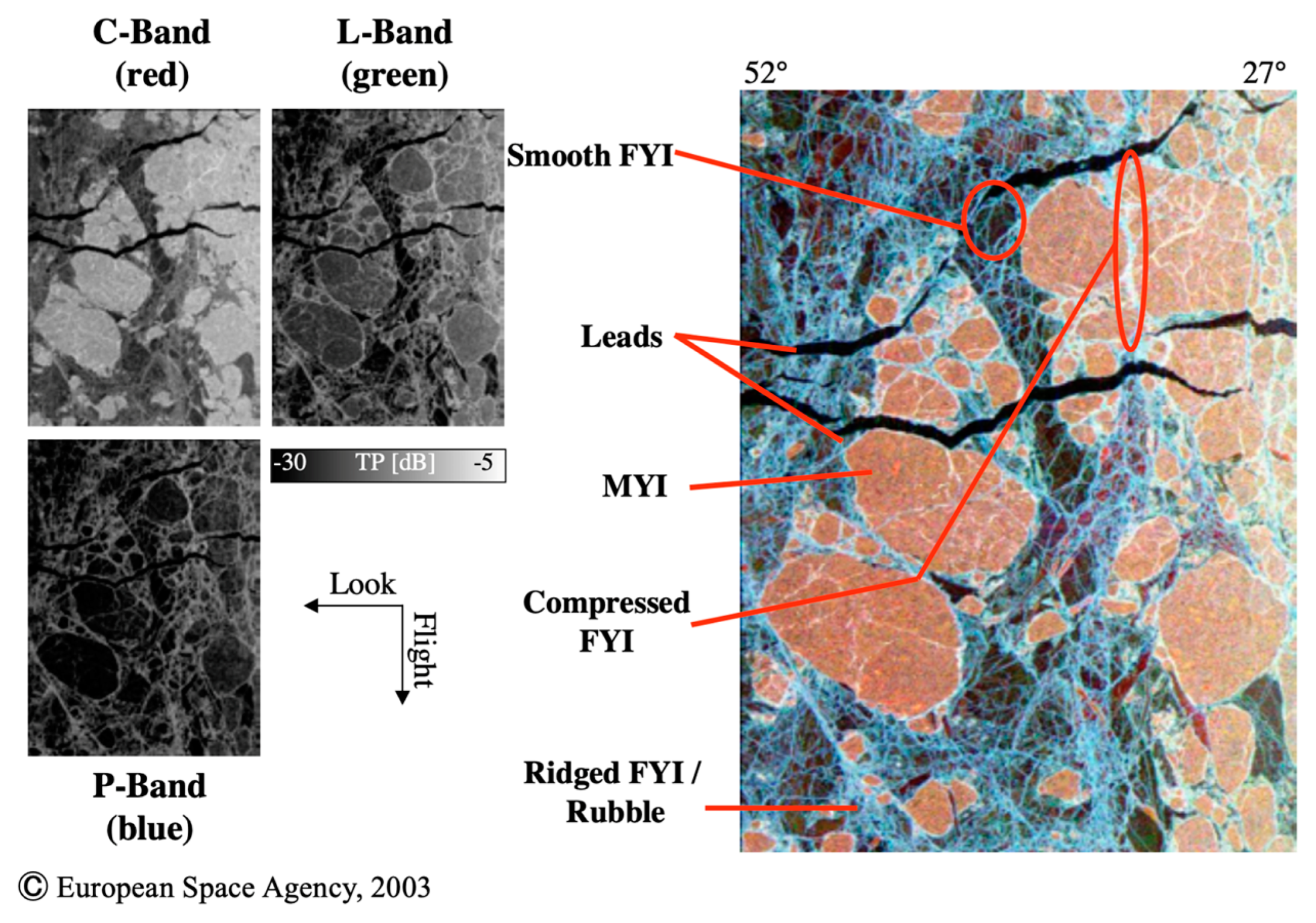
9.2. Sea Ice
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Ouchi, K. Recent trend and advance of synthetic aperture radar with selected topics. Remote Sens. 2013, 5, 716–807. [Google Scholar] [CrossRef]
- Huber, S.; de Almeida, F.Q.; Villano, M.; Younis, M.; Krieger, G.; Moreira, A. Tandem–L: A technical prospective on future spaceborne SAR sensors for earth observation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4792–4807. [Google Scholar] [CrossRef]
- Shimada, M. Imaging from Spaceborne and Airborne SARs, Calibration, and Applications; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Jackson, C.R.; Apel, J.R. (Eds.) Synthetic Aperture Radar Marine User’s Manual; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2004; pp. 1–457.
- Bamler, R.; Hartle, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Fletcher, K. (Ed.) InSAR Principles: Guidance for SAR Interferometry Processing and Interpretation; ESA Publication, ESTEC: Noordwijk, The Netherland, 2007. [Google Scholar]
- Rosen, P.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Yague-Martinez, M.; Prats-Iraola, P.; Gonzalez, F.R.; Brcic, R.; Shau, R.; Geudtner, D.; Eineder, M.; Bamler, R. Interferometric processing of Sentinel-1 TOPS fata. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2220–2234. [Google Scholar] [CrossRef]
- Wang, R.; Deng, Y. Bistatic InSAR. In Bistatic SAR System and Signal Processing Technology; Springer: Singapore, 2018. [Google Scholar]
- Romeiser, R.; Runge, H. Theoretical evaluation of several possible along-track InSAR modes of TerraSAR-X for ocean current measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 21–35. [Google Scholar] [CrossRef]
- Romeiser, R.; Runge, H.; Suchandt, S.; Kahle, R.; Rossi, C.; Bell, P.S. Quality assessment of surface current fields from TerraSAR-X and TanDEM-X along-track interferometry and Doppler centroid analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2759–2772. [Google Scholar] [CrossRef]
- Suchandt, S.; Runge, H. Ocean surface observations using the TanDEM-X satellite formation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5096–5105. [Google Scholar] [CrossRef]
- Wollstadt, S.; López-Dekker, P.; Zen, D.F.; Younis, M. Design principles and considerations for spaceborne ATI SAR-based observations of ocean surface velocity vectors. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4500–4519. [Google Scholar] [CrossRef]
- Ouchi, K.; Yoshida, T.; Yang, C.-S. A theory of multiaperture along-track interferometric synthetic aperture radar. IEEE Geosc. Remote Sens. Lett. 2019, 16, 1565–1569. [Google Scholar] [CrossRef]
- Yoshida, T.; Ouchi, K.; Yang, C.-S. Application of MA-ATI SAR for estimating the direction of moving water surface currents. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2724–2730. [Google Scholar] [CrossRef]
- Boerner, W.-M.; Yan, W.L.; Xi, A.-Q.; Yamaguchi, Y. On the basic principles of radar polarimetry: The target characteristic polarization state theory of Kennaugh, Huynen’s polarization folk concept, and its extension to the partially polarized case. Proc. IEEE 1991, 79, 1538–1550. [Google Scholar] [CrossRef]
- Cloude, S.R. A review of target decomposition theorem in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basic to Applications; CRS Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Yamaguchi, Y. Polarimetric SAR Imaging: Theory and Applications; CRS Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Deng, L.; Yu, D. Deep learning: Method and Applications. Signal Process. 2013, 7, 197–387. Available online: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/DeepLearning-NowPublishing-Vol7-SIG-039.pdf (accessed on 15 November 2022).
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Xu, F.; Jin, Y.-Q. Target classification using the deep convolution networks for SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.-Q. Complex valued convolution neural network and its application in polarimetrc SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Haenlein, M.; Kaplan, A. A brief history of artificial intelligence: On the past, present, and future of artificial intelligence. Calif. Manag. Rev. 2019, 61, 5–14. [Google Scholar] [CrossRef]
- Oveis, A.H.; Giusti, E.; Ghio, S.; Martorella, M. A survey on the applications of convolutional neural networks for synthetic aperture radar: Recent advances. IEEE Aerosp. Electron. Syst. Mag. 2022, 37, 18–42. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, Z.; Gan, H.; Xiang, D.; Zhu, S.; Yang, J. PolSAR ship detection using the joint polarimetric information. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8225–8241. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Maghsoudi, Y.; Salehi, M.; Bordbari, R. Exploitation of sub-look analysis and polarimetric signatures for ship detection in PolSAR data. Int. J. Remote Sens. 2022, 43, 1178–1198. [Google Scholar] [CrossRef]
- Lin, H.; Wang, H.; Wang, J.; Yuin, J.; Yang, J. A novel ship detection method via generalized polarization relative entropy for PolSAR images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4401205. [Google Scholar] [CrossRef]
- Won, E.-S.; Ouchi, K.; Yang, C.-S. Extraction of underwater laver cultivation nets by SAR polarimetric entropy. IEEE Geosci. Remote Sens. Lett. 2013, 10, 231–235. [Google Scholar]
- Scheuchl, B.; Hajnsek, I.; Cumming, I. Classification strategies for polarimetric SAR sea ice data. In Proceedings of the Workshop on POLinSAR, Frascati, Italy, 14–16 January 2003. [Google Scholar]
- Zhang, X.; Dierking, W.; Zhang, J.; Meng, J. A polarimetric decomposition method for ice in the Bohai Sea using C-band PolSAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 47–66. [Google Scholar] [CrossRef]
- He, L.; Hui, F.; Ye, Y.; Zhang, T.; Cheng, X. Investigation of polarimetric decomposition for arctic summer sea ice classification using Gaofen-3 polarimetric SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3904–3915. [Google Scholar] [CrossRef]
- Skrunes, S.; Brekke, C.; Eltoft, T. Characterization of marine surface slicks by Radarsat-2 multipolarization features. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5302–5319. [Google Scholar] [CrossRef]
- Skrunes, S.; Brekke, C.; Jones, C.E.; Holt, B. A multisensor comparison of experimental oil spill in polarimetric SAR for high wind condition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4948–4961. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Hou, Y.; Wang, X.; Wang, L. Marine oil slick detection using improved polarimetric feature parameters based on polarimetric synthetic aperture radar data. Remote Sens. 2021, 13, 1607. [Google Scholar] [CrossRef]
- Al-Ruzouq, R.; Gibril, M.B.A.; Shanableh, A.; Kais, A.; Hamed, O.; Al-Mansoori, S.; Khalil, M.A. Sensors, features, and machine learning for oil spill detection and monitoring: A review. Remote Sens. 2020, 12, 3338. [Google Scholar] [CrossRef]
- Fan, W.; Zhou, F.; Bai, X.; Tao, M.; Tian, Y. Ship detection using deep convolution neural networks for PolSAR images. Remote Sens. 2019, 11, 2862. [Google Scholar] [CrossRef]
- Hou, X.; Ao, W.; Song, Q.; Lai, J.; Wang, H.; Xu, F. FUSAR-SHIP: Building a high-resolution SAR-AIS matchup dataset of Gaofen-3 for ship detection and recognition. Sci. China Inf. Sci. 2020, 63, 140303. [Google Scholar] [CrossRef]
- Cui, J.; Jia, H.; Wang, H.; Xu, F. A fast threshold neural network for ship detection in large-scene SAR images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6016–6032. [Google Scholar] [CrossRef]
- Yoshida, T.; Ouchi, K. Detection of ships cruising in the azimuth direction using Spotlight SAR images with a deep learning method. Remote Sens. 2022, 14, 4691. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Zhang, H.; Dong, Y.; Wei, S. Automatic ship detection based on RetinaNet using multi-resolution Gaofen-3 imagery. Remote Sens. 2019, 11, 531. [Google Scholar] [CrossRef]
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc/s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C. Evidence of Bragg scattering in microwave Doppler spectra of sea return. J. Geophys. Res. 1990, 95, 16299–16310. [Google Scholar] [CrossRef]
- Alpers, W.; Rufenach, C.L. The effect of orbital motion on synthetic aperture radar imagery of ocean waves. IEEE Trans. Antennas Propag. 1979, AP-27, 685–690. [Google Scholar] [CrossRef]
- Hasselmann, K.; Raney, K.; Plant, W.J.; Alpers, W.; Shuchman, R.A.; Lyzenga, D.R.; Rufenach, C.L.; Tucker, M.J. Theory of synthetic aperture radar ocean imaging: A MAESEN view. J. Geophys. Res. 1985, 90, 4659–4686. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Shuchman, R.A.; Lyden, J.D. SAR imaging of waves in water and ice: Evidence for velocity bunching. J. Geophys. Res. 1985, 90, 1031–1036. [Google Scholar] [CrossRef]
- Ouchi, K. Synthetic aperture radar imagery of range traveling waves. IEEE Trans. Geosci. Remote Sens. 1988, GE-26, 30–37. [Google Scholar] [CrossRef]
- Ouchi, K. Two-dimensional imaging mechanism of ocean waves by synthetic aperture radars. J. Phys. D Appl. Phys. 1994, 17, 25–42. [Google Scholar] [CrossRef]
- Ouchi, K.; Maedoi, S.; Mitsuyasu, H. Determination of ocean wave propagation direction by split-look processing using JERS-1 SAR data. IEEE Trans. Geosci. Remote Sens. 1999, GE-37, 849–855. [Google Scholar] [CrossRef]
- Li, J.-G.; Holt, M. Comparison of Envisat ASAR ocean wave spectra with buoy and altimeter data via a wave model. J. Atmos. Ocean. Technol. 2009, 26, 593–614. [Google Scholar] [CrossRef]
- Li, h.; Chapron, B.; Mouche, A.; Stopa, J.E. A new ocean SAR cross-spectral parameter: Definition and directional property using the global Sentinel-A measurements. J. Geophys. Res. Oceans 2019, 124, 1566–1577. [Google Scholar] [CrossRef]
- Brasil-Correa, Y.O.; Violante-Carvalho, N.; Santos, F.M.; Carvalho, L.M.; Santos, A.L.C.; Costa, L.P.F.; Portilla-Yandun, J.; Romeiser, R. Evaluation of a linear inversion method for retrieval of directional wave spectra from SAR look cross spectra. Remote Sens. Environ. 2022, 282, 13265. [Google Scholar] [CrossRef]
- Quach, B.; Glaser, Y.; Stopa, J.E.; Mouche, A.A.; Sadowski, P. Deep learning for predicting significant wave height from synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1859–1867. [Google Scholar] [CrossRef]
- Xue, S.; Geng, X.; Yan, X.-H.; Xie, T.; Yu, Q. Significant wave height retrieval from Sentinel-1 SAR imagery by convolutional neural network. J. Oceanogr. 2020, 76, 465–477. [Google Scholar] [CrossRef]
- Ekman, V.W. On Dead Water. In The Norwegian North Polar Expedition 1893–1896: Scientific Results; Nansen, F., Ed.; Longmans, Green and Co.: New York, NY, USA, 1904; Volume V, Chapter XV; pp. 1–152. [Google Scholar]
- Fourdrinoy, J.; Dambrine, J.; Petcu, M.; Rousseaux, G. The dual nature of the dead-water phenomenology: Nansen verses Ekman wave-making drags. Appl. Phys. Sci. 2020, 117, 16770–16775. [Google Scholar] [CrossRef] [PubMed]
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing of ocean internal waves: An overview. J. Coast. Res. 2012, 28, 540–546. [Google Scholar] [CrossRef]
- Jackson, C.R.; da Silva, J.C.B.; Jeans, G.; Alpers, W.; Caruso, M.J. Nonlinear internal waves in synthetic aperture radar imagery. Oceanography 2013, 26, 68–79. [Google Scholar] [CrossRef]
- Hong, D.-B.; Yang, C.-S.; Ouchi, K. Estimation of internal wave velocity in the shallow South China Sea using single and multiple satellite images. Remote Sens. Lett. 2015, 6, 448–457. [Google Scholar] [CrossRef]
- Dwi Susanto, R.; Mitnik, L.; Zheng, Q. Ocean internal waves observed in the Lombok Strait. Oceanography 2005, 18, 80–87. [Google Scholar] [CrossRef]
- Li, L.; Pawlowicz, R.; Wang, C. Seasonal variability and generation mechanisms of nonlinear internal waves in the Strait of Georgia. J. Geophys. Res. Oceans 2018, 123, 5706–5726. [Google Scholar] [CrossRef]
- Feng, Y.; Tang, Q.; Li, J.; Sun, J.; Zhan, W. Internal solitary waves observed on the continental shelf in the northern South China Sea from acoustic backscatter data. Front. Marine Sci. 2021, 8, 734075. [Google Scholar] [CrossRef]
- Leichter, J.J.; Shellenbarger, G.; Genovese, S.J.; Wing, S.R. Breaking internal waves on a Florida (USA) coral reef: A plankton pump at work? Mar. Ecol. Prog. Ser. 1998, 166, 83–97. [Google Scholar] [CrossRef]
- Alford, M.H. Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature 2003, 423, 159–162. [Google Scholar] [CrossRef] [PubMed]
- Matthews, J.P.; Aiki, H.; Masuda, S.; Awaji, T.; Ishikawa, Y. Monsoon regulation of Lombok Strait internal waves. J. Geophys. Res. 2011, 116, C05007. [Google Scholar] [CrossRef]
- Garwood, J.C.; Musgrave, R.C.; Lucus, A.J. Life in internal waves. Oceanography 2020, 33, 38–49. [Google Scholar] [CrossRef]
- Whalen, C.B.; de Lavergne, C.; Naveira Carabato, A.C.; Klymak, J.M.; Mackinnon, J.A.; Sheen, K. Internal wave-driven mixing: Governing processes and consequences for climate. Nat. Rev. Earth Environ. 2020, 1, 606–621. [Google Scholar] [CrossRef]
- da Silva, J.C.B.; Ermakov, S.A.; Robinson, I.S. Role of surface films in ERS SAR signatures of internal waves on the shelf 3. Mode transitions. J. Geophys. Res. 2000, 105, 24089–24104. [Google Scholar] [CrossRef]
- Muacho, S.; de Silva, J.C.B.; Brotas, V.; Oliveira, P.B. Effect of internal waves on near-surface chlorophyll concentration and primary production in the Nazare Canyon (west of the Iberian Peninsula). Deep-Sea Res. 2013, 81, 89–96. [Google Scholar] [CrossRef]
- Bao, S.; Meng, J.; Sun, L.; Liu, Y. Detection of ocean internal waves based on Faster R-CNN in SAR images. J. Ocean. Limnol. 2020, 38, 55–63. [Google Scholar] [CrossRef]
- Liu, B.; Yang, H.; Zhao, Z.; Li, X. Internal solitary wave propagation observed by tandem satellites. Geophys. Res. Lett. 2014, 41, 2077–2085. [Google Scholar] [CrossRef]
- Munk, W. Internal waves and small-scale processes. In Evolution of Physical Oceanography; Warren, B.A., Wunsh, C., Eds.; The MIT Press: Cambridge, UK, 2007; pp. 264–291. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Apel, J.R. A new analytical model for internal solitons in the ocean. J. Phys. Oceanogr. 2003, 33, 2247–2269. [Google Scholar] [CrossRef]
- Dejak, S.I.; Sigal, I.M. Long-time dynamics of KdV solitary waves over a variable bottom. Commun. Pure Appl. Math. 2006, 59, 869–905. [Google Scholar] [CrossRef]
- Bocharov, A.A.; Khabakhpashev, G.A.; Tsvelodub, O.Y. Numerical simulation of plane and spatial nonlinear stationary waves in a two-layer fluid of arbitrary depth. Fluid Dyn. 2008, 43, 118–124. [Google Scholar] [CrossRef]
- Hong, D.-B.; Yang, C.-S.; Ouchi, K. Preliminary study of internal solitary wave amplitude off the east coast of Korea based on synthetic aperture radar data. J. Mar. Sci. Technol. 2016, 24, 1194–1203. [Google Scholar]
- Thompson, D.R.; Gasparovic, R.F. Intensity modulation in SAR images of internal waves. Nature 1986, 320, 343–348. [Google Scholar] [CrossRef]
- Holliday, D.; St-Cyr, G.; Woods, E.E. Comparison of a new ocean imaging model with SARSEX internal wave image data. Int. J. Remote Sens. 1988, 9, 1423–1430. [Google Scholar] [CrossRef]
- Hogan, G.G.; Chapman, R.D.; Watson, G.; Thompson, D.R. Observations of ship-generated internal waves in SAR images from Loch Linnhe, Scotland, and comparison with theory and in situ internal wave measurements. IEEE Trans. Geosci. Remote Sens. 1996, 34, 532–542. [Google Scholar] [CrossRef]
- Ouchi, K. Modulation of waveheight spectrum and radar cross section by varying surface currents. IEEE Trans. Geosci. Remote Sens. 1994, GE-32, 995–1003. [Google Scholar] [CrossRef]
- Ouchi, K.; Stapleton, N.R.; Barber, B.C. Multi-frequency SAR images of ship-generated internal waves. Int. J. Remote Sens. 1997, 18, 3709–3718. [Google Scholar] [CrossRef]
- Thompson, D.R.; Jensen, J.R. Synthetic aperture radar interferometry applied to ship-generated internal waves in the 1989 Loch Linnhe experiment. J. Geophys. Res. 1993, 98, 10259–10269. [Google Scholar] [CrossRef]
- Garber, H.C.; Thompson, D.R.; Carande, R.E. Ocean surface features and currents measured with synthetic aperture radar interferometry and HF radar. J. Geophys. Res. 1996, 101, 25813–35832. [Google Scholar] [CrossRef]
- Romeiser, R.; Graber, H.C. Advanced remote sensing of internal waves in speceborne along-track InSAR-A demonstration with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6735–6751. [Google Scholar] [CrossRef]
- Gabele, M.; Brautigam, B.; Shulze, D.; Tous-Ramon, N.; Younis, M. Fore and aft channel reconstruction in the TerraSAR-X dual receive antenna mode. IEEE Trans. Geosci. Remote Sens. 2010, 48, 795–806. [Google Scholar] [CrossRef]
- Leifer, L.; Lehr, B.; Semecek-Beatty, D.; Clark, E.; Dannison, P.; Hu, Y.; Matheson, S.; Jones, C.; Holt, B.; Reif, M.; et al. State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ. 2012, 124, 185–209. [Google Scholar] [CrossRef]
- Garcia-Pineda, O.; MacDonald, I.; Hu, C.; Svejkovsky, J.; Hess, M.; Dukhovskoy, D.; Morey, S.L. Detection of floating oil anomalies from the Deepwater Horizon oil spill with synthetic aperture radar. Oceanography 2013, 26, 124–137. [Google Scholar] [CrossRef]
- Marghany, M. Automatic Mexico Gulf oil spill detection from Radarsat-2 SAR satellite data using genetic algorithm. Acta Geophys. 2016, 64, 1916–1941. [Google Scholar] [CrossRef]
- Pallardy, R. Deepwater Horizon Oil Spill: Environmental Disaster, Gulf of Mexico [2010]. Britannica. Available online: https://www.britannica.com/event/Deepwater-Horizon-oil-spill#ref294126 (accessed on 3 November 2022).
- Oil Tanker Spill Statistics 2021. Available online: https://www.itopf.org/knowledge-resources/data-statistics/statistics/ (accessed on 3 November 2022).
- Kim, D.-J.; Moon, W.M.; Kim, Y.-S. Application of TerraSAR-X data for emergent oil-spill monitoring. IEEE Trans. Geosci. Remote Sens. 2010, 48, 852–863. [Google Scholar]
- Alpers, W.; Holt, B.; Zeng, K. Oil spill detection by imaging radars: Challenges and pitfalls. Remote Sens. Environ. 2017, 201, 133–147. [Google Scholar] [CrossRef]
- Brekke, K.; Solberg, A.H.D. Classifiers and confidence estimation for oil spill detection in ENVISAT ASAR images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 65–69. [Google Scholar] [CrossRef]
- Fingas, M.; Brown, C.E. A review of oil spill remote sensing. Sensors 2018, 18, 91. [Google Scholar] [CrossRef]
- Brekke, K.; Solberg, A.H.D. Oil spill detection by satellite remote sensing. Remote Sens. Environ. 2005, 95, 1–13. [Google Scholar] [CrossRef]
- Solberg, A.H.D.; Brekke, K.; Husoy, P.O. Oil spill detection in Radarsat and Envisat SAR images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 746–755. [Google Scholar] [CrossRef]
- Carvalho, C.d.A.; Minnett, P.J.; Ebecken, N.F.F.; Landau, L. Oil spills or look-alikes? Classification rank of surface ocean slick signatures in satellite data. Remote Sens. 2021, 13, 3466. [Google Scholar] [CrossRef]
- Migliaccio, M.; Nunziata, F.; Buono, A. SAR polarimetry for sea oil slick observation. Int. J. Remote Sens. 2015, 36, 3243–3273. [Google Scholar] [CrossRef]
- Espeseth, M.; Skrunes, S.; Jones, C.E.; Brekke, C.; Holt, B.; Doulgeris, A.P. Analysis of evolving oil spills in full-polarimetric and hybrid-polarity SAR. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4190–4210. [Google Scholar] [CrossRef]
- Shaban, M.; Salim, R.; Abu Khalifeh, H.; Khelifi, A.; Shalaby, A.; El-Mashad, S.; Mahmoud, A.; Ghazal, M.; El-Baz, A. A deep-learning framework for the detection of oil spills from SAR data. Sensors 2021, 21, 2351. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, Z. Marine oil spill detection from SAR images based on attention U-Net model using polarimetric and wind speed information. Int. J. Environ. Res. Public Health 2022, 19, 12315. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, Y.; Li, Z.; Yan, X.; Guan, Q.; Zhong, Y.; Zhang, L.; Li, D. Oil spill contextual and boundary-supervised detection network based on Marine SAR images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5213910. [Google Scholar] [CrossRef]
- Song, D.; Ding, Y.; Li, X.; Zhang, B.; Xu, M. Ocean oil spill classification with RADARSAT-2 SAR based on an optimized wavelet neural network. Remote Sens. 2017, 9, 799. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, Y.; Wang, Y. Polarimetric Features Analysis of Oil Spills in C-band and L-band SAR Images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Angelliaume, S.; Minchew, B.; Cataing, S.; Martineau, P.; Miegebielle, V. Multifrequency radar imagery and characterization of hazardous and noxious substance at sea. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3051–3066. [Google Scholar] [CrossRef]
- Mohr, V.; Gade, M. Marine oil pollution in an area of high economic use: Statistical analyses of SAR data from the western Java Sea. Remote Sens. 2022, 14, 880. [Google Scholar] [CrossRef]
- Kongsberg Satellite Services. Oil Spill Detection Service. Available online: https://www.ksat.no/earth-observation/environmental-monitoring/oil-spill-detection-service/ (accessed on 15 November 2022).
- Beegle-Krause, C.J. General NOAA oil modeling environment (GNOME): A new spill trajectory model. In Proceedings of the 2001 International Oil Spill Conference, Florida, FL, USA, 26–29 March 2001. [Google Scholar]
- General NOAA Operational Modeling Environment. Available online: https://response.restoration.noaa.gov/oil-and-chemical-spills/oil-spills/oil-spills/response-tools/ (accessed on 14 November 2022).
- IMO. Manual on Oil Pollution: Section IV-Combating Oil Spills (2005 edition); The Nautical Mind: Toronto, ON, Canada, 2006. [Google Scholar]
- Espeseth, M.M.; Brekke, C.; Jones, C.E.; Holt, B.; Freeman, A. The impact of system noise in polarimetric SAR imagery on oil spill observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4194–4214. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSDSingle Shot Multibox Dector// European Conference on Computer Vision; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Chang, Y.-L.; Anagaw, A.; Chang, L.; Wang, Y.C.; Hsiao, C.-Y.; Lee, W.-H. Ship detection based on YOLOv2 for SAR imagery. Remote Sens. 2019, 11, 786. [Google Scholar] [CrossRef]
- Jiang, J.; Fu, X.; Qin, R.; Wang, X.; Ma, Z. High-speed lightweight ship detection algorithm based on YOLO-V4 for three-channels RGB SAR Image. Remote Sens. 2021, 13, 1909. [Google Scholar] [CrossRef]
- Hong, Z.; Yang, T.; Tong, X.; Zhang, Y.; Jiang, S.; Zhou, R.; Han, Y.; Wang, J.; Yang, S.; Liu, S. Multi-scale ship detection from SAR and optical imagery via A More Accurate YOLOv3. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6083–6101. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fisher, P.; Brox, T. U-Net: Convolution Networks for Biomedical Image Segmentation. MICCAI 2015, 9351, 234–241. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Singha, S.; Bellerby, T.J.; Trieschmann, O. Satellite oil spill detection using artificial neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2355–2363. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; He, Y.; Jian, T. Supervised oil spill classification based on full polarimetric features. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Fan, Y.; Rui, X.; Zhang, G.; Yu, T.; Xu, X.; Poslad, S. Feature merged network for oil spill detection using SAR images. Remote Sens. 2021, 13, 3174. [Google Scholar] [CrossRef]
- Amri, E.; Dardouillet, P.; Benoit, A.; Courteille, H.; Bolon, P.; Dubucq, D.; Credoz, A. Offshore oil slick detection: From photo-interpreter to explainable multi-modal deep learning models using SAR images and contextual data. Remote Sens. 2022, 14, 3565. [Google Scholar] [CrossRef]
- Wang, D.; Wan, J.; Liu, S.; Chen, Y.; Yasir, M.; Xu, M.; Ren, P. BO-DRNet: An improved deep learning model for oil spill detection by polarimetric features from SAR images. Remote Sens. 2022, 14, 264. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Huang, X.; Zhang, B.; Perrie, W.; Lu, Y.; Wang, C. A novel deep learning method for marine oil spill detection from satellite synthetic aperture radar imagery. Mar. Pollut. Bull. 2022, 179, 113666. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free surface, topography-following-coordinate oceanic model. Ocean Model 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Dietrich, J.R.; Tanaka, S.; Westerink, J.J.; Dawsom, C.N.; Luettich, R.A., Jr.; Zijlema, M.; Holthuijsen, L.H.; Smith, J.M.; Westerink, L.G.; Westerink, H.J. Performance of the unstructured-mesh, SWAN+ADCIRC model in computing hurricane waves and surge. J. Sci. Comput. 2012, 52, 468–497. [Google Scholar] [CrossRef]
- Dietrich, J.C.; Trahan, C.J.; Howard, M.T.; Fleming, J.G.; Weaver, R.J.; Tanaka, S.; Yu, I.; Luettich, R.A., Jr.; Dawson, C.N.; Westerink, J.J.; et al. Surface trajectories of oil transport along the northern coastline of the Gulf of Mexico. Cont. Shelf Res. 2012, 41, 17–47. [Google Scholar] [CrossRef]
- Lehr, W.J.; Simecek-Beatty, D. The relation of Langmuir circulation processes to the standard oil spill spreading, dispersion, and transport algorithms. Spill Sci. Technol. Bull. 2000, 6, 247–253. [Google Scholar] [CrossRef]
- Abascal, A.J.; Castanedo, S.; Mendez, F.J.; Medina, R.; Losada, I.J. Calibration of a Lagrangian transport model using drifting buoys deployed during the Prestige oil spill. J. Coast. Res. 2009, 25, 80–90. [Google Scholar] [CrossRef]
- Fingas, M.F. The evaporation of oil spills: Development and implementation of new prediction methodology. In Proceedings of the 1999 International Oil Spill Conference, Seattle, WA, USA, 8–11 March 1999. [Google Scholar]
- Kim, T.-H.; Yang, C.-S.; Oh, J.-H.; Ouchi, K. Analysis of the contribution of wind drift factor to oil slick movement under strong tidal condition: Hebei Spirit oil spill case. PLoS ONE 2014, 9, e87393. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.-H.; Yang, C.-S.; Ouchi, K. Application of synthetic aperture radar imagery for forward and backward tracking of oil slicks. Terr. Atmos. Ocean. Sci. 2019, 30, 509–519. [Google Scholar] [CrossRef]
- Chaturvedi, S.K.; Yang, C.-S.; Ouchi, K.; Shanmugam, P. Ship recognition by integration of SAR and AIS. J. Navigat. 2012, 65, 323–337. [Google Scholar] [CrossRef]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. 2005, 110, C07008. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Chapron, B.; Collard, F.; Kudryavtsev, V.; Mouche, A.; Akimov, D.; Dagestad, K.-F. Direct ocean surface velocity measurements from space: Improved quantitative interpretation of Envisat ASAR observations. Geophys. Res. Lett. 2008, 35, L22608. [Google Scholar] [CrossRef]
- Jackson, G.; Fornaro, G.; Beradino, P.; Esposito, C.; Lanari, R.; Pauciullo, A.; Reale, D.; Zamparelli, V.; Perna, S. Experiments on sea surface current estimation with space and airborne SAR systems. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Zamparelli, V.; De Santi, F.; Cucco, A.; Zecchetto, S.; De Carolis, G.; Fornaro, G. Suface currents derived from SAR Doppler processing: An analysis over the Naples coastal region in South Italy. J. Mar. Sci. Eng. 2020, 8, 203. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A. Interferometric radar measurement of ocean surface currents. Nature 1987, 328, 707–709. [Google Scholar] [CrossRef]
- Ainsworth, T.L.; Lee, J.-S. (Naval Research Laboratory, Washington, DC, USA). Personal communication, 2002.
- Ainsworth, T.L.; Chubb, S.R.; Fusina, R.A.; Goldsteim, R.M.; Jansen, R.W.; Lee, J.-S.; Valenzuela, G.R. INSAR imagery of surface currents, wave fields, and fronts. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1117–1123. [Google Scholar] [CrossRef]
- Romeiser, R. Current measurements by airborne along-track InSAR: Measuring technique and experimental results. IEEE J. Ocean. Eng. 2005, 30, 552–569. [Google Scholar] [CrossRef]
- Kojima, S.; Umehara, T.; Umeno, J.; Kobayashi, T.; Satake, M.; Uratsuka, S. Development of Pi-SAR2 along-track interferometric system. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Romeiser, R.; Seibt-Winckler, A.; Heineke, M.; Eppel, D. Validation of current and bathymetry measurements in the German Bight by airborne along-track interferometric SAR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Romeiser, R.; Breit, H.; Einder, M.; Runge, H.; Flament, P.; de Long, K.; Vogelzang, J. Current measurements by SAR along-track interferometry from a space shuttle. IEEE Geosci. Remote Sens. 2005, 43, 2315–2324. [Google Scholar] [CrossRef]
- Rashid, M.; Gierull, C.H. Retrieval of ocean surface radial velocities with RADARSAT-2 along-track interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9597–9608. [Google Scholar] [CrossRef]
- Romeiser, R. The future of SAR-based oceanography: High-resolution current measurements by along-track interferometry. Oceanography 2013, 26, 92–99. [Google Scholar] [CrossRef]
- Frasier, S.J.; Camps, A.J. Dual-beam interferometry for ocean surface current vector mapping. IEEE Trans. Geosci. Remote Sens. 2001, 39, 401–414. [Google Scholar] [CrossRef]
- Farquharson, G.; Junek, W.N.; Ramanathan, A.; Frasier, G.; Tessier, R.; McLaughlin, D.J.; Sletten, M.A.; Toporkov, J.V. A pod-based dual-beam SAR. IEEE Geosci. Remote Sens. Lett. 2004, 1, 62–65. [Google Scholar] [CrossRef]
- Yoshida, T.; Ouchi, K.; Yang, C.-S. Validation of MA-ATI SAR theory using numerical simulation for estimating the direction of moving targets and ocean currents. IEEE Geosci. Remote Sens. Lett. 2021, 18, 677–681. [Google Scholar] [CrossRef]
- Kim, T.-H.; Yang, C.-S.; Ouchi, K. Interpretation of SAR image modulation by the interaction of current and bottom topography in Gyeonggi bay with microwave scattering models. J. Marine Sci. Technol. 2016, 24, 1171–1180. [Google Scholar]
- Cesbron, G.; Melet, A.; Almar, R.; Lifemann, A.; Tullot, D.; Crosnier, L. Pan-European satellite-derived coastal bathymetry-Review. Use needs and future services. Front. Mar. Sci. 2021, 8, 740830. [Google Scholar] [CrossRef]
- Alpers, W.; Hennings, I. A theory of imaging mechanism of underwater bottom topography by real and synthetic aperture radar. J. Geophys. Res. 1983, 99, 10529–10546. [Google Scholar] [CrossRef]
- Calkoen, C.J.; Hasselmans, G.H.F.M.; Wesink, G.J.; Vogelzang, J. The bathymetry assessment system: Efficient depth mapping in shallow seas using radar images. Int. J. Remote Sens. 2001, 22, 2973–2998. [Google Scholar] [CrossRef]
- De Valk, C.F.; Wensink, G.J. Measuring the bathymetry of shallow seas using radar imagery from satellite and aircraft. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2002. [Google Scholar]
- Alpers, W.; Campbell, G.; Wensink, H.; Zhang, Q. Underwater Topography. In Synthetic Aperture Radar Marine User’s Manual; Jackson, C.R., Apel, J.R., Eds.; National Oceanic and Atmospheric Administration (NOAA): Washington, DC, USA, 2004; pp. 245–262. [Google Scholar]
- Monteriro, F.J.M. Advanced Bathymetry Retrieval from Swell Patterns in High-Resolution SAR Images. Master’s Thesis, Miami University, Miami, FL, USA, December 2013; p. 466. [Google Scholar]
- European Marine Observation Data Network. Available online: https://emodnet.ec.europa.eu/en (accessed on 16 November 2022).
- Pleskachevsky, A.; Lehner, S.; Heege, T.; Mott, C. Synergy and fusion of optical and synthetic aperture radar satellite data for underwater topography estimation in coastal areas. Ocean Dyn. 2011, 61, 2099–2120. [Google Scholar] [CrossRef]
- Wiehle, S.; Pleskachevsky, A.; Gebhardt, C. Automatic bathymetry retrieval from SAR images. CEAS Space J. 2019, 11, 105–114. [Google Scholar] [CrossRef]
- Pereira, P.; Baptista, P.; Cunba, T.; Silva, P.A.; Romao, S.; Lafon, B. Estimation of nearshore bathymetry from high temporal resolution Sentinel-1A C-band SAR data–A case study. Remote Sens. Environ. 2019, 223, 166–178. [Google Scholar] [CrossRef]
- General Bathymetric Charts of the Oceans (GEBCO). Available online: http://www.gebco.net/ (accessed on 16 November 2022).
- Munk, W.H.; Scully-Power, P.; Zachariasen, F. Ships from space. Proc. R. Soc. Lond. A 1987, 412, 231–254. [Google Scholar]
- An Introduction to Maritime Domain Awareness (MDA). Available online: https://www.polestarglobal.com/resources/an-introduction-to-maritime-domain-awareness-mda (accessed on 16 November 2022).
- 19 Satellites in ExactEarth’s Real-Time Constellation Now in Service. Available online: https://newspaceglobal.com/exactearth-now-has-18-operational-satellites-ais-ship-tracking-hosted-payloads-10/ (accessed on 17 November 2022).
- Eyes on Every Ship. Available online: https://www.kongsberg.com/ru/maritime/the-full-picture-magazine/2016/1/eyes-on-every-ship/ (accessed on 17 November 2022).
- Greidanus, H.; Jackson, A.M. DECLIMS; State of the Art and User Needs; Report D1-A-v2-1.doc, Nr EVG2-CT-2002-20002; Joint Research Centre: Ispra, Italy, 2005. [Google Scholar]
- Arnesen, T.N.; Olsen, R.B. Literature Review on Vessel Detection; FFI/RAPPORT-2004/02619; Norwegian Defence Research Establishment: Kjeller, Norway, 2004; Available online: https://www.ffi.no/en/publications-archive/literature-review-on-vessel-detection (accessed on 15 February 2023).
- Zhang, T.; Zhang, X.; Li, J.; Xu, X.; Wang, B.; Zhan, X.; Xu, Y.; Ke, X.; Zeng, T.; Su, H.; et al. SAR ship detection dataset (SSDD): Official release and comprehensive data analysis. Remote Sens. 2021, 13, 3690. [Google Scholar] [CrossRef]
- Trunk, G. Range resolution of targets using automatic detector. IEEE Trans. Aerosp. Electron. Syst. 1978, 14, 750–755. [Google Scholar] [CrossRef]
- Rohling, H. Radar CFAR thresholding in clutter and multiple target situation. IEEE Trans. Aerosp. Electron. Eng. 1983, 19, 608–621. [Google Scholar] [CrossRef]
- Armstrong, B.C.; Griffiths, H.D. CFAR detection of fluctuating targets in spatially correlated K-distribution clutter. IEE. Proc. F Rad. Sig. Proc. 1991, 138, 139–152. [Google Scholar]
- Vachon, P.; Campbell, J.; Bjerkelund, C.; Dobson, F.; Rey, M. Ship detection by the radarsat SAR: Validation of detection model predictions. Can. J. Remote Sens. 1997, 23, 48–59. [Google Scholar] [CrossRef]
- Papas, O.; Achim, A.; Bull, A. Superpixel-level CFAR detector for ship detection in SAR imager. IEEE Geosc. Remote Sens. Lett. 2018, 15, 1397–1401. [Google Scholar] [CrossRef]
- Smith, M.; Varshney, P. Intelligent CFAR processor based on data variability. IEEE Trans. Aersp. Electron. Syst. 2000, 36, 837–847. [Google Scholar] [CrossRef]
- Li, M.D.; Cui, X.C.; Chen, S.W. Adaptive superpixel-level CFAR detector for SAR inshore dense ship detection. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4010405. [Google Scholar] [CrossRef]
- Eldhuset, K. An automatic ship and ship wake detection system for spaceborne SAR images in coastal regions. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1010–1019. [Google Scholar] [CrossRef]
- Crisp, D. The State-of-the-Art in Ship Detection in Synthetic Aperture Radar Imagery; Defence Science and Technology Organization (DSTO) Information Science Laboratory: Edinburgh, UK, 2004.
- Tello, M.; Lopez-Martinez, C.; Mallorqui, J.J. A novel algorithm for ship detection in SAR imagery based on the wavelet transform. IEEE Geosci. Remote Sens. Lett. 2005, 2, 201–205. [Google Scholar] [CrossRef]
- Tello, M.; Lopez-Martinez, C.; Mallorqui, J.J.; Bonastre, R. Automatic detection of spots and extraction of frontiers in SAR images by means of the wavelet transform: Application to ship and coastline detection. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Ouchi, K.; Tamaki, S.; Yaguchi, S.; Iehara, M. Ship detection based on coherence images derived from cross correlation of multilook SAR images. IEEE Geosci. Remote Sens. Lett. 2004, 1, 184–187. [Google Scholar] [CrossRef]
- Brekke, C.; Anfinsen, S.N.; Larsen, Y. Subband extraction strategies in ship detection with the subaperture cross-correlation magnitude. IEEE Geosci. Remote Sens. Lett. 2013, 10, 786–790. [Google Scholar] [CrossRef]
- Hwang, S.-I.; Ouchi, K. On a novel approach using MLCC and CFAR for the improvement of ship detection by synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2010, 7, 391–395. [Google Scholar] [CrossRef]
- Marino, A.; Sanjuan-Ferrer, M.J.; Hajnsek, I.; Ouchi, K. Ship detectors spectral analysis of synthetic aperture radar: A comparison of new and well-known algorithms. Remote Sens. 2015, 7, 5416–5439. [Google Scholar] [CrossRef]
- Renga, A.; Graziano, M.D.; Moccia, A. Segmentation of marine SAR images by sublook analysis and application to sea traffic monitoring. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1463–1477. [Google Scholar] [CrossRef]
- Sanjuan-Ferrer, M.J.; Hajnsek, I.; Papathanassiou, K.P.; Moreira, A. A new detection algorithm for coherent scatterers in SAR data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6293–6307. [Google Scholar] [CrossRef]
- Arii, M. Improvement of ship-SAR clutter ratio of SAR imagery using standard deviation filter. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 13–28 July 2011. [Google Scholar]
- Ren, Y.; Li, X.; Xu, H. A deep learning model to extract ship size from Sentinel-1 SAR images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5203414. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Boisbunon, A.; Canu, S.; Fourdrinier, D.; Strawderman, W.; Wells, M.T. Akaike’s information criterion, Cp and estimators of loss for elliptically symmetric distributions. Int. Stat. Rev. 2014, 82, 422–439. [Google Scholar] [CrossRef]
- Ouchi, K. Vessel detection and classification by spaceborne synthetic aperture radar for maritime security and safety. NMIO Bull. 2017, 12, 22–29. [Google Scholar]
- Margarit, G.; Mallorqui, J.J.; Fabregas, X. Single-pass polarimetric SAR interferometry for vessel classification. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3494–3502. [Google Scholar] [CrossRef]
- Margarit, G.; Tabasco, A. Ship classification in single-pol SAR images based on fuzzy logic. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3129–3138. [Google Scholar] [CrossRef]
- Xing, X.; Ji, K.; Zou, H.; Chen, W.; Sun, J. Ship classification in TerraSAR-X images with feature space based sparse representation. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1562–1566. [Google Scholar] [CrossRef]
- Lang, H.; Zhang, J.; Zhang, T.; Zhao, D. Hierarchical ship detection and recognition with high-resolution polarimetic synthetic aperture radar imagery. J. Appl. Remote Sens. 2014, 8, 083623. [Google Scholar] [CrossRef]
- Ouchi, K.; Martin, G.M.; Yang, C.-S. Ship detection and classification by TerraSAR-X in Tokyo Bay, Japan and Alboran Sea in the Mediterranean Sea: A summary. In Proceedings of the International Conference on Remote, Sensing 2018, Pyeongchang, Republic of Korea, 9–11 May 2018. [Google Scholar]
- Dechesne, C.; Lefevre, S.; Vadaone, R.; Hajduch, G.; Fabiet, R. Ship identification and characterization in Sentinel-1 SAR images with Multi-Task Deep Learning. Remote Sens. 2019, 11, 2997. [Google Scholar] [CrossRef]
- Ma, M.; Chen, J.; Liu, W.; Yang, W. Ship classification and detection based on CNN using GF-3 SAR Images. Remote Sens. 2018, 10, 2043. [Google Scholar] [CrossRef]
- Bentes, C.; Velotto, D.; Tings, B. Ship classification in TerraSAR-X images with convolutional neural networks. IEEE J. Ocean. Eng. 2018, 43, 258–266. [Google Scholar] [CrossRef]
- Stoffelem, A.; Anderson, D. Scatterometer data interpretation: Derivation of the transfer function CMOD4. J. Geophys. Res. 1997, 102, 5767–5780. [Google Scholar] [CrossRef]
- Isoguchi, O.; Shimada, M. An L-band ocean geophysical model function derived from PALSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1925–1936. [Google Scholar] [CrossRef]
- Stoffelem, A.; Verspeek, J.A.; Vogelzang, J.; Verhoef, A. The CMOD7 geophysical model function for ASCAT and ERS wind retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2123–2134. [Google Scholar] [CrossRef]
- Moutuori, A.; de Ruggiero, P.; Migliaccio, M.; Pierini, S.; Spezie, G. X-band COSMO-SkyMed wind field retrieval, with application to coastal circulation modeling. Ocean Sci. 2013, 9, 121–132. [Google Scholar] [CrossRef]
- Quik Scatterometer (QuikSCAT). Available online: https://podaac.jpl.nasa.gov/QuikSCAT?tab=-mission-objectives (accessed on 10 December 2022).
- Horstmann, J.; Lehner, S.; Koch, W.; Tonboe, R. Computation of wind vectors over the ocean using spaceborne synthetic aperture radar. Johns Hopkins APL Tec. Dig. 2000, 21, 100–107. [Google Scholar]
- Lu, Y.R.; Zhang, B.; Perrie, W.; Mouche, A.A.; Li, X.F.; Wang, H. A C-band geophysical model function for determining coastal wind speed using synthetic aperture radar. IEEE J. Sel. Tops. Apply. Earth Observ. Remote Sens. 2018, 11, 2417–2418. [Google Scholar] [CrossRef]
- Lin, H.; Xu, Q.; Zheng, Q. An overview on SAR measurement of sea surface wind. Prog. Nat. Sci. 2008, 18, 913–919. [Google Scholar] [CrossRef]
- Vachon, P.W.; Wolfe, J. C-band cross-polarization wind speed retrieval. IEEE Geosci. Remote Sens. Lett. 2011, 8, 456–459. [Google Scholar] [CrossRef]
- Qin, T.; Jia, T.; Feng, Q.; Li, X. Sea surface wind speed retrieval from Sentinel-1 HH polarization data using conventional and neural network methods. Acta Oceanol. Sin. 2021, 40, 13–21. [Google Scholar] [CrossRef]
- Kerbaol, V.; Chapron, B.; Vachon, P.W. Analysis of ERS-1/2 synthetic aperture radar wave mode imagettes. J. Geophys. Res. 1998, 103, 7833–7846. [Google Scholar] [CrossRef]
- Lehner, S.; Schulz-Stellenfleth, J.; Schattler, B.; Brei, H.; Horstmann, J. Wind and wave measurements using complex ERS-2 SAR wave mode data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2246–2257. [Google Scholar] [CrossRef]
- Nunziata, F.; Migliaccio, M.; Buono, A.; Ferrentino, E.; Alparone, A.; Zecchetto, S.; Zanchetta, A.; Portabella, M.; Grieco, G. Ocean wind field estimation using multi-frequency SAR imagery. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Kuala Lumpur, Malaysia, 17–22 July 2022. [Google Scholar]
- FAO. World Fisheries and Aquaculture Overview 2018; FAO Fisheries Department: Rome, Italy, 2018; Available online: https://www.fao.org/documents/card/en/c/I9540EN/ (accessed on 10 December 2022).
- Petit, M.; Stretta, J.-M.; Farrugio, H.; Wadsworth, A. Synthetic aperture radar imaging of sea surface life and fishing activity. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1085–1108. [Google Scholar] [CrossRef]
- Travaglia, C.; Profeti, G.; Aguilar-Manjarrez, J.; Lopes, N.A. Mapping coastal aquaculture and fisheries structures by satellite imaging radar. Case study of the Lingayen Gulf, the Philippines. FAD Fish. Tech. Paper 2004, 459, 1–46. [Google Scholar]
- Ottinger, M.; Bachofer, F.; Huth, J.; Kuenzer, C. Mapping aquaculture ponds for the coastal zone of Asia with Sentinel-1 and Sentinel-2 time series. Remote Sens. 2022, 14, 153. [Google Scholar] [CrossRef]
- Kurekin, A.A.; Miller, P.I.; Avilanosa, A.L.; Sumeldan, J.D.C. Monitoring of coastal aquaculture sites in the Philippines through automated time series analysis of Sentinel-1 SAR images. Remote Sens. 2022, 14, 2862. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Ji, Y.; Chen, J.; Deng, Y.; Chen, J.; Jie, Y. Combining segmentation network and nonsubsampled contourlet transform for automatic maritime raft aquaculture area extraction from Sentinel-1 images. Remote Sens. 2020, 12, 4182. [Google Scholar] [CrossRef]
- Ferriby, H.; Nejadhashemi, A.P.; Hernandez-Suarez, J.S.; Moor, N.; Kpodo, J.; Kropp, I.; Eeswaran, R.; Belton, B.; Haque, M.M. Harnessing machine learning techniques for mapping aquaculture waterbodies in Bangladesh. Remote Sens. 2021, 13, 4890. [Google Scholar] [CrossRef]
- Gao, L.; Su, H.; Wang, C.; Liu, K.; Chen, S. Extraction of floating raft aquaculture areas from Sentinel-1 SAR images by a dense residual U-Net model with pre-trained ResNet34 as the encoder. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Kuala Lumpur, Malaysia, 17–22 July 2022. [Google Scholar]
- Sugimoto, M.; Ouchi, K.; Nakamura, Y. Comprehensive contrast comparison of laver cultivation area extraction using parameters derived from polarimetric synthetic aperture radar. J. Appl. Remote Sens. 2013, 7, 073566. [Google Scholar] [CrossRef]
- How Does Sea Ice Affect Global Climate. National Ocean Service NOOA. Available online: https://oceanservice.noaa.gov/facts/sea-ice-climate.html (accessed on 16 December 2022).
- Grahn, J.; Brekke, C.; Eltoft, T.; Holt, B. On sea ice characterization by multi-frequency SAR. In Proceedings of the ESA Living Planet Symposium 2013, Edinburgh, UK, 9–23 September 2013. [Google Scholar]
- Dieking, W. Sea ice monitoring by synthetic aperture radar. Oceanography 2013, 26, 100–111. [Google Scholar]
- Hwang, B.; Wang, Y. Multi-scale satellite observations of Arctic sea ice: New insight into the life cycle of the floe size distribution. Philos. Trans. R. Soc. A 2021, 380, 20210259. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Yang, Y.; Shokr, M.; Mi, C.; Li, X.-M.; Cheng, X.; Hui, F. Deep learning based sea ice classification with Gaofen-3 fully polarimetric SAR data. Remote Sens. 2021, 13, 1452. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Hu, Y.; Chu, Q.; Liu, L. An improved sea ice classification algorithm with Gaofen-3 dual-polarization SAR data based on deep convolutional neural networks. Remote Sens. 2022, 14, 906. [Google Scholar] [CrossRef]
- de Gélis, I.; Colin, A.; Longépé, N. Prediction of categorized sea ice concentration from Sentinel-1 SAR images based on a fully convolutional network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5831–5841. [Google Scholar] [CrossRef]

















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouchi, K.; Yoshida, T. On the Interpretation of Synthetic Aperture Radar Images of Oceanic Phenomena: Past and Present. Remote Sens. 2023, 15, 1329. https://doi.org/10.3390/rs15051329
Ouchi K, Yoshida T. On the Interpretation of Synthetic Aperture Radar Images of Oceanic Phenomena: Past and Present. Remote Sensing. 2023; 15(5):1329. https://doi.org/10.3390/rs15051329
Chicago/Turabian StyleOuchi, Kazuo, and Takero Yoshida. 2023. "On the Interpretation of Synthetic Aperture Radar Images of Oceanic Phenomena: Past and Present" Remote Sensing 15, no. 5: 1329. https://doi.org/10.3390/rs15051329
APA StyleOuchi, K., & Yoshida, T. (2023). On the Interpretation of Synthetic Aperture Radar Images of Oceanic Phenomena: Past and Present. Remote Sensing, 15(5), 1329. https://doi.org/10.3390/rs15051329






