Efficient Underground Target Detection of Urban Roads in Ground-Penetrating Radar Images Based on Neural Networks
Abstract
1. Introduction
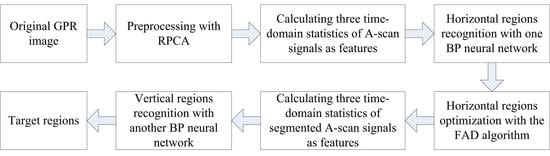
2. Theory and Method
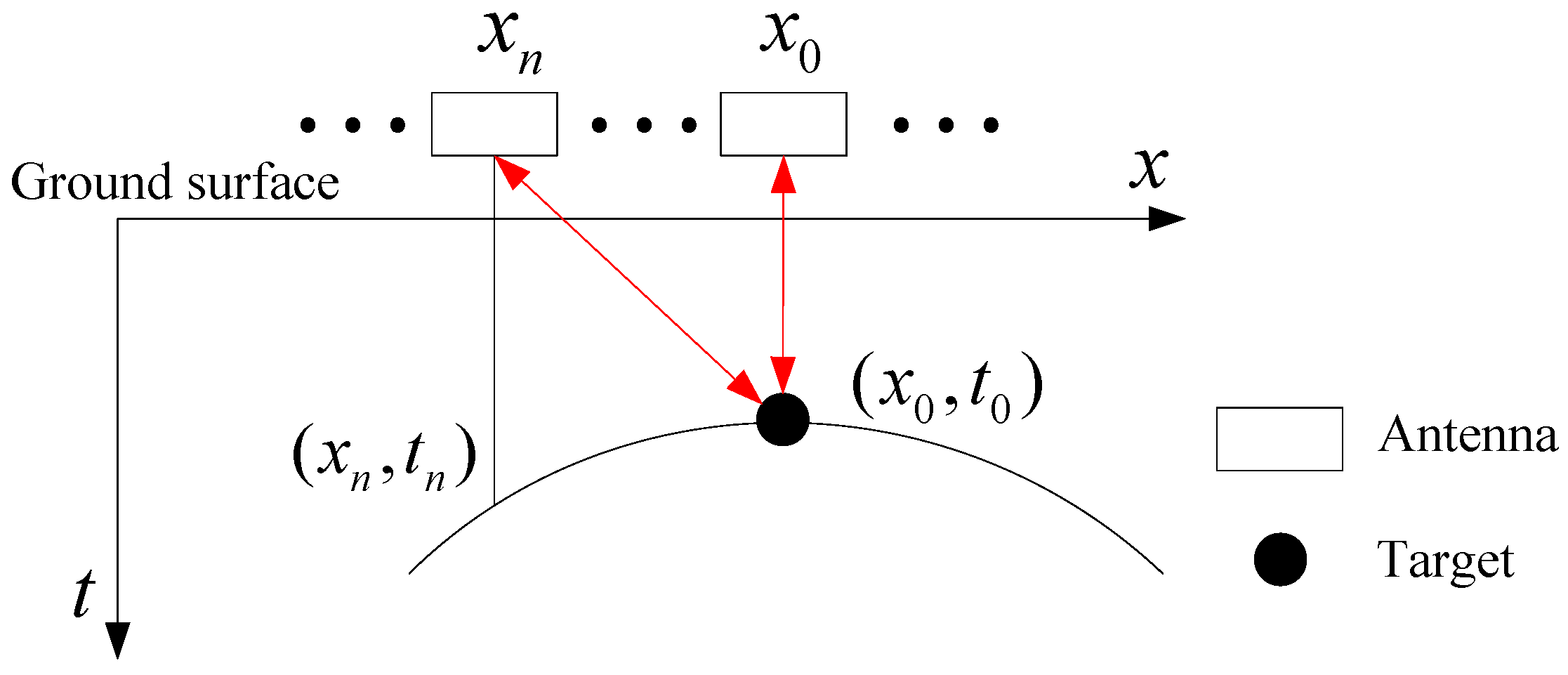
2.1. Detection Model of GPR
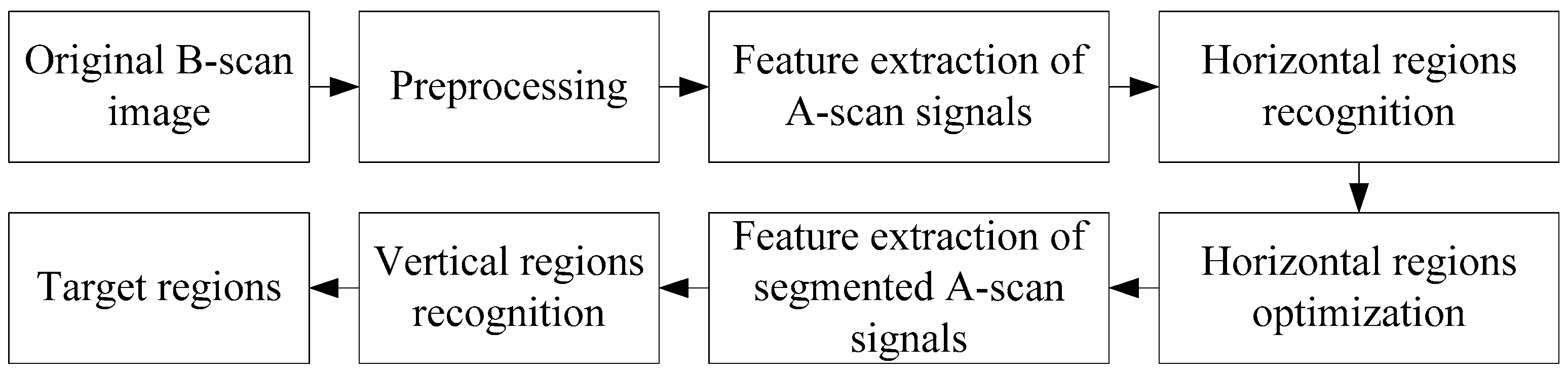
2.2. Detection Method
2.2.1. Preprocessing
2.2.2. Feature Extraction of A-Scan Signals
- (1)
- Mean absolute deviation
- (2)
- Standard deviation
- (3)
- Fourth root of the fourth moment
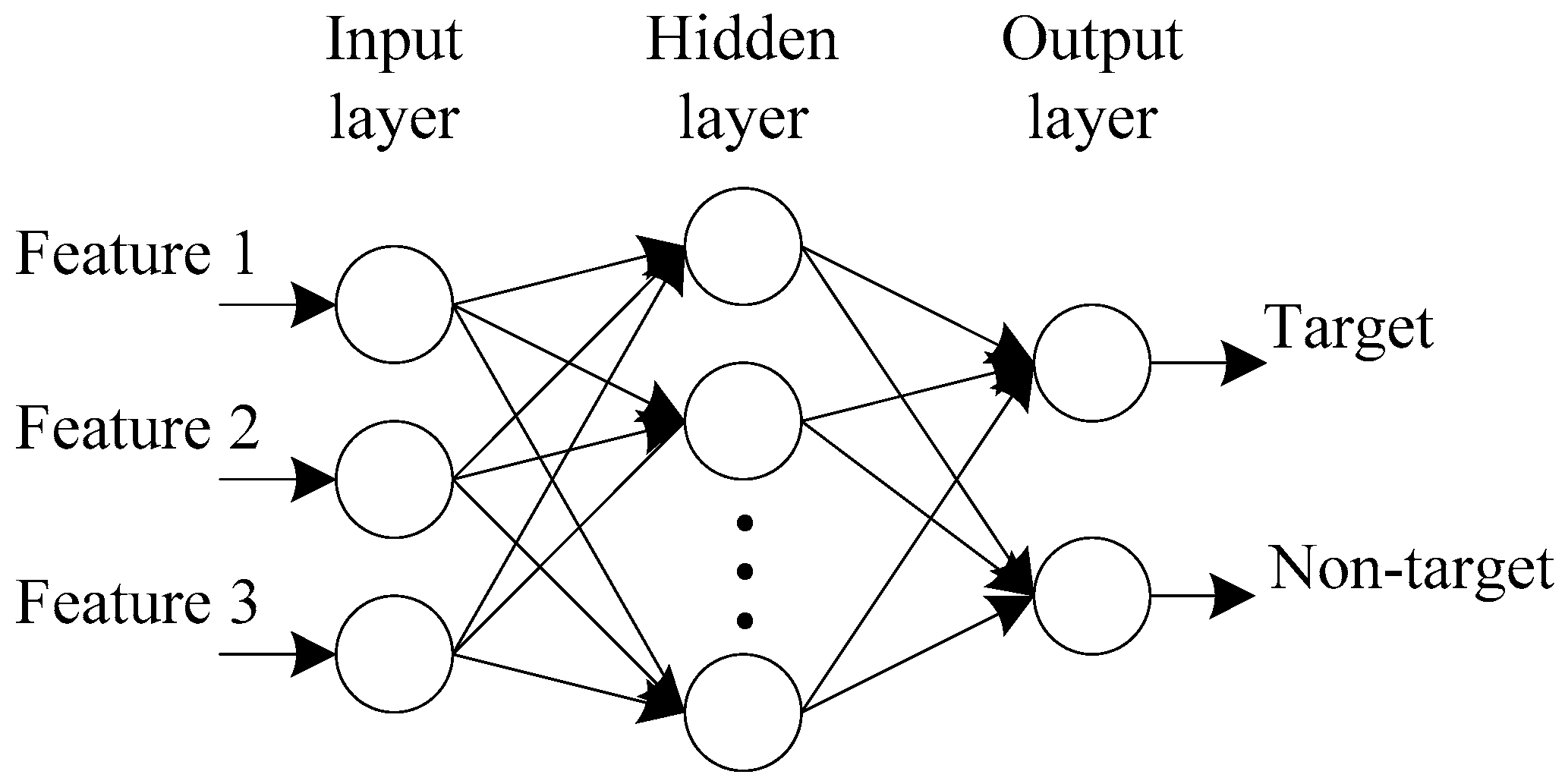
2.2.3. Target Horizontal Region Recognition
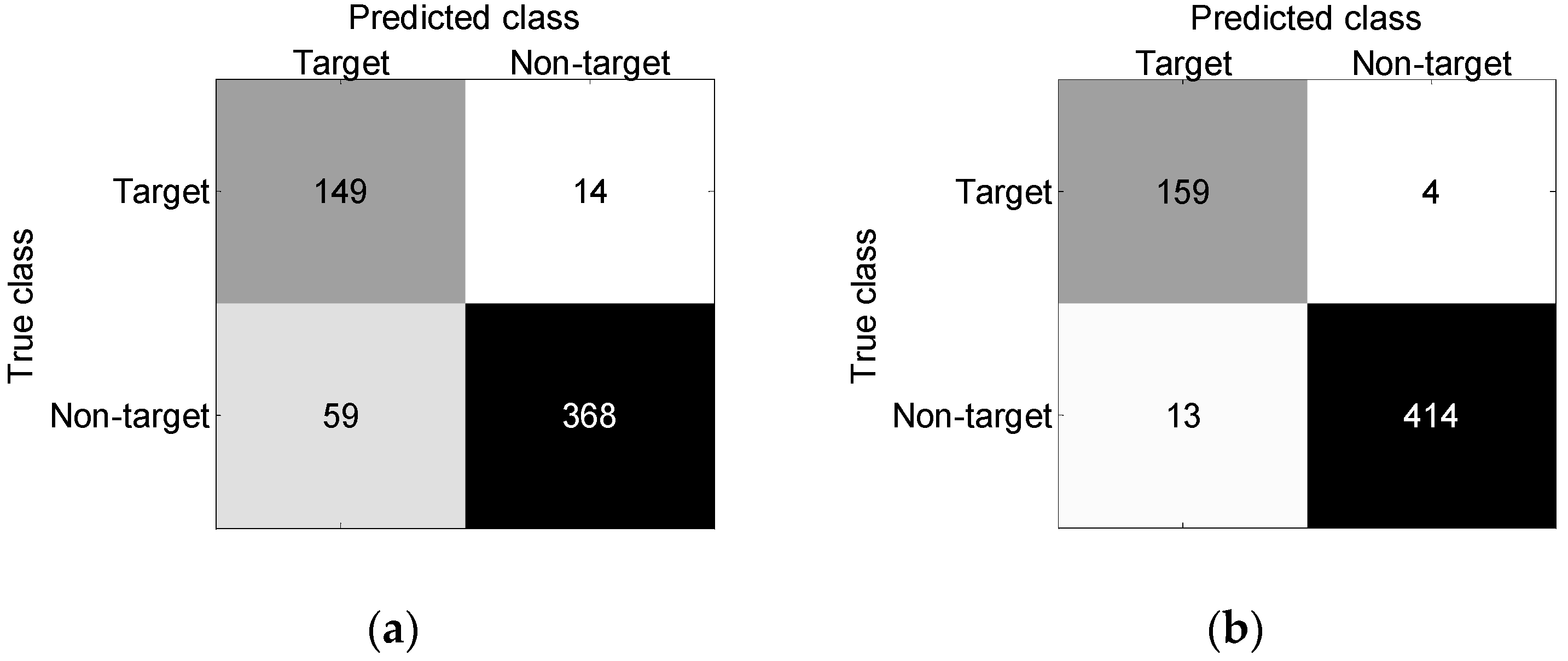
- Training set construction. Km1 A-scan signals with target reflections and kn1 A-scan signals without target reflections are selected from the B-scan images for training, and three features of each selected A-scan signal are extracted. Then, the features are normalized to construct the training set TR1, including km1 positive samples and kn1 negative samples. The output of the positive sample is set to [1 0], and the output of the negative sample is set to [0 1].
- Network training. The training set TR1 is used to train the designed BP neural network, and the network model NET1 is obtained.
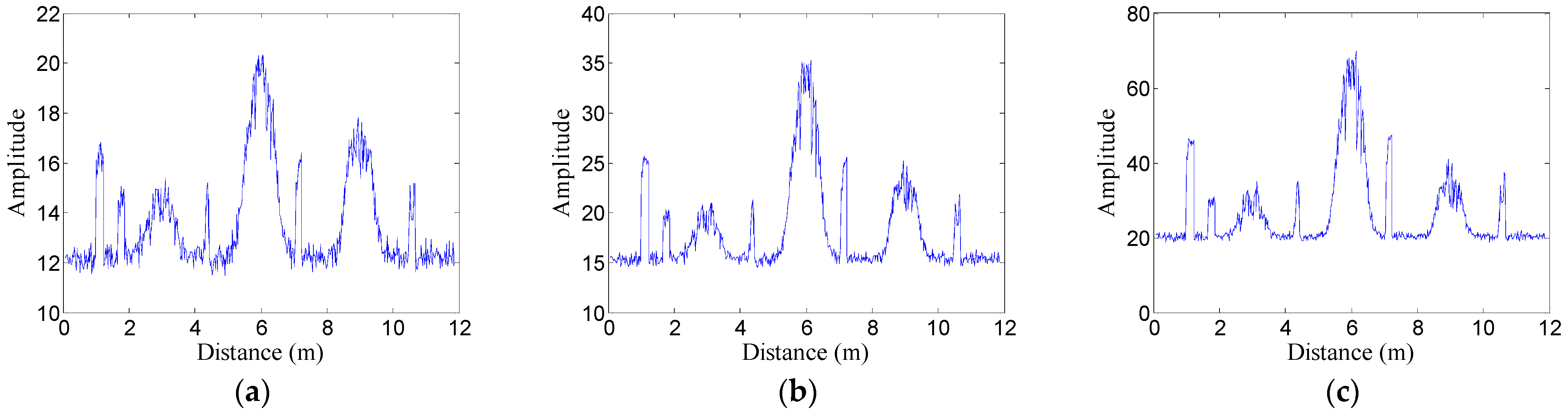
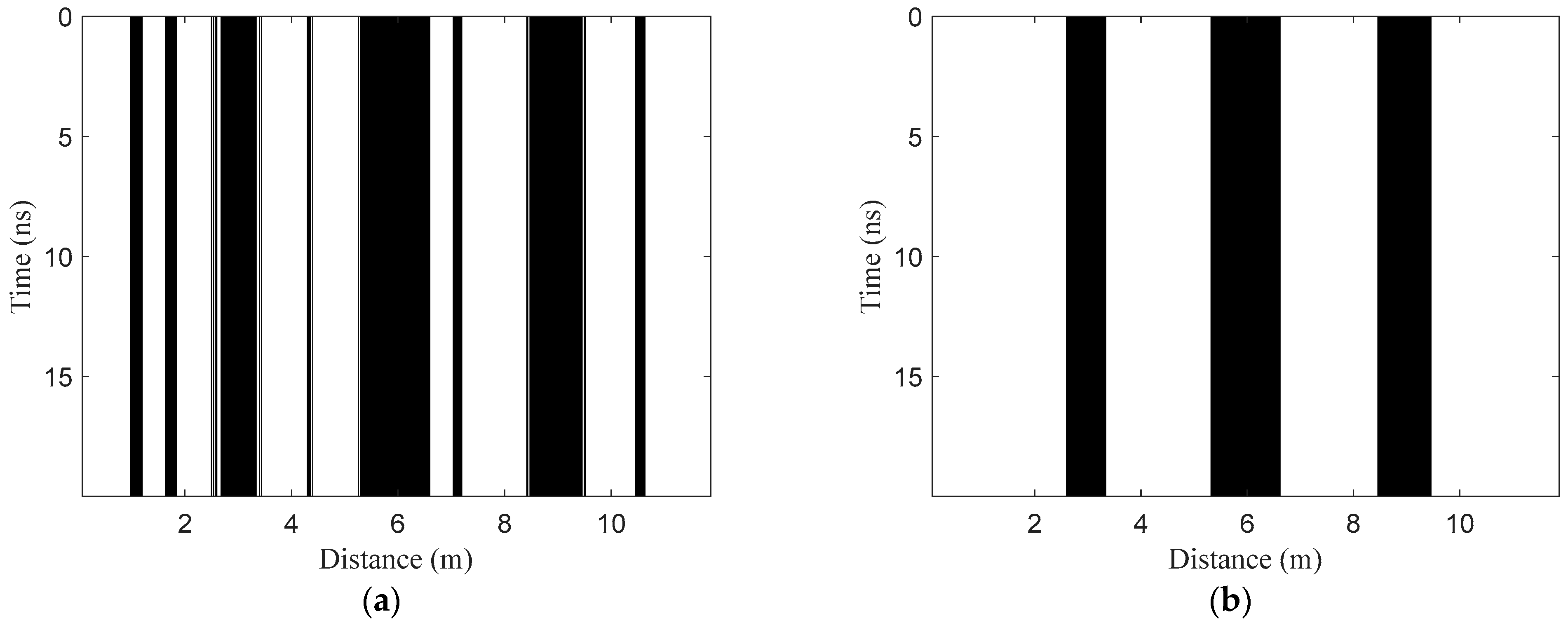
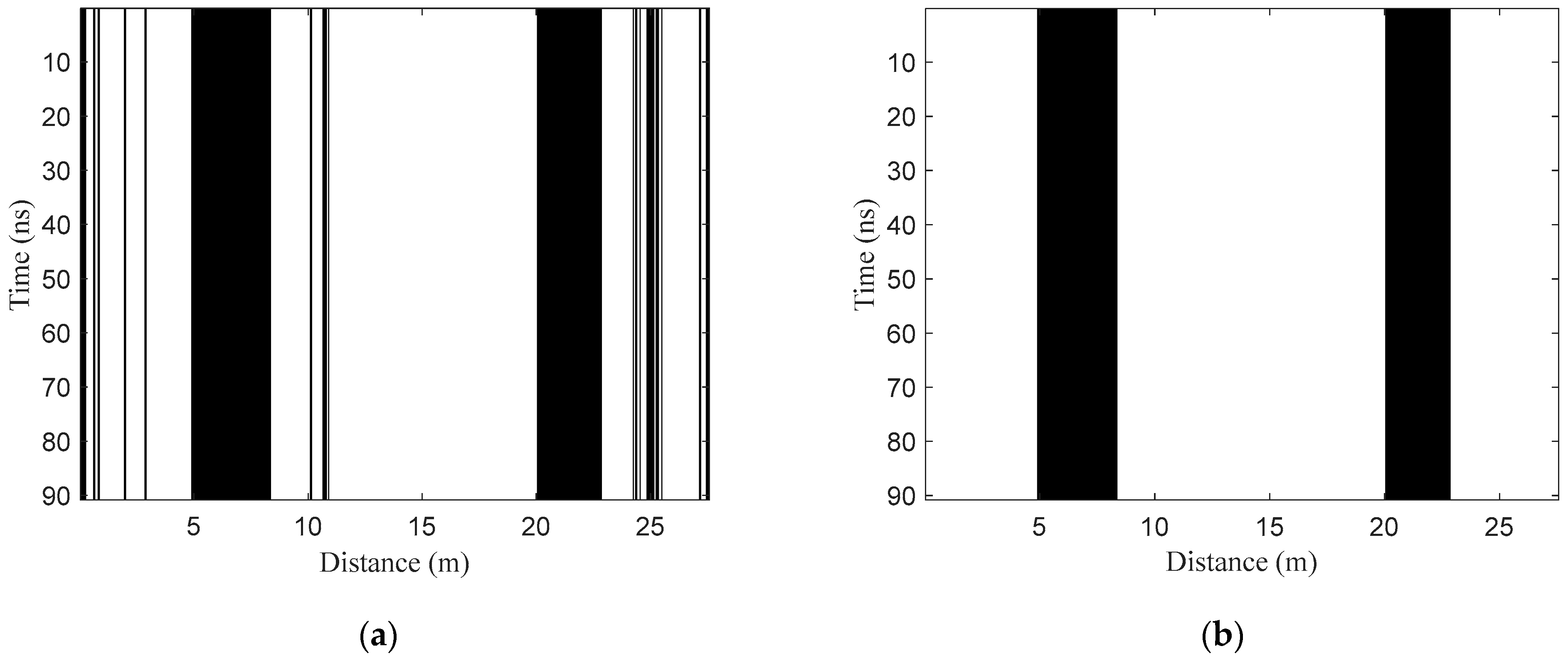
- Horizontal region recognition. The three features of all A-scan signals in the test B-scan image are extracted and normalized to construct the test set TE1. Then, the model NET1 is used to classify the samples in TE1. Assuming that K1 samples are identified as positive samples, the corresponding A-scan signals can be written as . Then, the target horizontal regions can be denoted as , where is the trace interval.
2.2.4. Optimization of Target Horizontal Regions
- Fusion processing. Fusion processing refers to further judgment for non-target A-scan signals between two adjacent target regions, which aims to reduce the false negative rate (missing detection). The judgment can be expressed aswhere is the non-target A-scan signal between two discontinuous target A-scan signals and in H1 and dth is the horizontal interval threshold. Through the processing, the two adjacent target regions with intervals less than dth will be fused together. Then, the horizontal region after fusion processing can be described as , where .
- 2.
- Deletion processing. Deletion processing further judges the target horizontal regions after fusion processing, which aims to decrease the false positive rate (false detection). The judgment can be represented aswhere is the continuous target A-scan signal in one target region in H2 and wth is the horizontal width threshold. Through the processing, the target region with width less than wth in H2 will be deleted. If , is an isolated target signal, and the location point will also be deleted. Then, the final optimized horizontal regions after fusion and deletion processing can be denoted as , where .
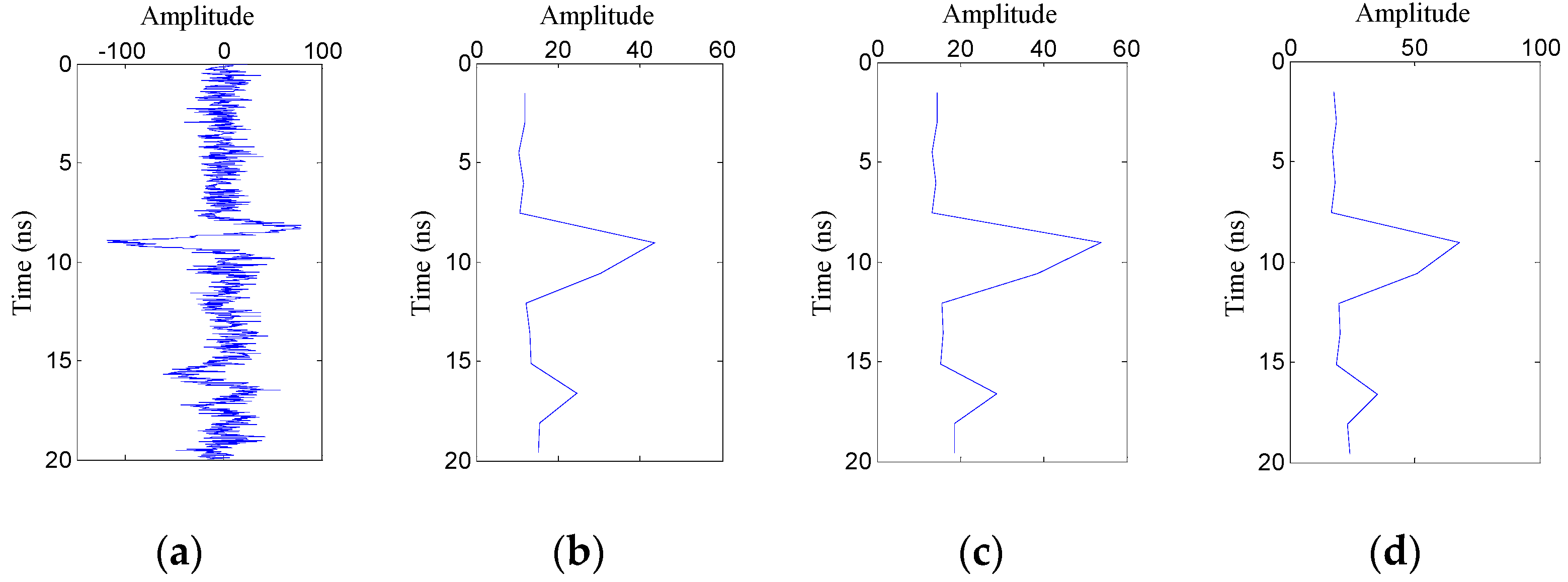
2.2.5. Feature Extraction of Segmented A-Scan Signals
- (1)
- Mean absolute deviation
- (2)
- Standard deviation
- (3)
- Fourth root of the fourth moment
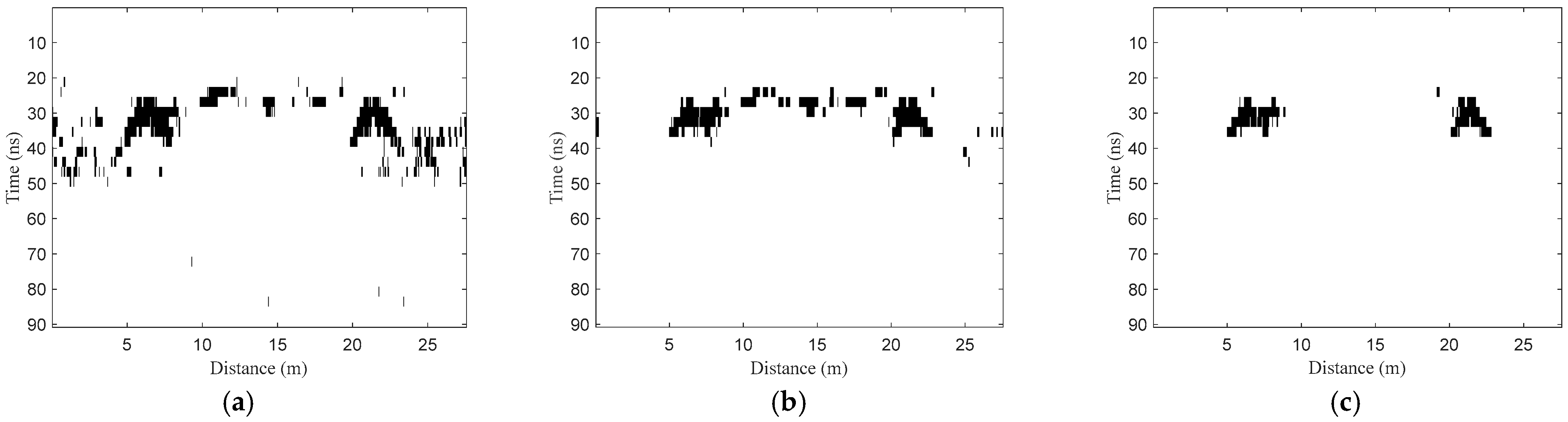
2.2.6. Target Vertical Region Recognition
- Training set construction. Km2 segments with target reflections and kn2 segments without target reflections are selected from the segmented A-scan signals for training, and three features of each selected segment are extracted. Then, the features are normalized to construct the training set TR2, including km2 positive samples and kn2 negative samples. The output of the positive sample is set to [1 0], and the output of the negative sample is set to [0 1].
- Network training. The training set TR2 is used to train the BP neural network, and the network model NET2 is obtained.
- Vertical region recognition. The three features of all segments in the optimized horizontal regions H3 of the test B-scan image are extracted and normalized to form the test set TE2. Then, the model NET2 is used to classify the samples in TE2. Assuming that samples are identified as positive samples in the A-scan signal , the corresponding segments can be written as . Then, the target vertical regions in the A-scan signal can be denoted as .
- The recognized segments are arranged in the two-dimensional image, and then the final target regions can be obtained.
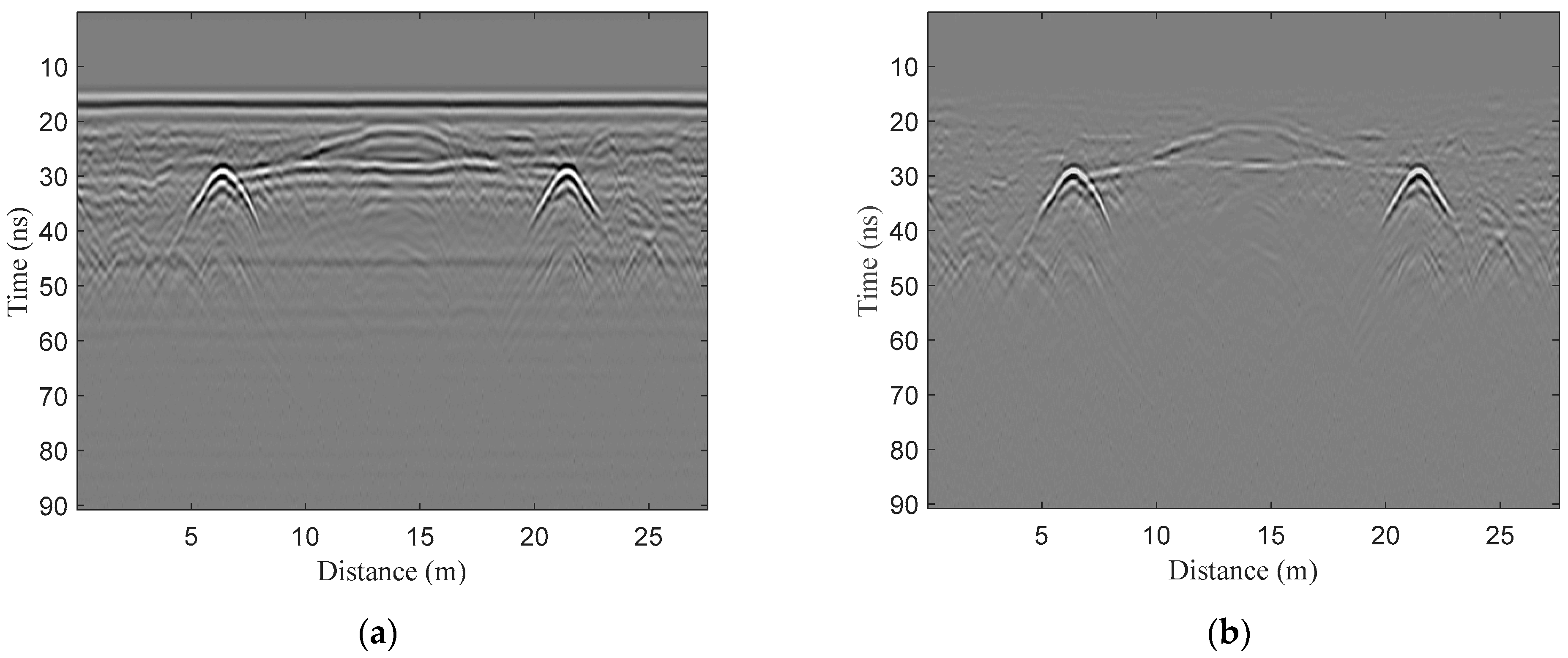
3. Results
3.1. Numerical Simulations
3.2. Field Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saarenketo, T.; Scullion, T. Road evaluation with ground penetrating radar. J. Appl. Geophys. 2000, 43, 119–138. [Google Scholar] [CrossRef]
- Dong, Z.; Ye, S.; Gao, Y.; Fang, G.; Zhang, X.; Xue, Z.; Zhang, T. Rapid Detection Methods for Asphalt Pavement Thicknesses and Defects by a Vehicle-Mounted Ground Penetrating Radar (GPR) System. Sensors 2016, 16, 2067. [Google Scholar] [CrossRef] [PubMed]
- Lai, W.W.; Dérobert, X.; Annan, P. A review of ground penetrating radar application in civil engineering: A 30-year journey from locating and testing to imaging and diagnosis. NDT E Int. 2018, 96, 58–78. [Google Scholar]
- Park, B.; Kim, J.; Lee, J.; Kang, M.S.; An, Y.K. Underground Object Classification for Urban Roads Using Instantaneous Phase Analysis of Ground-Penetrating Radar (GPR) Data. Remote Sens. 2018, 10, 1417. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, X.; Li, W.; Zhang, S.; Jia, Y. Automatic detection of moisture damages in asphalt pavements from GPR data with deep CNN and IRS method. Autom. Constr. 2020, 113, 103119. [Google Scholar] [CrossRef]
- Rasol, M.; Pais, J.C.; Pérez-Gracia, V.; Solla, M.; Fernandes, F.M.; Fontul, S.; Ayala-Cabrera, D.; Schmidt, F.; Assadollahi, H. GPR monitoring for road transport infrastructure: A systematic review and machine learning insights. Constr. Build. Mater. 2022, 324, 126686. [Google Scholar] [CrossRef]
- Gao, Y.; Pei, L.; Wang, S.; Li, W. Intelligent Detection of Urban Road Underground Targets by Using Ground Penetrating Radar based on Deep Learning. J. Phys. Conf. Ser. 2021, 1757, 012081. [Google Scholar] [CrossRef]
- Shao, W.; Bouzerdoum, A.; Phung, S.L.; Su, L.; Indraratna, B.; Rujikiatkamjorn, C. Automatic Classification of Ground-Penetrating-Radar Signals for Railway-Ballast Assessment. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3961–3972. [Google Scholar] [CrossRef]
- Al-Nuaimy, W.; Huang, Y.; Nakhkash, M.; Fang, M.T.C.; Nguyen, V.T.; Eriksen, A. Automatic detection of buried utilities and solid objects with GPR using neural networks and pattern recognition. J. Appl. Geophys. 2000, 43, 157–165. [Google Scholar] [CrossRef]
- Wu, J.; Mao, T.; Zhou, H. Feature Extraction and Recognition Based on SVM. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), Dalian, China, 12–14 October 2008. [Google Scholar]
- Frigui, H.; Gader, P. Detection and discrimination of land mines in ground-penetrating radar based on edge histogram descriptors and a possibilistic K-nearest neighbor classifier. IEEE Trans. Fuzzy Syst. 2009, 17, 185–199. [Google Scholar] [CrossRef]
- Torrione, P.; Morton, K.D.; Sakaguchi, R.; Collins, L. Histograms of oriented gradients for landmine detection in ground-penetrating radar data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1539–1550. [Google Scholar] [CrossRef]
- Xie, X.; Qin, H.; Yu, C.; Liu, L. An automatic recognition algorithm for GPR images of RC structure voids. J. Appl. Geophys. 2013, 99, 125–134. [Google Scholar] [CrossRef]
- Núñez-Nieto, X.; Solla, M.; Gómez-Pérez, P.; Lorenzo, H. GPR Signal Characterization for Automated Landmine and UXO Detection Based on Machine Learning Techniques. Remote Sens. 2014, 6, 9729–9748. [Google Scholar] [CrossRef]
- Harkat, H.; Ruano, A.E.; Ruano, M.G.; Bennani, S.D. GPR target detection using a neural network classifier designed by a multi-objective genetic algorithm. Appl. Soft Comput. 2019, 79, 310–325. [Google Scholar] [CrossRef]
- Tong, Z.; Gao, J.; Zhang, H. Innovative method for recognizing subgrade defects based on a convolutional neural network. Constr. Build. Mater. 2018, 169, 69–82. [Google Scholar] [CrossRef]
- Xue, W.; Dai, X.; Liu, L. Remote Sensing Scene Classification Based on Multi-Structure Deep Features Fusion. IEEE Access 2020, 8, 28746–28755. [Google Scholar] [CrossRef]
- Huang, W.; Zhao, Z.; Sun, L.; Ju, M. Dual-Branch Attention-Assisted CNN for Hyperspectral Image Classification. Remote Sens. 2022, 14, 6158. [Google Scholar] [CrossRef]
- Tong, Z.; Gao, J.; Zhang, H. Recognition, location, measurement, and 3D reconstruction of concealed cracks using convolutional neural networks. Constr. Build. Mater. 2017, 146, 775–787. [Google Scholar] [CrossRef]
- Dinh, K.; Gucunski, N.; Duong, T.H. An algorithm for automatic localization and detection of rebars from GPR data of concrete bridge decks. Autom. Constr. 2018, 89, 292–298. [Google Scholar] [CrossRef]
- Liu, H.; Lin, C.; Cui, J.; Fan, L.; Xie, X.; Spencer, B.F. Detection and localization of rebar in concrete by deep learning using ground penetrating radar. Autom. Constr. 2020, 118, 103279. [Google Scholar] [CrossRef]
- Ozkaya, U.; Melgani, F.; Bejiga, M.B.; Seyfi, L.; Donelli, M. GPR B Scan Image Analysis with Deep Learning Methods. Measurement 2020, 165, 107770. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, W.; Gu, X.; Li, S. Application of Combining YOLO Models and 3D GPR Images in Road Detection and Maintenance. Remote Sens. 2021, 13, 1081. [Google Scholar] [CrossRef]
- Qiao, L.; Qin, Y.; Ren, X.; Wang, Q. Identification of buried objects in GPR using amplitude modulated signals extracted from multiresolution monogenic signal analysis. Sensors 2015, 15, 30340–30350. [Google Scholar] [CrossRef] [PubMed]
- Tivive, F.H.C.; Bouzerdoum, A.; Abeynayake, C. GPR Target Detection by Joint Sparse and Low-Rank Matrix Decomposition. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2583–2595. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust Principal Component Analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- He, Z.; Peng, P.; Wang, L.; Jiang, Y. PickCapsNet: Capsule Network for Automatic P-Wave Arrival Picking. IEEE Geosci. Remote Sens. Lett. 2021, 18, 617–621. [Google Scholar] [CrossRef]
- Gamba, P.; Lossani, S. Neural Detection of Pipe Signatures in Ground Penetrating Radar Images. IEEE Trans. Geosci. Remote Sens. 2000, 38, 790–797. [Google Scholar] [CrossRef]
- Gao, D.; Wu, S. An optimization method for the topological structures of feed-forward multi-layer neural networks. Pattern Recognit. 1998, 31, 1337–1342. [Google Scholar]
- Liu, H.; Liu, J.; Wang, Y.; Xia, Y.; Guo, Z. Identification of grouting compactness in bridge bellows based on the BP neural network. Structures 2021, 32, 817–826. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Giannakis, I.; Giannopoulos, A.; Warren, C. A Realistic FDTD Numerical Modeling Framework of Ground Penetrating Radar for Landmine Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 37–51. [Google Scholar] [CrossRef]
- Song, X.; Liu, T.; Xiang, D.; Su, Y. GPR Antipersonnel Mine Detection Based on Tensor Robust Principal Analysis. Remote Sens. 2019, 11, 984. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Antenna central frequency | 400 MHz |
| Excitation waveform | Ricker wavelet |
| Time window | 20 ns |
| Number of time samples | 848 |
| Trace interval | 0.02 m |
| Number of traces | 590 |
| Model Number | Void | Metal Pipe | PVC Pipe | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Depth | Lateral Distance | Radius | Depth | Lateral Distance | Radius (Outer/Inner) | Depth | Lateral Distance | Radius (Outer/Inner) | |
| 1 | 0.30 m | 3 m | 0.10 m | 0.30 m | 6 m | 0.10 m/0.05 m | 0.30 m | 9 m | 0.10 m/0.05 m |
| 2 | 0.50 m | 3 m | 0.10 m | 0.50 m | 6 m | 0.10 m/0.05 m | 0.50 m | 9 m | 0.10 m/0.05 m |
| 3 | 0.70 m | 3 m | 0.10 m | 0.70 m | 6 m | 0.10 m/0.05 m | 0.70 m | 9 m | 0.10 m/0.05 m |
| 4 | 0.35 m | 3 m | 0.15 m | 0.35 m | 6 m | 0.15 m/0.10 m | 0.35 m | 9 m | 0.15 m/0.10 m |
| 5 | 0.55 m | 3 m | 0.15 m | 0.55 m | 6 m | 0.15 m/0.10 m | 0.55 m | 9 m | 0.15 m/0.10 m |
| 6 | 0.75 m | 3 m | 0.15 m | 0.75 m | 6 m | 0.15 m/0.10 m | 0.75 m | 9 m | 0.15 m/0.10 m |
| 7 | 0.40 m | 3 m | 0.20 m | 0.40 m | 6 m | 0.20 m/0.15 m | 0.40 m | 9 m | 0.20 m/0.15 m |
| 8 | 0.60 m | 3 m | 0.20 m | 0.60 m | 6 m | 0.20 m/0.15 m | 0.60 m | 9 m | 0.20 m/0.15 m |
| 9 | 0.80 m | 3 m | 0.20 m | 0.80 m | 6 m | 0.20 m/0.15 m | 0.80 m | 9 m | 0.20 m/0.15 m |
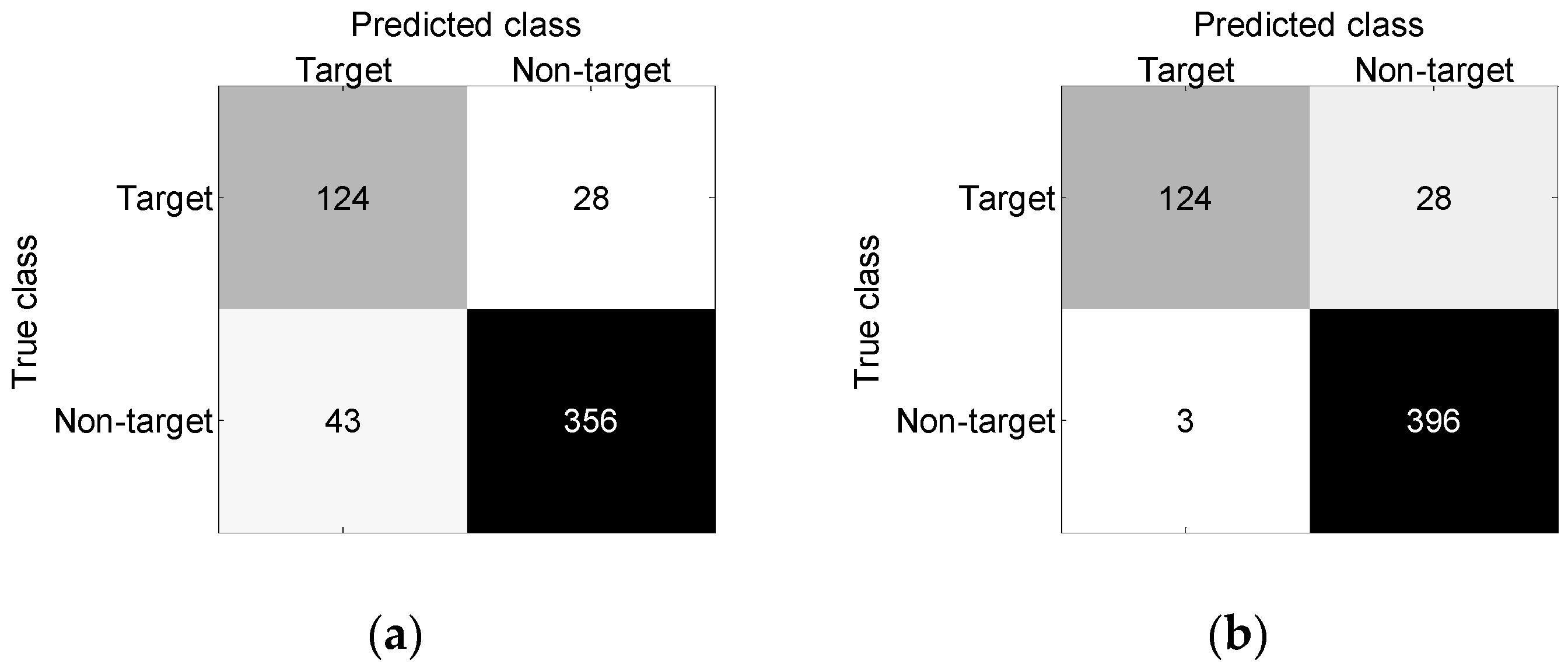
| Method | Accuracy | FPR | FNR |
|---|---|---|---|
| BP neural network | 87.6% | 13.8% | 8.6% |
| BP neural network + FAD | 97.1% | 3.0% | 2.5% |
| Method | Accuracy | FPR | FNR |
|---|---|---|---|
| Traditional segmentation recognition method based on BP neural network | 95.1% | 4.4% | 15.5% |
| Traditional segmentation recognition method based on SVM | 96.6% | 2.6% | 20.6% |
| Proposed method | 98.7% | 0.4% | 18.9% |
| Method | Processing Time (s) | ||
|---|---|---|---|
| Clutter Suppression | Target Recognition | Total | |
| Traditional segmentation recognition method based on BP neural network | 0.38 | 0.63 | 1.01 |
| Traditional segmentation recognition method based on SVM | 0.38 | 0.65 | 1.03 |
| Proposed method | 0.38 | 0.44 | 0.82 |
| Method | Accuracy | FPR | FNR |
|---|---|---|---|
| BP neural network | 87.1% | 10.8% | 18.4% |
| BP neural network + FAD | 94.4% | 0.8% | 18.4% |
| Method | Accuracy | FPR | FNR |
|---|---|---|---|
| Traditional segmentation recognition method based on BP neural network | 96.8% | 2.8% | 23.3% |
| Traditional segmentation recognition method based on SVM | 97.7% | 1.8% | 26.8% |
| Proposed method | 99.1% | 0.3% | 28.4% |
| Method | Processing Time (s) | ||
|---|---|---|---|
| Clutter Suppression | Target Recognition | Total | |
| Traditional segmentation recognition method based on BP neural network | 0.54 | 0.93 | 1.47 |
| Traditional segmentation recognition method based on SVM | 0.54 | 0.91 | 1.45 |
| Proposed method | 0.54 | 0.74 | 1.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, W.; Chen, K.; Li, T.; Liu, L.; Zhang, J. Efficient Underground Target Detection of Urban Roads in Ground-Penetrating Radar Images Based on Neural Networks. Remote Sens. 2023, 15, 1346. https://doi.org/10.3390/rs15051346
Xue W, Chen K, Li T, Liu L, Zhang J. Efficient Underground Target Detection of Urban Roads in Ground-Penetrating Radar Images Based on Neural Networks. Remote Sensing. 2023; 15(5):1346. https://doi.org/10.3390/rs15051346
Chicago/Turabian StyleXue, Wei, Kehui Chen, Ting Li, Li Liu, and Jian Zhang. 2023. "Efficient Underground Target Detection of Urban Roads in Ground-Penetrating Radar Images Based on Neural Networks" Remote Sensing 15, no. 5: 1346. https://doi.org/10.3390/rs15051346
APA StyleXue, W., Chen, K., Li, T., Liu, L., & Zhang, J. (2023). Efficient Underground Target Detection of Urban Roads in Ground-Penetrating Radar Images Based on Neural Networks. Remote Sensing, 15(5), 1346. https://doi.org/10.3390/rs15051346