Multi-GNSS Differential Inter-System Bias Estimation for Smartphone RTK Positioning: Feasibility Analysis and Performance
Abstract
:1. Introduction
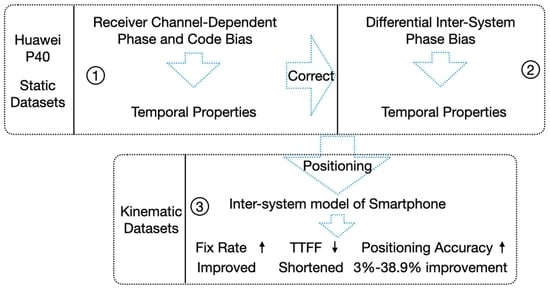
2. Methodology
2.1. Inter-System Model for Smartphone
2.2. Statistical Hypothesis Test of DISB
3. Receiver Channel-Dependent Bias and DISB Characteristics
3.1. Experimental Setup and Processing Methods
3.2. Temporal Properties of Receiver Channel-Dependent Bias
3.3. Temporal Properties of Phase DISB
4. Impact of DISB on Kinematic RTK Positioning
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, B.; Hou, P.; Zha, J.; Liu, T. PPP–RTK functional models formulated with undifferenced and uncombined GNSS observations. Satell. Navig. 2022, 3, 3. [Google Scholar] [CrossRef]
- Zhang, Z.; Yuan, H.; He, X.; Li, B.; Geng, J. Best Integer Equivariant Estimation With Quality Control in GNSS RTK for Canyon Environments. IEEE Trans. Aerosp. Electron. Syst. 2023, 1–15. [Google Scholar] [CrossRef]
- Ye, J. Research on Pedestrian Navigation Algorithm Based on Multi-Sensor Fusion; Chang’an University: Xi’an, China, 2020. [Google Scholar]
- Ge, Y.; Cao, X.; Lyu, D.; He, Z.; Ye, F.; Xiao, G.; Shen, F. An investigation of PPP time transfer via BDS-3 PPP-B2b service. GPS Solut. 2023, 27, 61. [Google Scholar] [CrossRef]
- Sikirica, N.; Malić, E.; Rumora, I.; Filjar, R. Exploitation of Google GNSS measurement API for risk assessment of GNSS applications. In Proceedings of the 2017 25th Telecommunication Forum (TELFOR), Belgrade, Serbia, 21–22 November 2017; pp. 1–3. [Google Scholar]
- Banville, S.; Van Diggelen, F. Precise positioning using raw GPS measurements from Android smartphones. GPS World 2016, 27, 43–48. [Google Scholar]
- Chen, B.; Gao, C.; Liu, Y.; Sun, P. Real-time precise point positioning with a Xiaomi MI 8 android smartphone. Sensors 2019, 19, 2835. [Google Scholar] [CrossRef] [Green Version]
- Bahadur, B. A study on the real-time code-based GNSS positioning with Android smartphones. Measurement 2022, 194, 111078. [Google Scholar] [CrossRef]
- Li, Z.; Wang, L.; Wang, N.; Li, R.; Liu, A. Real-time GNSS precise point positioning with smartphones for vehicle navigation. Satell. Navig. 2022, 3, 19. [Google Scholar] [CrossRef]
- Li, G.; Geng, J. Characteristics of raw multi-GNSS measurement error from Google Android smart devices. GPS Solut. 2019, 23, 90. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Gao, Y.; Shen, Y. Real-time carrier phase multipath detection based on dual-frequency C/N0 data. GPS Solut. 2019, 23, 7. [Google Scholar] [CrossRef]
- Geng, J.; Li, G. On the feasibility of resolving Android GNSS carrier-phase ambiguities. J. Geod. 2019, 93, 2621–2635. [Google Scholar] [CrossRef]
- Darugna, F.; Wübbena, J.; Ito, A.; Wübbena, T.; Wübbena, G.; Schmitz, M. RTK and PPP-RTK using smartphones: From short-baseline to long-baseline applications. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 3932–3945. [Google Scholar]
- Bochkati, M.; Sharma, H.; Lichtenberger, C.A.; Pany, T. Demonstration of fused RTK (fixed)+ inertial positioning using Android smartphone sensors only. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1140–1154. [Google Scholar]
- Sun, R.; Wang, J.; Cheng, Q.; Mao, Y.; Ochieng, W.Y. A new IMU-aided multiple GNSS fault detection and exclusion algorithm for integrated navigation in urban environments. GPS Solut. 2021, 25, 147. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, C.; Shang, R.; Peng, Z.; Zhang, R.; Gan, L.; Gao, W. NLOS signal detection and correction for smartphone using convolutional neural network and variational mode decomposition in urban environment. GPS Solut. 2023, 27, 31. [Google Scholar] [CrossRef]
- Xia, Y.; Pan, S.; Meng, X.; Gao, W.; Ye, F.; Zhao, Q.; Zhao, X. Anomaly detection for urban vehicle GNSS observation with a hybrid machine learning system. Remote Sens. 2020, 12, 971. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Meng, X.; Yang, Y.; Pan, S.; Zhao, Q.; Gao, W. First results of BDS positioning for LBS applications in the UK. Satell. Navig. 2021, 2, 8. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Murrian, M.; Van Diggelen, F.; Podshivalov, S.; Pesyna, K.M. On the feasibility of cm-accurate positioning via a smartphone’s antenna and GNSS chip. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GR, USA, 11–14 April 2016; pp. 232–242. [Google Scholar]
- Riley, S.; Lentz, W.; Clare, A. On the path to precision-observations with android GNSS observables. In Proceedings of the 30th International Technical Meeting of The Satellite Division of The Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 116–129. [Google Scholar]
- Paziewski, J.; Sieradzki, R.; Baryla, R. Signal characterization and assessment of code GNSS positioning with low-power consumption smartphones. GPS Solut. 2019, 23, 98. [Google Scholar] [CrossRef] [Green Version]
- Paziewski, J. Recent advances and perspectives for positioning and applications with smartphone GNSS observations. Meas. Sci. Technol. 2020, 31, 091001. [Google Scholar] [CrossRef]
- Paziewski, J.; Fortunato, M.; Mazzoni, A.; Odolinski, R. An analysis of multi-GNSS observations tracked by recent Android smartphones and smartphone-only relative positioning results. Measurement 2021, 175, 109162. [Google Scholar] [CrossRef]
- Li, G.; Geng, J. Android multi-GNSS ambiguity resolution in the case of receiver channel-dependent phase biases. J. Geod. 2022, 96, 72. [Google Scholar] [CrossRef]
- Li, B.; Miao, W.; Chen, G.; Li, Z. Ambiguity resolution for smartphone GNSS precise positioning: Effect factors and performance. J. Geod. 2022, 96, 63. [Google Scholar] [CrossRef]
- Julien, O.; Alves, P.; Cannon, M.E.; Zhang, W. A tightly coupled GPS/GALILEO combination for improved ambiguity resolution. In Proceedings of the European Navigation Conference (ENC-GNSS’03), Calgary, AB, Canada, 9 September 2003; pp. 1–14. [Google Scholar]
- Zhang, B.; Teunissen, P.J.; Yuan, Y. On the short-term temporal variations of GNSS receiver differential phase biases. J. Geod. 2017, 91, 563–572. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps. Navig. J. Inst. Navig. 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P.J. Characterization of between-receiver GPS-Galileo inter-system biases and their effect on mixed ambiguity resolution. GPS Solut. 2013, 17, 521–533. [Google Scholar] [CrossRef]
- Paziewski, J.; Wielgosz, P. Accounting for Galileo–GPS inter-system biases in precise satellite positioning. J. Geod. 2015, 89, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Nadarajah, N.; Khodabandeh, A.; Teunissen, P.J. Assessing the IRNSS L5-signal in combination with GPS, Galileo, and QZSS L5/E5a-signals for positioning and navigation. GPS Solut. 2016, 20, 289–297. [Google Scholar] [CrossRef]
- Odijk, D.; Nadarajah, N.; Zaminpardaz, S.; Teunissen, P.J. GPS, Galileo, QZSS and IRNSS differential ISBs: Estimation and application. GPS Solut. 2017, 21, 439–450. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J. Single-frequency, dual-GNSS versus dual-frequency, single-GNSS: A low-cost and high-grade receivers GPS-BDS RTK analysis. J. Geod. 2016, 90, 1255–1278. [Google Scholar] [CrossRef]
- Wu, M.; Liu, W.; Wang, W.; Zhang, X. Differential inter-system biases estimation and initial assessment of instantaneous tightly combined RTK with BDS-3, GPS, and Galileo. Remote Sens. 2019, 11, 1430. [Google Scholar] [CrossRef] [Green Version]
- Yuan, H.; Zhang, Z.; He, X.; Zeng, J. Tight integration of BDS-3/BDS-2/GPS/Galileo observations considering the new overlapping DISBs and its application in obstructed environments. Adv. Space Res. 2022, 71, 2879–2891. [Google Scholar] [CrossRef]
- Gao, W.; Meng, X.; Gao, C.; Pan, S.; Wang, D. Combined GPS and BDS for single-frequency continuous RTK positioning through real-time estimation of differential inter-system biases. GPS Solut. 2018, 22, 20. [Google Scholar] [CrossRef]
- Mi, X.; Zhang, B.; Yuan, Y.; Luo, X. Characteristics of GPS, BDS2, BDS3 and Galileo inter-system biases and their influence on RTK positioning. Meas. Sci. Technol. 2019, 31, 015009. [Google Scholar] [CrossRef]
- Mi, X.; Zhang, B.; Yuan, Y. Multi-GNSS inter-system biases: Estimability analysis and impact on RTK positioning. GPS Solut. 2019, 23, 81. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, W.; Li, J. Multi-GNSS relative positioning with fixed inter-system ambiguity. Remote Sens. 2019, 11, 454. [Google Scholar] [CrossRef] [Green Version]
- Shang, R.; Meng, X.; Gao, C.; Pan, S.; Gao, W.; Peng, Z. Particle filter-based inter-system positioning model for non-overlapping frequency code division multiple access systems. J. Navig. 2020, 73, 953–970. [Google Scholar] [CrossRef]
- Liu, J.; Tu, R.; Han, J.; Zhang, R.; Zhang, P.; Fan, L. Estimability analysis of differential inter-system biases and differential inter-frequency biases for dual-frequency GPS and BDS combined RTK. Meas. Sci. Technol. 2019, 31, 025009. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P. Zero-baseline Analysis of GPS/BeiDou/Galileo Between-Receiver Differential Code Biases (BR-DCBs): Time-wise Retrieval and Preliminary Characterization. Navig. J. Inst. Navig. 2016, 63, 181–191. [Google Scholar] [CrossRef] [Green Version]
- Xiaohong, Z.; Mingkui, W.; Wanke, L. Model and Performance Analysis of Tightly Combined BeiDou B2 and Galileo E5b Relative Positioning for Short Baseline. Acta Geod. Et Cartogr. Sin. 2017, 45, 1. [Google Scholar]
- Zhang, Z.; Li, Y.; He, X.; Chen, W.; Li, B. A composite stochastic model considering the terrain topography for real-time GNSS monitoring in canyon environments. J. Geod. 2022, 96, 79. [Google Scholar] [CrossRef]
- Sui, M.; Gong, C.; Shen, F. An optimized stochastic model for smartphone GNSS positioning. Front. Earth Sci. 2022, 10, 1018420. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, Z.; He, X.; Li, G.; Wang, S. Stochastic model assessment of low-cost devices considering the impacts of multipath effects and atmospheric delays. Measurement 2022, 188, 110619. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Modeling and assessment of combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]












| Baseline | Device | Antenna | Duration (UTC Time) | Systems and Frequencies | |
|---|---|---|---|---|---|
| L | P | ||||
| JSJN-HP40 | CHCNAV P5 (base) | HI-TARGET AT-53501 | 1 h (08:00–09:00, 18 December 2022) | G:L1/L5; E:E1/E5a; C:B1I B1C B2a; J:L1/L5 | G:L1/L5; E:E1/E5a; C:B1I; J:L1/L5 |
| HP40 (rover) | Embedded antenna | G:L1/L5; E:E1/E5a; C:B1I B1C B2a; J:L1/L5 | G:L1/L5; E:E1/E5a; C:B1I B1C B2a; J:L1/L5 | ||
| CUT0-CUTB | Trimble NetR9 (base) | TRM59800.00 | 24 h (31 May 2020) | G:L1/L5; E:E1/E5a; C:B1I B1C B2a; J:L1/L5 | G:L1/L5; E:E1/E5a; C:B1I B1C B2a; J:L1/L5 |
| Trimble NetR9 (rover) | TRM59800.00 | G:L1/L5; E:E1/E5a; C:B1I B1C B2a; J:L1/L5 | G:L1/L5; E:E1/E5a; C:B1I B1C B2a; J:L1/L5 | ||
| Baseline | Phase Combination | T | |
|---|---|---|---|
| JSJN-HP40 | GPS L1/Galileo E1 | 471.1 | 3740.7 |
| GPS L1/QZSS L1 | 102.8 | 3740.7 | |
| BDS-2 B1I/BDS-3 B1I | 106.9 | 3740.7 | |
| CUT0-CUTB | GPS L1/Galileo E1 | 368.4 | 3006.0 |
| GPS L1/QZSS L1 | 261.4 | 3006.0 | |
| GPS L1/BDS-2 B1I | 745.1 | 3006.0 |
| Base Receiver | Rover Device | Antenna | Baseline Length | Duration (UTC Time) |
|---|---|---|---|---|
| JSJN | HP40 | SinoGNSS AT340 | 0.4–0.6 km | 25 min (03:35–04:00, 13 December 2022) |
| CHCNAV i90 |
| Case | Fix Rate (%) | TTFF (s) | ||
|---|---|---|---|---|
| Intra | Inter | Intra | Inter | |
| GPS + 2 Galileo | 82.9 | 90.4 | 45 | 25 |
| GPS + 3 Galileo | 95.3 | 99.5 | 16 | 11 |
| GPS + 4 Galileo | 99.2 | 99.6 | 12 | 5 |
| GPS + 5 Galileo | 99.3 | 99.6 | 9 | 5 |
| Case | Positioning Accuracy (cm) | Improvement (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Intra | Inter | ||||||||
| N | E | U | N | E | U | N | E | U | |
| GPS + 2 Galileo | 0.37 | 0.37 | 1.80 | 0.33 | 0.26 | 1.10 | 8.9 | 30.6 | 38.9 |
| GPS + 3 Galileo | 0.34 | 0.28 | 1.17 | 0.32 | 0.25 | 1.05 | 5.5 | 10.3 | 10.2 |
| GPS + 4 Galileo | 0.31 | 0.25 | 1.03 | 0.30 | 0.24 | 0.94 | 4.7 | 6.5 | 9.3 |
| GPS + 5 Galileo | 0.31 | 0.24 | 0.89 | 0.30 | 0.24 | 0.85 | 3.3 | 2.5 | 4.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, R.; Gao, C.; Gan, L.; Zhang, R.; Gao, W.; Meng, X. Multi-GNSS Differential Inter-System Bias Estimation for Smartphone RTK Positioning: Feasibility Analysis and Performance. Remote Sens. 2023, 15, 1476. https://doi.org/10.3390/rs15061476
Shang R, Gao C, Gan L, Zhang R, Gao W, Meng X. Multi-GNSS Differential Inter-System Bias Estimation for Smartphone RTK Positioning: Feasibility Analysis and Performance. Remote Sensing. 2023; 15(6):1476. https://doi.org/10.3390/rs15061476
Chicago/Turabian StyleShang, Rui, Chengfa Gao, Lu Gan, Ruicheng Zhang, Wang Gao, and Xiaolin Meng. 2023. "Multi-GNSS Differential Inter-System Bias Estimation for Smartphone RTK Positioning: Feasibility Analysis and Performance" Remote Sensing 15, no. 6: 1476. https://doi.org/10.3390/rs15061476
APA StyleShang, R., Gao, C., Gan, L., Zhang, R., Gao, W., & Meng, X. (2023). Multi-GNSS Differential Inter-System Bias Estimation for Smartphone RTK Positioning: Feasibility Analysis and Performance. Remote Sensing, 15(6), 1476. https://doi.org/10.3390/rs15061476