Method of Infrared Small Moving Target Detection Based on Coarse-to-Fine Structure in Complex Scenes
Abstract
:1. Introduction
- The contrast ratio is less than 15%.
- The target size is less than 0.15% of the whole image.
1.1. Related Works
1.2. Motivation
- 1.
- A novel method for extracting coarse potential target regions is proposed. The preprocessed image is obtained by smooth filtering through a Laplacian filter kernel and enhanced with a new prior weight. Next, the multiscale local contrast features (MLCF) and multiscale local variance (MLV) are proposed to compute the contrast difference and obtain the potential region of the target (PRT).
- 2.
- A novel robust region intensity level (RRIL) method is proposed to weight the spatial domain of the PRT at a finer level.
- 3.
- A new time domain weighting approach is proposed through the kurtosis features of the temporal signals to eliminate the false alarms further and finely.
- 4.
- By testing on real datasets as well as qualitative, quantitative, comparative, ablation and noise immunity experiments, the proposed coarse-to-fine structure (MCFS) can achieve superior performance for infrared small moving target detection.
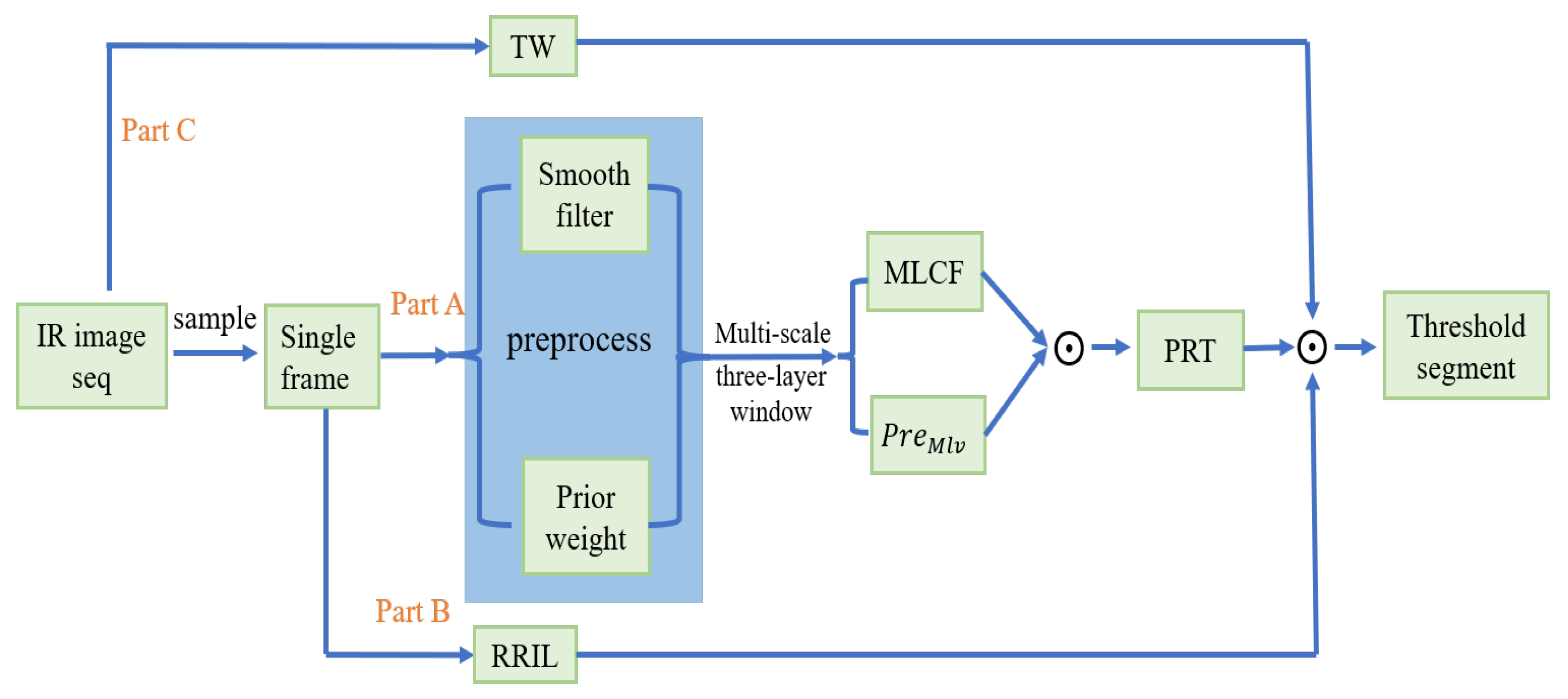
2. Proposed Algorithm
- 1.
- Firstly, the image is smoothed by Laplacian filtering and combined with the proposed weighted prior weight for image preprocessing, and afterward, the proposed MLCV and MLV incorporating multi-scale strategies are used for local feature calculation to obtain PRT.
- 2.
- Secondly, using the proposed algorithm to calculate a robust region intensity level (RRIL) to obtain the spatial weight of the target.
- 3.
- Then, by using the different moving information of the target and background components, the time domain characteristics of the target are obtained to calculate the temporal weight (TW).
- 4.
- Finally, use the temporal and the spatial weight to finely weigh the PRT and detect the target through threshold segmentation.
2.1. Calculation of PRT
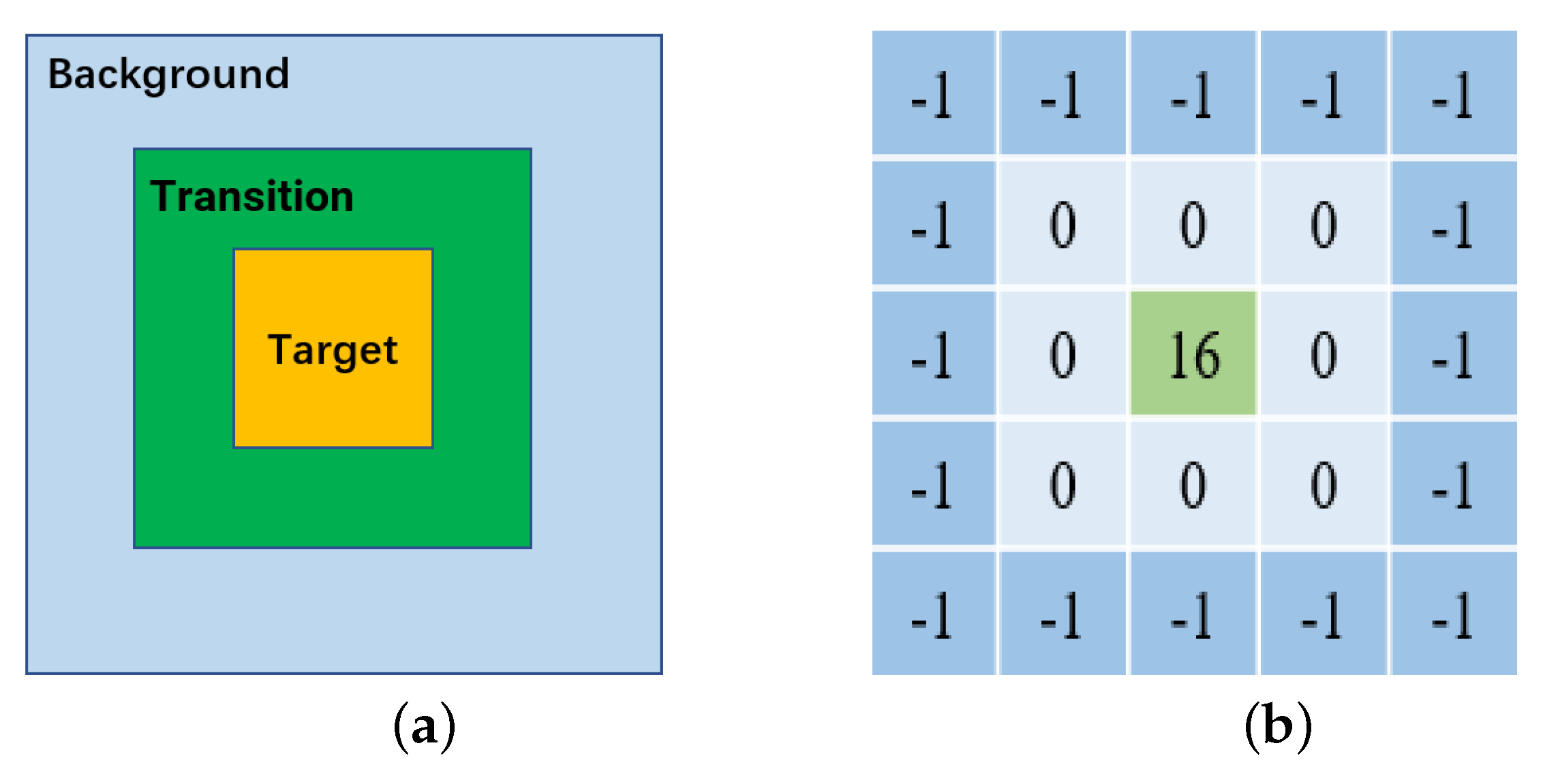
2.1.1. Smoothing Filter
2.1.2. Weighted Harmonic Prior
2.1.3. Calculation of MLCF and MLV
2.1.4. Multiscale Strategy
2.2. Calculation of Spatial Weighting Map
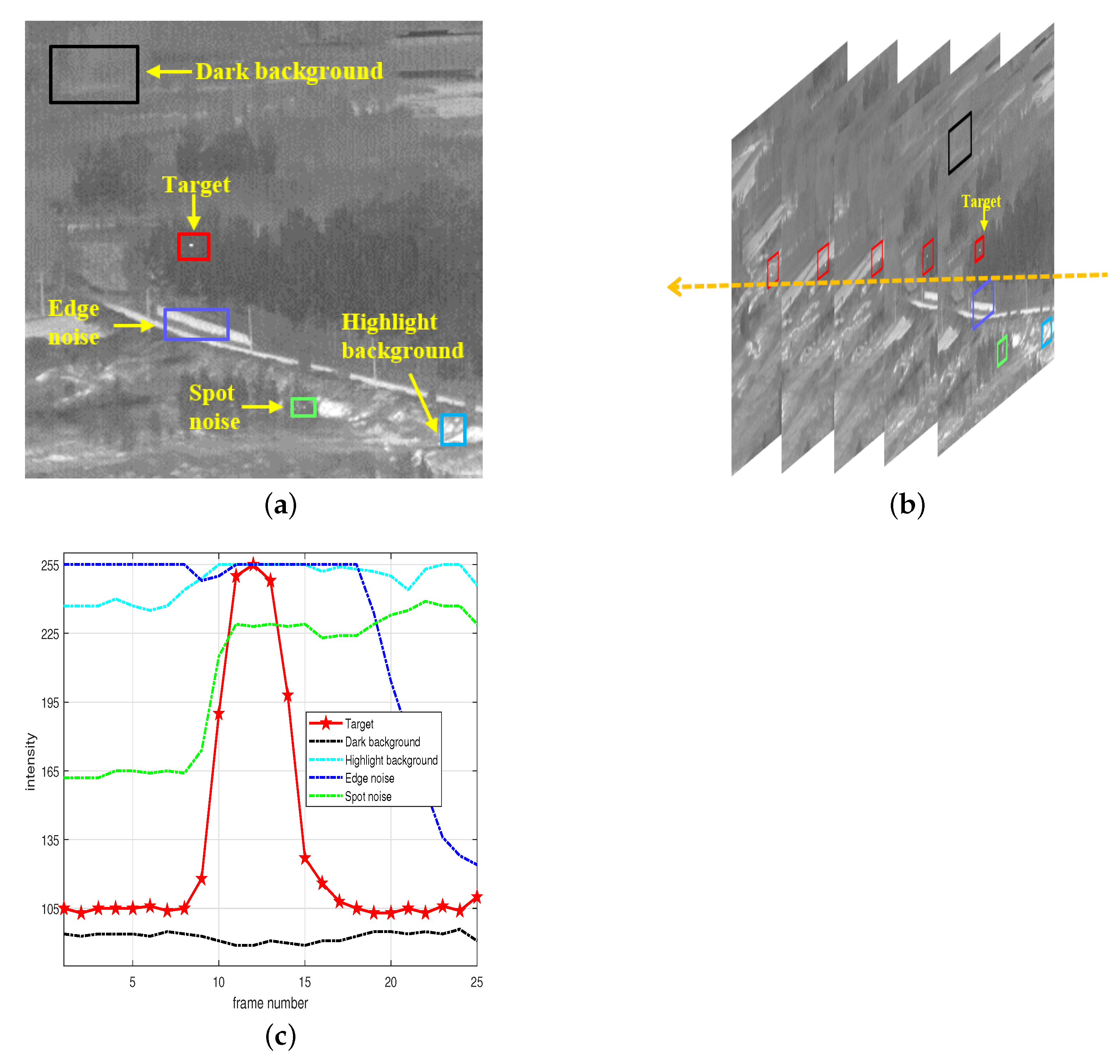
- 1.
- In most cases, the relationship between the target and the background in infrared images is shown in (a). The target is bright, and all the surrounding background areas are dark. At this time, the response of the target processed by either ARRIL or BRRIL calculation is large. So the multiplied response must also be large.
- 2.
- There is sparse point-like bright noise around the target, as shown in (b). The response of the target calculated by BRRIL is large. Due to the existence of the median value in ARRIL, the calculated response is also large. So the multiplied response is also large.
- 3.
- There are multiple point noises around the target or the target is at the edge of the bright background region, as shown in (c). At this time, although the response obtained by the target through ARRIL is small, the response obtained by BRRIL is large. So the response of the final target is large.
- 4.
- The target is in the highlighted background region, as shown in (d). Although both ARRIL and BRRIL will be small, the background response is smaller. At the same time, this situation will be suppressed during the extraction of PRT.
2.3. Calculation of Temporal Weighting Map
2.4. Calculation of Target Feature Map
3. Experiment and Analysis
3.1. Dataset Introduction
3.2. Parametric Analysis
3.3. Ablation Experiments
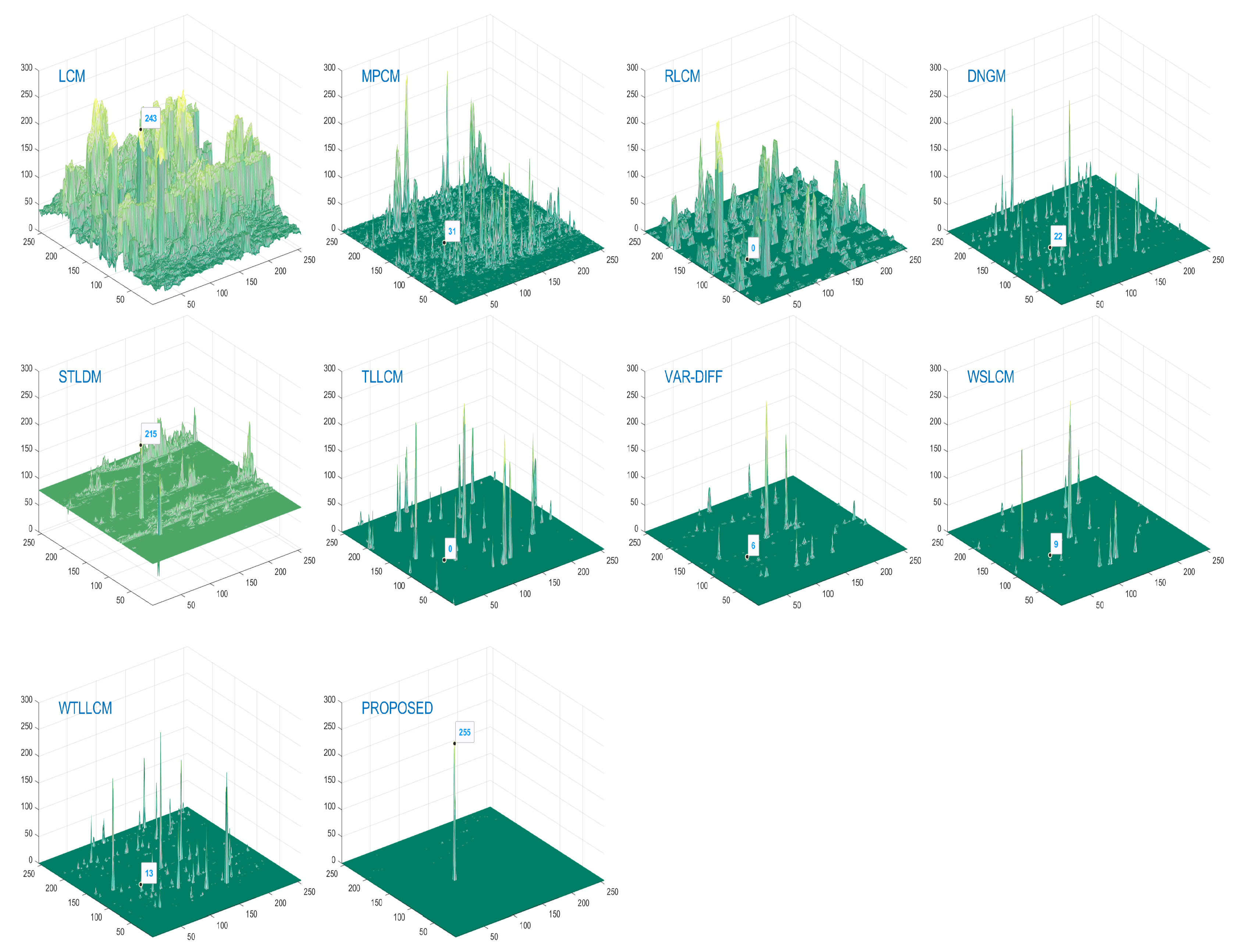
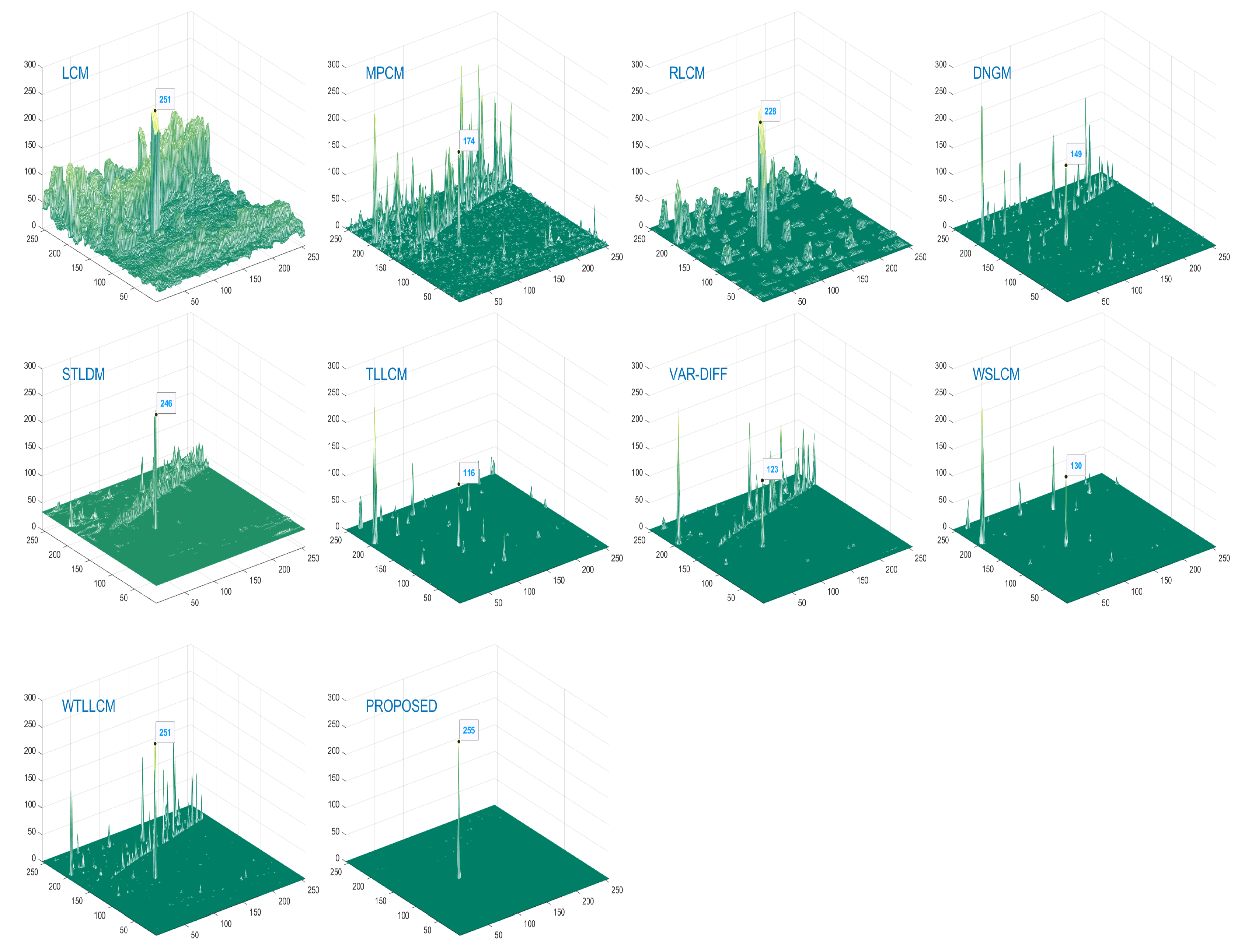
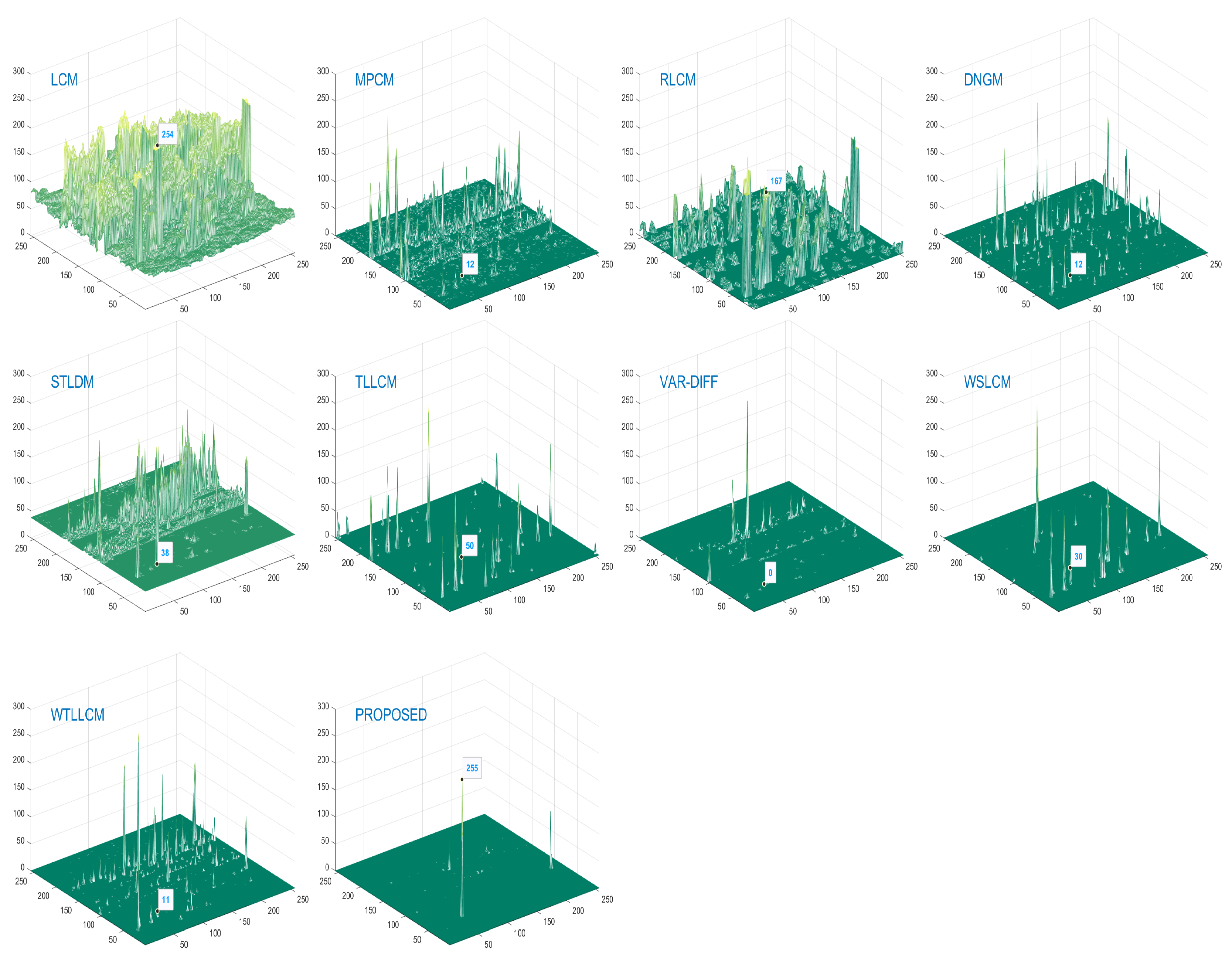
3.4. Qualitative Analysis
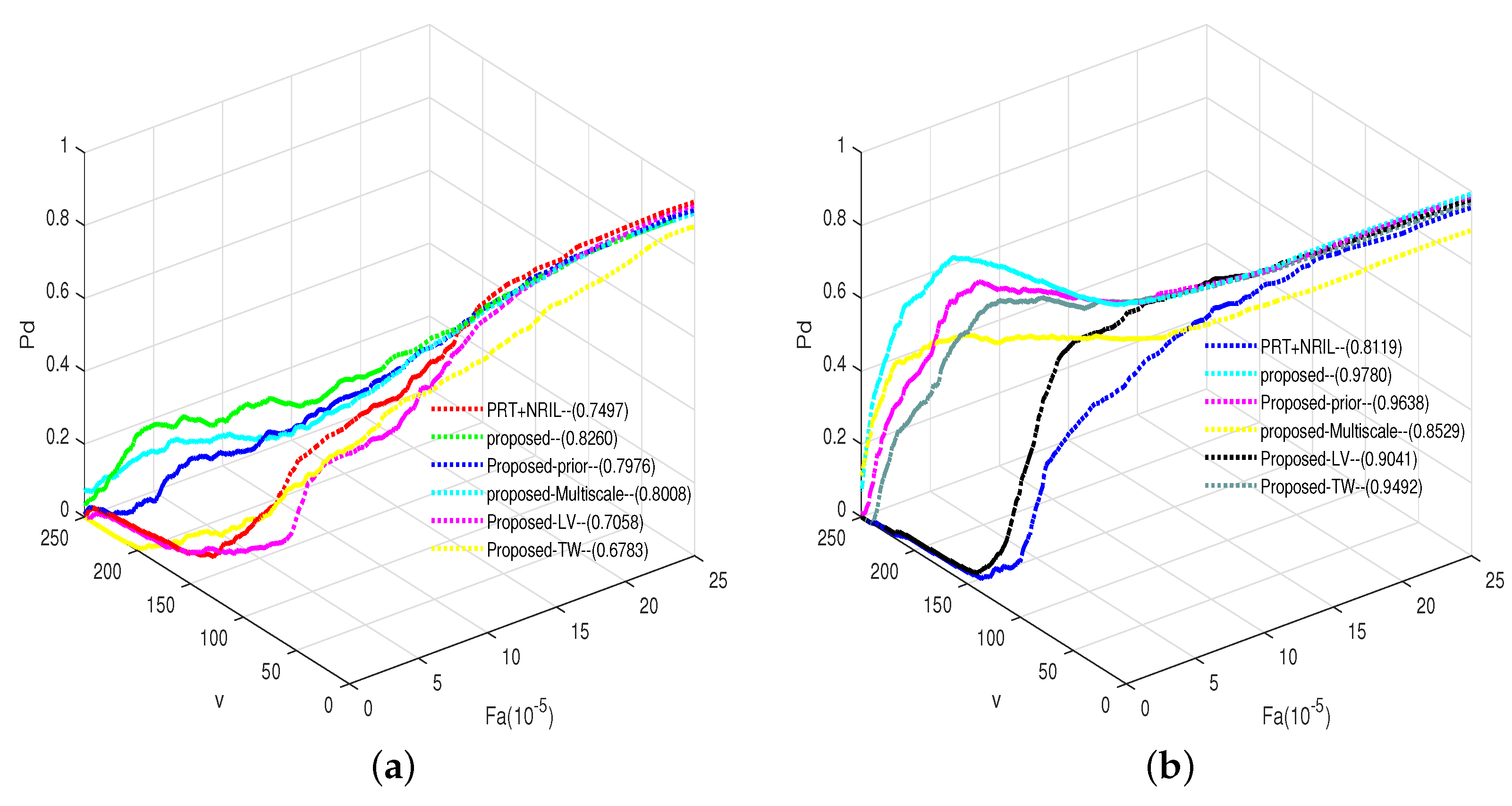
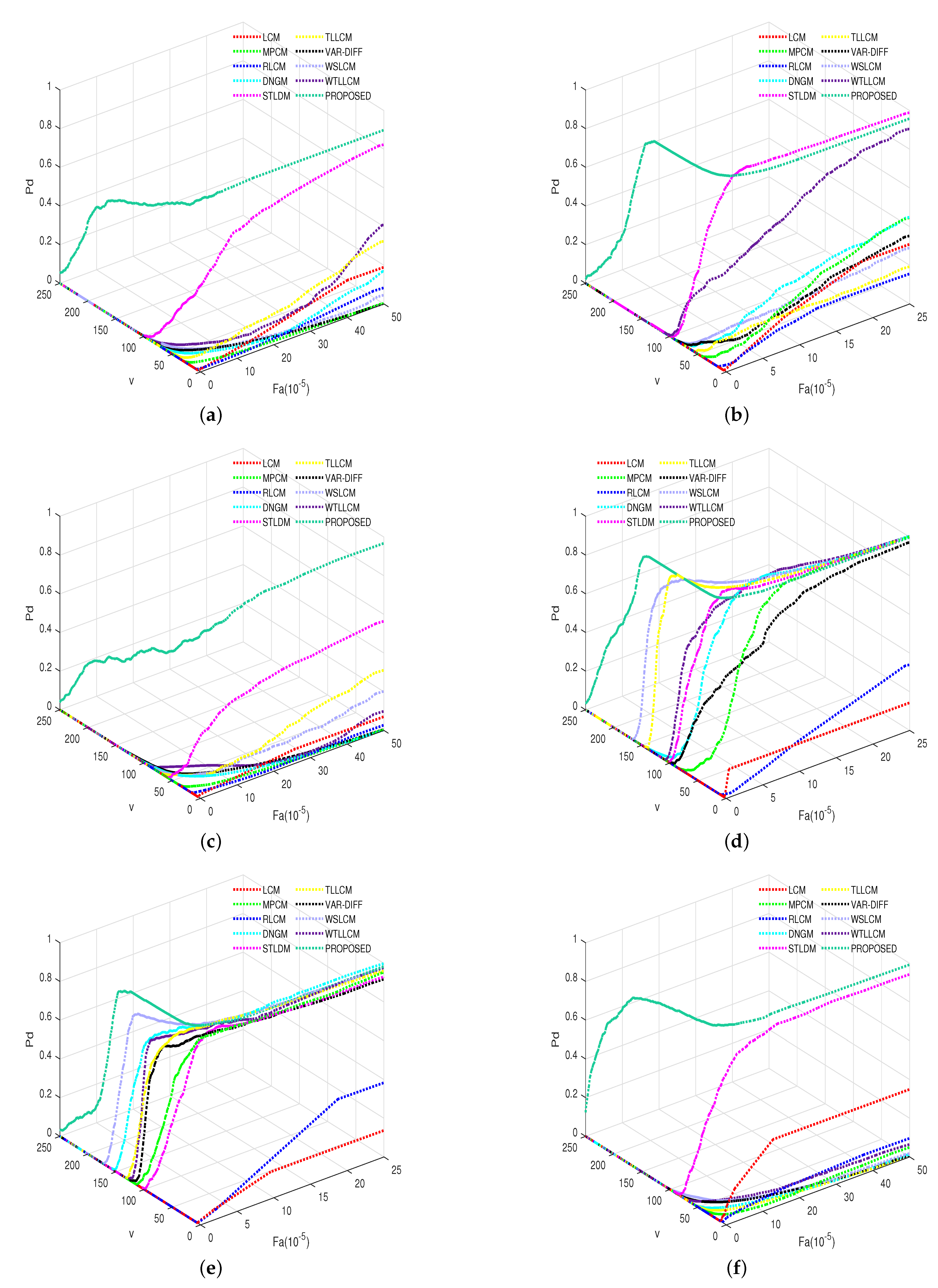
3.5. Quantitative Analysis
3.5.1. Evaluation Indicators
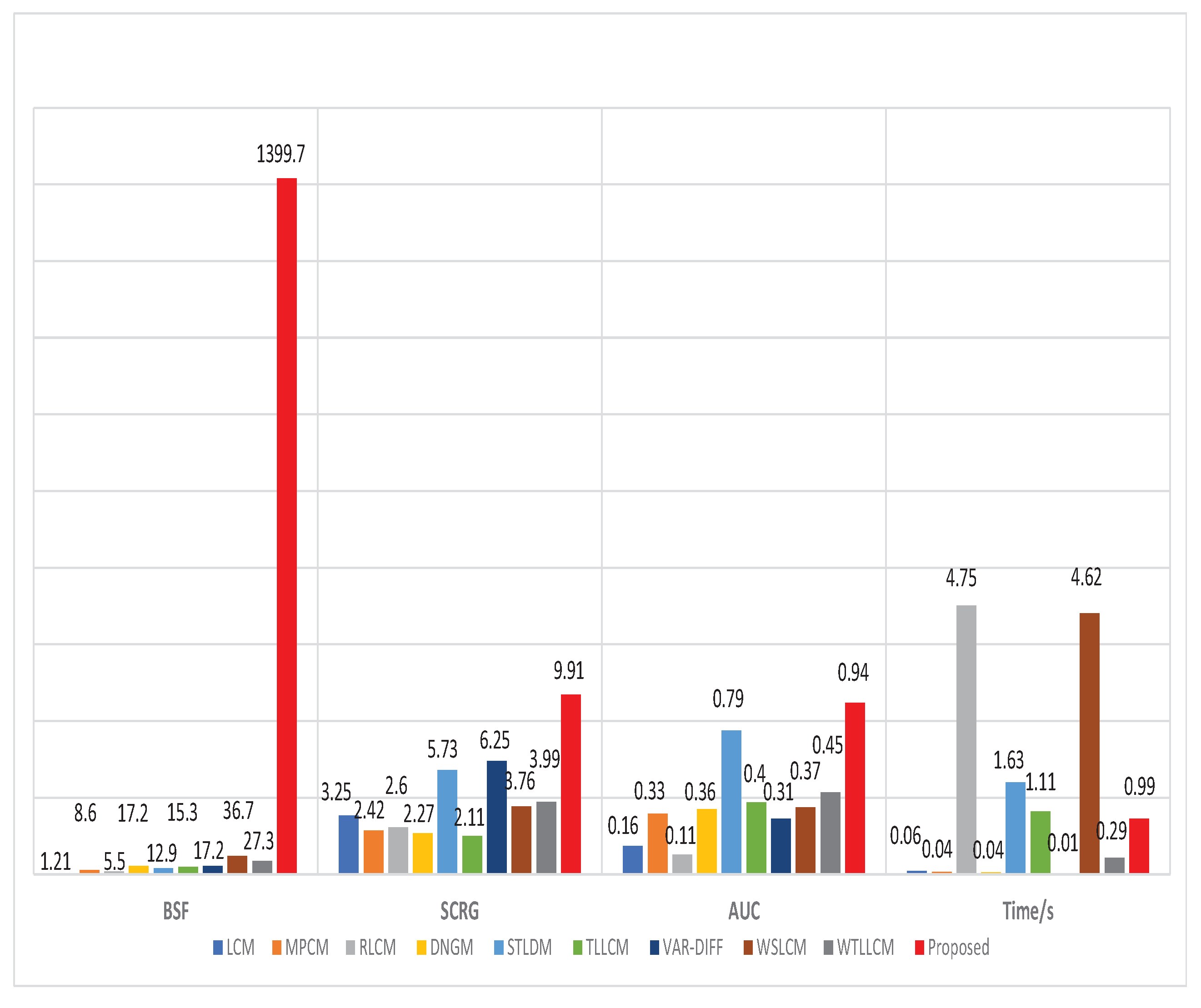
- Background suppression factor (BSF) [55]:BSF is a measure of the ability of the algorithm to suppress the whole background. represents the standard deviation of the whole background region of the processed image. represents the standard deviation of the whole background region of the input image.
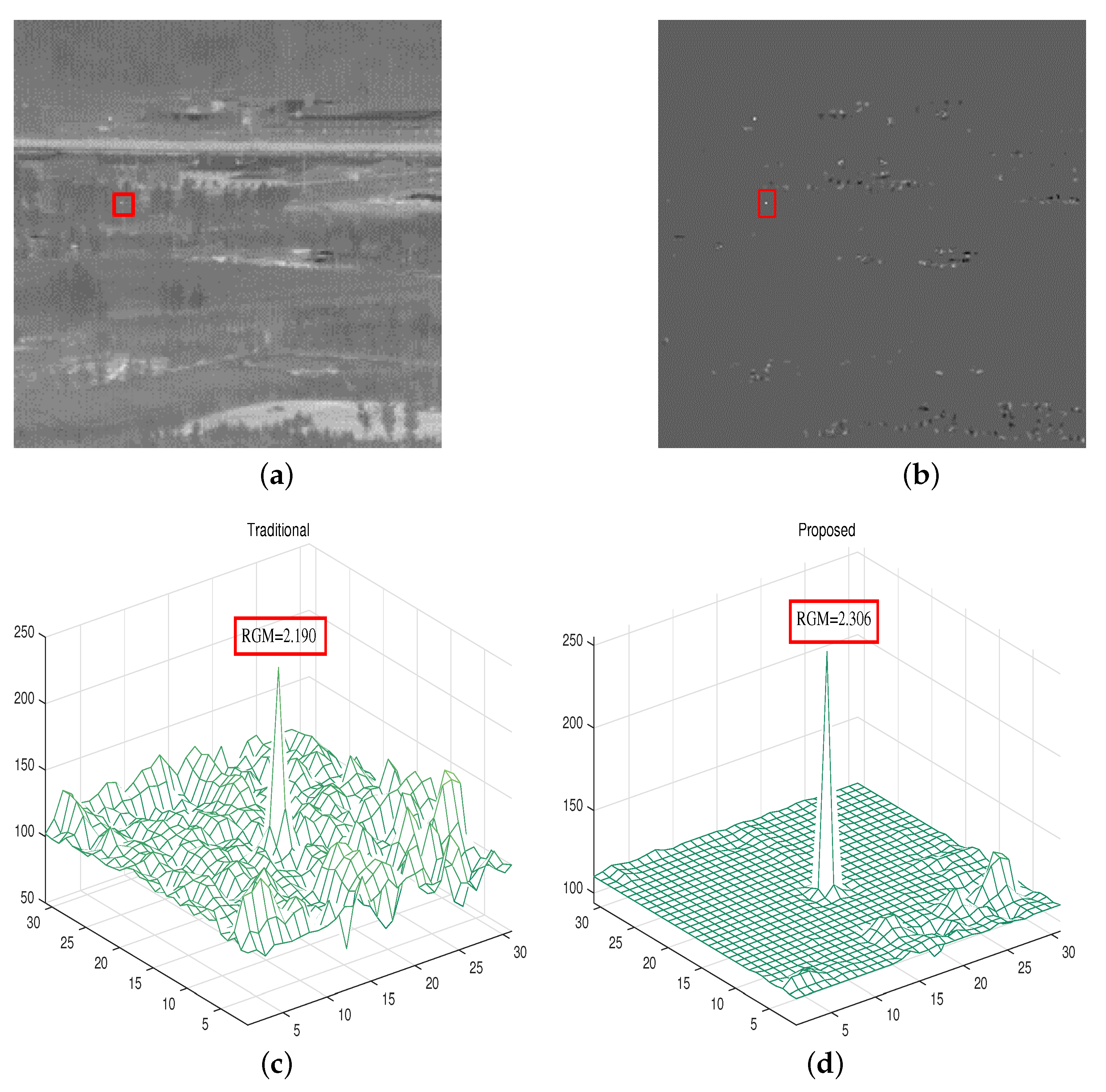
- Signal-to-clutter ratio gain (SCRG):SCRG is an indicator used to measure the ability of the algorithm to improve the local contrast of the target. represents the gray mean of the target. and represent the gray mean and the variance of the local background region around the target as shown in Figure 6. In this experiment, we take b as 25. and represent the processed image and the SCR of the input image, respectively.
- Area under the curve (AUC). AUC is related to detection probability () and false alarm rate ():
3.5.2. Quantitative Evaluation
3.6. Robustness to Noise
3.7. Computation Time
3.8. Intuitive Effect
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MCFS | Method of infrared small moving target detection based on coarse-to-fine structure |
| RIL | Regional intensity levels |
| RRIL | Robust region intensity level |
| SPIE | Society of Photo-Optical Instrumentation Engineers |
| SNR | Signal-to-noise ratio |
| HVS | Human visual system |
| LCM | Local contrast measure |
| MPCM | Multiscale patch contrast measure |
| RLCM | Relative local contrast measure |
| TLLCM | Three-layer local contrast measurement |
| DNGM | Double-neighborhood gradient method |
| NRIL | New regional intensity levels |
| WTLLCM | Weighted three-layer window local contrast measure |
| IRIL | Improved regional intensity levels |
| WSLCM | Weighted strengthened local contrast measure |
| VAR-DIFF | Variance difference |
| IFCM | Improved fuzzy C-means |
| NTRS | Non-convex tensor rank surrogate |
| PSTNN | Partial sum of the tensor nuclear norm |
| TV | Total variation |
| LogTFNN | (Log)tensor-fibered nuclear norm |
| GIPT | Group image-patch tensor |
| STLDM | Spatial–temporal local difference measure |
| ASTFDF | Anisotropic spatial-temporal fourth-order diffusion filter |
| MFSTPT | Multi-frame spatial-temporal patch-tensor model |
| RISTDnet | Robust infrared small target detection network |
| DRUnet | Dilated residual networks |
| LCF | Local contrast features |
| MLCF | Multiscale local contrast features |
| MLV | Multiscale local variance |
| PRT | Potential region of the target |
| RGM | Ratio of the gray mean |
| LV | Local variances |
| MLV | Multiscale local variances |
| TW | Temporal weighting |
| AUC | Area under curve |
| BSF | Background suppression factor |
| SCRG | Signal-to-clutter ratio gain |
| ROC | Receiver operating characteristic |
Appendix A. Some Figures



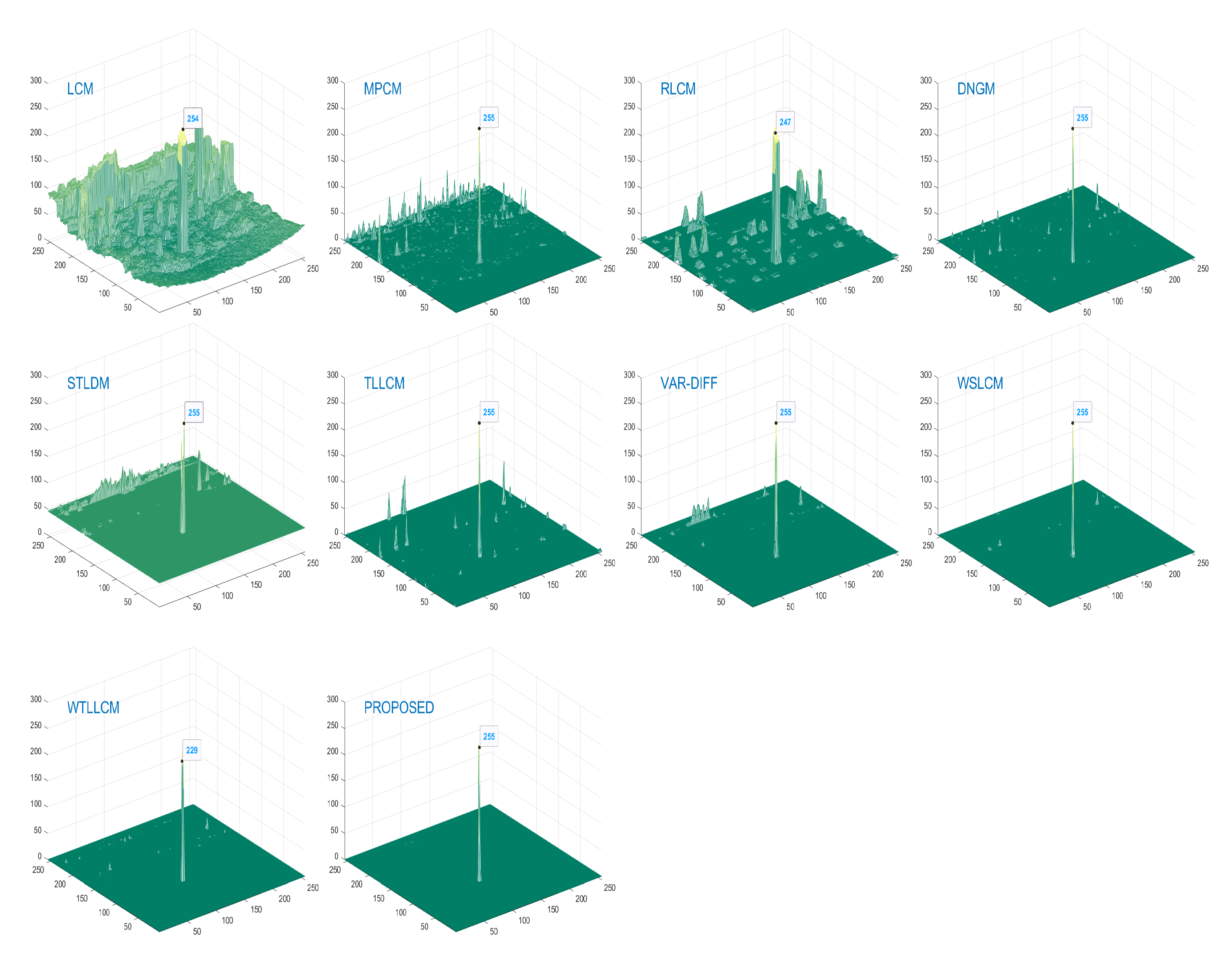


References
- Planinsic, G. Infrared Thermal Imaging: Fundamentals, Research and Applications. 2011. Available online: https://dialnet.unirioja.es/descarga/articulo/3699916.pdf (accessed on 2 December 2022).
- Zhang, X.; Jin, W.; Yuan, P.; Qin, C.; Wang, H.; Chen, J.; Jia, X. Research on passive wide-band uncooled infrared imaging detection technology for gas leakage. In Proceedings of the 2019 International Conference on Optical Instruments and Technology: Optical Systems and Modern Optoelectronic Instruments, Beijing, China, 26–28 October 2019; Volume 11434, pp. 144–157. [Google Scholar]
- Cuccurullo, G.; Giordano, L.; Albanese, D.; Cinquanta, L.; Di Matteo, M. Infrared thermography assisted control for apples microwave drying. J. Food Eng. 2012, 112, 319–325. [Google Scholar] [CrossRef]
- Jia, L.; Rao, P.; Zhang, Y.; Su, Y.; Chen, X. Low-SNR Infrared Point Target Detection and Tracking via Saliency-Guided Double-Stage Particle Filter. Sensors 2022, 22, 2791. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Li, W.; Li, L.; Hu, J.; Ma, P.; Tao, R. Single-Frame Infrared Small-Target Detection: A survey. IEEE Geosci. Remote Sens. Mag. 2022, 10, 87–119. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T. Clutter-adaptive infrared small target detection in infrared maritime scenarios. Opt. Eng. 2011, 50, 067001. [Google Scholar] [CrossRef]
- Pang, D.; Shan, T.; Ma, P.; Li, W.; Liu, S.; Tao, R. A novel spatiotemporal saliency method for low-altitude slow small infrared target detection. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Hu, Y.; Ma, Y.; Pan, Z.; Liu, Y. Infrared Dim and Small Target Detection from Complex Scenes via Multi-Frame Spatial–Temporal Patch-Tensor Model. Remote Sens. 2022, 14, 2234. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y.; Guo, J. Non-negative infrared patch-image model: Robust target-background separation via partial sum minimization of singular values. Infrared Phys. Technol. 2017, 81, 182–194. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, L.; Huang, S.; Peng, Z. Infrared small target detection via non-convex tensor rank surrogate joint local contrast energy. Remote Sens. 2020, 12, 1520. [Google Scholar] [CrossRef]
- Zhao, B.; Lu, F.; Hu, X.; Liu, D.; Wang, W. Infrared moving dim point target detection based on spatial-temporal local contrast. In Proceedings of the 2021 4th International Conference on Computer Information Science and Application Technology (CISAT 2021), Lanzhou, China, 30 July–1 August 2021; Volume 2010, p. 012189. [Google Scholar]
- Huang, S.; Liu, Y.; He, Y.; Zhang, T.; Peng, Z. Structure-adaptive clutter suppression for infrared small target detection: Chain-growth filtering. Remote Sens. 2019, 12, 47. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Han, J.; Liang, K.; Zhou, B.; Zhu, X.; Zhao, J.; Zhao, L. Infrared small target detection utilizing the multiscale relative local contrast measure. IEEE Geosci. Remote Sens. Lett. 2018, 15, 612–616. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, G.; Ma, Y.; Kang, J.U.; Kwan, C. Small infrared target detection based on fast adaptive masking and scaling with iterative segmentation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Liu, C.; Zhang, H.; Zhao, Q. A local contrast method for infrared small-target detection utilizing a tri-layer window. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1822–1826. [Google Scholar] [CrossRef]
- Wu, L.; Ma, Y.; Fan, F.; Wu, M.; Huang, J. A double-neighborhood gradient method for infrared small target detection. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1476–1480. [Google Scholar] [CrossRef]
- Lv, P.; Sun, S.; Lin, C.; Liu, G. A method for weak target detection based on human visual contrast mechanism. IEEE Geosci. Remote Sens. Lett. 2018, 16, 261–265. [Google Scholar] [CrossRef]
- Cui, H.; Li, L.; Liu, X.; Su, X.; Chen, F. Infrared Small Target Detection Based on Weighted Three-Layer Window Local Contrast. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Zhang, H.; Zhao, Q.; Zhang, X.; Li, N. Infrared small target detection based on the weighted strengthened local contrast measure. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1670–1674. [Google Scholar] [CrossRef]
- Ma, T.; Yang, Z.; Ren, X.; Wang, J.; Ku, Y. Infrared Small Target Detection Based on Smoothness Measure and Thermal Diffusion Flowmetry. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Nasiri, M.; Chehresa, S. Infrared small target enhancement based on variance difference. Infrared Phys. Technol. 2017, 82, 107–119. [Google Scholar] [CrossRef]
- Chen, L.; Lin, L. Improved Fuzzy C-Means for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y. Reweighted infrared patch-tensor model with both nonlocal and local priors for single-frame small target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Peng, Z. Infrared small target detection based on partial sum of the tensor nuclear norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef] [Green Version]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–21. [Google Scholar] [CrossRef]
- Yang, L.; Yan, P.; Li, M.; Zhang, J.; Xu, Z. Infrared Small Target Detection Based on a Group Image-Patch Tensor Model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liu, H.K.; Zhang, L.; Huang, H. Small target detection in infrared videos based on spatio-temporal tensor model. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8689–8700. [Google Scholar] [CrossRef]
- Du, P.; Hamdulla, A. Infrared moving small-target detection using spatial–temporal local difference measure. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1817–1821. [Google Scholar] [CrossRef]
- Zhu, H.; Guan, Y.; Deng, L.; Li, Y.; Li, Y. Infrared moving point target detection based on an anisotropic spatial-temporal fourth-order diffusion filter. Comput. Electr. Eng. 2018, 68, 550–556. [Google Scholar] [CrossRef]
- Hou, Q.; Wang, Z.; Tan, F.; Zhao, Y.; Zheng, H.; Zhang, W. RISTDnet: Robust infrared small target detection network. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, C.; Fu, Q.; Han, Z. A novel pattern for infrared small target detection with generative adversarial network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4481–4492. [Google Scholar] [CrossRef]
- Liu, T.; Yang, J.; Li, B.; Xiao, C.; Sun, Y.; Wang, Y.; An, W. Nonconvex Tensor Low-Rank Approximation for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Asymmetric contextual modulation for infrared small target detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 950–959. [Google Scholar]
- Fang, H.; Xia, M.; Zhou, G.; Chang, Y.; Yan, L. Infrared small UAV target detection based on residual image prediction via global and local dilated residual networks. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Han, J.; Ma, Y.; Zhou, B.; Fan, F.; Liang, K.; Fang, Y. A robust infrared small target detection algorithm based on human visual system. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2168–2172. [Google Scholar]
- Liu, J.; He, Z.; Chen, Z.; Shao, L. Tiny and dim infrared target detection based on weighted local contrast. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1780–1784. [Google Scholar] [CrossRef]
- Qin, Y.; Li, B. Effective infrared small target detection utilizing a novel local contrast method. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1890–1894. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Yuan, D.; Chen, H. Infrared small target detection based on local intensity and gradient properties. Infrared Phys. Technol. 2018, 89, 88–96. [Google Scholar] [CrossRef]
- Jiang, Y.; Dong, L.; Chen, Y.; Xu, W. An infrared small target detection algorithm based on peak aggregation and Gaussian discrimination. IEEE Access 2020, 8, 106214–106225. [Google Scholar] [CrossRef]
- Hsieh, T.H.; Chou, C.L.; Lan, Y.P.; Ting, P.H.; Lin, C.T. Fast and robust infrared image small target detection based on the convolution of layered gradient kernel. IEEE Access 2021, 9, 94889–94900. [Google Scholar] [CrossRef]
- Guan, X.; Peng, Z.; Huang, S.; Chen, Y. Gaussian scale-space enhanced local contrast measure for small infrared target detection. IEEE Geosci. Remote Sens. Lett. 2019, 17, 327–331. [Google Scholar] [CrossRef]
- Distante, A.; Distante, C.; Distante, W.; Wheeler. Handbook of Image Processing and Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Qin, Y.; Bruzzone, L.; Gao, C.; Li, B. Infrared small target detection based on facet kernel and random walker. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7104–7118. [Google Scholar] [CrossRef]
- Gao, C.Q.; Tian, J.W.; Wang, P. Generalised-structure-tensor-based infrared small target detection. Electron. Lett. 2008, 44, 1349–1351. [Google Scholar] [CrossRef]
- Brown, M.; Szeliski, R.; Winder, S. Multi-image matching using multi-scale oriented patches. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 510–517. [Google Scholar]
- Deng, H.; Sun, X.; Liu, M.; Ye, C.; Zhou, X. Small infrared target detection based on weighted local difference measure. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4204–4214. [Google Scholar] [CrossRef]
- Chapple, P.B.; Bertilone, D.C.; Caprari, R.S.; Angeli, S.; Newsam, G.N. Target detection in infrared and SAR terrain images using a non-Gaussian stochastic model. In Proceedings of the Targets and Backgrounds: Characterization and Representation V, Orlando, FL, USA, 14 July 1999; Volume 3699, pp. 122–132. [Google Scholar]
- Hui, B.; Song, Z.; Fan, H.; Zhong, P.; Hu, W.; Zhang, X.; Lin, J.; Su, H.; Jin, W.; Zhang, Y.; et al. A dataset for dim-small target detection and tracking of aircraft in infrared image sequences. Sci. DB 2019. [Google Scholar]
- Leng, X.; Ji, K.; Zhou, S.; Xing, X. Ship detection based on complex signal kurtosis in single-channel SAR imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6447–6461. [Google Scholar] [CrossRef]
- Hui, B.; Song, Z.; Fan, H.; Zhong, P.; Hu, W.; Zhang, X.; Ling, J.; Su, H.; Jin, W.; Zhang, Y.; et al. A dataset for infrared detection and tracking of dim-small aircraft targets under ground/air background. China Sci. Data 2020, 5, 291–302. [Google Scholar]
- Zhang, T.; Wu, H.; Liu, Y.; Peng, L.; Yang, C.; Peng, Z. Infrared small target detection based on non-convex optimization with Lp-norm constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Yang, J.; Long, Y.; Shang, Z.; An, W. Infrared patch-tensor model with weighted tensor nuclear norm for small target detection in a single frame. IEEE Access 2018, 6, 76140–76152. [Google Scholar] [CrossRef]














| Data | Frames | Average SCR | Scene Introduction |
|---|---|---|---|
| Data 1 | 800 | 5.45 | long distance, ground background, long time |
| Data 2 | 399 | 6.07 | ground background, alternating near and far |
| Data 3 | 500 | 3.42 | Target maneuver, ground background |
| Data 4 | 400 | 3.84 | Irregular movement of target, ground background |
| Data 5 | 400 | 3.01 | Target maneuver, sky ground background |
| Data 6 | 400 | 2.20 | Target from far to near, single target, ground background |
| Methods | Parameter Settings |
|---|---|
| LCM [13] | window size: 3∗3 |
| MPCM [14] | window size: 3∗3, 5∗5, 7∗7, mean filter size: 3 ∗ 3 |
| RLCM [15] | (K1, K2) = (2, 4), (5, 9), and (9, 16) |
| DNGM [18] | sub-window size: 3∗3 |
| STLDM [30] | frames = 5 |
| TLLCM [17] | Gaussian filter kernel |
| VAR-DIFF [23] | window size: 3∗3, 5∗5, 7∗7 |
| WSLCM [21] | window size: 3∗3, 5∗5, 7∗7, 9∗9 |
| WTLLCM [20] | sub-window size: 3∗3, K = 4 |
| Proposed | sub-window size: 3∗3, K = 2, = 2, = 1 |
| Methods | Seq.1 | Seq.2 | Seq.3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BSF | SCRG | AUC | BSF | SCRG | AUC | BSF | SCRG | AUC | |
| LCM | 0.481 | 1.842 | 0.108 | 0.497 | 1.816 | 0.203 | 0.819 | 5.331 | 0.054 |
| MPCM | 2.405 | 1.791 | 0 | 4.094 | 6.371 | 0.252 | 5.403 | 3.581 | 0.010 |
| RLCM | 1.117 | 3.637 | 0.05 | 2.224 | 3.822 | 0.112 | 2.637 | 2.300 | 0.010 |
| DNGM | 4.607 | 4.033 | 0.044 | 7.902 | 2.142 | 0.272 | 10.240 | 1.941 | 0 |
| STLDM | 5.565 | 4.702 | 0.654 | 8.593 | 3.406 | 0.930 | 6.381 | 3.632 | 0.457 |
| TLLCM | 3.744 | 2.486 | 0.153 | 6.224 | 1.848 | 0.128 | 8.492 | 1.827 | 0.149 |
| VAR-DIFF | 4.895 | 16.061 | 0.001 | 7.487 | 11.91 | 0.189 | 10.798 | 3.001 | 0.001 |
| WSLCM | 5.818 | 11.073 | 0.009 | 8.460 | 3.071 | 0.169 | 9.526 | 3.398 | 0.086 |
| WTLLCM | 5.194 | 11.488 | 0.170 | 10.285 | 4.771 | 0.632 | 10.171 | 2.181 | 0.020 |
| Proposed | 577.2 | 23.162 | 0.856 | 1805.9 | 5.823 | 0.955 | 37.288 | 6.934 | 0.893 |
| Methods | Seq.4 | Seq.5 | Seq.6 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BSF | SCRG | AUC | BSF | SCRG | AUC | BSF | SCRG | AUC | |
| LCM | 1.755 | 2.087 | 0.139 | 1.625 | 1.004 | 0.112 | 2.104 | 7.418 | 0.315 |
| MPCM | 12.986 | 0.160 | 0.814 | 16.674 | 2.603 | 0.899 | 9.893 | 0.010 | 0.022 |
| RLCM | 14.715 | 0.583 | 0.174 | 9.143 | 1.302 | 0.235 | 3.417 | 3.981 | 0.074 |
| DNGM | 20.232 | 2.222 | 0.880 | 45.693 | 2.125 | 0.952 | 14.527 | 1.129 | 0.001 |
| STLDM | 18.681 | 2.086 | 0.963 | 18.939 | 1.988 | 0.855 | 19.358 | 18.588 | 0.883 |
| TLLCM | 31.576 | 2.548 | 0.999 | 28.143 | 2.676 | 0.943 | 13.844 | 1.270 | 0.001 |
| VAR-DIFF | 15.164 | 1.179 | 0.756 | 46.245 | 2.956 | 0.893 | 18.492 | 2.386 | 0.001 |
| WSLCM | 56.679 | 1.862 | 0.997 | 117.64 | 2.127 | 0.953 | 22.017 | 0.999 | 0.005 |
| WTLLCM | 23.771 | 2.401 | 0.931 | 97.467 | 2.404 | 0.920 | 16.663 | 0.705 | 0.030 |
| Proposed | 2355.2 | 1.785 | 0.997 | 3247.4 | 1.815 | 0.980 | 375.16 | 19.945 | 0.978 |
| Methods | Seq.1(/s) | Seq.2(/s) | Seq.3(/s) | Seq.4(/s) | Seq.5(/s) | Seq.6(/s) |
|---|---|---|---|---|---|---|
| LCM | 0.042 | 0.057 | 0.063 | 0.054 | 0.080 | 0.057 |
| MPCM | 0.037 | 0.038 | 0.043 | 0.041 | 0.041 | 0.041 |
| RLCM | 4.567 | 5.499 | 6.201 | 4.525 | 3.829 | 3.905 |
| DNGM | 0.037 | 0.037 | 0.043 | 0.039 | 0.037 | 0.039 |
| STLDM | 1.629 | 1.618 | 1.609 | 1.627 | 1.607 | 1.693 |
| TLLCM | 1.147 | 1.129 | 1.152 | 1.087 | 1.084 | 1.090 |
| VAR-DIFF | 0.010 | 0.012 | 0.014 | 0.009 | 0.009 | 0.013 |
| WSLCM | 4.570 | 4.477 | 4.579 | 4.415 | 4.461 | 5.192 |
| WTLLCM | 0.327 | 0.266 | 0.288 | 0.276 | 0.296 | 0.316 |
| Proposed | 0.999 | 0.993 | 1.010 | 0.963 | 0.973 | 0.994 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Liu, Y.; Pan, Z.; Hu, Y. Method of Infrared Small Moving Target Detection Based on Coarse-to-Fine Structure in Complex Scenes. Remote Sens. 2023, 15, 1508. https://doi.org/10.3390/rs15061508
Ma Y, Liu Y, Pan Z, Hu Y. Method of Infrared Small Moving Target Detection Based on Coarse-to-Fine Structure in Complex Scenes. Remote Sensing. 2023; 15(6):1508. https://doi.org/10.3390/rs15061508
Chicago/Turabian StyleMa, Yapeng, Yuhan Liu, Zongxu Pan, and Yuxin Hu. 2023. "Method of Infrared Small Moving Target Detection Based on Coarse-to-Fine Structure in Complex Scenes" Remote Sensing 15, no. 6: 1508. https://doi.org/10.3390/rs15061508
APA StyleMa, Y., Liu, Y., Pan, Z., & Hu, Y. (2023). Method of Infrared Small Moving Target Detection Based on Coarse-to-Fine Structure in Complex Scenes. Remote Sensing, 15(6), 1508. https://doi.org/10.3390/rs15061508







