Next Article in Journal
Absolute Localization of Targets Using a Phase-Measuring Sidescan Sonar in Very Shallow Waters
Previous Article in Journal
Accurate and Serialized Dense Point Cloud Reconstruction for Aerial Video Sequences
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 6
10.3390/rs15061623
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Technical Note

GNSS High-Precision Augmentation for Autonomous Vehicles: Requirements, Solution, and Technical Challenges

by
Liang Chen
1,
Fu Zheng
2,*,
Xiaopeng Gong
3 and
Xinyuan Jiang
4
1
School of Geomatics, Liaoning Technical University, 47 Zhonghua Road, Fuxin 123000, China
2
School of Electronic and Information Engineering, Beihang University, 37 Xueyuan Road, Beijing 100191, China
3
GNSS Research Center, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
4
German Research Centre for Geosciences (GFZ), 14473 Potsdam, Germany
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(6), 1623; https://doi.org/10.3390/rs15061623
Submission received: 13 February 2023 / Revised: 14 March 2023 / Accepted: 15 March 2023 / Published: 17 March 2023
(This article belongs to the Topic Recent Advances in PNT Technology with GNSS as the Core and Its Application in Emerging Fields)
Browse Figures
Versions Notes

Abstract

:
Autonomous driving is becoming a pivotal technology that can realize intelligent transportation and revolutionize the future of mobility. Various types of sensors, including perception sensors and localization sensors, are essential for high-level autonomous and intelligent vehicles (AIV). In this paper, the characteristics of different sensors are compared, and the application characteristics and requirements of AIV are analyzed in depth. These analyses indicate that: GNSS, as the unique localization sensor that can obtain an absolute position, can not only provide all-weather position and time information for internal multi-sensor fusion but also act as a standard spatiotemporal reference for all autonomous systems; Furthermore, AIVs aim to provide safety for a mass user base ranging from tens to hundreds of millions; for this, AIVs require a global wide-area and instantaneous precise positioning service with location privacy protection. Based on a “geometry-bound” description of road grade and vehicle size, it has been found that GNSS requirements in autonomous vehicles include decimeter-level positioning with the assurance of high integrity. Combined with high-integrity GNSS implementation in the civil aviation field, GNSS different technology routes, and commercial solutions, a state space representation (SSR)-based GNSS high-precision augmentation positioning solution for AIV is summarized and introduced. The solution can achieve instantaneous, precise positioning with high integrity in a wide area by utilizing passive positioning mode with location privacy protection. In addition, the research progress on key technologies in the solution and existing challenges is investigated in detail by reviewing a series of publications.

1. Introduction

Unmanned autonomous systems are high-tech, intelligent machines capable of carrying out operations or management by means of advanced technologies and traveling by air, land, or sea without human intervention [1]. With the significant advancement of multi-sensor technology and obstacle detection algorithms, autonomous driving is becoming a pivotal technology that can realize intelligent transportation and revolutionize the future of mobility [2]. According to the definition of the Society of Automotive Engineers (SAE), there are six levels (0 to 5) of vehicles, i.e., Level 0: No Driving Automation, Level 1: Driver Assistance, Level 2: Partial Driving Automation, Level 3: Conditional Driving Automation, Level 4: High Driving Automation, and Level 5: Full Driving Automation [3]. High-level AIV rely on various types of sensors to make logical decisions based on the information gathered, similar to humans [4]. These sensors can be divided into two categories: perception sensors and localization sensors. Perception sensors, e.g., RADAR, LiDAR, ultrasonic, camera, etc., are mainly used to perceive the surrounding environment of the vehicle [5]. However, harsh weather conditions, such as glare, snow, mist, rain, haze, fog, etc., can significantly reduce the performance of purely perception-based approaches for perception and navigation [2], which is a major challenge for AIVs. Therefore, in order to achieve seamless and reliable perception and decision-making, AIVs require not only internal multi-sensor fusion [6,7] but also interoperability with external autonomous systems, e.g., a vehicle road coordination system [5,8], which requires sharing common spatial reference frames and timing [5,9]. Localization sensors include GNSS, IMU, odometry, etc. [10,11]. These sensors, especially GNSS, not only provide all-weather position and altitude information for internal multi-sensor fusion [4], but also provide the only source of globally consistent precise positioning and timing, acting as a standard reference for all autonomous systems [5]. Thus, GNSS is essential for AIVs.
GNSSs, e.g., GPS, GLONASS, BDS, and Galileo, commonly consist of three components: the space segment, the control segment, and the user segment [12]. The positioning principle of GNSS is that the user segment determines its position by measuring the distance from several GNSS satellites to the receiver at the same time. GNSS observations suffer from several errors, including satellite-related ephemeris errors (orbit error, clock error, and signal bias), transmission-related atmosphere delay (ionospheric and tropospheric), and receiver-related observation error, which degrades the positioning accuracy significantly [4,12]. In order to achieve GNSS precise positioning, there are currently two implementation routes: observation space representation (OSR) and state space representation (SSR) [13,14]. OSR uses observations of a reference station directly or uses the derived distance-related corrections to eliminate users’ observation errors based on the high correlation of adjacent GNSS stations’ observations, while SSR uses actual state-space data, i.e., improved ephemeris (orbit and clock, satellite biases), ionospheric and tropospheric models, etc., to represent the complete GNSS state [13].
According to the implementation routes of SSR and OSR, the development of GNSS positioning technology is shown in Figure 1. Single point positioning (SPP), based on pseudorange observations and SSR broadcast ephemeris, the standard positioning service (SPS) provided by GNSS [15,16,17], can deliver global meter-level absolute positioning, which is widely used in the mass market [18] and can be considered the first-generation of positioning technology. On the basis of SPP, precise point positioning (PPP) can achieve global decimeter- or centimeter-level precise positioning after convergence by processing undifferenced (UD) pseudorange and carrier-phase observations from a stand-alone GNSS receiver together with SSR precise ephemeris [19,20]. Developed in the 1990s to fulfill the special needs of the aviation community, the satellite-based augmentation system (SBAS) can improve the user’s positioning performance by broadcasting differential corrections and integrity monitoring information [21]. Thus, it can be considered an augmentation version of the SPS. There are four operational SBAS for aviation, including the UAS’s WAAS, Europe’s EGNOS, Japan’s MSAS, and India’s GAGAN [18]. Currently, the SBAS concept also covers the global correction service based on PPP technology [18], and the construction of an SBAS service for aviation and a global PPP correction service can be coordinated and optimized by employing the same ground tracking network, computing center, and correction information [22]. The SBAS global PPP correction service includes open or authorized precision positioning services provided by GNSS providers, e.g., Galileo’s HAS, QZSS’s CLAS, and BDS’s PPP [14,23,24,25], and other commercial augmentation services provided, e.g., Hemisphere’s Altas, John Deere’s Starfire, Trimble’s RTX and OmniSTAR, Hexagon AB’s VERIPOS, TerraStar, etc. [18].
As mentioned above, OSR routes take advantage of the slowly varying characteristics of ephemeris errors and ionospheric and tropospheric delays with timing and the strong correlation between the user and the reference station. The pseudorange-based differential GNSS (DGNSS) technique can obtain meter-level positioning by computing and broadcasting either corrections to the position or to the measurements [26], whereas the carrier-phase-dominated real-time kinematic (RTK) technique can achieve centimeter-level precise positioning by relying on double-differenced (DD) ambiguity resolution [27]. On this basis, LAAS, known as a GBAS, is developed for aircraft approach and landing and can guarantee the positioning requirements of aircraft in different flight categories together with WAAS [28]. As an effective means to overcome single-base RTK’s distance limit of 10–20 km between reference station and rover receiver, CORS, another high-precision GBAS service based on network RTK (NRTK), can extend the distance to about 75 km and can provide service for a larger area [26].
PPP-RTK, an innovative PPP using SSR in RTK networks [13,29], can achieve rapid convergence of several seconds to reliable centimeter-level positioning accuracy [30]. All individual GNSS SSR correction components include (a) orbits and clocks, the standard products for PPP service estimated by a global sparse network of 100 stations [31]; (b) pseudorange and carrier-phase biases; and (c) ionospheric and tropospheric estimated by a regional dense network with approximately 200 km station spacing [32].
A comparison of the most widespread GNSS positioning technologies based on SSR and OSR for observations, corrections, communication links, service area, convergence, accuracy, application fields, etc., is shown in Table 1.
Based on a review of AIV application characteristics and requirements, combined with the developments in GNSS technology, a GNSS high-precision augmentation positioning solution for AIV is summarized and introduced in this paper. The article structure is as follows: Firstly, the technology development and comparison of different GNSS implementation routes are introduced in Section 1. The application characteristics and positioning requirements of AIV are described in Section 2, including integrity, positioning accuracy, etc. The then-current GNSS augmentation solution for AIV is summarized in Section 3 by comparing and analyzing the different GNSS positioning technologies. Section 4 describes in detail the key technologies of the GNSS high-precision augmentation positioning solution for AIVs, and its progress and challenges are also analyzed to clarify the technical direction and research focus for the future application of GNSS in AIVs. Finally, some conclusions are offered in Section 5.

2. Survey of AIV Requirements

2.1. Application Characteristics of AIVs

Recently emerging autonomous applications have experienced rapid development. Different from traditional GNSS high-precision applications, e.g., surveying and mapping, emerging autonomous GNSS applications, e.g., AIV, drones, etc., have significant application characteristics, which are summarized as follows:
  • Globally, about 70 million cars are sold each year (https://www.statista.com/statistics/200002/international-car-sales-since-1990/ (accessed on 14 March 2023)). The proportion of high-level assistance vehicles is increasing. According to market forecasts, there will be 25 million AIVs at Level 3 or above by 2025 [33]. Thus, AIVs aim to reach tens to hundreds of millions of users.
  • The emerging field of autonomous applications faces the global market, in which users may be active anywhere all over the world at any time, including in the air, on land, and at sea [18]. Different from professional work, it is almost intolerable for AIV users to wait too long to obtain positioning requirements. Therefore, instantaneous global wide-area positioning services are required.
  • AIV often involves safety-of-life issues. AIVs of Level 3 and above will require shifting all the safety and legal responsibilities from humans to the automated driving system [34]. In addition, the ISO (International Organization for Standardization) formulated the standard “Road vehicles-Functional safety ISO 26262” guidance to mitigate safety-related risk caused by the complex system [35]. For AIVs, safety is critical.
  • Currently, the government pays increasing attention to individuals’ rights to privacy [36], and the privacy principles for vehicle technologies and services clarify that consumer privacy should be considered and protected [37]. Location privacy protection in mass applications is becoming a key issue [18,38].

2.2. Integrity Requirements

As mentioned above, safety is one of the key issues in the development of AIV [39]. With the trend of increasing technological complexity, software content, and mechatronic implementation, there are increasing risks of systematic failures and random hardware failures [35]. Integrity is defined as the trust that can be placed in the correctness of a service’s information, including the ability to provide timely alerts to users when the service cannot be used for positioning [15], which can express the more stringent performance requirements of AIVs.
Integrity, as one of the most essential performance parameters of GNSS, was originally developed in the civil aviation framework as part of the International Civil Aviation Organization (ICAO) requirements for using GNSS in the communications, navigation, and surveillance/air traffic management systems [40]. International Standards and Recommended Practices (SARPS) developed by ICAO are binding on the member states [41]. Requirements for GNSS signal-in-space service are contained in Annex 10 to the convention on civil aviation of SARPs, as shown in Table 2 [42]. The integrity risk for GNSS systems used in aviation is generally set to a probability of 10−7, which includes the probability of a missed alarm (positioning error exceeding the alert limit without a warning to the user) and a false alarm (a warning to the user while positioning error satisfies the alert limit).
Similar to the requirements of civil aviation, in the interest of assuring safety for AIVs, the autonomous vehicle field also formulates strict safety access standards, i.e., “Road vehicles-Functional safety ISO 26262”, which provides requirements for relations between customers and suppliers. The standard applies to all activities during the safety lifecycle of safety-related systems comprised of electrical, electronic, and software components and provides guidance to mitigate safety-related risks caused by the complex system by providing an automotive-specific risk-based approach to determine an automotive safety integrity level (ASIL) [35]. Table 3 shows the ASIL level and safety risk probability from A to D [43]. The higher the ASIL level, the stricter the functional safety requirements. The entire design domain and overall process of the vehicles, including the necessary means to provide high-precision absolute positioning for AIV-GNSS positioning services and products, should adopt and follow ISO 26262 [36].

2.3. Accuracy Requirements

The sole purpose of all sensors on an autonomous vehicle is to ensure that the vehicle knows it is within its lane, where horizontal positioning limits can be calculated by lateral and longitudinal components and a multi-layer road can be distinguished in a vertical direction. Based on the “geometry bound” method of measuring road grade and vehicle size proposed by Reid et al. [43], the accuracy requirements of AIVs are briefly mentioned again in this section.
Figure 2 shows the geometric relationship between the vehicle size and road information, which shows the allowable maximum position error of the vehicle to ensure it is within the lane known as the alert limits, i.e., the red dotted box. From the figure, it can be seen that alert limits are a function of vehicle size (length l v and width w v ) and road information (lane width w R and radius of circular curve r R ). In the figure, x and y are lateral and longitudinal geometry bounds, respectively. d l o and d l a are lateral and longitudinal alert limits, respectively. According to the geometric relationship of the right-angled triangle in the figure, we can obtain the equation according to the Pythagorean theorem as follows:
y 2 2 + r R − w R 2 + x 2 = r R + w R 2 2
The lateral and longitudinal alert limits can be obtained as follows:
d l a = x − w v / 2 d l o = y − l v / 2
Combining Equations (1) and (2), the functional relationship of alert limits in lateral d l a and longitudinal d l o can be obtained as follows:
d l o = 2 r R ⋅ w R − 2 d l a + w v 2 + w R − 2 r R ⋅ 2 d l a + w v − l v 2
From the equation above, the functional relationship between lateral ( d l a ) and longitudinal ( d l o ) alert limits can be obtained based on the vehicle size and road information provided (road width w R and radius of circular curve r R ). According to China’s design specification for highway alignment [44], the relationship between the vehicle’s design speed and the road’s curvature radius is shown in Table 4.
For example, in the highway scenario, where autonomous driving is easier to implement [45], the current design speed of China’s highways is 80–120 km/h, and the design lane width is 3.75 m [44]. Assuming that the size of the passenger car is 2 m × 5 m, the function relationship of the lateral and longitudinal alert limits corresponding to each scenario in Table 4 can be obtained as shown in Figure 3.
As shown in Figure 3, the lateral and longitudinal alert limits of vehicles are different; a series of application scenarios corresponds to road grades. Combined with Table 4, it can be seen that the straighter the highway design is, the higher the design speed limit.
For quantitative analysis, the lateral and longitudinal alarm limits are considered to be equal based on the uniform error characteristics of GNSS, i.e., d l a = d l o . The most stringent standard, the 220 m radius of a circular curve, is chosen for analysis in Table 4 and Figure 3. From Figure 3, we can get the alarm limits d l a = d l o = 0.86 m and then the horizontal alarm limits d l a 2 + d l o 2 ≈ 1.22 m. Assuming that the positioning error is a normal distribution with a zero mean, Figure 4 illustrates the relationship between integrity risk, alert limit, and a 95% or 2 σ accuracy requirement. The probability of a 5.73 σ alert limit in normal distribution is about 99.999999%, which satisfies the requirements of the integrity risk probability of 10−8 of ASIL D. The 2 σ (about 95%) horizontal accuracy requirements are 0.42 m.
The vertical requirements are mainly to identify which road level the vehicle is on; 1.47 m, or 1/3 of the minimum vertical clearance, is sufficient and can be set as the vertical alert limit [43]. The corresponding 95% vertical accuracy is 0.51 m.
Based on this preliminary analysis, the location accuracy requirements of AIV are at the decimeter level.

2.4. Issues of Availability and Continuity

The application characteristics of AIV determine the need for available and continuous positioning. Currently, there is no one localization sensor that can meet the requirements of AIV in all weather, road, and traffic scenarios [43], so multi-sensor fusion is an essential approach [6,7]. Availability is the percentage of the positioning error that is less than the protection level (PL) when the PL satisfies the alert limit, i.e., no integrity risk occurs, while continuity is the probability that the positioning performance meeting the AIV requirements will be maintained for a certain duration [46]. Hence, both availability and continuity together express the stable and reliable operation of AIV for positioning.

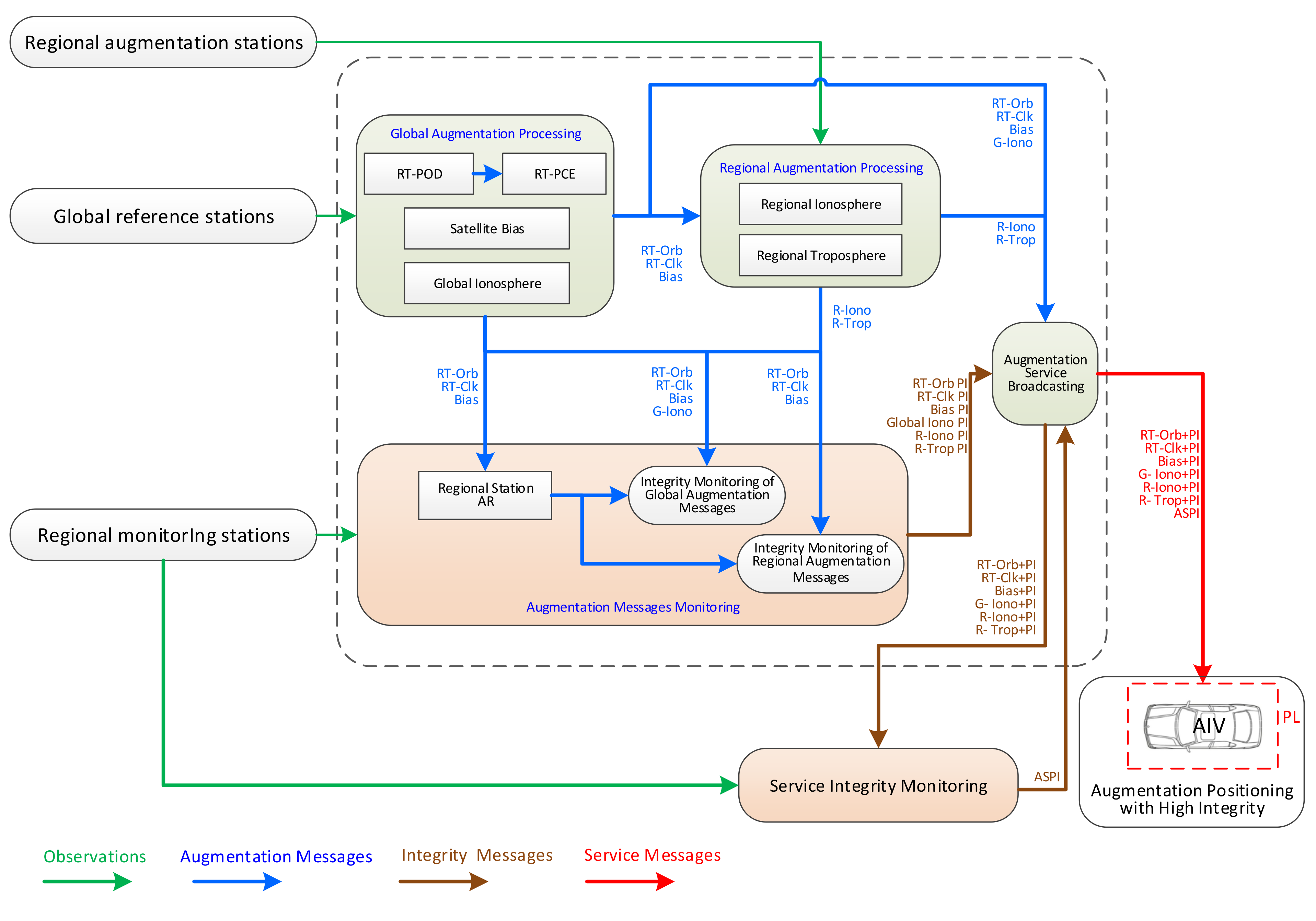
3. GNSS Augmentation Solution for AIV: A Case

According to the application characteristics of AIVs outlined in Section 2.1, active positioning often requires the uploading of the initial position, which makes it impossible to achieve user location privacy protection and high-concurrency services for mass users. Therefore, the characteristics of the requirements for AIV applications represented by autonomous vehicles using GNSS technology can be summarized as follows: wide-area services, passive positioning, high-integrity, and instantaneous decimeter-level positioning.
According to the analysis in Section 1 Introduction, high-precision carrier-phase observations are necessary in order to achieve GNSS centimeter- to decimeter-level positioning. NRTK technology can achieve instantaneous centimeter-level positioning in local coverage, including mainstream virtual reference stations (VRS) and master-auxiliary concepts (MAC). However, VRS technology requires users to upload their initial position to the service center, which is active positioning. Even though it was initially developed to provide a passive broadcast solution, MAC is not suitable for larger networks, such as those with 50–100 stations, due to the data rate limits of communication and the number of stations in the sub-network [47]. Civil aviation has established a complete integrity monitoring theory and method [48,49]. GNSS signal-in-space (SIS) integrity information can be provided by GBAS and SBAS by comparing the ground truth of the monitoring station with the position solution computed using the GNSS SSR (orbit, clock, atmosphere delay, etc.) [50], providing an important reference for the design and implementation of a GNSS high-precision augmentation solution for AIV. As mentioned in Section 1. Introduction, due to the broadcast of these SIS and atmosphere corrections to users through the Internet or communication satellites, positioning technology based on SSR can realize a wide-area passive positioning service. In addition, the high-precision SSR corrections obtained by combining carrier-phase and pseudorange observations, especially atmosphere corrections, can achieve instantaneous decimeter-level high-precision positioning [50,51].
With a view to the GNSS augmentation application of AIV, there are some commercial safety-critical GNSS augmentation service solutions such as Trimble RTX Fast Service [52], Sapcorda’s Safe and Precise Augmentation (SAPA) (https://www.embedded.com/gnss-correction-service-enhances-position-accuracy/ (accessed on 14 March 2023)), Swift Skylark Precise Positioning Service (https://www.swiftnav.com/skylark (accessed on 14 March 2023)) etc. Based on the analysis and commercial solutions above, the GNSS high-precision augmentation solution for AIVs is summarized as shown in Figure 5. The solution mainly includes six parts: global augmentation processing, regional augmentation processing, augmentation messages monitoring, augmentation service broadcasting, service integrity monitoring, and augmentation positioning with high integrity.
  • The global augmentation processing part is largely responsible for obtaining global real-time augmentation messages based on global reference stations, including real-time precise satellite orbit (RT-Orb) and clock (RT-Clk), satellite bias (Bias), global ionospheric (G-Iono), etc.;
  • The regional augmentation processing part mainly uses the global augmentation messages and the regional augmentation stations to obtain the regional ionospheric (R-Iono) and tropospheric delay (R-Trop), and then outputs the modeling information;
  • The augmentation message monitoring part mainly uses the monitoring stations in the service area to monitor the integrity of global and regional augmentation messages and then generates the corresponding performance index (PI);
  • The augmentation service broadcasting part is responsible for encoding global and regional augmentation messages and then broadcasting that information through the Internet or communication satellites;
  • The service integrity monitoring part is responsible for monitoring the performance and generating the augmentation service performance factor (ASPI) by using regional monitoring stations’ known precise coordinates based on broadcasted wide-area and regional augmentation messages. If there is a service integrity problem, it will promptly alert the public;
  • The augmentation positioning with high integrity part aims to achieve precise positioning for AIVs based on these global and regional augmentation messages as well as monitoring messages.
From the analysis above and Figure 5, the system-level key technologies of the GNSS high-precision augmentation solution for AIV include GNSS real-time precise orbit determination (RT-POD), real-time precise clock estimation (RT-PCE), signal bias estimation, atmosphere estimation and modeling (global/regional ionospheric, regional tropospheric), integrity monitoring on augmentation messages and services, etc. The key user-level technologies include integrity fault detection and exclusion, real-time, instantaneous, precise positioning, etc.

4. Progress and Challenges of Key Technologies

4.1. RT-POD

As shown in Figure 5, RT-POD is the basis of global augmentation processing. International GNSS Service (IGS) is a nonprofit organization devoted to the generation of high-precision GNSS data and products by operating the global infrastructure of network stations [53], including ultra-rapid, rapid, and final productions with varying accuracies and latencies. In order to obtain low-latency orbits, IGS utilizes prior normal equation systems and appends a few hours of new data to generate an ultra-rapid solution to avoid recomputing the measurement model and partial derivatives of overlapping observation arcs [54], then predicts orbital arcs. The predicted ultra-rapid IGS orbits with centimeter-level accuracy [55,56] are usually applied in its real-time service [57,58], which is widely used to produce real-time GNSS solutions [59]. Position and Navigation Data Analyst (PANDA) software developed by Wuhan University, one of the Analysis Centers of IGS, has achieved centimeter-level multi-GNSS POD [60,61] and improves orbit accuracy significantly by improving orbit models and algorithms [62,63,64,65,66].

4.2. RT-PCE

Even though the accuracy of IGS ultra-rapid products [53] has met the real-time requirements [67], its clocks, with an accuracy of about 3 ns and a sampling of 5 min, cannot be used in real-time high-precision applications [58]. A real-time PCE filter based on real-time data streams in a network is an effective solution, but it is also a time-consuming task [68]. The ultra-rapid orbit can be input and held fixed in the real-time GNSS clock filter to reduce the computational burden and complexity of the real-time process, which estimates only clock, tropospheric, ambiguity, etc. parameters [59]. The traditional RT-PCE UD model has been modified based on UD pseudorange and epoch-differenced carrier-phase observations (referred to as the mixed-differenced model, MD) to eliminate that great number of ambiguity parameters [68,69,70]. In order to achieve the development of multi-GNSS fusion solutions, the RT-PCE MD model was further upgraded by introducing pre-estimated bias corrections [71,72] to correct the receiver-/satellite-dependent and inter-system biases, which can obtain ~100 ps multi-GNSS precision clock with sub-second estimation efficiency for a single epoch.

4.3. Bias Estimations

Multi-frequencies and multi-constellations tend to lead to signal hardware delays in multi-GNSS observations, which are split into satellite-specific and receiver-specific delays [73].
Among these, pseudorange or code delays will greatly correct pseudorange accuracy and then affect precise data processing [74], e.g., PPP convergence [75], wide-lane ambiguity resolution [76], estimation of bias-free ionospheric accuracy [77], etc. The precise satellite clock products of IGS are commonly computed by ionosphere-free (IF) combined observations [56]; as a result, the satellite-specific code bias can be considered ignorable in IF combination precise positioning [78]. Satellite-specific code bias of inter-frequency (e.g., P1–P2) and intra-frequency (e.g., P1-C1, P2-C2) can also be corrected by the satellite differential code bias (DCB) products of IGS [79,80] as well as by receiver-specific code bias [81]. It has been confirmed that signal distortion biases (SDBs) in pseudorange caused by the differences in correlation processing within GNSS receivers [82] are inconsistent for different satellites from the same constellation [74]. The common practice for IGS of estimating only one DCB per station considered identical for all satellites [83] cannot totally describe those SDBs. Preliminary analysis finds that SDBs remain stable over a short period of time [84] and can be used to correct pseudorange accuracy for multi-GNSS fusion solutions among inhomogeneous receivers.
These carrier-phase biases originating from satellites and receivers, also called uncalibrated phase delays (UPD) [85] or fractional cycle biases (FCBs) [86], are not integer values; thus, they prevent the resolution of the integer ambiguities. The receiver-specific carrier-phase biases can be eliminated by satellite-satellite single-difference (SD); then, the fractional parts of the satellite-specific SD UPDs in wide- and narrow-lane from a global reference network can be estimated [85,87], which can be applied as corrections to SD ambiguities at a single station to recover its natural integer feature.

4.4. Atmosphere Estimation and Modeling

The GNSS high-precision augmentation solution for AIVs designed above is based on SSR, and a great deal of research has proven that external atmosphere constraints or corrections, including ionospheric [51,88,89] and tropospheric [90,91,92] corrections, provide an efficient route to accelerate the instantaneous convergence of SSR positioning, e.g., PPP.
Currently, precise ionospheric modeling includes two implementations: one based on vertical total electron content (VTEC), e.g., the IGS Global Ionospheric Map (GIM) [93], and another based on directly slant total electron content (STEC) [94]. The introduction of the ionospheric mapping function [95] in VTEC modeling limits the accuracy of real-time GIM to about 2–8 total electron content units (TECU) [96,97] compared to STEC, which can achieve an accuracy of about 1 TECU from the nearby stations [98] (1 TECU corresponds to 16.2 cm in the GPS L1 frequency). Experiments show that the VTEC of GIM-constrained PPP can improve positioning accuracy by about 26% after a convergence time of 1 min, compared to about 67% for STEC-constrained positioning [94]. These results indicate that regional GNSS networks can provide more accurate ionosphere delays than IGS GIM [99], and the accuracy of ionosphere delays is very critical for shortening PPP convergence [100]. Thus, STEC is fundamental for achieving instant PPP [101]. Therefore, the VTEC and STEC can be applied in global augmentation processing and regional augmentation processing, respectively.
The line-of-sight tropospheric delay can be expressed by the zenith total delay (ZTD) of receivers with mapping functions, which can further be decomposed as the sum of the zenith hydrostatic delay (ZHD) and the zenith wet delay (ZWD) [102]. ZHD with millimeter-level accuracy can be derived from existing models [103,104], while ZWD is usually estimated as an additional epoch-wise parameter in GNSS processing and then used to form empirical models with centimeter-level accuracy, e.g., GPT2 (global pressure and temperature 2) [105] and TropGrid2 [106,107]. Compared to empirical models, it would be more appropriate to reflect the actual tropospheric delays, such as those retrieved from numerical weather models (NWM) [108,109]), as well as real-time regional tropospheric models represented by interpolation [110], fitting coefficients [90,111], or grid points [112]. Note that Japan’s QZSS broadcasts the tropospheric corrections with the grid model in the L1-SAIF (L1 submeter-class augmentation with integrity function) augmentation signal [113].
Benefits from the development of real-time orbit and clock products and precise real-time ionospheric and tropospheric delays can be derived directly by implementing a PPP model when ambiguity is fixed [114,115].

4.5. Integrity Monitoring

GNSS integrity analysis can be implemented at the system-level and user-level [50]. GNSS itself can generate basic system-level integrity messages, e.g., satellite and signal faults, SIS user range accuracy (URA), etc., and broadcast them to users [116,117], which, however, cannot meet the stringent civil aviation integrity requirements as specified by ICAO [40]. For this reason, various augmentation systems, including GBAS, SBAS, etc., have been developed to reduce integrity risk and generate other additional integrity information, e.g., ionospheric anomalies [50]. The typical user-level integrity monitoring is receiver autonomous integrity monitoring (RAIM), which can detect and exclude faults by residual-based or solution-separation analysis [118,119] to obtain the user’s protection level compared to the alert limit [120,121].
Different from civil aviation’s use of GNSS SPS application based on pesudorange observations and broadcast ephemeris, the GNSS high-precision augmentation solution for AIVs involves more observations, especially carrier-phase observations influenced by ambiguities and cycle slips, and precise augmentation products and correction models; as a result, additional integrity-monitoring models need to be developed [46,50]. Similar to the SIS integrity generated by GBAS or SBAS, global and regional augmentation corrections for AIV applications, including orbit, clock, ionospheric, tropospheric bias, etc., can be validated by residual-based analysis of different carrier-phase combinations [113]. However, there is little research that discusses the procedures of augmentation message quality control and user PL calculation, which impact the analysis of different faults and user solutions [50].
Although some studies have carried out user-level integrity analysis based on augmentation messages [52,122,123,124,125,126,127], further research still needs to be carried out in order to obtain acceptable models and methods [50].

4.6. RT Instant Precise Positioning

Single-receiver users can obtain their centimeter-level positions by double-frequency ionospheric-free PPP based on global SSR augmentation messages, i.e., orbit, clock, etc. and the popular double-frequency ionospheric-free combination process [19], which is constantly plagued by slow initialization and convergence [29]. The convergence is actually the process of PPP ambiguity resolution (AR) [128], and there are several routes proposed to try to resolve this problem, including (a) PPP AR based on multi-GNSS and multi-frequency GNSS uncombined or combined data [129,130,131] or (b) introducing internal or external ionospheric or tropospheric corrections, etc. [51].
PPP-AR can be achieved by introducing a predetermined UPD into the float ambiguity estimation [85] or using an integer recovery clock/decoupled satellite clock product [132,133]. Multi-GNSS data can be integrated to promote PPP rapid AR [129], which could be fixed in several minutes based on GPS/GLONASS/BDS fusion data [134,135]. It has been proven that the convergence period for PPP will not be changed completely by simply implementing AR procedures and multi-GNSS observation processing [51,136], and further algorithms are required to reduce the convergence time, e.g., triple-frequency PPP or ionospheric corrections [51].
A single epoch of triple-frequency observations can be used to accomplish multi-GNSS PPP wide-lane AR, which can achieve global instantaneous decimeter-level positioning [137]. The self-predicted ionospheric delays can be used in succeeding epochs to accelerate the re-convergence of ambiguity resolution within several epochs [138,139]. The initialization time can also be further shortened to several minutes by introducing external global ionospheric corrections [88], and instant centimeter-level positioning can be achieved by introducing ionospheric and tropospheric corrections obtained based on regional networks [32,88]. On those bases, multi-frequency uncombined GNSS data can demonstrate better performance with higher positioning accuracy and fewer outliers compared to double-frequency data [115,140].
The goal of GNSS applications of AIV is to achieve instant and reliable decimeter-level positioning with the lowest hardware and software costs. Considering the cost and the limitations of complex observation environments, the utilization of multi-frequency observation data has always been a problem worthy of further study. In addition, it is difficult to achieve a 100% AR fixing rate [115,137], and there is incorrect ambiguity fixing. Therefore, one must ask, “Is PPP AR essential for reliable, decimeter-level AIV positioning?” [141]. Despite those problems, there is no doubt that multi-GNSS, multi-frequency UD, and uncombined observations are the future direction of AIV applications [115].

5. Conclusions

This paper gives a brief review of GNSS application in the field of AIVs and discusses its requirements for GNSS high-precision augmentation, summarizes a GNSS augmentation positioning solution for AIVs, and then investigates research progress on key technologies in the solution as well as existing challenges.
The characteristics of different sensors used by AIV, including GNSS, are first discussed and compared. Among them, GNSS, as the unique localization sensor that can achieve absolute positioning and timing, is essential for AIV. Furthermore, AIVs aim to provide safety for a mass user base ranging from tens to hundreds of millions; for this, AIVs require a global wide-area and instantaneous precise positioning service with location privacy protection. For positioning accuracy, the “geometry bound” analysis between road grade and vehicle size indicates that GNSS requirements in autonomous vehicles include decimeter-level positioning with the assurance of high integrity.
An SSR-based GNSS high-precision augmentation positioning solution for AIV is summarized and introduced in this paper, combined with GNSS high-integrity implementation in the civil aviation field, GNSS different technology routes, and commercial solutions. The solution includes six main parts: global augmentation processing, regional augmentation processing, augmentation messages monitoring, augmentation service broadcasting, service integrity monitoring, and augmentation positioning with high integrity and can obtain instantaneous precise positioning with high-integrity in a wide area by passive positioning mode, which can also achieve location privacy protection.
After reviewing a variety of literature, the research progress of most key technologies, e.g., RT-POD, RT-PCE, signal bias estimation, atmosphere estimation and modeling, etc., has met the implementation requirements of the GNSS high-precision augmentation positioning solution for AIV. However, there are also a series of challenges that need to be overcome to satisfy the AIV application, mainly system-level integrity monitoring for high-precision augmentation messages, user-level integrity monitoring based on those augmentation messages, and achieving instant and reliable decimeter-level positioning with the lowest hardware and software costs.

Author Contributions

Conceptualization, L.C. and F.Z.; methodology, L.C. and F.Z.; software, L.C.; validation, F.Z.; writing—original draft preparation, L.C.; writing—review and editing, X.G.; visualization, L.C.; supervision, X.J.; funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Young Elite Scientists Sponsorship Program by CAST (YESS20200308), a project funded by the China Postdoctoral Science Foundation (2021M690192), the Beijing Postdoctoral Research Foundation (2021-ZZ-088), and the Beijing Nova Program (Z211100002121068).

Acknowledgments

The authors would like to thank the editor in chief and the anonymous reviewers for their valuable comments and improvements to this manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

AIVAutonomous and Intelligent Vehicle
ARAmbiguity Resolution
ASILAutomotive Safety Integrity Level
BDSBeiDou Navigation Satellite System
CLASCentimeter Level Augmentation Service
CORSContinuously Operating Reference Stations
DCBDifferential Code Bias
EGNOSEuropean Geostationary Navigation Overlay Service
FCBFractional Cycle Bias
GAGANGPS Aided GEO Augmented Navigation
GalileoGalileo Navigation Satellite System
GBASGround-Based Augmentation System
GIMGlobal Ionospheric Map
GLONASSGLObal NAvigation Satellite System
GNSSGlobal Navigation Satellite System
GPSGlobal Positioning System
HASHigh Accuracy Service
IMUInertial Measurement Unit
LAASLocal Area Augmentation System
LiDARLight Detection And Ranging
MACMaster-Auxiliary Concept
MSASMTSAT Satellite-based Augmentation System
NRTKNetwork Real-Time Kinematic
OSRObservation Space Representation
PCEPrecise Clock Estimation
PIPerformance Index
PLProtection Level
PODPrecise Orbit Determination
PPPPrecise Point Positioning
QZSSQuasi-Zenith Satellite System
RADARRAdio Detection And Ranging
RAIMReceiver Autonomous Integrity Monitoring
SBASSatellite-Based Augmentation System
SDBSignal Distortion Bias
SISSignal-in-Space
SPPSingle Point Positioning
SPSStandard Positioning Service
SSRState Space Representation
TECTotal Electron Content
TECUTotal Electron Content Unit
UPDUncalibrated Phase Delays
UPDUncalibrated Phase Delay
VRSVirtual Reference Station
VTECVertical TEC
WAASWide Area Augmentation System
ZHDZenith Hydrostatic Delay
ZTDZenith Total Delay
ZWDZenith Wet Delay

References

  1. Zhang, T.; Li, Q.; Zhang, C.; Liang, H.; Li, P.; Wang, T.; Li, S.; Zhu, Y.; Wu, C. Current trends in the development of intelligent unmanned autonomous systems. Front. Inf. Technol. Electron. Eng. 2017, 18, 68–85. [Google Scholar] [CrossRef] [Green Version]
  2. Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
  3. J3016-2021; Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles. SAE International: Warrendale, PA, USA, 2021.
  4. Vargas, J.; Alsweiss, S.; Toker, O.; Razdan, R.; Santos, J. An Overview of Autonomous Vehicles Sensors and Their Vulnerability to Weather Conditions. Sensors 2021, 21, 5397. [Google Scholar] [CrossRef] [PubMed]
  5. Joubert, N.; Reid, T.G.R.; Noble, F. Developments in Modern GNSS and Its Impact on Autonomous Vehicle Architectures. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 April 2020; pp. 2029–2036. [Google Scholar]
  6. Varghese, J.Z. Overview of Autonomous Vehicle Sensors and Systems. In Proceedings of the 2015 International Conference on Operations Excellence and Service Engineering, Orlando, FL, USA, 10–11 September 2015. [Google Scholar]
  7. Gogineni, S. Multi-Sensor Fusion and Sensor Calibration for Autonomous Vehicles. Int. Res. J. Eng. Technol. (IRJET) 2020, 7, 1073–1078. [Google Scholar]
  8. Yang, D.; Jiang, K.; Zhao, D.; Yu, C.; Cao, Z.; Xie, S.; Xiao, Z.H.; Jiao, X.; Wang, S.; Zhang, K. Intelligent and connected vehicles: Current status and future perspectives. Sci. China Technol. Sci. 2018, 61, 1446–1471. [Google Scholar] [CrossRef]
  9. Toulminet, G.; Boussuge, J.; Laurgeau, C. Comparative Synthesis of the 3 Main European Projects Dealing with Cooperative Systems (CVIS, SAFESPOT and COOPERS) and Description of COOPERS Demonstration Site 4. In Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 12–15 October 2008; pp. 809–814. [Google Scholar]
  10. Jahromi, B.S.; Tulabandhula, T.; Cetin, S. Real-Time Hybrid Multi-Sensor Fusion Framework for Perception in Autonomous Vehicles. Sensors 2019, 19, 4357. [Google Scholar] [CrossRef] [Green Version]
  11. Ayala, R.; Mohd, T.K. Sensors in Autonomous Vehicles: A Survey. ASME J. Auton. Veh. Syst. 2021, 1, 031003. [Google Scholar] [CrossRef]
  12. Langley, R.B.; Teunissen, P.J.G.; Montenbruck, O. Introduction to GNSS. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 3–23. [Google Scholar]
  13. Wübbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise Point Positioning Using State-Space Representation in RTK Networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 2584–2594. [Google Scholar]
  14. Chen, L.; Zhou, G.; Chen, G.; Sun, W.; Pan, L. Signal-in-space and positioning performance of BDS open augmentation service. Math. Probl. Eng. 2022, 2022, 1112646. [Google Scholar] [CrossRef]
  15. GPS SPS. Global Positioning System Standard Positioning Service Performance Standard, 5th ed.; Department of Defense: Washington, DC, USA, 2020. [Google Scholar]
  16. BDS OS PS. BeiDou Navigation Satellite System Open Service Performance Standard; China Satellite Navigation Office: Beijing, China, 2021.
  17. Galileo OS SDD. European GNSS (Galileo) Open Service Service Definition Document Issue 1.2; European GNSS Service Centre: Madrid, Spain, 2021. [Google Scholar]
  18. Galileo GNSS Agency. GNSS User Technology Report, Issue 3; Publications Office of the EU, Galileo GNSS Agency: Paris, France, 2020. [Google Scholar]
  19. Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
  20. Huisman, L.; Teunissen, P.J.G.; Hu, C. GNSS precise point positioning in regional reference frames using real-time broadcast corrections. J. Appl. Geod. 2012, 6, 15–23. [Google Scholar] [CrossRef] [Green Version]
  21. Walter, T. Satellite Based Augmentation Systems. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 339–361. [Google Scholar]
  22. Yang, Y.; Ding, Q.; Gao, W.; Li, J.; Xu, Y.; Sun, B. Principle and performance of BDSBAS and PPP-B2b of BDS-3. Satell. Navig. 2022, 3, 5. [Google Scholar] [CrossRef]
  23. European GNSS Agency. Galileo High Accuracy Service (HAS); Publications Office of the EU, Galileo GNSS Agency: Paris, France, 2020. [Google Scholar]
  24. IS-QZSS-L6-003; Quasi-Zenith Satellite System Interface Specification Centimeter Level Augmentation Service. Cabinet Office: Tokyo, Japan, 2020.
  25. China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Precise Point Positioning Service Signal PPP-B2b; China Satellite Navigation Office: Beijing, China, 2020. [Google Scholar]
  26. Odijk, D.; Wanninger, L. Differential Positioning. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 753–780. [Google Scholar]
  27. Weng, D.; Ji, S.; Lu, Y.; Chen, W.; Li, Z. Improving DGNSS Performance through the Use of Network RTK Corrections. Remote Sens. 2021, 13, 1621. [Google Scholar] [CrossRef]
  28. Pervan, B.; Pullen, S.; Lawrence, D.G.; Gromov, K.; Christie, J.; Opshaug, G.; Lu, V.; Ko, P.; Enge, P.; Parkinson, B.W. Prototype LAAS Architecture Design Considerations. GPS Solut. 1998, 2, 49–61. [Google Scholar] [CrossRef]
  29. Bisnath, S.; Gao, Y. Current State of Precise Point Positioning and Future Prospects and Limitations. In Observing Our Changing Earth; Sideris, M.G., Ed.; Springer: New York, NY, USA, 2009; pp. 615–623. [Google Scholar]
  30. Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A.H. Towards PPP-RTK: Ambiguity resolution in real-time precise point positioning. Adv. Space Res. 2011, 47, 1664–1673. [Google Scholar] [CrossRef] [Green Version]
  31. Li, X.; Ge, M.; Douša, J.; Wickert, J. Real-time precise point positioning regional augmentation for large GPS reference networks. GPS Solut. 2014, 18, 61–71. [Google Scholar] [CrossRef] [Green Version]
  32. Nardo, A.; Drescher, R.; Brandl, M.; Chen, X.; Landau, H.; Rodriguez-Solano, C.; Seeger, S.; Weinbach, U. Experiences with Trimble CenterPoint RTX with Fast Convergence. In Proceedings of the European Navigation Conference 2015, Bordeaux, France, 7–10 April 2015. [Google Scholar]
  33. Müller, F.; Nenninger, P.; Sax, E. Analysis of Requirements for Autonomous Driving Systems. In Proceedings of the 11th IEEE Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 4–7 November 2020; pp. 87–93. [Google Scholar]
  34. Ilkova, V.; Ilka, A. Legal Aspects of Autonomous Vehicles—An Overviewo. In Proceedings of the 21st International Conference on Process Control (PC), Strbske Pleso, Slovakia, 6–9 July 2017; pp. 428–433. [Google Scholar] [CrossRef] [Green Version]
  35. ISO26262; Road Vehicles-Functional Safety. The International Organization for Standardization. ISO: London, UK, 2018.
  36. NHTSA. Federal Automated Vehicles Policy. Accelerating the Next Revolution in Roadway Safety; U.S. Department of Transportation–National Highway Traffic Safety Administration: Washington, DC, USA, 2016. [Google Scholar]
  37. Alliance for Automotive Innovation, Inc. Consumer Privacy Protection Principles-Privacy Principles for Vehicle Technologies and Services; Alliance for Automotive Innovation: Washington, DC, USA, 2014. [Google Scholar]
  38. Chen, L.; Thombre, S.; Jarvinen, K.; Lohan, E.S.; Alen-Savikko, A.K.; Leppäkoski, H.; Bhuiyan, M.Z.H.; Bu-Pasha, S.; Ferrara, G.N.; Honkala, H. Robustness, Security and Privacy in Location-Based Services for Future IoT: A Survey. IEEE Access 2017, 5, 8956–8977. [Google Scholar] [CrossRef]
  39. AI Hage, J.; Xu, P.; Bonnifait, P.; Ibanez-Guzman, J. Localization Integrity for Intelligent Vehicles through Fault Detection and Position Error Characterization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2978–2990. [Google Scholar] [CrossRef]
  40. Salos, D.; Martineau, A.; Macabiau, C.; Bonhoure, B.; Kubrak, D. Receiver autonomous integrity monitoring of GNSS signals for electronic toll collection. IEEE Trans. Intell. Transp. Syst. 2014, 15, 94–103. [Google Scholar] [CrossRef]
  41. Farnworth, R. Aviation Applications. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 877–903. [Google Scholar]
  42. International Civil Aviation Organization (ICAO). International Standards and Recommended Practices, Annex 10 to the Convention on Civil Aviation, Aeronautical Telecommunications; Radio Navigation Aids 7th edition; ICAO: Montreal, QC, Canada, 2018; Volume 1. [Google Scholar]
  43. Reid, T.; Houts, S.; Cammarata, R.; Mills, G.; Agarwal, S.; Vora, A.; Pandey, G. Localization Requirements for Autonomous Vehicles. SAE Int. J. Connect. Autom. Veh. 2019, 2, 173–190. [Google Scholar] [CrossRef] [Green Version]
  44. JTG D20-2017; Design Specification for Highway Alignment. China Ministry of Transport: Beijing, China, 2017.
  45. Chai, Z.; Nie, T.; Becker, J. Autonomous Driving Changes the Future. China Machine Press: Beijing, China; Springer Nature Singapore Pte Ltd.: Singapore, 2021. [Google Scholar]
  46. Zhu, N.; Marais, J.; Bétaille, D.; Berbineau, M. GNSS position integrity in urban environments: A review of literature. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2762–2778. [Google Scholar] [CrossRef] [Green Version]
  47. Chen, X.; Allison, T.; Cao, W.; Ferguson, K.; Grünig, S.; Gomez, V.; Kipka, A.; Köhler, J.; Landau, H.; Leandro, R.; et al. Trimble RTX, an Innovative New Approach for Network RTK. In Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 19–23 September 2011; pp. 2214–2219. [Google Scholar]
  48. Roturier, B.; Chatre, E.; Ventura-Traveset, J. The SBAS integrity concept standardised by ICAO-application to EGNOS. Navig. Paris 2001, 49, 65–77. [Google Scholar]
  49. Jin, B.; Chen, S.; Li, D.; Wang, Y.; Takka, E. Performance analysis of SBAS ephemeris corrections and integrity algorithms in China region. Satell. Navig. 2021, 2, 15. [Google Scholar] [CrossRef]
  50. Du, Y.; Wang, J.; Rizos, C.; EI-Mowafy, A. Vulnerabilities and integrity of precise point positioning for intelligent transport systems: Overview and analysis. Satell. Navig. 2021, 2, 3. [Google Scholar] [CrossRef]
  51. Choy, S.; Bisnath, S.; Rizos, C. Uncovering common misconceptions in GNSS Precise Point Positioning and its future prospect. GPS Solut. 2017, 21, 13–22. [Google Scholar] [CrossRef]
  52. Weinbach, U.; Brandl, M.; Chen, X.; Landau, H.; Pastor, F.; Reussner, N.; Rodriguez-Solano, C. Integrity of the Trimble® CenterPoint® RTX Correction Service. In Proceedings of the 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 1902–1909. [Google Scholar]
  53. Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar]
  54. Weiss, J.P.; Steigenberger, P.; Springer, T. Orbit and Clock Product Generation. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 983–1010. [Google Scholar]
  55. Li, B.; Ge, H.; Bu, Y.; Zheng, Y.; Yuan, L. Comprehensive assessment of real-time precise products from IGS analysis centers. Satell. Navig. 2022, 3, 12. [Google Scholar] [CrossRef]
  56. Montenbruck, O.; Steigenberger, P.; Parange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The multi-GNSS experiment (MGEX) of the international GNSS service (IGS)-achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
  57. Weber, G.; Mervart, L.; Lukes, Z.; Rocken, C.; Dousa, J. Real-Time Clock and Orbit Corrections for Improved Point Positioning via NTRIP. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 1992–1998. [Google Scholar]
  58. Chen, L.; Zhao, Q.; Hu, Z.; Ge, M.; Shi, C. GNSS global real-time augmentation positioning: Real-time precise satellite clock estimation, prototype system construction and performance analysis. Adv. Space Res. 2018, 61, 367–384. [Google Scholar] [CrossRef]
  59. Hauschild, A.; Montenbruck, O. Real-Time clock Estimation for Precise Orbit Determination of LEO-Satellites. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 581–589. [Google Scholar]
  60. Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar]
  61. Shi, C.; Zhao, Q.; Geng, J.; Lou, Y.; Ge, M.; Liu, J. Recent Development of PANDA Software in GNSS Data Processing. In Proceedings of the International Conference on Earth Observation Data Processing and Analysis (ICEODPA), Bellingham, WA, USA, 28–30 December 2008. [Google Scholar]
  62. Shi, C.; Zhao, Q.; Li, M.; Tang, W.; Hu, Z.; Lou, Y.; Zhang, H.; Niu, X.; Liu, J. Precise orbit determination of Beidou Satellites with precise positioning. Sci. China Earth Sci. 2012, 55, 1079–1086. [Google Scholar] [CrossRef]
  63. Zhao, Q.; Guo, J.; Li, M.; Qu, L.; Hu, Z.; Shi, C.; Liu, J. Initial results of precise orbit and clock determination for COMPASS navigation satellite system. J. Geod. 2013, 87, 475–486. [Google Scholar] [CrossRef]
  64. Dai, X.; Ge, M.; Lou, Y.; Shi, C.; Wickert, J.; Schuh, H. Estimating the yaw-attitude of BDS IGSO and MEO satellites. J. Geod. 2015, 89, 1005–1018. [Google Scholar] [CrossRef]
  65. Guo, J.; Chen, G.; Zhao, Q.; Liu, J.; Liu, X. Comparison of solar radiation pressure models for BDS IGSO and MEO satellites with emphasis on improving orbit quality. GPS Solut. 2016, 21, 511–522. [Google Scholar] [CrossRef] [Green Version]
  66. Liu, Y.; Ge, M.; Shi, C.; Lou, Y.; Wickert, J.; Schuh, H. Improving integer ambiguity resolution for GLONASS precise orbit determination. J. Geod. 2016, 90, 715–726. [Google Scholar] [CrossRef]
  67. Griffiths, J.; Ray, J. On the precision and accuracy of IGS orbits. J. Geod. 2009, 83, 277–287. [Google Scholar] [CrossRef]
  68. Bock, H.; Dach, R.; Jaggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083–1094. [Google Scholar] [CrossRef] [Green Version]
  69. Zhang, X.; Li, X.; Guo, F. Satellite clock estimation at 1 Hz for realtime kinematic PPP applications. GPS Solut. 2011, 15, 315–324. [Google Scholar] [CrossRef]
  70. Ge, M.; Chen, J.; Dousa, J.; Gendt, G.; Wickert, J. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime. GPS Solut. 2012, 16, 9–17. [Google Scholar] [CrossRef]
  71. Chen, L.; Li, M.; Zhao, Y.; Hu, Z.; Zheng, F.; Shi, C. Multi-GNSS real-time precise clock estimation considering the correction of inter-satellite code biases. GPS Solut. 2021, 25, 32. [Google Scholar] [CrossRef]
  72. Gong, X.; Gu, S.; Zheng, F.; Wu, Q.; Liu, S.; Lou, Y. Improving GPS and Galileo Precise Data Processing Based on Calibration of Signal Distortion Biases. Measurement 2021, 174, 108981. [Google Scholar] [CrossRef]
  73. Montenbruck, O.; Hauschild, A.; Hessels, U. Characterization of GPS/GIOVE sensor stations in the CONGO network. GPS Solut. 2011, 15, 193–205. [Google Scholar] [CrossRef]
  74. Chen, L.; Li, M.; Zhao, Y.; Zheng, F.; Zhang, X.; Shi, C. Clustering Code Biases between BDS-2 and BDS-3 Satellites and Effects on Joint Solution. Remote Sens. 2021, 12, 15. [Google Scholar] [CrossRef]
  75. Geng, J.; Meng, X.; Dodson, A.; Teferle, F. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef] [Green Version]
  76. Loyer, S.; Perosanz, F.; Mercier, F.; Capdeville, H.; Marty, J.C. Zero-difference GPS ambiguity resolution at CNES–CLS IGS Analysis Center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
  77. Li, Z.; Yuan, Y.; Wang, N.; Hernandez-Pajares, M.; Huo, X. SHPTS:towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J. Geod. 2015, 89, 331–345. [Google Scholar] [CrossRef]
  78. Schaer, S.; Gurtner, W.; Feltens, J. IONEX: The Ionosphere Map Exchange Format Version 1. In Proceedings of the IGS AC Workshop, Darmstadt, Germany, 9–11 February 1998. [Google Scholar]
  79. Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps. Navigation 2014, 61, 191–201. [Google Scholar] [CrossRef]
  80. Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
  81. Ge, Y.; Zhou, F.; Sun, B.; Wang, S.; Shi, B. The Impact of Satellite Time Group Delay and Inter-Frequency Differential Code Bias Corrections on Multi-GNSS Combined Positioning. Sensors 2017, 17, 602. [Google Scholar] [CrossRef] [Green Version]
  82. Hauschild, A.; Steigenberger, P.; Montenbruck, O. Inter-Receiver GNSS Pseudorange Biases and Their Effect on Clock and DCB Estimation. In Proceedings of the ION GNSS+ 2019, Institute of Navigation, Miami, FL, USA, 16–20 September 2019; pp. 3675–3685. [Google Scholar]
  83. Hauschild, A.; Montenbruck, O. A study on the dependency of GNSS pseudorange biases on correlator spacing. GPS Solut. 2016, 20, 159–171. [Google Scholar] [CrossRef]
  84. Gong, X.; Zheng, F.; Gu, S.; Zhang, Z.; Lou, Y. The long-term characteristics of GNSS signal distortion biases and their empirical corrections. GPS Solut. 2022, 26, 52. [Google Scholar] [CrossRef]
  85. Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
  86. Xiao, G.; Sui, L.; Heck, B.; Zeng, T.; Tian, Y. Estimating satellite phase fractional cycle biases based on Kalman filter. GPS Solut. 2018, 22, 82. [Google Scholar] [CrossRef]
  87. Gabor, M.J.; Nerem, R.S. GPS carrier phase AR Using Satellite-Satellite Single Difference. In Proceedings of the ION GPS 1999, 14–17 September 1999; pp. 1569–1578. [Google Scholar]
  88. Banville, S.; Collins, P.; Zhang, W.; Langley, R. Global and regional ionospheric corrections for faster PPP convergence. Navigation 2014, 61, 115–124. [Google Scholar] [CrossRef]
  89. Zhang, X.; Ren, X.; Chen, J.; Zuo, X.; Mei, D.; Liu, W. Investigating GNSS PPP–RTK with external ionospheric constraints. Satell. Navig. 2022, 3, 6. [Google Scholar] [CrossRef]
  90. Shi, J.; Xu, C.; Guo, J.; Gao, Y. Local troposphere augmentation for real-time precise point positioning. Earth Planets Space 2014, 66, 1–13. [Google Scholar] [CrossRef] [Green Version]
  91. Yao, Y.; Peng, W.; Xu, C.; Cheng, S. Enhancing real-time precise point positioning with zenith troposphere delay products and the determination of corresponding tropospheric stochastic models. Geophys. J. Int. 2017, 208, 1217–1230. [Google Scholar] [CrossRef]
  92. Cui, B.; Wang, J.; Li, P.; Ge, M.; Schuh, H. Modeling wide-area tropospheric delay corrections for fast PPP ambiguity resolution. GPS Solut. 2022, 26, 56. [Google Scholar] [CrossRef]
  93. Li, Z.; Wang, N.; Hernández-Pajares, M.; Yuan, Y.; Krankowski, A.; Liu, A.; Zha, J.; García-Rigo, A.; Roma-Dollase, D.; Yang, H.; et al. IGS real-time service for global ionospheric total electron content modeling. J. Geod. 2020, 94, 32. [Google Scholar] [CrossRef]
  94. Xiang, Y.; Gao, Y.; Li, Y. Ionospheric STEC and VTEC Constraints for Fast PPP. In Proceeding of the China Satellite Navigation Conference (CSNC), CSNC 2017: Volume II; Lecture Notes in Electrical Engineering; Springer: Singapore, 2017; Volume 438, pp. 257–269. [Google Scholar]
  95. Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Thesis, Astronomical Institute, University of Bernese, Bern, Switzerland, 1999. [Google Scholar]
  96. Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, C. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2018, 92, 691–706. [Google Scholar] [CrossRef] [Green Version]
  97. Liu, Q.; Hernández-Pajares, M.; Yang, H.; Monte-Moreno, E.; Roma-Dollase, D.; García-Rigo, A.; Li, Z.; Wang, N.; Laurichesse, D.; Blot, A.; et al. The cooperative IGS RT-GIMs: A reliable estimation of the global ionospheric electron content distribution in real time. Earth Syst. Sci. Data 2021, 13, 4567–4582. [Google Scholar] [CrossRef]
  98. Li, W.; Li, Z.; Wang, N.; Liu, A.; Zhou, K.; Yuan, H.; Krankowski, A. A satellite-based method for modeling ionospheric slant TEC from GNSS observations: Algorithm and validation. GPS Solut. 2022, 26, 14. [Google Scholar] [CrossRef]
  99. Abdelazeem, M.; Çelik, R.N.; Elrabbany, A. An Enhanced Real-Time Regional Ionospheric Model Using IGS Real-Time Service (IGS-RTS) Products. J. Navig. 2016, 69, 521–530. [Google Scholar] [CrossRef] [Green Version]
  100. Zhang, H.; Gao, Z.; Ge, M.; Niu, X.; Huang, L.; Tu, R.; Li, X. On the convergence of ionospheric constrained precise point positioning (IC-PPP) based on undifferential uncombined raw GNSS observations. Sensors 2013, 13, 15708–15725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  101. Rovira-Garcia, A.; Juan, J.; Sanz, J.; González-Casado, G. A worldwide ionospheric model for fast precise point positioning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4596–4604. [Google Scholar] [CrossRef] [Green Version]
  102. Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
  103. Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Geophys. Monogr. Ser. 1972, 15, 247–251. [Google Scholar]
  104. Collins, J.P.; Langley, R.B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System; Department of Geodesy and Geomatics Engineering, University of New Brunswick: Fredericton, NB, Canada, 1997. [Google Scholar]
  105. Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [Green Version]
  106. Schüler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
  107. Yao, Y.; Xu, C.; Shi, J.; Cao, N.; Zhang, B.; Yang, J. ITG: A new global GNSS tropospheric correction model. Sci. Rep. 2015, 5, 10273. [Google Scholar] [CrossRef] [Green Version]
  108. Lu, C.; Zus, F.; Ge, M.; Heinkelmann, R.; Dick, G.; Wickert, J.; Schuh, H. Tropospheric delay parameters from numerical weather models for multi-GNSS precise positioning. Atmos. Meas. Tech. 2016, 9, 5965–5973. [Google Scholar] [CrossRef] [Green Version]
  109. Wilgan, K.; Hadas, T.; Hordyniec, P.; Bosy, J. Real-time precise point positioning augmented with high-resolution numerical weather prediction model. GPS Solut. 2017, 21, 1341–1353. [Google Scholar] [CrossRef] [Green Version]
  110. Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
  111. de Oliveira, P.S.; Morel, L.; Fund, F.; Legros, R.; Monico, J.F.G.; Durand, S.; Durand, F. Modeling tropospheric wet delays with dense and sparse network configurations for PPP-RTK. GPS Solut. 2017, 21, 237–250. [Google Scholar] [CrossRef] [Green Version]
  112. Zheng, F.; Lou, Y.; Gu, S.; Gong, X.; Shi, C. Modeling tropospheric wet delays with national GNSS reference network in China for BeiDou precise point positioning. J. Geod. 2018, 92, 545–560. [Google Scholar] [CrossRef]
  113. Takeichi, N.; Sakai, T.; Fukushima, S.; Ito, K. Tropospheric delay correction with dense GPS network in L1-SAIF augmentation. GPS Solut. 2010, 14, 185–192. [Google Scholar] [CrossRef]
  114. Zhang, B.; Ou, J.; Yuan, Y.; Li, Z. Extraction of line-of-sight ionospheric observables from GPS data using precise point positioning. Sci. China Earth Sci. 2012, 55, 1919–1928. [Google Scholar] [CrossRef]
  115. Li, X.; Wang, B.; Li, X.; Huang, J.; Lyu, H.; Han, X. Principle and performance of multi-frequency and multi-GNSS PPP-RTK. Satell. Navig. 2022, 3, 7. [Google Scholar] [CrossRef]
  116. Weiss, M.; Shome, P.; Beard, R. On-board Signal Integrity for GPS. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2010), Portland, OR, USA, 21–24 September 2010; pp. 3199–3212. [Google Scholar]
  117. Kovach, K.; Dobyne, J.; Crews, M.; Miles, C. GPS III Integrity Concept. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 2250–2257. [Google Scholar]
  118. Gunning, K.; Blanch, J.; Walter, T.; de Groot, L.; Norman, L. Design and Evaluation of Integrity Algorithms for PPP in Kinematic Applications. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+2018), Miami, FL, USA, 24–28 September 2018; pp. 1910–1939. [Google Scholar]
  119. Speidel, J.; Tossaint, M.; Wallner, S.; Ávila-Rodríguez, J. Integrity for aviation: Comparing future concepts. Inside GNSS 2013, 4, 54–64. [Google Scholar]
  120. Brown, R.G. Receiver Autonomous Integrity Monitoring. Global Positioning System: Theory and Applications American Institute of Aeronautics and Astronautics; Parkinson, B.W., Spilker, J.J., Jr., Eds.; American Institute of Aeronautics and Astronautics: National Harbor, MD, USA, 1996; Volume II, pp. 143–165. [Google Scholar]
  121. Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A. Advanced RAIM User Algorithm Description: Integrity Support Message Processing, Fault Detection, Exclusion, and Protection Level Calculation. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 2828–2849. [Google Scholar]
  122. Seepersad, G.; Bisnath, S. Integrity Monitoring in Precise Point Positioning. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2013), Nashville, TN, USA, 16–20 September 2013; pp. 1164–1175. [Google Scholar]
  123. Jokinen, A.; Feng, S.; Schuster, W.; Ochieng, W.; Hide, C.; Moore, T.; Hill, C. Integrity monitoring of fixed ambiguity Precise Point Positioning (PPP) solutions. Geospat. Inf. Sci. 2013, 16, 141–148. [Google Scholar] [CrossRef] [Green Version]
  124. Laurichesse, D.; Privat, A. An Open-Source PPP Client Implementation for the CNES PPP-WIZARD Demonstrator. In Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+2015), Tampa, FL, USA, 14–18 September 2015; pp. 2780–2789. [Google Scholar]
  125. Gunning, K.; Blanch, J.; Walter, T. SBAS Corrections for PPP Integrity with Solution Separation. In Proceedings of the 2019 International Technical Meeting of the Institute of Navigation, Reston, VA, USA, 28–31 January 2019; pp. 707–719. [Google Scholar]
  126. Gunning, K.; Blanch, J.; Walter, T.; de Groot, L.; Norman, L. Integrity for Tightly Coupled PPP and IMU. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS + 2019), Miami, FL, USA, 16–20 September 2019; pp. 3066–3078. [Google Scholar]
  127. Blanch, J.; Walter, T.; Norman, L.; Gunning, K.; de Groot, L. Solution Separation-Based FD to Mitigate the Effects of Local Threats on PPP Integrity. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1085–1092. [Google Scholar]
  128. Teunissen, P.J.G.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
  129. Geng, J.; Guo, J.; Meng, X.; Gao, K. Speeding up PPP ambiguity resolution using triple-frequency GPS/BeiDou/Galileo/QZSS data. J. Geod. 2020, 94, 6. [Google Scholar] [CrossRef] [Green Version]
  130. Naciri, N.; Bisnath, S. An uncombined triple-frequency user implementation of the decoupled clock model for PPP-AR. J. Geod. 2021, 95, 60. [Google Scholar] [CrossRef]
  131. Wu, Z.; Wang, Q.; Hu, C.; Yu, Z.; Wu, W. Modeling and assessment of five-frequency BDS precise point positioning. Satell. Navig. 2022, 3, 8. [Google Scholar] [CrossRef]
  132. Laurichesse., D.; Mercier, F. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and its Application to PPP. In Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 839–848. [Google Scholar]
  133. Collins, P. Isolating and estimating undifferenced GPS integer ambiguities. In Proceedings of the ION NTM, Savannah, GA, USA, 16–19 September 2008; pp. 720–732. [Google Scholar]
  134. Liu, Y.; Lou, Y.; Ye, S.; Zhang, R.; Song, W.; Zhang, X.; Li, Q. Assessment of PPP integer ambiguity resolution using GPS, GLONASS and BeiDou (IGSO, MEO) constellations. GPS Solut. 2017, 21, 1647–1659. [Google Scholar] [CrossRef]
  135. Zhao, Q.; Guo, J.; Liu, S.; Tao, J.; Hu, Z.; Chen, G. A variant of raw observation approach for BDS/GNSS precise point positioning with fast integer ambiguity resolution. Satell. Navig. 2021, 2, 29. [Google Scholar] [CrossRef]
  136. Collins, P.; Bisnath, S. Issues in Ambiguity Resolution for Precise Point Positioning. In Proceedings of the ION GNSS Meeting, Portland, OR, USA, 19–23 September 2011; pp. 679–687. [Google Scholar]
  137. Geng, J.; Guo, J.; Chang, H.; Li, X. Toward global instantaneous decimeter-level positioning using tightly coupled multi-constellation and multi-frequency GNSS. J. Geod. 2019, 93, 977–991. [Google Scholar] [CrossRef] [Green Version]
  138. Geng, J.; Meng, X.; Dodson, A.; Ge, M.; Teferle, F. Rapid re-convergences to ambiguity-fixed solutions in precise point positioning. J. Geod. 2010, 84, 705–714. [Google Scholar] [CrossRef] [Green Version]
  139. Geng, J.; Shi, C. Rapid initialization of real-time PPP by resolving undifferenced GPS and GLONASS ambiguities simultaneously. J. Geod. 2017, 91, 361–374. [Google Scholar] [CrossRef]
  140. Zhang, B.; Hou, P.; Zha, J.; Liu, T. PPP–RTK functional models formulated with undifferenced and uncombined GNSS observations. Satell. Navig. 2022, 3, 3. [Google Scholar] [CrossRef]
  141. Seepersad, G.; Aggrey, J.; Bisnath, S. Do We Need Ambiguity Resolution in Multi-GNSS PPP for Accuracy or Integrity? In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 2204–2218. [Google Scholar]
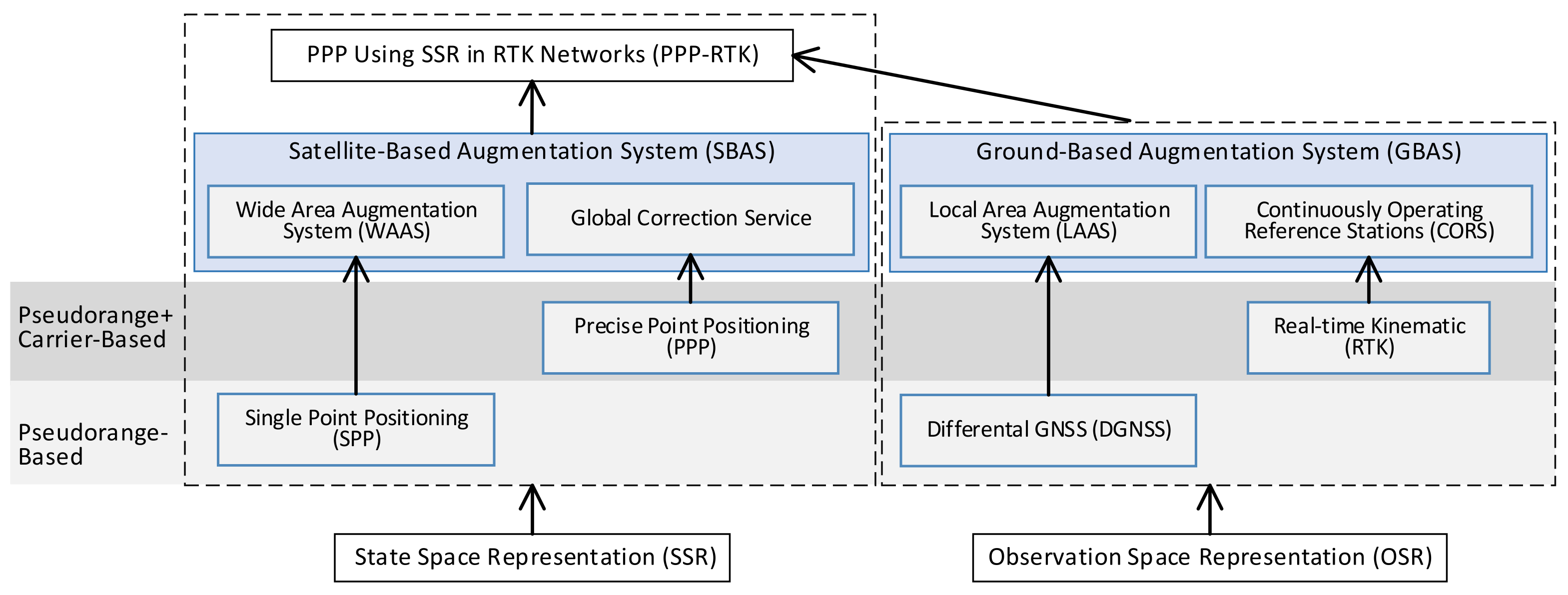
Remotesensing 15 01623 g001 550
Figure 1. GNSS positioning technology routes and development.
Figure 1. GNSS positioning technology routes and development.
Remotesensing 15 01623 g001
Remotesensing 15 01623 g002 550
Figure 2. Geometric relationship between vehicle size and road.
Figure 2. Geometric relationship between vehicle size and road.
Remotesensing 15 01623 g002
Remotesensing 15 01623 g003 550
Figure 3. Relationship of lateral ( d l a ) and longitudinal ( d l o ) alert limits corresponding to the different highway radius of circular curve r R .
Figure 3. Relationship of lateral ( d l a ) and longitudinal ( d l o ) alert limits corresponding to the different highway radius of circular curve r R .
Remotesensing 15 01623 g003
Remotesensing 15 01623 g004 550
Figure 4. Relationship of integrity risk, alert limits and accuracy.
Figure 4. Relationship of integrity risk, alert limits and accuracy.
Remotesensing 15 01623 g004
Remotesensing 15 01623 g005 550
Figure 5. GNSS high-precision augmentation solution for AIV. POD: precise orbit determination, PCE: precise clock estimation.
Figure 5. GNSS high-precision augmentation solution for AIV. POD: precise orbit determination, PCE: precise clock estimation.
Remotesensing 15 01623 g005
Table
Table 1. Comparison of most widespread GNSS positioning technologies based on SSR and OSR.
Table 1. Comparison of most widespread GNSS positioning technologies based on SSR and OSR.
RoutesSSROSR
ModeSPP (SPS)SBAS (WAAS)PPPPPP-RTKLAAS (DGNSS)RTKCORS (NRTK)
ObservationsUD PseudorangeUD Pseudorange + carrier-phaseDD PseudorangeDD Pseudorange + carrier-phase
CorrectionsNoneOrbit, clock, ionosphericOrbit, clockOrbit, clock, bias, ionospheric, troposphericCombined range correction
Communication LinkNoYesYesYesYes
Service AreaGlobalRegionalGlobalGlobal/regionalLocalLocalRegional
ConvergenceInstantInstantMinutes to tens of minutesSeconds to Tens of secondsInstantSeveral seconds
AccuracyMeter-levelDecimeter to meter-levelCentimeter-levelDecimeter to meter-levelCentimeter-level
Application fieldsMass marketAviationMaritime and ocean-going operationsAviationSurveying and mapping
Table
Table 2. ICAO GNSS Signal-in-Space performance requirements (ICAO, 2018 [42]).
Table 2. ICAO GNSS Signal-in-Space performance requirements (ICAO, 2018 [42]).
Typical OperationHorizontal AccuracyVertical AccuracyIntegrity RiskTime-to-Alert
95%Alert Limit95%Alert Limit
En-route3.7 km7.4 km (oceanic/continental low density) 3.7 km (continental)//10−7/h5 min
Terminal740 m1.85 km//10−7/h15 s
NPA *220 m556 m//10−7/h10 s
APV-I **16 m40 m20 m50 m2 × 10−7 in any approach10 s
APV-II16 m40 m8 m20 m6 s
CAT-I ***16 m40 m4–6 m10–35 m6 s
* Non-precision approach. ** Approach with Vertical Guidance. *** Category I precision approach.
Table
Table 3. ISO 26262 ASIL safety level and integrity risk.
Table 3. ISO 26262 ASIL safety level and integrity risk.
Safety LevelIntegrity Risk
ASIL-A10−6–10−5/h
ASIL-B/C10−7–10−6/h
ASIL-D10−8–10−7/h
Table
Table 4. Relationship of vehicle’s design speed and road’s radius of circular curve.
Table 4. Relationship of vehicle’s design speed and road’s radius of circular curve.
Design Speed (km/h)1201008060
r R Minimum radius of circular curve (m)1000700400200
Minimum radius of circular curve (m)Maximum of road superelevation *4%810500300150
6%710440270135
8%650400250125
10%570360220115
* Road superelevation is the transverse slope throughout the length of the horizontal curve to counteract the effect of centrifugal force and to minimize the tendency of the vehicle to overturn or skid by raising the outer edge of the pavement with respect to the inner edge.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chen, L.; Zheng, F.; Gong, X.; Jiang, X. GNSS High-Precision Augmentation for Autonomous Vehicles: Requirements, Solution, and Technical Challenges. Remote Sens. 2023, 15, 1623. https://doi.org/10.3390/rs15061623

AMA Style

Chen L, Zheng F, Gong X, Jiang X. GNSS High-Precision Augmentation for Autonomous Vehicles: Requirements, Solution, and Technical Challenges. Remote Sensing. 2023; 15(6):1623. https://doi.org/10.3390/rs15061623

Chicago/Turabian Style

Chen, Liang, Fu Zheng, Xiaopeng Gong, and Xinyuan Jiang. 2023. "GNSS High-Precision Augmentation for Autonomous Vehicles: Requirements, Solution, and Technical Challenges" Remote Sensing 15, no. 6: 1623. https://doi.org/10.3390/rs15061623

APA Style

Chen, L., Zheng, F., Gong, X., & Jiang, X. (2023). GNSS High-Precision Augmentation for Autonomous Vehicles: Requirements, Solution, and Technical Challenges. Remote Sensing, 15(6), 1623. https://doi.org/10.3390/rs15061623

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop