A Partial Reconstruction Method for SAR Altimeter Coastal Waveforms Based on Adaptive Threshold Judgment
Abstract
:1. Introduction
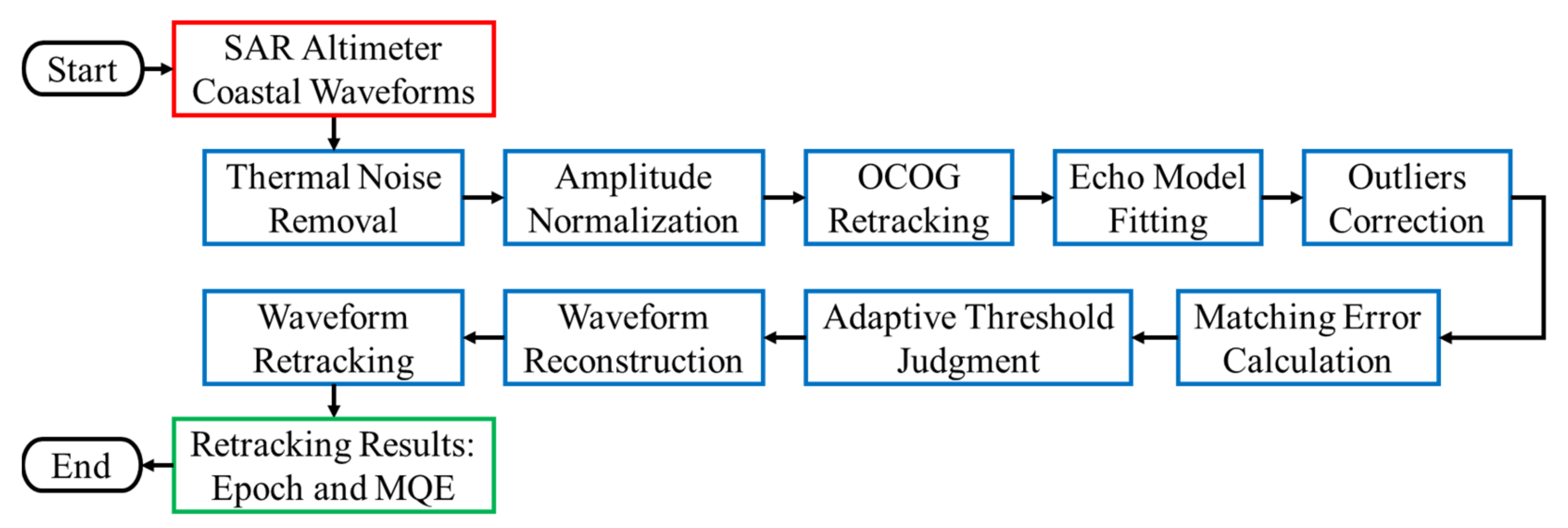
2. Materials and Methods
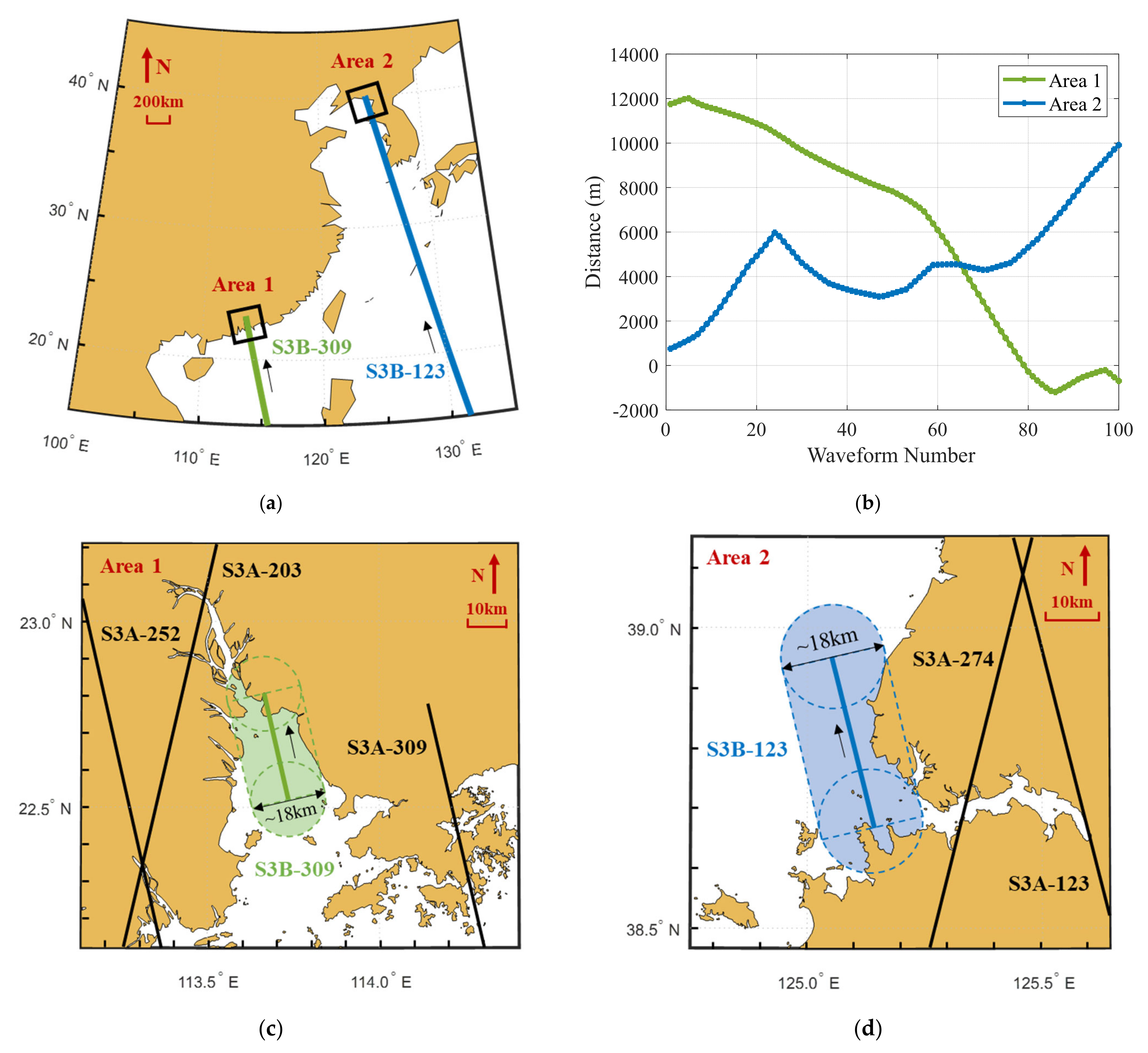
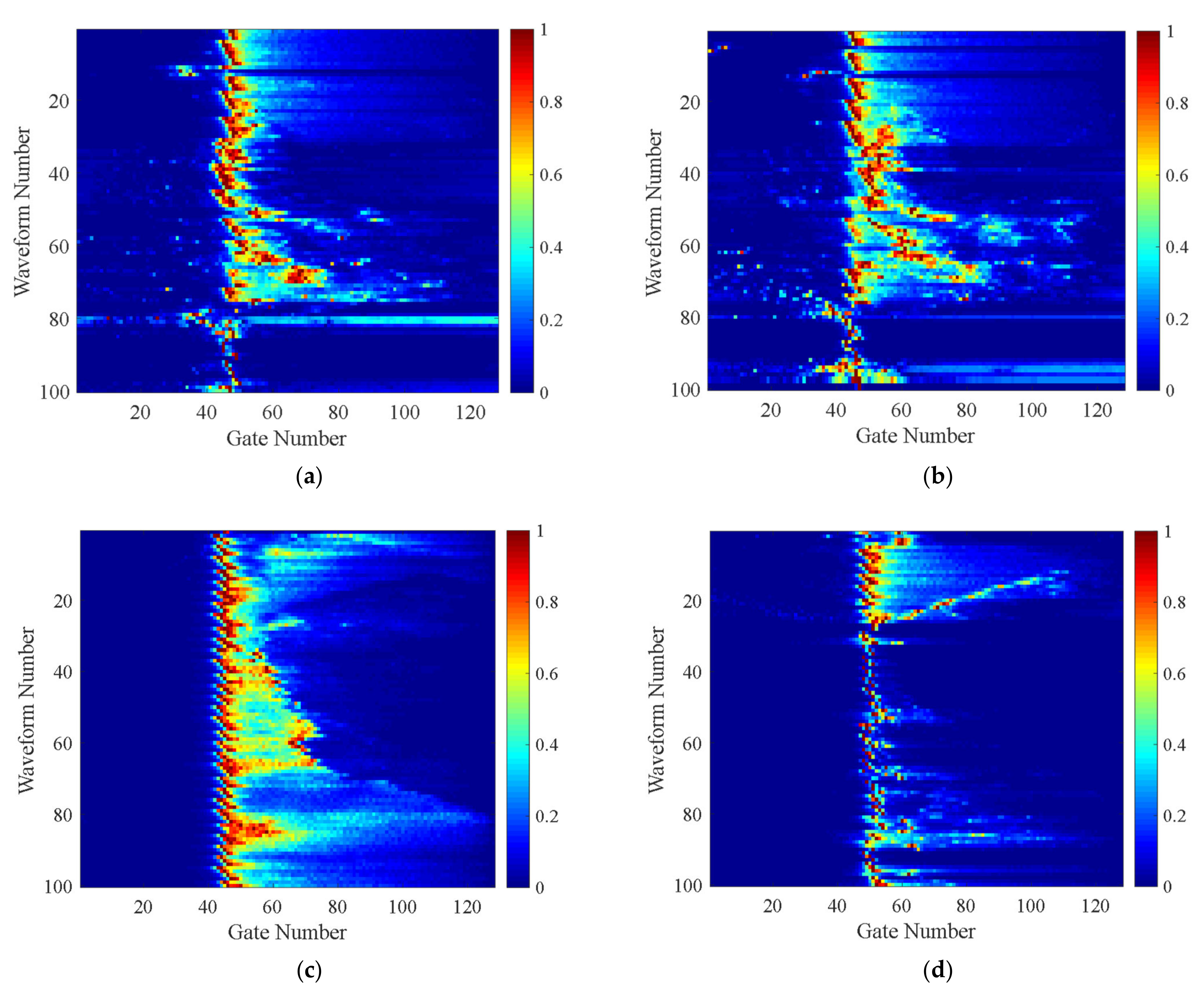
2.1. Coastal Waveform Data of the Sentinel-3 SAR Altimeter
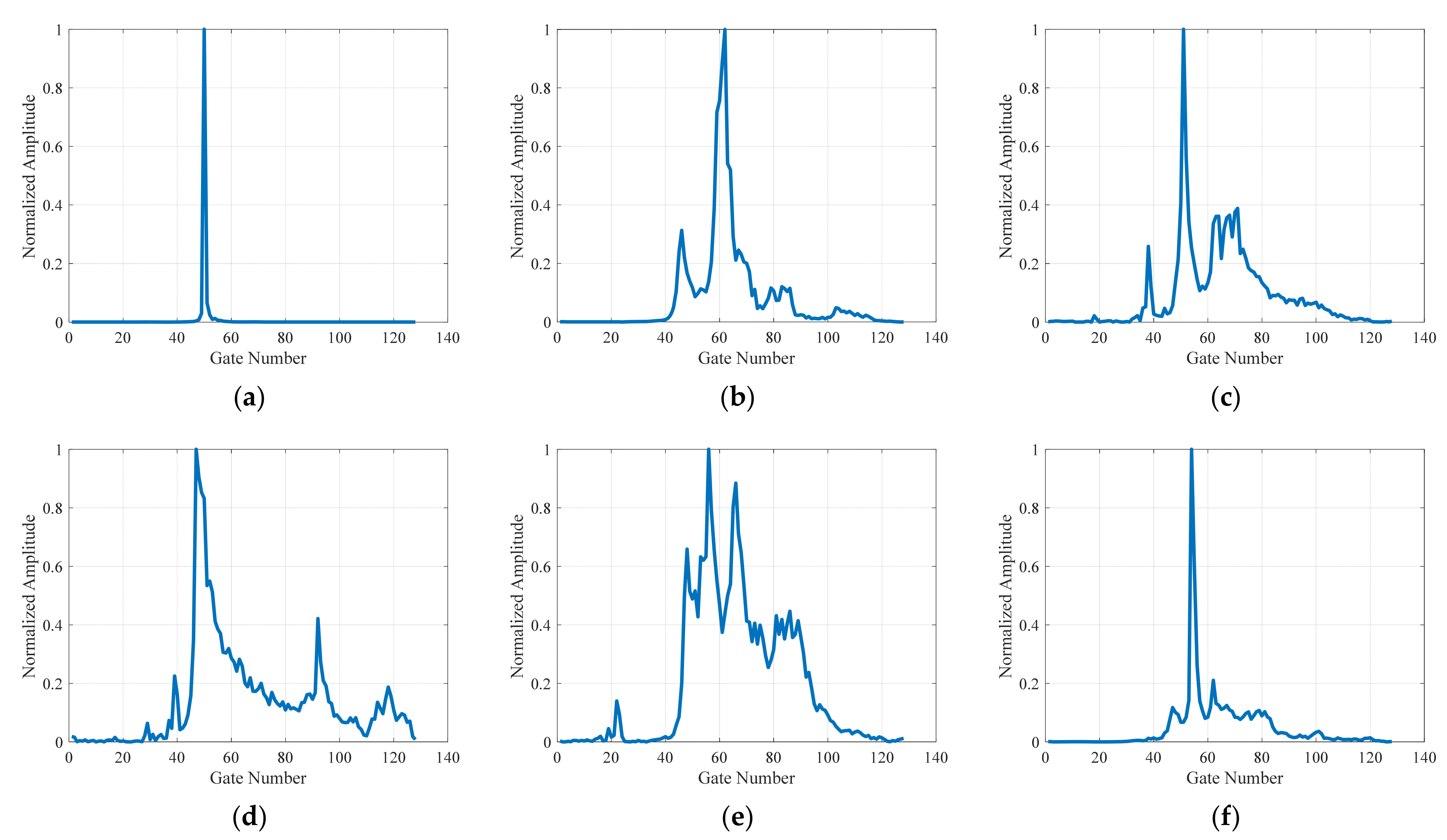
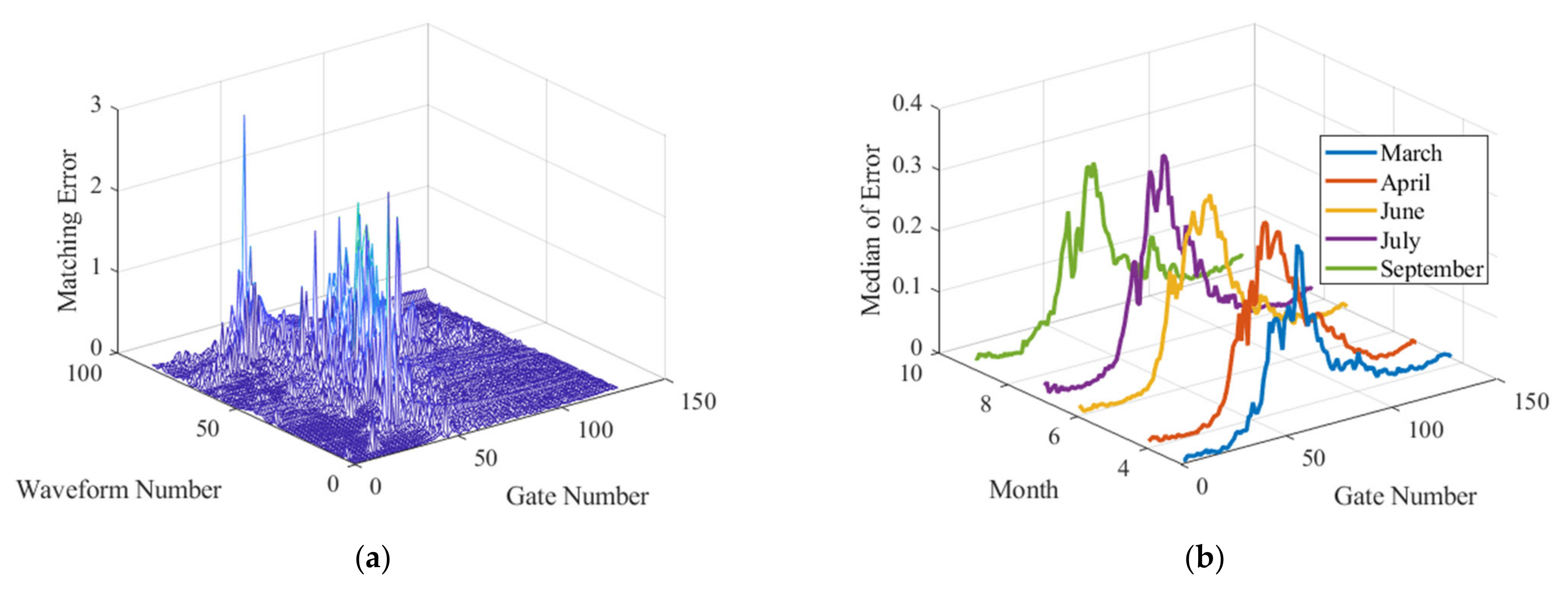
2.2. Echo Model Fitting and Matching Error Calculation
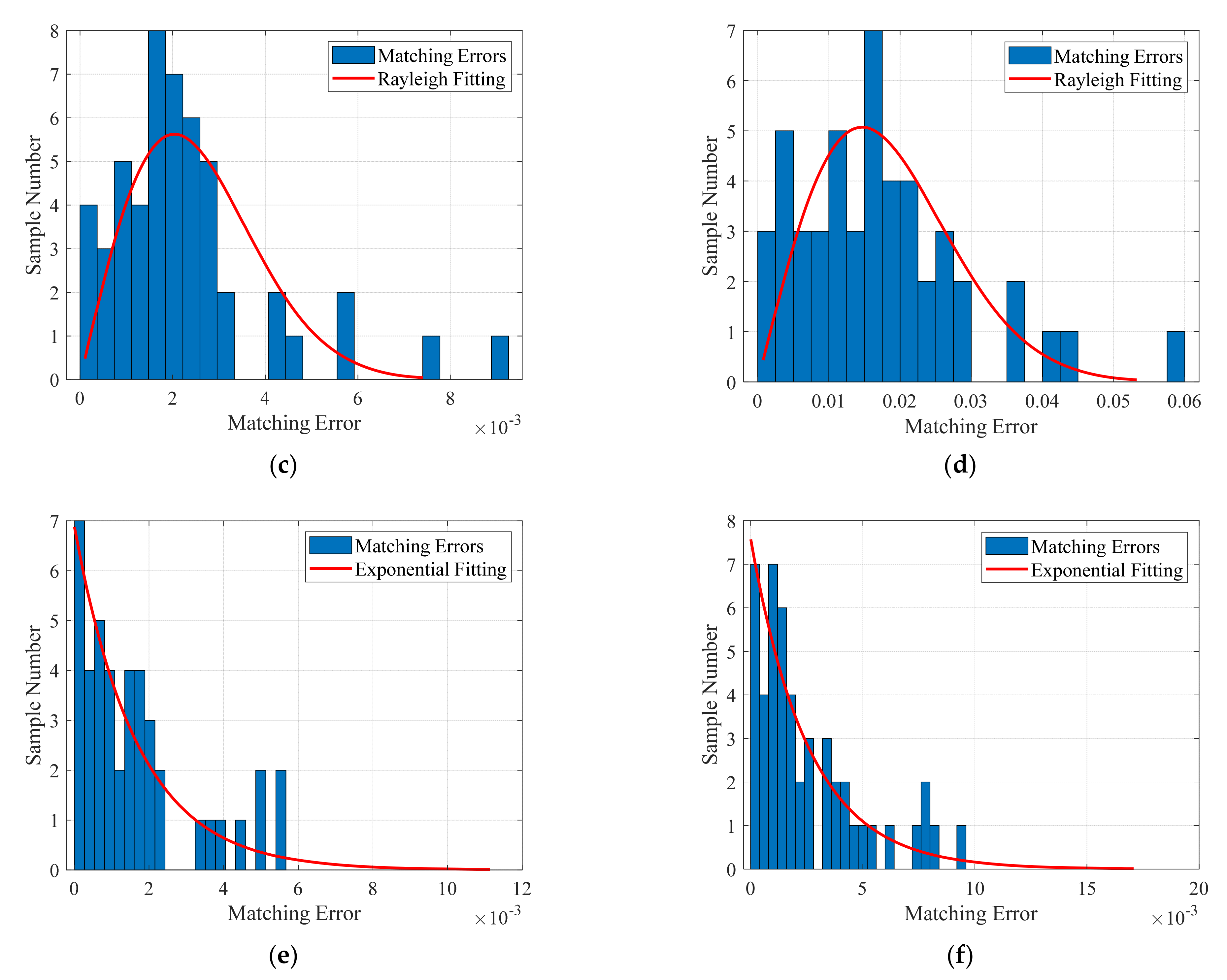
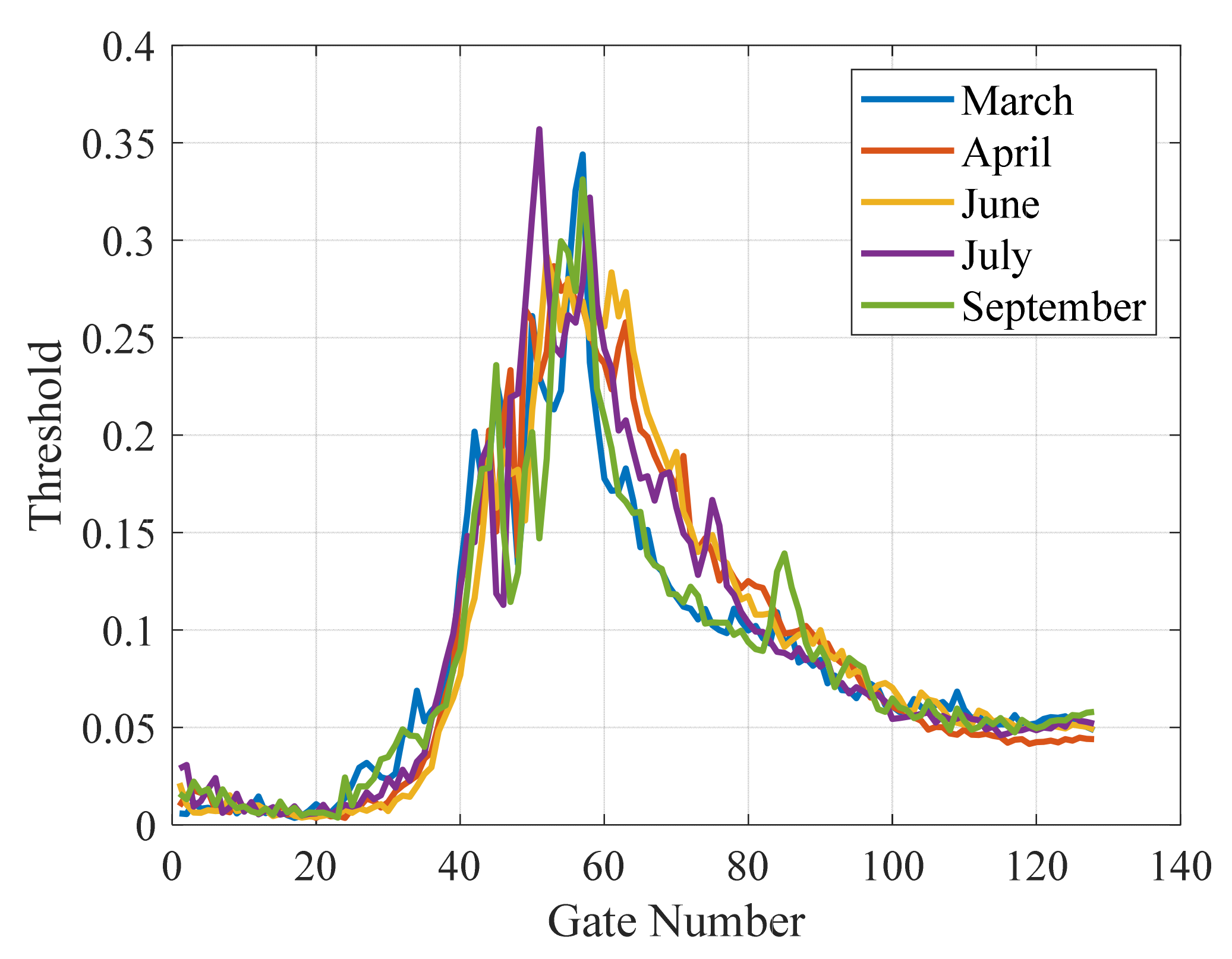
2.3. Adaptive Threshold Judgment Based on Error Distribution
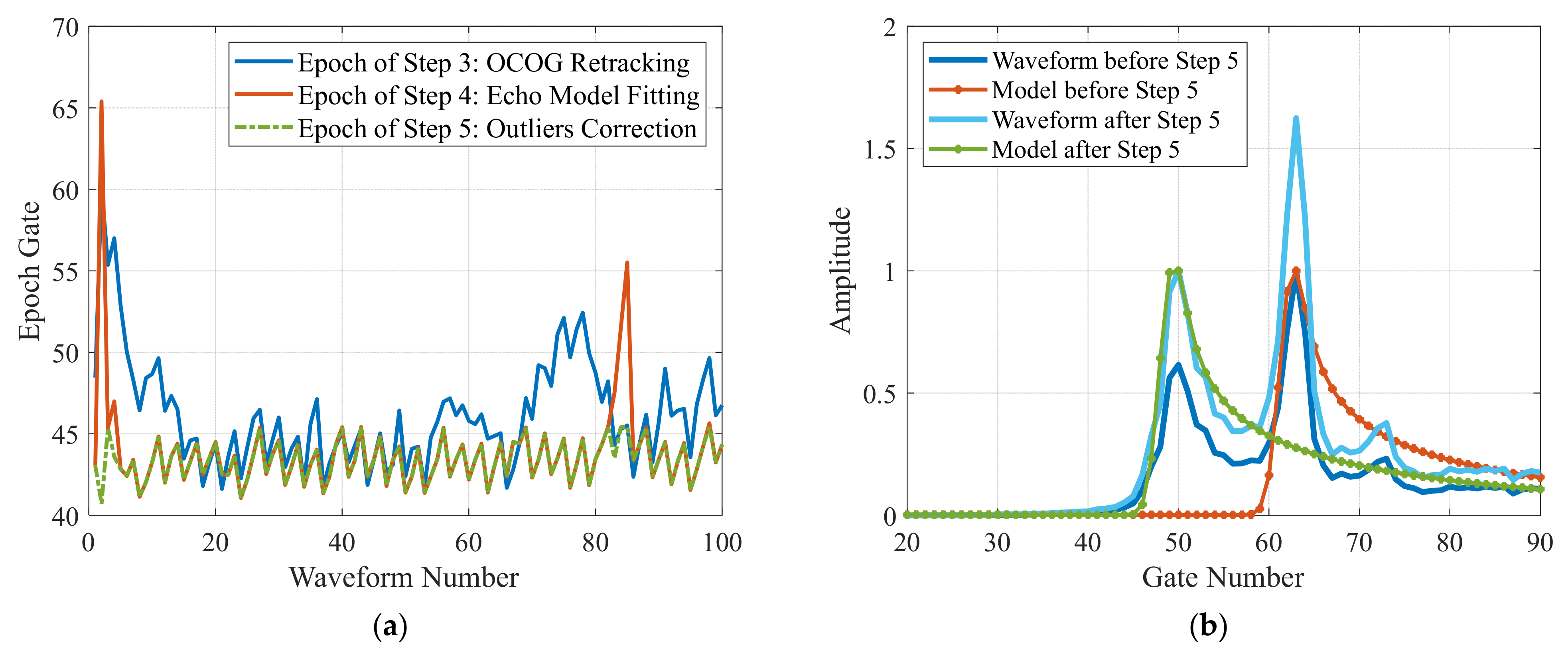
2.4. Waveform Reconstruction and Retracking Method
3. Results
3.1. MQE Comparison and Retracking Results for Area 1
3.2. SSH Retrieval Results and Precision Validation of Area 2
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bannoura, W.J.; Wade, A.; Srinivas, D.N. NOAA ocean surface topography mission Jason-2 project overview. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; pp. 2155–2159. [Google Scholar]
- Phalippou, L.; Enjolras, V. Re-tracking of SAR altimeter ocean power-waveforms and related accuracies of the retrieved sea surface height, significant wave height and wind speed. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Barcelona, Spain, 23–28 July 2007; pp. 3533–3536. [Google Scholar]
- Tournadre, J.; Chaprono, B. Altimeter as an imager of the sea surface roughness: Comparison of SAR and LRM modes. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3541–3544. [Google Scholar]
- Jiang, M.; Xu, K.; Xu, X.; Shi, L.; Yu, X.; Liu, P. 2019: Range noise level estimation of the HY-2B radar altimeter and its comparison with Jason-2 and Jason-3 altimeters. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 8312–8315. [Google Scholar]
- Dinardo, S.; Lucas, B.; Benveniste, J. Sentinel-3 STM SAR ocean retracking algorithm and SAMOSA model. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5320–5323. [Google Scholar]
- Donlon, C.J.; Cullen, R.; Giulicchi, L.; Vuilleumier, P.; Francis, C.R.; Kuschnerus, M.; Simpson, W.; Bouridah, A.; Caleno, M.; Bertoni, R.; et al. The Copernicus Sentinel-6 mission: Enhanced continuity of satellite sea level measurements from space. Remote Sens. Environ. 2021, 258, 112395. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J.; Wang, C. Sentinel-3A SRAL global statistical assessment and cross-calibration with Jason-3. Remote Sens. 2019, 11, 1573. [Google Scholar] [CrossRef] [Green Version]
- Donlon, C.; Cullen, R.; Giulicchi, L.; Fornari, M.; Vuilleumier, P. Copernicus Sentinel-6 Michael Freilich satellite mission: Overview and preliminary in orbit results. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Brussels, Belgium, 11–16 July 2021; pp. 7732–7735. [Google Scholar]
- Hithin, N.K.; Remya, P.G.; Nair, T.M.B.; Harikumar, R.; Kumar, R.; Nayak, S. Validation and Intercomparison of SARAL/AltiKa and PISTACH-Derived Coastal Wave Heights Using In-Situ Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4120–4129. [Google Scholar] [CrossRef]
- Gower, J.F.R. Intercalibration of wave and wind data from TOPEX/POSEIDON and moored buoys off the west coast of Canada. J. Geophys. Res. 1996, 101, 3817–3829. [Google Scholar] [CrossRef]
- Dinardo, S.; Fenoglio-Marc, L.; Buchhaupt, C.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Benveniste, J. Coastal SAR and PLRM altimetry in German Bight and West Baltic Sea. Adv. Space Res. 2018, 62, 1371–1404. [Google Scholar] [CrossRef]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Raney, R.K. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G.G. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. 1994, 99, 24821–24852. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Cui, X.; Dong, W.; Sun, H.; Lu, Y. Simulation of wet atmospheric delay correction for interferometric imaging altimeter based on radiometer. In Proceedings of the IET International Radar Conference 2020 (IET IRC 2020), Online, 4–6 November 2020; pp. 511–516. [Google Scholar]
- Fernandes, M.J.; Pires, N.; Lazáro, C.; Nunes, A. L Tropospheric delays from GNSS for application in coastal altimetry. Adv. Space Res. 2013, 51, 1352–1368. [Google Scholar] [CrossRef]
- Lebedev, S.; Sirota, A.; Medvedev, D.; Khlebnikova, S.; Vignudelli, S.; Snaith, H.M.; Cipollini, P.; Venuti, F.; Lyard, F.; Bouffard, J.; et al. Exploiting satellite altimetry in coastal ocean through the ALTICORE project. Russ. J. Earth Sci. 2008, 10, ES1002. [Google Scholar] [CrossRef] [Green Version]
- Coastal and Hydrology Altimetry Product (PISTACH) Handbook; CLS-DOS-NT-10–246, SALP-MU-P-OP-16031-CN01/00; National Center of Spatial Studies: Paris, France, 2010.
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR altimeter backscattered waveform model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 911–919. [Google Scholar] [CrossRef]
- Martin, T.V.; Zwally, H.J.; Brenner, A.C.; Bindschadler, R.A. Analysis and retracking of continental ice sheet radar altimeter waveforms. J. Geophys. Res. 1983, 88, 1608–1616. [Google Scholar] [CrossRef]
- Legresy, B.; Remy, F. Surface characteristics of the Antarctic ice sheet and altimetric observations. J. Glaciol. 1997, 43, 197–206. [Google Scholar] [CrossRef] [Green Version]
- Wingham, D.J.; Rapley, C.G.; Griffiths, H. New techniques in satellite altimeter tracking system. In Proceedings of the 1986 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Zurich, Switzerland, 8–11 September 1986; pp. 1339–1344. [Google Scholar]
- Davis, C.H. A robust threshold retracking algorithm for measuring ice-sheet surface elevation change from satellite radar altimeter. IEEE Trans. Geosci. Remote Sens. 1997, 35, 974–979. [Google Scholar] [CrossRef]
- Dabo-Niang, S.; Ferraty, F.; Vieu, P. On the using of modal curves for radar waveforms classification. Comput. Statist. Data. Anal. 2007, 51, 4878–4890. [Google Scholar] [CrossRef]
- Yang, L. Study on Satellite Radar Altimeter Retrieval Algorithms over Coastal Seas and under High Sea State Events. Ph.D. Thesis, Nanjing University of Science & Technology, Nanjing, China, 2009. [Google Scholar]
- Ganguly, D.; Chander, S.; Desai, S.; Chauhan, P. A Subwaveform-Based Retracker for Multipeak Waveforms: A Case Study over Ukai Dam/Reservoir. Mar. Geod. 2015, 38, 581–596. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef] [Green Version]
- Passaro, M.; Rose, S.; Andersen, O.; Boergens, E.; Calafat, F.; Dettmering, D.; Benveniste, J. ALES+: Adapting a homogenous ocean retracker for satellite altimetry to sea ice leads, coastal and inland waters. Remote Sens. Environ. 2018, 211, 456–471. [Google Scholar] [CrossRef] [Green Version]
- Passaro, M.; Rautiainen, L.; Dettmering, D.; Restano, M.; Hart-Davis, M.G.; Schlembach, F.; Särkkä, J.; Müller, F.L.; Schwatke, C.; Benveniste, J. Validation of an empirical subwaveform retracking strategy for SAR altimetry. Remote Sens. 2022, 14, 4122. [Google Scholar] [CrossRef]
- Jain, M.; Andersen, O.B.; Dall, J.; Stenseng, L. Sea surface height determination in the Arctic using Cryosat-2 SAR data from primary peak empirical retrackers. Adv. Space Res. 2015, 55, 40–50. [Google Scholar] [CrossRef]
- The European Space Agency. Available online: https://www.esa.int/ (accessed on 10 January 2023).
- Aviso+ Satellite Altimetry Data. Available online: https://www.aviso.altimetry.fr/en/home.html (accessed on 10 January 2023).
- EUMETSAT Data Store. Available online: https://data.eumetsat.int/extended?query=SRAL%20Level%202%20Altimetry%20Global%20-%20Sentinel-3# (accessed on 10 January 2023).
- Guccione, P. Beam sharpening of Delay/Doppler altimeter data through chirp Zeta transform. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2517–2526. [Google Scholar] [CrossRef]
- Scagliola, M.; Guccione, P.; Giudici, D. Fully focused SAR processing for radar altimeter: A frequency domain approach. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 6699–6702. [Google Scholar]
- Wingham, D.J.; Phalippou, L.; Mavrocordatos, C.; Wallis, D. The mean echo and echo cross product from a beamforming interferometric altimeter and their application to elevation measurement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2305–2323. [Google Scholar] [CrossRef]
- Egido, A.; Smith, W.H.F. Fully focused SAR altimetry: Theory and applications. IEEE Trans. Geosci. Remote Sens. 2017, 55, 392–406. [Google Scholar] [CrossRef]
- Wingham, D.J.; Giles, K.A.; Galin, N.; Cullen, R.; Armitage, T.W.; Smith, W.H. A semianalytical model of the synthetic aperture, interferometric radar altimeter mean echo, and echo cross-product and its statistical fluctuations. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2539–2553. [Google Scholar] [CrossRef]
- Scagliola, M.; Guccione, P. Datation and range calibration of radar altimeter exploiting fully focused SAR processing. IEEE Geosci. Remote Sens. Lett. 2021, 18, 480–483. [Google Scholar] [CrossRef]
- Liu, X.; Kong, W.; Sun, H.; Lu, Y. Performance analysis of Ku/Ka dual-band SAR altimeter from an airborne experiment over South China Sea. Remote Sens. 2022, 14, 2362. [Google Scholar] [CrossRef]
- Garcia, E.S.; Sandwell, D.T.; Smith, W.H.F. Retracking CryoSat-2, Envisat and Jason-1 radar altimetry waveforms for improved gravity field recovery. Geophys. J. Int. 2013, 196, 1402–1422. [Google Scholar] [CrossRef] [Green Version]
- Halimi, A.; Mailhes, C.; Tourneret, J.; Thibaut, P.; Boy, F. A semi-analytical model for Delay/Doppler altimetry and its estimation algorithm. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4248–4258. [Google Scholar] [CrossRef] [Green Version]
- Taburet, N.; Zawadzki, L.; Vayre, M.; Blumstein, D.; Le Gac, S.; Boy, F.; Raynal, M.; Labroue, S.; Crétaux, J.-F.; Femenias, P. S3MPC: Improvement on Inland Water Tracking and Water Level Monitoring from the OLTC Onboard Sentinel-3 Altimeters. Remote Sens. 2020, 12, 3055. [Google Scholar] [CrossRef]
- Liu, X.; Kong, W.; Sun, H.; Xu, Y.; Lu, Y. An improved altimeter in-orbit range noise-level estimation approach based on along-track differential method. Remote Sens. 2022, 14, 6250. [Google Scholar] [CrossRef]



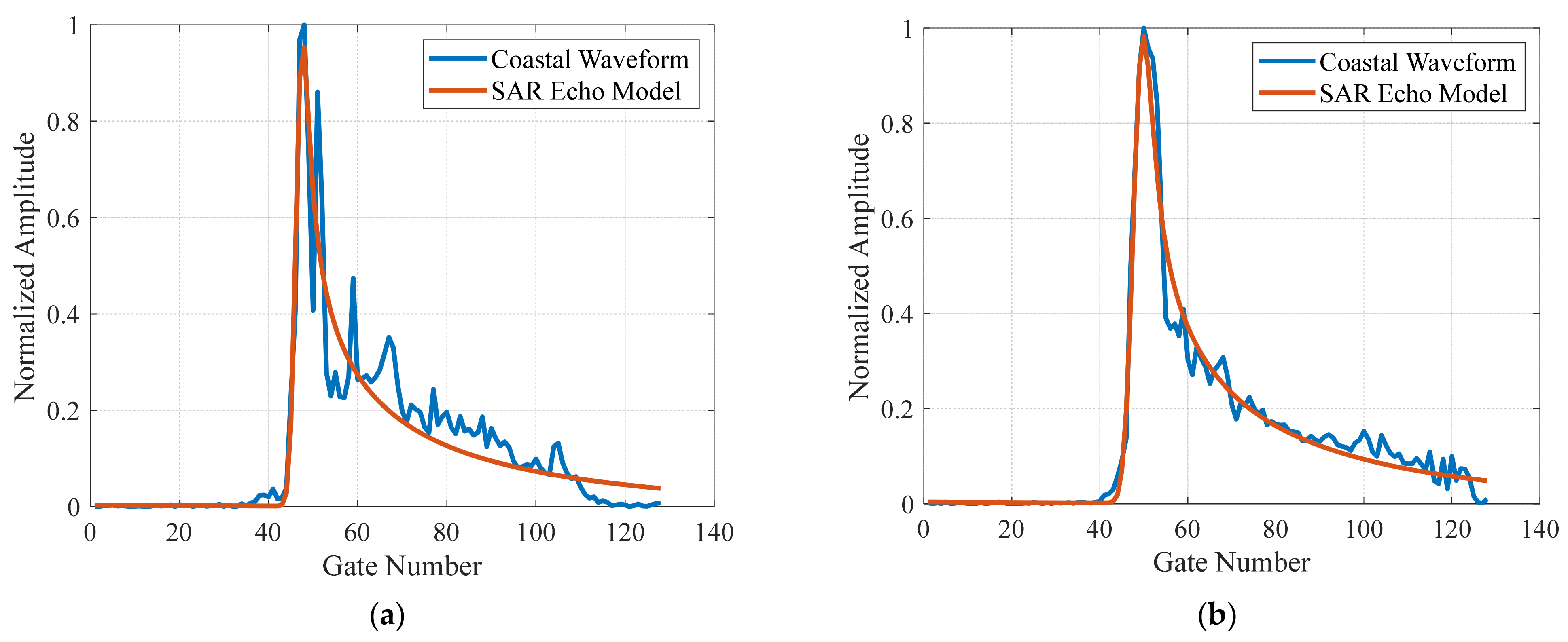


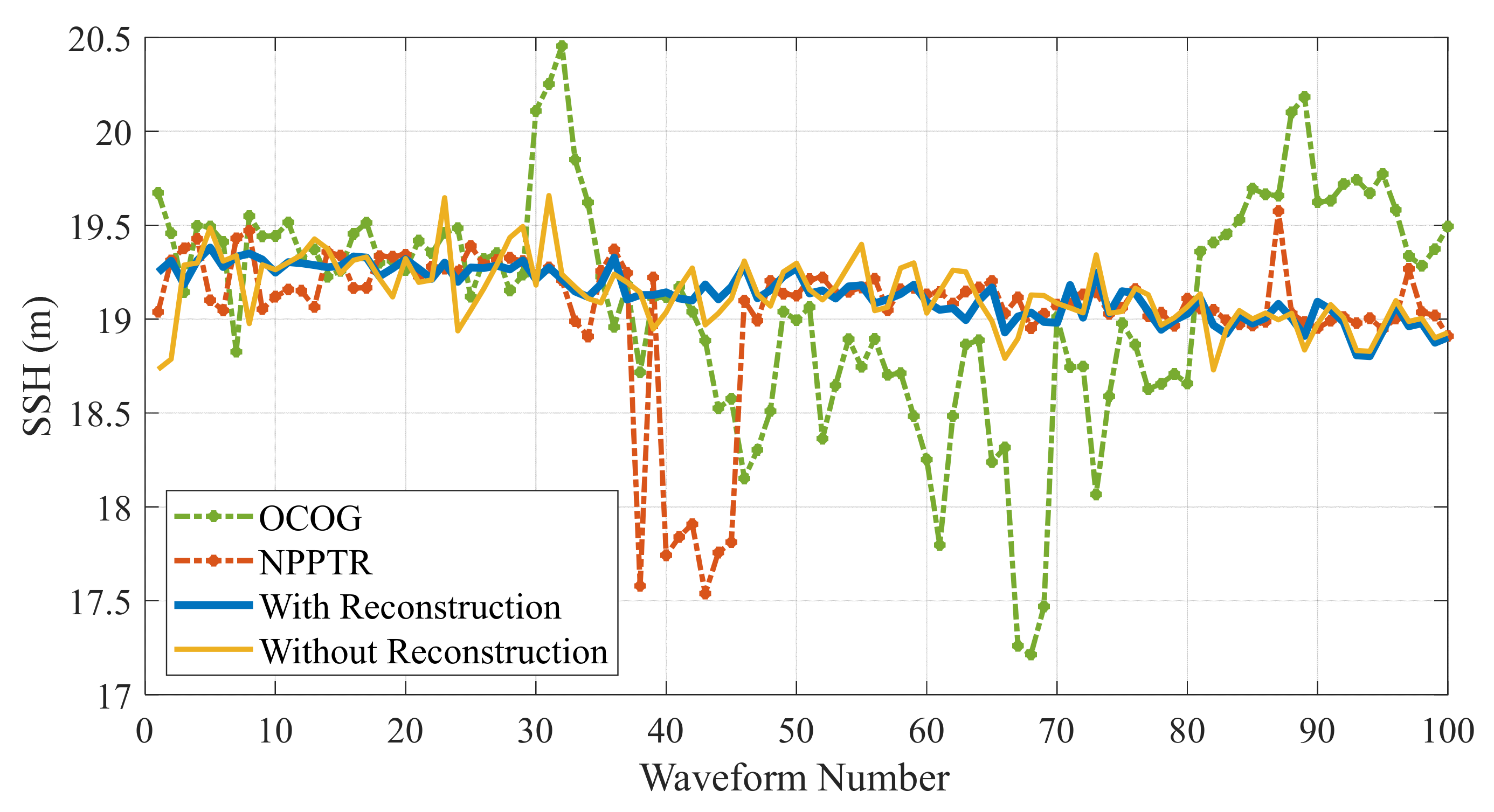
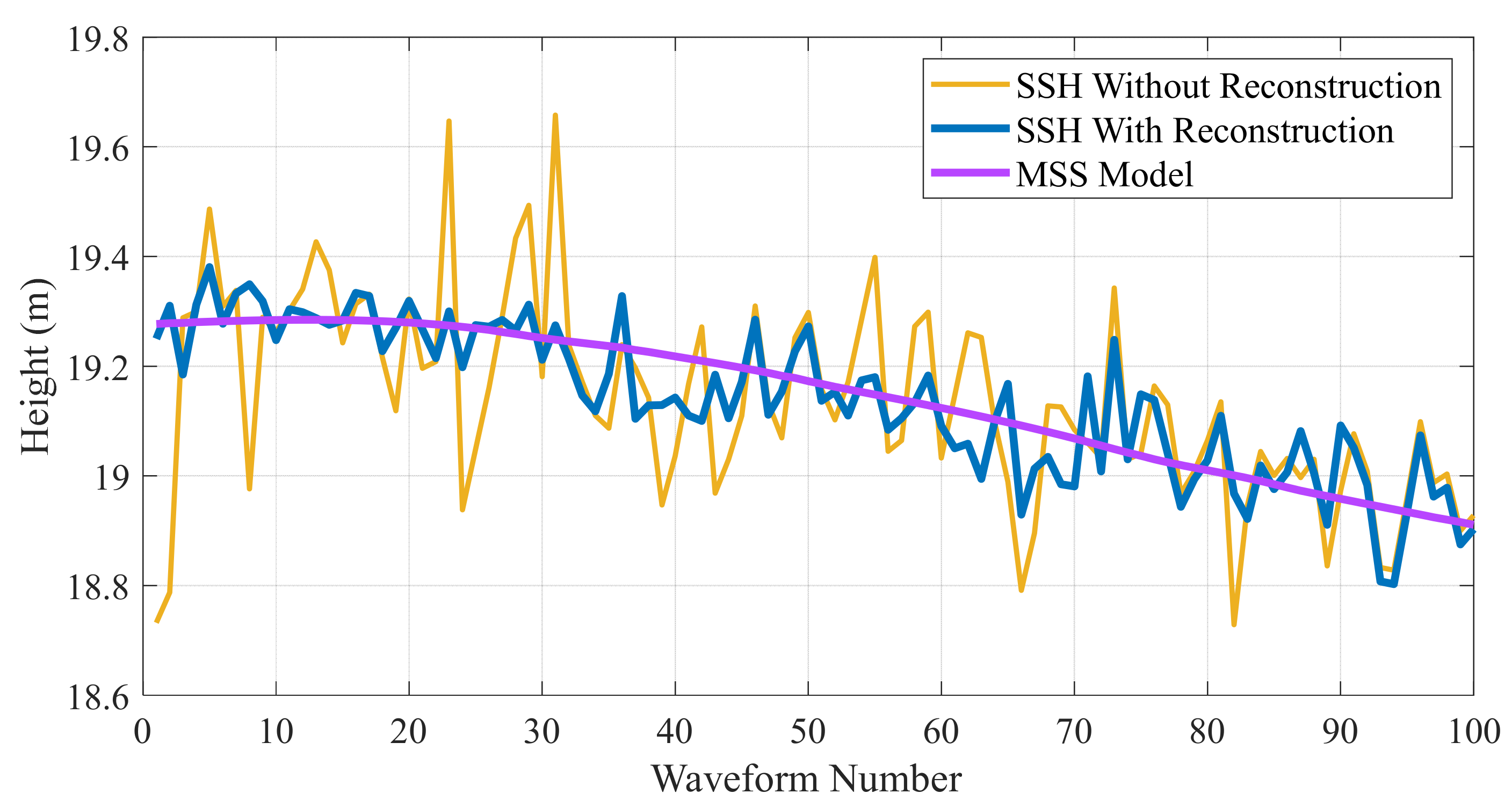
| Item | Area 1 | Area 2 |
|---|---|---|
| Measure Satellite | Sentinel-3B | |
| Measure Mode | SAR | |
| Measure Year | 2022 | |
| Measure Pass | 309 | 123 |
| Measure Month | 3, 4, 6, 7, 9 | a whole year |
| Data Rate | 20 Hz | |
| Data Level | L2 GDR | |
| No. Month | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| MQE improvement proportion | 91.86% | 84.44% | 84.88% | 78.49% | 91.86% | |
| Retracking success rate | Without Reconstruction | 37.21% | 42.22% | 51.16% | 40.86% | 38.37% |
| With Reconstruction | 90.70% | 73.33% | 76.58% | 79.57% | 87.21% | |
| Increasing Percentage | 53.49% | 31.11% | 25.42% | 38.71% | 48.84% | |
| No. Pass | MQE Improvement Proportion | Retracking Success Rate | ||
|---|---|---|---|---|
| without Reconstruction | with Reconstruction | Increasing Percentage | ||
| 1 | 68.13% | 21.98% | 53.85% | 31.87% |
| 2 | 93.94 % | 42.42% | 97.98% | 55.56% |
| 3 | 63.64% | 49.09% | 61.82% | 12.73% |
| 4 | 92.06% | 65.08% | 93.65% | 28.57% |
| 5 | 59.14% | 65.59% | 69.89% | 4.30% |
| 6 | 83.00% | 54.00% | 91.00% | 37.00% |
| 7 | 63.00% | 86.00% | 88.00% | 2.00% |
| 8 | 79.59% | 58.16% | 96.94% | 38.78% |
| 9 | 88.33% | 61.67% | 86.67% | 25.00% |
| 10 | 91.23% | 42.11% | 87.72% | 45.61% |
| 11 | 84.09% | 57.95% | 94.32% | 36.37% |
| 12 | 82.83 % | 58.59% | 92.93% | 34.34% |
| 13 | 94.95% | 47.47% | 97.98% | 50.51% |
| Mean | 80.30% | 54.62% | 85.60% | 30.98% |
| Method | OCOG | NPPTR | without Reconstruction | with Reconstruction |
|---|---|---|---|---|
| Noise level | 26.23 cm | 27.53 cm | 12.75 cm | 6.32 cm |
| RMSE | 59.87 cm | 39.82 cm | 15.24 cm | 7.06 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Kong, W.; Sun, H.; Lu, Y. A Partial Reconstruction Method for SAR Altimeter Coastal Waveforms Based on Adaptive Threshold Judgment. Remote Sens. 2023, 15, 1717. https://doi.org/10.3390/rs15061717
Liu X, Kong W, Sun H, Lu Y. A Partial Reconstruction Method for SAR Altimeter Coastal Waveforms Based on Adaptive Threshold Judgment. Remote Sensing. 2023; 15(6):1717. https://doi.org/10.3390/rs15061717
Chicago/Turabian StyleLiu, Xiaonan, Weiya Kong, Hanwei Sun, and Yaobing Lu. 2023. "A Partial Reconstruction Method for SAR Altimeter Coastal Waveforms Based on Adaptive Threshold Judgment" Remote Sensing 15, no. 6: 1717. https://doi.org/10.3390/rs15061717
APA StyleLiu, X., Kong, W., Sun, H., & Lu, Y. (2023). A Partial Reconstruction Method for SAR Altimeter Coastal Waveforms Based on Adaptive Threshold Judgment. Remote Sensing, 15(6), 1717. https://doi.org/10.3390/rs15061717






