Forward Electromagnetic Induction Modelling in a Multilayered Half-Space: An Open-Source Software Tool
Abstract
:1. Introduction
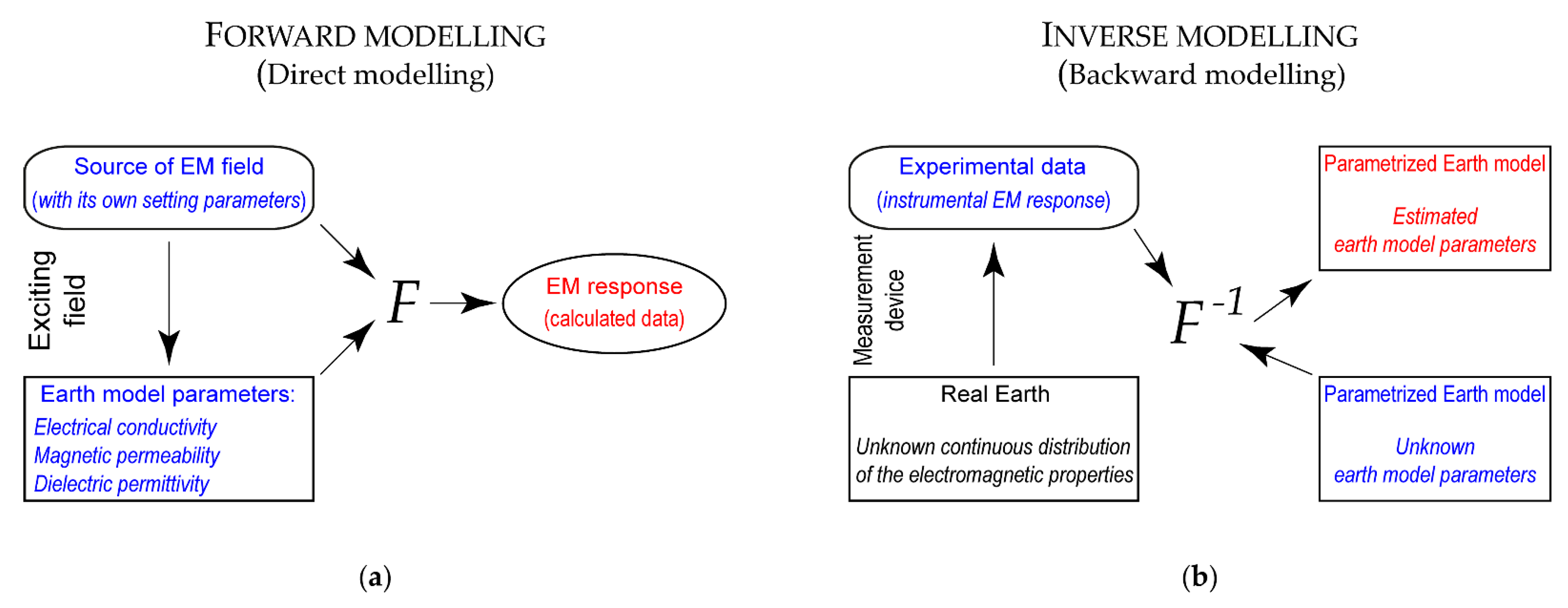
2. EMI Theory Overview
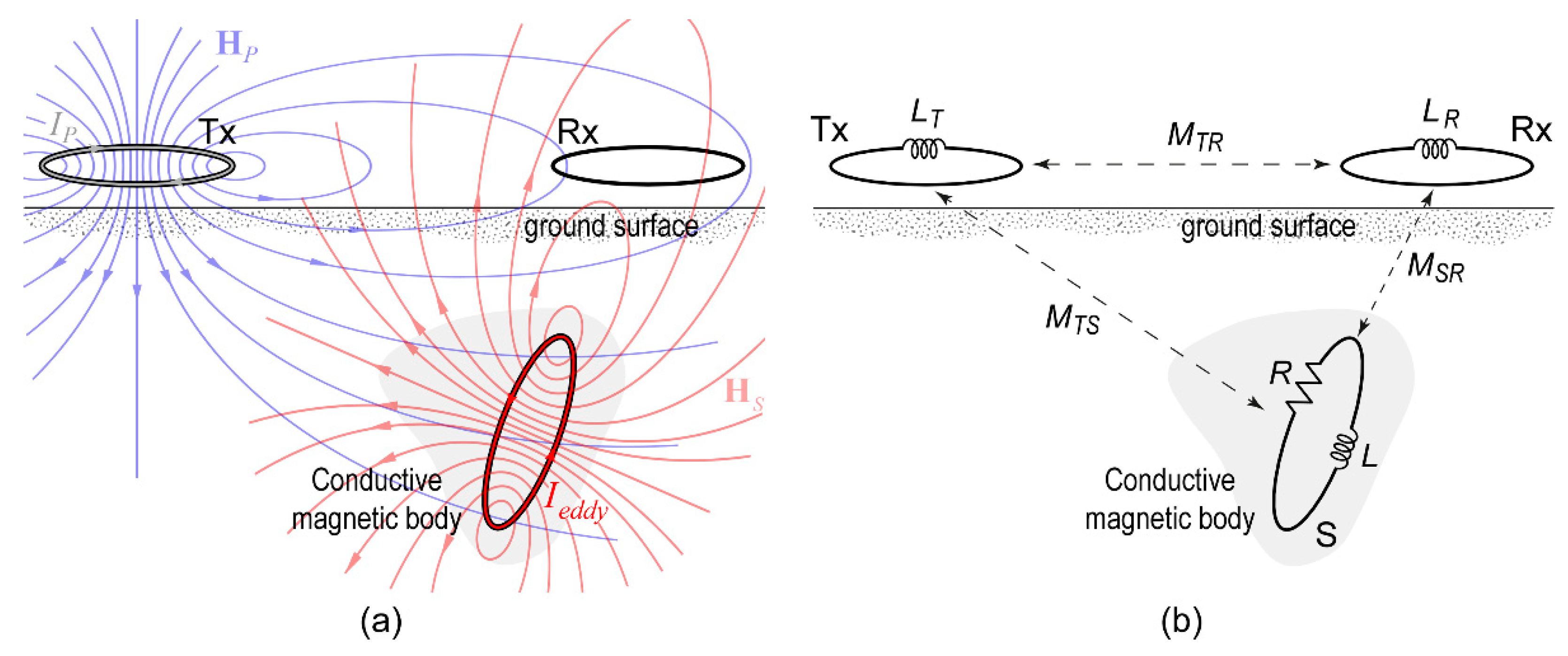
2.1. Basics of Electromagnetic Induction
2.2. 1D forward Modelling
2.2.1. 1D layered Ground Model and Loop-Loop Configurations of Measuring Devices
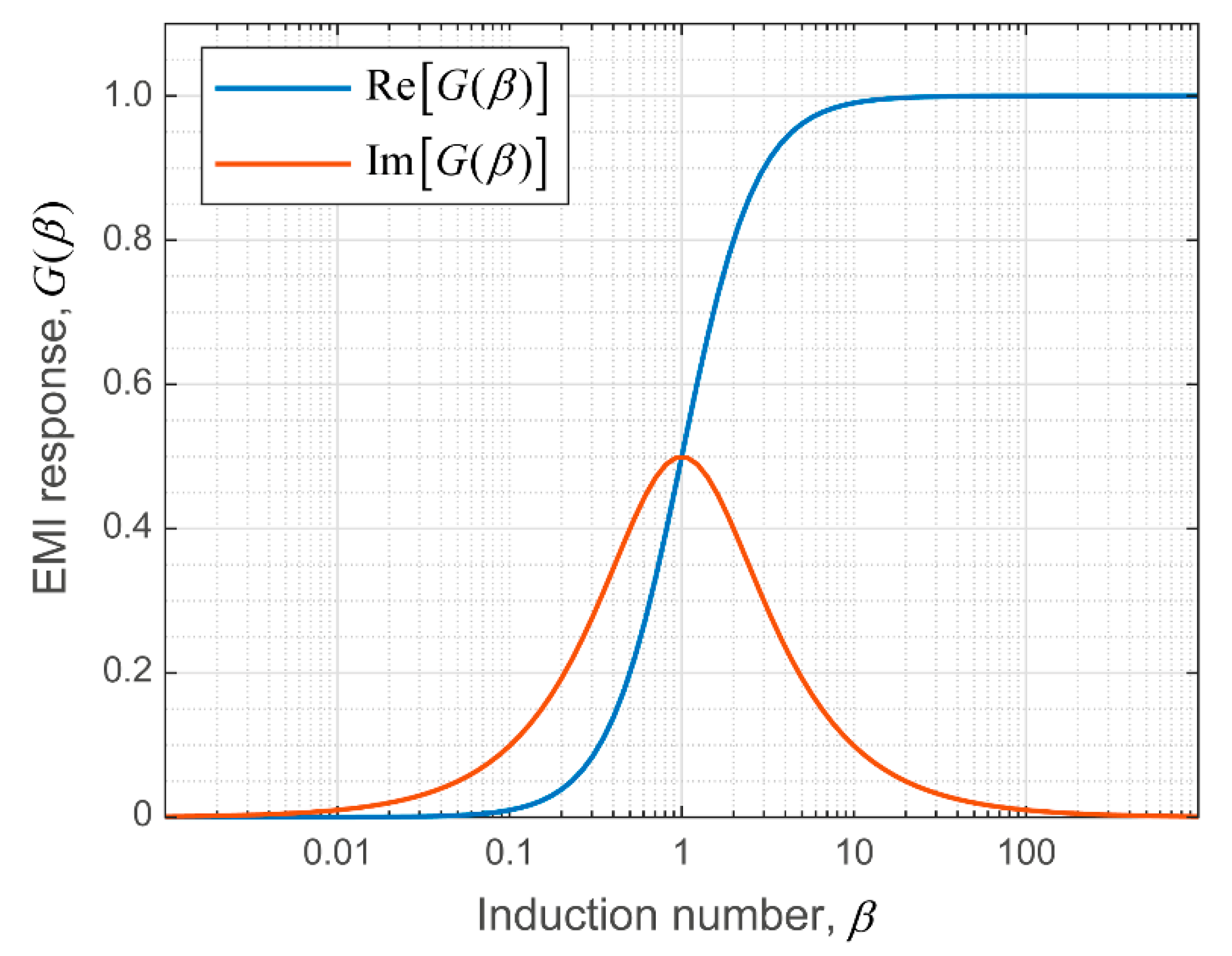
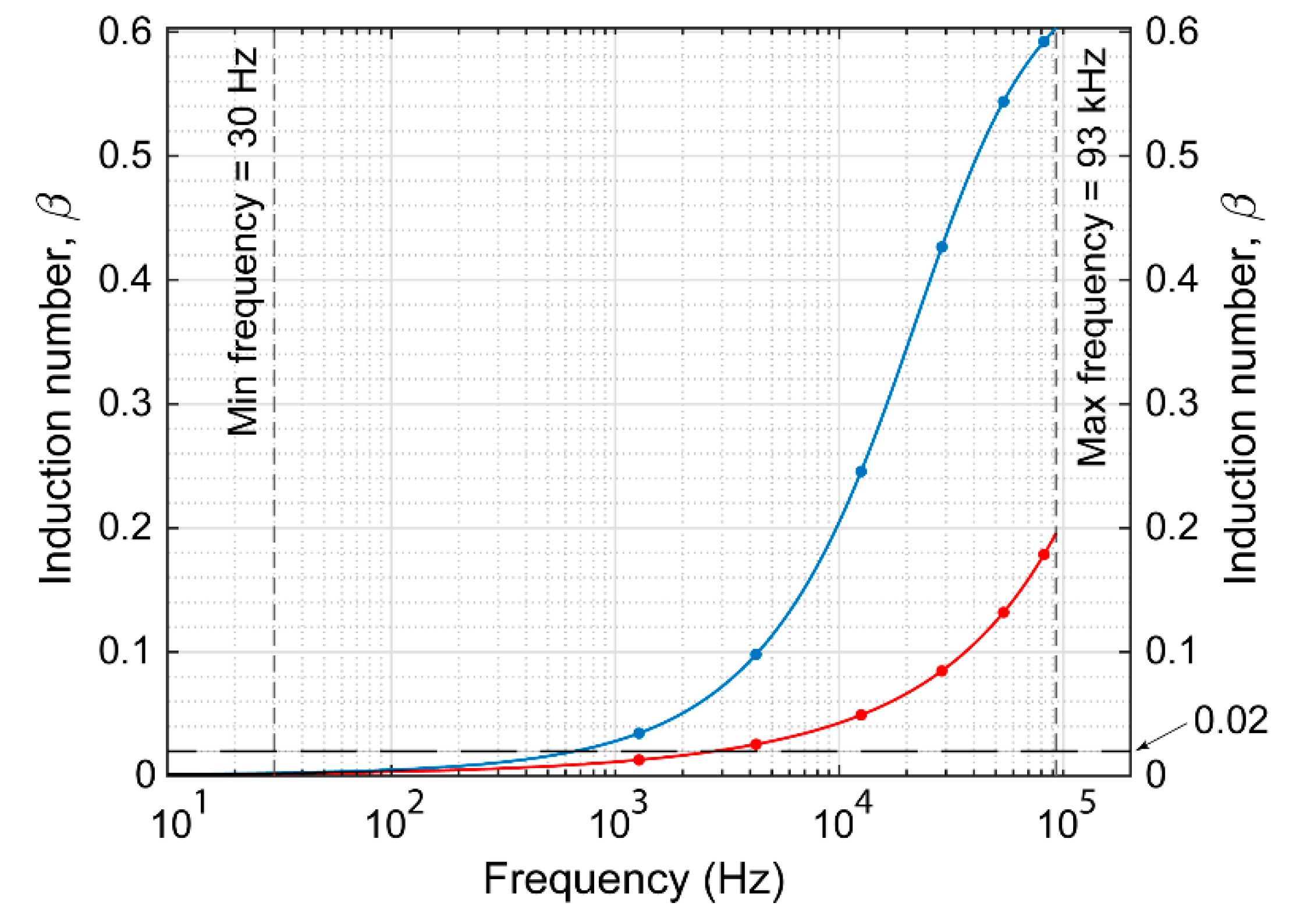
2.2.2. Skin Depth and Induction Number
2.2.3. Nonlinear Forward Modelling
2.2.4. Linear Approximation of the Forward Modelling
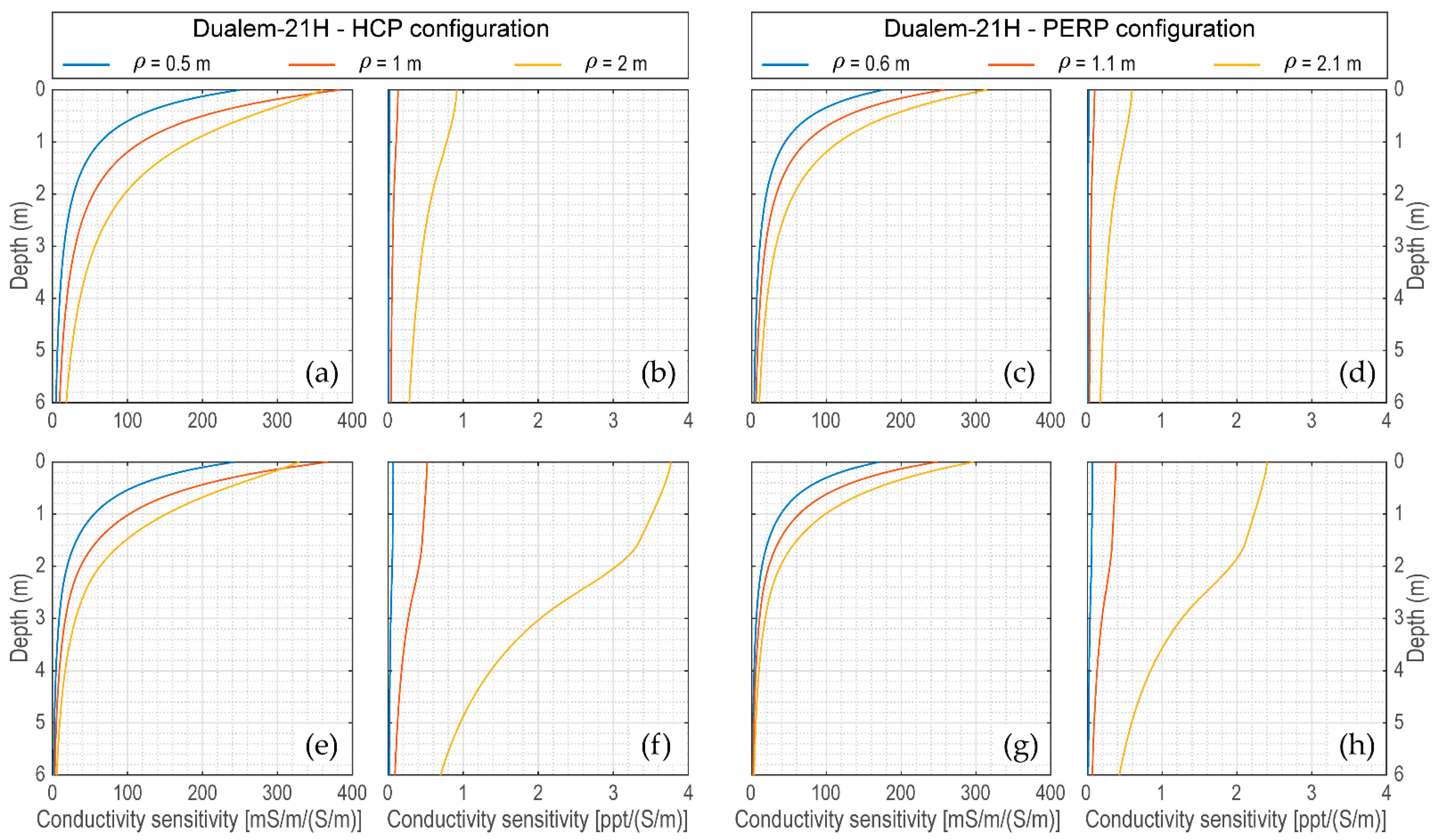
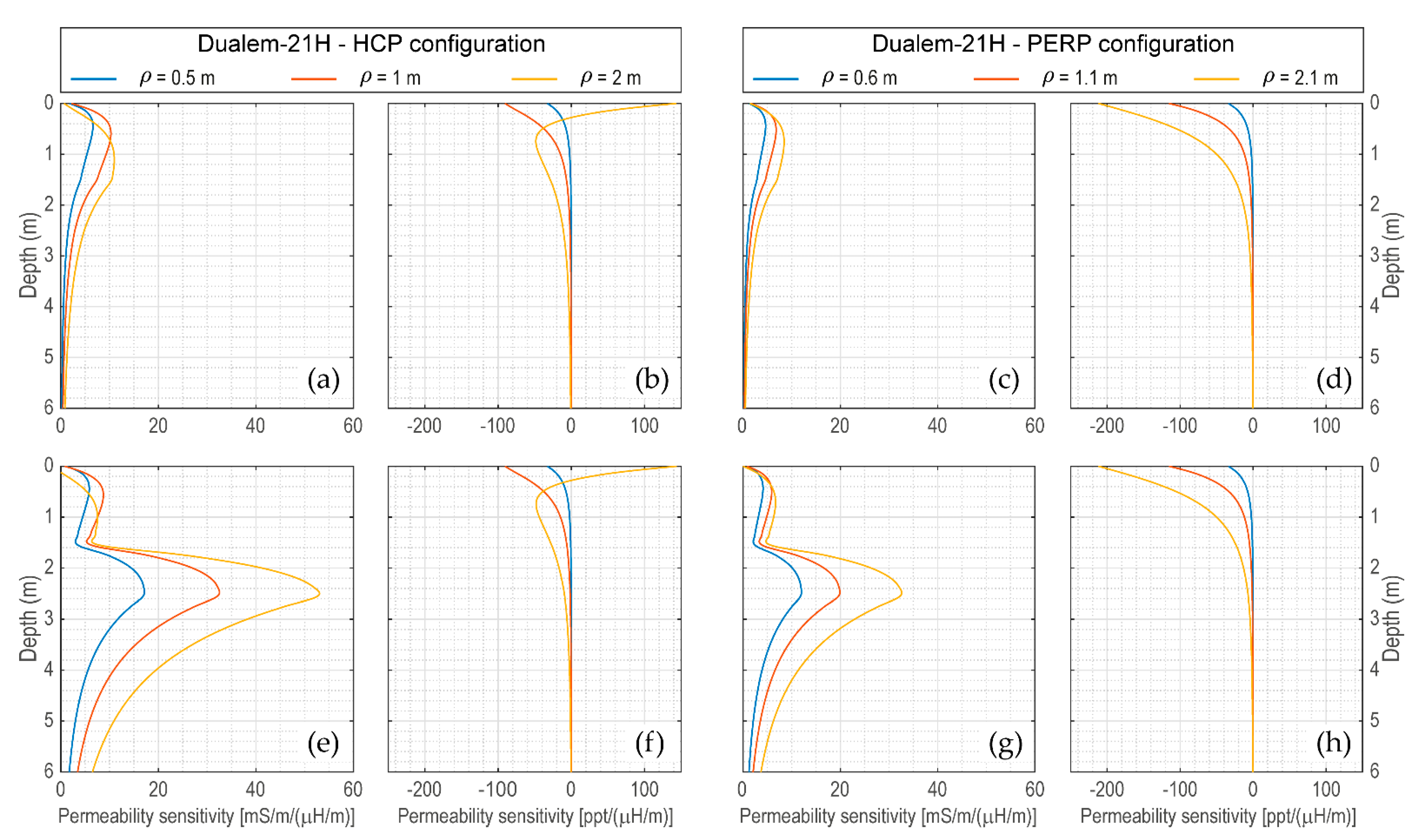
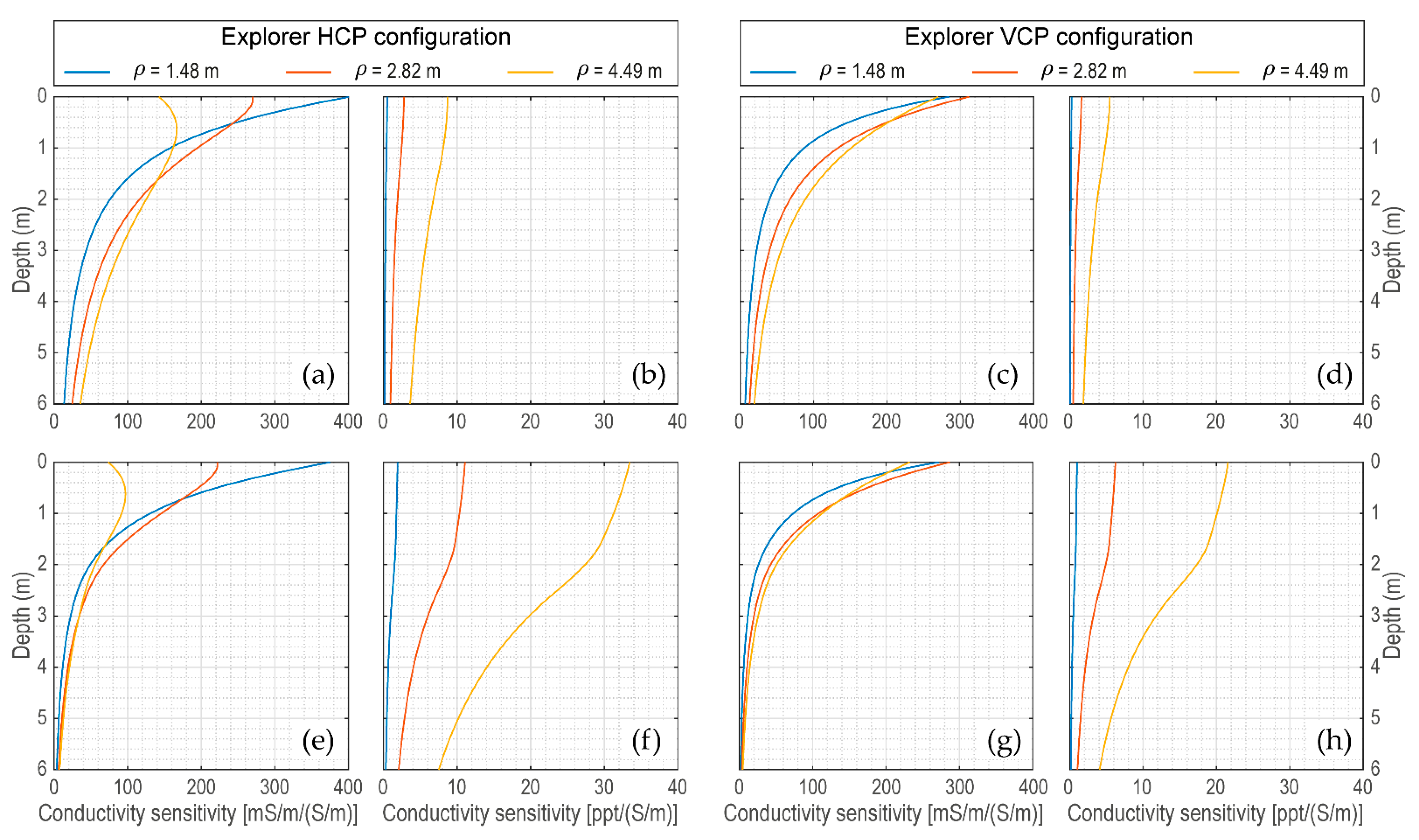
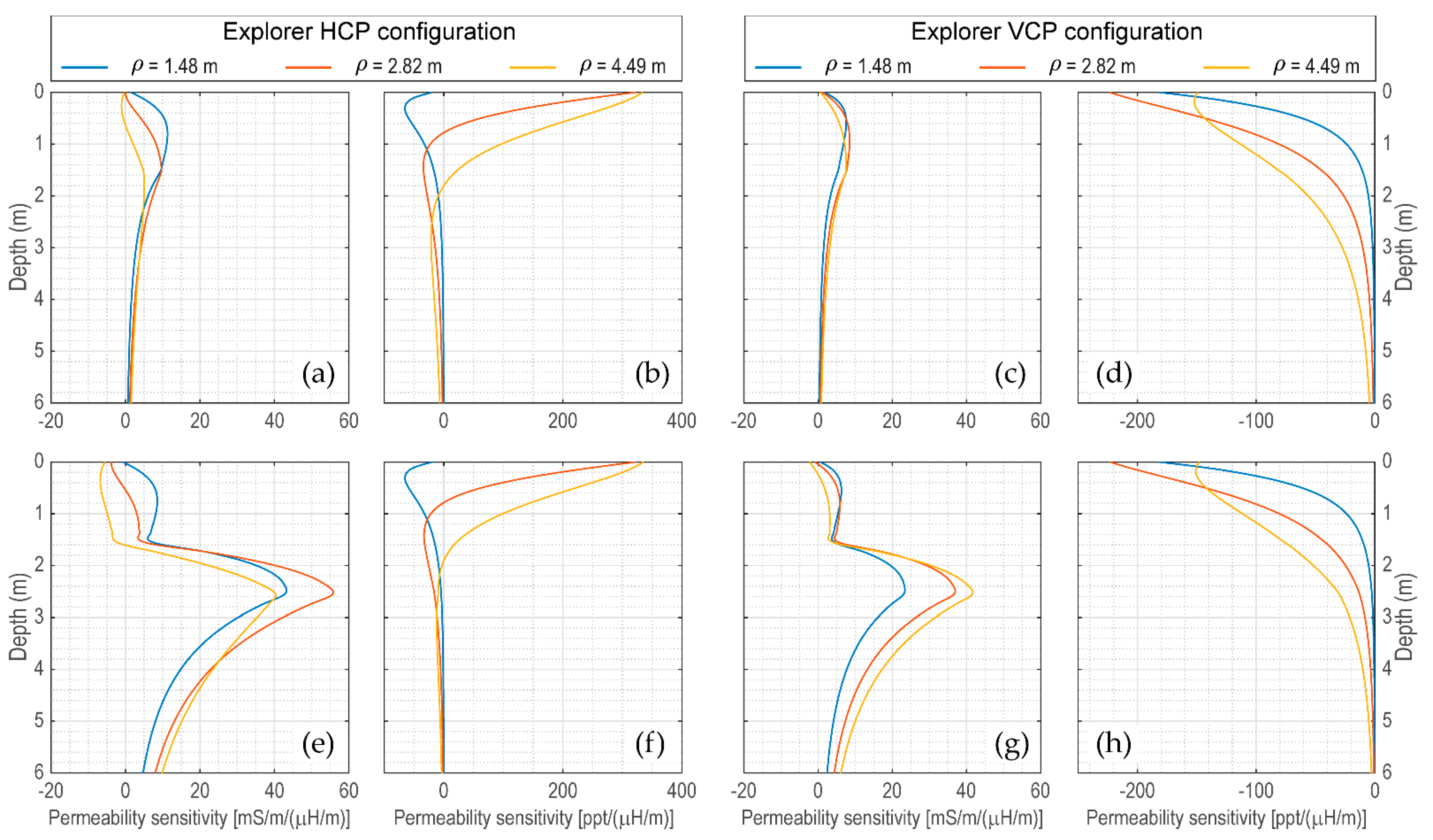
2.3. Sensitivity Function of EMI Measuring Devices
2.4. Depth of Investigation (DOI)
3. Inversion Algorithm
Minimal-Norm Solution
- MNGN
- MNGN2(α): in [71], a further damping parameter has been introduced for the projection term, through a second-order analysis of the residual , as well as a strategy to automatically tune it. A simple choice is to consider a parameter to control both terms,and estimate it by the Armijo–Goldstein principle.
- MNGN2(α,β): another possibility is to consider two independent parameters
- MNGN2(α,β,δ): this implementation is identical to the previous one, but the parameter is estimated by a different adaptive technique, which proved to be superior in the numerical simulations reported in [71].
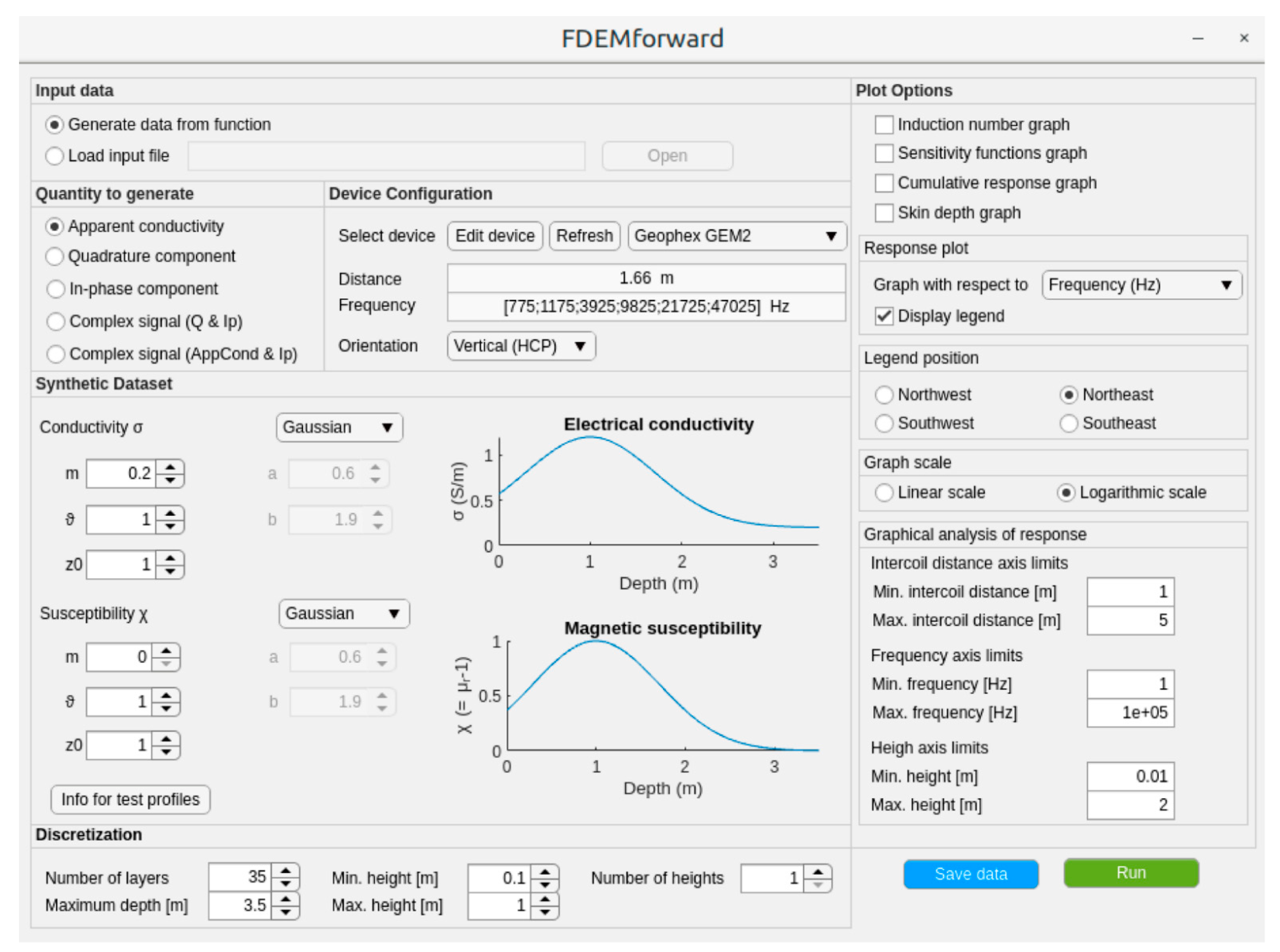
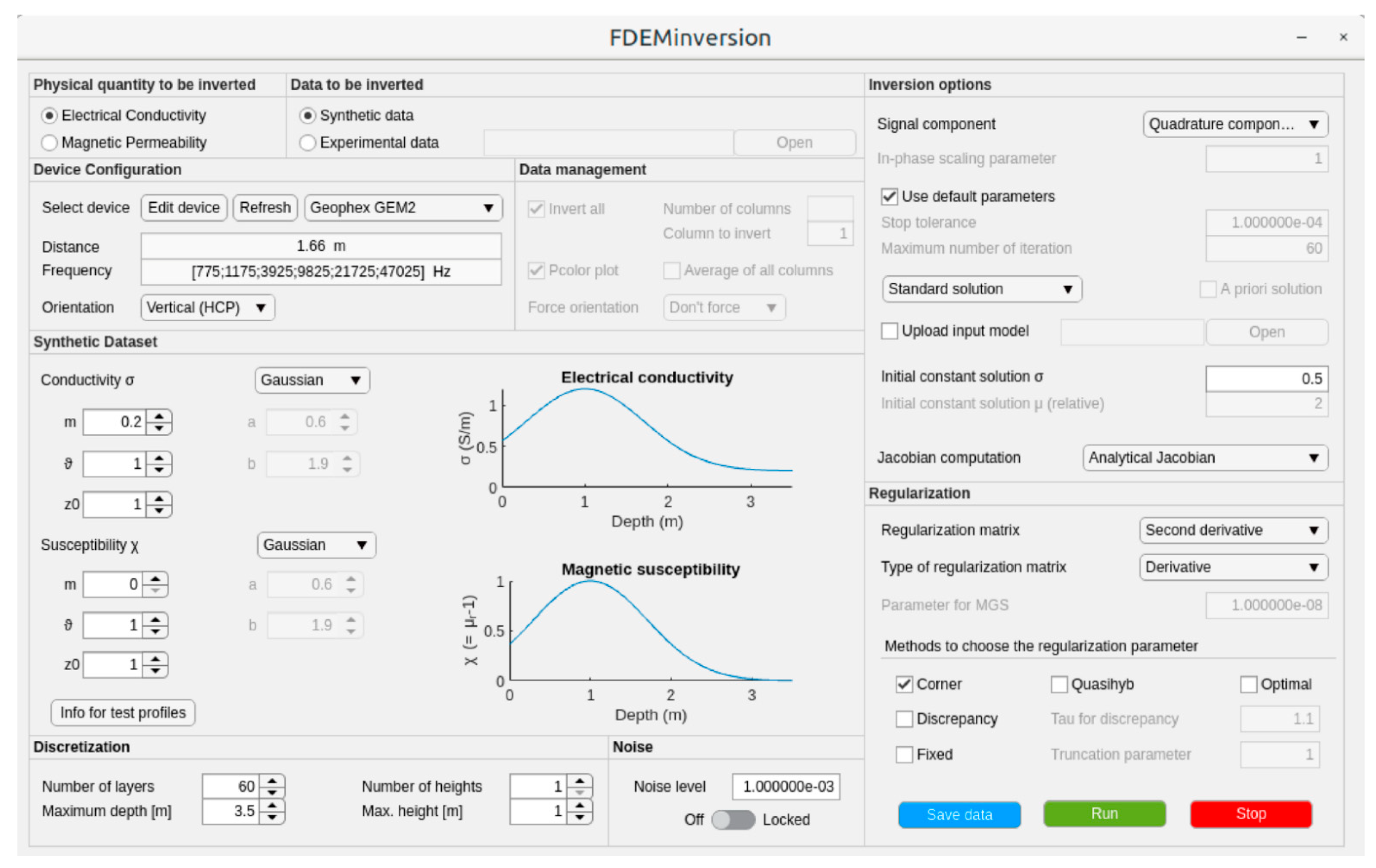
4. Software Package
- FDEMforward
- Input data;
- Quantity to generate;
- Device configuration;
- Synthetic datasets;
- Discretization
- Plot options;
- FDEMinversion
- Physical quantity to be inverted;
- Data to be inverted;
- Device configuration;
- Data management;
- Synthetic Dataset;
- Discretization;
- Noise;
- Inversion options;
- Regularization.
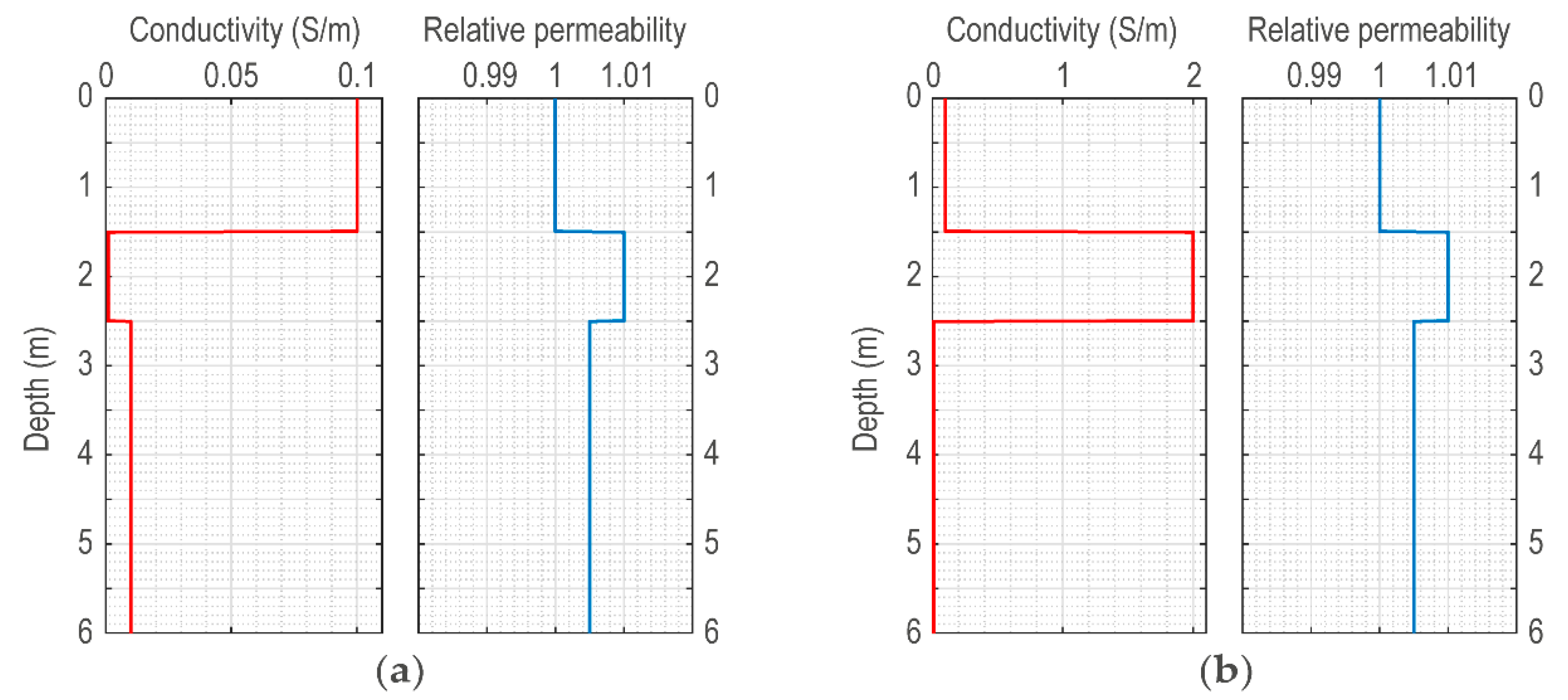
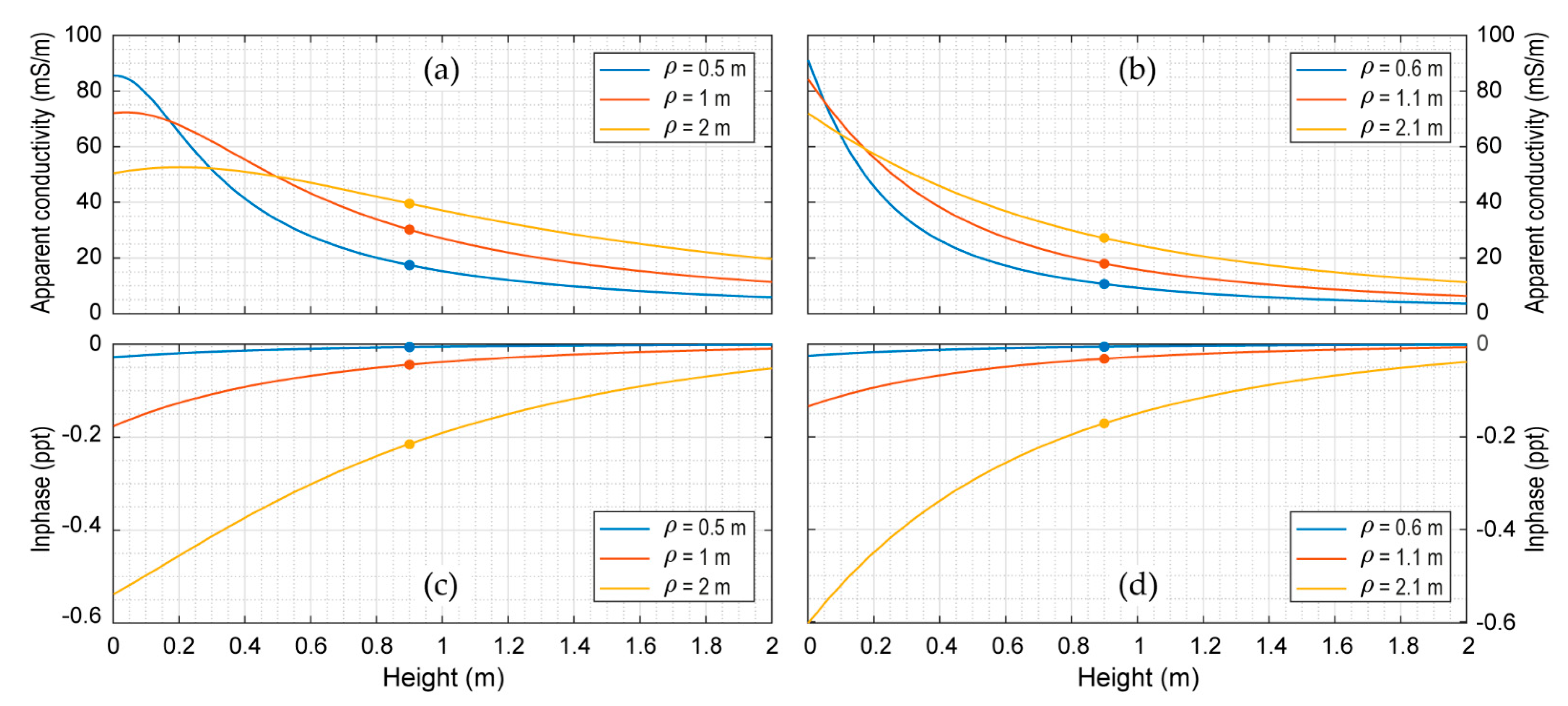
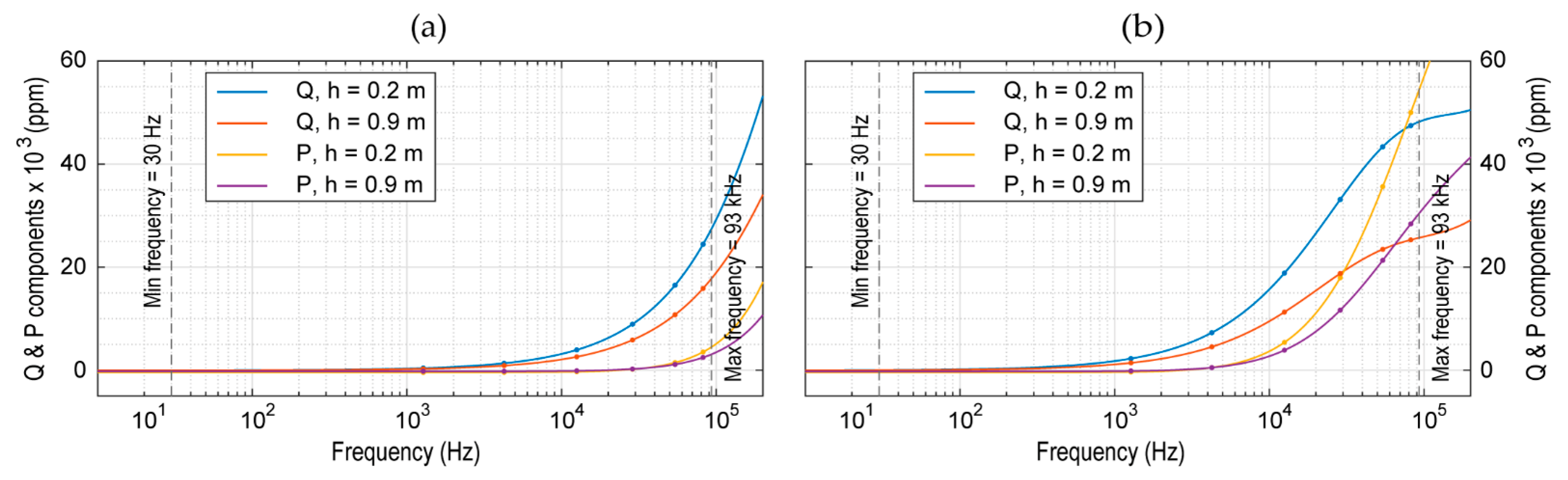
5. Numerical Examples and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Brief Review of the Maxwell Equations
Appendix A.1. Quasi-Stationary Approximation
Appendix B. Step-by-Step Electromagnetic Induction
Appendix B.1. Step 1
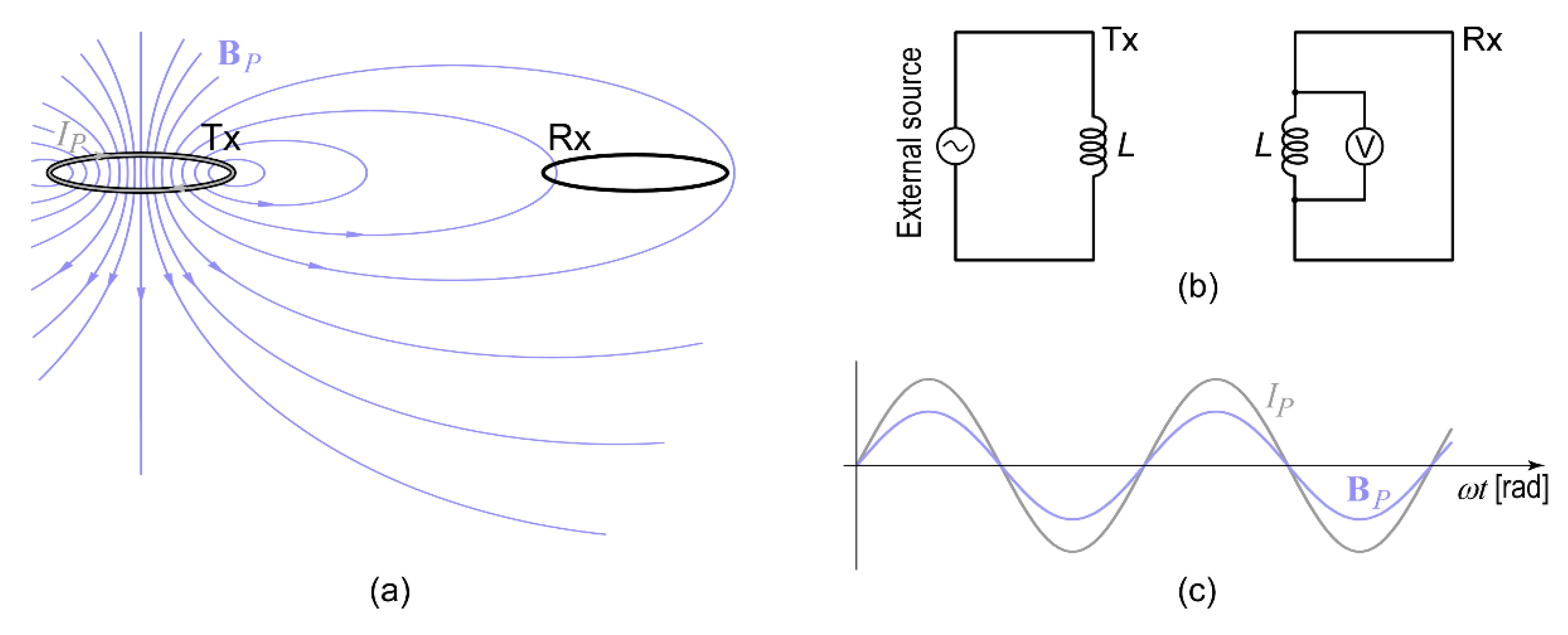
Appendix B.2. Step 2

Appendix B.3. Step 3
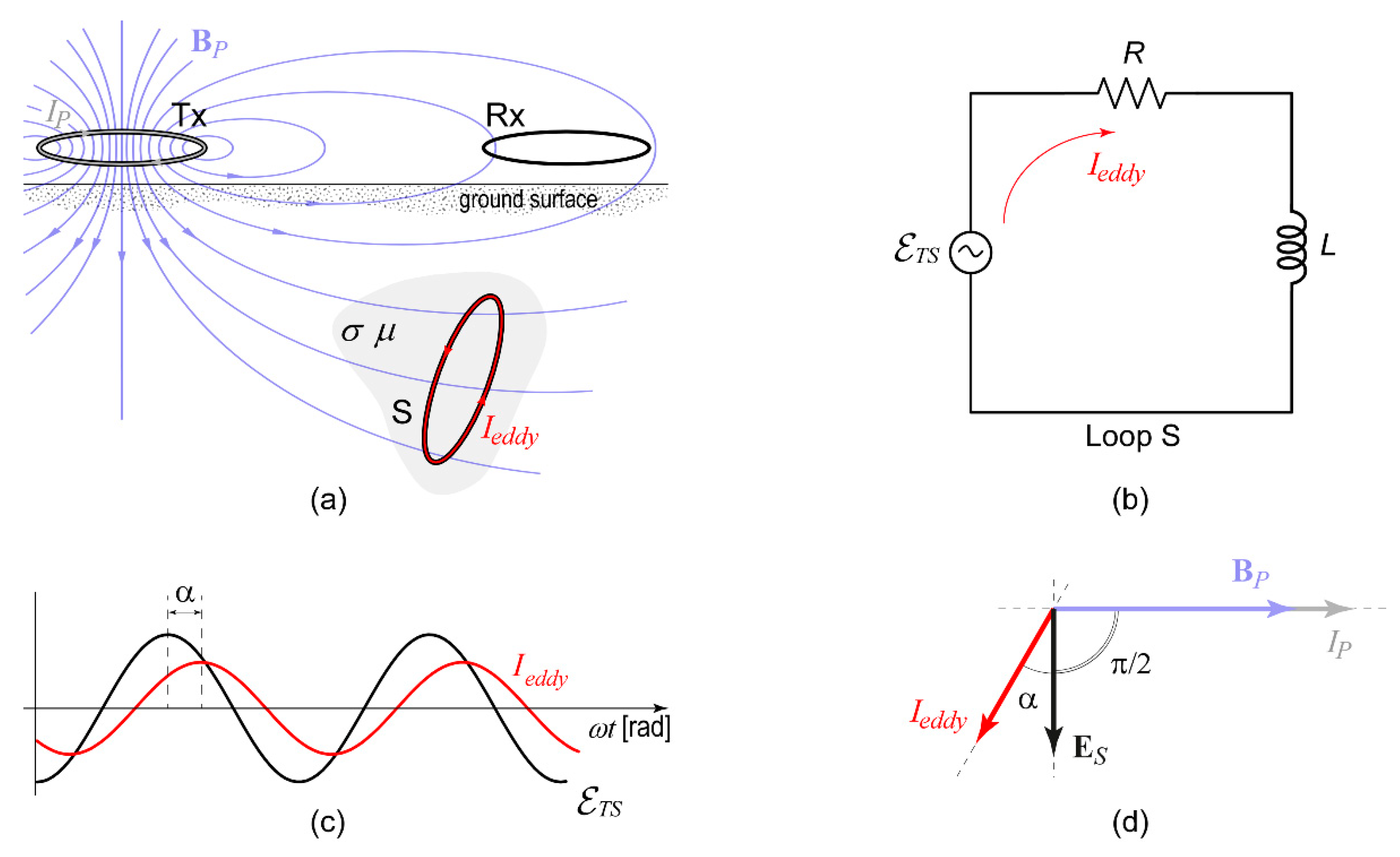
Appendix B.4. Step 4
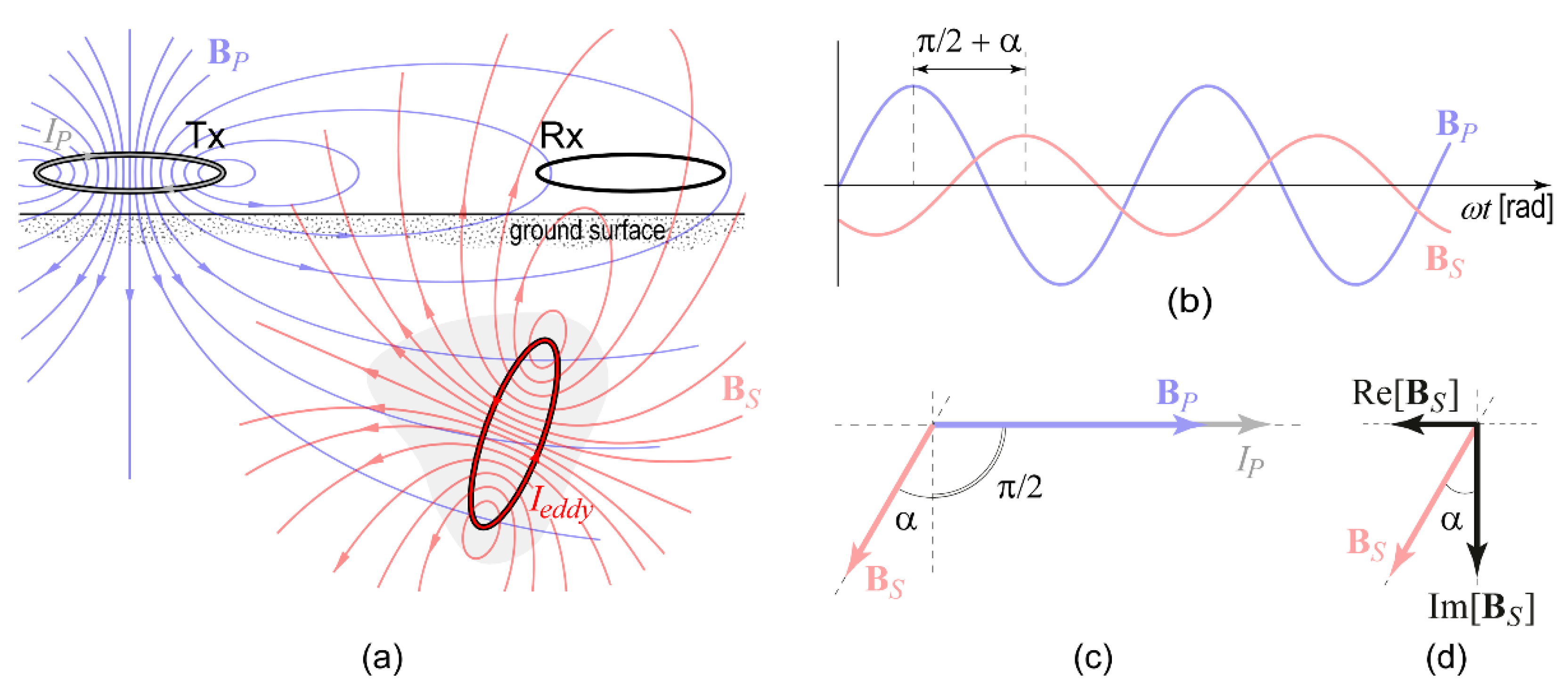
References
- Pellerin, L. Applications of Electrical and Electromagnetic Methods for Environmental and Geotechnical Investigations. Surv. Geophys. 2002, 23, 101–132. [Google Scholar] [CrossRef]
- Martinelli, P.; Duplaá, M.C. Laterally filtered 1D inversions of small-loop, frequency-domain EMI data from a chemical waste site. Geophysics 2008, 73, F143–F149. [Google Scholar] [CrossRef] [Green Version]
- Boaga, J. The use of FDEM in hydrogeophysics: A review. J. Appl. Geophys. 2017, 139, 36–46. [Google Scholar] [CrossRef]
- McLachlan, P.; Blanchy, G.; Chambers, J.; Sorensen, J.; Uhlemann, S.; Wilkinson, P.; Binley, A. The Application of Electromagnetic Induction Methods to Reveal the Hydrogeological Structure of a Riparian Wetland. Water Resour. Res. 2021, 57, e2020WR029221. [Google Scholar] [CrossRef]
- Jansen, J.; Haddad, B.; Fassbender, W.; Jurcek, P. Frequency Domain Electromagnetic Induction Sounding Surveys for Landfill Site Characterization Studies. Groundw. Monit. Remediat. 1992, 12, 103–109. [Google Scholar] [CrossRef]
- Dumont, G.; Pilawski, T.; Dzaomuho-Lenieregue, P.; Hiligsmann, S.; Delvigne, F.; Thonart, P.; Robert, T.; Nguyen, F.; Hermans, T. Gravimetric water distribution assessment from geoelectrical methods (ERT and EMI) in municipal solid waste landfill. Waste Manag. 2016, 55, 129–140. [Google Scholar] [CrossRef]
- Deidda, G.P.; De Carlo, L.; Caputo, M.C.; Cassiani, G. Frequency domain electromagnetic induction imaging: An effective method to see inside a capped landfill. Waste Manag. 2022, 144, 29–40. [Google Scholar] [CrossRef]
- Deidda, G.P.; Himi, M.; Barone, I.; Cassiani, G.; Ponsati, A.C. Frequency-Domain Electromagnetic Mapping of an Abandoned Waste Disposal Site: A Case in Sardinia (Italy). Remote Sens. 2022, 14, 878. [Google Scholar] [CrossRef]
- Paine, J.G. Determining salinization extent, identifying salinity sources, and estimating chloride mass using surface, borehole, and airborne electromagnetic induction methods. Water Resour. Res. 2003, 39, 1059. [Google Scholar] [CrossRef] [Green Version]
- Yao, R.; Yang, J. Quantitative evaluation of soil salinity and its spatial distribution using electromagnetic induction method. Agric. Water Manag. 2010, 97, 1961–1970. [Google Scholar] [CrossRef]
- Jadoon, K.Z.; Moghadas, D.; Jadoon, A.; Missimer, T.M.; Al-Mashharawi, S.K.; McCabe, M.F. Estimation of soil salinity in a drip irrigation system by using joint inversion of multicoil electromagnetic induction measurements. Water Resour. Res. 2015, 51, 3490–3504. [Google Scholar] [CrossRef] [Green Version]
- Koganti, T.; Narjary, B.; Zare, E.; Pathan, A.L.; Huang, J.; Triantafilis, J. Quantitative mapping of soil salinity using the DUALEM-21S instrument and EM inversion software. L. Degrad. Dev. 2018, 29, 1768–1781. [Google Scholar] [CrossRef]
- Khongnawang, T.; Zare, E.; Srihabun, P.; Khunthong, I.; Triantafilis, J. Digital soil mapping of soil salinity using EM38 and quasi-3d modelling software (EM4Soil). Soil Use Manag. 2022, 38, 277–291. [Google Scholar] [CrossRef]
- Huang, J.; Scudiero, E.; Clary, W.; Corwin, D.L.; Triantafilis, J. Time-lapse monitoring of soil water content using electromagnetic conductivity imaging. Soil Use Manag. 2017, 33, 191–204. [Google Scholar] [CrossRef]
- Dragonetti, G.; Comegna, A.; Ajeel, A.; Deidda, G.P.; Lamaddalena, N.; Rodriguez, G.; Vignoli, G.; Coppola, A. Calibrating electromagnetic induction conductivities with time-domain reflectometry measurements. Hydrol. Earth Syst. Sci. 2018, 22, 1509–1523. [Google Scholar] [CrossRef] [Green Version]
- Dragonetti, G.; Farzamian, M.; Basile, A.; Monteiro Santos, F.; Coppola, A. In situ estimation of soil hydraulic and hydrodispersive properties by inversion of electromagnetic induction measurements and soil hydrological modeling. Hydrol. Earth Syst. Sci. 2022, 26, 5119–5136. [Google Scholar] [CrossRef]
- Robinet, J.; von Hebel, C.; Govers, G.; van der Kruk, J.; Minella, J.P.G.; Schlesner, A.; Ameijeiras-Mariño, Y.; Vanderborght, J. Spatial variability of soil water content and soil electrical conductivity across scales derived from Electromagnetic Induction and Time Domain Reflectometry. Geoderma 2018, 314, 160–174. [Google Scholar] [CrossRef]
- Murad, M.O.F.; Minasny, B.; Bramley, H.; McBratney, A.B. Development of a crop water use monitoring system using electromagnetic induction survey. Soil Tillage Res. 2022, 223, 105451. [Google Scholar] [CrossRef]
- Doolittle, J.A.; Brevik, E.C. The use of electromagnetic induction techniques in soils studies. Geoderma 2014, 223, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Boaga, J.; Ghinassi, M.; D’Alpaos, A.; Deidda, G.P.; Rodriguez, G.; Cassiani, G. Geophysical investigations unravel the vestiges of ancient meandering channels and their dynamics in tidal landscapes. Sci. Rep. 2018, 8, 1708. [Google Scholar] [CrossRef] [Green Version]
- Beucher, A.; Koganti, T.; Iversen, B.V.; Greve, M.H. Mapping of Peat Thickness Using a Multi-Receiver Electromagnetic Induction Instrument. Remote Sens. 2020, 12, 2458. [Google Scholar] [CrossRef]
- Bellizia, E.; Tognin, D.; Boaga, J.; Cassiani, G.; Leardi, R.; Finotello, A.; D’alpaos, A.; Ghinassi, M. From electromagnetic to sediment textural maps: An integrated approach to unravel the intra-point-bar variability of sediment properties. J. Geol. Soc. 2022, 179. [Google Scholar] [CrossRef]
- Bonsall, J.; Fry, R.; Gaffney, C.; Armit, I.; Beck, A.; Gaffney, V. Assessment of the CMD Mini-Explorer, a New Low-frequency Multi-coil Electromagnetic Device, for Archaeological Investigations. Archaeol. Prospect. 2013, 20, 219–231. [Google Scholar] [CrossRef]
- Dabas, M.; Anest, A.; Thiesson, J.; Tabbagh, A. Slingram EMI Devices for Characterizing Resistive Features Using Apparent Conductivity Measurements: Check of the DualEM-421S Instrument and Field Tests. Archaeol. Prospect. 2016, 23, 165–180. [Google Scholar] [CrossRef] [Green Version]
- Deiana, R.; Vicenzutto, D.; Deidda, G.P.; Boaga, J.; Cupitò, M. Remote Sensing, Archaeological, and Geophysical Data to Study the Terramare Settlements: The Case Study of Fondo Paviani (Northern Italy). Remote Sens. 2020, 12, 2617. [Google Scholar] [CrossRef]
- Deiana, R.; Deidda, G.P.; Cusí, E.D.; van Dommelen, P.; Stiglitz, A. FDEM and ERT measurements for archaeological prospections at Nuraghe S’Urachi (West-Central Sardinia). Archaeol. Prospect. 2022, 29, 69–86. [Google Scholar] [CrossRef]
- Casas, A.; Castanyer, P.; Himi, M.; Lovera, R.; Rivero, L.; Santos, M.; Tremoleda, J.; Sendrós, A.; García-Artigas, R.; Urruela, A. Frequency Domain Electromagnetic mapping for delineating subsurface structures related to the historical port of Emporiae. Archaeol. Prospect. 2022, 29, 33–43. [Google Scholar] [CrossRef]
- Zhang, Z.; Oldenburg, D.W. Simultaneous reconstruction of 1-D susceptibility and conductivity from electromagnetic data. Geophysics 1999, 64, 33–47. [Google Scholar] [CrossRef]
- Huang, H.; Won, I.J. Conductivity and Susceptibility Mapping Using Broadband Electromagnetic Sensors. J. Environ. Eng. Geophys. 2000, 5, 31–41. [Google Scholar] [CrossRef]
- Simon, F.X.; Sarris, A.; Thiesson, J.; Tabbagh, A. Mapping of quadrature magnetic susceptibility/magnetic viscosity of soils by using multi-frequency EMI. J. Appl. Geophys. 2015, 120, 36–47. [Google Scholar] [CrossRef] [Green Version]
- Benech, C.; Lombard, P.; Rejiba, F.; Tabbagh, A. Demonstrating the contribution of dielectric permittivity to the in-phase EMI response of soils: Example from an archaeological site in Bahrain. Near Surf. Geophys. 2016, 14, 337–344. [Google Scholar] [CrossRef] [Green Version]
- Simon, F.X.; Tabbagh, A.; Donati, J.C.; Sarris, A. Permittivity mapping in the VLF–LF range using a multi-frequency EMI device: First tests in archaeological prospection. Near Surf. Geophys. 2019, 17, 27–41. [Google Scholar] [CrossRef] [Green Version]
- Knapp, R.W.; Steeples, D.W. High-resolution common-depth-point reflection profiling: Field acquisition parameter design. Geophysics 1986, 51, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Guérin, R.; Méhéni, Y.; Rakotondrasoa, G.; Tabbagh, A. Interpretation of slingram conductivity mapping in near-surface geophysics: Using a single parameter fitting with 1D model. Geophys. Prospect. 1996, 44, 233–249. [Google Scholar] [CrossRef]
- Cox, L.H.; Zhdanov, M.S. Advanced Computational Methods of Rapid and Rigorous 3-D Inversion of Airborne Electromagnetic Data. Commun. Comput. Phys. 2008, 3, 160–179. [Google Scholar]
- Yi, M.J.; Sasaki, Y. 2-D and 3-D joint inversion of loop–loop electromagnetic and electrical data for resistivity and magnetic susceptibility. Geophys. J. Int. 2015, 203, 1085–1095. [Google Scholar] [CrossRef] [Green Version]
- Thiesson, J.; Tabbagh, A.; Simon, F.X.; Dabas, M. 3D linear inversion of magnetic susceptibility data acquired by frequency domain EMI. J. Appl. Geophys. 2017, 136, 165–177. [Google Scholar] [CrossRef] [Green Version]
- Deidda, G.P.; Díaz de Alba, P.; Fenu, C.; Lovicu, G.; Rodriguez, G. FDEMtools: A MATLAB package for FDEM data inversion. Numer. Algorithms 2020, 84, 1313–1327. [Google Scholar] [CrossRef] [Green Version]
- Heagy, L.J.; Cockett, R.; Kang, S.; Rosenkjaer, G.K.; Oldenburg, D.W. A framework for simulation and inversion in electromagnetics. Comput. Geosci. 2017, 107, 1–19. [Google Scholar] [CrossRef]
- Elwaseif, M.; Robinson, J.; Day-Lewis, F.D.; Ntarlagiannis, D.; Slater, L.D.; Lane, J.W.; Minsley, B.J.; Schultz, G. A matlab-based frequency-domain electromagnetic inversion code (FEMIC) with graphical user interface. Comput. Geosci. 2017, 99, 61–71. [Google Scholar] [CrossRef] [Green Version]
- McLachlan, P.; Blanchy, G.; Binley, A. EMagPy: Open-source standalone software for processing, forward modeling and inversion of electromagnetic induction data. Comput. Geosci. 2021, 146, 104561. [Google Scholar] [CrossRef]
- EM4Soil. Available online: http://www.emtomo.com/products/em4soil (accessed on 13 March 2023).
- Aarhus Workbench Overview—Aarhus GeoSoftware. Available online: https://www.aarhusgeosoftware.dk/aarhus-workbench (accessed on 13 March 2023).
- Grant, F.S.; West, G.F. Interpretation Theory in Applied Geophysics, 1st ed.; McGraw-Hill Bool Co.: New York, NY, USA, 1965; ISBN 0070241007. [Google Scholar]
- Wait, J.R. Geo-Electromagnetism; Elsevier: New York, NY, USA, 1982. [Google Scholar]
- Ward, S.H.; Hohmann, G.W. Electromagnetic Theory for Geophysical Applications. In Electromagnetic Methods in Applied Geophysics; Nabighian, M.N., Ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 1988; pp. 130–311. [Google Scholar]
- Weaver, J.T. Mathematical Methods for Geo-Electromagnetic Induction; Wiley: New York, NY, USA, 1994; ISBN 086380165X, 0471944416. [Google Scholar]
- Ward, S.H. Part C—The Electromagnetic Method. In Mining Geophysics, Volume II—Theory; Hansen, D.A., MacDougall, R.E., Rogers, G.R., Suner, J.S., Ward, S.H., Eds.; Society of Exploration Geophysicists: Tulsa, OK, USA, 1967; pp. 224–372. [Google Scholar]
- Wait, J.R. Mutual coupling of loops lying on the ground. Geophysics 1954, 19, 290–296. [Google Scholar] [CrossRef]
- Wait, J.R. Mutual Electromagnetic Coupling of Loops Over a Homogeneous Ground. Geophysics 1955, 20, 630–637. [Google Scholar] [CrossRef]
- McNeill, J.D. Electromagnetic Terrain Conductivity Measurements at Low Induction Numbers; Geonics Limited: Mississauga, ON, Canada, 1980. [Google Scholar]
- Spies, B.R.; Eggers, D.E. The use and misuse of apparent resistivity in electromagnetic methods. Geophysics 1986, 51, 1462–1471. [Google Scholar] [CrossRef]
- Beamish, D. Low induction number, ground conductivity meters: A correction procedure in the absence of magnetic effects. J. Appl. Geophys. 2011, 75, 244–253. [Google Scholar] [CrossRef] [Green Version]
- GF Instruments. GF Instruments Short Guide for Electromagnetic Conductivity Mapping; GF Instruments: Brno, Czech Republic, 2020. [Google Scholar]
- Deidda, G.P.; Fenu, C.; Rodriguez, G. Regularized solution of a nonlinear problem in electromagnetic sounding. Inverse Probl. 2014, 30, 125014. [Google Scholar] [CrossRef] [Green Version]
- Deidda, G.P.; Díaz de Alba, P.; Rodriguez, G. Identifying the magnetic permeability in multi-frequency EM data inversion. Electron. Trans. Numer. Anal. 2017, 47, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Oldenburg, D.W.; Li, Y. Estimating depth of investigation in dc resistivity and IP surveys. Geophysics 1999, 64, 403–416. [Google Scholar] [CrossRef]
- Fitterman, D.V. Detectability levels for central induction transient soundings. Geophysics 1989, 54, 127–129. [Google Scholar] [CrossRef]
- Spies, B.R. Depth of investigation in electromagnetic sounding methods. Geophysics 1989, 54, 872–888. [Google Scholar] [CrossRef]
- Nabighian, M.N.; Macnae, J.C. Time Domain Electromagnetic Prospecting Methods. In Investigations in Geophysics, Electromagnetic Methods in Applied Geophysics, Volume 2, Application, Ptarts A and B; Nabighian, M.N., Ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 1991; pp. 427–520. [Google Scholar]
- Reid, J.E.; Macnae, J.C. Doubling the effective skin depth with a local source. Geophysics 1999, 64, 732–738. [Google Scholar] [CrossRef]
- Callegary, J.B.; Ferré, T.P.A.; Groom, R.W. Vertical Spatial Sensitivity and Exploration Depth of Low-Induction-Number Electromagnetic-Induction Instruments. Vadose Zo. J. 2007, 6, 158–167. [Google Scholar] [CrossRef]
- Morris, E.R. Height-above-ground effects on penetration depth and response of electromagnetic induction soil conductivity meters. Comput. Electron. Agric. 2009, 68, 150–156. [Google Scholar] [CrossRef]
- Saey, T.; Simpson, D.; Vermeersch, H.; Cockx, L.; Meirvenne, M. Van Comparing the EM38DD and DUALEM-21S Sensors for Depth-to-Clay Mapping. Soil Sci. Soc. Am. J. 2009, 73, 7–12. [Google Scholar] [CrossRef]
- Christiansen, A.V.; Auken, E. A global measure for depth of investigation. Geophysics 2012, 77, WB171–WB177. [Google Scholar] [CrossRef]
- Heil, K.; Schmidhalter, U. Comparison of the EM38 and EM38-MK2 electromagnetic induction-based sensors for spatial soil analysis at field scale. Comput. Electron. Agric. 2015, 110, 267–280. [Google Scholar] [CrossRef]
- Deidda, G.P.; Díaz de Alba, P.; Rodriguez, G.; Vignoli, G. Inversion of Multiconfiguration Complex EMI Data with Minimum Gradient Support Regularization: A Case Study. Math. Geosci. 2020, 52, 945–970. [Google Scholar] [CrossRef] [Green Version]
- Díaz de Alba, P.; Rodriguez, G. Regularized inversion of multi-frequency EM data in geophysical applications. In SEMA SIMAI Springer Series; Springer: Berlin/Heidelberg, Germany, 2016; Volume 8, pp. 357–369. [Google Scholar]
- Buccini, A.; Díaz De Alba, P. A variational non-linear constrained model for the inversion of FDEM data. Inverse Probl. 2021, 38, 014001. [Google Scholar] [CrossRef]
- Pes, F.; Rodriguez, G. The Minimal-Norm Gauss-Newton Method and Some of Its Regularized Variants. ETNA Electron. Trans. Numer. Anal. 2020, 53, 459–480. [Google Scholar] [CrossRef]
- Pes, F.; Rodriguez, G. A doubly relaxed minimal-norm Gauss–Newton method for underdetermined nonlinear least-squares problems. Appl. Numer. Math. 2022, 171, 233–248. [Google Scholar] [CrossRef]
- Hansen, P.C. Regularization Tools version 4.0 for Matlab 7.3. Numer. Algorithms 2007, 46, 189–194. [Google Scholar] [CrossRef]
- Anderson, W.L. Numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering. Geophysics 1979, 44, 1287–1305. [Google Scholar] [CrossRef]
- Reichel, L.; Rodriguez, G. Old and new parameter choice rules for discrete ill-posed problems. Numer. Algorithms 2012, 63, 65–87. [Google Scholar] [CrossRef]
- Deidda, G.P.; Bonomi, E.; Manzi, C. Inversion of electrical conductivity data with Tikhonov regularization approach: Some considerations. Ann. Geophys. 2003, 46, 549–558. [Google Scholar]
- Hendrickx, J.M.H.; Borchers, B.; Corwin, D.L.; Lesch, S.M.; Hilgendorf, A.C.; Schlue, J. Inversion of Soil Conductivity Profiles from Electromagnetic Induction Measurements. Soil Sci. Soc. Am. J. 2002, 66, 673–685. [Google Scholar] [CrossRef]
- Díaz de Alba, P.; Fermo, L.; van der Mee, C.; Rodriguez, G. Recovering the electrical conductivity of the soil via a linear integral model. J. Comput. Appl. Math. 2019, 352, 132–145. [Google Scholar] [CrossRef]
- Díaz de Alba, P.; Fermo, L.; Pes, F.; Rodriguez, G. Minimal-norm RKHS solution of an integral model in geo-electromagnetism. In Proceedings of the 2021 21st International Conference on Computational Science and Its Applications (ICCSA), Calgari, Italy, 13–16 September 2021; pp. 21–28. [Google Scholar] [CrossRef]
- Díaz de Alba, P.; Fermo, L.; Pes, F.; Rodriguez, G. Regularized minimal-norm solution of an overdetermined system of first kind integral equations. Numer. Algorithms 2023, 92, 471–502. [Google Scholar] [CrossRef]
- Huang, H.; Won, I.J. Real-time resistivity sounding using a hand-held broadband electromagnetic sensor. Geophysics 2003, 68, 1224–1231. [Google Scholar] [CrossRef]
- Abraham, J.D.; Deszcz-Pan, M.; Fitterman, D.V.; Burton, B.L. Use of a handheld broadband EM induction system for deriving resistivity depth images. In Proceedings of the 19th EEGS Symposium on the Application of Geophysics to Engineering and Environmental Problems; European Association of Geoscientists & Engineers, Seattle, WA, USA, 2–6 April 2006; p. cp-181-00175. [Google Scholar]
- Huang, H.; Fraser, D.C. Inversion of helicopter electromagnetic data to a magnetic conductive layered earth. Geophysics 2003, 68, 1211–1223. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Oldenburg, D.W.; Routh, P.S. Simultaneous 1D inversion of loop–loop electromagnetic data for magnetic susceptibility and electrical conductivity. Geophysics 2003, 68, 1857–1869. [Google Scholar] [CrossRef]





| Manufacturer | Device | Configuration | Frequency (kHz) | Coil Spacing (m) | Measurement * |
|---|---|---|---|---|---|
| Gf Instruments | CMD Mini-Explorer | HCP | 30 | 0.32, 0.71, 1.18 | Q (mS/m), P (ppt) |
| VCP | 30 | 0.32, 0.71, 1.18 | Q (mS/m), P (ppt) | ||
| CMD Explorer | HCP | 10 | 1.48, 2.82, 4.49 | Q (mS/m), P (ppt) | |
| VCP | 10 | 1.48, 2.82, 4.49 | Q (mS/m), P (ppt) | ||
| CMD DUO | HCP | 0.925 | 10, 20, 40 | Q (mS/m), P (ppt) | |
| VCP | 0.925 | 10, 20, 40 | Q (mS/m), P (ppt) | ||
| Dualem Inc. | Dualem-21 | HCP | 9 | 1, 2 | Q (mS/m), P (ppt) |
| PERP | 9 | 1.1, 2.1 | Q (mS/m), P (ppt) | ||
| Dualem-21H | HCP | 9 | 0.5, 1, 2 | Q (mS/m), P (ppt) | |
| PERP | 9 | 0.6, 1.1, 2.1 | Q (mS/m), P (ppt) | ||
| Dualem-421 | HCP | 9 | 1, 2, 4 | Q (mS/m), P (ppt) | |
| PERP | 9 | 1.1, 2.1, 4.1 | Q (mS/m), P (ppt) | ||
| Geonics Limited | EM38-MK2 | HCP | 14.5 | 0.5, 1 | Q (mS/m), P (ppt) |
| VCP | 14.5 | 0.5, 1 | Q (mS/m), P (ppt) | ||
| EM31-MK2 | HCP | 9.8 | 3.66 | Q (mS/m), P (ppt) | |
| VCP | 9.8 | 3.66 | Q (mS/m), P (ppt) | ||
| Geophex Ltd. | GEM-2 | HCP | 0.03–93 | 1.66 | Q (ppm), P (ppm) |
| VCP | 0.03–93 | 1.66 | Q (ppm), P (ppm) |
| Forward Model Routines | |
|---|---|
| aconduct | compute the apparent conductivity |
| hratio | compute the ratio HS/HP, i.e., the device readings |
| inphase | compute the in-phase (real) component of the ratio HS/HP |
| quadracomp | compute the quadrature (complex) component of HS/HP |
| reflfact | compute the reflection factor |
| Computational Routines | |
| emsolvenlsig | reconstruct the electrical conductivity |
| emsolvenlmu | reconstruct the magnetic permeability |
| tsvdnewt | Gauss–Newton method regularized by T(G)SVD |
| jack | approximate the Jacobian matrix by finite differences |
| hankelpts | quadrature nodes for Hankel transform; see [73] |
| hankelwts | quadrature weights for Hankel transform; see [73] |
| FDEM | general graphical user interface (GUI) |
| FDEMforward | GUI for forward modelling |
| FDEMinversion | GUI for data inversion |
| Test Scripts | |
| drawfigures | test program for plotting the Figures in Section 5 |
| driverforward | test program for analyzing the forward model |
| driver | test program for the inversion problem |
| driver2D | test program for 2D inversion |
| Auxiliary Routines | |
| addnoise | add noise to data |
| chooseparam | define default parameters and test functions |
| chooseparambis | define default parameters |
| cumulativeresp | compute the cumulative response |
| fdemcomp | main code for the inversion algorithm |
| fdemdoi | compute the depth of investigation (DOI); see [67] |
| fdemplot | plot the reconstructed solution and, if available, the exact one |
| fdemprint | print information about the whole process |
| fdemsimp | compute an integral by Simpson’s rule |
| forwardcomp | main code for the forward algorithm |
| mgsreg | compute the MGS regularization term; see [67] |
| morozov | choose regularization parameter by discrepancy principle |
| plotcumulative | display the cumulative response |
| plotforward | display intermediate results during forward modelling |
| plotresults | display intermediate results during inversion |
| plotsensfunc | display the sensitivity functions |
| quasihybrid | choose regularization parameter by quasi-hybrid method; see [74] |
| skindepth | compute the skin depth |
| sensitivityfunc | compute the sensitivity functions |
| Auxiliary Files | |
| FDEMdevices | GUI for managing the device database |
| dev.mat | data file containing the device database |
| information.pdf | file displayed by FDEMinversion |
| FDEMfwoutput.mat | data file produced by FDEMforward |
| FDEMoutput.mat | data file produced by FDEMinversion |
| Device | ρ (m) | f (Hz) | δ1 (m) | β1 | δ2 (m) | β2 |
|---|---|---|---|---|---|---|
| Dualem-21H 1 | 0.5 (0.6) | 9000 | 41.4 | 0.012 (0.015) | 8.8 | 0.057 (0.068) |
| 1 (1.1) | 9000 | 41.4 | 0.024 (0.027) | 8.8 | 0.113 (0.124) | |
| 2 (2.1) | 9000 | 41.4 | 0.048 (0.051) | 8.8 | 0.226 (0.237) | |
| CMD Explorer | 1.48 | 10,000 | 38.8 | 0.038 | 8.1 | 0.183 |
| 2.82 | 10,000 | 38.8 | 0.073 | 8.1 | 0.348 | |
| 4.49 | 10,000 | 38.8 | 0.116 | 8.1 | 0.554 | |
| GEM-2 | 1.66 | 1275 | 127.9 | 0.013 | 48.2 | 0.034 |
| 1.66 | 4250 | 64.9 | 0.026 | 16.9 | 0.098 | |
| 1.66 | 12,525 | 33.7 | 0.049 | 6.8 | 0.246 | |
| 1.66 | 28,725 | 19.6 | 0.085 | 3.9 | 0.427 | |
| 1.66 | 54,150 | 12.6 | 0.132 | 3.1 | 0.544 | |
| 1.66 | 82,150 | 9.3 | 0.179 | 2.8 | 0.592 |
| Model | Dualem-21H | CMD Explorer | GEM-2 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HCPρ1 | HCPρ2 | HCPρ3 | PERPρ1 | PERPρ2 | PERPρ3 | HCPρ1 | HCPρ2 | HCPρ3 | VCPρ1 | VCPρ2 | VCPρ3 | f1 | f2 | f3 | f4 | f5 | f6 | |
| M1 | 2.7 | 3.5 | 6.7 | 2.7 | 2.8 | 3.9 | 5.5 | 5.9 | 7.9 | 3.2 | 5.1 | 8.3 | 8.3 | 8.3 | 8.3 | 8.3 | 8.3 | 7.9 |
| M2 | 2.7 | 3.5 | 6.3 | 2.4 | 2.8 | 3.9 | 5.1 | 5.6 | 7.1 | 3.2 | 4.7 | 7.5 | 8.3 | 8.3 | 7.2 | 6.4 | 5.5 | 4.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deidda, G.P.; Díaz de Alba, P.; Pes, F.; Rodriguez, G. Forward Electromagnetic Induction Modelling in a Multilayered Half-Space: An Open-Source Software Tool. Remote Sens. 2023, 15, 1772. https://doi.org/10.3390/rs15071772
Deidda GP, Díaz de Alba P, Pes F, Rodriguez G. Forward Electromagnetic Induction Modelling in a Multilayered Half-Space: An Open-Source Software Tool. Remote Sensing. 2023; 15(7):1772. https://doi.org/10.3390/rs15071772
Chicago/Turabian StyleDeidda, Gian Piero, Patricia Díaz de Alba, Federica Pes, and Giuseppe Rodriguez. 2023. "Forward Electromagnetic Induction Modelling in a Multilayered Half-Space: An Open-Source Software Tool" Remote Sensing 15, no. 7: 1772. https://doi.org/10.3390/rs15071772
APA StyleDeidda, G. P., Díaz de Alba, P., Pes, F., & Rodriguez, G. (2023). Forward Electromagnetic Induction Modelling in a Multilayered Half-Space: An Open-Source Software Tool. Remote Sensing, 15(7), 1772. https://doi.org/10.3390/rs15071772







