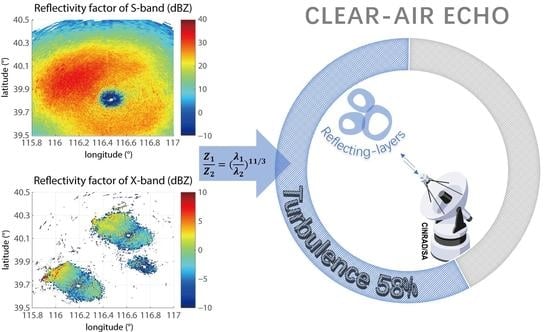
Turbulence: A Significant Role in Clear-Air Echoes of CINRAD/SA at Night
Abstract
:1. Introduction
2. Concepts and Theory
2.1. Dual-Polarization Radar Products
2.2. Turbulence
2.3. Bragg Scattering
2.4. Biological Scattering
3. Instruments and Data
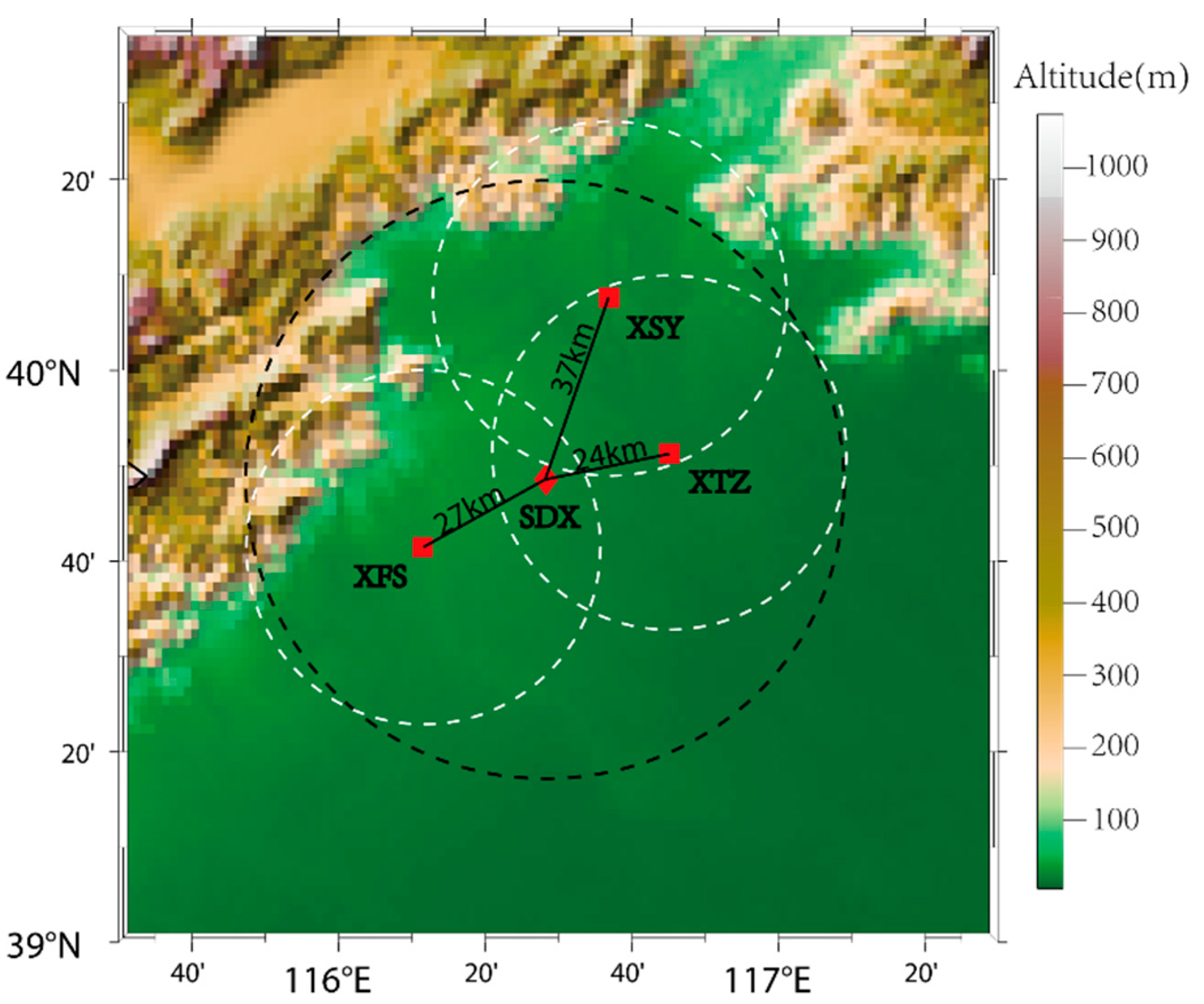
3.1. Instruments
3.2. Preprocessing
3.2.1. Threshold
3.2.2. Vertical Profiles
3.2.3. Dual-Wavelength Ratio
4. Results
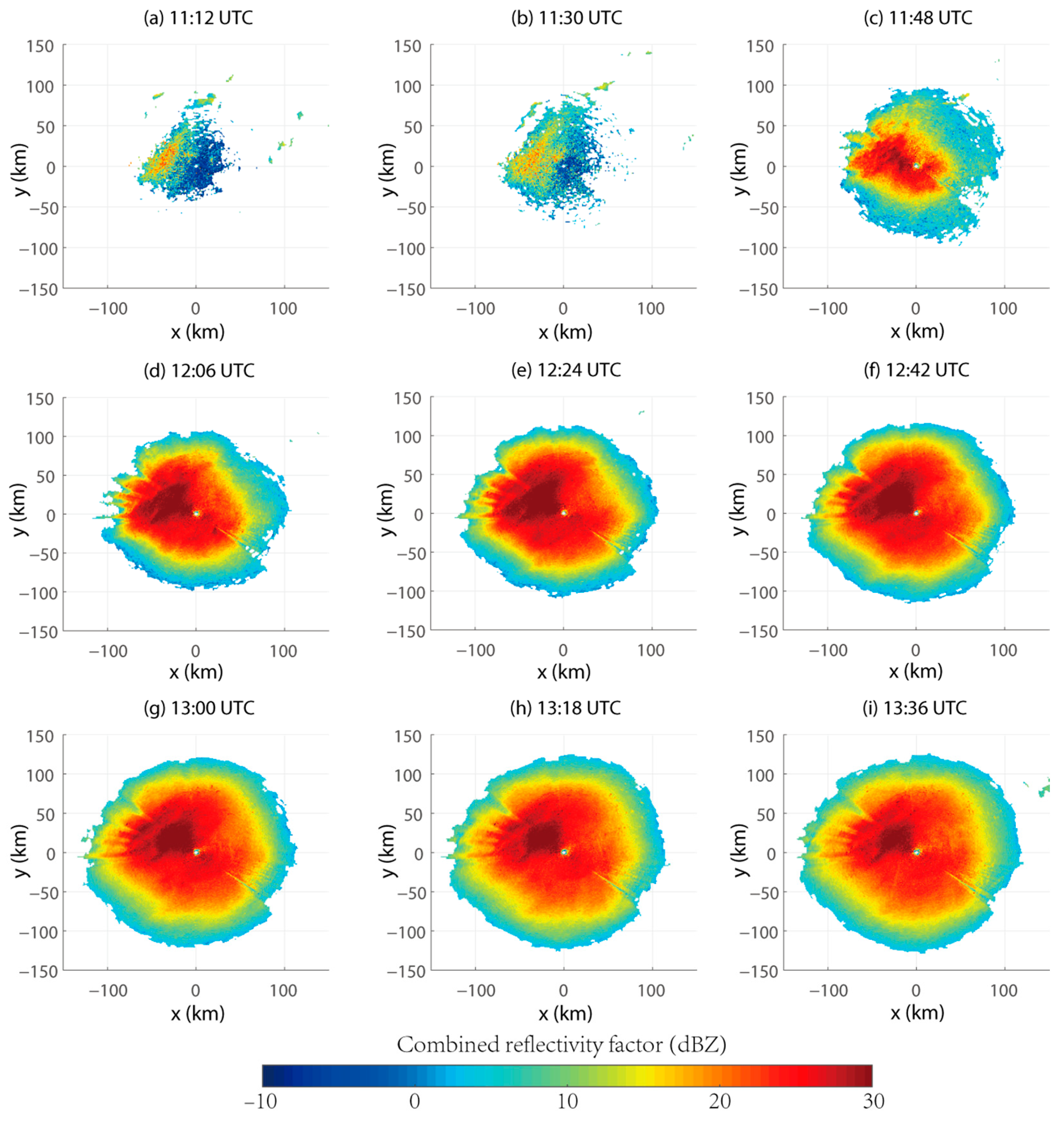
4.1. Plan Position Indicator
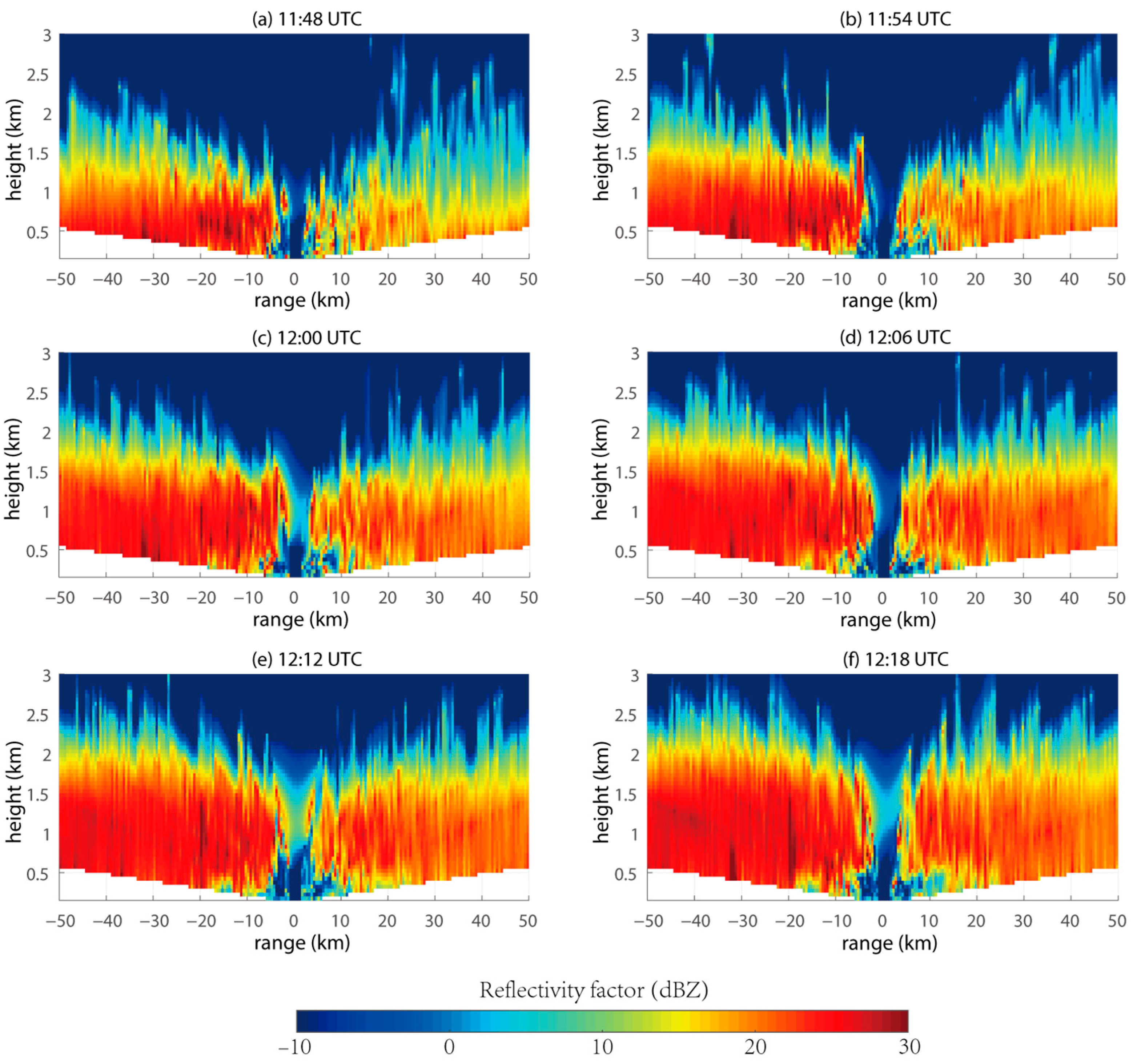
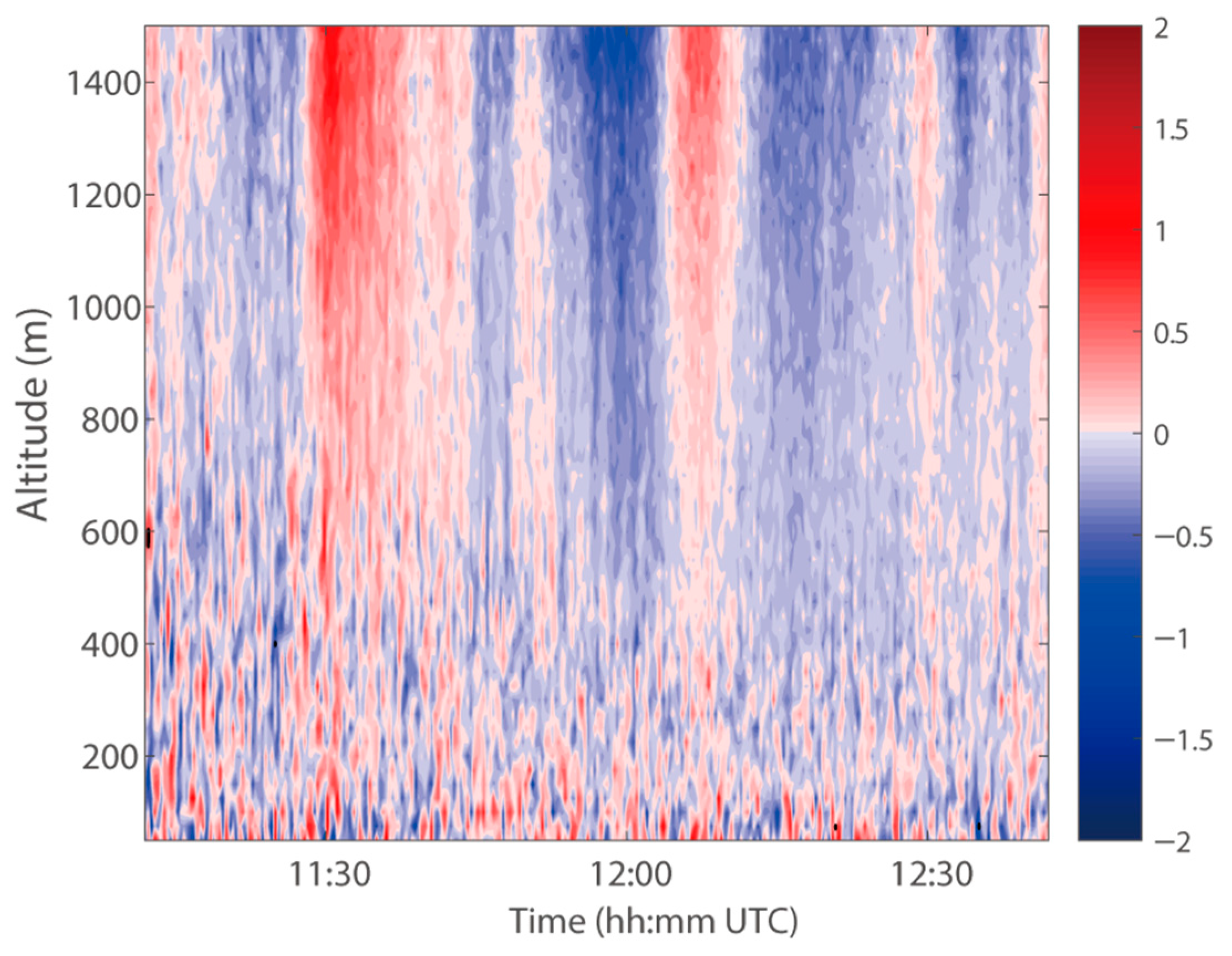
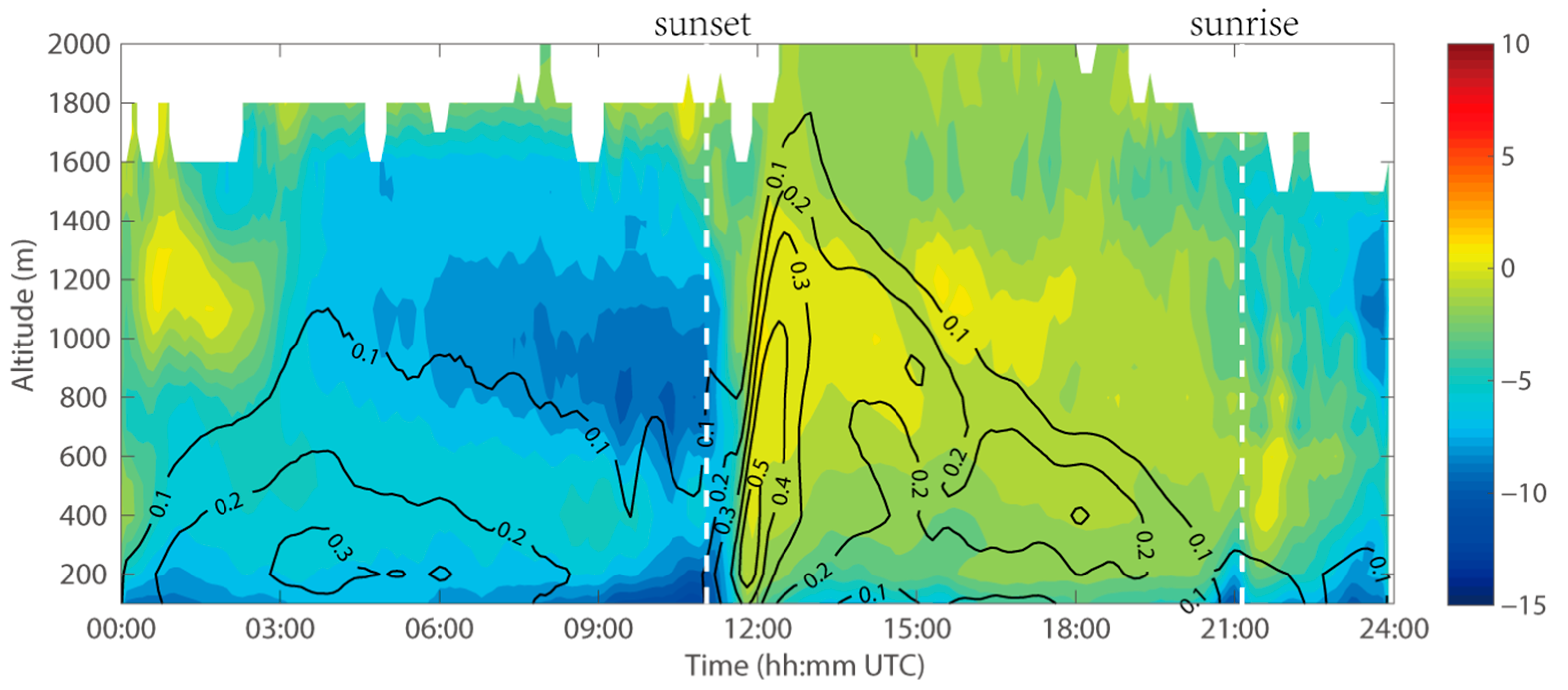
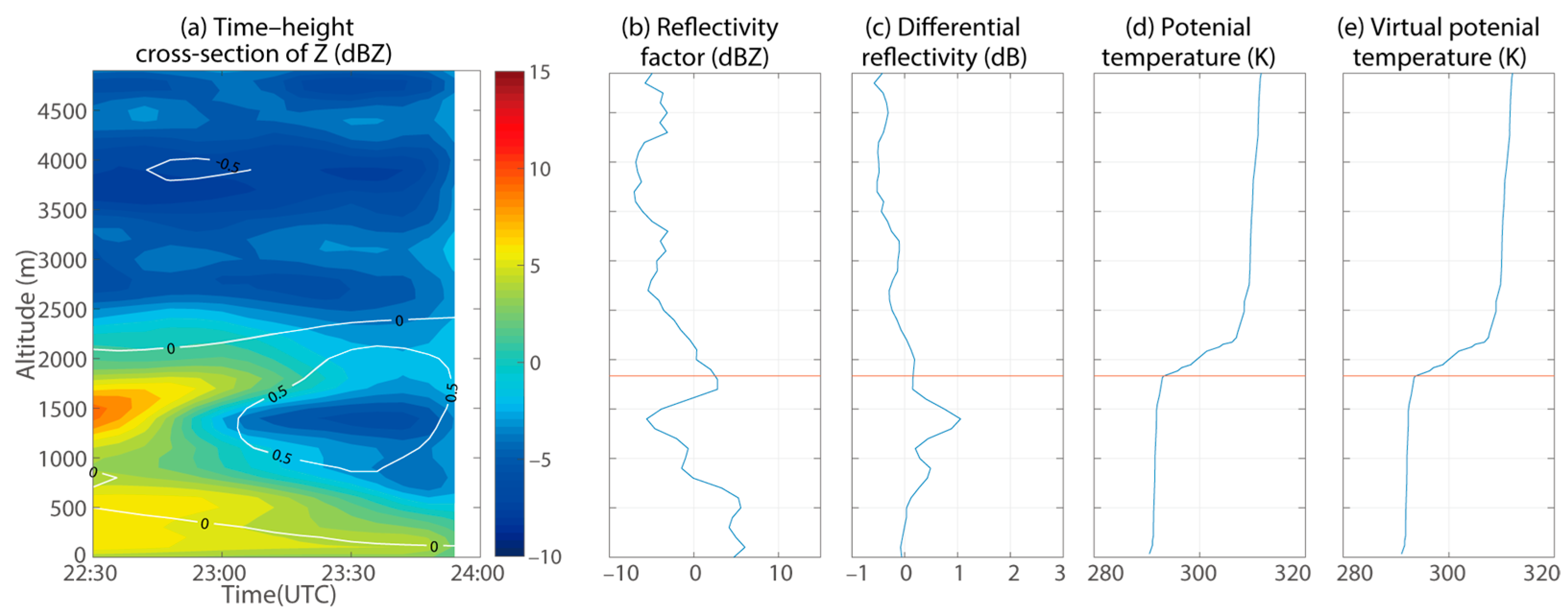
4.2. Time–Height Cross-Section
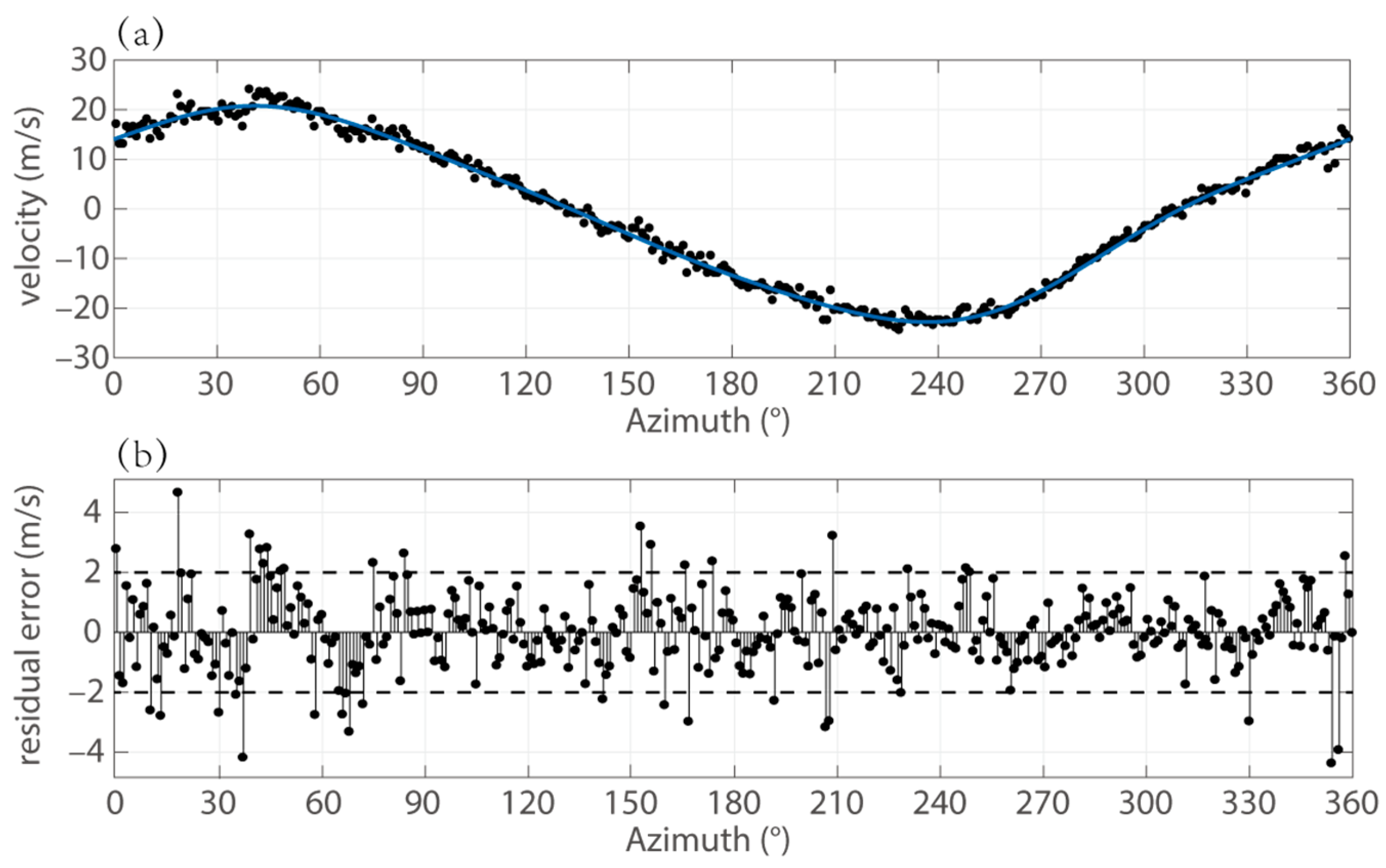
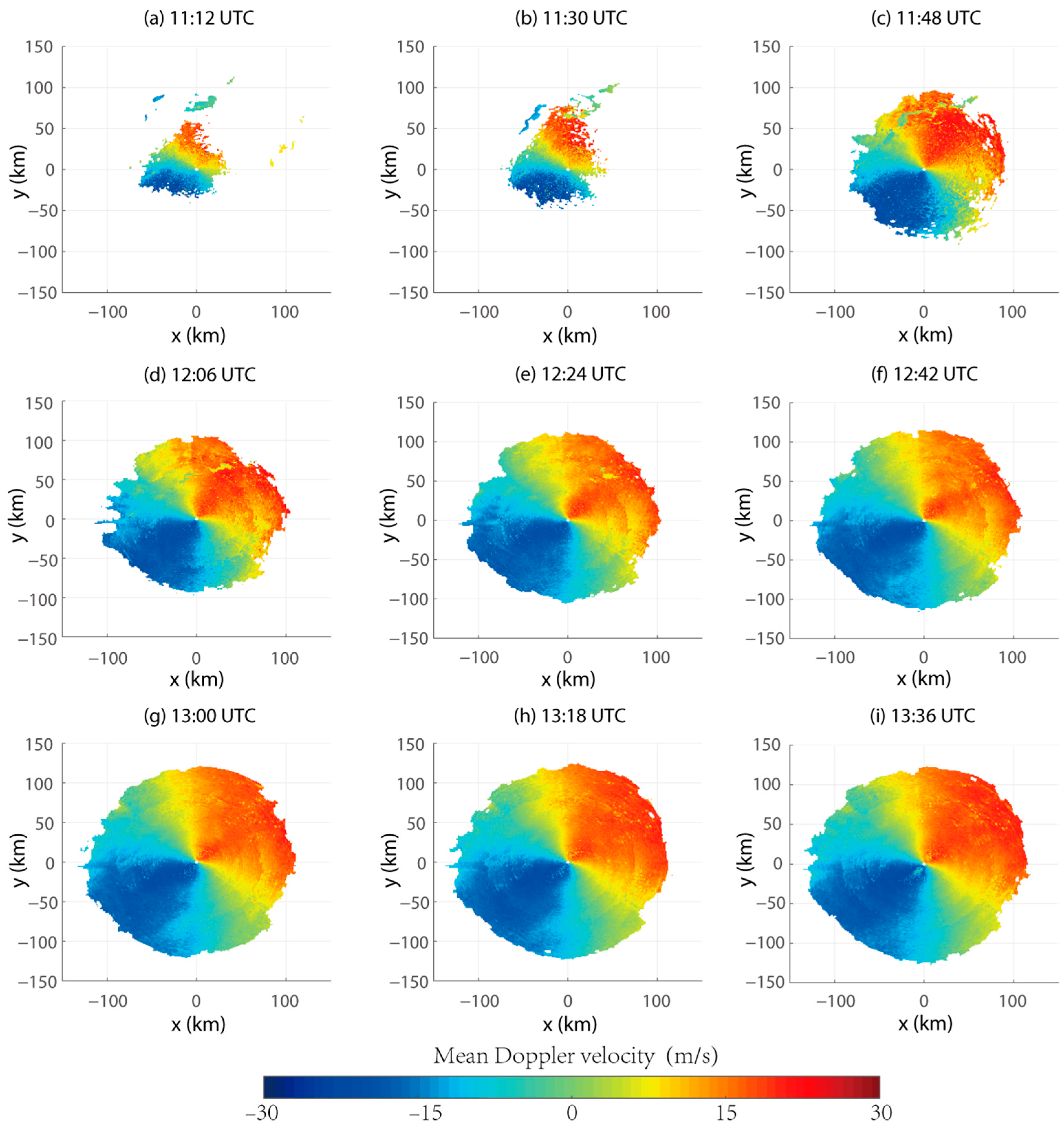
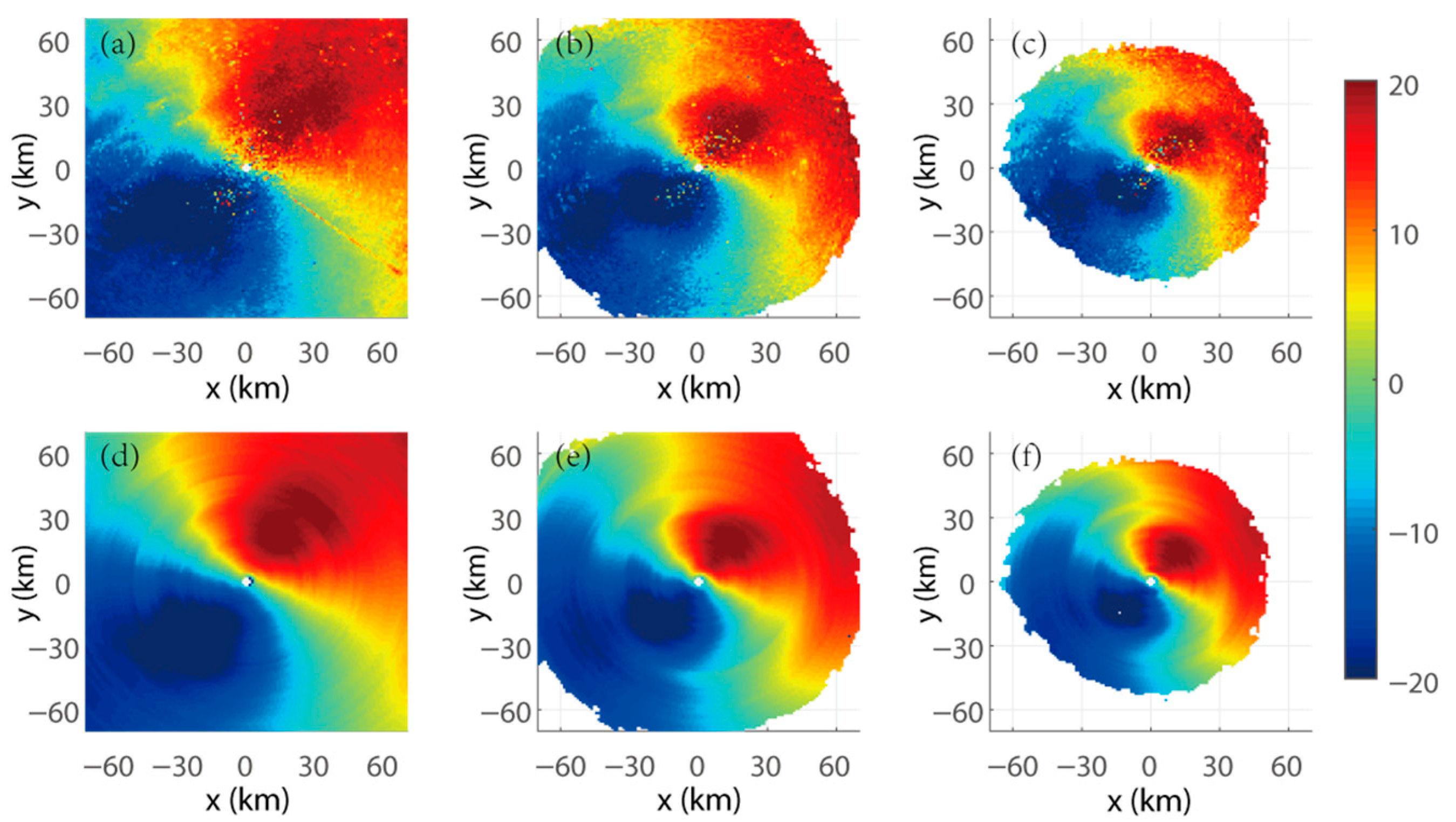
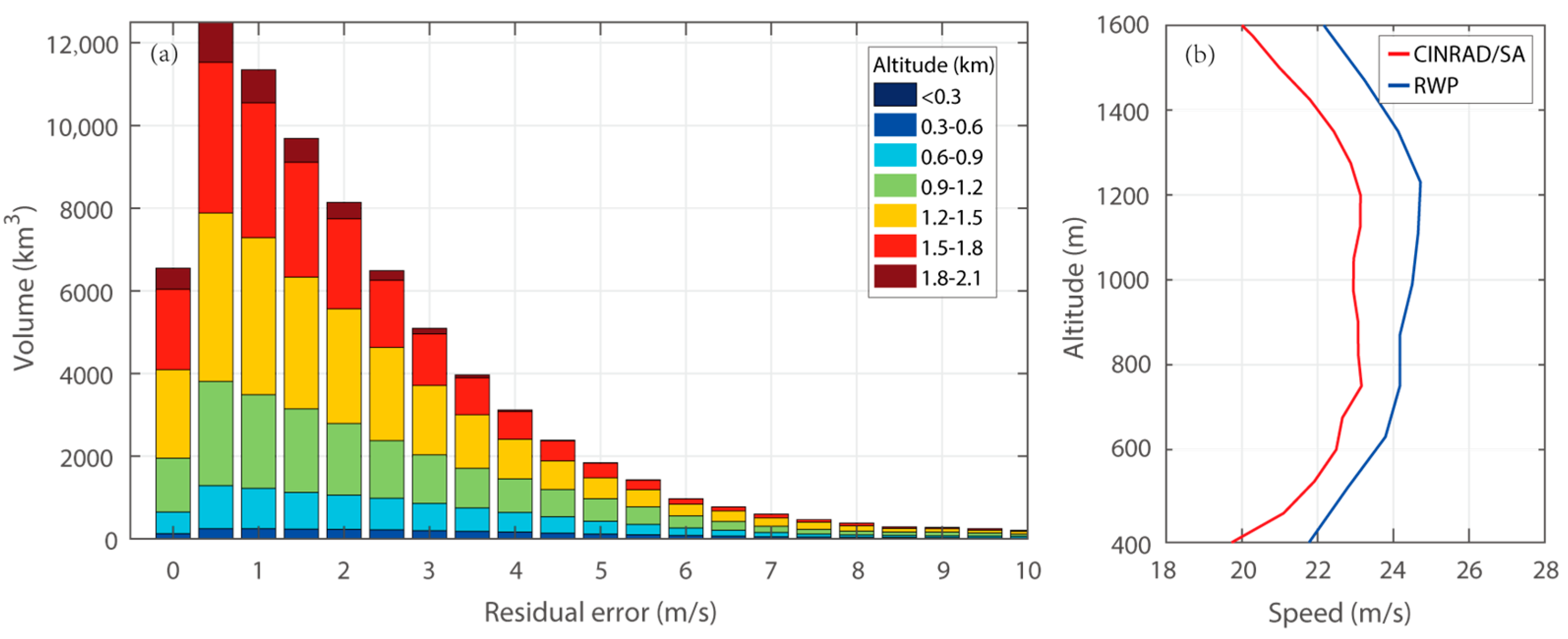
4.3. Velocity Analysis
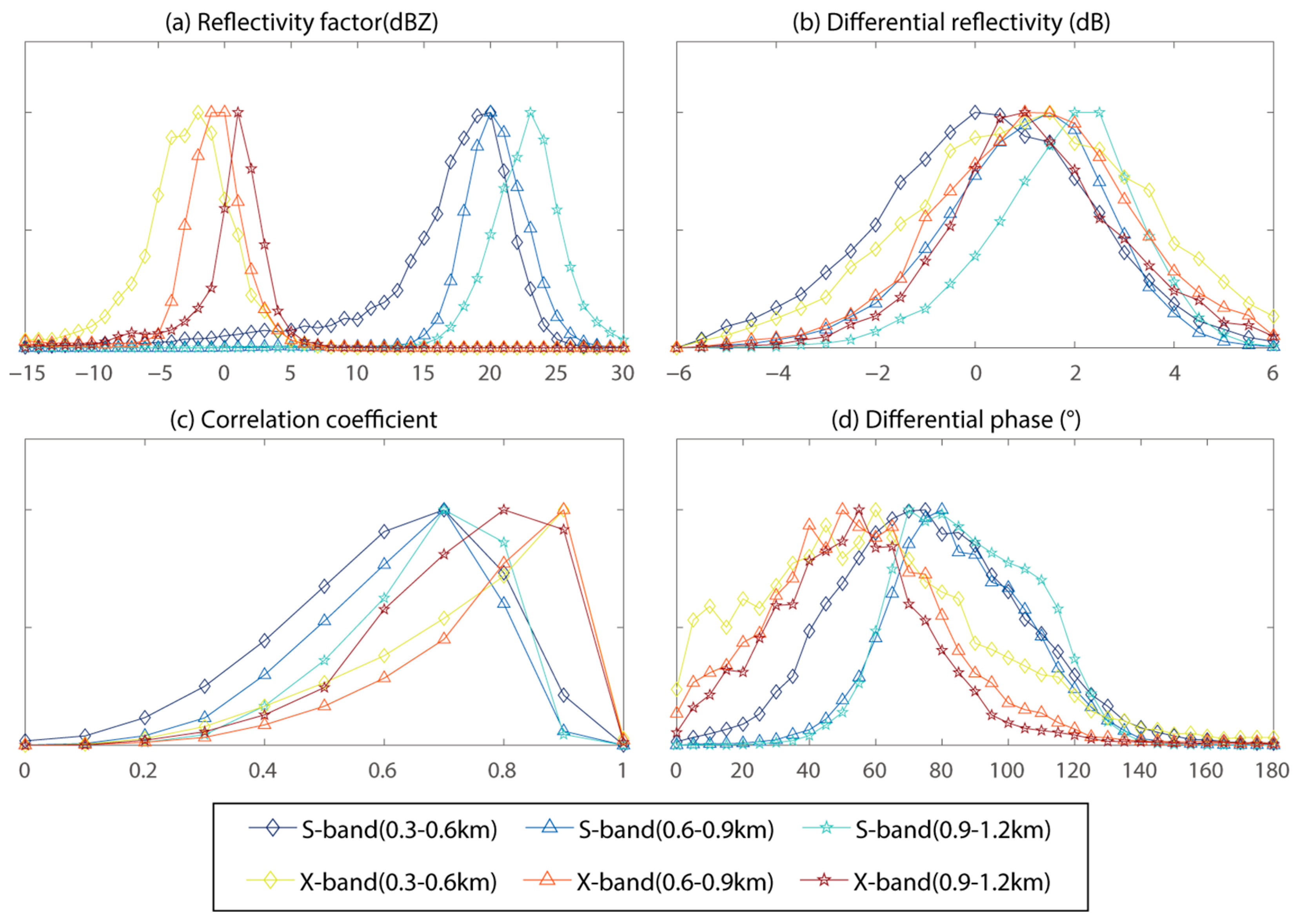
4.4. Comparison of the S-Band and X-Band
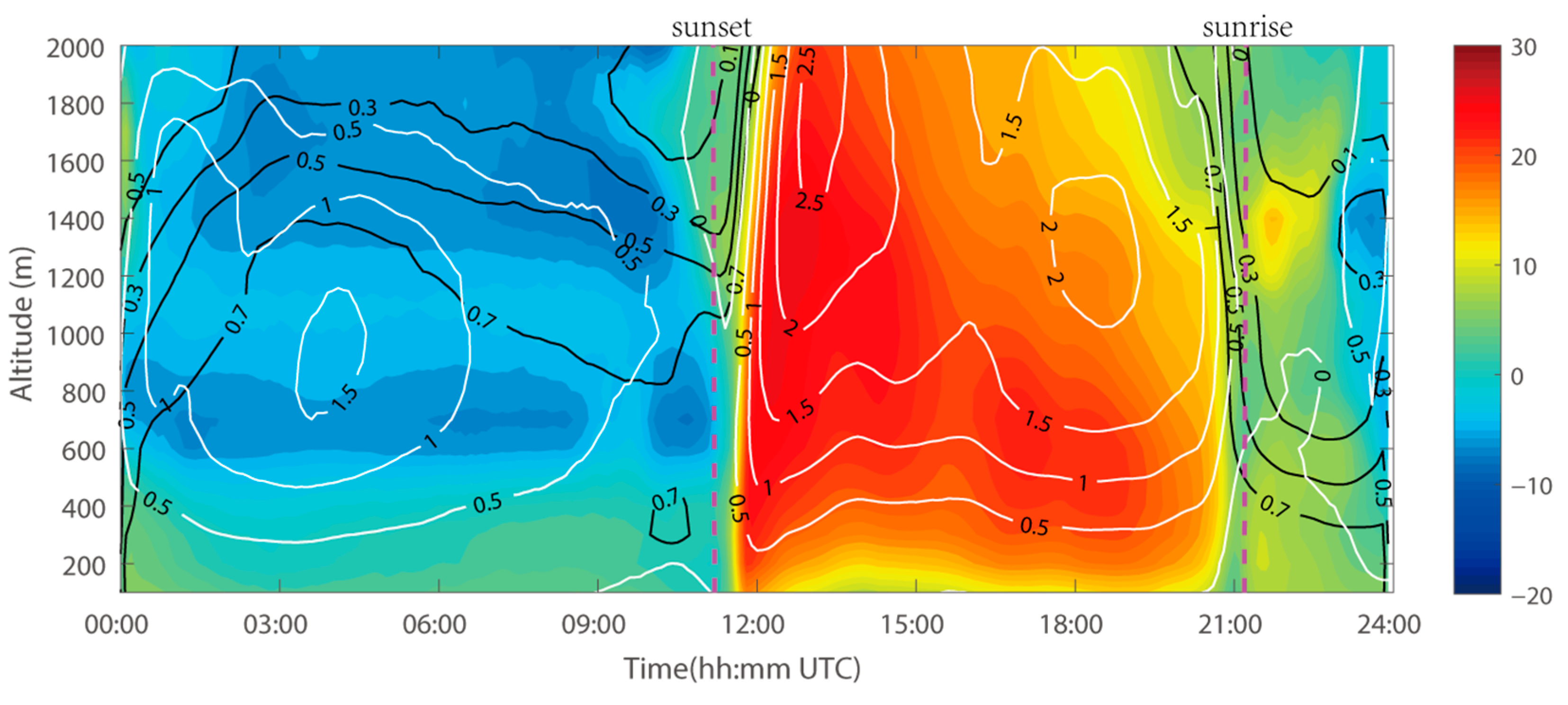
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Doren, B.M.; Horton, K.G. A continental system for forecasting bird migration. Science 2018, 361, 1115–1117. [Google Scholar] [CrossRef] [PubMed]
- Bruderer, B. The study of bird migration by radar part 1: The technical basis. Naturwissenschaften 1997, 84, 1–8. [Google Scholar] [CrossRef]
- Wilson, J.W.; Weckwerth, T.M.; Vivekanandan, J.; Wakimoto, R.M.; Russell, R.W. Boundary Layer Clear-Air Radar Echoes: Origin of Echoes and Accuracy of Derived Winds. J. Atmos. Ocean. Technol. 1994, 11, 1184–1206. [Google Scholar] [CrossRef]
- Martin, W.J.; Shapiro, A. Discrimination of bird and insect radar echoes in clear air using high-resolution radars. J. Atmos. Ocean. Technol. 2007, 24, 1215–1230. [Google Scholar] [CrossRef]
- Van den Broeke, M.S. Polarimetric Radar Observations of Biological Scatterers in Hurricanes Irene (2011) and Sandy (2012). J. Atmos. Ocean. Technol. 2013, 30, 2754–2767. [Google Scholar] [CrossRef] [Green Version]
- Westbrook, J.K.; Eyster, R.S.; Wolf, W.W. WSR-88D doppler radar detection of corn earworm moth migration. Int. J. Biometeorol. 2014, 58, 931–940. [Google Scholar] [CrossRef] [PubMed]
- Zrnic, D.S.; Ryzhkov, A.V. Observations of insects and birds with a polarimetric radar. IEEE Trans. Geosci. Remote Sens. 1998, 36, 661–668. [Google Scholar] [CrossRef]
- Ottersten, H. Atmospheric Structure and Radar Backscattering in Clear Air. Radio Sci. 1969, 4, 1179–1193. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Levin, V.; Hunt, J.C.R.; Phillips, O.M.; Williams, D. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Rep. AS USSR 1941, 434, 9–13. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B. Intermittent turbulence and fractal dimension: Kurtosis and the spectral exponent 5/3 + B. In Multifractals and 1/ƒ Noise: Wild Self-Affinity in Physics (1963–1976); Mandelbrot, B.B., Ed.; Springer: New York, NY, USA, 1976; pp. 389–415. [Google Scholar]
- Ringuet, E.; Rozé, C.; Gouesbet, G. Experimental observation of type-II intermittency in a hydrodynamic system. Phys. Rev. E 1993, 47, 1405–1407. [Google Scholar] [CrossRef] [PubMed]
- Batchelor, G.K.; Townsend, A.A.; Jeffreys, H. The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1949, 199, 238–255. [Google Scholar] [CrossRef]
- Pomeau, Y.; Manneville, P. Intermittent transition to turbulence in dissipative dynamical systems. Commun. Math. Phys. 1980, 74, 189–197. [Google Scholar] [CrossRef]
- Siggia, E.D. Numerical study of small-scale intermittency in three-dimensional turbulence. J. Fluid Mech. 1981, 107, 375–406. [Google Scholar] [CrossRef] [Green Version]
- Paladin, G.; Vulpiani, A. Anomalous scaling laws in multifractal objects. Phys. Rep. 1987, 156, 147–225. [Google Scholar] [CrossRef]
- Huang, Y.N.; Huang, Y.D. On the transition to turbulence in pipe flow. Phys. D Nonlinear Phenom. 1989, 37, 153–159. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. Interface dimension in intermittent turbulence. Phys. Rev. A 1990, 41, 2246–2248. [Google Scholar] [CrossRef]
- Vassilicos, J.C. Turbulence and intermittency. Nature 1995, 374, 408–409. [Google Scholar] [CrossRef]
- Benzi, R.; Biferale, L. Intermittency in Turbulence. In Theories of Turbulence; Oberlack, M., Busse, F.H., Eds.; Springer: Vienna, Austria, 2002; pp. 1–76. [Google Scholar]
- Jiménez, J. Intermittency in Turbulence. In Encyclopedia of Mathematical Physics; Françoise, J.-P., Naber, G.L., Tsun, T.S., Eds.; Academic Press: Oxford, UK, 2006; pp. 144–151. [Google Scholar]
- Belen’kii, M.S. Effect of the stratosphere on star image motion. Opt. Lett. 1995, 20, 1359–1361. [Google Scholar] [CrossRef]
- Korotkova, O.; Toselli, I. Non-Classic Atmospheric Optical Turbulence: Review. Appl. Sci. 2021, 11, 8487. [Google Scholar] [CrossRef]
- Rao, C.; Jiang, W.; Ling, N. Spatial and temporal characterization of phase fluctuations in non-Kolmogorov atmospheric turbulence. J. Mod. Opt. 2000, 47, 1111–1126. [Google Scholar] [CrossRef]
- Andrews, L.C. Free-space optical system performance for laser beam propagation through non-Kolmogorov turbulence. Opt. Eng. 2008, 47, 026003. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhu, W.; Wu, X.; Rao, R. Equivalent refractive-index structure constant of non-Kolmogorov turbulence. Opt. Express 2015, 23, 23004–23012. [Google Scholar] [CrossRef]
- Ruizhong, R.; Yujie, L. Light Propagation through Non-Kolmogorov-Type Atmospheric Turbulence and Its Effects on Optical Engineering. Acta Opt. Sin. 2015, 35, 0501003. [Google Scholar] [CrossRef]
- Yang, H.; Fang, Z.; Li, C.; Deng, X.; Xing, K.; Xie, C. Atmospheric Optical Turbulence Profile Measurement and Model Improvement over Arid and Semi-arid regions. Atmos. Meas. Tech. Discuss. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Richardson, L.M.; Cunningham, J.G.; Zittel, W.D.; Lee, R.R.; Ice, R.L.; Melnikov, V.M.; Hoban, N.P.; Gebauer, J.G. Bragg Scatter Detection by the WSR-88D. Part I: Algorithm Development. J. Atmos. Ocean. Technol. 2017, 34, 465–478. [Google Scholar] [CrossRef]
- Villars, F.; Weisskopf, V.F. The scattering of electromagnetic waves by turbulent atmospheric fluctuations. Phys. Rev. 1954, 94, 232–240. [Google Scholar] [CrossRef]
- Stepanian, P.M.; Horton, K.G.; Melnikov, V.M.; Zrnic, D.S.; Gauthreaux, S.A. Dual-polarization radar products for biological applications. Ecosphere 2016, 7, 27. [Google Scholar] [CrossRef]
- Park, H.S.; Ryzhkov, A.V.; Zrnić, D.S.; Kim, K.-E. The Hydrometeor Classification Algorithm for the Polarimetric WSR-88D: Description and Application to an MCS. Weather Forecast. 2009, 24, 730–748. [Google Scholar] [CrossRef] [Green Version]
- Kilambi, A.; Fabry, F.; Meunier, V. A Simple and Effective Method for Separating Meteorological from Nonmeteorological Targets Using Dual-Polarization Data. J. Atmos. Ocean. Technol. 2018, 35, 1415–1424. [Google Scholar] [CrossRef]
- Koistinen, J. Bird migration patterns on weather radars. Phys. Chem. Earth Pt B-Hydrol. Ocean. Atmos. 2000, 25, 1185–1193. [Google Scholar] [CrossRef]
- Hu, C.; Fang, L.; Wang, R.; Zhou, C.; Li, W.; Zhang, F.; Lang, T.; Long, T. Analysis of Insect RCS Characteristics. J. Electron. Inf. Technol. 2020, 42, 140–153. [Google Scholar]
- Wang, C.; Wu, C.; Liu, L.; Liu, X.; Chen, C. Integrated Correction Algorithm for X Band Dual-Polarization Radar Reflectivity Based on CINRAD/SA Radar. Atmosphere 2020, 11, 119. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zou, Q.; Han, J.; Cluckie, I. Cinrad data quality control and precipitation estimation. Proc. Inst. Civ. Eng.—Water Manag. 2009, 162, 95–105. [Google Scholar] [CrossRef]
- Vignal, B.; Andrieu, H.; Creutin, J.D. Identification of Vertical Profiles of Reflectivity from Volume Scan Radar Data. J. Appl. Meteorol. 1999, 38, 1214–1228. [Google Scholar] [CrossRef]
- Joss, J.; Lee, R. The Application of Radar Gauge Comparisons to Operational Precipitation Profile Corrections. J. Appl. Meteorol. 1995, 34, 2612–2630. [Google Scholar] [CrossRef]
- Joss, J.; Waldvogel, A.; Collier, C.G. Precipitation Measurement and Hydrology. In Radar in Meteorology: Battan Memorial and 40th Anniversary Radar Meteorology Conference; Atlas, D., Ed.; American Meteorological Society: Boston, MA, USA, 1990; pp. 577–606. [Google Scholar]
- Cuihong, W.; Yufa, W.; Tao, W.; Hongxiang, J. Vertical Profile of Radar Echo and Its Deteermination Methods. J. Appl. Meteorol. Sci. 2006, 17, 232–239. [Google Scholar]
- Melnikov, V.M.; Istok, M.J.; Westbrook, J.K. Asymmetric Radar Echo Patterns from Insects. J. Atmos. Ocean. Technol. 2015, 32, 659–674. [Google Scholar] [CrossRef]
- Farisenkov, S.E.; Kolomenskiy, D.; Petrov, P.N.; Engels, T.; Lapina, N.A.; Lehmann, F.O.; Onishi, R.; Liu, H.; Polilov, A.A. Novel flight style and light wings boost flight performance of tiny beetles. Nature 2022, 602, 96–100. [Google Scholar] [CrossRef]
- Xingfu, J. The Physiological and Genetic Characteristics of Migratory Behavior and Genetic Diversity, as Determined by AFLP in the Oriental Armyworm, Mythimna Separata (Walker). Ph.D. Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2004. [Google Scholar]
- Holleman, I.; van Gasteren, H.; Bouten, W. Quality Assessment of Weather Radar Wind Profiles during Bird Migration. J. Atmos. Ocean. Technol. 2008, 25, 2188–2198. [Google Scholar] [CrossRef] [Green Version]
- Dokter, A.M.; Liechti, F.; Stark, H.; Delobbe, L.; Tabary, P.; Holleman, I. Bird migration flight altitudes studied by a network of operational weather radars. J. R. Soc. Interface 2011, 8, 30–43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pei, L.; Qiu, C. The assessment of velocity azimuth display technique of doppler weather radar. J. Trop. Meteorol. 2013, 29, 597–606. [Google Scholar]
- Benedict, L.H.; Gould, R.D. Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 1996, 22, 129–136. [Google Scholar] [CrossRef]
- Moraghan, A.; Kim, J.; Yoon, S.-J. Density distributions of outflow-driven turbulence. Mon. Not. R. Astron. Soc. Lett. 2013, 432, L80–L84. [Google Scholar] [CrossRef] [Green Version]
- Cael, B.B.; Mashayek, A. Log-Skew-Normality of Ocean Turbulence. Phys. Rev. Lett. 2021, 126, 224502. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, X.; Wu, L.; Mu, T.; Yu, F.; Kearsley, L.; Liang, X.; Fu, J.; Hou, X.; Peng, P.; et al. A 30,000-km journey by Apus apus pekinensis tracks arid lands between northern China and south-western Africa. Mov. Ecol. 2022, 10, 29. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Y.; Liu, Y. Using light-level geolocations to monitor incubation behaviour of a cavity-nesting bird Apus apus pekinensis. Avian Res. 2021, 12, 9. [Google Scholar] [CrossRef]
- Li, L.; Wu, Z.S.; Lin, L.K.; Zhang, R.; Zhao, Z.W. Study on the Prediction of Troposcatter Transmission Loss. IEEE Trans. Antennas Propag. 2016, 64, 1071–1079. [Google Scholar] [CrossRef]
- Zhang, M.G. Tropospheric Scatter Propagation; Publishing House of Electronics Industry: Beijing, China, 2004; Volume 10. [Google Scholar]
- Bullington, K. Reflections from an exponential atmosphere. Bell Syst. Tech. J. 1963, 42, 2849–2867. [Google Scholar] [CrossRef]
- Zoumakis, N.M. On the relationship between the gradient and the bulk Richardson number for the atmospheric surface layer. Il Nuovo Cim. C 1992, 15, 111–114. [Google Scholar] [CrossRef]
- Ren, G.; Liu, J.; Wan, J.; Li, F.; Guo, Y.; Yu, D. The analysis of turbulence intensity based on wind speed data in onshore wind farms. Renew. Energy 2018, 123, 756–766. [Google Scholar] [CrossRef]
- Day, J.P.; Trolese, L.G. Propagation of Short Radio Waves over Desert Terrain. Proc. IRE 1950, 38, 165–175. [Google Scholar] [CrossRef]
- Katzin, M.; Bauchman, R.W.; Binnian, W. 3- and 9-Centimeter Propagation in Low Ocean Ducts. Proc. IRE 1947, 35, 891–905. [Google Scholar] [CrossRef]
- Melnikov, V.; Zrnić, D.S. Observations of Convective Thermals with Weather Radar. J. Atmos. Ocean. Technol. 2017, 34, 1585–1590. [Google Scholar] [CrossRef]
- Melnikov, V.M.; Doviak, R.J.; Zrnić, D.S.; Stensrud, D.J. Structures of Bragg Scatter Observed with the Polarimetric WSR-88D. J. Atmos. Ocean. Technol. 2013, 30, 1253–1258. [Google Scholar] [CrossRef]
- Richardson, L.M.; Zittel, W.D.; Lee, R.R.; Melnikov, V.M.; Ice, R.L.; Cunningham, J.G. Bragg Scatter Detection by the WSR-88D. Part II: Assessment of Z(DR) Bias Estimation. J. Atmos. Ocean. Technol. 2017, 34, 479–493. [Google Scholar] [CrossRef]
- Banghoff, J.R.; Stensrud, D.J.; Kumjian, M.R. Convective Boundary Layer Depth Estimation from S-Band Dual-Polarization Radar. J. Atmos. Ocean. Technol. 2018, 35, 1723–1733. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Hufford, G.L.; Kelley, H.L.; Sparkman, W.; Moore, R.K. Use of Real-Time Multisatellite and Radar Data to Support Forest Fire Management. Weather Forecast. 1998, 13, 592–605. [Google Scholar] [CrossRef]
- Melnikov, V.M.; Zrnic, D.S.; Rabin, R.M.; Zhang, P. Radar polarimetric signatures of fire plumes in Oklahoma. Geophys. Res. Lett. 2008, 35, L14815. [Google Scholar] [CrossRef]
- Zhang, G.; Doviak, R.; Palmer, R. Bistatic interferometry to measure clear air wind. In Proceedings of the 32nd Conference on Radar Meteorology, Albuquerque, NM, USA, 24–29 October 2005. [Google Scholar]

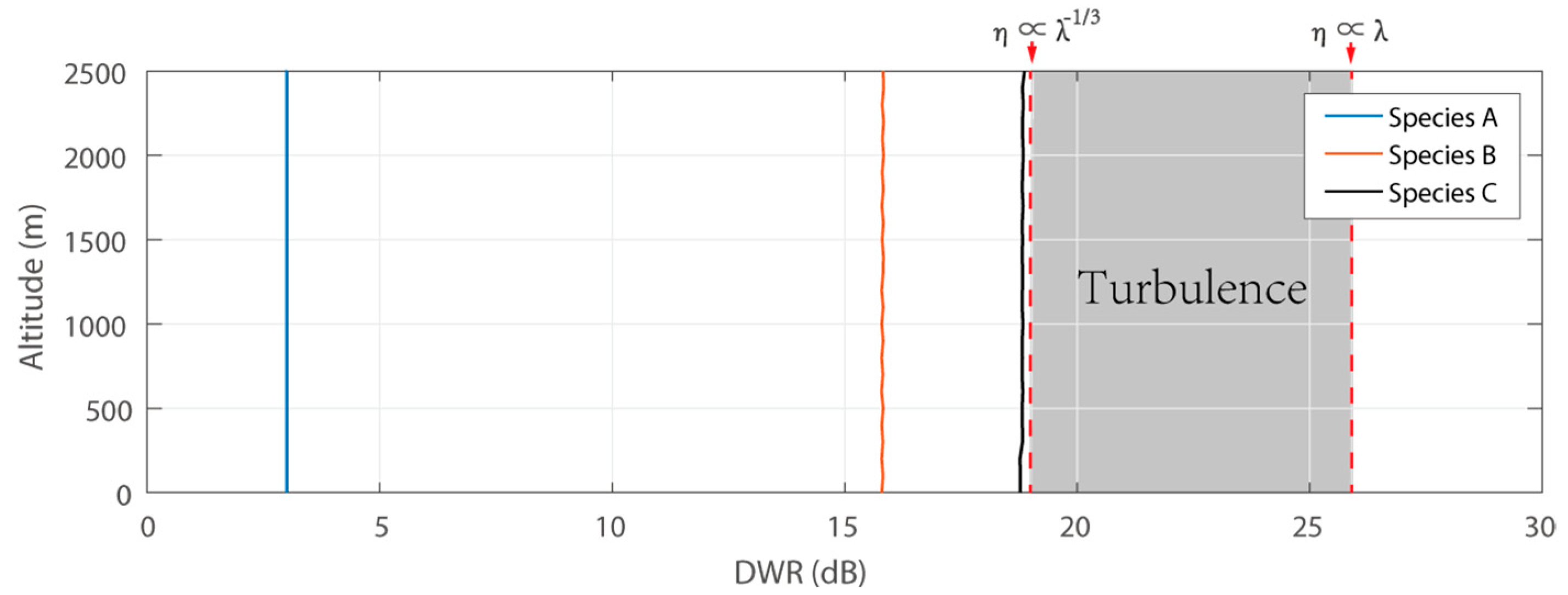



| Species | Average Weight (mg) | Average Length (mm) | Average Width (mm) | RCS of S-Band (dBsm) | RCS of X-Band (dBsm) |
|---|---|---|---|---|---|
| Conogethes punctiferalis, Hawaiian beet webworm, Athetis lepigone | 22.1 | 13.0 | 3.2 | −52.5 | −25.0 |
| Cotton bollworms, Plusia agnata | 114.8 | 16.7 | 5.4 | −39.8 | −34.2 |
| Armyworms, Black cutworms, Sprodoptera litura | 145.4 | 19.0 | 5.8 | −36.2 | −33.8 |
| Parameter | CINRAD/SA Radar | X-POL Radars |
|---|---|---|
| Frequency | 2700–3000 MHz | 9300–9500 MHz |
| Antenna cover diameter | 11.9 m | ≥4 m |
| Polarization | Linear H and V | Linear H and V |
| Volume coverage patterns | VCP 21 | VCP 21 |
| Time of VCP 21 | 6 min | 3 min |
| Range resolution | 250 m | 75 m |
| Minimum detectable reflectivity | −7.5 dBZ @ 50 km | 5 dBZ @ 60 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, Y.; Li, T.; Ma, S.; Chen, H. Turbulence: A Significant Role in Clear-Air Echoes of CINRAD/SA at Night. Remote Sens. 2023, 15, 1781. https://doi.org/10.3390/rs15071781
Teng Y, Li T, Ma S, Chen H. Turbulence: A Significant Role in Clear-Air Echoes of CINRAD/SA at Night. Remote Sensing. 2023; 15(7):1781. https://doi.org/10.3390/rs15071781
Chicago/Turabian StyleTeng, Yupeng, Tianyan Li, Shuqing Ma, and Hongbin Chen. 2023. "Turbulence: A Significant Role in Clear-Air Echoes of CINRAD/SA at Night" Remote Sensing 15, no. 7: 1781. https://doi.org/10.3390/rs15071781
APA StyleTeng, Y., Li, T., Ma, S., & Chen, H. (2023). Turbulence: A Significant Role in Clear-Air Echoes of CINRAD/SA at Night. Remote Sensing, 15(7), 1781. https://doi.org/10.3390/rs15071781