Abstract
Due to space environment interference, imperfect data processing model, and the performance of atomic clocks, real-time satellite clock products often contain outliers or irregular biases. We propose a real-time linear moving short-term prediction algorithm to predict clock offsets and detect abnormalities. The proposed algorithm mainly includes phase/frequency anomaly detection and real-time prediction part. Both the phase and frequency domains are used to detect abnormal clock offsets with previous epochs for building the clock prediction model accurately. The real-time moving prediction module utilizes the high short-term prediction performance to check the clock abnormality. The performance of the algorithm is then evaluated for all satellites with real-time estimated satellite clock offsets. To verify the feasibility and effectiveness of the proposed linear moving model and algorithm, the results of the grey model GM(1,1) and the ARIMA model are also compared. The experimental results indicated that the algorithm can detect clock outliers, frequency modulation, and phase jumps, and the linear model has a better clock performance improvement. After the abnormalities are removed with the proposed algorithm, the average STD accuracy of the real-time clock offsets for all satellites is improved by 15.5%, compared to an improvement of 11.4% by the GM(1,1) model and 11.5% by the ARIMA model. The PPP results demonstrate that the proposed clock prediction algorithm improves the positioning accuracy by 8.1%, 13.3%, and 16.9% in the east, north, and up components, respectively.
1. Introduction
With the completion of the networking of the Chinese Beidou satellite navigation system (BDS), positioning navigation and timing (PNT) technology has been increasingly applied in many fields [1,2]. Some scholars demonstrate that satellite clock offset is one of the core products of this technology, and some scholars provide effective data for evaluating the performance of onboard satellite atomic clocks [3,4]. The effective and reliable clock offset product is a prerequisite for clock offset prediction and atomic clock performance evaluation and the key to achieving high-precision positioning [5,6,7]. However, other scholars point out that owing to various uncertain factors, such as the clock estimation strategy, poor precision of the satellite orbit products [8], the performance of the atomic clock, and the influence of the space environment, the estimated clock data often contain outliers or irregular biases, which will have a serious impact on the Precise Point Position (PPP) and other applications. Therefore, it is necessary to deal with abnormal clock offsets.
Common methods to detect these abnormal values can be divided into two categories. The first category is the direct detection method. Some scholars [9,10] proposed the Bayesian, median, Allan, and other expansion methods to detect outliers. Other scholars develop the second category, including indirect detection methods, by establishing suitable clock offset models based on the data and using prediction models to detect abnormal values, such as the semi-parametric mean-shift model [11,12], an autoregressive moving average model (ARIMA) [13,14], outlier repair model based on the convolutional neural network [15,16], and other clock offset prediction models [17,18,19]. Some methods with clock offset models to detect outliers have gradually been recognized by most scholars. However, there are also many defects among the above methods. For example, although the median method is simple and convenient, it is not sensitive to small gross offsets. The Bayesian method is cumbersome in the iterative update weight process. The ARIMA model can deal with the phase outlier with frequency data, but it needs to go through a complicated sampling process and multiple iterations. GM(1,1) is a method to get the approximate exponential law from the original data, but it is only suitable for short-and medium-term forecasting or for forecasting the approximate exponential growth [20]. The convolutional neural network model needs to convert the data into an image first to identify and deal with outliers, and it must extract training samples. Generally, the second type of detection method has better recognition and processing of outliers than the first, but there are also a series of problems, such as cumbersome processes and easy misjudgments. At present, these existing methods are not sufficient to recognize and deal with abnormal real-time BDS clock offsets since most of the above methods for detecting outliers are based on post-processed products rather than real-time BDS clock offsets. Besides, validation experiments often artificially introduce phase disturbances and then detect them according to their respective proposed models.
In this study, we propose an efficient linear moving real-time short-term prediction model algorithm in both frequency and phase domains to deal with abnormal real-time BDS clock offsets. Moreover, the grey model GM(1,1) and the ARIMA model are used for comparison with the moving short-term clock prediction algorithm. The linear clock offset prediction model and the phase/frequency detecting function are first established. Subsequently, the real-time sliding prediction is initiated, and the threshold is set according to the fitting accuracy to determine whether the clock offset is abnormal. Next, real-time BDS clock data are used to conduct experimental validation. Finally, the algorithm performance is verified with the standard deviation (STD) precision of the detected clean BDS clock offsets compared with the final products provided by the Wuhan university analysis center (WHU), and the positioning accuracy is validated with the PPP method.
2. Materials and Methods
2.1. Linear Clock Prediction Model and Prediction Threshold Set
The outlier detection algorithm is mainly based on the clock prediction model. Thus, the function model of the clock prediction and the rule of outlier detection is proposed in detail as follows. Furthermore, ARIMA and GM(1,1) proposed in detail could be seen in reference [21].
The BDS onboard satellite clock has good short-term frequency stability characteristics, and the period terms have a small impact on short-term clock fitting and prediction [22,23]. Thus, the clock offset variation can be expressed with a linear model. We propose a linear model for short-term clock offset prediction, which can be denoted as follows:
where is the epoch time at the epoch; is the known real-time clock offset estimated in a real-time way when fitting the clock model; and are the model parameters, which are the frequency and phase of the atomic clock, respectively; and is white noise. To solve these parameters, the observation equation is constructed as follows:
where is the residual vector, is the coefficient matrix, is the parameter matrix to be solved, and is the clock offset matrix. According to the least-squares method, the parameters can be estimated as follows:
where , , ; is the clock offset corresponding to the fitted epoch. Using (1) and (3), the prediction value can be obtained with the estimated parameters.
To avoid the influence of abnormal clock offsets, we use both the phase and frequency domains to detect outliers among the clock offsets at previous epochs for accurately building the clock prediction model. Since the clock frequency, which is the first derivative of the clock phase versus time, is easy to identify outliers, the first step is to convert the clock phase data of all satellites into frequency data. The formula is as follows:
where is the frequency of the epoch .
The frequency data are passed into the frequency anomaly detection function. The main steps of the function are described below. First, the standard deviation of the frequency data is calculated as follows:
where is the average value of all frequency data, and is the total number of frequency data.
Then, the maximum value of the frequency data is computed with the formula . According to different satellite orbit types, different thresholds could be designed as follows.
where is the defined detection threshold. defines the tolerance of random errors, is empirical hour-boundary bias, and different MEO/GEO/IGSO orbit types are set different values such as 0.016 × 10−9, 0.033 × 10−9. For MEO satellites in the real-time clock estimation process, the orbit error seems too small to consider setting another empirical threshold. The reason for setting different hour-boundary biases is that the real-time satellite clock is estimated with the hourly updated ultra-rapid orbit, and the IGSO/GEO satellite absorbs larger hour-boundary orbit error than the MEO satellite. Too large clock bias should be deleted since it will affect the positioning result due to large interpolation errors. Thus, this algorithm can automatically regulate the detection threshold to a reasonable range at hour-boundary epochs or other normal epochs.
The equation for judging whether the detected clock offset exceeds the limit is as follows:
If Equation (7) is satisfied, will be identified as an abnormal frequency point. Then, the next maximum frequency point is continuously detected until there is no abnormal frequency.
The second step of the algorithm is to complete the real-time clock offset fitting model. Some previous epochs are imported for building a preliminary fitting model, and the corresponding residuals are checked whether contain abnormal values before clock prediction. The clock detection threshold in the phase domain can be computed by the root mean square error (RMS) of the fitting clock residual and the empirical hour-boundary bias. The calculation formula of the RMS accuracy is as follows:
where is the root mean square offset, is the known clock offset, is the fitting value, and is the total number of the fitting epoch.
After the short-term clock model is built, the real-time clock prediction can be carried out by a moving window with one epoch step. Finally, it is determined whether the predicted clock exceeds the threshold range. If so, it is eliminated. Otherwise, it moves forward one epoch, and fitting–prediction–detection is performed again until there is no new epoch.
2.2. Linear Moving Short-Term Clock Prediction and Anomaly Detection Algorithm
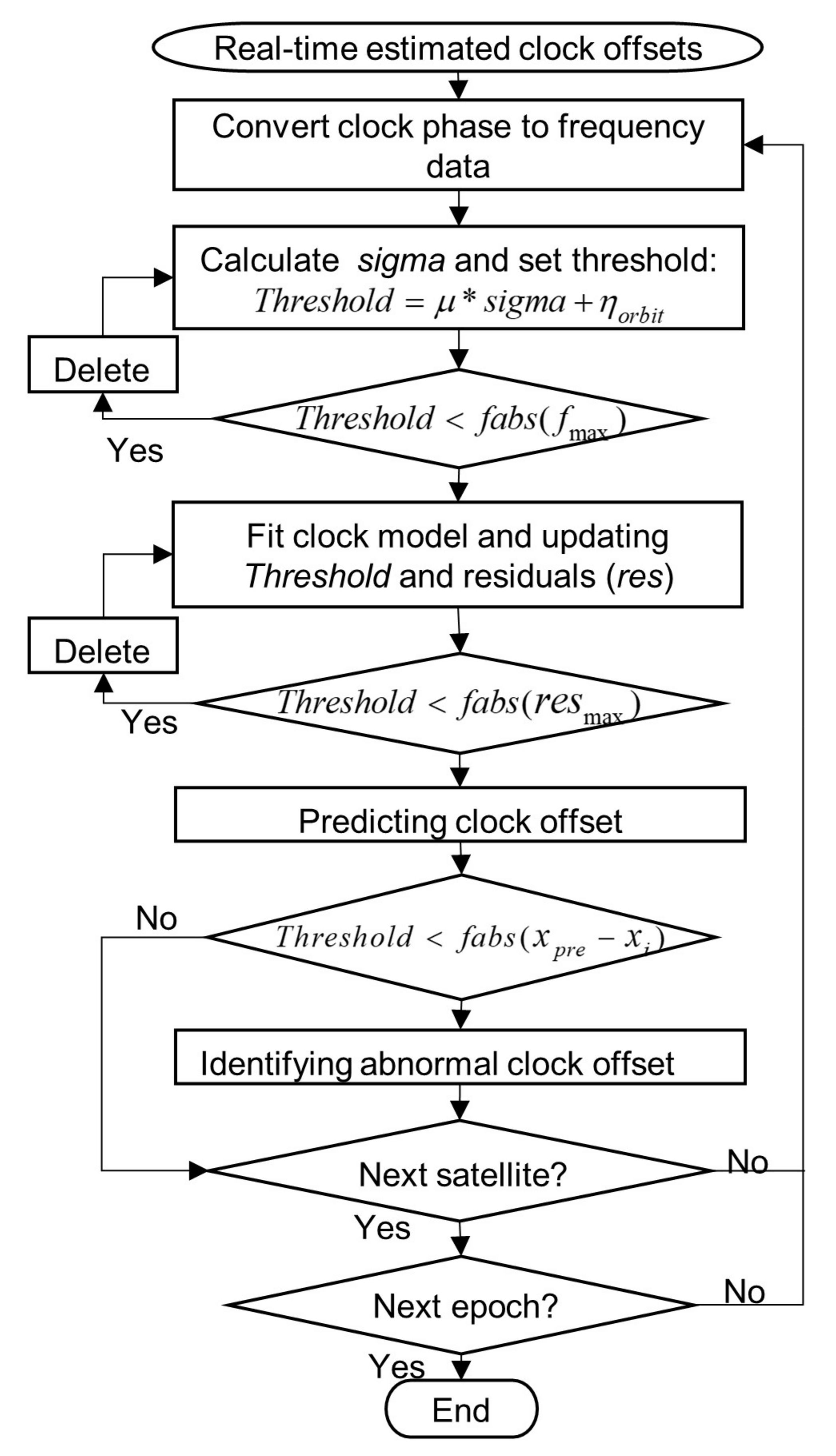
A linear moving short-term clock detection algorithm is proposed to control the clock abnormalities and has been embedded into the real-time clock estimation program. The algorithm mainly contains three steps, as shown in Figure 1. The first step is to obtain real-time estimated satellite clock offsets of some previous epochs as the input of the abnormal clock detection at the current time. To fit the clock model precisely, we convert them to frequency data for outlier detection. Secondly, the linear clock model is fitted with a sequential least-squares adjustment, and the quality control is also carried out in the phase domain. Thirdly, the clock offset at the current epoch is predicted with the fitted model. Since the prediction time length is very short, the predicted clock offset is accurate enough to check the estimated clock offset. After all satellite clock offsets are detected at the current epoch, the algorithm procedure moves forward and is repeated at the next new epoch. Only real-time estimated clocks are used to build a clock prediction model during the detection procedure. If abnormal clock values are identified and removed correctly, the clock difference time series will have less fluctuation, and the STD of the differences will be improved.
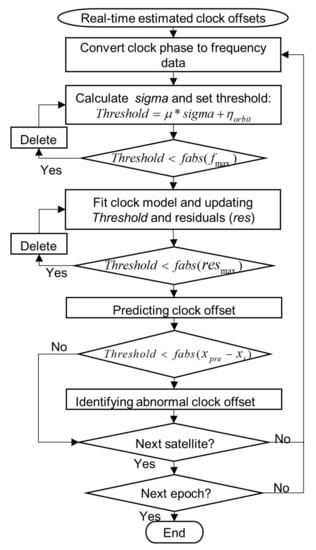
Figure 1.
Flowchart of the linear moving short-term clock prediction and detection algorithm at one epoch.
3. Experiments, Results, and Discussion
3.1. Abnormal Values in the Estimated Real-Time BDS-2/BDS-3 Clock Offsets
To verify the effectiveness of the linear moving short-term clock detection algorithm, the clock precision before detection and the steps of the algorithm need to be described. This section mainly introduced real-time clock sources and origin precision and also described the algorithm in detail.
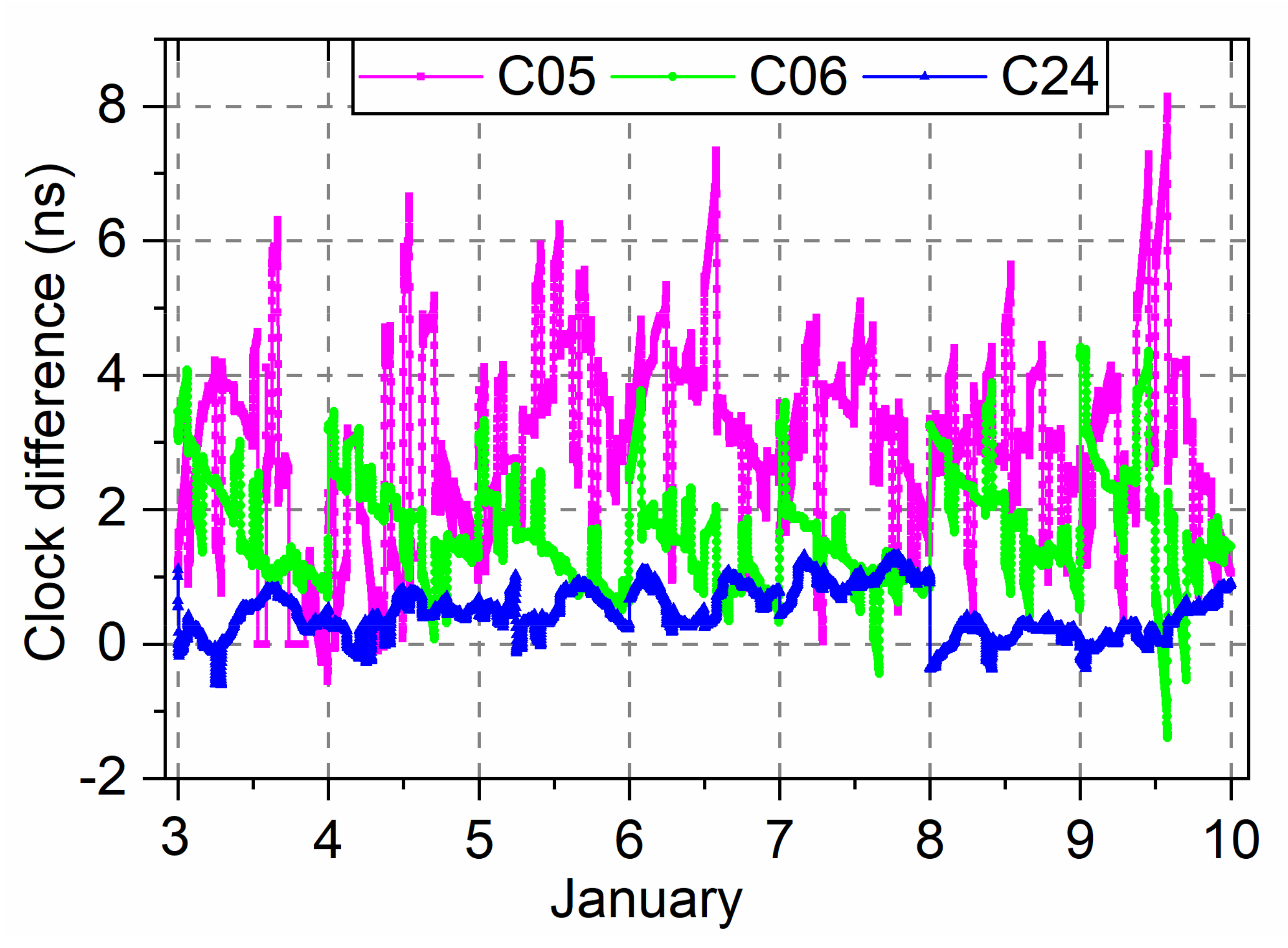
The real-time BDS-2/BDS-3 satellite clock offsets with a sampling interval of 30 s from 3–9 January 2021, which are estimated with the overlapping B1I/B3I signal using a global station network and the WHU ultra-rapid orbit products, are selected as the known clock offsets for detecting abnormal clock offsets. The real-time clock estimation program is developed by us and has good product performance [24]. To explain the abnormal values in the estimated BDS-2/BDS-3 clock offsets and evaluate the accuracy improved by the abnormal clock detection, the differences between our real-time estimated clock and the WHU final clock product are computed [25]. The final product of WHU is based on the global station, which adopts the post-processing method. The precise orbit, troposphere, and ambiguity parameters are processed first, and then these parameters are fixed by an epoch loop to solve the clock difference parameters. So, the WHU final clock product with better accuracy is treated as the true value since it is obtained in a post-processed way with the final orbit product. To remove the influence of different clock datums between these two products, the clock offsets of the reference satellite C19 are deducted from other satellite clock offsets. The clock difference time series of the C05, C06, and C24 satellites from GEO, IGSO, and MEO, respectively, are first presented in Figure 2. The average STD of all satellite clocks is presented in Figure 3.
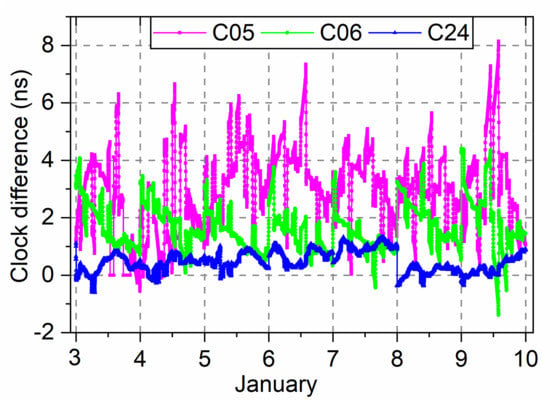
Figure 2.
Clock difference of the C05, C06, and C24 satellites between real-time estimated clock offsets and WHU final products.
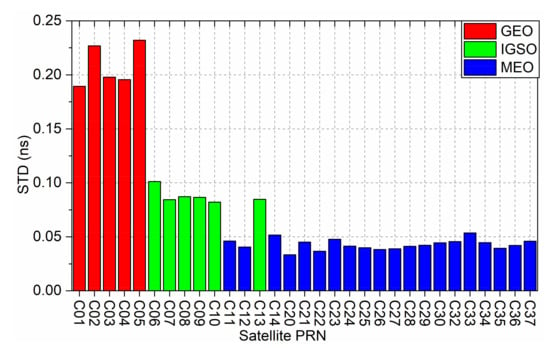
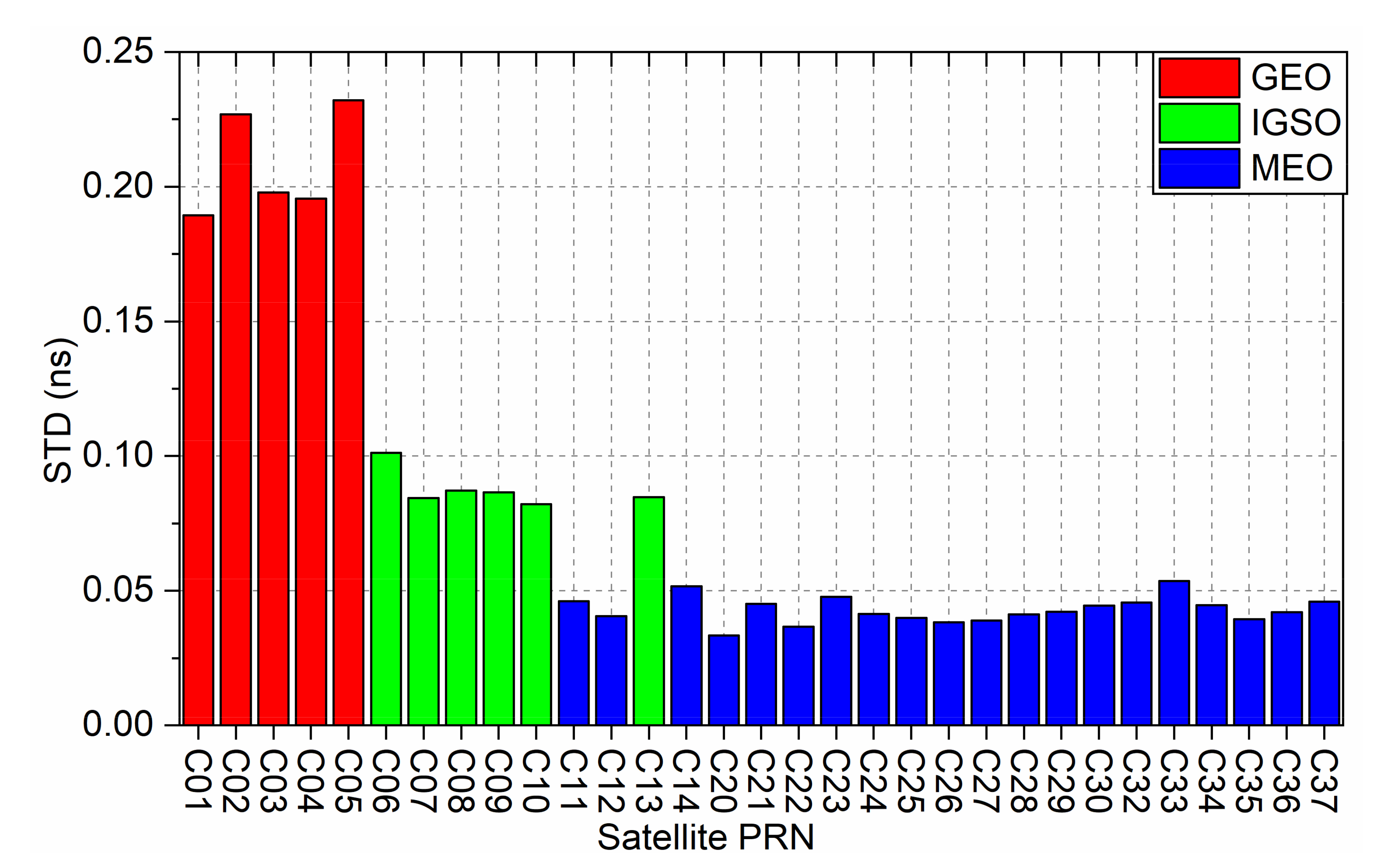
Figure 3.
Average STD of the real-time estimated BDS-2/BDS-3 satellite clock.
The BDS satellite atomic clock should have high-frequency stability, and its short-term phase variation should have shown a linear law. However, the real-time clock offsets are obtained by estimating with a global station network with ultra-rapid orbit products. The real-time estimated clock offset products inevitably contain some anomalies, such as gross offsets, phase jumps, and missing data. These abnormal values are mainly due to the influence of orbital error, other unmodeled errors, or poor observation error during the clock estimation process, resulting in a part of irregular orbital errors or outliers absorbed into the real-time clock offset. Figure 1 shows that the amplitude of the C05 sequence has the largest fluctuation, with an obvious jump phenomenon at the hour boundary. The C06 and C24 satellites have small fluctuation amplitude, but there are still some abnormal clock offsets.
Figure 2 shows that there are 31 satellite clocks including 5 GEO satellites, 6 IGSO satellites, and 20 MEO satellites. The MEO satellite has the highest accuracy of approximately 0.043 ns. The STD accuracy of the IGSO satellite is approximately 0.088 ns, while the GEO satellite has the lowest STD accuracy of approximately 0.208 ns. Due to the influence of larger GEO orbit errors, the accuracy of clock estimation is lower than that of MEO and IGSO satellites [26].
3.2. Three Kinds of Typical Abnormal Real-Time Clock Offsets and Detection Algorithm Validation
To illustrate the performance of the proposed abnormal clock detection method, three kinds of typical abnormalities are first selected to validate the algorithm. The experimental analysis of all real-time BDS-2/BDS-3 satellite clock offsets from 3 to 9 January 2021 is carried out first, and then validation experiment and results analysis are carried out to assess the performance improvement with the proposed linear method. As a comparison, the results of the GM(1,1) and the ARIMA model are also presented in this section. The clock prediction performance of the linear model is evaluated with different prediction time lengths and compared to the other two models.
The abnormal real-time estimated satellite clock offsets must be detected and removed since these abnormalities could cause large positioning errors in PPP applications [27]. The linear moving clock detection algorithm embedded into real-time clock estimation is thus proposed to solve the issue. To validate the effectiveness of the detection algorithm, three kinds of typical abnormal real-time clock offsets, such as outliers, frequency jumps, phase jumps, and so on, are taken as examples.
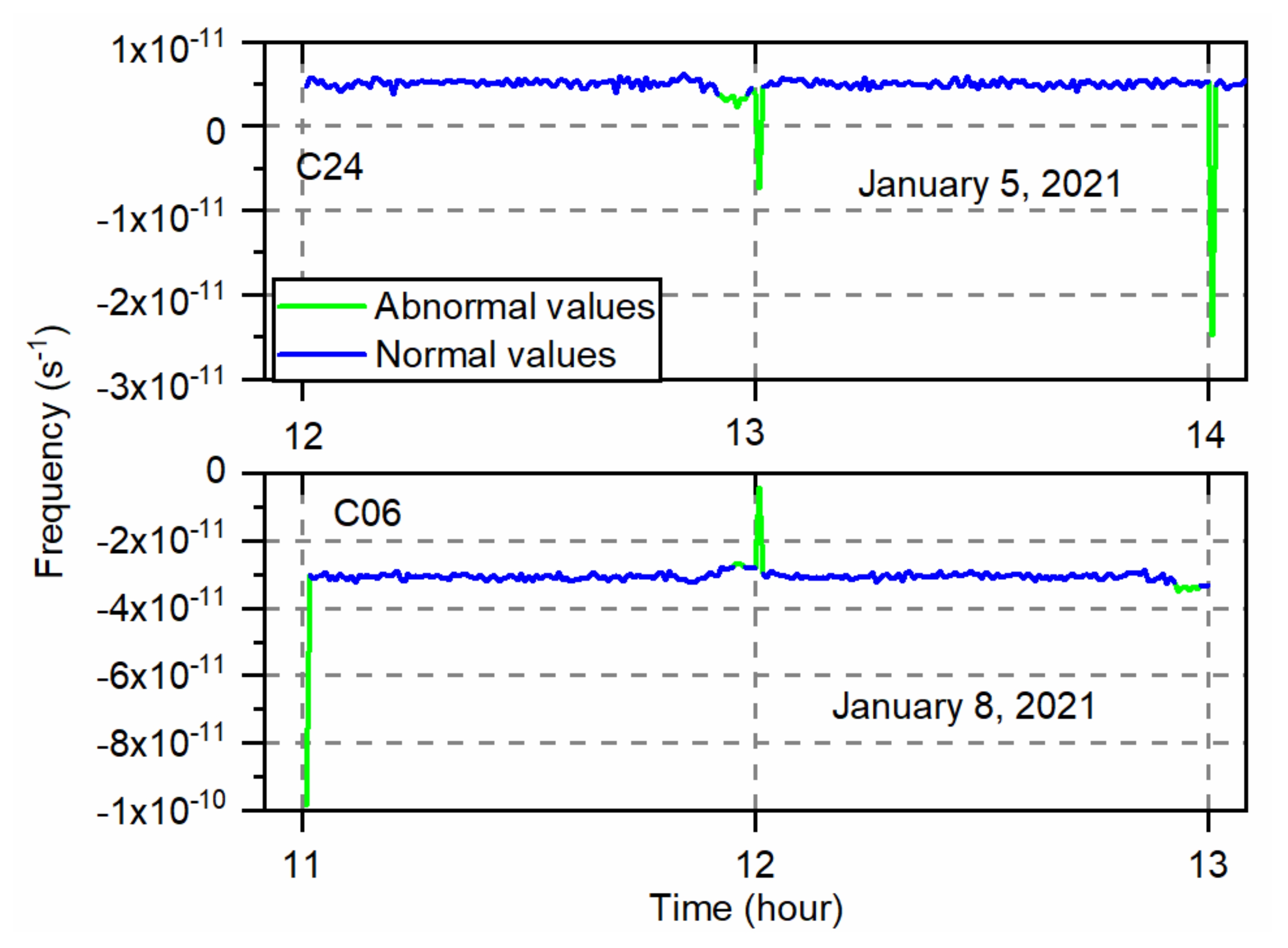
The first example uses the real-time estimated clock offsets of the IGSO satellite C06 on 8 January 2021 and the MEO satellite C24 on 5 January 2021 to illustrate the detection of clock outliers. The frequency detection is more effective than the phase for some isolated outliers since the normal satellite atomic clock frequency is stable during a short-term period. The frequency data and outlier detection results are shown in Figure 4. The blue line shows that most frequency data are stable, and some large frequency points denoted with the green line are detected as outliers. The C06 frequency presents larger fluctuations than the C24 at the hour boundary due to large hourly updated IGSO orbit error. The frequency detection algorithm module can detect hour-boundary biases and remove the corresponding outliers.
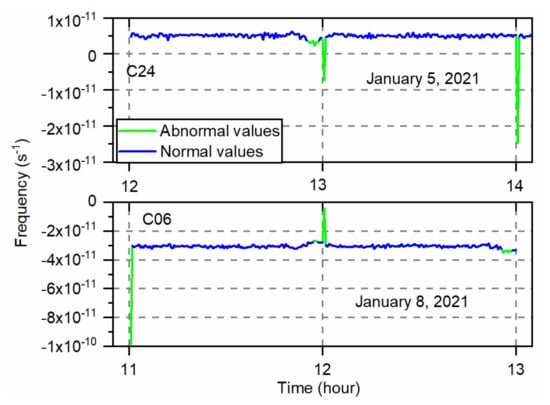
Figure 4.
Frequency data of C06 and C24 satellite clocks and the outlier detection results.
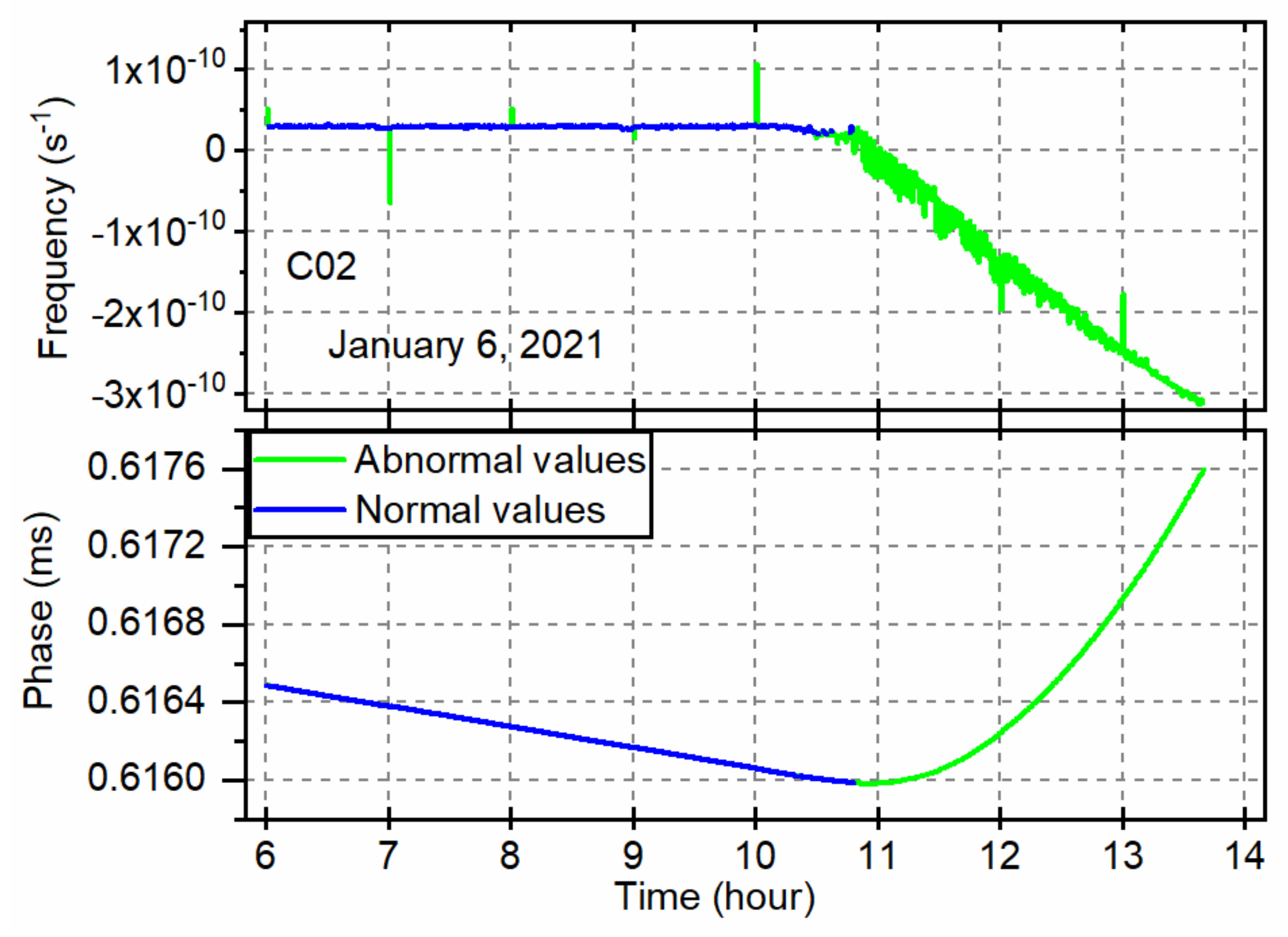
The second example presents the abnormal clock offsets of the GEO satellite C02 caused by frequency modulation on 6 January 2021. Figure 5 shows the frequency modulation on the C02 satellite and abnormal clock detection results. The top and bottom panel is the frequency and phase time series, respectively. As shown by the green line, the proposed algorithm can correctly identify abnormal clock offsets caused by frequency modulation and eliminate abnormal parts. The phenomenon lasts about three hours leading to an obvious trend in the frequency data and a parabolic trend in the phase data. The abnormal clock offsets should be remarked unavailable after the frequency modulation happens to avoid the adverse influence on the PPP.
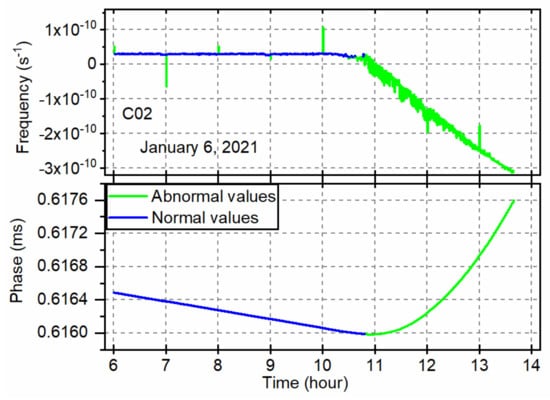
Figure 5.
Frequency modulation on the C02 satellite and abnormal clock detection results in the frequency (top) and phase (bottom) domains. The frequency modulation causes the real-time estimated clock offsets to be unavailable after about UTC 11:00.
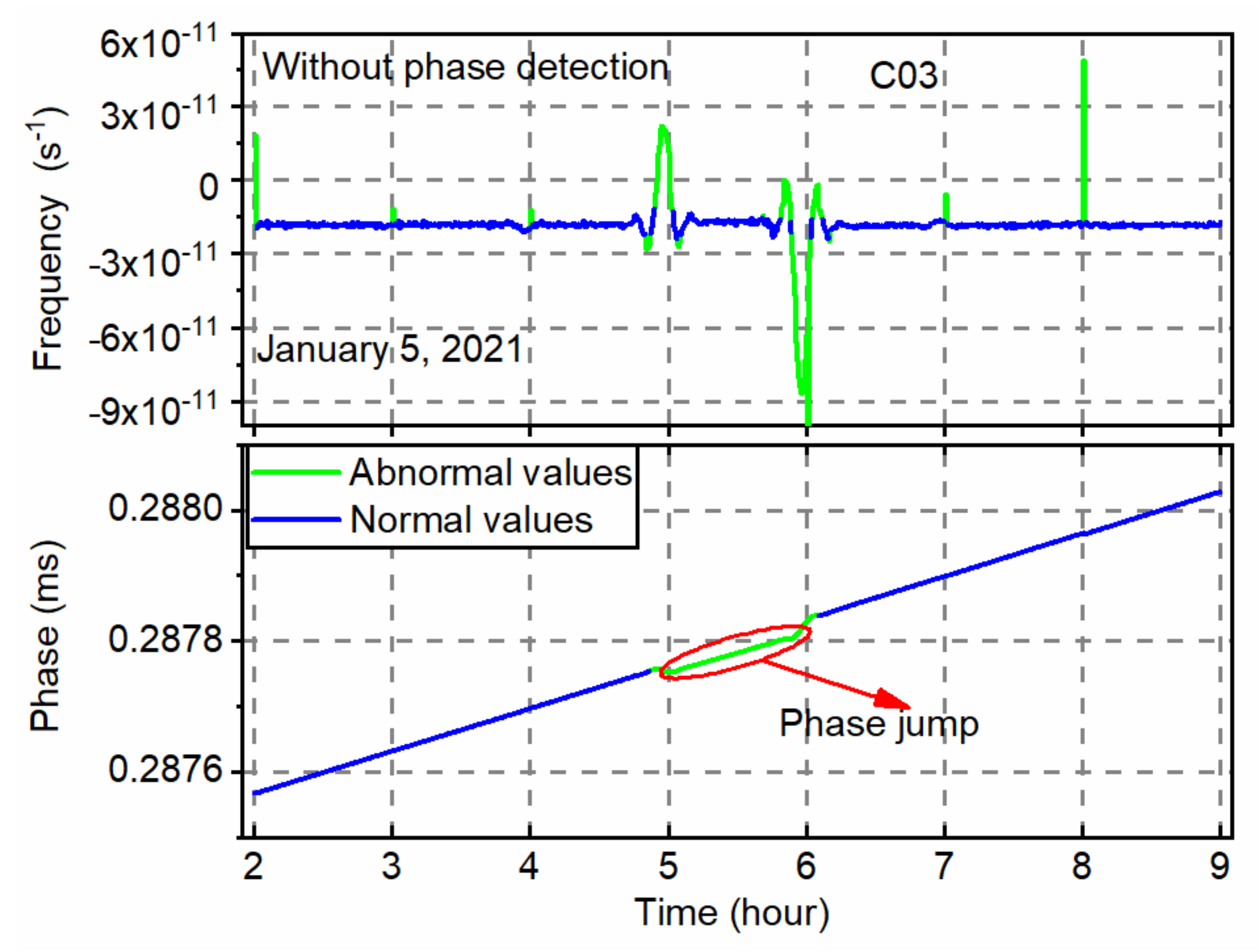
The third example presents the abnormal clock offsets of the GEO satellite C03 caused by phase modulation on 5 January 2021. Figure 6 shows the phase jump on the C03 satellite and abnormal clock detection results. The top and bottom panel is the frequency and phase time series, respectively. The frequency data at the hour boundary fluctuates significantly, but the time series from UTC 05:00 to 06:00 varies stable. The frequency detection part is not effective for the phase jump. However, it can be detected by the phase detection part since all phase data during this period deviate from the primary variation trend. The clock jump value is approximately 10 ns. The phase jump will cause a large interpolation error, which can affect the positioning performance. Therefore, the short-term abnormal clock offsets caused by the phase jump should be detected. As shown by the green line, the proposed algorithm can detect abnormal clock offsets, including large outliers and phase jumps.
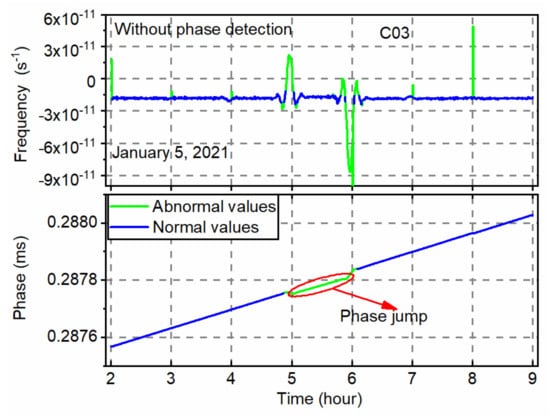
Figure 6.
Phase jump on the C03 satellite and abnormal clock detection results in the frequency (top) and phase (bottom) domains. The phase jump causes the real-time estimated clock offsets to be unavailable from UTC 05:00 to 06:00.
3.3. Improvement of Clock Performance after Removing Abnormal Values
To reflect the performance of the linear moving short-term clock detection algorithm, the improved STD accuracy of the real-time estimated satellite clock offsets is assessed in this section after the abnormal clock values are removed. First, the GEO satellite C05, the IGSO satellite C06, and the MEO satellite C24 are selected to analyze the improvement of the clock STD accuracy each day. Secondly, the assessment of average real-time clock performance improvement of all days is carried out on all satellites. The results of the abnormal real-time satellite clocks detected with the grey model and the ARIMA model, respectively, are also compared to the proposed method.
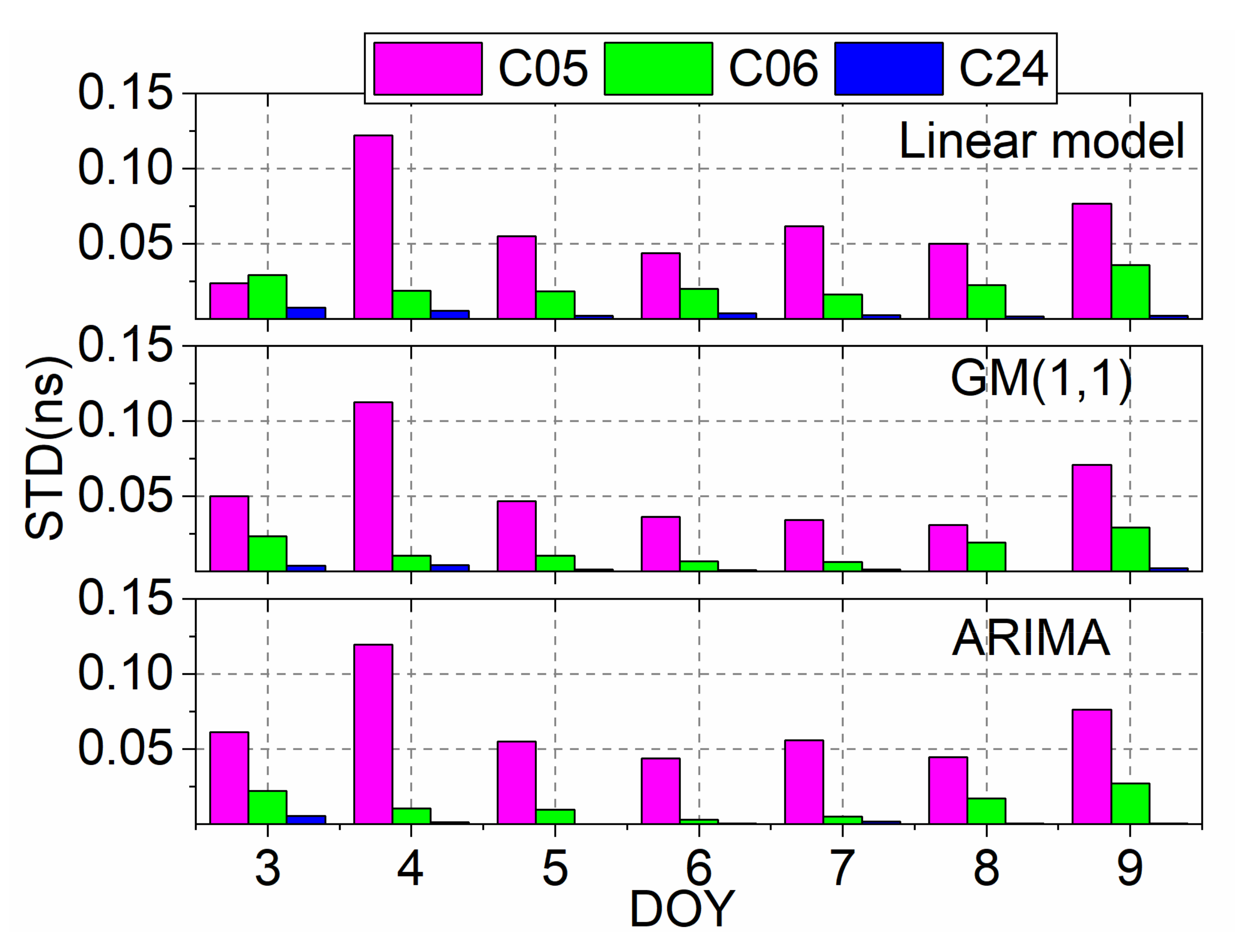
Figure 7 shows the daily improvement of the C05, C06, and C24 clock offsets by the proposed linear model and the comparison with the grey model and the ARIMA model. Abscissa is the day of the year (DOY). For the C05 satellite, the average improvement is 0.064 ns, 0.055 ns, and 0.065 ns, respectively, for the linear model, the grey model, and the ARIMA model. The most obvious improvement is on 4 January 2021, reaching 0.126 ns, 0.112 ns, and 0.119 ns, respectively, for the three models since large abnormal clock offsets are removed. The C06 satellite average improves 0.023 ns with the linear model, and it is 0.015 ns and 0.013 ns for the grey model and the ARIMA model, respectively. The C24 satellite has a small improvement since the MEO satellite clock offsets have fewer outliers due to good orbit products. Compared to the other two models, the linear model has a better clock performance improvement for these satellites of different orbit types.
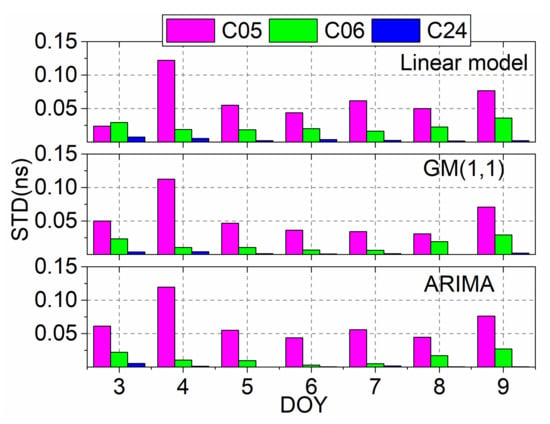
Figure 7.
Daily clock STD accuracy improvement of the GEO satellite C05, the IGSO satellite C06, and the MEO satellite C24.
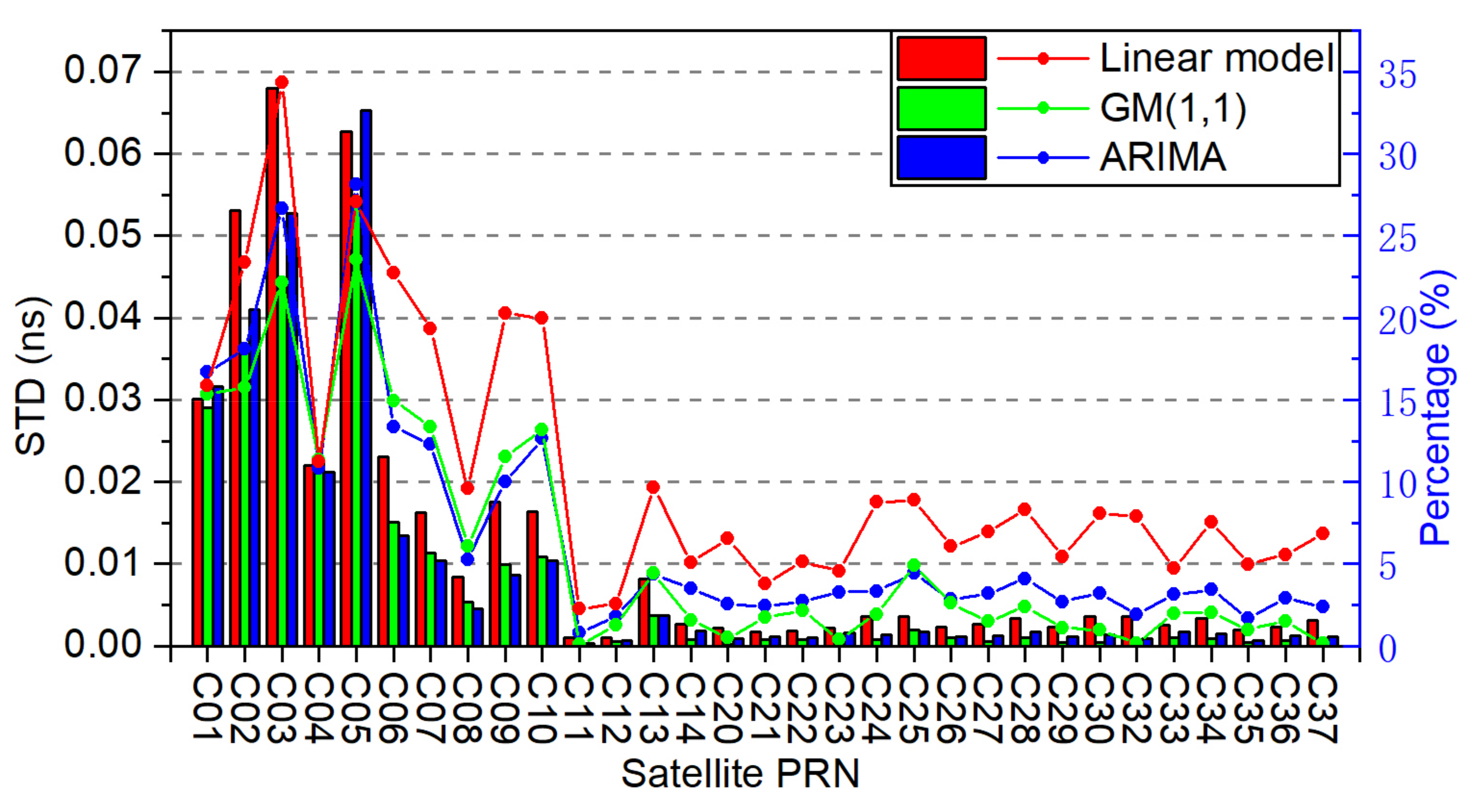
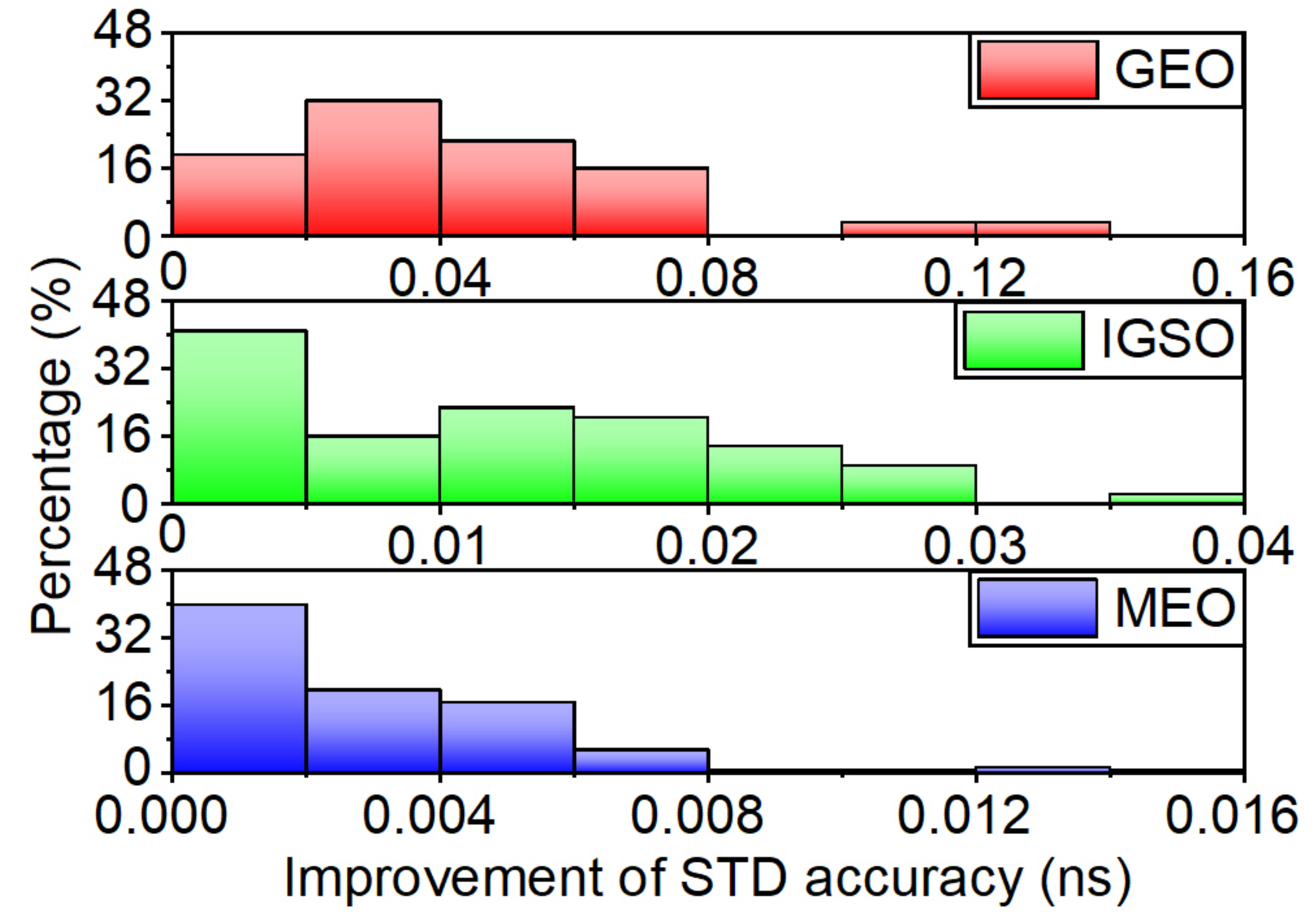
To comprehensively assess the STD accuracy of the real-time satellite clock offsets after removing the abnormal values, the average improvement of each satellite with these three models is presented in Figure 8. The clock improvement distribution of different orbit types with the proposed method is also shown in Figure 9 to illustrate the effect of controlling abnormal clock offsets. The overall clock STD improvement percentage of the three orbit types is summarized in Table 1. As shown in Figure 9, a total number can be obtained by calculating the STD accuracy of the clock per hour per satellite. For MEO satellites, the number of improvements per 0.002 ns range divided by this total number is the ratio shown in Figure 9. For GEO and IGSO satellites, 0.020 ns and 0.005 ns are set, respectively.
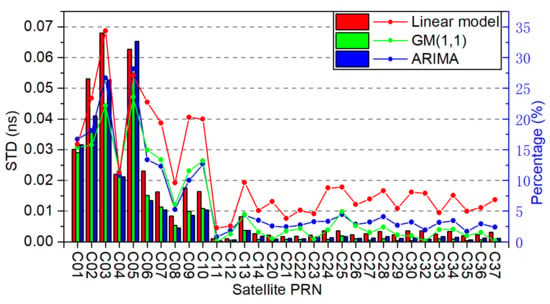
Figure 8.
Average clock STD improvement and the percentage of each satellite with the three models.
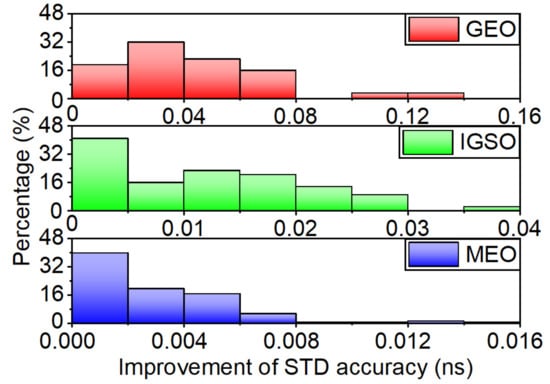
Figure 9.
Frequency histogram of the clock STD improvement of the GEO, IGSO, and MEO satellites with the linear model.

Table 1.
Average STD improvement of the GEO, IGSO, and MEO satellites with the three models.
Figure 8 shows that the proposed linear moving clock detection method has a better performance than the other two models in general and shows varying degrees of improvement for the satellites of different orbit types. The average STD accuracy of all satellites is improved by 15.5% from 0.078 to 0.066 ns with the linear model, while the grey model and the ARIMA model are 10.3% and 11.5% by 0.008 ns and 0.009 ns, respectively. The BDS-2 satellites have a significant improvement with 19.7%, 13.9%, and 14.9% for the linear model, GM(1,1), and ARIMA, respectively. While BDS-3 STD accuracy improved by 0.002 ns, 0.001 ns, and 0.001 ns for the three models. Additionally, the GEO satellite has the most significant improvement, then the IGSO satellite and the last is the MEO satellite. Figure 9 shows that most experimental results of the GEO satellite uniformly distributed within accuracy improvement of 0.08 ns, it is 0.03 ns and 0.008 ns for the IGSO and MEO satellite, respectively, with the proposed linear model. The average STD improvement is 0.048 ns, 0.014 ns, and 0.002 ns for the GEO, IGSO, and MEO satellites, respectively, with the linear model. For comparison, the GM(1,1) improves by 0.037 ns, 0.009 ns, and 0.001 ns, while the ARIMA improves by 0.048 ns, 0.009 ns, and 0.001 ns for these three kinds of orbit types. Table 1 shows the corresponding percentage of improvement in STD accuracy relative to the real-time estimated clock products. This indicates that the algorithm greatly improves the accuracy of the real-time estimated satellite clock offsets, and its detection performance is better than the grey model and the ARIMA model.
3.4. Performance of the Real-Time Linear Clock Prediction Algorithm
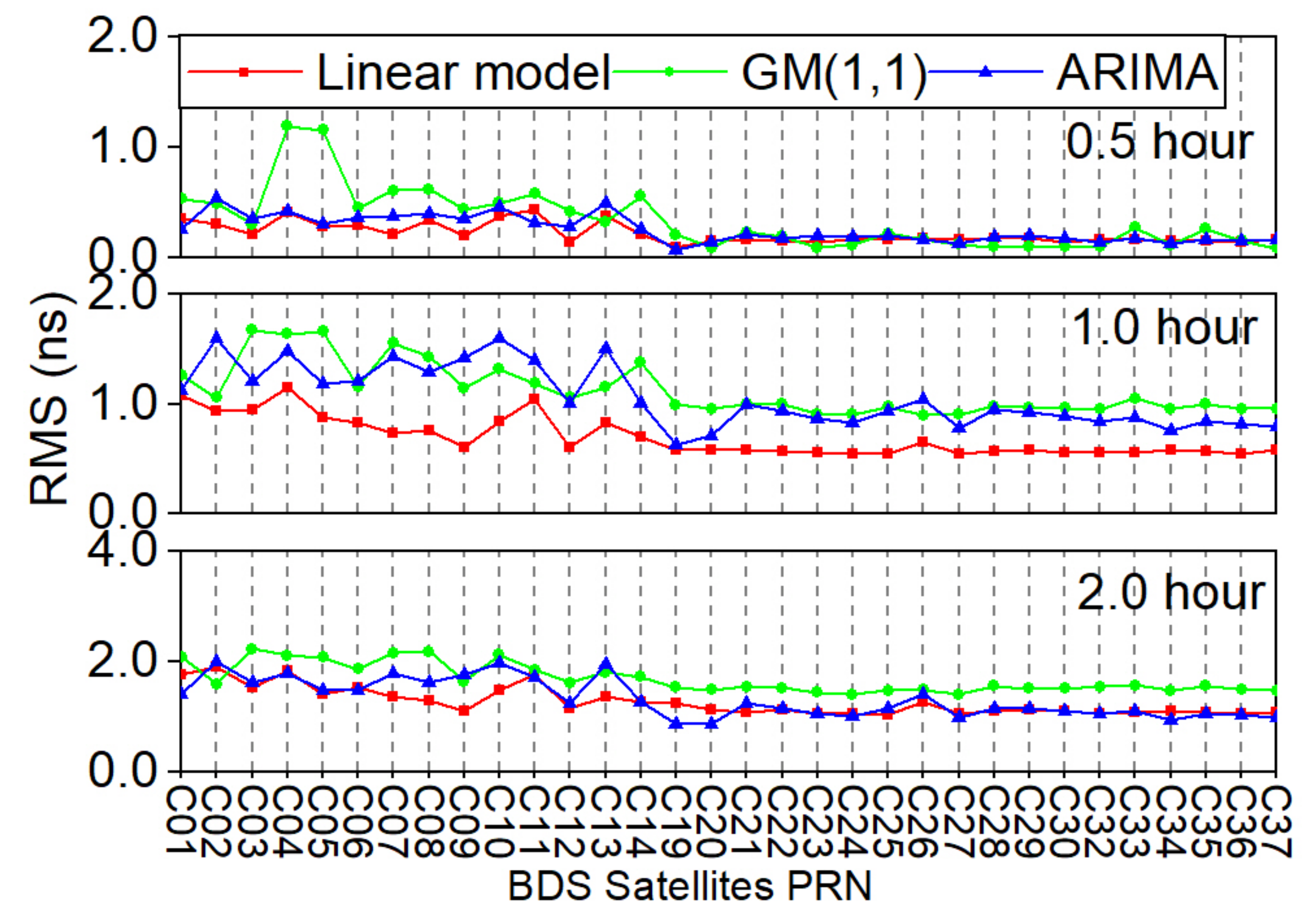
The core part of the algorithm is the clock prediction model, and good clock prediction performance is the premise of detecting outliers correctly. To further validate the proposed method, the prediction accuracy of the linear model is evaluated for different clock prediction time lengths. The fitting model is built with 20 min clock offset data, and the prediction time length is 0.5 h, 1.0 h, and 2.0 h, respectively. According to the predicted residuals of the three models, the RMS accuracy is computed and shown in Figure 10 and Figure 11.
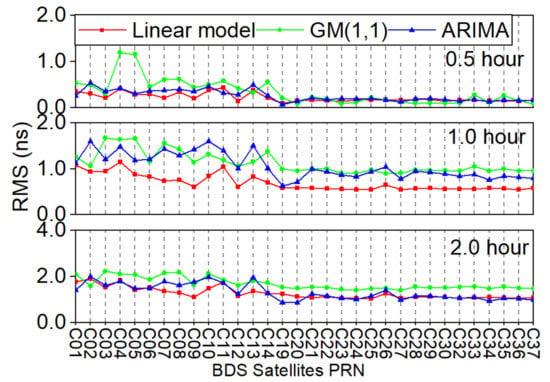
Figure 10.
Clock accuracy of predicting 0.5 h, 1.0 h, and 2.0 h satellite clock offsets with the linear model, the grey model, and the ARIMA model.
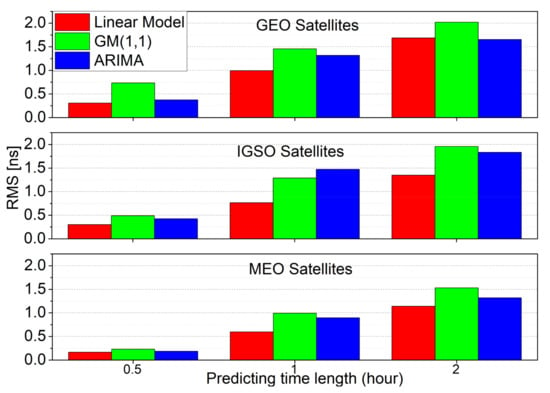
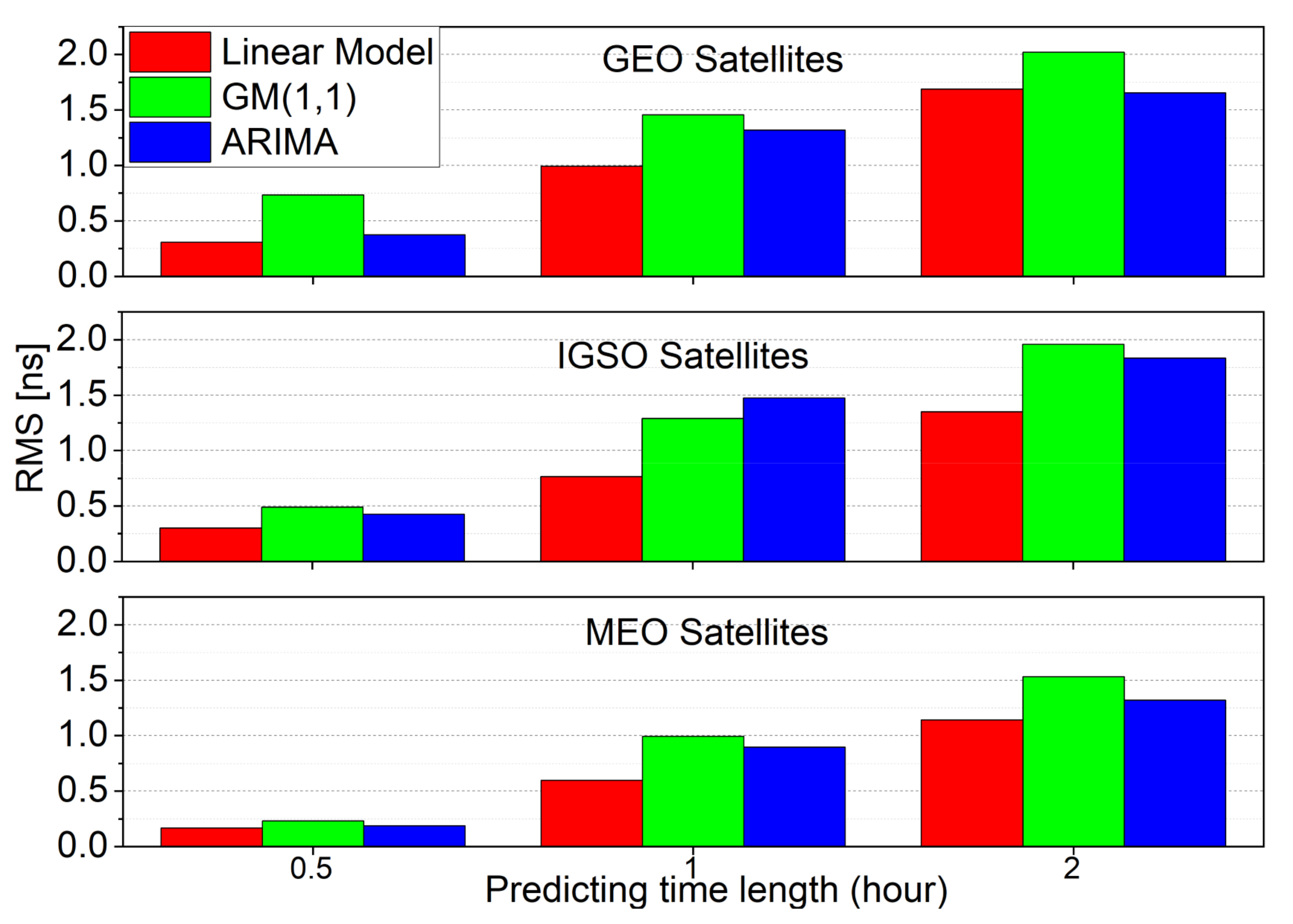
Figure 11.
Average clock prediction accuracy for different prediction time lengths with the three models for different orbit types.
Figure 10 reflects the average RMS accuracy of the predicted clock offsets for each satellite with three models, and the corresponding average accuracy for three orbits is shown in Figure 11. In general, the clock prediction accuracy of the GEO and IGSO satellites is worse than the MEO satellites, which is consistent with the above results. The linear model has the best average prediction accuracy, which is 0.214 ns, 0.687 ns, and 1.284 ns for the prediction time length of 0.5 h, 1.0 h, and 2.0 h, respectively. The three orbits’ average prediction accuracy for the GM(1,1) is 0.360 ns, 1.166 ns, 1.768 ns, and 0.263 ns, 1.090 ns, 1.359 ns for the ARIMA model. Besides, the precision of BDS-2 and BDS-3 clock prediction is also consistent with the above. BDS-2 obtains average RMS of 0.289 ns, 0.839 ns, and 1.465 ns for the prediction time length of 0.5 h, 1.0 h, and 2.0 h, respectively. While BDS-3 gets 0.153 ns, 0.569 ns, and 1.099 ns with the linear model. Furthermore, BDS-2 could reach 0.613 ns, 1.317 ns, 1.917 ns, 0.369 ns, 1.327 ns, and 1.655 ns for GM(1,1) and ARIMA with 0.5 h, 1.0 h, and 2.0 h prediction time length. In contrast, BDS-3 gets 0.149 ns, 0.961 ns, 1.500 ns, 0.175 ns, 0.857 ns, and 1.071 ns with a different model. With the increase of the prediction time length, the accuracy of the predicted clock offsets decreases. Thus, it is necessary to adopt the moving short-term clock prediction method for maintaining good prediction accuracy. The clock prediction performance shows that the linear model is more suitable for predicting and detecting abnormal satellite clock offsets in the proposed method.
3.5. PPP Validation
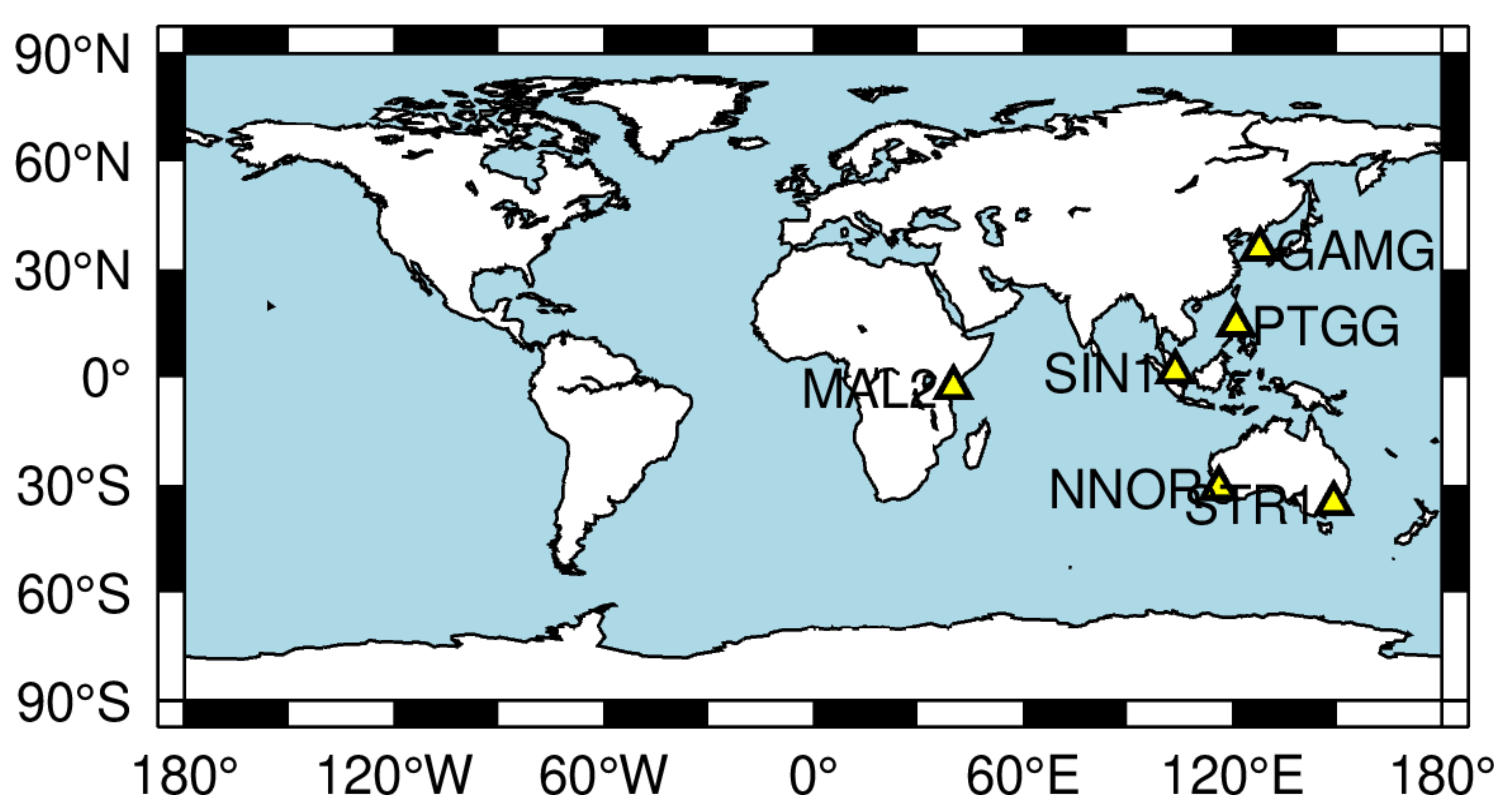
To verify the effectiveness of the proposed method, the real-time kinematic PPP is carried out with the real-time estimated satellite clock products before and after the abnormal clock detection. The PPP model and parameters are displayed in Table 2. Six IGS stations are selected, and the distribution is shown in Figure 12. The undifferenced BDS B1I/B3I phase and code ionosphere-free combination observations and the WHU ultra-rapid orbit products are used in the PPP processing model. To avoid the influence of day-boundary orbit error, the PPP experiment starts from the UTC 2:00 to 22:00 on each day. The daily positioning error of the PPP in the east, north, and up components is computed with respect to the post-processed IGS reference coordinates, and an example of the station PTGG on 4 January 2021 is shown in Figure 13. The average RMS accuracy of all days is presented in Figure 14, and the accuracy improvement is shown in Table 3.

Table 2.
Models and parameters for PPP.
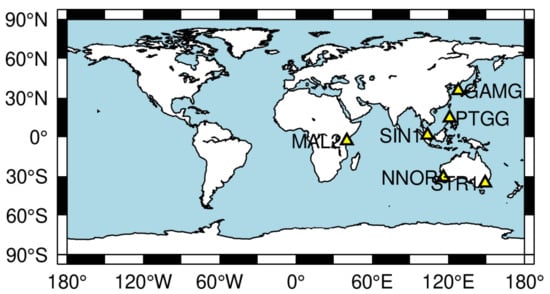
Figure 12.
Station distribution for PPP validation.
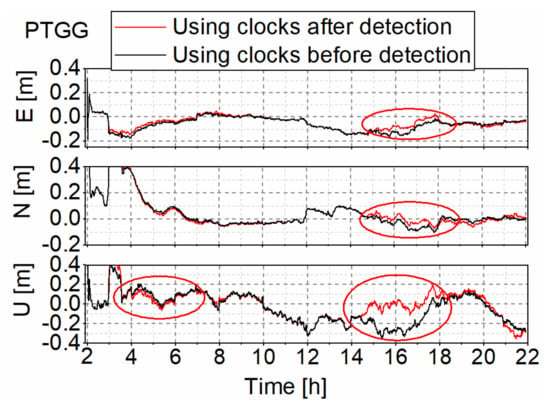
Figure 13.
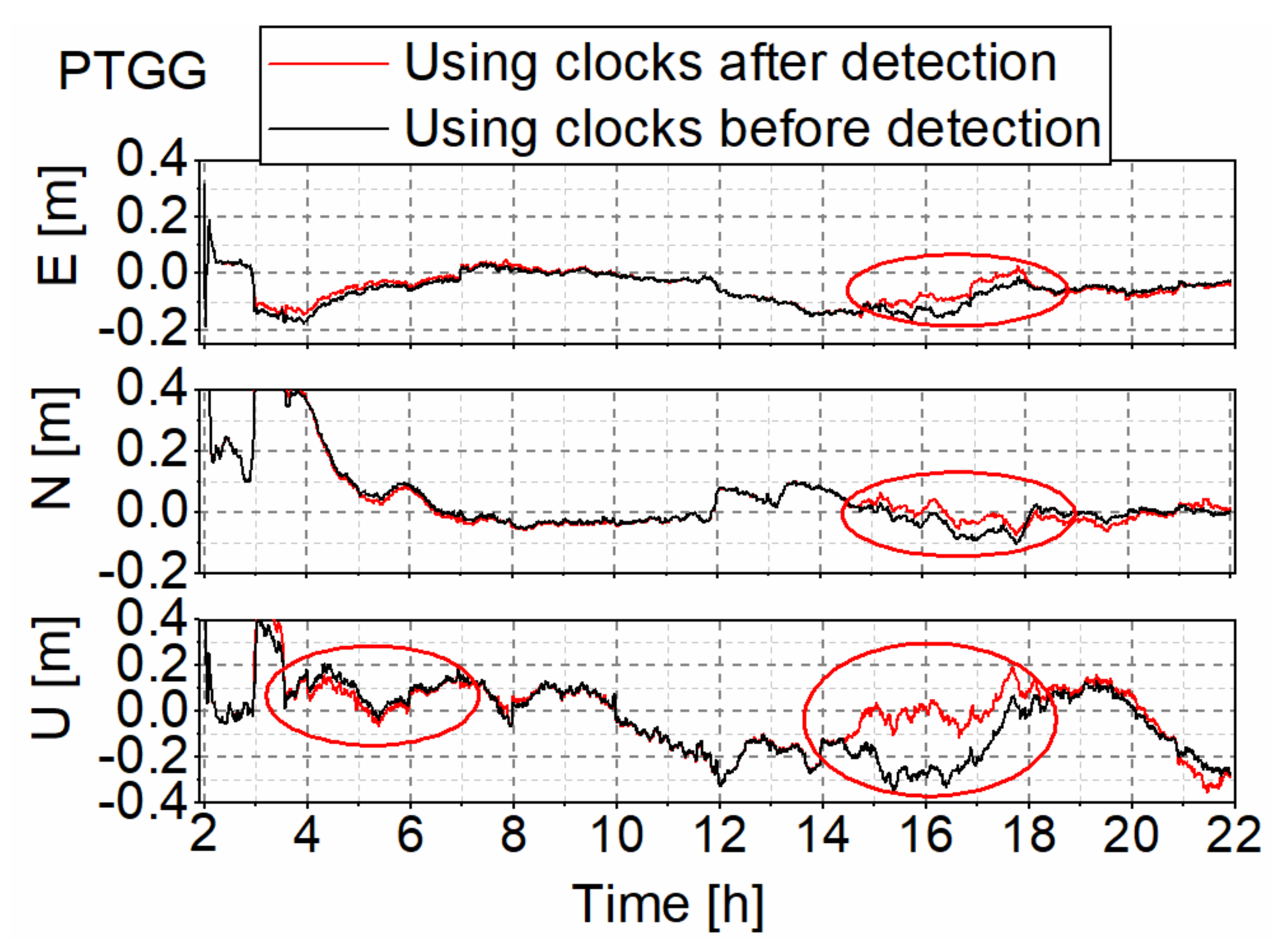
Positioning errors of the real-time kinematic PPP at the station PTGG on 4 January 2021.
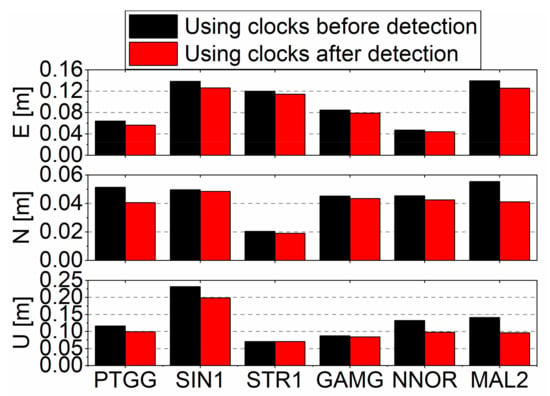
Figure 14.
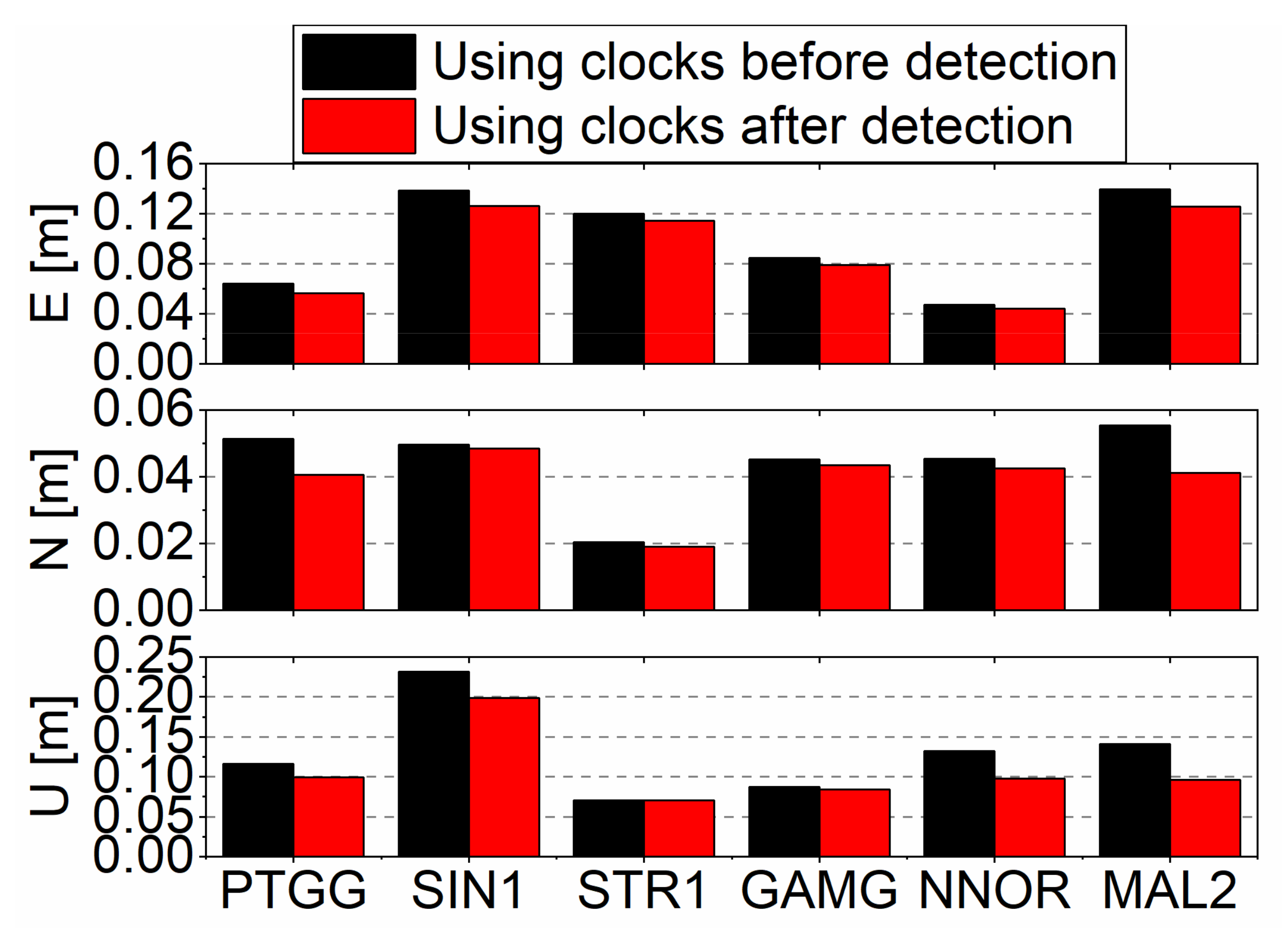
Average RMS accuracy of the real-time kinematic PPP at each station.

Table 3.
Average RMS accuracy improvement.
Figure 13 shows that the position errors of the station PTGG are improved significantly from UTC 14:00 to 17:00. This is because many abnormal clock data are detected and removed during this period by the abnormal satellite clock detection. The RMS accuracy in east, north, and up components is improved by 0.004 m, 0.009 m, and 0.026 m, respectively. In general, the horizontal direction improved by 0.010 m. Figure 14 and Table 2 show that the average RMS accuracy with the original real-time clocks amounts to 0.099 m, 0.045 m, and 0.130 m in the east, north, and up components, respectively, while the corresponding accuracies of 0.091 m, 0.039 m, and 0.108 m are achieved with the clocks after removing abnormal values. In comparison, the improvement is 8.1%, 13.3%, and 16.9%, respectively. In other words, the precision of horizontal direction could improve by 8.3% after clock outliers detection. This demonstrates that the abnormal clock detection algorithm could improve the positioning quality of the real-time estimated satellite clock.
4. Conclusions
Precise real-time satellite clock offset product is the basis for obtaining reliable real-time PPP solutions. However, the real-time estimated BDS clock offsets often contain abnormal values. This study proposes a linear real-time moving short-term prediction model and algorithm to detect outliers after analyzing the abnormal values in the real-time estimated BDS-2/BDS-3 clock offset. The algorithm includes real-time clock data preparation, frequency detection, phase detection, and real-time linear moving prediction. Some typical abnormal types of satellite clock offsets, such as outliers, frequency jumps, and phase jumps, are first discussed to validate the proposed algorithm. The performance of the algorithm is then evaluated for all satellites with one-week real-time clock offset data. The grey model and the ARIMA model are compared with the linear model in both the quality of abnormal clock detection and the performance of clock prediction for illustrating the advantage of the linear model. Finally, the PPP with the real-time estimated satellite clock products before and after the abnormal clock detection is carried out to verify the effectiveness of the proposed method.
Experimental results show that the proposed algorithm can detect hour-boundary biases, identify abnormal clock offsets caused by the phase or frequency modulation, and correctly remove the corresponding BDS-2/BDS-3 clock outliers. Compared to the grey model and the ARIMA model, the linear model has a better clock performance improvement for the GEO, IGSO, and MEO satellites. The GEO satellite has the most significant improvement, then the IGSO satellite, and the last is the MEO satellite since the accuracy of the real-time clock is related to the satellite orbit type due to poor orbital error of the GEO and IGSO satellite. The average STD accuracy of all satellites is improved by 15.5%, 10.3%, and 11.5% with the linear model, the grey model, and the ARIMA model, respectively. The clock prediction experiments show that the linear model has the best prediction accuracy, and the accuracy of the predicted clock offsets decreases rapidly with the increase of the prediction time length. Thus, it is more suitable to adopt the moving short-term linear clock prediction method to maintain good prediction and detection performance accuracy. The PPP results demonstrate that the abnormal clock detection algorithm could improve the positioning accuracy by 8.1%, 13.3%, and 16.9% in the east, north, and up components, respectively.
In conclusion, it indicates that the linear moving short-term clock detection algorithm is effective and feasible for controlling the abnormal values in the estimated real-time satellite clock offsets. This method also has a good perspective on monitoring the performance variation of the onboard BDS satellite clocks in real time. In future studies, we will focus on how to classify the abnormal clock types automatically for providing a reliable real-time clock monitoring and alerting service. Moreover, there are some deficiencies in the algorithm. When switching the reference clock in the real-time clock estimation process, subsequent periods of the clock will contain systematic bias from this reference. We set additional empirical values in the clock prediction threshold to avoid deleting normal epochs by mistake. However, some huge systematic biases would be remarked as outliers. So, in future work, we want to find math rules to replace the empirical values in the prediction threshold.
Author Contributions
Conceptualization, G.C. and W.F.; methodology, G.C.; software, X.C.; validation, Y.G., G.C. and L.M.; formal analysis, G.C.; investigation, W.F.; resources, W.F.; data curation, W.F.; writing original draft preparation, G.C.; writing—review and editing, T.L. and D.X.; supervision, Y.G.; project administration, Y.G.; funding acquisition, Y.G. and W.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Program of the National Natural Science Foundation of China (No. 41904038), the China Postdoctoral Science Foundation (No. 2019M662713); the Science and Technology Open Fund of Sichuan Society of Surveying, Mapping and Geographic Information (CCX202114), Sichuan Provincial Applied Fundamental Research Fund (2020YJ0362) and Scientific Research Fund of Sichuan Provincial Science and Technology Commission (2018GZDZX0047).
Data Availability Statement
The BDS satellite final clock and ultra-rapid orbit products that support the findings of this study are available from the IGS with access to https://cddis.nasa.gov/archive/gnss/products.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Xu, A.G.; Xu, Z.Q.; Xu, X.C.; Zhu, H.Z.; Sui, X.; Sun, H.S. Precise Point Positioning Using the Regional BeiDou Navigation Satellite Constellation. J. Navig. 2014, 64, 523–537. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Li, B.F.; Nie, L.W.; Wei, C.X.; Jia, S.; Jiang, S.Q. Initial assessment of BeiDou-3 global navigation satellite system: Signal quality, RTK and PPP. GPS Solut. 2019, 23, 111. [Google Scholar] [CrossRef]
- Hauschild, A.; Montenbruck, O.; Steigenberger, P. Short-term analysis of GNSS clocks. GPS Soult. 2013, 17, 295–307. [Google Scholar] [CrossRef]
- Galleani, L.; Tavella, P. Detection and identification of atomic clock anomalies. Metrologia 2008, 45, S127–S133. [Google Scholar] [CrossRef]
- El-Mowafy, A. Impact of predicting real-time clock corrections during their outages on precise point positioning. Surv. Rev. 2019, 51, 183–192. [Google Scholar] [CrossRef]
- Wang, K.; El-Mowafy, A. LEO satellite clock analysis and prediction for positioning applications. Geospat. Inf. Sci. 2021, 25, 14–33. [Google Scholar] [CrossRef]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Soult. 2018, 19, 93–105. [Google Scholar] [CrossRef]
- Chen, M.L.; Zhan, X.Q.; Du, G.; Liu, M.H. Compass/BeiDou-2 spaceborne clock performance assessment and its error detection, mitigation. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 438–446. [Google Scholar] [CrossRef]
- Sesia, I.; Tavella, P. Estimating the Allan variance in the presence of long periods of missing data and outliers. Metrologia 2008, 45, S134–S142. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Gui, Q.M. Bayesian methods for outliers detection in GNSS time series. J. Geod. 2013, 87, 609–627. [Google Scholar]
- Yang, Y.F.; Pan, X.; Qing, C.X.; Mei, C.S.; Lai, Z.L. Detection and repair of outliers in BDS satellite clock offset based on semiparametric mean drift model. Chin. J. Sci. Instrum. 2020, 41, 47–54. [Google Scholar]
- Pan, X.; Lv, Y.T.; Wang, Y.; Luo, J.; Xu, J.T. Research of the Location and Valuation of Gross Offsets Based on Semi-parametric Adjustment Model. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 1421–1426. [Google Scholar]
- Louni, H. Outier Detection in ARMA Models. J. Time Ser. Anal. 2008, 29, 1057–1065. [Google Scholar] [CrossRef]
- Ma, C.Z.; Zhu, J.Q.; Han, S.H. Model Selection Method Based on ARIMA Model in Outliers Detection of Satellite Clock Offset. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 167–172. [Google Scholar]
- Huang, B.H.; Ji, Z.X.; Zhai, R.J.; Xiao, C.F.; Yang, F.; Yang, B.H.; Wang, Y.P. Clock bias prediction algorithm for navigation satellites based on a supervised learning long short-term memory neural network. GPS Soult. 2021, 25, 80. [Google Scholar] [CrossRef]
- Wen, T.L.; Ou, G.; Tang, X.M.; Zhang, P.Y.; Wang, P.C. A Novel Long Short-Term Memory Predicted Algorithm for BDS Short-Term Satellite Clock Offsets. Int. J. Aerosp. Eng. 2021, 4066275. [Google Scholar] [CrossRef]
- Kirsten, L.; Penina, A. Improved prediction of GPS satellite clock sub-daily variations based on daily repeat. GPS Soult. 2018, 22, 58. [Google Scholar]
- Lee, S.W.; Kim, J.; Jeong, M.S.; Lee, Y.J. Monitoring atomic clocks on board GNSS satellites. Adv. Space Res. 2011, 47, 1654–1663. [Google Scholar] [CrossRef]
- Huang, G.W.; Zhang, Q.; Xu, G.C. Real-time clock offset prediction with an improved model. GPS Soult. 2014, 18, 95–104. [Google Scholar] [CrossRef]
- Ye, Y.U.; Zhang, H.; Xiaohui, L.I. A new method of GM(1,1)satellite clock bias prediction with error prediction correction. Sci. Surv. Mapp. 2019, 44, 814. [Google Scholar]
- Ge, H.B.; Li, B.F.; Wu, T.H.; Jiang, S.H. Prediction models of GNSS satellite clock errors: Evaluation and application in PPP. Adv. Space Res. 2021, 6, 2470–2487. [Google Scholar] [CrossRef]
- Yu, H.L.; Hao, J.M.; Liu, W.P.; Tian, Y.G.; Zhang, H. Analysis of Model In Ultra Short-term Predicting Satellite Clock Error. J. Geod. Geodyn. 2014, 34, 161–164. [Google Scholar]
- Wang, B.; Lou, Y.D.; Liu, J.N.; Zhao, Q.L.; Su, X. Analysis of BDS satellite clocks in orbit. GPS Soult. 2016, 20, 783–794. [Google Scholar] [CrossRef]
- Fu, W.J.; Wang, L.; Chen, R.Z.; Han, Y.; Zhou, H.T.; Li, T. Combined BDS-2/BDS-3 real-time satellite clock estimation with the overlapping B1I/B3I signals. Adv. Space Res. 2021, 68, 4470–4483. [Google Scholar] [CrossRef]
- Chen, G.; Gao, Y.P.; Fu, W.J.; Chen, X.; Yang, J.L. Availability and Prediction Performance Evaluation of BDS-3 Satellite Clock Error Products. In China Satellite Navigation Conference (CSNC 2021) Proceedings; Lecture Notes in Electrical Engineering; Springer: Singapore, 2021; Volume 772. [Google Scholar]
- Chen, L.; Zhao, Q.; Hu, Z.; Jiang, X.; Geng, C.; Ge, M.; Shi, C. GNSS global real-time augmentation positioning: Real-time precise satellite clock estimation, prototype system construction and performance analysis. Adv. Space Res. 2018, 61, 367–384. [Google Scholar] [CrossRef]
- Yu, D.Y.; Ji, B.; Liu, Y.; Wu, S.G.; Li, H.P.; Bian, S.F. Performance assessment of RTPPP positioning with SSR corrections and PPP-AR positioning with FCB for multi-GNSS from MADOCA products. Adv. Space Res. 2023, 6, P2924–P2937. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).