Combination of InSAR with a Depression Angle Model for 3D Deformation Monitoring in Mining Areas
Abstract
:1. Introduction
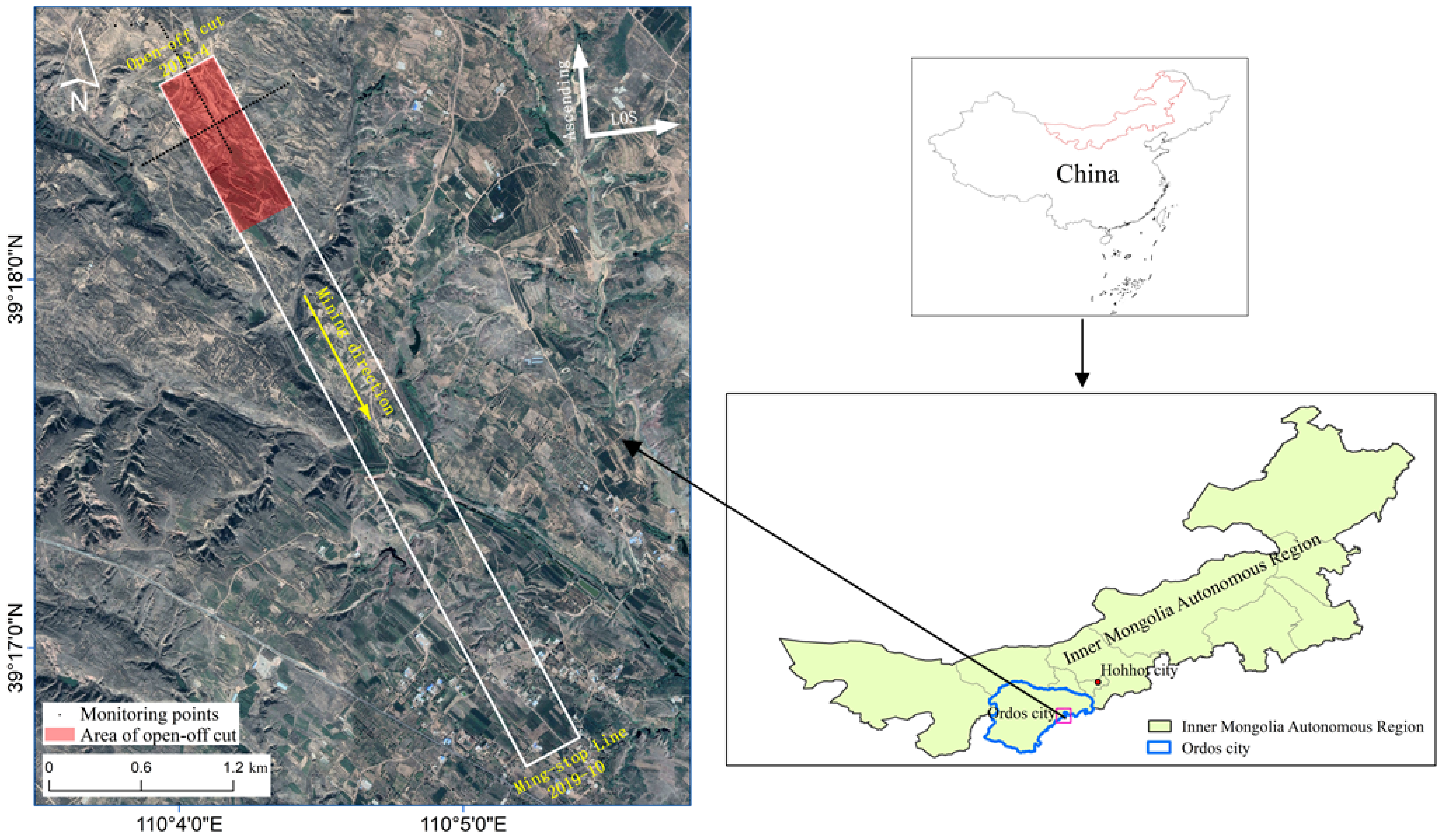
2. Study Areas and Data Source
3. Methodology
3.1. Basic Theories of InSAR Technology and PIM
3.2. Research Methods
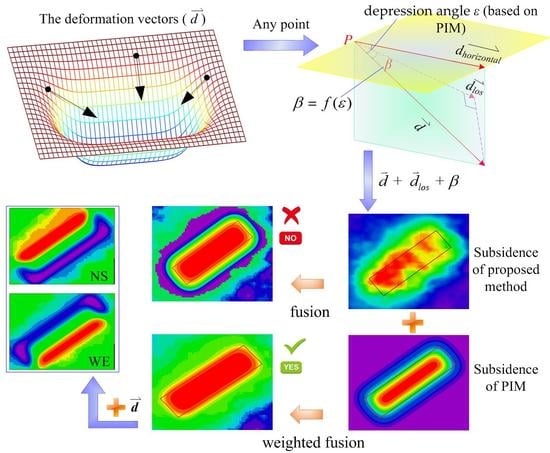
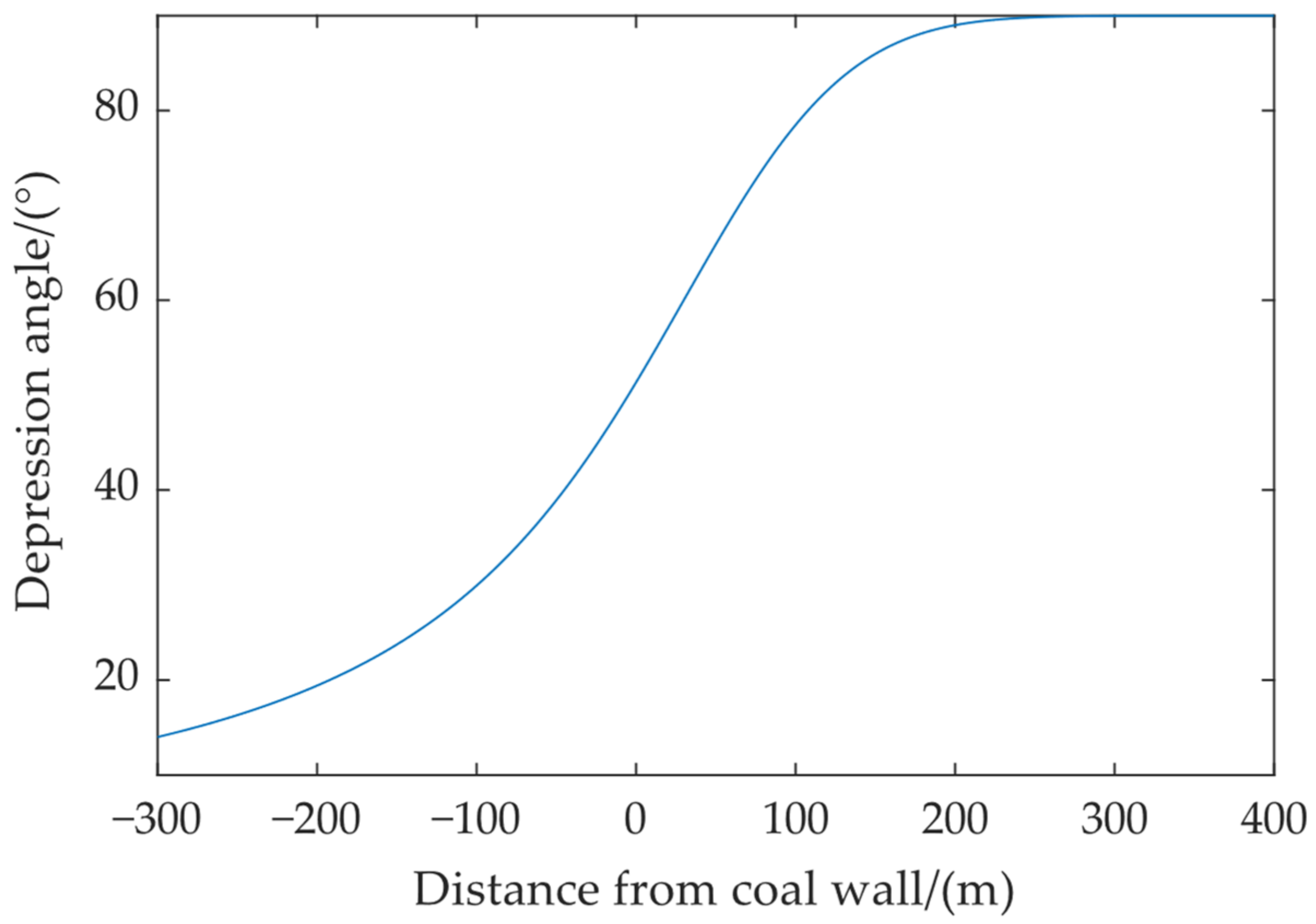
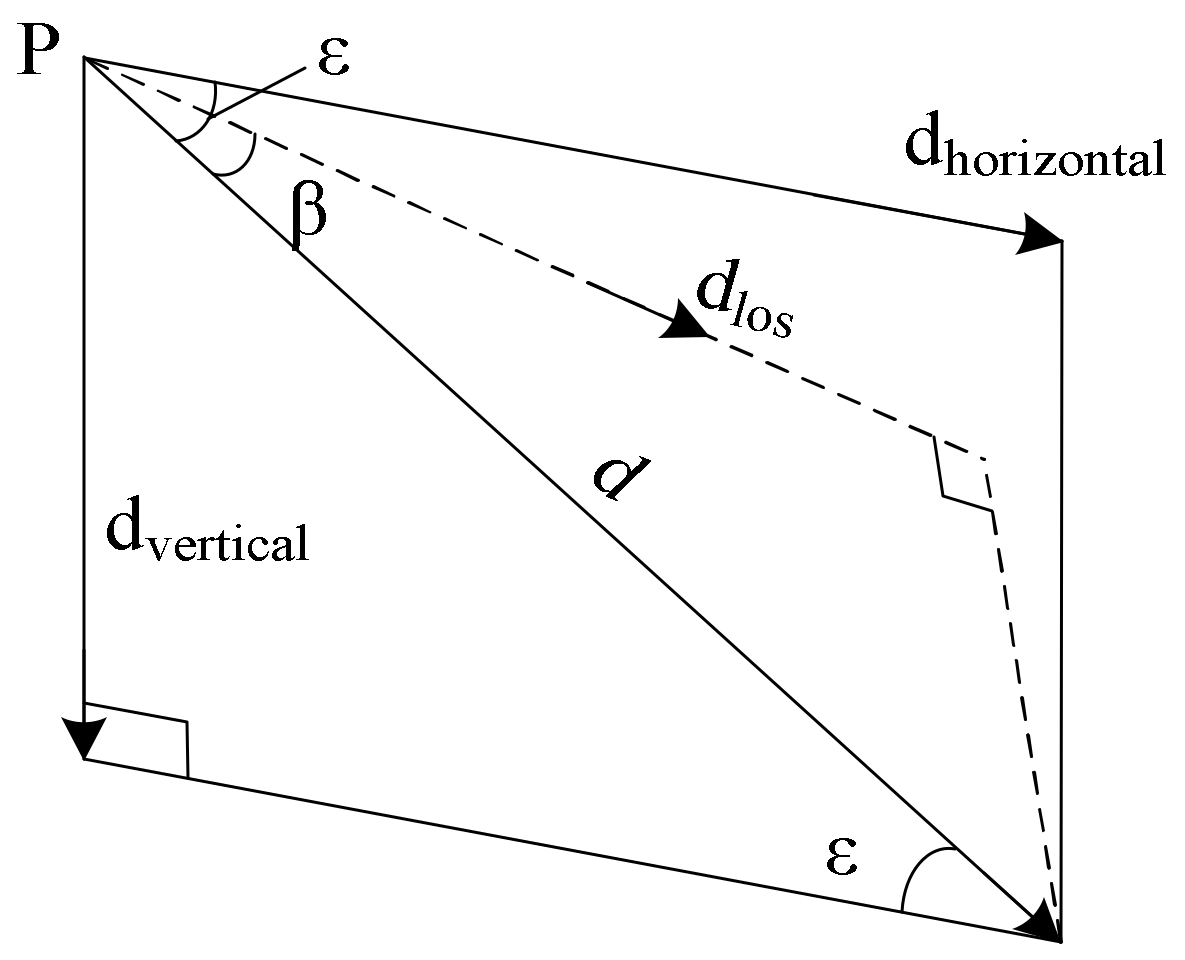
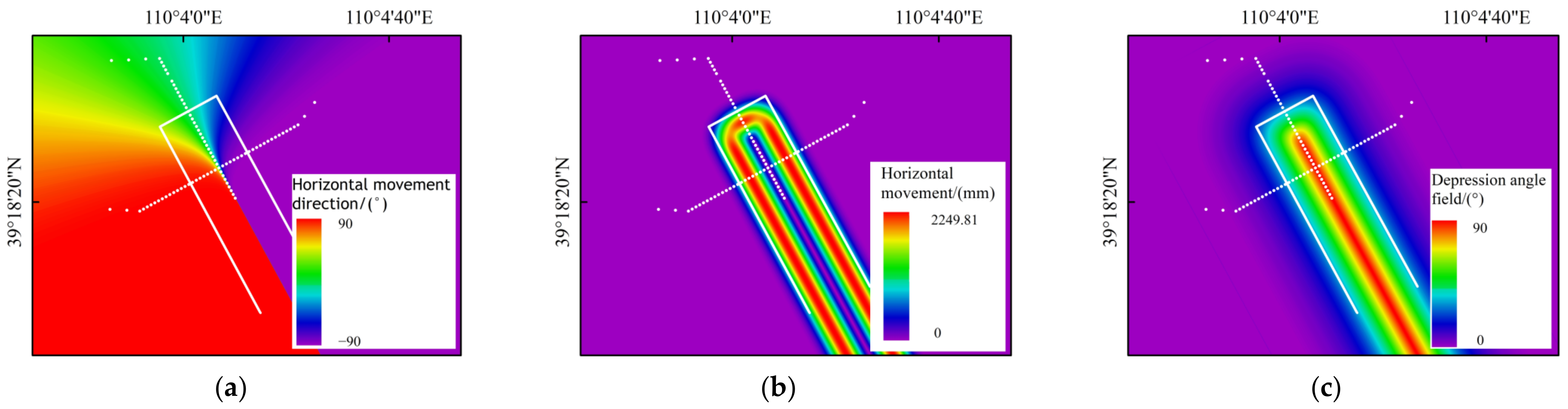
3.2.1. Depression Angle Model of Surface Displacement Vector
3.2.2. Method for Calculating the Surface Displacement Vector Combined InSAR with the Depression Angle Model
4. Results
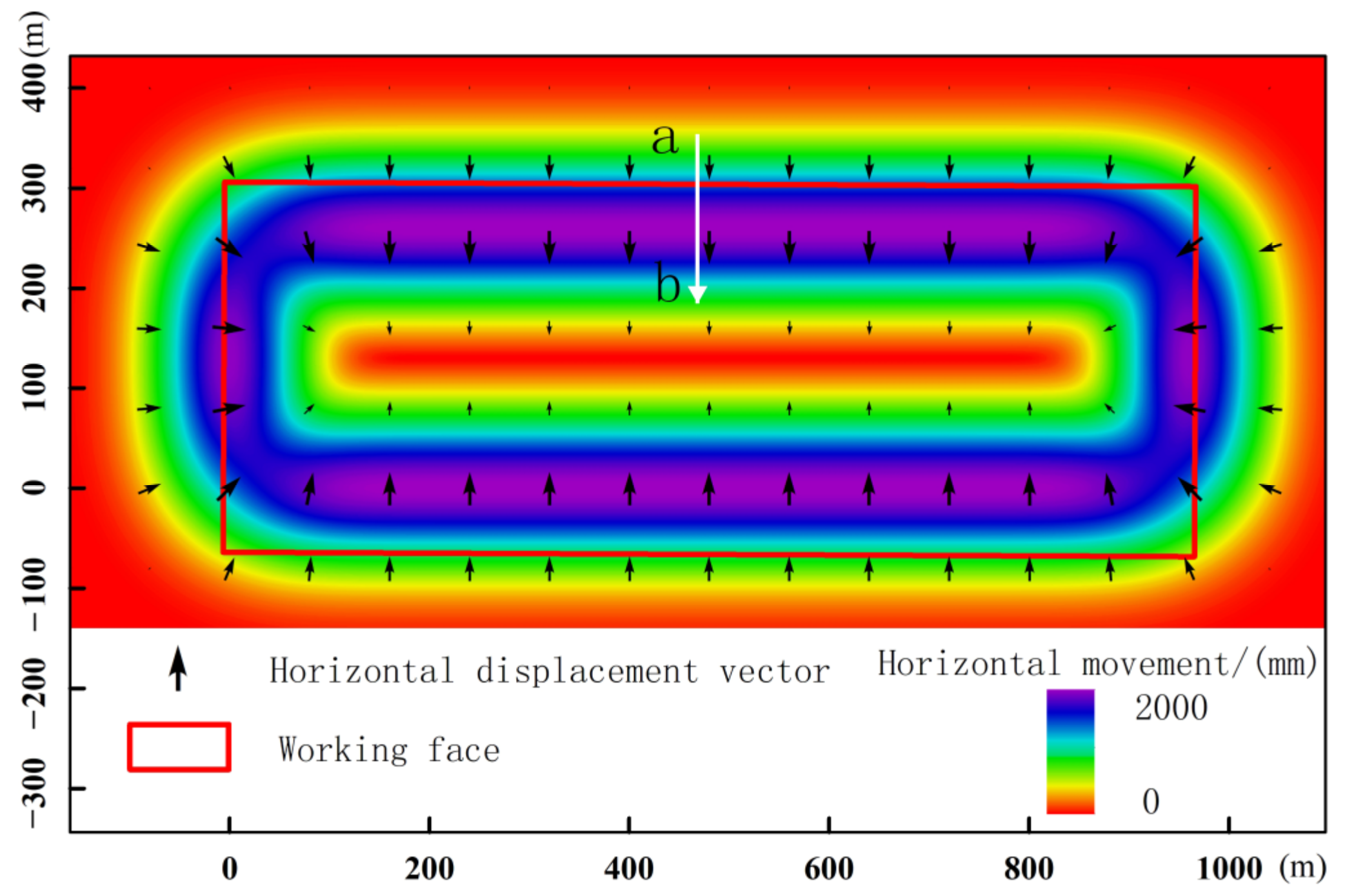
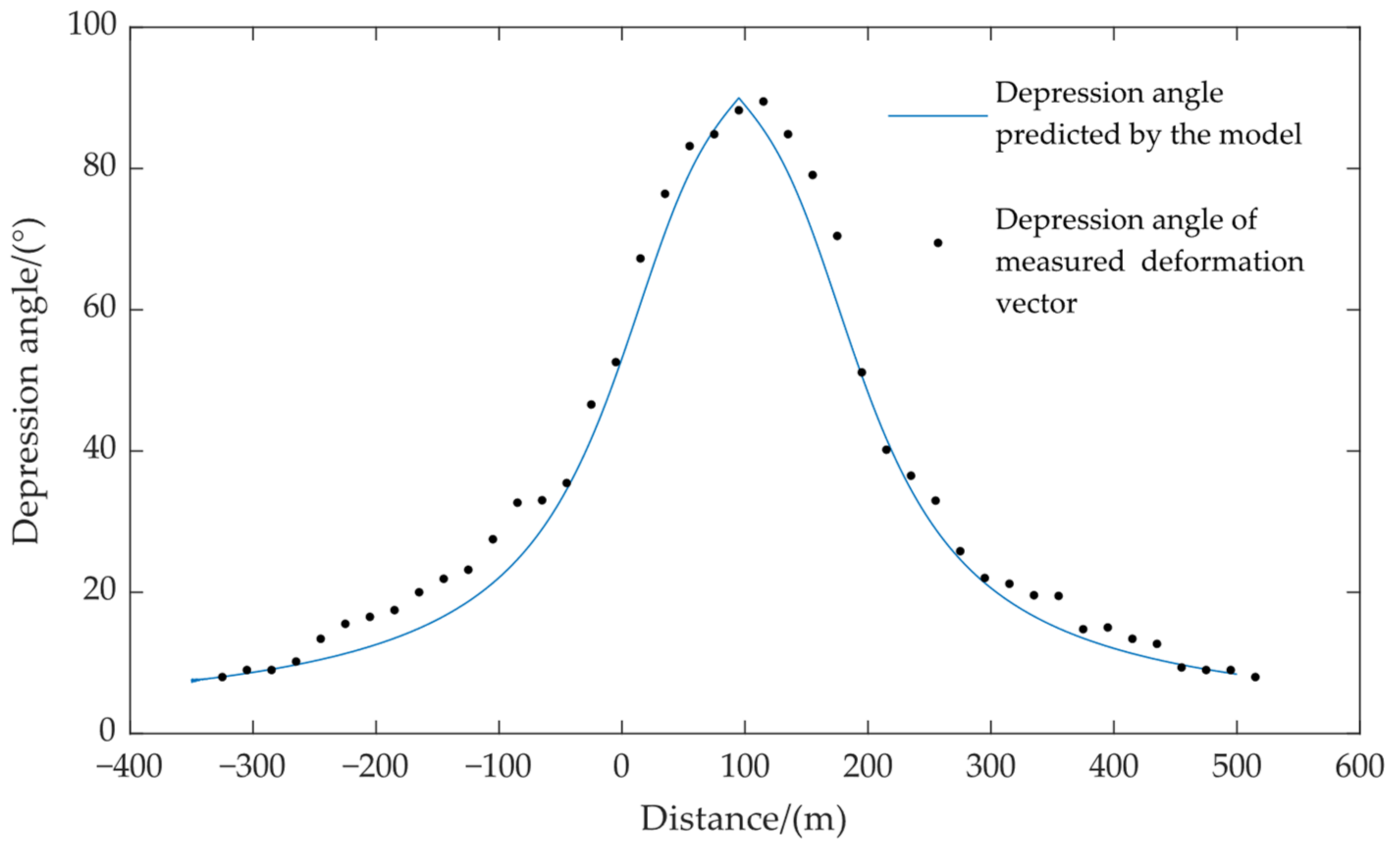
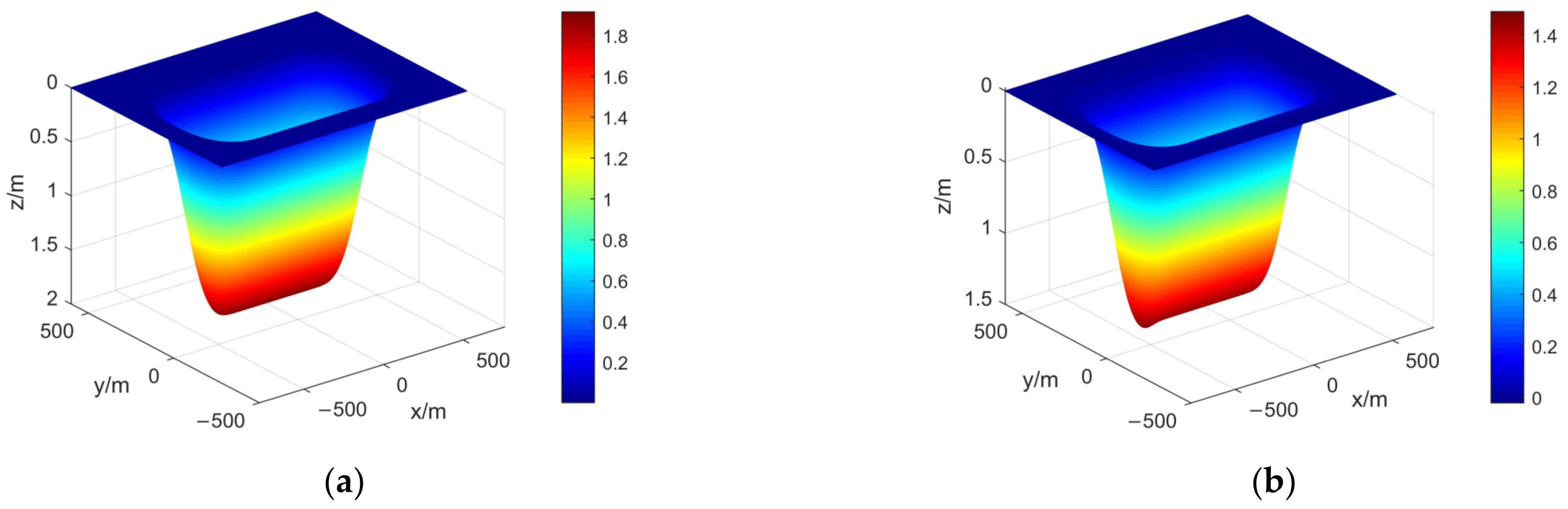
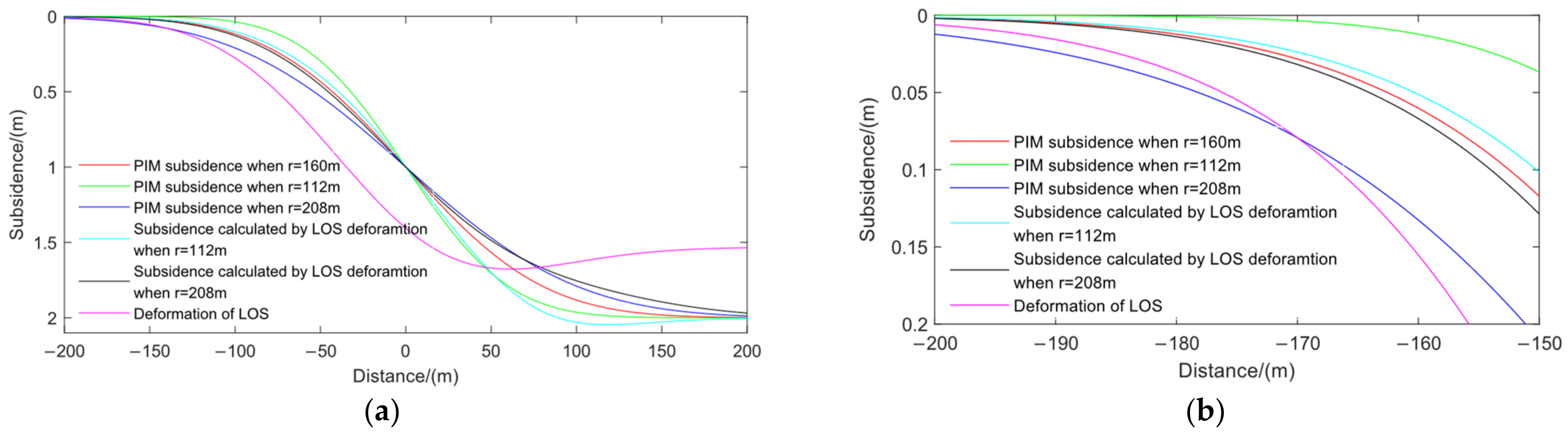
4.1. Application Analysis of the Depression Angle Model
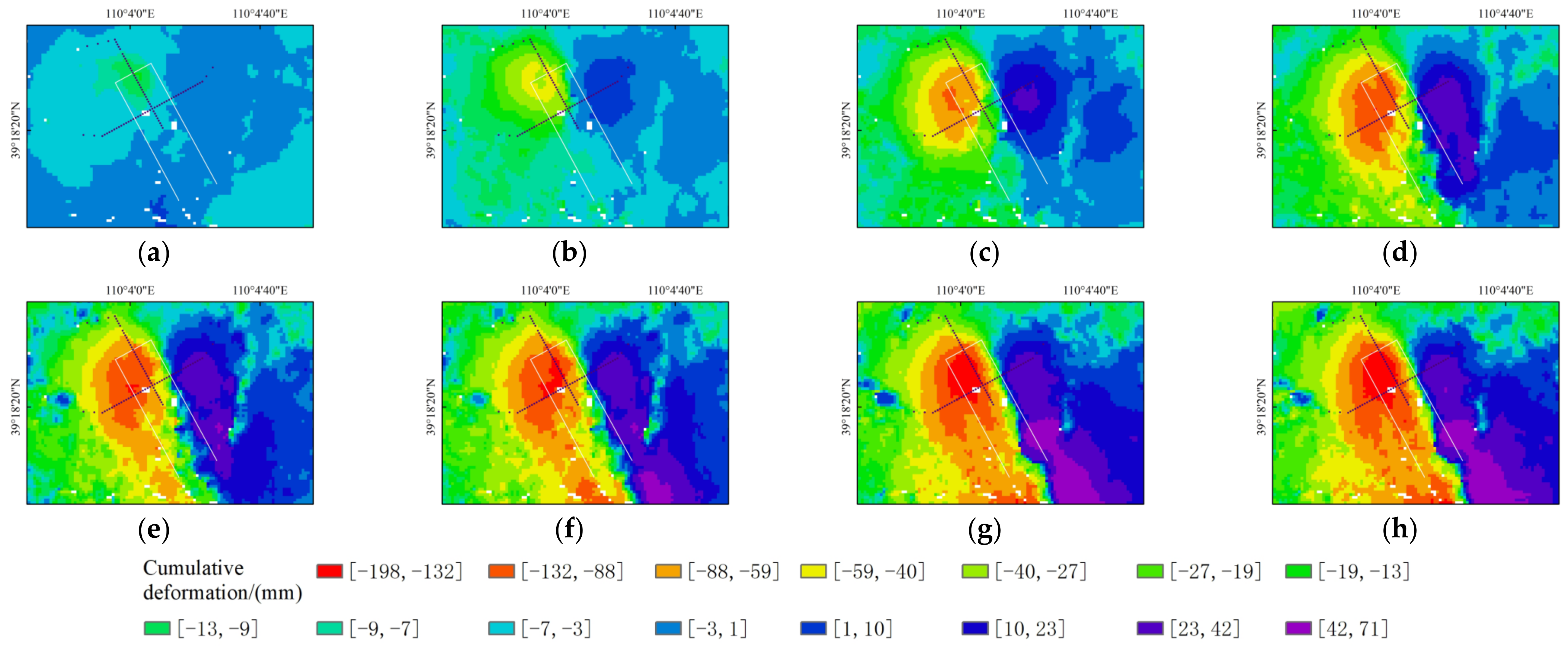
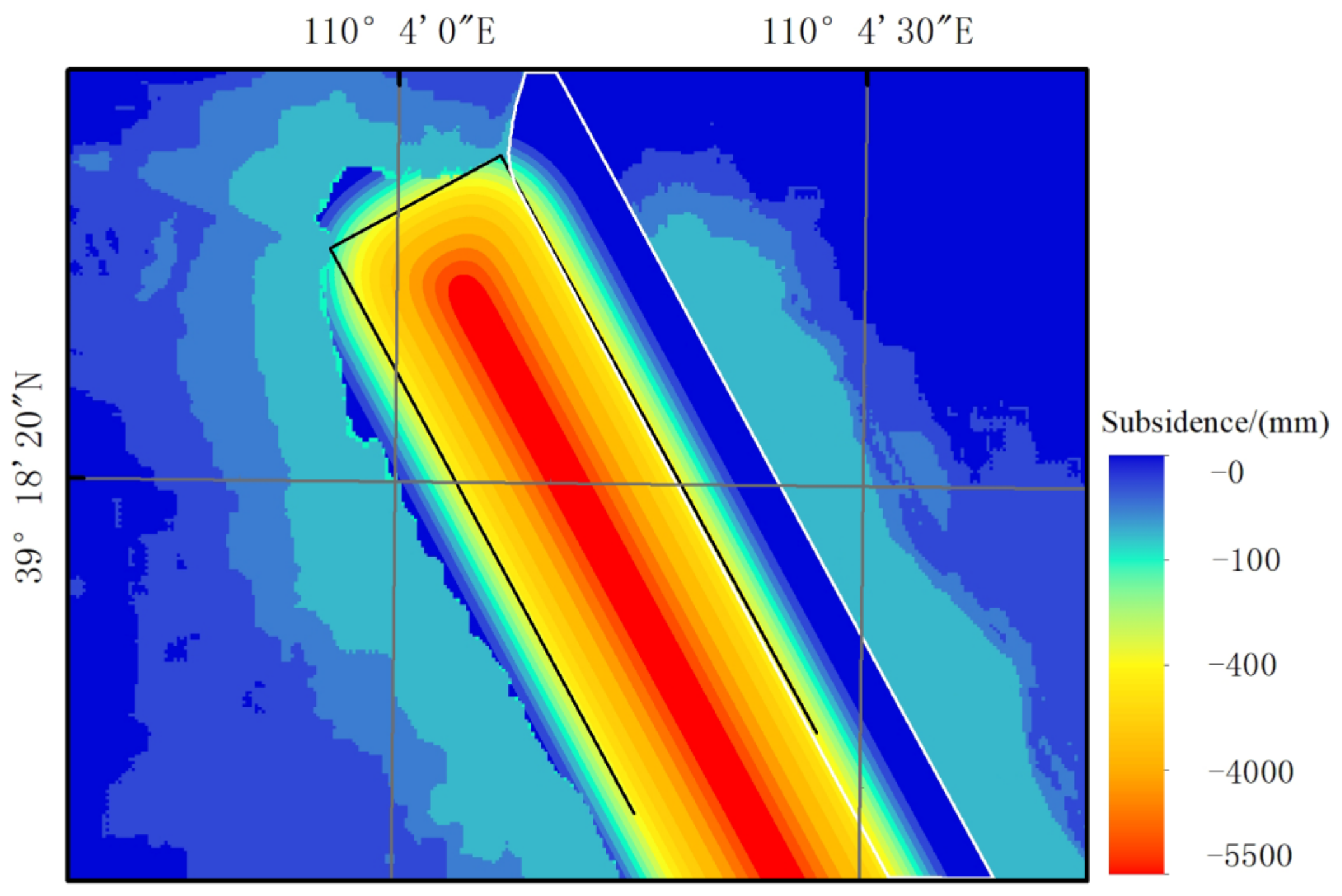
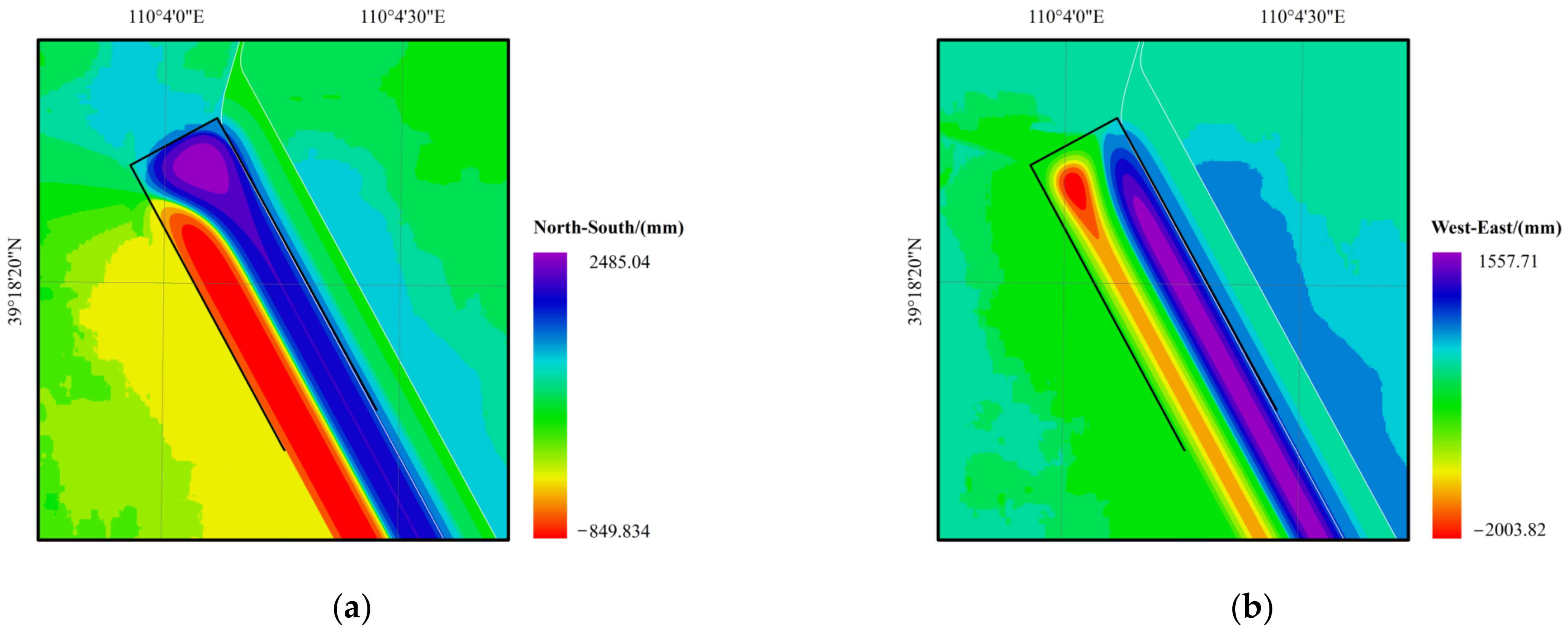
4.2. InSAR Deformation Monitoring in the Mining Area
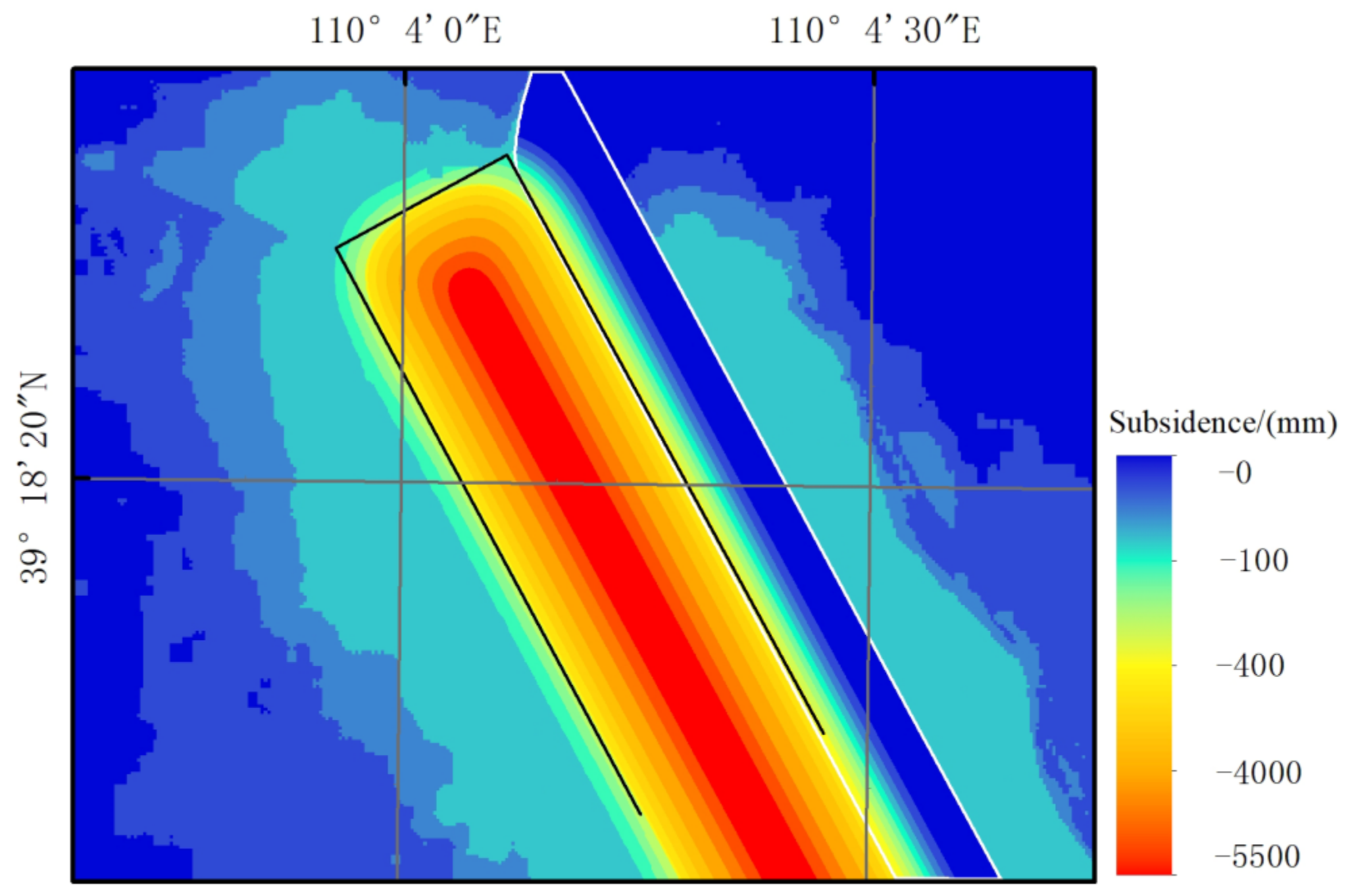
4.3. 3D Deformation Monitoring Based on PIM and InSAR Combined with Depression Angle Model
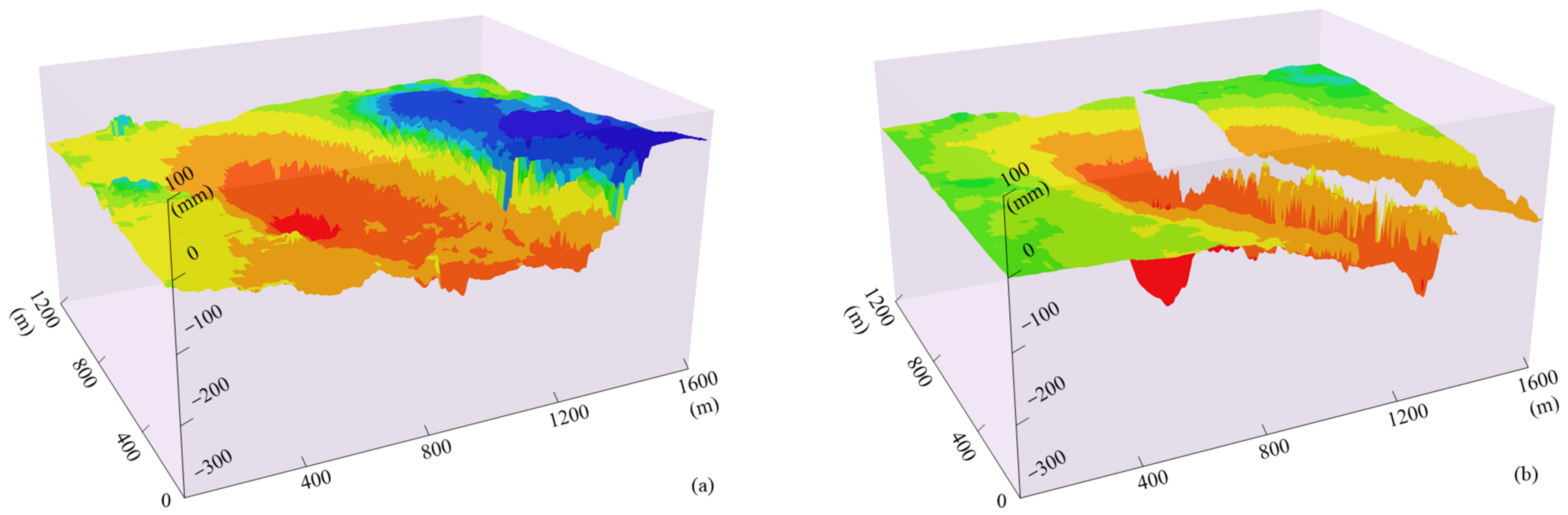
4.4. Accuracy Analysis of Vertical Deformation
- (1)
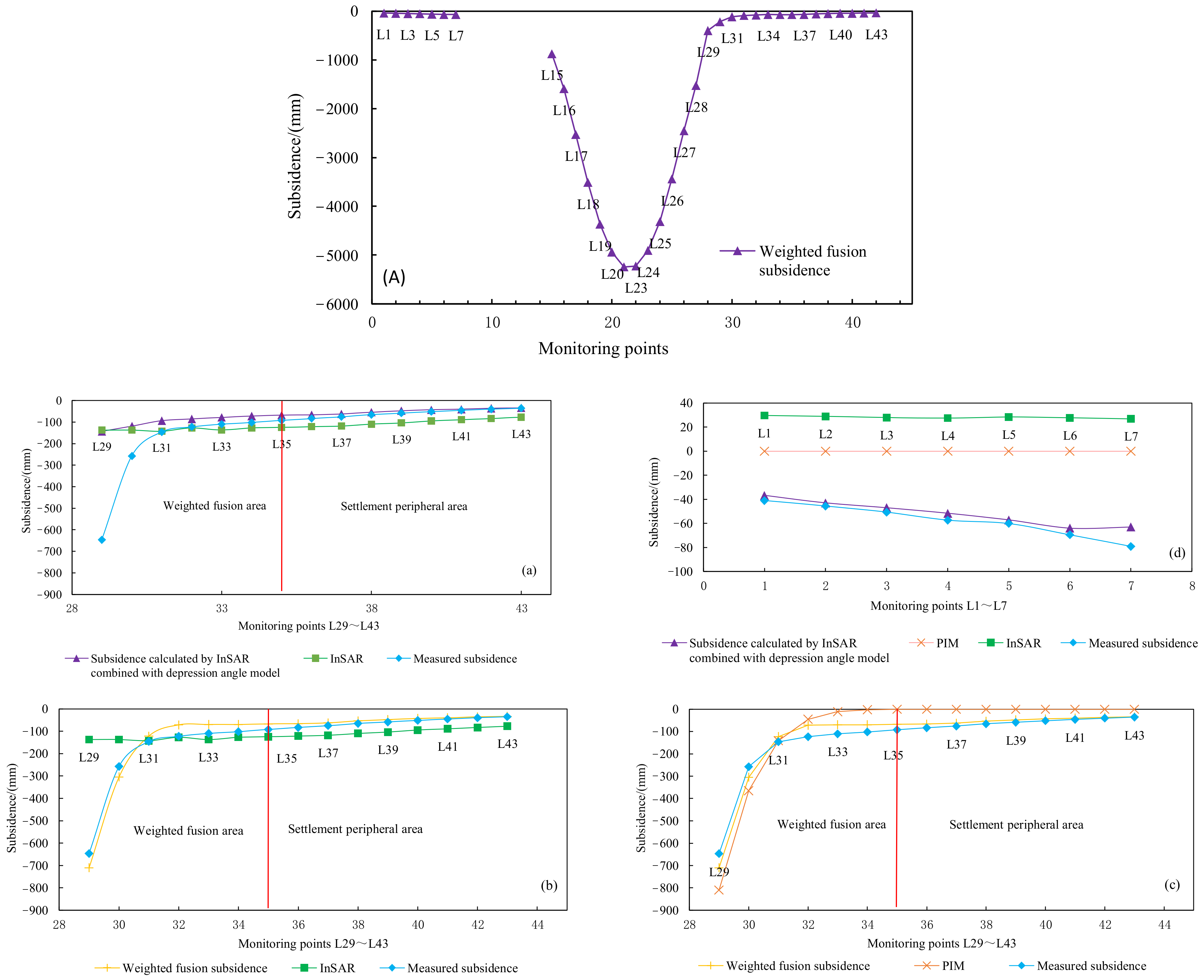
- The edge settlement area: The PIM converges too fast, and the predicted result is zero (Figure 20c,d). The difference between the InSAR-monitored results and the measured values is large, especially the InSAR-monitored results in Figure 20d, which shows that the ground surface is uplifted. The settlement after the weighted fusion of L35~L43 in Figure 20a and L1~L7 in Figure 20d (the edge area is equivalent to the settlement calculated by InSAR+ depression angle model) is highly consistent with the measured leveling value, with the RMSE equals 10 mm, which has a monitoring accuracy that is much higher than the 65 mm of InSAR and the 61 mm of PIM, and the monitoring accuracy is increased by 85% and 84%, respectively.
- (2)
- The weighted fusion area: The predicted result of the PIM increases from almost zero of L34 toward the center of the mining area, and it is gradually consistent with the measured value (Figure 20c). InSAR has begun losing surface deformation information gradually in this area as a result, and the subsidence calculated by InSAR+ depression angle model can only obtain part of the settlement information, which is less than the leveling value (Figure 20a). Through weighted fusion, the monitoring settlement accuracy is improved compared with the PIM, and the RMSE is reduced from 133 mm to 80 mm.
- (3)
- The overall results (edge settlement area and weighted fusion area): The overall monitoring accuracy RMSE of the edge settlement area and weighted fusion area is 42 mm, which is 66% and 44% higher than that of InSAR and PIM, respectively.
5. Discussion
6. Conclusions
- (1)
- The depression angle model of the displacement vector based on PIM is more consistent with the actual ground movement, which has a high fitting accuracy with the depression angles calculated from the measured values, in which R2 is 0.9981 and the RMSE is 2.9°. This shows that the depression angle model converges gently in the edge region, which is conducive to the inversion of edge subsidence.
- (2)
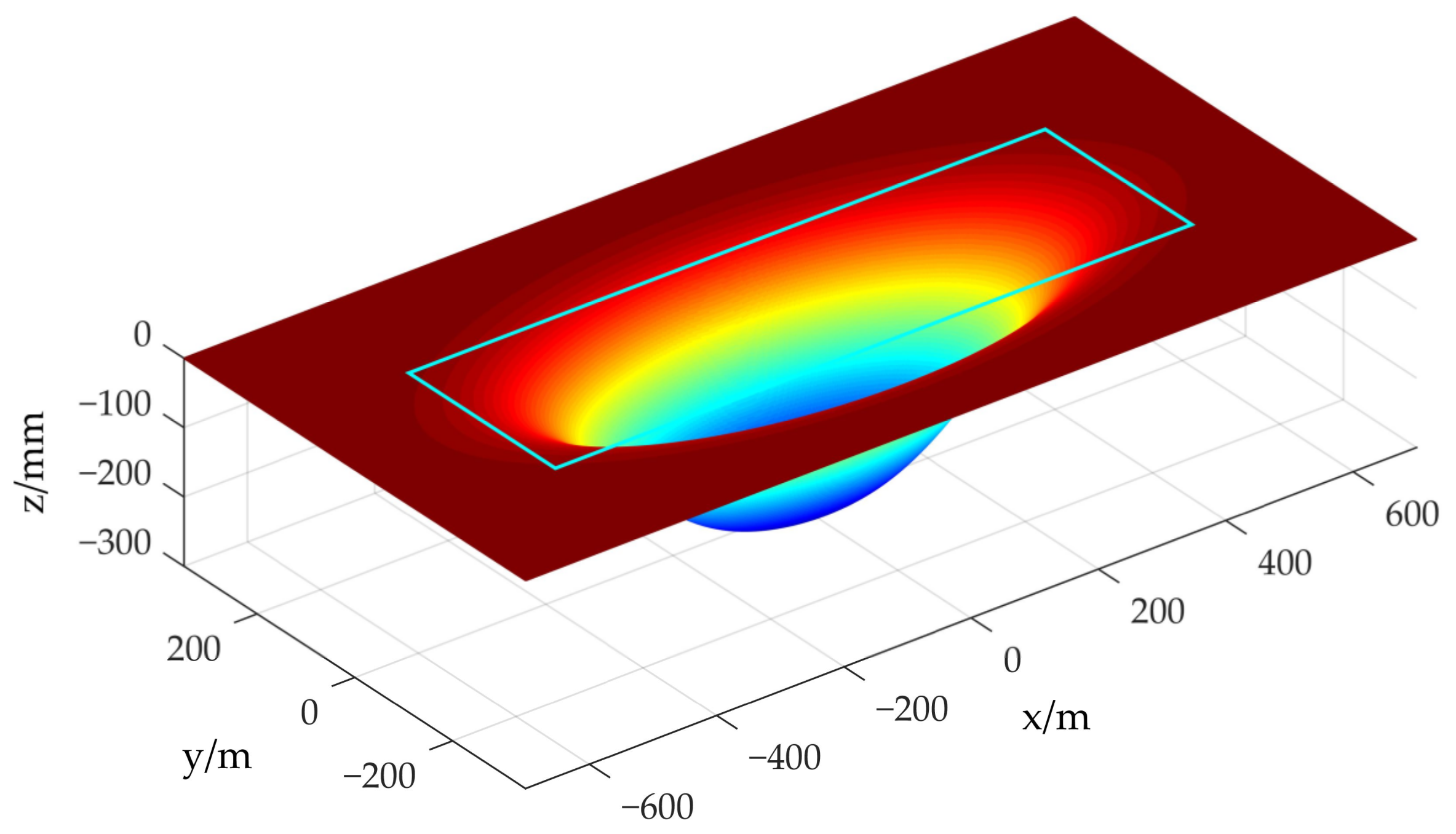
- The subsidence basins monitored by InSAR generally show a certain degree of skewness, and even some regions show surface uplift, which is difficult to reflect in the real surface deformation. The horizontal movement direction field of the mining area surface based on the PIM is consistent with the characteristics of the horizontal displacement of the surface. Compared with the depression angle field of the displacement vector and the surface subsidence information obtained by the method, the 3D deformation information of the whole basin is obtained, which makes up for the shortage of using the PIM or InSAR technology alone.
- (3)
- For the subsidence basin obtained with the proposed method, the subsidence in the edge area is obtained by the depression angle model combined with InSAR, and the RMSE tested by the measured value is 10 mm. The monitoring accuracy is 85% and 84% higher than that of InSAR and PIM, respectively. The RMSE of the weighted fusion area is 80 mm, and the monitoring accuracy improved by 63% and 40%, respectively. The overall RMSE of the two areas is 42 mm, and the monitoring accuracy improved by 66% and 44%, respectively. This shows that the proposed method can obtain more accurate surface subsidence information around the mining area, and the overall subsidence is more consistent with the actual situation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cui, X.M.; Che, Y.H.; Malinowska, A.; Zhao, Y.L.; Li, P.X.; Hu, Q.F.; Kang, X.L.; Bai, Z.H. Method and problems for subsidence prediction in entire process induced by underground mining. J. China Coal Soc. 2022, 47, 2170–2181. [Google Scholar]
- Wang, L.; Teng, C.Q.; Jiang, K.G.; Jiang, C.; Zhu, S.J. D-InSAR Monitoring Method of Mining Subsidence Based on Boltzmann and Its Application in Building Mining Damage Assessment. KSCE J. Civ. Eng. 2022, 26, 353–370. [Google Scholar] [CrossRef]
- Yang, Z.; Li, W.P.; Li, X.Q.; Wang, Q.Q.; He, J.H. Assessment of eco-geo-environment quality using multivariate data: A case study in a coal mining area of Western China. Ecol. Indic. 2019, 107, 105651. [Google Scholar] [CrossRef]
- Tang, F.Q. Mining subsidence monitoring using the method of combining InSAR and GPS technology. J. Coal Sci. Eng. 2011, 17, 133–136. [Google Scholar] [CrossRef]
- Klein, E.; Vigny, C.; Fleitout, L.; Grandin, R.; Jolivet, R.; Rivera, E.; Métois, M. A comprehensive analysis of the Illapel 2015 Mw8.3 earthquake from GPS and InSAR data. Earth Planet. Sci. Lett. 2017, 469, 123–134. [Google Scholar] [CrossRef] [Green Version]
- Vajedian, S.; Motagh, M.; Mousavi, Z.; Motaghi, K.; Fielding, E.J.; Akbari, B.; Wetzel, H.-U.; Darabi, A. Coseismic Deformation Field of the Mw 7.3 12 November 2017 Sarpol-e Zahab (Iran) Earthquake: A Decoupling Horizon in the Northern Zagros Mountains Inferred from InSAR Observations. Remote Sens. 2018, 10, 1589. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, T.J.; Wright, A.J.; Hooper, C.; Jordan, A.; Novellino, L.; Bateson, J. Biggs, Benchmarking and inter-comparison of Sentinel-1 InSAR velocities and time series. Remote Sens. Environ. 2021, 256, 112306. [Google Scholar]
- Eshqi Molan, Y.; Kim, J.-W.; Lu, Z.; Wylie, B.; Zhu, Z. Modeling Wildfire-Induced Permafrost Deformation in an Alaskan Boreal Forest Using InSAR Observations. Remote Sens. 2018, 10, 405. [Google Scholar] [CrossRef] [Green Version]
- Del Soldato, M.; Solari, L.; Raspini, F.; Bianchini, S.; Ciampalini, A.; Montalti, R.; Ferretti, A.; Pellegrineschi, V.; Casagli, N. Monitoring Ground Instabilities Using SAR Satellite Data: A Practical Approach. ISPRS Int. J. Geo-Inf. 2019, 8, 307. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.P.; Wang, Y.J. InSAR- and PIM-Based Inclined Goaf Determination for Illegal Mining Detection. Remote Sens. 2020, 12, 3884. [Google Scholar] [CrossRef]
- Shi, M.; Yang, H.; Wang, B.; Peng, J.; Gao, Z.; Zhang, B. Improving Boundary Constraint of Probability Integral Method in SBAS-InSAR for Deformation Monitoring in Mining Areas. Remote Sens. 2021, 13, 1497. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, S.; Tao, Q.; Liu, G.; Wang, L.; Wang, F. Accuracy Verification and Correction of D-InSAR and SBAS-InSAR in Monitoring Mining Surface Subsidence. Remote Sens. 2021, 13, 4365. [Google Scholar] [CrossRef]
- Xu, Y.; Li, T.; Tang, X.; Zhang, X.; Fan, H.; Wang, Y. Research on the Applicability of DInSAR, Stacking-InSAR and SBAS-InSAR for Mining Region Subsidence Detection in the Datong Coalfield. Remote Sens. 2022, 14, 3314. [Google Scholar] [CrossRef]
- Li, Y.x.; Yang, K.m.; Zhang, J.h.; Hou, Z.x.; Wang, S.; Ding, X.m. Research on time series InSAR monitoring method for multiple types of surface deformation in mining area. Nat. Hazards. 2022, 114, 2479–2508. [Google Scholar] [CrossRef]
- Palamà, R.; Crosetto, M.; Rapinski, J.; Barra, A.; Cuevas-González, M.; Monserrat, O.; Crippa, B.; Kotulak, N.; Mróz, M.; Mleczko, M. A Multi-Temporal Small Baseline Interferometry Procedure Applied to Mining-Induced Deformation Monitoring. Remote Sens. 2022, 14, 2182. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.; Zhang, H.; Tang, Y.; Zhang, X.; Zhang, Z. Small-Baseline Approach for Monitoring the Freezing and Thawing Deformation of Permafrost on the Beiluhe Basin, Tibetan Plateau Using TerraSAR-X and Sentinel-1 Data. Sensors 2020, 20, 4464. [Google Scholar] [CrossRef]
- Luebeck, D.; Wimmer, C.F.; Moreira, L.; Alcântara, M.; Oré, G.A.; Góes, J.P.; Oliveira, L.; Teruel, B.S.; Bins, L.H.; Gabrielli, L.; et al. Drone-borne Differential SAR Interferometry. Remote Sens. 2020, 12, 778. [Google Scholar] [CrossRef] [Green Version]
- Tao, Q.X.; Liu, G.L.; Liu, W.K. Analysis of capabilities of L and C-band SAR data to monitor mining-induced subsidence. Chin. J. Geophys. 2012, 55, 3681–3689. [Google Scholar]
- Zhu, J.J.; Yang, Z.F.; Li, Z.W. Recent progress in retrieving and predicting mining induced 3D displacements using InSAR. Acta Geodaetica et Cartographica Sinica 2019, 48, 135–144. [Google Scholar]
- Samsonov, S.; d’Oreye, N.; Smets, B. Ground deformation associated with post-mining activity at the French–German border revealed by novel InSAR time series method. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 142–154. [Google Scholar]
- Zhu, J.J.; Li, Z.W.; Hu, J. Research progress and methods of InSAR for deformation monitoring. Acta Geod. Cartogr. Sinica 2017, 46, 1717–1733. [Google Scholar]
- Yang, Z.; Li, Z.; Zhu, J.; Feng, G.; Wang, Q.; Hu, J.; Wang, C. Deriving time-series three-dimensional displacements of mining areas from a single-geometry InSAR dataset. J. Geod. 2018, 92, 529–544. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Preusse, A.; Hu, J.; Feng, G.C.; Yi, H.W.; Papst, M. An alternative method for estimating 3-D large displacements of mining areas from a single SAR amplitude pair using offset tracking. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3645–3656. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, L.; Yu, X.X.; Chi, S.S.; Tao, W.; Wang, X.L. DPIM-Based InSAR Phase Unwrapping Model and a 3D Mining-Induced Surface Deformation Extracting Method: A Case of Huainan Mining Area. KSCE J. Civ. Eng. 2021, 25, 654–668. [Google Scholar] [CrossRef]
- Diao, X.P.; Wu, K.; Hu, D.H.; Li, L.; Zhou, D.W. Combining differential SAR interferometry and the probability integral method for three-dimensional deformation monitoring of mining areas. Int. J. Remote Sens. 2016, 37, 5196–5212. [Google Scholar] [CrossRef]
- Tang, F.Q.; Dong, L.K.; Wang, Z.L.; Huang, J.C. A 3-D inversion model for InSAR detected displacements based on ground subsidence symmetry induced by horizontal coal mining. J. China Coal Soc. 2019, 44, 210–220. [Google Scholar]
- Fan, H.D.; Wang, L.; Wen, B.F.; Du, S. A new model for three-dimensional deformation extraction with single-track insar based on mining subsidence characteristics. Int. J. Appl. Earth Obs. Geoinf. 2021, 94, 102223. [Google Scholar] [CrossRef]
- Luo, H.B.; Li, Z.H.; Chen, J.J.; Pearson, C.; Wang, M.M.; Lv, W.C.; Ding, H.Y. Integration of range split spectrum interfer-ometry and conventional InSAR to monitor large gradient surface displacements. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 130–137. [Google Scholar]
- He, G.Q. Mining Subsidence; China University of Mining and Technology Press: Xuzhou, China, 1991. [Google Scholar]
- Chen, Y.; Tao, Q.X.; Liu, G.L.; Wang, L.Y.; Wang, F.Y.; Wang, K. Detailed mining subsidence monitoring combined with InSAR and probability integral method. Chin. J. Geophys. 2021, 64, 3554–3566. [Google Scholar]
- Tan, Z.X.; Yang, J.W.; Deng, K.Z. Study on method of mining subsidence parameters calculating for whole basin of mining area based on SBAS-InSAR. Coal Sci. Technol. 2021, 49, 312–318. [Google Scholar]
- Hou, Z.X.; Yang, K.M.; Li, Y.R.; Gao, W.; Wang, S.; Ding, X.M.; Li, Y.X. Dynamic prediction model of mining subsidence combined with D-InSAR technical parameter inversion. Environ. Earth Sci. 2022, 81, 307. [Google Scholar] [CrossRef]
- Zhang, W.H.; Shi, J.C.; Yi, H.W.; Zhu, Y.; Xu, B. Underground Goaf Parameters Estimation by Cross-Iteration with InSAR Measurements. Remote Sens. 2021, 13, 3204. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Lian, X.G.; Ge, L.L.; Liu, X.Y.; Du, Z.Y.; Yang, W.F.; Wu, Y.R.; Hu, H.F.; Cai, Y.F. Surface Subsidence Monitoring Induced by Underground Coal Mining by Combining DInSAR and UAV Photogrammetry. Remote Sens. 2022, 14, 4711. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Q.S.; Dai, H.Y.; Guo, J.T.; Yan, Y.G. Research on integrated monitoring technology and practice of “space-sky-ground” on surface movement in mining area. Coal Sci. Technol. 2020, 48, 207–213. [Google Scholar]
- Baran, I.; Stewart, M.; Claessens, S. A new functional model for determining minimum and maximum detectable deformation gradient resolved by satellite radar interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 675–682. [Google Scholar] [CrossRef]
- Hao, Y.J.; Wu, L.X.; Dai, H.Y. Establish ground settlement prediction model with elastic slab theory. Chin. J. Rock Mech. Eng. 2006, 25, 2958–2962. [Google Scholar]
- Wang, J.B.; Liu, X.R.; Liu, X.J. Dynamic prediction model for mining subsidence. J. China Coal Soc. 2015, 40, 516–521. [Google Scholar]








| Basic Parameters | Sentinel-1A |
|---|---|
| Orbit | Sun synchronous orbit |
| Orbital altitude/km | 693 |
| Orbit inclination/(°) | 98.18 |
| Angle of incidence | 18.3°~46.8° |
| Revisit period/d | 12 |
| Imaging mode | IW |
| Band | C |
| Central incidence angle/(°) | 38.92 |
| Cartographic resolution/m | 20 × 20 |
| Methods | Edge Subsidence Area (L1~L7, L35~L43) RMSE/mm | Weighted Fusion Area (L29~L34) RMSE/mm | Overall Results (L1~L7, L35~L43, and L29~L34) RMSE/mm |
| InSAR | 65 | 214 | 124 |
| InSAR+ depression angle model | 10 | 180 | 113 |
| PIM | 61 | 133 | 75 |
| weighted fusion | 10 | 80 | 42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Dai, H.; Yan, Y.; Liu, J.; Ren, J. Combination of InSAR with a Depression Angle Model for 3D Deformation Monitoring in Mining Areas. Remote Sens. 2023, 15, 1834. https://doi.org/10.3390/rs15071834
Wang Z, Dai H, Yan Y, Liu J, Ren J. Combination of InSAR with a Depression Angle Model for 3D Deformation Monitoring in Mining Areas. Remote Sensing. 2023; 15(7):1834. https://doi.org/10.3390/rs15071834
Chicago/Turabian StyleWang, Zhihong, Huayang Dai, Yueguan Yan, Jibo Liu, and Jintong Ren. 2023. "Combination of InSAR with a Depression Angle Model for 3D Deformation Monitoring in Mining Areas" Remote Sensing 15, no. 7: 1834. https://doi.org/10.3390/rs15071834
APA StyleWang, Z., Dai, H., Yan, Y., Liu, J., & Ren, J. (2023). Combination of InSAR with a Depression Angle Model for 3D Deformation Monitoring in Mining Areas. Remote Sensing, 15(7), 1834. https://doi.org/10.3390/rs15071834