Improved Geometric Optics with Topography (IGOT) Model for GNSS-R Delay-Doppler Maps Using Three-Scale Surface Roughness
Abstract
:1. Introduction
2. Theoretical Model
2.1. Ground Surface Modeling
2.2. BRCS DDM Modeling
3. Validation Cases
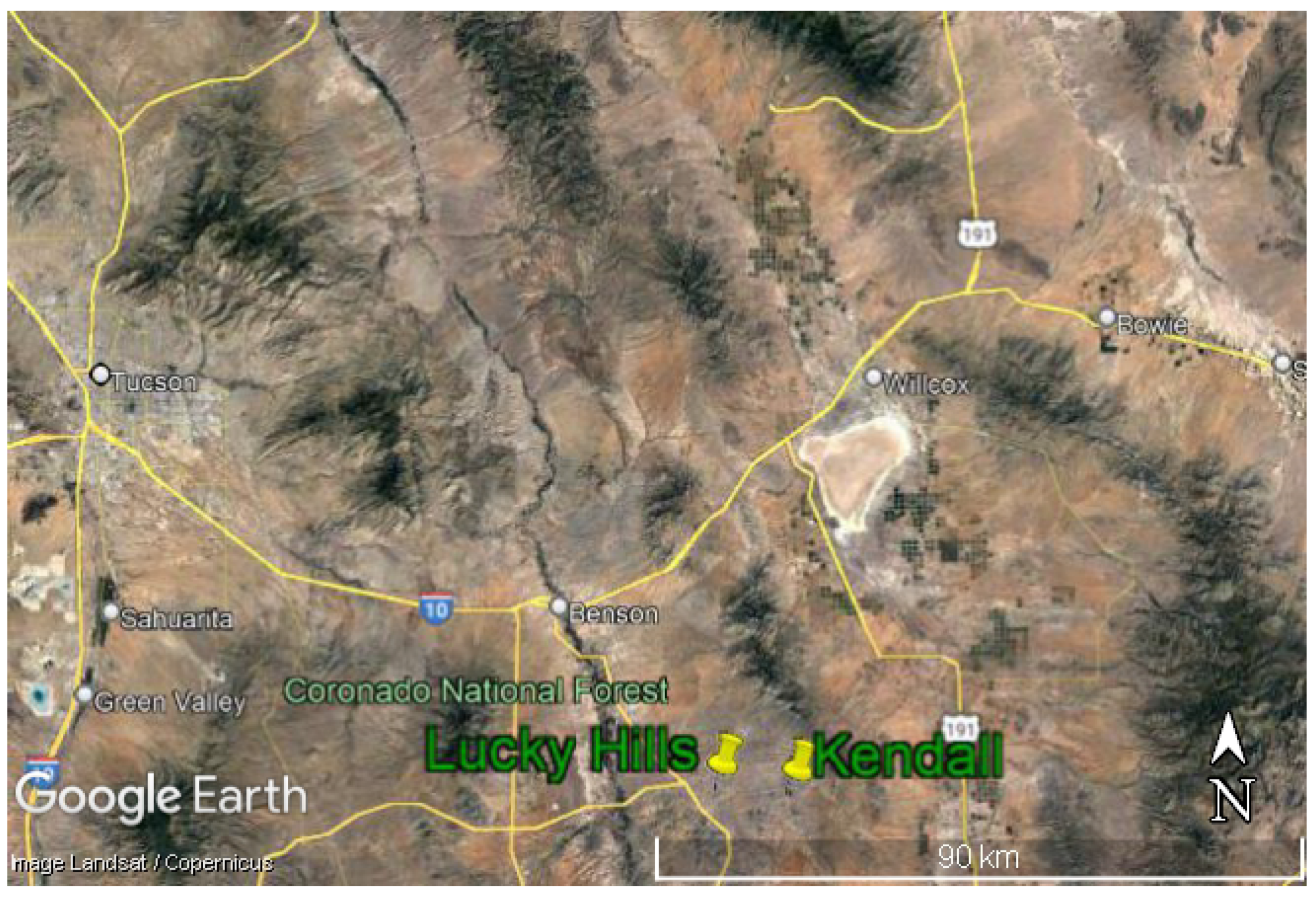
3.1. Validation Sites
3.1.1. Walnut Gulch (WG)
3.1.2. Jornada Experimental Range (JER)
3.2. Surface Roughness Measurements
3.3. CYGNSS and Ancillary Data
4. Validation Results
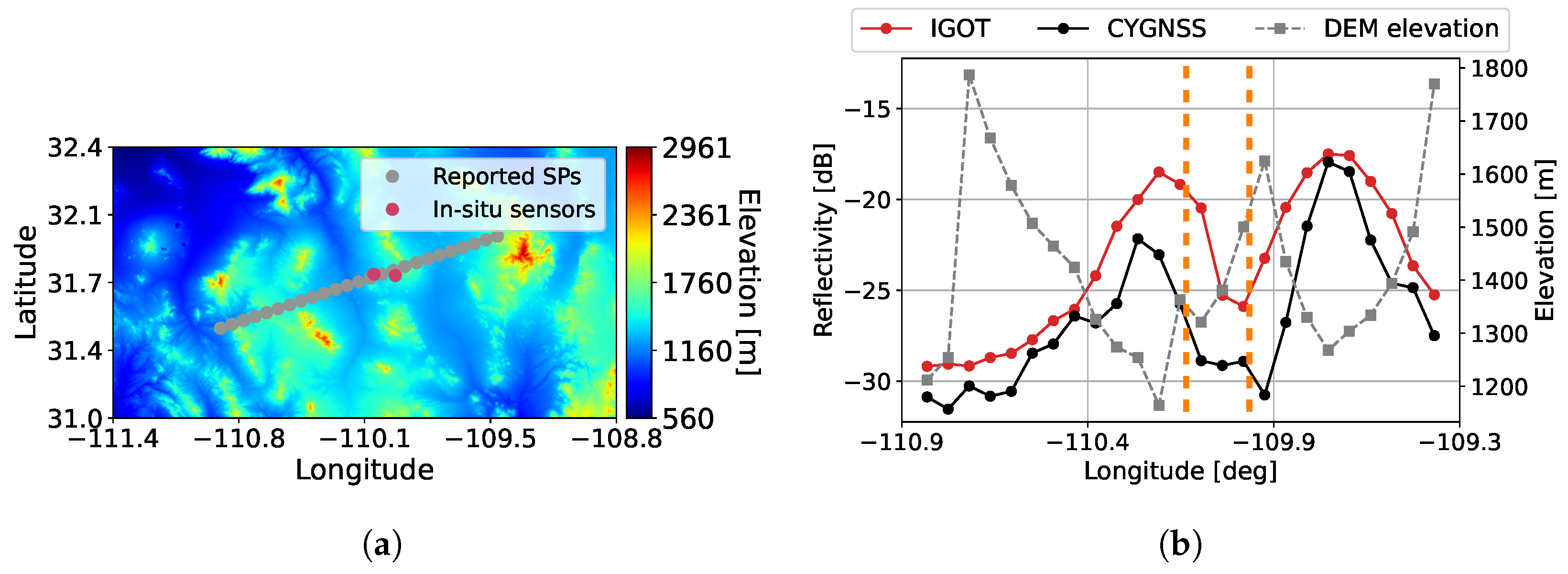
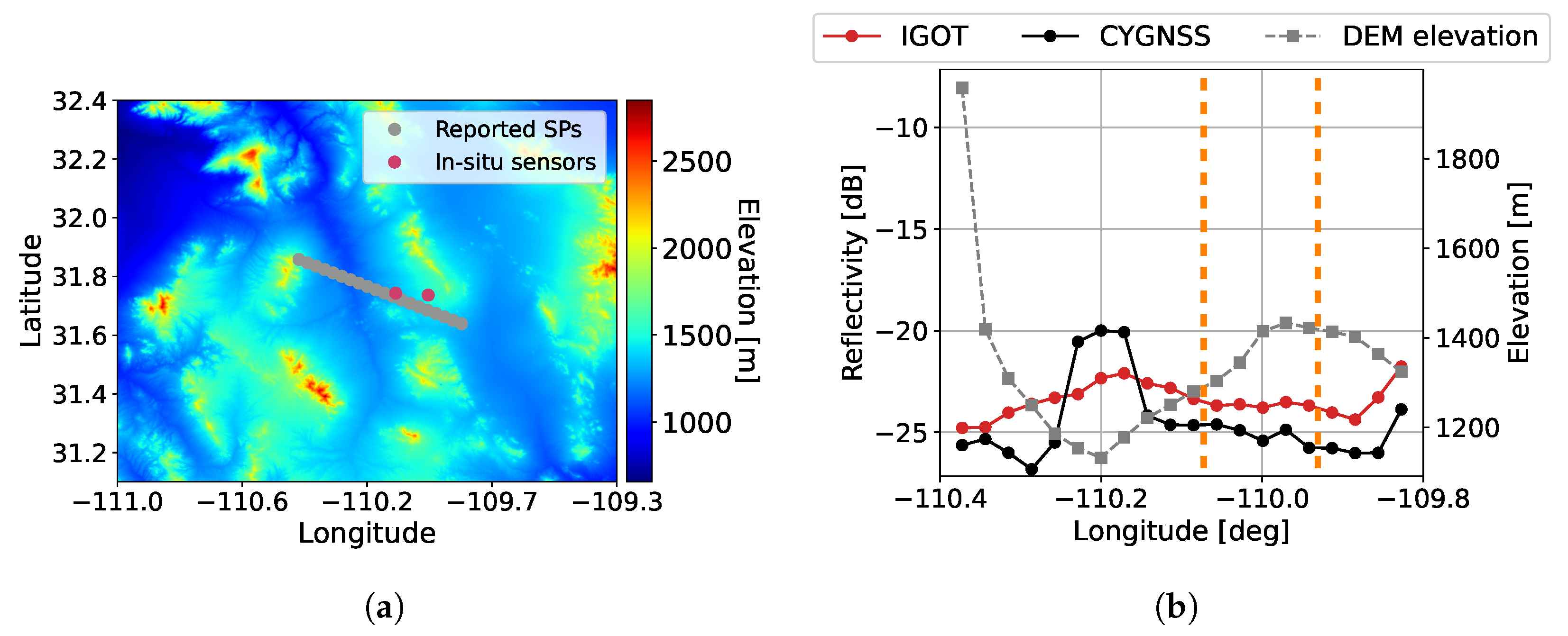
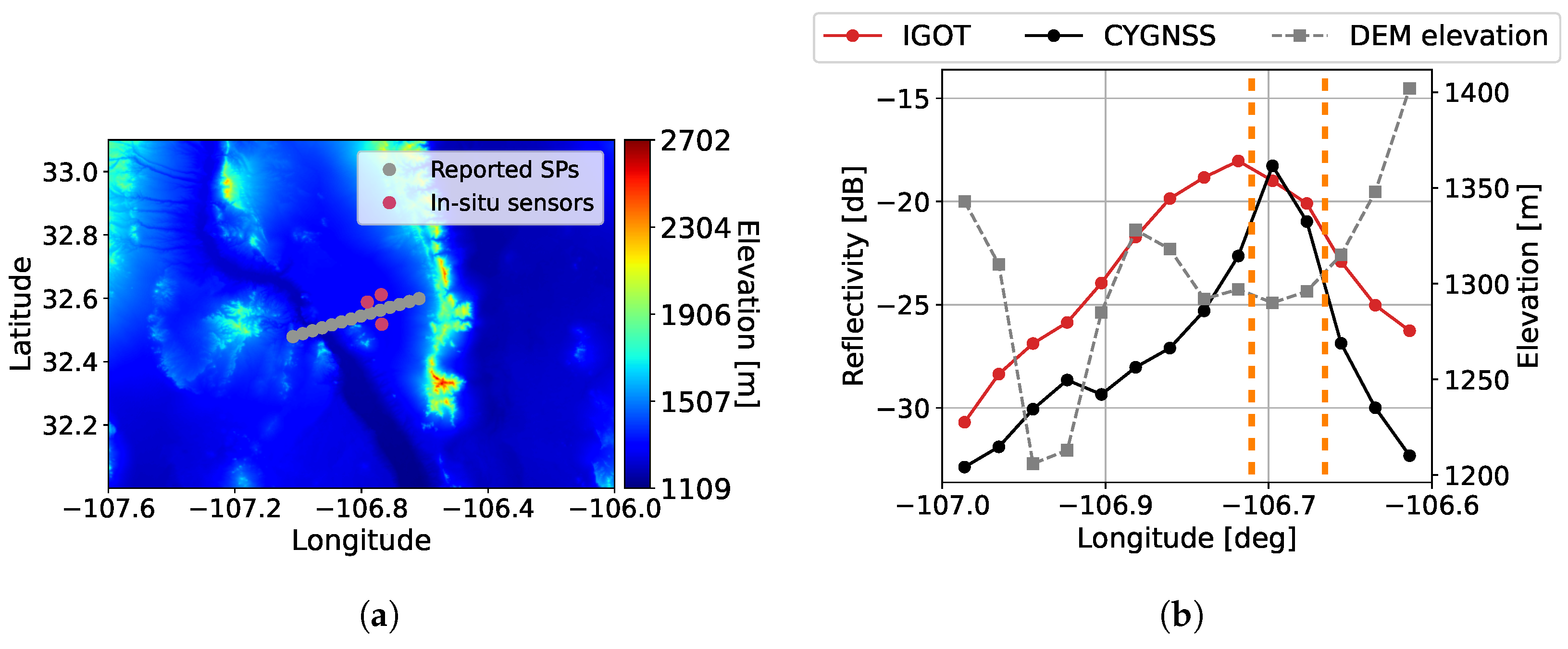
4.1. Along-Track Results
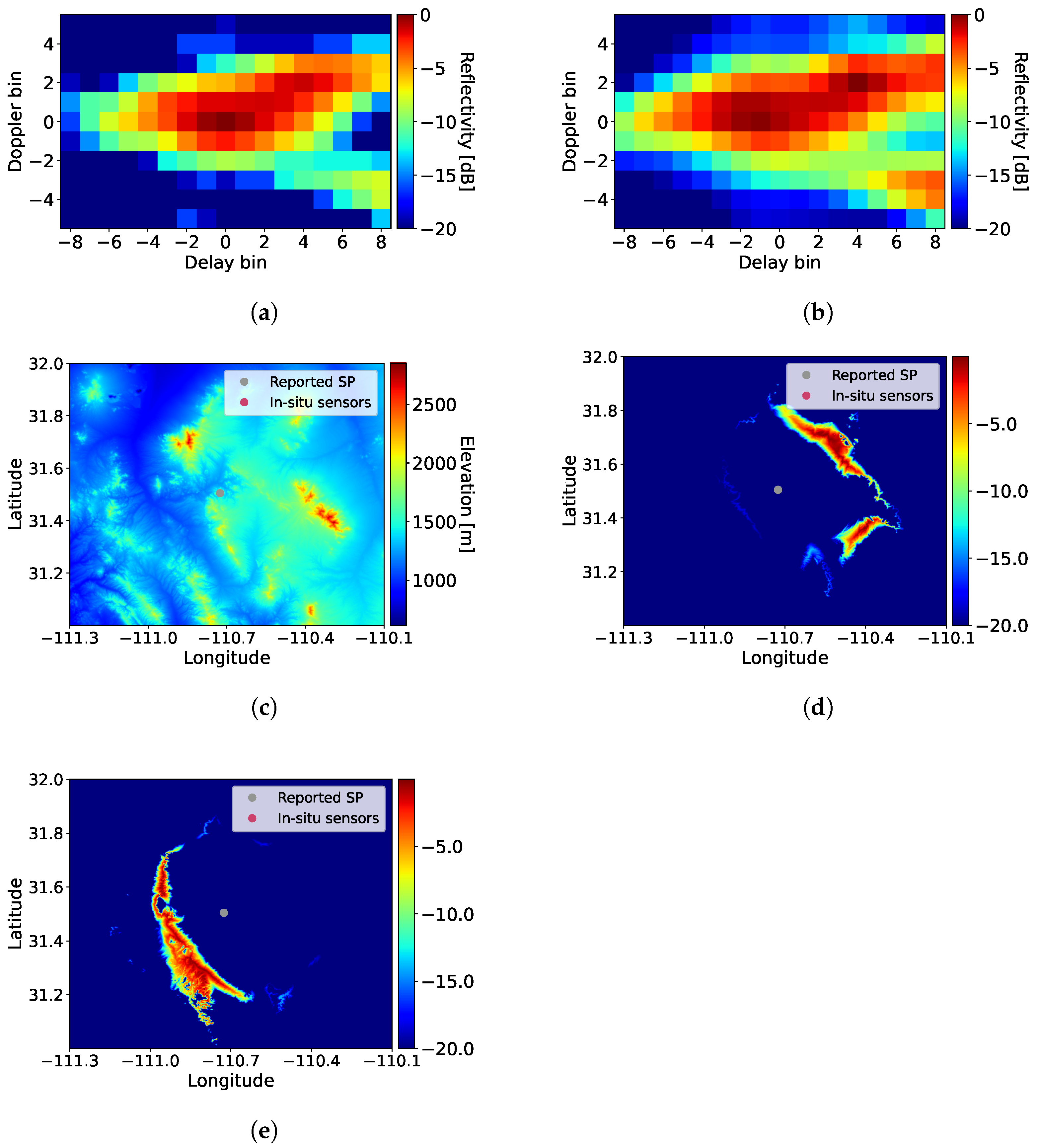
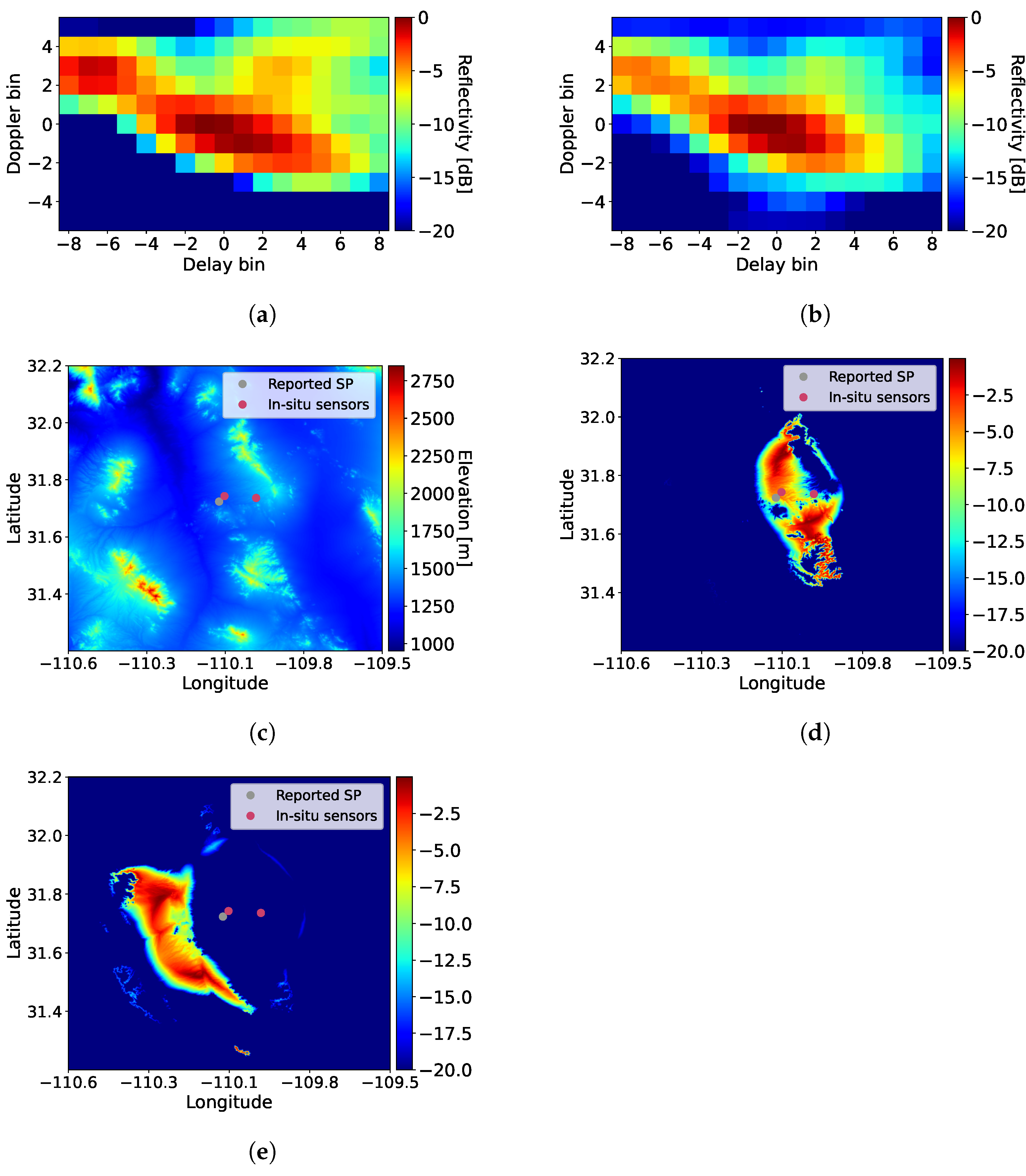
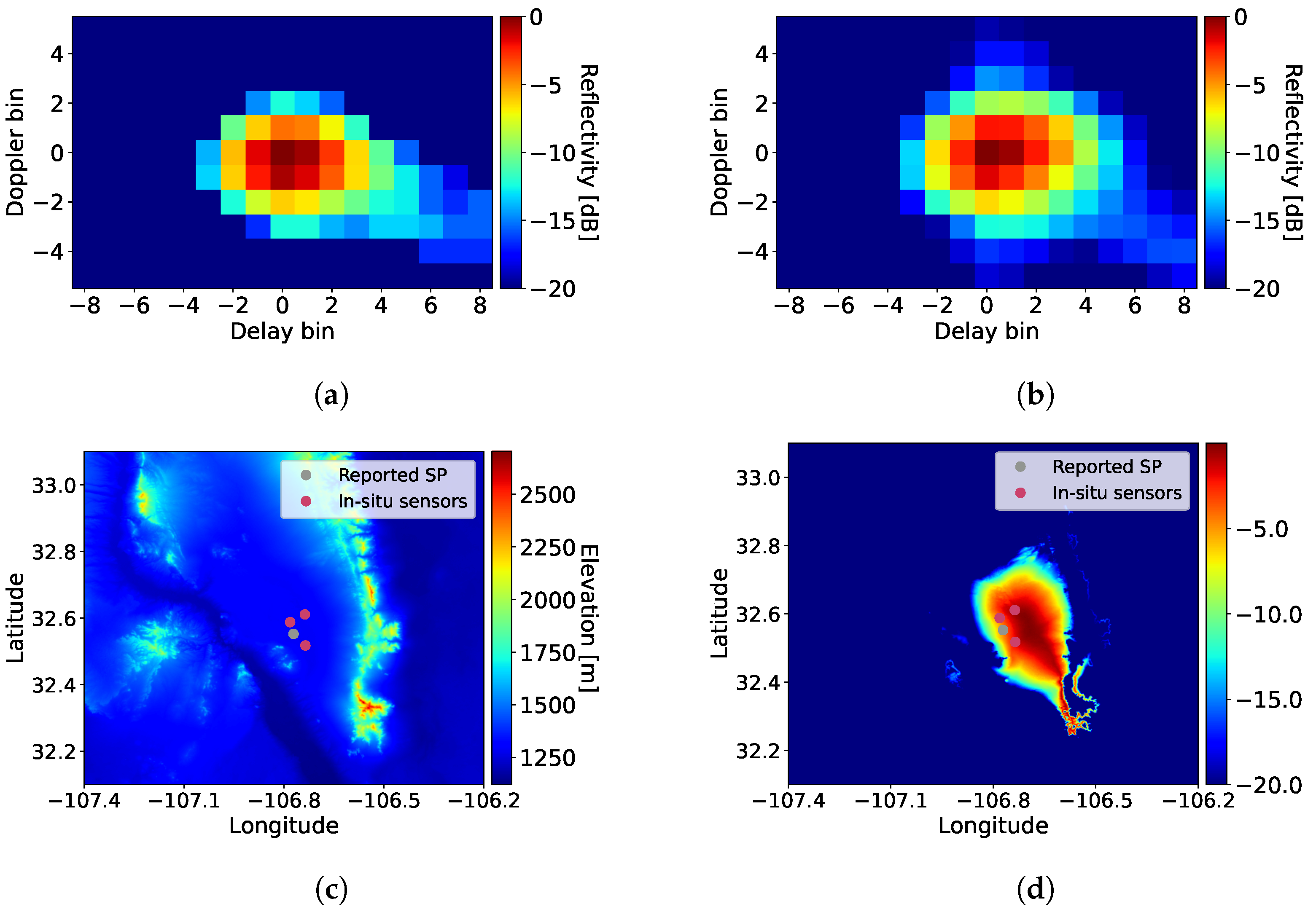
4.2. DDM Results
5. Discussion and Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gleason, S.; Hodgart, S.; Yiping, S.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and Processing of Bistatically Reflected GPS Signals from Low Earth Orbit for the Purpose of Ocean Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef] [Green Version]
- Unwin, M.; Duncan, S.; Jales, P.; Blunt, P.; Tye, J. Implementing GNSS-Reflectometry in Space on the TechDemoSat-1 Mission. In Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2014), Tampa, FL, USA, 8–12 September 2014; pp. 1222–1235. [Google Scholar]
- Ruf, C.S.; Gleason, S.; Jelenak, Z.; Katzberg, S.; Ridley, A.; Rose, R.; Scherrer, J.; Zavorotny, V. The CYGNSS Nanosatellite Constellation Hurricane Mission. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 214–216. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Fernandez, L.; Perez, A.; Ruiz-De-azua, J.A.; Park, H.; Camps, A.; Domínguez, B.C.; Pastena, M. In-Orbit Validation of the FMPL-2 Instrument—The GNSS-R and L-Band Microwave Radiometer Payload of the FSSCat Mission. Remote Sens. 2020, 13, 121. [Google Scholar] [CrossRef]
- Freeman, V.; Masters, D.; Jales, P.; Esterhuizen, S.; Ebrahimi, E.; Irisov, V.; Khadhra, K.B. Earth Surface Monitoring with Spire’s New GNSS Reflectometry (GNSS-R) CubeSats. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020. EGU2020-13766. [Google Scholar] [CrossRef]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef] [Green Version]
- Ruf, C.S.; Chew, C.; Lang, T.; Morris, M.G.; Nave, K.; Ridley, A.; Balasubramaniam, R. A New Paradigm in Earth Environmental Monitoring with the CYGNSS Small Satellite Constellation. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wan, W.; Liu, B.; Zeng, Z.; Chen, X.; Wu, G.; Xu, L.; Chen, X.; Hong, Y. Using CYGNSS Data to Monitor China’s Flood Inundation during Typhoon and Extreme Precipitation Events in 2017. Remote Sens. 2019, 11, 854. [Google Scholar] [CrossRef] [Green Version]
- Chew, C.; Small, E. Description of the UCAR/CU Soil Moisture Product. Remote Sens. 2020, 12, 1558. [Google Scholar] [CrossRef]
- Wu, X.; Ma, W.; Xia, J.; Bai, W.; Jin, S.; Calabia, A. Spaceborne GNSS-R Soil Moisture Retrieval: Status, Development Opportunities, and Challenges. Remote Sens. 2020, 13, 45. [Google Scholar] [CrossRef]
- Campbell, J.D.; Melebari, A.; Moghaddam, M. Modeling the Effects of Topography on Delay-Doppler Maps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1740–1751. [Google Scholar] [CrossRef]
- Dente, L.; Guerriero, L.; Comite, D.; Pierdicca, N. Space-Borne GNSS-R Signal over a Complex Topography: Modeling and Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1218–1233. [Google Scholar] [CrossRef]
- Comite, D.; Ticconi, F.; Dente, L.; Guerriero, L.; Pierdicca, N. Bistatic Coherent Scattering from Rough Soils with Application to GNSS Reflectometry. IEEE Trans. Geosci. Remote Sens. 2020, 58, 612–625. [Google Scholar] [CrossRef]
- Zhu, J.; Tsang, L.; Xu, H. A Physical Patch Model for GNSS-R Land Applications. Prog. Electromagn. Res. 2019, 165, 93–105. [Google Scholar] [CrossRef] [Green Version]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Zavorotny, V.U.; Larson, K.M.; Braun, J.J.; Small, E.E.; Gutmann, E.D.; Bilich, A.L. A Physical Model for GPS Multipath Caused by Land Reflections: Toward Bare Soil Moisture Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 100–110. [Google Scholar] [CrossRef]
- Ren, B.; Zhu, J.; Tsang, L.; Xu, H. Analytical Kirchhoff Solutions (AKS) and Numerical Kirchhoff Approach (NKA) for First-Principle Calculations of Coherent Waves and Incoherent Waves at P Band and L Band in Signals of Opportunity (SoOp). Prog. Electromagn. Res. 2021, 171, 35–73. [Google Scholar] [CrossRef]
- Kurum, M.; Deshpande, M.; Joseph, A.T.; O’Neill, P.E.; Lang, R.H.; Eroglu, O. SCoBi-Veg: A Generalized Bistatic Scattering Model of Reflectometry From Vegetation for Signals of Opportunity Applications. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1049–1068. [Google Scholar] [CrossRef]
- Park, H.; Camps, A.; Castellvi, J.; Muro, J. Generic Performance Simulator of Spaceborne GNSS-Reflectometer for Land Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3179–3191. [Google Scholar] [CrossRef]
- Campbell, J.D.; Akbar, R.; Bringer, A.; Comite, D.; Dente, L.; Gleason, S.T.; Guerriero, L.; Hodges, E.; Johnson, J.T.; Kim, S.B.; et al. Intercomparison of Electromagnetic Scattering Models for Delay-Doppler Maps along a CYGNSS Land Track with Topography. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Akbar, R.; Campbell, J.; Silva, A.R.; Chen, R.; Melebari, A.; Hodges, E.; Entekhabi, D.; Ruf, C.; Moghaddam, M. SoilSCAPE Wireless in Situ Networks in Support of CYGNSS Land Applications. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5042–5044. [Google Scholar] [CrossRef]
- Thompson, D.; Elfouhaily, T.; Garrison, J. An Improved Geometrical Optics Model for Bistatic GPS Scattering from the Ocean Surface. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2810–2821. [Google Scholar] [CrossRef]
- Pascual, D.; Park, H.; Camps, A.; Arroyo, A.A.; Onrubia, R. Simulation and Analysis of GNSS-R Composite Waveforms Using GPS and Galileo Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1461–1468. [Google Scholar] [CrossRef]
- Goodrich, D.C.; Keefer, T.O.; Unkrich, C.L.; Nichols, M.H.; Osborn, H.B.; Stone, J.J.; Smith, J.R. Long-Term Precipitation Database, Walnut Gulch Experimental Watershed, Arizona, United States. Water Resour. Res. 2008, 44, 5. [Google Scholar] [CrossRef]
- Osborn, H.B. Persistence of Summer Rainy and Drought Periods on a Semiarid Rangeland Watershed. Int. Assoc. Sci. Hydrol. Bull. 1968, 13, 14–19. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing; The University of Michigan Press: Ann Arbor, MI, USA, 2015; pp. 1–1116. [Google Scholar]
- Havstad, K.M.; Huenneke, L.F.; Schlesinger, W.H. Structure and Function of a Chihuahuan Desert Ecosystem: The Jornada Basin Long-Term Ecological Research Site; Oxford University Press: Oxford, UK, 2006. [Google Scholar] [CrossRef]
- Diamond, H.J.; Karl, T.R.; Palecki, M.A.; Baker, C.B.; Bell, J.E.; Leeper, R.D.; Easterling, D.R.; Lawrimore, J.H.; Meyers, T.P.; Helfert, M.R.; et al. U.S. Climate Reference Network After One Decade of Operations Status and Assessment. Bull. Am. Meteorol. Soc. 2013, 94, 485–498. [Google Scholar] [CrossRef]
- CYGNSS. CYGNSS Level 1 Science Data Record Version 3.1; Dataset; PO.DAAC: Pasadena, CA, USA, 2021. Available online: https://podaac.jpl.nasa.gov/dataset/CYGNSS_L1_V3.1 (accessed on 15 January 2023).
- Earth Resources Observation and Science (EROS) Center. Shuttle Radar Topography Mission 1 Arc-Second Global; U.S. Geological Survey: Reston, VA, USA, 2018. [CrossRef]
- Hodges, E.; Campbell, J.D.; Melebari, A.; Bringer, A.; Johnson, J.T.; Moghaddam, M. Using Lidar Digital Elevation Models for Reflectometry Land Applications. IEEE Trans. Geosci. Remote Sens. 2023, 12, 2308. [Google Scholar] [CrossRef]
- Burgin, M.S.; Khankhoje, U.K.; Duan, X.; Moghaddam, M. Generalized Terrain Topography in Radar Scattering Models. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3944–3952. [Google Scholar] [CrossRef]
- Comite, D.; Pierdicca, N. Decorrelation of the Near-Specular Scattering in GNSS Reflectometry from Space. IEEE Trans. Geosci. Remote Sens. 2022, 60, 2005213. [Google Scholar] [CrossRef]
- DI Martino, G.; DI Simone, A.; Iodice, A.; Riccio, D. Bistatic Scattering from Anisotropic Rough Surfaces via a Closed-Form Two-Scale Model. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3656–3671. [Google Scholar] [CrossRef]
- Azemati, A.; Melebari, A.; Campbell, J.D.; Walker, J.P.; Moghaddam, M. GNSS-R Soil Moisture Retrieval for Flat Vegetated Surfaces Using a Physics-Based Bistatic Scattering Model and Hybrid Global/Local Optimization. Remote Sens. 2022, 14, 3129. [Google Scholar] [CrossRef]



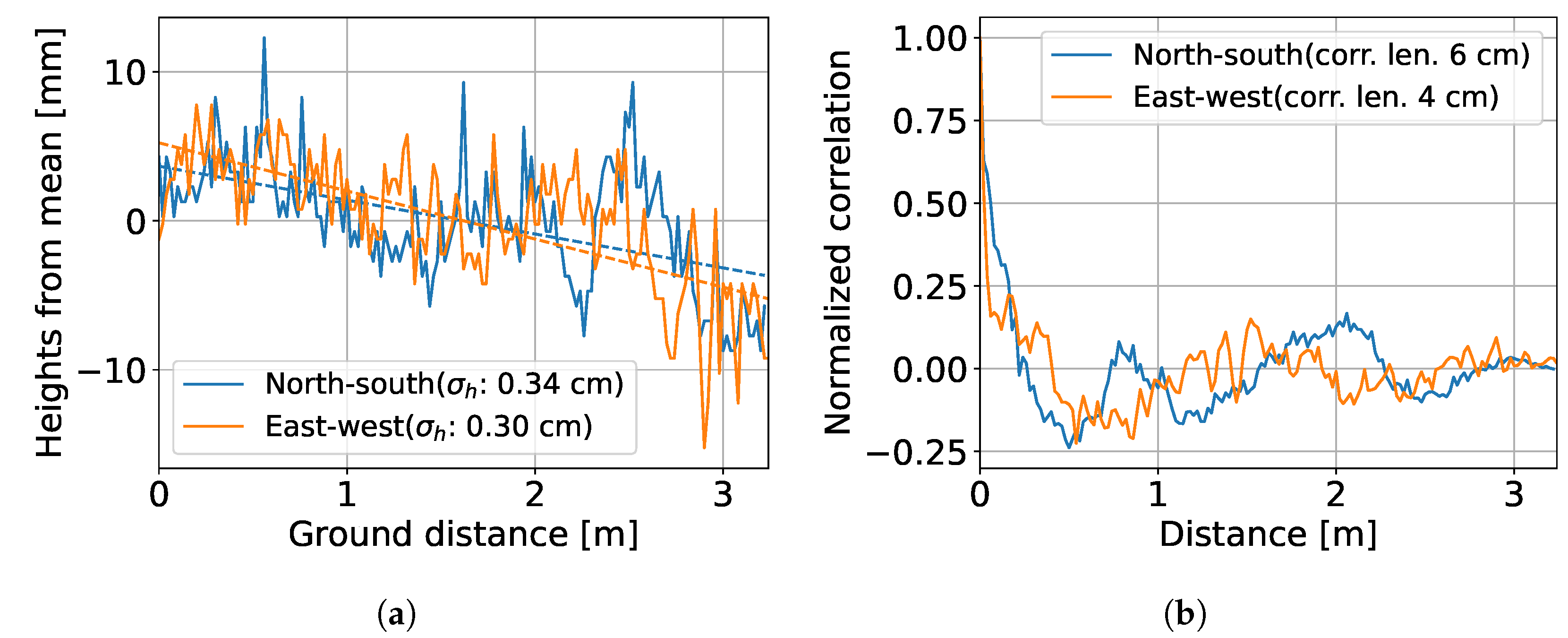

| Location | Orientation | [cm] | Correlation Length [cm] | Correlation Length/ |
|---|---|---|---|---|
| JR-1 | N-S | 0.34 | 6 | 17.8 |
| E-W | 0.30 | 4 | 13.1 | |
| JR-2 | N-S | 0.56 | 16 | 28.7 |
| E-W | 0.56 | 26 | 46.7 | |
| JR-3 | N-S | 1.44 | 26 | 18.0 |
| E-W | 0.67 | 6 | 8.9 | |
| KN | N-S | 0.73 | 4 | 5.5 |
| E-W | 0.46 | 2 | 4.3 | |
| LH | N-S | 0.88 | 4 | 4.5 |
| E-W | 0.34 | 2 | 5.8 |
| WG Track 1 | WG Track 2 | JER Track 1 | JER Track 2 | |
|---|---|---|---|---|
| Date | 5 February 2019 | 15 September 2019 | 30 May 2022 | 30 May 2022 |
| Time [UTC] | 19:41 | 14:31 | 14:27 | 17:57 |
| Spacecraft ID | 8 | 6 | 4 | 5 |
| Channel number | 4 | 4 | 3 | 4 |
| Starting sample ID | 70,680 | 104,540 | 10,419 | 128,830 |
| Number of DDM | 25 | 20 | 14 | 18 |
| SNR range [dB] | 4–13 | 5–10 | 2–10 | 2–10 |
| Soil moisture [m3 m−3] | 0.18 | 0.51 * | 0.01 | 0.01 |
| Soil clay percentage | 20% | 20% | 20% | 20% |
| 0.4° | 0.4° | 0.1° | 0.1° | |
| [cm] | 1.25 | 1.25 | 1.25 | 1.25 |
| DEM window size | 9 | 9 | 15 | 15 |
| 0 | 0.2 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melebari, A.; Campbell, J.D.; Hodges, E.; Moghaddam, M. Improved Geometric Optics with Topography (IGOT) Model for GNSS-R Delay-Doppler Maps Using Three-Scale Surface Roughness. Remote Sens. 2023, 15, 1880. https://doi.org/10.3390/rs15071880
Melebari A, Campbell JD, Hodges E, Moghaddam M. Improved Geometric Optics with Topography (IGOT) Model for GNSS-R Delay-Doppler Maps Using Three-Scale Surface Roughness. Remote Sensing. 2023; 15(7):1880. https://doi.org/10.3390/rs15071880
Chicago/Turabian StyleMelebari, Amer, James D. Campbell, Erik Hodges, and Mahta Moghaddam. 2023. "Improved Geometric Optics with Topography (IGOT) Model for GNSS-R Delay-Doppler Maps Using Three-Scale Surface Roughness" Remote Sensing 15, no. 7: 1880. https://doi.org/10.3390/rs15071880
APA StyleMelebari, A., Campbell, J. D., Hodges, E., & Moghaddam, M. (2023). Improved Geometric Optics with Topography (IGOT) Model for GNSS-R Delay-Doppler Maps Using Three-Scale Surface Roughness. Remote Sensing, 15(7), 1880. https://doi.org/10.3390/rs15071880









