Abstract
With the increase in rainfall intensity, population, and urbanised areas, surface water flooding (SWF) is an increasing concern impacting properties, businesses, and human lives. Previous studies have shown that microtopography significantly influences flow paths, flow direction, and velocity, impacting flood extent and depth, particularly for the shallow flow associated with urban SWF. This study compares two survey strategies commonly used by flood practitioners, S1 (using Unmanned Aerial Systems-based RGB data) and S2 (using manned aircraft with LiDAR scanners), to develop guidelines on where to use each strategy to better characterise microtopography for a range of flood features. The difference between S1 and S2 in elevation and their accuracies were assessed using both traditional and robust statistical measures. The results showed that the difference in elevation between S1 and S2 varies between 11 cm and 37 cm on different land use and microtopographic flood features. Similarly, the accuracy of S1 ranges between 3 cm and 70 cm, and the accuracy of S2 ranges between 3.8 cm and 30.3 cm on different microtopographic flood features. Thus, this study suggests that the flood features of interest in any given flood study would be key to select the most suitable survey strategy. A decision framework was developed to inform data collection and integration of the two surveying strategies to better characterise microtopographic features. The findings from this study will help improve the microtopographic representation of flood features in flood models and, thus, increase the ability to identify high flood-risk prompt areas accurately. It would also help manage and maintain drainage assets, spatial planning of sustainable drainage systems, and property level flood resilience and insurance to better adapt to the effects of climate change. This study is another step towards standardising flood extent and impact surveying strategies.
1. Introduction
The climate around the world is changing. The World Meteorological Organisation reports that the global mean temperature in 2022 was estimated to have risen 1.11 ± 0.13 °C above the 1850–1900 pre-industrial average [1]. Abnormally high annual precipitation totals were observed in South and South-East Asia, eastern China, and the West Siberian plain [1]. In the recent decade (2010–2019), UK summers and winters are, on average, 11% and 4% wetter compared to previous decades (1981–2010) [2]. The increase in heavy short-duration storms results in frequent surface water flooding (SWF). The increased impermeable area and insufficient drainage capacity due to population growth and urbanisation further contribute to SWF [3]. SWF is most prevalent in urban areas, impacting properties, businesses, infrastructure, and human lives [3]. In England, approximately 5.6 million properties are at risk of SWF, whereas 3.1 million properties are at risk of flooding due to rivers and the sea [3,4,5]. There are established risk assessment and management approaches for fluvial flooding [6]. However, surface water flood risk assessment and management are more challenging due to the complex interactions between the urban environment’s source, pathway, and receptor. The surface runoff generated by heavy rainfall flows through drains, ditches, or open channels to discharge into the buried surface water or combined sewer pipes. In the case of surface water pipes, the runoff is ultimately discharged into a watercourse. For combined sewer systems, the pipes carry sewage and surface water flows into treatment facilities, with flows exceeding the capacity of the sewer pipes or the treatment sites being discharged to water bodies.
A critical task in managing SWF is accurately identifying flood risk areas. Although surface water flood maps prepared from flood models help identify flood risk areas, there is a disconnect between the modelled surface water flood maps and the actual flood extent and depth [7]. The accuracy of a flood model depends on factors such as quality of input data, boundary conditions, reproduction of the complex interaction between surface flow and sub-surface drainage networks, and an accurate representation of elements such as building, vegetation, and other small-scale features related to microtopography [7]. Various studies have demonstrated the importance of uncertainty quantification for models associated to the management of natural resources, to understand and predict the phenomena more accurately and make informed decisions based on it [8,9]. Box et al. [9] demonstrated that Leaf Area Index (LAI)-based approaches can be reliably extended from low to high LAI values, for (non-)submerged vegetation, to represent the vegetative friction factor for modelling river flows. Previous studies indicate that microtopography [10,11] is a critical factor influencing the extent and risk of local flooding. It influences the flow path, particularly during shallow water flow associated with urban SWF [7,12,13,14]. Microtopography guides the surface water runoff flow direction and velocity and impacts the flood extent and depth. In the context of SWF, microtopography is defined as the undulations on the ground surface due to features such as road kerbs, speed bumps, drainage gullies, hedgerow bunds, drainage ditches, flood gates, walls, and steps [7,10,11]. With the steady progress in data availability and computational power, flood models have become more sophisticated, representing the heterogeneity of urban topography in more detail [15,16]. To capture small-scale features such as kerbs, steps, road cambers, and walls that influence the flow path, high-resolution topographic data as fine as 10 cm [7,17,18,19] are required. Within the context of this study, microtopography is defined as variations in elevation (planimetry and altimetry) in the order of 10 cm. A detailed characterisation of microtopography will advance both experimental and numerical models of the prediction of flood phenomena. The inclusion of microtopographic features in flood models involves high computational expenses [20]. Some studies have suggested using simplified models [16] or merged data [21] to manage this high computational expense. There are also studies indicating the use of data-driven models such as Artificial Neural Networks (ANN) to reduce computational costs [16].
Microtopography can be captured and visualised at a range of scales with appropriate technologies. Different technologies have already been used to map microtopography for various applications such as archaeology, soil mapping, and flow modelling. Some digital technologies used for mapping microtopography include Total Stations, the Global Navigation Satellite System (GNSS), Terrestrial Laser Scanners, and Airborne Laser scanners (LiDAR—Light Detection and Ranging) [22]. Roosevelt [22] compared the implementation and efficiency of mapping microtopography by Unmanned Aerial Systems (UAS) and ground-based Rover Real-Time Kinematic (RTK) GNSS. The study suggested that the use of UAS is more labour- and cost-efficient, with a significant gain in data quality (average data density of 95.14 points m−2) compared to RTK GNSS (0.76 points m−2). Regarding accuracy, the UAS Digital Elevation Model (DEM) showed an average root mean squared error (RMSE) of 0.21 m at three out of four survey sites. Brubaker et al. [23] investigated LiDAR data to model microtopography and surface roughness accurately for landscape analysis. Their study proved that high-resolution (i.e., ≈10 points m−2) LiDAR data could model microtopography with a mean difference in elevations of −0.3 m.
Mazzoleni et al. [24] tested the reliability of UAS–RGB-derived microtopography for hydraulic modelling in tropical environments, where weather conditions and remoteness of the study area might affect the quality of the retrieved data. The UAS–RGB-derived (25 cm DEM) geometry was compared with three other DEMs derived from LiDAR (1 m DEM), RTK–GPS (50 cm DEM), and shuttle radar topography mission (SRTM) (30 m DEM) data. Results showed that the RMSE of the UAS DEMs of river cross-sections was higher than RTK–GPS DEMs. Their study also assessed the suitability of UAS-based topography data for hydraulic modelling and compared it against other DEMs, considering LiDAR DEMS as the benchmark used by practitioners. The results showed that the UAS-based model (RMSE = 0.75 m) outperformed the RTK–GPS (RMSE = 0.83 m) for the estimation of maximum water depth. Backes et al. [14] investigated the effect of using UAS high-resolution data, with an average Ground Sampling Distance (GSD) of 2 cm, to achieve accurate flood predictions. The study confirmed the impact of microtopographic features on flow, pooling and water depth and identified the importance of investigating it in further detail. Ozdemir et al. [19] demonstrated that when the DEM resolution changes from 1 m to 10 cm, the flood extent decreases by 6%, flood depth increases by 37%, and velocity increases by 32% [19]. In addition, Sampson et al. [25] proved that using DEMs at a 10 cm resolution improves the representation of hydraulic connectivity in flood models with a significant impact on flood risk assessment.
Aguera Vega et al. [26] investigated the effect of 3D point cloud density on the accuracy of a UAS-derived Digital Terrain Model (DTM) (GSD ≈ 0.4 cm) at the microtopography level (0.4 cm to 4.01 cm). The results revealed that the accuracy of their DTM increased with point density. The maximum accuracy obtained in elevation for the totality of the point cloud was ≈1.1 cm. When the point cloud density was reduced by 20%, the RMSE increased by 3%, and when the point cloud density was reduced by >85%, the RMSE increased exponentially (i.e., a 45% RMSE increase for a 99% reduction in point cloud density). The authors also reported that the pixel size that minimised the RMSE for densities ≥20% of the raw data set was 1 cm, which is two times the GSD of the images used in the data processing.
Kopysc [27] concluded in their study that the accuracy of UAS DEMs was not superior to aerial laser scanning at a microtopographic level. A UAS DEM with a 5 cm horizontal and 1 cm vertical RMSE was used and compared with a similar aerial LiDAR. Kopysc [27] measured the level of soil degradation on hiking trails over four years with the use of DEMs derived from aerial LiDAR point clouds (24 points m−2) and Structure from Motion point clouds across two fields. The comparison between the DEMs showed an absolute difference in height ranging from 0.01 0.01 m to 0.09 0.01 m for the first field and from 0 0.01 m to 0.13 0.01 m for the second field. The author suggested that UAS would be an easy-to-use and cheaper method to collect up-to-date high-accuracy topographic data for smaller areas to supplement aerial laser scanning, which is a costly method where time intervals between every scan are counted in years.
Photogrammetry-based UAS and LiDAR data have been studied for flood modelling [20,28,29] and flood mapping [30,31] applications. Leitao et al. [29] compared a 5 cm resolution UAS-derived raster with a conventional LiDAR raster (Swisstopo; 2 m resolution) for flood modelling purposes. The accuracy of the vertical dimension of the LiDAR dataset was 0.5 to 1.5 m, whereas that from the UAS DEM was 0.1 to 0.2 m. The elevation difference between both rasters ranged between −0.468 m and 0.306 m, with a mean of 0.06 m and a standard deviation of 0.119 m. Leitao et al. [28] presented the application of the MBlend merging method of DEM rasters (0.5 × 0.5 m resolution) from UAS imagery and terrestrial LiDAR and proved its impact on flood models. The flood modelling results of the reference DEM and merged DEMs showed that the difference in water depth ranged between −9.8 m to 0.2 mm, and the difference in velocity ranged between 0.003 to 0.024 m s−1. Similarly, Muthusamy et al. [21] explored the use of merged DEMs where higher resolution DEMs (1 m) were used to characterise the river channel in conjunction with a 30 m resolution DEM for the wider area. The results showed that merged DEMs reduced the mean flood depth from 3.3 m to 1.81 m and the RMSE in flood depths from 2.6 m to 0.9 m at a 30 m resolution.
Annis et al. [30] compared the performance of photogrammetry-based UAS DEM (0.25 m) (vertical accuracy ≈ 0.10 m) and a high-resolution DEM (TINITALY) (10 m) (vertical accuracy ≈ 16 m) to represent floodplain topography for flood simulations, using a 1 m LiDAR DEM (vertical accuracy ≈ 0.15–0.3 m) as a benchmark. The different DEMs were compared as input to hydrologic–hydraulic modelling. The results proved that the performance of UAS DEM flood simulations were significantly better than the TINITALY DEM (there was a 72% flood extension matching from TINITALY versus 98% from UAS DEM flood maps for the 200-year return period simulation) and a good alternative to LiDAR DEM for flood mapping. Hashemi-Beni et al. [32] performed an accuracy analysis of the water surface extracted from an UAS-derived DEM (3 cm) with the water surface data from a nearby stream gauge station and LiDAR data (90 cm). The results showed that UAS-based water surface was higher and had a difference of 27 cm with a standard deviation of 15 cm from the USGS stream level elevation [32].
The Environment Agency in England collects airborne LiDAR data regularly to provide accurate elevation information at a 1 m spatial resolution to the whole of England [33]. UAS–RGB imagery is collected by authorities, companies, and research institutions for surveillance, infrastructure inspection, and search and rescue missions pre-, during and post-event. The potential benefits of combining geomatic products derived from UAS–RGB and aircraft LiDAR data have been highlighted by several authors [28,34,35]. Similarly, the potential use of UAS–RGB to characterise microtopography has been recognised in a wide range of studies. However, to date, no studies have focussed on identifying the microtopographic configuration of flood features in urban areas to aid surface water flood management at a property level. Better knowledge about the microtopographic features would help improve flood risk assessment and management, prepare effective emergency response and evacuation plans, and accurate damage assessment [19,25,36]. Similarly, a better understanding of the effectiveness of different surveying strategies for the characterisations of various microtopographic features would also help improve surface water flood management through accurate flood predictions and flood risk assessment and management [25,37,38]. Villanueva et al. [39] investigated the possibility of using LIDAR elevation data for DEM-generation of UAS imaging for flood applications. The results for their study proved that the accuracy of the DEM generated is comparable to other studies and also demonstrated the complementarity of these two datasets.
To the authors’ knowledge, limited efforts have been dedicated to developing guidelines to choose fit-for-purpose surveying strategies, specially between UAS–RGB and aircraft LiDAR. The works by [39,40] are perhaps one of the most recent efforts but do not specifically focus on characterising topographic features that influence surface water flooding. This paper aims to develop a conceptual survey decision framework for aircraft-LiDAR vs UAS–RGB strategies to better characterise microtopography features in urban landscapes. The following three overarching objectives would help achieve the aim.
O1. To identify the data characteristics of the geomatic products derived from standard UAS–RGB and aircraft–LiDAR surveying strategies used for flood management purposes.
O2. To assess the accuracy and the elevation difference in microtopography of each surveying strategy for a range of land use classes and flood features.
O3. To devise a decision framework and set of guidelines to collect data and integrate UAS–RGB and aircraft-LiDAR surveying strategies based on the lessons learnt from O1 and O2.
2. Materials and Methods
2.1. Study Area
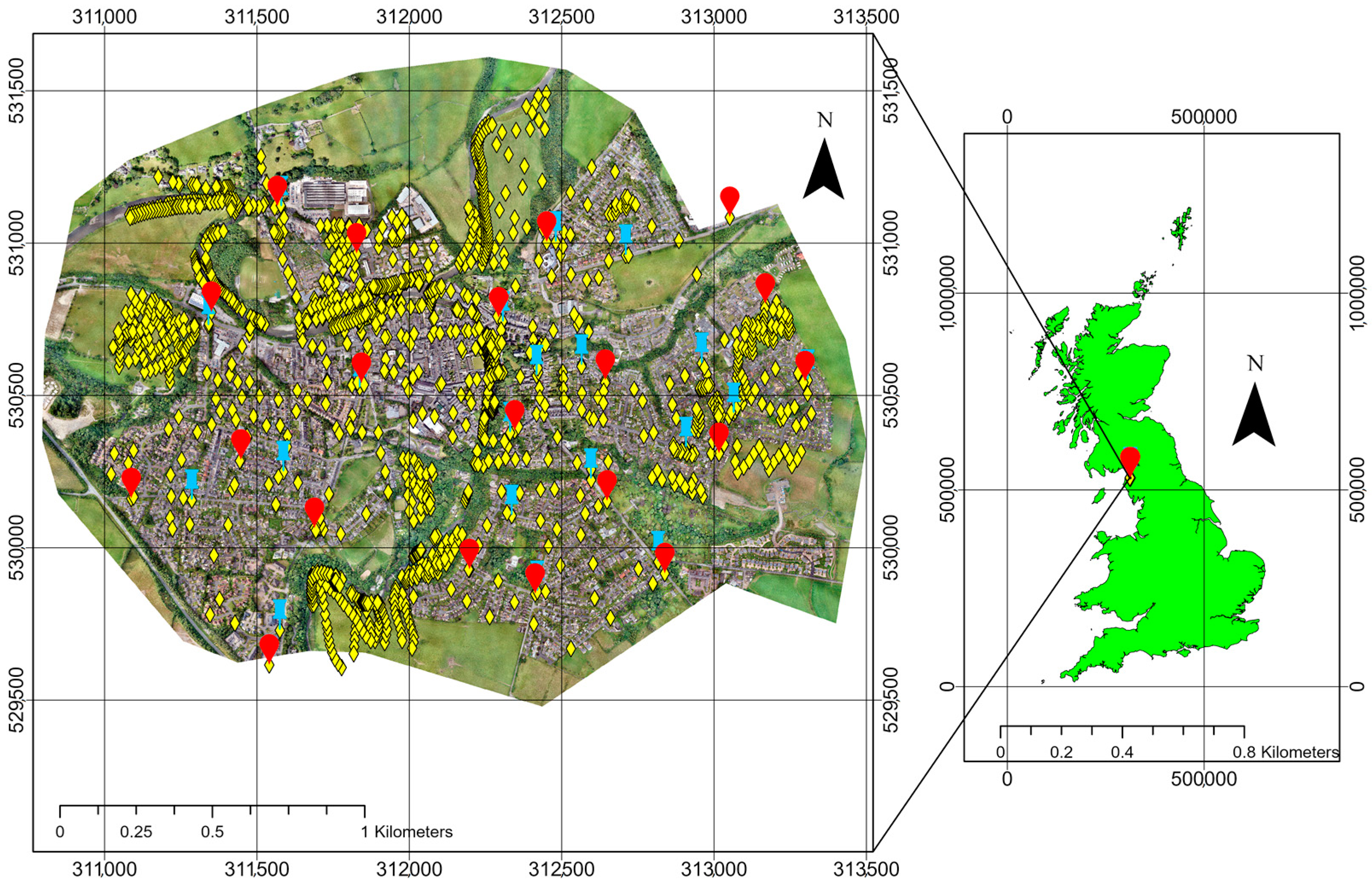
This study focuses on Cockermouth, Cumbria, UK (Figure 1). The town’s estimated population was around 9494 inhabitants during the 2020 census survey [41], with a population growth of 0.4% estimated from 2011 to 2020 [42]. The site is prone to extreme floods, with the most recent storm event in October 2021. The 2015 storm event caused by Storm Desmond impacted around 5500 homes and 1000 businesses in Cumbria [43]. It also damaged 400 km of road and destroyed 792 bridges and 44 schools [43]. Cockermouth was one of the worst affected towns in this area [44] with an estimated cost of repair and reinstatement of around £7 million [43].
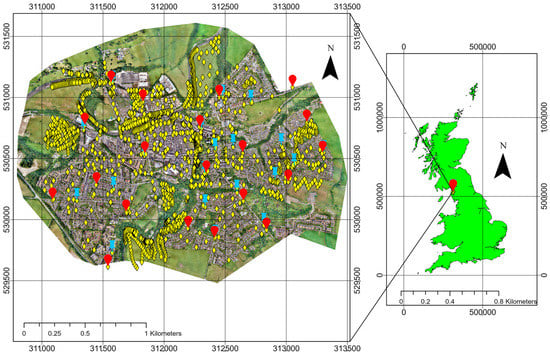
Figure 1.
Study area at Cockermouth town, Cumbria, UK (surveyed area: 471 hectares). The red tear markers represent the 20 ground control points used for data collection purposes. The blue push pin markers represent check points (20), whereas the yellow diamond markers represent 2031 additional ground points considered in this study.
2.2. Data Collection
Two sampling strategies commonly used by flood risk managers, emergency responders and flood scientists, were implemented. The first focussed on using a UAS platform with an embedded RGB sensor. The second strategy relied on a LiDAR sensor mounted on a manned aircraft. These surveying strategies are usually carried out to characterize the configuration of the terrain or quantify flood extent and impact, amongst others.
2.2.1. UAS–RGB Data (Survey Strategy S1)
High-resolution aerial imagery in the visible spectrum was collected over the study area using a Sirius Pro UAS (Topcon Positioning System Inc., Livermore, CA, USA). The UAS platform, powered by a 5300 mAh Lippo battery (30C, 18.5V), had a wingspan of 163 cm and a length of 120 cm. It was equipped with a Sony Alpha ILCE 6300 PRO camera (Sony Europe Limited, Weybridge, Surrey, UK). The GSD was 2.23 cm pixel−1 at a flying altitude of 125 m. The platform also included a 9DOF IMU. The take-off payload of the platform was 2.7 kg. The flight plan was defined by a multi-pass trajectory with image capture at predetermined waypoints, ensuring 85% and 65% across the track overlap. Each waypoint had associated GPS coordinates that defined the centre of the frame and yaw, pitch, and roll information. The GPS was a GNSS-RTK- L1/L2 and GLONASS with a planimetric accuracy of 0.01 cm and altimetric accuracy of 0.015 cm. The survey was conducted between 17 July 2019 and 19 July 2019. The weather conditions during these days, based on data from Spadeadam meteorological aerodrome report (METAR), were surface wind speeds between 2 km h−1 to 14 km h−1 and directions varying from 180° to 290° with excellent visibility [45]. A total of 11 flights were required to cover the 4.71 km2 surveyed area. All flights were conducted by fully qualified UAS pilots, always following CAA regulations (CAP 722 and CAP393). This survey strategy will be referred to as S1.
2.2.2. LiDAR Data (Survey Strategy S2)
High-density LiDAR data were collected from a Partenavia P68 Aircraft with a Teledyne Optech Galaxy (Teledyne Optech, Toronto, ON, Canada) (Table 1) topographic laser, emitting pulses at 18 pulses per minute (ppm) during a flight (2000 feet) conducted between 14:05 and 17:50 on 23 July 2019. The flight plan was designed to maximise data quality and consisted of ten overlapping swaths with an ancillary perpendicular swath across the surveyed area. The Optech Galaxy laser integrates PulseTRAKTM and SwathTRAKTM technologies. It combines a 27 kg 0.34 m × 0.34 m × 0.25 m sensor with a 6.5 kg 0.42 m × 0.33 m × 0.10 m power distribution unit (PDU), powered by a 28 V battery (12 A) that distributes 300 W appropriately to the different components. PulseTRAKTM provides high pulse repetition frequencies (PRFs) at high altitudes [46]. SwathTRAKTM enables a constant swath width on the ground by dynamically changing the scan field-of-view (FOV), thus providing a consistent point density across the surveyed area [46]. The centre of each LiDAR exposure had associated GPS (Trimble Applanix L1/L2 Card within the position and orientation module Rover Receiver incorporated into the Optech Galaxy system) coordinates and yaw, pitch, and roll information. A minimum of five satellites were locked during data capture to ensure an adequate GPS signal. The weather conditions during the flight, based on the Spadeadam METAR, were surface wind speeds between 2.5 m s−1 and 4.1 m s−1 and directions varying from 200° to 210°, with a prevailing visibility of 10 km or more and clear weather conditions (no weather to report) at 25 °C [47]. The flying speed ranged between 56 m s−1 and 76 m s−1. The total surveyed area was 4.71 km2. This survey strategy will be referred to as S2.

Table 1.
Configuration of the Teledyne Optech (Teledyne Optech, Toronto, Canada) laser for the data collection on 23/07/19. FOV stands for field-of-view.
2.2.3. RTK–GPS Data
A Topcon Hiper V RTK Network RTK–GPS (Topcon Positioning System Inc., Livermore, CA, USA) was used to take ground truth measurements at 20 ground control points (GCPs) and 20 checkpoints (XPs). The GPS planimetric and the altimetric accuracy was 15 mm and 30 mm, respectively. The GCPs were used to ensure the correct external orientation for the S1 imagery. The XPs were used to validate the accuracy of the geomatic products.
An ancillary data set with 2031 RTK–GPS measurements was obtained (in addition to the XPs) at walls, floodgates, drainage points, vegetated crests, roads, and grassland areas. These measurements were used to quantify the accuracy in elevation of both surveying strategies at key features of interest (Table 2). The land classes were chosen to assess the efficiency of the two survey strategies on manmade impermeable areas such as roofs and roads against permeable areas such as grasslands. The microtopographic features were chosen based on their influence on surface runoff and potential use in surface water management and flood risk assessment, as well as based on accessibility criteria. Drainage points were chosen as they are the first entry point of surface water into both surface water and combined sewer pipes; the location and elevation of drainage are critical to managing surface water. Likewise, physical barriers such as walls, floodgates, and vegetated crests were chosen as they influence the direction and velocity of surface runoff. Roofs, roads, and grasslands were selected to represent impervious and pervious surfaces, respectively. All points’ measurements were collected on the same day as the S1 data.

Table 2.
Land uses and microtopographic features used in the analysis. * Indicates RTK–GPS ground control points (GCPs; total 2031) that were collected. The number of GCPs collected is provided in brackets. Data used for each analysis (differences in elevation (D) or validation (V)) are identified.
2.3. Data Processing
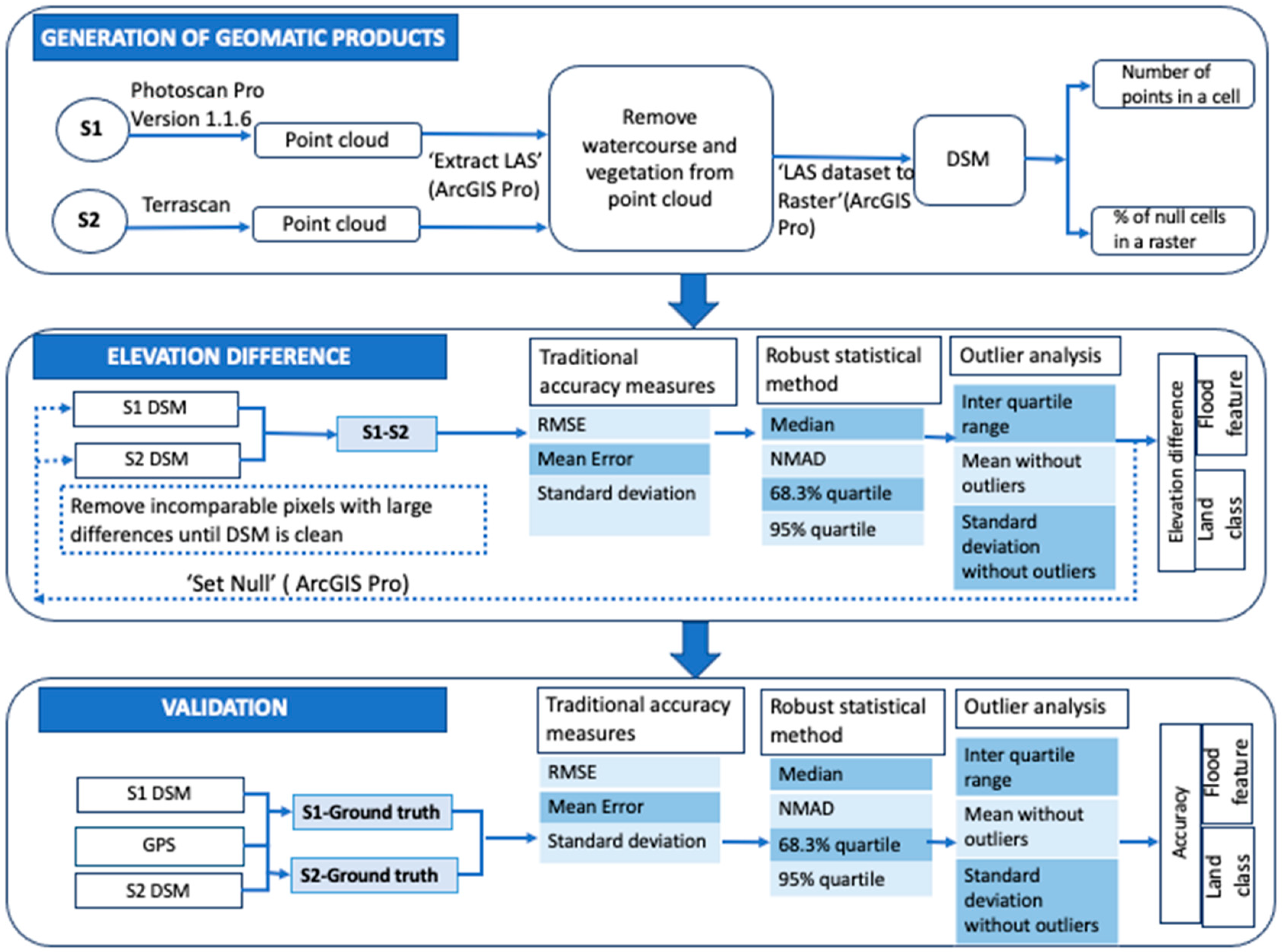
The data analysis workflow (Figure 2) required (i) the pixel size determination for S1 and S2, (ii) the quantification of the elevation difference between surveying strategies at the microtopographic level, and (iii) the validation of both surveying strategies for a range of microtopographic features.
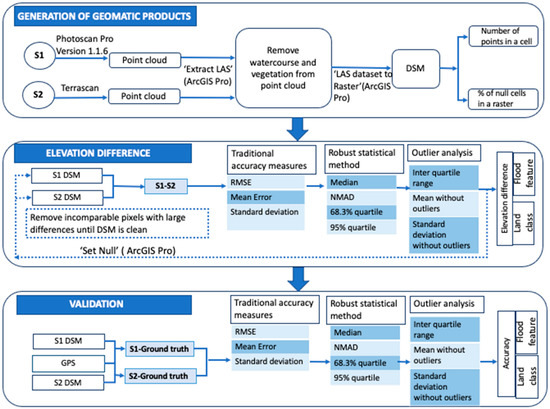
Figure 2.
Data processing workflow followed in this study.
2.3.1. Pixel Size Determination for S1 and S2
The S1 RGB imagery was processed with Photoscan Pro version 1.1.6 (Agisoft LLC, St. Petersburg, Russia). The S1 geomatic products (orthoimage and point cloud) were generated on a computer with Windows 6bit Operating System, Intel® Core™ i7-5960X CPU @300GHz CPU and GeoForce GTX TITAN X GPU. Only those images that met the quality control criteria of spatial coverage, image quality, and image overlap were included in the photogrammetric process. This process generated geomatic products, including the orthoimage and the point cloud. To minimise distortion, the 20 GCPs were used to georeference (i.e., locate, translate, and rotate) the individual frames into the World Geodetic System WGS84. This process involved manually assigning the field RTK–GPS coordinates to the centroids of GCP in all the frames. Photoscan calculates the co-registration error for X, Y, and Z directions automatically by root mean squared error (RMSEco) (Equation (1)).
where x, y, and z are RTK–GPS positions of the GCPs. ,, and are image-derived coordinates at point, j, and N is the total number of GCPs.
LiDAR data were processed using TerraScan (Terra Solid, Helsinki, Finland). The multiple swaths were matched, calibrated, and rectified prior to generating the point cloud. The inter-swatch relative accuracy was better than 0.06 m with the intra-swatch accuracy being better than 1 cm. All points falling in the river channel and trees were excluded from further analysis as they are incomparable between S1 and S2. For that purpose, polygons delineating the tree canopy and the river channel were digitised. The ‘Extract LAS’ function in ArcGIS Pro (Esri, Redlands, CA, USA) was used to exclude the points on water and trees from the S2 point cloud and the S1-derived geomatic products.
The point clouds were then rasterised to DSMs using the ‘LAS dataset to Raster’ function in ArcGIS Pro (Esri, Redlands, CA). A dataset layer with the first returns was used in all instances to generate the DSM for the LiDAR data. The elevation points in the DSM raster were calculated by the IDW interpolation method and binning without filling the voids.
The average point cloud spacings of the S1 and S2 data were obtained automatically from ArcGIS Pro (Esri, Redlands, CA). The percentage of empty pixels and the number of points per pixel were calculated for a range of pixel sizes to understand the distribution of points on both datasets and choose the optimum pixel size for further comparative study. This operation was carried out in ArcGIS Pro (Esri, Redlands, CA, USA) using the ‘IsNull’ and ‘LAS Point Statistics as Raster’ functions. Within this context, empty pixels refer to those pixels that contain no elevation measurements. Chow et al. [48] stated that the general rule of generating DSM from LiDAR point clouds is that the pixel size should be equal to or greater than the point cloud spacing to achieve reasonable data coverage. Within the context of this study, the DSM pixel size must also be fine enough to capture microtopographic features. As this study aims to compare the two survey strategies to characterise flood information at the microtopographic level, the optimum pixel size must be small enough to capture microtopographic flood features with a reasonable data coverage of the study area by both datasets. Thus, the optimum pixel size for comparison was identified by finding the midpoint value of the smallest pixel value achievable for the two strategies based on the point cloud spacing.
2.3.2. Difference in Elevation between S1 and S2
The difference in elevation between S1 and S2 DSMs was assessed by subtracting the elevation of S2 from S1 for each pixel in ArcGIS Pro (Esri, Redlands, CA). Positive values indicated the elevation from S1 was higher than S2. Both traditional and robust statistical metrics [49] were calculated using R studio (Integrated development platform for R, Boston, MA, USA).
Traditional statistical metrics assume that the variable of interest (i.e., the difference in elevation) follows a Gaussian distribution and that no outliers exist. The traditional metrics rely on the estimation of mean error, standard deviation, and RMSEe metrics (Table 3). Instead, the robust statistical metrics [49] remove the influence of outliers and detach the assumption of normal distribution from the metrics. The robust metrics are the median, normalised median absolute deviation, 68.3% quantile, and 95% quantile [49] (Table 3). Values outside the interquartile range were mapped to visually identify areas and features with large elevation differences and exclude incomparable pixels from further analysis. Incomparable pixels included pixels on shadows, moving vehicles, and photogrammetric processing errors. These pixels were incomparable as the large differences in elevation were either a result of moving objects between survey campaigns or data processing errors. Exclusion of such pixels was carried out using the ‘Set Null’ function in ArcGIS Pro (Esri, Redlands, CA, USA).

Table 3.
Traditional and robust statistical metrics for errors. N is the total number of independent observations. Δ denotes the individual elevation differences between strategies or errors and I = 1,…,n are independent observations. stands for standard deviation. RMSEe stands for root mean squared error, n denotes the number of data points, denotes mean, denotes median, and NMAD denotes normalized median absolute deviation.
The differences in elevation were analysed for both land use classes and microtopographic flood features (Table 2). Land use classes were identified from Ordnance Survey data [50], whereas microtopographic features were identified visually in the orthoimage and manually digitised. Only pixels where both S1 and S2 had elevation values were considered for analysis. The analysis was carried out in a GIS environment (ArcGIS Pro, Esri, Redlands, CA, USA). A non-parametric Kruskal–Wallis test was carried out to identify whether the differences in elevation between S1 and S2 were statistically significant between features and land classes.
2.3.3. Validation
Twenty XPs were used to validate the accuracy of the S1 orthoimage in X, Y, and Z dimensions. The ancillary ground truth data set (2031 points) was used to compare the accuracy in the vertical dimension of both S1 and S2 DSMs at key features (Table 2). The accuracy was calculated by subtracting RTK–GPS measurements from S1 and S2 measurements. Positive values indicated the elevation from the surveying strategy was higher than the ground truth measurement, whereas negative values indicated the elevation was lower than the ground truth. Only RTK–GPS measurements where both S1 and S2 values were available were considered for analysis. Both traditional and robust statistical metrics were calculated in R studio (Integrated development platform for R, Boston, MA). The interquartile range of the resulting values (errors) was calculated to determine the dataset’s mid-spread and outliers (i.e., values outside the interquartile range). The outliers were mapped to identify those areas and features that were error prone. The accuracy was also assessed over the flood features identified in Table 2.
3. Results
3.1. Pixel Size Determination for S1 and S2
Under S1, the photogrammetric analysis was carried out on 6073 UAS–RGB aerial images that met the quality criteria. An orthoimage of a 3 cm GSD and a dense point cloud with an average 8 cm point spacing was generated. The co-registration error of X, Y, and Z at the GCPs was 3.85 cm, 3.57 cm, and 3.57 cm, respectively. The LiDAR data produced ten tiles of LAS files with point cloud spacing between 12 cm and 17 cm (average: 15.5 cm, SD: 1.8 cm). After the removal of the river channel and tree canopy from the dataset, the point cloud spacing of the LAS files ranged from 13 cm and 17 cm (average: 16.2 cm, SD: 1.3 cm).
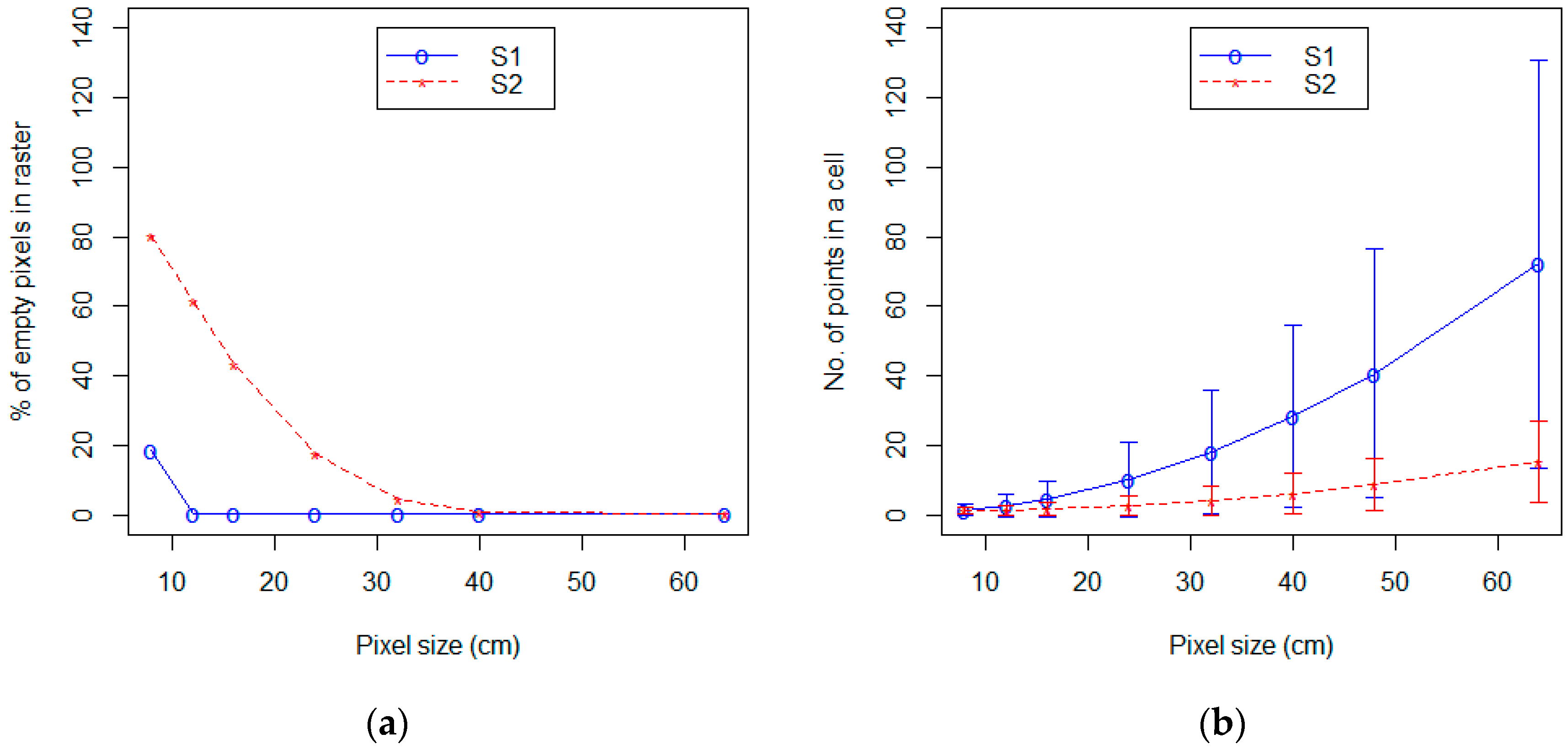
Figure 3 shows the effect of pixel size on the number of empty pixels and the effect on the number of points per pixel for both surveying strategies. As the pixel size increases, the % of empty pixels reduces. However, the rate of reduction is not the same for both strategies. The empty pixels in S1 reduce to less than 1% at pixel sizes that are 1.5 times the point cloud spacing (i.e., 12 cm). However, for S2, the percentage of empty pixels reduces to less than 1% only when the pixel size is increased to 3 times the average point cloud spacing (i.e., 48 cm).
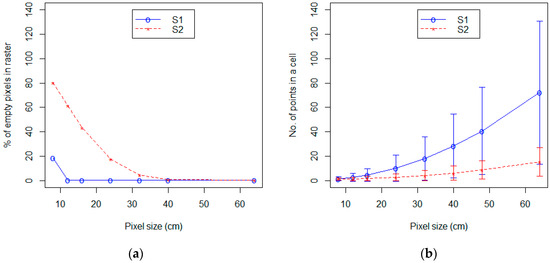
Figure 3.
Graph showing (a) the percentage of empty pixels in the raster and (b) the number of points in a pixel as the pixel size changes.
The average number of points in a pixel and their standard deviation (Figure 3) increases at a similar rate for both strategies when the pixel size increases. Figure 3b shows a flatter curve and a smaller standard deviation for S2 data than for S1.
As this study aims to capture microtopographic features, the midpoint of the smallest possible pixel size of both strategies was selected for further analysis. This was 12 cm, considering the point cloud spacing for S1 is 8 cm, and the average point cloud spacing for S2 is 16 cm. S1 and S2 point cloud data were both rasterized to DSMs of 12 cm pixel sizes.
3.2. Difference in Elevation between S1 and S2
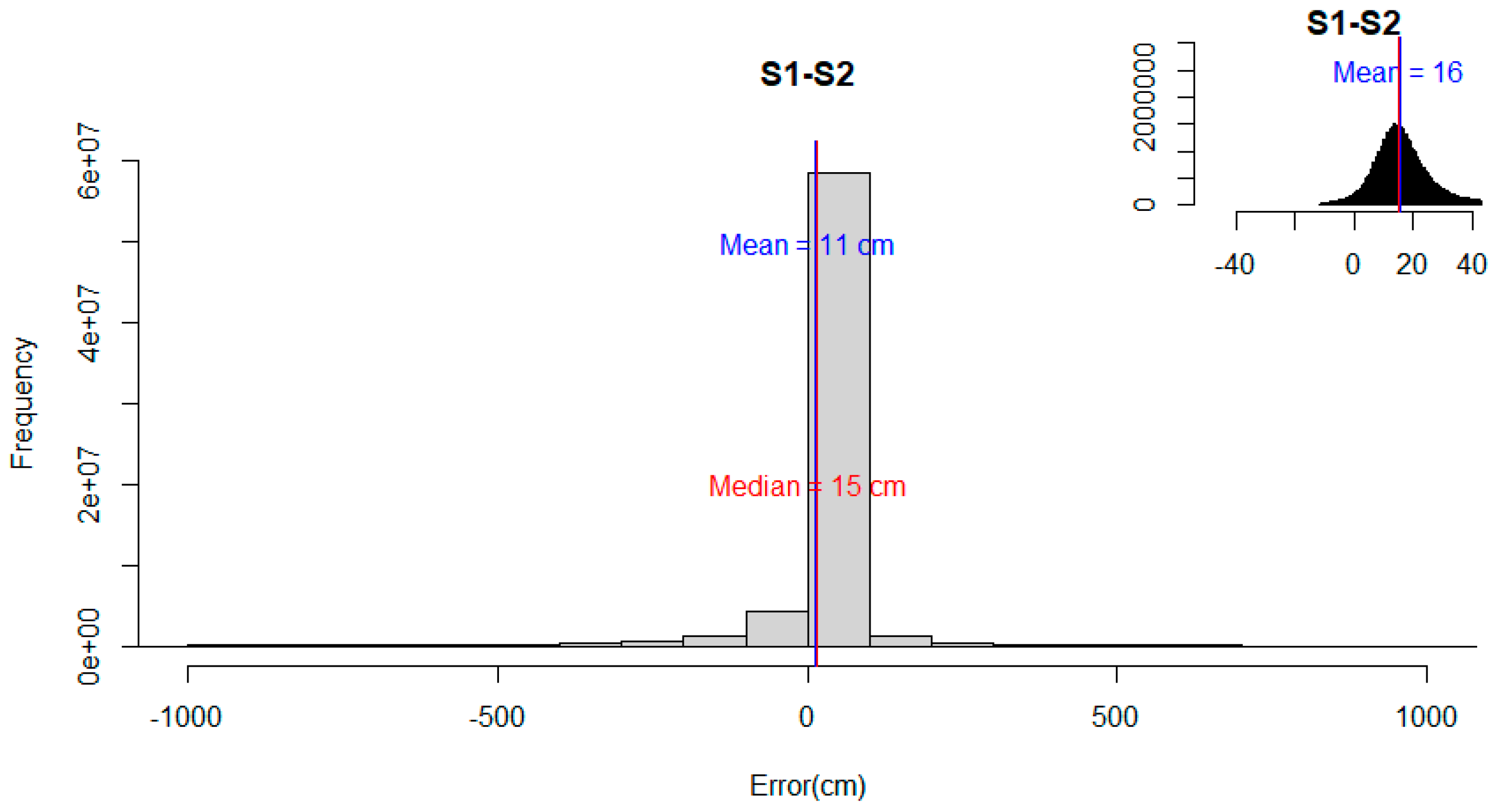
The histogram of the elevation difference between S1 and S2 presented negative skewness and showed leptokurtic patterns. When the outliers are removed, the distribution changed substantially (Figure 4), thus affecting the configuration of minimum (from ≈−540 m to ≈−11 cm), maximum (≈70 m to ≈43 cm), and mean values (10.9 cm to 15.8 cm). The NMAD value, the robust estimator of the deviation, was 9.9 cm. The 68.3% and 95% quantile values were 22.4 cm and 13.3 m. These results reinstated that the distribution of the difference in elevation between strategies was not normal, and, therefore, the use of robust statistical metrics is recommended.
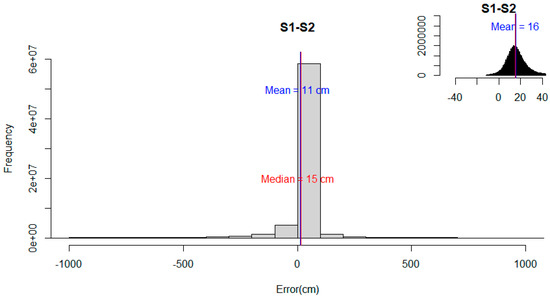
Figure 4.
Histogram showing distribution of difference between S1 and S2 for an extent (−1000 cm, 1000 cm). Inset plot shows data distribution without outliers.
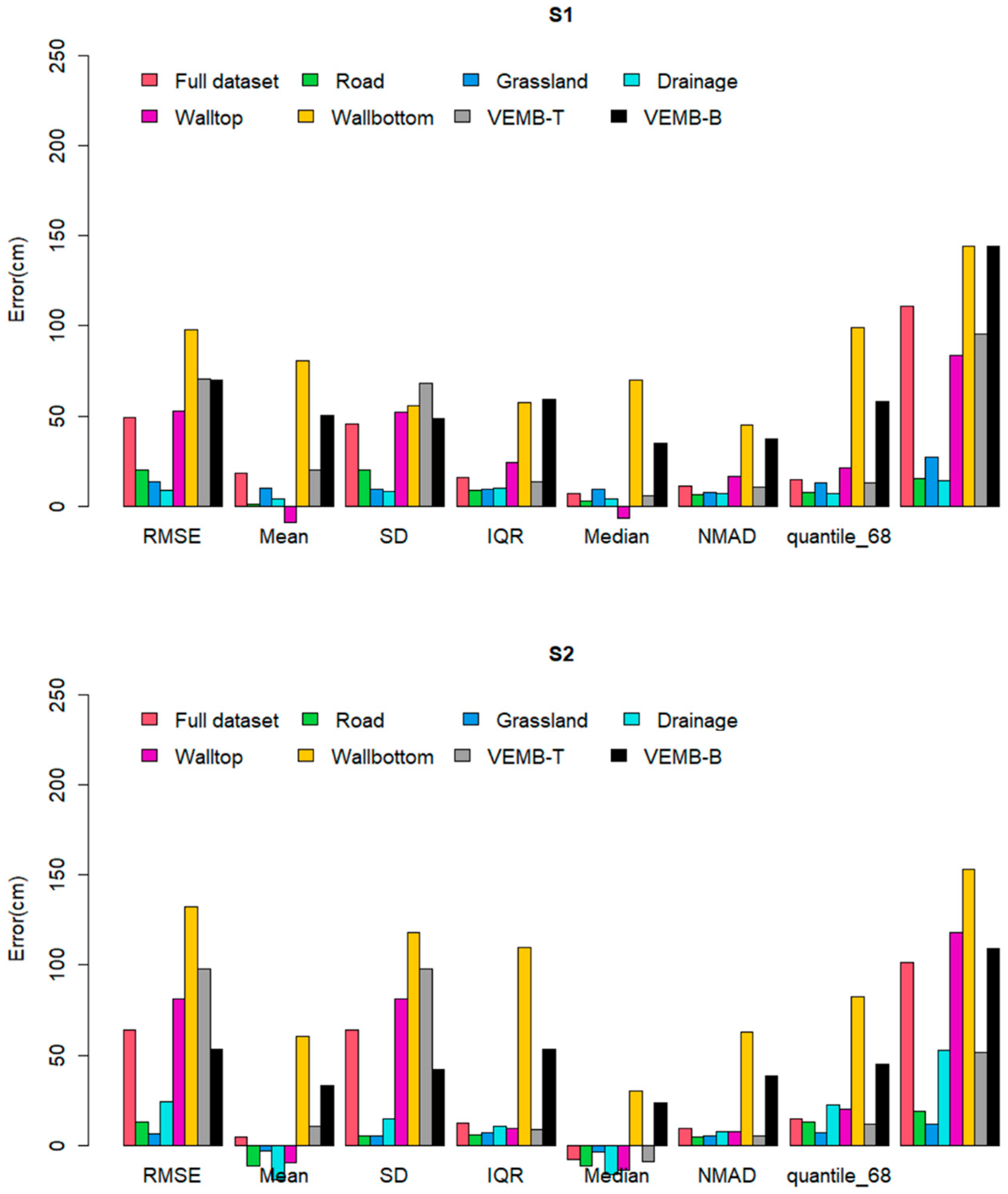
When the land classes were considered (Figure 5), the median of the elevation difference was between 13 cm and 17 cm for all classes (always >10 cm). All medians were positive which indicated that the elevation from S1 was systematically higher than S2. The 68.3% quantile and NMAD presented >10 cm of difference for all land classes. When the microtopographic flood features were considered (Figure 5), the median elevation difference was between 11 cm and 37 cm for all flood features except kerbs (≈8 cm). The mean error and median were always positive. The NMAD had a difference of >10 cm on all flood features (except kerbs). The Kruskal–Wallis test showed that the median ranks of the differences were significantly different among land use classes and flood features (p-value < 0.001).
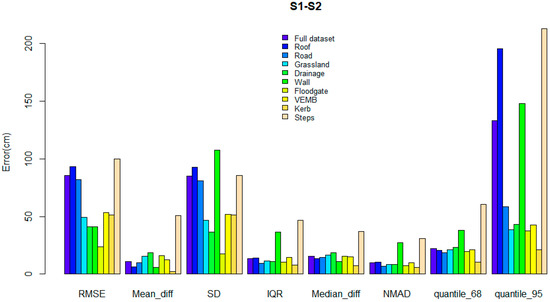
Figure 5.
Plot showing traditional and robust statistical metrics of the difference in elevation between S1 and S2 for all classes combined and per land class and microtopographic feature. IQR stands for interquartile range. NMAD stands for normalized median absolute deviation. quantile_68 stands for 68.3% quantile. quantile_95 stands for 95% quantile. VEMB stands for vegetated embankment.
The elevation difference of 50% of the pixels was 15.3 cm, and 68.3% of the pixels fell within 22.4 cm. The outliers identified were outside the interval [−11 cm, 43 cm] and fell on the edge of the roofs, trees, and shrubs, as well as hedgerows and narrow bridges (Figure 6). Some random points on the road and the roof of buildings were outliers, with a large difference of more than 500 m in elevation difference.

Figure 6.
Spatial distribution of differences in elevation (cm) between S1 and S2 on various features.
3.3. Validation
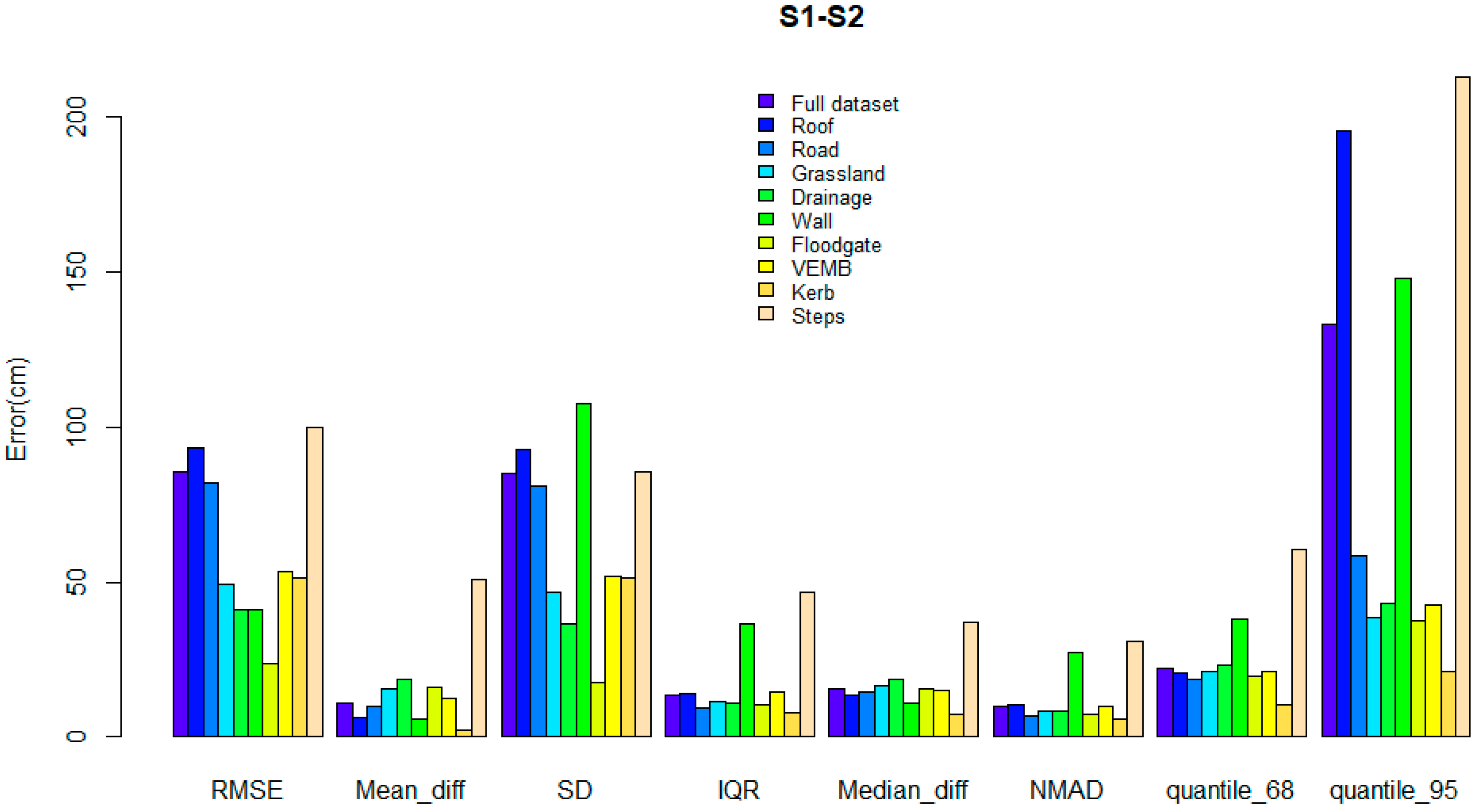
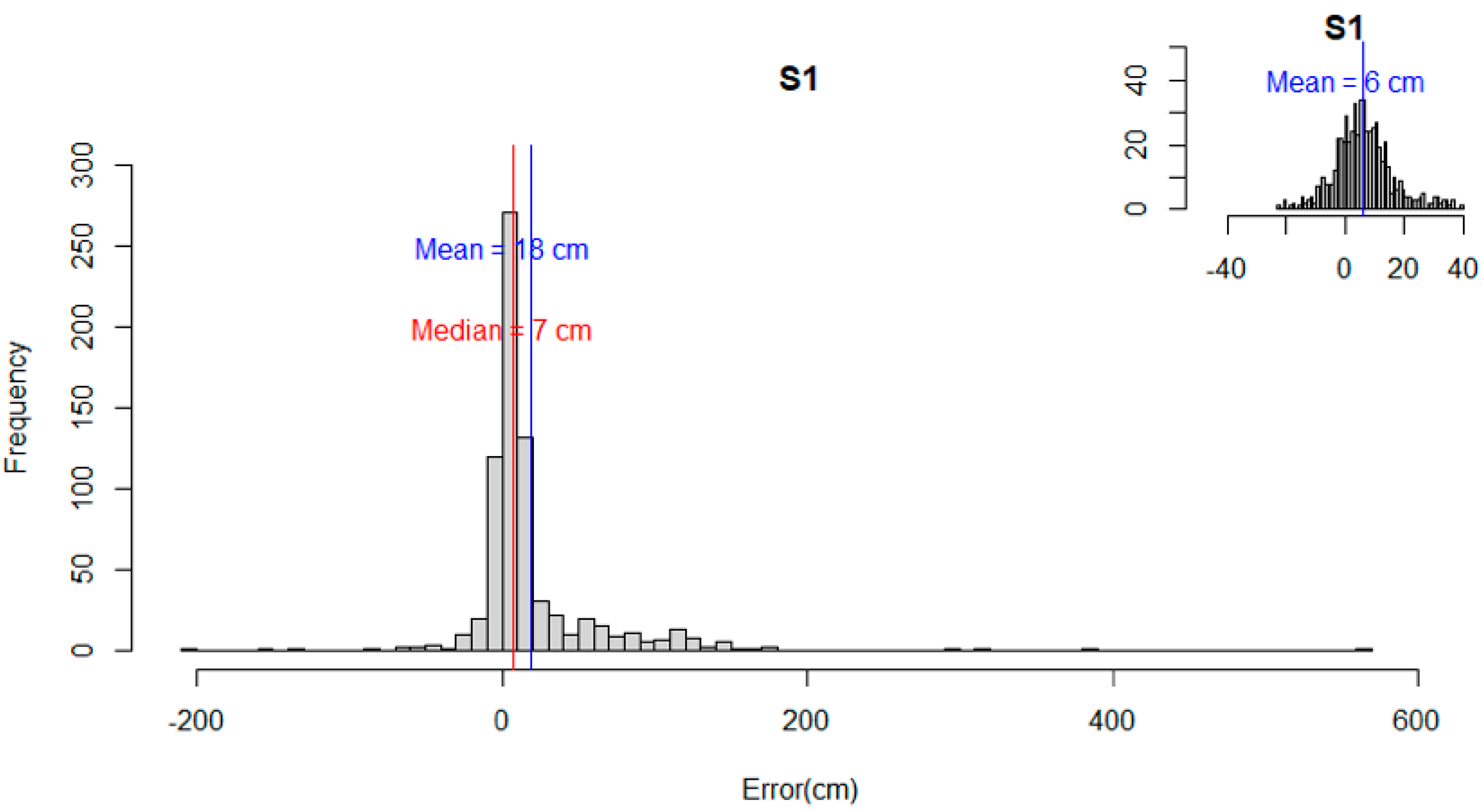
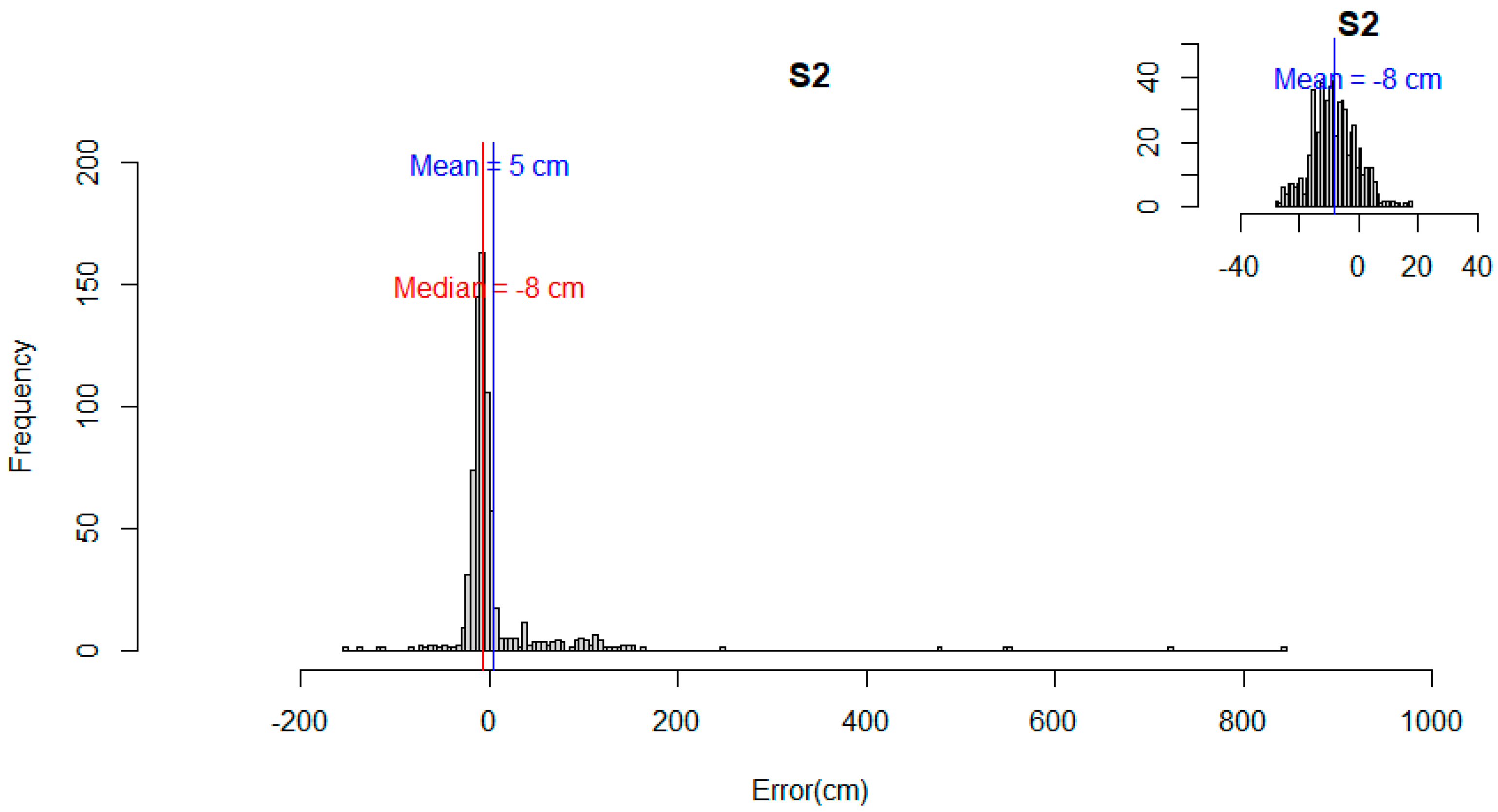
The distribution of the errors for S1 and S2 (Figure 7 and Figure 8) showed a departure from normality. Both distributions presented positive skew and leptokurtic patterns. The outliers identified had an impact on the statistical metrics calculated, thus affecting the measures of central tendency and dispersion. For example, the mean error of S1 reduced from 18 cm to 6 cm, and the mean error of S2 changed from a positive to a negative value. A similar pattern was observed for the reported maximum values, which changed from ≈560 cm to ≈40 cm (S1) and from >800 cm to <20 cm (S2). The NMAD for both S1 (i.e., 11 cm) and S2 (i.e., 9 cm) was slightly different from the 68.3% quantile (i.e., 15 cm for both S1 and S2). This indicated that the data were not normally distributed when outliers are present and confirmed the need to use robust statistical metrics [49]. For all combined features and land classes (Figure 9), the absolute mean error (excluding the outliers) and the median were approximately the same for S1 and S2 and always below 8.5 cm. The NMAD was higher than the median for both strategies. The NMAD and the 95% quantile were larger for S1 than S2, whereas the 68.3% quantile was similar for both S1 and S2.
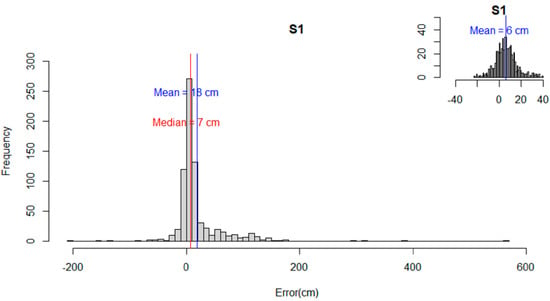
Figure 7.
Histogram showing distribution of the difference between S1 for an extent. Inset plot shows data distribution when outliers are removed.
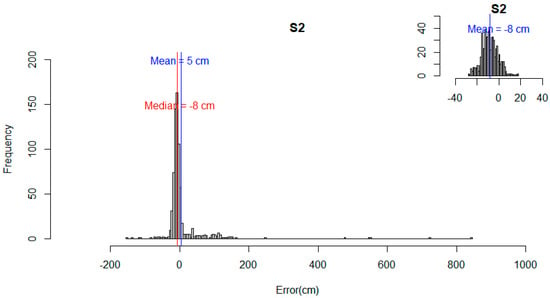
Figure 8.
Histogram showing distribution of error of S2. Inset plot shows data distribution when outliers are removed.
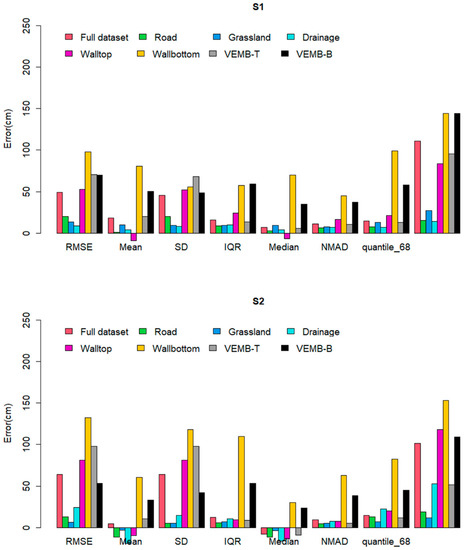
Figure 9.
Plot summarizing traditional and robust statiscal metrics (Table 3) for S1 and S2 (for all classes combined as well as per land class and microtopographic feature) when compared to Ground Control Point measurements. RMSE denotes root mean squared error. IQR stands for interquartile range. NMAD stands for normalized median absolute deviation. quantile_68 stands for 68.3% quantile. quantile_95 stands for 95% quantile. VEMB-T stands for the top of the vegetated embankment and VEMB-B stands for vegetated embankment.
The traditional and robust metrics confirmed the non-normality of the data for each land class (Figure 9). S1 presented a smaller median on roads, while S2 showed a smaller median on grasslands. The mean and median for roads and grasslands were negative for S2 (underestimation), while for S1 they were positive (overestimation). This was consistent with the results obtained in the previous section where the difference in elevation of S2 from S1 (S1–S2) was always positive. The mean error before and after removing outliers was close to the median for both S1 and S2 on roads and grasslands. However, the standard deviation changed when the outliers were removed.
The traditional and robust statistical metrics also highlighted the non-normality of data at the feature level (Figure 9) and differences in error magnitudes per feature. S1 presented a smaller median for drainage, the top of the wall, and the top of the vegetated crest, and S2 offered a smaller median for the bottom of the wall and the bottom of the vegetated crest. The medians of both S1 and S2 were >10 cm at the bottom of the wall and at the bottom of the vegetated crest. The median for S1 was positive (overestimated) at drainage and the top of the vegetated crest and was negative (underestimated) at the top of the wall. The median for S2 was negative (underestimated) at drainage, the top of the wall and at the top of the vegetated crest and >10 cm at all features, except for the top of the vegetated crest. Figure 9 also depicts the patterns for the quantiles for each feature. S2 presented a smaller median on the bottom of the wall and the top and bottom of the vegetated crest.
For both strategies, outliers were identified on uneven surfaces, vegetated areas, walls, bridges, drains, and shadows of tall structures (Figure 10). The number of outliers was more significant for S1 than for S2. For S1, most outliers were found at the bottom of the brick wall, at the bottom of the vegetated crest, and where the surface was either uneven or vegetated. There were also a few outliers on the top of the brick wall and features such as roads or drains in the shadow of tall structures were also outliers. The outliers for S2 were generally detected in the same features as in the S1 data and were mainly found at the bottom of the vegetated crest and at the top and bottom of the brick wall. The number of outliers was larger for S2 compared to S1 on drain points. The percentage of outliers never exceeded 27% for a given feature. Note that the outliers of S1 that fell on the road bridge were not outliers under S2. Where there was a tall structure casting a shadow on the road, both S1 and S2 gave a significant difference in elevation from the ground truth.

Figure 10.
Examples of features where outliers are identified for both S1 and S2. Blue markers indicate outliers. Pink markers are points which fell within the interquartile range.
In general, S1 data captured more points at all flood features compared to S2.
4. Discussion
4.1. Framework Development
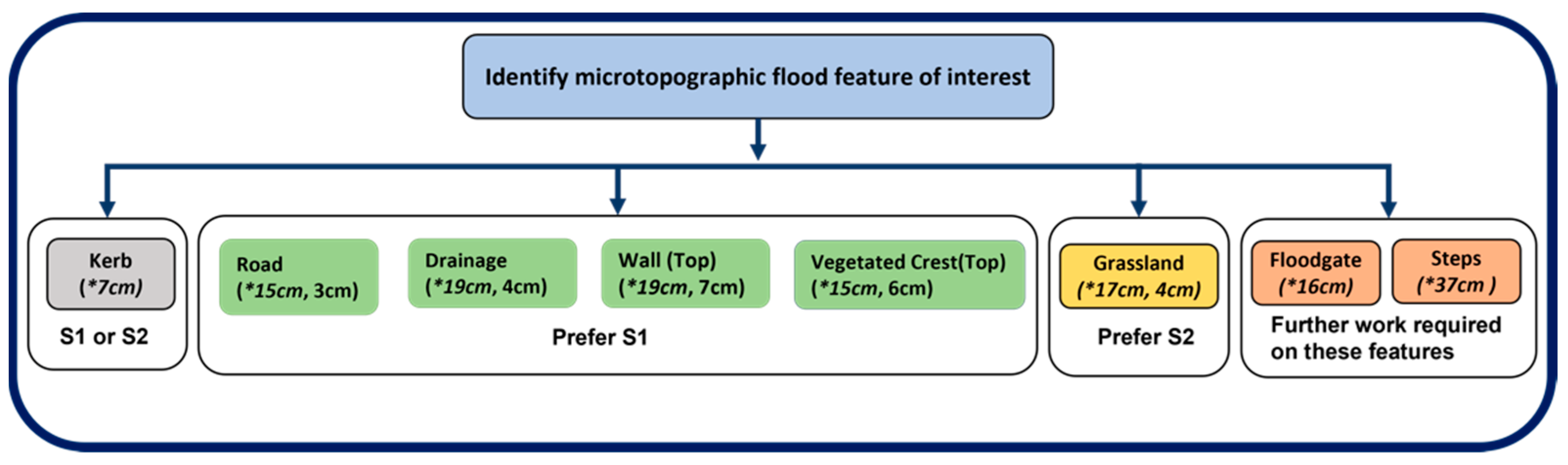
This study compared a typical survey specification for a UAS-based RGB survey (S1) and for a manned aircraft LiDAR survey (S2) commonly used for flood risk management activities. Both survey techniques can generate high-resolution geomatic products that enable the characterization of microtopography. Based on the results, a decision framework (Figure 11) was developed to identify the most appropriate survey strategy (S1 or S2) to characterize different microtopographic features. The framework helps identify whether these two strategies could be used interchangeably or should be specific to a certain feature. The decision criterion is driven by the features of interest, the median value of the differences in elevation between the two strategies considered, their accuracies and thresholds of tolerable discrepancy, and error. As the study focuses on characterizing microtopographic features, these thresholds are set to 10 cm. The threshold, as well as the decision criteria, could be defined differently depending on the purpose of the survey.
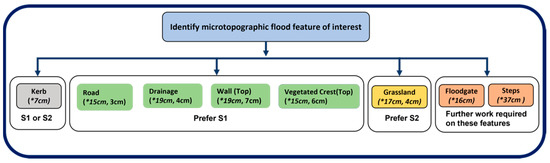
Figure 11.
Survey decision framework for S1 (UAS–RGB) and S2 (aircraft–LiDAR) for the characterization of microtopographic features. Values in brackets show the (*) median elevation difference between S1 and S2 and the elevation accuracy.
The choice of survey strategy depends on the microtopographic features present within the survey extent. When the median value of the elevation difference between S1 and S2 on a feature is <10 cm, both strategies would give similar outcomes and, therefore, both strategies can be used interchangeably. The median accuracy will further inform which strategy to use to minimize the error. However, when the median difference is >10 cm, the choice of strategy can yield considerably different results. The median accuracy will inform which strategy to use in a particular set of circumstances. When multiple features are to be surveyed, combining the different surveying approaches would be most beneficial. Based on these criteria, both surveying strategies can be used interchangeably when characterizing kerbs. The difference in elevation between S1 and S2 was less than the 10 cm threshold set up to characterize microtopography. Therefore, both strategies would provide elevation values that would enable a similar characterization of kerbs.
For any land classes and features other than kerbs, the median difference in elevation between S1 and S2 was >10 cm. Therefore, a further median accuracy assessment guided the choice of the best survey strategy. The median accuracy was used to assess which strategy was best placed for a given feature or land class. For roads, drainage, walls, and vegetated crests, surveyors are recommended to use S1 as it provides smaller median error values than S2. For grasslands, S2 is recommended when applying the same reasoning. For floodgates and steps, the accuracy could not be estimated due to a lack of available data points and, therefore, further research is required to identify the best sampling strategy. For land classes and features with large (>10 cm) median differences in elevation and median accuracy, ground-based sensors and UAS oblique imagery may be most appropriate. It should be noted that there could be seasonal variation in elevation for some features. For example, some types of grassland areas could experience seasonal changes of more than 30 cm between summer and winter surveys as the vegetation experiences the spring seasonal growth. The cost-effectiveness of surveying these areas, as well as the surveying frequency will be defined by these seasonal patterns.
This framework suggests that the features of interest within the survey area will need to be identified prior to survey commencement. Currently, this would have to be determined by visual inspection.
The range of results obtained in this present study are consistent with those by Leitao et al. [29]. The authors compared the elevation between UAS–RGB and LiDAR DEMs. The mean and standard deviation of the elevation differences were 6 cm and 11.9 cm, respectively. In the present work, the mean and standard deviation were 10.9 cm and 9.2 cm, respectively.
The difference between S1 and S2 was consistently positive, showing that S1 systematically provided larger elevation readings than S2. The difference between strategies was approximately 13 cm on buildings, 15 cm on roads, and 17 cm on grasslands (Figure 5).
A large difference between strategies was found at the edge of the roofs. This could be due to the difference in the angle of both the imagery (S1) and laser rays (S2). It is to be noted that S1 captures nadir imagery and, therefore, does not enable the characterisation of critical water ingress points such as property windows and doors. UAS oblique imagery could possibly address this challenge, improving flood risk assessment at the property level [51,52,53,54]. This in turn will help identify those properties in need of flood resilience and resistance measures. The large difference in elevation between strategies on drainage, walls and steps, as well as the large errors at the bottom of urban features (wall and vegetated embankments), could be explained by the same principle. It was also noted that thin features such as floodgates and flood barriers on the nadir images had a low number of points. The framework could be further enhanced by integrating the use of oblique imagery from either UASs or ground-based scanners.
It has to be noted that the accuracy analysis in the present study showed that S2 underestimated elevation systematically, whereas S1 systematically overestimated. Overestimation could mislead flood managers to believe that properties are better protected than they actually are. It could lead to inaccurate flood prediction, an inadequate design of flood remedial work, and an incorrect flood risk assessment and cost estimation.
The framework proposed here will promote the use and uptake of surveying technologies for microtopographic characterisation. There is a major role of parameter uncertainty in flood model selection and the resulting accuracy. Recent studies [55] report the effect that the uncertainty in the estimated topographic levels can have in urban flood simulations when using GIS-based dual coupled hydraulic models. Amongst other factors, the spatial discretization associated with local meshing, the small-scale variability of the physical parameters and the seasonal variation of the vegetation are reasons for the uncertainty. Microtopographic information could contribute to address these sources of uncertainty and enhance both model calibration and validation. This framework will directly contribute to enhance flood modelling and management practices by a better representation of microtopographic features. Several authors have already demonstrated the impact microtopography can have in flood modelling outcomes. For example, the studies by Ozdemir et al. [19] and Shreshtha et al. [56] have demonstrated the importance of high-resolution spatial data and completeness of data for urban flood modelling. As the resolution becomes finer, small-scale features are easily identifiable, thus improving the flood predictions for shallow surface water flows in urban environments [19], as demonstrated by previous authors.
A better characterisation of microtopography enhances surface water flow models, identifying areas at risk of SWF more accurately and implementing appropriate flood remedial works. Better surface water flow simulation will also support the planning and implementation of sustainable urban drainage systems (SUDS) [19]. The microtopographic information from high-resolution data would also help to identify microtopographic flood resilience measures installed in properties and help flood managers to prioritise their emergency resources accordingly [51]. The benefit of assessing the flood resilience of a property would also support flood insurance companies. The outcomes presented here will also contribute to the development of indicators on the “mitigation and adaptation to increasing flood” of the 25-Year Environmental Plan under the Resilience theme [57,58].
Inclusion of more microtopographic features by use of high-resolution data on flood modelling would require a high processing capacity of computers and increased simulation time, due to the complexity of the calculation for a hydraulic model with a prohibitively high-resolution mesh [59]. Other studies have established the possibility of integrating high-resolution datasets on critical features and merging different datasets to address this challenge [60]. Muthusamy et al. [21] demonstrated the use of merged high-resolution (1 m) DEMs with coarser resolution (50 m) DEMs in fluvial flood modelling to improve the characterisation of the river channel and how it reduces the error in mean flood depth from 150% to 20% and the overall RMSE in flood depth from 5.26 m to 0.98 m at a 50 m resolution. Leitao et al. [28] explored three DEM merging methods with LiDAR and UAS–RGB DEMs and concluded the MBlend method performed better in combining two DEMs where the elevation artefacts were similar to the reference DEM. The study also showed DEM merging could be used to improve the quality of flood modelling results by the use of higher quality DEMs [60,61]. This framework developed as part of this study would help to improve the quality of topographic data by identifying an accurate dataset for each feature to support the integration or merging of different datasets to improve the accuracy of microtopographic information.
4.2. Limitations and Future Work
This study compares two typical survey specifications used for flood studies. Both survey strategies could be improved by changing the survey specifications to maximise the characterisation of microtopography. Further work is required to identify the survey specifications that maximise the capture of microtopographic detail with each strategy. The study is carried out only on limited flood features, and the inclusion of other relevant flood features should be further explored. The analysis presented here has excluded vegetation from the analysis. Exclusion of vegetation could be automated using machine learning, image classification, or the techniques-based estimation of Leaf Area Index [62]. The use of GPS-based equipment is usually challenging in these locations. Further work should explore this type of coverage using optical surveys (e.g., total stations and ground-based scanners).
The framework is limited to a single criterion of accuracy and elevation difference between the two survey strategies. This could be further improved by including other important aspects such as cost and operational constraints [63]. UAS capital costs are lower than those associated with aircraft equipment. There is also the cost associated with successful deployment, including training, crew size, and other additional operational costs such as those required for the provision of health and safety measures [63]. As UAS become more popular, sub-contractor costs are expected to decrease [63]. Further work would be required to quantify how the improved accuracy in SWF predictions with the use of high-quality topographic data could help in mitigating flood risk on properties and critical infrastructure as well as managing drainage assets and storm water discharges into rivers.
To date, no clear guidelines or standards have been proposed for the error levels to be targeted for specific flood management purposes. To the authors’ knowledge, this study is another attempt towards quantifying the effect that surveying strategies can have on the characterisation of flood features and permeable/impervious surfaces at the microtopographic level.
5. Conclusions
This paper reports the data characteristics of point clouds derived from a typical survey specification of UAS–RGB and manned aircraft LiDAR. The findings reinstate that careful thought needs to be put on choosing a survey strategy to obtain accurate microtopographic information. The decision framework developed as part of this study will aid the selection of the most appropriate survey strategy based on an accuracy threshold of 10 cm. In brief, features such as roads, drainage, walls, and vegetated crests (top) are best characterized following UAS–RGB (S1), whereas manned aircraft LIDAR (S2) is best suited for grasslands. Kerbs are well characterized with either S1 or S2 for the targeted threshold (10 cm). In areas where multiple features are present, the combined use of S1 and S2 is proposed. Systematic overestimation of elevation (S1) and underestimations (S2) need to be considered when making flood assessments on flood risk or flood damages. For the elevation data on features such as the edge of buildings, thin features should be used for flood assessment with careful consideration as they are error prone. The results presented here are for a set of typical specification. It is to be noted that an impact on the accuracy values is to be expected when/if the survey specifics, such as flight altitude and UAS speed, are changed.
In addition to the accuracy of features of interest, the surveyors also need to carefully consider other factors such as the extent of the survey area, cost, safety, resource availability, time, and operational constraints [63]. This decision framework for data collection could be further developed to include other survey aspects (e.g., alternative sensors and oblique imagery).
Accurate topographic information is critical for planning, design, and maintenance of existing drainage assets and sustainable urban drainage systems (SUDS). Knowledge about urban features that manage the flood property level would support the flood manager and practitioner in making cost-effective, efficient flood management strategies and managing their limited resources efficiently. This study is another step towards developing a set of guidelines and standards that facilitate the selection of fit-for-purpose surveying strategies to inform flood management decisions.
Author Contributions
Conceptualization, R.R., M.R.C., Y.B.F. and P.L.; methodology, R.R., M.R.C. and Y.B.F.; software, R.R., M.R.C. and I.T.; validation, R.R. and M.R.C.; formal analysis, R.R.; investigation, R.R.; resources, M.R.C., Y.B.F., C.C., R.C. and P.L.; data curation, R.R.; writing—original draft preparation, R.R.; writing—review and editing, R.R., M.R.C., Y.B.F., I.T., C.C., R.C. and P.L.; visualisation, R.R.; supervision, M.R.C. and Y.B.F.; project administration, M.R.C.; funding acquisition, M.R.C., Y.B.F., C.C., R.C. and P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Atkins Global and the Engineering and Physical Sciences Research Council (EPSRC), under an EPSRC Industrial Case Studentship, voucher 20000021. This research was also funded under EPSRC project EP/N010329/1. The APC was funded by Remote Sensing MDPI.
Data Availability Statement
Data supporting this study are not publicly available due to commercial reasons. Please contact m.rivas-casado@cranfield.ac.uk.
Acknowledgments
We would like to thank the reviewers for their useful and constructive comments. We believe the manuscript is easier to read and follow thanks to their input.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Meteorological Organisation WMO. Provisional State of the Global Climate 2022. Available online: https://library.wmo.int/index.php?lvl=notice_display&id=22156#.ZCj4ktOS2Um (accessed on 16 May 2021).
- Kendon, M.; McCarthy, M.; Jevrejeva, S.; Matthews, A.; Sparks, T.; Garforth, J. State of the UK Climate 2019. Int. J. Climatol. 2020, 40, 1–69. [Google Scholar] [CrossRef]
- Environment Agency Surface Water: The Biggest Flood Risk of All. Available online: https://www.gov.uk/government/news/surface-water-the-biggest-flood-risk-of-all (accessed on 16 May 2021).
- Environment Agency Social Deprivation and the Likelihood of Flooding. Available online: http://www.gov.uk/government/organisations/environme (accessed on 25 August 2021).
- Environment Agency Flooding in England: A National Assessment of Flood Risk. Available online: www.environment-agency.gov.uk (accessed on 25 August 2021).
- Hunter, N.; Dale, A.; Hankin, B.; Lamb, R.; Lowis, A. Framework and Tools for Local Flood Risk Assessment: Project Report SC070059/R3; Environment Agency: Bristol, UK, 2014.
- Dottori, F.; di Baldassarre, G.; Todini, E. Detailed Data Is Welcome, but with a Pinch of Salt: Accuracy, Precision, and Uncertainty in Flood Inundation Modeling. Water Resour. Res. 2013, 49, 6079–6085. [Google Scholar] [CrossRef]
- Smith, R.C. Uncertainty Quantification: Theory, Implementation, and Applications; Siam: Philadelphia, PA, USA, 2013; Volume 12. [Google Scholar]
- Box, W.; Järvelä, J.; Västilä, K. Flow Resistance of Floodplain Vegetation Mixtures for Modelling River Flows. J. Hydrol. 2021, 601, 126593. [Google Scholar] [CrossRef]
- Fewtrell, T.J.; Duncan, A.; Sampson, C.C.; Neal, J.C.; Bates, P.D. Benchmarking Urban Flood Models of Varying Complexity and Scale Using High Resolution Terrestrial LiDAR Data. Phys. Chem. Earth 2011, 36, 281–291. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Urban Fluvial Flood Modelling Using a Two-Dimensional Diffusion-Wave Treatment, Part 2: Development of a Sub-Grid-Scale Treatment. Process 2006, 20, 1567–1583. [Google Scholar] [CrossRef]
- Aronica, G.T.; Lanza, L.G. Drainage Efficiency in Urban Areas: A Case Study. Hydrol. Process 2005, 19, 1105–1119. [Google Scholar] [CrossRef]
- Palla, A.; Colli, M.; Candela, A.; Aronica, G.T.; Lanza, L.G. Pluvial Flooding in Urban Areas: The Role of Surface Drainage Efficiency. J. Flood Risk Manag. 2018, 11, S663–S676. [Google Scholar] [CrossRef]
- Backes, D.; Schumann, G.; Teferele, F.N.; Boehm, J. Towards a High-Resolution Drone-Based 3D Mapping Dataset to Optimise Flood Hazard Modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2-W13, 181–187. [Google Scholar] [CrossRef]
- Fewtrell, T.J.; Bates, P.D.; Horritt, M.; Hunter, N.M. Evaluating the Effect of Scale in Flood Inundation Modelling in Urban Environments. Hydrol. Process. Int. J. 2008, 22, 5107–5118. [Google Scholar] [CrossRef]
- Guo, K.; Guan, M.; Yu, D. Urban Surface Water Flood Modelling-a Comprehensive Review of Current Models and Future Challenges. Hydrol. Earth Syst. Sci. 2021, 25, 2843–2860. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Interactions between Subgrid-Scale Resolution, Feature Representation and Grid-Scale Resolution in Flood Inundation Modelling. Hydrol. Process 2011, 25, 36–53. [Google Scholar] [CrossRef]
- Utlu, M.; Özdemir, H. How Much Spatial Resolution Do We Need to Model a Local Flood Event? Benchmark Testing Based on UAV Data from Biga River (Turkey). Arab. J. Geosci. 2020, 13, 1293. [Google Scholar] [CrossRef]
- Ozdemir, H.; Sampson, C.C.; De Almeida, G.A.M.; Bates, P.D. Evaluating Scale and Roughness Effects in Urban Flood Modelling Using Terrestrial LIDAR Data. Hydrol. Earth Syst. Sci. 2013, 17, 4015–4030. [Google Scholar] [CrossRef]
- Muthusamy, M.; Casado, M.R.; Salmoral, G.; Irvine, T.; Leinster, P. A Remote Sensing Based Integrated Approach to Quantify the Impact of Fluvial and Pluvial Flooding in an Urban Catchment. Remote Sens. 2019, 11, 577. [Google Scholar] [CrossRef]
- Muthusamy, M.; Casado, M.R.; Butler, D.; Leinster, P. Understanding the Effects of Digital Elevation Model Resolution in Urban Fluvial Flood Modelling. J. Hydrol. 2021, 596, 126088. [Google Scholar] [CrossRef]
- Roosevelt, C.H. Mapping Site-Level Microtopography with Real- Time Kinematic Global Navigation Satellite Systems (RTK GNSS) and Unmanned Aerial Vehicle Photogrammetry (UAVP). Open Archaeol. 2015, 1, 29–53. [Google Scholar] [CrossRef]
- Brubaker, K.M.; Myers, W.L.; Drohan, P.J.; Miller, D.A.; Boyer, E.W. The Use of LiDAR Terrain Data in Characterizing Surface Roughness and Microtopography. Appl. Environ. Soil Sci. 2013, 2013. [Google Scholar] [CrossRef]
- Mazzoleni, M.; Paron, P.; Reali, A.; Juizo, D.; Manane, J.; Brandimarte, L. Testing UAV-Derived Topography for Hydraulic Modelling in a Tropical Environment. Nat. Hazards 2020, 103, 139–163. [Google Scholar] [CrossRef]
- Sampson, C.C.; Fewtrell, T.J.; Duncan, A.; Shaad, K.; Horritt, M.S.; Bates, P.D. Use of Terrestrial Laser Scanning Data to Drive Decimetric Resolution Urban Inundation Models. Adv. Water Resour. 2012, 41, 1–17. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Agüera-Puntas, M.; Martínez-Carricondo, P.; Mancini, F.; Carvajal, F. Effects of Point Cloud Density, Interpolation Method and Grid Size on Derived Digital Terrain Model Accuracy at Micro Topography Level. Int. J. Remote Sens. 2020, 2020, 8281–8299. [Google Scholar] [CrossRef]
- Kopyść, P.T. The Use of Aerial Lidar and Structure from Motion (SFM) Photogrammetry Data in Analyzing Microtopographic Changes on Hiking Trails on the Example of Kielce (Poland). Carpathian J. Earth Environ. Sci. 2020, 15, 461–470. [Google Scholar] [CrossRef]
- Leitão, J.P.; de Sousa, L.M. Towards the Optimal Fusion of High-Resolution Digital Elevation Models for Detailed Urban Flood Assessment. J. Hydrol. 2018, 561, 651–661. [Google Scholar] [CrossRef]
- Leitão, J.P.; de Vitry, M.M.; Scheidegger, A.; Rieckermann, J. Assessing the Quality of Digital Elevation Models Obtained from Mini Unmanned Aerial Vehicles for Overland Flow Modelling in Urban Areas. Hydrol. Earth Syst. Sci. 2016, 20, 1637–1653. [Google Scholar] [CrossRef]
- Annis, A.; Nardi, F.; Petroselli, A.; Apollonio, C.; Arcangeletti, E.; Tauro, F.; Belli, C.; Bianconi, R.; Grimaldi, S. UAV-DEMs for Small-Scale Flood Hazard Mapping. Water 2020, 12, 1717. [Google Scholar] [CrossRef]
- Hashemi-Beni, L.; Gebrehiwot, A.A. Flood Extent Mapping: An Integrated Method Using Deep Learning and Region Growing Using UAV Optical Data. IEEE J. Sel. Top Appl. Earth Obs. Remote Sens. 2021, 14, 2127–2135. [Google Scholar] [CrossRef]
- Hashemi-Beni, L.; Jones, J.; Thompson, G.; Johnson, C.; Gebrehiwot, A. Challenges and Opportunities for UAV-Based Digital Elevation Model Generation for Flood-Risk Management: A Case of Princeville, North Carolina. Sensors 2018, 18, 3843. [Google Scholar] [CrossRef]
- National LIDAR Programme-Data.Gov.Uk. Available online: https://www.data.gov.uk/dataset/f0db0249-f17b-4036-9e65-309148c97ce4/national-lidar-programme (accessed on 24 August 2022).
- Nex, F.; Rinaudo, F. LiDAR or Photogrammetry? Integration Is the Answer. Ital. J. Remote Sens. 2011, 43, 107–121. [Google Scholar] [CrossRef]
- Abily, M.; Duluc, C.-M. Photogrammetric and LiDAR Data for High Resolution Runoff Modeling over Industrial and Urban Sites. In 2013 IAHR World Congress; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Zawadzka, J.; Truckell, I.; Khouakhi, A.; Rivas Casado, M.; Alexakis, D. Detection of Flood Damage in Urban Residential Areas Using Object-Oriented UAV Image Analysis Coupled with Tree-Based Classifiers. Remote Sens. 2021, 13, 3913. [Google Scholar] [CrossRef]
- Wedajo, G.K. LiDAR DEM Data for Flood Mapping and Assessment; Opportunities and Challenges: A Review. J. Remote Sens. GIS 2017, 06, 210. [Google Scholar] [CrossRef]
- Trepekli, K.; Friborg, T.; Balstrøm, T.; Fog, B.; Allotey, A.; Kofie, R.Y.; Møller-Jensen, L. UAV-LiDAR Observations Increase the Precision of Urban Flood Modelling in Accra by Detecting Critical Micro-Topographic Features. In Proceedings of the EGU General Assembly 2021, online, 19–30 April 2021. [Google Scholar] [CrossRef]
- Villanueva, J.R.E.; Martínez, L.I.; Montiel, J.I.P. DEM Generation from Fixed-Wing UAV Imaging and LiDAR-Derived Ground Control Points for Flood Estimations. Sensors 2019, 19, 3205. [Google Scholar] [CrossRef]
- Salmoral, G.; Casado, M.R.; Muthusamy, M.; Butler, D.; Menon, P.P.; Leinster, P. Guidelines for the Use of Unmanned Aerial Systems in Flood Emergency Response. Water 2020, 12, 521. [Google Scholar] [CrossRef]
- Office for National Statistics Population Estimates for the UK, England and Wales, Scotland and Northern Ireland. Available online: https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationestimates/bulletins/annualmidyearpopulationestimates/mid2020#local-area-population-change (accessed on 29 July 2021).
- Population Statistics. Available online: http://citypopulation.de/en/uk/northwestengland/cumbria/E34004122__cockermouth/ (accessed on 4 November 2021).
- Cumbria County Council. Cumbria Resilience A Review of Recovery Processes Following Storm Desmond’s Impacts on Cumbria (5 Th/6 Th Dec 2015); Cumbria County Council: Carlisle, UK, 2018.
- Casado, M.R.; Irvine, T.; Johnson, S.; Palma, M.; Leinster, P. The Use of Unmanned Aerial Vehicles to Estimate Direct Tangible Losses to Residential Properties from Flood Events: A Case Study of Cockermouth Following the Desmond Storm. Remote Sens. 2018, 10, 1548. [Google Scholar] [CrossRef]
- Cockermouth, Cumbria, United Kingdom Historical Weather Almanac. Available online: https://www.worldweatheronline.com/cockermouth-weather-history/cumbria/gb.aspx (accessed on 5 November 2021).
- Galaxy|Teledyne Geospatial. Available online: http://www.teledyneoptech.com/en/products/airborne-survey/galaxy/ (accessed on 1 April 2022).
- Formulario Para Peticion de Mensajes Aeronauticos. Available online: https://ogimet.com/metars.phtml.en (accessed on 1 April 2022).
- Chow, T.E.; Hodgson, M.E. Effects of Lidar Post-Spacing and DEM Resolution to Mean Slope Estimation. Int. J. Geogr. Inf. Sci. 2009, 23, 1277–1295. [Google Scholar] [CrossRef]
- Höhle, J.; Höhle, M. Accuracy Assessment of Digital Elevation Models by Means of Robust Statistical Methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- OS MasterMap® Topography Layer [FileGeoDatabase Geospatial Data], Scale 1:1250, Tiles: GB, Updated: 6 August 2020, Ordnance Survey (GB), Using: EDINA Digimap Ordnance Survey Service. Available online: https://Digimap.Edina.Ac.Uk (accessed on 17 June 2021).
- Feng, Y.; Xiao, Q.; Brenner, C.; Peche, A.; Yang, J.; Feuerhake, U.; Sester, M. Determination of Building Flood Risk Maps from LiDAR Mobile Mapping Data. Comput. Environ. Urban Syst. 2022, 93, 101759. [Google Scholar] [CrossRef]
- Chen, K.; Blong, R. Extracting Building Features from High Resolution Aerial Imagery for Natural Hazards Risk Assessment; Extracting Building Features from High Resolution Aerial Imagery for Natural Hazards Risk Assessment. Int. Geosci. Remote Sens. Symp. (IGARSS) 2002, 4, 2039–2041. [Google Scholar] [CrossRef]
- Vacca, G.; Dessì, A.; Sacco, A. The Use of Nadir and Oblique UAV Images for Building Knowledge. ISPRS Int. J. Geo-Inf. 2017, 6, 393. [Google Scholar] [CrossRef]
- Piech, I.; Ruzyczka, A. Generating of Building Facades Orthophotoplans with UAV and Terrestrial Photos. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 012074. [Google Scholar] [CrossRef]
- Sinagra, M.; Nasello, C.; Tucciarelli, T. Urban Flood Prediction through GIS-Based Dual-Coupled Hydraulic Models. Hydrology 2022, 9, 174. [Google Scholar] [CrossRef]
- Shrestha, A.; Mascaro, G.; Garcia, M. Effects of Stormwater Infrastructure Data Completeness and Model Resolution on Urban Flood Modeling. J. Hydrol. 2022, 607, 127498. [Google Scholar] [CrossRef]
- 25 Year Environment Plan Annual Progress Report-April 2021 to March 2022; HH Associates Ltd.: London, UK, 2021; ISBN 978-1-5286-3643-8.
- DEFRA. Measuring Environmental Change: Outcome Indicator Framework for the 25 Year Environment Plan; DEFRA: London, UK, 2019.
- Shen, D.; Wang, J.; Cheng, X.; Rui, Y.; Ye, S. Integration of 2-D Hydraulic Model and High-Resolution Lidar-Derived DEM for Floodplain Flow Modeling. Hydrol. Earth Syst. Sci. 2015, 19, 3605–3616. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Bates, P.D. Editorial: The Need for a High-Accuracy, Open-Access Global Digital Elevation Model. Front. Earth Sci. 2020, 8, 544. [Google Scholar] [CrossRef]
- Backes, D.J.; Teferle, F.N. Multiscale Integration of High-Resolution Spaceborne and Drone-Based Imagery for a High-Accuracy Digital Elevation Model Over Tristan Da Cunha. Front. Earth Sci. 2020, 8, 319. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Errico, A.; Francalanci, S.; Solari, L.; Preti, F.; Chirico, G.B. Evaluation of Flow Resistance Models Based on Field Experiments in a Partly Vegetated Reclamation Channel. Geosciences 2020, 10, 47. [Google Scholar] [CrossRef]
- Comparison of Aerial Surveying with a Manned Aircraft or UAS for Mapping and 3D Modelling?|Geo-Matching.Com. Available online: https://geo-matching.com/content/comparison-of-aerial-surveying-with-a-manned-aircraft-or-uas-for-mapping-and-3d-modelling (accessed on 24 February 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).