Water Temperature Reconstruction via Station Position Correction Method Based on Coastal Acoustic Tomography Systems

Abstract

Underwater acoustic tomography is an advanced technology in water environment observation. Sound propagation duration between transceivers is used for underwater parameter distribution profile reconstruction in the inverse problem. The key points of acoustic tomography are accurate station distance and time synchronization. Two methods are introduced in this study for sound station position correction. The direct signal transmission correction (DSC) method corrects the multi-peak (expect direct ray) travel time via the travel time difference between different sound rays and reference direct ray. The ray-model position correction (RMC) method calculates exact station position by the station drift distance obtained from transceiver depth variations to correct direct ray travel time; the other multi-peak travel time is revised by the corrected direct ray travel time. A water temperature observation experiment was carried out in a reservoir using coastal acoustic tomography (CAT) systems to verify the flexibility of these two methods. Multi-ray arrival peaks are corrected using DSC and RMC methods; water temperature inversion results in a 2D vertical profile are obtained. The reliability of the method is proved by comparison with temperature depth sensor (TD) data. The methods improve the quality of initial data and can be attempted for further water environment observation in acoustic tomography observation studies.

1. Introduction

Underwater acoustic tomography is widely used for underwater environmental observation using sound propagation information. As remote sensing techniques, ocean acoustic tomography (OAT) and coastal acoustic tomography (CAT) are both underwater acoustic tomography techniques and are widely applied for dynamical processes observation in oceans, rivers, coastal regions, etc. [1,2,3,4]. Compared with fixed-point measurement devices, such as acoustic Doppler current profilers (ADCPs) and conductivity temperature depth probes (CTDs), underwater acoustic tomography is not limited by shipping, navigation and observation scale [2]. In recent years, CAT observations via multi-station networking were widely conducted in several countries for underwater environment observation [5,6,7,8,9,10,11,12].

The critical idea of acoustic tomography observation is reconstructing an environment field by the travel time information of multi-rays between acoustic station pairs. However, travel times of sound signals are influenced by system clock error, acoustic station position error, and environment variations (temperature, salinity, and flow). The first two errors are generated by time synchronization differences and surface waves, which increase the error of inversion results. Time synchronization is awarded by GPS or atomic clock and the clock difference is less than 0.6 us. Besides, environment variations are the target of our observation experiment, which also influence the processing of acoustic signal transmission. Therefore, it is crucial to remove the effects of system clock error and acoustic station position error from the observation results and retain the effects of environment variations. In contrast, the station drifts caused by the influence of surface waves will produce a larger travel time difference.

In previous studies, researchers usually directly removed the travel time error caused by station drift during the observation period or only solved the flow field. Yong Guo et al. (2019) [7] carried out a CAT experiment in the Panzhinan waterway, but acoustic stations were moved by a strong flow field; thus, only vertical profiles inversion results of current filed were obtained [8]. In addition, the travel time error caused by station drift is corrected via the direct sound ray in the early experiment. Chuanzheng Zhang et al. (2017) [5] considered station drift as a constant value during the experiment period, and the actual station distance was corrected by the projected distance of direct ray travel time multiplier reference sound speed [13,14]. However, the station distance is changing in real time in the ocean observation, which means the sound ray structure is changing in real time and ray simulations are required at each sending moment. In the latest research, Dai et al. (2023) [14] simulated a random swing of about 5 m of the acoustic station position, which results in an inversion sound speed error of less than 1 m/s. The data with random swing showed good agreement with the original data, but it is a complex work for eliminating the errors of travel time, especially in high-frequency small-scale observation [15]. Thus, a fast and reasonable method for travel time correction (station correction) is urgently necessary.

Different from the acoustic station moving or dragging, the station drift does not produce strong Doppler effects [16]. In other words, the distance of station drift is much smaller than the acoustic station pair distance, and the acoustic channel models are almost constant between station pair. This means that the received acoustic signal information can be used to correct the sound travel time. In this paper, two methods are proposed to correct signal travel time: the first way corrects the multi-peak travel time directly via the travel time difference of arrival signal peaks. Another way finds the exact station position first and then the correct travel time by referring to the distance of new station positions. To verify the methods, a four-station CAT experiment deployed along one vertical profile in the Huangcai Reservoir, Changsha, is introduced and used. The travel times corrected by the two methods are compared and discussed. Besides, the water temperature variation patterns during the observation period are reconstructed using the corrected travel time, and the inversion results are compared with TDs.

The rest of this paper is structured as follows: two types of travel time correction methods are introduced in Section 2. In Section 3, a vertical profile observation experiment is presented. Section 4 focuses on multi-peak identification and matching, and also, the feasibility of the travel time correction methods is compared and discussed based on inversion results in this section. Discussion and conclusions are given in Section 5.

2. Methodology

The effect of station position drift on the reciprocal signal transmission results in the distortion between ray simulation results and actual received signals. In underwater acoustic tomography, multi-peak travel times are identified via the correlation of received signals with transmitted sound waves [16]. It can be simply expressed as [1,2]:

$$t_{ij/ji}={\displaystyle {\int }_{{\mathsf{\Gamma }}^{\pm }}\frac{ds}{C\pm U}\approx \frac{L_{ij/ji}}{C_m\pm U_m}}$$

(1)

where $C_m$ is the range-averaged sound speed, and $U_m$ is the range-averaged current velocity. $L_{ij}$ is the ray path length between station i and station j. $t_{ij}$ is the travel time of the sound wave along each ray path. The average current and sound speed filed are inversed by two-way signal travel time difference and travel time deviation obtained from the CAT systems, as follows:

$$\begin{array}{l}{U}_m=\frac{L_{ij}}{2}\left(\frac{1}{t_{ij}}-\frac{1}{t_{ji}}\right)\approx \frac{L_{ij}}{2t_0{}^2}\Delta t=\frac{L_{ij}}{2{\overline{t}}^2}\Delta t\\ C_m=\frac{L_{ij}}{2}\left(\frac{1}{t_{ij}}+\frac{1}{t_{ji}}\right)\approx \frac{L_{ij}}{\overline{t}}\end{array}$$

(2)

where $\Delta t$ is travel time difference ($\Delta t=t_{ij}-t_{ji}$); $\overline{t}$ is the mean travel time ($\overline{t}=\frac{t_{ij}+t_{ji}}{2}$); $t_0$ and $C_0$ are the reference sound travel time and reference sound speed, respectively ($t_0\approx \overline{t}$). The full differentiations of Equation (2) are as follows (Equation (3)):

$$\begin{array}{l}d{U}_m=\frac{\partial U_m}{\partial L_{ij}}d{L}_{ij}+\frac{\partial U_m}{\partial \Delta t}d\left(\Delta t\right)+\frac{\partial U_m}{\partial \left(\overline{t}\right)}d\left(\overline{t}\right)=\frac{\Delta t}{2{\overline{t}}^2}d{L}_{ij}+\frac{L_{ij}}{2{\overline{t}}^2}d(\Delta t)-\frac{L_{ij}\Delta t}{{\overline{t}}^3}d\left(\overline{t}\right)\\ d{C}_m=\frac{\partial C_m}{\partial L_{ij}}d{L}_{ij}+\frac{\partial C_m}{\partial \left(\overline{t}\right)}d\left(\overline{t}\right)=\frac{1}{\overline{t}}d{L}_{ij}+\frac{-L_{ij}}{{\overline{t}}^2}d\left(\overline{t}\right)\end{array}$$

(3)

Multiply Equation (3) with Equation (2) will produce Equation (4):

$$\begin{array}{l}\frac{d{U}_m}{U_m}=\frac{d{L}_{ij}}{L_{ij}}+\frac{d\left(\Delta t\right)}{\Delta t}-2\frac{d(\overline{t})}{\overline{t}}\\ \frac{d{C}_m}{C_m}=\frac{d{L}_{ij}}{L_{ij}}-\frac{d(\overline{t})}{\overline{t}}\end{array}$$

(4)

From Equation (4), the distance error between station pairs and the errors of signal travel time difference are the main factors in flow field inversion. Normally, the variations of velocity represent the movement of the flow field in the observation area. The errors of signal travel time difference are due to the clock synchronization differences. The system is synchronized by GPS or atomic clock; the clock error of GPS is less than 0.6 us, and the error of the atomic clock is less than the GPS. On the contrary, the error caused by acoustic station movement is larger than the clock error. For example, it assumes a station drift of 10 m at a distance of 200 m (reference travel time is about 0.1 s) with the average current velocity of 0.5 m/s. In this situation, the error of flow velocity caused by station drift is about 0.025 m/s via Equation (3), and that caused by an error of the signal travel time difference is about 0.0035 m/s. Both the 0.025 m/s caused by station drift and the 0.0035 m/s caused by clock synchronization error are acceptable in a flow field inversion problem.

As for average sound-speed calculating, the distance error also affects the sound speed [17]; in addition, the error of sound travel time deviation is another affect factor. The distributions of sound speed in water are mainly determined by temperature, salinity, and depth [18]; water temperature variations are the greatest factors to sound speed in a shallow water environment. At the same depth, a 1 °C increase of water corresponds to about a 4.5 m/s sound speed increase [2,19,20]. The error of sound travel time deviation is caused by clock synchronization differences and systematic calculation errors, which is assumed to be 0.001 s at 5 k frequency (the value is different at different acoustic frequency). Similarly, assuming a station drift of 50 m at a distance of 30 km, when the average sound speed is 1500 m/s, the error of sound speed caused by station drift is about 2.5 m/s, while the error caused by travel time deviation is 1.5 m/s, resulting in temperature errors of about 0.5 °C and 0.3 °C, respectively. Such a big error from Equation (3) is unacceptable in temperature field inversion and needs to be reduced.

In conclusion, acoustic station drift existing in experiments will increase the errors in both inversions of temperature and flow. Especially, more intense flow field effects and topographic fluctuations increase acoustic station drift distance in a shallow water area. Generally, a station moves in circles around the anchored position because of the surface waves. In addition, with the variations of terrain and distance, the sound structure between acoustic station pairs changes significantly. Currently, oceanographers normally use other devices for secondary positioning or direct positioning compensation with direct arrival rays. For this purpose, the estimation of station position and the travel time correction are performed with the received reciprocal transmission acoustic signals. Two methods are developed to solve this problem. It should be noted that acoustic station drift is different from station moving; station drift is a slow process without a Doppler effect.

2.1. Direct Signal Transmission Correction

The core idea of direct signal transmission correction is correct signal travel time using the difference between multi-ray travel time with direct ray travel time. When the experiment area has little terrain fluctuations, despite station drift existing, the acoustic channel structure can be considered as a constant. From this point, direct signal transmission correction is a way to correct other signals via the one received reference signal plus other arrival peak-time differences. The detailed process is as follows:

Identify the multi-peak arrival time at each moment during the sound reciprocal transmission. Generally, the first arrival peak time denotes the travel time of a direct ray and the rest of the arrival peaks denote deflected rays or reflected rays. It should note that the first arrival peak is or not the direct ray is not critical in this method.

The travel time of a direct ray in the earliest recorded signal group ($G_0$) is selected as the reference travel time (${}^{0}t_{ij}^1$). Each group represents the result of signal transmission for each station pair at each sending moment, and the travel times in each group are the identified arrival peaks. The model of direct signal transmission correction is established as follows:

$$\begin{array}{c}{G}_0[{}^{0}t_{ij}^1,{}^{0}t_{ij}^2,\dots ,{}^{0}t_{ij}^k,\dots ,{}^{0}t_{ij}^K],\cdots ,G_n,\cdots ,G_N[{}^{N}t_{ij}^1,{}^{N}t_{ij}^2,\dots ,{}^{N}t_{ij}^k,\dots ,{}^{N}t_{ij}^K];\\ G_{\mathrm{Cn}}=\left[\begin{array}{c}{}^{Cn}t_{ij}^1\\ {}^{Cn}t_{ij}^2\\ \dots \\ \begin{array}{c}{}^{Cn}t_{ij}^k\\ \dots \\ {}^{Cn}t_{ij}^K\end{array}\end{array}\right]=\left[\begin{array}{c}{}^{0}t_{ij}^1\\ {}^{0}t_{ij}^1\\ \dots \\ \begin{array}{c}{}^{0}t_{ij}^1\\ \dots \\ {}^{0}t_{ij}^1\end{array}\end{array}\right]+\left[\begin{array}{c}0\\ {}^{n}t_{ij}^2-{}^{n}t_{ij}^1\\ \dots \\ \begin{array}{c}{}^{n}t_{ij}^k-{}^{n}t_{ij}^1\\ \dots \\ {}^{n}t_{ij}^K-{}^{n}t_{ij}^1\end{array}\end{array}\right]=\left[\begin{array}{c}{}^{0}t_{ij}^1\\ {}^{0}t_{ij}^1+{}^{n}t_{ij}^2-{}^{n}t_{ij}^1\\ \dots \\ \begin{array}{c}{}^{0}t_{ij}^1+{}^{n}t_{ij}^k-{}^{n}t_{ij}^1\\ \dots \\ {}^{0}t_{ij}^1+{}^{n}t_{ij}^K-{}^{n}t_{ij}^1\end{array}\end{array}\right]\end{array}$$

(5)

where $G_n$ denotes the original travel time group, and the $G_{Cn}$ denotes the group after travel time correction. i and j denote station number, n (1, …, N) denotes different moment number of received travel time series, and k (1, …, K) denotes number of multi-peaks’ travel time. ${}^{Cn}t_{ij}^k$ is the travel time of kth sound ray between station i and station j (nth moment). ‘C’ means the travel time is corrected. K is the sum of matched sound ray number.

Direct signal transmission correction is a rapid travel time correction method. It is empirically concluded that the sound-ray path of an acoustic signal passing through remains unchanged when the station shift is slight. This indicates that the identified arrival peaks in each sending moment (group) are moving together. Thus, the group with the earliest travel time of the first arrival peak is used as a reference group for correcting and matching other travel time groups. The travel time difference between identified multiple arrival peaks (except first peak) and first arrival peak in the same group is caused by environment variation (ray deflection or ray reflection). The travel time corrections of a multi-ray is to add this difference to the reference travel time of the first arrival peak. The travel time of an acoustic station pair after direct signal transmission correction can be expressed as follows:

$$T_{ij}=\left[\begin{array}{c}{G}_{C0}\\ G_{C1}\\ \dots \\ \begin{array}{c}{G}_{Cn}\\ \dots \\ G_{CN}\end{array}\end{array}\right]=\left[\begin{array}{cccccc}{}^{0}t_{ij}^1& {}^{0}t_{ij}^2& \dots & {}^{0}t_{ij}^k& \dots & {}^{0}t_{ij}^K\\ {}^{0}t_{ij}^1& {}^{0}t_{ij}^1+\left({}^{1}t_{ij}^2-{}^{1}t_{ij}^1\right)& \dots & {}^{0}t_{ij}^1+\left({}^{1}t_{ij}^k-{}^{1}t_{ij}^1\right)& \dots & {}^{0}t_{ij}^1+\left({}^{1}t_{ij}^K-{}^{1}t_{ij}^1\right)\\ \dots & \dots & \dots & \dots & \dots & \dots \\ {}^{0}t_{ij}^1& {}^{0}t_{ij}^1+\left({}^{n}t_{ij}^2-{}^{n}t_{ij}^1\right)& \dots & {}^{0}t_{ij}^1+\left({}^{n}t_{ij}^k-{}^{n}t_{ij}^1\right)& \dots & {}^{0}t_{ij}^1+\left({}^{n}t_{ij}^K-{}^{n}t_{ij}^1\right)\\ \dots & \dots & \dots & \dots & \dots & \dots \\ {}^{0}t_{ij}^1& {}^{0}t_{ij}^1+\left({}^{N}t_{ij}^2-{}^{N}t_{ij}^1\right)& \dots & {}^{0}t_{ij}^1+\left({}^{N}t_{ij}^k-{}^{N}t_{ij}^1\right)& \dots & {}^{0}t_{ij}^1+\left({}^{N}t_{ij}^K-{}^{N}t_{ij}^1\right)\end{array}\right]$$

(6)

where $T_{ij}$ denotes corrected reciprocal signal transmission between station i and station j.

The advantage of this method is that it can correct the multi-ray travel time quickly, but its disadvantage is that the first arrival peak cannot be used for the subsequent solution. In addition, it cannot be used of error correction when the station drift is large.

2.2. Ray-Model Position Correction

This method uses the projection of direct ray distances and drift distances between station pairs to revise the position after station drift, and then corrects the travel time of the multi-ray arrival peaks. Normally, the transceiver fluctuates around the anchored position. Reference station distances between station pairs are calculated via the travel time of a direct ray projected in a horizontal direction at each moment. The station drifts are obtained using the depth variation of a transceiver recorded by co-located TD. In this paper, a three-station travel time correction process via ray-model position correction is introduced. The station position correction model with three stations is shown in Figure 1a. Figure 1b shows correction processing of position projection and Figure 1c shows the transceiver position variation at vertical direction.

In tomography observation experiments, station distance affects the accuracy of results. Different station distances produce different patterns of sound rays. Direct rays (D) always exist with a high signal-to-noise ratio (SNR) and the earliest travel time that can be easily identified. Bottom-reflected rays (BR), surface-reflected rays (SR), or other arrival ray patterns depend on the observation zone terrain.

The steps of the position correction method based on ray model are as follows:

Step 1: identify multi-peak travel times of a sound wave at different moments and conduct sound ray simulations (BEELHOP [1]) with pre-set GPS positions. Obtain sound ray path patterns and structures by ray simulation.

Step 2: obtain station drift distance by the depth variation of a transceiver, then calculate the actual station position via the reference three-station distance and station drift distance.

Step 3: obtain exact station distance and corrected travel time of direct ray by removing the station drift error from the reference station distance. The travel time differences between other multi-peak and first peak in the same group are used to correct the travel times of other rays.

The symbols in Figure 1 are defined as follows: initial station coordinates indicate as $S_i(x_i,y_i,z_i)$; drifting station coordinates indicate as $S_i(x_i^{\prime },y_i^{\prime },z_i^{\prime })$; initial station distance between S_i and S_j indicates as $L_{ij}$; actual station distance indicates as $L_{\mathrm{ij}}^{\prime }$; station drift distance indicates as $\Delta d_i$; i and j are acoustic station numbers.

Due to the influence of flow current field, this method requires prior prediction and calculation of the reference current velocity before station position correction. The reference current velocity $U_{ij}^r$ is estimated by Equation (7) at each moment. The reference distance $L_{{}_{ij}}^r$ between station i and j is obtained via GPS and the reference sound speed $C_0^{ij}$ between station pair is obtained via CTD.

$$U_{ij}^r\approx U_m=\frac{L_{ij}^r}{2}\left(\frac{1}{t_{ij}}-\frac{1}{t_{ji}}\right)\approx \frac{L_{ij}^r}{2t_0{}^2}\Delta t=\frac{{\left(C_0^{ij}\right)}^2}{2L_{ij}}\Delta t$$

(7)

The results of the reference current velocity are used in Equation (10).

The exact station position after station drift is determined by the solution matrix between multi-stations. Project the station $S_i(x_i,y_i,z_i)$ to the horizontal plane $S_i(x_i,y_i)$ as Figure 1b. According to the principle of intersection of geometric circles, the relationship of station drift distance can be expressed as Equation (8).

$$\begin{array}{c}{L}_{12}^{\prime }{}^2={\left(x_2^{\prime }-x_1\right)}^2+{\left(y_2^{\prime }-y_1\right)}^2=\mathrm{Pro}\left({(C_0^{12}+U_{{}_{12}}^r)}^2{\left(t_{12}^1\right)}^2\right)\\ L_{13}^{\prime }{}^2={\left(x_3^{\prime }-x_1\right)}^2+{\left(y_3^{\prime }-y_1\right)}^2=\mathrm{Pro}\left({(C_0^{13}+U_{{}_{13}}^r)}^2{\left(t_{13}^1\right)}^2\right)\\ L_{23}^{\prime }{}^2={\left(x_3^{\prime }-x_2^{\prime }\right)}^2+{\left(y_3^{\prime }-y_2^{\prime }\right)}^2=\mathrm{Pro}\left({(C_0^{23}+U_{{}_{23}}^r)}^2{\left(t_{23}^1\right)}^2\right)\end{array}$$

(8)

where $\mathrm{Pro}\left({(C_0^{ij}+U_{{}_{ij}}^r)}^2{\left(t_{ij}^1\right)}^2\right)$ is the projection of direct ray path in horizontal direction. $t_{ij}^1$ is the travel time of direct ray between station i and j. The horizontal drift distance from the fixed point of the station is calculated by the depth variation of the transceiver and pre-set rope length as Equation (9) (Figure 1c), where the station drift distance can be obtained via $\Delta d_i=\sqrt{R_i{}^2-{\left(Z_i^{\prime }\right)}^2}\times \frac{Z_i^{\prime }}{Z_{0i}}$, $R_i$ is the rope length between transceiver to bottom weight, $Z_i^{\prime }$ is the water depth minus recorded transceiver depth, and $Z_{0i}$ is the depth measured by depth gauge at original fixed point of the station.

$$\begin{array}{c}{\left(x_2^{\prime }-x_2\right)}^2+{\left(y_2^{\prime }-y_2\right)}^2=\Delta d_2{}^2={\left(\frac{Z_2^{\prime }}{Z_{02}}\right)}^2\times \left(R_2{}^2-{\left(Z_2^{\prime }\right)}^2\right)\\ {\left(x_3^{\prime }-x_3\right)}^2+{\left(y_3^{\prime }-y_3\right)}^2=\Delta d_3{}^2={\left(\frac{Z_3^{\prime }}{Z_{03}}\right)}^2\times \left(R_2{}^2-{\left(Z_2^{\prime }\right)}^2\right)\end{array}$$

(9)

Note that to simplify the ray-model solution process of three stations, we append one station drift to the other two stations, which assumes that the stations did not move in the ray-model correction. Therefore, the corrected station positions of $S_{{}_2}^{\prime }(x_{{}_2}^{\prime },y_{{}_2}^{\prime })$ and $S_{{}_3}^{\prime }(x_{{}_3}^{\prime },y_{{}_3}^{\prime })$ can be quickly calculated by Equations (8) and (9), and the new station position after station drift is obtained.

As for travel time correction via the new station position, the station drift produces different effects along station pair lines, which cannot be easily defined by subtracting the drift distance of the exact station distance. The travel time corrections of a direct ray at the new position are defined as Equation (10). The reference sound speed and reference current velocity are used to correct travel time $t_{ij}^{1\prime }$.

$$\mathrm{Pro}\left(\left(C_0^{ij}+U_{ij}^r\right)t_{ij}^{1\prime }\right)=L_{ij}^{\prime }+\Delta d_j\cdot \cos {\theta }_{ij}+\Delta d_i\cdot \cos {\theta }_{ji}$$

(10)

where $L_{ij}^{\prime }=\sqrt{{\left(x_j^{\prime }-x_i\right)}^2+{\left(y_j^{\prime }-y_i\right)}^2}$, and ${\theta }_{ij}$ is the angle between drift direction and initial station pair direction. It should be explained that a small projected error exists in this correction method, but it can be ignored because that station distance is much larger than the station drift error.

Via the corrected travel time of a direct ray, the travel time of other multi-rays can be obtained by corrected direct ray travel time plus travel time differences between other ray patterns and direct rays as Equation (11), which is similar to the direct signal transmission correction method.

$$T_{ij}=\left[\begin{array}{ccccc}{}^{0}t_{ij}^{1\prime }& \dots & {}^{n}t_{ij}^{1\prime }& \dots & {}^{N}t_{ij}^{1\prime }\\ {}^{0}t_{ij}^{1\prime }+\left({}^{0}t_{ij}^2-{}^{0}t_{ij}^1\right)& \dots & {}^{n}t_{ij}^{1\prime }+\left({}^{n}t_{ij}^2-{}^{n}t_{ij}^1\right)& \dots & {}^{N}t_{ij}^{1\prime }+\left({}^{N}t_{ij}^2-{}^{N}t_{ij}^1\right)\\ \dots & \dots & \dots & \dots & \dots \\ {}^{0}t_{ij}^{1\prime }+\left({}^{0}t_{ij}^k-{}^{0}t_{ij}^1\right)& \dots & {}^{n}t_{ij}^{1\prime }+\left({}^{n}t_{ij}^k-{}^{n}t_{ij}^1\right)& \dots & {}^{N}t_{ij}^{1\prime }+\left({}^{N}t_{ij}^k-{}^{N}t_{ij}^1\right)\\ \dots & \dots & \dots & \dots & \dots \\ {}^{0}t_{ij}^{1\prime }+\left({}^{0}t_{ij}^K-{}^{0}t_{ij}^1\right)& \dots & {}^{n}t_{ij}^{1\prime }+\left({}^{n}t_{ij}^K-{}^{n}t_{ij}^1\right)& \dots & {}^{N}t_{ij}^{1\prime }+\left({}^{N}t_{ij}^K-{}^{N}t_{ij}^1\right)\end{array}\right]$$

(11)

In summary, the ray-model position correction method solves station position by a triangulation relationship of three stations first and then corrects the travel time of multi-peaks at the new station position. Compared to the direct signal transmission correction method, this method has no sound ray loss and also does not need extensive ray simulation calculations.

The corrected two-way travel time is used to reconstruct a grid-averaged temperature profile as follows. The inversion method via grid slice was introduced in previous research [19,21], which is not the focus in this study.

3. Experiment

A series of water temperature and flow current observation experiments were conducted using high-frequency CAT systems in the Huangcai Reservoir, Changsha, China, from 28 February to 7 March 2022. This paper mainly introduces an experiment with four acoustic stations that were deployed along the same vertical section on 6 March to 7 March. The aim of this experiment was to reconstruct a high-precision current field in vertical profile via a multi-station uniform setting. However, during the experiment, the rope between transceiver and floating ball was too long, so the transceiver produced a station drift because of the influence of current and surface waves. The received signals at station pairs produced fluctuations. Thus, methods for travel time correction are developed and the experiment data are used to test the feasibility of these methods.

The experiment setting and sound transmission paths are shown in Figure 2. Each transceiver was moored at a depth range of 15~18 m by an anchored buoy and a weight; it was tied with a TD (temperature and pressure sensor) at 20 cm above the sound transceiver. The TD array was moored by floats and weights and was deployed along the observation section. Each acoustic station transmitted seventh-order M sequence phase-modulated signals with a carrier center frequency of 50 kHz at 1 min sound transmission intervals. The transmitted signal contained 381 digits and the digit length was 7.62 ms. The SNR of received signals in this experiment was improved by 42.076 dB.

Figure 2e shows the sound velocity profiles with negative gradients measured by CTD [20]. The two-way reciprocal signal transmissions were successfully performed between three station pairs (S1, S3, and S4), but S2 only sends acoustic signals and did not receive data because of a system problem. Therefore, in this paper, sound communications between S1, S3, and S4 are used to verify the travel time correction methods. During the two-day observation period, we obtained a total of 880 valid pieces of data. After the correction and inversion, the water temperature results are discussed and compared.

4. Results

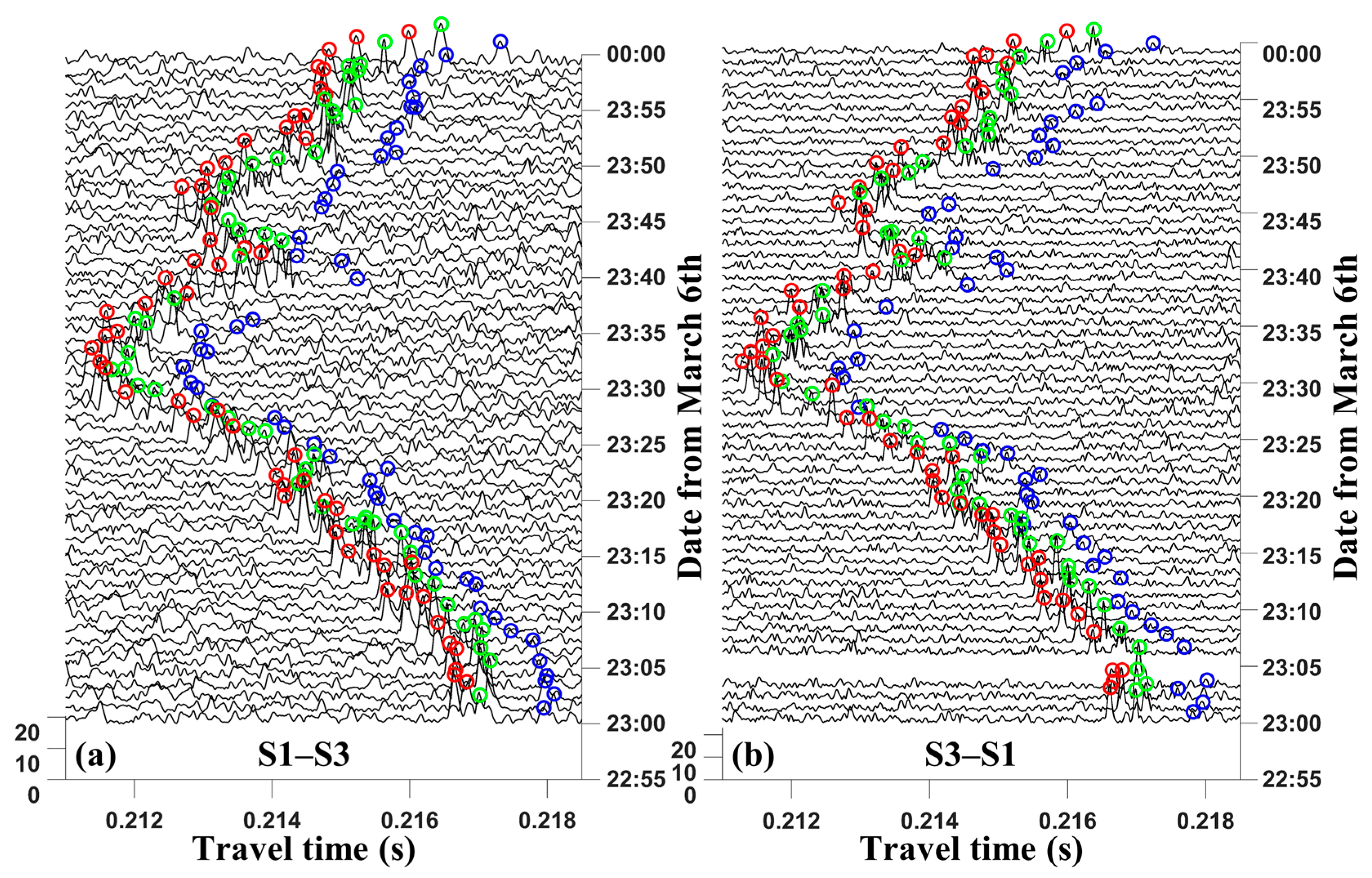
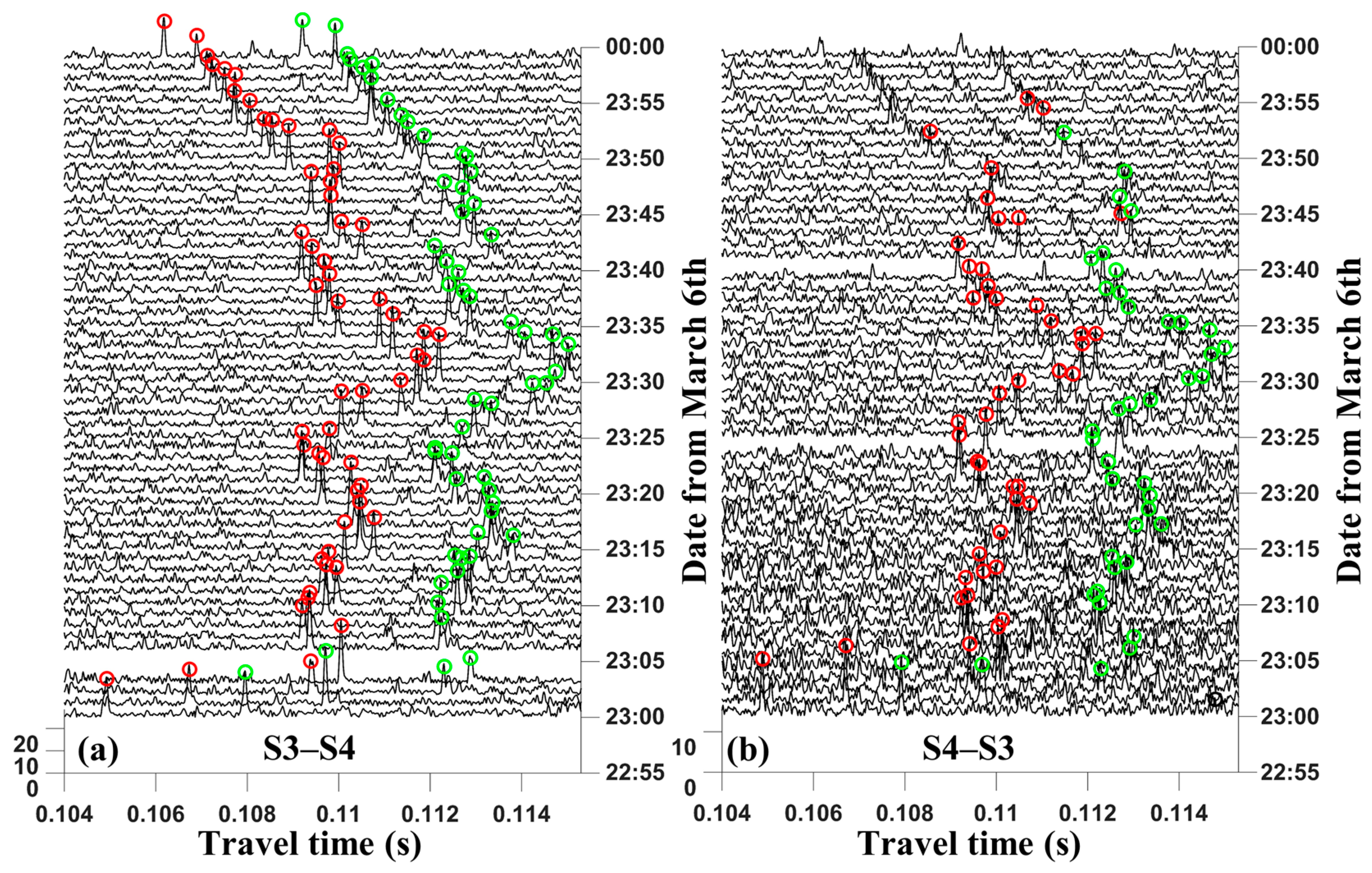
4.1. Multi-Peak Identification and Matching

The identification and matching of multi-peaks are determined by the high SNR of signals and the different arrival time delays [19,20,21]. Figure 3, Figure 4 and Figure 5 show two-way multi-peak identification of S1 to S3, S1 to S4, and S3 to S4, respectively. The data presented in these figures are the results from 23:00 to 24:00 on 6 March after signal correlation. Generally, the first peak denotes the direct ray and has the highest SNR and the smallest travel time; the second and third peaks represent the sound rays reflected or deflected, respectively.

From the multi-peak identification results, the significant time delay peak drifts exist because of the acoustic station drift. Meanwhile, it can be seen from the moving patterns of peaks that multi-peaks are synchronized, moving as a group; in other words, the sound ray structure is almost unchanged. The peak drifts between each station pair are almost the same. The effect of station drift is completely different when the same station is in different acoustic station pairs (such as S1 at S1 to S3 with S1 to S4). Each peak group produces a different signal drift at a different moment.

Both Figure 3 and Figure 4 show that three peaks are identified as S1–S3 and S1–S4, respectively. However, only two peaks are identified between S3 to S4 because of the relatively short distance, resulting in the incomplete reflection transmission of the acoustic signal.

The ray simulation is used for matching the signal travel time after correction. Figure 6 shows the multi-ray path structure and launch angle results via ray simulation. This result is obtained by tiling all three stations in a whole two-dimensional (2D) vertical profile. A station pair is directly divided into nine grids for comparison of the inversion data and validation of the results. The result is plotted in the same 2D vertical profile and gridded in three station pairs. Each station pair is divided into 3 × 3 grids for comparison and validation. In Figure 6, red lines represent direct rays (D), green lines represent surface reflected rays (SR), and blue lines represent bottom reflected rays (BR).

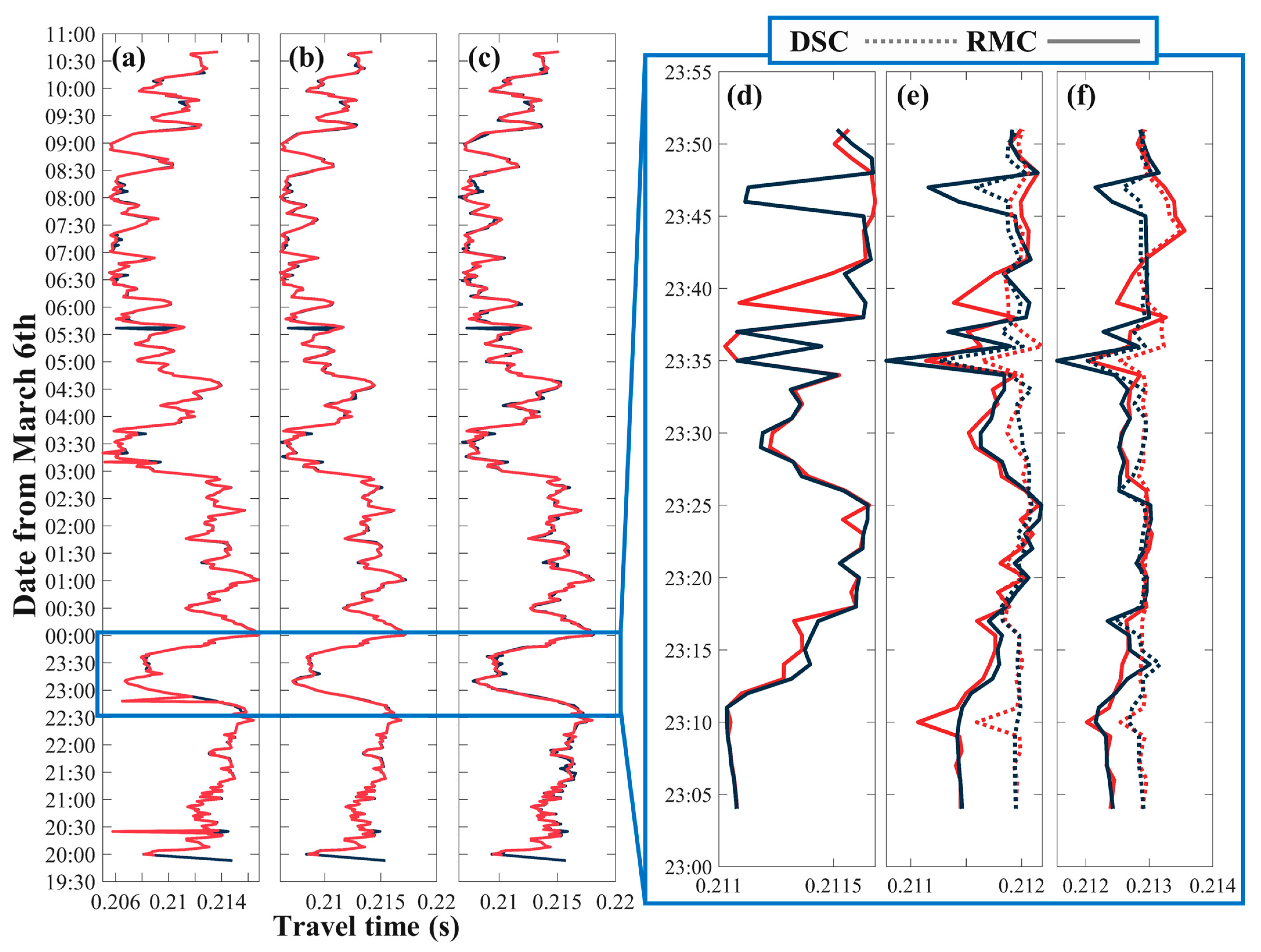
4.2. Travel Time Correction

The travel time of all reciprocal transmissions between three station pairs are corrected during the obsecration period. Figure 7 shows the identification of three initial arrival peaks between S1 and S3 on the left and the corrected travel time during 23:00 to 24:00 on the right. From the results of the three peaks in Figure 7a–c, the travel time fluctuations of different peaks are similar, which corresponds to the multi-peak drift together as a group in part 4.1. In addition, Figure 7d–f compare the travel times corrected by two methods. Both the direct signal transmission correction method and ray-model position correction method are able to correct the travel time of multi-peaks effectively. The correction results of the two methods are similar, but compared with the direct signal transmission correction (DSC) method, the ray-model position correction (RMC) method retained more variations in the travel time of the acoustic signal; in other words, RMC retained more environmental information.

Table 1. Standard deviation comparison of initial and correction travel times.

	Initial
Multi-peak	1st peak		2nd peak		3rd peak
Station pair	S1–S3	S3–S1	S1–S3	S3–S1	S1–S3	S3–S1
Standard deviation of initial (ms)	1.4985	1.4969	1.4841	1.4969	1.4639	1.525
	Correction
Station pair	S1–S3	S3–S1	S1–S3	S3–S1	S1–S3	S3–S1
Standard deviation of RMC (ms)	0.2332	0.2316	0.1028	0.1359	0.1677	0.1777
Standard deviation of DSC (ms)	/	/	0.1019	0.166	0.1347	0.1764

shows the standard deviation comparison of multi-peak travel time before and after the correction. The comparison of standard deviation also verifies the feasibility of the two methods. Both methods have advantages and disadvantages: DSC is faster and simpler, and RMC is more complex and keeps more information of signal variations.

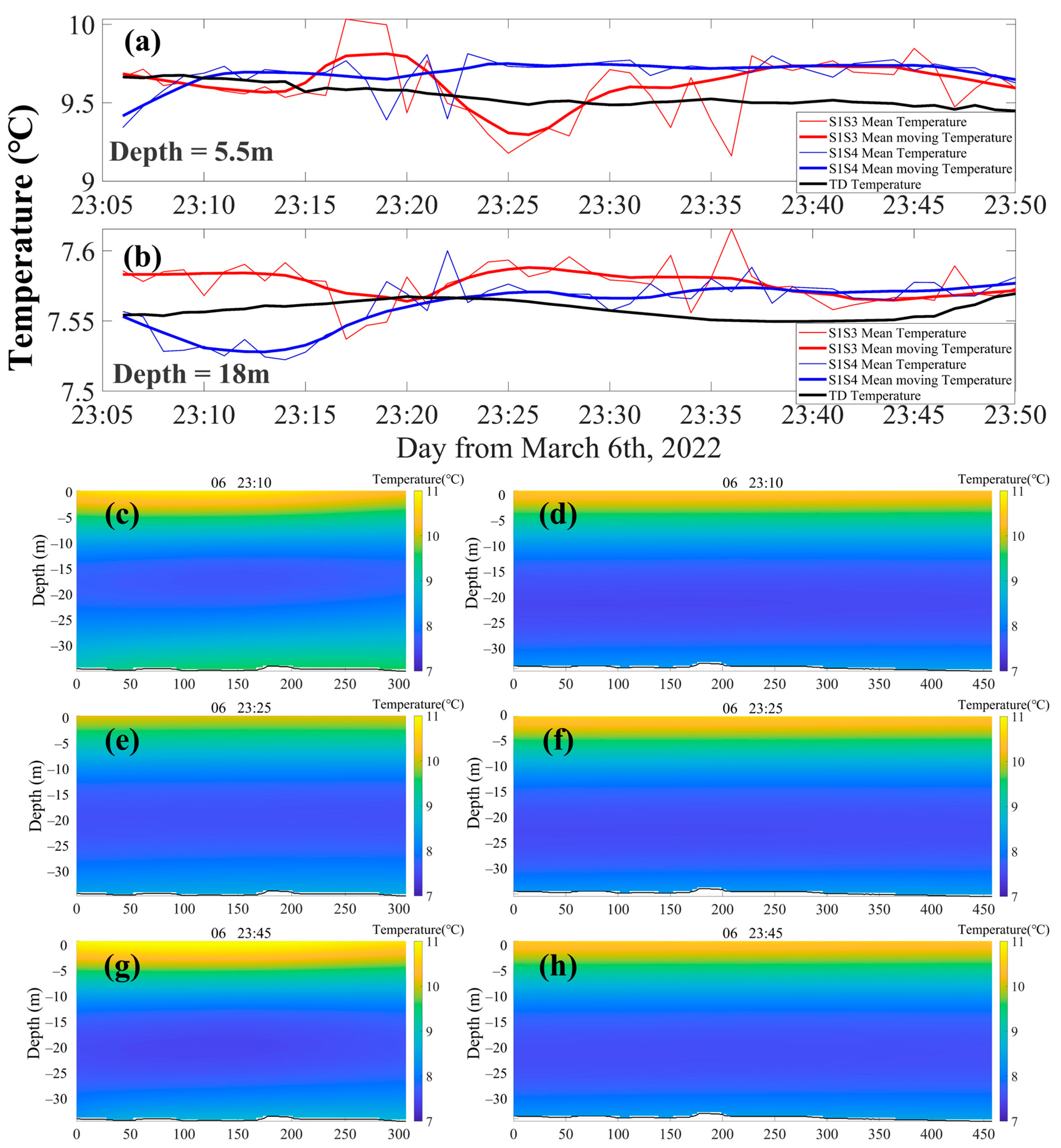
4.3. Inversion Result

Since sound rays are less matched via the DSC method, the inversion results are reconstructed by the corrected travel time via the RMC method. The layer-averaged temperature inversion result comparisons of S1 to S3 using initial travel time and corrected travel time are shown in Figure 8. Three layers are divided: 0 m–10 m, 10 m–20 m, and 20 m–bottom. From Figure 8, it is clear that the significant errors exist in the inversion results of the initial travel time. The correction inversion water temperature result demonstrates the precision of the correction method after station position drift.

Figure 9a,b show the inversion water temperature variations of S1–S3 and S1–S4 at the same depth, comparing with TD arrays at depths of 5.5 m and 18 m from 23:00 to 24:00. Due to the TD array not passing the vertical profile of S3–S4, the temperature inversion results of S3–S4 are not shown in Figure 9. The thick lines indicate the inversion results using 5 min weighted moving average. The lines of temperature inversion results fluctuate around TD data. The root mean square error (RSME) of temperature difference between corrected inversion results and TD data of S1–S3 are 0.131 °C and 0.0096 °C at depths of 5.5 m and 18 m. In addition, the RSME of temperatures of S1–S4 are 0.122 °C and 0.0175 °C. The RMSE at a depth of 5 m is larger than that at 18 m; it shows that a large temperature fluctuation exists at the surface. Error still exists after travel time correction, which needs future study. The 2D temperature profile at 23:10, 23:25, and 23:30 of S1–S3 and S1–S4 are shown in Figure 9c–h. At three times (Figure 9c–h), the inversion results are different from TD data. Figure 9c–h show a clear temperature layer stratification, and the 2D temperature color maps of S1–S3 and S1–S4 are similar. The inversion result in this paper still has a small error, but these two methods can largely reduce the travel time error caused by station drift.

5. Discussion and Conclusions

Travel time drifts caused by station drift are analyzed and developed in this study. From the comparison in Figure 7, the drifted travel time is corrected via two methods. Compared with the DSC method, the RMC method needs more complete transmission information and peak groups. The RMC method is suitable in deep sea sound transmission, where multi-path sound transmission is more possible. However, the RMC method needs to determine the station location first and, then, perform ray simulations according to corrected station distance at each moment to identify and match multiple arrival peaks. It is a time-consuming and complicated process but retains the information of direct ray transmission. As for the DSC method, although it is faster, the missing travel time of a direct ray makes the sound ray structure incomplete and produces more inversion errors than the RMC method. The DSC method can be used in a deeper area compared with the other method, where multi-path-propagated sound rays can be much easier identified.

Discussing the comparisons between the inversion temperature and TD data (Figure 9), the layer-averaged temperature inversion results fluctuate around the TD temperature. In addition, the temperature variations in Figure 8 are more significant in the surface and bottom layers, but slower in the middle layer. This is due to the sound rays having less information in the surface and bottom layers. On the other hand, errors may still exist after travel time correction. These errors come from the over-smoothing during the inversion process and occur by the travel time correction calculation.

The corrected travel time improves the data quality. On the one hand, the standard deviation comparison of initial and correction travel time in Table 1 shows the travel time correction and improvement. On the other hand, the RSME between TD and inversion results prove the feasibility of corrected travel time.

The experiment in this paper is a small-scale observational experiment; the RSMEs for the inversion temperature are small. If the correction methods are used in large-scale ocean experiments or array observations, the signal fluctuations can be greatly mitigated. In particular, acoustic station networking transmission has become a common tool used for marine science investigations, while the station location drift by the marine environment is commonly existing. Thus, the acoustic experiments require not only a pre-planning of the station setting but also recovery and correction for the drifted data. The direct signal transmission correction method and ray-model position correction method proposed in this paper are both useful in improving data quality.

In addition, the influence of environmental variation is often related to climate change [22,23], and how to derive climate change mode by observation of water environment results can be further studied.

6. Conclusions

Two underwater sound travel time correction methods for acoustic tomography research are proposed in this study. A water temperature profile observation experiment was carried out in a reservoir via high-frequency CAT systems. Multi-path propagating sound waves are corrected and compared with ray simulation results based on the DSC and RMC methods. The reliability of these two methods are proved by comparing 2D vertical water temperature inversion results with TD array observation data.

The main conclusions of this research are as follows:

• Two methods for travel time error caused by station position drift are developed and verified. The standard deviation of corrected data is around 0.15 ms, and uncorrected data is about 1.5 ms. Thus, the quality of 2D vertical water temperature variations is improved 90% via new methods.
• A two-dimensional vertical water temperature profile among three stations is successfully established by the corrected travel time data, and the errors of the inversion results are within the experience requirements.
• The correction methods have improved the initial data and can be attempted for further water environment observation in acoustic tomography observation studies.