Road-Side Individual Tree Segmentation from Urban MLS Point Clouds Using Metric Learning
Abstract
:1. Introduction
- A novel individual tree segmentation framework that combines semantic and instance segmentation network is designed to separate instance-level road-side trees from point clouds.
- Extensive experiments on two mobile laser scanning (MLS) and one airborne laser scanning (ALS) point clouds have been carried out to demonstrate the effectiveness and generalization of the proposed tree segmentation method for urban scenes.
2. Related Work
2.1. Point Cloud Semantic Segmentation
2.2. Point Cloud Instance Segmentation
2.3. Individual Tree Segmentation
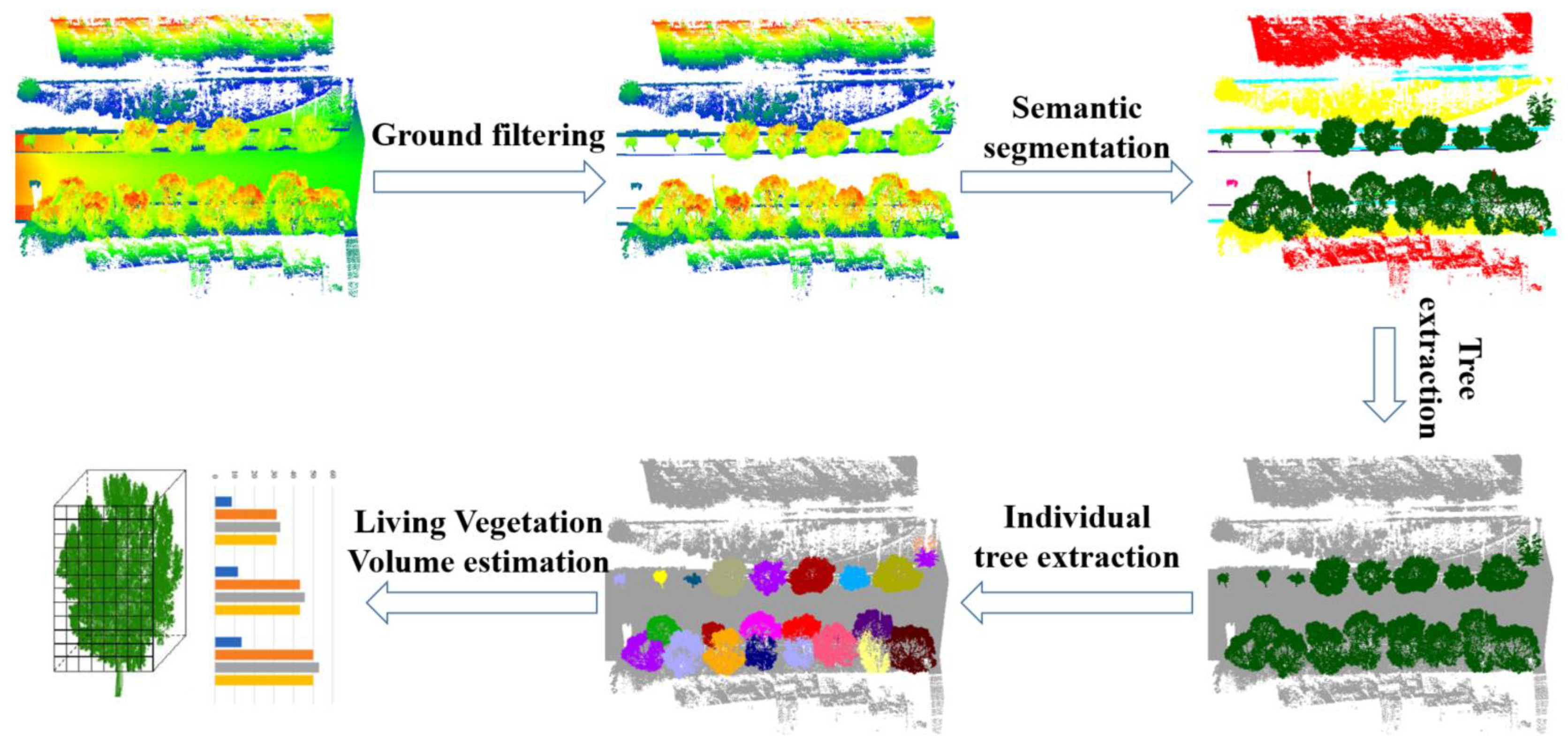
3. Methodology
3.1. Tree Point Extraction
3.2. Individual Tree Segmentation
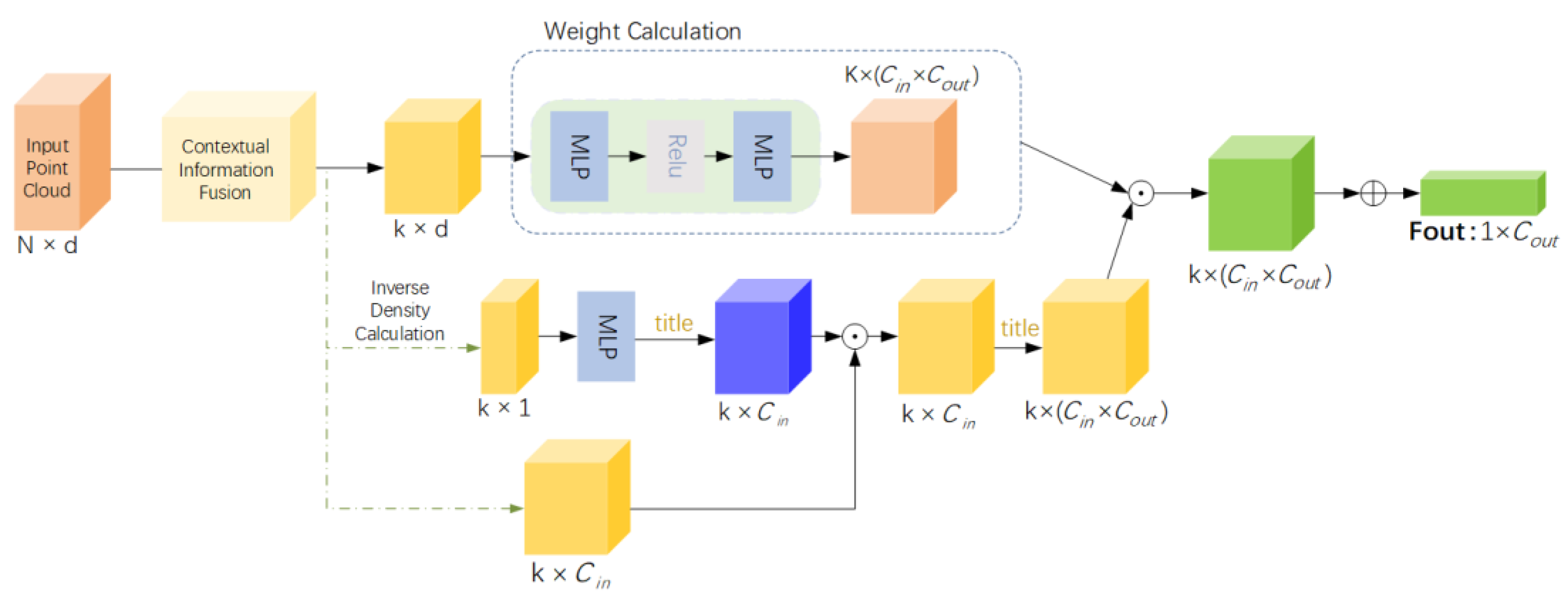
3.2.1. Density-Based Point Convolution (DPC)
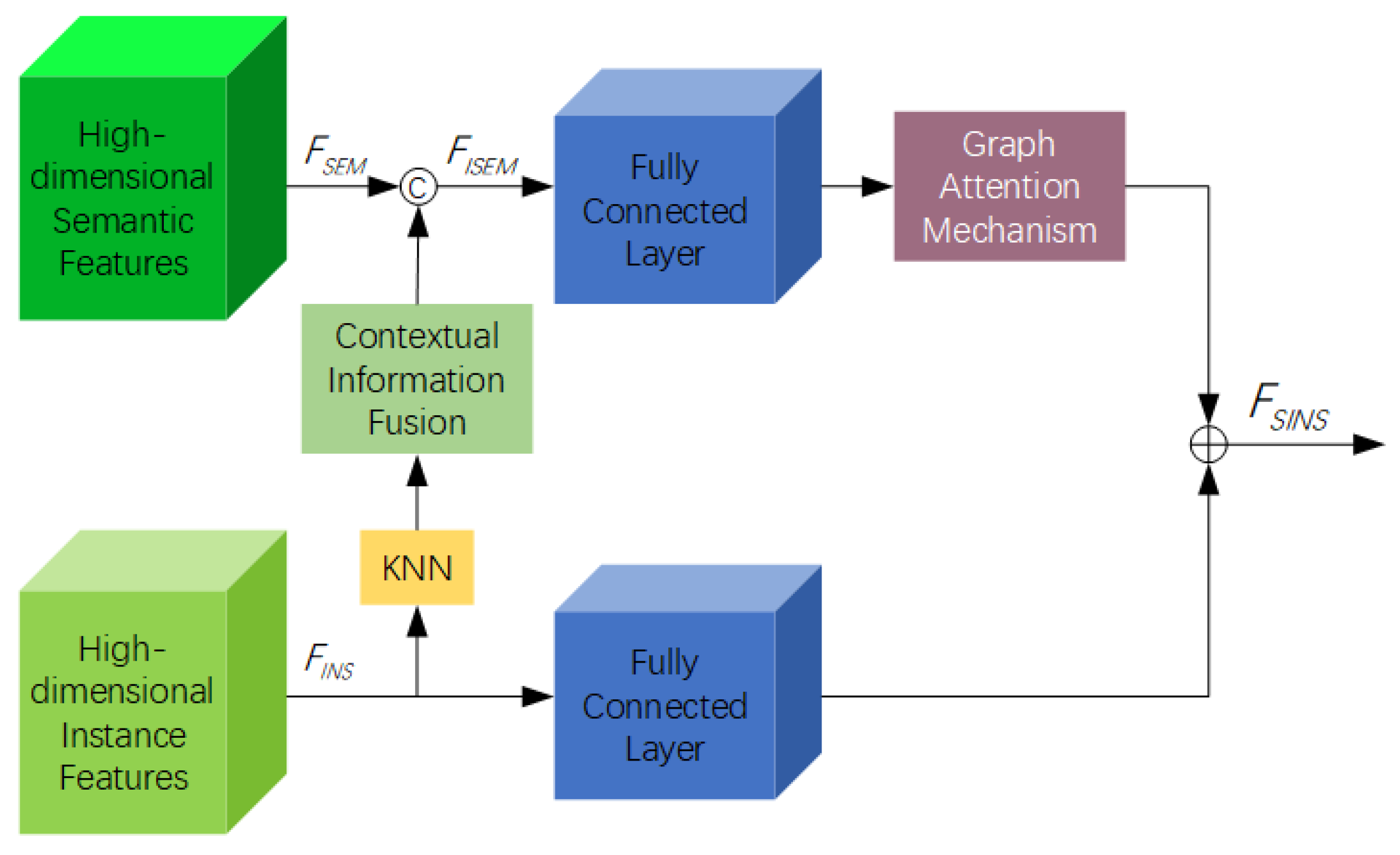
3.2.2. Associatively Segmenting Instances and Semantics in Tree Point Clouds
3.2.3. Loss Function Based on Metric Learning
3.3. Estimation of Living Vegetation Volume
4. Experimental Results
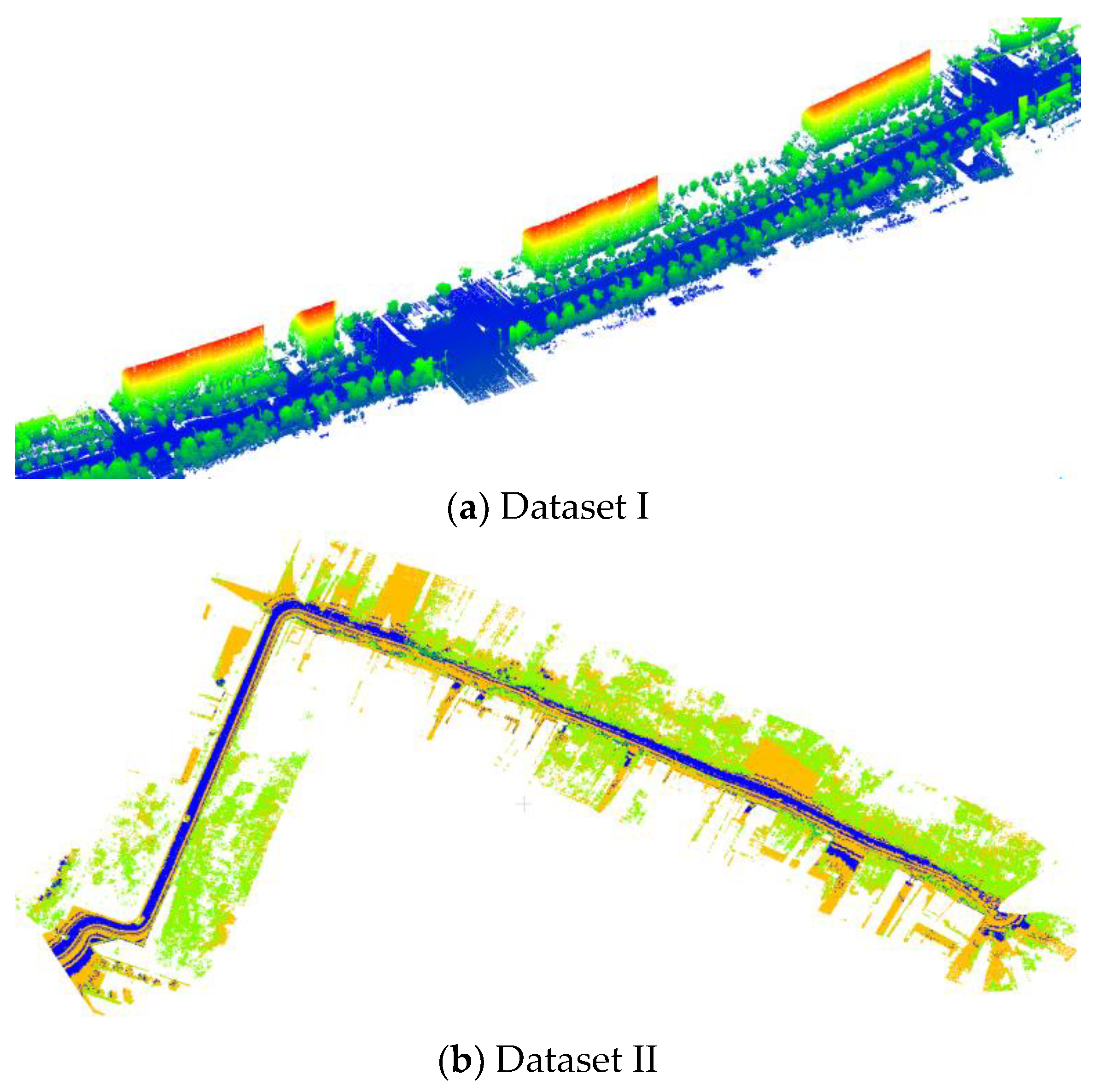
4.1. Dataset Description
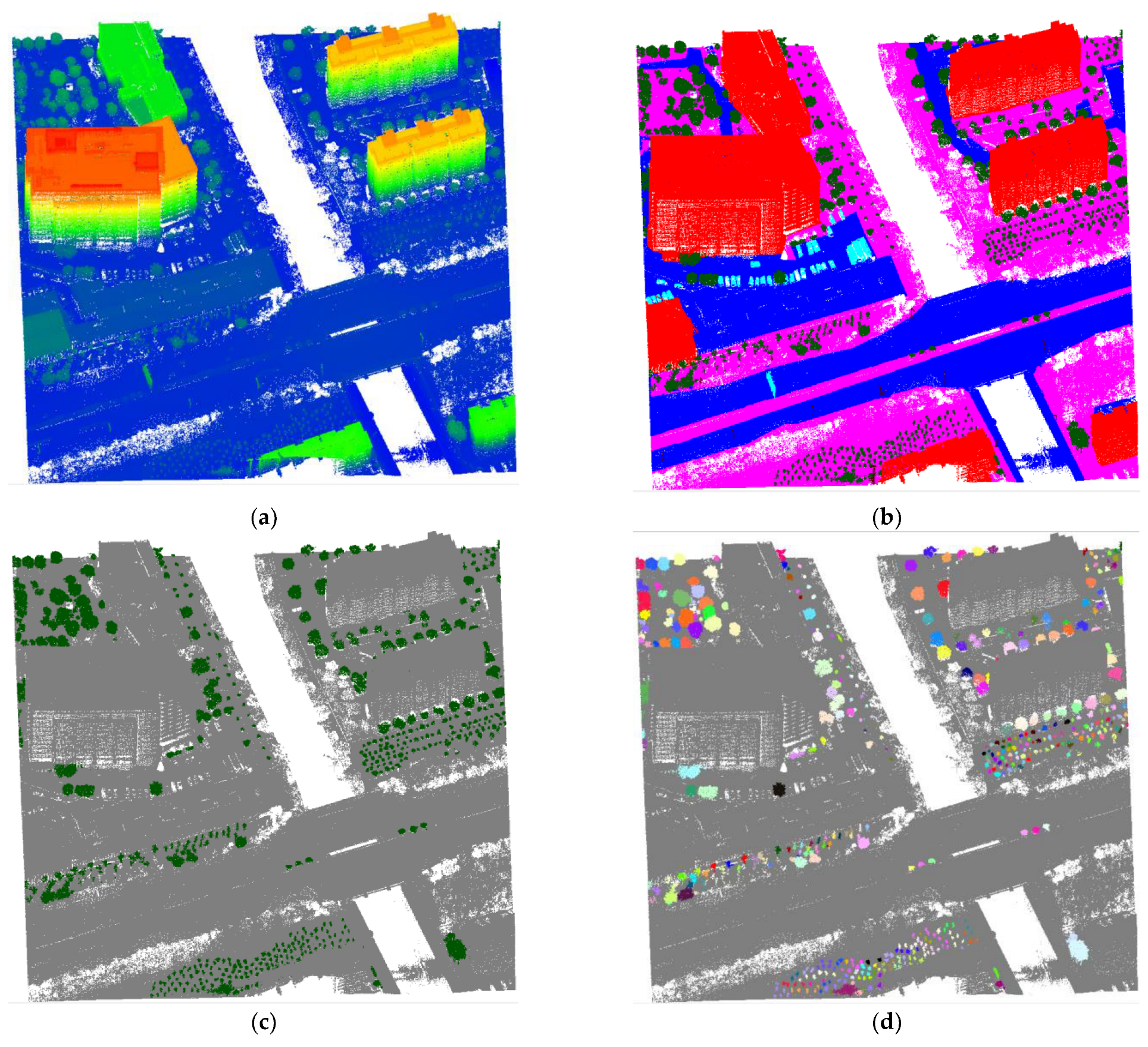
4.2. Semantic Segmentation Performances
4.2.1. Semantic Segmentation Results
4.2.2. Comparison with Other Published Methods
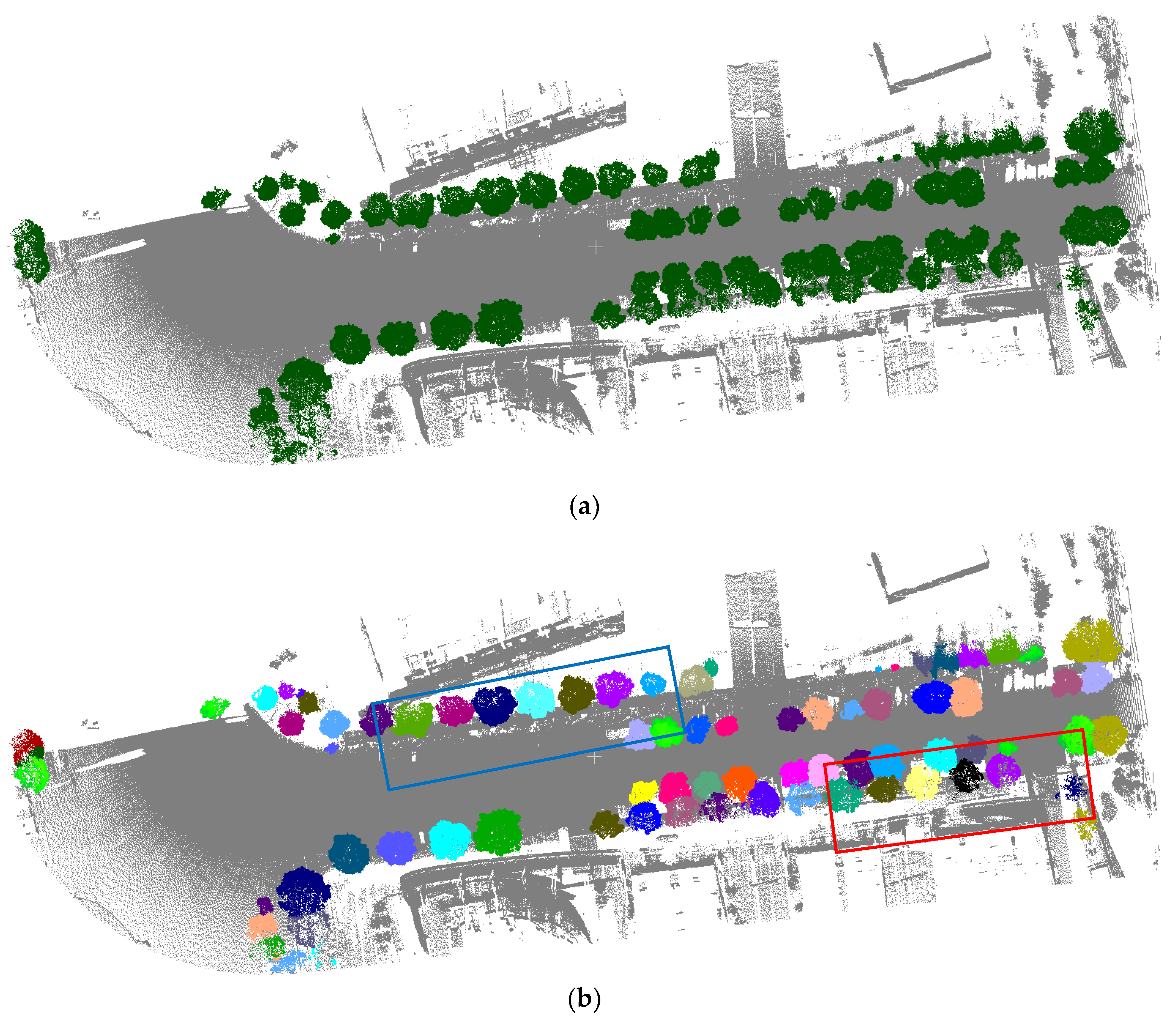
4.3. Individual Tree Segmentation Perfromances
4.3.1. Tree Segmentation Results
4.3.2. Comparative Studies
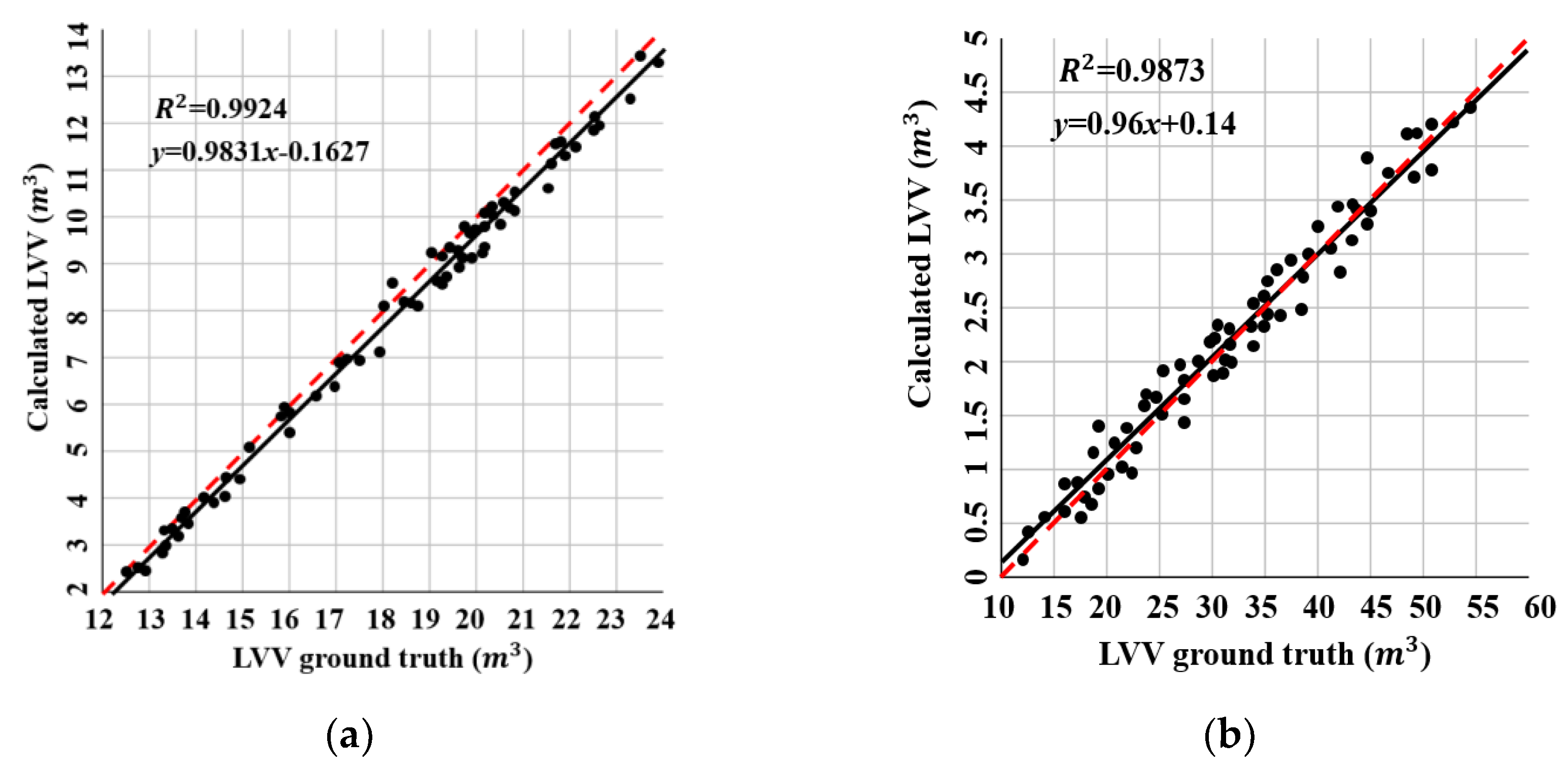
4.4. LVV Calculatation Results
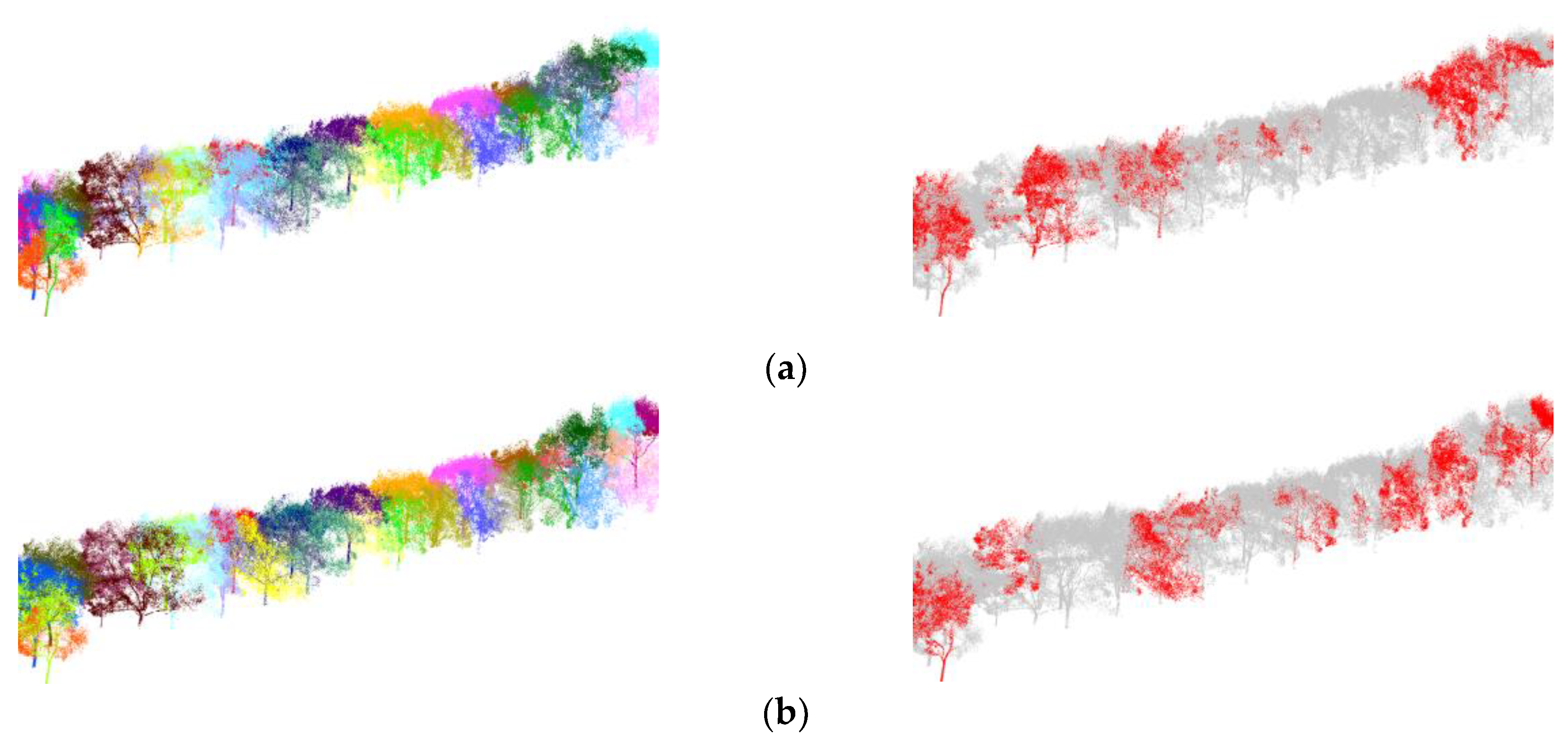
4.5. Generalization Capability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huo, L.; Lindberg, E.; Holmgren, J. Towards low vegetation identification: A new method for tree crown segmentation from LiDAR data based on a symmetrical structure detection algorithm (SSD). Remote Sens. Environ. 2022, 270, 112857. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, F.; Li, S.; Mao, J.; Xu, H.; Ju, W.; Liu, X.; Wu, J.; Min, K.; Zhang, X.; et al. Solar energy potential of urban buildings in 10 cities of China. Energy 2020, 196, 117038. [Google Scholar] [CrossRef]
- Lan, H.; Gou, Z.; Xie, X. A simplified evaluation method of rooftop solar energy potential based on image semantic segmentation of urban streetscapes. Sol. Energy 2021, 230, 912–924. [Google Scholar] [CrossRef]
- Gong, F.; Zeng, Z.; Ng, E.; Norford, L.K. Spatiotemporal patterns of street-level solar radiation estimated using Google Street View in a high-density urban environment. Build. Environ. 2019, 148, 547–566. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z.; Liu, Y.; Liang, F.; Wang, Y. Computing multiple aggregation levels and contextual features for road facilities recognition using mobile laser scanning data. ISPRS J. Photogramm. Remote Sens. 2017, 126, 180–194. [Google Scholar] [CrossRef]
- Yun, T.; Jiang, K.; Li, G.; Eichhorn, M.P.; Fan, J.; Liu, F.; Chen, B.; An, F.; Cao, L. Individual tree crown segmentation from airborne LiDAR data using a novel Gaussian filter and energy function minimization-based approach. Remote Sens. Environ. 2021, 256, 112307. [Google Scholar] [CrossRef]
- Jiang, T.; Liu, S.; Zhang, Q.; Zhao, L.; Sun, J.; Wang, Y. ShrimpSeg: A local-global structure for mantis shrimp point cloud segmentation network with contextual reasoning. Appl. Opt. 2023, 62, 97–103. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, Y.; Liu, S.; Cong, Y.; Dai, L.; Sun, J. Local and global structure for urban ALS point cloud semantic segmentation with ground-aware attention. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5702615. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Li, S.; Cheng, L.; Li, M. Hierarchical Classification of Urban ALS Data by Using Geometry and Intensity Information. Sensors 2019, 19, 4583. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Jiang, T.; Yu, M.; Tao, S.; Sun, J.; Liu, S. Semantic-Based Building Extraction from LiDAR Point Clouds Using Contexts and Optimization in Complex Environment. Sensors 2020, 20, 3386. [Google Scholar] [CrossRef]
- Lei, X.; Guan, H.; Ma, L.; Yu, Y.; Dong, Z.; Gao, K.; Delavar, M.R.; Li, J. WSPointNet: A multi-branch weakly supervised learning network for semantic segmentation of large-scale mobile laser scanning point clouds. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103129. [Google Scholar] [CrossRef]
- Hu, T.; Wei, D.; Su, Y.; Wang, X.; Zhang, J.; Sun, X.; Liu, Y.; Guo, Q. Quantifying the shape of urban street trees and evaluating its influence on their aesthetic functions based on mobile lidar data. ISPRS J. Photogramm. Remote Sens. 2022, 184, 203–214. [Google Scholar] [CrossRef]
- Yang, B.; Dai, W.; Dong, Z.; Liu, Y. Automatic Forest Mapping at Individual Tree Levels from Terrestrial Laser Scanning Point Clouds with a Hierarchical Minimum Cut Method. Remote Sens. 2016, 8, 372. [Google Scholar] [CrossRef] [Green Version]
- Klouček, T.; Klápště, P.; Marešová, J.; Komárek, J. UAV-Borne Imagery Can Supplement Airborne Lidar in the Precise Description of Dynamically Changing Shrubland Woody Vegetation. Remote Sens. 2022, 14, 2287. [Google Scholar] [CrossRef]
- Liu, J.; Skidmore, A.K.; Wang, T.; Zhu, X.; Premier, J.; Heurich, M.; Beudert, B.; Jones, S. Variation of leaf angle distribution quantified by terrestrial LiDAR in natural European beech forest. ISPRS J. Photogramm. Remote Sens. 2019, 148, 208–220. [Google Scholar] [CrossRef]
- Moudrý, V.; Gdulová, K.; Fogl, M.; Klápště, P.; Urban, R.; Komárek, J.; Moudrá, L.; Štroner, M.; Barták, V.; Solský, M. Comparison of leaf-off and leaf-on combined UAV imagery and airborne LiDAR for assessment of a post-mining site terrain and vegetation structure: Prospects for monitoring hazards and restoration success. Appl. Geogr. 2019, 104, 32–41. [Google Scholar] [CrossRef]
- Wang, D.; Takoudjou, S.M.; Casella, E. LeWoS: A universal leaf-wood classification method to facilitate the 3D modelling of large tropical trees using terrestrial LiDAR. Methods Ecol. Evol. 2020, 11, 376–389. [Google Scholar] [CrossRef]
- Zou, Y.; Weinacker, H.; Koch, B. Towards Urban Scene Semantic Segmentation with Deep Learning from LiDAR Point Clouds: A Case Study in Baden-Württemberg, Germany. Remote Sens. 2021, 13, 3220. [Google Scholar] [CrossRef]
- Jiang, T.; Sun, J.; Liu, S.; Zhang, X.; Wu, Q.; Wang, Y. Hierarchical semantic segmentation of urban scene point clouds via group proposal and graph attention network. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102626. [Google Scholar] [CrossRef]
- Luo, H.; Chen, C.; Fang, L.; Khoshelham, K.; Shen, G. MS-RRFSegNet: Multiscale regional relation feature segmentation network for semantic segmentation of urban scene point clouds. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8301–8315. [Google Scholar] [CrossRef]
- Huang, R.; Xu, Y.; Stilla, U. GraNet: Global relation-aware attentional network for semantic segmentation of ALS point clouds. ISPRS J. Photogramm. Remote Sens. 2021, 177, 1–20. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, Z.; Chen, S.; Wen, S.; Ma, H.; Xu, Z. A self-attention based global feature enhancing network for semantic segmentation of large-scale urban street-level point clouds. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 102974. [Google Scholar] [CrossRef]
- Kang, Z.; Yang, J. A probabilistic graphical model for the classification of mobile LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 143, 108–123. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Y.; Gu, X.; Chen, D.; Gao, F.; Shuang, F. Point Cloud Classification Algorithm Based on the Fusion of the Local Binary Pattern Features and Structural Features of Voxels. Remote Sens. 2021, 13, 3156. [Google Scholar] [CrossRef]
- Tong, G.; Li, Y.; Chen, D.; Xia, S.; Peethambaran, J.; Wang, Y. Multi-View Features Joint Learning with Label and Local Distribution Consistency for Point Cloud Classification. Remote Sens. 2020, 12, 135. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Sun, L.; Zhong, R.; Chen, D.; Zhang, L.; Li, X.; Wang, Q.; Chen, S. Hierarchical Aggregated Deep Features for ALS Point Cloud Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1686–1699. [Google Scholar] [CrossRef]
- Lin, Y.; Vosselman, G.; Cao, Y.; Yang, M.Y. Local and global encoder network for semantic segmentation of Airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2021, 176, 151–168. [Google Scholar] [CrossRef]
- Yang, B.; Jiang, T.; Wu, W.; Zhou, Y.; Dai, L. Automated Semantics and Topology Representation of Residential-Building Space Using Floor-Plan Raster Maps. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 7809–7825. [Google Scholar] [CrossRef]
- Yuan, Z.; Cheng, M.; Zeng, W.; Su, Y.; Liu, W.; Yu, S.; Wang, C. Prototype-Guided Multitask Adversarial Network for Cross-Domain LiDAR Point Clouds Semantic Segmentation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5700613. [Google Scholar] [CrossRef]
- Feng, H.; Chen, Y.; Luo, Z.; Sun, W.; Li, W.; Li, J. Automated extraction of building instances from dual-channel airborne LiDAR point clouds. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103042. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3D point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Jiang, W.; Xu, B.; Zhu, Q.; Jiang, S.; Huang, W. A convolutional neural network-based 3D semantic labeling method for ALS point clouds. Remote Sens. 2017, 9, 936. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Tan, B.; Pei, H.; Jiang, W. Segmentation and multiscale convolutional neural network-based classification of airborne laser scanner data. Sensors 2018, 18, 3347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lei, X.; Wang, H.; Wang, C.; Zhao, Z.; Miao, J.; Tian, P. ALS point cloud classification by integrating an improved fully convolutional network into transfer learning with multi-scale and multi-view deep features. Sensors 2020, 20, 6969. [Google Scholar] [CrossRef] [PubMed]
- Choy, C.; Gwak, J.; Savarese, S. 4D spatio-temporal convnets: Minkowski convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 3075–3084. [Google Scholar]
- Zhang, J.; Hu, X.; Dai, H. A graph-voxel joint convolution neural network for ALS point cloud segmentation. IEEE Access 2020, 8, 139781–139791. [Google Scholar] [CrossRef]
- Qin, N.; Hu, X.; Wang, P.; Shan, J.; Li, Y. Semantic labeling of ALS point cloud via learning voxel and pixel representations. IEEE Geosci. Remote Sens. Lett. 2020, 17, 859–863. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.-E.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv: Flexible and deformable convolution for point clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October 2019–2 November 2019; pp. 6411–6420. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-scale point cloud semantic segmentation with superpoint graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Chen, S.; Miao, Z.; Chen, H.; Mukherjee, M.; Zhang, Y. Point-attention Net: A graph attention convolution network for point cloud segmentation. Appl. Intell. 2022. [Google Scholar] [CrossRef]
- Zou, J.; Zhang, Z.; Chen, D.; Li, Q.; Sun, L.; Zhong, R.; Zhang, L.; Sha, J. GACM: A Graph Attention Capsule Model for the Registration of TLS Point Clouds in the Urban Scene. Remote Sens. 2021, 13, 4497. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11105–11114. [Google Scholar]
- Hou, J.; Dai, A.; Nießner, M. 3D-SIS: 3D semantic instance segmentation of RGB-D scans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4416–4427. [Google Scholar]
- Yi, L.; Zhao, W.; Wang, H.; Sung, M.; Guibas, L.J. GSPN: Generative shape proposal network for 3D instance segmentation in point cloud. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3942–3951. [Google Scholar]
- Yang, B.; Wang, J.; Clark, R.; Hu, Q.; Wang, S.; Markham, A.; Trigoni, N. Learning object bounding boxes for 3D instance segmentation on point clouds. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 6737–6746. [Google Scholar]
- Engelmann, F.; Bokeloh, M.; Fathi, A.; Leibe, B.; Nießner, M. 3D-MPA: Multi-proposal aggregation for 3D semantic instance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9028–9037. [Google Scholar]
- Jiang, L.; Zhao, H.; Shi, S.; Liu, S.; Fu, C.W.; Jia, J. Pointgroup: Dual-set point grouping for 3d instance segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4867–4876. [Google Scholar]
- Wang, X.; Liu, S.; Shen, X.; Shen, C.; Jia, J. Associatively segmenting instances and semantics in point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4091–4100. [Google Scholar]
- Han, L.; Zheng, T.; Xu, L.; Fang, L. Occuseg: Occupancy-aware 3D instance segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2937–2946. [Google Scholar]
- Wang, Y.; Zhang, Z.; Zhong, R.; Sun, L.; Leng, S.; Wang, Q. Densely connected graph convolutional network for joint semantic and instance segmentation of indoor point clouds. ISPRS J. Photogramm. Remote Sens. 2021, 182, 67–77. [Google Scholar] [CrossRef]
- Chen, S.; Fang, J.; Zhang, Q.; Liu, W.; Wang, X. Hierarchical Aggregation for 3D Instance Segmentation. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 15447–15456. [Google Scholar]
- Vu, T.; Kim, K.; Luu, T.M.; Nguyen, T.; Yoo, C.D. SoftGroup for 3D instance segmentation on point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 2698–3007. [Google Scholar]
- Chen, F.; Wu, F.; Gao, G.; Ji, Y.; Xu, J.; Jiang, G.; Jing, X. JSPNet: Learning joint semantic & instance segmentation of point clouds via feature self-similarity and cross-task probability. Pattern Recognit. 2022, 122, 108250. [Google Scholar]
- Chen, Y.; Wang, S.; Li, J.; Ma, L.; Wu, R.; Luo, Z.; Wang, C. Rapid urban roadside tree inventory using a mobile laser scanning system. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 3690–3700. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An individual tree segmentation method based on watershed algorithm and three-dimensional spatial distribution analysis from airborne LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Yan, W.; Guan, H.; Cao, L.; Yu, Y.; Li, C.; Lu, J. A self-adaptive mean shift tree-segmentation method using UAV LiDAR data. Remote Sens. 2020, 12, 515. [Google Scholar] [CrossRef] [Green Version]
- Dai, W.; Yang, B.; Dong, Z.; Shaker, A. A new method for 3D individual tree extraction using multispectral airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 144, 400–411. [Google Scholar] [CrossRef]
- Yang, W.; Liu, Y.; He, H.; Lin, H.; Qiu, G.; Guo, L. Airborne LiDAR and photogrammetric point cloud fusion for extraction of urban tree metrics according to street network segmentation. IEEE Access 2021, 9, 97834–97842. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Z.; Tang, Y.; Qu, Y. Individual tree crown detection from high spatial resolution imagery using a revised local maximum filtering. Remote Sens. Environ. 2021, 258, 112397. [Google Scholar] [CrossRef]
- Windrim, L.; Bryson, M. Forest tree detection and segmentation using high resolution airborne LiDAR. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 3898–3904. [Google Scholar]
- Mäyrä, J.; Keski-Saari, S.; Kivinen, S.; Tanhuanpää, T.; Hurskainen, P.; Kullberg, P.; Poikolainen, L.; Viinikka, A.; Tuominen, S.; Kumpula, T.; et al. Tree species classification from airborne hyperspectral and LiDAR data using 3D convolutional neural networks. Remote Sens. Environ. 2021, 256, 112322. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, T.; Liu, J.; Li, X.; Liang, C. Hierarchical instance recognition of individual roadside trees in environmentally complex urban areas from UAV laser scanning point clouds. ISPRS Int. J. GeoInf. 2020, 9, 595. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, R.; Yang, C.; Lin, Y. Urban vegetation segmentation using terrestrial LiDAR point clouds based on point non-local means network. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102580. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Z.; Li, W.; Chen, Y.; Wang, C.; Nurunnabi, A.A.M.; Li, J. Detection of individual trees in UAV LiDAR point clouds using a deep learning framework based on multichannel representation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5701715. [Google Scholar] [CrossRef]
- Luo, H.; Khoshelham, K.; Chen, C.; He, H. Individual tree extraction from urban mobile laser scanning point clouds using deep pointwise direction embedding. ISPRS J. Photogramm. Remote Sens. 2021, 175, 326–339. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Zhao, X.; Hu, T.; Guo, Q. A point-based fully convolutional neural network for airborne LiDAR ground point filtering in forested environments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3958–3974. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef] [Green Version]
- Simonovsky, M.; Komodakis, N. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3693–3702. [Google Scholar]
- Yue, B.; Fu, J.; Liang, J. Residual recurrent neural networks for learning sequential representations. Information 2018, 9, 56. [Google Scholar] [CrossRef] [Green Version]
- Shu, X.; Zhang, L.; Sun, Y.; Tang, J. Host–Parasite: Graph LSTM-in-LSTM for group activity recognition. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 663–674. [Google Scholar] [CrossRef] [PubMed]
- Dersch, S.; Heurich, M.; Krueger, N.; Krzystek, P. Combining graph-cut clustering with object-based stem detection for tree segmentation in highly dense airborne lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2021, 172, 207–222. [Google Scholar] [CrossRef]
- Wu, W.; Qi, Z.; Li, F. PointConv: Deep Convolutional Networks on 3D Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9613–9622. [Google Scholar]
- Tusa, E.; Monnet, J.M.; Barré, J.B.; Mura, M.D.; Dalponte, M.; Chanussot, J. Individual Tree Segmentation Based on Mean Shift and Crown Shape Model for Temperate Forest. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2052–2056. [Google Scholar] [CrossRef]
- Wang, Y.; Pyörälä, J.; Liang, X.; Lehtomäki, M.; Kukko, A.; Yu, X.; Kaartinen, H.; Hyyppä, J. In situ biomass estimation at tree and plot levels: What did data record and what did algorithms derive from terrestrial and aerial point clouds in boreal forest. Remote Sens. Environ. 2019, 232, 111309. [Google Scholar] [CrossRef]
- Tatarchenko, M.; Park, J.; Koltun, V.; Zhou, Q. Tangent convolutions for dense prediction in 3D. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3887–3896. [Google Scholar]
- Roynard, X.; Deschaud, J.E.; Goulette, F. Classification of Point Cloud for Road Scene Understanding with Multiscale Voxel Deep Network. In Proceedings of the 10th Workshop on Planning, Perception and Navigation for Intelligent Vehicules (PPNIV), Madrid, Spain, 1 October 2018; pp. 13–18. [Google Scholar]
- Li, D.; Shi, G.; Li, J.; Chen, Y.; Zhang, Y.; Xiang, S.; Jin, S. PlantNet: A dual-function point cloud segmentation network for multiple plant species. ISPRS J. Photogramm. Remote Sens. 2021, 184, 243–263. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Shendryk, I.; Broich, M.; Tulbure, M.G.; Alexandrov, S.V. Bottom-up delineation of individual trees from full-waveform airborne laser scans in a structurally complex eucalypt forest. Remote Sens. Environ. 2016, 179, 69–83. [Google Scholar]










| Ref. | OA | mIoU | Ground | Building | Tree | Light | Parterre | Pedestrain | Fence | Pole | Car | Others | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset I | [39] | 61.9 | 45.3 | 60.4 | 59.9 | 60.8 | 62.5 | 45.1 | 9.6 | 7.3 | 34.7 | 78.0 | 34.2 |
| [77] | 52.3 | 37.4 | 58.7 | 29.9 | 50.8 | 49.1 | 29.1 | 10.7 | 33.5 | 8.6 | 81.2 | 38.1 | |
| [78] | 52.9 | 40.1 | 60.2 | 67.1 | 53.4 | 50.8 | 13.8 | 15.4 | 2.9 | 60.8 | 78.3 | 4.8 | |
| [41] | 85.6 | 61.7 | 88.1 | 81.3 | 81.5 | 82.9 | 60.2 | 30.2 | 26.8 | 50.2 | 90.7 | 50.3 | |
| [40] | 80.2 | 59.2 | 80.1 | 82.1 | 65.1 | 79.4 | 65.2 | 70.3 | 3.9 | 23.4 | 91.2 | 12.7 | |
| [44] | 82.5 | 61.3 | 79.2 | 77.1 | 90.3 | 89.5 | 45.8 | 56.2 | 30.1 | 66.2 | 88.3 | 10.3 | |
| [20] | 75.2 | 49.6 | 72.3 | 80.4 | 70.2 | 79.1 | 23.0 | 33.6 | 78.4 | 8.5 | 96.1 | 30.5 | |
| Ours | 89.1 | 63.8 | 85.3 | 88.9 | 87.2 | 90.8 | 25.6 | 59.7 | 34.6 | 49.8 | 95.2 | 20.7 | |
| Dataset II | [39] | 59.8 | 39.6 | 55.8 | 65.1 | 52.7 | 37.9 | 46.4 | 15.3 | 10.8 | 31.7 | 51.0 | 29.7 |
| [77] | 51.0 | 37.7 | 45.7 | 30.2 | 39.7 | 52.7 | 11.5 | 8.7 | 40.1 | 9.6 | 35.7 | 26.9 | |
| [78] | 52.3 | 39.8 | 56.7 | 70.5 | 46.7 | 54.7 | 12.8 | 20.7 | 10.9 | 45.8 | 67.1 | 12.5 | |
| [41] | 84.9 | 62.6 | 85.4 | 73.2 | 85.7 | 78.4 | 55.7 | 36.9 | 22.4 | 58.7 | 70.1 | 60.4 | |
| [40] | 79.8 | 50.9 | 76.9 | 83.7 | 70.2 | 79.9 | 52.1 | 44.1 | 10.2 | 15.7 | 66.7 | 9.9 | |
| [44] | 80.7 | 54.6 | 70.8 | 70.2 | 86.7 | 82.7 | 23.7 | 57.1 | 40.8 | 51.7 | 50.4 | 12.4 | |
| [20] | 72.9 | 45.0 | 53.4 | 77.1 | 70.4 | 70.4 | 40.2 | 12.1 | 10.4 | 1.0 | 75.7 | 40.1 | |
| Ours | 88.8 | 64.3 | 63.8 | 70.8 | 88.6 | 83.7 | 53.4 | 30.7 | 68.4 | 60.1 | 45.2 | 73.0 |
| Ref. | Prec (%) | Rec (%) | mCov (%) | mWCov (%) | |
|---|---|---|---|---|---|
| Dataset I | [80] | 80.22 | 80.10 | 79.06 | 81.23 |
| [81] | 82.14 | 81.67 | 82.01 | 83.54 | |
| [64] | 84.56 | 85.22 | 83.96 | 85.24 | |
| [67] | 86.11 | 85.89 | 84.66 | 86.74 | |
| Ours | 90.27 | 89.75 | 86.39 | 88.98 | |
| Dataset II | [80] | 82.54 | 82.69 | 80.12 | 81.95 |
| [81] | 83.96 | 83.42 | 82.45 | 84.02 | |
| [64] | 85.47 | 84.55 | 84.23 | 86.33 | |
| [67] | 88.53 | 87.86 | 85.74 | 86.78 | |
| Ours | 90.86 | 89.27 | 87.20 | 88.56 |
| This Scheme (m3) | Traditional Method (m3) | Platform Method (m3) | (%) | (%) | ||
|---|---|---|---|---|---|---|
| Dataset I | Road 1 | 9.23 | 10.80 | 9.79 | 17.0 | 6.1 |
| Road 2 | 22.70 | 25.56 | 23.32 | 12.6 | 2.7 | |
| Road 3 | 25.34 | 33.88 | 28.89 | 33.7 | 14.0 | |
| Average | 19.9 | 7.8 | ||||
| Dataset II | Road 4 | 13.41 | 16.77 | 15.37 | 25.0 | 14.6 |
| Road 5 | 32.11 | 36.48 | 34.29 | 13.6 | 6.8 | |
| Road 6 | 39.76 | 46.40 | 42.29 | 16.7 | 6.4 | |
| Average | 16.5 | 8.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Tang, Y.; Liao, Z.; Yan, Y.; Dai, L.; Liu, S.; Jiang, T. Road-Side Individual Tree Segmentation from Urban MLS Point Clouds Using Metric Learning. Remote Sens. 2023, 15, 1992. https://doi.org/10.3390/rs15081992
Wang P, Tang Y, Liao Z, Yan Y, Dai L, Liu S, Jiang T. Road-Side Individual Tree Segmentation from Urban MLS Point Clouds Using Metric Learning. Remote Sensing. 2023; 15(8):1992. https://doi.org/10.3390/rs15081992
Chicago/Turabian StyleWang, Pengcheng, Yong Tang, Zefan Liao, Yao Yan, Lei Dai, Shan Liu, and Tengping Jiang. 2023. "Road-Side Individual Tree Segmentation from Urban MLS Point Clouds Using Metric Learning" Remote Sensing 15, no. 8: 1992. https://doi.org/10.3390/rs15081992
APA StyleWang, P., Tang, Y., Liao, Z., Yan, Y., Dai, L., Liu, S., & Jiang, T. (2023). Road-Side Individual Tree Segmentation from Urban MLS Point Clouds Using Metric Learning. Remote Sensing, 15(8), 1992. https://doi.org/10.3390/rs15081992








