Abstract
The article proposes a methodology for analyzing the performance of S-lidars (S comes from Scheimpflug) as a new class of environmental remote sensors operating under conditions of wide variability of optical weather and sky background brightness. The novelty of the problem statement, the methods used and the results obtained are determined by their application to laser sensing systems with unconventional design principles and the consequent need to revise the traditional ways of assessing their potential capabilities. The research method is based on a dimensionless-parametric approach, which allows comparing phenomena and systems of different scales and combining complementary characteristics and parameters. Effects of the dimensionless optical weather factor on lidar potential are shown being investigated under various environmental conditions, from the clear atmosphere through haze and mist to fog when probing in Vis/SWIR spectral bands and using Si/InGaAs detector arrays. It is shown exactly how and to what extent the significant differences in their spectral sensitivity and internal noise parameters are susceptible to the wide spectral and energy variability of the sky background brightness observed at very different angles to the Sun. A detailed analysis of the two most important influencing factors within the system, “S-Lidar instrument + Optical weather + External background source”, taking into account their wide variability, allowed us to describe their joint nonlinear influence and, thus, to anticipate the imposed limitations. The proposed dimensionless-parametric concept for predicting the potential capabilities of S-lidars with Si/InGaAs arrays is aimed at expanding applications of this rapidly developing class of remote sensors in a wide variety of environments.
1. Introduction
When developing and using sensors for laser remote sensing of the environment, it is customary to rely on generalized approaches and to look for solutions that would be able to focus on the strengths of a certain class of sensors aiming to exploit specific features, characteristic differences and advantages on this basis [1,2,3,4,5,6]. On the other hand, it is important to anticipate possible ambient situations and related conditions to ensure reliable operation in a real environment with a wide variability of its properties and influencing parameters.
In this regard, speaking about traditional methods and instrumentation on range-resolved laser remote sensing, first of all, we shall name pulsed lidars with all their numerous and undoubted advantages. Simultaneously, the complexity of transceiver subsystems and their high cost should be noted [4,5,6,7,8,9,10,11]. Other commonly used laser-based sensors for environmental monitoring are CW frequency-modulated lidars with optical or RF-heterodyning [4,7,8,9,10,12], which are also capable of providing high spatial resolution but are difficult in hardware implementation and very demanding for tuning accuracy. These features, to some extent, limit the wide commercial application of mentioned remote sensors.
The paper focuses on S-lidars (S comes from Scheimpflug) as a relatively new class of atmospheric lidars, implementing non-traditional principles of system design [13,14,15] and actively using the latest achievements of optical instrumentation and modern nanophotonic technologies. They are successfully used for atmospheric aerosol monitoring [16], aquatic ecosystems profiling [17], detection of oil pollution [18], vertical atmospheric transmittance detection [19,20], trace gases and air pollution monitoring [21], volumetric profiling of targets [22] and in many other applications [23,24,25,26,27,28,29,30,31,32].
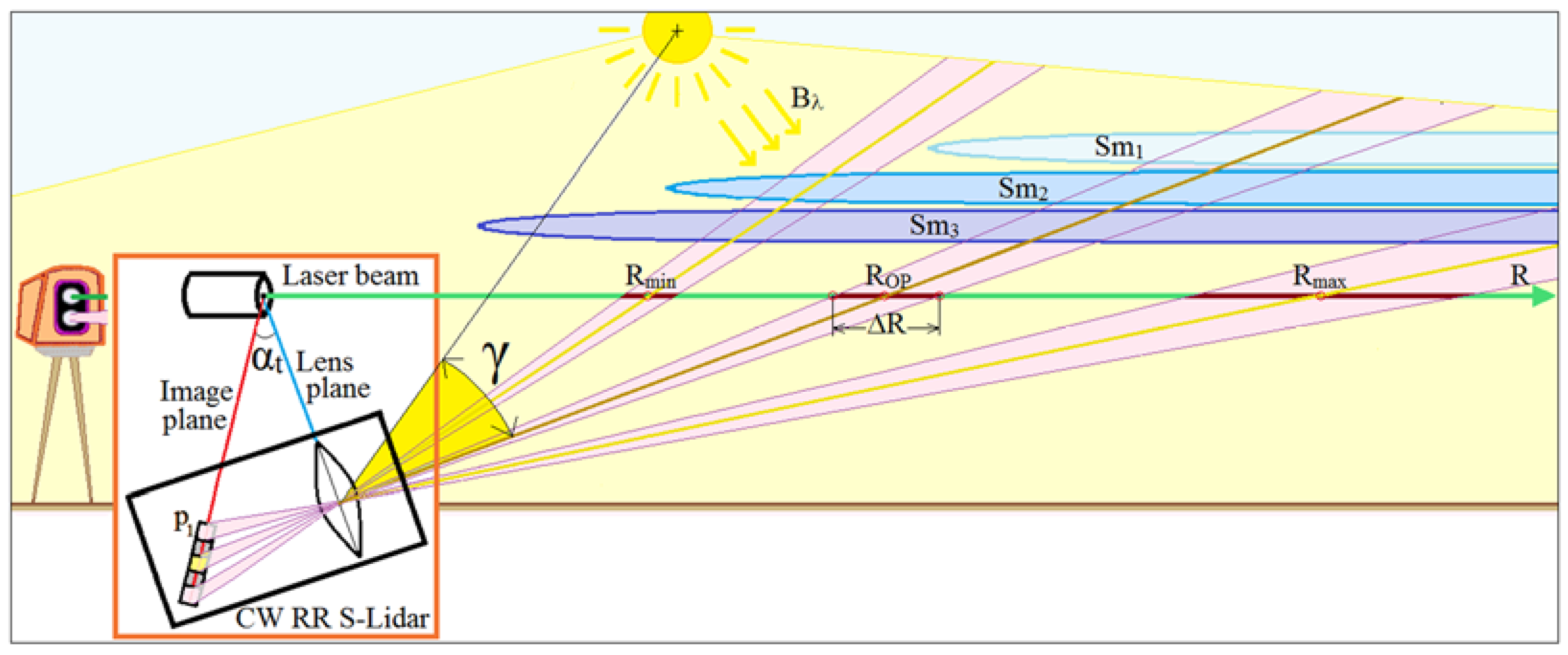
S-lidars use CW laser emitters and implement the triangular range control scheme, providing detection of echo signals by receiving optics equipped with array detectors (Figure 1). In this method, each microcell forms its own partial field of view, tracks a partial volume along the sound path and determines the current range resolution (RR) of the sensor [33,34,35].
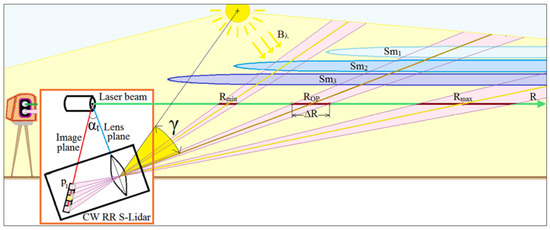
Figure 1.
Generalized representation of the “S-lidar + Optical Weather + External Background” system under discussion.
In Figure 1, the geometric proportions are deliberately altered so as to shrink on the range scale while, in contrast, the transceiver dimensions are stretched. This is done to illustrate the technique of providing a large depth-of-field of sharply focused images. The belonging to the backscatter lidar is seen from the fact that both the near Rmin and far Rmax borders of the depth-of-field (DoF) can be very far (many hundreds of meters and kilometers) from the sensor, and the base L of the implemented S-lidars does not exceed 1 m.
Characteristic features of S-lidars are disclosed, with emphasis on the study of hardware capabilities for reliable operation under a wide variety of optical weather conditions Sm and sky background brightness Bλ. We consider that in the first approximation, a variety of ambient atmospheric conditions can be generalized by different meteorological visibility ranges Sm. As shown, a generalized analysis of possible constraints imposed by the real environment on the potential capabilities of S-lidars makes it possible to develop optimal design solutions in a wide range of specific applications.
The common point that unites complementary sub-directions of the conducted research is a dimensionless approach based on forming normalized categories and factors reduced to some pre-proposed reference values. This allows for predicting and comparing a wide range of design solutions within the considered class of atmospheric S-lidars.
2. Methods and Approaches
2.1. S-Lidars: Features of Received Signals Description
Depending on the lidar system type, the potentially achievable range resolution ΔRpot is determined differently. For pulsed (time-of-flight—ToF) lidars, it is determined by the pulse duration τp: ; for continuous-wave frequency-modulated (CW-FM) lidars [4,9,12] it is equal to ΔRCWFM = ½ c∙ΔFf/Δfdev∙frep and even = ½ c/Δfdev if ΔFfmin = frep. Here, Δfdev is the frequency deviation; frep is the repetition frequency; and ΔFf is the receiver filter bandwidth. S-lidars under discussion have their own peculiarities that should be taken into account.
2.1.1. Range–Domain Characteristic of S-Lidars
As we discussed earlier [33], in CW S-lidars, the current range resolution can be represented by this relation:
where K1 is the combined optical–geometric parameter
which takes into account the focal distance f, the lidar base L, the cell size p1 and the tilt angle αt.
It should be noted that some publications on S-lidars [16,17,21,31,36,37] mention the term “infinite depth of field”, although they talk about the increase in range resolution ΔR as the range square, but are often silent about what values ΔR reaches the far border Rmax of the operating range. From (1), it is easy to see that with insufficiently large K1, the range resolution can be up to hundreds of meters, which in many remote sensing applications is unacceptably large and devalues the measurement results.
To avoid this unwittingly hidden uncertainty, in [33] (Equation (21)), we suggested using the factor
as an indicator of the range–domain quality, characterizing the specificity of S-lidars. On this basis, it was shown how to predict the far border of lidars at a pre-selected or available value of the combined parameter K1 and the given quality requirements:
Q(R) = R/ΔR
Conversely, what should be the value of K1-parameter to provide the required far border of the remote sensor at a given quality factor Q:
2.1.2. Lidar Equation in Its S-Lidar-Specific Form
Received signals of lidar systems for environmental monitoring are described by the so-called lidar equation [1,2,38], which is generally represented as
where Er is the echo-signal energy; ΔRgen is the range resolution in generalized form. Taking into account the considered relations (1)–(6), this equation adapted to the features of S-lidars will look as follows:
where is the received signal energy; Tobs is the observation time; ξ is the transceiver’s optical efficiency; Ar is the receiving optics area; βπ is the backscattering coefficient.
Er(λ,R) = E0∙ξ(λ)∙Ar∙ΔRgen ∙βπ(λ,R)∙T2(λ,R)/R2
Table 1 shows typical parameters of S-lidars for environmental remote sensing.

Table 1.
Parameters of S-Lidars designed for various environmental applications.
2.1.3. From Pixel Numbers i to Current Ranges Ri: A Simple Transition Algorithm
Operation principles and specific features of the considered class of S-lidars, among other things, assume an uncommon method of processing “images”. We put the term “image” in quotes because array detectors of S-lidars receive and process information about optical parameters of layers of the investigated medium, which are located along the probing beam rather than across the beam or view field, as in traditional imaging. In this case, each array cell gathers information from its own layer along the probing path.
In this regard, let us briefly consider issues related to the «current distance—number of a pixel» interrelation. Relations [16,17,18,21,36,37,39] describing the range Ri to the i-th layer as a function of the pixel number i are often found in the literature. They are associated with the necessity of using high-precision values of angles of inclination of both the lens plane and the image plane, which is not always convenient to use. Therefore, in [33] (Equation (20)), we proposed another approach to describe the dependence Ri = f(i) based on generalized parameters of S-lidars:
where Rop is the tuning distance of receiving optics; K0 = ½∙n∙Rop/K1 is the combined system parameter; n is the number of cells in the linear array. Given that f/Rop ≪ 1 and the relation of [34] (Equation (17)), we can reduce (8) to such a simple form:
As can be seen, the range to the i-th layer can be easily calculated based on the system parameter K1 from (2), the number of cells n of the linear array and the required quality parameter Qreq value, which together with the available K1 defines the far border of S-lidars according to (4).
2.2. S-Lidar Potential in Real Environment
2.2.1. Dimensionless Parameterization for Potential Prediction
In order to predict potential capabilities of any atmospheric lidar under arbitrary environmental conditions, whether micro-lidars or, conversely, powerful lidar systems, as well as to compare the effectiveness of the most different design solutions, it seems appropriate to highlight the influencing factors as follows. Let us call the dimensionless potential of any lidar the ratio of the signal power Pr received from the reference distance R0 when probing an arbitrary homogeneous medium to the achieved threshold power Pt. We will present it as a product of three dimensionless factors to account for the variability of real environmental factors, namely the meteorological visibility Sm and the sky background brightness Bλ:
Here, characterizes the virtual potential of any type of lidar when probing the reference medium with visibility Sm0 at dark night (DN) with sky background brightness ; the factor describes the influence of optical weather on the lidar potential; is the factor of external background influence. As a reference medium, we have chosen a molecular atmosphere (Sm0 = ), whose optical characteristics are considered to be known and stable [2,3,40], and the reference distance R0 can be chosen differently in specific applications.
By introducing three dimensionless factors into (10), it is possible to make reasonable predictions about the extent to which real environmental conditions affect the potential of a particular lidar instrument even before field measurements are made. Moreover, we consider system capacities not by themselves but in comparison with a hypothetical lidar sensing a reference molecular atmosphere on a dark night. If such integral approaches obtained are applied to existing or just being developed lidar instruments, it is easy to adapt the generalized solutions to specific conditions of particular applications based on the own parameters of the used remote sensing system.
2.2.2. Virtual Potential of S-Lidar under Reference Conditions
Reference potentials of different lidars in a molecular atmosphere with minimal influence of sky background can be written down as follows:
When adapting (11) to S-lidars as a relatively new and promising class of environmental remote sensing tools, one should take into account their range–domain features specified in (1) and (4), namely, the range resolution and the far border of operation range. The latter leads to the seemingly obvious conclusion that when predicting the initial virtual potential of any available S-lidar with the aggregate parameter K1 and the formulated requirements to Q, it is reasonable to choose :
Next, we show how, based on the concept (10) of representing the potential of any lidar instrument, to predict the influence of specific conditions of both the ambient atmosphere and sky brightness. The introduced factors of normalized weather Π and sensitivity to the external background Φ allow us to quantitatively predict changes in the virtual potential Ψ0, which is tied to the molecular atmosphere and the lowest sky background.
3. Results and Discussion
3.1. Ambient Optical Weather and S-Lidar Potential
3.1.1. Optical Weather: Components of Dimensionless Description
Under dimensionless approaches (10)–(12), let us return to the normalized potential (10) and consider its second-factor Π characterizing the contribution of real optical weather versus the molecular atmosphere by presenting it in this form:
with .
In the analytical description of relations (13), we assumed that the atmospheric extinction coefficient σ can be written as [3,41,42]
Additionally, assuming for simplicity the absence of absorption (σ = α) and following the experimental data [43,44], we supposed [45] that the relation between the backscattering coefficient βπ and the total scattering α can be described in some cases as
with the known lidar ratio βπ/α = 3/8π in the molecular atmosphere.
3.1.2. Influence of Optical Weather Conditions on S-Lidar Potential Capabilities
Based on (13)–(15), it is possible to properly account for the surrounding weather conditions when conducting or planning monitoring activities and predict the effect of their variability on lidar potential. This can directly affect the accuracy of measurements and retrieval of atmospheric optical parameters. To gain insight and illustrate the degree of variation in normalized optical “weather” Π and how it can affect lidar potential, we considered a wide range of visibility Sm variations from the clear atmosphere to heavy fog.
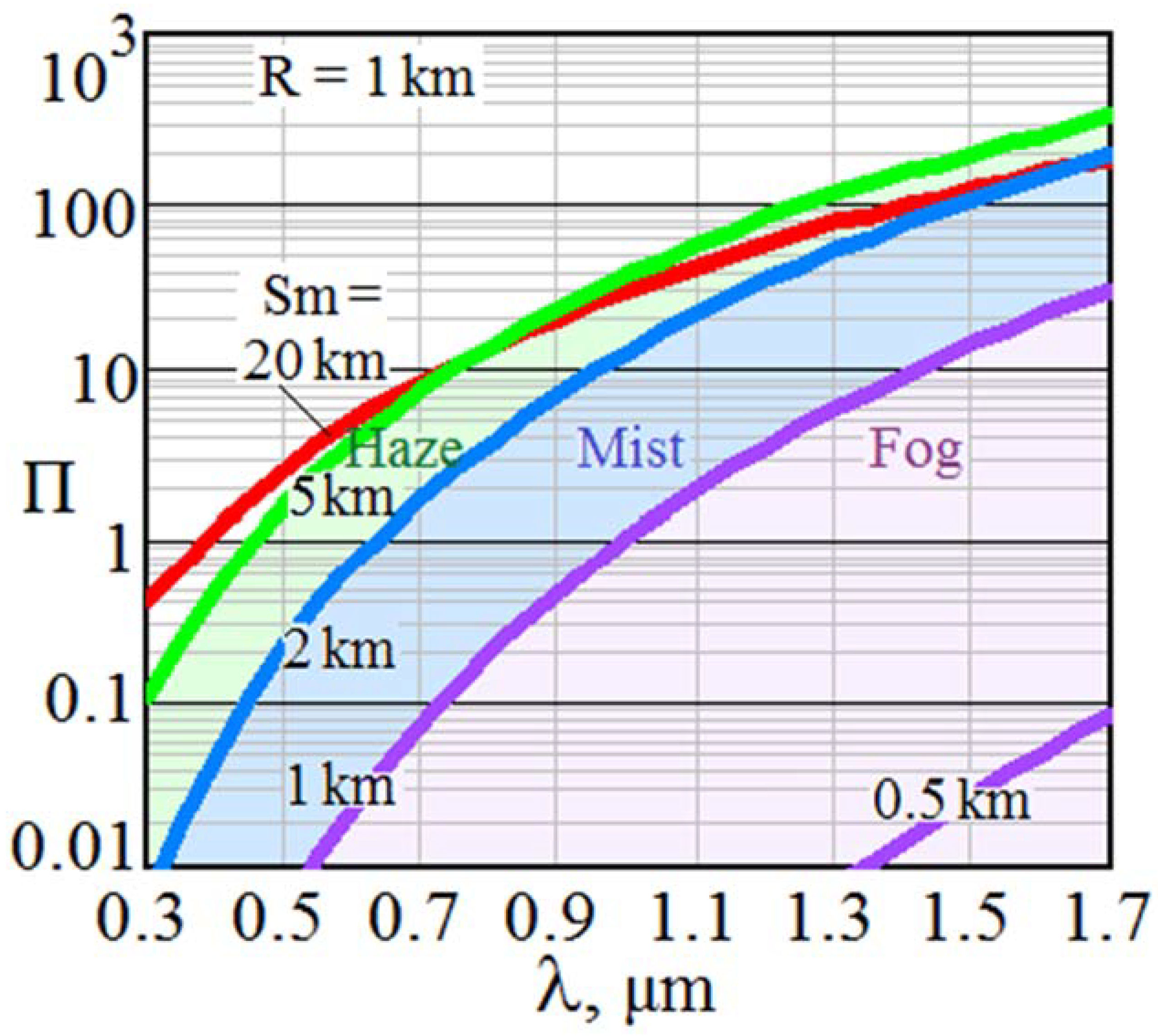
For subsequent analysis adapted to CW RR S-lidars, we chose the spectral range of 0.3…1.7 μm, in which manufacturers offer a wide choice of Si and InGaAs array detectors capable of overlapping the left and right halves of this range. As shown in Figure 2, where the common gradations of meteorological conditions are highlighted, the optical weather factor Π is significantly higher at the long-wave boundary of the range in question.
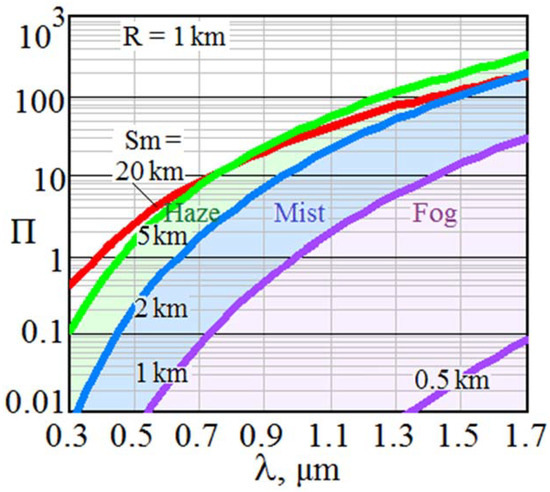
Figure 2.
Spectral course of dimensionless optical weather factor Π in clear day, haze, mist and fog conditions.
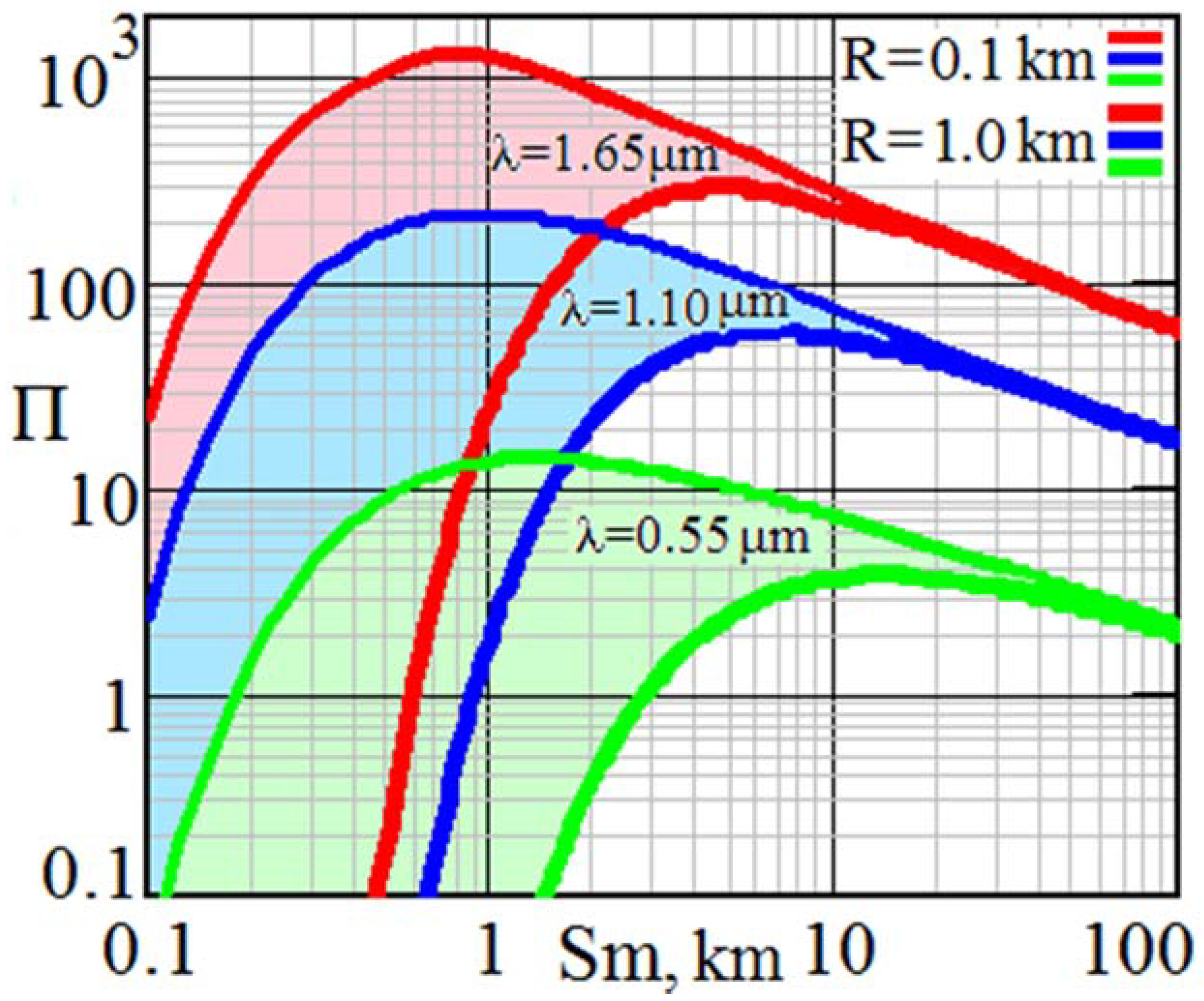
Figure 3 and Figure 4 show the behavior of the Π factor under the wide variability of Sm visibility in the Vis+SWIR range at the three selected wavelengths multiple of 0.55 μm. They illustrate the ability to predict lidar potential under certain environmental conditions even before in situ measurements are made. Since, in S-lidars, the near and far boundaries of the depth of field of sharply focused images are always predetermined by hardware, the operation range between Rmin = 0.1 km and Rmax = 1 km is chosen as an example.
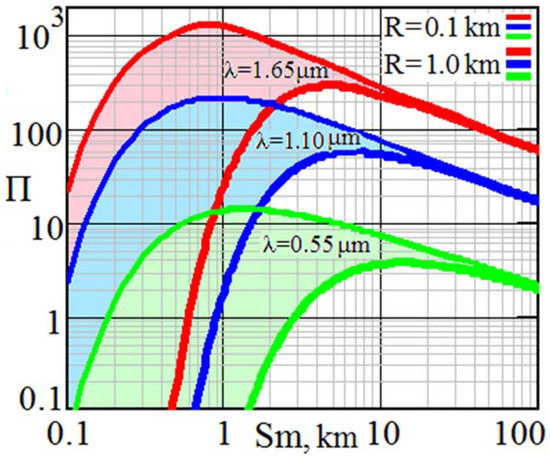
Figure 3.
Variability bands of dimensionless optical weather Π within the depth of field between 0.1 km and 1.0 km at three wavelengths in the Vis/SWIR region where Si/InGaAs arrays are sensitive.
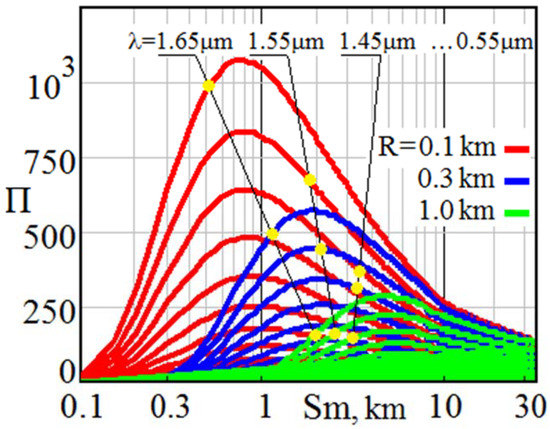
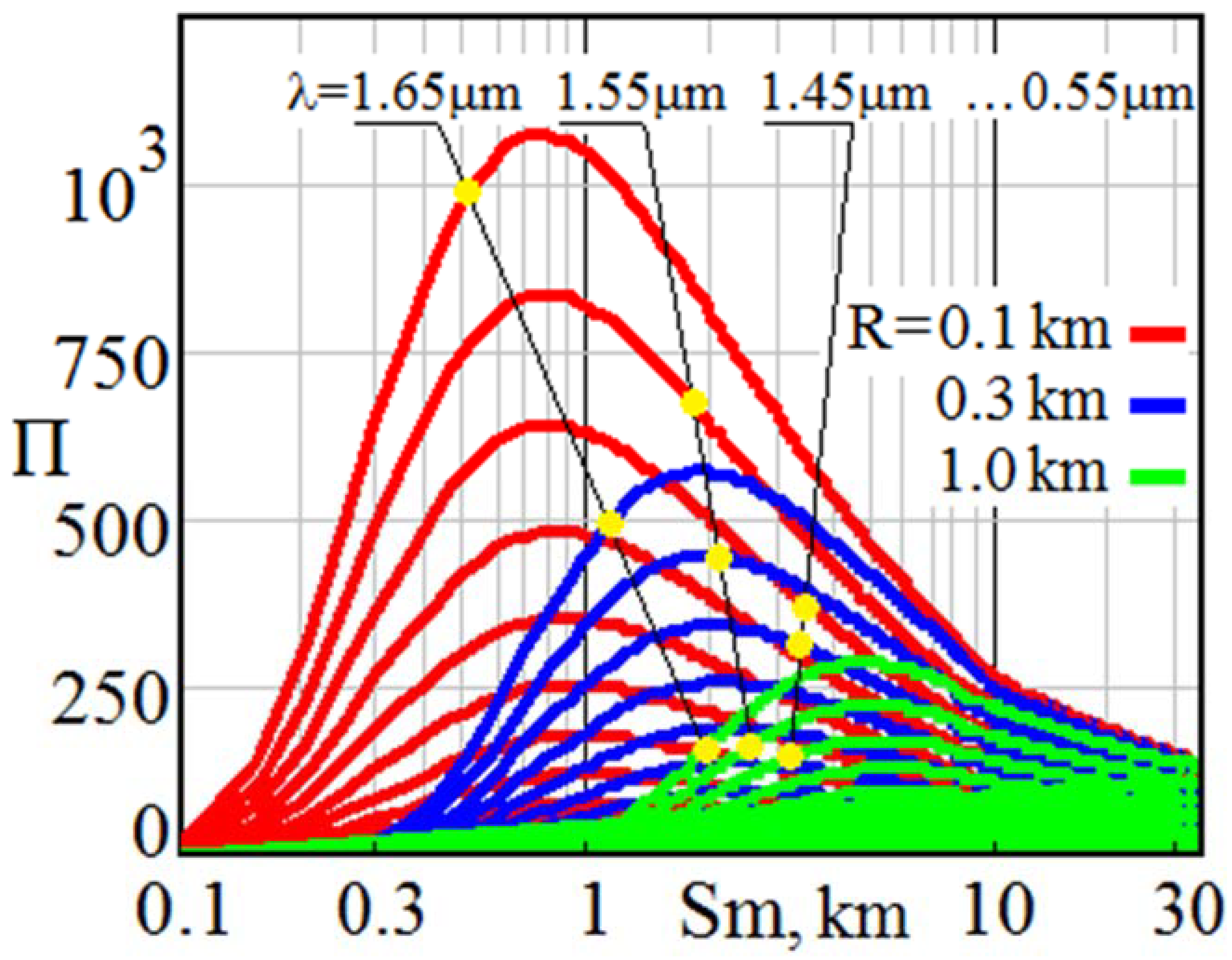
Figure 4.
Variability of optical weather Π as a function of current visibility Sm and sensing range R at wavelengths of Si/InGaAs arrays sensitivity.
So, near its right border (λ = 1.65 μm) with visibility from moderate fog to light haze (Sm~0.5…5.0 km), Π-factor may increase to 3∙102 when receiving signals from R~1 km and exceed 103 when receiving signals from a shorter distance R~0.1 km. Although in the SWIR range, the scattering coefficient decreases compared to the visible range according to (14), the contribution of atmospheric transmission in the double path in (13) plays a much smaller role than in the visible spectral range, which explains the illustrated dependences.
When one shifts to visible wavelengths, the weather-dependent factor of lidar potential normalized to the reference atmospheric conditions becomes significantly lower. For example, in the green region (λ = 0.55 μm), when receiving signals from a range of R~1 km, only 4-fold excess over probing in the virtual molecular atmosphere is maximally achieved with Π(Sm = 15 km) = 4, and at R = 0.1 km, only Π(Sm = 15 km) = 15 can be obtained.
Thus, the optical weather coefficient applied to S-lidars with Si/InGaAs array detectors operating in the spectral region of 0.3…1.7 µm gives the following predictions. When probing in visible spectral range at short distances with R ~ 0.1 km, application of Π factor indicates advantages of operation under mist conditions (Sm ~ 1…2 km), and at ranges about R ~ 1 km confirms kind of optimality at Sm ~ 10…15 km. In SWIR range, the weather factor indicates an increase of lidar potential in somewhat less transparent conditions; for example, when receiving signals from the range R ~ 1 km, it turns out to be maximal at Sm ~ 4…8 km. At the same time, it is obvious that when visibility deteriorates significantly, and the beam attenuation factor plays a decisive role, the normalized lidar potential at λ < 1 μm is always much lower than in virtual reference conditions.
3.2. Sky Background and S-Lidars with Vis/SWIR Array Detectors
3.2.1. Normalized Spectral Brightness of Sunlight
In laser remote sensing of the environment, the received echo signals are often accompanied by background illumination. In contrast to laboratory experiments, where background sources are negligible or can be compensated for, in open-path field measurements, the brightness of background interference can be significant, and its influence is not easily overcome. When ambient background radiation is mentioned, it refers to a flow or single photons that interfere with the proper reception and processing of sounding echoes. It is assumed that the nature of background photons is not related to the laser sensing signals, and their spectrum falls within the sensitivity bandwidth of the photodetector. Mitigating and preventing the effects of background interference seems to be very important tasks in laser remote sensing [2,3,6,40,46,47,48].
Scattered solar radiation at wavelengths shorter than 3 μm is the main source of daytime sky background accompanying the laser sensing. Usually, the Sun’s brightness is described as [1,3,46]
and the color temperature of the Sun is often taken to be Tsun = 6000 K, which determines the radiation maximum at wavelength λBmax = 0.002898/Tsun = 0.483 μm [2,3]. Assuming the same brightness of the sky, it is frequently considered to be about 10−5 of the Sun brightness, and the maximum sky brightness is estimated up to BλBmax = 109 W∙m−2∙m−1∙sr−1. The normalized spectral brightness of the sky can be represented as
In the following analysis, we will assume that the background brightness distribution coincides with the spectrum of solar radiation.
3.2.2. Background Power Reaching a Single Pixel
Let us estimate the power of background illumination received together with the lidar echo signal. Consider that in the angular field Ω of the optical receiver, there is an elementary volume Ω·R2·dR, remote at a distance R, the atmosphere inside which is homogeneous and has a volume scattering coefficient βγ at arbitrary angle γ. If the monochromatic illumination by the incident flow of background radiation is equal to Hλ, the intensity of radiation scattered by the elementary volume can be represented as Hλ βγ Ω R2 dR. If the receiver with an entrance pupil area Ar subtends a solid angle equal approximately to Ar/R2, then the power of background radiation scattered by the volume and then passed through the atmosphere with transparency T = exp [− ], the receiving optical system and the spectral band-pass filter
where ξ0 is the total transmission of receiving optics.
Integrating (18) by R from 0 to ∞, we obtain the total power of the sky background collected from the whole sounding path in the receiving field of view:
where iγ is the scattering indicatrix (phase function). As a special case of (19), one can obtain an expression usually used in the estimation of background radiation power at the photodetector input [1,3,8,48]. Since the spectral brightness density is
the power can be obtained when α does not depend on R:
Βλ = Hλ iγ
A feature of S-lidars under study is a very narrow field of view formed by a single pixel of the array: , hence
From (21) follows a simple estimate of the background illumination power affecting a single detector pixel:
3.2.3. Normalized Sky Background in Photon Counting Mode: Spectral Features
Since S-lidars usually use detectors with Si/InGaAs arrays, it is useful to present the characteristic dependencies in the spectral band of interest. Keeping in mind the photon counting mode, we note that the spectrum of background photon numbers is shifted to the right compared to in accordance with (16), (17) and (21)–(23), since the photon energy Eph = hc/λ is inversely proportional to the wavelength:
As a result, the normalized spectrum of background photons will look like
For example, at the Sun temperature T = 6000 K, when λBmax = 0.483 μm, the spectrum shift leads to λNbmax = 0.612 μm.
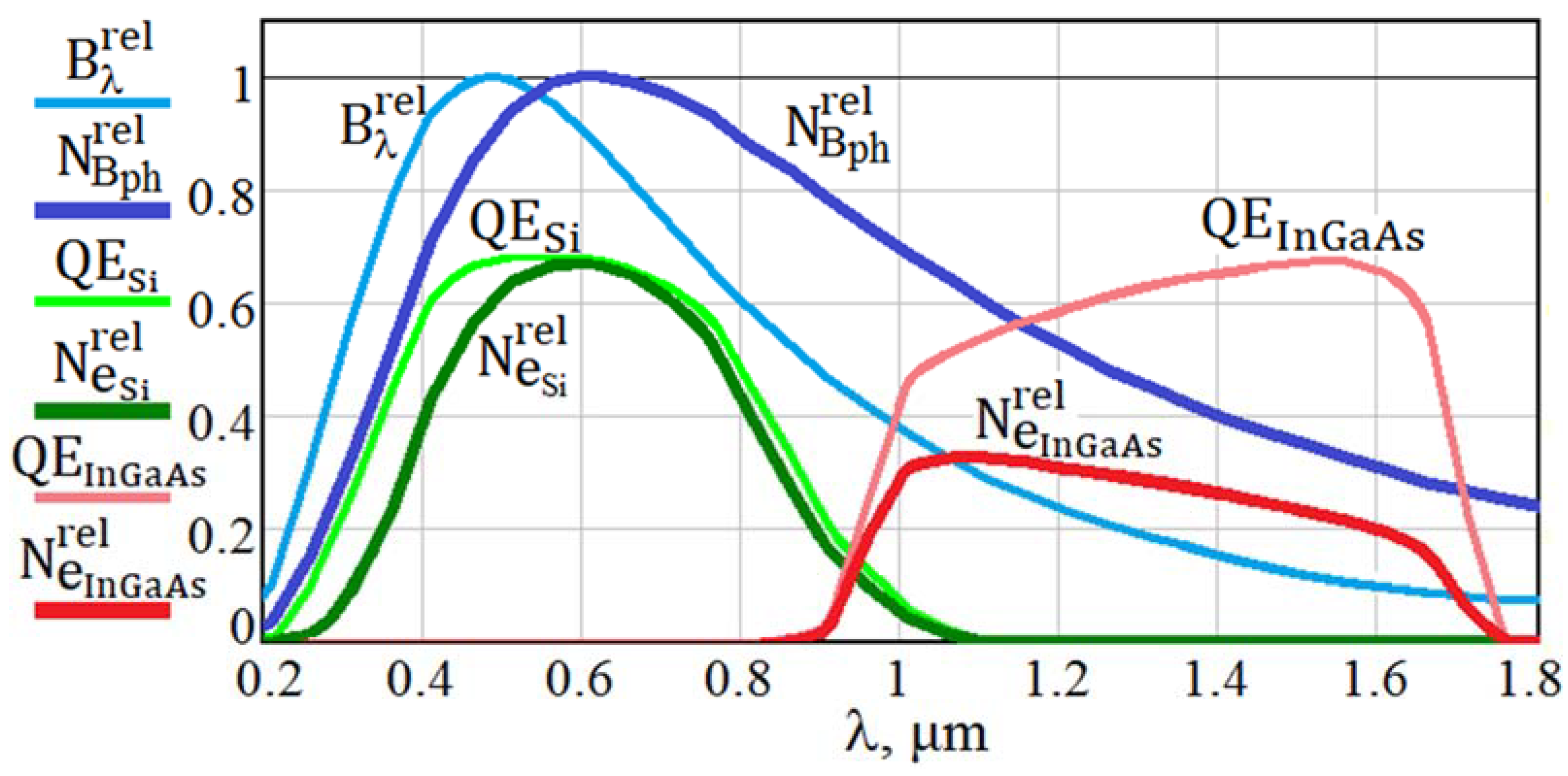
Figure 5 shows the spectra of the normalized sky background brightness and the number of background photons at the array input from (25), typical quantum efficiencies QESi and QEInGaAs of Si and InGaAs detectors at room temperature and numbers of generated photoelectrons and at the output of detectors.
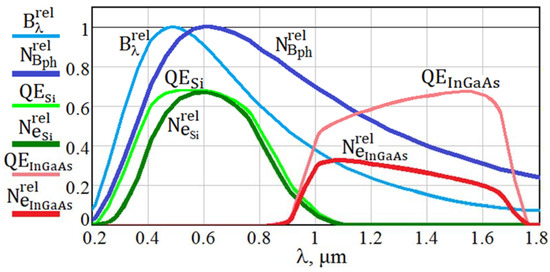
Figure 5.
Normalized spectra of solar irradiance and background photon numbers ; typical quantum efficiencies QESi and QEInGaAs of Si and InGaAs arrays at room temperature and background photoelectron numbers and generated at the output of Si and InGaAs arrays. Observation time Tobs = 20 ms.
3.3. Sky Light at Different Weather Conditions and Background Stability of Si- and InGaAs-Arrays
3.3.1. Description of Mildly-Sloping Scattering Indicatrices
The right-hand side of (21) is commonly used in the remote sensing literature [1,3,8,47] for simplified estimation of the incoming background illumination power. To further understand the effects of optical weather, consider that the background brightness Βλ = f(iγ) depends on the shape of scattering indicatrices iγ, which, in turn, are very sensitive to atmospheric conditions. It is known that scattering indicatrices iγ, or phase functions, associated with different atmospheric conditions have been well studied and repeatedly classified [2,5,49,50,51,52]. In particular, the range of variability of the directional light scattering coefficient βγ = iγ∙α∙increases with decreasing atmospheric transparency. The molecular indicatrix is usually described as , assuming that it is independent of wavelength in the Vis+SWIR range.
In many cases, such as molecular scattering, scattering on spherical aerosol particles, and in several others, indicatrices do not depend on the scattering azimuth, so for simplicity, we will consider only them. Our analysis of experimental indicatrices [43,44] showed [8,45] that the correlation between iγ and α can be approximated by such a functional relationship
implying for angles γ at the sun that at γ < 50° coefficient bγ > 0 and at γ > 60 coefficient bγ < 0. With a relative error of no more than 20%, sufficient to make estimates, let us take the following set of angle-dependent power function approximations for mildly-sloping scattering indicatrices [8,45] shown in Table 2.
iγ = aγ ∙αbγ

Table 2.
Power function approximations of experimental indicatrices.
3.3.2. Angles at the Sun, Scattering Indicatrices and Sky Background Power at the Input
Our results of spline interpolation of the normalized indicatrices from Table 2 are shown in Figure 6.
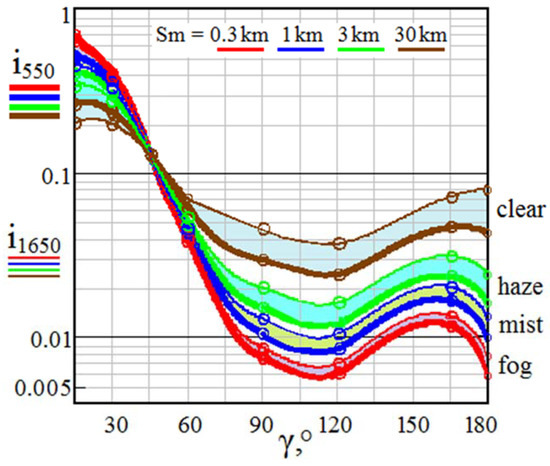
Figure 6.
Modeling of normalized scattering indicatrices (phase functions) in the spectral range 0.55…1.65 μm under different visibility conditions Sm = 0.3…30 km according to (26) and Table 2.
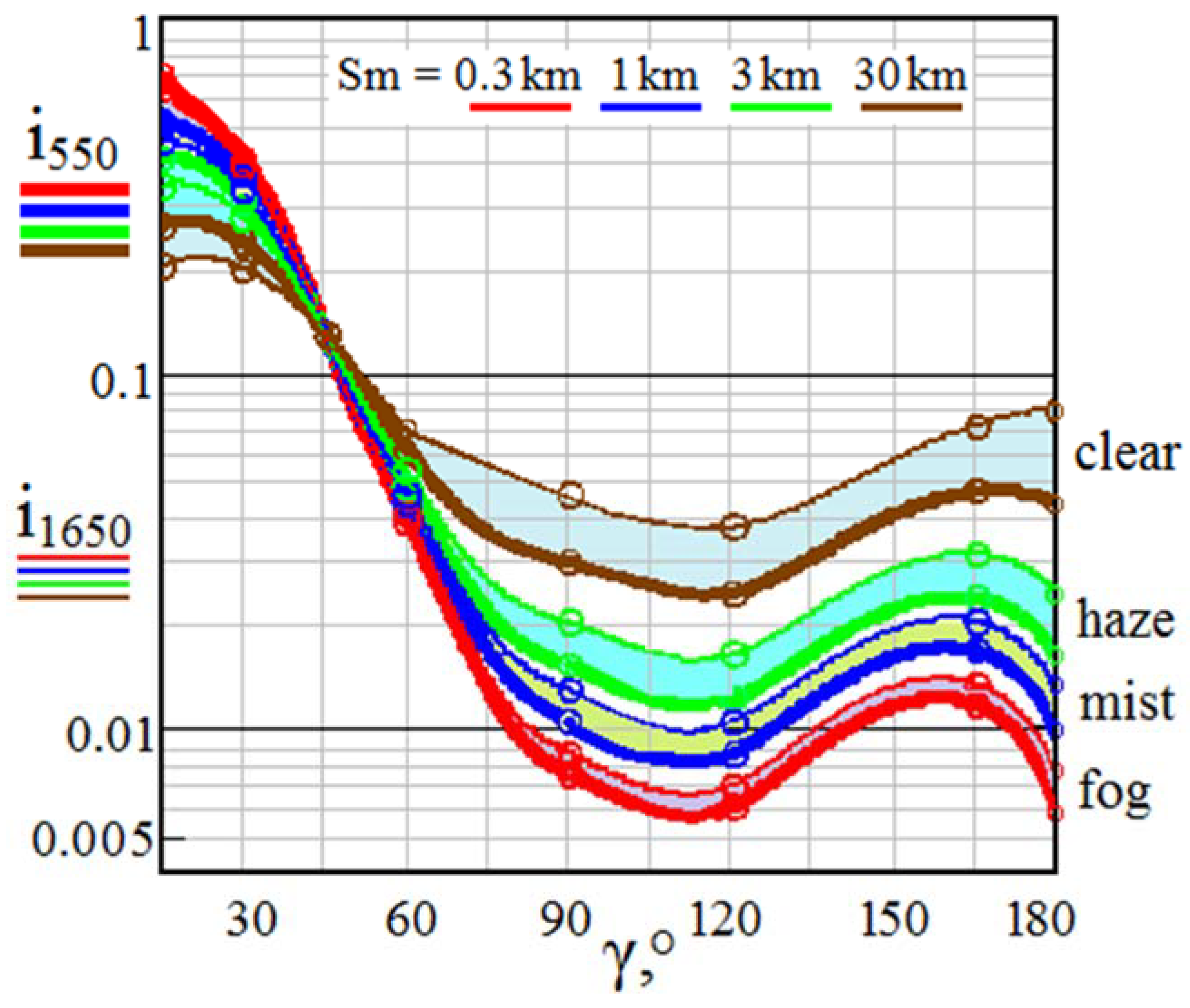
It can be seen that the range of indicatrices variability iγ expands significantly with decreasing transparency from a clear atmosphere through haze and mist to fog. Based on this, the nature of weather-dependent variability of the normalized sky background power in the spectral range λ = 0.3…1.7 μm with a discrete set of angles between the receiving optical axis and the direction to the Sun (say ROADS-angles) γ = 15°…165° is shown in Figure 7.
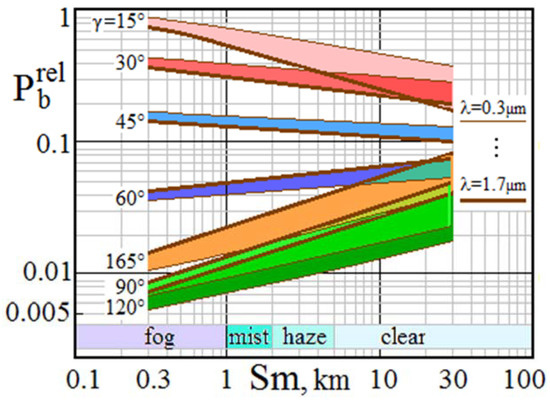
Figure 7.
Power of received sky background as a function of visibility Sm at different angles γ at the Sun in the Vis+SWIR spectral range. Here, γ is the angle between the receiving optical axis and the direction to the Sun.
As follows from Figure 7, environmental conditions have a significant influence on the background level at the receiver input at all angles of inclination to the Sun. It is also obvious that ROADS-angles γ greater than 50° are preferable to limit the influence of bright sky background, both in clear weather and when probing in a hazy atmosphere.
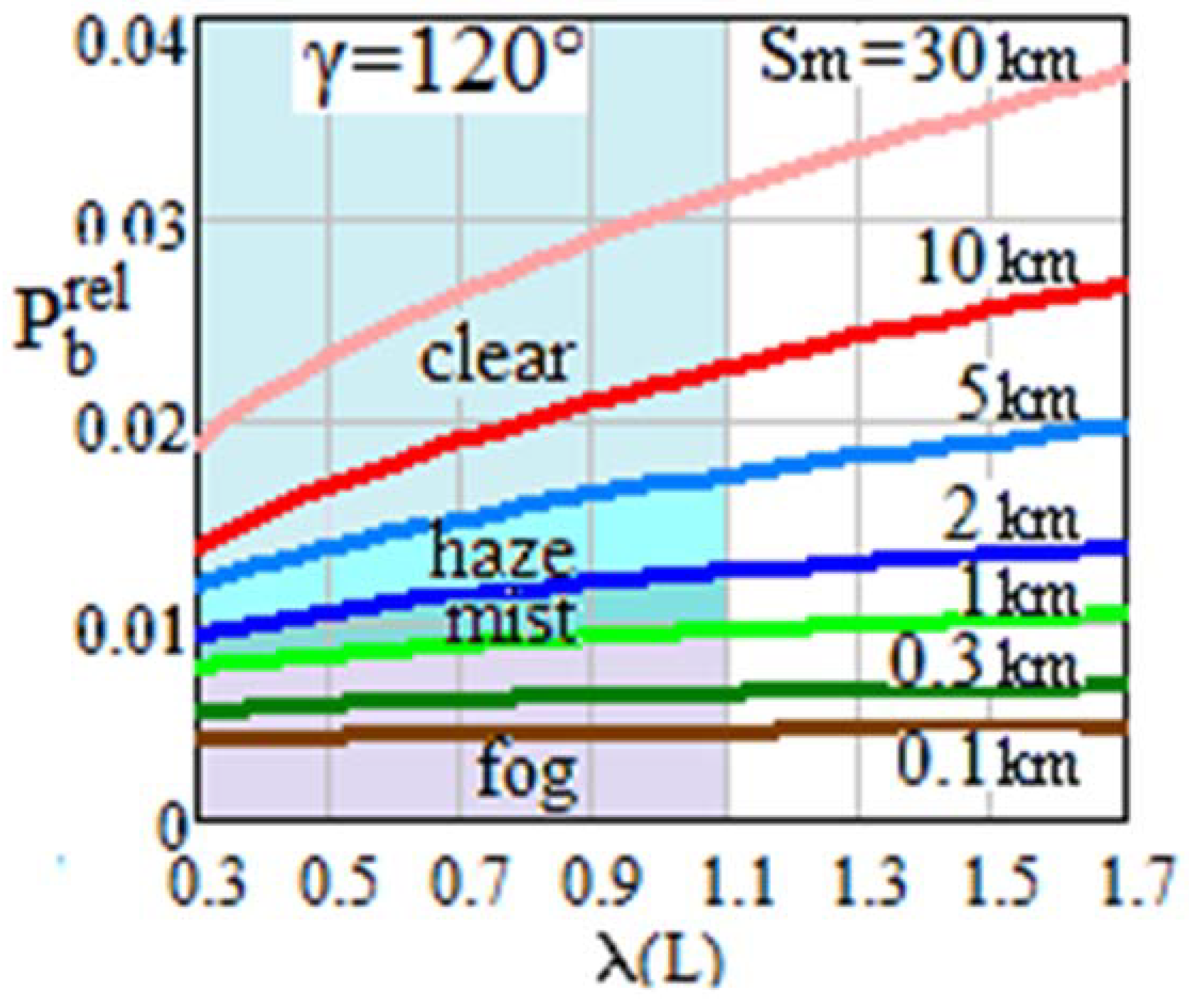
Spectral distribution examples of the normalized power of external background illumination at visibility Sm variations for two angles on the Sun γ = 30° and 120° are presented in Figure 8 and Figure 9.
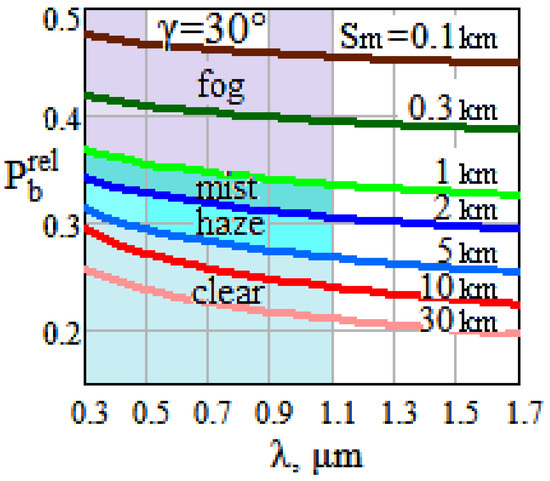
Figure 8.
Spectral distributions of at variations of visibility Sm and Sun angles γ = 30°.
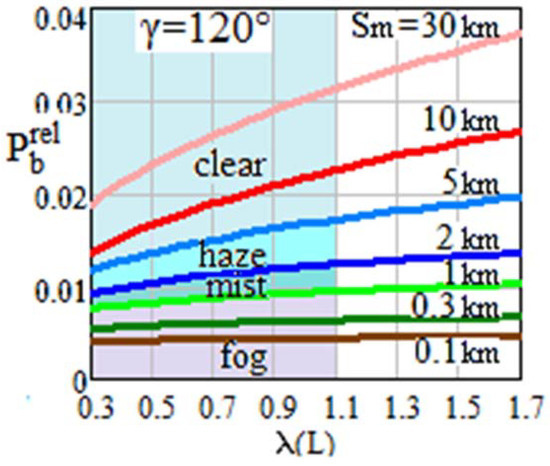
Figure 9.
Spectral distributions of at variations of visibility Sm and Sun angles γ = 120°.
When the Sun is in the forward hemisphere, the less transparent the atmosphere, the greater the background illumination at the lidar receiver input. Conversely, when the Sun shines from behind, the sky background is more significant in clear weather. Along with this, the background power at the lidar input is always less than in the first case.
The results obtained should be considered as first approximation estimates. The purpose of such estimates is to pay attention and provide insight into how solar illumination can limit the capabilities of reliable laser sensing under changing optical weather conditions, along with how to foresee the influence of sun angles, etc., to account for their contribution to lidar design. A deeper analysis should consider factors such as the homogeneity of optical weather conditions, especially for solar flux and the presence of cirrus clouds or aerosols at altitude. Correct consideration of their influence in specific applications will provide more reliable sensing data and more accurate results for their retrieval.
3.3.3. Background Stability of Si- and InGaAs-Arrays
To estimate possible degradations of S-lidar potential, we will calculate the factor Φ from (10) as the ratio of sensitivity thresholds at the minimum dark night illumination (DN) and the real daytime background for array detectors with known intrinsic dark currents:
Here, Pt0 is the threshold power; is the number of dark electrons; is the number of background photons; η(λ) is the quantum efficiency; Bλ is the sky background brightness.
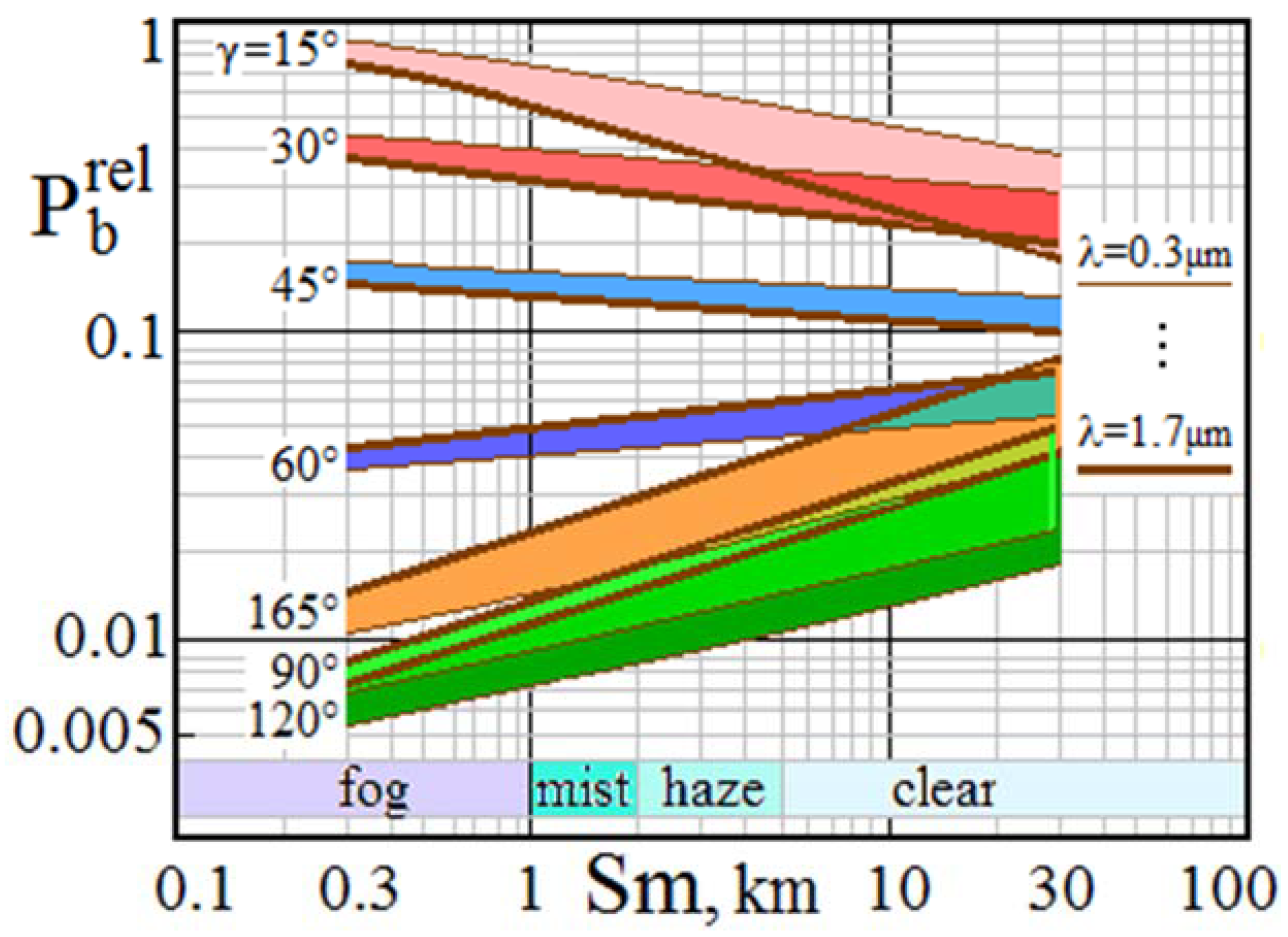
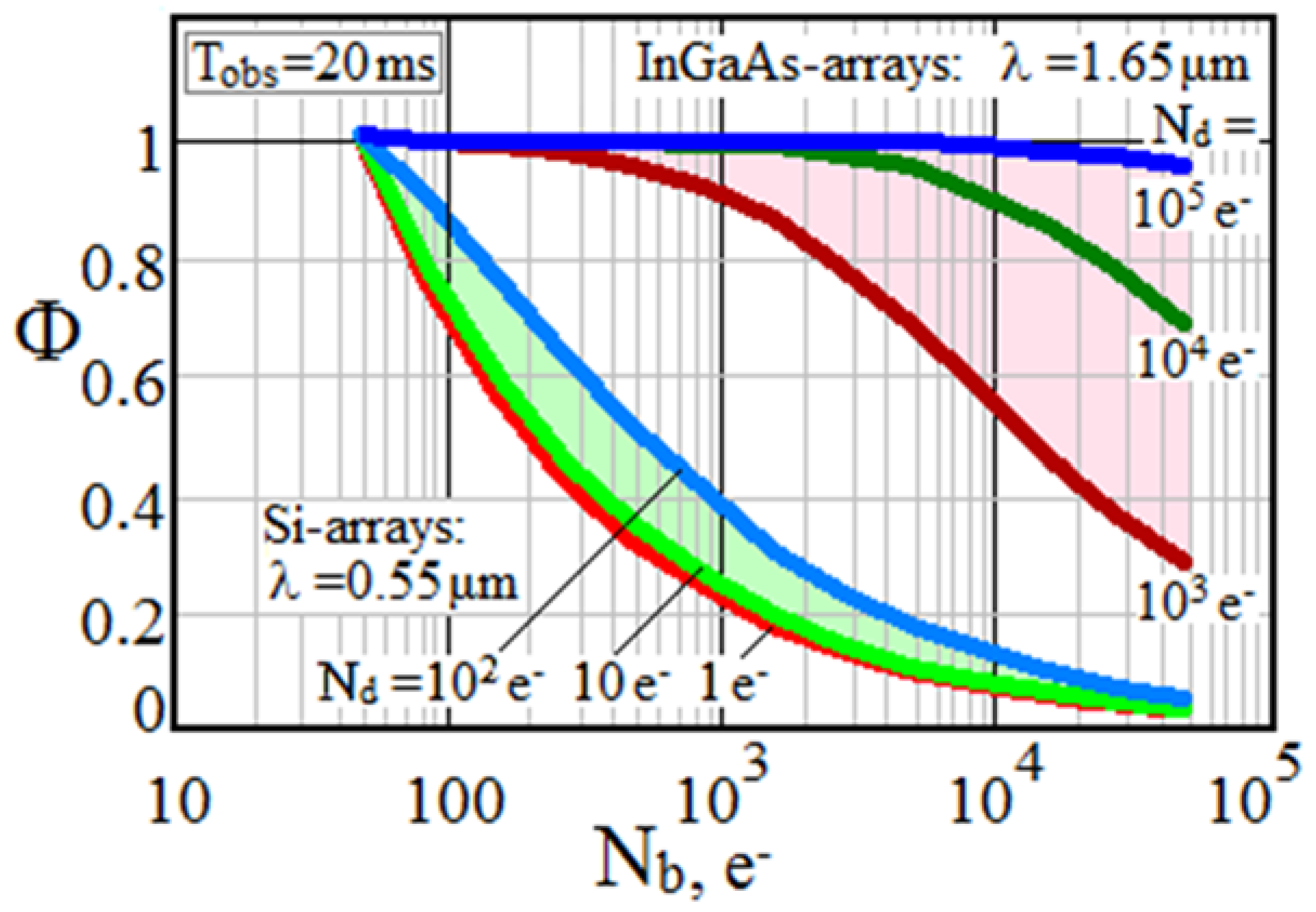
Figure 10 shows families of dependences Φ = f(Nb), illustrating the effect of external background on the potential of lidar with Si and InGaAs arrays, whose behavior differs.
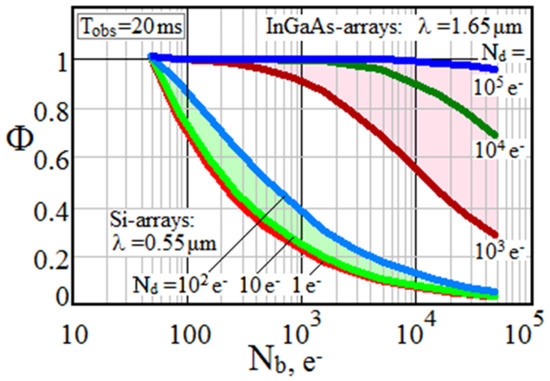
Figure 10.
Effect of external background on potential capabilities of S-lidars. Si-arrays: Id = 10−17/10−16/10−15 A. InGaAs-arrays: Id = 10−14/10−13/10−12 A. Tobs = 20 ms. T = 20 °C.
Obviously, the most significant reason for such dissimilarity of characteristics is the large difference in their dark currents. As can be seen, lidars with low-noise Si-arrays are very sensitive to external backgrounds, and under bright daytime sky conditions, their potential can easily degrade to Φ ≪ 1. Under the same conditions, lidars with uncooled InGaAs array detectors are much less sensitive to sky backgrounds, and at Nd~105 e− (corresponding to Id~1 pA at Tint~20 ms), they are virtually insensitive to ambient light.
Note that the considered illustrations reflect the variability of lidar sensitivity to the sky’s light in relation to a sensor with the same dark current but which operates under a weak background of the dark night sky. Therefore, the Φ curves at 10- and 100-fold increases in the number of dark electrons show a higher immunity to the external background.
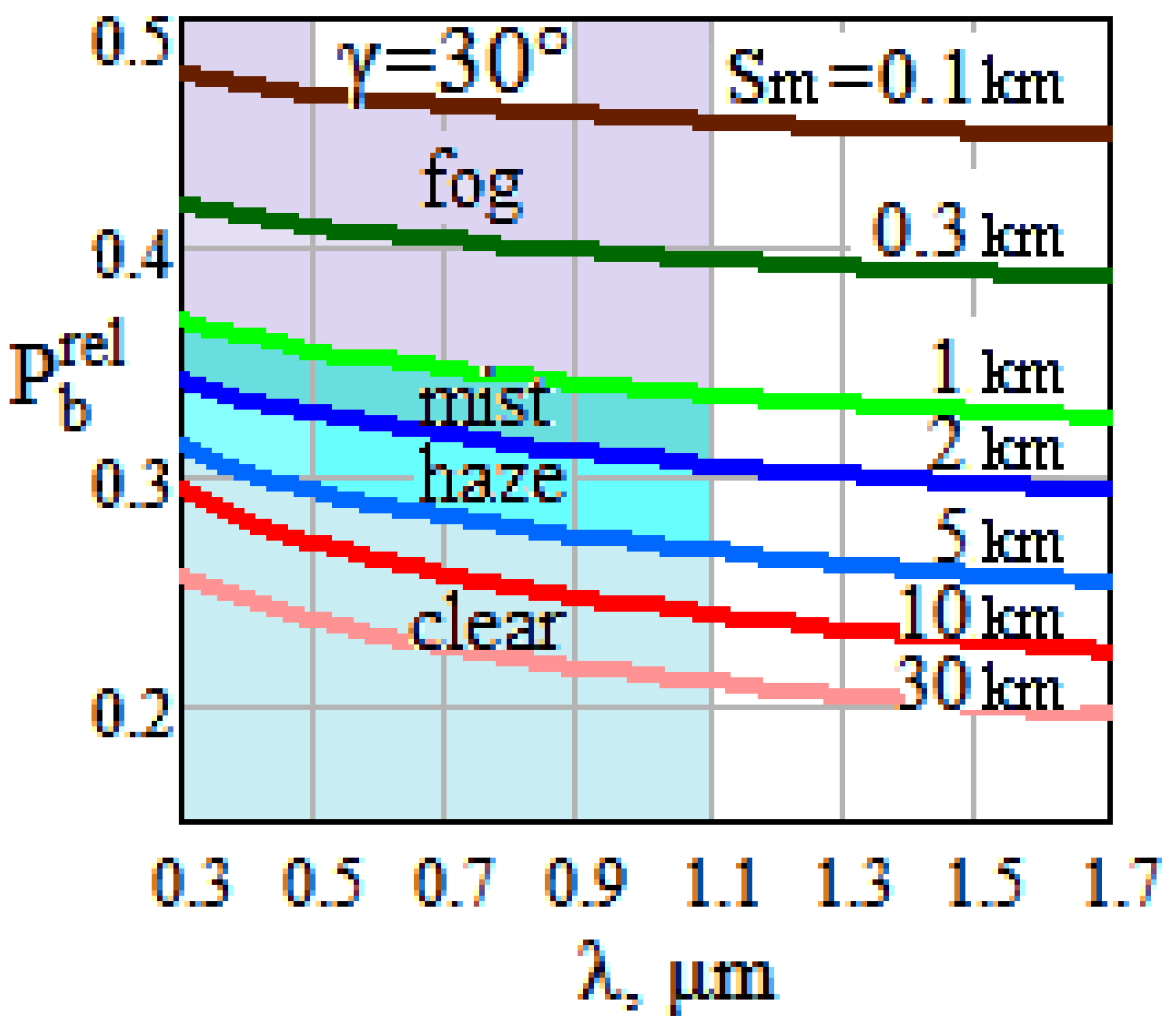
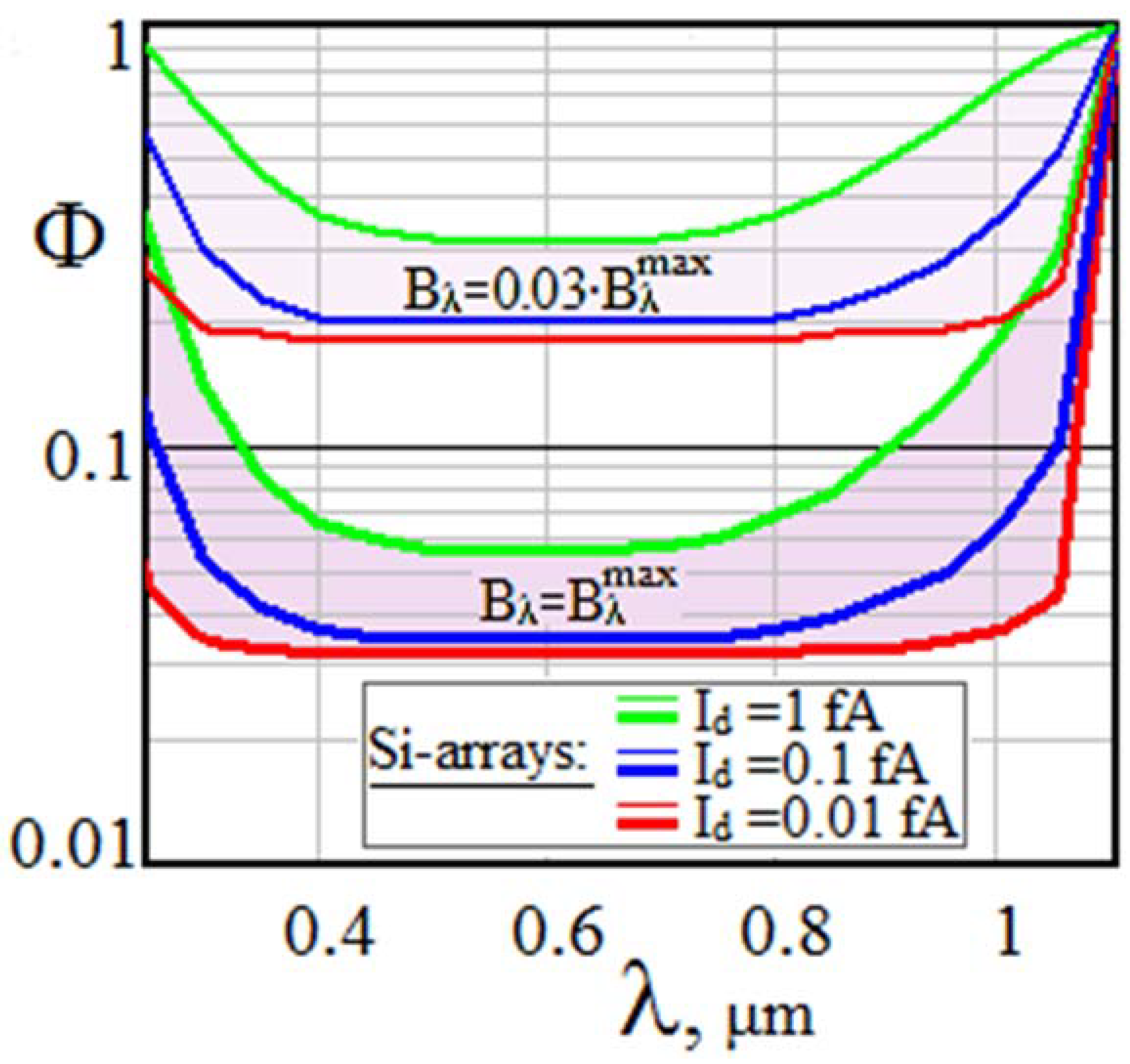
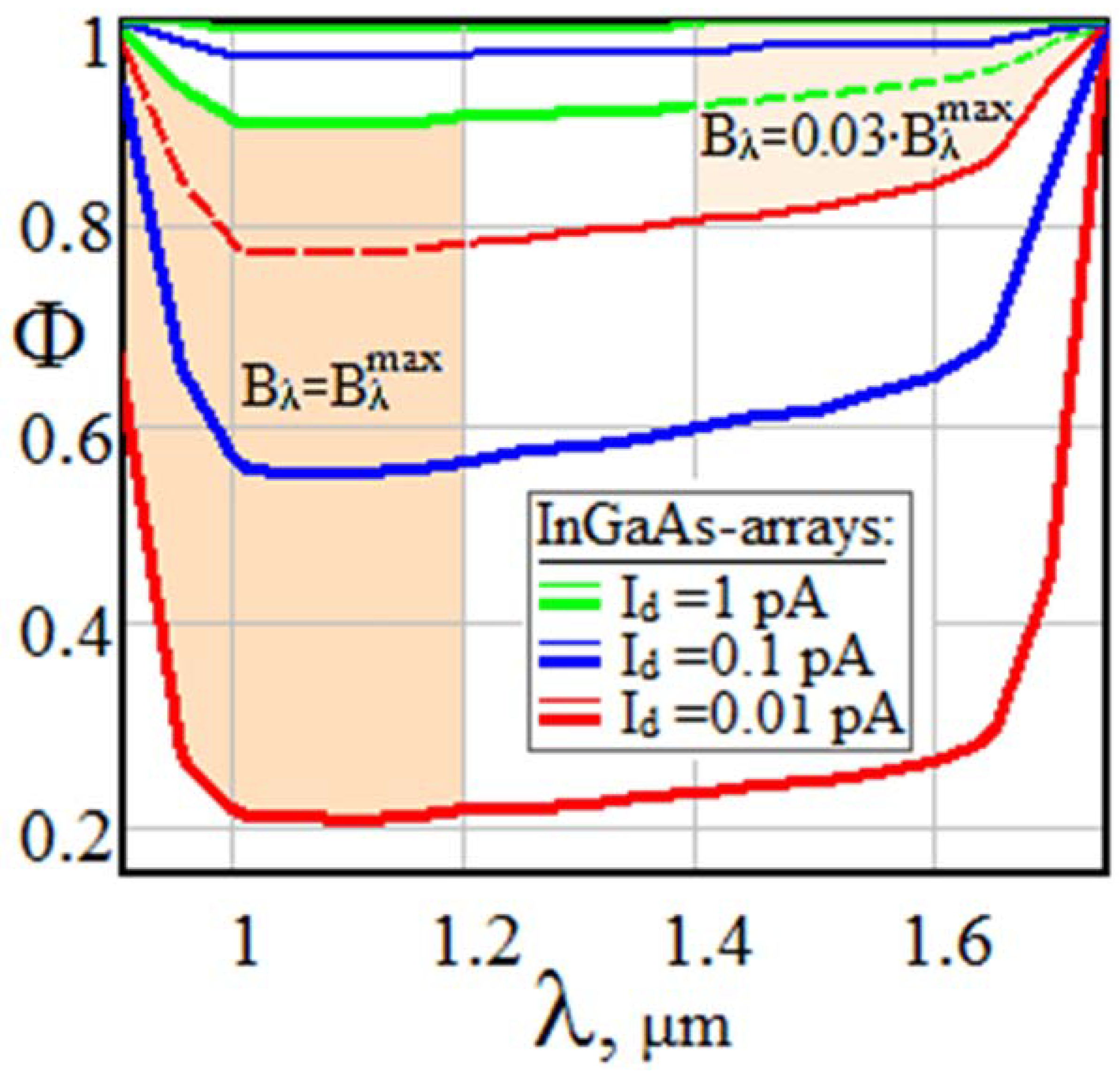
Spectral dependences in Figure 11 and Figure 12, typical for lidars with Si and InGaAs detectors, illustrate a similar situation.
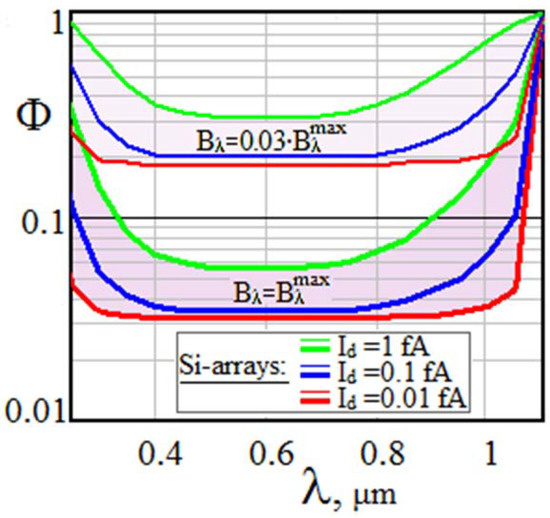
Figure 11.
Spectral dependences of sensitivity Φ to external background characteristic of Si-arrays.
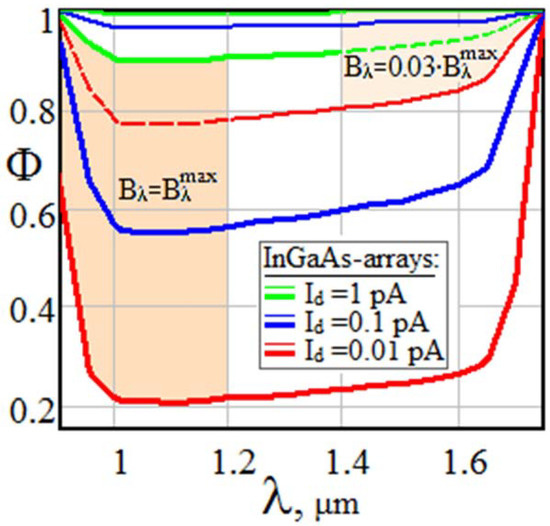
Figure 12.
Spectral dependences of sensitivity Φ to external background characteristic of InGaAs-arrays.
The potential of lidars with low-noise Si-arrays (Figure 11) falls significantly to values Φ = 0.2…0.3 already at a moderate sky background (the upper family of curves) and may decrease 10-fold more against a very bright background (the lower family). As for InGaAs-based S-lidars (Figure 12), their sensitivity to external background is significant only when using cooled cameras with dark current Id < 0.1 pA, while typical uncooled detectors with Id~1 pA feel almost no influence of the sky’s light on potential capabilities of S-lidars.
Adapting the generalized modeling parameters to any particular instrument makes it possible to quantitatively predict the sky background influence on the reduction of potential capabilities for different S-lidar designs.
4. Conclusions
This paper proposes a methodology for analyzing S-lidar performance under wide variability of optical weather conditions and sky background brightness. The novelty of the problem statement and obtained results are determined by their application to remote laser systems with (described) non-traditional principles of design, such as S-lidars, which represent a relatively new class of environmental lidars. We used a dimensionless approach, which allows us to compare phenomena and systems of different scales and integrates complementary fields of study.
To analyze the influence of changing environment on the lidar potential, we introduced normalized factors of optical weather and background influence. Effects of optical weather on the lidar potential under different environmental conditions, from clear atmosphere through haze and mist to fog, have been shown in the Vis+SWIR bands in which S-lidars with Si/InGaAs detectors operate.
Studies of external background influence on the S-lidar potential began based on estimates of spectral and energy variability of the sky brightness and identification of response features of Si and InGaAs detector arrays used in the photon counting mode. Along with this, significant differences in their spectral sensitivity and intrinsic noise characteristics were taken into account.
Based on the proposed model for describing mildly-sloping scattering indicatrices, we further show significant differences in the sky-light power at the receiver input, which are observed at different angles to the Sun. On this basis, it became possible to predict the joint effect of the current visibility, phase functions and angles to the Sun on the background power received. We then proposed algorithms and quantified the degree of lidar sensitivity to external backgrounds with differences in spectral characteristics and intrinsic noises of Vis/SWIR array detectors used. Possible cases and situations of both significant deterioration of lidar potential and its insensitivity to accompanying sky background were illustrated.
To summarize, we note that the proposed concept of predicting the influence of external factors on the potential capabilities of S-lidars with Si/InGaAs array detectors is intended to expand possible applications of this rapidly developing class of remote sensors in a variety of environmental conditions.
Author Contributions
Conceptualization and methodology, R.A.; investigation, R.A., Z.W. and D.L.; writing—review and editing, R.A.; resources and funding acquisition, Z.W. and D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Chinese Academy of Sciences (CAS-PIFI, 2023VEA0004); the National Natural Science Foundation of China (41975038); the Key Research and Development Program of Anhui Province (2022h11020008); HFIPS director’s Fund (2021YZGH01).
Data Availability Statement
No data were generated or analyzed in the presented research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hinkley, E. Laser Monitoring of the Atmosphere; Springer: Berlin/Heidelberg, Germany, 1976; p. 397. [Google Scholar]
- Measures, R. Laser Remote Sensing: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 1984; p. 320. [Google Scholar]
- Rees, W. Physical Principles of Remote Sensing; Cambridge University Press: Cambridge, UK, 2006; p. 470. [Google Scholar]
- Molebny, V.; McManamon, P.; Steinvall, O.; Kobayashi, T.; Chen, W. Laser radar: Historical prospective—From the East to the West. Opt. Eng. 2016, 56, 031220–031224. [Google Scholar] [CrossRef]
- Ball, J.E.; Anderson, D.T.; Chan, C.S. Comprehensive survey of deep learning in remote sensing: Theories, tools, and challenges for the community. J. Appl. Remote Sens. 2017, 11, 42609. [Google Scholar] [CrossRef]
- Comerón, A.; Muñoz-Porcar, C.; Rocadenbosch, F.; Rodríguez-Gómez, A.; Sicard, M. Current research in lidar technology used for the remote sensing of atmospheric aerosols. Sensors 2017, 17, 1450. [Google Scholar] [CrossRef]
- Dang, R.; Yang, Y.; Hu, X.-M.; Wang, Z.; Zhang, S. A Review of Techniques for Diagnosing the Atmospheric Boundary Layer Height Using Aerosol Lidar Data. Remote Sens. 2019, 11, 1590. [Google Scholar] [CrossRef]
- Agishev, R. Laser Remote Sensing of the Environment; Phys-Math-Lit: Moscow, Russia, 2019; p. 264. [Google Scholar]
- McManamon, P. Lidar Technologies and Systems; SPIE Press: Bellingham, WA, USA, 2019; p. 520. [Google Scholar]
- Zhou, B.; Zhang, S.; Xue, R.; Li, J.; Wang, S. A review of space-air-ground integrated remote sensing techniques for atmospheric monitoring. J. Environ. Sci. 2021, 123, 3–14. [Google Scholar] [CrossRef]
- She, C.-Y.; Friedman, J. Atmospheric Lidar Fundamentals; Cambridge University Press: Cambridge, UK, 2022; p. 400. [Google Scholar]
- Agishev, R.; Gross, B.; Moshary, F.; Gilerson, A.; Ahmed, S. Range-resolved pulsed and CWFM lidars: Potential capabilities comparison. Appl. Phys. B Lasers Opt. 2006, 85, 149–162. [Google Scholar] [CrossRef]
- Scheimpflug, T. Improved Method and Apparatus for the Systematic Alteration or Distortion of Plane Pictures and Images by Means of Lenses and Mirrors for Photography and for Other Purposes. GB Patent GB190401196A, 12 May 1904. [Google Scholar]
- Barnes, J.; Bronner, S.; Beck, R.; Parikh, N. Boundary layer scattering measurements with a charge-coupled device camera lidar. Appl. Opt. 2003, 42, 2647–2652. [Google Scholar] [CrossRef]
- Cilingiroglu, U.; Chen, S. Range sensing with a Scheimpflug camera and a CMOS sensor/processor chip. IEEE Sens. J. 2004, 4, 36–44. [Google Scholar] [CrossRef]
- Mei, L.; Brydegaard, M. Atmospheric aerosol monitoring by an elastic Scheimpflug lidar system. Opt. Express 2015, 23, A1613–A1628. [Google Scholar] [CrossRef]
- Zhao, G.; Ljungholm, M.; Malmqvist, E.; Bianco, G.; Hansson, L.; Svanberg, S.-A.; Brydegaard, M. Inelastic hyperspectral lidar for profiling aquatic ecosystems. Laser Photonics Rev. 2016, 10, 807–813. [Google Scholar] [CrossRef]
- Gao, F.; Li, J.; Lin, H.; He, S. Oil pollution discrimination by an inelastic hyperspectral Scheimpflug lidar system. Opt. Express 2017, 25, 25515–25522. [Google Scholar] [CrossRef]
- Sun, G.; Qin, L.; Hou, Z.; Jing, X.; He, F.; Tan, F.; Zhang, S. Small-scale Scheimpflug lidar for aerosol extinction coefficient and vertical atmospheric transmittance detection. Opt. Express 2018, 26, 7423–7436. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Li, H.; Mei, L. Preliminary studies on atmospheric monitoring by employing a portable unmanned Mie-scattering Scheimpflug lidar system. Remote Sens. 2019, 11, 837. [Google Scholar] [CrossRef]
- Brydegaard, M.; Larsson, J.; Török, S.; Malmqvist, E.; Zhao, G.; Jansson, S.; Andersson, M.; Svanberg, S.; Åkesson, S.; Laurell, F.; et al. Short-wave infrared atmospheric Scheimpflug lidar. EPJ Web Conf. 2018, 176, 01012. [Google Scholar] [CrossRef]
- Luo, L.; Chen, X.; Xu, Z.; Li, S.; Sun, Y.; He, S. A parameter-free calibration process for a Scheimpflug Lidar for volumetric profiling. Prog. Electromagn. Res. 2020, 169, 117–127. [Google Scholar] [CrossRef]
- Mei, L.; Brydegaard, M. Continuous-wave differential absorption lidar. Laser Photon. Rev. 2015, 9, 629–636. [Google Scholar] [CrossRef]
- Malmqvist, E.; Brydegaard, M.; Aldén, M.; Bood, J. Scheimpflug lidar for combustion diagnostics. Opt. Express 2018, 26, 14842–14858. [Google Scholar] [CrossRef]
- Wang, X.; Duan, Z.; Brydegaard, M.; Svanberg, S.; Zhao, G.Y. Drone-based area scanning of vegetation fluorescence height profiles using a miniaturized hyperspectral lidar system. Appl. Phys. A 2018, 124, 207. [Google Scholar] [CrossRef]
- Gao, F.; Lin, H.; Chen, K.; Chen, X.; He, S. Light-sheet based two-dimensional Scheimpflug lidar system for profile measurements. Opt. Express 2018, 26, 338056. [Google Scholar] [CrossRef]
- Mei, L.; Zhang, L.; Kong, Z.; Li, H. Noise modeling, evaluation and reduction for the atmospheric lidar technique employing an image sensor. Opt. Commun. 2018, 426, 463–470. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Li, Z.; Liu, B.; Yin, B.; Wu, S.-H. Small angle scattering intensity measurement by an improved ocean Scheimpflug lidar system. Remote Sens. 2021, 13, 2390. [Google Scholar] [CrossRef]
- Li, N.; Ho, C.P.; Wang, I.-T.; Pitchappa, P.; Fu, Y.H.; Zhu, Y.; Lee, L.Y.T. Spectral imaging and spectral LIDAR systems: Moving toward compact nanophotonics-based sensing. Nanophotonics 2021, 10, 1437–1467. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Z.; Zhang, H.; Shan, H.; Han, J.; Zhao, S.; Wang, S.; Liu, D.; Wang, Y.; Tao, Z. Detecting aerosol backscattering coefficient across the whole troposphere by the side-scattering lidar system with three CCD cameras. Opt. Express 2022, 30, 29969–29978. [Google Scholar] [CrossRef]
- Chen, R.; Li, Y.; Xue, G.; Tao, Y.; Li, X. Laser triangulation measurement system with Scheimpflug calibration based on the Monte Carlo optimization strategy. Opt. Express 2022, 30, 25290. [Google Scholar] [CrossRef]
- Xing, L.; Dai, W.; Zhang, Y. Scheimpflug camera-based technique for multi-point displacement monitoring of bridges. Sensors 2022, 22, 4093. [Google Scholar] [CrossRef]
- Agishev, R. CW range-resolved S-lidars: Capabilities and limitations in range domain. Opt. Lasers Eng. 2020, 134, 106260. [Google Scholar] [CrossRef]
- Agishev, R.R. Imaging S-lidars enhancement by optimizing range-domain characteristics. Opt. Eng. 2021, 60, 034110. [Google Scholar] [CrossRef]
- Agishev, R. Application of imaging S-lidars: Functional and diagnostic capabilities for remote air pollution detection. Opt. Eng. 2021, 60, 084104. [Google Scholar] [CrossRef]
- Brydegaard, M.; Kouakou, B.; Jansson, S.; Rydell, J.; Zoueu, J. High dynamic range in entomological Scheimpflug lidars. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 6900711. [Google Scholar] [CrossRef]
- Yi, S.; Min, S. Composition of sharp-focused image by rotation of Scheimpflug camera. Opt. Laser Technol. 2022, 155, 108406. [Google Scholar] [CrossRef]
- Blais, F. Review of 20 years of range sensor development. J. Electronic Imaging 2004, 13, 231–243. [Google Scholar] [CrossRef]
- Manefjord, H.; Muller, L.; Li, M.; Salvador, J.; Blomqvist, S.; Runemark, A.; Kirkeby, C.; Ignell, R.; Bood, J.; Brydegaard, M. 3D-printed fluorescence hyperspectral lidar for monitoring tagged insects. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 1–9. [Google Scholar] [CrossRef]
- Kovalev, V.; Eichinger, W. Elastic Lidar: Theory Practice and Analysis Methods; Wiley Interscience: New York, NY, USA, 2004; p. 214. [Google Scholar]
- Wiegner, M. Lidar for aerosol remote sensing. In Atmospheric Physics: Background Methods Trends; Schumann, U., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 449–464. [Google Scholar]
- Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Weitkamp, C., Ed.; Springer: New York, NY, USA, 2005; p. 466. [Google Scholar]
- Barteneva, O.; Dovgyallo, O.; Polyakova, E. Experimental Studies of Optical Properties of Near-the-Ground Atmospheric Layers; Petersburg, S., Ed.; Hydromet: Leningrad, Russia, 1987; p. 237. [Google Scholar]
- Pyaskovskaya, E. Studies of Light Scattering in the Earth’s Atmosphere; Academy of Science: Moscow, Russia, 1977; p. 220. [Google Scholar]
- Agishev, R. Estimation of sky background power and signal-to-noise ratio in lidar measurements. Proc. High. Edu. Inst. Instrum. Eng. 1991, 34, 98–104. [Google Scholar]
- Ross, M. Laser Receivers: Devices, Techniques, Systems; Wiley: New York, NY, USA, 1966; p. 405. [Google Scholar]
- Osche, G. Optical Detection Theory for Laser Applications; Wiley: New York, NY, USA, 2011; p. 442. [Google Scholar]
- Agishev, R. Environmental CW range-resolved S-lidars with Si/InGaAs arrays: Limitations and capabilities under sky background. Appl. Opt. 2022, 61, 8889–8897. [Google Scholar] [CrossRef]
- Kokhanovsky, A. Aerosol Optics: Light Absorption and Scattering by Particles in the Atmosphere; Springer: Berlin/Heidelberg, Germany, 2008; p. 172. [Google Scholar]
- Fujii, T.; Fukuchi, T. Laser Remote Sensing; CRC Press: Boca Raton, FL, USA, 2005; p. 240. [Google Scholar]
- Kovalev, V. Solutions in Lidar Profiling of the Atmosphere; Wiley: New York, NY, USA, 2015; p. 248. [Google Scholar]
- Deirmendjian, D. Electromagnetic Scattering on Spherical Polydispersions; Elsevier: New York, NY, USA, 1969; p. 378. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).