Faint Echo Extraction from ALB Waveforms Using a Point Cloud Semantic Segmentation Model
Abstract
:1. Introduction
2. The Mapper4000U and Study Area
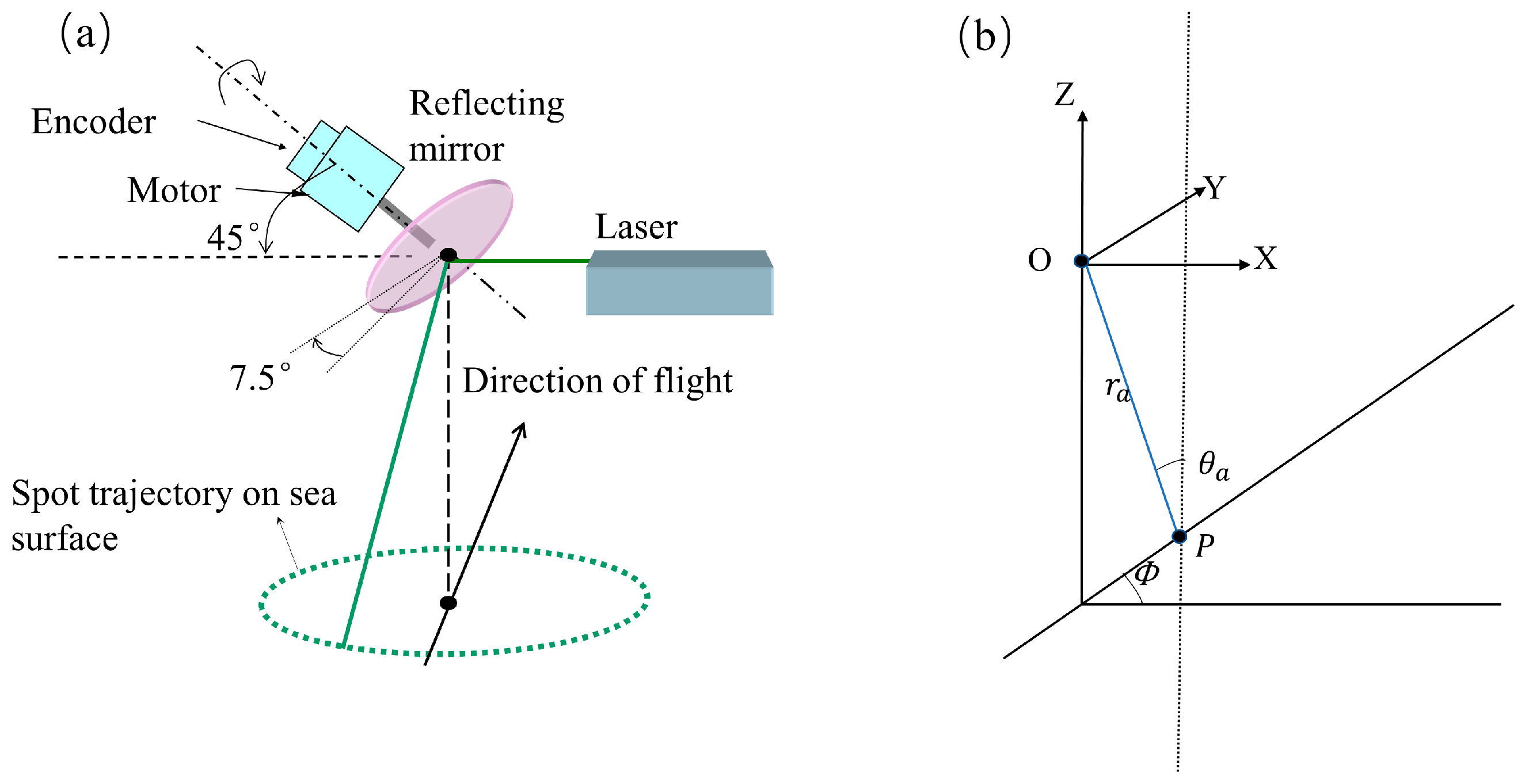
2.1. Mapper4000U
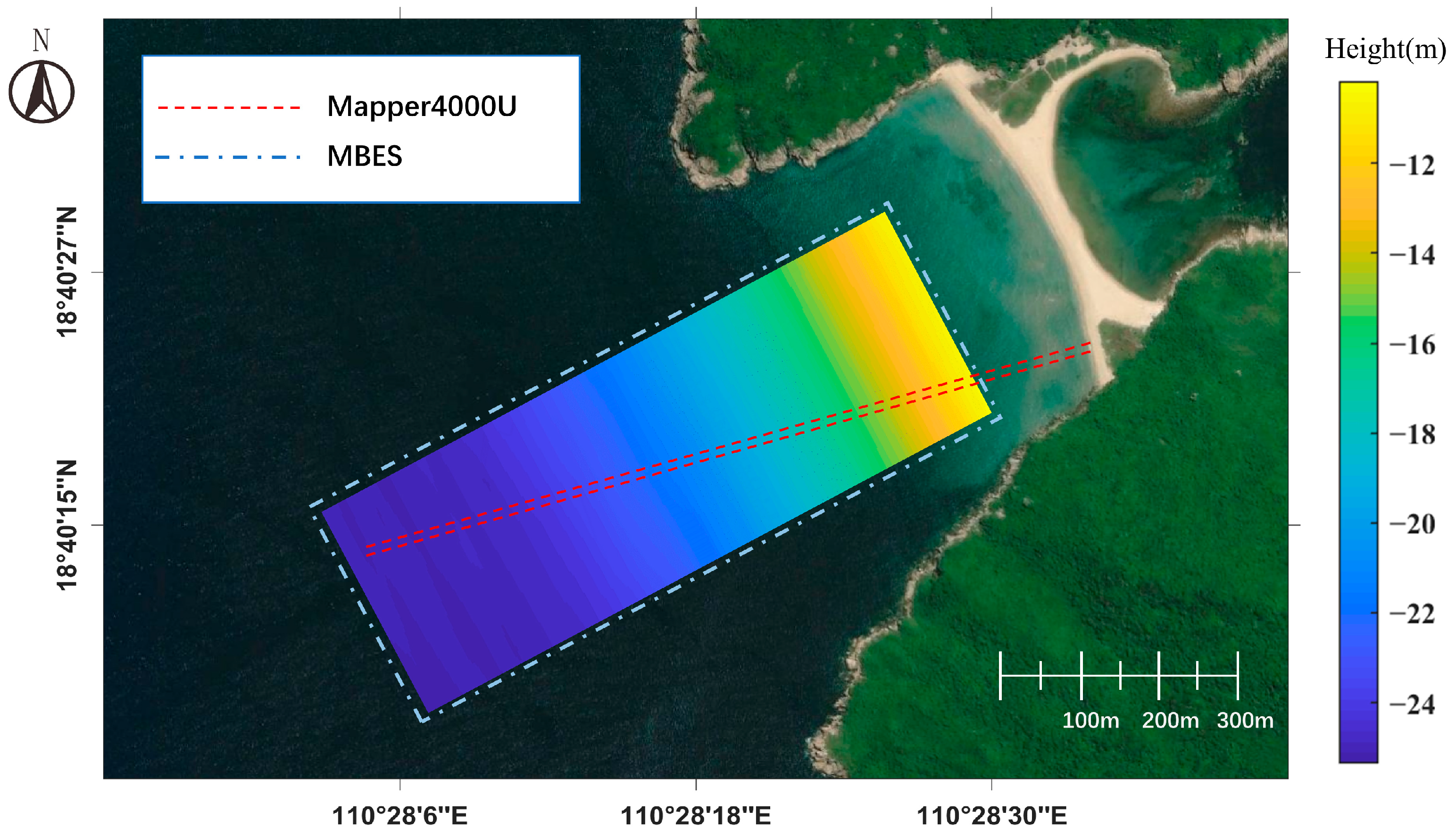
2.2. Study Area
3. Method
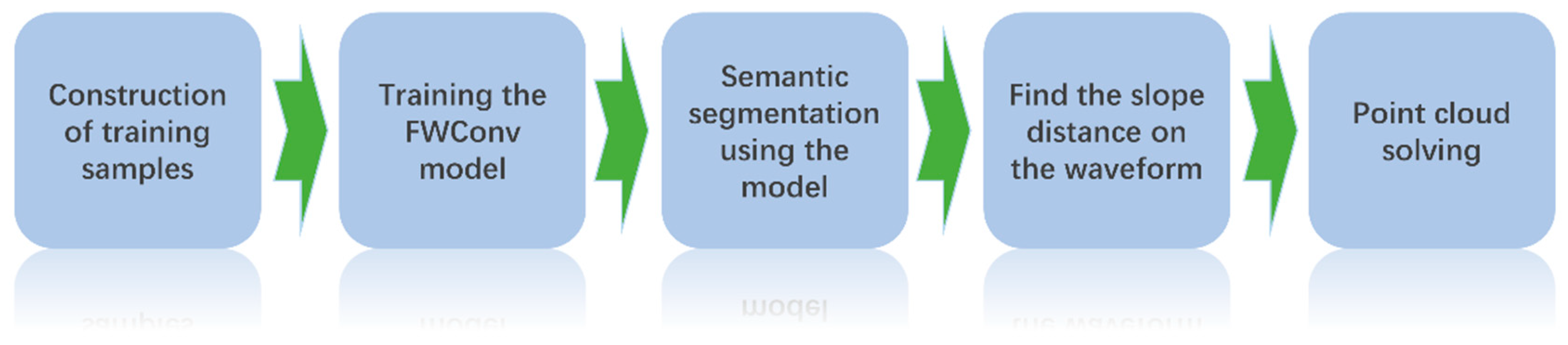
3.1. Workflow
3.2. Construction of Training Samples
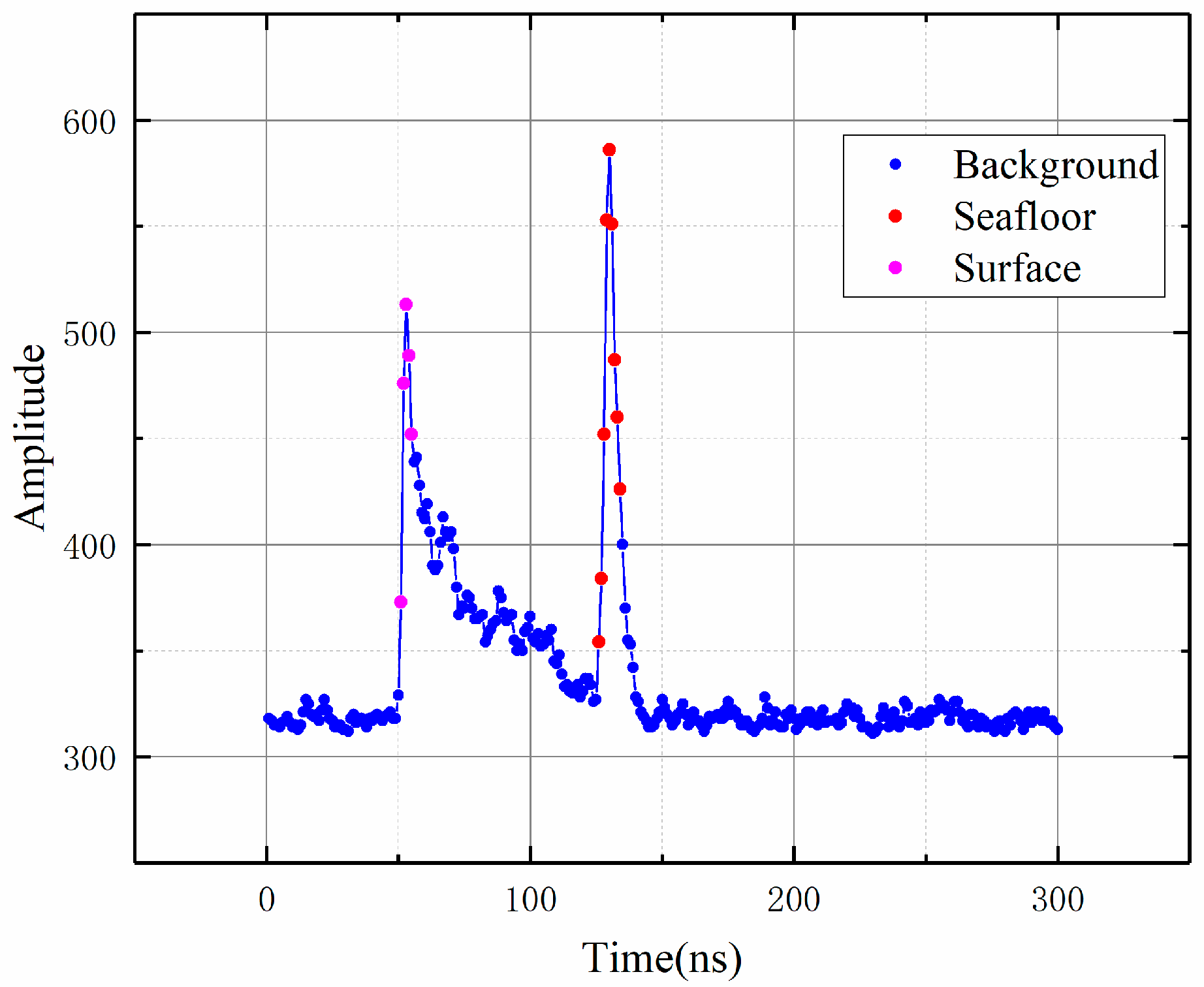
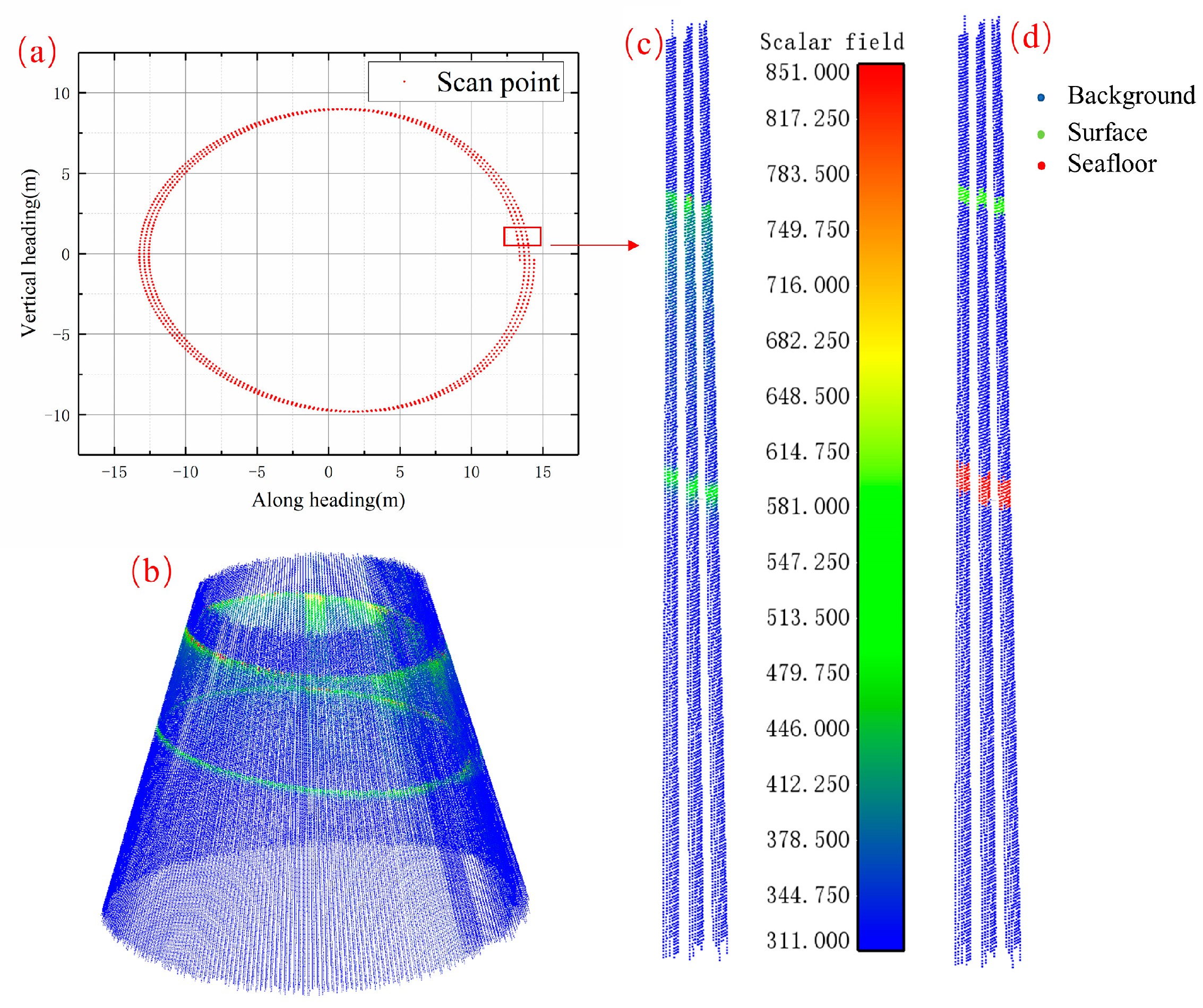
3.2.1. Semantic Labeling of Points
3.2.2. Convert Waveform to Point Cloud
3.2.3. Selection of Spatial Neighborhood Waveforms
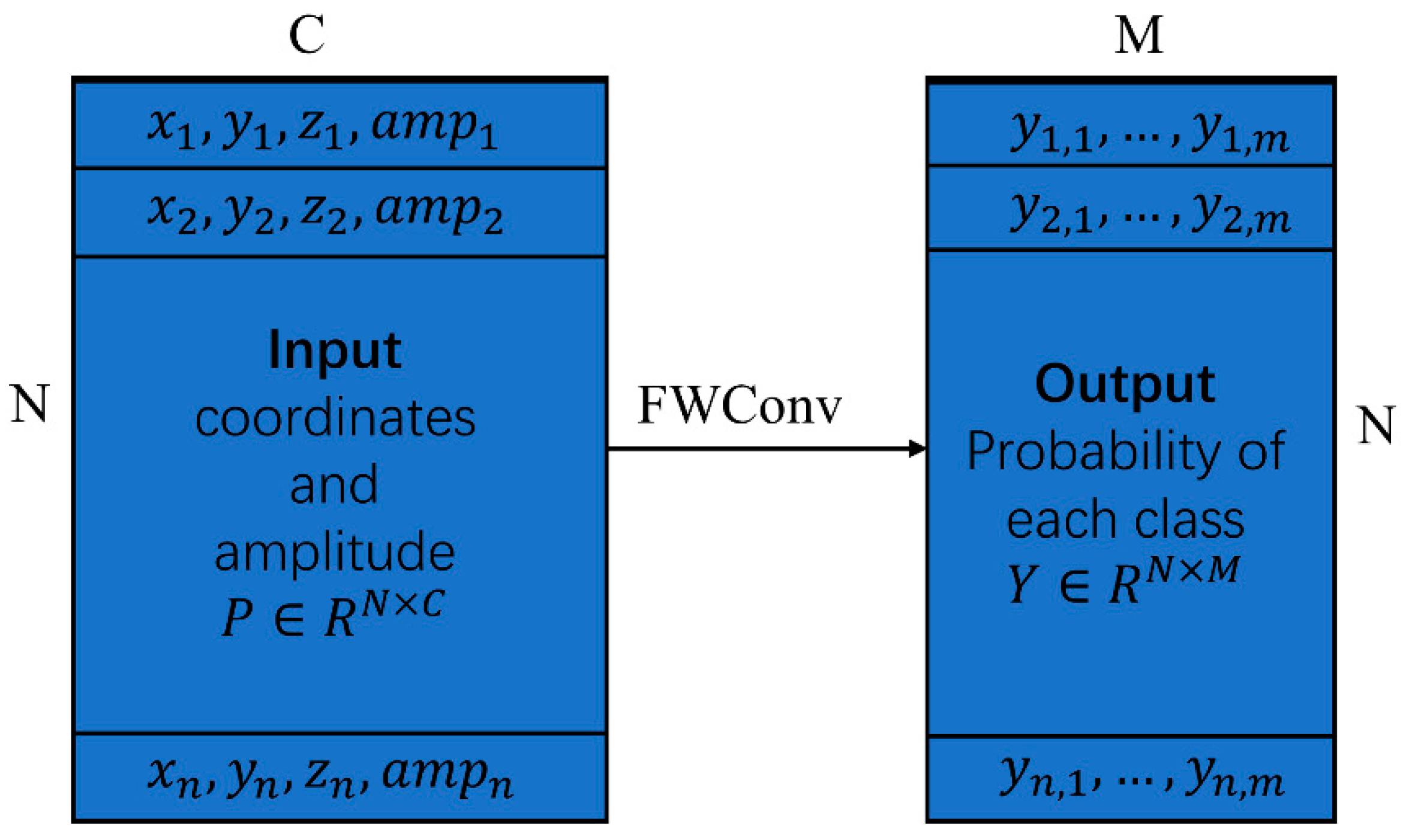
3.3. FWConv
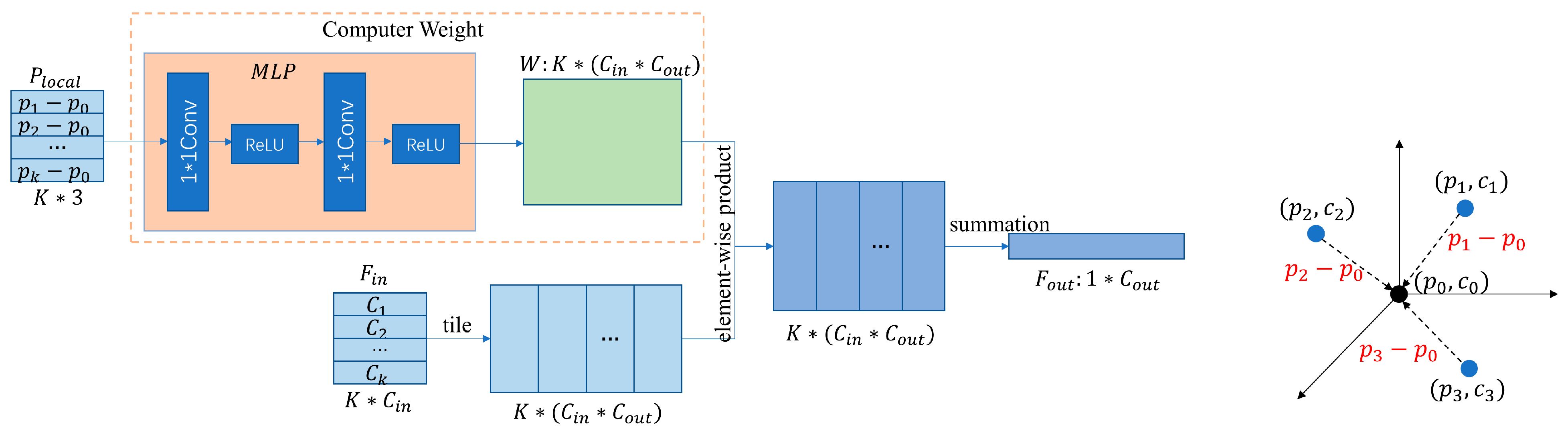
3.3.1. PointConv and Problem Statement
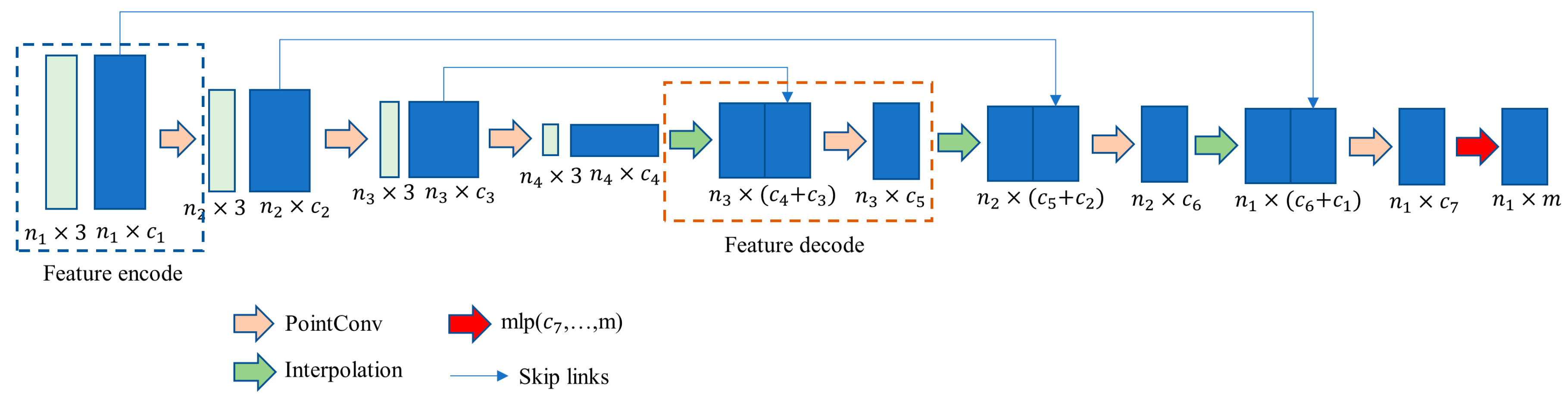
3.3.2. Semantic Segmentation Architecture
3.4. Obtain Slope Distance from the Point Cloud
3.5. Methods for the Evaluation
4. Results
4.1. Accuracy of Sea Surface Points
4.2. Detection Rate and Correctness
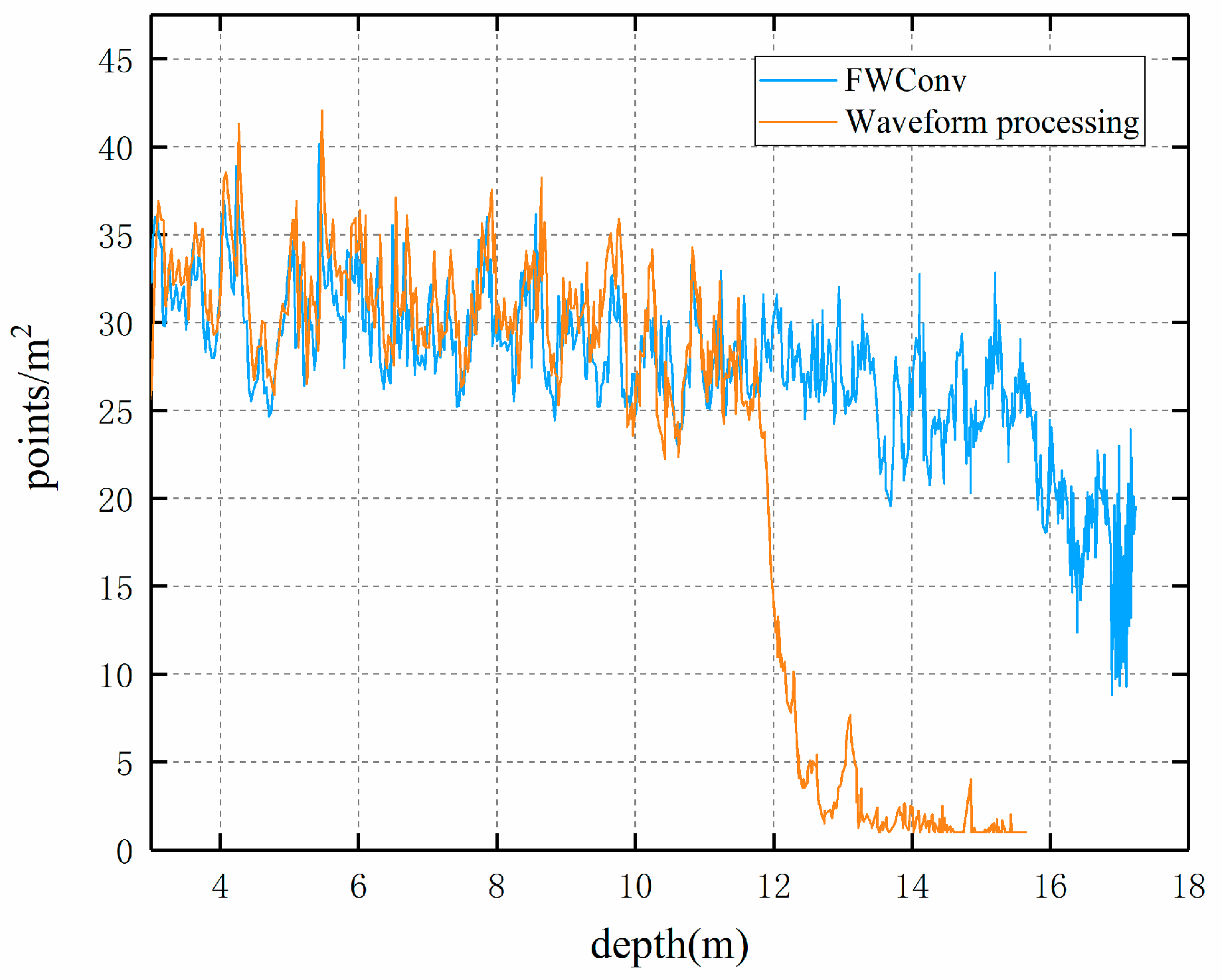
4.3. Maximum Water Depth and Point Density
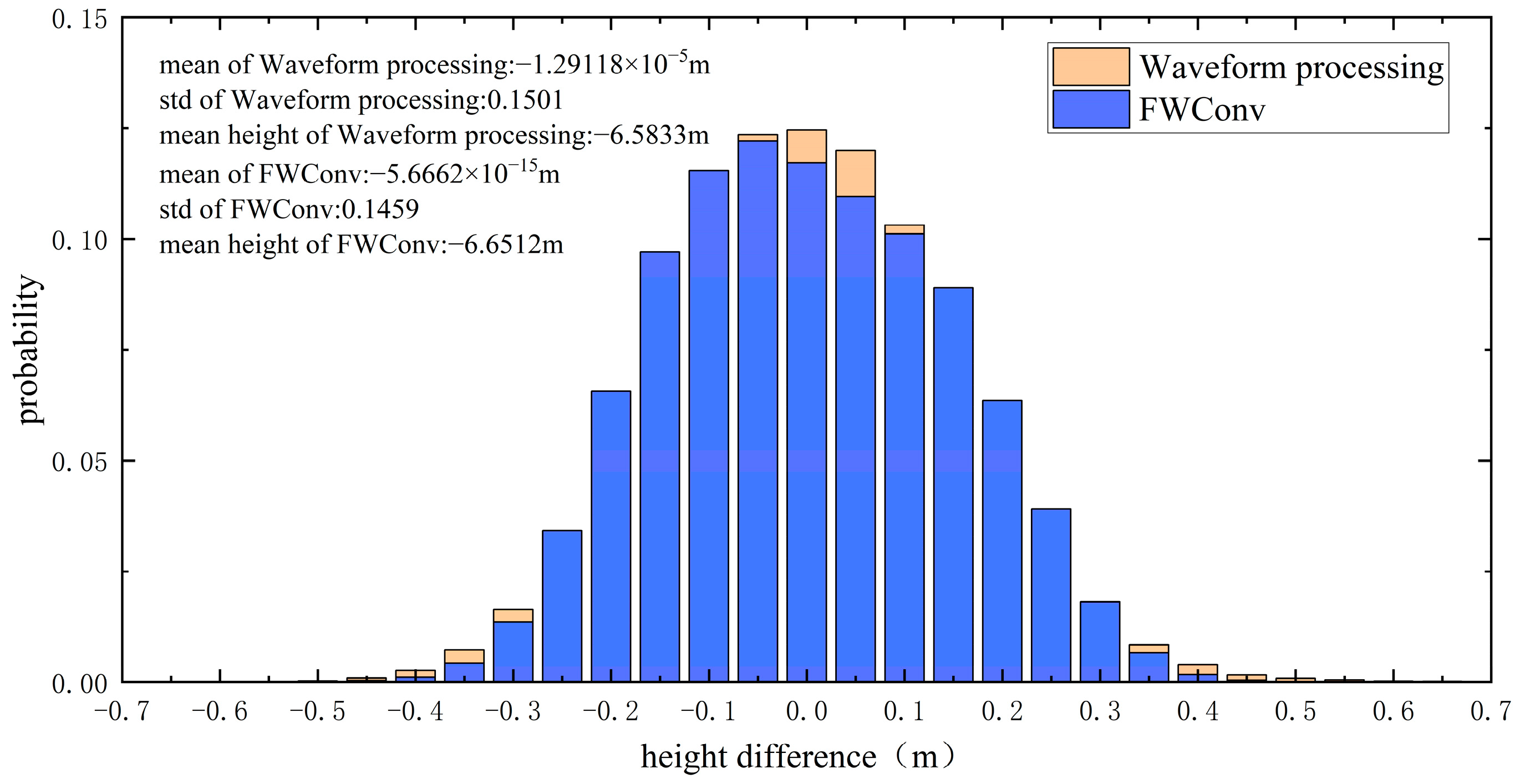
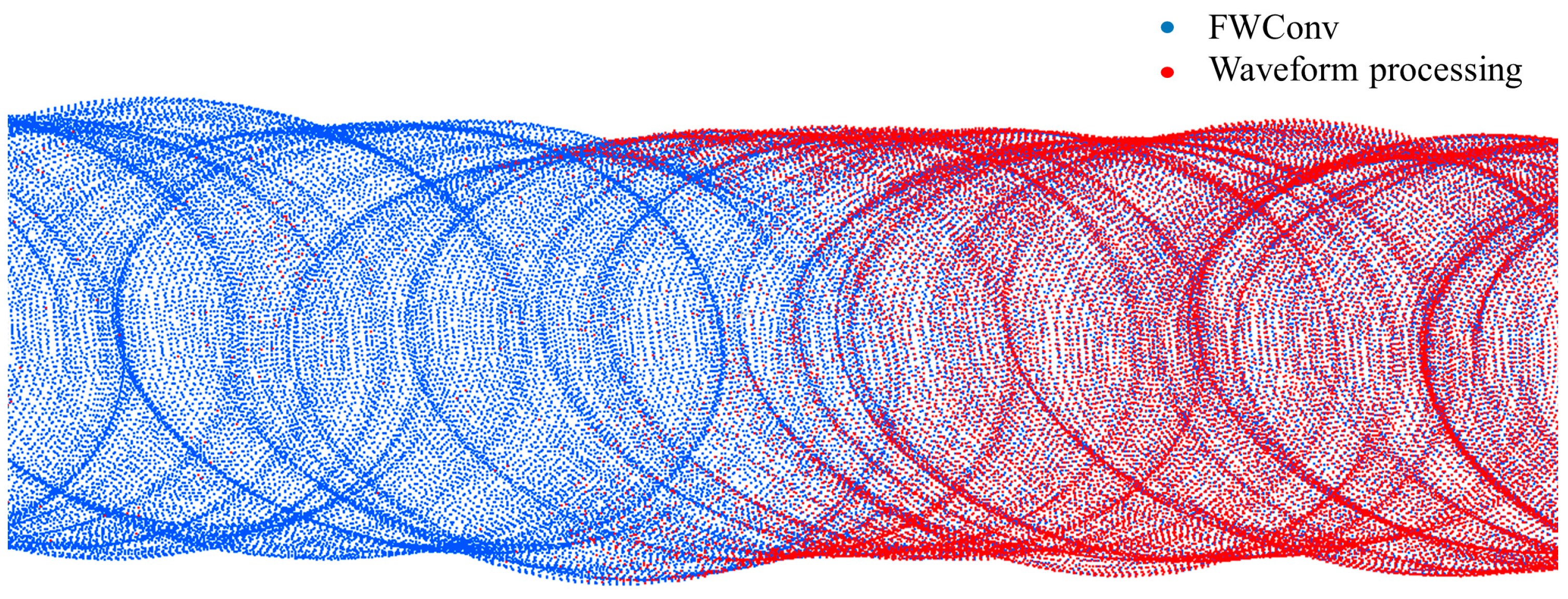
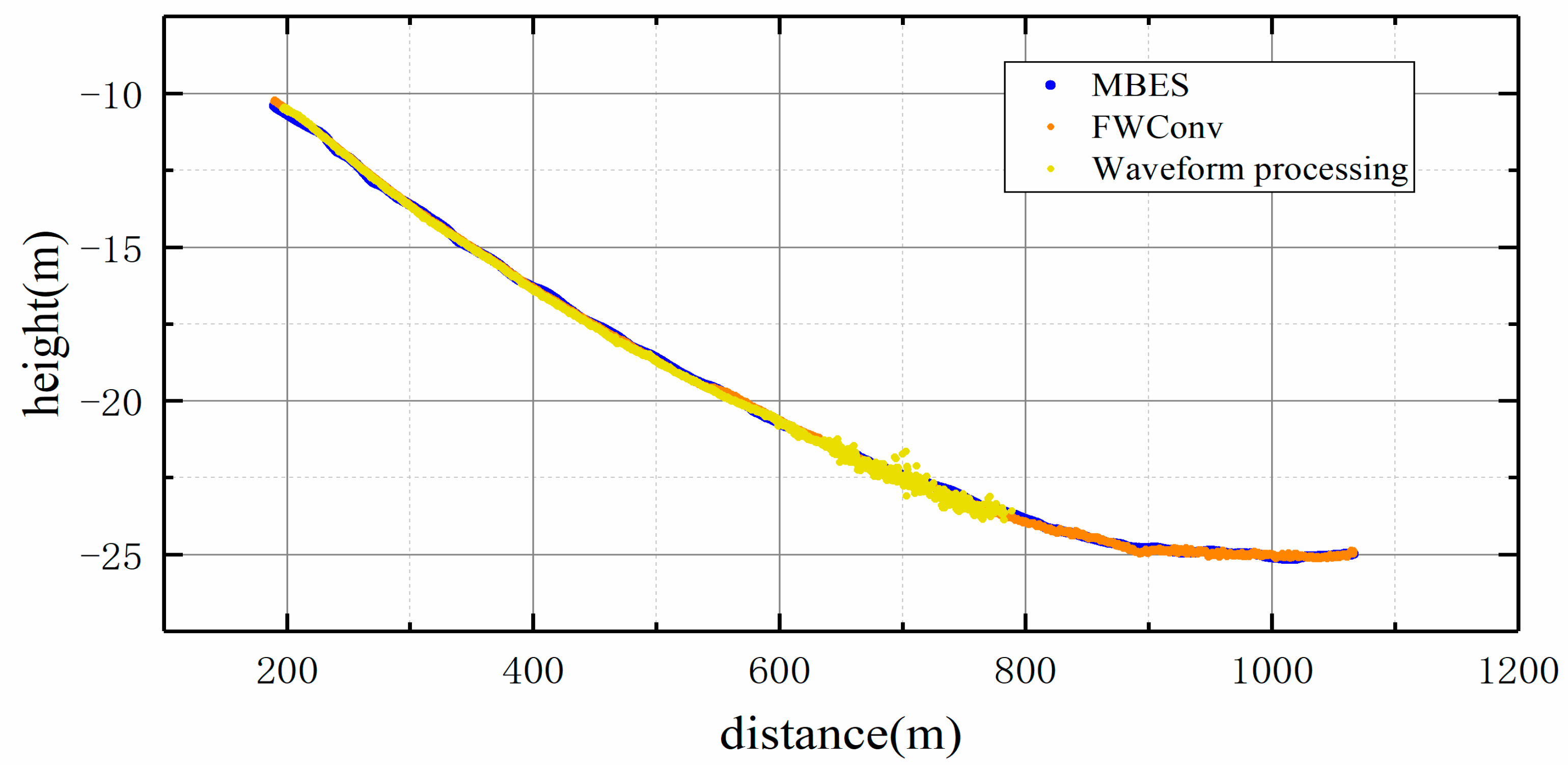
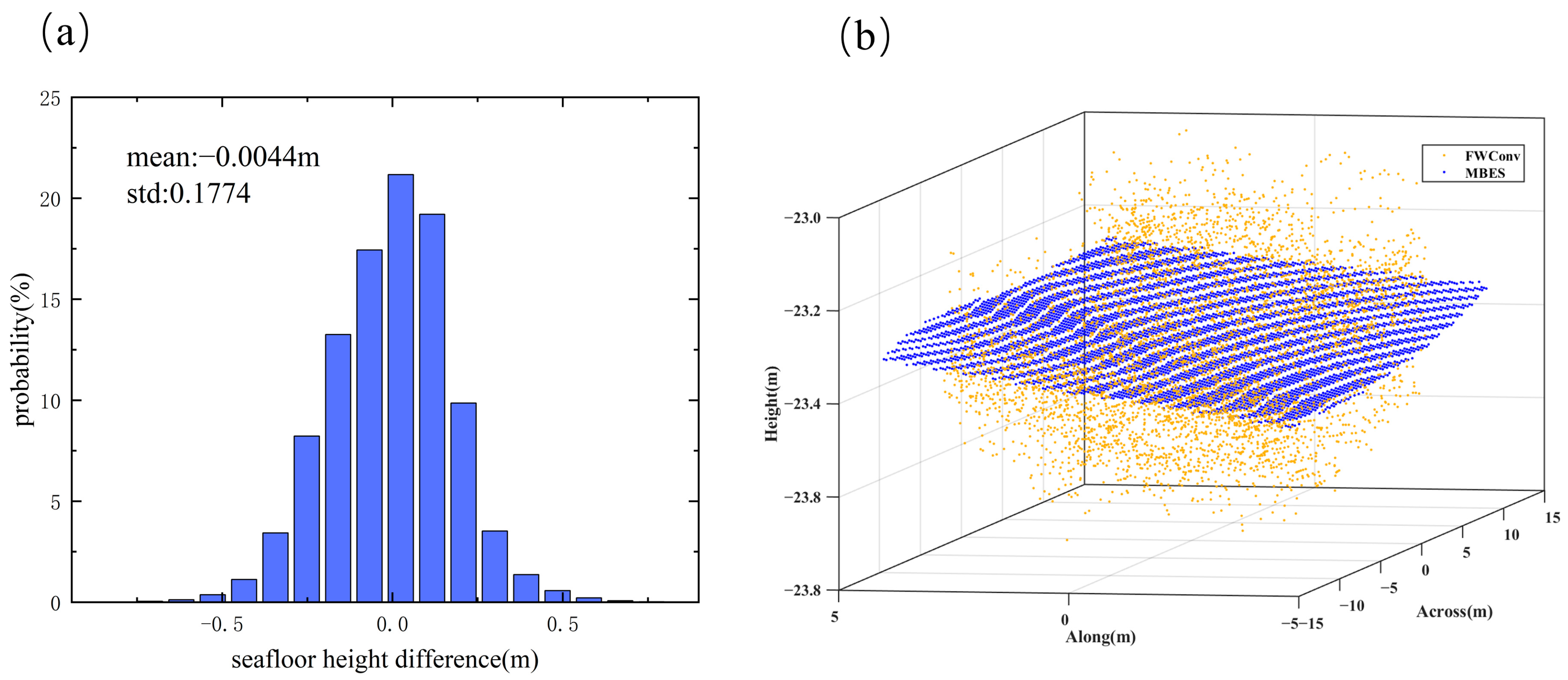
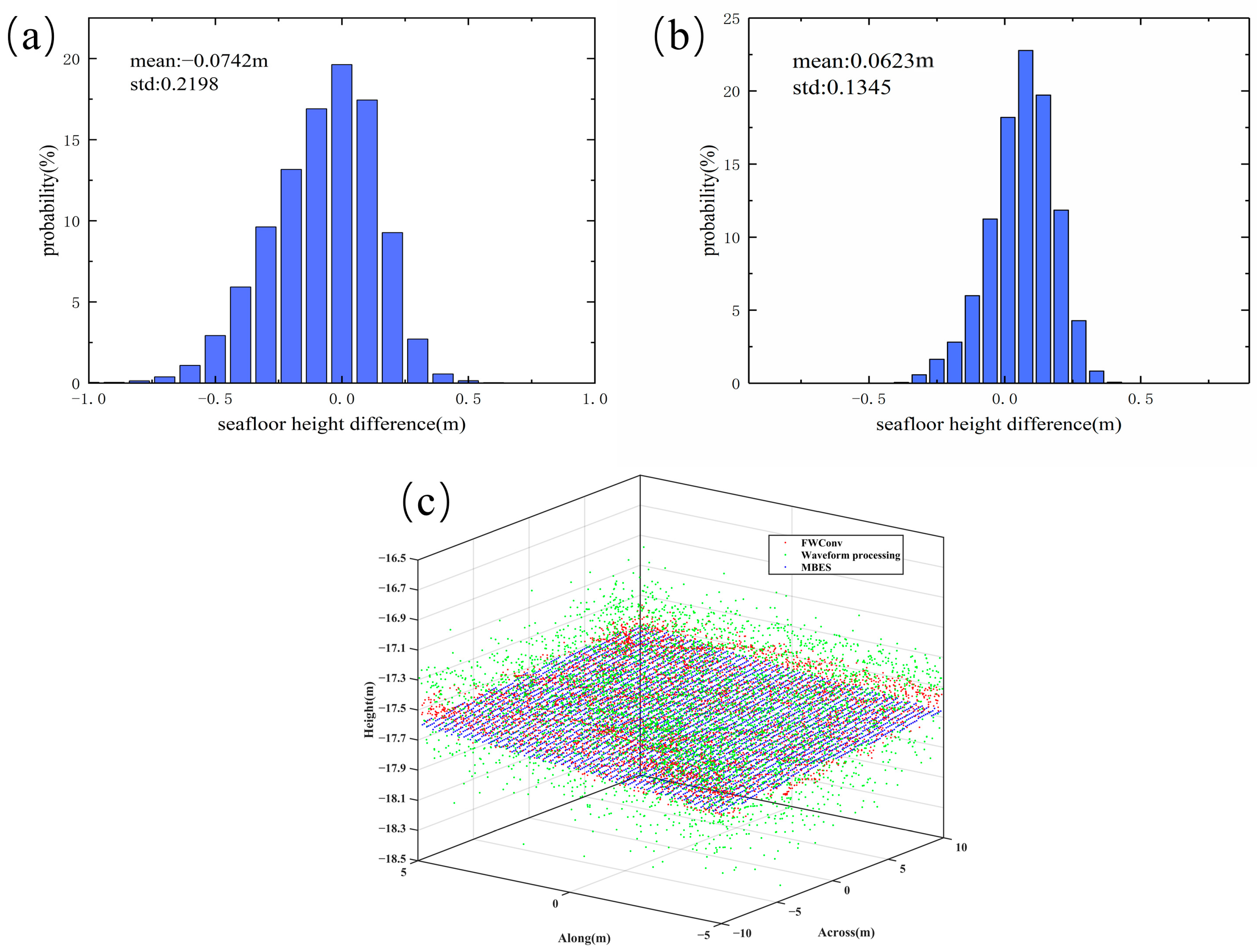
4.4. Accuracy Analysis Using MBES
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saylam, K.; Brown, R.A.; Hupp, J.R. Assessment of depth and turbidity with airborne Lidar bathymetry and multiband satellite imagery in shallow water bodies of the Alaskan North Slope. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 191–200. [Google Scholar] [CrossRef]
- Wang, C.S.; Li, Q.Q.; Liu, Y.X.; Wu, G.F.; Liu, P.; Ding, X.L. A comparison of waveform processing algorithms for single-wavelength LiDAR bathymetry. ISPRS J. Photogramm. Remote Sens. 2015, 101, 22–35. [Google Scholar] [CrossRef]
- Wu, J.Y.; van Aardt, J.A.N.; Asner, G.P. A Comparison of Signal Deconvolution Algorithms Based on Small-Footprint LiDAR Waveform Simulation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2402–2414. [Google Scholar] [CrossRef]
- Wagner, W.; Roncat, A.; Melzer, T.; Ullrich, A. Waveform analysis techniques in airborne laser scanning. In Proceedings of the ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007. [Google Scholar]
- Kogut, T.; Bakula, K. Improvement of Full Waveform Airborne Laser Bathymetry Data Processing based on Waves of Neighborhood Points. Remote Sens. 2019, 11, 1255. [Google Scholar] [CrossRef]
- Yao, W.; Stilla, U. Mutual Enhancement of Weak Laser Pulses for Point Cloud Enrichment Based on Full-Waveform Analysis. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3571–3579. [Google Scholar] [CrossRef]
- Mader, D.; Richter, K.; Westfeld, P.; Maas, H.G. Potential of a Non-linear Full-Waveform Stacking Technique in Airborne LiDAR Bathymetry. Pfg-J. Photogramm. Remote Sens. Geoinf. Sci. 2021, 89, 139. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Yu, X.M.; Hu, B.; Chen, R. A Multi-Source Convolutional Neural Network for Lidar Bathymetry Data Classification. Mar. Geod. 2022, 45, 232–250. [Google Scholar] [CrossRef]
- Kogut, T.; Slowik, A. Classification of Airborne Laser Bathymetry Data Using Artificial Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1959–1966. [Google Scholar] [CrossRef]
- Roshandel, S.; Liu, W.Q.; Wang, C.; Li, J. Semantic Segmentation of Coastal Zone on Airborne Lidar Bathymetry Point Clouds. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, D.D.; Xing, S.; He, Y.; Yu, J.Y.; Xu, Q.; Li, P.C. Evaluation of a New Lightweight UAV-Borne Topo-Bathymetric LiDAR for Shallow Water Bathymetry and Object Detection. Sensors 2022, 22, 1379. [Google Scholar] [CrossRef]
- Allouis, T.; Bailly, J.S.; Pastol, Y.; Le Roux, C. Comparison of LiDAR waveform processing methods for very shallow water bathymetry using Raman, near-infrared and green signals. Earth Surf. Process. Landf. 2010, 35, 640–650. [Google Scholar] [CrossRef]
- Abdallah, H.; Bailly, J.S.; Baghdadi, N.N.; Saint-Geours, N.; Fabre, F. Potential of Space-Borne LiDAR Sensors for Global Bathymetry in Coastal and Inland Waters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 202–216. [Google Scholar] [CrossRef]
- Xing, S.; Wang, D.D.; Xu, Q.; Lin, Y.Z.; Li, P.C.; Jiao, L.; Zhang, X.L.; Liu, C.B. A Depth-Adaptive Waveform Decomposition Method for Airborne LiDAR Bathymetry. Sensors 2019, 19, 5065. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.L.; Liang, G.; Liang, Y.; Zhao, J.H.; Zhou, F.N. Background noise reduction for airborne bathymetric full waveforms by creating trend models using Optech CZMIL in the Yellow Sea of China. Appl. Opt. 2020, 59, 11019–11026. [Google Scholar] [CrossRef] [PubMed]
- Nie, S.; Wang, C.; Li, G.C.; Pan, F.F.; Xi, X.H.; Luo, S.Z. Signal-to-noise ratio-based quality assessment method for ICESat/GLAS waveform data. Opt. Eng. 2014, 53, 103104. [Google Scholar] [CrossRef]
- Guo, Y.L.; Wang, H.Y.; Hu, Q.Y.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4338–4364. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet plus plus: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wu, W.X.; Qi, O.G.; Li, F.X.; Soc, I.C. PointConv: Deep Convolutional Networks on 3D Point Clouds. In Proceedings of the 32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 9613–9622. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.M.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef]
- Do, J.D.; Jint, J.Y.; Kim, C.H.; Kim, W.H.; Lee, B.G.; Wie, G.J.; Chang, Y.S. Measurement of Nearshore Seabed Bathymetry using Airborne/Mobile LiDAR and Multibeam Sonar at Hujeong Beach, Korea. J. Coast. Res. 2020, 95, 1067–1071. [Google Scholar] [CrossRef]
- Janowski, L.; Wroblewski, R.; Rucinska, M.; Kubowicz-Grajewska, A.; Tysiac, P. Automatic classification and mapping of the seabed using airborne LiDAR bathymetry. Eng. Geol. 2022, 301, 106615. [Google Scholar] [CrossRef]
- Liu, F.H.; He, Y.; Chen, W.B.; Luo, Y.; Yu, J.Y.; Chen, Y.Q.; Jiao, C.M.; Liu, M.Z. Simulation and Design of Circular Scanning Airborne Geiger Mode Lidar for High-Resolution Topographic Mapping. Sensors 2022, 22, 3656. [Google Scholar] [CrossRef]
- Štular, B.; Lozić, E. Airborne LiDAR data in landscape archaeology. Introd. Non-Archaeol. 2022, 64, 247–260. [Google Scholar]
- Van Den Eeckhaut, M.; Poesen, J.; Verstraeten, G.; Vanacker, V.; Nyssen, J.; Moeyersons, J.; van Beek, L.P.H.; Vandekerckhove, L. Use of LIDAR-derived images for mapping old landslides under forest. Earth Surf. Process. Landf. 2007, 32, 754–769. [Google Scholar] [CrossRef]
- Magruder, L.A.; Neuenschwander, A.L.; Marmillion, S.P. Lidar waveform stacking techniques for faint ground return extraction. J. Appl. Remote Sens. 2010, 4, 043501. [Google Scholar] [CrossRef]



| Parameter | Mapper4000U |
|---|---|
| Laser re-frequency | 4 kHz |
| Pulse energy | 12 uJ@1064 nm 24 uJ@532 nm |
| Laser pulse width | 1.5 ns |
| Weight | 4.4 kg |
| Scan mode | Elliptical scanning |
| Scan rate | 900 rpm |
| Size | 235 mm × 184 mm × 148 mm |
| Parameter | Hydro-Tech MS400U |
|---|---|
| Working Frequency | 400 kHz |
| Depth Resolution | 0.75 cm |
| No. of Beams | 512 |
| Working Modes | Equiangular or Equidistance |
| Vertical Receiving Beam Width | 1° |
| Parallel Transmitting Beam Width | 2° |
| Sounding Range | 0.2–150 m |
| Ours | |||||||
|---|---|---|---|---|---|---|---|
| ASDF | RLD | ASDF | RLD | ASDF | RLD | ||
| Total number of waveforms | 632,807 | 632,807 | 632,807 | 632,807 | 632,807 | 632,807 | 632,807 |
| Detected points | 537,246 | 624,146 | 626,356 | 631,917 | 628,650 | 632,786 | 628,754 |
| Detection rate (%) | 84.90 | 98.63 | 98.98 | 99.86 | 99.34 | 99.99 | 99.36 |
| Correct points | 536,296 | 282,231 | 316,193 | 285,113 | 338,334 | 260,999 | 279,166 |
| Correctness (%) | 99.82 | 45.22 | 50.48 | 45.12 | 53.82 | 41.25 | 44.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; He, Y.; Zhu, X.; Yu, J.; Chen, Y. Faint Echo Extraction from ALB Waveforms Using a Point Cloud Semantic Segmentation Model. Remote Sens. 2023, 15, 2326. https://doi.org/10.3390/rs15092326
Huang Y, He Y, Zhu X, Yu J, Chen Y. Faint Echo Extraction from ALB Waveforms Using a Point Cloud Semantic Segmentation Model. Remote Sensing. 2023; 15(9):2326. https://doi.org/10.3390/rs15092326
Chicago/Turabian StyleHuang, Yifan, Yan He, Xiaolei Zhu, Jiayong Yu, and Yongqiang Chen. 2023. "Faint Echo Extraction from ALB Waveforms Using a Point Cloud Semantic Segmentation Model" Remote Sensing 15, no. 9: 2326. https://doi.org/10.3390/rs15092326
APA StyleHuang, Y., He, Y., Zhu, X., Yu, J., & Chen, Y. (2023). Faint Echo Extraction from ALB Waveforms Using a Point Cloud Semantic Segmentation Model. Remote Sensing, 15(9), 2326. https://doi.org/10.3390/rs15092326





