Can Water-Detection Indices Be Reliable Proxies for Water Discharges in Mid-Sized Braided Rivers Using Coarse-Resolution Landsat Archives?
Abstract
:1. Introduction
2. Materials and Methods
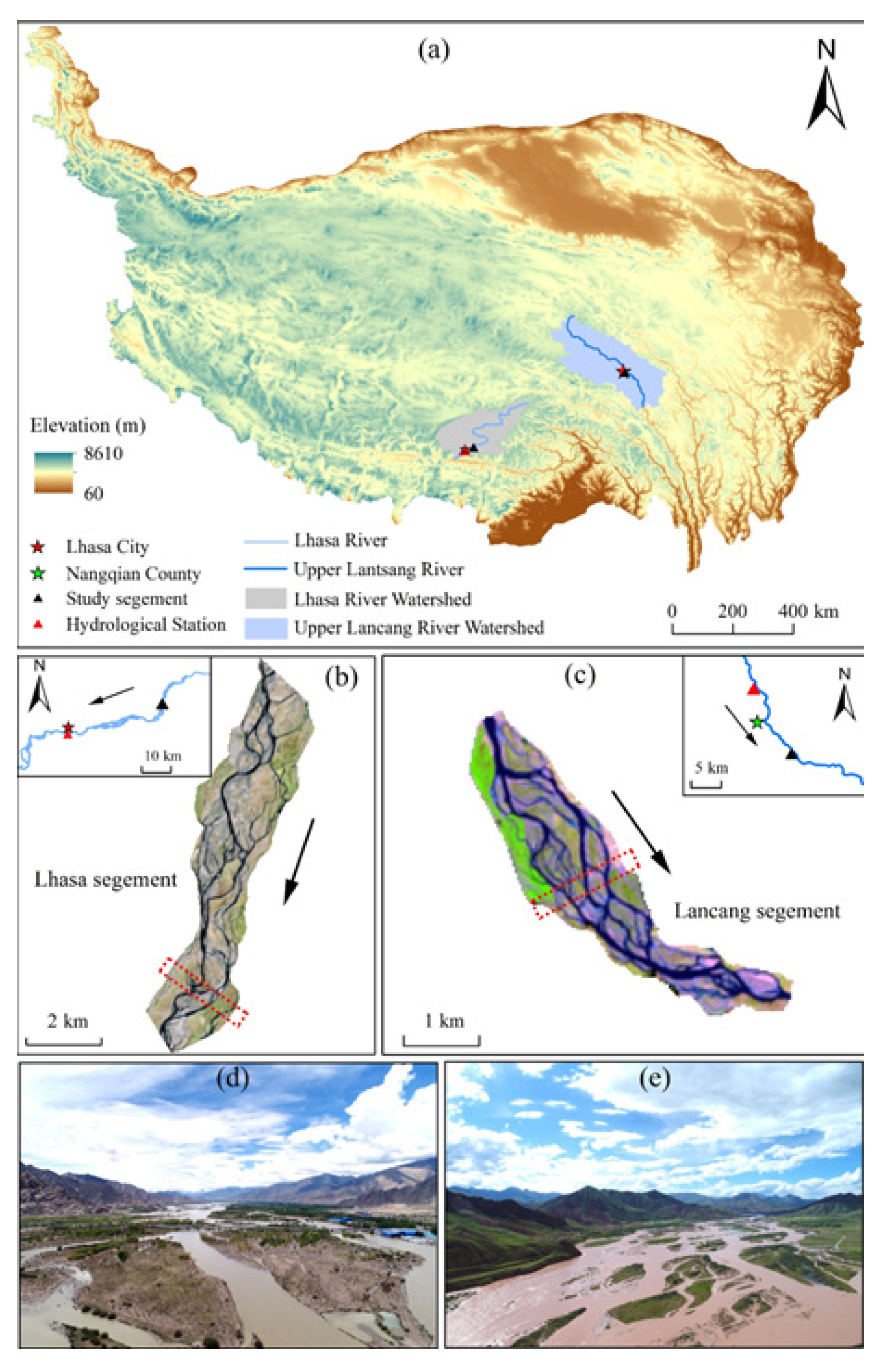
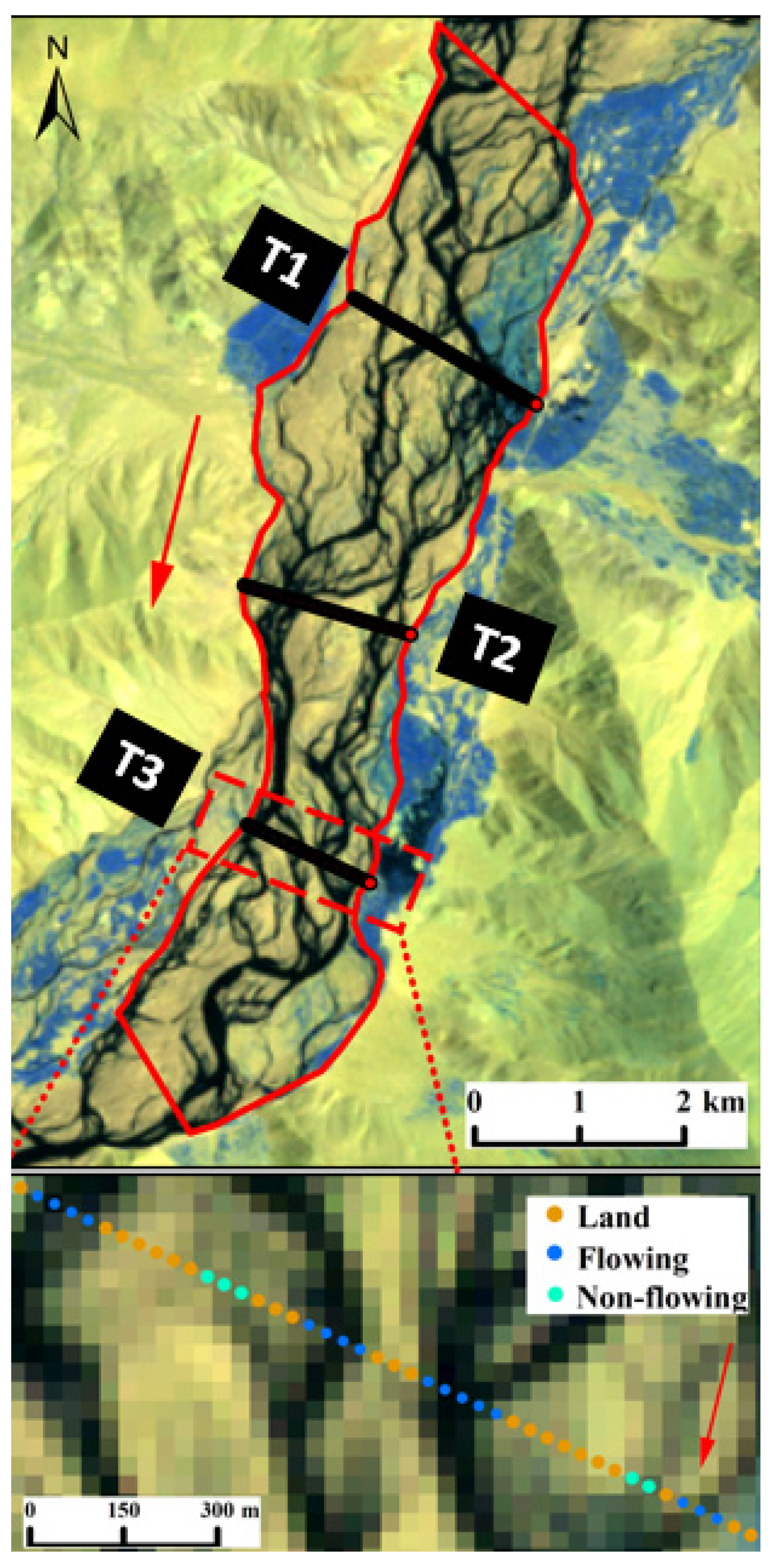
2.1. The Studied Braided Reaches
2.2. Methods
3. Results
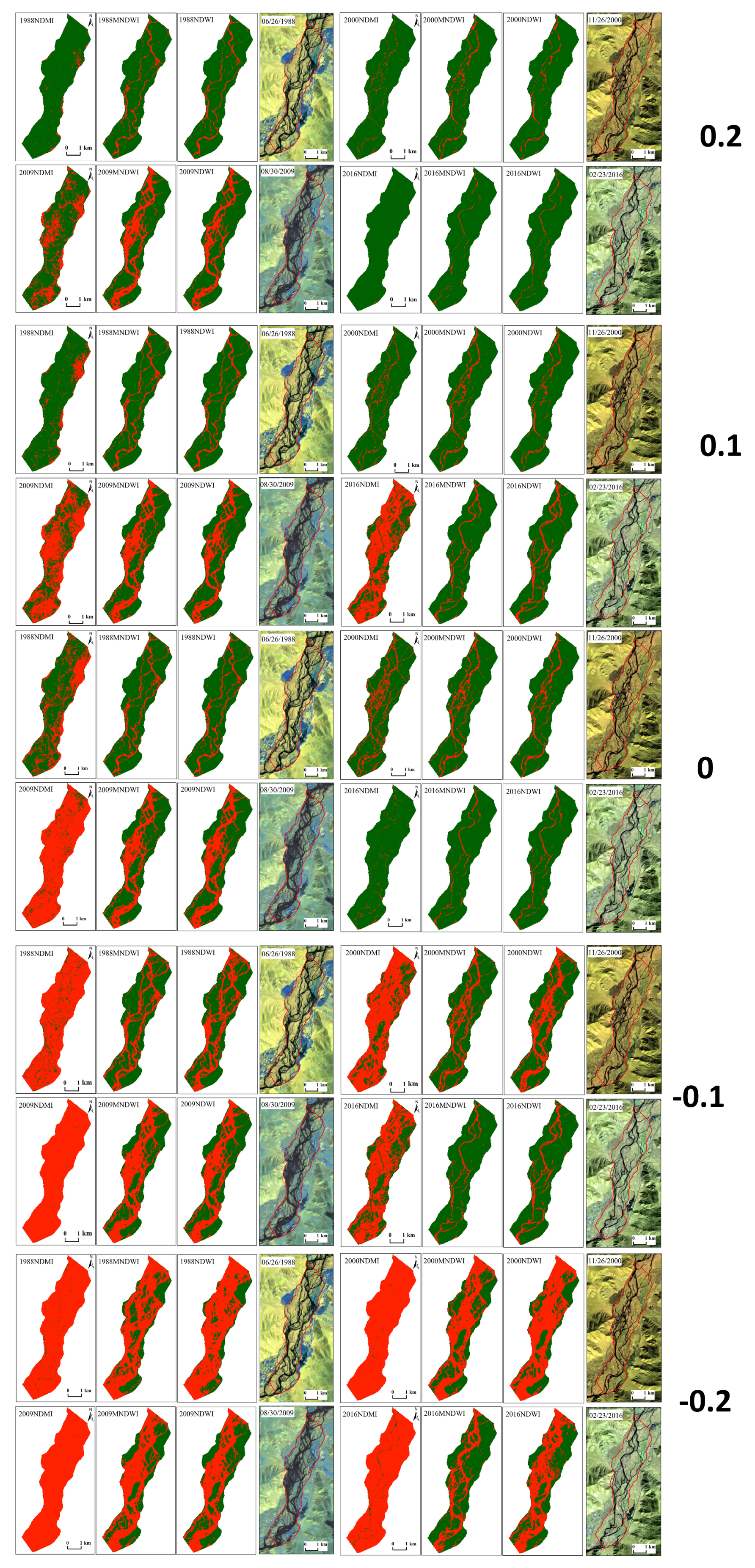
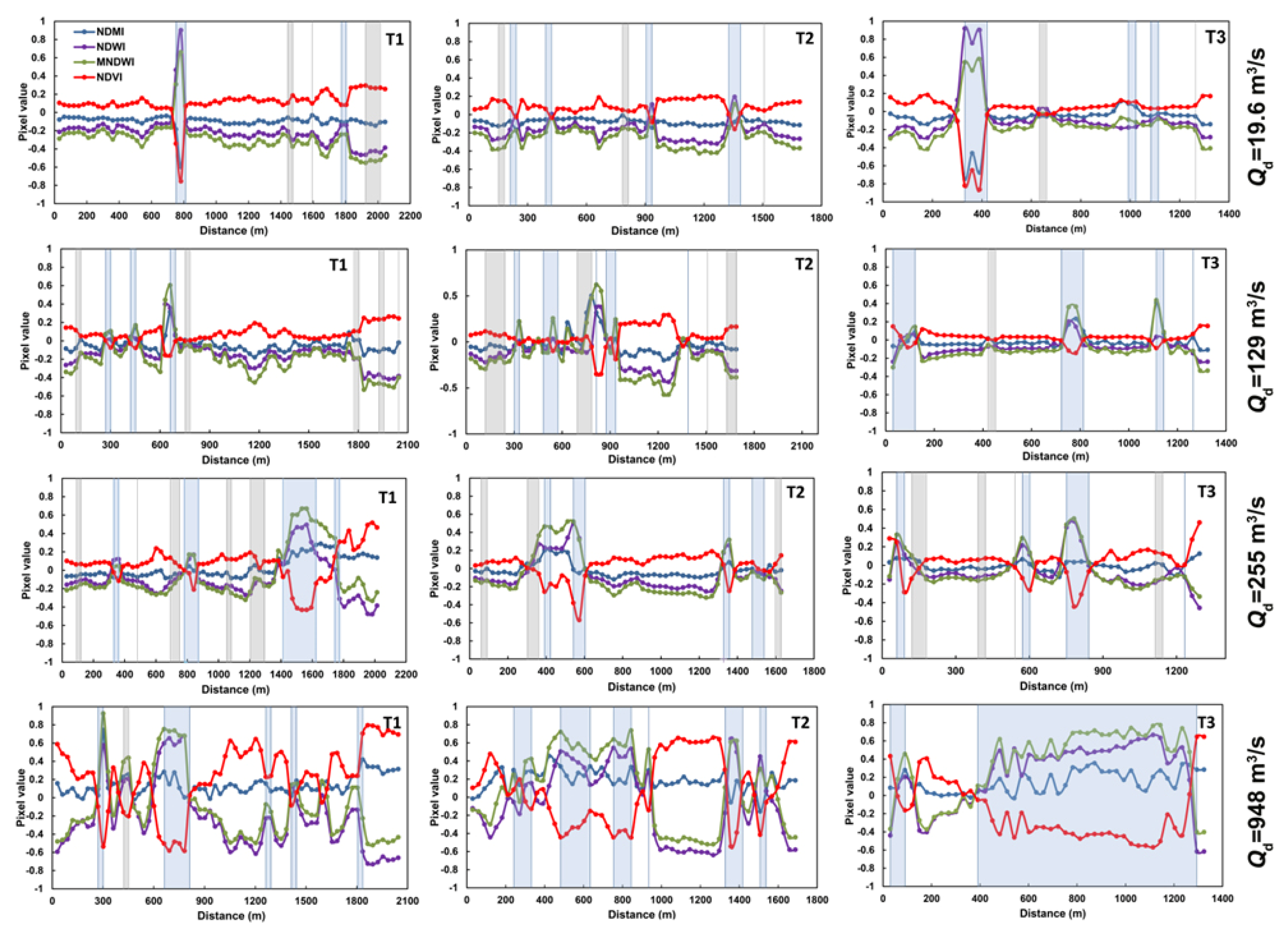
3.1. Characteristics of Water-Detection Indices
3.2. Temporal and Hydrological Characteristics of the Detected River Morphological Metrics
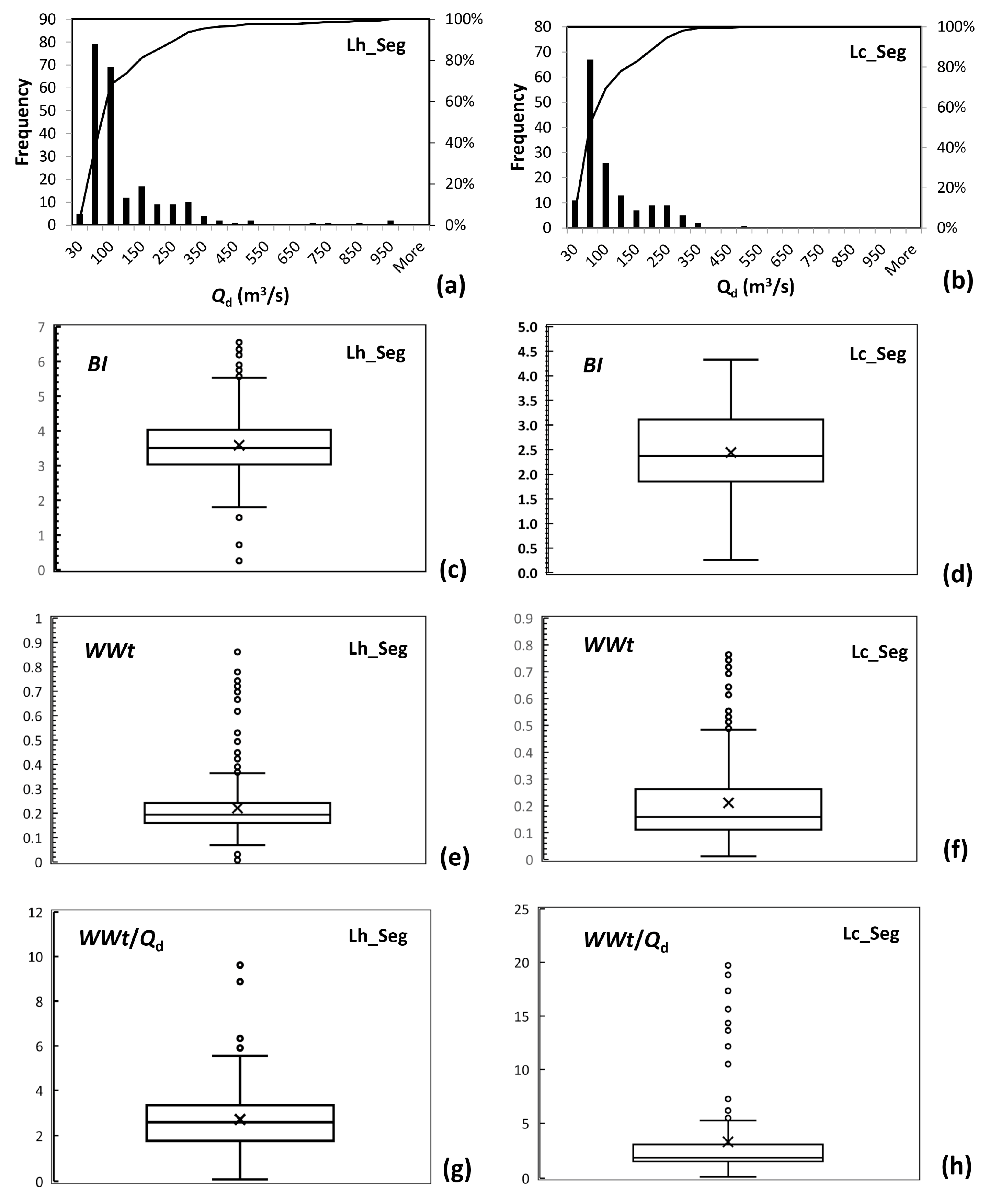
3.2.1. Characteristics of Qd, BI, and WWt in the Two Braided Segments
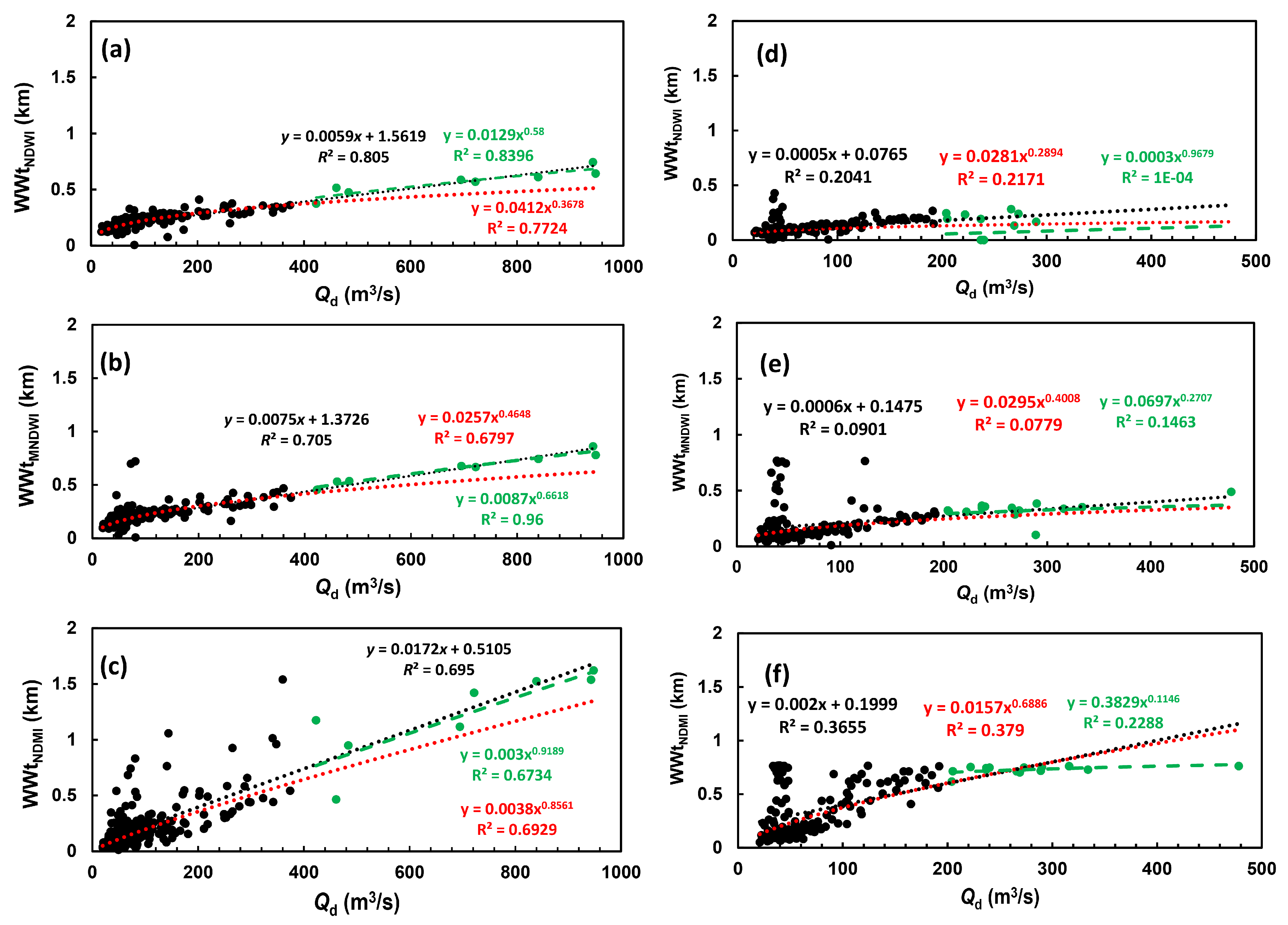
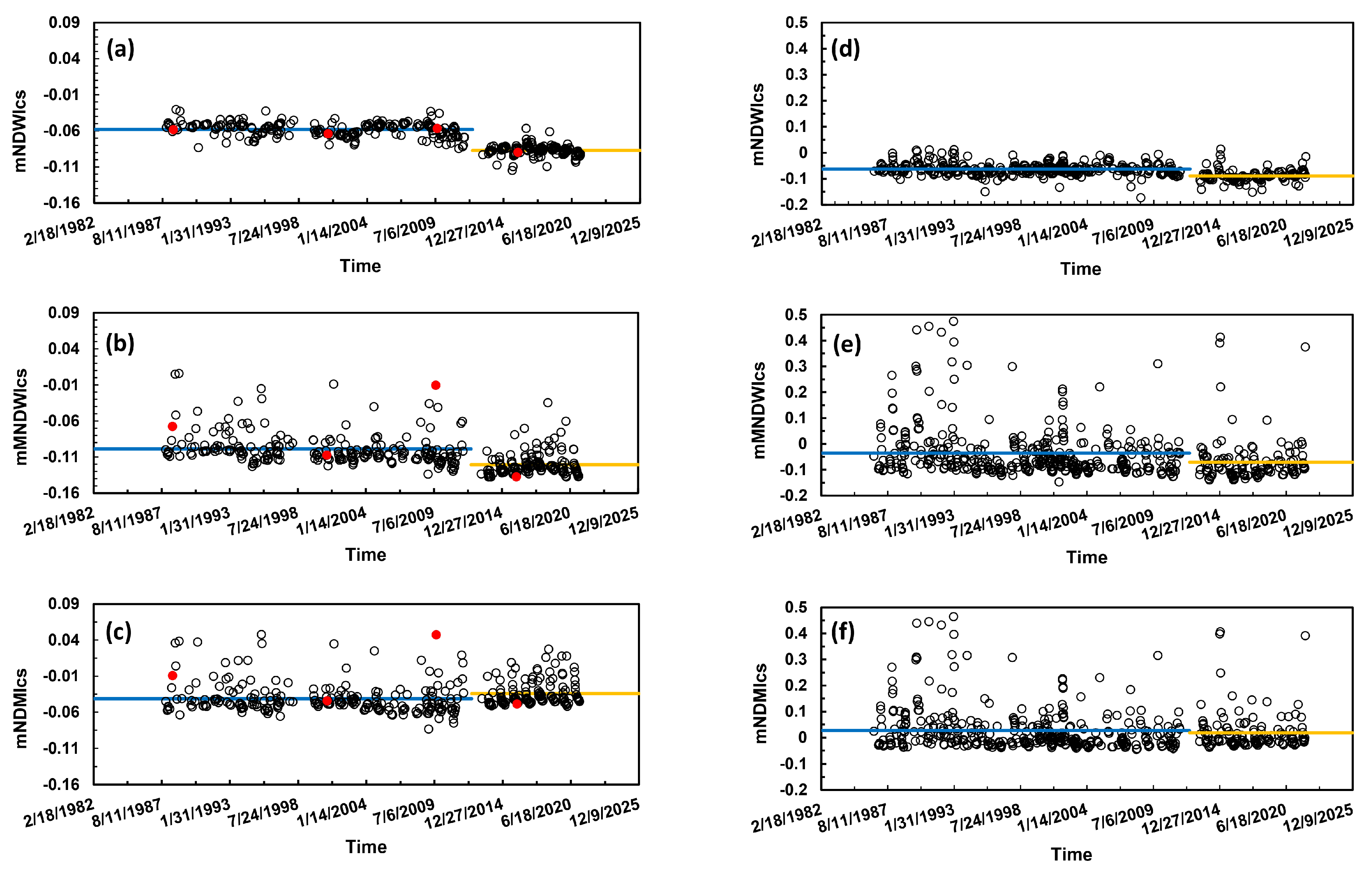
3.2.2. Temporal Trends of WWt Values and Their Relationship with Daily Discharges
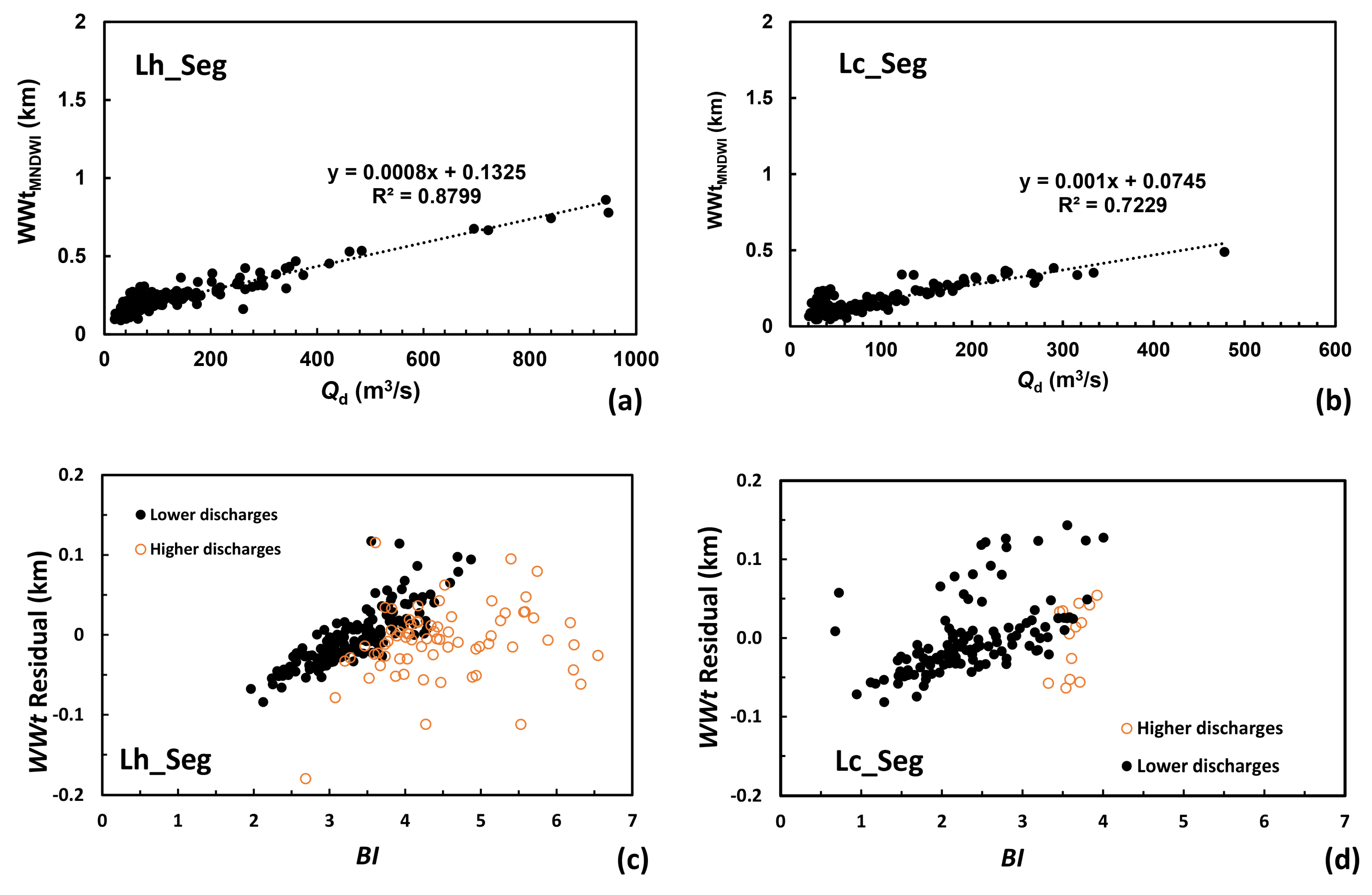
3.2.3. Mean Water-Detection Indices at the Braided Corridor Scale and Their Relationships with Daily Discharges
4. Discussions
4.1. Pitfalls of Using WWt as a Proxy for the Water Discharges
4.2. Mechanisms of Index Performance in Relating to Water Discharges
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Acharya, B.S.; Bhandari, M.; Bandini, F.; Pizarro, A.; Perks, M.; Joshi, D.R.; Wang, S.; Dogwiler, T.; Ray, R.L.; Kharel, G.; et al. Unmanned Aerial Vehicles in Hydrology and Water Management: Applications, Challenges, and Perspectives. Water Resour. Res. 2021, 57, e2021WR029925. [Google Scholar] [CrossRef]
- Acharya, T.D.; Subedi, A.; Lee, D.H. Evaluation of Water Indices for Surface Water Extraction in a Landsat 8 Scene of Nepal. Sensors 2018, 18, 2580. [Google Scholar] [CrossRef] [PubMed]
- Allen, G.H.; Yang, X.; Gardner, J.; Holliman, J.; David, C.H.; Ross, M. Timing of Landsat Overpasses Effectively Captures Flow Conditions of Large Rivers. Remote Sens. 2020, 12, 1510. [Google Scholar] [CrossRef]
- Ashmore, P. Morphology and dynamics of braided rivers. In Treatise on Geomorphology; Shroder, J., Wohl, E., Eds.; Academic Press: San Diego, CA, USA, 2013; pp. 289–312. [Google Scholar]
- Ashmore, P.; Sauks, E. Prediction of discharge from water surface width in a braided river with implications for at-a-station hydraulic geometry. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Ashworth, P.J.; Lewin, J. How do big rivers come to be different? Earth-Sci. Rev. 2012, 114, 84–107. [Google Scholar] [CrossRef]
- Bhangale, U.; More, S.; Shaikh, T.; Patil, S.; More, N. Analysis of Surface Water Resources Using Sentinel-2 Imagery. Procedia Comput. Sci. 2020, 171, 2645–2654. [Google Scholar] [CrossRef]
- Bonnema, M.G.; Sikder, S.; Hossain, F.; Durand, M.; Gleason, C.J.; Bjerklie, D.M. Benchmarking wide swath altime-try-based river discharge estimation algorithms for the Ganges river system. Water Resour. Res. 2016, 52, 2439–2461. [Google Scholar] [CrossRef]
- Boothroyd, R.J.; Nones, M.; Guerrero, M. Deriving Planform Morphology and Vegetation Coverage from Remote Sensing to Support River Management Applications. Front. Environ. Sci. 2021, 9, 657354. [Google Scholar] [CrossRef]
- Boothroyd, R.J.; Williams, R.D.; Hoey, T.B.; Barrett, B.; Prasojo, O.A. Applications of Google Earth Engine in fluvial geomorphology for detecting river channel change. WIREs Water 2020, 8, e21496. [Google Scholar] [CrossRef]
- Brakenridge, G.R.; Nghiem, S.V.; Anderson, E.; Mic, R. Orbital microwave measurement of river discharge and ice status. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Coe, M.T.; Birkett, C.M. Calculation of river discharge and prediction of lake height from satellite radar altimetry: Example for the Lake Chad basin. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Costa, J.E.; Spicer, K.R.; Cheng, R.T.; Haeni, P.F.; Melcher, N.B.; Thurman, E.M.; Plant, W.J.; Keller, W.C. measuring stream discharge by non-contact methods: A Proof-of-Concept Experiment. Geophys. Res. Lett. 2000, 27, 553–556. [Google Scholar] [CrossRef]
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An intercom-parison of remote sensing river discharge estimation algorithms from measurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Egozi, R.; Ashmore, P. Defining and measuring braiding intensity. Earth Surf. Process. Landf. 2008, 33, 2121–2138. [Google Scholar] [CrossRef]
- Elmi, O.; Tourian, M.J.; Bárdossy, A.; Sneeuw, N. Spaceborne River Discharge from a Nonparametric Stochastic Quantile Mapping Function. Water Resour. Res. 2021, 57, e2021WR030277. [Google Scholar] [CrossRef]
- Feng, D.M.; Gleason, C.J.; Yang, X.; Pavelsky, T.M. Comparing Discharge Estimates Made via the BAM Algorithm in High-Order Arctic Rivers Derived Solely From Optical CubeSat, Landsat, and Sentinel-2 Data. Water Resour. Res. 2019, 55, 7753–7771. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Gao, P. Understanding watershed suspended sediment transport. Prog. Phys. Geogr. Earth Environ. 2008, 32, 243–263. [Google Scholar]
- Gao, P.; Li, Z.W.; You, Y.; Zhou, Y.; Piégay, H. Assessing functional characteristics of a braided river in the Qinghai-Tibet Plateau, China. Geomorphology 2022, 403, 108180. [Google Scholar] [CrossRef]
- Gleason, C.J.; Durand, M.T. Remote Sensing of River Discharge: A Review and a Framing for the Discipline. Remote Sens. 2020, 12, 1107. [Google Scholar] [CrossRef]
- Gleason, C.J.; Smith, L.C.; Lee, J. Retrieval of river discharge solely from satellite imagery and at-many-stations hy-draulic geometry: Sensitivity to river form and optimization parameters. Water Resour. Res. 2014, 50, 9604–9619. [Google Scholar] [CrossRef]
- Gleason, C.J.; Wang, J.D. Theoretical basis for at-many-stations hydraulic geometry. Geophys. Res. Lett. 2015, 42, 7107–7114. [Google Scholar] [CrossRef]
- Hong, L.B.; Davies, T.R.H. A study of stream braiding. Geol. Soc. Am. Bull. 90 1979, 90 Pt II, 1839–1859. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Zhang, S.; Wu, J. Detecting, Extracting, and Monitoring Surface Water from Space Using Optical Sensors: A Review. Rev. Geophys. 2018, 56, 333–360. [Google Scholar] [CrossRef]
- Ishitsuka, Y.; Gleason, C.J.; Hagemann, M.W.; Beighley, E.; Allen, G.H.; Feng, D.M.; Lin, P.R.; Pan, M.; Andreadis, K.; Pavelsky, T.M. Combining Optical Remote Sensing, McFLI Discharge Estimation, Global Hydrologic Modeling, and Data Assim-ilation to Improve Daily Discharge Estimates Across an Entire Large Watershed. Water Resour. Res. 2021, 57, e2020WR027794. [Google Scholar] [CrossRef]
- Jackson, T.J.; Chen, D.; Cosh, M.; Li, F.; Anderson, M.; Walthall, C.; Doriaswamy, P.; Hunt, E. Vegetation water content mapping using Landsat data derived normalized difference water index for corn and soybeans. Remote Sens. Environ. 2004, 92, 475–482. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, U. Object-based water body extraction model using Sentinel-2 satellite imagery. Eur. J. Remote Sens. 2017, 50, 137–143. [Google Scholar] [CrossRef]
- Knighton, D. Fluvial Forms & Processes: A New Perspective; Arnold: London, UK, 1998. [Google Scholar]
- LeFavour, G.; Alsdorf, D. Water slope and discharge in the Amazon River estimated using the shuttle radar topography mission digital elevation model. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Leopoid, L.B. Some relations among velocity, depth and slope in braided rivers. EOS Trans. AGU 1985, 66, 912. [Google Scholar]
- Marcus, W.A.; Fonstad, M.A.; Legleiter, C.J. Management applications of optical remote sensing in the active river channel. In Fluvial Remote Sensing for Science and Management; Carbonneau, P.E., Piégay, H., Eds.; Wiley: Chichester, UK, 2012; pp. 19–41. [Google Scholar]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Morel, M.; Tamisier, V.; Pella, H.; Booker, D.J.; Navratil, O.; Piégay, H.; Gob, F.; Lamouroux, N. Revisiting the drivers of at-a-station hydraulic geometry in stream reaches. Geomorphology 2019, 328, 44–56. [Google Scholar] [CrossRef]
- Mosley, P.M. Response of braided rivers to changing discharge. J. Hydrol. N. Z. 1983, 22, 18–67. [Google Scholar]
- Mutanga, O.; Kumar, L. Google Earth Engine Applications. Remote Sens. 2019, 11, 591. [Google Scholar] [CrossRef]
- Freden, S.C.; Mercanti, E.P.; Becker, M.A. (Eds.) NASA Third Earth Resources Technology Satellite-1 Symposium—Volume 1: Technical Presentations; Scientific and Technical Information Office, National Aeronautics and Space Administration: Washington, DC, USA, 1974; pp. 309–317.
- Ogilvie, A.; Belaud, G.; Delenne, C.; Bailly, J.-S.; Bader, J.-C.; Oleksiak, A.; Ferry, L.; Martin, D. Decadal monitoring of the Niger Inner Delta flood dynamics using MODIS optical data. J. Hydrol. 2015, 523, 368–383. [Google Scholar] [CrossRef]
- Omute, P.; Corner, R.; Awange, J.L. The use of NDVI and its Derivatives for Monitoring Lake Victoria’s Water Level and Drought Conditions. Water Resour. Manag. 2012, 26, 1591–1613. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Piégay, H.; Alber, A.; Slater, L.; Bourdin, L. Census and typology of braided rivers in the French Alps. Aquat. Sci. 2009, 71, 371–388. [Google Scholar] [CrossRef]
- Rhoads, B.L. River Dynamics: Geomorphology to Support Management; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Riggs, R.M.; Allen, G.H.; David, C.H.; Lin, P.R.; Pan, M.; Yang, X.; Gleason, C. RODEO: An algorithm and Google Earth Engine application for river discharge retrieval from Landsat. Environ. Model. Softw. 2022, 148, 105254. [Google Scholar] [CrossRef]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water Feature Extraction and Change Detection Using Multitemporal Landsat Imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Smith, L.C.; Isacks, B.L.; Forster, R.R.; Bloom, A.L.; Preuss, I. Estimation of discharge from braided gla-cial rivers using ers-1 synthetic-aperture radar-first results. Water Resour. Res. 1995, 31, 1325–1329. [Google Scholar] [CrossRef]
- Smith, L.C.; Pavelsky, T.M. Estimation of river discharge, propagation speed, and hydraulic geometry from space: Lena River, Siberia. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, X.; Qin, Y.; Dong, J.; Wu, J.; Li, B. Improved maps of surface water bodies, large dams, reservoirs, and lakes in China. Earth Syst. Sci. Data 2022, 14, 3757–3771. [Google Scholar] [CrossRef]
- Wilson, E.H.; Sader, S.A. Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sens. Environ. 2002, 80, 385–396. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, J.; Watanabe, M.; Sun, C. Estimating river discharge from very high-resolution satellite data: A case study in the Yangtze River, China. Hydrol. Process. 2004, 18, 1927–1939. [Google Scholar] [CrossRef]
- Yoon, Y.; Garambois, P.; Paiva, R.C.; Durand, M.; Roux, H.; Beighley, E. Improved error estimates of a discharge algorithm for remotely sensed river measurements: Test cases on Sacramento and Garonne Rivers. Water Resour. Res. 2016, 52, 278–294. [Google Scholar] [CrossRef]
- You, Y.; Li, Z.; Gao, P.; Hu, T. Impacts of dams and land-use changes on hydromorphology of braided channels in the Lhasa River of the Qinghai-Tibet Plateau, China. Int. J. Sediment Res. 2022, 37, 214–228. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, P.; Belletti, B.; Piégay, H.; You, Y.; Li, Z. Can Water-Detection Indices Be Reliable Proxies for Water Discharges in Mid-Sized Braided Rivers Using Coarse-Resolution Landsat Archives? Remote Sens. 2024, 16, 137. https://doi.org/10.3390/rs16010137
Gao P, Belletti B, Piégay H, You Y, Li Z. Can Water-Detection Indices Be Reliable Proxies for Water Discharges in Mid-Sized Braided Rivers Using Coarse-Resolution Landsat Archives? Remote Sensing. 2024; 16(1):137. https://doi.org/10.3390/rs16010137
Chicago/Turabian StyleGao, Peng, Barbara Belletti, Hervé Piégay, Yuchi You, and Zhiwei Li. 2024. "Can Water-Detection Indices Be Reliable Proxies for Water Discharges in Mid-Sized Braided Rivers Using Coarse-Resolution Landsat Archives?" Remote Sensing 16, no. 1: 137. https://doi.org/10.3390/rs16010137
APA StyleGao, P., Belletti, B., Piégay, H., You, Y., & Li, Z. (2024). Can Water-Detection Indices Be Reliable Proxies for Water Discharges in Mid-Sized Braided Rivers Using Coarse-Resolution Landsat Archives? Remote Sensing, 16(1), 137. https://doi.org/10.3390/rs16010137








