A General Deep Learning Point–Surface Fusion Framework for RGB Image Super-Resolution
Abstract
:1. Introduction
- (1)
- The proposed method has both the non-linear feature extraction ability of deep learning and the interpretability and clarity of the physical model;
- (2)
- With the help of spectral data, the proposed method can save time and effort in obtaining HRHS images that are not limited to the visible light range;
- (3)
- Compared with pure deep learning-based methods, GRSS-Net requires fewer training parameters and does not need image registration;
- (4)
- More importantly, the proposed method provides a point–surface fusion framework, which can solve the problem of difficulty in obtaining hyperspectral images effectively.
2. Methodology
2.1. Related Work
2.1.1. Compressed Sensing
2.1.2. Gradient Descent
2.1.3. Iterative Soft-Threshold Shrinkage
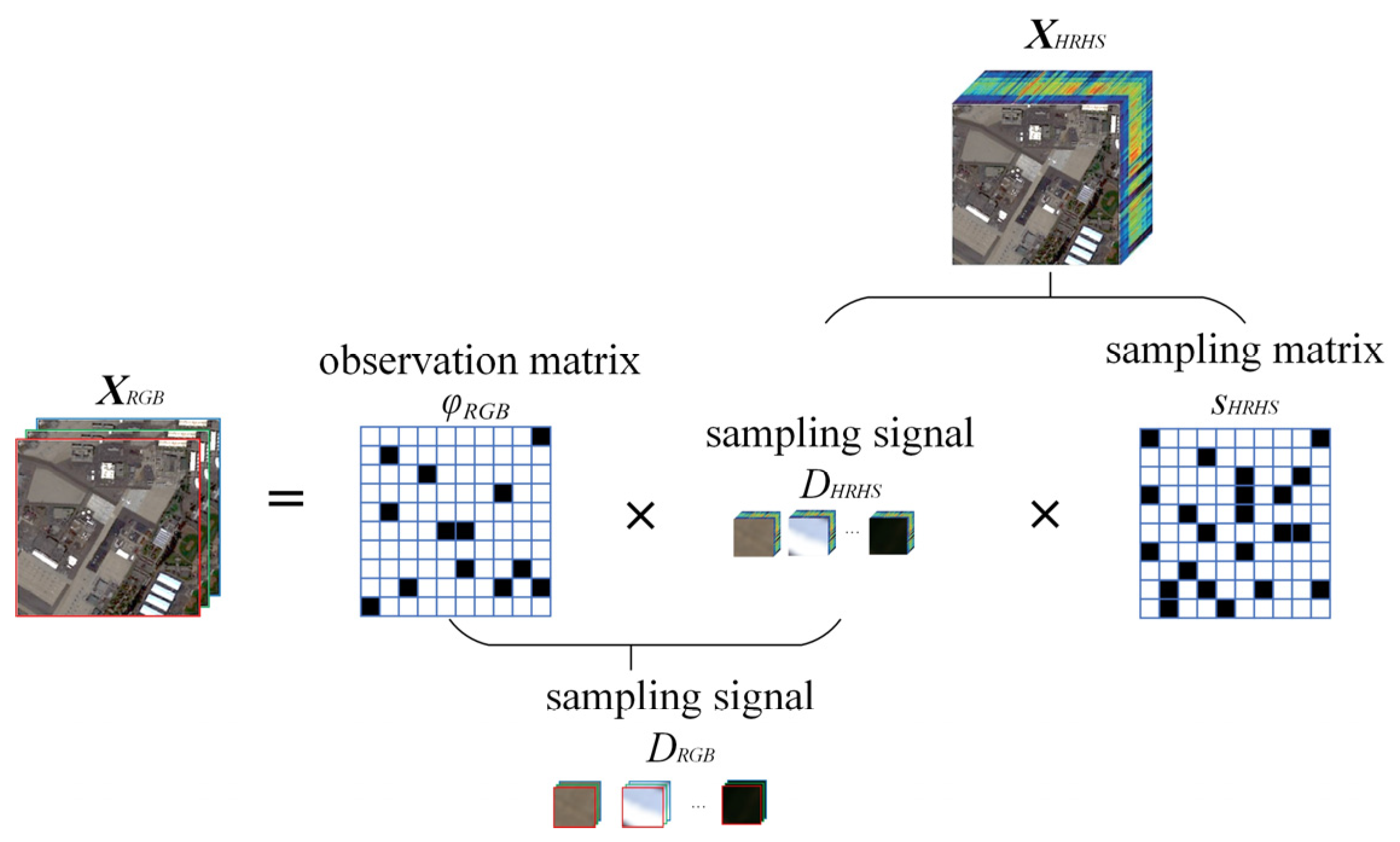
2.2. Observation Model
2.3. Fundamental Formula Derivation of GRSS-Net
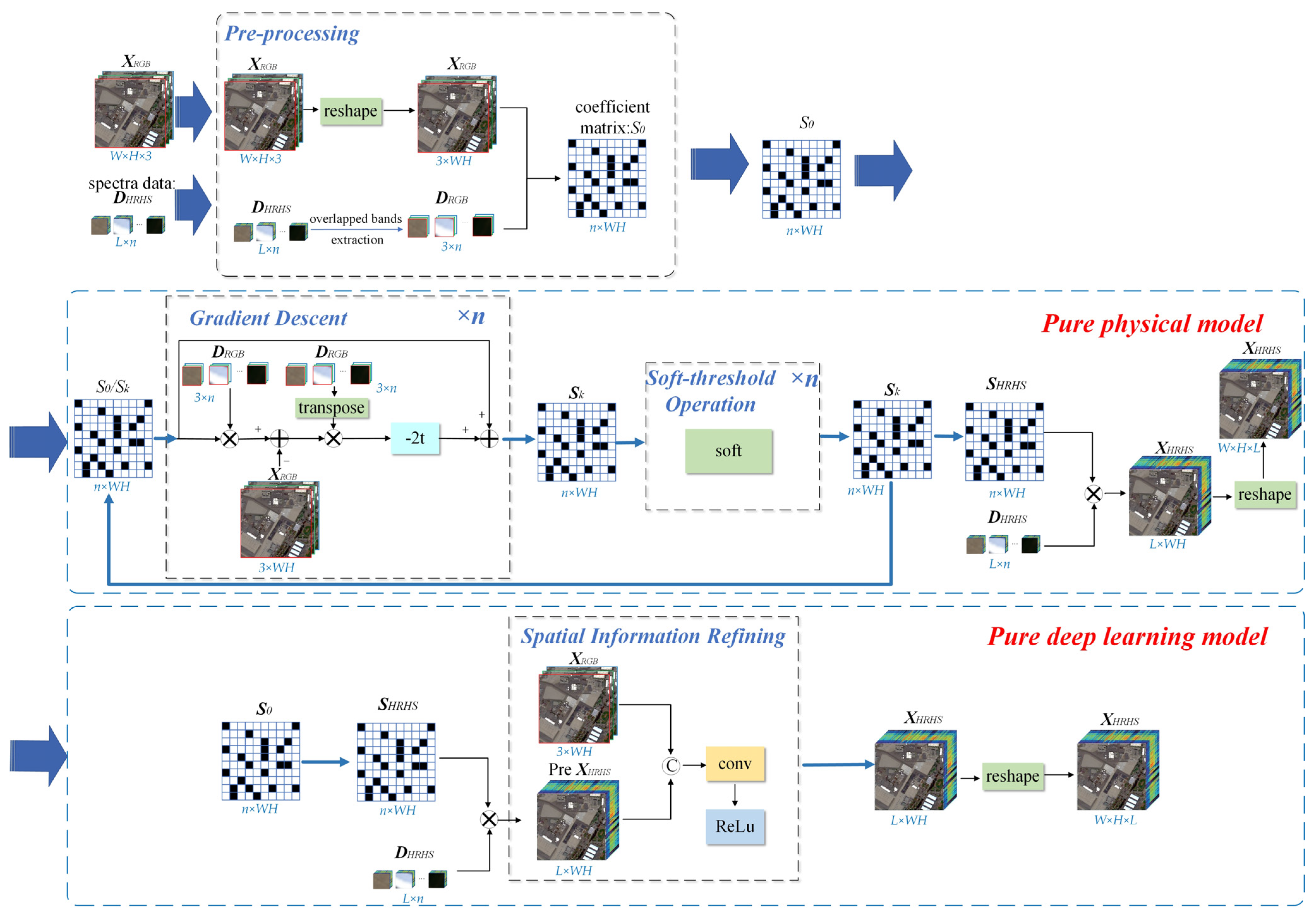
2.4. Architecture of GRSS-Net
2.4.1. Pre-Processing
2.4.2. Gradient Descent Calculation
2.4.3. Soft-Threshold Operation
2.4.4. Spatial Information Refining
2.4.5. Parameter Initialization
3. Experiments and Results
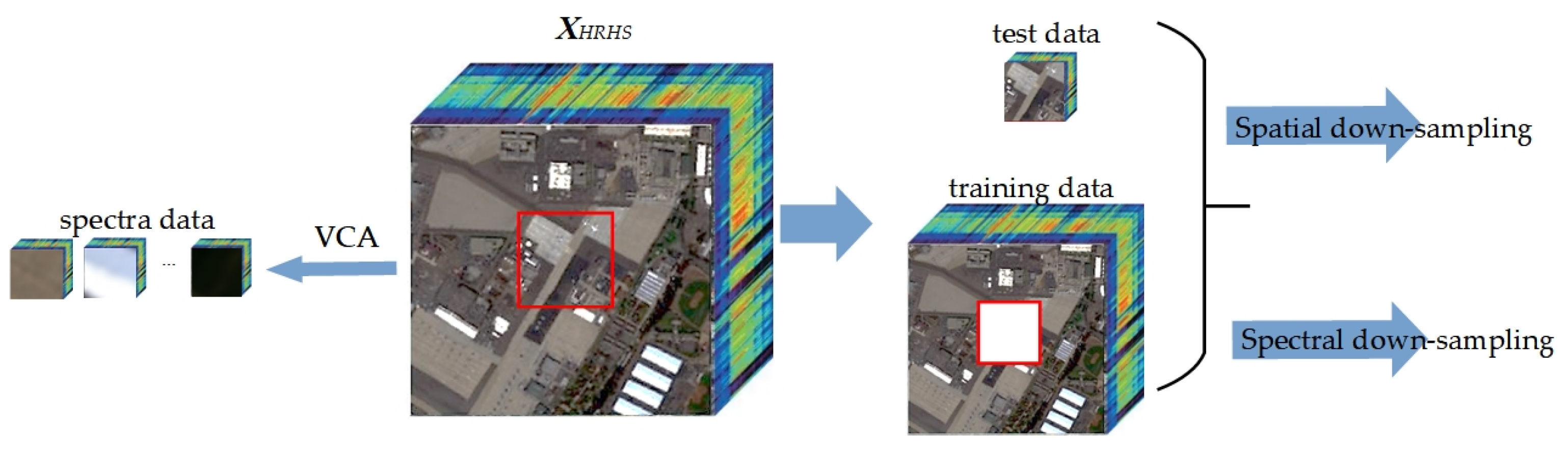
3.1. Datasets
- (1)
- San Diego Airport: These data are acquired by the AVIRIS hyperspectral sensor, with a size of 400 × 400 pixels. The spectral range of San Diego Airport data is from 400 nm to 2500 nm. It has 189 valid spectral bands.
- (2)
- Pavia University: The Pavia University data were obtained by the ROSIS sensor, with a size of 610 × 340 pixels. The spectral range of Pavia University data is from 430 nm to 860 nm, with 103 bands in total. The main ground objects in the Pavia University scene consist of buildings, meadows, Bare Soil, and so on.
- (3)
- XiongAn [34]: The XiongAn dataset was acquired using a full-spectrum multi-modal imaging spectrometer. The spectral range is from 400 nm to 1000 nm with 250 bands in total. The spatial resolution of this scene is 0.5 m with a size of 3750 × 1580 pixels.
3.2. Evaluation Metrics
- (1)
- Root mean square error (RMSE). RMSE is a direct quantitative evaluation index and it measures reconstructed error by calculating pixel value differences between reference and reconstructed images directly. It can be written as follows:where M, N, and L are the width, height, and band number of HRHS images, respectively; and denote pixel value in reference and reconstructed images, respectively.
- (2)
- Peak signal-to-noise ratio (PSNR). The PSNR of a single spectral band is defined in the following equation. The final PSNR value is calculated by averaging the PSNRs of all bands.where represents the maximum function.
- (3)
- Relative dimensionless global error in synthesis (ERGAS). ERGAS reflects the image quality of an entire image. The smaller the value, the better the reconstructed effect. The equation of ERGAS is defined as follows:where r represents the spatial resolution ratio between hyperspectral images and HRHS images; denotes the average function.
- (4)
- Spectral angle mapping (SAM). The SAM index measures the average spectral similarity between reference and reconstructed images, and it is defined as follows:
- (5)
- Structural similarity (SSIM). SSIM is a typical metric indicating the similarity of an entire image. The best value of SSIM is 1. The closer to 1, the more similar the two images are. The SSIM is defined as follows:where and represent the mean of the reference and reconstructed images, respectively; and represent the standard deviation of the reference and reconstructed images, respectively; represents covariance between the reference and reconstructed images; and are constants used for adjustment.
3.3. Network Settings
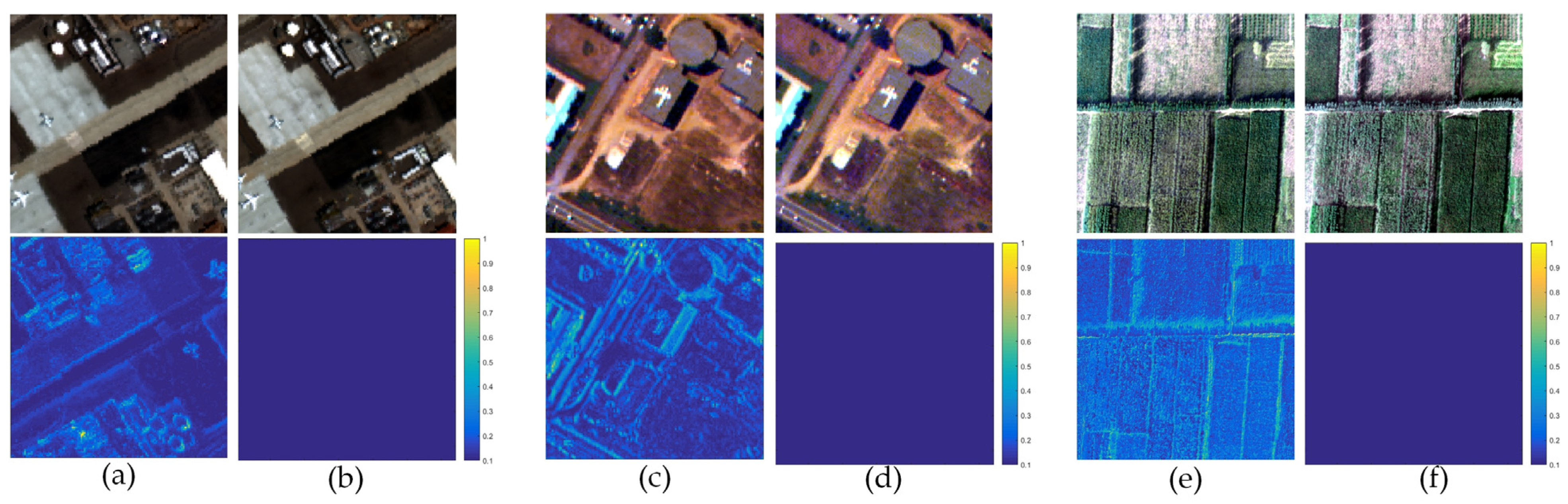
3.4. Quantitative Evaluation
3.5. Ablation Study
4. Discussion
4.1. Effect Validation in Spatial Misalignment Scenes
4.2. Validation Experiments on ZY1E Images
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Farzaneh, D.; Farhad, S.; Soroosh, M.; Ahmad, T.; Reza, K.; Alfred, S. A review of image fusion techniques for pan-sharpening of high-resolution satellite imagery. ISPRS J. Photogramm. 2021, 171, 101–117. [Google Scholar]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification With Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Qi, W.; Huang, C.; Wang, Y.; Zhang, X.; Sun, W.; Zhang, L. Global-Local Three-Dimensional Convolutional Transformer Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5510820. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Y.; Xu, M.; Li, W.; Zhang, G.; Liu, L.; Yu, D. An Improved Low Rank and Sparse Matrix Decomposition-Based Anomaly Target Detection Algorithm for Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 2663–2672. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, H.; Tian, X.; Jiang, J.; Ma, J. Image fusion meets deep learning: A survey and perspective. Inform. Fusion 2021, 76, 323–336. [Google Scholar] [CrossRef]
- Han, X.; Yu, J.; Xue, J.H.; Sun, W. Hyperspectral and Multispectral Image Fusion Using Optimized Twin Dictionaries. IEEE Trans. Image Process. 2020, 29, 4709–4720. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, M.; Zhao, Q.; Xu, Z.; Meng, D. MHF-Net: An Interpretable Deep Network for Multispectral and Hyperspectral Image Fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1457–1473. [Google Scholar] [CrossRef]
- Arad, B.; Ben Shahar, O. Sparse Recovery of Hyperspectral Signal from Natural RGB Images. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–10 and 15–16 October 2016. [Google Scholar]
- Hu, J.; Huang, T.; Deng, L.; Dou, H.; Hong, D.; Vivone, G. Fusformer: A Transformer-Based Fusion Network for Hyperspectral Image Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6012305. [Google Scholar] [CrossRef]
- Jia, S.; Min, Z.; Fu, X. Multiscale spatial–spectral transformer network for hyperspectral and multispectral image fusion. Inform. Fusion 2023, 96, 117–129. [Google Scholar] [CrossRef]
- Li, S.; Dian, R.; Liu, B. Learning the external and internal priors for multispectral and hyperspectral image fusion. Sci. China Inform. Sci. 2022, 66, 140303. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Sun, B.; Guo, A. Recent advances and new guidelines on hyperspectral and multispectral image fusion. Inform. Fusion 2021, 69, 40–51. [Google Scholar] [CrossRef]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and Multispectral Image Fusion based on a Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, H.J.; Liu, T.; Wang, F.; Li, H.S. Remote sensing image fusion via wavelet transform and sparse representation. ISPRS J. Photogramm. 2015, 104, 158–173. [Google Scholar] [CrossRef]
- Deng, S.; Deng, L.; Wu, X.; Ran, R.; Hong, D.; Vivone, G. PSRT: Pyramid Shuffle-and-Reshuffle Transformer for Multispectral and Hyperspectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5503715. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, Y.; Han, X.H. Deep Unsupervised Fusion Learning for Hyperspectral Image Super Resolution. Sensors 2021, 21, 2348. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Liu, H.; Hou, J.; Jia, S.; Zhang, Q. Deep Amended Gradient Descent for Efficient Spectral Reconstruction From Single RGB Images. IEEE Trans. Comput. Imaging 2021, 7, 1176–1188. [Google Scholar] [CrossRef]
- Vivone, G. Multispectral and hyperspectral image fusion in remote sensing: A survey. Inform. Fusion 2023, 89, 405–417. [Google Scholar] [CrossRef]
- Li, J.; Hong, D.; Gao, L.; Yao, J.; Zheng, K.; Zhang, B.; Chanussot, J. Deep learning in multimodal remote sensing data fusion: A comprehensive review. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102926. [Google Scholar] [CrossRef]
- Peng, Y. Blind Fusion of Hyperspectral Multispectral Images Based on Matrix Factorization. Remote Sens. 2021, 13, 4219. [Google Scholar]
- Guo, H.; Bao, W.X.; Feng, W.; Sun, S.S.; Mo, C.; Qu, K. Multispectral and Hyperspectral Image Fusion Based on Joint-Structured Sparse Block-Term Tensor Decomposition. Remote Sens. 2023, 15, 4610. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Li, Z. Spectral Super-Resolution Network Guided by Intrinsic Properties of Hyperspectral Imagery. IEEE Trans. Image Process. 2021, 30, 7256–7265. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, Y.; Wang, C.; Ye, X.; Heidrich, W. BUSIFusion: Blind Unsupervised Single Image Fusion of Hyperspectral and RGB Images. IEEE Trans. Comput. Imaging 2023, 9, 94–105. [Google Scholar] [CrossRef]
- Gao, L.; Hong, D.; Yao, J.; Zhang, B.; Gamba, P.; Chanussot, J. Spectral Superresolution of Multispectral Imagery with Joint Sparse and Low-Rank Learning. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2269–2280. [Google Scholar] [CrossRef]
- Selesnick, I.W. Sparse Signal Restoration. Connexions Web Site. 2009. Available online: http://cnx.org/content/m32168/1.3/contentinfo (accessed on 28 April 2019).
- Liang, D.; Liu, B.; Wang, J.; Ying, L. Accelerating Sense Using Compressed Sensing. Magn. Reson. Med. 2009, 62, 1574–1584. [Google Scholar] [CrossRef]
- Sun, T.; Tang, K.; Li, D. Gradient Descent Learning with Floats. IEEE Trans. Cybern. 2022, 52, 1763–1771. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. Siam J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Wellington, New Zealand, 14–16 December 2018. [Google Scholar]
- Olshausen, B.A.; Field, D.J. Emergence of simple-cell receptive fieldproperties by learning a sparse code for natural images. Nature 1996, 381, 607–609. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Zhang, X.T.; Huang, W.; Wang, Q.; Li, X.L. SSR-NET: SpatialSpectral Reconstruction Network for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5953–5965. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Q.; Wang, Y. Remote sensing image fusion based on two-stream fusion network. Inform. Fusion 2020, 55, 1–15. [Google Scholar] [CrossRef]
- Cen, Y.; Zhang, L.; Zhang, X.; Wang, Y.; Qi, W.; Tang, S.; Zhang, P. Aerial hyperspectral remote sensing classification dataset of Xiongan New Area (Matiwan Village). J. Remote Sens. 2020, 24, 1299–1306. [Google Scholar]
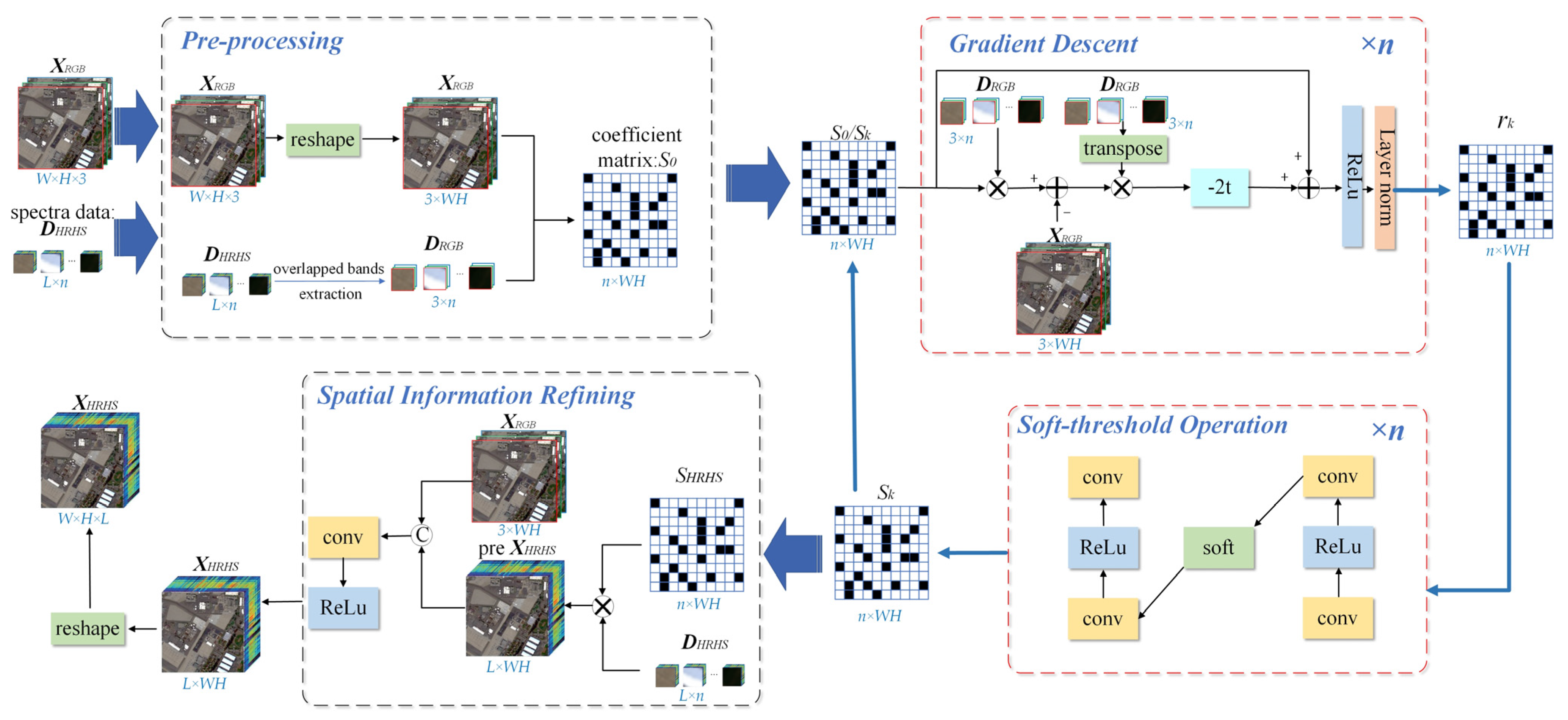






| Input | Output | |
|---|---|---|
| pre-processing | , | , |
| gradient descent calculation | , , | |
| soft-threshold operation | ||
| spatial information refining | , , |
| RMSE (↓,0) | PSNR (↑,+∞) | ERGAS (↓,0) | SAM (↓,0) | SSIM (↑,1) | |
|---|---|---|---|---|---|
| Sparse coding | 23.720 | 41.034 | 7.674 | 10.850 | 0.775 |
| CNMF | 29.553 | 37.232 | 5.796 | 6.170 | 0.769 |
| TFNet | 1.043 | 47.796 | 1.546 | 2.445 | 0.883 |
| ResTFNet | 0.952 | 47.587 | 1.398 | 2.196 | 0.953 |
| SSR-NET | 1.075 | 47.532 | 1.590 | 2.507 | 0.945 |
| GRSS-Net | 1.299 | 46.889 | 1.912 | 3.318 | 0.962 |
| RMSE (↓,0) | PSNR (↑,+∞) | ERGAS (↓,0) | SAM (↓,0) | SSIM (↑,1) | |
|---|---|---|---|---|---|
| Sparse coding | 12.245 | 33.969 | 7.131 | 6.577 | 0.702 |
| CNMF | 10.202 | 32.707 | 6.229 | 5.625 | 0.779 |
| TFNet | 2.831 | 38.112 | 1.957 | 2.643 | 0.989 |
| ResTFNet | 2.967 | 38.404 | 2.106 | 2.586 | 0.990 |
| SSR-NET | 3.999 | 36.810 | 2.709 | 3.253 | 0.983 |
| GRSS-Net | 3.558 | 38.674 | 3.186 | 3.385 | 0.982 |
| RMSE (↓,0) | PSNR (↑,+∞) | ERGAS (↓,0) | SAM (↓,0) | SSIM (↑,1) | |
|---|---|---|---|---|---|
| Sparse coding | 9.245 | 31.834 | 6.928 | 3.183 | 0.773 |
| CNMF | 8.638 | 33.670 | 6.318 | 2.882 | 0.820 |
| TFNet | 2.238 | 38.474 | 1.413 | 2.672 | 0.996 |
| ResTFNet | 2.588 | 37.213 | 1.584 | 2.554 | 0.995 |
| SSR-NET | 2.783 | 36.583 | 1.982 | 2.968 | 0.989 |
| GRSS-Net | 3.091 | 35.671 | 2.772 | 2.501 | 0.980 |
| RMSE (↓,0) | PSNR (↑,+∞) | ERGAS (↓,0) | SAM (↓,0) | SSIM (↑,1) | |
|---|---|---|---|---|---|
| Pure physical model | 6.558 | 31.828 | 9.601 | 8.006 | 0.929 |
| Pure deep learning model | 8.354 | 27.259 | 11.956 | 12.289 | 0.773 |
| GRSS-Net | 1.299 | 45.889 | 1.912 | 3.318 | 0.962 |
| RMSE (↓,0) | PSNR (↑,+∞) | ERGAS (↓,0) | SAM (↓,0) | SSIM (↑,1) | |
|---|---|---|---|---|---|
| San Diego Airport | 1.355 | 46.279 | 2.012 | 3.348 | 0.952 |
| Pavia University | 3.719 | 38.441 | 2.417 | 3.172 | 0.978 |
| XiongAn | 3.185 | 35.637 | 2.648 | 2.483 | 0.974 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, L.; Song, R.; Tong, Q. A General Deep Learning Point–Surface Fusion Framework for RGB Image Super-Resolution. Remote Sens. 2024, 16, 139. https://doi.org/10.3390/rs16010139
Zhang Y, Zhang L, Song R, Tong Q. A General Deep Learning Point–Surface Fusion Framework for RGB Image Super-Resolution. Remote Sensing. 2024; 16(1):139. https://doi.org/10.3390/rs16010139
Chicago/Turabian StyleZhang, Yan, Lifu Zhang, Ruoxi Song, and Qingxi Tong. 2024. "A General Deep Learning Point–Surface Fusion Framework for RGB Image Super-Resolution" Remote Sensing 16, no. 1: 139. https://doi.org/10.3390/rs16010139
APA StyleZhang, Y., Zhang, L., Song, R., & Tong, Q. (2024). A General Deep Learning Point–Surface Fusion Framework for RGB Image Super-Resolution. Remote Sensing, 16(1), 139. https://doi.org/10.3390/rs16010139







