Investigating the Spatial, Proximity, and Multiscale Effects of Influencing Factors in the Snowmelt Process in the Manas River Basin Using a Novel Zonal Spatial Panel Model
Abstract
:1. Introduction
2. Study Area and Data Integration
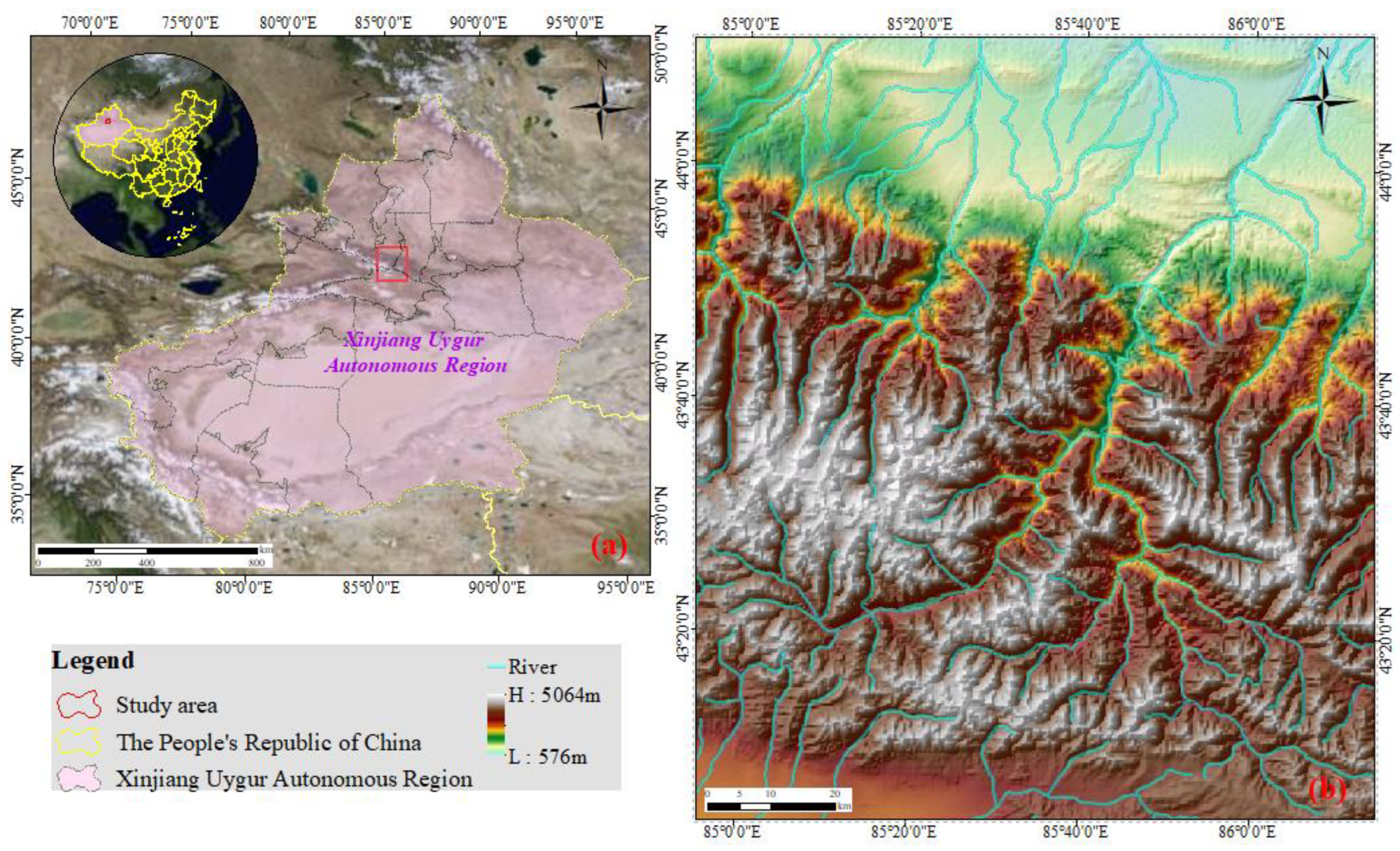
2.1. Study Area
2.2. Data Sources
2.3. Integration of the Influencing Factors
3. Methodologies
3.1. Overall Methodology
3.2. Snow Cover Index Calculations
- is the value that normalizes the reflectance in the green and shortwave infrared bands [46], represents the reflectance of the red band, represents the maximum reflectance of the red band, and is the shadow regulator. The optimum matching algorithm is used to determine the value of shadow adjusting factor . First, select the terrain effect prominent area, the initial value of a given equals 0 and 0.001 as a step for circulation, until the shadow area and highlight areas of snow index value equal or similar (the general difference is less than 0.01) end loop adjustment factor value.
3.3. Spatial Panel Regression (SPR) Modelling and Evaluation
3.4. Multiscale Partitioning Scheme and Zonal Spatial Panel Model
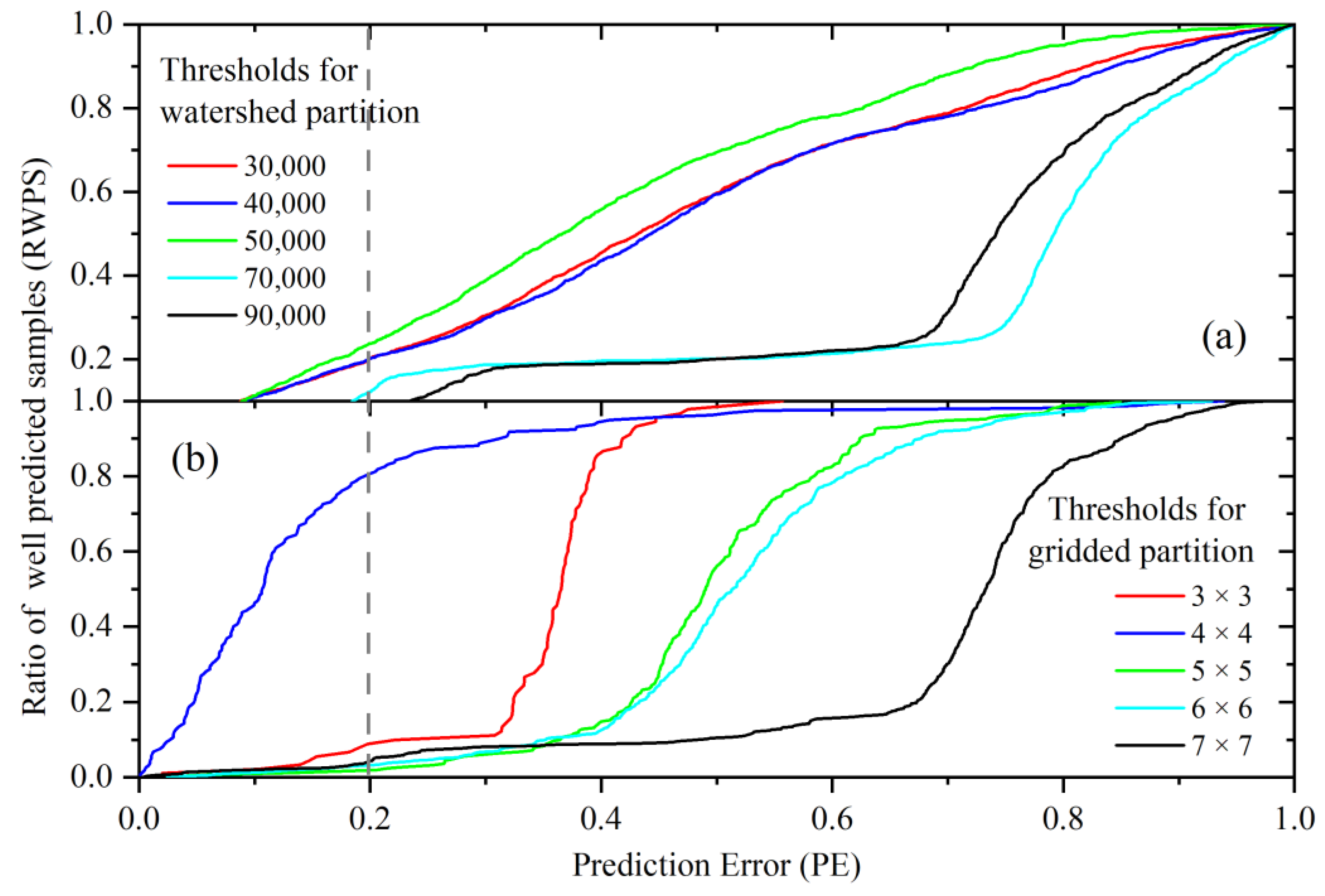
3.5. Determination and Evaluation of Optimal Partition Zone
4. Results
4.1. Results of Extracted SESI during the Snow Melting Period
4.2. Mechanism of Spatial and Proximity Effect of Snow Influence Factors
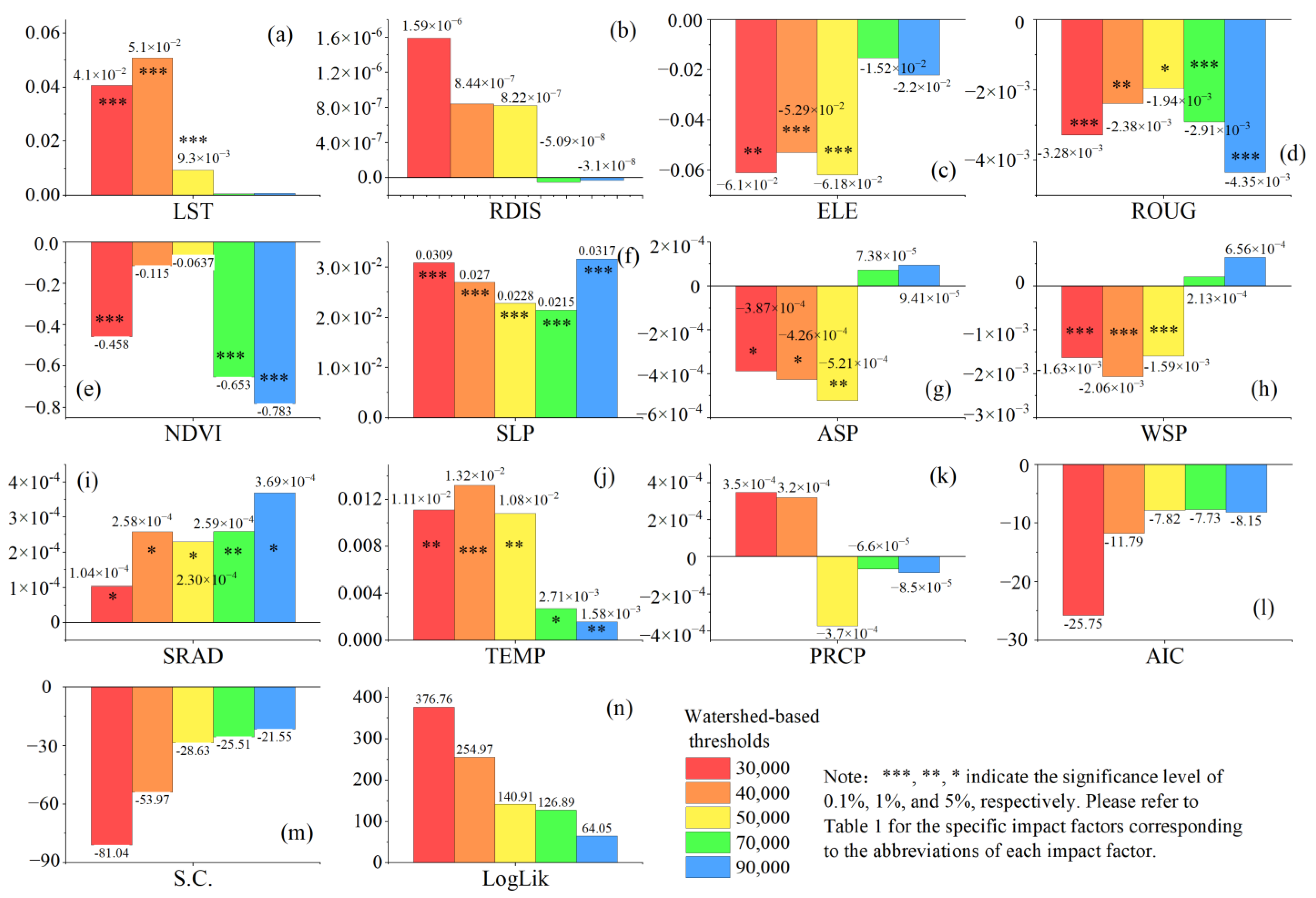
4.3. Characteristics of Influence Factors under Multiple Scales
4.4. Spatial Heterogeneity of Each Influencing Factor Based on Optimal Partition Scale
5. Discussions
5.1. The Spatial and Proximity Interaction in the Snow Melting Process
5.2. The Differences in Dominant Factors Affecting Snow Melting at Varied Scales
5.3. Heterogeneity of Local Influencing Factors
5.4. Comparison with Existing Methods
5.5. Limitations and Perspectives
6. Conclusions
7. Patent
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B
References
- Ahluwalia, R.S.; Rai, S.P.; Meetei, P.N.; Kumar, S.; Sarangi, S.; Chauhan, P.; Karakoti, I. Spatial-diurnal variability of snow/glacier melt runoff in glacier regime river valley: Central Himalaya, India. Quat. Int. 2021, 585, 183–194. [Google Scholar] [CrossRef]
- Guo, D.L.; Pepin, N.; Yang, K.; Sun, J.Q.; Li, D. Local changes in snow depth dominate the evolving pattern of elevation-dependent warming on the Tibetan Plateau. Sci. Bull. 2021, 66, 1146–1150. [Google Scholar] [CrossRef] [PubMed]
- Beniston, M. Is snow in the Alps receding or disappearing? Clim. Chang. 2012, 3, 349–358. [Google Scholar] [CrossRef]
- Matiu, M.; Crespi, A.; Bertoldi, G.; Carmagnola, C.M.; Marty, C.; Morin, S.; Schöner, W.; Berro, D.C.; Chiogna, G.; De Gregorio, L.; et al. Observed snow depth trends in the European Alps 1971 to 2019. Cryosphere Discuss. 2021, 15, 1343–1382. [Google Scholar] [CrossRef]
- Yi, Y.; Kimball, S.J.; Rawlins, A.M.; Moghaddam, M.; Euskirchen, E.S. The role of snow cover affecting boreal-arctic soil freeze–thaw and carbon dynamics. Biogeosciences 2015, 12, 5811–5829. [Google Scholar] [CrossRef]
- Aanderud, Z.T.; Jones, S.E.; Schoolmaster, D.R., Jr.; Fierer, N.; Lennon, J.T. Sensitivity of soil respiration and microbial communities to altered snowfall. Soil. Biol. Biochem. 2013, 57, 217–227. [Google Scholar] [CrossRef]
- Notarnicola, C. Hotspots of snow cover changes in global mountain regions over 2000–2018. Remote Sens. Environ. 2020, 243, 111781. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Lei, X.; Ju, Y.; Bu, X.; Li, H. Quantitative determination of environmental factors governing the snow melting: A geodetector case study in the central Tienshan Mountains. Sci. Rep. 2022, 12, 11565. [Google Scholar] [CrossRef]
- Schweizer, J.; Kronholm, K. Snow cover spatial variability at multiple scales: Characteristics of a layer of buried surface hoar. Cold Reg. Sci. Technol. 2007, 47, 207–223. [Google Scholar] [CrossRef]
- Zhang, T. Influence of the seasonal snow cover on the ground thermal regime: An overview. Rev. Geophys. 2005, 43, RG4002. [Google Scholar] [CrossRef]
- Sharma, A.; Bhattacharya, A.; Venkataraman, C. Influence of aerosol radiative effects on surface temperature and snow melt in the Himalayan region. Sci. Total Environ. 2021, 810, 151299. [Google Scholar] [CrossRef] [PubMed]
- Burazerovic, D.; Heylen, R.; Geens, B.; Sterckx, S.; Scheunders, P. Detecting the Adjacency Effect in Hyperspectral Imagery with Spectral Unmixing Techniques. IEEE J. Sel. Top. Appl. 2013, 6, 1070–1078. [Google Scholar] [CrossRef]
- Garg, P.K. Effect of contamination and adjacency factors on snow using spectroradiometer and hyperspectral images. In Hyperspectral Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2020; pp. 167–196. [Google Scholar]
- Roots, E.F.; Glen, J. Hydrological aspects of Alpine and high mountain areas. In Proceedings of the Exeter Symposium, Exeter, UK, 19–30 July 1982; International Association of Hydrological Sciences: Oxfordshire, UK, 1982; pp. V–VI. [Google Scholar]
- Currier, W.R.; Lundquist, J.D. Snow depth variability at the forest edge in multiple climates in the western United States. Water Resour. Res. 2018, 54, 8756–8773. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Storck, P.; Lettenmaier, D.P. Modeling snow accumulation and ablation processes in forested environments. Water Resour. Res. 2009, 45, W05429. [Google Scholar] [CrossRef]
- Sanmiguel-Vallelado, A.; McPhee, J.; Carreño, P.E.O.; Morán-Tejeda, E.; Camarero, J.J.; López-Moreno, J.I. Sensitivity of forest–snow interactions to climate forcing: Local variability in a Pyrenean valley. J. Hydrol. 2022, 605, 127311. [Google Scholar] [CrossRef]
- Watson, F.G.; Anderson, T.N.; Kramer, M.; Detka, J.; Masek, T.; Cornish, S.S.; Moore, S.W. Effects of wind, terrain, and vegetation on snow pack. Terr. Ecol. 2008, 3, 67–84. [Google Scholar]
- Verbunt, M.; Gurtz, J.; Jasper, K.; Lang, H.; Warmerdam, P.; Zappa, M. The hydrological role of snow and glaciers in alpine river basins and their distributed modeling. J. Hydrol. 2003, 282, 36–55. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Gascoin, S.; Herrero, J.; Sproles, E.A.; Pons, M.; Alonso-González, E.; Hanich, L.; Boudhar, A.; Musselman, K.N.; Molotch, N.P.; et al. Different sensitivities of snowpacks to warming in Mediterranean climate mountain areas. Environ. Res. Lett. 2007, 12, 074660. [Google Scholar] [CrossRef]
- Bi, Y.; Xie, H.; Huang, C.; Ke, C. Snow cover variations and controlling factors at upper Heihe River Basin, Northwestern China. Remote Sens. 2015, 7, 6741–6762. [Google Scholar] [CrossRef]
- Mott, R.; Vionnet, V.; Grünewald, T. The Seasonal Snow Cover Dynamics: Review on Wind-Driven Coupling Processes. Front. Earth Sci. 2018, 6, 197. [Google Scholar] [CrossRef]
- Walker, D.A.; Billings, W.D.; Molenaar, J.G.D. Snow-vegetation interactions in tundra environments. Snow Ecol. 2001, 20, 207–223. [Google Scholar]
- Dankers, R.; Christensen, O.B. Climate change impact on snow coverage, evaporation and river discharge in the Sub-Arctic Tana Basin, Northern Fennoscandia. Clim. Chang. 2005, 69, 367–392. [Google Scholar] [CrossRef]
- Han, S.Z. Linkage of the preceding winter mid-latitude Eurasian atmospheric circulation with the spring northern East Asian snow cover. Atmos. Res. 2023, 293, 106926. [Google Scholar] [CrossRef]
- Han, S.Z.; Ren, H.L.; Su, B.H.; Li, J.X. Connection between the North Atlantic Sea surface temperature and the late autumn snow cover anomalies over the central Tibetan Plateau. Atmos. Res. 2022, 279, 106926. [Google Scholar] [CrossRef]
- Tang, Z.G.; Deng, G.; Hu, G.J.; Zhang, H.B.; Pan, H.Z.; Sang, G.Q. Satellite observed spatiotemporal variability of snow cover and snow phenology over high mountain Asia from 2002 to 2021. J. Hydrol. 2022, 613, 128438. [Google Scholar] [CrossRef]
- Strom, J.; Svensson, J.; Moosmuller, H.; Meinander, O.; Virkkula, A.; Hyvarinen, A.; Asmi, E. Snow cover duration in northern Finland and the influence of key variables through a conceptual framework based on observed variations in snow depth. Sci. Total Environ. 2023, 903, 166333. [Google Scholar] [CrossRef] [PubMed]
- Mankin, J.S.; Diffenbaugh, N.S. Influence of temperature and precipitation variability on near-term snow trends. Clim. Dyn. 2015, 45, 1099–1116. [Google Scholar] [CrossRef]
- Valt, M.; Guyennon, N.; Salerno, F.; Petrangeli, A.B.; Salvatori, R.; Cianfarra, P.; Romano, E. Predicting new snow density in the Italian Alps: A variability analysis based on 10 years of measurements. Hydrol. Process. 2018, 32, 3174–3187. [Google Scholar] [CrossRef]
- Roh, H.-J.; Sahu, P.K.; Sharma, S.; Datla, S.; Mehran, B. Statistical investigations of snowfall and temperature interaction with passenger car and truck traffic on primary highways in Canada. J. Cold Reg. End. 2016, 30, 04015006. [Google Scholar] [CrossRef]
- Dedieu, J.P.; Lessard-Fontaine, A.; Ravazzani, G.; Cremonese, E.; Shalpykova, G.; Beniston, M. Shifting mountain snow patterns in a changing climate from remote sensing retrieval. Sci. Total Environ. 2014, 493, 1267–1279. [Google Scholar] [CrossRef]
- Qin, D.H.; Liu, S.Y.; Li, P.J. Snow cover distribution, variability, and response to climate change in western China. J. Clim. 2006, 19, 1820–1833. [Google Scholar]
- Jost, G.; Weiler, M.; Gluns, D.R.; Alila, Y. The influence of forest and topography on snow accumulation and melt at the watershed-scale. J. Hydrol. 2007, 347, 101–115. [Google Scholar] [CrossRef]
- López-Moreno, J.; Fassnacht, S.; Heath, J.; Musselman, K.; Revuelto, J.; Latron, J.; Morán-Tejeda, E.; Jonas, T. Small scale spatial variability of snow density and depth over complex alpine terrain: Implications for estimating snow water equivalent. Adv. Water Resour. 2013, 55, 40–52. [Google Scholar] [CrossRef]
- Nicholls, N. Climate variability, climate change and the Australian snow season. Aust. Meteorol. Mag. 2005, 54, 177–185. [Google Scholar]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Elhorst, J.P. Serial and spatial error correlation. Econ. Lett. 2008, 100, 422–424. [Google Scholar] [CrossRef]
- De Blas, C.S.; Valcarce-Diñeiro, R.; Sipols, A.E.; Martín, N.S.; Arias-Pérez, B.; Santos-Martín, M.T. Prediction of crop biophysical variables with panel data techniques and radar remote sensing imagery. Biosyst. Eng. 2021, 205, 76–92. [Google Scholar] [CrossRef]
- Li, C.; Managi, S.; Wang, M.H. Estimating monthly global ground-level NO2 concentrations using geographically weighted panel regression. Remote Sens. Environ. 2022, 280, 113152. [Google Scholar] [CrossRef]
- Fu, M.; Kelly, A.; Clinch, J.P. Prediction of PM2.5 daily concentrations for grid points throughout a vast area using remote sensing data and an improved dynamic spatial panel model. Atmos. Environ. 2020, 237, 117667. [Google Scholar] [CrossRef]
- Hu, B.D.; McAleer, M. Estimation of Chinese agricultural production efficiencies with panel data. Math. Comput. Simulat. 2005, 68, 475–484. [Google Scholar] [CrossRef]
- Jiang, C.; Zhao, L.; Dai, J.; Liu, H.; Li, Z.; Wang, X.; Yang, Z.; Zhang, H.; Wen, M.; Wang, J. Examining the soil erosion responses to ecological restoration programs and landscape drivers: A spatial econometric perspective. J. Arid. Environ. 2020, 183, 104255. [Google Scholar] [CrossRef]
- Hu, R.Y. The Natural Geography of Tianshan Mountain in China; China Environmental Science Press: Beijing, China, 2004. [Google Scholar]
- Li, H.; Liu, J.; Bu, X.; Feng, X.; Xiao, P. An Integrated Shadow-Adjusted Snow-Aging Index for Alpine Regions. Remote Sens. 2020, 12, 1249. [Google Scholar] [CrossRef]
- Negi, H.S.; Singh, S.K.; Kulkarni, A.V.; Semwal, B.S. Field-based spectral reflectance measurements of seasonal snow cover in the Indian Himalaya. Int. J. Remote Sens. 2010, 31, 2393–2417. [Google Scholar] [CrossRef]
- Elhorst, J.P. Spatial Panel Data Analysis. Encycl. GIS 2017, 2, 2050–2058. [Google Scholar]
- Elhorst, J.P. Spatial panel models and common factors. In Handbook of Regional Science; Springer: Berlin/Heidelberg, Germany, 2021; pp. 2141–2159. [Google Scholar]
- Elhorst, J.P. Spatial panel data models. In Spatial Econometrics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 37–93. [Google Scholar]
- Gu, Y.L.; You, X.Y. A Spatial Quantile Regression Model for Driving Mechanism of Urban Heat Island by Considering the Spatial Dependence and Heterogeneity: An Example of Beijing, China. Sustain. Cities Soc. 2022, 79, 103692. [Google Scholar] [CrossRef]
- Elhorst, J.; Paul, D.J.; Piras, G. On model specification and parameter space definitions in higher order spatial econometric models. Reg. Sci. Urban Econ. 2012, 42, 211–220. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Prucha, I.R. Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances. J. Econom. 2010, 157, 53–67. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Piras, G. Estimation of spatial models with endogenous weighting matrices, and an application to a demand model for cigarettes. Reg. Sci. Urban Econ. 2014, 46, 140–149. [Google Scholar] [CrossRef]
- Lee, L.F. Asymptotic distributions of quasi-maximum likelihood estimators for spatial autor-egressive models. Econometrica 2004, 72, 140–149. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. Announcement of the Ministry of Water Resources on approval and release of water conservancy industry standards (specification for division and encoding of the small watershed, SDESW). Bull. Minist. Water Resour. People’s Repub. China 2013, 4, 51. [Google Scholar]
- Immerzeel, W.W.; Lutz, A.F.; Andrade, M.; Bahl, A.; Biemans, H.; Bolch, T.; Hyde, S.; Brumby, S.; Davies, B.J.; Elmore, A.C.; et al. Importance and vulnerability of the world’s water towers. Nature 2020, 577, 364–369. [Google Scholar] [CrossRef]
- Gao, X.L.; Asami, Y.; Chung, C.J.F. An empirical evaluation of spatial regression models. Comput. Geosci. 2006, 32, 1040–1051. [Google Scholar] [CrossRef]
- Lu, H.; Wei, W.S.; Liu, M.Z.; Han, X.; Hong, W. Observations and modeling of incoming longwave radiation to snow beneath forest canopies in the west Tianshan Mountains, China. J. Mt. Sci. 2020, 11, 1138–1153. [Google Scholar] [CrossRef]
- Sturm, M.; McFadden, J.P.; Liston, G.E.; Chapin, F.S.; Racine, C.H.; Holmgren, J. Snow–Shrub Interactions in Arctic Tundra: A Hypothesis with Climatic Implications. J. Clim. 2001, 14, 336–344. [Google Scholar] [CrossRef]
- Golding, D.L.; Swanson, R.H. Snow distribution patterns in clearings and adjacent forest. Water Resour. Res. 1986, 22, 1931–1940. [Google Scholar] [CrossRef]
- Marchand, W.D.; Killingtveit, A. Analyses of the relation between spatial snow distribution and terrain characteristics. In Proceedings of the 58th Eastern Snow Conference, Ottawa, ON, Canada, 17–19 May 2001; pp. 71–84. [Google Scholar]
- Lundquist, J.D.; Pepin, N.; Rochford, C. Automated algorithm for mapping regions of cold-air pooling in complex terrain. J. Geophys. Res. Atmos. 2008, 113, D22107. [Google Scholar] [CrossRef]
- Anand, P.; Janardhanan, J.; Nair, A.P.; Suresh, I.; Suneel, V.; Gopika, S.; Thadathil, P. Role of subsurface layer temperature inversion in cyclone induced warming in the northern Bay of Bengal. Dynam. Atmos. Oceans 2023, 103, 101389. [Google Scholar]
- Vitasse, Y.; Klein, G.; Kirchner, J.W.; Rebetez, M. Intensity, frequency and spatial configuration of winter temperature inversions in the closed La Brevine valley, Switzerland. Theor. Appl. Clim. 2017, 130, 1073–1083. [Google Scholar] [CrossRef]
- Ford, K.R.; Ettinger, A.K.; Lundquist, J.D.; Raleigh, M.S.; Lambers, J.H.R. Spatial heterogeneity in ecologically important climate variables at coarse and fine scales in a high-snow mountain landscape. PLoS ONE 2013, 8, e65008. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- He, J.; Zhao, W.; Li, A.; Wen, F.; Yu, D. The impact of the terrain effect on land surface temperature variation based on Landsat-8 observations in mountainous areas. Int. J. Remote Sens. 2019, 40, 1808–1827. [Google Scholar] [CrossRef]
- Lubitz, W.D.; White, B.R. Wind-tunnel and field investigation of the effect of local wind direction on speed-up over hills. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 639–661. [Google Scholar] [CrossRef]
- Yan, G.; Jiao, Z.-H.; Wang, T.; Mu, X. Modeling surface longwave radiation over high-relief terrain. Remote Sens. Environ. 2020, 237, 111556. [Google Scholar] [CrossRef]
- Zuo, J.; Xu, J.; Chen, Y.; Wang, C. Downscaling precipitation in the data-scarce inland river basin of Northwest China based on Earth system data products. Atmosphere 2019, 10, 613. [Google Scholar] [CrossRef]
- Jain, S.K.; Goswami, A.; Saraf, A.K. Role of elevation and aspect in snow distribution in snow distribution in Western Himalaya. Water Resour. Manag. 1986, 23, 71–83. [Google Scholar] [CrossRef]
- Lopez-Moreno, J.I.; Pomeroy, J.W.; Revuelto, J.; Vicente-Serrano, S.M. Response of snow processes to climate change: Spatial variability in a small basin in the Spanish Pyrenees. Hydrol. Process. 2013, 18, 2637–2650. [Google Scholar] [CrossRef]
- Lopez-Moreno, J.I.; Revuelto, J.; Gilaberte, M.; Moran-Tejeda, E.; Pons, M.; Jover, E.; Esteban, P.; García, C.; Pomeroy, J.W. The effect of slope aspect on the response of snowpack to climate warming in the Pyrenees. Theor. Appl. Climatol. 2014, 117, 207–219. [Google Scholar] [CrossRef]
- Thapa, S.; Zhang, F.; Zhang, H.B.; Zeng, C.; Wang, L.; Xu, C.Y.; Thapa, A.; Nepal, S. Assessing the snow cover dynamics and its relationship with different hydro-climatic characteristics in Upper Ganges river basin and its sub-basins. Sci. Total Environ. 2021, 793, 148648. [Google Scholar] [CrossRef]
- Yan, W.; Wang, Y.; Ma, X.; Tan, Y.; Yan, J.; Liu, M.; Liu, S. What Is the Threshold Elevation at Which Climatic Factors Determine Snow Cover Variability? A Case Study of the Keriya River Basin. Remote Sens. 2023, 15, 4725. [Google Scholar] [CrossRef]
- Wu, S.Y.; Zhang, X.L.; Du, J.K.; Zhou, X.B.; Tuo, Y.; Li, R.J.; Duan, Z. The vertical influence of temperature and precipitation on snow cover variability in the Central Tianshan Mountains, Northwest China. Hydrol. Process. 2019, 33, 1686–1697. [Google Scholar] [CrossRef]
- Li, K.M.; Li, H.L.; Wang, L.; Gao, W.Y. On the relationship between local topography and small glacier change under climatic warming on Mt. Bogda, eastern Tian Shan, China. J. Earth Sci. 2011, 22, 515–527. [Google Scholar] [CrossRef]
- Hock, R. A distributed temperature-index ice- and snowmelt model including potential direct solar radiation. J. Glaciol. 1999, 45, 101–111. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Cao, T.; Kan, X.; Wang, J.G.; Tian, W. Spatial and temporal variation analysis of snow cover using MODIS over Qinghai-Tibetan Plateau during 2003–2014. J. Indian Soc. Remote Sens. 2017, 45, 887–897. [Google Scholar] [CrossRef]
- Wisnumurti, R.D.; Pratiwi, H.; Handajani, S.S. Spatial Lag Fixed Effect Panel Model with Weights Queen Contiguity for Economic Growth Data of ASEAN Member Countries. J. Phys. Conf. Series. IOP Publ. 2019, 1306, 012033. [Google Scholar] [CrossRef]
- Lee, L.; Yu, J. QML estimation of spatial dynamic panel data models with time-varying spatial weights matrices. Spat. Econ. Anal. 2012, 7, 31–74. [Google Scholar] [CrossRef]




| Data Type | Data Name | Description | Abbreviations | Spatio-Temporal Resolution | Data Source | Periods |
|---|---|---|---|---|---|---|
| Reflectance data L-1 | Landsat8 OLI/TIRS | Shady eliminated snow index | SESI | 30 m/16 days | https://earthexplorer.usgs.gov/ | Accessed on 15 dates as 10 and 26 February 2015, 3 and 19 March 2015, 12 and 24 April 2015, 23 March 2017, 24 April 2017, 10 May 2017, 10 and 13 March 2018, 14 April 2019, 13 and 15 March 2020, and 2 May 2020. |
| Meteorological variables | MOD02HKM | Land surface temperature | LST | 500 m/Daily | https://modsi.gsfc.nasa.gov/ | |
| China meteorological forcing dataset | Ai temperature | TEMP | 5 km/Daily | https://data.tpdc.ac.cn/zh-hans/data/8028b944-daaa-4511-8769-965612652c49 | ||
| Wind speed | WSP | |||||
| Solar radiation | SRAD | |||||
| Precipitation | PRCP | |||||
| Terrain parameters | GDEM v2 | Elevation | ELE | 30 m/- | https://www.gscloud.cn/sources/accessdata/421?pid=302 | |
| Slope | SLP | |||||
| Aspect | ASP | |||||
| Roughness | ROUG | |||||
| Hydrological parameters | Distribution data of lakes and rivers in Xinjiang | Distance from the river | RDIS | 1:250,000 Vector data/Annual | http://www.ncdc.ac.cn/portal/metadata/d9c87a38-cdec-43f6-9c8c-f6ce82a8bce4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, J.; Xiao, M.; Bao, X. Investigating the Spatial, Proximity, and Multiscale Effects of Influencing Factors in the Snowmelt Process in the Manas River Basin Using a Novel Zonal Spatial Panel Model. Remote Sens. 2024, 16, 26. https://doi.org/10.3390/rs16010026
Li H, Liu J, Xiao M, Bao X. Investigating the Spatial, Proximity, and Multiscale Effects of Influencing Factors in the Snowmelt Process in the Manas River Basin Using a Novel Zonal Spatial Panel Model. Remote Sensing. 2024; 16(1):26. https://doi.org/10.3390/rs16010026
Chicago/Turabian StyleLi, Haixing, Jinrong Liu, Mengge Xiao, and Xiaolong Bao. 2024. "Investigating the Spatial, Proximity, and Multiscale Effects of Influencing Factors in the Snowmelt Process in the Manas River Basin Using a Novel Zonal Spatial Panel Model" Remote Sensing 16, no. 1: 26. https://doi.org/10.3390/rs16010026
APA StyleLi, H., Liu, J., Xiao, M., & Bao, X. (2024). Investigating the Spatial, Proximity, and Multiscale Effects of Influencing Factors in the Snowmelt Process in the Manas River Basin Using a Novel Zonal Spatial Panel Model. Remote Sensing, 16(1), 26. https://doi.org/10.3390/rs16010026





