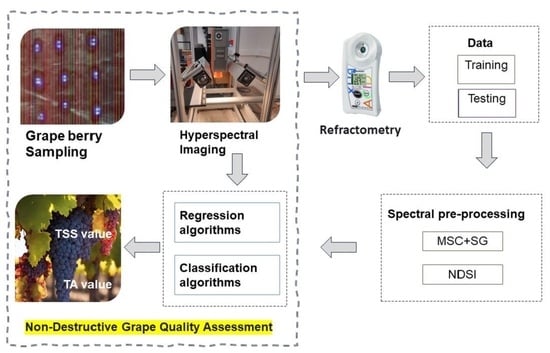
Hyperspectral Imaging Spectroscopy for Non-Destructive Determination of Grape Berry Total Soluble Solids and Titratable Acidity
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Acquisition
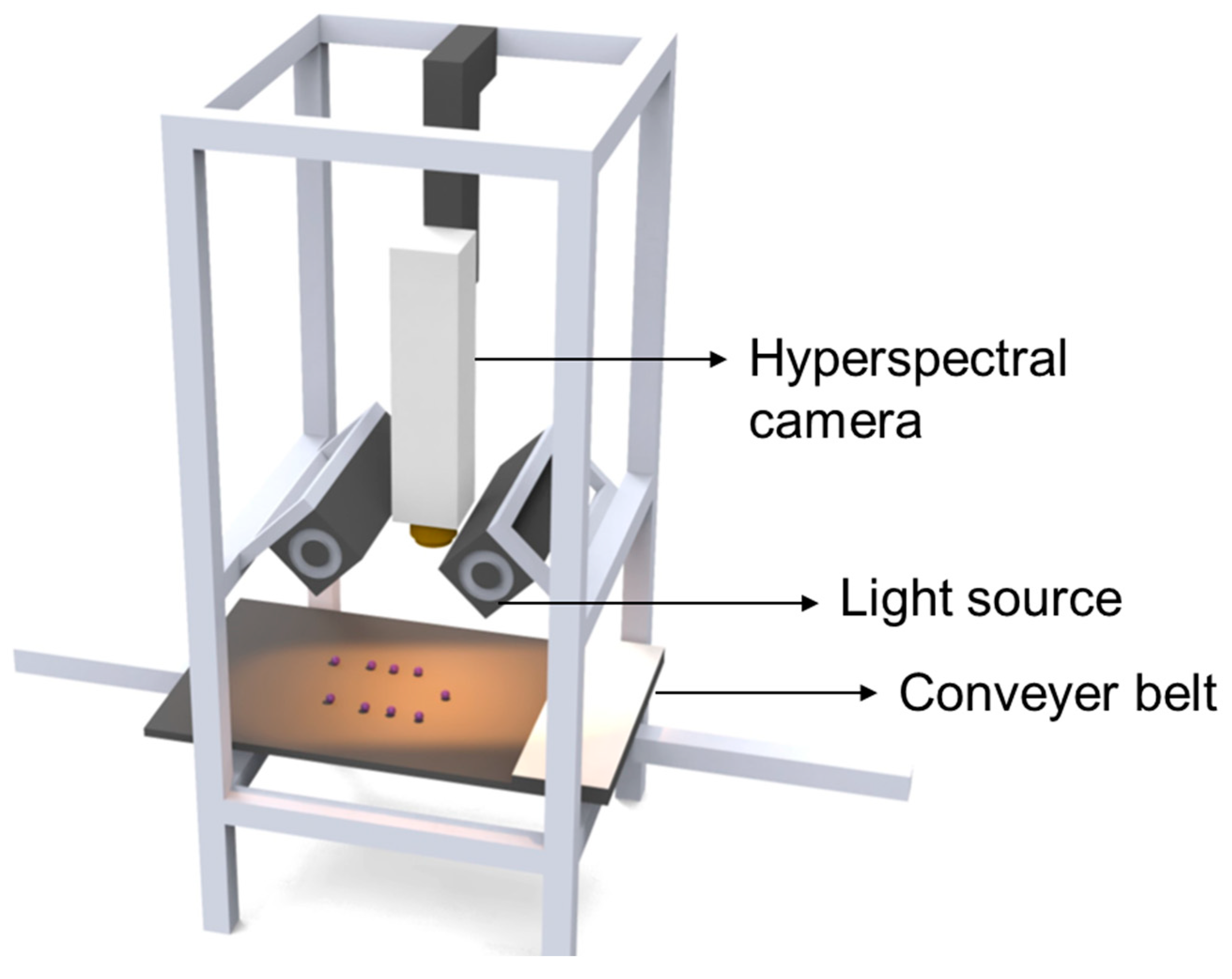
2.2. Hyperspectral Image Acquisition and Analysis
2.3. Enological Parameter Measurements
2.4. Data Analysis
2.4.1. Development of Regression Model
2.4.2. Development of Classification Model
3. Results
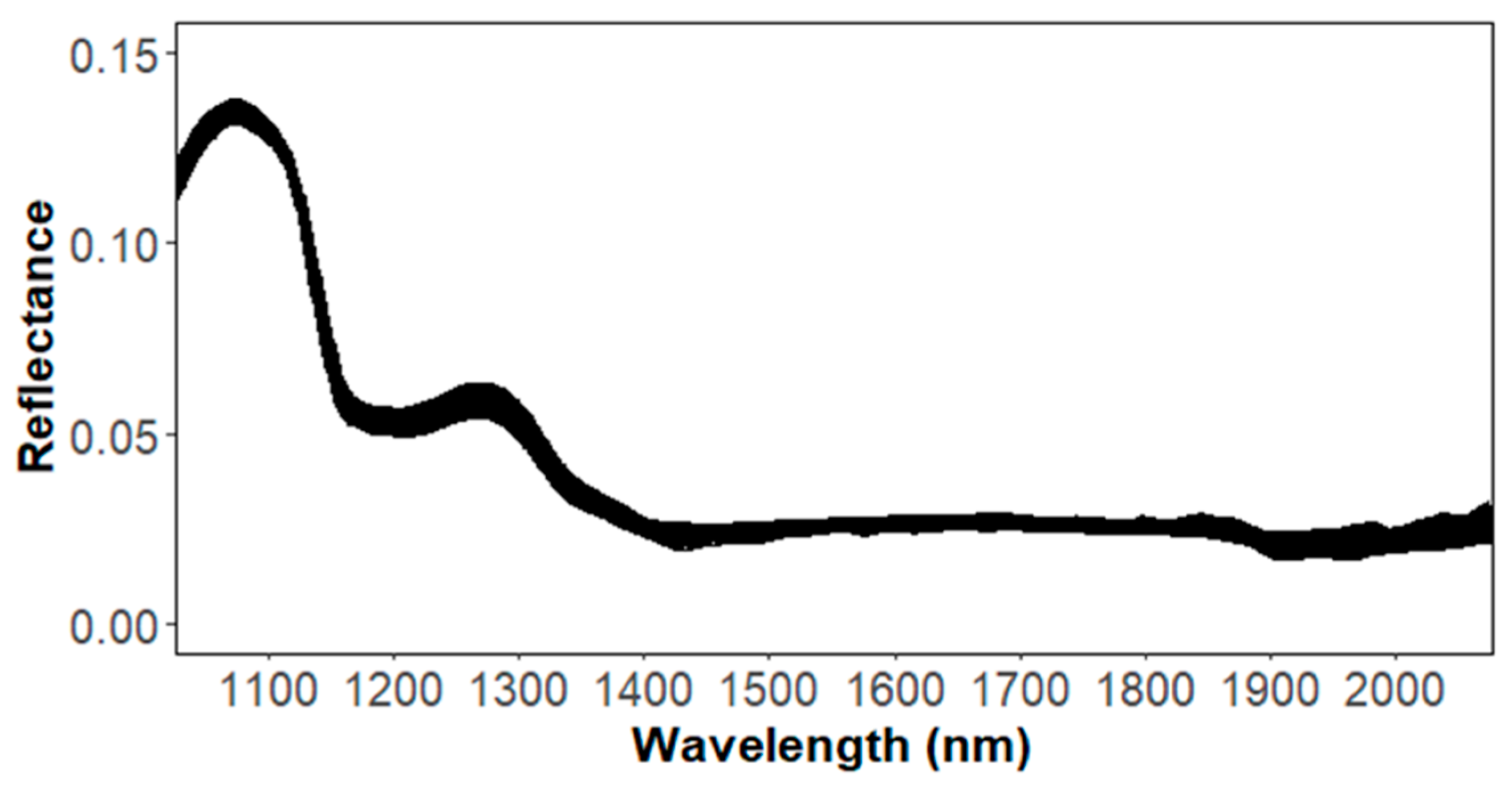
3.1. Statistical Analysis of Measured TSS, TA and Hyperspectral Reflectance
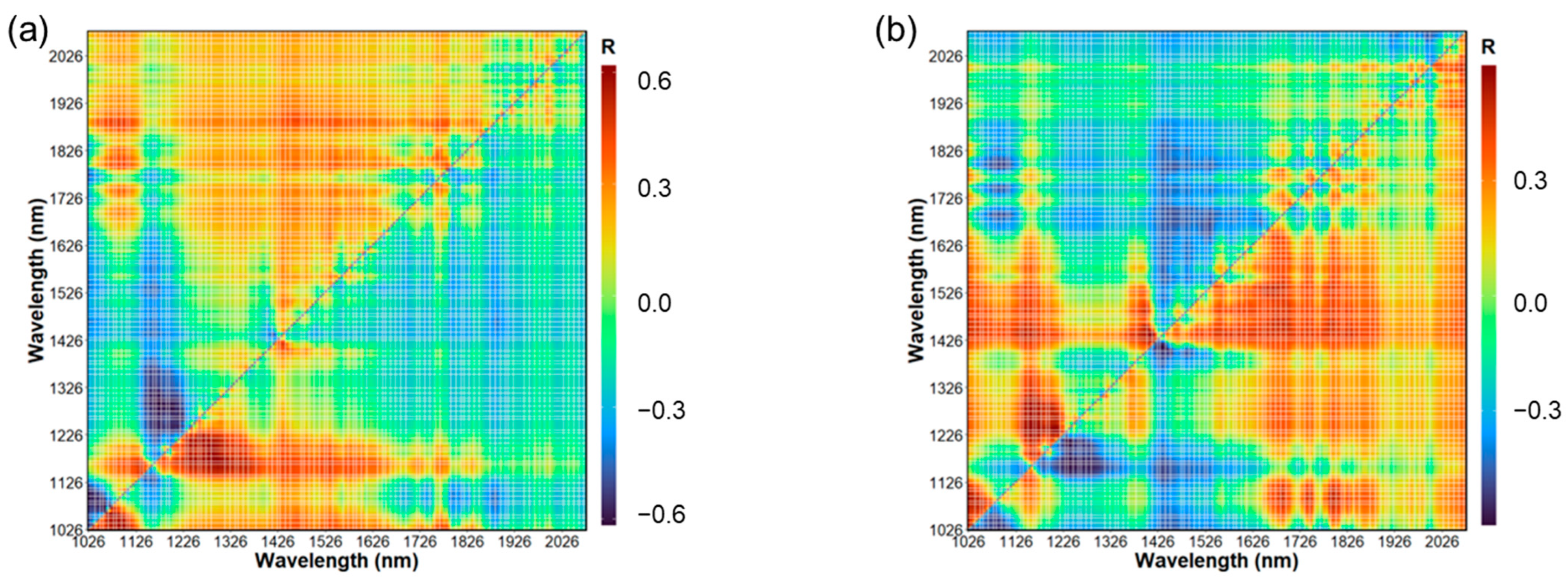
3.2. TSS and TA Estimation Based on Hyperspectral Narrowband NDSI
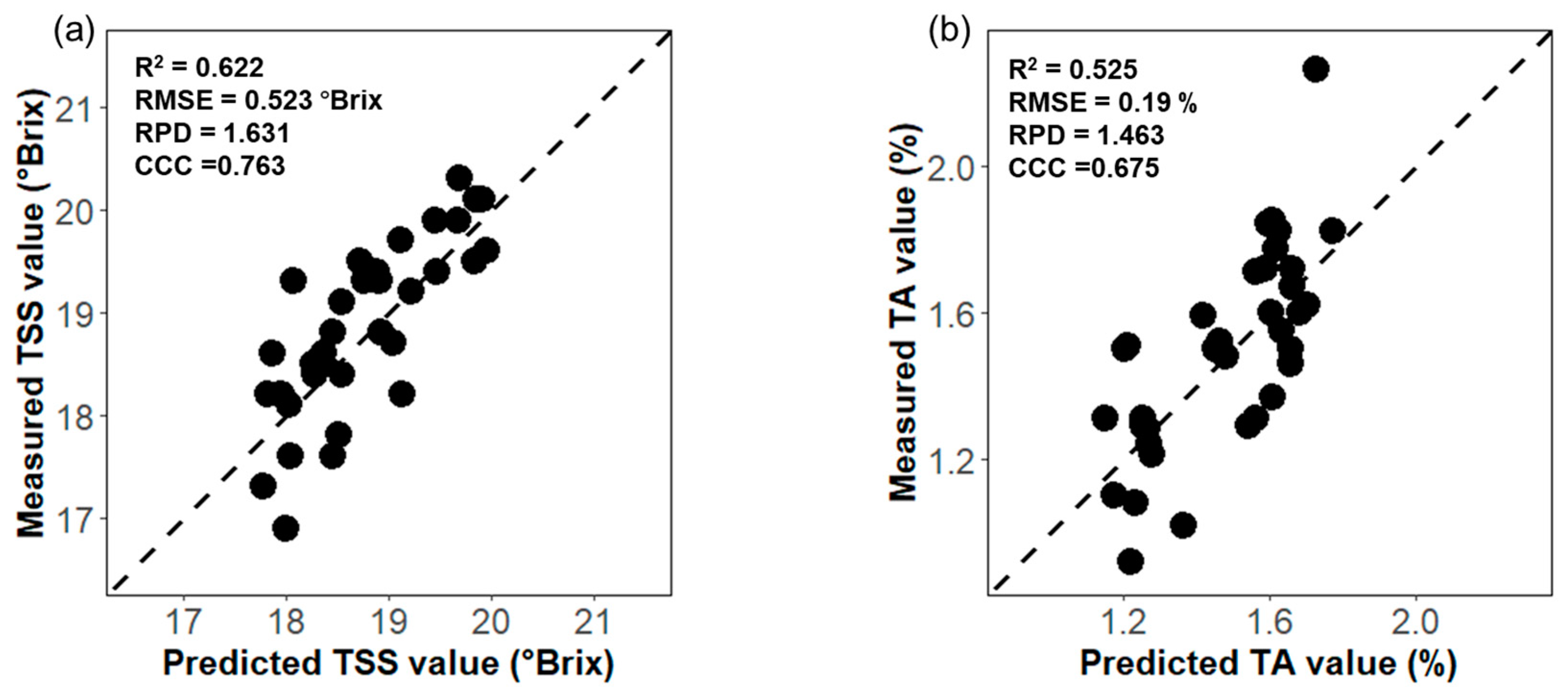
3.3. Predictive Model Performance Based on Regression Models
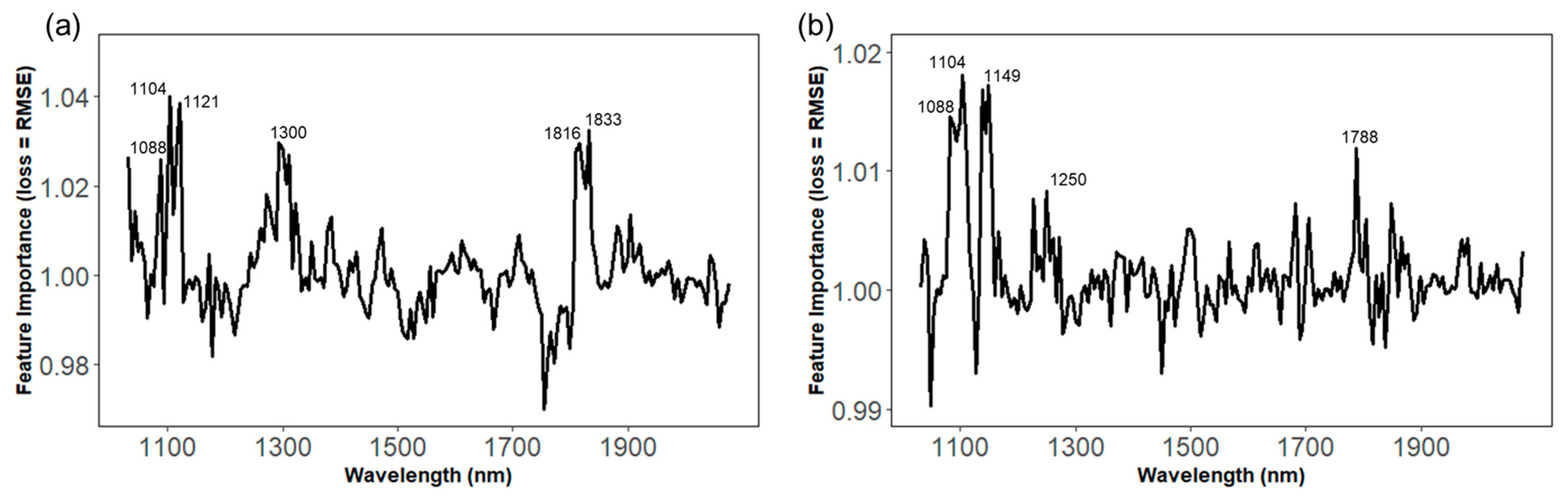
3.4. Spectral Feature Importance of TSS and TA
3.5. Discrimination Capacity Based on Classification Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Gomes, V.; Fernandes, A.; Faia, A.; Melo-Pinto, P. Comparison of Different Approaches for the Prediction of Sugar Content in New Vintages of Whole Port Wine Grape Berries Using Hyperspectral Imaging. Comput. Electron. Agric. 2017, 140, 244–254. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kang, T.H.; Um, B.H.; Sohn, E.-H.; Han, W.-C.; Ji, S.-H.; Jang, K.-H. Evaluation of Physicochemical Properties and Fermenting Qualities of Apple Wines Added with Medicinal Herbs. Food Sci. Biotechnol. 2013, 22, 1039–1046. [Google Scholar] [CrossRef]
- Baluja, J.; Tardaguila, J.; Ayestaran, B.; Diago, M.P. Spatial Variability of Grape Composition in a Tempranillo (Vitis Vinifera L.) Vineyard over a 3-Year Survey. Precis. Agric. 2013, 14, 40–58. [Google Scholar] [CrossRef]
- Bramley, R.; Pearse, B.; Chamberlain, P. Being Profitable Precisely -A Case Study of Precision Viticulture from Margaret River. Aust. New Zealand Grapegrow. Winemak. Annu. Tech. Issue 2003, 473a, 84–87. [Google Scholar]
- Zhao, M.; Cang, H.; Chen, H.; Zhang, C.; Yan, T.; Zhang, Y.; Gao, P.; Xu, W. Determination of Quality and Maturity of Processing Tomatoes Using Near-Infrared Hyperspectral Imaging with Interpretable Machine Learning Methods. LWT 2023, 183, 114861. [Google Scholar] [CrossRef]
- Li, S.; Luo, H.; Hu, M.; Zhang, M.; Feng, J.; Liu, Y.; Dong, Q.; Liu, B. Optical Non-Destructive Techniques for Small Berry Fruits: A Review. Artif. Intell. Agric. 2019, 2, 85–98. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, F.; Ning, J.; Liu, X.; Zhang, Z.; Yang, S. Predicting the Anthocyanin Content of Wine Grapes by NIR Hyperspectral Imaging. Food Chem. 2015, 172, 788–793. [Google Scholar] [CrossRef]
- Silva, R.; Gomes, V.; Mendes-Faia, A.; Melo-Pinto, P. Using Support Vector Regression and Hyperspectral Imaging for the Prediction of Oenological Parameters on Different Vintages and Varieties of Wine Grape Berries. Remote Sens. 2018, 10, 312. [Google Scholar] [CrossRef]
- Ferrer-Gallego, R.; Hernández-Hierro, J.M.; Rivas-Gonzalo, J.C.; Escribano-Bailón, M.T. Determination of Phenolic Compounds of Grape Skins during Ripening by NIR Spectroscopy. LWT-Food Sci. Technol. 2011, 44, 847–853. [Google Scholar] [CrossRef]
- González-Caballero, V.; Sánchez, M.-T.; Fernández-Novales, J.; López, M.-I.; Pérez-Marín, D. On-Vine Monitoring of Grape Ripening Using near-Infrared Spectroscopy. Food Anal. Methods 2012, 5, 1377–1385. [Google Scholar] [CrossRef]
- Urraca, R.; Sanz-Garcia, A.; Tardaguila, J.; Diago, M.P. Estimation of Total Soluble Solids in Grape Berries Using a Hand-held NIR Spectrometer under Field Conditions. J. Sci. Food Agric. 2016, 96, 3007–3016. [Google Scholar] [CrossRef]
- dos Santos Costa, D.; Mesa, N.F.O.; Freire, M.S.; Ramos, R.P.; Mederos, B.J.T. Development of Predictive Models for Quality and Maturation Stage Attributes of Wine Grapes Using Vis-Nir Reflectance Spectroscopy. Postharvest Biol. Technol. 2019, 150, 166–178. [Google Scholar] [CrossRef]
- Dambergs, R.G.; Cozzolino, D.; Esler, M.B. The Use of near Infrared Spectroscopy for Rape Quality Measurement. Aust. New Zealand Grapegrow. Winemak. 2003, 69–76. [Google Scholar]
- Guidetti, R.; Beghi, R.; Bodria, L. Evaluation of Grape Quality Parameters by a Simple Vis/NIR System. Trans. ASABE 2010, 53, 477–484. [Google Scholar] [CrossRef]
- Wei, H.-E.; Grafton, M.; Bretherton, M.; Irwin, M.; Sandoval, E. Evaluation of Point Hyperspectral Reflectance and Multivariate Regression Models for Grapevine Water Status Estimation. Remote Sens. 2021, 13, 3198. [Google Scholar] [CrossRef]
- Lyu, H.; Grafton, M.; Ramilan, T.; Irwin, M.; Sandoval, E. Assessing the Leaf Blade Nutrient Status of Pinot Noir Using Hyperspectral Reflectance and Machine Learning Models. Remote Sens. 2023, 15, 1497. [Google Scholar] [CrossRef]
- Lyu, H.; Grafton, M.; Ramilan, T.; Irwin, M.; Wei, H.-E.; Sandoval, E. Using Remote and Proximal Sensing Data and Vine Vigor Parameters for Non-Destructive and Rapid Prediction of Grape Quality. Remote Sens. 2023, 15, 5412. [Google Scholar] [CrossRef]
- Pullanagari, R.R.; Li, M. Uncertainty Assessment for Firmness and Total Soluble Solids of Sweet Cherries Using Hyperspectral Imaging and Multivariate Statistics. J. Food Eng. 2021, 289, 110177. [Google Scholar] [CrossRef]
- Williams, P.; Norris, K. Near-Infrared Technology in the Agricultural and Food Industries; American Association of Cereal Chemists, Inc.: St Paul, MN, USA, 1987; ISBN 0-913250-49-X. [Google Scholar]
- Iqbal, A.; Sun, D.-W.; Allen, P. Prediction of Moisture, Color and pH in Cooked, Pre-Sliced Turkey Hams by NIR Hyperspectral Imaging System. J. Food Eng. 2013, 117, 42–51. [Google Scholar] [CrossRef]
- Fairuz Omar, A. Spectroscopic Profiling of Soluble Solids Content and Acidity of Intact Grape, Lime, and Star Fruit. Sens. Rev. 2013, 33, 238–245. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, C.; Yang, H.; Jiang, H.; Li, L.; Yang, G. Non-Destructive and in-Site Estimation of Apple Quality and Maturity by Hyperspectral Imaging. Comput. Electron. Agric. 2022, 195, 106843. [Google Scholar] [CrossRef]
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-infrared Reflectance Spectroscopy–Principal Components Regression Analyses of Soil Properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, D.; Wang, J.; Triantafilis, J. Soil Organic Carbon (SOC) Prediction in Australian Sugarcane Fields Using Vis–NIR Spectroscopy with Different Model Setting Approaches. Geoderma Reg. 2022, 30, e00566. [Google Scholar] [CrossRef]
- Grafton, M.; Kaul, T.; Palmer, A.; Bishop, P.; White, M. Regression Analysis of Proximal Hyperspectral Data to Predict Soil pH and Olsen P. Agriculture 2019, 9, 55. [Google Scholar] [CrossRef]
- Golic, M.; Walsh, K.; Lawson, P. Short-Wavelength near-Infrared Spectra of Sucrose, Glucose, and Fructose with Respect to Sugar Concentration and Temperature. Appl. Spectrosc. 2003, 57, 139–145. [Google Scholar] [CrossRef]
- Gutiérrez, S.; Tardáguila, J.; Fernández-Novales, J.; Diago, M.P. On-the-go Hyperspectral Imaging for the In-field Estimation of Grape Berry Soluble Solids and Anthocyanin Concentration. Aust. J. Grape Wine Res. 2019, 25, 127–133. [Google Scholar] [CrossRef]
- González-Caballero, V.; Pérez-Marín, D.; López, M.-I.; Sánchez, M.-T. Optimization of NIR Spectral Data Management for Quality Control of Grape Bunches during On-Vine Ripening. Sensors 2011, 11, 6109–6124. [Google Scholar] [CrossRef]
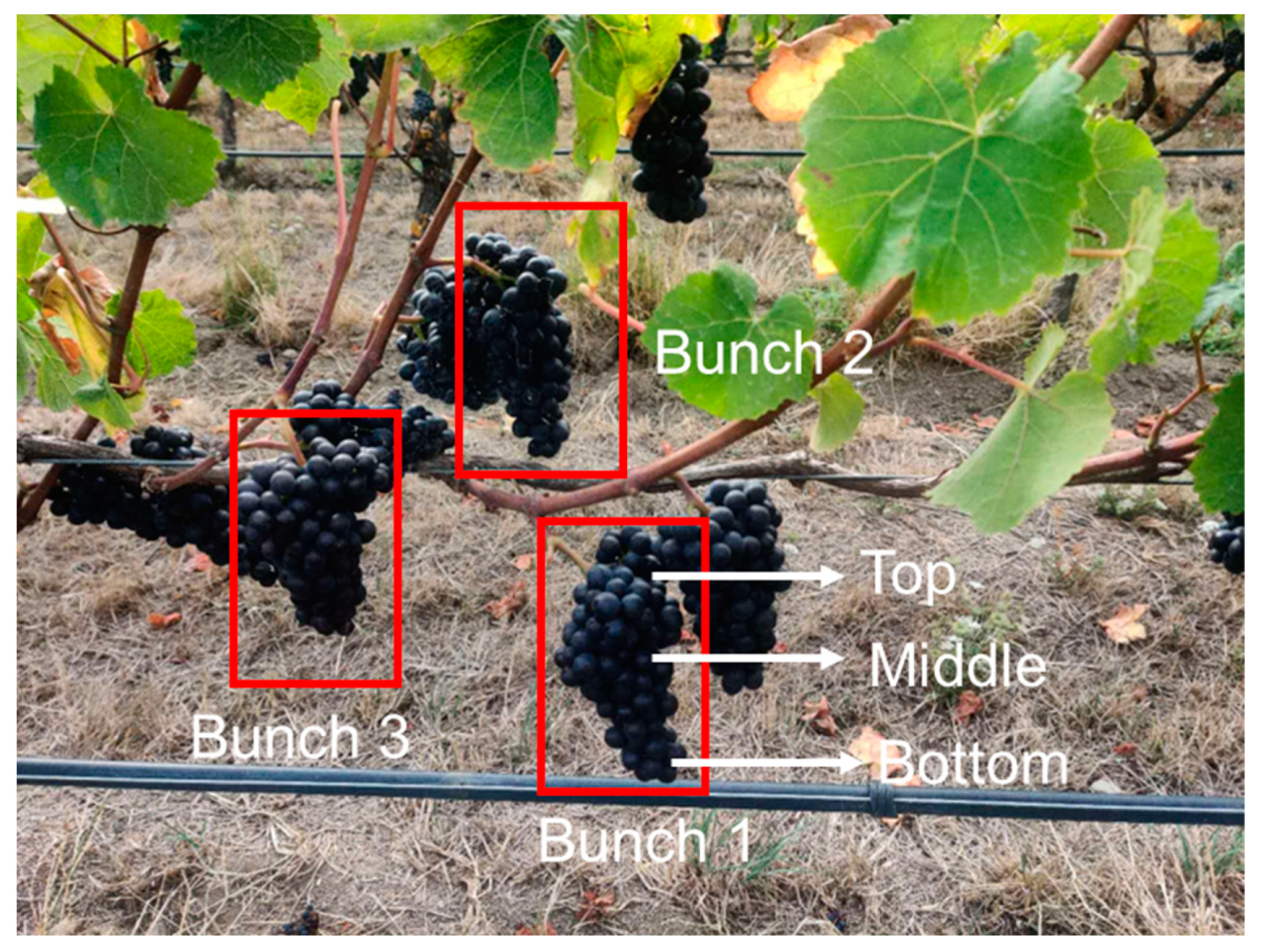

| Date | Number of Samples |
|---|---|
| 7 March | 22 |
| 15 March | 57 |
| 27 March | 33 |
| Parameter | Date | N | Minimum | Maximum | Mean | SD |
|---|---|---|---|---|---|---|
| °Brix | 7 March | 21 | 17.3 | 19 | 18.21 | 0.58 |
| 15 March | 53 | 16.9 | 19.9 | 18.63 | 0.67 | |
| 27 March | 33 | 18.8 | 21.2 | 19.59 | 0.49 | |
| TA | 7 March | 21 | 1.28 | 2.26 | 1.72 | 0.33 |
| 15 March | 53 | 1.17 | 1.93 | 1.59 | 0.17 | |
| 27 March | 33 | 0.92 | 1.51 | 1.23 | 0.14 |
| Parameter | Feature | Model | RMSE | RPD | R2 | CCC |
|---|---|---|---|---|---|---|
| TSS (°Brix) | MSC+SG | PLSR | 0.554 | 1.54 | 0.583 | 0.693 |
| MSC+SG | SVR | 0.523 | 1.631 | 0.622 | 0.763 | |
| MSC+SG | RFR | 0.642 | 1.368 | 0.449 | 0.549 | |
| NDSI | PLSR | 0.726 | 1.114 | 0.305 | 0.548 | |
| NDSI | SVR | 0.543 | 1.49 | 0.589 | 0.655 | |
| NDSI | RFR | 0.592 | 1.429 | 0.531 | 0.687 | |
| TA (%) | MSC+SG | PLSR | 0.305 | 0.82 | 0.025 | 0.15 |
| MSC+SG | SVR | 0.333 | 0.751 | 0.03 | 0.168 | |
| MSC+SG | RFR | 0.217 | 1.346 | 0.43 | 0.595 | |
| NDSI | PLSR | 0.207 | 1.343 | 0.51 | 0.54 | |
| NDSI | SVR | 0.19 | 1.463 | 0.525 | 0.675 | |
| NDSI | RFR | 0.198 | 1.444 | 0.5 | 0.652 |
| Parameter | Feature | Model | Acc | FP | Recall | Ce |
|---|---|---|---|---|---|---|
| TSS (°Brix) | MSC+SG | LDA | 0.75 | 1 | 0.588 | 0.25 |
| MSC+SG | SVM | 0.781 | 5 | 0.846 | 0.219 | |
| MSC+SG | RF | 0.844 | 2 | 0.8 | 0.156 | |
| NDSI | LDA | 0.688 | 7 | 0.769 | 0.313 | |
| NDSI | SVM | 0.938 | 1 | 0.933 | 0.0625 | |
| NDSI | RF | 0.906 | 2 | 0.933 | 0.094 | |
| TA (%) | MSC+SG | LDA | 0.75 | 7 | 0.933 | 0.25 |
| MSC+SG | SVM | 0.781 | 1 | 0.667 | 0.219 | |
| MSC+SG | RF | 0.844 | 2 | 0.8 | 0.156 | |
| NDSI | LDA | 0.75 | 7 | 0.941 | 0.25 | |
| NDSI | SVM | 0.844 | 3 | 0.857 | 0.156 | |
| NDSI | RF | 0.844 | 3 | 0.857 | 0.156 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, H.; Grafton, M.; Ramilan, T.; Irwin, M.; Sandoval, E. Hyperspectral Imaging Spectroscopy for Non-Destructive Determination of Grape Berry Total Soluble Solids and Titratable Acidity. Remote Sens. 2024, 16, 1655. https://doi.org/10.3390/rs16101655
Lyu H, Grafton M, Ramilan T, Irwin M, Sandoval E. Hyperspectral Imaging Spectroscopy for Non-Destructive Determination of Grape Berry Total Soluble Solids and Titratable Acidity. Remote Sensing. 2024; 16(10):1655. https://doi.org/10.3390/rs16101655
Chicago/Turabian StyleLyu, Hongyi, Miles Grafton, Thiagarajah Ramilan, Matthew Irwin, and Eduardo Sandoval. 2024. "Hyperspectral Imaging Spectroscopy for Non-Destructive Determination of Grape Berry Total Soluble Solids and Titratable Acidity" Remote Sensing 16, no. 10: 1655. https://doi.org/10.3390/rs16101655
APA StyleLyu, H., Grafton, M., Ramilan, T., Irwin, M., & Sandoval, E. (2024). Hyperspectral Imaging Spectroscopy for Non-Destructive Determination of Grape Berry Total Soluble Solids and Titratable Acidity. Remote Sensing, 16(10), 1655. https://doi.org/10.3390/rs16101655