Mobile Laser Scanning Data Collected under a Forest Canopy with GNSS/INS-Positioned Systems: Possibilities of Processability Improvements
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Mobile Laser Scanning Data
2.3. Navigation System Data
2.4. Mobile Laser Scanning Data Processing
2.5. GNSS Time-Based Point Clustering
2.6. GNSS Data Processing
2.7. Statistical Analyses
2.7.1. Derivation of the Point Cloud Parameters
2.7.2. Stand-to-Stand Comparison of the Processability and GNSS Signal Availability
2.7.3. Correlation and Regression Analysis
3. Results
3.1. Differences in Processability between the Young and the Mature Stand
3.2. Influence of Point Cloud Parameters on the Processability of the MLS Point Cloud Collected under a Forest Canopy
3.3. Influence of GNSS Signal Availability on the Processability of the MLS Point Cloud Collected under a Forest Canopy
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hyyppä, E.; Yu, X.; Kaartinen, H.; Hakala, T.; Kukko, A.; Vastaranta, M.; Hyyppä, J. Comparison of Backpack, Handheld, Under-Canopy UAV, and Above-Canopy UAV Laser Scanning for Field Reference Data Collection in Boreal Forests. Remote Sens. 2020, 12, 3327. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Vastaranta, M.; Holopainen, M.; Yu, X.; Haapanen, R.; Melkas, T.; Hyyppä, J.; Hyyppä, H. Individual tree detection and area-based approach in retrieval of forest inventory characteristics from low-pulse airborne laser scanning data. Photogramm. J. Finl. 2011, 22, 1–13. [Google Scholar]
- Sačkov, I.; Kulla, L.; Bucha, T. A Comparison of Two Tree Detection Methods for Estimation of Forest Stand and Ecological Variables from Airborne LiDAR Data in Central European Forests. Remote Sens. 2019, 11, 1431. [Google Scholar] [CrossRef]
- Goodbody, T.R.; Tompalski, P.; Coops, N.C.; Hopkinson, C.; Treitz, P.; van Ewijk, K. Forest Inventory and Diversity Attribute Modelling Using Structural and Intensity Metrics from Multi-Spectral Airborne Laser Scanning Data. Remote Sens. 2020, 12, 2109. [Google Scholar] [CrossRef]
- Parkitna, K.; Krok, G.; Miscicki, S.; Ukalski, K.; Lisanczuk, M.; Mitelsztedt, K.; Magnussen, S.; Markiewicz, A.; Sterenczak, K. Modelling growing stock volume of forest stands with various ALS area-based approaches. For. Int. J. For. Res. 2021, 94, 630–650. [Google Scholar] [CrossRef]
- Brovkina, O.; Navrátilová, B.; Novotný, J.; Albert, J.; Slezák, L.; Cienciala, E. Influences of vegetation, model, and data parameters on forest aboveground biomass assessment using an area-based approach. Ecol. Inform. 2022, 70, 101754. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Hyyppä, E.; Hyyppä, J.; Hakala, T.; Kukko, A.; Wulder, M.A.; White, J.C.; Pyörälä, J.; Yu, X.; Wang, Y.; Virtanen, J.-P.; et al. Under-canopy UAV laser scanning for accurate forest field measurements. ISPRS J. Photogramm. Remote Sens. 2020, 164, 41–60. [Google Scholar] [CrossRef]
- Bruggisser, M.M. Improving Forest Mensurations with High Resolution Point Clouds. Doctoral Dissertation, Technische Universität Wien, Vienna, Austria, 2021. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.; Onda, Y.; Hashimoto, A.; Gomi, T.; Chiu, C.; Inokoshi, S. A tree detection method based on trunk point cloud section in dense plantation forest using drone LiDAR data. For. Ecosyst. 2023, 10, 100088. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest Inventory with Long Range and High-Speed Personal Laser Scanning (PLS) and Simultaneous Localization and Mapping (SLAM) Technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Aguiar, A.S.; dos Santos, F.N.; Cunha, J.B.; Sobreira, H.; Sousa, A.J. Localization and Mapping for Robots in Agriculture and Forestry: A Survey. Robotics 2020, 9, 97. [Google Scholar] [CrossRef]
- Di Stefano, F.; Chiappini, S.; Gorreja, A.; Balestra, M.; Pierdicca, R. Mobile 3D scan LiDAR: A literature review. Geomat. Nat. Hazards Risk 2021, 12, 2387–2429. [Google Scholar] [CrossRef]
- Liang, X.; Kukko, A.; Balenovic, I.; Saarinen, N.; Junttila, S.; Kankare, V.; Holopainen, M.; Mokros, M.; Surovy, P.; Kaartinen, H.; et al. Close-Range Remote Sensing of Forests: The state of the art, challenges, and opportunities for systems and data acquisitions. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–71. [Google Scholar] [CrossRef]
- Brolly, G.; Király, G. Algorithms for Stem Mapping by Means of Terrestrial Laser Scanning. Acta Silv. Et Lignaria Hung. 2009, 5, 119–130. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree Stem and Height Measurements using Terrestrial Laser Scanning and the RANSAC Algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef]
- Koreň, M.; Mokroš, M.; Bucha, T. Accuracy of tree diameter estimation from terrestrial laser scanning by circle-fitting methods. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 122–128. [Google Scholar] [CrossRef]
- Saarinen, N.; Kankare, V.; Vastaranta, M.; Luoma, V.; Pyörälä, J.; Tanhuanpää, T.; Liang, X.; Kaartinen, H.; Kukko, A.; Jaakkola, A.; et al. Feasibility of Terrestrial laser scanning for collecting stem volume information from single trees. ISPRS J. Photogramm. Remote Sens. 2017, 123, 140–158. [Google Scholar] [CrossRef]
- Rönnholm, P.; Liang, X.; Kukko, A.; Jaakkola, A.; Hyyppä, J. Quality analysis and correction of mobile backpack laser scanning data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-1, 41–47. [Google Scholar] [CrossRef]
- Tjernqvist, M. Backpack-Based Inertial Navigation and LiDAR Mapping in Forest Environments; Umeå University: Umeå, Sweden, 2017. [Google Scholar]
- Hyyppä, E.; Kukko, A.; Kaijaluoto, R.; White, J.C.; Wulder, M.A.; Pyörälä, J.; Liang, X.; Yu, X.; Wang, Y.; Kaartinen, H.; et al. Accurate derivation of stem curve and volume using backpack mobile laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 161, 246–262. [Google Scholar] [CrossRef]
- Chudá, J.; Kadlečík, R.; Mokroš, M.; Mikita, T.; Tuček, J.; Chudý, F. Slam and ins based positional accuracy assessment of natural and artificial objects under the forest canopy. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, XLIII-B1-2, 197–205. [Google Scholar] [CrossRef]
- Ryding, J.; Williams, E.; Smith, M.J.; Eichhorn, M.P. Assessing Handheld Mobile Laser Scanners for Forest Surveys. Remote Sens. 2015, 7, 1095–1111. [Google Scholar] [CrossRef]
- Zhou, S.; Kang, F.; Li, W.; Kan, J.; Zheng, Y.; He, G. Extracting Diameter at Breast Height with a Handheld Mobile LiDAR System in an Outdoor Environment. Sensors 2019, 19, 3212. [Google Scholar] [CrossRef]
- Tockner, A.; Gollob, C.; Kraßnitzer, R.; Ritter, T.; Nothdurft, A. Automatic tree crown segmentation using dense forest point clouds from Personal Laser Scanning (PLS). Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103025. [Google Scholar] [CrossRef]
- Tomaštík, J.; Saloň, Š.; Tunák, D.; Chudý, F.; Kardoš, M. Tango in forests—An initial experience of the use of the new Google technology in connection with forest inventory tasks. Comput. Electron. Agric. 2017, 141, 109–117. [Google Scholar] [CrossRef]
- McGlade, J.; Wallace, L.; Hally, B.; White, A.; Reinke, K.; Jones, S. An early exploration of the use of the Microsoft Azure Kinect for estimation of urban tree Diameter at Breast Height. Remote Sens. Lett. 2020, 11, 963–972. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Kraßnitzer, R.; Tockner, A.; Nothdurft, A. Measurement of Forest Inventory Parameters with Apple iPad Pro and Integrated LiDAR Technology. Remote Sens. 2021, 13, 3129. [Google Scholar] [CrossRef]
- Bobrowski, R.; Winczek, M.; Zięba-Kulawik, K.; Wężyk, P. Best practices to use the iPad Pro LiDAR for some procedures of data acquisition in the urban forest. Urban For. Urban Green. 2023, 79, 127815. [Google Scholar] [CrossRef]
- Giannetti, F.; Puletti, N.; Quatrini, V.; Travaglini, D.; Bottalico, F.; Corona, P.; Chirici, G. Integrating terrestrial and airborne laser scanning for the assessment of single-tree attributes in Mediterranean forest stands. Eur. J. Remote Sens. 2018, 51, 795–807. [Google Scholar] [CrossRef]
- Maltamo, M.; Hauglin, M.; Naesset, E.; Gobakken, T. Estimating stand level stem diameter distribution utilizing harvester data and airborne laser scanning. Silva Fenn. 2019, 53, 1–19. [Google Scholar] [CrossRef]
- Keefe, R.F.; Zimbelman, E.G.; Picchi, G. Use of Individual Tree and Product Level Data to Improve Operational Forestry. Curr. For. Rep. 2022, 8, 148–165. [Google Scholar] [CrossRef]
- Gallo, R.; Visser, R.; Mazzetto, F. Developing an Automated Monitoring System for Cable Yarding Systems. Croat. J. For. Eng. 2021, 42, 213–225. [Google Scholar] [CrossRef]
- Gollob, C.; Krassnitzer, R.; Nothdurft, A.; Ritter, T.; Tockner, A.; Erber, G.; Kühmaier, M.; Hönigsberger, F.; Varch, T.; Holzinger, A.; et al. Measurement of Individual Tree Parameters with Carriage-Based Laser Scanning in Cable Yarding Operations. Croat. J. For. Eng. 2023, 44, 401–417. [Google Scholar] [CrossRef]
- Demol, M.; Verbeeck, H.; Gielen, B.; Armston, J.; Burt, A.; Disney, M.; Duncanson, L.; Hackenberg, J.; Kükenbrink, D.; Lau, A.; et al. Estimating forest above-ground biomass with terrestrial laser scanning: Current status and future directions. Methods Ecol. Evol. 2022, 13, 1628–1639. [Google Scholar] [CrossRef]
- Borsah, A.A.; Nazeer, M.; Wong, M.S. LIDAR-Based Forest Biomass Remote Sensing: A Review of Metrics, Methods, and Assessment Criteria for the Selection of Allometric Equations. Forests 2023, 14, 2095. [Google Scholar] [CrossRef]
- Loudermilk, E.L.; Pokswinski, S.; Hawley, C.M.; Maxwell, A.; Gallagher, M.R.; Skowronski, N.S.; Hudak, A.T.; Hoffman, C.; Hiers, J.K. Terrestrial Laser Scan Metrics Predict Surface Vegetation Biomass and Consumption in a Frequently Burned Southeastern U.S. Ecosystem. Fire 2023, 6, 151. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H. Estimation of LAI with the LiDAR Technology: A Review. Remote Sens. 2020, 12, 3457. [Google Scholar] [CrossRef]
- Patočka, Z.; Novosadová, K.; Haninec, P.; Pokorný, R.; Mikita, T.; Klimánek, M. Comparison of LiDAR-based Models for True Leaf Area Index and Effective Leaf Area Index Estimation in Young Beech Forests. Acta Univ. Agric. Et Silvic. Mendel. Brun. 2020, 68, 559–566. [Google Scholar] [CrossRef]
- Valbuena, R.; O’connor, B.; Zellweger, F.; Simonson, W.; Vihervaara, P.; Maltamo, M.; Silva, C.; Almeida, D.; Danks, F.; Morsdorf, F.; et al. Standardizing Ecosystem Morphological Traits from 3D Information Sources. Trends Ecol. Evol. 2020, 35, 656–667. [Google Scholar] [CrossRef]
- Koma, Z.; Zlinszky, A.; Bekő, L.; Burai, P.; Seijmonsbergen, A.C.; Kissling, W.D. Quantifying 3D vegetation structure in wetlands using differently measured airborne laser scanning data. Ecol. Indic. 2021, 127, 107752. [Google Scholar] [CrossRef]
- Yrttimaa, T. Characterizing tree communities in space and time using point clouds. Diss. For. 2021, 2021, 314. [Google Scholar] [CrossRef]
- Neuville, R.; Bates, J.S.; Jonard, F. Estimating Forest Structure from UAV-Mounted LiDAR Point Cloud Using Machine Learning. Remote Sens. 2021, 13, 352. [Google Scholar] [CrossRef]
- Kissling, W.; Shi, Y. Which metrics derived from airborne laser scanning are essential to measure the vertical profile of ecosystems? Divers. Distrib. 2023, 29, 1315–1320. [Google Scholar] [CrossRef]
- Moudrý, V.; Cord, A.F.; Gábor, L.; Laurin, G.V.; Barták, V.; Gdulová, K.; Malavasi, M.; Rocchini, D.; Stereńczak, K.; Prošek, J.; et al. Vegetation structure derived from airborne laser scanning to assess species distribution and habitat suitability: The way forward. Divers. Distrib. 2022, 29, 39–50. [Google Scholar] [CrossRef]
- Qian, C.; Liu, H.; Tang, J.; Chen, Y.; Kaartinen, H.; Kukko, A.; Zhu, L.; Liang, X.; Chen, L.; Hyyppä, J. An Integrated GNSS/INS/LiDAR-SLAM Positioning Method for Highly Accurate Forest Stem Mapping. Remote Sens. 2016, 9, 3. [Google Scholar] [CrossRef]
- Liang, X.; Kukko, A.; Hyyppä, J.; Lehtomäki, M.; Pyörälä, J.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Wang, Y. In-situ measurements from mobile platforms: An emerging approach to address the old challenges associated with forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 143, 97–107. [Google Scholar] [CrossRef]
- Bienert, A.; Georgi, L.; Kunz, M.; von Oheimb, G.; Maas, H.-G. Automatic extraction and measurement of individual trees from mobile laser scanning point clouds of forests. Ann. Bot. 2021, 128, 787–804. [Google Scholar] [CrossRef] [PubMed]
- Vatandaşlar, C.; Seki, M.; Zeybek, M. Assessing the potential of mobile laser scanning for stand-level forest inventories in near-natural forests. For. Int. J. For. Res. 2023, 96, 448–464. [Google Scholar] [CrossRef]
- Åkerblom, M.; Kaitaniemi, P. Terrestrial laser scanning: A new standard of forest measuring and modelling? Ann. Bot. 2021, 128, 653–662. [Google Scholar] [CrossRef]
- Hunčaga, M.; Chudá, J.; Tomaštík, J.; Slámová, M.; Koreň, M.; Chudý, F. The Comparison of Stem Curve Accuracy Determined from Point Clouds Acquired by Different Terrestrial Remote Sensing Methods. Remote Sens. 2020, 12, 2739. [Google Scholar] [CrossRef]
- Jung, J.; Che, E.; Olsen, M.J.; Parrish, C. Efficient and robust lane marking extraction from mobile lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 147, 1–18. [Google Scholar] [CrossRef]
- Balado, J.; González, E.; Arias, P.; Castro, D. Novel Approach to Automatic Traffic Sign Inventory Based on Mobile Mapping System Data and Deep Learning. Remote Sens. 2020, 12, 442. [Google Scholar] [CrossRef]
- Justo, A.; Soilán, M.; Sánchez-Rodríguez, A.; Riveiro, B. Scan-to-BIM for the infrastructure domain: Generation of IFC-compliant models of road infrastructure assets and semantics using 3D point cloud data. Autom. Constr. 2021, 127, 103703. [Google Scholar] [CrossRef]
- Xu, Y.; Stilla, U. Toward Building and Civil Infrastructure Reconstruction From Point Clouds: A Review on Data and Key Techniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2857–2885. [Google Scholar] [CrossRef]
- Puente, I.; González-Jorge, H.; Martínez-Sánchez, J.; Arias, P. Review of mobile mapping and surveying technologies. Measurement 2013, 46, 2127–2145. [Google Scholar] [CrossRef]
- DeCesare, N.J.; Squires, J.R.; Kolbe, J.A. Effect of forest canopy on GPS-based movement data. Wildl. Soc. Bull. 2005, 33, 935–941. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Vastaranta, M.; Kukko, A.; Jaakkola, A.; Yu, X.; Pyörälä, J.; Liang, X.; Liu, J.; Wang, Y.; et al. Accuracy of Kinematic Positioning Using Global Satellite Navigation Systems under Forest Canopies. Forests 2015, 6, 3218–3236. [Google Scholar] [CrossRef]
- Brach, M.; Stereńczak, K.; Bolibok, L.; Kwaśny, Ł.; Krok, G.; Laszkowski, M. Impacts of forest spatial structure on variation of the multipath phenomenon of navigation satellite signals. Folia For. Pol. Ser. A For. 2019, 61, 3–21. [Google Scholar] [CrossRef]
- Feng, T.; Chen, S.; Feng, Z.; Shen, C.; Tian, Y. Effects of Canopy and Multi-Epoch Observations on Single-Point Positioning Errors of a GNSS in Coniferous and Broadleaved Forests. Remote Sens. 2021, 13, 2325. [Google Scholar] [CrossRef]
- Rybansky, M.; Kratochvíl, V.; Dohnal, F.; Gerold, R.; Kristalova, D.; Stodola, P.; Nohel, J. GNSS Signal Quality in Forest Stands for Off-Road Vehicle Navigation. Appl. Sci. 2023, 13, 6142. [Google Scholar] [CrossRef]
- Merry, K.; Bettinger, P. Smartphone GPS accuracy study in an urban environment. PLoS ONE 2019, 14, e0219890. [Google Scholar] [CrossRef] [PubMed]
- Boguspayev, N.; Akhmedov, D.; Raskaliyev, A.; Kim, A.; Sukhenko, A. A Comprehensive Review of GNSS/INS Integration Techniques for Land and Air Vehicle Applications. Appl. Sci. 2023, 13, 4819. [Google Scholar] [CrossRef]
- Zhang, H.; Xiong, H.; Hao, S.; Yang, G.; Wang, M.; Chen, Q. A Novel Multidimensional Hybrid Position Compensation Method for INS/GPS Integrated Navigation Systems During GPS Outages. IEEE Sens. J. 2023, 24, 962–974. [Google Scholar] [CrossRef]
- Danskin, S.; Bettinger, P.; Jordan, T. Multipath Mitigation under Forest Canopies: A Choke Ring Antenna Solution. For. Sci. 2009, 55, 109–116. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, C.; Chen, T.; Zhao, X.; Liu, C.; Hu, H.; Zhou, T.; Xin, H. Real-Time Multipath Mitigation in Multi-GNSS Short Baseline Positioning via CNN-LSTM Method. Math. Probl. Eng. 2021, 2021, 6573230. [Google Scholar] [CrossRef]
- Brach, M. Rapid Static Positioning Using a Four System GNSS Receivers in the Forest Environment. Forests 2022, 13, 45. [Google Scholar] [CrossRef]
- Li, T.; Pei, L.; Xiang, Y.; Zuo, X.; Yu, W.; Truong, T. P3-LINS: Tightly Coupled PPP-GNSS/INS/LiDAR Navigation System With Effective Initialization. IEEE Trans. Instrum. Meas. 2023, 72, 1–13. [Google Scholar] [CrossRef]
- Pires, R.d.P.; Olofsson, K.; Persson, H.J.; Lindberg, E.; Holmgren, J. Individual tree detection and estimation of stem attributes with mobile laser scanning along boreal forest roads. ISPRS J. Photogramm. Remote Sens. 2022, 187, 211–224. [Google Scholar] [CrossRef]
- Ferenčík, M.; Kardoš, M.; Allman, M.; Slatkovská, Z. Detection of forest road damage using mobile laser profilometry. Comput. Electron. Agric. 2019, 166, 105010. [Google Scholar] [CrossRef]
- Kweon, H.; Seo, J.I.; Lee, J.-W. Assessing the Applicability of Mobile Laser Scanning for Mapping Forest Roads in the Republic of Korea. Remote Sens. 2020, 12, 1502. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Lu, Z.; Hu, Z.; Uchimura, K. SLAM Estimation in Dynamic Outdoor Environments: A Review. In Proceedings of the Intelligent Robotics and Applications: Second International Conference, ICIRA 2009, Singapore, 16–18 December 2009. [Google Scholar]
- Tourani, A.; Bavle, H.; Sanchez-Lopez, J.L.; Voos, H. Visual SLAM: What Are the Current Trends and What to Expect? Sensors 2022, 22, 9297. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Tan, J.; Liu, H.; Xie, H.; Chen, C. Automatic non-rigid registration of multi-strip point clouds from mobile laser scanning systems. Int. J. Remote Sens. 2017, 39, 1713–1728. [Google Scholar] [CrossRef]
- Chen, W.; Zhou, C.; Shang, G.; Wang, X.; Li, Z.; Xu, C.; Hu, K. SLAM Overview: From Single Sensor to Heterogeneous Fusion. Remote Sens. 2022, 14, 6033. [Google Scholar] [CrossRef]
- Nevalainen, P.; Li, Q.; Melkas, T.; Riekki, K.; Westerlund, T.; Heikkonen, J. Navigation and Mapping in Forest Environment Using Sparse Point Clouds. Remote Sens. 2020, 12, 4088. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, B.; Zhou, J.; Yan, Y.; Tian, G.; Gu, B. Recent developments and applications of simultaneous localization and mapping in agriculture. J. Field Robot. 2022, 39, 956–983. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, T.; Fei, S.; Habib, A. Forest feature lidar slam (f2-lslam) and integrated scan simultaneous trajectory enhancement and mapping (is2-team) for accurate forest inventory using backpack systems. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-1/W, 1823–1830. [Google Scholar] [CrossRef]
- Tang, J.; Chen, Y.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Khoramshahi, E.; Hakala, T.; Hyyppä, J.; Holopainen, M.; Hyyppä, H. SLAM-Aided Stem Mapping for Forest Inventory with Small-Footprint Mobile LiDAR. Forests 2015, 6, 4588–4606. [Google Scholar] [CrossRef]
- Balenović, I.; Liang, X.; Jurjević, L.; Hyyppä, J.; Seletković, A.; Kukko, A. Hand-Held Personal Laser Scanning. Croat. J. For. Eng. 2020, 42, 165–183. [Google Scholar] [CrossRef]
- Del Perugia, B.; Giannetti, F.; Chirici, G.; Travaglini, D. Influence of Scan Density on the Estimation of Single-Tree Attributes by Hand-Held Mobile Laser Scanning. Forests 2019, 10, 277. [Google Scholar] [CrossRef]
- Chahine, G.; Vaidis, M.; Pomerleau, F.; Pradalier, C. Mapping in unstructured natural environment: A sensor fusion framework for wearable sensor suites. SN Appl. Sci. 2021, 3, 1–14. [Google Scholar] [CrossRef]
- Jia, F.; Lichti, D.D. A Practical Algorithm for the Viewpoint Planning of Terrestrial Laser Scanners. Geomatics 2022, 2, 181–196. [Google Scholar] [CrossRef]
- Kuželka, K.; Marušák, R.; Surový, P. Inventory of close-to-nature forest stands using terrestrial mobile laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103104. [Google Scholar] [CrossRef]
- Čerňava, J.; Mokroš, M.; Tuček, J.; Antal, M.; Slatkovská, Z. Processing Chain for Estimation of Tree Diameter from GNSS-IMU-Based Mobile Laser Scanning Data. Remote Sens. 2019, 11, 615. [Google Scholar] [CrossRef]
- Angelats, E.; Colomina, I. ONE STEP MOBILE MAPPING LASER AND CAMERA DATA ORIENTATION AND CALIBRATION. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-3/W1. [Google Scholar] [CrossRef]
- Yang, B.; Li, Y.; Zou, X.; Dong, Z. A marker-free calibration method for mobile laser scanning point clouds correction. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B2-2, 347–354. [Google Scholar] [CrossRef]
- Almqvist, H.; Magnusson, M.; Kucner, T.P.; Lilienthal, A.J. Learning to detect misaligned point clouds. J. Field Robot. 2017, 35, 662–677. [Google Scholar] [CrossRef]
- Li, L.; Wang, R.; Zhang, X. A Tutorial Review on Point Cloud Registrations: Principle, Classification, Comparison, and Technology Challenges. Math. Probl. Eng. 2021, 2021, 1–32. [Google Scholar] [CrossRef]
- Han, J.-Y.; Chen, C.-S.; Lo, C.-T. Time-Variant Registration of Point Clouds Acquired by a Mobile Mapping System. IEEE Geosci. Remote Sens. Lett. 2013, 11, 196–199. [Google Scholar] [CrossRef]
- Takai, S.; Date, H.; Kanai, S.; Niina, Y.; Oda, K.; Ikeda, T. Accurate registration of MMS point clouds of urban areas using trajectory. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, II-5/W2, 277–282. [Google Scholar] [CrossRef]
- Huang, X.; Mei, G.; Zhang, J.; Abbas, R. A comprehensive survey on point cloud registration. arXiv 2021, arXiv:2103.02690. [Google Scholar]
- Lyu, Y.; Huang, X.; Zhang, Z. CoFi: Coarse-to-Fine ICP for LiDAR Localization in an Efficient Long-lasting Point Cloud Map. arXiv 2021, arXiv:2110.10194. [Google Scholar]
- Guo, D.; Qi, B.; Wang, C. Fast clustering method of LiDAR point clouds from coarse-to-fine. Infrared Phys. Technol. 2023, 129, 104544. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Proceedings Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Glira, P.; Pfeifer, N.; Briese, C.; Ressl, C. A Correspondence Framework for ALS Strip Adjustments based on Variants of the ICP Algorithm. Photogramm. Fernerkund. Geoinf. 2015, 2015, 275–289. [Google Scholar] [CrossRef]
- Tazir, M.L.; Gokhool, T.; Checchin, P.; Malaterre, L.; Trassoudaine, L. Cluster ICP: Towards Sparse to Dense Registration. In Intelligent Autonomous Systems 15; Strand, M., Dillmann, R., Menegatti, E., Ghidoni, S., Eds.; IAS 2018, Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2019; Volume 867. [Google Scholar] [CrossRef]
- CLOUD COMPARE. CloudCompare Version 2.6.1—User Manual. 2015. Available online: https://www.danielgm.net/cc/doc/qCC/CloudCompare%20v2.6.1%20-%20User%20manual.pdf (accessed on 14 April 2023).
- Yang, X.-S. Cuckoo Search (cs) Algorithm. mATLAB Central File Exchange. 2021. Available online: https://www.mathworks.com/matlabcentral/fileexchange/29809-cuckoo-search-cs-algorithm (accessed on 14 April 2023).
- Yin, C.; Yang, B.; Cheng, J.C.; Gan, V.J.; Wang, B.; Yang, J. Label-efficient semantic segmentation of large-scale industrial point clouds using weakly supervised learning. Autom. Constr. 2023, 148, 104757. [Google Scholar] [CrossRef]
- Kim, M.; Kim, H. Optimal Pre-processing of Laser Scanning Data for Indoor Scene Analysis and 3D Reconstruction of Building Models. KSCE J. Civ. Eng. 2024, 28, 1–14. [Google Scholar] [CrossRef]
- Zhao, K.; Xu, Y.C.; Wang, R.D. A preprocessing method of 3D point clouds registration in urban environments. Opto-Electron. Eng. 2018, 45, 180266. [Google Scholar]
- Wang, P.; Gu, T.; Sun, B.; Huang, D.; Sun, K. Research on 3D Point Cloud Data Preprocessing and Clustering Algorithm of Obstacles for Intelligent Vehicle. World Electr. Veh. J. 2022, 13, 130. [Google Scholar] [CrossRef]
- Wu, C.; Yuan, Y.; Tang, Y.; Tian, B. Application of Terrestrial Laser Scanning (TLS) in the Architecture, Engineering and Construction (AEC) Industry. Sensors 2021, 22, 265. [Google Scholar] [CrossRef] [PubMed]
- Bae, K.; Belton, D.; Lichti, D.D. Pre-processing procedures for raw point clouds from terrestrial laser scanners. J. Spat. Sci. 2007, 52, 65–74. [Google Scholar] [CrossRef]
- Zhu, M.; Leng, B.; Xiao, C.; Hou, G.; Yao, X.; Li, K. Research on Fast Pre-Processing Method of Tunnel Point Cloud Data in Complex Environment. J. Phys. Conf. Ser. 2022, 2185, 012038. [Google Scholar] [CrossRef]
- Boavida, J.; Oliveira, A. Precise Long Tunnel Survey using the Riegl VMX-250 Mobile Laser Scanning System. In Proceedings of the 2012 RIEGL International Airborne and Mobile User Conference, Orlando, FL, USA, 27 February–1 March 2012. [Google Scholar]
- Bienert, A.; Georgi, L.; Kunz, M.; Maas, H.-G.; Von Oheimb, G. Comparison and Combination of Mobile and Terrestrial Laser Scanning for Natural Forest Inventories. Forests 2018, 9, 395. [Google Scholar] [CrossRef]
- Levene, H. Robust tests for equality of variances. In Contributions to Probability and Statistics, Stanford Studies in Mathematics and Statistics, 2; Stanford University Press: Stanford, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Gastwirth, J.L.; Gel, Y.R.; Miao, W. The Impact of Levene’s Test of Equality of Variances on Statistical Theory and Practice. Stat. Sci. 2009, 24, 343–360. [Google Scholar] [CrossRef]
- West, R.M. Best practice in statistics: The use of log transformation. Ann. Clin. Biochem. Int. J. Biochem. Lab. Med. 2021, 59, 162–165. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Wang, H.; Lu, N.; Chen, T.; He, H.; Lu, Y.; Tu, X.M. Log-transformation and its implications for data analysis. Shanghai Arch. Psychiatry 2014, 26, 105–109. [Google Scholar]
- Langley, R.B. Dilution of precision. GPS World 1999, 10, 52–59. [Google Scholar]
- Kurum, M.; Farhad, M.M.; Boyd, D.R. Gnss transmissometry (GNSS-T): Modeling propagation of GNSS signals through forest canopy. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 4695–4698. [Google Scholar]
- Faitli, T.; Hakala, T.; Kaartinen, H.; Hyyppä, J.; Kukko, A. Real-time lidar-inertial positioning and mapping for forestry automation. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-1/W, 145–150. [Google Scholar] [CrossRef]
- Muhojoki, J.; Hakala, T.; Kukko, A.; Kaartinen, H.; Hyyppä, J. Comparing positioning accuracy of mobile laser scanning systems under a forest canopy. Sci. Remote Sens. 2024, 9, 100121. [Google Scholar] [CrossRef]
- Wang, G.; Han, Y.; Chen, J.; Wang, S.; Zhang, Z.; Du, N.; Zheng, Y. A GNSS/INS Integrated Navigation Algorithm Based on Kalman Filter. IFAC-Pap. 2018, 51, 232–237. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Zhang, L.; Li, Q.; Wu, J. Tightly Coupled GNSS/INS Integration with Robust Sequential Kalman Filter for Accurate Vehicular Navigation. Sensors 2020, 20, 561. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, J.; Zhang, C.; Li, Y.; Yan, P.; Meng, X. A Novel Optimal Robust Adaptive Scheme for Accurate GNSS RTK/INS Tightly Coupled Integration in Urban Environments. Remote Sens. 2023, 15, 3725. [Google Scholar] [CrossRef]
- Boer, J.D.; Calmettes, V.; Tourneret, J.; Lesot, B. Outage mitigation for GNSS/MEMS navigation using neural networks. In Proceedings of the 2009 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 2156–2160. [Google Scholar]
- Torino, P.D.; Wu, F.; Dovis, F. SINS/GNSS Tighty Coupled Integration based on a Radial Basis Function Neural Network. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2020. [Google Scholar]
- Siemuri, A.; Selvan, K.; Kuusniemi, H.; Valisuo, P.; Elmusrati, M.S. A Systematic Review of Machine Learning Techniques for GNSS Use Cases. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5043–5077. [Google Scholar] [CrossRef]
- Zhao, S.; Zhou, Y.; Huang, T. A Novel Method for AI-Assisted INS/GNSS Navigation System Based on CNN-GRU and CKF during GNSS Outage. Remote Sens. 2022, 14, 4494. [Google Scholar] [CrossRef]
- Lee, W.-J.; Yu, W.-S.; Choi, Y.-S.; Yoon, H.-S. Improvement of Network RTK Positioning in Urban and Forest Land Using BeiDou. J. Digit. Contents Soc. 2020, 21, 2057–2064. [Google Scholar] [CrossRef]
- Al Bitar, N.; Gavrilov, A.; Khalaf, W. Artificial Intelligence Based Methods for Accuracy Improvement of Integrated Navigation Systems During GNSS Signal Outages: An Analytical Overview. Gyroscopy Navig. 2020, 11, 41–58. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L. A Hybrid Intelligent Algorithm DGP-MLP for GNSS/INS Integration during GNSS Outages. J. Navig. 2018, 72, 375–388. [Google Scholar] [CrossRef]
- Fang, W.; Jiang, J.; Lu, S.; Gong, Y.; Tao, Y.; Tang, Y.; Yan, P.; Luo, H.; Liu, J. A LSTM Algorithm Estimating Pseudo Measurements for Aiding INS during GNSS Signal Outages. Remote Sens. 2020, 12, 256. [Google Scholar] [CrossRef]
- Zhi, Z.; Liu, D.; Liu, L. A performance compensation method for GPS/INS integrated navigation system based on CNN–LSTM during GPS outages. Measurement 2021, 188, 110516. [Google Scholar] [CrossRef]
- Chiang, K.; Tsai, G.; Chang, H.; Joly, C.; El-Sheimy, N. Seamless navigation and mapping using an INS/GNSS/grid-based SLAM semi-tightly coupled integration scheme. Inf. Fusion. 2019, 50, 181–196. [Google Scholar] [CrossRef]
- Chiang, K.; Le, D.T.; Duong, T.T.; Sun, R. The Performance Analysis of INS/GNSS/V-SLAM Integration Scheme Using Smartphone Sensors for Land Vehicle Navigation Applications in GNSS-Challenging Environments. Remote Sens. 2020, 12, 1732. [Google Scholar] [CrossRef]
- You, B.; Zhong, G.; Chen, C.; Li, J.; Ma, E. A Simultaneous Localization and Mapping System Using the Iterative Error State Kalman Filter Judgment Algorithm for Global Navigation Satellite System. Sensors 2023, 23, 6000. [Google Scholar] [CrossRef]
- Khoshelham, K.; Ramezani, M. Vehicle positioning in the absence of GNSS signals: Potential of visual-inertial odometry. In Proceedings of the 2017 Joint Urban Remote Sensing Event (JURSE), Dubai, United Arab Emirates, 6–8 March 2017; pp. 1–4. [Google Scholar]
- Abosekeen, A.; Karamat, T.B.; Noureldin, A.; Korenberg, M.J. Adaptive cruise control radar-based positioning in GNSS challenging environment. IET Radar Sonar Navig. 2019, 13, 1666–1677. [Google Scholar] [CrossRef]
- Zhu, K.; Guo, X.; Jiang, C.; Xue, Y.; Li, Y.; Han, L.; Chen, Y. MIMU/Odometer Fusion with State Constraints for Vehicle Positioning during BeiDou Signal Outage: Testing and Results. Sensors 2020, 20, 2302. [Google Scholar] [CrossRef]
- Saleh, S.; Bader, Q.; Karaim, M.; Elhabiby, M.; Noureldin, A. Integrated 5G mmWave Positioning in Deep Urban Environments: Advantages and Challenges. arXiv 2023, arXiv:2305.02284v1. [Google Scholar]
- Chang, L.; Niu, X.; Liu, T.; Tang, J.; Qian, C. GNSS/INS/LiDAR-SLAM Integrated Navigation System Based on Graph Optimization. Remote Sens. 2019, 11, 1009. [Google Scholar] [CrossRef]
- Abdelaziz, N.; El-Rabbany, A. An Integrated INS/LiDAR SLAM Navigation System for GNSS-Challenging Environments. Sensors 2022, 22, 4327. [Google Scholar] [CrossRef] [PubMed]
- Chong, T.; Tang, X.; Leng, C.; Yogeswaran, M.; Ng, O.; Chong, Y. Sensor Technologies and Simultaneous Localization and Mapping (SLAM). Procedia Comput. Sci. 2015, 76, 174–179. [Google Scholar] [CrossRef]
- Gupta, H.; Andreasson, H.; Lilienthal, A.J.; Kurtser, P. Robust Scan Registration for Navigation in Forest Environment Using Low-Resolution LiDAR Sensors. Sensors 2023, 23, 4736. [Google Scholar] [CrossRef]
- Agunbiade, O.Y.; Zuva, T. Simultaneous Localization and Mapping in Application to Autonomous Robot. In Proceedings of the 2018 International Conference on Intelligent and Innovative Computing Applications (ICONIC), Mon Tresor, Mauritius, 6–7 December 2018; pp. 1–5. [Google Scholar]
- Li, J.; Liu, Y.; Wang, J.; Yan, M.; Yao, Y. 3D Semantic Mapping Based on Convolutional Neural Networks. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 9303–9308. [Google Scholar]
- Abbas, I.; Liu, J.; Faheem, M.; Noor, R.S.; Shaikh, S.A.; Solangi, K.A.; Raza, S.M. Different sensor based intelligent spraying systems in Agriculture. Sens. Actuators A Phys. 2020, 316, 112265. [Google Scholar] [CrossRef]
- Aldibaja, M.; Suganuma, N.; Yanase, R.; Yoneda, K.; Cao, L. On LIDAR Map Combination: A Graph Slam Module to Generate Accurate and Largescale Maps for Autonomous Driving. In Proceedings of the 2022 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Sapporo, Japan, 11–15 July 2022; pp. 736–743. [Google Scholar]
- Kukko, A.; Kaijaluoto, R.; Kaartinen, H.; Lehtola, V.V.; Jaakkola, A.; Hyyppä, J. Graph SLAM correction for single scanner MLS forest data under boreal forest canopy. ISPRS J. Photogramm. Remote Sens. 2017, 132, 199–209. [Google Scholar] [CrossRef]
- Chudá, J.; Výbošťok, J.; Tomaštík, J.; Chudý, F.; Tunák, D.; Skladan, M.; Tuček, J.; Mokroš, M. Prompt Mapping Tree Positions with Handheld Mobile Scanners Based on SLAM Technology. Land 2024, 13, 93. [Google Scholar] [CrossRef]
- Bienert, A.; Maas, H. Methods for the automatic geometric registration of terrestrial laser scanner point clouds in forest stands. ISPRS Int. Arch. Photogramm. Rem. Sens. Spat. Inf. Sci. 2009, 93–98. [Google Scholar]
- Schaer, P.; Vallet, J. Trajectory Adjustment of Mobile Laser Scan Data in GPS Denied Environments. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 40, 61–64. [Google Scholar] [CrossRef]
- Yogender; Raghavendra, S.; Kushwaha, S.K.P. Role of Ground Control Points (GCPs) in Integration of Terrestrial Laser Scanner (TLS) and Close-range Photogrammetry (CRP). In Applications of Geomatics in Civil Engineering; Ghosh, J., da Silva, I., Eds.; Lecture Notes in Civil Engineering; Springer: Singapore, 2020; Volume 33. [Google Scholar] [CrossRef]
- Kalvoda, P.; Nosek, J.; Kalvodova, P. Influence of Control Points Configuration on the Mobile Laser Scanning Accuracy. IOP Conf. Ser. Earth Environ. Sci. 2021, 906, 012091. [Google Scholar] [CrossRef]
- Yadav, M.; Singh, A.K.; Lohani, B. Extraction of road surface from mobile LiDAR data of complex road environment. Int. J. Remote Sens. 2017, 38, 4655–4682. [Google Scholar] [CrossRef]
- McElhinney, C.P.; Kumar, P.; Cahalane, C.; McCarthy, T. Initial Results From European Road Safety Inspection (EURSI) Mobile Mapping Project. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences: Part 5 Commission V Symposium, Newcastle upon Tyne, UK, 21–24 June 2010; Volume XXXVIII. [Google Scholar]
- Yu, Y.; Li, J.; Guan, H.; Jia, F.; Wang, C. Learning Hierarchical Features for Automated Extraction of Road Markings From 3-D Mobile LiDAR Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 709–726. [Google Scholar] [CrossRef]
- Puente, I.; Akinci, B.; González-Jorge, H.; Díaz-Vilariño, L.; Arias, P. A semi-automated method for extracting vertical clearance and cross sections in tunnels using mobile LiDAR data. Tunn. Undergr. Space Technol. 2016, 59, 48–54. [Google Scholar] [CrossRef]
- Wang, H.; Luo, H.; Wen, C.; Cheng, J.; Li, P.; Chen, Y.; Wang, C.; Li, J. Road Boundaries Detection Based on Local Normal Saliency From Mobile Laser Scanning Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2085–2089. [Google Scholar] [CrossRef]
- Balado, J.; Díaz-Vilariño, L.; Arias, P.; Garrido, I. Point clouds to indoor/outdoor accessibility diagnosis. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume IV-2/W4, 2017 ISPRS Geospatial Week 2017, Wuhan, China, 18–22 September 2017. [Google Scholar]
- Yang, B.; Fang, L.; Li, J. Semi-automated extraction and delineation of 3D roads of street scene from mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 79, 80–93. [Google Scholar] [CrossRef]
- Zhong, M.; Sui, L.; Wang, Z.; Yang, X.; Zhang, C.; Chen, N. Recovering Missing Trajectory Data for Mobile Laser Scanning Systems. Remote Sens. 2020, 12, 899. [Google Scholar] [CrossRef]
- Tam, G.K.; Cheng, Z.-Q.; Lai, Y.-K.; Langbein, F.C.; Liu, Y.; Marshall, D.; Martin, R.R.; Sun, X.-F.; Rosin, P.L. Registration of 3D Point Clouds and Meshes: A Survey from Rigid to Nonrigid. IEEE Trans. Vis. Comput. Graph. 2012, 19, 1199–1217. [Google Scholar] [CrossRef]
- Bellekens, B.; Spruyt, V.; Berkvens, R.; Weyn, M. A survey of rigid 3d pointcloud registration algorithms. In Proceedings of the AMBIENT 2014: The Fourth International Conference on Ambient Computing, Applications, Services and Technologies, Rome, Italy, 24–28 August 2014; pp. 8–13. [Google Scholar]
- Yang, B.; Dong, Z.; Liang, F.; Liu, Y. Automatic registration of large-scale urban scene point clouds based on semantic feature points. ISPRS J. Photogramm. Remote Sens. 2016, 113, 43–58. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, B.; Liang, F.; Dong, Z. Iterative global similarity points: A robust coarse-to-fine integration solution for pairwise 3d point cloud registration. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 180–189. [Google Scholar]
- Huang, X.; Zhang, J.; Wu, Q.; Fan, L.; Yuan, C. A Coarse-to-Fine Algorithm for Matching and Registration in 3D Cross-Source Point Clouds. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2965–2977. [Google Scholar] [CrossRef]
- Choy, C.B.; Dong, W.; Koltun, V. Deep Global Registration. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 2511–2520. [Google Scholar]
- He, Y.; Liang, B.; Yang, J.; Li, S.; He, J. An Iterative Closest Points Algorithm for Registration of 3D Laser Scanner Point Clouds with Geometric Features. Sensors 2017, 17, 1862. [Google Scholar] [CrossRef]
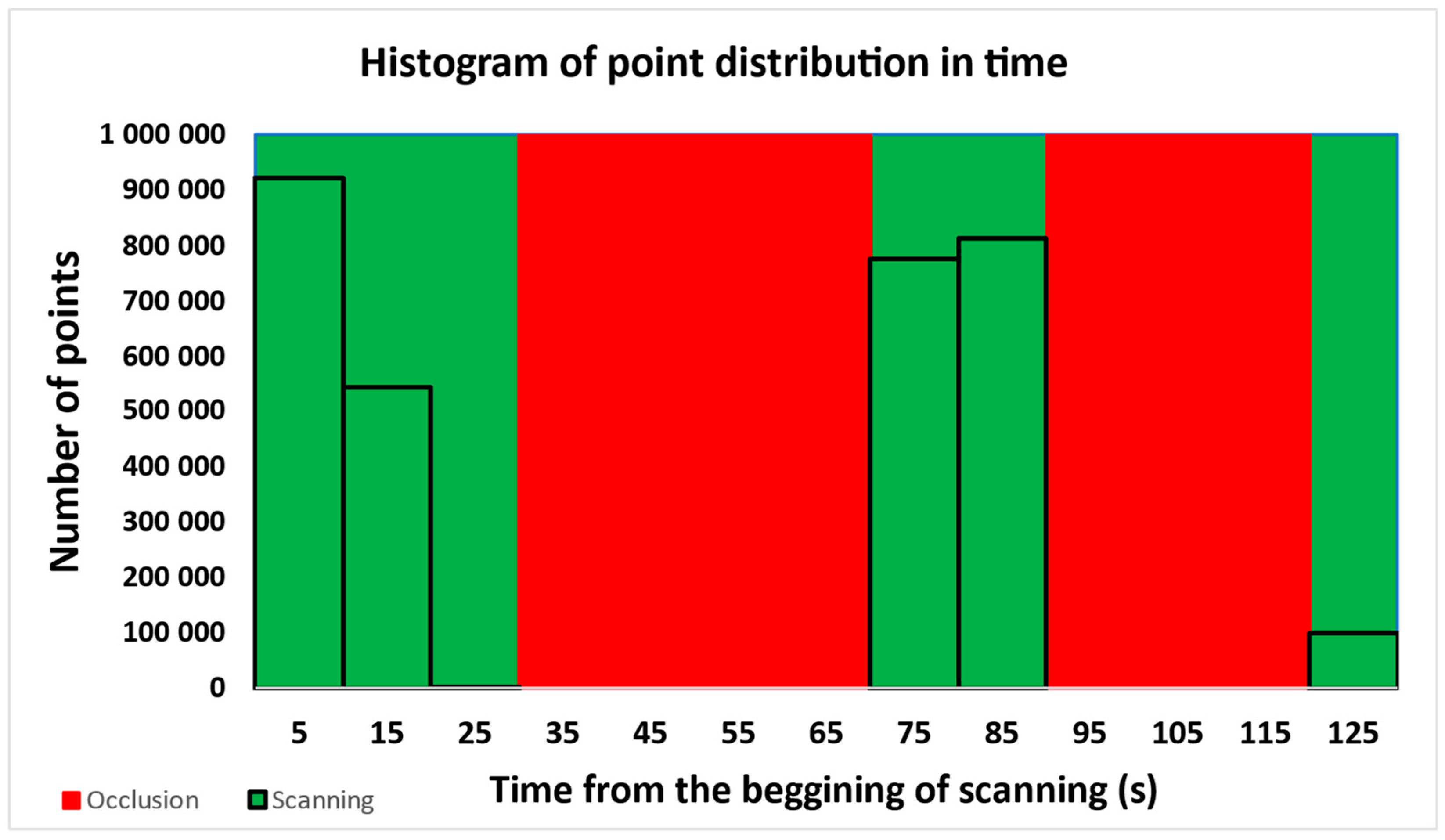




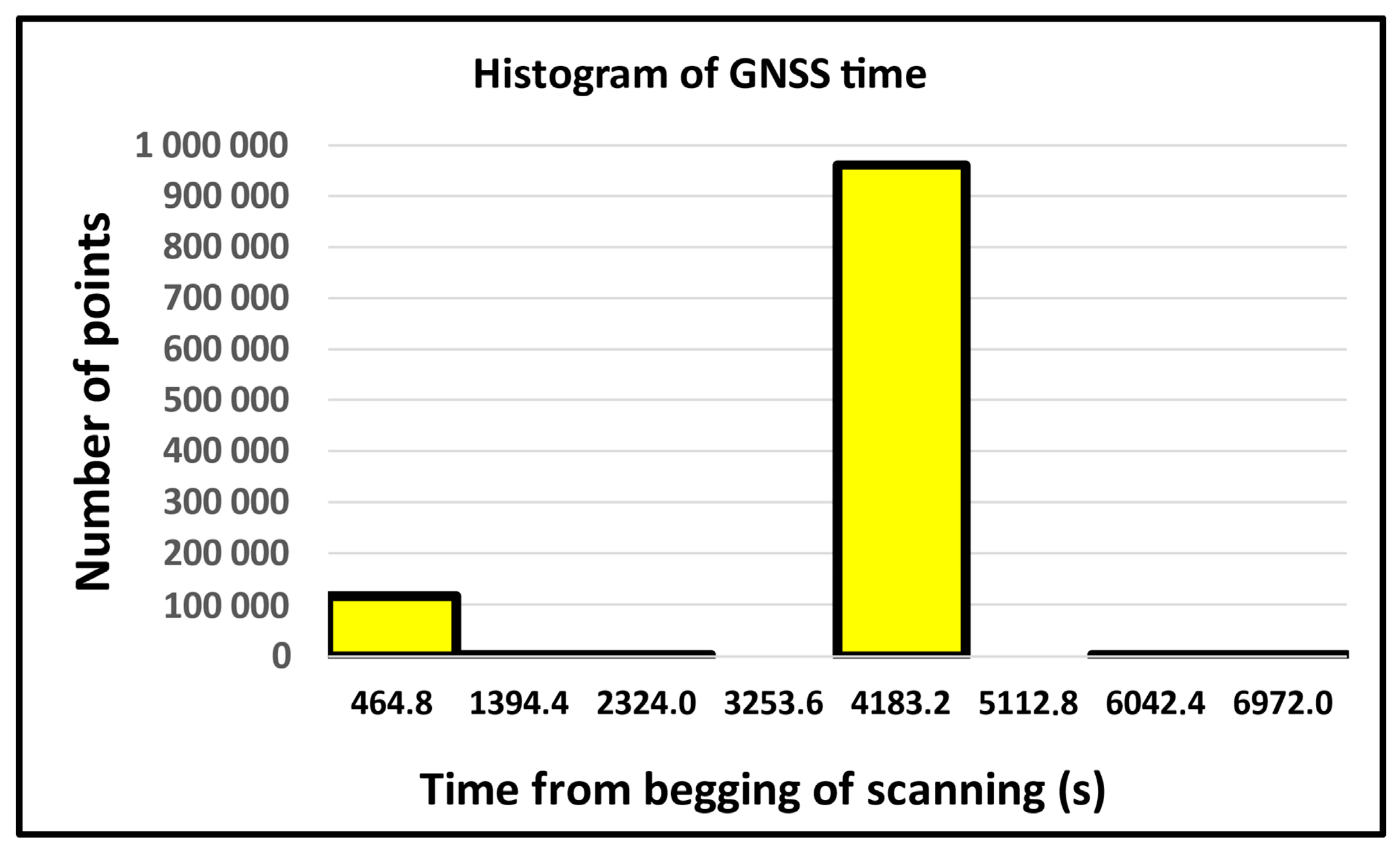

| Number of Points | |||||
|---|---|---|---|---|---|
| Hrabiny-South | Hrabiny-North | Total | |||
| Filtering Stage | Scanner 1 | Scanner 2 | Scanner 1 | Scanner 2 | |
| Original sample | 65 | 65 | 69 | 69 | 268 |
| Non-empty point clouds | 65 | 62 | 69 | 69 | 265 |
| Successfully processed | 62 | 62 | 67 | 64 | 255 |
| First stage clustering input | 62 | 62 | 67 | 64 | 255 |
| Second stage clustering input | 77 | 73 | 69 | 64 | 283 |
| Optimal bin width < 100 | 77 | 73 | 68 | 57 | 275 |
| Variable | Plot | N | Mean | t-Value * | STD | F-Value ** |
|---|---|---|---|---|---|---|
| Threshold (s) | Hrabiny-South | 150 | 3.908 | 1.263 | 9.583 | 7.183 |
| Hrabiny-North | 125 | 6.034 | 17.743 | |||
| Number of points | Hrabiny-South | 150 | 1,495,638.6 | 0.037 | 2,353,039.376 | 0.054 |
| Hrabiny-North | 125 | 1,485,118.056 | 2,359,536.157 | |||
| Spatial density (pnts/m3) | Hrabiny-South | 150 | 5138.44 | 0.322 | 7429.08 | 0.001 |
| Hrabiny-North | 125 | 5421.47 | 7032.71 | |||
| Temporal density (pnts/s) | Hrabiny-South | 150 | 42,650.54 | 0.097 | 54,853.25 | 0.326 |
| Hrabiny-North | 125 | 41,998.36 | 56,888.53 | |||
| Point loss | Hrabiny-South | 150 | 451,904.827 | −0.265 | 835,113.829 | 0.002 |
| Hrabiny-North | 125 | 479,734.664 | 906,416.109 | |||
| % Point loss | Hrabiny-South | 150 | 39.006 | −1.508 | 40.09 | 0.839 |
| Hrabiny-North | 125 | 46.219 | 38.797 | |||
| Time range (s) | Hrabiny-South | 150 | 43.589 | −1.384 | 40.292 | 1.991 |
| Hrabiny-North | 125 | 51.155 | 50.37 | |||
| Total scanning duration (s) | Hrabiny-South | 150 | 35.063 | 0.286 | 25.754 | 7.694 |
| Hrabiny-North | 125 | 34.258 | 19.924 | |||
| Mean scan duration (s) | Hrabiny-South | 150 | 24.052 | −0.422 | 22.721 | 1.401 |
| Hrabiny-North | 125 | 25.244 | 24.014 | |||
| Total duration of occlusions (s) | Hrabiny-South | 150 | 8.525 | −1.922 | 25.704 | 15.079 |
| Hrabiny-North | 125 | 16.898 | 45.335 | |||
| Max duration of occlusion (s) | Hrabiny-South | 150 | 6.167 | −1.18 | 16.459 | 6.13 |
| Hrabiny-North | 125 | 9.276 | 26.762 | |||
| Number of outages | Hrabiny-South | 150 | 45.787 | −2.128 | 89.422 | 10.823 |
| Hrabiny-North | 125 | 75.04 | 136.933 | |||
| Mean PDOP | Hrabiny-South | 150 | 14.867 | 0.324 | 18.908 | 0.008 |
| Hrabiny-North | 125 | 14.119 | 16.994 | |||
| Max outage (s) | Hrabiny-South | 150 | 11.401 | −0.371 | 7.425 | 4.824 |
| Hrabiny-North | 125 | 11.901 | 14.388 | |||
| Mean outage (s) | Hrabiny-South | 150 | 2.618 | −0.881 | 3.259 | 5.978 |
| Hrabiny-North | 125 | 2.261 | 4.591 |
| Variable | LN (Number of Points) | LN (Temporal Density) | LN (Spatial Density) |
|---|---|---|---|
| F-value | 70.156 | 243.545 | 57.032 |
| F-critical | 3.8415 | 3.8415 | 3.8415 |
| R2 | 0.204 | 0.471 | 0.173 |
| Best-fitting model | Linear | Linear | Linear |
| b coeficient sign | - | - | - |
| Variable | Statitstic | F-Value | F-Critical | R2 | Model | b Coef. Sign |
|---|---|---|---|---|---|---|
| Time range | Total | 415.191 | 3.8415 | 0.603 | Linear | + |
| LN (Scanning duration) | Total | 19.358 | 3.8415 | 0.066 | Power | + |
| Mean | 257.436 | 3.8415 | 0.485 | Power | − | |
| Max | 10.709 | 3.8415 | 0.038 | Power | − | |
| Occlusion duration | Total | 870.335 | 3.8415 | 0.761 | Linear | + |
| Mean | 114.827 | 3.8415 | 0.296 | Linear | + | |
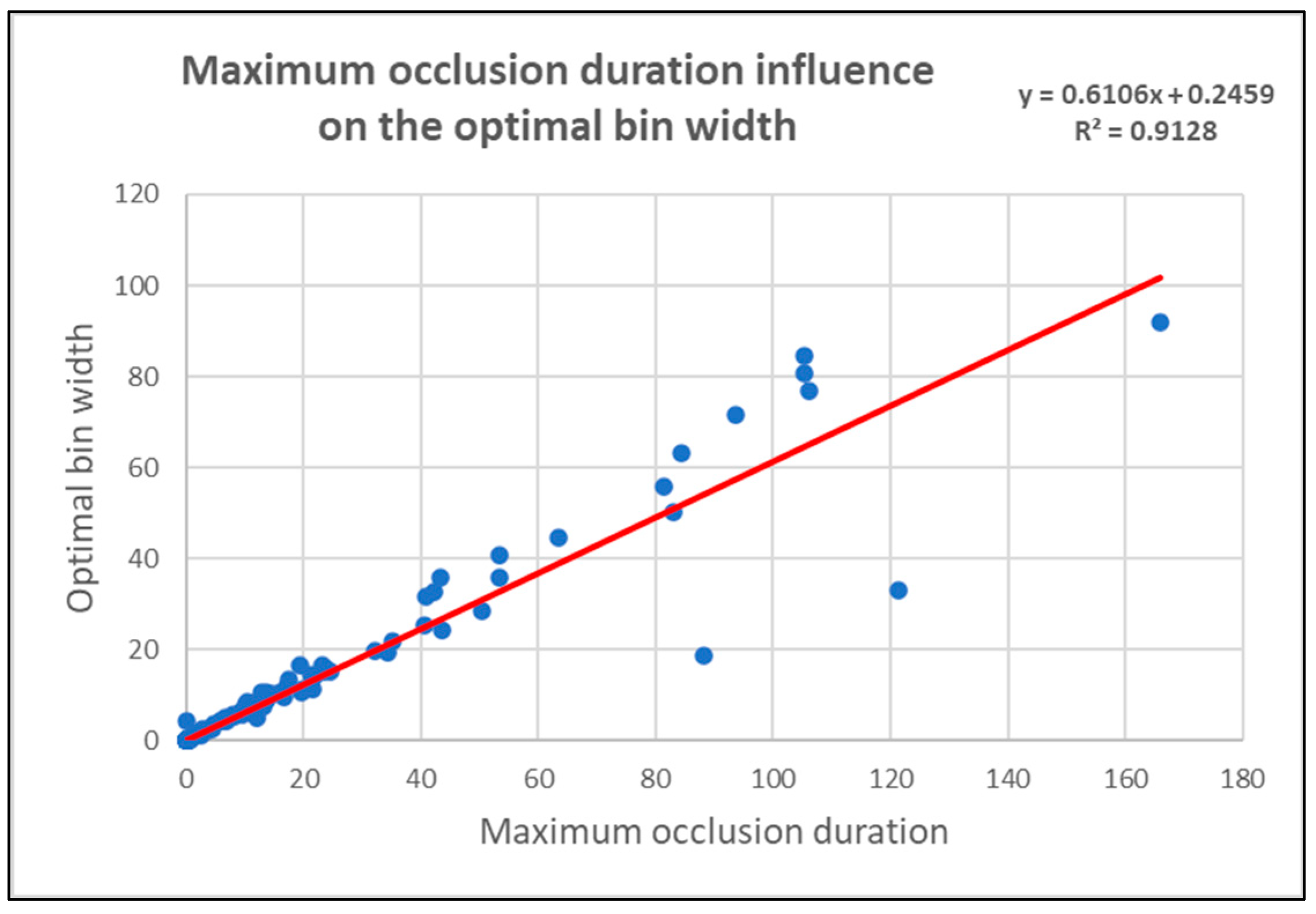
| Max | 2856.492 | 3.8415 | 0.913 | Linear | + |
| Variable | Statitstic | F-Value | F-Critical | R2 | Model | b Coef. Sign |
|---|---|---|---|---|---|---|
| Overall outage | Number | 48.502 | 3.8415 | 0.151 | Linear | + |
| Mean | 3.322 | 3.8415 | 0.012 | Exp | + | |
| Max | 82.696 | 3.8415 | 0.232 | Linear | + | |
| Outage during the scanning | Number | 12.055 | 3.8415 | 0.042 | Linear | + |
| Mean | 8.515 | 3.8415 | 0.03 | Exp | − | |
| Max | 0.117 | 3.8415 | 0 | Exp | − | |
| Outage during the occlusion | Number | 138.668 | 3.8415 | 0.337 | Linear | + |
| Mean | 3.958 | 3.8415 | 0.057 | Power | + | |
| Max | 400.651 | 3.8415 | 0.595 | Linear | + |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čeňava, J.; Tuček, J.; Chudá, J.; Koreň, M. Mobile Laser Scanning Data Collected under a Forest Canopy with GNSS/INS-Positioned Systems: Possibilities of Processability Improvements. Remote Sens. 2024, 16, 1734. https://doi.org/10.3390/rs16101734
Čeňava J, Tuček J, Chudá J, Koreň M. Mobile Laser Scanning Data Collected under a Forest Canopy with GNSS/INS-Positioned Systems: Possibilities of Processability Improvements. Remote Sensing. 2024; 16(10):1734. https://doi.org/10.3390/rs16101734
Chicago/Turabian StyleČeňava, Juraj, Ján Tuček, Juliána Chudá, and Milan Koreň. 2024. "Mobile Laser Scanning Data Collected under a Forest Canopy with GNSS/INS-Positioned Systems: Possibilities of Processability Improvements" Remote Sensing 16, no. 10: 1734. https://doi.org/10.3390/rs16101734
APA StyleČeňava, J., Tuček, J., Chudá, J., & Koreň, M. (2024). Mobile Laser Scanning Data Collected under a Forest Canopy with GNSS/INS-Positioned Systems: Possibilities of Processability Improvements. Remote Sensing, 16(10), 1734. https://doi.org/10.3390/rs16101734







