WDFA-YOLOX: A Wavelet-Driven and Feature-Enhanced Attention YOLOX Network for Ship Detection in SAR Images
Abstract
:1. Introduction
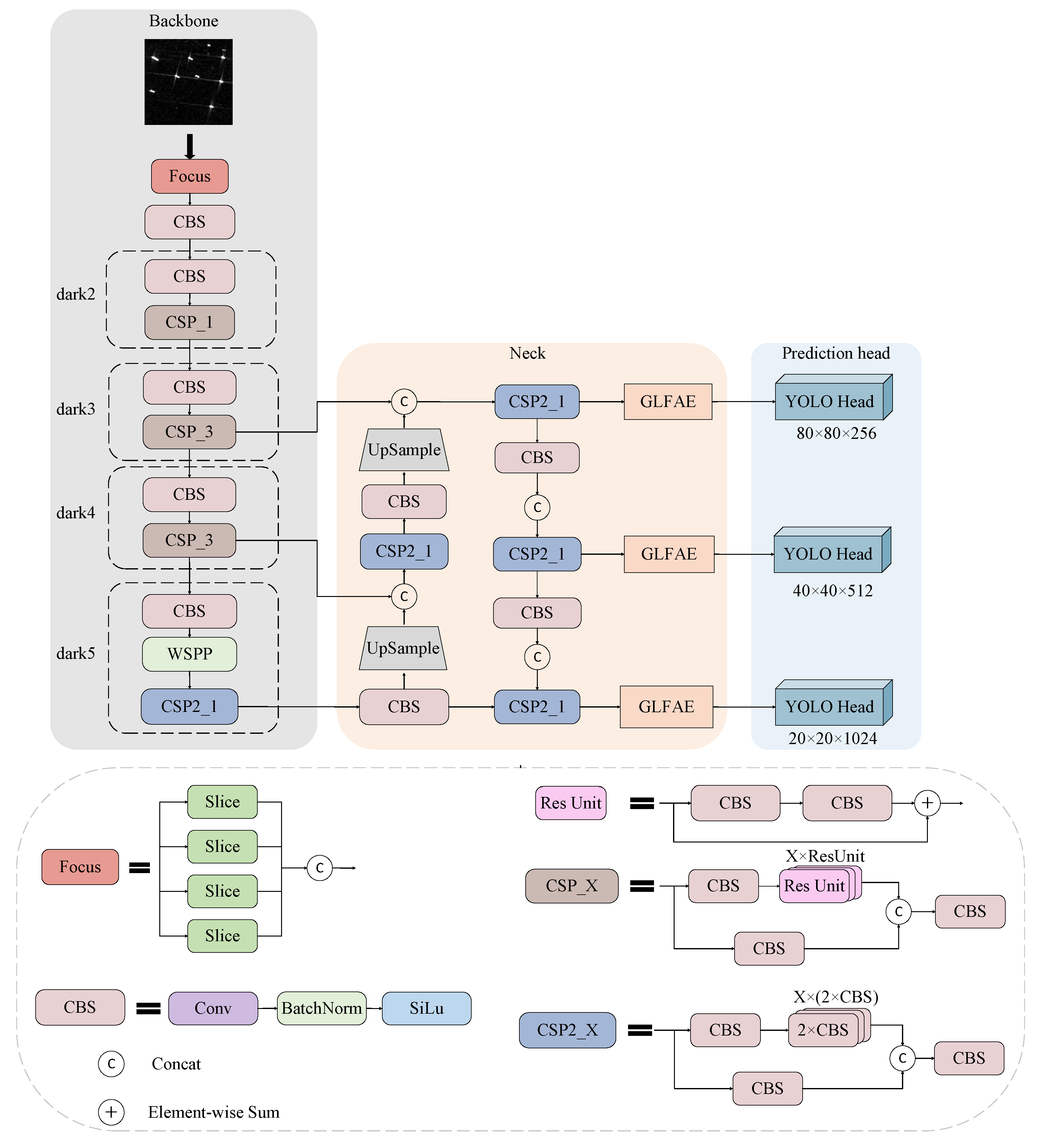
- Addressing the complexities inherent in SAR images, including complex background interference, limited available feature information, and the dense arrangement of ships in coastal areas, we propose a novel Wavelet Cascade Residual (WCR) module. This module is integrated into the Spatial Pyramid Pooling (SPP) module to propose a new wavelet transform-based SPP module (WSPP). By incorporating the wavelet transform into a CNN, spatial- and frequency-domain features are captured. It not only compensates for the loss of fine-grained feature information during pooling but also extends the receptive field of feature maps, ultimately reducing false positives.
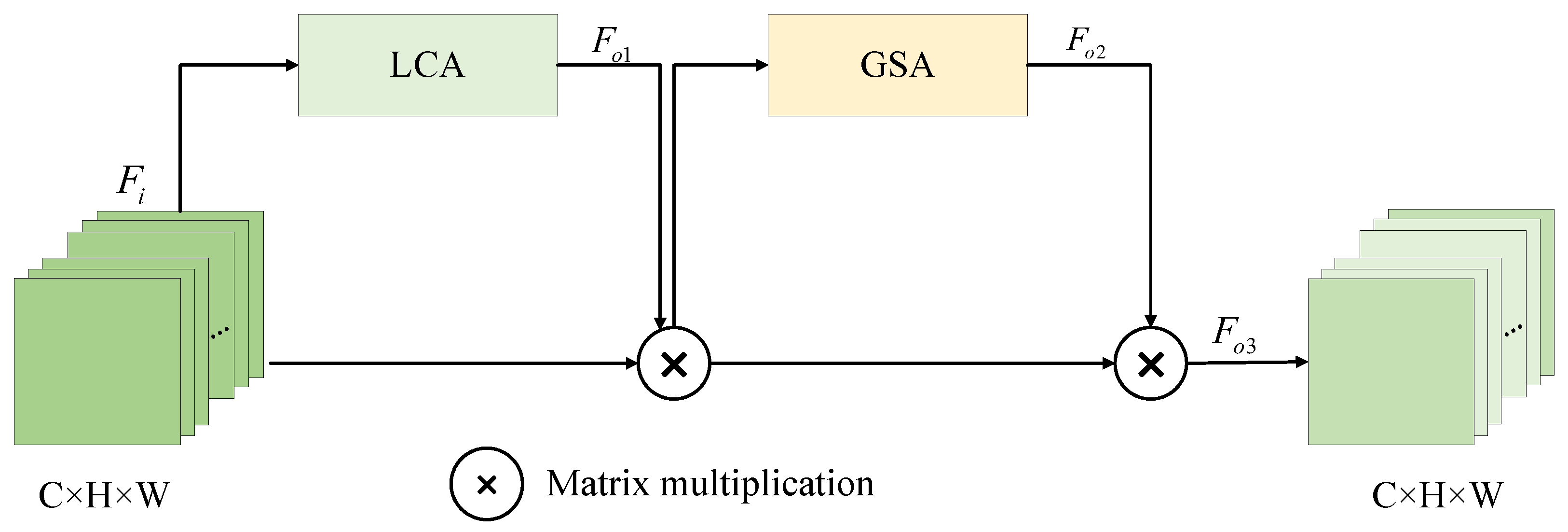
- In response to the prevalence of numerous small-sized ships, which have weak representation capabilities in SAR datasets, we propose a Global and Local Feature Attention Enhancement (GLFAE) module. Through a parallel structure, we fuse the outputs of channel and spatial attention mechanisms with those of the transformer module, which assigns greater importance to regions of interest while suppressing unnecessary features and enables the capturing of both local and global information related to ships.
- To address the issue of slow convergence speed in the model, which adversely affects model performance, we replace the loss function with GIOU and introduce the Chebyshev distance with dual penalty terms on top of that, which is called the Chebyshev distance-based generalised IoU loss function. It improves the ability to accurately align and match bounding boxes, which helps with the convergence and stability of the training process and strikes a balance between model accuracy and speed.
2. Methodology
2.1. Overall Network Structure
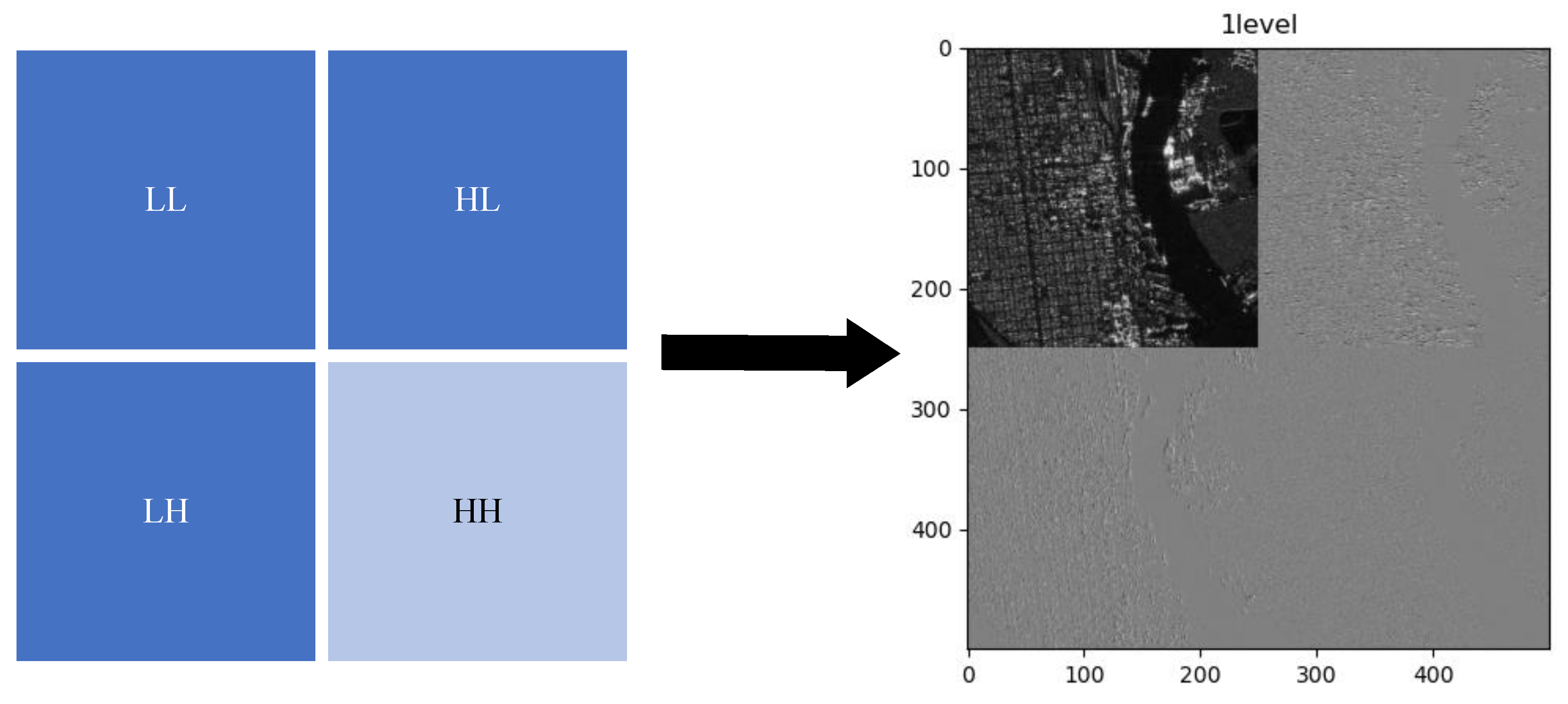
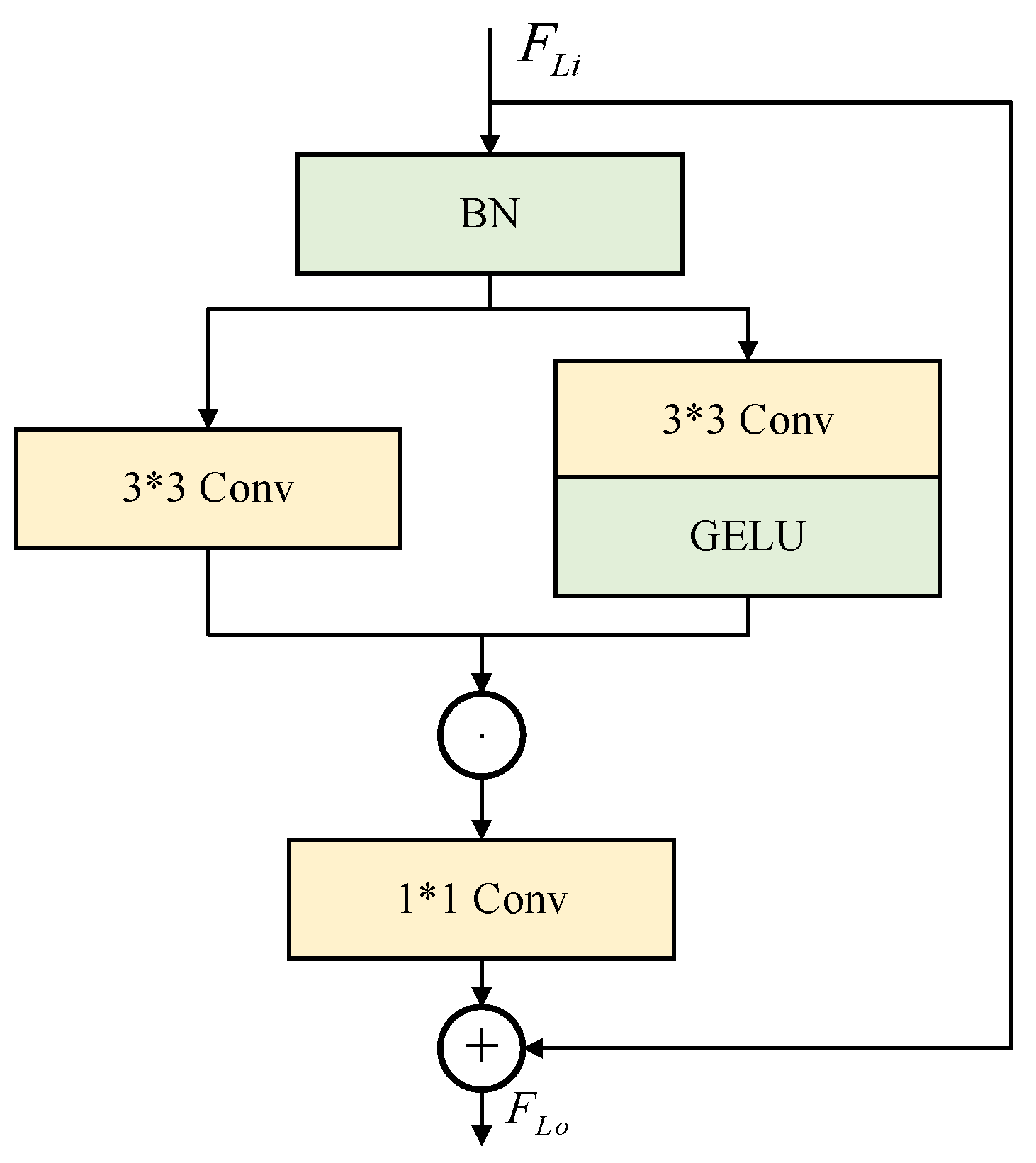
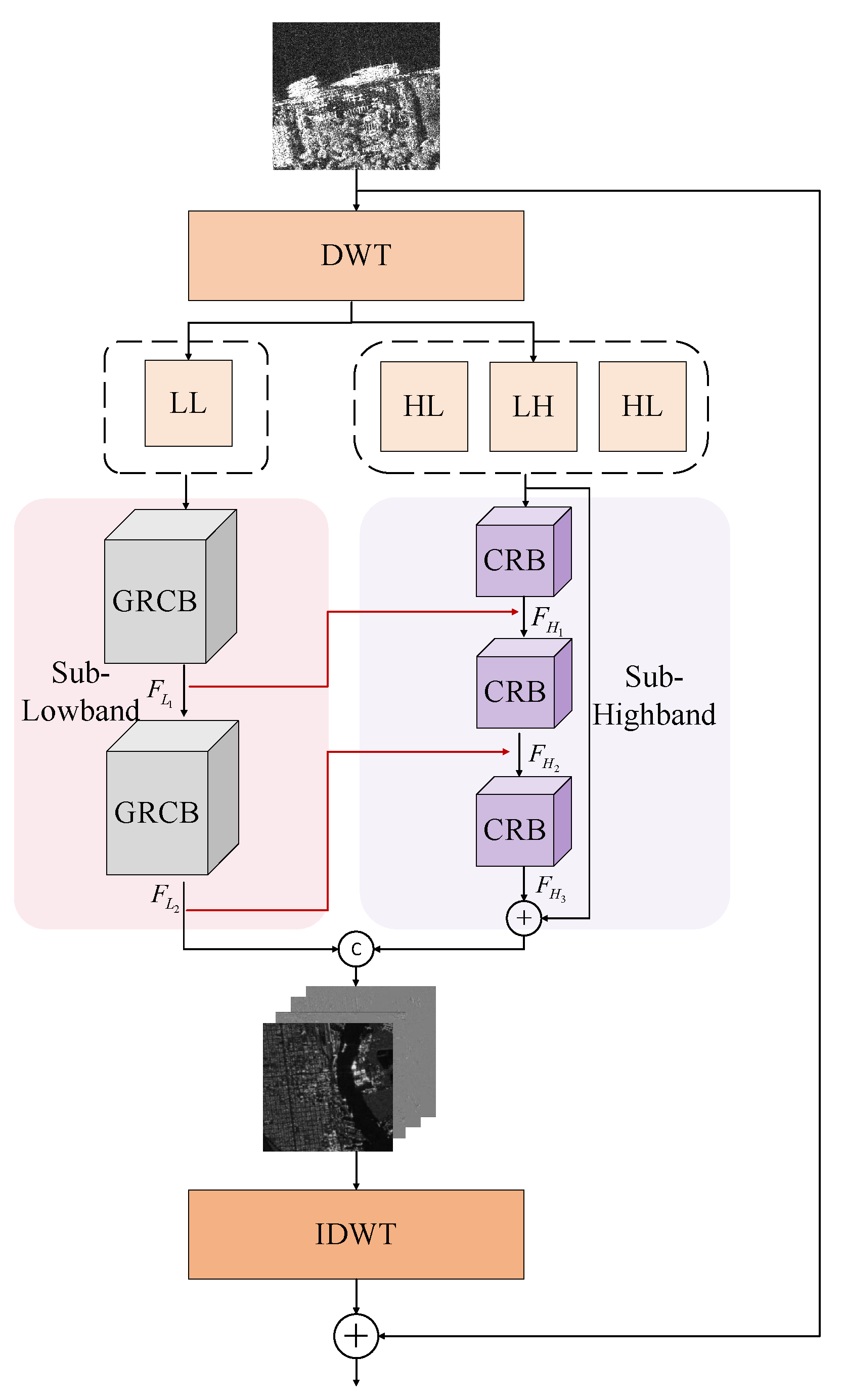
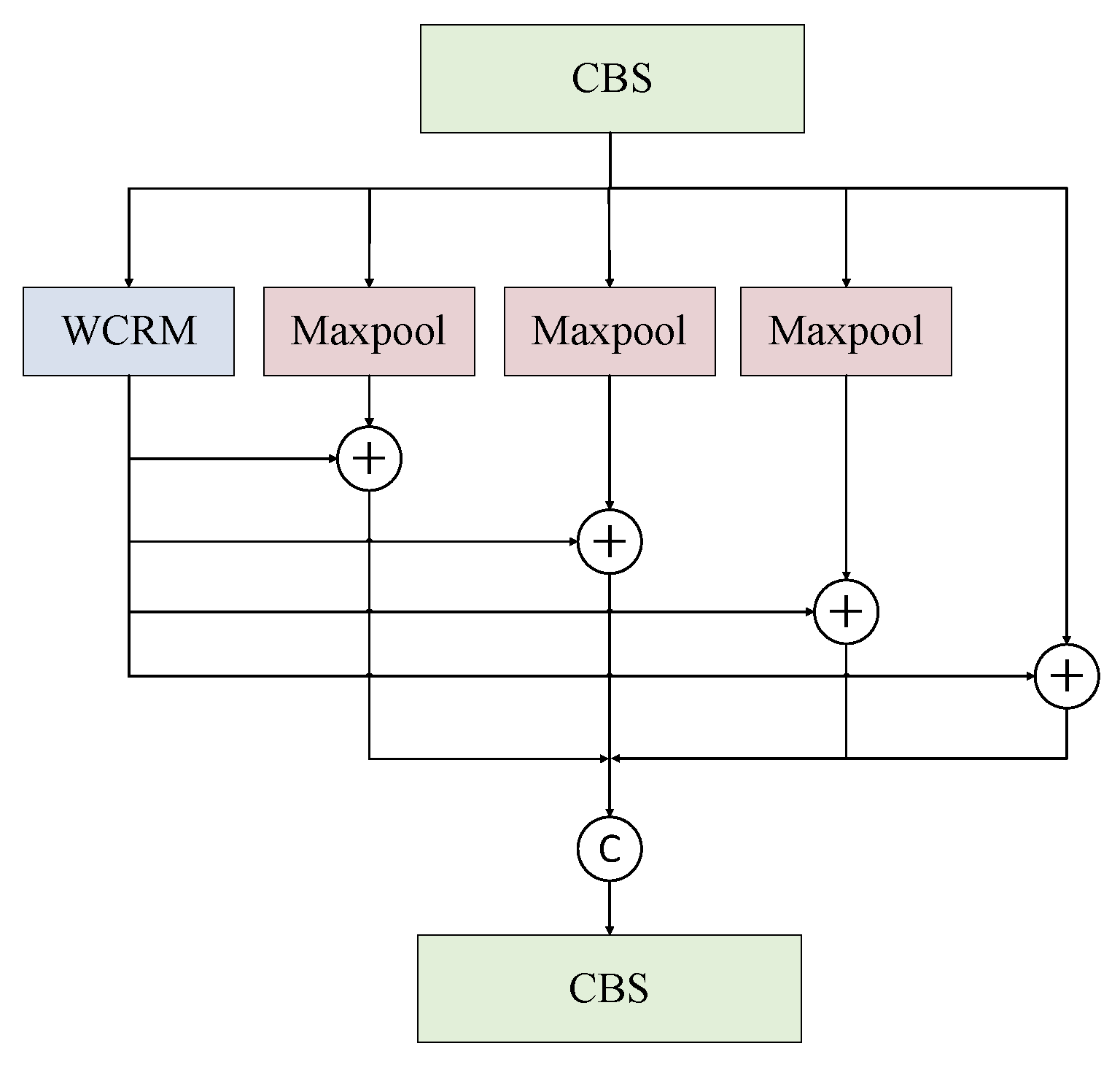
2.2. Wavelet Cascade Residual Module
2.3. Wavelet Transform-Based Spatial Pyramid Pooling
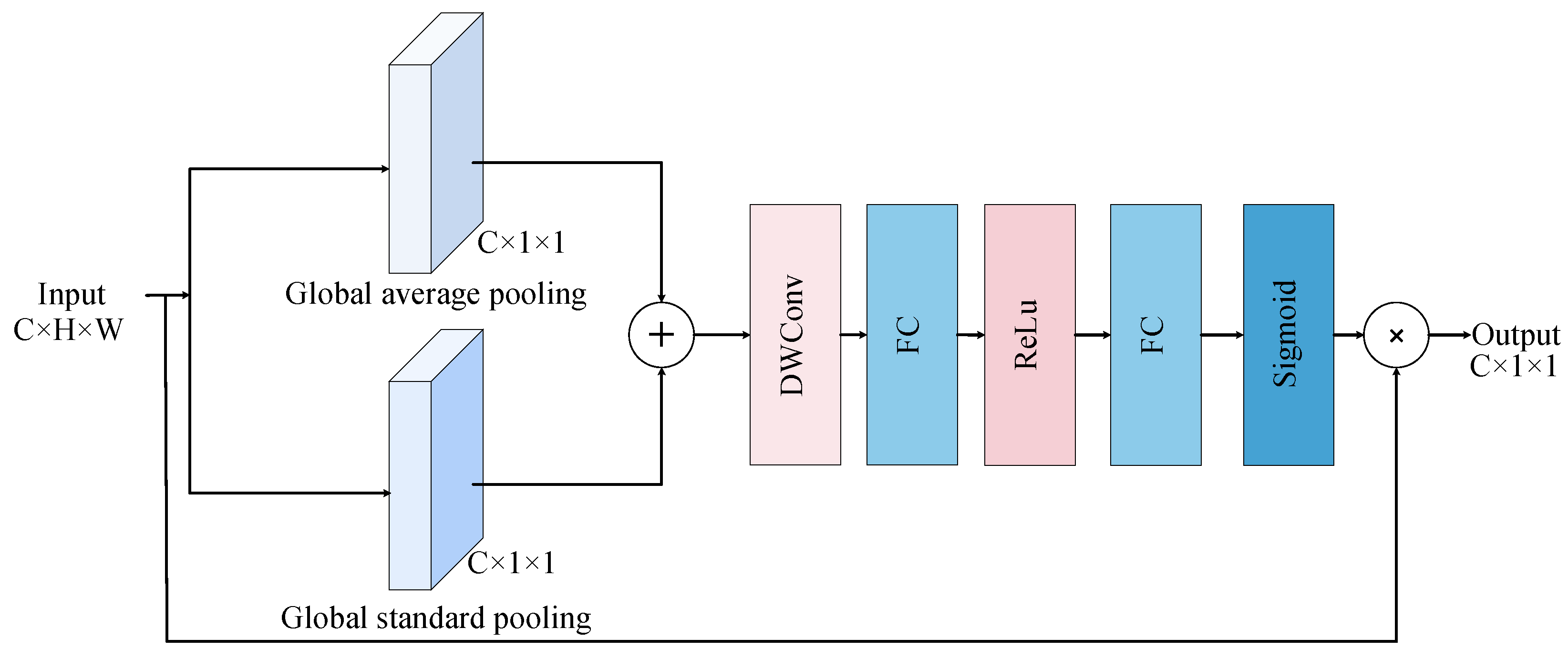
2.4. Global and Local Feature Attention Enhancement Module
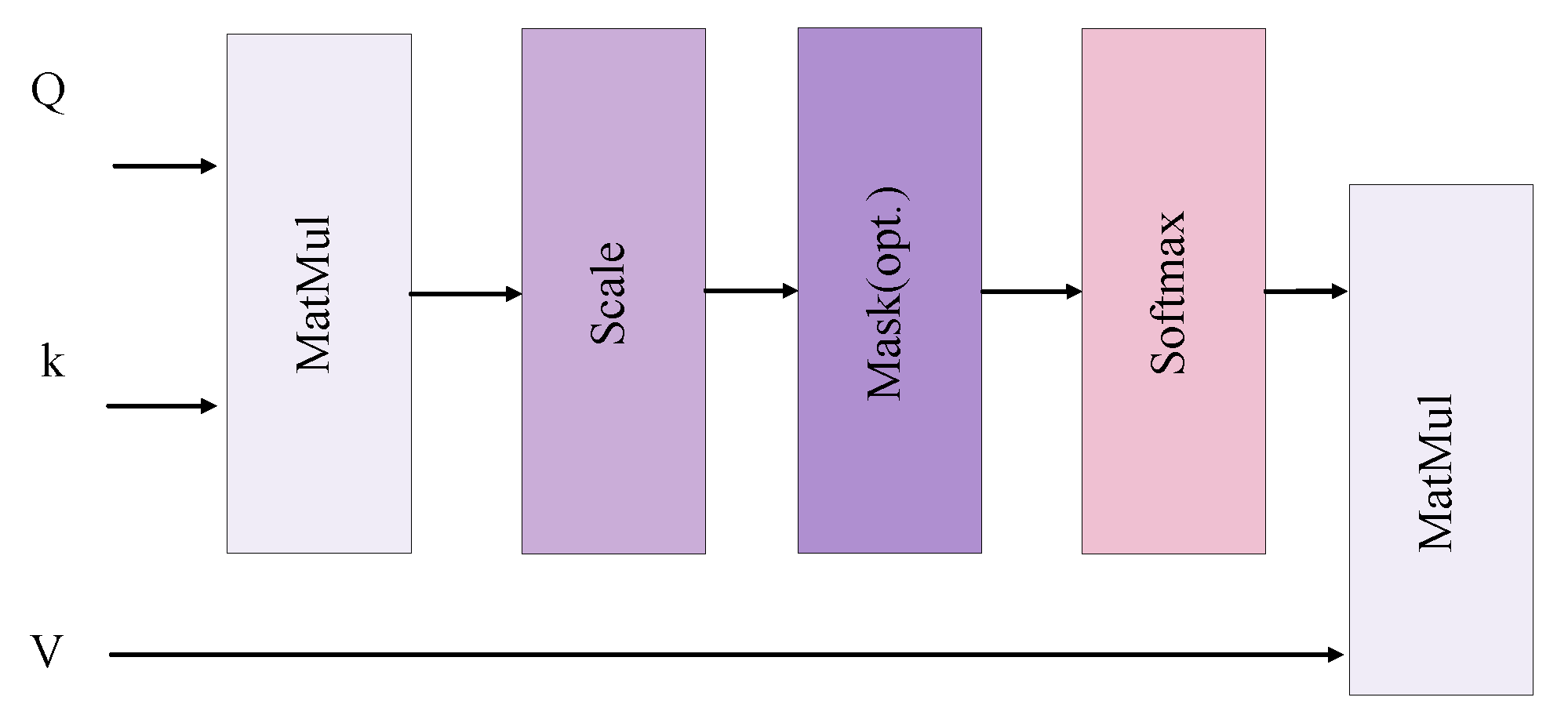
2.5. The Chebyshev Distance-Generalised IoU Loss Function
3. Experiments
3.1. Implementation Details
3.1.1. Datasets
3.1.2. Evaluation Metrics
3.1.3. Implementation Details
3.2. Ablation Experiment
3.3. Comparison with Other Methods
3.4. Visualisation Comparison of Detection Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Average precision | |
| CNN | Convolutional neural network |
| CRB | Convolution residual block |
| Dconv | Deformable convolution |
| DWT | Discrete wavelet transform |
| Frame per second | |
| GRCB | Gated residual convolution block |
| GLFAE | Global and Local Feature Attention Enhancement |
| GSA | Global spatial attention |
| HRSID | High-Resolution SAR Images Dataset |
| LCA | Local channel attention |
| P | Precision |
| R | Recall |
| R-CNN | Region-convolutional neural network |
| SAR | Synthetic Aperture Radar |
| SPP | Spatial pyramid pooling |
| SSD | Single-shot multibox detector |
| SSDD | SAR Ship Detection Dataset |
| WCR | Wavelet cascade residual |
| WDFA-YOLOX | Wavelet-Driven Feature-Enhanced Attention–You Only Look Once X Network |
| WSPP | Wavelet transform-based SPP module |
| YOLO | You Only Look Once |
References
- Asiyabi, R.M.; Datcu, M.; Anghel, A.; Nies, H. Complex-Valued End-to-End Deep Network With Coherency Preservation for Complex-Valued SAR Data Reconstruction and Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5206417. [Google Scholar] [CrossRef]
- Du, L.; Wang, Z.; Wang, Y. Survey of research progress on target detection and discrimination of single-channel SAR images for complex scenes. J. Radars 2020, 9, 34–54. [Google Scholar] [CrossRef]
- Mullissa, A.G.; Marcos, D.; Tuia, D.; Herold, M.; Reiche, J. deSpeckNet: Generalizing Deep Learning-Based SAR Image Despeckling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5200315. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Z.; Lei, B. What, Where, and How to Transfer in SAR Target Recognition Based on Deep CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2324–2336. [Google Scholar] [CrossRef]
- Li, J.; Xu, C.; Su, H.; Gao, L.; Wang, T. Deep Learning for SAR Ship Detection: Past, Present and Future. Remote Sens. 2022, 14, 2712. [Google Scholar] [CrossRef]
- Leng, X.; Ji, K.; Yang, K.; Zou, H. A Bilateral CFAR Algorithm for Ship Detection in SAR Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1536–1540. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, J.; Gao, G.; Yang, J.; Marino, A. CFAR Ship Detection in Polarimetric Synthetic Aperture Radar Images Based on Whitening Filter. IEEE Trans. Geosci. Remote Sens. 2020, 58, 58–81. [Google Scholar] [CrossRef]
- Wang, S.; Wang, M.; Yang, S.; Jiao, L. New Hierarchical Saliency Filtering for Fast Ship Detection in High-Resolution SAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 351–362. [Google Scholar] [CrossRef]
- Kapur, J.; Sahoo, P.; Wong, A. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vision, Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Egbert, S.L.; Kastens, J.H. Analysis of time-series MODIS 250 m vegetation index data for crop classification in the US Central Great Plains. Remote Sens. Environ. 2007, 108, 290–310. [Google Scholar] [CrossRef]
- Wu, F.; He, J.; Zhou, G.; Li, H.; Liu, Y.; Sui, X. Improved Oriented Object Detection in Remote Sensing Images Based on a Three-Point Regression Method. Remote Sens. 2021, 13, 4517. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the 30TH IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar] [CrossRef]
- Shen, L.; Tao, H.; Ni, Y.; Wang, Y.; Stojanovic, V. Improved YOLOv3 model with feature map cropping for multi-scale road object detection. Meas. Sci. Technol. 2023, 34, 045406. [Google Scholar] [CrossRef]
- Jocher. YOLOv5 by Ultralytics. Available online: https://github.com/ultralytics/yolov5 (accessed on 8 January 2024).
- Wang, C.Y.; Bochkovskiy, A.; Liao, H.Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar] [CrossRef]
- Hou, H.; Chen, M.; Tie, Y.; Li, W. A Universal Landslide Detection Method in Optical Remote Sensing Images Based on Improved YOLOX. Remote Sens. 2022, 14, 4939. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Computer Vision—ECCV 2016, PT I, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; Volume 9905, pp. 21–37. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Li, J.; Xu, X.; Wang, B.; Zhan, X.; Xu, Y.; Ke, X.; Zeng, T.; Su, H.; et al. SAR Ship Detection Dataset (SSDD): Official Release and Comprehensive Data Analysis. Remote Sens. 2021, 13, 3690. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Zhang, H.; Dong, Y.; Wei, S. A SAR Dataset of Ship Detection for Deep Learning under Complex Backgrounds. Remote Sens. 2019, 11, 765. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X.; Zhan, X.; Shi, J.; Wei, S.; Pan, D.; Li, J.; Su, H.; Zhou, Y.; et al. LS-SSDD-v1.0: A Deep Learning Dataset Dedicated to Small Ship Detection from Large-Scale Sentinel-1 SAR Images. Remote Sens. 2020, 12, 2997. [Google Scholar] [CrossRef]
- Wei, S.; Zeng, X.; Qu, Q.; Wang, M.; Su, H.; Shi, J. HRSID: A High-Resolution SAR Images Dataset for Ship Detection and Instance Segmentation. IEEE Access 2020, 8, 120234–120254. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X. Quad-FPN: A Novel Quad Feature Pyramid Network for SAR Ship Detection. Remote Sens. 2021, 13, 2771. [Google Scholar] [CrossRef]
- Fu, J.; Sun, X.; Wang, Z.; Fu, K. An Anchor-Free Method Based on Feature Balancing and Refinement Network for Multiscale Ship Detection in SAR Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1331–1344. [Google Scholar] [CrossRef]
- Hu, Q.; Hu, S.; Liu, S. BANet: A Balance Attention Network for Anchor-Free Ship Detection in SAR Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5222212. [Google Scholar] [CrossRef]
- Zhang, P.; Luo, H.; Ju, M.; He, M.; Chang, Z.; Hui, B. Brain-Inspired Fast Saliency-Based Filtering Algorithm for Ship Detection in High-Resolution SAR Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5201709. [Google Scholar] [CrossRef]
- Zhu, M.; Hu, G.; Li, S.; Zhou, H.; Wang, S.; Feng, Z. A Novel Anchor-Free Method Based on FCOS plus ATSS for Ship Detection in SAR Images. Remote Sens. 2022, 14, 2034. [Google Scholar] [CrossRef]
- Zhang, J.; Sheng, W.; Zhu, H.; Guo, S.; Han, Y. MLBR-YOLOX: An Efficient SAR Ship Detection Network With Multilevel Background Removing Modules. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5331–5343. [Google Scholar] [CrossRef]
- Huang, M.; Liu, T.; Chen, Y. CViTF-Net: A Convolutional and Visual Transformer Fusion Network for Small Ship Target Detection in Synthetic Aperture Radar Images. Remote Sens. 2023, 15, 4373. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Qu, L.; Cai, J.; Fang, J. A Spatial Cross-Scale Attention Network and Global Average Accuracy Loss for SAR Ship Detection. Remote Sens. 2023, 15, 350. [Google Scholar] [CrossRef]
- Qiu, Z.; Rong, S.; Ye, L. YOLF-ShipPnet: Improved RetinaNet with Pyramid Vision Transformer. Int. J. Comput. Intell. Syst. 2023, 16, 58. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Zhang, T. Lite-YOLOv5: A Lightweight Deep Learning Detector for On-Board Ship Detection in Large-Scene Sentinel-1 SAR Images. Remote Sens. 2022, 14, 1018. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Hu, R.; Yu, Y. ESarDet: An Efficient SAR Ship Detection Method Based on Context Information and Large Effective Receptive Field. Remote Sens. 2023, 15, 3018. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.Y.; Chang, W.C. Recurrent wavelet structure-preserving residual network for single image deraining. Pattern Recognit. 2023, 137, 109294. [Google Scholar] [CrossRef]
- Hsu, W.Y.; Jian, P.W. Detail-Enhanced Wavelet Residual Network for Single Image Super-Resolution. IEEE Trans. Instrum. Meas. 2022, 71, 5016913. [Google Scholar] [CrossRef]
- Sun, K.; Tian, Y. DBFNet: A Dual-Branch Fusion Network for Underwater Image Enhancement. Remote Sens. 2023, 15, 1195. [Google Scholar] [CrossRef]
- Zi, Y.; Ding, H.; Xie, F.; Jiang, Z.; Song, X. Wavelet Integrated Convolutional Neural Network for Thin Cloud Removal in Remote Sensing Images. Remote Sens. 2023, 15, 781. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning (ICML’15), Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Lee, M. Mathematical Analysis and Performance Evaluation of the GELU Activation Function in Deep Learning. J. Math. 2023, 2023, 2314–4629. [Google Scholar] [CrossRef]
- Xie, F.; Lin, B.; Liu, Y. Research on the Coordinate Attention Mechanism Fuse in a YOLOv5 Deep Learning Detector for the SAR Ship Detection Task. Sensors 2022, 22, 3370. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression. In Proceedings of the 2019 Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; pp. 658–666. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression. In Proceedings of the 34th AAAI Conference on Artificial Intelligence/32nd Innovative Applications of Artificial Intelligence Conference/10th AAAI Symposium on Educational Advances in Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12993–13000. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]

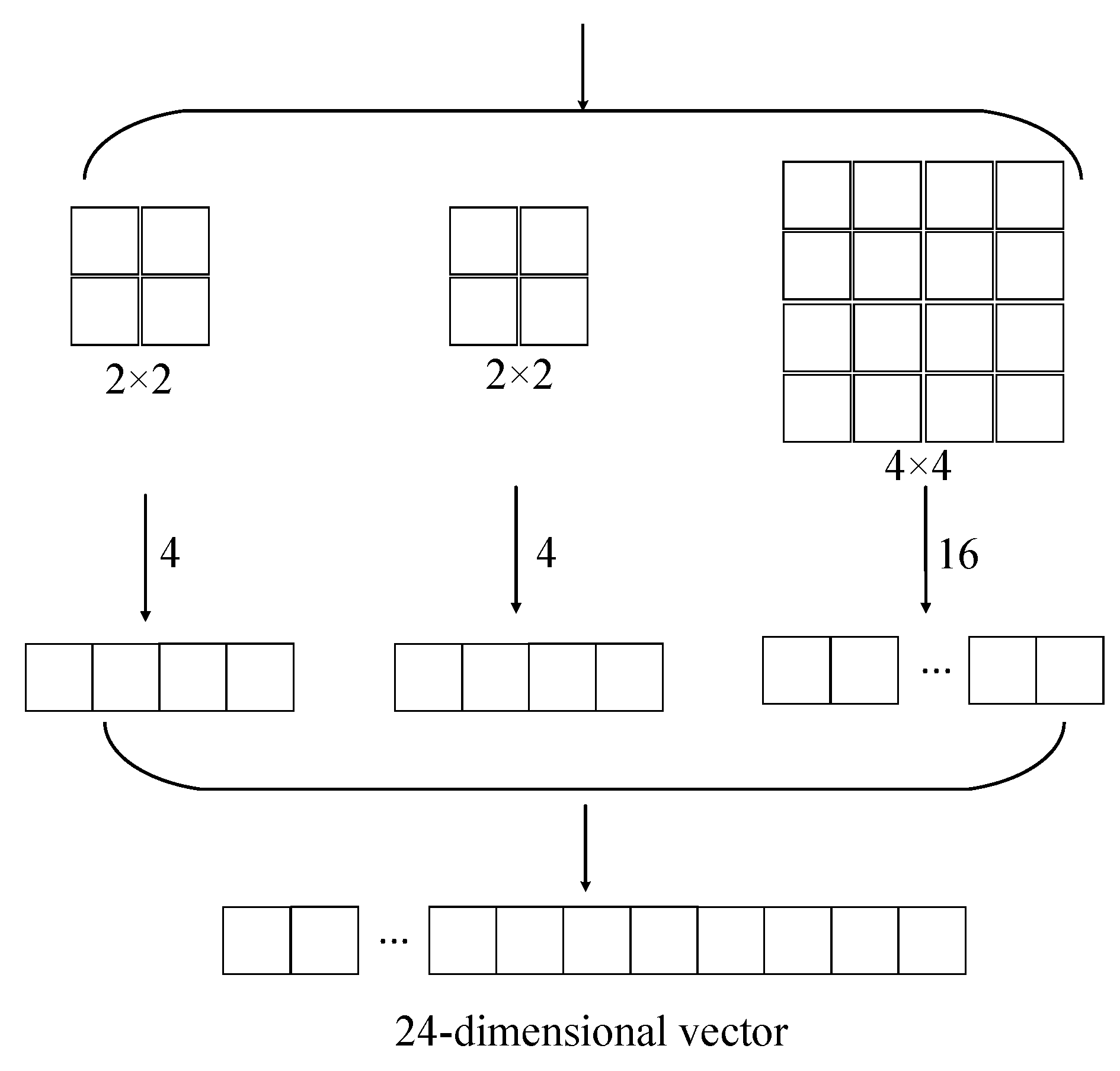


| SSDD | HRSID | |
|---|---|---|
| RadarSat-2, | Sentinel-1B, | |
| Data sources | TerraSAR-X, | TerraSAR-X, |
| Sentinel-1 | TanDEM-X | |
| Polarisation mode | HH, VV, VH, HV | HH, VV, VH, HV |
| Band | X and C bands | X and C bands |
| Resolution (m) | 1–15 | 0.5–3 |
| Category | ship | ship |
| Number (sheets) | 1160 | 5604 |
| Image size (pixels) | 28 × 28 − 256 × 256 | 800 × 800 |
| Ship number | 2456 | 16,951 |
| Configuration | Parameter |
|---|---|
| GPU | NVIDIA GeForce GTX 3090 GPU ×3 |
| Operating system | Ubuntu 20.04.4 LTS |
| Development tools | Python 3.10, Pytorch 1.13.0+cul17 |
| Dataset | WSPP | GLAFE | LossCGIOU | P(%) | R(%) | AP(%) | FPS |
|---|---|---|---|---|---|---|---|
| SSDD | 92.81 | 96.95 | 96.92 | 28.28 | |||
| ✓ | 94.14 | 95.30 | 97.66 | 27.31 | |||
| ✓ | 93.29 | 95.24 | 97.30 | 28.19 | |||
| ✓ | 91.63 | 94.83 | 94.08 | 60.53 | |||
| ✓ | ✓ | 95.92 | 96.32 | 98.98 | 20.27 | ||
| ✓ | ✓ | 95.01 | 97.43 | 98.03 | 57.11 | ||
| ✓ | ✓ | 94.93 | 96.77 | 97.29 | 58.75 | ||
| ✓ | ✓ | ✓ | 95.07 | 98.33 | 99.11 | 58.34 | |
| HRSID | 89.02 | 93.73 | 92.61 | 28.42 | |||
| ✓ | 92.59 | 95.98 | 94.53 | 27.26 | |||
| ✓ | 91.84 | 94.96 | 93.29 | 28.41 | |||
| ✓ | 90.85 | 88.32 | 91.29 | 60.33 | |||
| ✓ | ✓ | 93.80 | 95.70 | 96.19 | 27.35 | ||
| ✓ | ✓ | 92.90 | 95.62 | 95.89 | 57.28 | ||
| ✓ | ✓ | 92.72 | 95.23 | 94.37 | 59.29 | ||
| ✓ | ✓ | ✓ | 93.25 | 95.89 | 96.20 | 59.13 |
| Dataset | Model | P(%) | R(%) | AP(%) | FPS |
|---|---|---|---|---|---|
| SSDD | Faster-RCNN [14] | 81.63 | 85.31 | 89.62 | 11.37 |
| RetinaNet [23] | 93.34 | 87.54 | 92.13 | 23.82 | |
| YOLOv5 [19] | 95.14 | 90.01 | 96.61 | 98.80 | |
| YOLOv7 [20] | 91.05 | 84.92 | 93.68 | 51.63 | |
| YOLOX [21] | 92.81 | 96.95 | 96.92 | 28.28 | |
| MLBR-YOLOX [33] | 86.70 | 95.70 | 96.69 | 120.71 | |
| CviTF-Net [34] | 94.30 | 98.18 | 97.80 | - | |
| SCSA-Net [35] | 98.19 | 94.72 | 98.70 | 22.01 | |
| WDFA-YOLOX | 95.07 | 98.33 | 99.11 | 58.34 | |
| HRSID | Faster-RCNN [14] | 83.81 | 72.57 | 77.98 | 11.41 |
| RetinaNet [23] | 78.40 | 83.4 | 88.80 | 24.80 | |
| YOLOv5 [19] | 78.24 | 83.41 | 88.89 | 24.76 | |
| YOLOv7 [20] | 91.52 | 80.58 | 89.64 | 51.82 | |
| YOLOX [21] | 89.02 | 93.73 | 92.61 | 28.42 | |
| MLBR-YOLOX [33] | 92.72 | 88.61 | 92.16 | 121.25 | |
| CviTF-Net [34] | 90.95 | 93.69 | 92.98 | - | |
| SCSA-Net [35] | 96.45 | 90.02 | 95.40 | 22.29 | |
| WDFA-YOLOX | 93.25 | 95.89 | 96.20 | 59.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Hu, T.; Xia, Y.; Ma, B.; Sarwar, S.; Zhang, C. WDFA-YOLOX: A Wavelet-Driven and Feature-Enhanced Attention YOLOX Network for Ship Detection in SAR Images. Remote Sens. 2024, 16, 1760. https://doi.org/10.3390/rs16101760
Wu F, Hu T, Xia Y, Ma B, Sarwar S, Zhang C. WDFA-YOLOX: A Wavelet-Driven and Feature-Enhanced Attention YOLOX Network for Ship Detection in SAR Images. Remote Sensing. 2024; 16(10):1760. https://doi.org/10.3390/rs16101760
Chicago/Turabian StyleWu, Falin, Tianyang Hu, Yu Xia, Boyi Ma, Saddam Sarwar, and Chunxiao Zhang. 2024. "WDFA-YOLOX: A Wavelet-Driven and Feature-Enhanced Attention YOLOX Network for Ship Detection in SAR Images" Remote Sensing 16, no. 10: 1760. https://doi.org/10.3390/rs16101760
APA StyleWu, F., Hu, T., Xia, Y., Ma, B., Sarwar, S., & Zhang, C. (2024). WDFA-YOLOX: A Wavelet-Driven and Feature-Enhanced Attention YOLOX Network for Ship Detection in SAR Images. Remote Sensing, 16(10), 1760. https://doi.org/10.3390/rs16101760






