Constrained Iterative Adaptive Algorithm for the Detection and Localization of RFI Sources Based on the SMAP L-Band Microwave Radiometer
Abstract
:1. Introduction
2. Materials and Methods
2.1. SMAP L1B_TB Data
2.2. Theoretical Analysis of RFI Influence Characteristics
2.3. SMAP RFI Detection Algorithm
- (1)
- (2)
- The substantial transition in brightness temperature that occurs at land–water and ice–water boundaries can also cause false alarms. Several algorithms have too high FAR at land–water and ice–water coastal boundaries, and only increasing the threshold can be used to reduce the FAR. However, increasing the threshold may result in the missed detection of weak RFI at coastal boundaries [11,12].
- (3)
- The influence of an RFI source on a satellite-borne L-band microwave radiometer through sidelobes is not limited by the RFI source position. As long as there is a line-of-sight propagation path between the transmitting antenna and the receiving antenna, the RFI source will influence the satellite observation results [12,14,34,35].
- (4)
- The emission characteristic of terrestrial RFI sources dynamically varies over time, and this increases the difficulty in setting a threshold for the detection algorithm [12].
- (5)
2.4. Construction of RFI Detection, Identification, and Localization Algorithms
- Step I: Detect and extract suspected RFI samples
- Step II: Perform iterative clustering of RFI samples
- Step III: Identify and localize RFI sources
3. Results
3.1. Detection of RFI Suspected Samples
3.1.1. Extraction of RFI Detection Samples
3.1.2. Classification of RFI Detection Samples at the Water–Land Boundary
3.2. Iterative Clustering of RFI Samples
3.2.1. DBSCAN Clustering
3.2.2. Multiple Iterations Clustering
3.2.3. Sidelobe Clusters Filtering
3.2.4. Water–Land Boundary Clusters Filtering
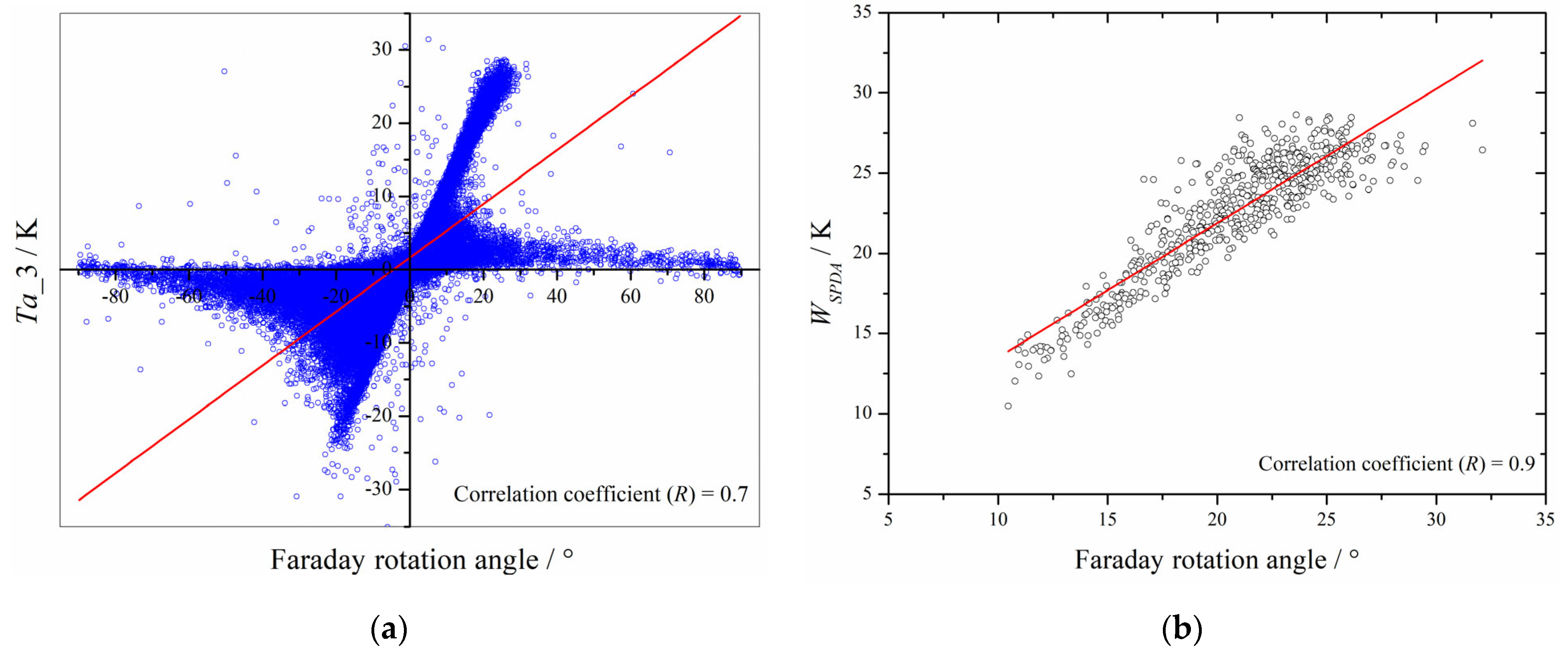
3.2.5. Faraday Rotation Clusters Filtering
3.3. Localization of RFI Sources
3.3.1. RFI Source Identification Algorithm
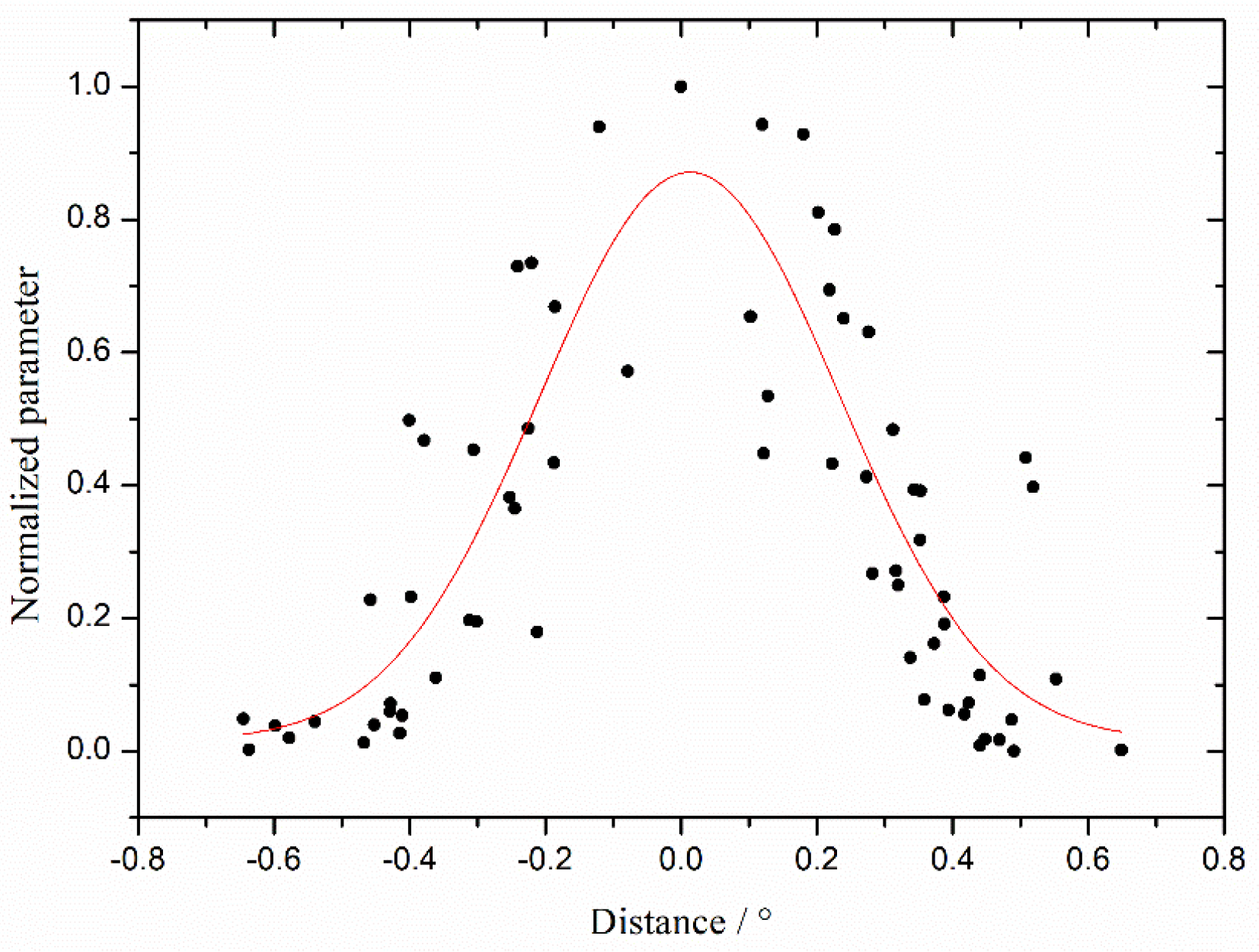
3.3.2. Data Normalization
3.3.3. Normalized Data Quality Control
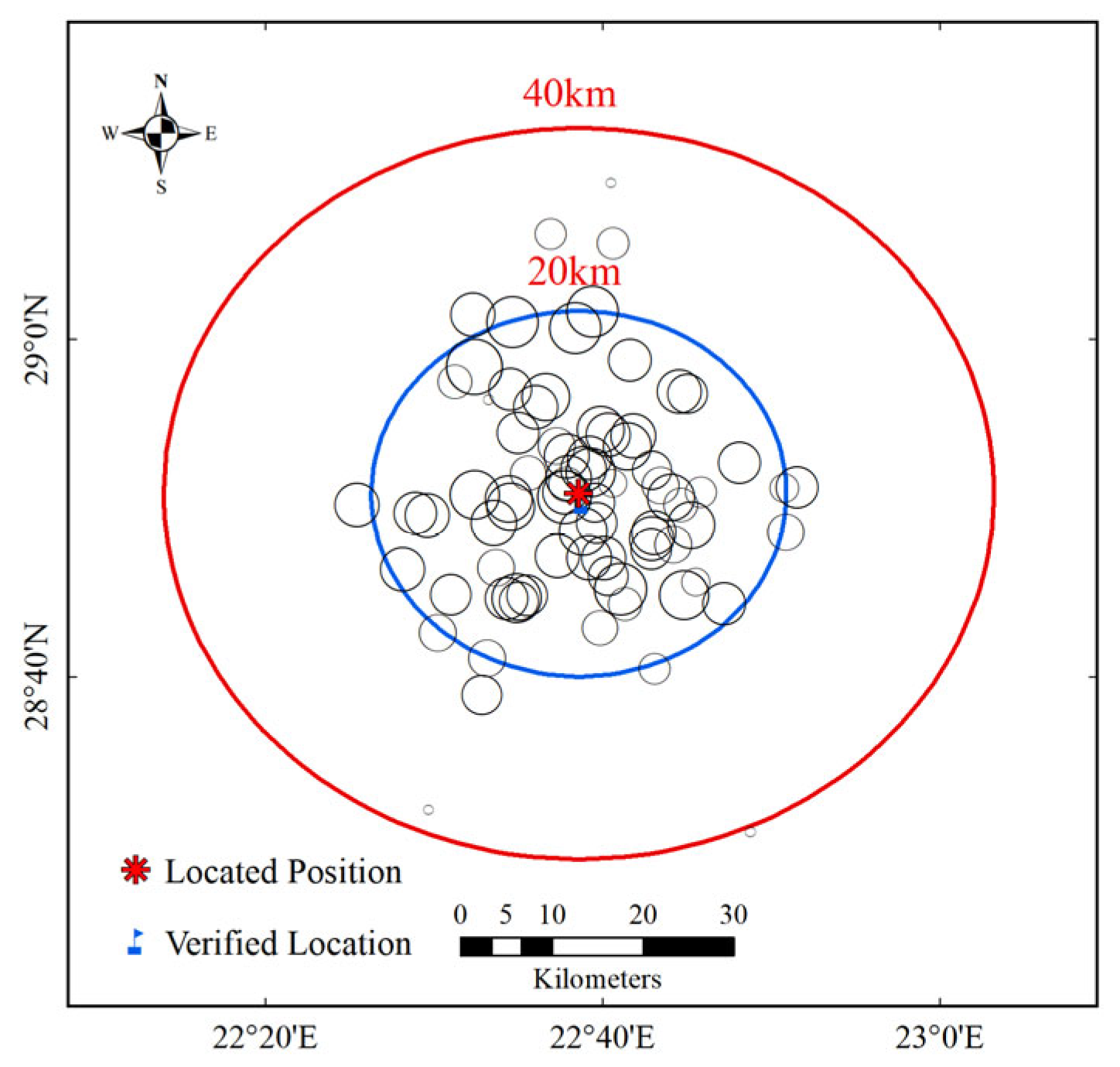
3.3.4. RFI Source Identification Results
3.3.5. Long-Time-Series Data Location of RFI Sources
4. Discussion
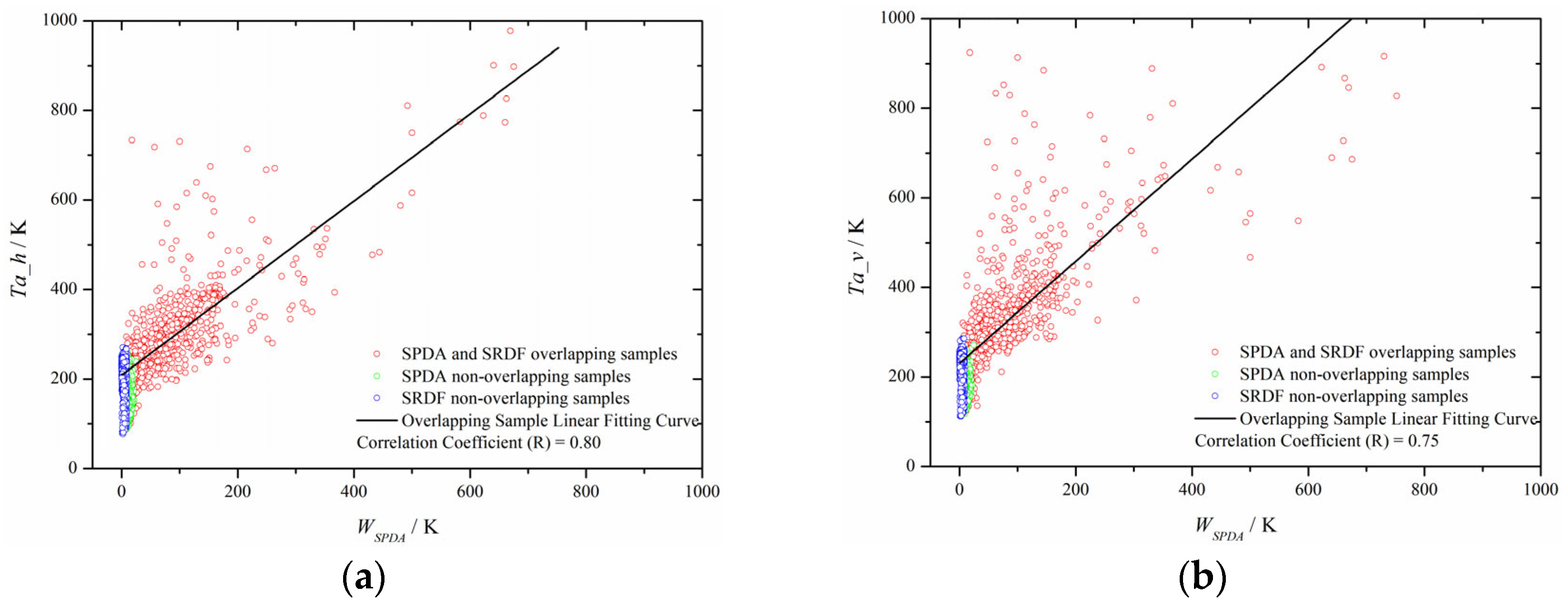
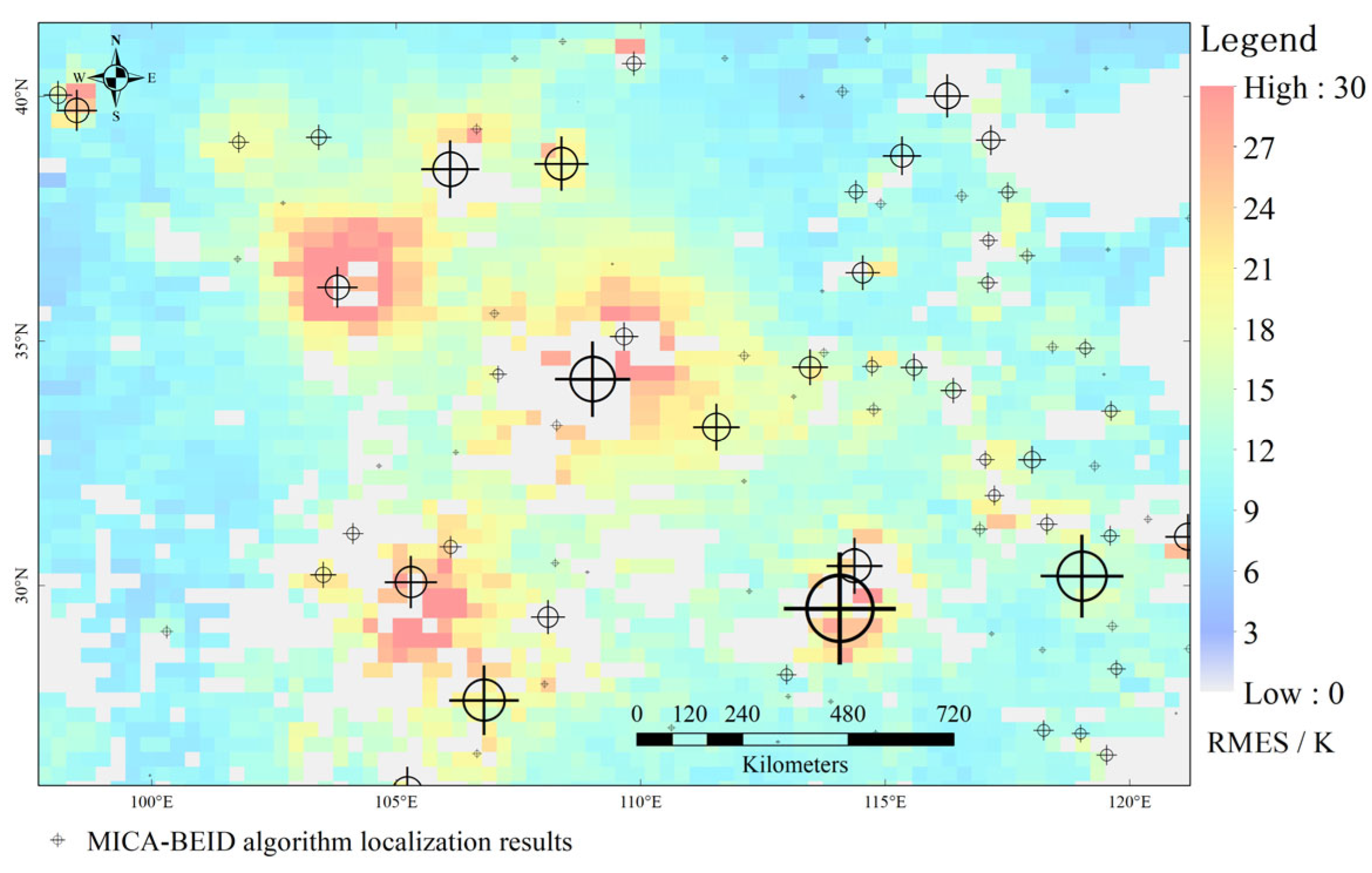
4.1. Information Carried by the Parameter WSPDA
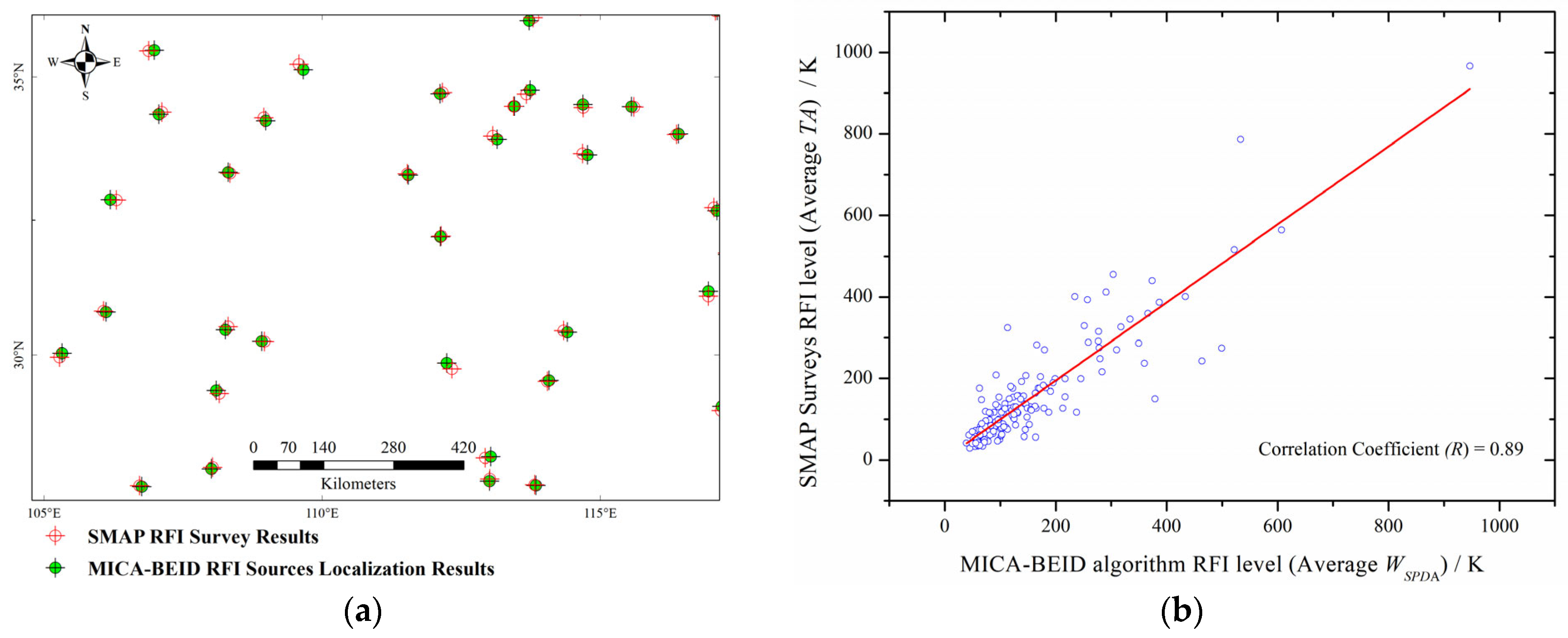
4.2. Comparison with the ITU’s RFI Survey Results
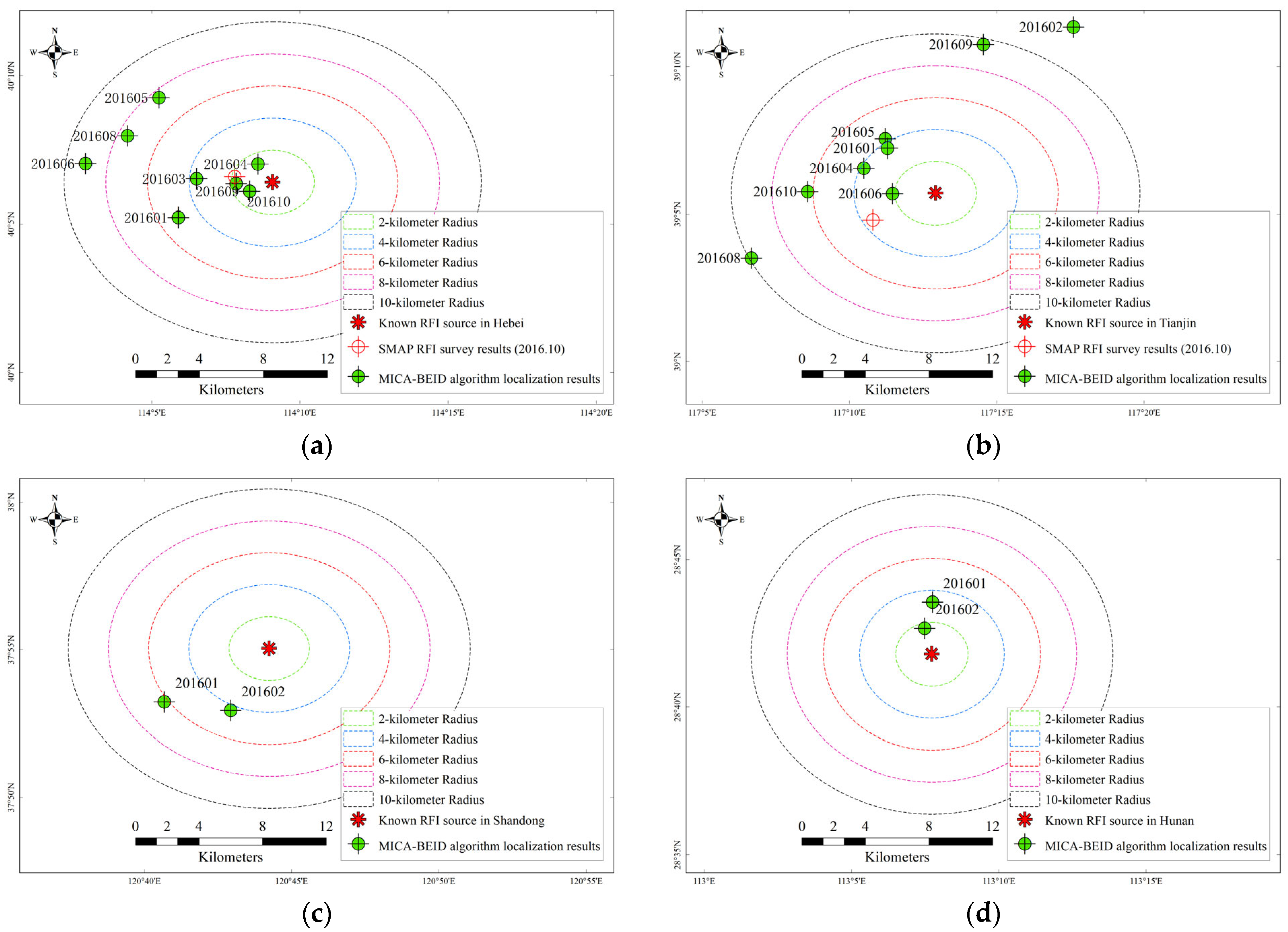
4.3. Comparison with Known Sources
4.4. Comparison with SMOS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salisbury, J.; Vandemark, D.; Joensson, B.; Balch, W.; Chakraborty, S.; Lohrenz, S.; Chapron, B.; Hales, B.; Mannino, A.; Mathis, J.T.; et al. How can present and future satellite missions support scientific studies that address ocean acidification? Oceanography 2015, 28, 108–121. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Tang, W.; Yueh, S.; Yang, D.; Fore, A.; Hayashi, A.; Lee, T.; Fournier, S.; Holt, B. The Potential and Challenges of Using Soil Moisture Active Passive (SMAP) Sea Surface Salinity to Monitor Arctic Ocean Freshwater Changes. Remote Sens. 2018, 10, 869. [Google Scholar] [CrossRef]
- Dinnat, E.P.; Le Vine, D.M.; Boutin, J.; Meissner, T. Satellite Sea Surface Salinity: Evaluation of Products and Impact of Retrieval Algorithms. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 7936–7939. [Google Scholar] [CrossRef]
- Fore, A.; Yueh, S.; Tang, W.; Hayashi, A. The JPL SMAP Sea Surface Salinity Algorithm. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 7920–7923. [Google Scholar] [CrossRef]
- Klein, L.; Swift, C. An Improved Model for the Dielectric Constant of Sea Water at Microwave Frequencies. IEEE Trans. Antennas Propag. 1977, 25, 104–111. [Google Scholar] [CrossRef]
- Yueh, S.H.; West, R.; Wilson, W.J.; Li, F.K.; Njoku, E.G.; Rahmat-Samii, Y. Error sources and feasibility for microwave remote sensing of ocean surface salinity. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1049–1060. [Google Scholar] [CrossRef]
- Toose, P.; Roy, A.; Solheim, F.; Derksen, C.; Royer, A.; Walker, A. Radio frequency interference mitigating hyperspectral L-band radiometer. Geosci. Instrum. Method Data Syst. 2017, 6, 39–51. [Google Scholar] [CrossRef]
- Oliva, R.; Daganzo, E.; Kerr, Y.H.; Mecklenburg, S.; Nieto, S.; Richaume, P.; Gruhier, C. SMOS Radio Frequency Interference Scenario: Status and Actions Taken to Improve the RFI Environment in the 1400–1427-MHz Passive Band. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1427–1439. [Google Scholar] [CrossRef]
- Le Vine, D.M.; de Matthaeis, P.; Ruf, C.S.; Chen, D.D. Aquarius RFI detection and mitigation algorithm: Assessment and examples. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4574–4584. [Google Scholar] [CrossRef]
- Mohammed, P.N.; Aksoy, M.; Piepmeier, J.R.; Johnson, J.T.; Bringer, A. SMAP L-band microwave radiometer: RFI mitigation prelaunch analysis and first year on-orbit observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6035–6047. [Google Scholar] [CrossRef]
- Soldo, Y.; Le Vine, D.M.; de Matthaeis, P.; Richaume, P. L-Band RFI Detected by SMOS and Aquarius. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4220–4235. [Google Scholar] [CrossRef]
- Llorente, A.; Daganzo, E.; Oliva, R.; Uranga, E.; Kerr, Y.; Richaume, P.; de la Fuente, A.; Martin-Neira, M.; Mecklenburg, S. Lessons Learnt from SMOS RFI Activities after 10 Years in Orbit: RFI Detection and Reporting to Claim Protection and Increase Awareness of the Interference Problem in the 1400–1427 MHZ Passive Band. In Proceedings of the 2019 RFI Workshop—Coexisting with Radio Frequency Interference (RFI), Toulouse, France, 23–26 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Soldo, Y.; Le Vine, D.M.; Bringer, A.; de Matthaeis, P.; Oliva, R.; Johnson, J.T.; Piepmeier, J.R. Location of Radio-Frequency Interference Sources Using the SMAP L-Band Radiometer. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6854–6866. [Google Scholar] [CrossRef]
- Dinnat, E.; Le Vine, D. L-band radiometer calibration consistency assessment for the SMOS, SMAP and Aquarius instruments. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2047–2049. [Google Scholar] [CrossRef]
- Camps, A.; Gourrion, J.; Tarongí, J.; Vall-llossera, M.; Gutierrez, A.; Castro, J.B.Y.R. Radio-Frequency Interference Detection and Mitigation Algorithms for Synthetic Aperture Radiometers. Algorithms 2011, 4, 155–182. [Google Scholar] [CrossRef]
- Johnson, J.T.; Mohammed, P.N.; Piepmeier, J.R.; Bringer, A.; Aksoy, M. Soil Moisture Active Passive (SMAP) Microwave Radiometer Radio-Frequency Interference (RFI) Mitigation: Algorithm Updates and Performance Assessment. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 123–124. [Google Scholar] [CrossRef]
- Piepmeier, J.R.; Johnson, J.T.; Mohammed, P.N.; Bradley, D.; Ruf, C.; Aksoy, M.; Garcia, R.; Hudson, D.; Miles, L.; Wong, M. Radio-Frequency Interference Mitigation for the Soil Moisture Active Passive Microwave Radiometer. IEEE Trans. Geosci. Remote Sens. 2013, 52, 761–775. [Google Scholar] [CrossRef]
- Aksoy, M. Radio Frequency Interference Characterization and Detection in L-Band Microwave Radiometry. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2015. [Google Scholar]
- Piepmeier, J.R.; Focardi, P.; Horgan, K.A.; Knuble, J.; Ehsan, N.; Lucey, J. SMAP L-band microwave radiometer: Instrument design and first year on orbit. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1954–1966. [Google Scholar] [CrossRef]
- Nazar, I.M.; Aksoy, M. Radio Frequency Interference detection in microwave radiometry using Multi–Dimensional Semi Supervised Learning. In Proceedings of the IGARSS 2023–2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 589–591. [Google Scholar] [CrossRef]
- Owfi, A.; Afghah, F. Autoencoder-based radio frequency interference mitigation for SMAP passive radiometer. In Proceedings of the IGARSS 2023-2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 6783–6786. [Google Scholar] [CrossRef]
- Wang, X.X.; Wang, X.; Han, Z.; Yang, J.H. Radio Frequency Interference Detection and Characteristic Analysis Based on the L Band Stokes Parameters Remote Sensing Data. JEIT 2015, 37, 2342–2348. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Bao, Z.; Ao, T.; Wang, G.; Wu, H.; Wang, J. Evaluation of Multi-Source Soil Moisture Datasets over Central and Eastern Agricultural Area of China Using In Situ Monitoring Network. Remote Sens. 2021, 13, 1175. [Google Scholar] [CrossRef]
- Gabarró, P.C. Study of Salinity Retrieval Errors for the SMOS Mission. Ph.D. Thesis, University Politècnica de Catalunya, Barcelona, Spain, 2004. [Google Scholar]
- Yin, X.B. A Study on the Passive Microwave Remote Sensing of Sea Surface Wind Vector, Temperature and Salinity and the Effect of Wind on Remote Sensing of Temperature and Salinity. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2007. [Google Scholar]
- Pardé, M.; Zribi, M.; Fanise, P.; Dechambre, M. Analysis of RFI Issue Using the CAROLS L-Band Experiment. IEEE Trans. Geosci. Remote Sens 2011, 49, 1063–1070. [Google Scholar] [CrossRef]
- Kristensen, S.S.; Balling, J.E.; Skou, N.; Søbjærg, S.S. RFI detection in SMOS data using 3rd and 4th Stokes parameters. In Proceedings of the 2012 12th Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment (MicroRad), Rome, Italy, 5–9 March 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Soldo, Y.; Le Vine, D.M.; Dinnat, E. SMAP Observations of the Fourth Stokes Parameter At L-Band. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8407–8410. [Google Scholar] [CrossRef]
- Hartmann, J.; Habersack, J.; Steiner, H.J. Accurate and Efficient Satellite Payload Testing in Compact Ranges. In Proceedings of the 28th ESA Antenna Workshop on Space Antenna Systems and Technologies, Noordwijk, The Netherlands, 31 May–3 June 2005. [Google Scholar]
- Recommendation ITU-R RS.2106-0. Detection and Resolution of Radio Frequency Interference to Earth Exploration-Satellite Service (Passive) Sensors. (07/2017), RS Series, Remote Sensing Systems. Posted on 12 March 2017. Available online: https://www.itu.int/rec/R-REC-RS.2106-0-201707-I (accessed on 1 April 2024).
- Aksoy, M.; Rajabi, H.; Atrey, P.; Mohamed Nazar, I. Characteristics of the Global Radio Frequency Interference in the Protected Portion of L-Band. Remote Sens. 2021, 13, 253. [Google Scholar] [CrossRef]
- Fournier, S.; Bingham, F.M.; González-Haro, C.; Hayashi, A.; Ulfsax Carlin, K.M.; Brodnitz, S.K.; González-Gambau, V.; Kuusela, M. Quantification of Aquarius, SMAP, SMOS and Argo-Based Gridded Sea Surface Salinity Product Sampling Errors. Remote Sens. 2023, 15, 422. [Google Scholar] [CrossRef]
- Soldo, Y.; Cabot, F.; Khazaal, A.; Miernecki, M.; Slominska, E.; Fieuzal, R.; Kerr, Y.H. Localization of RFI sources for the SMOS mission: A means for assessing SMOS pointing performances. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 617–627. [Google Scholar] [CrossRef]
- Corbella, I.; Martin-Neira, M.; Oliva, R.; Torres, F.; Duffo, N. Reduction of Secondary Lobes in Aperture Synthesis Radiometry. IEEE Geosci. Remote Sens. Lett. 2012, 9, 977–979. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, W.T.; et al. SMAP Handbook–Soil Moisture Active Passive: Mapping Soil Moisture and Freeze/Thaw from Space; JPL Publication: Pasadena, CA, USA, 2014.
- Report ITU-R RS.2491-0; Global Survey of Radio Frequency Interference Observed by the SMAP Radar in the 1215 to 1300 MHz Band and the SMAP Radiometer in the 1400 to 1427 MHz Band. International Telecommunications Union, 2021; ITU RS Series, Remote Sensing Systems. Posted on September 2021. Available online: https://www.itu.int/pub/R-REP-RS.2491 (accessed on 2 April 2024).
- Wigneron, J.-P.; Li, X.; Frappart, F.; Fan, L.; Al-Yaari, A.; De Lannoy, G.; Liu, X.; Wang, M.; Le Masson, E.; Moisy, C. SMOS-IC data record of soil moisture and L-VOD: Historical development, applications and perspectives. Remote Sens. Environ. 2021, 254, 112238. [Google Scholar] [CrossRef]


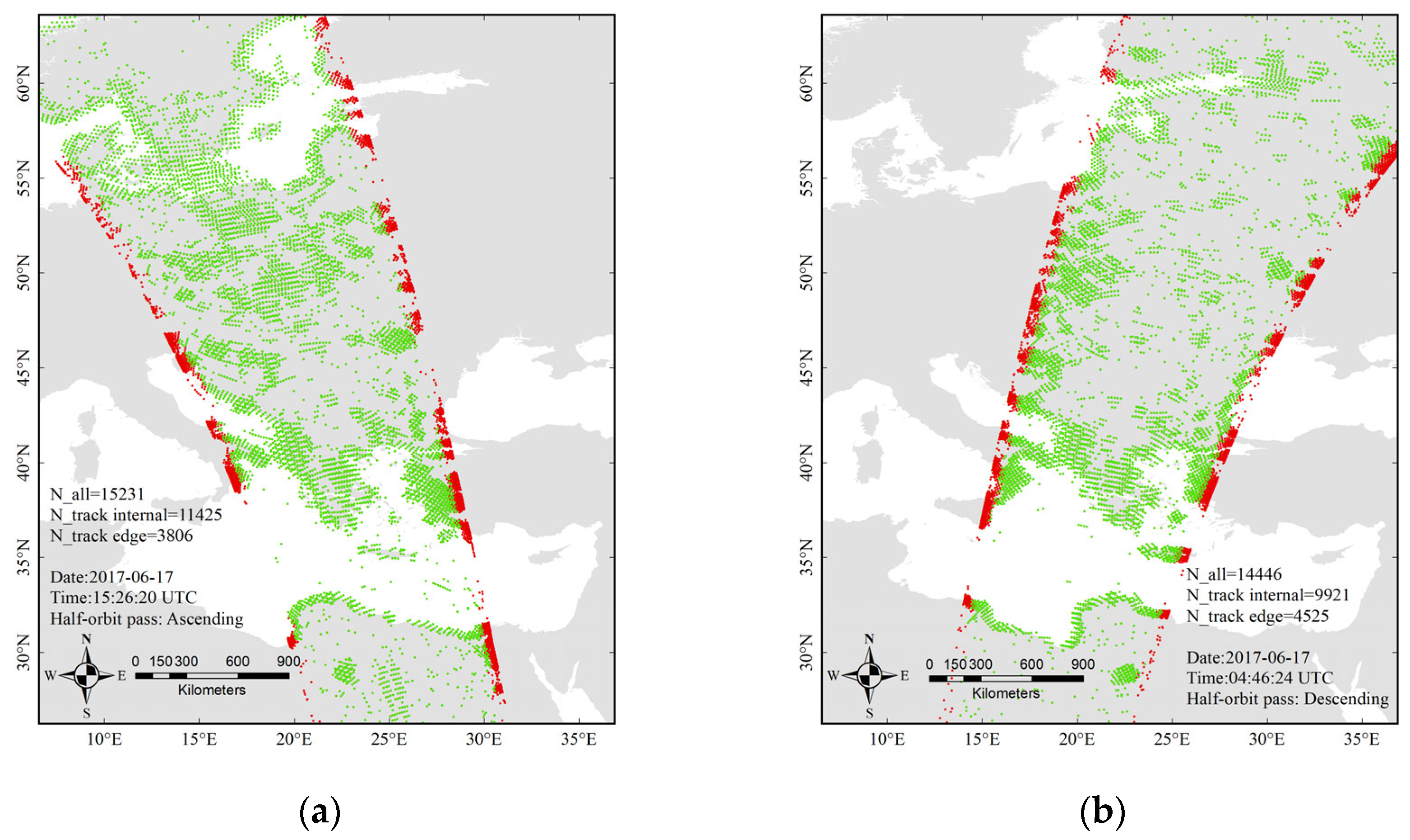

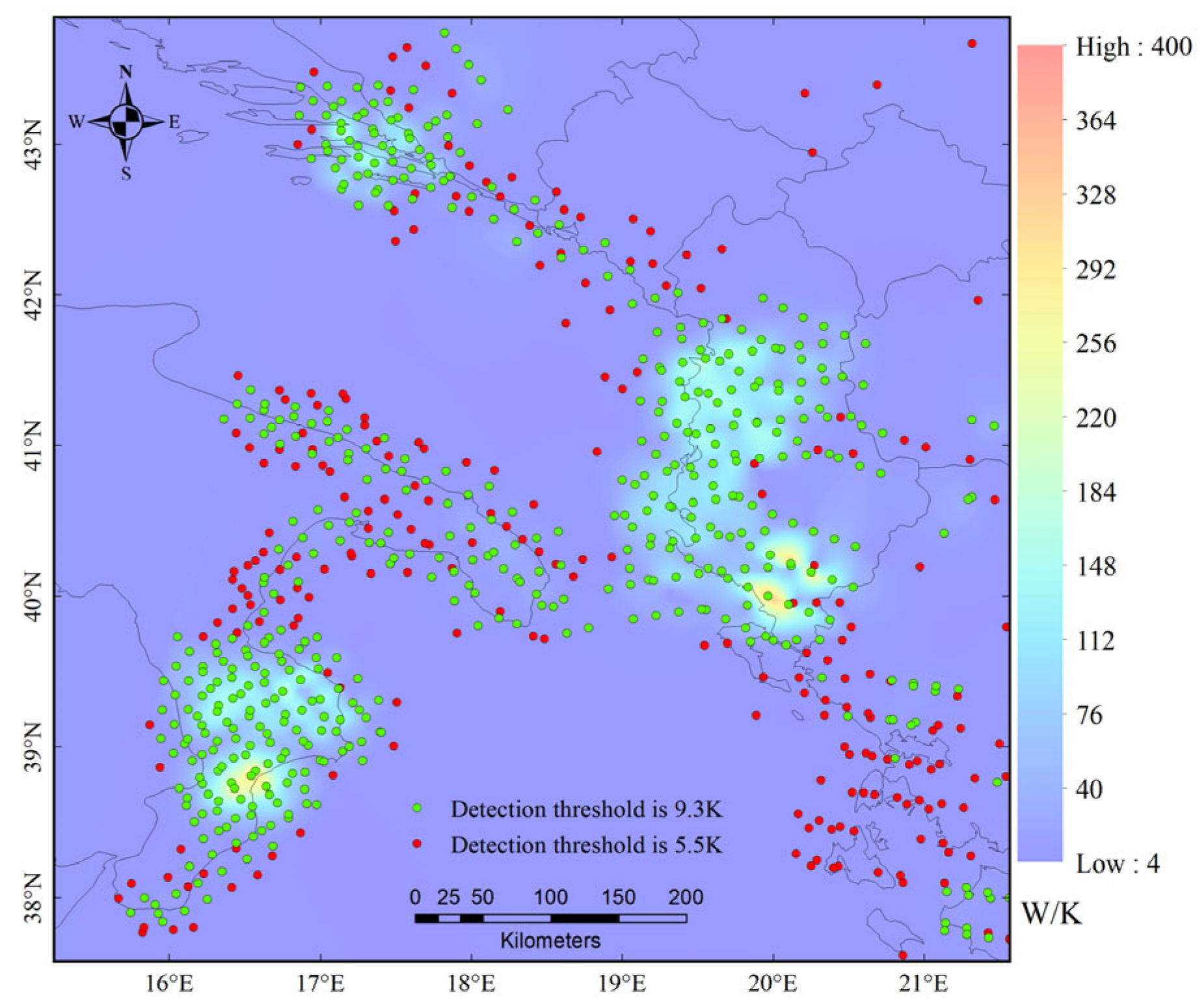


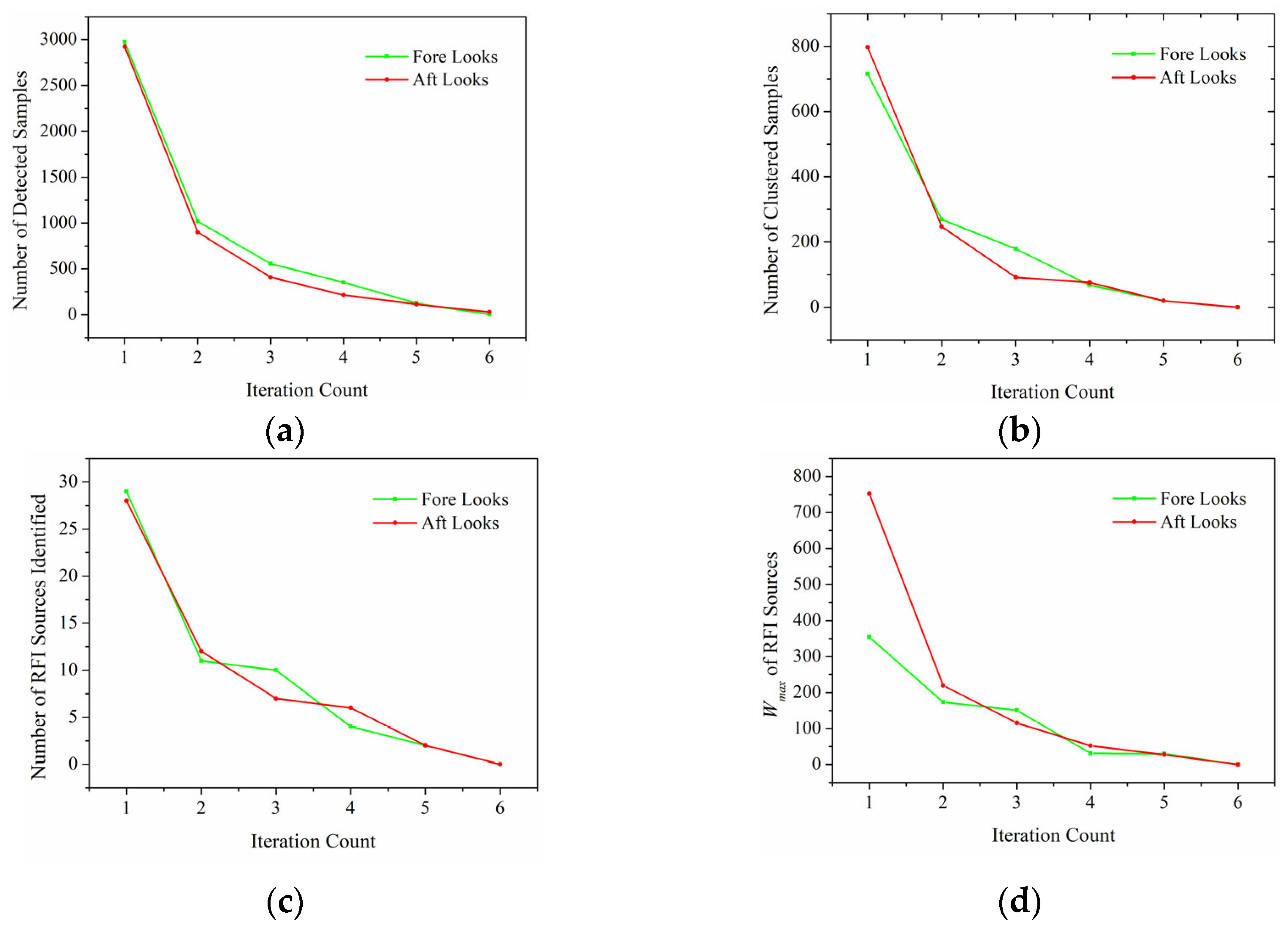
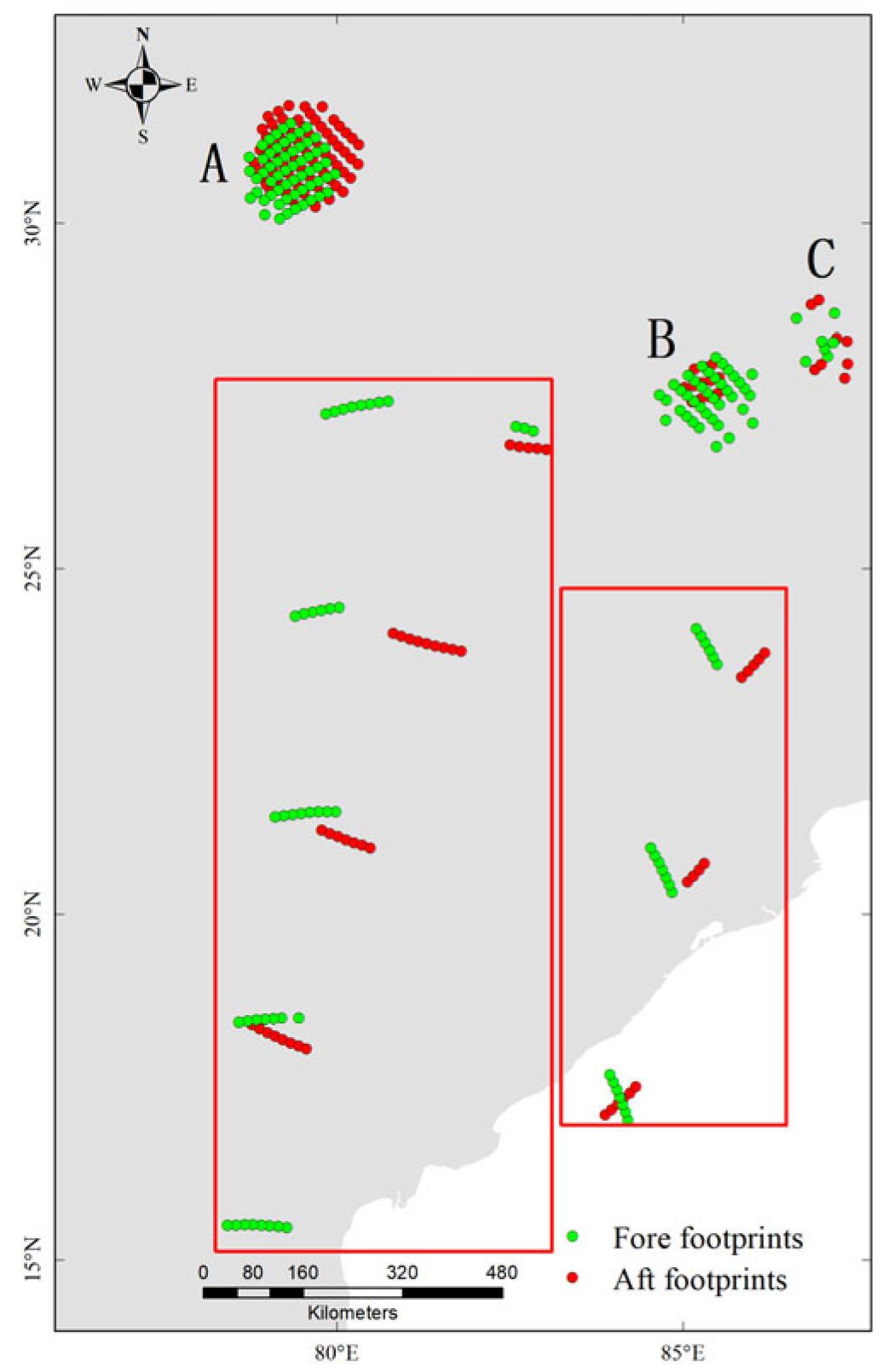




| Orbit | Total Number of RFI Detection Samples | Number of Samples on Orbit Edge | Number of Samples inside Orbit | Number of SRDF Samples inside Orbit | Number of SPDA Samples inside Orbit | Number of Overlapped Samples |
|---|---|---|---|---|---|---|
| Ascending | 15,231 | 3806 | 11,425 | 7436 | 7853 | 3864 |
| Descending | 14,446 | 4525 | 9921 | 4915 | 7608 | 2602 |
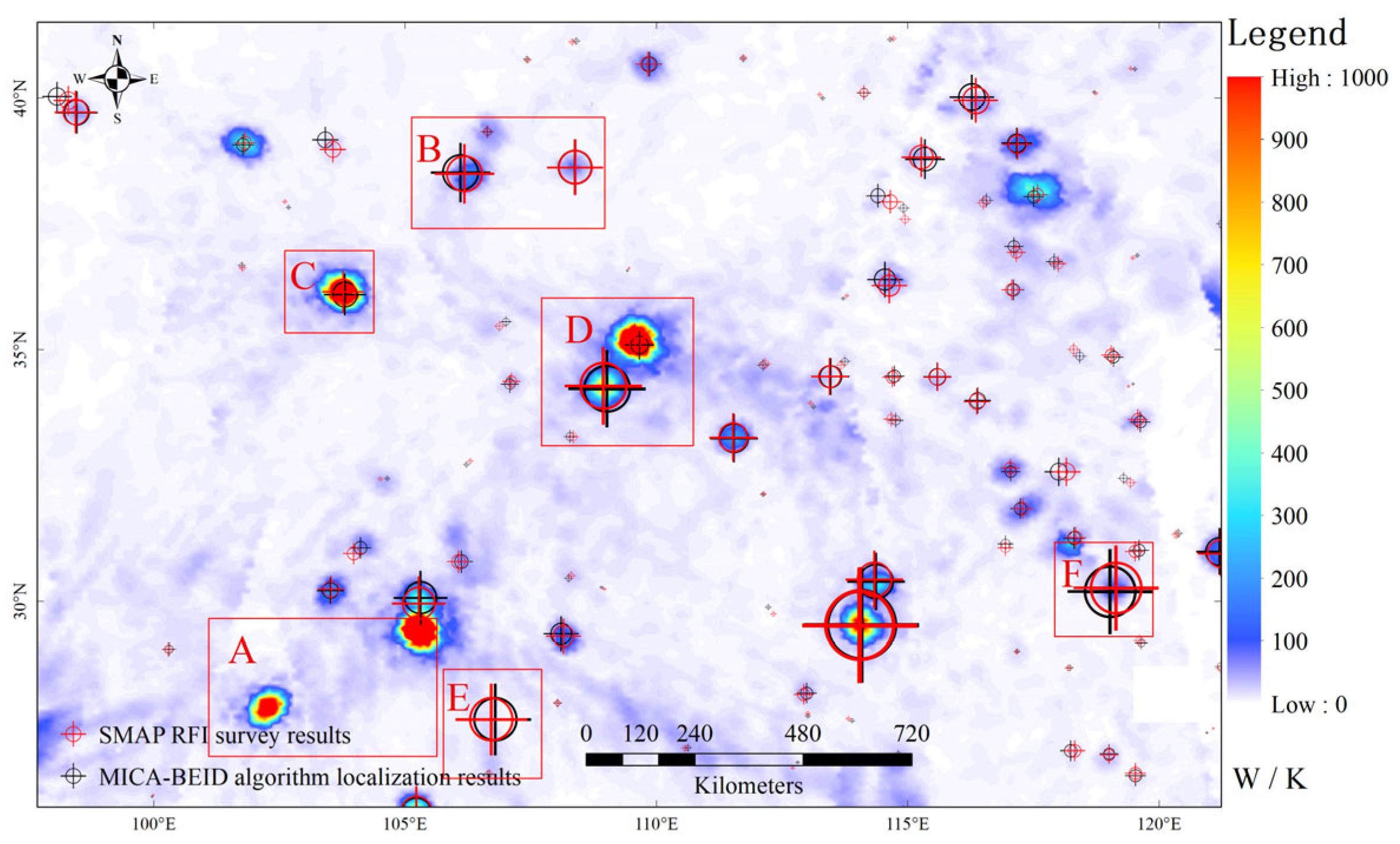
| Clusters | Minimum Value (K) | Maximum Value (K) | Standard Deviation (K) | Number of Samples |
|---|---|---|---|---|
| A | 9.9 | 216.2 | 76.3 | 80 |
| B | 9.9 | 18.7 | 2.2 | 112 |
| C | 10.1 | 366.7 | 115.1 | 54 |
| D | 9.8 | 21.7 | 3.1 | 108 |
| E | 9.8 | 21 | 2.6 | 131 |
| Region | Optimal Location Distance (km) | Wmax (K) | Types of Known RFI Sources | Date Turned Off |
|---|---|---|---|---|
| Hebei | 1.2 | 200.4 | Broadcast and television tower | 2017-08 |
| Tianjin | 2.1 | 434.7 | Video surveillance equipment. | 2017-08 |
| Shandong | 3.8 | 959.1 | Broadcast and television tower | 2016-03 |
| Hunan | 1.7 | 1340.7 | Microwave transmission antenna | 2016-03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, X.; Wang, L.; Fan, J.; Wei, E. Constrained Iterative Adaptive Algorithm for the Detection and Localization of RFI Sources Based on the SMAP L-Band Microwave Radiometer. Remote Sens. 2024, 16, 1791. https://doi.org/10.3390/rs16101791
Wang X, Wang X, Wang L, Fan J, Wei E. Constrained Iterative Adaptive Algorithm for the Detection and Localization of RFI Sources Based on the SMAP L-Band Microwave Radiometer. Remote Sensing. 2024; 16(10):1791. https://doi.org/10.3390/rs16101791
Chicago/Turabian StyleWang, Xinxin, Xiang Wang, Lin Wang, Jianchao Fan, and Enbo Wei. 2024. "Constrained Iterative Adaptive Algorithm for the Detection and Localization of RFI Sources Based on the SMAP L-Band Microwave Radiometer" Remote Sensing 16, no. 10: 1791. https://doi.org/10.3390/rs16101791
APA StyleWang, X., Wang, X., Wang, L., Fan, J., & Wei, E. (2024). Constrained Iterative Adaptive Algorithm for the Detection and Localization of RFI Sources Based on the SMAP L-Band Microwave Radiometer. Remote Sensing, 16(10), 1791. https://doi.org/10.3390/rs16101791






