Enhanced Underwater Single Vector-Acoustic DOA Estimation via Linear Matched Stochastic Resonance Preprocessing
Abstract
:1. Introduction
- (1)
- What are the theoretical restrictions of preprocessing methods for vector DOA estimation?
- (2)
- How can vector acoustic DOA estimation performance be improved under low-SNR conditions and complex background noise?
- (1)
- A generalized vector acoustic preprocessing optimization model is established in a comprehensive theoretical analysis of UAVSsignal preprocessing, which indicates that the gain-phase constraints for vector DOA estimation are independent of the P channel.
- (2)
- A novel preprocessing method named linear matched stochastic resonance (LMSR) is proposed within the framework of matched stochastic resonance theory, which can naturally guarantee linear gain-phase restrictions, as well as achieving effective denoising performance.
- (3)
- Superior vector acoustic DOA estimation performance is achieved in comparison with classical intensity-based AAIM and CAIM methods, especially under low-SNR conditions and non-Gaussian impulsive noise circumstances.
- (4)
- This work can lay a solid foundation to break through the challenges of underwater remote vector acoustic DOA estimation under low SNR and complex ocean ambient noise and can provide important guidance for future research work.
2. Generalized Vector Acoustic Preprocessing Optimization Model with Theoretical Analyses
2.1. Vector Acoustic Preprocessing Analysis Model Subject to Gain-Phase Uncertainties
2.2. Theoretical Analysis of Gain-Phase Constraints for AAIM
2.3. Theoretical Analysis of Gain-Phase Constraints for CAIM
2.4. Generalized Vector Acoustic Preprocessing Optimization Model
3. Linear Matched Stochastic Resonance
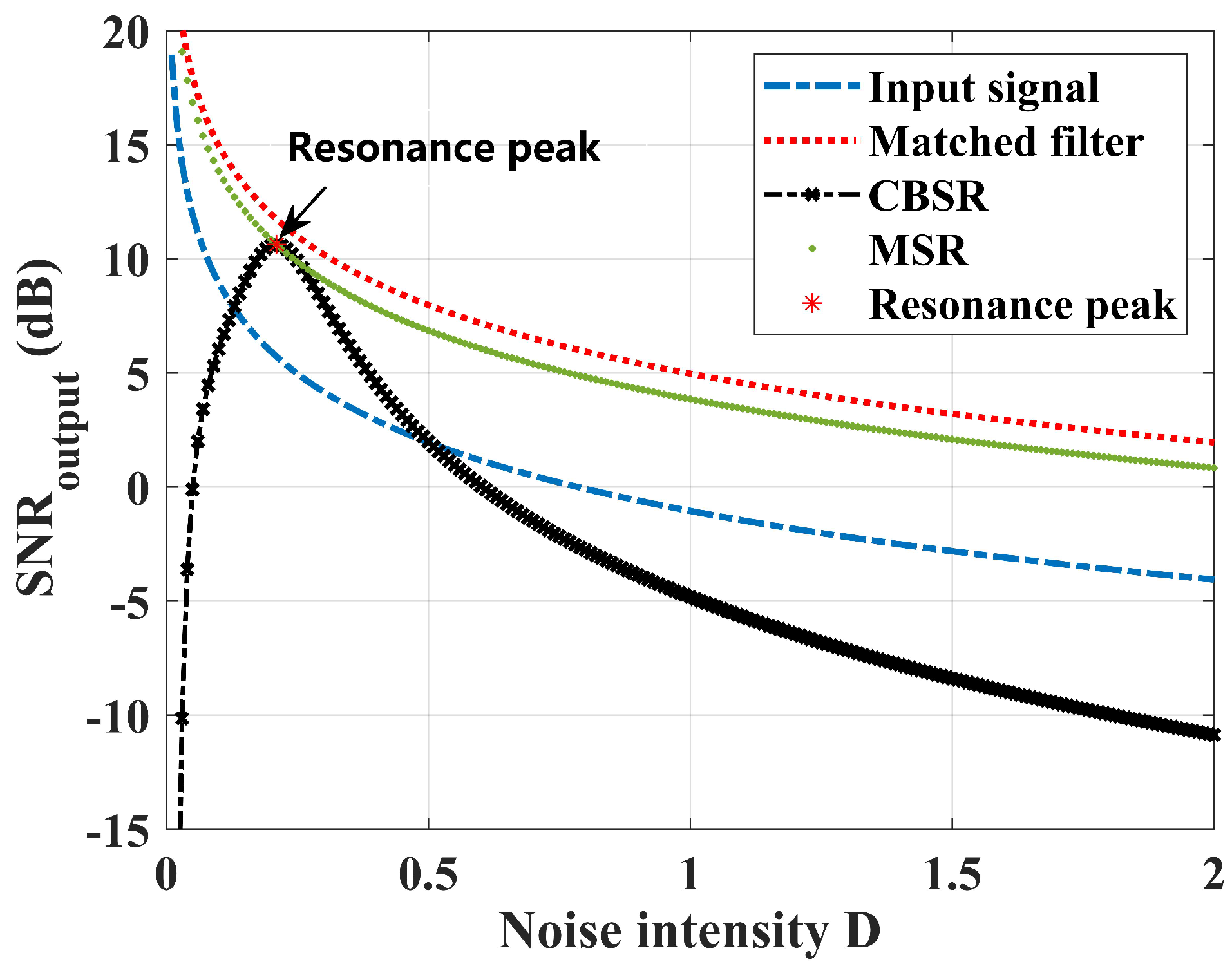
3.1. Classical Bistable Stochastic Resonance (CBSR)
3.2. Theory of Matched Stochastic Resonance (MSR)
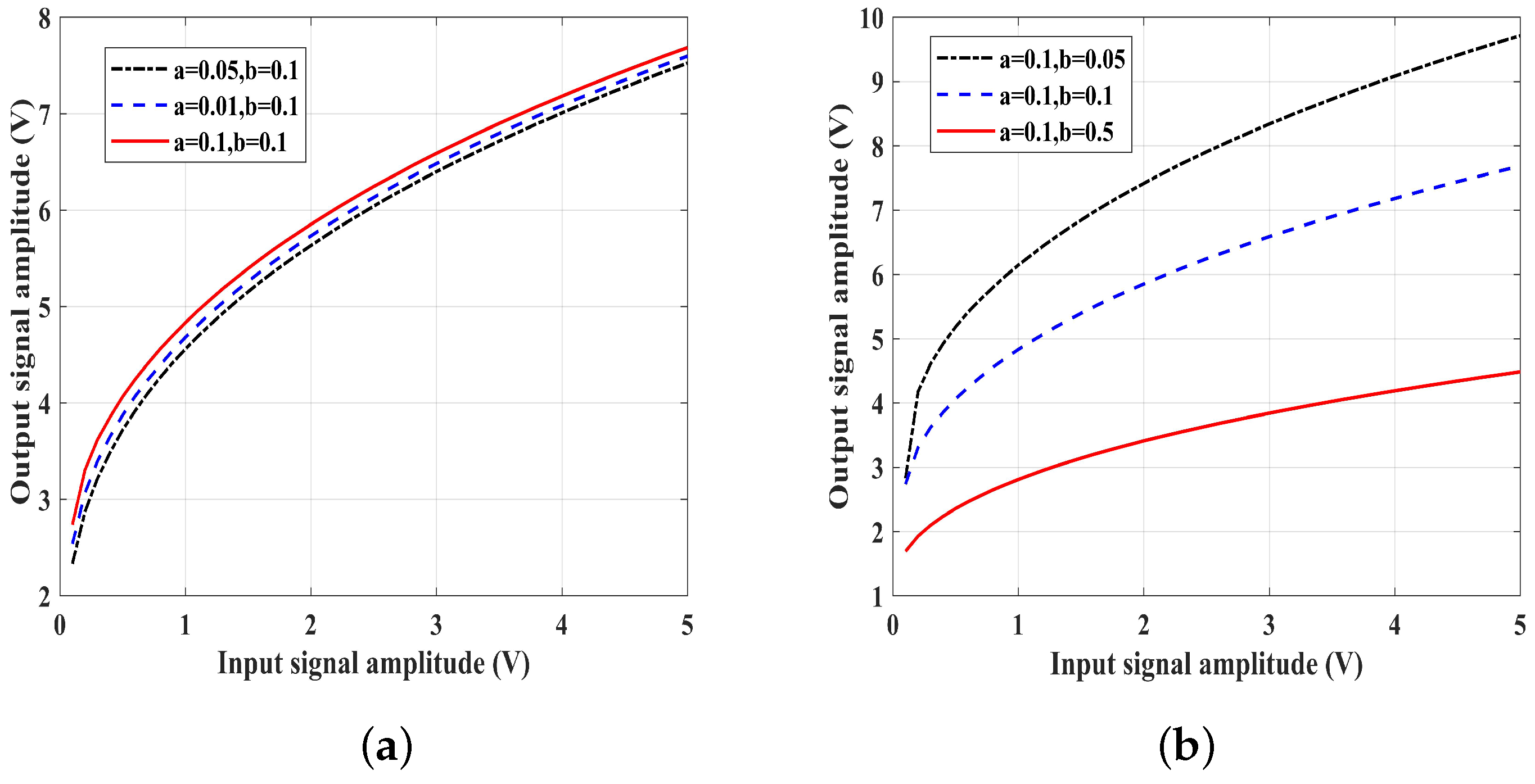
3.3. Linear Matched Stochastic Resonance for Vector Acoustic Preprocessing (LMSR)
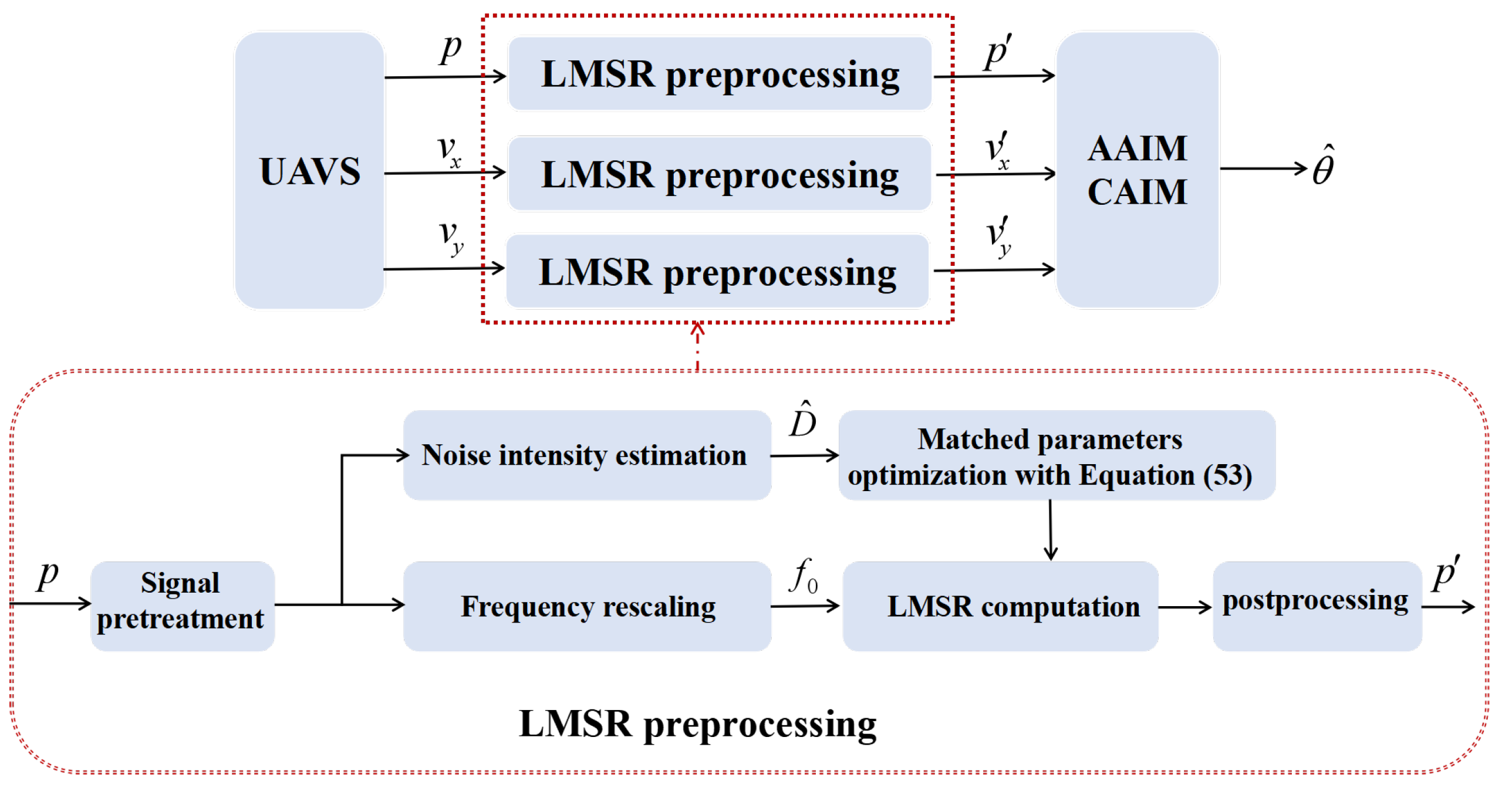
3.4. Implementation of LMSR-Based Vector Acoustic DOA Estimation
- (1)
- Signal pretreatment: Common techniques such as band-pass filtering, data normalization, or envelope extraction are executed to better reveal the signal periodicity of the actual received noisy signals.
- (2)
- Frequency rescaling: According to the adiabatic approximation theorem, the SR system is restricted by input signals with a low frequency () of Hz. For practical high input-signal frequencies of tens to thousands of hertz, a frequency rescaling preprocessing technique can be utilized to satisfy the assumption. By introducing a scaling factor () in the process of solving the Runge–Kutta algorithm, the signal frequency () is equivalently converted to a desirable value () as below.in which is the sampling time. Generally, the should be small enough; in this paper, the empirical value is set to Hz.
- (3)
- Noise intensity estimation: The noise intensity estimator () is obtained following a penalization-based least squares method by minimizing the generalized cross-validation score [48].
- (4)
- Parameter optimization: The reference frequency is initialized as Hz, and the optimal parameters ( and ) can be obtained according to Equation (53).
- (5)
- LMSR computation: The LMSR output corresponding to all the received AVS-channel signals is computer. The fourth-order Runge–Kutta (RK4) method is adopted to obtain the numerical solution of the LMSR output under Gaussian noise [35]. For the circumstance of Lévy impulsive noise, the numerical solution is reported in [49].
- (6)
- Post-processing: The Lorentz effect of SR, DC offset, and low-frequency interference removal are applied.
- (7)
- Vector acoustic DOA estimation: The estimation results are calculated by using the AAIM and CAIM methods with the processed multichannel UAVS signals.
4. Simulation Analyses
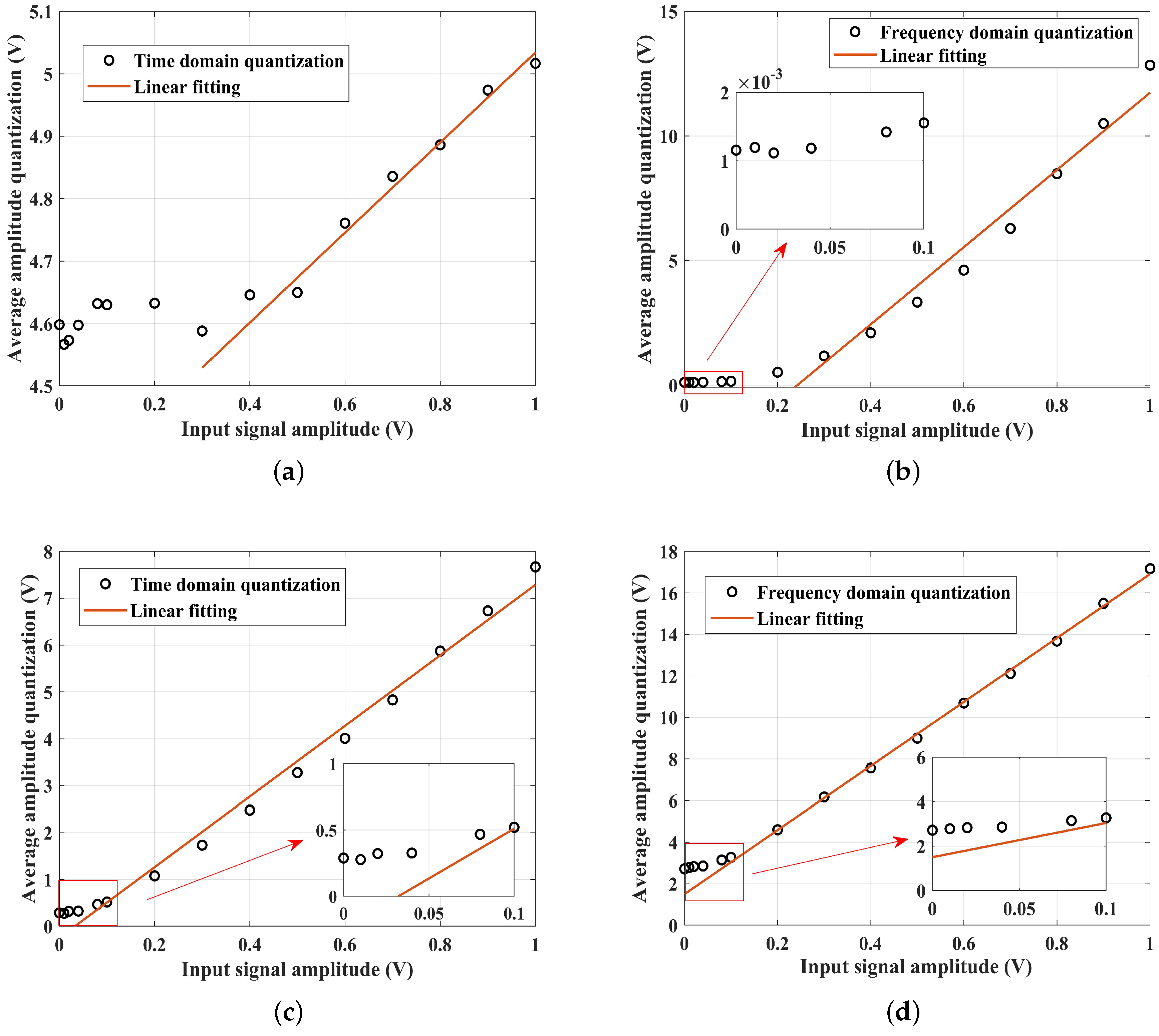
4.1. Linear Amplitude Response Characteristic Analysis
- (1)
- For the time-domain average amplitude quantization, we use peak averaging, which can be defined aswhere M is the number of sliding windows, and and represent the maximum and minimum amplitude within the i-th sliding window, respectively.
- (2)
- For the frequency domain, we calculate the average amplitude value corresponding to the signal frequency via fast Fourier transform (FFT).where is the number of points of the FFT, represents the amplitude of FFT corresponding to the signal frequency (), and ∗ denotes the complex conjugation.
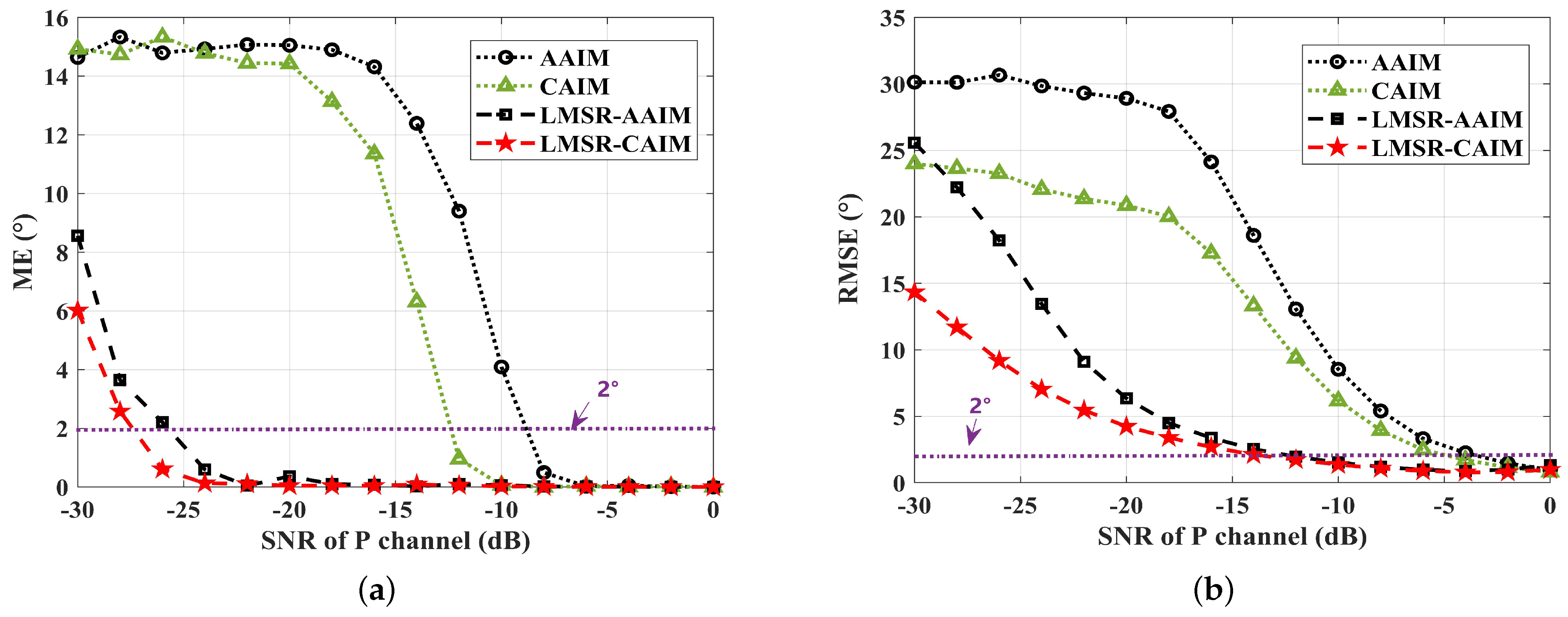
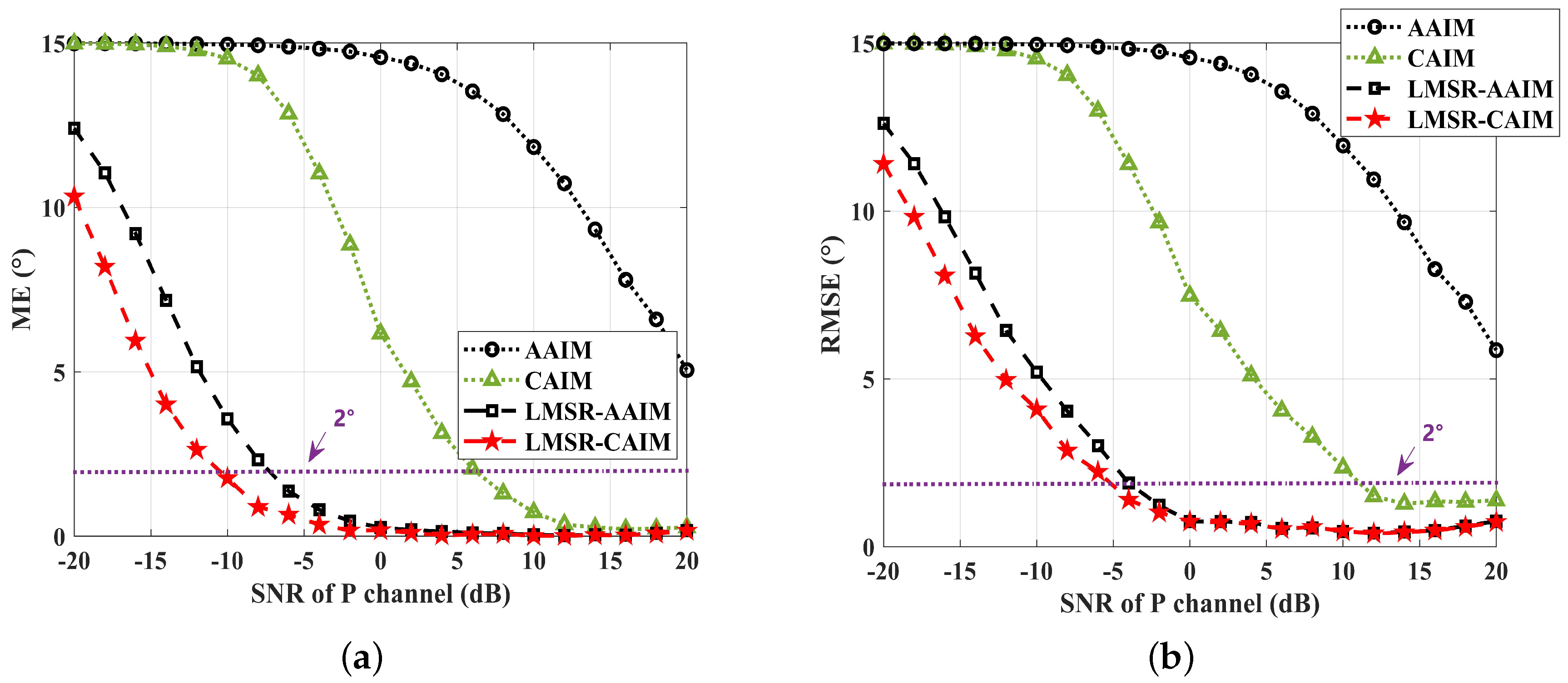
4.2. Estimation Performance Analysis under White Gaussian Noise (WGN)
4.3. Estimation Performance Analysis under Non-Gaussian Impulsive Noise
5. Experimental Verification
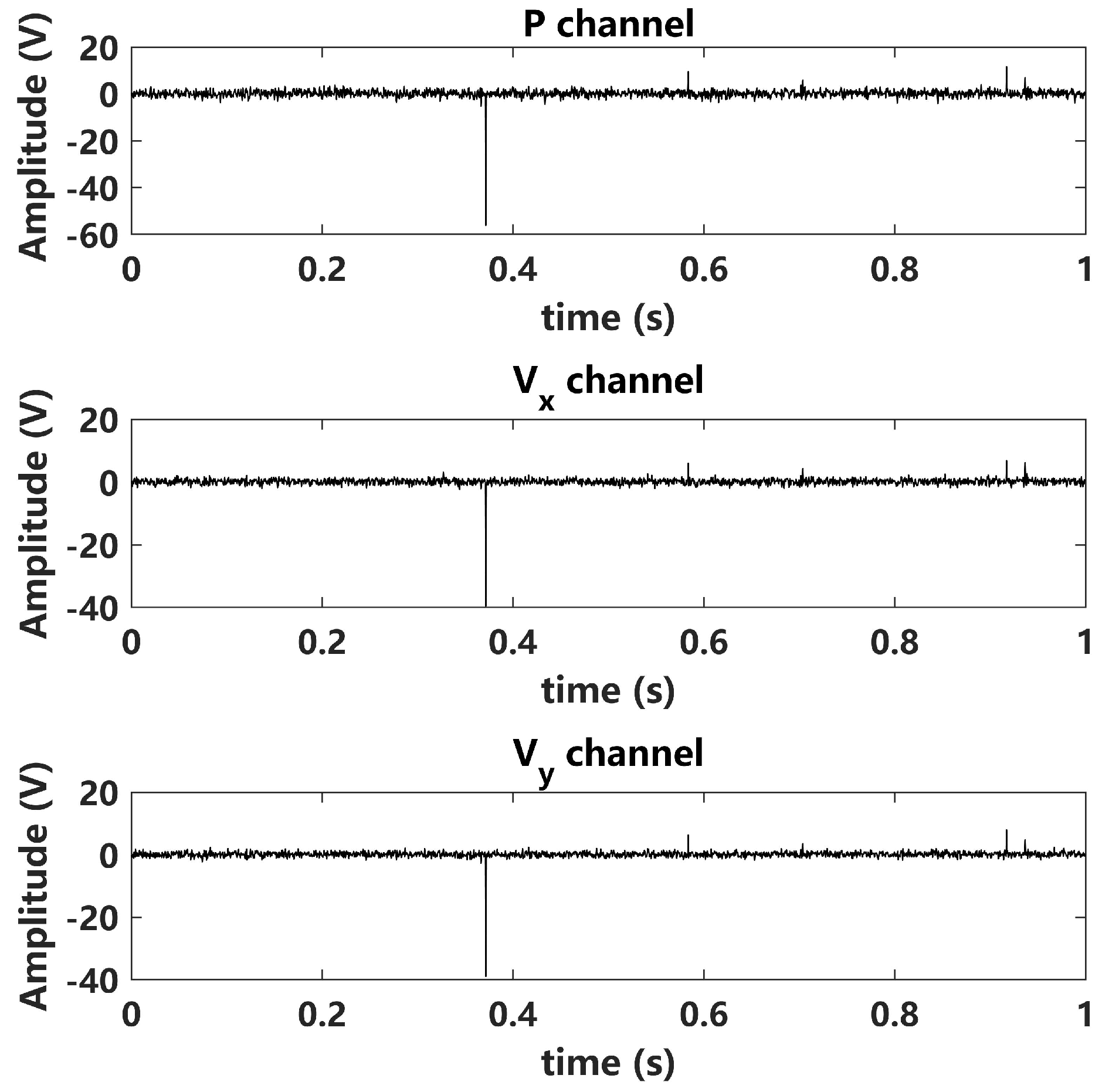
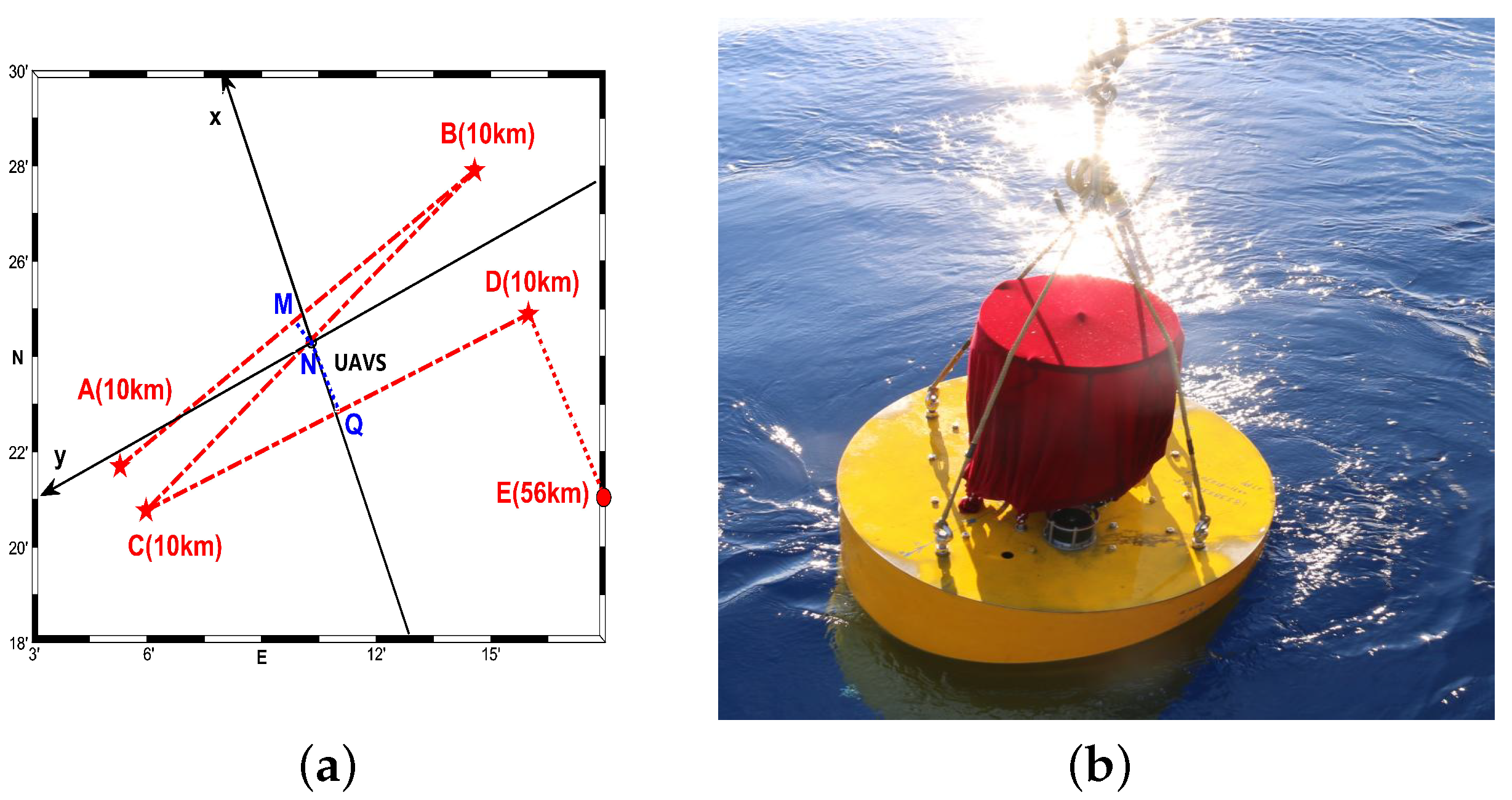
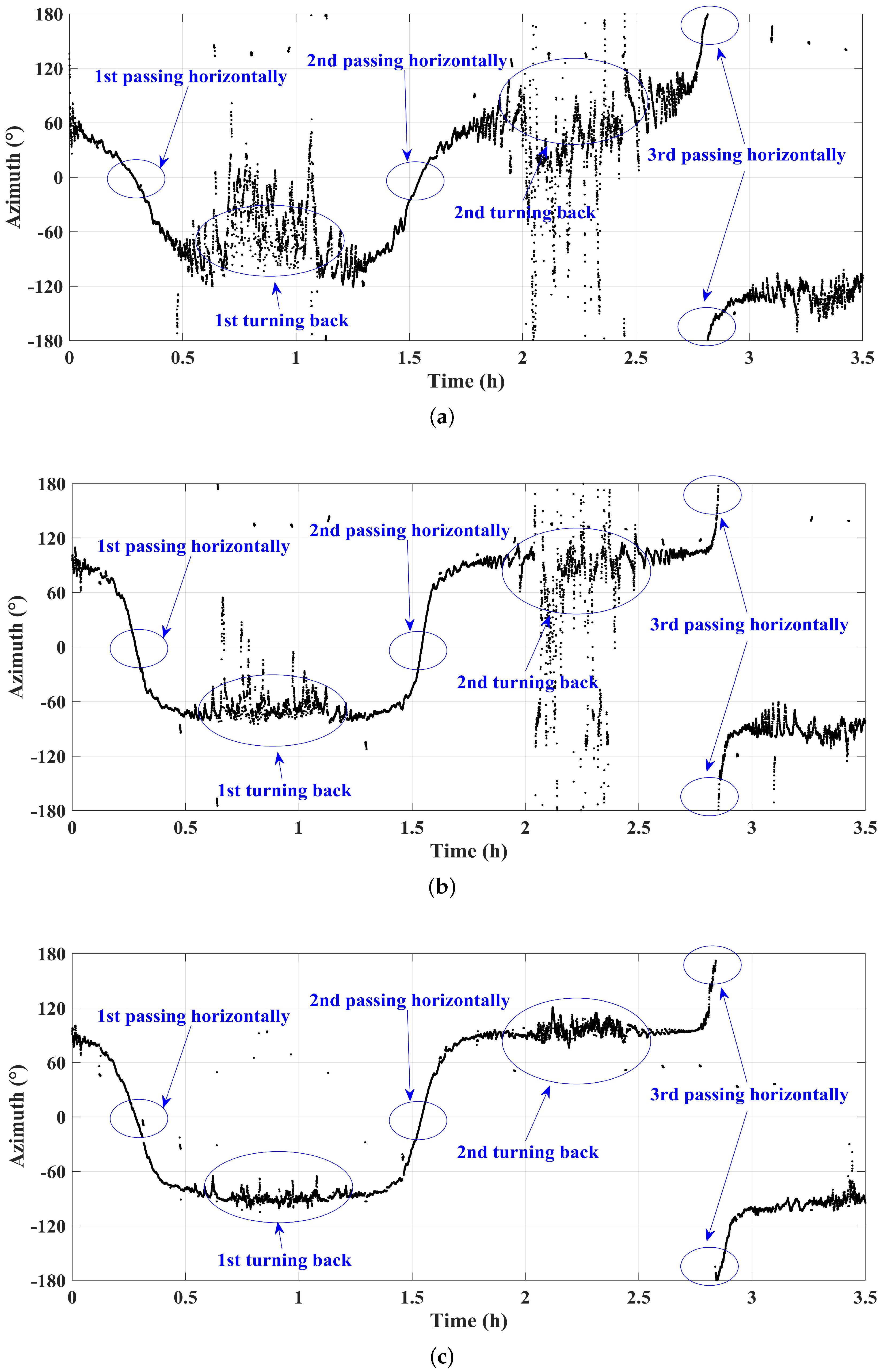
5.1. Experimental Description
5.2. DOA Estimation Performance Analysis
6. Discussion
- (1)
- With the development of advanced ship shock absorption and noise reduction technology, active or passive sonar detection tends toward lower-frequency bands ( Hz) or very low-frequency bands ( Hz). However, ambient ocean noise in the low-frequency band is generally non-Gaussian and impulsive [51,52,53]. Therefore, how to improve vector DOA estimation performance under low-SNR conditions and complex background noise is a key problem for underwater vector acoustic signal processing in the future.
- (2)
- Stochastic resonance has merits in dealing with non-Gaussian noise, which can provide new insights with respect to vector signal processing using nonlinear approaches. In Section 3, we demonstrated that within the framework of matched stochastic resonance theory, the linear gain-phase response can be guaranteed. The aforementioned numerical and practical analyses reveal the effectiveness of our proposed LMSR method. A considerable amount of research work has focused on the SR effect [32,33,34,35], and in previous work, we proposed PMSR, SMSR, IMSR, AIMSR, etc., which can achieve better nonlinear filtering performance than LMSR [35,36,37,38]. Therefore, there should be a number of approaches to improve the overall performance and stability. These can be further studied in the future.
- (3)
- In recent years, deep learning has led to rapid development in a variety of research fields. For vector signal processing, such an approach has already been adopted to improve AVS-DOA estimation performance [30]. However, learning tasks generally require guidance to determine a better loss function design. In Section 2, a generalized vector acoustic preprocessing optimization model was described as ’maximizing denoising performance in under the constraints of equivalent amplitude-gain response and phase-bias response’. We thought this would be important guidance for future research work.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, J.; Liu, J.; Wang, J.; Lai, X. Acoustic vector sensor: Reviews and future perspectives. IET Signal Process. 2016, 11, 1–9. [Google Scholar] [CrossRef]
- Wu, K.; Reju, V.G.; Khong, A.W. Multisource DOA estimation in a reverberant environment using a single acoustic vector sensor. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1848–1859. [Google Scholar] [CrossRef]
- Stinco, P.; Tesei, A.; Dreo, R.; Micheli, M. Detection of envelope modulation and direction of arrival estimation of multiple noise sources with an acoustic vector sensor. J. Acoust. Soc. Am. 2021, 149, 1596–1608. [Google Scholar] [CrossRef] [PubMed]
- Nehorai, A.; Paldi, E. Acoustic vector-sensor array processing. IEEE Trans. Signal Process. 1994, 42, 2481–2491. [Google Scholar] [CrossRef]
- Wong, K.T.; Zoltowski, M.D. Uni-vector-sensor ESPRIT for multisource azimuth, elevation, and polarization estimation. IEEE Trans. Antennas Propag. 1997, 45, 1467–1474. [Google Scholar] [CrossRef]
- Miron, S.; Le Bihan, N.; Mars, J.I. Quaternion-MUSIC for vector-sensor array processing. IEEE Trans. Signal Process. 2006, 54, 1218–1229. [Google Scholar] [CrossRef]
- Han, K.; Nehorai, A. Nested vector-sensor array processing via tensor modeling. IEEE Trans. Signal Process. 2014, 62, 2542–2553. [Google Scholar] [CrossRef]
- Najeem, S.; Kiran, K.; Malarkodi, A.; Latha, G. Open lake experiment for direction of arrival estimation using acoustic vector sensor array. Appl. Acoust. 2017, 119, 94–100. [Google Scholar] [CrossRef]
- Weiss, A. Blind direction-of-arrival estimation in acoustic vector-sensor arrays via tensor decomposition and Kullback-Leibler divergence covariance fitting. IEEE Trans. Signal Process. 2020, 69, 531–545. [Google Scholar] [CrossRef]
- Dreo, R.; Trabattoni, A.; Stinco, P.; Micheli, M.; Tesei, A. Detection and localization of multiple ships using acoustic vector sensors on buoyancy gliders: Practical design considerations and experimental verifications. IEEE J. Ocean. Eng. 2022, 48, 577–591. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, S.; Qi, Y.; Liang, Y.; Sui, Y. Characteristics of very-low-frequency pulse acoustic fields measured by vector sensor and ocean bottom seismometer in shallow water. J. Acoust. Soc. Am. 2018, 144, 1916. [Google Scholar] [CrossRef]
- Silvia, M.T.; Richards, R.T. A theoretical and experimental investigation of low-frequency acoustic vector sensors. In Proceedings of the OCEANS’02 MTS/IEEE, Biloxi, MI, USA, 29–31 October 2002; Volume 3, pp. 1886–1897. [Google Scholar]
- Thode, A.; Skinner, J.; Scott, P.; Roswell, J.; Straley, J.; Folkert, K. Tracking sperm whales with a towed acoustic vector sensor. J. Acoust. Soc. Am. 2010, 128, 2681–2694. [Google Scholar] [CrossRef] [PubMed]
- Tichavsky, P.; Wong, K.T.; Zoltowski, M.D. Near-field/far-field azimuth and elevation angle estimation using a single vector hydrophone. IEEE Trans. Signal Process. 2001, 49, 2498–2510. [Google Scholar] [CrossRef]
- Zhao, A.; Ma, L.; Hui, J.; Zeng, C.; Bi, X. Open-lake experimental investigation of azimuth angle estimation using a single acoustic vector sensor. J. Sens. 2018, 2018, 1–18. [Google Scholar] [CrossRef]
- Bereketli, A.; Guldogan, M.B.; Kolcak, T.; Gudu, T.; Avsar, A.L. Experimental results for direction of arrival estimation with a single acoustic vector sensor in shallow water. J. Sens. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Zhao, A.; Ma, L.; Ma, X.; Hui, J. An improved azimuth angle estimation method with a single acoustic vector sensor based on an active sonar detection system. Sensors 2017, 17, 412. [Google Scholar] [CrossRef]
- Wu, Y.I.; Wong, K.T.; Yuan, X.; Lau, S.k.; Tang, S.k. A directionally tunable but frequency-invariant beamformer on an acoustic velocity-sensor triad to enhance speech perception. J. Acoust. Soc. Am. 2012, 131, 3891–3902. [Google Scholar] [CrossRef] [PubMed]
- Thode, A.M.; Kim, K.H.; Norman, R.G.; Blackwell, S.B.; Greene, C.R., Jr. Acoustic vector sensor beamforming reduces masking from underwater industrial noise during passive monitoring. J. Acoust. Soc. Am. 2016, 139, EL105–EL111. [Google Scholar] [CrossRef] [PubMed]
- Suo, J.; Dong, H.; Shen, X.; Wang, H. Bistable stochastic resonance with linear amplitude response enhanced vector DOA estimation under low SNR conditions. Chaos Solitons Fract. 2020, 136, 109825. [Google Scholar] [CrossRef]
- Terracciano, D.S.; Costanzi, R.; Manzari, V.; Stifani, M.; Caiti, A. Passive bearing estimation using a 2-D acoustic vector sensor mounted on a hybrid autonomous underwater vehicle. IEEE J. Ocean. Eng. 2022, 47, 799–814. [Google Scholar] [CrossRef]
- Suo, J.; Wang, H.; Dong, H.; Shen, X.; Yan, Y.; Zhang, H. Single acoustic vector sensor DOA enhanced by unsaturated bistable stochastic resonance with linear amplitude response constrained. Appl. Acoust. 2023, 214, 109695. [Google Scholar] [CrossRef]
- Hochwald, B.; Nehorai, A. Identifiability in array processing models with vector-sensor applications. IEEE Trans. Signal Process. 1996, 44, 83–95. [Google Scholar] [CrossRef]
- Agarwal, A.; Agrawal, M.; Kumar, A. Higher-order-statistics-based direction-of-arrival estimation of multiple wideband sources with single acoustic vector sensor. IEEE J. Ocean. Eng. 2019, 45, 1439–1449. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, X.; Chen, Z.; Bao, M.; Zhang, X.P.; Yang, J. High-resolution DOA estimation algorithm for a single acoustic vector sensor at low SNR. IEEE Trans. Signal Process. 2020, 68, 6142–6158. [Google Scholar] [CrossRef]
- Wang, D.; Zou, Y.; Wang, W. Learning soft mask with DNN and DNN-SVM for multi-speaker DOA estimation using an acoustic vector sensor. J. Frankl. Inst. 2018, 355, 1692–1709. [Google Scholar] [CrossRef]
- Zhong, X.; Premkumar, A.B. Particle filtering approaches for multiple acoustic source detection and 2-D direction of arrival estimation using a single acoustic vector sensor. IEEE Trans. Signal Process. 2012, 60, 4719–4733. [Google Scholar] [CrossRef]
- Gunes, A.; Guldogan, M.B. Joint underwater target detection and tracking with the Bernoulli filter using an acoustic vector sensor. Digit. Signal Process. 2016, 48, 246–258. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, W.; Wang, Z.; Xia, B. A source counting method using acoustic vector sensor based on sparse modeling of DOA histogram. IEEE Signal Process. Lett. 2019, 26, 69–73. [Google Scholar] [CrossRef]
- Cao, H.; Wang, W.; Su, L.; Ni, H.; Gerstoft, P.; Ren, Q.; Ma, L. Deep transfer learning for underwater direction of arrival using one vector sensor. J. Acoust. Soc. Am. 2021, 149, 1699–1711. [Google Scholar] [CrossRef]
- Dong, H.; Suo, J.; Zhu, Z.; Li, S. Improved Underwater Single-Vector Acoustic DOA Estimation via Vector Convolution Preprocessing. Electronics 2024, 13, 1796. [Google Scholar] [CrossRef]
- Lu, S.; He, Q.; Wang, J. A review of stochastic resonance in rotating machine fault detection. Mech. Syst. Signal Process. 2019, 116, 230–260. [Google Scholar] [CrossRef]
- Qiao, Z.; Lei, Y.; Li, N. Applications of stochastic resonance to machinery fault detection: A review and tutorial. Mech. Syst. Signal Process. 2019, 122, 502–536. [Google Scholar] [CrossRef]
- He, D.; Lin, Y.; He, C.; Jiang, L. A novel spectrum-sensing technique in cognitive radio based on stochastic resonance. IEEE Trans. Veh. Technol. 2010, 59, 1680–1688. [Google Scholar]
- Dong, H.; Wang, H.; Shen, X.; He, K. Parameter matched stochastic resonance with damping for passive sonar detection. J. Sound Vib. 2019, 458, 479–496. [Google Scholar] [CrossRef]
- Dong, H.; Wang, H.; Shen, X.; Jiang, Z. Effects of Second-Order Matched Stochastic Resonance for Weak Signal Detection. IEEE Access 2018, 6, 46505–46515. [Google Scholar] [CrossRef]
- Dong, H.; Shen, X.; He, K.; Wang, H. Nonlinear filtering effects of intrawell matched stochastic resonance with barrier constrainted duffing system for ship radiated line signature extraction. Chaos Solitons Fract. 2020, 141, 110428. [Google Scholar] [CrossRef]
- Dong, H.; He, K.; Shen, X.; Ma, S.; Wang, H.; Qiao, C. Adaptive intrawell matched stochastic resonance with a potential constraint aided line enhancer for passive sonars. Sensors 2020, 20, 3269. [Google Scholar] [CrossRef] [PubMed]
- Ross, D. Mechanics of Underwater Noise; Pergamon Press: Los Altos, CA, USA, 1976; pp. 272–280. [Google Scholar]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–286. [Google Scholar] [CrossRef]
- McNamara, B.; Wiesenfeld, K. Theory of stochastic resonance. Phys. Rev. A 1989, 39, 4854. [Google Scholar] [CrossRef]
- Hu, N.Q. Theory and Methods for Weak Characteristic Signal Detection with Stochastic Resonance; National Defense Industry Press: Beijing, China, 2012; pp. 42–46. [Google Scholar]
- Xu, B.; Duan, F.; Bao, R.; Li, J. Stochastic resonance with tuning system parameters: The application of bistable systems in signal processing. Chaos Solitons Fract. 2002, 13, 633–644. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and Their Behaviour; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Stocks, N.G. Suprathreshold stochastic resonance in multilevel threshold systems. Phys. Rev. Lett. 2000, 84, 2310. [Google Scholar] [CrossRef]
- Herrmann, S.; Imkeller, P.; Pavlyukevich, I.; Peithmann, D. Stochastic Resonance; American Mathematical Society: Ann Arbor, MI, USA, 2013; Volume 194. [Google Scholar]
- Dong, H.; Wang, H.; Shen, X.; Huang, Z.; Ma, S. Detection of underwater weak signal via matched stochastic resonance. In Proceedings of the OCEANS 2017, Aberdeen, UK, 19–22 June 2017; pp. 1–7. [Google Scholar]
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Wang, H.; Shen, X.; Dong, H. Stochastic resonance for underwater vlf weak signal detection under lévy noise background. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar]
- Tan, J.; Chen, X.; Wang, J.; Chen, H.; Cao, H.; Zi, Y.; He, Z. Study of frequency-shifted and re-scaling stochastic resonance and its application to fault diagnosis. Mech. Syst. Signal Process. 2009, 23, 811–822. [Google Scholar] [CrossRef]
- Ma, S.; Wang, H.; Shen, X.; He, K.; Dong, H. Detection method of VLF acoustic signal in complex marine environmental noise. Acta Armamentarii 2020, 41, 2495. [Google Scholar]
- Ainslie, M.A.; Andrew, R.K.; Howe, B.M.; Mercer, J.A. Temperature-driven seasonal and longer term changes in spatially averaged deep ocean ambient sound at frequencies 63–125 Hz. J. Acoust. Soc. Am. 2021, 149, 2531–2545. [Google Scholar] [CrossRef]
- Siddagangaiah, S.; Li, Y.; Guo, X.; Yang, K. On the dynamics of ocean ambient noise: Two decades later. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 103117. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Suo, J.; Zhu, Z.; Wang, H.; Ji, H. Enhanced Underwater Single Vector-Acoustic DOA Estimation via Linear Matched Stochastic Resonance Preprocessing. Remote Sens. 2024, 16, 1802. https://doi.org/10.3390/rs16101802
Dong H, Suo J, Zhu Z, Wang H, Ji H. Enhanced Underwater Single Vector-Acoustic DOA Estimation via Linear Matched Stochastic Resonance Preprocessing. Remote Sensing. 2024; 16(10):1802. https://doi.org/10.3390/rs16101802
Chicago/Turabian StyleDong, Haitao, Jian Suo, Zhigang Zhu, Haiyan Wang, and Hongbing Ji. 2024. "Enhanced Underwater Single Vector-Acoustic DOA Estimation via Linear Matched Stochastic Resonance Preprocessing" Remote Sensing 16, no. 10: 1802. https://doi.org/10.3390/rs16101802
APA StyleDong, H., Suo, J., Zhu, Z., Wang, H., & Ji, H. (2024). Enhanced Underwater Single Vector-Acoustic DOA Estimation via Linear Matched Stochastic Resonance Preprocessing. Remote Sensing, 16(10), 1802. https://doi.org/10.3390/rs16101802









