Characterizing Canopy Structure Variability in Amazonian Secondary Successions with Full-Waveform Airborne LiDAR
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Selection and Age Assignment of Secondary Successions
2.2. Full-Waveform (FWF) Airborne LiDAR Data Acquisition and Derived Metrics
2.3. Data Analysis
3. Results
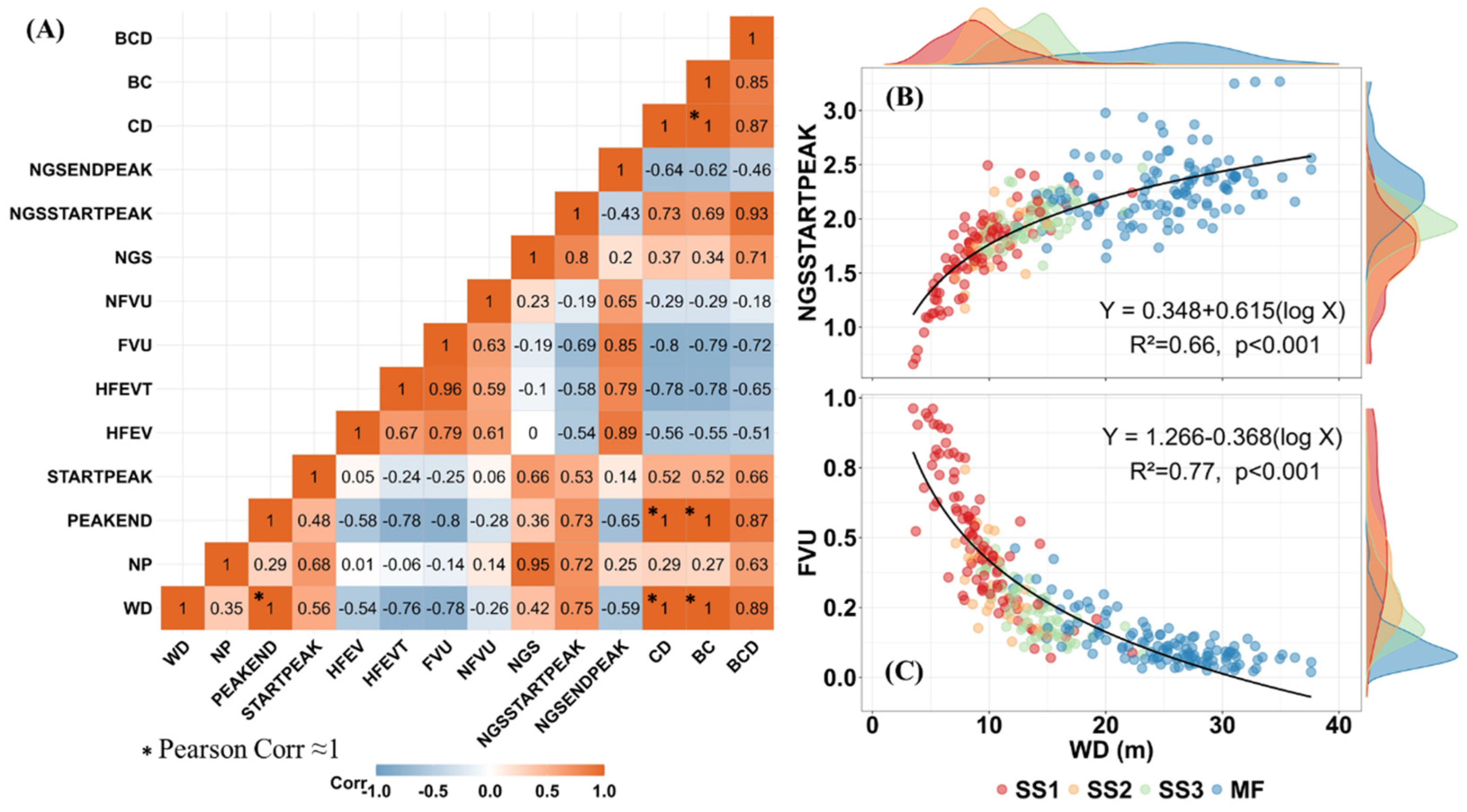
3.1. Variations in FWF Metrics within and across Circular Sample Plots
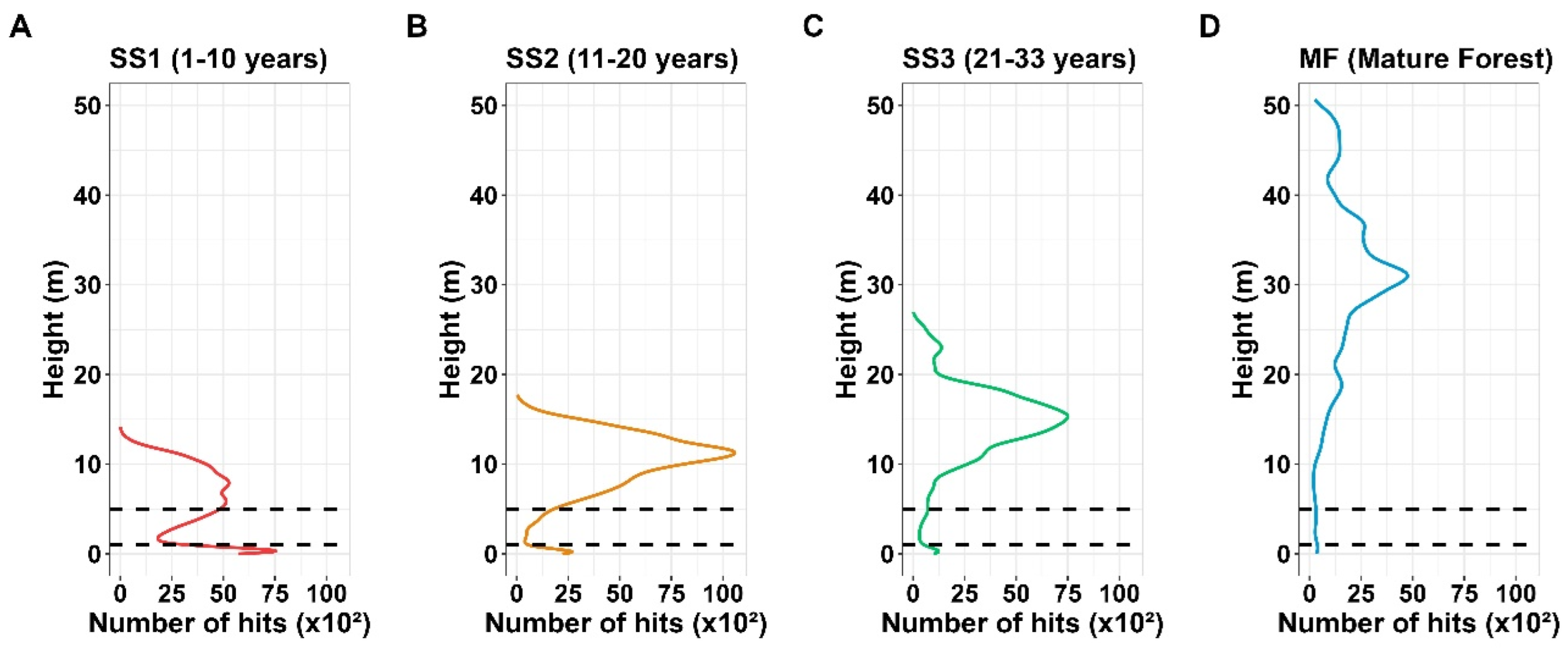
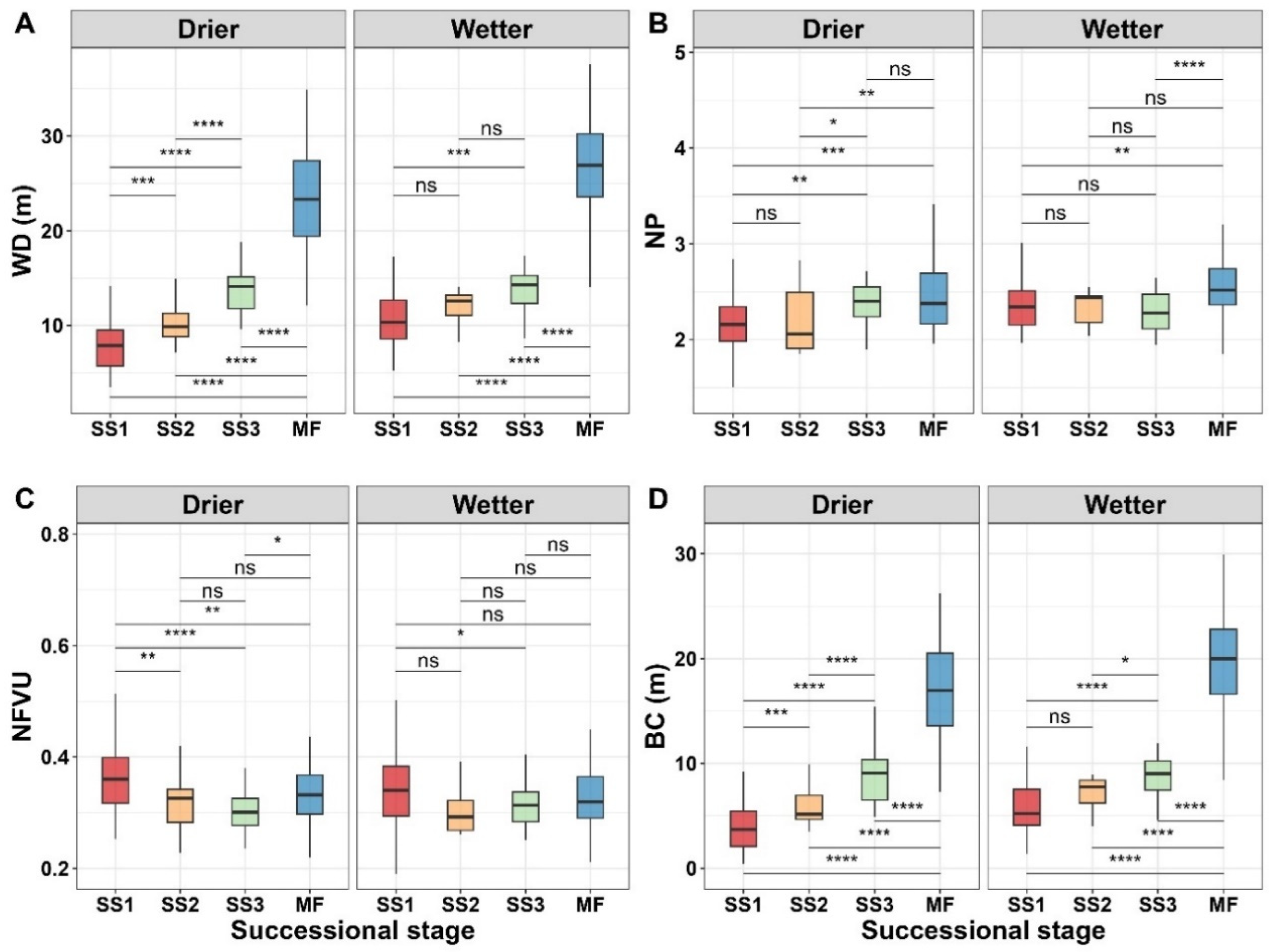
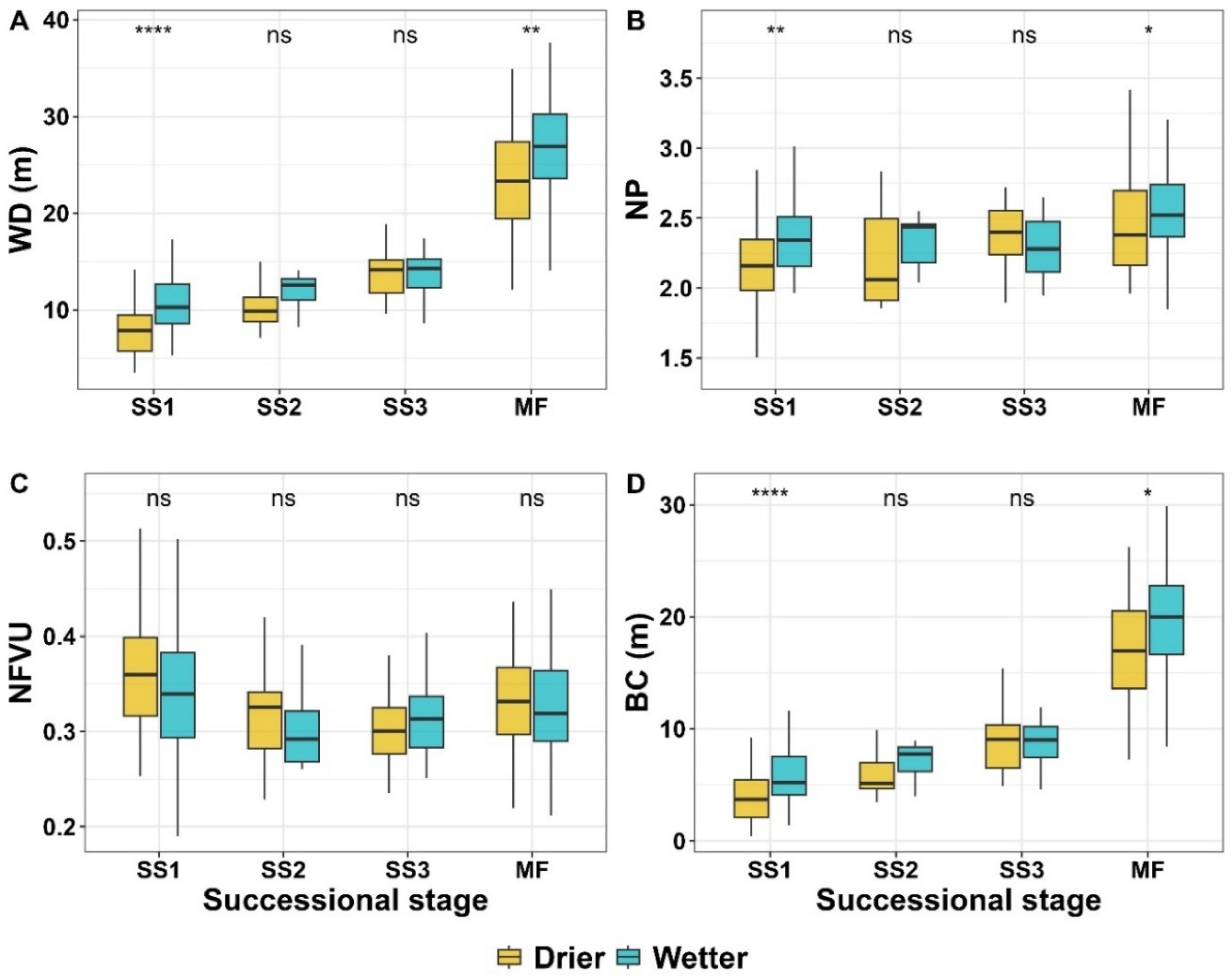
3.2. Differences in FWF Metrics between Successional Stages and Climatological Regions
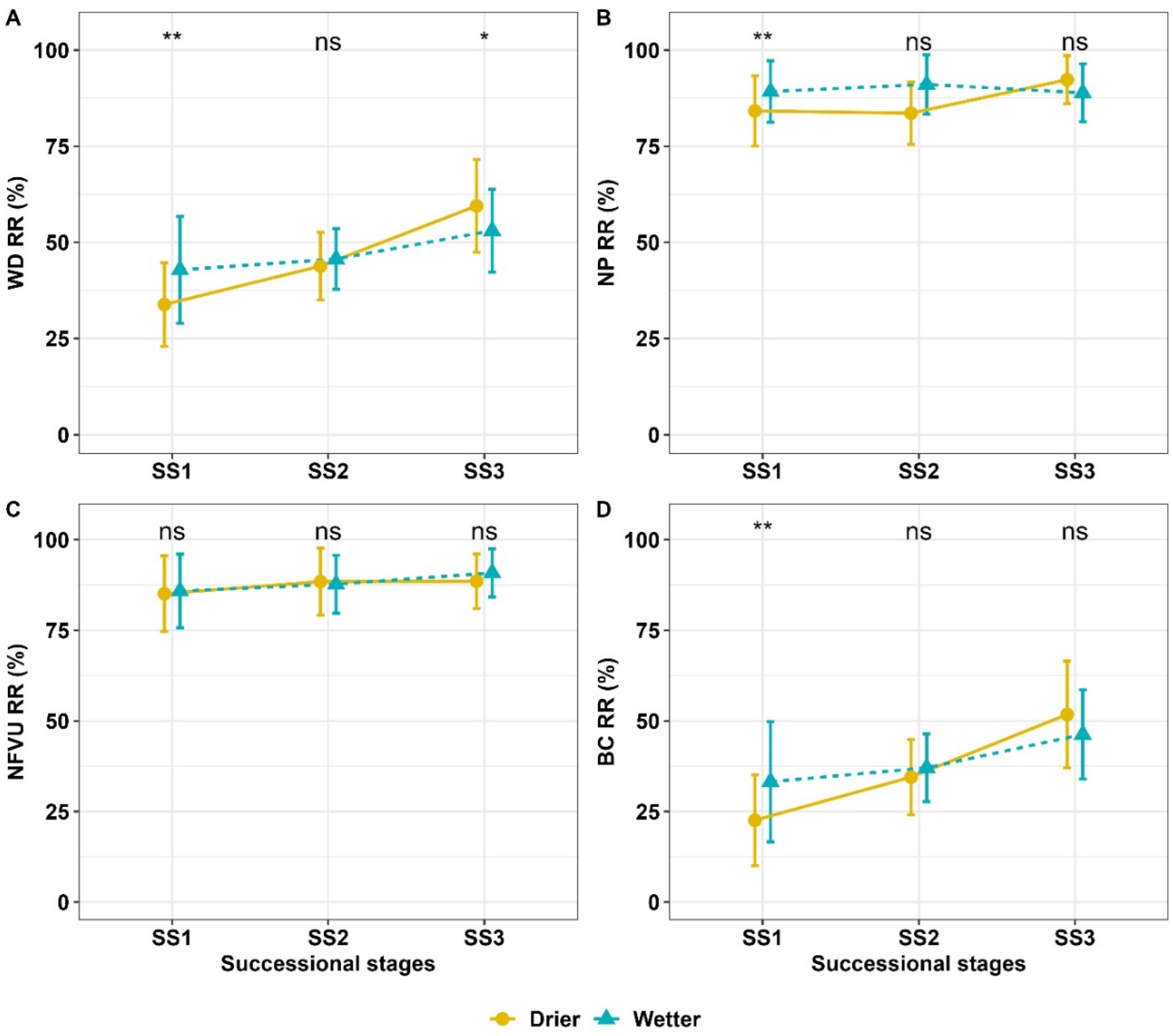
3.3. Relative Recovery of FWF Metrics with Vegetation Regrowth
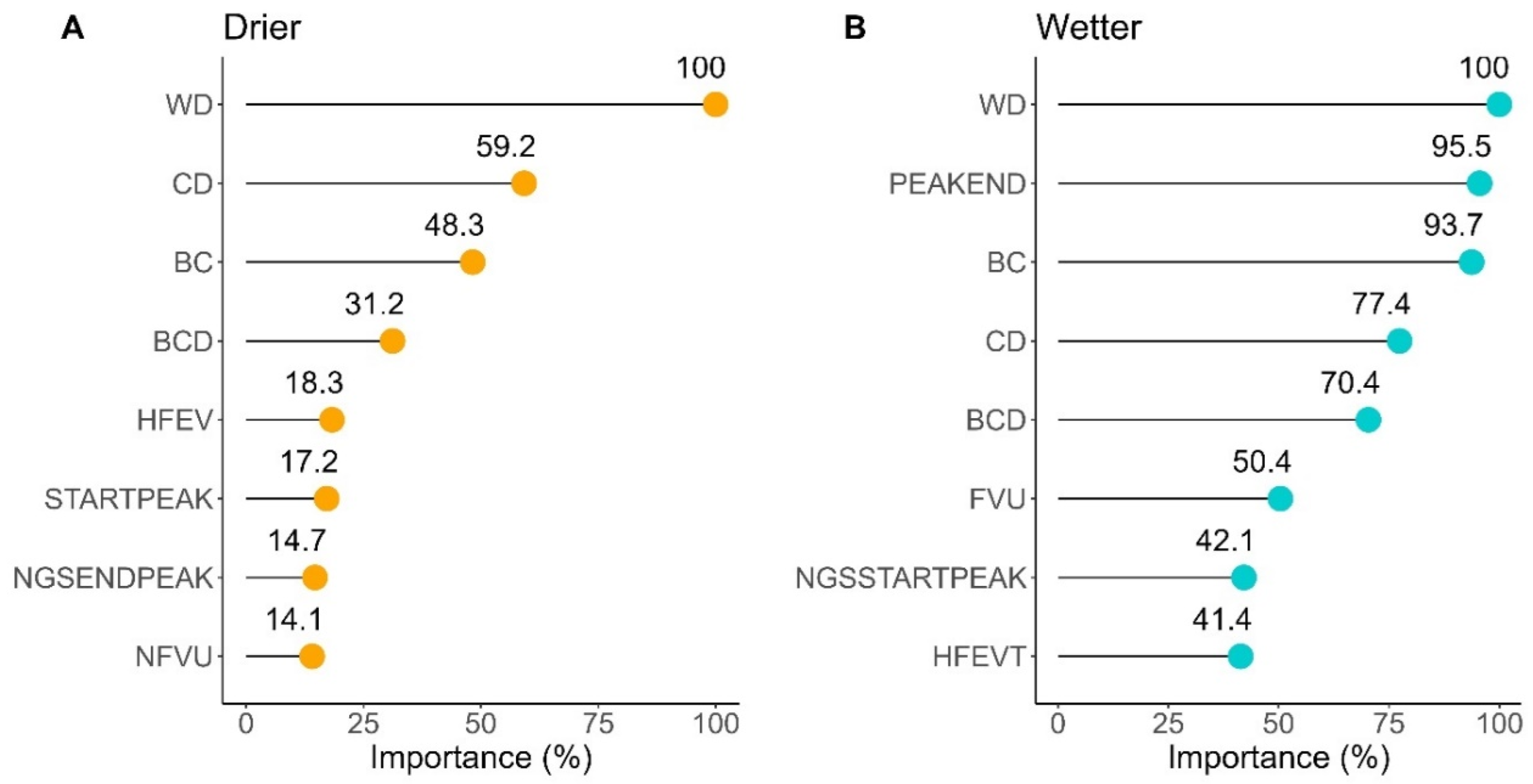
3.4. Potential of FWF Metrics to Discriminate Stages of Secondary Succession Using Random Forest (RF)
4. Discussion
5. Conclusions
- (i)
- The data analysis revealed notable differences in FWF metrics among successional stages, as well as within and between sample plots and regions. Generally, the Drier region displayed more pronounced variations between successional stages and lower FWF metric values than the Wetter region;
- (ii)
- In the initial stages of succession, the Drier region exhibited a slower rate of relative recovery in FWF metrics compared to the Wetter region. However, as succession progressed, the Drier region showed similar rates of recovery to those observed in the Wetter region;
- (iii)
- The WD metric, related to average canopy height, alongside the Gaussian Decomposition metrics (CD, BC, and BCD), associated with the lower forest stratum height, proved to be highly influential and stable in distinguishing successional stages in both analyzed regions. However, the Drier region exhibited superior discrimination between classes, achieving a weighted F1-score of 0.80, compared to 0.73 for the Wetter region.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poorter, L.; Craven, D.; Jakovac, C.C.; Van Der Sande, M.T.; Amissah, L.; Bongers, F.; Chazdon, R.L.; Farrior, C.E.; Kambach, S.; Meave, J.A.; et al. Multidimensional Tropical Forest Recovery. Science 2021, 374, 1370–1376. [Google Scholar] [CrossRef] [PubMed]
- Chazdon, R.L. Second Growth: The Promise of Tropical Forest Regeneration in an Age of Deforestation; University of Chicago Press: Chicago, IL, USA, 2014; ISBN 978-0-226-11807-9. [Google Scholar]
- Chazdon, R.L.; Broadbent, E.N.; Rozendaal, D.M.A.; Bongers, F.; Zambrano, A.M.A.; Aide, T.M.; Balvanera, P.; Becknell, J.M.; Boukili, V.; Brancalion, P.H.S.; et al. Carbon Sequestration Potential of Second-Growth Forest Regeneration in the Latin American Tropics. Sci. Adv. 2016, 2, e1501639. [Google Scholar] [CrossRef] [PubMed]
- Silva Junior, C.H.L.; Heinrich, V.H.A.; Freire, A.T.G.; Broggio, I.S.; Rosan, T.M.; Doblas, J.; Anderson, L.O.; Rousseau, G.X.; Shimabukuro, Y.E.; Silva, C.A.; et al. Benchmark Maps of 33 Years of Secondary Forest Age for Brazil. Sci. Data 2020, 7, 269. [Google Scholar] [CrossRef] [PubMed]
- Brancalion, P.H.S.; Niamir, A.; Broadbent, E.; Crouzeilles, R.; Barros, F.S.M.; Almeyda Zambrano, A.M.; Baccini, A.; Aronson, J.; Goetz, S.; Reid, J.L.; et al. Global Restoration Opportunities in Tropical Rainforest Landscapes. Sci. Adv. 2019, 5, eaav3223. [Google Scholar] [CrossRef] [PubMed]
- Rozendaal, D.M.A.; Bongers, F.; Aide, T.M.; Alvarez-Dávila, E.; Ascarrunz, N.; Balvanera, P.; Becknell, J.M.; Bentos, T.V.; Brancalion, P.H.S.; Cabral, G.A.L.; et al. Biodiversity Recovery of Neotropical Secondary Forests. Sci. Adv. 2019, 5, eaau3114. [Google Scholar] [CrossRef] [PubMed]
- Poorter, L.; Bongers, F.; Aide, T.M.; Almeyda Zambrano, A.M.; Balvanera, P.; Becknell, J.M.; Boukili, V.; Brancalion, P.H.S.; Broadbent, E.N.; Chazdon, R.L.; et al. Biomass Resilience of Neotropical Secondary Forests. Nature 2016, 530, 211–214. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, V.H.A.; Dalagnol, R.; Cassol, H.L.G.; Rosan, T.M.; De Almeida, C.T.; Silva Junior, C.H.L.; Campanharo, W.A.; House, J.I.; Sitch, S.; Hales, T.C.; et al. Large Carbon Sink Potential of Secondary Forests in the Brazilian Amazon to Mitigate Climate Change. Nat. Commun. 2021, 12, 1785. [Google Scholar] [CrossRef]
- Chazdon, R.L.; Guariguata, M.R. Natural Regeneration as a Tool for Large-Scale Forest Restoration in the Tropics. Biotropica 2016, 48, 716–730. [Google Scholar] [CrossRef]
- Crouzeilles, R.; Beyer, H.L.; Monteiro, L.M.; Feltran-Barbieri, R.; Pessôa, A.C.M.; Barros, F.S.M.; Lindenmayer, D.B.; Lino, E.D.S.M.; Grelle, C.E.V.; Chazdon, R.L.; et al. Achieving Cost-effective Landscape-scale Forest Restoration through Targeted Natural Regeneration. Conserv. Lett. 2020, 13, e12709. [Google Scholar] [CrossRef]
- Jakovac, C.C.; Junqueira, A.B.; Crouzeilles, R.; Peña-Claros, M.; Mesquita, R.C.G.; Bongers, F. The Role of Land-use History in Driving Successional Pathways and Its Implications for the Restoration of Tropical Forests. Biol. Rev. 2021, 96, 1114–1134. [Google Scholar] [CrossRef]
- Silva, R.D.; Galvão, L.S.; dos Santos, J.R.; de J. Silva, C.V.; de Moura, Y.M. Spectral/Textural Attributes from ALI/EO-1 for Mapping Primary and Secondary Tropical Forests and Studying the Relationships with Biophysical Parameters. GIScience Remote Sens. 2014, 51, 677–694. [Google Scholar] [CrossRef]
- Cao, S.; Yu, Q.; Sanchez-Azofeifa, A.; Feng, J.; Rivard, B.; Gu, Z. Mapping Tropical Dry Forest Succession Using Multiple Criteria Spectral Mixture Analysis. ISPRS J. Photogramm. Remote Sens. 2015, 109, 17–29. [Google Scholar] [CrossRef]
- Gu, Z.; Cao, S.; Sanchez-Azofeifa, G.A. Using LiDAR Waveform Metrics to Describe and Identify Successional Stages of Tropical Dry Forests. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 482–492. [Google Scholar] [CrossRef]
- Becknell, J.M.; Keller, M.; Piotto, D.; Longo, M.; Nara dos-Santos, M.; Scaranello, M.A.; Bruno de Oliveira Cavalcante, R.; Porder, S. Landscape-scale lidar analysis of aboveground biomass distribution in secondary Brazilian Atlantic Forest. Biotropica 2018, 50, 520–530. [Google Scholar] [CrossRef]
- Almeida, C.T.D.; Galvão, L.S.; Aragão, L.E.D.O.C.E.; Ometto, J.P.H.B.; Jacon, A.D.; Pereira, F.R.D.S.; Sato, L.Y.; Lopes, A.P.; Graça, P.M.L.D.A.; Silva, C.V.D.J.; et al. Combining LiDAR and Hyperspectral Data for Aboveground Biomass Modeling in the Brazilian Amazon Using Different Regression Algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- de Almeida, C.T. Integration of LiDAR and Hyperspectral Data for Forest Disturbance Characterization and Aboveground Biomass Estimation in the Brazilian Amazon; Instituto Nacional de Pesquisas Espaciais: São José dos Campos, Brazil, 2020. [Google Scholar]
- Martins-Neto, R.P.; Tommaselli, A.M.G.; Imai, N.N.; David, H.C.; Miltiadou, M.; Honkavaara, E. Identification of Significative LiDAR Metrics and Comparison of Machine Learning Approaches for Estimating Stand and Diversity Variables in Heterogeneous Brazilian Atlantic Forest. Remote Sens. 2021, 13, 2444. [Google Scholar] [CrossRef]
- Ometto, J.P.; Gorgens, E.B.; De Souza Pereira, F.R.; Sato, L.; De Assis, M.L.R.; Cantinho, R.; Longo, M.; Jacon, A.D.; Keller, M. A Biomass Map of the Brazilian Amazon from Multisource Remote Sensing. Sci. Data 2023, 10, 668. [Google Scholar] [CrossRef] [PubMed]
- Scheeres, J.; De Jong, J.; Brede, B.; Brancalion, P.H.S.; Broadbent, E.N.; Zambrano, A.M.A.; Gorgens, E.B.; Silva, C.A.; Valbuena, R.; Molin, P.; et al. Distinguishing Forest Types in Restored Tropical Landscapes with UAV-Borne LIDAR. Remote Sens. Environ. 2023, 290, 113533. [Google Scholar] [CrossRef]
- Torralba, J.; Crespo-Peremarch, P.; Ruiz, L.A. Evaluación Del Uso de LiDAR Discreto, Full-Waveform y TLS En La Clasificación Por Composición de Especies En Bosques Mediterráneos. Rev. Teledetección 2018, 27. [Google Scholar] [CrossRef]
- Crespo-Peremarch, P.; Tompalski, P.; Coops, N.C.; Ruiz, L.Á. Characterizing Understory Vegetation in Mediterranean Forests Using Full-Waveform Airborne Laser Scanning Data. Remote Sens. Environ. 2018, 217, 400–413. [Google Scholar] [CrossRef]
- Crespo-Peremarch, P.; Fournier, R.A.; Nguyen, V.-T.; Van Lier, O.R.; Ruiz, L.Á. A Comparative Assessment of the Vertical Distribution of Forest Components Using Full-Waveform Airborne, Discrete Airborne and Discrete Terrestrial Laser Scanning Data. For. Ecol. Manag. 2020, 473, 118268. [Google Scholar] [CrossRef]
- Marselis, S.M.; Abernethy, K.; Alonso, A.; Armston, J.; Baker, T.R.; Bastin, J.-F.; Bogaert, J.; Boyd, D.S.; Boeckx, P.; Burslem, D.F.R.P.; et al. Evaluating the Potential of Full-Waveform Lidar for Mapping Pan-Tropical Tree Species Richness. Glob. Ecol. Biogeogr. 2020, 29, 1799–1816. [Google Scholar] [CrossRef]
- Martins-Neto, R.P. Extraction of Structural Variables Using Lidar Data Combined with Hyperspectral Images for Classification of Upper Canopy Tree Species in Brazilian Atlantic Forest; Universidade Estadual Paulista: Presidente Prudente, Brazil, 2021. [Google Scholar]
- Duan, M.; Bax, C.; Laakso, K.; Mashhadi, N.; Mattie, N.; Sanchez-Azofeifa, A. Characterizing Transitions between Successional Stages in a Tropical Dry Forest Using LiDAR Techniques. Remote Sens. 2023, 15, 479. [Google Scholar] [CrossRef]
- Pirotti, F. Analysis of Full-Waveform LiDAR Data for Forestry Applications: A Review of Investigations and Methods. iForest 2011, 4, 100–106. [Google Scholar] [CrossRef]
- Crespo-Peremarch, P.; Ruiz, L.A. A Full-Waveform Airborne Laser Scanning Metric Extraction Tool for Forest Structure Modelling. Do Scan Angle and Radiometric Correction Matter? Remote Sens. 2020, 12, 292. [Google Scholar] [CrossRef]
- Sun, C.; Cao, S.; Sanchez-Azofeifa, G.A. Mapping Tropical Dry Forest Age Using Airborne Waveform LiDAR and Hyperspectral Metrics. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101908. [Google Scholar] [CrossRef]
- Zhao, G.; Sanchez-Azofeifa, A.; Laakso, K.; Sun, C.; Fei, L. Hyperspectral and Full-Waveform LiDAR Improve Mapping of Tropical Dry Forest’s Successional Stages. Remote Sens. 2021, 13, 3830. [Google Scholar] [CrossRef]
- MapBiomas Project Collection 6 of the Annual Land Use Land Cover Maps of Brazil. 2021. Available online: https://mapbiomas.org (accessed on 14 February 2023).
- Santoro, M.; Cartus, O. ESA Biomass Climate Change Initiative (Biomass_cci): Global Datasets of Forest above-Ground Biomass for the Years 2010, 2017, 2018, 2019 and 2020, V4 2023, 5183 Files, 302039459020 B. CEDA Archive. Available online: https://catalogue.ceda.ac.uk/ (accessed on 20 April 2023).
- Vancutsem, C.; Achard, F.; Pekel, J.-F.; Vieilledent, G.; Carboni, S.; Simonetti, D.; Gallego, J.; Aragão, L.E.O.C.; Nasi, R. Long-Term (1990–2019) Monitoring of Forest Cover Changes in the Humid Tropics. Sci. Adv. 2021, 7, eabe1603. [Google Scholar] [CrossRef] [PubMed]
- Vedovato, L.B. From Past to Present: Impacts of Fire on Amazonian Forests; University of Exeter: Exeter, UK, 2022. [Google Scholar]
- Miltiadou, M.; Grant, M.G.; Campbell, N.D.F.; Warren, M.; Clewley, D.; Hadjimitsis, D.G. Open Source Software DASOS: Efficient Accumulation, Analysis, and Visualisation of Full-Waveform Lidar. In Proceedings of the Seventh International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2019), Paphos, Cyprus, 18–21 March 2019; SPIE: Bellingham, WA, USA, 2019; Volume 11174, pp. 524–540. [Google Scholar]
- Hermosilla, T.; Coops, N.C.; Ruiz, L.A.; Moskal, L.M. Deriving Pseudo-Vertical Waveforms from Small-Footprint Full-Waveform LiDAR Data. Remote Sens. Lett. 2014, 5, 332–341. [Google Scholar] [CrossRef]
- Duong, V.H. Processing and Application of ICEsat Large Footprint Full Waveform Laser Range Data. Ph.D. Thesis, University of Technology, Delft, The Netherlands, 8 June 2010. [Google Scholar]
- Duncanson, L.I.; Niemann, K.O.; Wulder, M.A. Estimating forest canopy height and terrain relief from GLAS waveform metrics. Remote Sens. Environ. 2010, 114, 138–154. [Google Scholar] [CrossRef]
- Dalagnol, R.; Wagner, F.H.; Galvão, L.S.; Streher, A.S.; Phillips, O.L.; Gloor, E.; Pugh, T.A.M.; Ometto, J.P.H.B.; Aragão, L.E.O.C. Large-Scale Variations in the Dynamics of Amazon Forest Canopy Gaps from Airborne Lidar Data and Opportunities for Tree Mortality Estimates. Sci. Rep. 2021, 11, 1388. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Brownlee, J. Imbalanced Classification with Python: Better Metrics, Balance Skewed Classes, Cost-Sensitive Learning; Machine Learning Mastery: New York, NY, USA, 2020. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Soft. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Toledo, M.; Poorter, L.; Peña-Claros, M.; Alarcón, A.; Balcázar, J.; Leaño, C.; Licona, J.C.; Llanque, O.; Vroomans, V.; Zuidema, P.; et al. Climate Is a Stronger Driver of Tree and Forest Growth Rates than Soil and Disturbance. J. Ecol. 2011, 99, 254–264. [Google Scholar] [CrossRef]
- Crouzeilles, R.; Barros, F.S.M.; Molin, P.G.; Ferreira, M.S.; Junqueira, A.B.; Chazdon, R.L.; Lindenmayer, D.B.; Tymus, J.R.C.; Strassburg, B.B.N.; Brancalion, P.H.S. A New Approach to Map Landscape Variation in Forest Restoration Success in Tropical and Temperate Forest Biomes. J. Appl. Ecol. 2019, 56, 2675–2686. [Google Scholar] [CrossRef]
- Ruiz, L.; Crespo-Peremarch, P.; Torralba Pérez, J. Modelling Canopy Fuel Properties and Understory Vegetation with Full-Waveform LiDAR. In Proceedings of the International Conference on Smart Geoinformatics Applications (ICSGA 2021), Prince of Songkla University, Phuket, Thailand, 24 February 2021. [Google Scholar]
- Crespo-Peremarch, P.; Ruiz, L.Á.; Balaguer-Beser, Á.; Estornell, J. Analyzing the Role of Pulse Density and Voxelization Parameters on Full-Waveform LiDAR-Derived Metrics. ISPRS J. Photogramm. Remote Sens. 2018, 146, 453–464. [Google Scholar] [CrossRef]
- Almeida, D.R.A.D.; Stark, S.C.; Chazdon, R.; Nelson, B.W.; Cesar, R.G.; Meli, P.; Gorgens, E.B.; Duarte, M.M.; Valbuena, R.; Moreno, V.S.; et al. The Effectiveness of Lidar Remote Sensing for Monitoring Forest Cover Attributes and Landscape Restoration. For. Ecol. Manag. 2019, 438, 34–43. [Google Scholar] [CrossRef]
- de Almeida, D.R.A.; Almeyda Zambrano, A.M.; Broadbent, E.N.; Wendt, A.L.; Foster, P.; Wilkinson, B.E.; Salk, C.; de Almeida Papa, D.; Stark, S.C.; Valbuena, R.; et al. Detecting Successional Changes in Tropical Forest Structure Using GatorEye Drone-Borne Lidar. Biotropica 2020, 52, 1155–1167. [Google Scholar] [CrossRef]

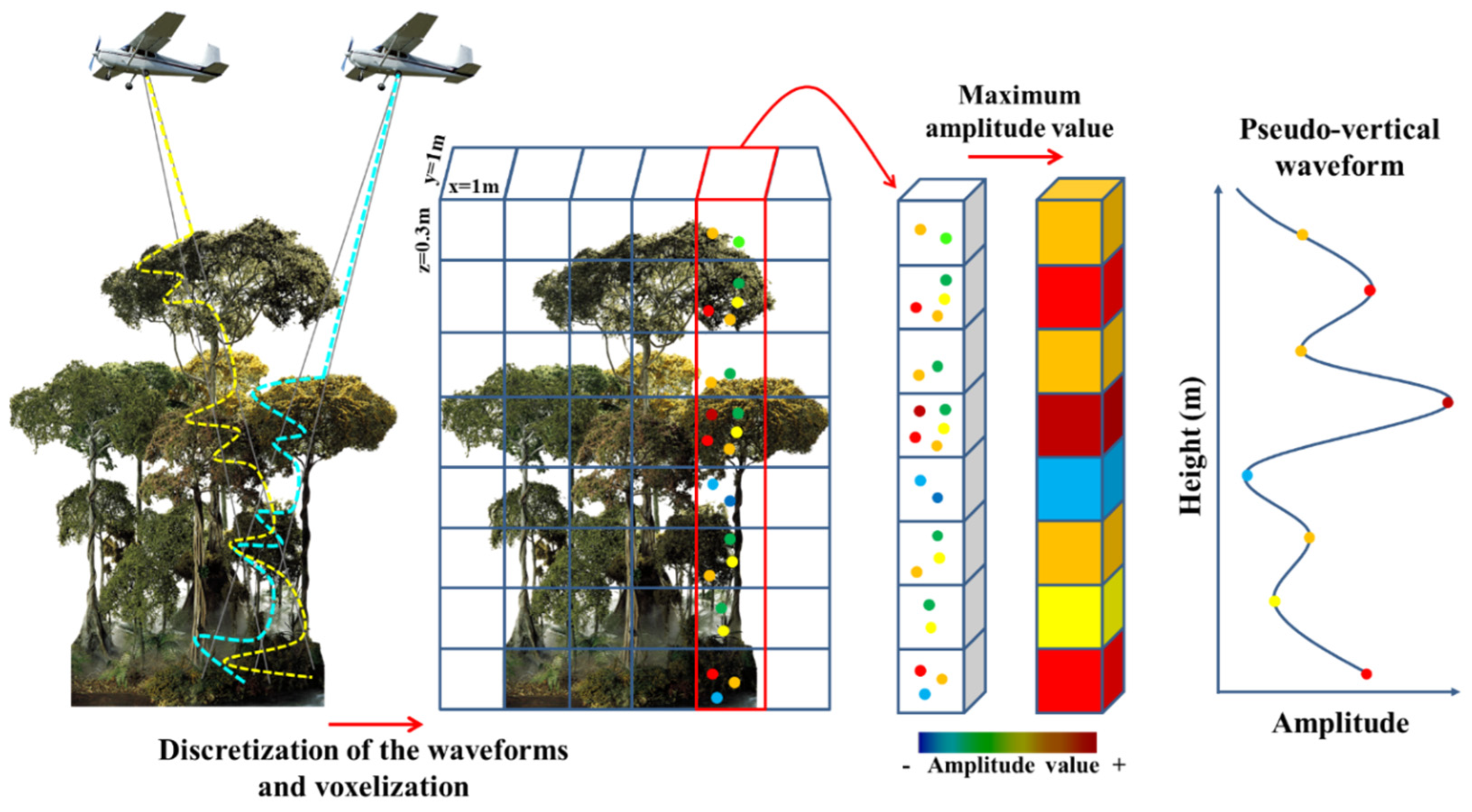
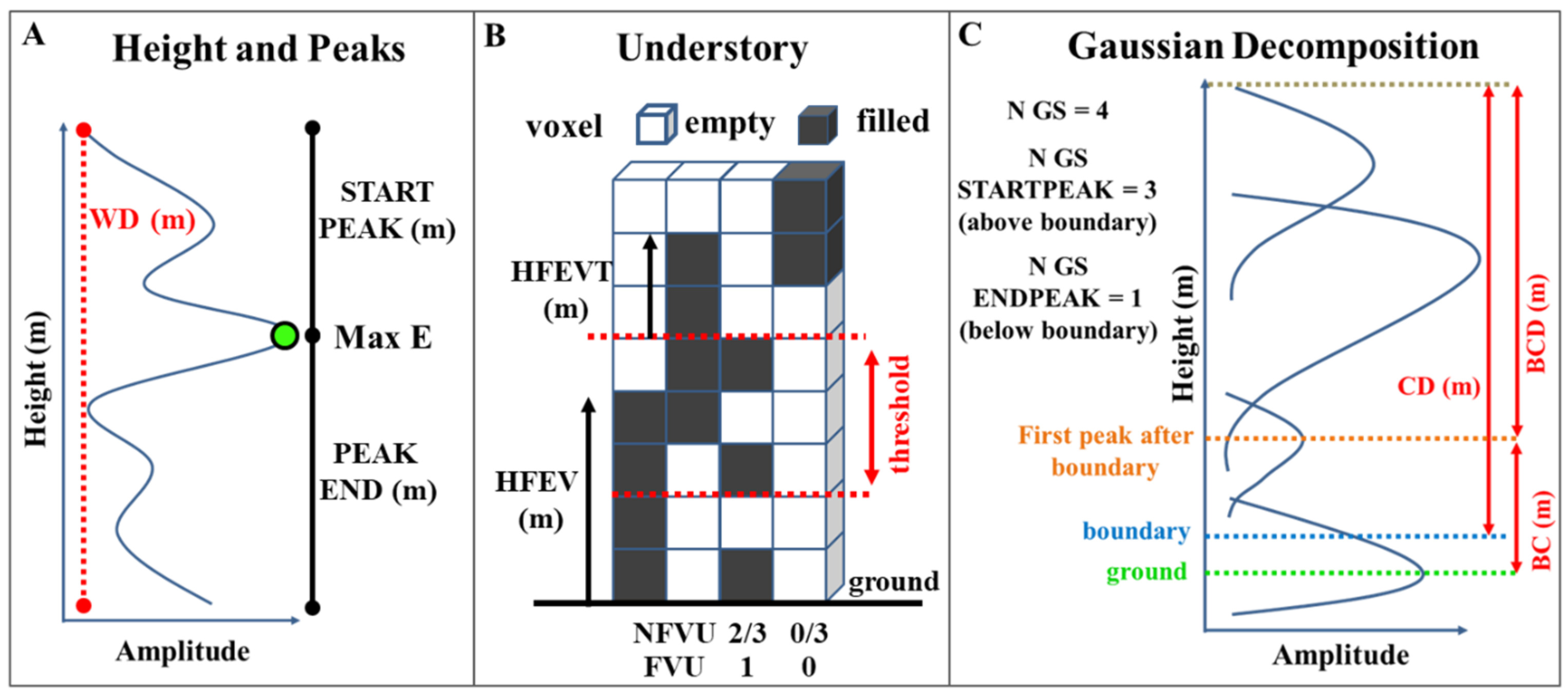
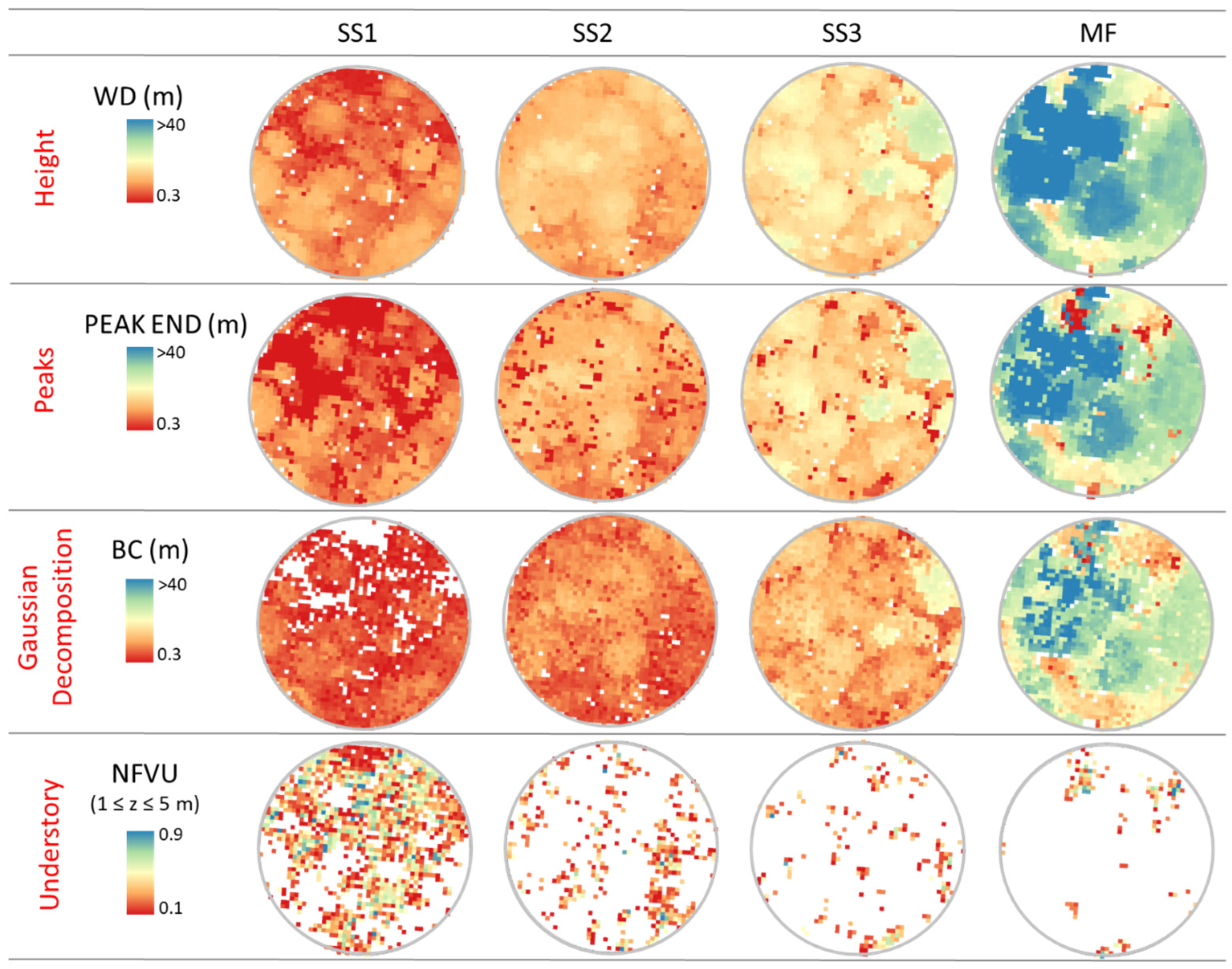

| Category | Metric [Reference] | Description (Units) |
|---|---|---|
| Height | WD [37] | Waveform distance (m)—Distance between the beginning of the waveform and the ground or height of the waveform. |
| Peaks | NP [37] | Number of peaks in the waveform. |
| START PEAK [38] | Distance between the beginning of the waveform and the height of maximum energy—MAX E (m). | |
| PEAK END [38] | Distance between the height of MAX E and the ground (m). | |
| Understory | HFEV [28] | Height of the first empty voxel from the ground upwards (m). |
| HFEVT [28] | Height of the first empty voxel from a max threshold (m). | |
| FVU [28] | Filled voxels at the understory. Examines if there are any filled voxels between min and max threshold (Yes/No = 1/0). | |
| NFVU [28] | Number of filled voxels at the understory divided by the total number of voxels between min and max threshold. | |
| Gaussian Decomposition | N GS [38] | Number of Gaussian curves in the waveform. |
| N GS STARTPEAK [38] | Number of Gaussian curves between the beginning of the waveform and the height of the boundary. | |
| N GS ENDPEAK [38] | Number of Gaussian curves between the height of the boundary and the ground. | |
| BC [28] | Bottom of canopy: the height from the ground to the first Gaussian curve above the boundary. | |
| BCD [28] | Bottom of canopy distance: the distance from BC to the top of the canopy. | |
| CD [28] | Canopy distance: distance from the beginning of the waveform to the boundary between ground and canopy (m). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jacon, A.D.; Galvão, L.S.; Martins-Neto, R.P.; Crespo-Peremarch, P.; Aragão, L.E.O.C.; Ometto, J.P.; Anderson, L.O.; Vedovato, L.B.; Silva-Junior, C.H.L.; Lopes, A.P.; et al. Characterizing Canopy Structure Variability in Amazonian Secondary Successions with Full-Waveform Airborne LiDAR. Remote Sens. 2024, 16, 2085. https://doi.org/10.3390/rs16122085
Jacon AD, Galvão LS, Martins-Neto RP, Crespo-Peremarch P, Aragão LEOC, Ometto JP, Anderson LO, Vedovato LB, Silva-Junior CHL, Lopes AP, et al. Characterizing Canopy Structure Variability in Amazonian Secondary Successions with Full-Waveform Airborne LiDAR. Remote Sensing. 2024; 16(12):2085. https://doi.org/10.3390/rs16122085
Chicago/Turabian StyleJacon, Aline D., Lênio Soares Galvão, Rorai Pereira Martins-Neto, Pablo Crespo-Peremarch, Luiz E. O. C. Aragão, Jean P. Ometto, Liana O. Anderson, Laura Barbosa Vedovato, Celso H. L. Silva-Junior, Aline Pontes Lopes, and et al. 2024. "Characterizing Canopy Structure Variability in Amazonian Secondary Successions with Full-Waveform Airborne LiDAR" Remote Sensing 16, no. 12: 2085. https://doi.org/10.3390/rs16122085
APA StyleJacon, A. D., Galvão, L. S., Martins-Neto, R. P., Crespo-Peremarch, P., Aragão, L. E. O. C., Ometto, J. P., Anderson, L. O., Vedovato, L. B., Silva-Junior, C. H. L., Lopes, A. P., Peripato, V., Assis, M., Pereira, F. R. S., Haddad, I., de Almeida, C. T., Cassol, H. L. G., & Dalagnol, R. (2024). Characterizing Canopy Structure Variability in Amazonian Secondary Successions with Full-Waveform Airborne LiDAR. Remote Sensing, 16(12), 2085. https://doi.org/10.3390/rs16122085










