Semi-Tightly Coupled Robust Model for GNSS/UWB/INS Integrated Positioning in Challenging Environments
Abstract
:1. Introduction
2. Related Work
3. The Proposed Model and Robust Method
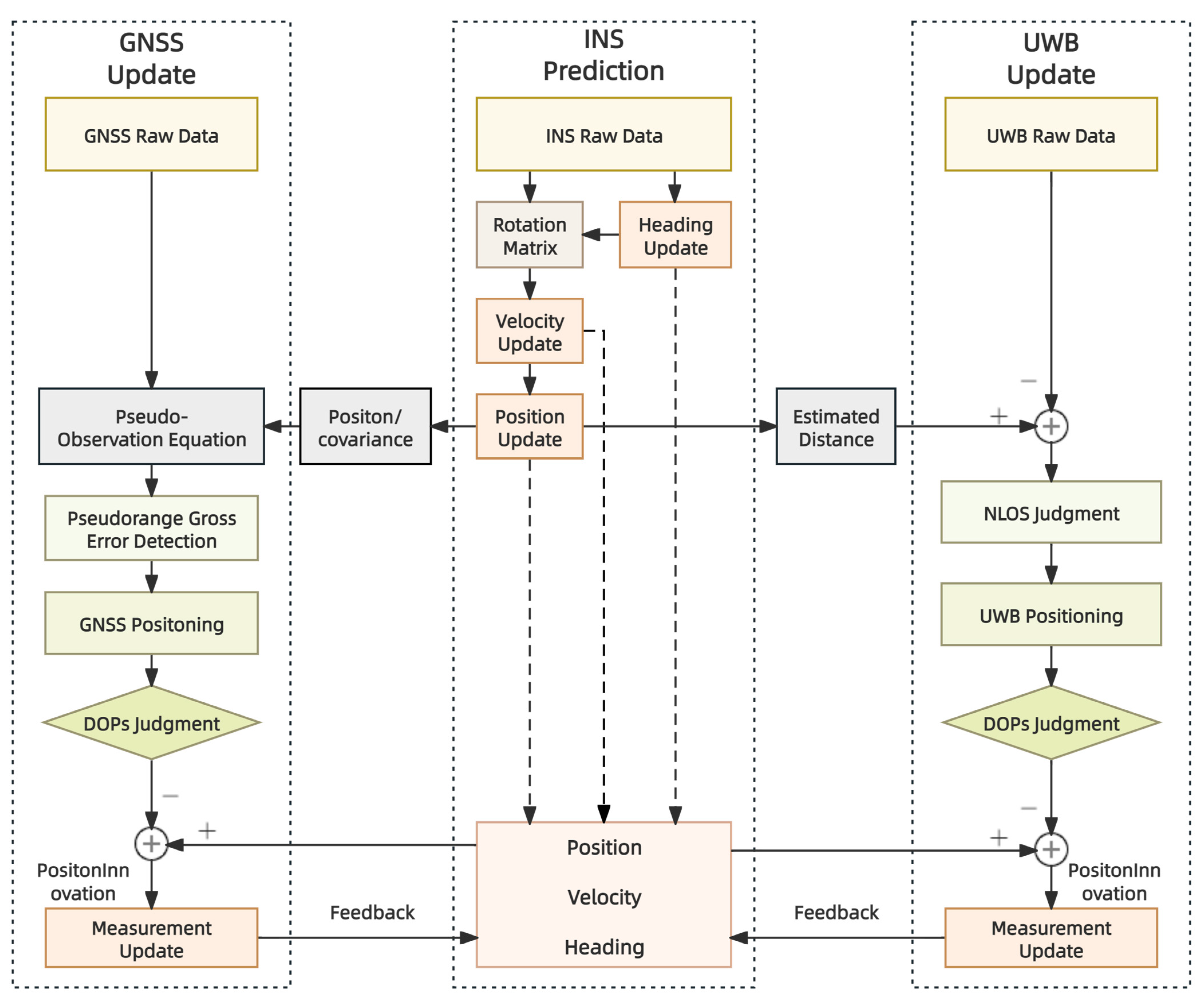
3.1. System Model
3.2. State Prediction by INS
3.3. STC Robust Method for GNSS/INS
3.3.1. GNSS Pseudorange Observation Equation
3.3.2. INS Pseudo-Observation Equation
3.3.3. (N + 3) Pseudo-Observation Equation
3.3.4. Robust EKF with INS Constraints
3.4. STC Robust Method for UWB/INS
3.4.1. Two-Dimensional Distance Calculated by INS
3.4.2. Two-Dimensional Distance Measured by UWB
3.4.3. NLOS Judgment Statistics
3.4.4. UWB Distance-Ranging Observation Equation
3.5. Judgment with DOPs
3.5.1. DOPs of GNSS
3.5.2. DOPs of UWB
3.6. Measurement Update for Integrated Navigation
4. Experiments and Analysis
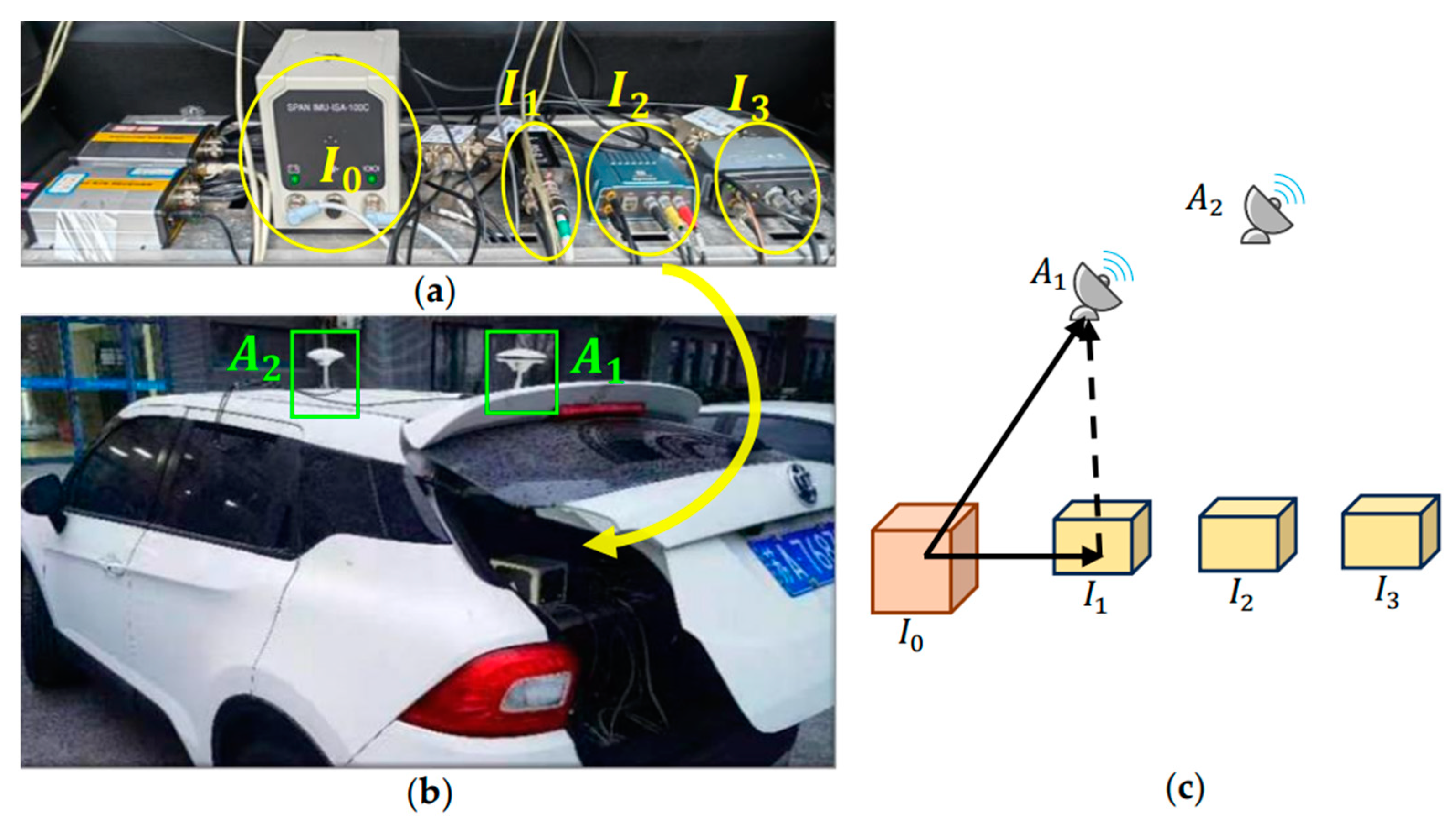
4.1. Equipment and Experiments
4.1.1. Equipment and Experiments of GNSS
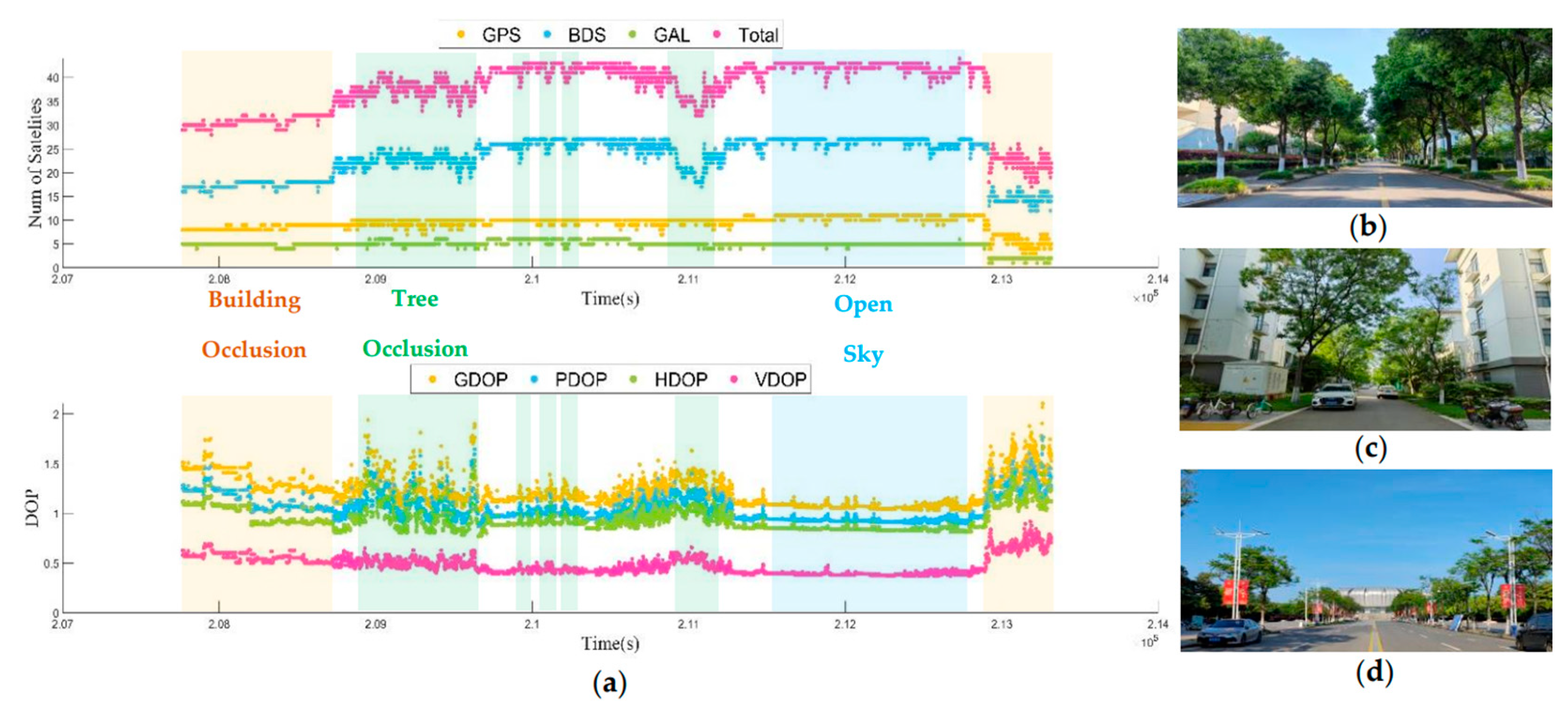
- Under the open sky, the number and configuration of observable satellites vary. Obviously, in an open sky environment, the number of satellites from the three satellite systems remains relatively stable at each epoch, with the total number of available satellites maintained at around 35 to 40, and the DOP values also remain within a small range, with minimal fluctuations. Therefore, under an open sky environment, the satellite signal quality is high, and it is expected to produce stable and reliable GNSS positioning results.
- Under tree occlusion, the number of available satellites at each epoch decreases, and the total number of available satellites and DOP values fluctuate significantly, with some epochs even having GDOP values close to 2.0. Hence, in a shaded environment, the satellite signal is unstable, which may affect positioning accuracy.
- Under building occlusion, the number of satellites at each epoch decreases significantly. Unlike the shaded environment, in this scenario, the changes in the number of satellites and DOP values at each epoch fluctuate less. For this road section, it is necessary to find other positioning sources to compensate for positioning accuracy.
4.1.2. Equipment and Experiments of INS
4.1.3. Equipment and Experiments of UWB
4.2. Results and Analysis
4.2.1. STC Robust Performance of GNSS/INS
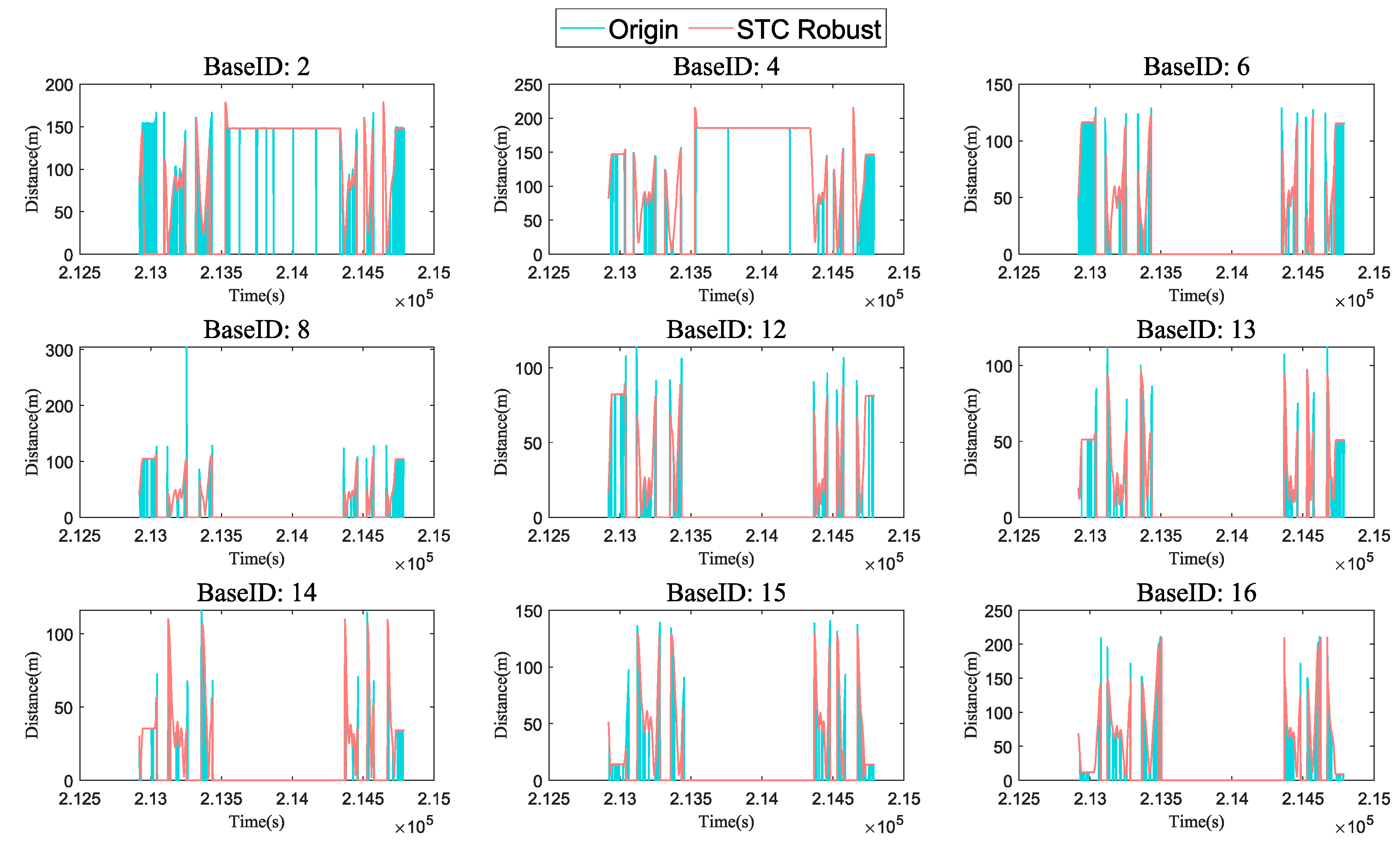
4.2.2. STC Robust Performance of UWB/INS
- First, the normal zone. The positioning error of the UWB/INS semi-tightly integrated system is stably smaller than that of the loosely integrated system, while the UWB single positioning source often exhibits meter-level positioning jumps in this area.
- Second, the signal dead zone. Due to the insufficient number of available base stations, positioning cannot be achieved solely relying on UWB, while the INS can provide inertial dead reckoning. Therefore, in the green region of the graph, UWB/INS integrated positioning does not experience interruption until the UWB signal recovers after 85 s, during which time the integrated navigation system accumulates a total drift error of 20 m.
- Third, the recovery zone. The INS drift error is corrected under the measurement update of the UWB, allowing the filter’s state to gradually return to normal accuracy. It is worth noting that, since the semi-tightly integrated system provides INS position domain information, it prevents excessive elimination from causing UWB positioning failures. Therefore, under the semi-tightly integrated structure, the INS enters the drift state later, which in a sense verifies the role and effectiveness of tightly integrated navigation in maintaining positioning continuity.
4.2.3. STC Performance of GNSS/UWB/INS Integrated System
- Firstly, the UWB signal normal zone. Due to severe building obstruction of the sky, the positioning accuracy of UWB/INS is significantly higher than that of GNSS/INS. Therefore, compared to GNSS/INS, the combined positioning accuracy of GNSS/UWB/INS is greatly improved.
- Secondly, the UWB signal dead zone. UWB cannot provide positioning, but relying on the positioning results of the GNSS, the combined navigation system can still achieve stable and continuous output. At this time, the positioning error of GNSS/UWB/INS is basically the same as that of GNSS/INS.
- Therefore, compared to the GNSS/INS and UWB/INS combined systems, the GNSS/UWB/INS positioning system designed in this paper can cope with dynamic and variable environments, achieving continuous and reliable positioning in challenging environments with both sky and ground obstructions.
5. Discussion
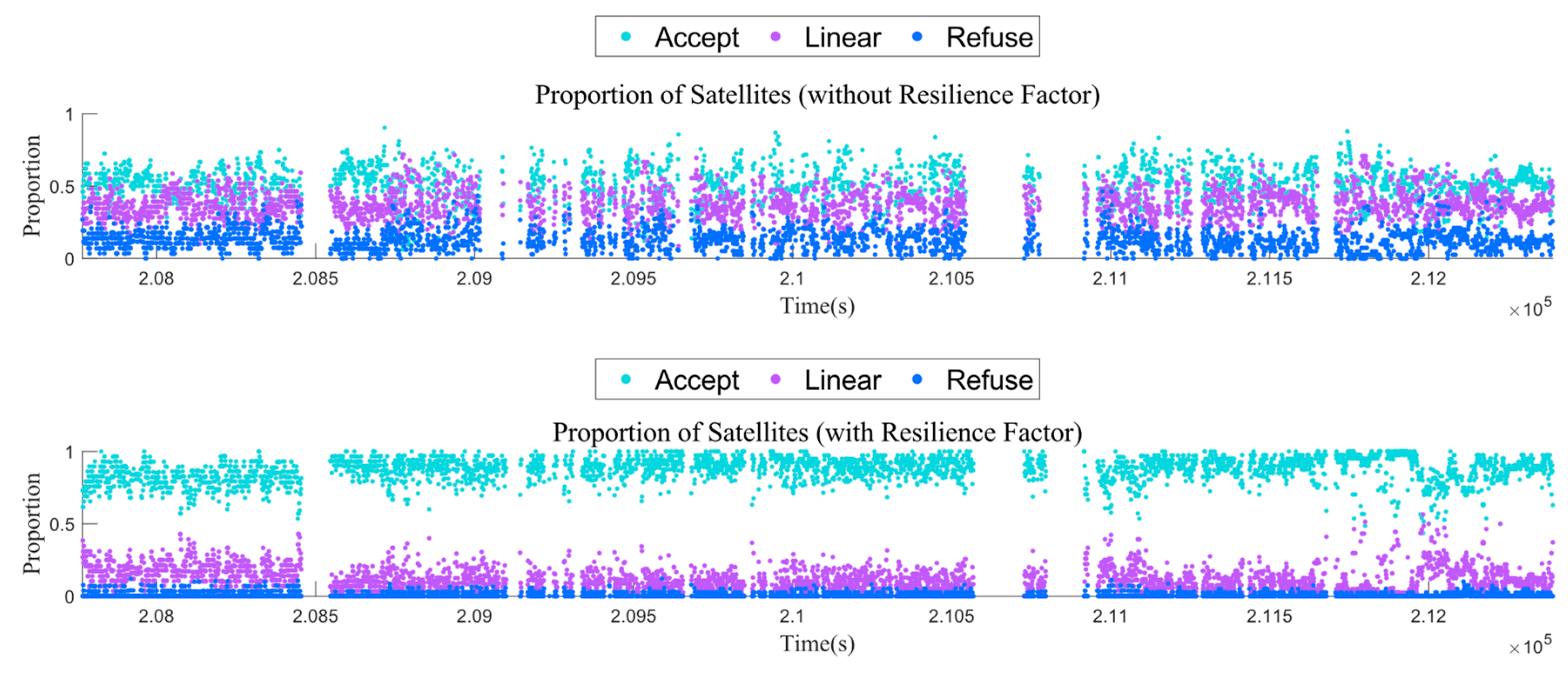
- Firstly, in terms of identifying gross errors, refer to Section 3.3 and Section 3.4. Due to the introduction of INS position domain information, it provides an a priori reference for the smaller-dimensional observations in challenging environments, enabling the identification of unacceptable gross errors within the accuracy range of the INS without causing systematic bias. Compared to the loosely coupled robust methods of similar complexity, this is a remarkable improvement.
- Secondly, in terms of suppressing gross errors, refer to Section 3.3.4 and Section 3.4.3. This paper, considering the differences in observation characteristics between the GNSS and UWB, employs the IGG III weighting degradation method based on resilience factors for GNSS pseudorange gross errors, and a threshold elimination method for UWB ranging NLOS gross errors. This can minimize the impact of gross errors on the system, while reducing information loss as much as possible.
- Finally, in terms of continuous and reliable positioning, refer to Section 4.2.3. This paper focuses on the challenges of reliability in complex sky–ground environments for GNSS and UWB positioning. A fusion framework based on DOP value judgments is proposed, which can achieve a complementary accuracy between the GNSS and UWB in dynamic and changing environments, while ensuring reliable positioning results.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Ren, X.; Jia, X. Development trends of the national secure PNT system based on BDS. Sci. China Earth Sci. 2023, 66, 929–938. [Google Scholar] [CrossRef]
- Prol, F.S.; Ferre, R.M.; Saleem, Z. Position, navigation, and timing (PNT) through low earth orbit (LEO) satellites: A survey on current status, challenges, and opportunities. IEEE Access 2022, 10, 83971–84002. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Shi, C. Robust M-estimation-Based ICKF for GNSS Outlier Mitigation in GNSS/SINS navigation applications. IEEE Trans. Instrum. Meas. 2023, 72, 8505617. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, P.; Zha, J. PPP–RTK functional models formulated with undifferenced and uncombined GNSS observations. Satell. Navig. 2022, 3, 3. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, C.; Odolinski, R. Functional model modification of precise point positioning considering the time-varying code biases of a receiver. Satell. Navig. 2021, 2, 1–10. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, T.; Lin, T. Implementation and performance of a deeply-coupled GNSS receiver with low-cost MEMS inertial sensors for vehicle urban navigation. Sensors 2020, 20, 3397. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Zhou, H.; Wang, Z. Improved Multi-sensor Fusion Positioning System Based on GNSS/LiDAR/Vision/IMU with Semi-tightly Coupling and Graph Optimization in GNSS Challenging Environments. IEEE Access 2023, 11, 95711–95723. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, Q.; Niu, X. Estimate the pitch and heading mounting angles of the IMU for land vehicular GNSS/INS integrated system. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6503–6515. [Google Scholar] [CrossRef]
- Jang, B.J. Principles and trends of UWB positioning technology. J. Korean Inst. Electromagn. Eng. Sci. 2022, 33, 1–11. [Google Scholar] [CrossRef]
- Brovko, T.; Chugunov, A.; Malyshev, A. Complex Kalman filter algorithm for smartphone-based indoor UWB/INS navigation systems. In Proceedings of the Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 13–14 May 2021; pp. 0280–0284. [Google Scholar]
- Wang, C.; Xu, A.; Sui, X.; Hao, Y.; Shi, Z.; Chen, Z. A seamless navigation system and applications for autonomous vehicles using a tightly coupled GNSS/UWB/INS/map integration scheme. Remote Sens. 2021, 14, 27. [Google Scholar] [CrossRef]
- Ren, Z.; Liu, S.; Dai, J. Research on Kinematic and Static Filtering of the ESKF Based on INS/GNSS/UWB. Sensors 2023, 23, 4735. [Google Scholar] [CrossRef]
- Yao, L.; Li, M.; Xu, T. GNSS/UWB/INS indoor and outdoor seamless positioning algorithm based on federal filtering. Meas. Sci. Technol. 2023, 35, 015135. [Google Scholar] [CrossRef]
- Boguspayev, N.; Akhmedov, D.; Raskaliyev, A. A comprehensive review of GNSS/INS integration techniques for land and air vehicle applications. Appl. Sci. 2023, 13, 4819. [Google Scholar] [CrossRef]
- Li, S.; Wang, S.; Zhou, Y. Tightly coupled integration of GNSS, INS, and LiDAR for vehicle navigation in urban environments. IEEE Internet Things J. 2022, 9, 24721–24735. [Google Scholar] [CrossRef]
- Falco, G.; Pini, M.; Marucco, G. Loose and tight GNSS/INS integrations: Comparison of performance assessed in real urban scenarios. Sensors 2017, 17, 255. [Google Scholar] [CrossRef] [PubMed]
- Lou, T.S.; Chen, N.H.; Chen, Z.W. Robust partially strong tracking extended consider Kalman filtering for INS/GNSS integrated navigation. IEEE Access 2019, 7, 151230–151238. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Niu, X.; Gao, Z. Tightly-coupled integration of multi-GNSS single-frequency RTK and MEMS-IMU for enhanced positioning performance. Sensors 2017, 17, 2462. [Google Scholar] [CrossRef]
- Jiang, Y.; Pan, S.; Meng, Q. Performance Analysis of Robust Tightly Coupled GNSS/INS Integration Positioning Based on M Estimation in Challenging Environments. In China Satellite Navigation Conference; Springer Nature: Singapore, 2022; pp. 400–414. [Google Scholar]
- Wang, D.; Dong, Y.; Li, Z. Constrained MEMS-based GNSS/INS tightly coupled system with robust Kalman filter for accurate land vehicular navigation. IEEE Trans. Instrum. Meas. 2019, 69, 5138–5148. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Liao, J. Semi-tightly coupled integration of multi-GNSS PPP and S-VINS for precise positioning in GNSS-challenged environments. Satell. Navig. 2021, 2, 1. [Google Scholar] [CrossRef]
- Ma, C.; Pan, S.; Gao, W. Variational Bayesian-based robust adaptive filtering for GNSS/INS tightly coupled positioning in urban environments. Measurement 2023, 223, 113668. [Google Scholar] [CrossRef]
- Yang, B.; Li, J.; Shao, Z. Robust UWB indoor localization for NLOS scenes via learning spatial-temporal features. IEEE Sens. J. 2022, 22, 7990–8000. [Google Scholar] [CrossRef]
- Pan, S.; Meng, X.; Gao, W. A new approach for optimising GNSS positioning performance in harsh observation environments. J. Navigat. 2014; 67, 1029–1048. [Google Scholar]
- Zaman, B.; Mahfooz, S.Z.; Mehmood, R. An adaptive EWMA control chart based on Hampel function to monitor the process location parameter. Qual. Reliab. Eng. Int. 2023, 39, 1277–1298. [Google Scholar] [CrossRef]
- Sinova, B.; Van Aelst, S. Advantages of M-estimators of location for fuzzy numbers based on Tukey’s biweight loss function. Int. J. Approx. Reason. 2018, 93, 219–237. [Google Scholar] [CrossRef]
- Huber, P.; Peter, J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Zhang, X. Robust Kalman filtering with constraints: A case study for integrated navigation. J. Geod. 2010, 84, 373–381. [Google Scholar] [CrossRef]
- Amami, M.M. The Advantages and Limitations of Low-Cost Single Frequency GPS/MEMS-Based INS Integration. Glob. J. Eng. Technol. Adv. 2022, 10, 018–031. [Google Scholar] [CrossRef]
- Fredeluces, E.; Ozeki, T.; Kubo, N. Modified RTK-GNSS for Challenging Environments. Sensors 2024, 24, 2712. [Google Scholar] [CrossRef] [PubMed]
- Su, M.; Chang, X.; Zheng, F. Theory and Experiment Analysis on the Influence of Floods on a GNSS Pseudo-Range Multipath and CNR Signal Based on Two Cases Study in China. Remote Sens. 2022, 14, 5874. [Google Scholar] [CrossRef]
- Xue, A.; Kong, H.; Lao, Y. A new robust identification method for transmission line parameters based on ADALINE and IGG Method. IEEE Access 2020, 8, 132960–132969. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Yuan, H. An enhanced outlier processing approach based on the resilient mathematical model compensation in GNSS precise positioning and navigation. Meas. Sci. Technol. 2023, 35, 015007. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Zheng, S. UWB/INS-based robust anchor-free relative positioning scheme for UGVs. Meas. Sci. Technol. 2022, 33, 125007. [Google Scholar] [CrossRef]
- Won, D.H.; Lee, E.; Heo, M. Selective integration of GNSS, vision sensor, and INS using weighted DOP under GNSS-challenged environments. IEEE Trans. Instrum. Meas. 2014, 63, 2288–2298. [Google Scholar] [CrossRef]
- Wang, H.S.; Kao, A. A behavioral approach to GNSS positioning and DOP determination. WSEAS Trans. Syst. 2008, 7, 854–869. [Google Scholar]
- Tahsin, M.; Sultana, S.; Reza, T. Analysis of DOP and its preciseness in GNSS position estimation. In Proceedings of the 2015 International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Savar, Bangladesh, 21–23 May 2015; pp. 1–6. [Google Scholar]
- Feng, G.; Shen, C.; Long, C. GDOP index in UWB indoor location system experiment. In Proceedings of the 2015 IEEE SENSORS, Busan, Republic of Korea, 1–4 November 2015; pp. 1–4. [Google Scholar]



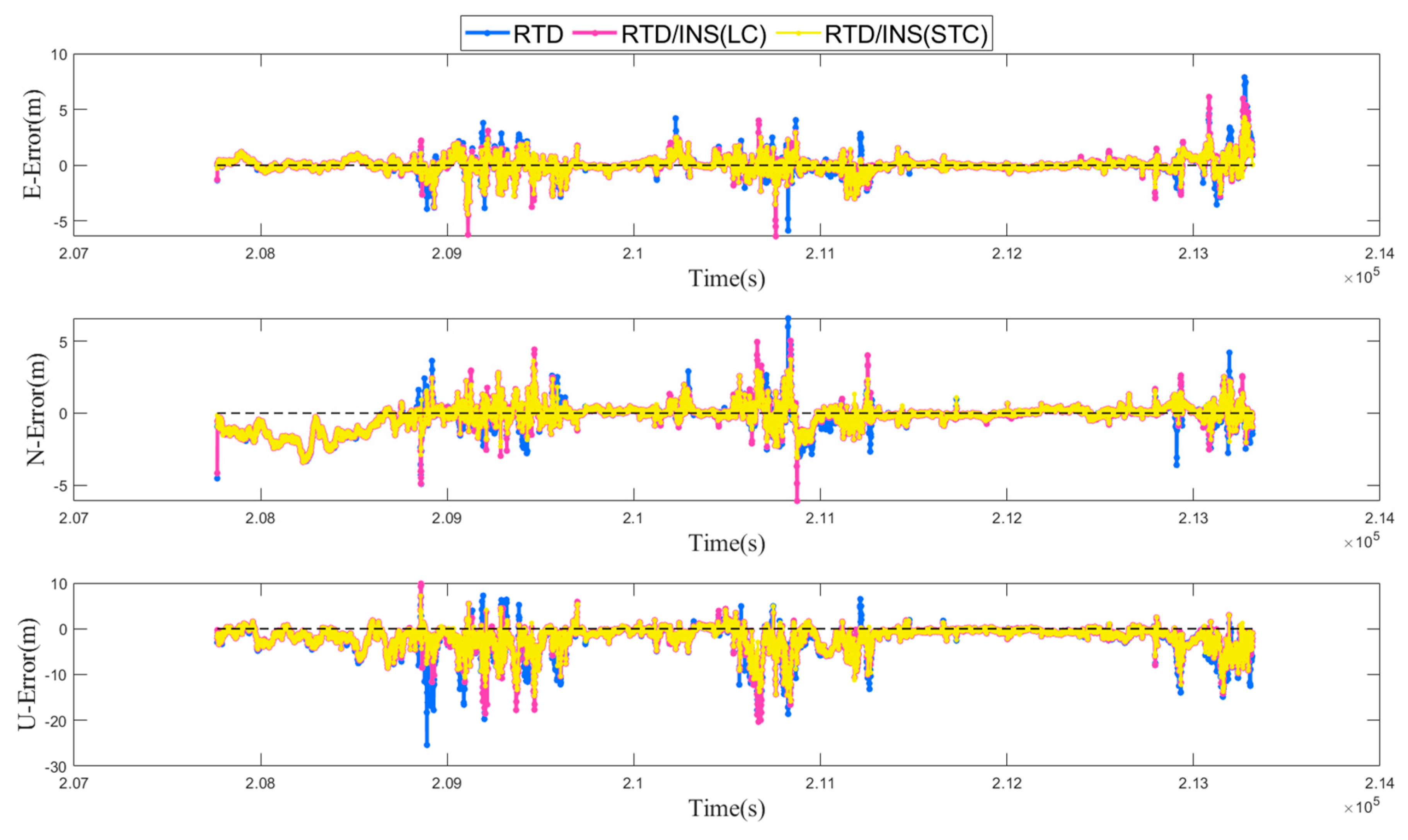



| RMS | GNSS 1 | GNSS/INS LC Robust | GNSS/INS STC Robust | UWB 2 | UWB/INS LC Robust | UWB/INS STC Robust | GNSS/UWB/INS STC Robust |
|---|---|---|---|---|---|---|---|
| E/m | 2.94 | 1.51 | 0.95 | 1.69 | 0.83 | 0.33 | 0.42 |
| N/m | 2.26 | 1.30 | 0.70 | 1.66 | 0.61 | 0.40 | 0.55 |
| U/m | 5.64 | 4.44 | 3.21 | -- | -- | -- | 3.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Gao, W.; Tao, X.; Pan, S.; Wu, P.; Huang, H. Semi-Tightly Coupled Robust Model for GNSS/UWB/INS Integrated Positioning in Challenging Environments. Remote Sens. 2024, 16, 2108. https://doi.org/10.3390/rs16122108
Sun Z, Gao W, Tao X, Pan S, Wu P, Huang H. Semi-Tightly Coupled Robust Model for GNSS/UWB/INS Integrated Positioning in Challenging Environments. Remote Sensing. 2024; 16(12):2108. https://doi.org/10.3390/rs16122108
Chicago/Turabian StyleSun, Zhihan, Wang Gao, Xianlu Tao, Shuguo Pan, Pengbo Wu, and Hong Huang. 2024. "Semi-Tightly Coupled Robust Model for GNSS/UWB/INS Integrated Positioning in Challenging Environments" Remote Sensing 16, no. 12: 2108. https://doi.org/10.3390/rs16122108




