Self-Calibration Strip Bundle Adjustment of High-Resolution Satellite Imagery
Abstract
:1. Introduction
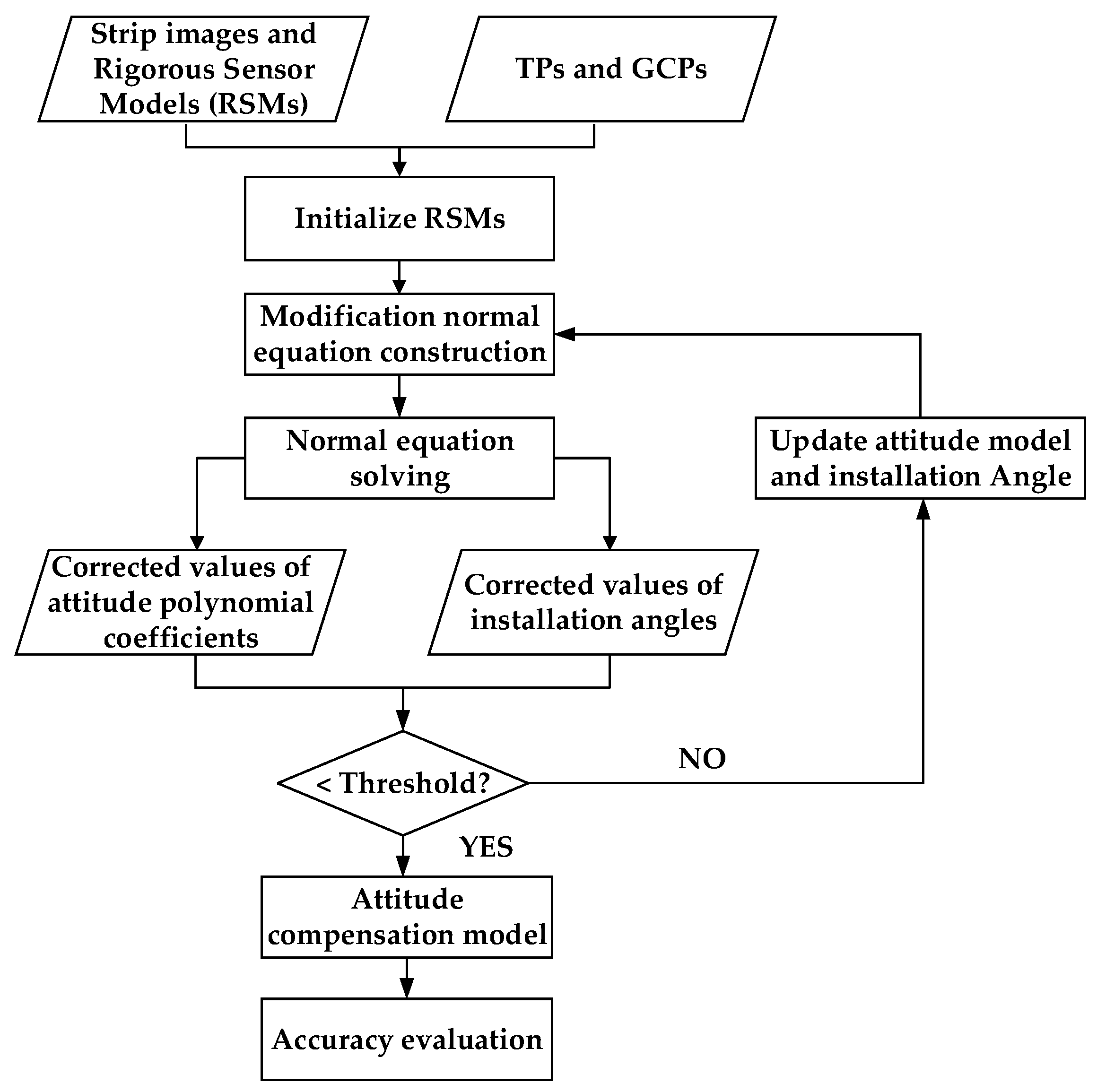
2. Methodology
2.1. Rigorous Sensor Model Taking into Account the Installation
2.2. Attitude Error Compensation
2.2.1. Satellite Attitude Representation
2.2.2. Attitude Compensation Model
2.3. Self-Calibration Strip Adjustment Taking into Account the Installation
3. Experimental Results
3.1. Experimental Datasets
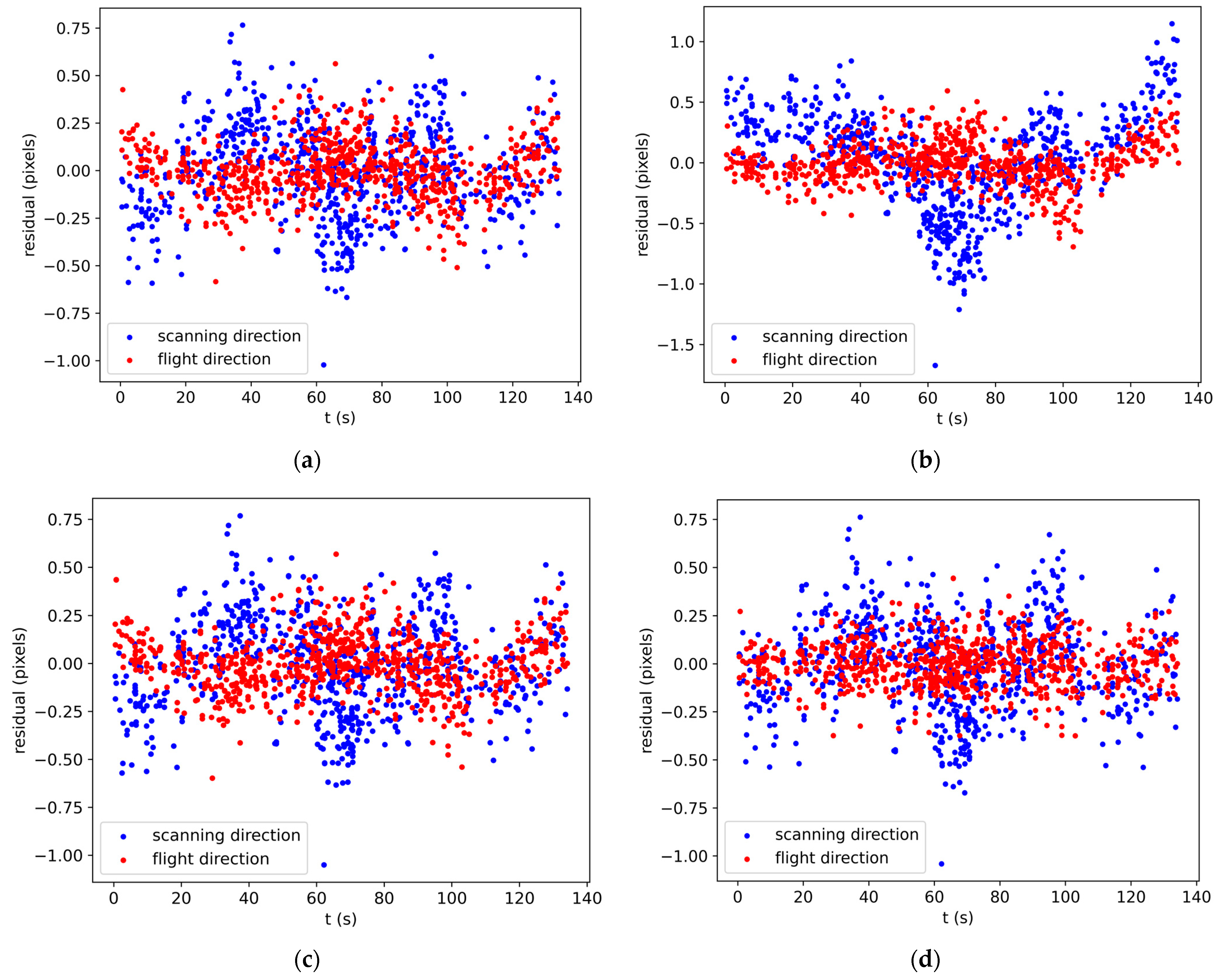
3.2. Bundle Adjustment without GCPs
- Plan A:
- Three-line-array-cameras independent adjustment with first-order attitude compensation model.
- Plan B:
- Self-calibration adjustment with translation attitude compensation model considering installation.
- Plan C:
- Self-calibration adjustment with first-order attitude compensation model considering installation.
- Plan D:
- Self-calibration adjustment with second-order attitude compensation model considering installation.
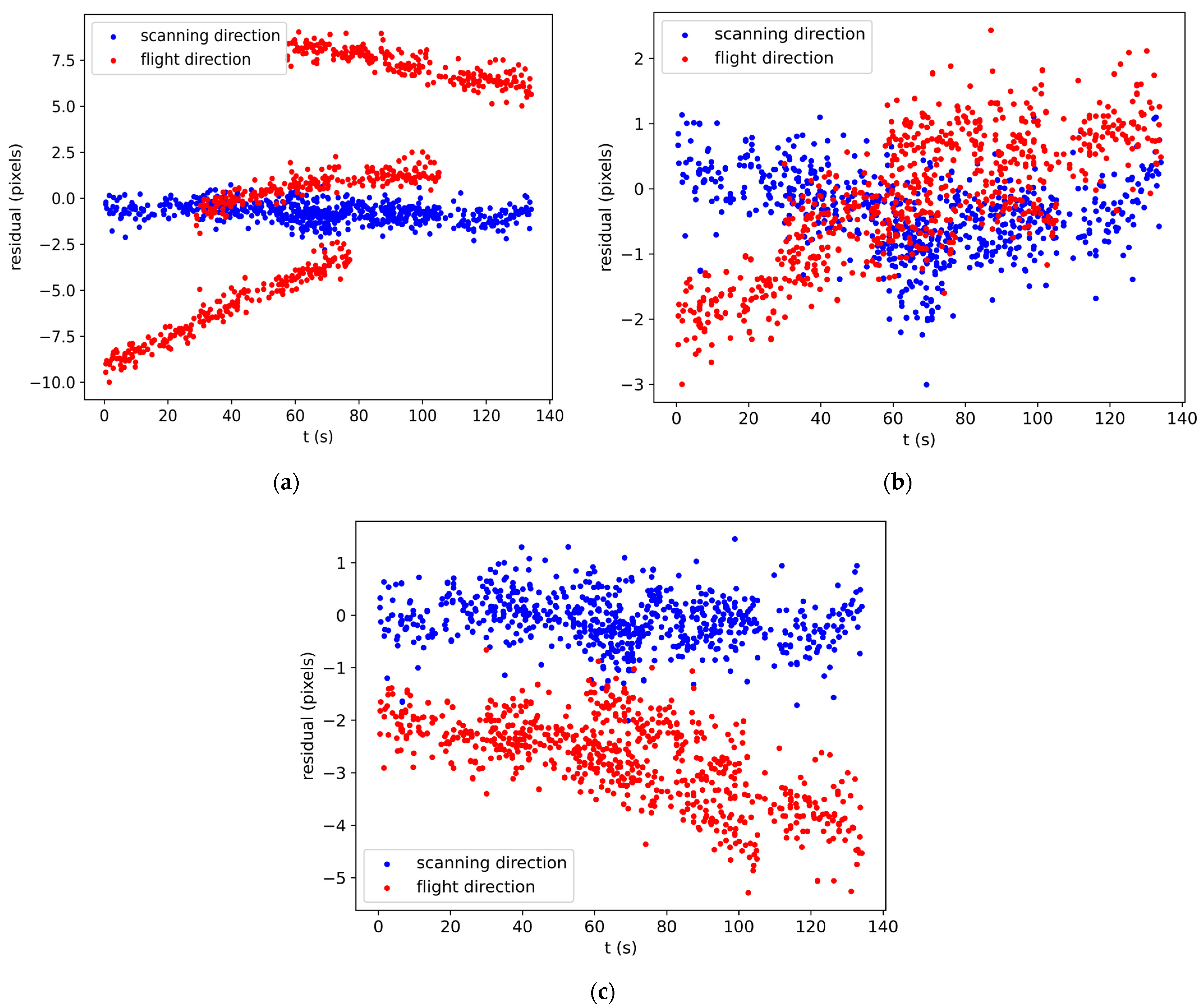
3.3. Bundle Adjustment with GCPs
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, D.; Wang, M. A review of high resolution optical satellite surveying and mapping technology. Spacecr. Recovery Remote Sens. 2020, 41, 1–11. [Google Scholar]
- Tadono, T.; Shimada, M.; Watanabe, M.; Hashimoto, T.; Iwata, T. Calibration and validation of PRISM onboard ALOS. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 13–18. [Google Scholar]
- Bouillon, A.; Bernard, M.; Gigord, P.; Orsoni, A.; Rudowski, V.; Baudoin, A. SPOT 5 HRS geometric performances: Using block adjustment as a key issue to improve quality of DEM generation. ISPRS J. Photogramm. Remote Sens. 2006, 60, 134–146. [Google Scholar] [CrossRef]
- Muralikrishnan, S.; Pillai, A.; Narender, B.; Reddy, S.; Venkataraman, V.R.; Dadhwal, V. Validation of Indian national DEM from Cartosat-1 data. J. Indian Soc. Remote Sens. 2013, 41, 1–13. [Google Scholar] [CrossRef]
- Wang, R.; Hu, X.; Wang, J. Photogrammetry of mapping satellite-1 without ground control points. Acta Geod. Cartogr. Sin. 2013, 42, 1–5. [Google Scholar]
- Cao, H.; Zhang, X.; Zhao, C.; Xu, C.; Mo, F.; Dai, J. System design and key technolongies of the GF-7 satellite. Chin. Space Sci. Technol. 2020, 40, 1. [Google Scholar]
- Barazzetti, L.; Roncoroni, F.; Brumana, R.; Previtali, M. Georeferencing accuracy analysis of a single worldview-3 image collected over milan. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 429–434. [Google Scholar] [CrossRef]
- Greslou, D.; de Lussy, F.; Amberg, V.; Dechoz, C.; Lenoir, F.; Delvit, J.-M.; Lebègue, L. Pleiades-HR 1A&1B image quality commissioning: Innovative geometric calibration methods and results. In Proceedings of the Earth Observing Systems XVIII; SPIE: San Diego, CA, USA, 2013; p. 886611. [Google Scholar]
- Luthcke, S.; Zelensky, N.; Rowlands, D.; Lemoine, F.; Williams, T. The 1-centimeter orbit: Jason-1 precision orbit determination using GPS, SLR, DORIS, and altimeter data special issue: Jason-1 calibration/validation. Mar. Geod. 2003, 26, 399–421. [Google Scholar] [CrossRef]
- Zhao, C.; Tang, X. Precise orbit determination for the ZY-3 satellite mission using GPS receiver. J. Astronaut. 2013, 34, 1202–1206. [Google Scholar]
- Jiang, Y.; Zhang, G.; Tang, X.; Zhu, X.; Qin, Q.; Li, D.; Fu, X. High accuracy geometric calibration of ZY-3 three-line image. Acta Geod. Cartogr. Sin. 2013, 42, 523–529. [Google Scholar]
- Hofmann, O.; Navé, P.; Ebner, H. DPS-A Digital Photogrammetric System for producing digital elevation models and orthophotos by means of linear array scanner imagery. Photogramm. Eng. Remote Sens. 1984, 50, 1135–1142. [Google Scholar]
- Wang, R. Satellite Photogrammetric Principle for Three-Line-Array CCD Imagery; Surveying and Mapping Press: Beijing, China, 2016; pp. 53–54. [Google Scholar]
- Wang, R.; Hu, X.; Wang, X.; Yang, J. The construction and application of mapping satellite-1 engineering. J. Remote Sens. 2012, 16, 2–5. [Google Scholar]
- Ebner, H.; Kornus, W.; Ohlhof, T.; Putz, E. Orientation of MOMS-02/D2 and MOMS-2P/PRIRODA imagery. ISPRS J. Photogramm. Remote Sens. 1999, 54, 332–341. [Google Scholar] [CrossRef]
- Poli, D. A rigorous model for spaceborne linear array sensors. Photogramm. Eng. Remote Sens. 2007, 73, 187–196. [Google Scholar] [CrossRef]
- Weser, T.; Rottensteiner, F.; Willneff, J.; Poon, J.; Fraser, C.S. Development and testing of a generic sensor model for pushbroom satellite imagery. Photogramm. Rec. 2008, 23, 255–274. [Google Scholar] [CrossRef]
- Kim, T.; Dowman, I. Comparison of two physical sensor models for satellite images: Position–rotation model and orbit–attitude model. Photogramm. Rec. 2006, 21, 110–123. [Google Scholar] [CrossRef]
- Li, R.; Hwangbo, J.; Chen, Y.; Di, K. Rigorous photogrammetric processing of HiRISE stereo imagery for Mars topographic mapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2558–2572. [Google Scholar]
- Radhadevi, P.; Nagasubramanian, V.; Mahapatra, A.; Solanki, S.; Sumanth, K.; Varadan, G. Potential of high-resolution Indian remote sensing satellite imagery for large scale mapping. In Proceedings of the ISPRS Hannover Workshop, High-Resolution Earth Imaging for Geospatial Information, Hannover, Germany, 2–5 June 2009. [Google Scholar]
- Rottensteiner, F.; Weser, T.; Lewis, A.; Fraser, C.S. A strip adjustment approach for precise georeferencing of ALOS optical imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4083–4091. [Google Scholar] [CrossRef]
- Di, K.; Liu, Y.; Liu, B.; Peng, M.; Hu, W. A Self-Calibration Bundle Adjustment Method for Photogrammetric Processing of Chang’E-2 Stereo Lunar Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 5432–5442. [Google Scholar]
- Zhang, Y.; Zheng, M.; Wang, X.; Huang, X. Strip-based bundle adjustment of Mapping Satellite-1 three-line array imagery. J. Remote Sens. Beijing 2012, 16, 84–89. [Google Scholar]
- Zheng, M.; Zhang, Y.; Zhu, J.; Xiong, X. Self-calibration adjustment of CBERS-02B long-strip imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3847–3854. [Google Scholar] [CrossRef]
- Cao, J.; Yuan, X.; Fu, J.; Gong, J. Precise sensor orientation of high-resolution satellite imagery with the strip constraint. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5313–5323. [Google Scholar] [CrossRef]
- Li, D. China’s first civilian three-line-array stereo mapping satellite: ZY-3. Acta Geod. Cartogr. Sin. 2012, 41, 317–322. [Google Scholar]
- Grodecki, J.; Dial, G. Block adjustment of high-resolution satellite images described by rational polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, M.; Xiong, J.; Lu, Y.; Xiong, X. On-orbit geometric calibration of ZY-3 three-line array imagery with multistrip data sets. IEEE Trans. Geosci. Remote Sens. 2013, 52, 224–234. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, M.; Xiong, X.; Xiong, J. Multistrip bundle block adjustment of ZY-3 satellite imagery by rigorous sensor model without ground control point. IEEE Geosci. Remote Sens. Lett. 2014, 12, 865–869. [Google Scholar] [CrossRef]
- Pan, H.; Tao, C.; Zou, Z. Precise georeferencing using the rigorous sensor model and rational function model for ZiYuan-3 strip scenes with minimum control. ISPRS J. Photogramm. Remote Sens. 2016, 119, 259–266. [Google Scholar] [CrossRef]
- Yuan, X.; Yu, X. Calibration of angular systematic errors for high resolution satellite imagery. Acta Geod. Cartogr. Sin. 2012, 41, 385–392. [Google Scholar]
- Cao, J.; Fu, J.; Yuan, X.; Gong, J. Nonlinear bias compensation of ZiYuan-3 satellite imagery with cubic splines. ISPRS J. Photogramm. Remote Sens. 2017, 133, 174–185. [Google Scholar] [CrossRef]
- Tao, C.V.; Hu, Y. A comprehensive study of the rational function model for photogrammetric processing. Photogramm. Eng. Remote Sens. 2001, 67, 1347–1358. [Google Scholar]
- Poli, D.; Toutin, T. Review of developments in geometric modelling for high resolution satellite pushbroom sensors. Photogramm. Rec. 2012, 27, 58–73. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.; Fan, D.; Lei, R.; Dai, H. Self-calibration Block Adjustment for Three-line-array Image of ZY-3. Acta Geod. Cartogr. Sin. 2014, 43, 1046. [Google Scholar]
| Number of Scenes | Image Acquisition Time | Image Coverage Ground Size | Image Coverage (Latitude and Longitude) |
|---|---|---|---|
| 12 × 3 | 3 February 2012 | 560 km × 51 km | E114.947709° N42.064374° |
| E115.547510° N41.956830° | |||
| E114.107452° N37.138009° | |||
| E113.544067° N37.226530° |
| Plan | The RMSE of TPs in the Image Space (Pixels) | ||
|---|---|---|---|
| Scanning Direction | Flight Direction | Plane | |
| Plan A | 0.240 | 0.145 | 0.280 |
| Plan B | 0.402 | 0.172 | 0.438 |
| Plan C | 0.241 | 0.145 | 0.281 |
| Plan D | 0.238 | 0.117 | 0.265 |
| Plan | The RMSE of CKPs in the Object Space (m) | |||
|---|---|---|---|---|
| East | North | Plane | Height | |
| Plan A | 3.873 | 2.553 | 4.639 | 53.270 |
| Plan B | 7.293 | 15.638 | 17.255 | 53.918 |
| Plan C | 2.308 | 3.217 | 3.960 | 53.287 |
| Plan D | 6.110 | 4.518 | 7.599 | 53.892 |
| GCP Layout Scheme | Plan | The RMSE of TPs in the Image Space (Pixels) | ||
|---|---|---|---|---|
| Scanning Direction | Flight Direction | Plane | ||
| 4 GCPs | Plan A | 0.248 | 0.145 | 0.287 |
| Plan C | 0.249 | 0.167 | 0.300 | |
| Plan D | 0.246 | 0.152 | 0.289 | |
| 16 GCPs | Plan A | 0.269 | 0.175 | 0.321 |
| Plan C | 0.269 | 0.194 | 0.331 | |
| Plan D | 0.263 | 0.181 | 0.319 | |
| 27 GCPs | Plan A | 0.290 | 0.218 | 0.363 |
| Plan C | 0.290 | 0.248 | 0.382 | |
| Plan D | 0.288 | 0.229 | 0.368 | |
| GCP Layout Scheme | Plan | The RMSE of CKPs in the Object Space (m) | |||
|---|---|---|---|---|---|
| East | North | Plane | Height | ||
| 4 GCPs | Plan A | 1.680 | 1.385 | 2.177 | 1.571 |
| Plan C | 1.679 | 1.355 | 2.158 | 2.313 | |
| Plan D | 1.297 | 1.332 | 1.859 | 1.876 | |
| 16 GCPs | Plan A | 1.333 | 1.331 | 1.884 | 1.505 |
| Plan C | 1.328 | 1.340 | 1.887 | 2.275 | |
| Plan D | 1.309 | 1.285 | 1.834 | 1.717 | |
| 27 GCPs | Plan A | 1.259 | 1.341 | 1.839 | 1.340 |
| Plan C | 1.260 | 1.343 | 1.841 | 2.224 | |
| Plan D | 1.233 | 1.298 | 1.790 | 1.360 | |
| Test Scheme | Comparison Plan | Plane | Height | ||
|---|---|---|---|---|---|
| ME (m) | p-Value | ME (m) | p-Value | ||
| Test 1 | Plan A | 1.904 | 0.924 | 0.751 | 0.455 |
| Plan C | 1.914 | 0.618 | |||
| Test 2 | Plan C | 1.914 | 2.190 × 10−4 | 0.618 | 0.194 |
| Plan D | 1.551 | 0.864 | |||
| Test Scheme | GCP Layout Scheme | Plane | Height | ||
|---|---|---|---|---|---|
| ME (m) | p-Value | ME (m) | p-Value | ||
| Test 3 | 4 GCPs | 1.551 | 0.895 | 0.864 | 0.009 |
| 16 GCPs | 1.538 | 0.436 | |||
| Test 4 | 16 GCPs | 1.538 | 0.676 | 0.436 | 0.020 |
| 27 GCPs | 1.496 | 0.079 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Pan, H.; Zhou, S.; Zhu, X. Self-Calibration Strip Bundle Adjustment of High-Resolution Satellite Imagery. Remote Sens. 2024, 16, 2196. https://doi.org/10.3390/rs16122196
Zhang X, Pan H, Zhou S, Zhu X. Self-Calibration Strip Bundle Adjustment of High-Resolution Satellite Imagery. Remote Sensing. 2024; 16(12):2196. https://doi.org/10.3390/rs16122196
Chicago/Turabian StyleZhang, Xue, Hongbo Pan, Shun Zhou, and Xiaoyong Zhu. 2024. "Self-Calibration Strip Bundle Adjustment of High-Resolution Satellite Imagery" Remote Sensing 16, no. 12: 2196. https://doi.org/10.3390/rs16122196






