Imaging Seafloor Features Using Multipath Arrival Structures
Abstract
:1. Introduction
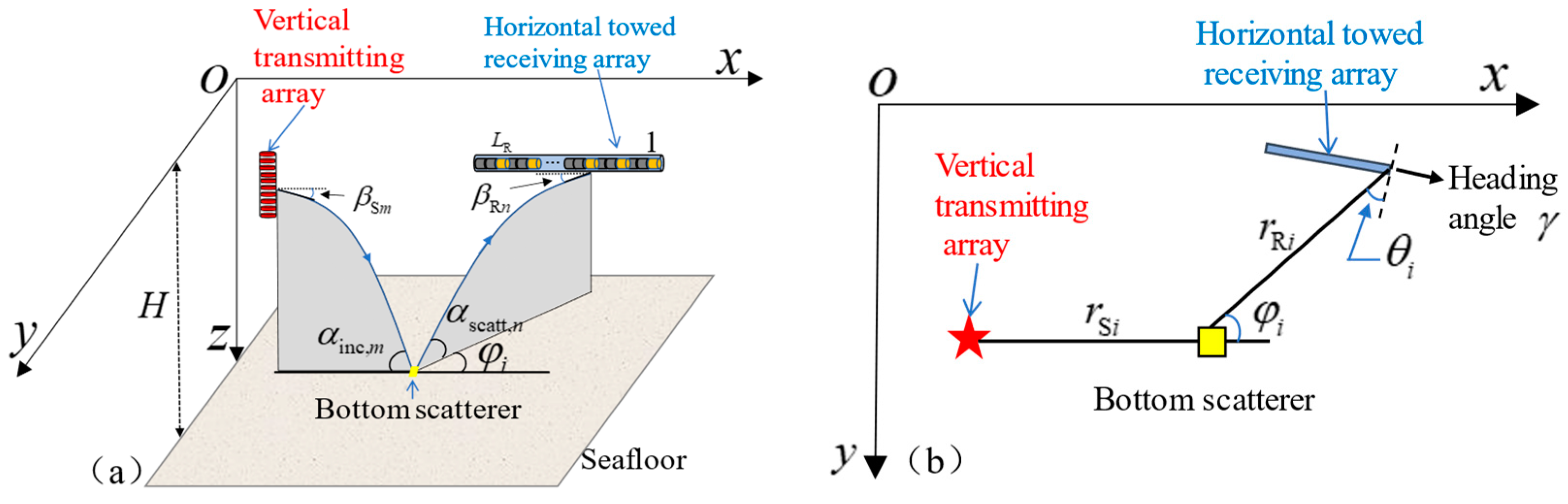
2. Receiving Signal Model
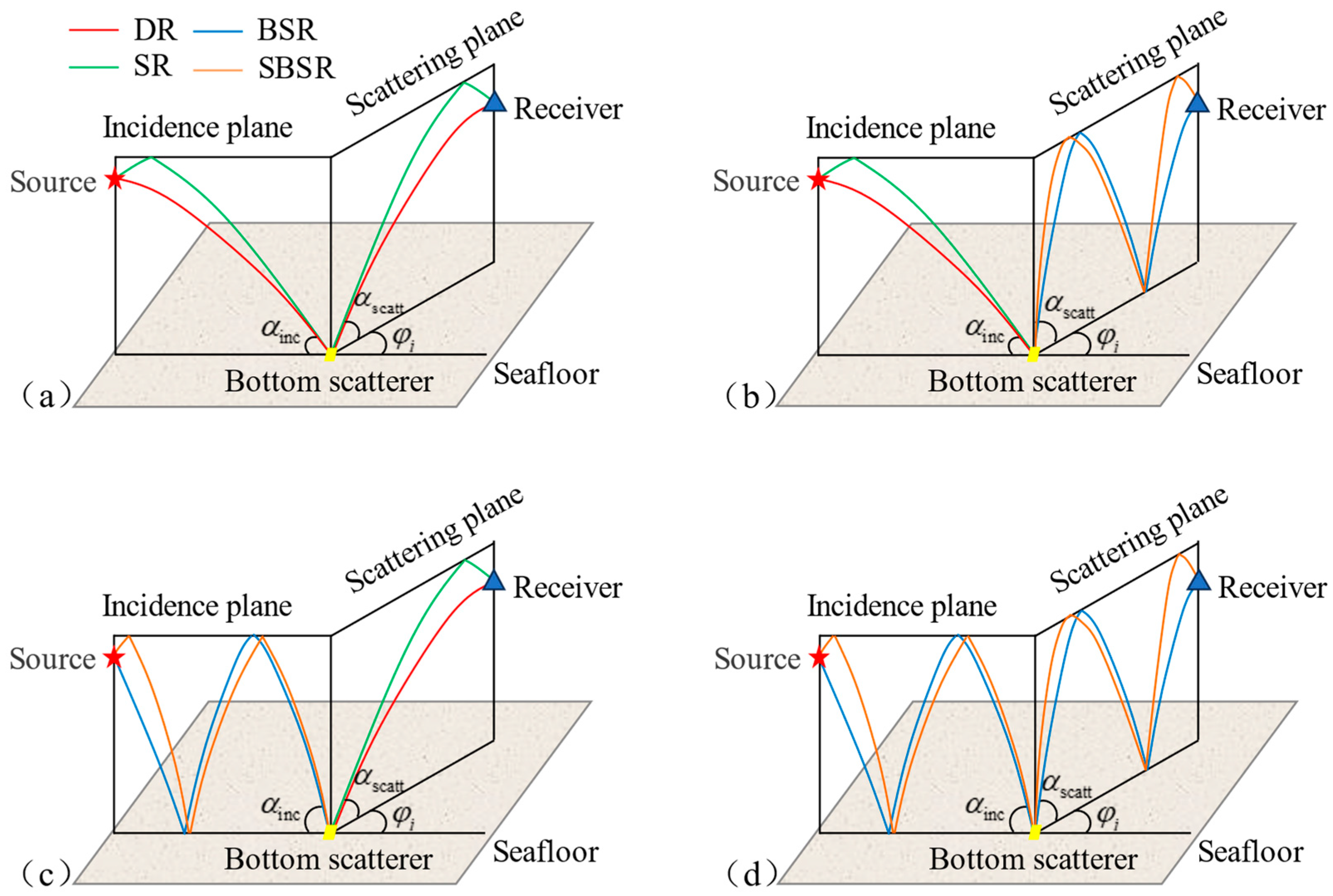
2.1. General Form of Receiving Signal Model
- M and N: the number of incident eigenrays and the number of scattered eigenrays.
- and : the amplitude and propagation delay of the mth incident eigenray.
- and : the amplitude and propagation delay of the nth scattered eigenray.
- and : the incident grazing angle of the mth incident eigenray and the scattered grazing angle of the nth scattered eigenray.
- : the direction of the arrival angle of the nth scattered eigenray, where .
2.2. Simplification of the Receiving Signal Model
3. Generating Seafloor Images Using Multipath Structures
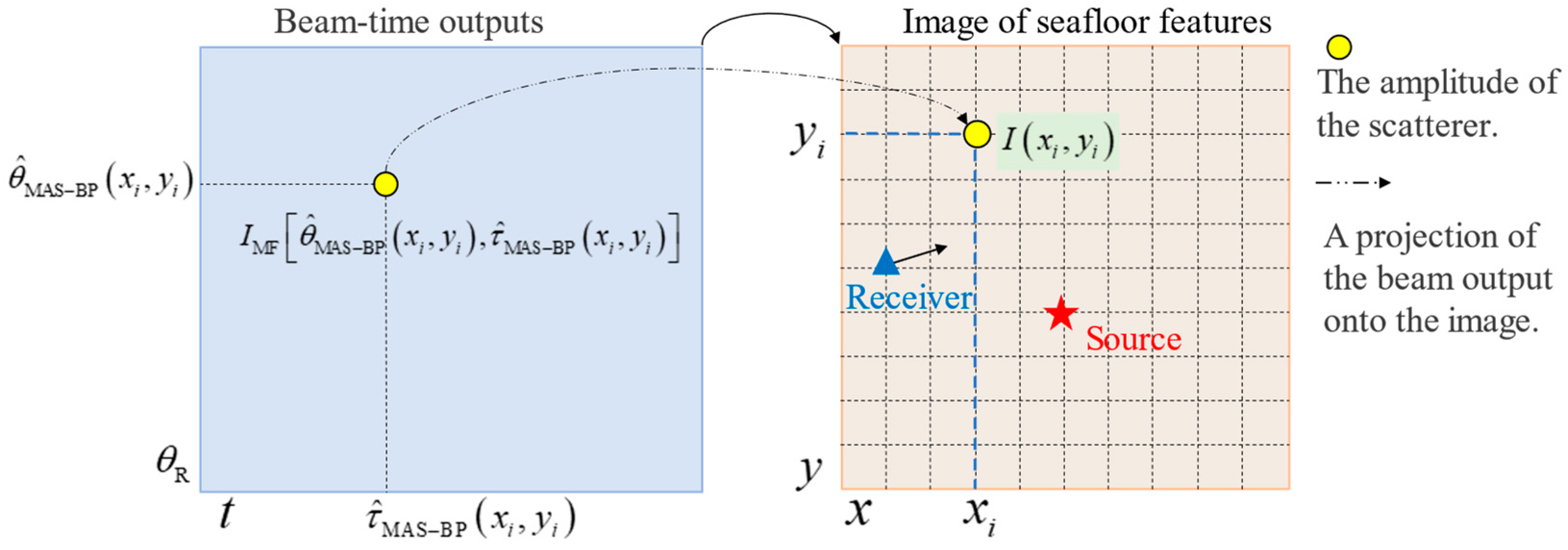
3.1. The Proposed MAS-BP Imaging Method
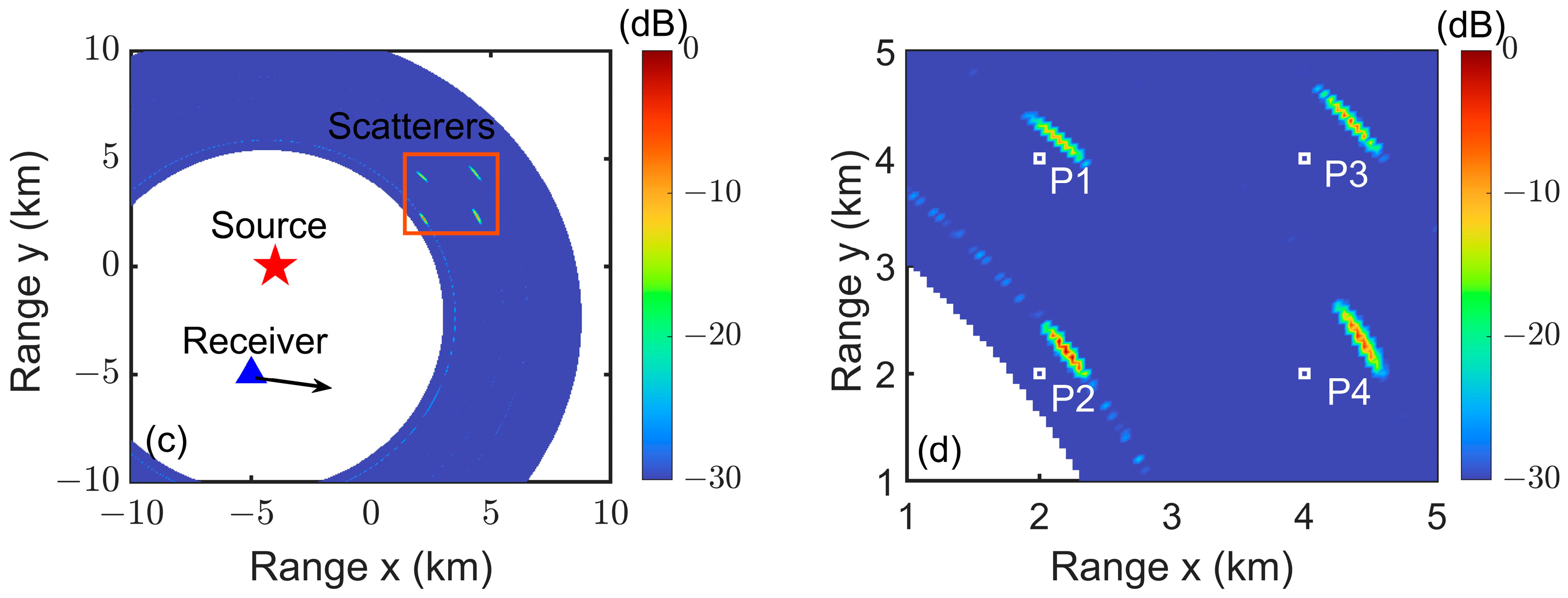
3.2. Comparison with the Conventional BP Method
4. Numerical Simulations
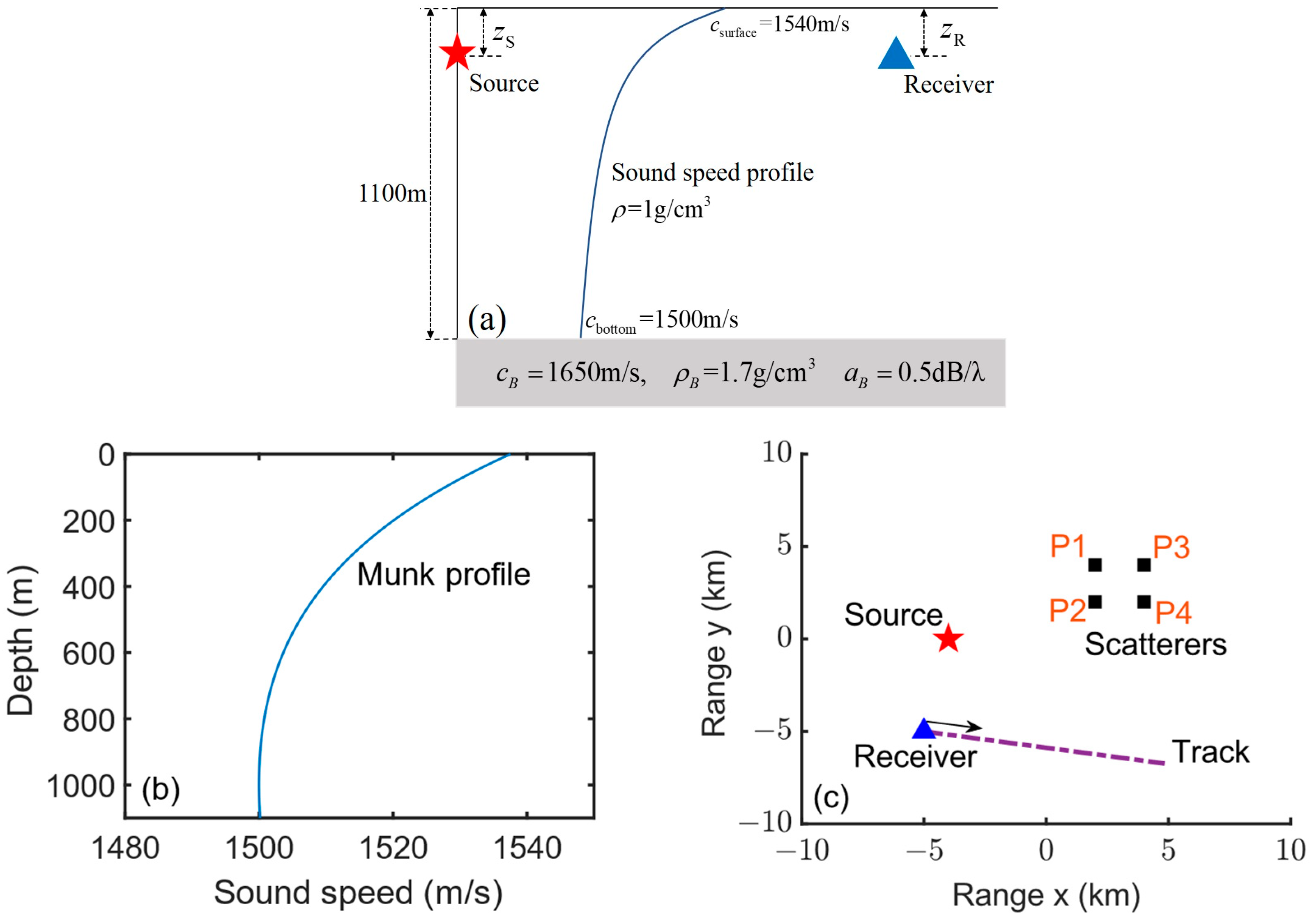
4.1. Simulation Environment and Parameters
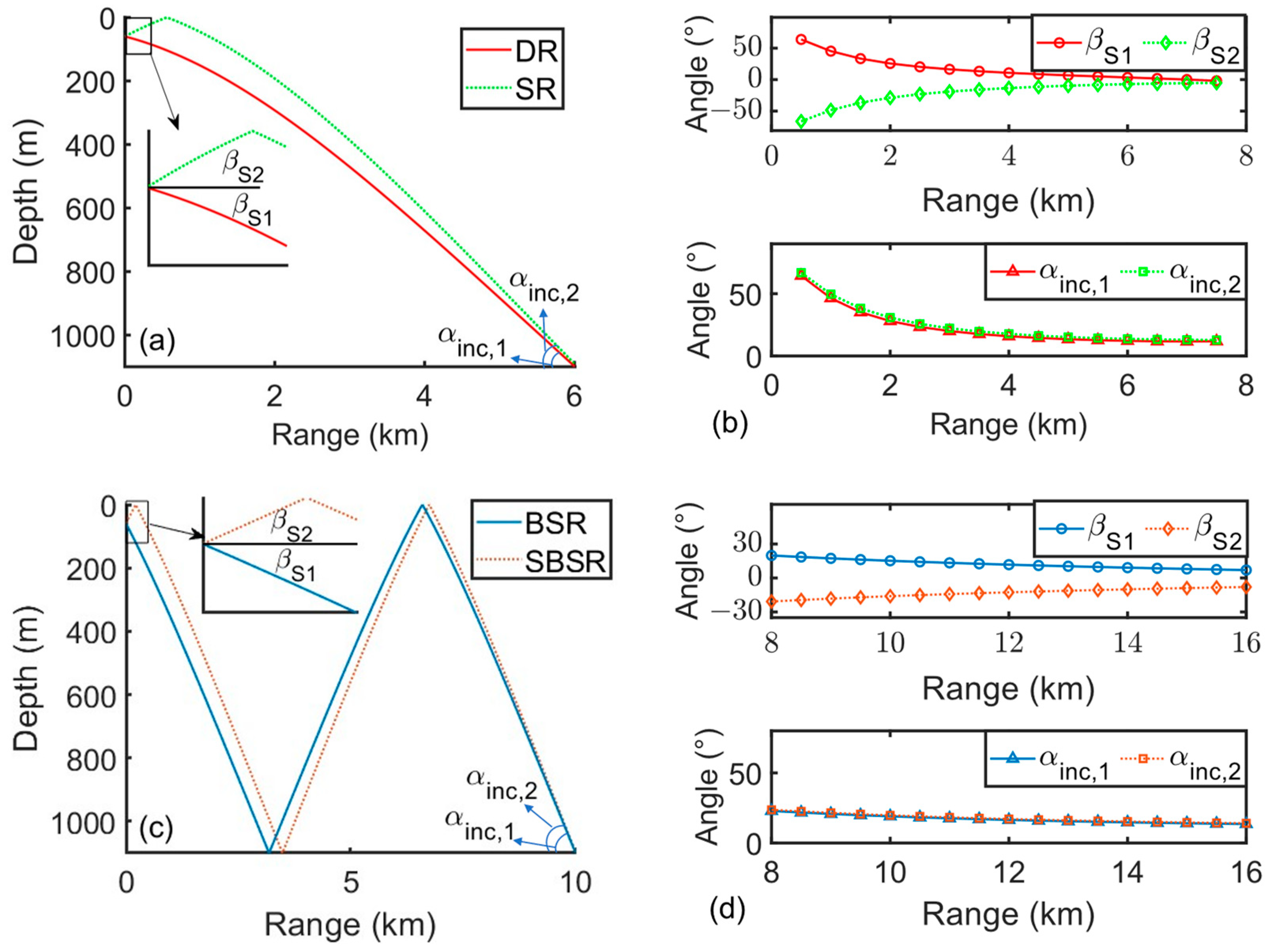
4.2. Comparison of Propagation Delay Values
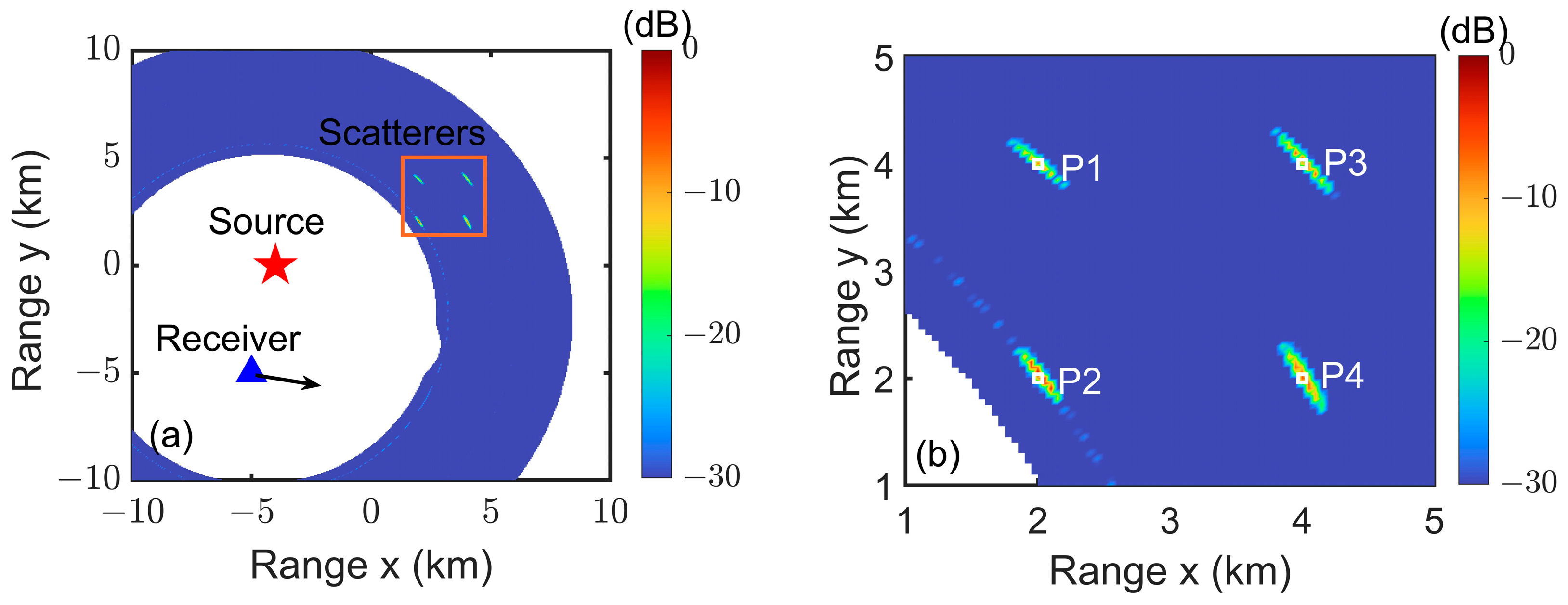
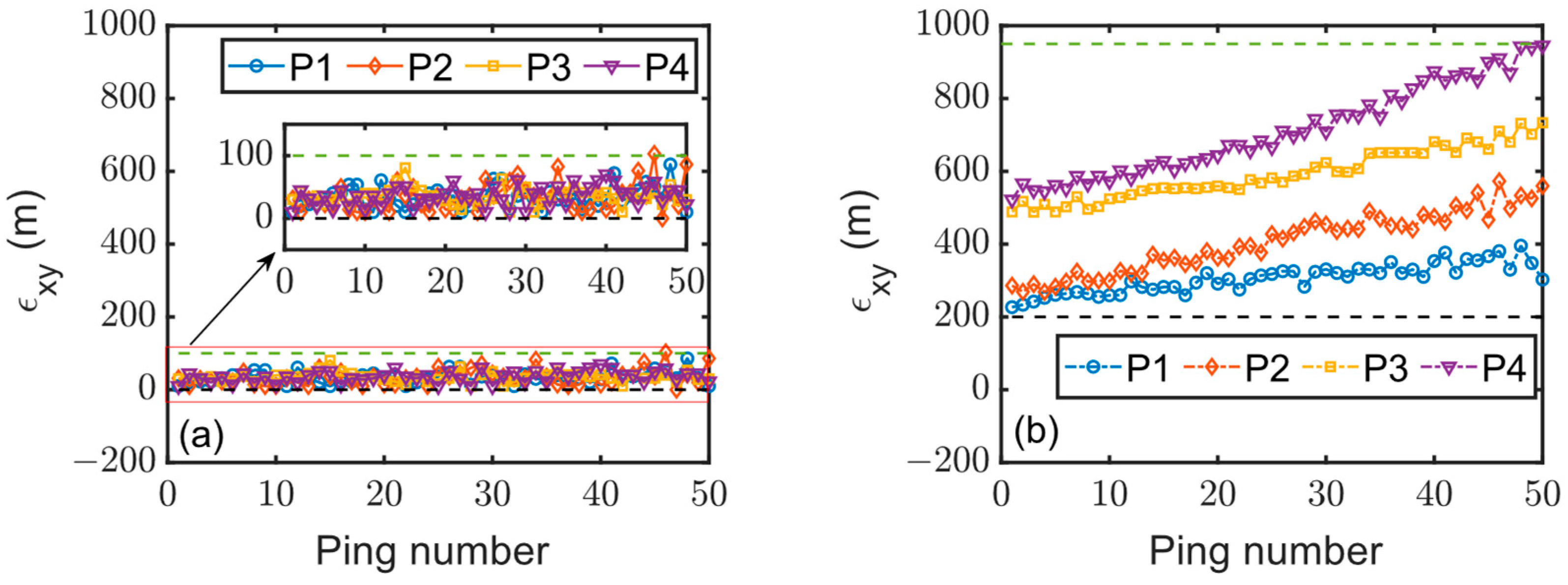
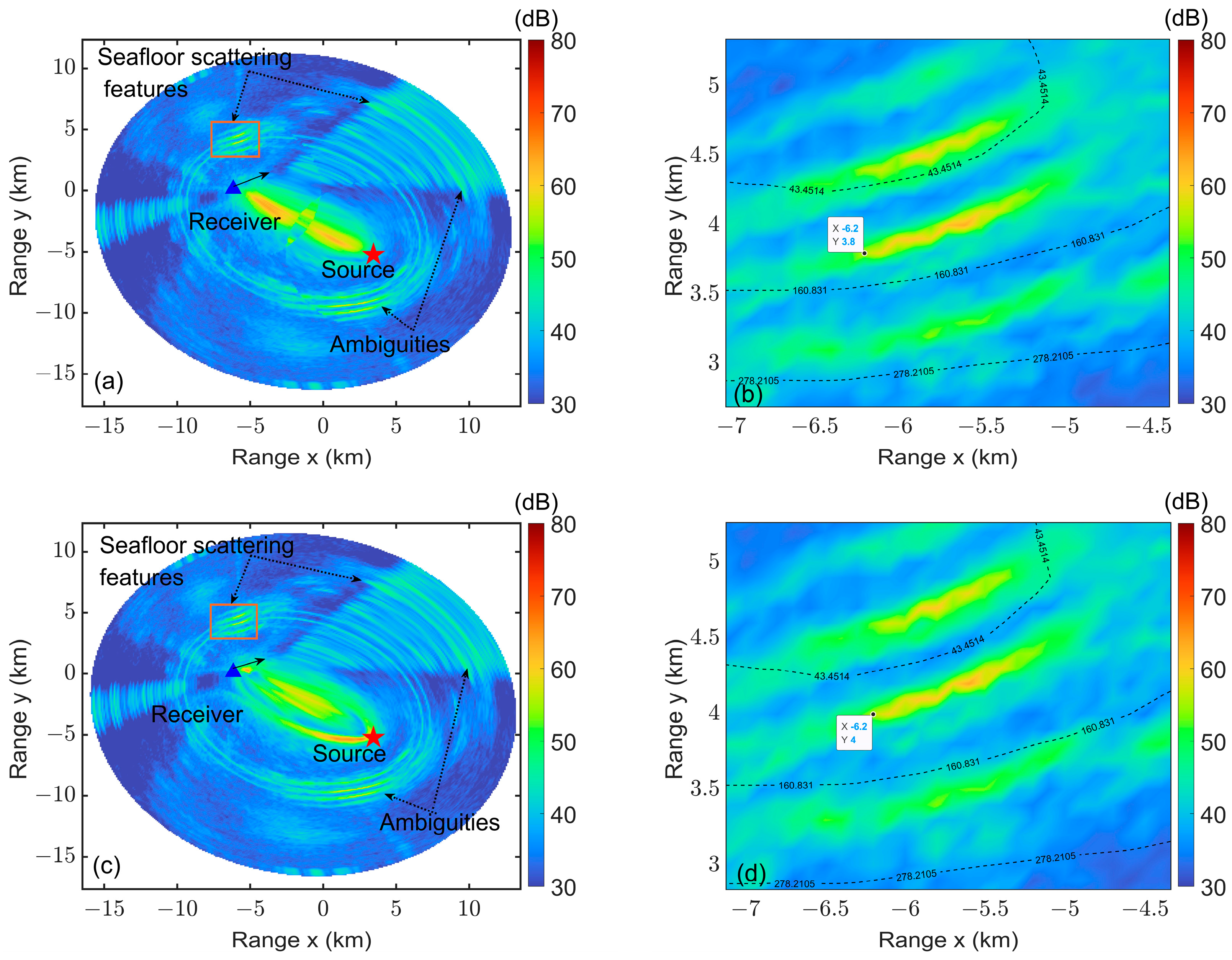
4.3. Imaging Results of Point Scatterers
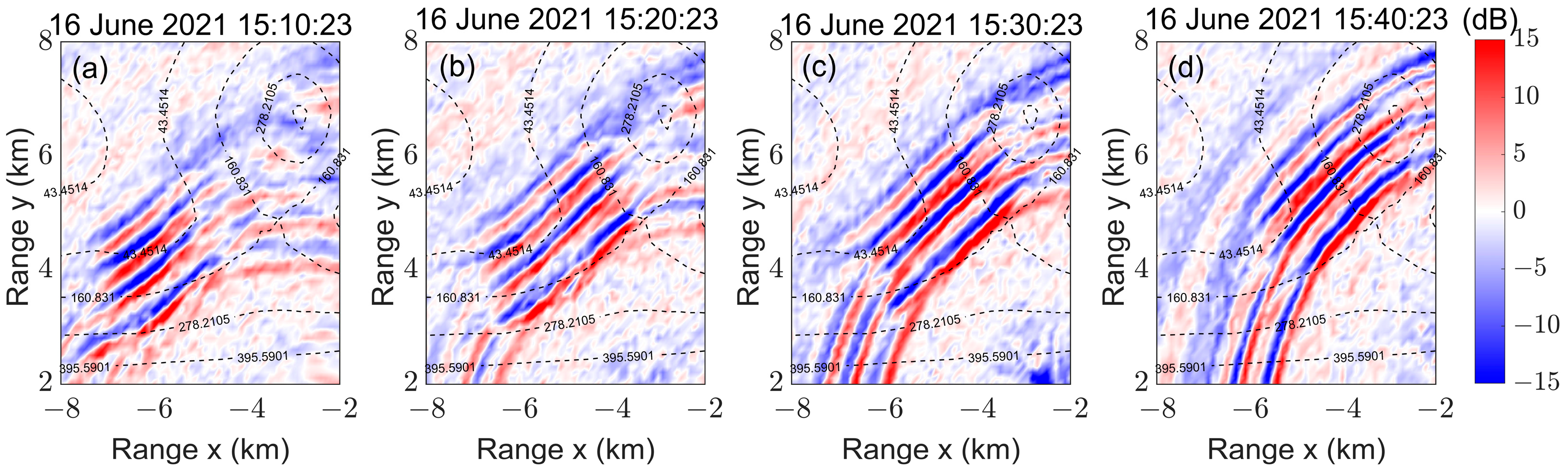
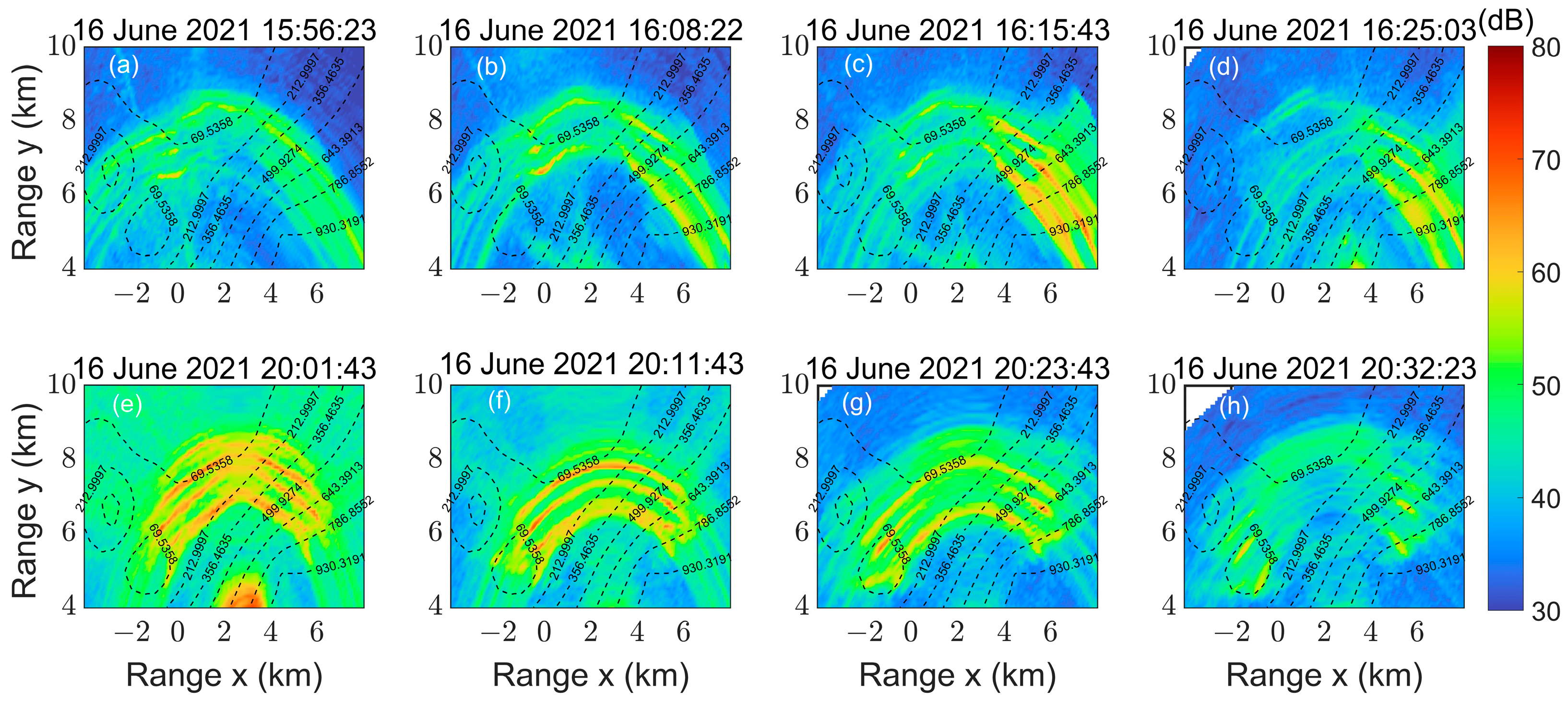
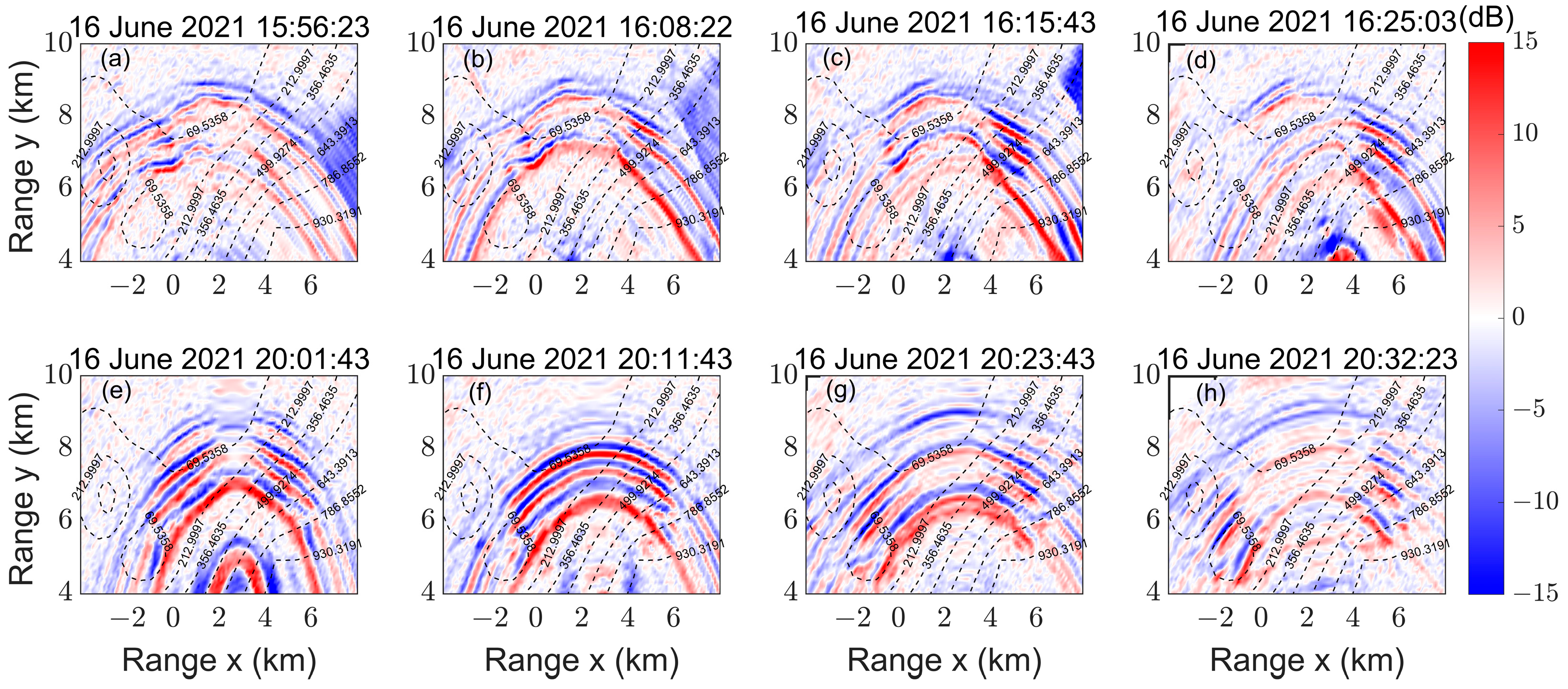
5. Application to Experimental Data
5.1. Experiment Description
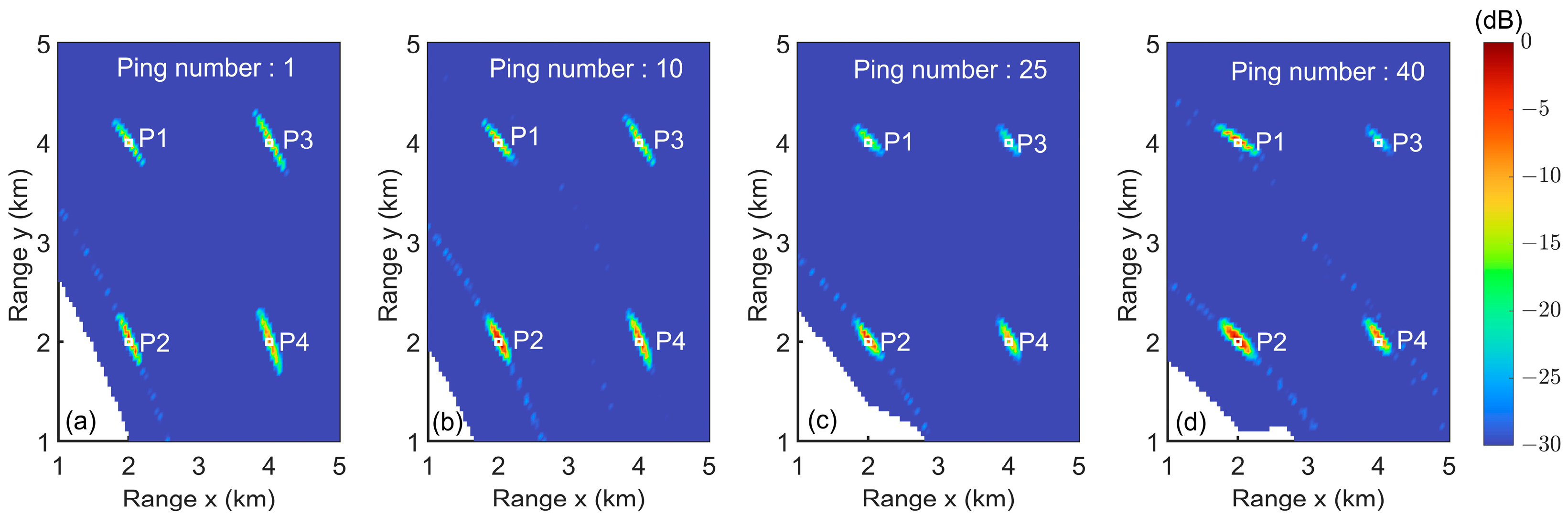
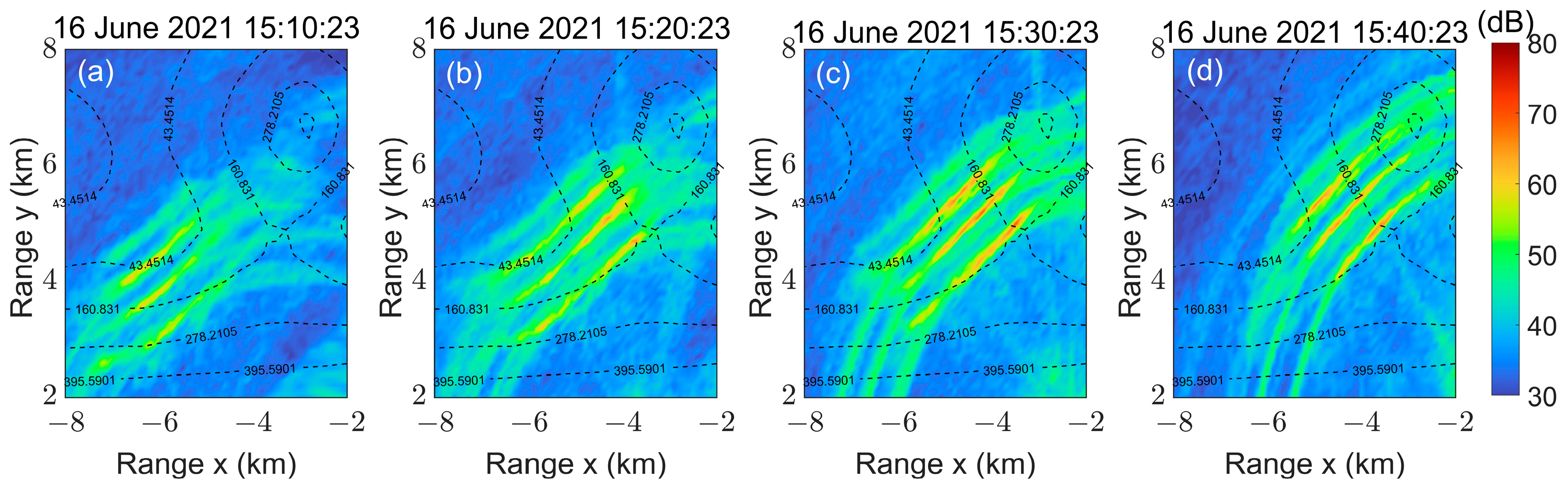
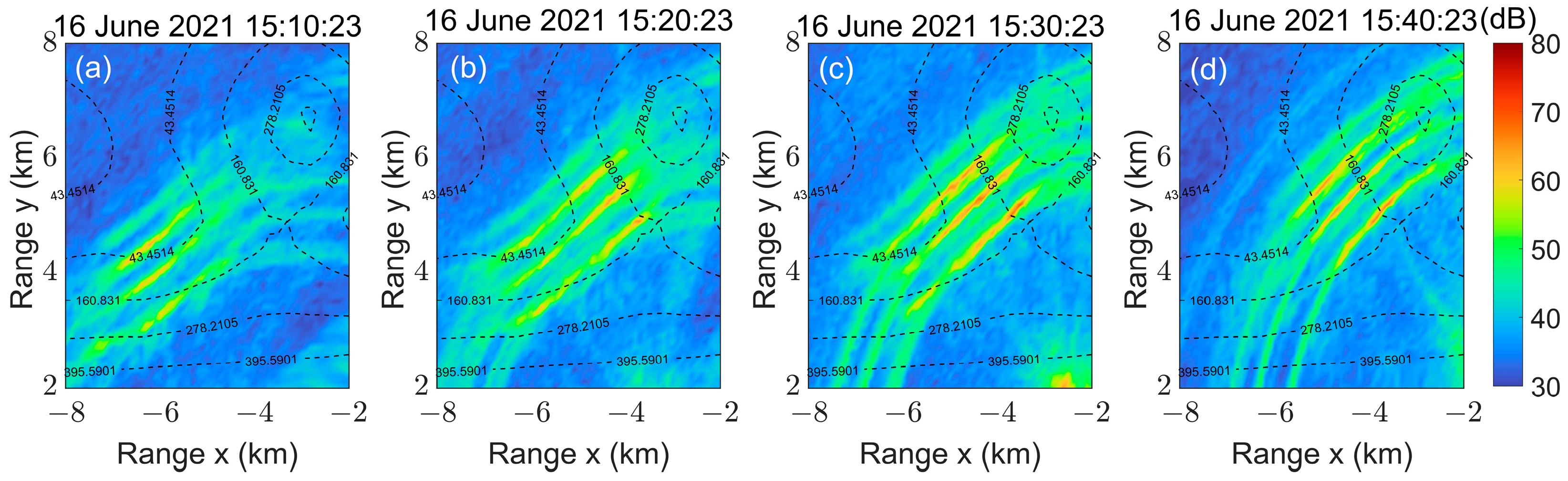
5.2. Experimental Results of Track 1
5.3. Experimental Results at Different Tracks
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Makris, N.C.; Jagannathan, S.; Ignisca, A. Ocean Acoustic Waveguide Remote Sensing: Visualizing Life Around Seamounts. Oceanography 2010, 23, 204–205. [Google Scholar] [CrossRef]
- Jagannathan, S.; Bertsatos, I.; Symonds, D.T.; Chen, T.; Nia, H.T.; Jain, A.D.; Andrews, M.J.; Gong, Z.; Nero, R.W.; Ngor, L.; et al. Ocean Acoustic Waveguide Remote Sensing (OAWRS) of marine ecosystems. Mar. Ecol. Prog. Ser. 2009, 395, 137–160. [Google Scholar] [CrossRef]
- Makris, N.C.; Avelino, L.Z.; Menis, R. Deterministic Reverberation from Ocean Ridges. J. Acoust. Soc. Am. 1995, 97, 3547–3574. [Google Scholar] [CrossRef]
- Makris, N.C.; Berkson, J.M. Long-Range Backscatter from the Mid-Atlantic Ridge. J. Acoust. Soc. Am. 1994, 95, 1865–1881. [Google Scholar] [CrossRef]
- Zheng, Y.; Ping, X.; Li, L.; Wang, D. Maximum Likelihood Deconvolution of Beamforming Images with Signal-Dependent Speckle Fluctuations. Remote Sens. 2024, 16, 1506. [Google Scholar] [CrossRef]
- Makris, N.C.; Ratilal, P.; Jagannathan, S.; Gong, Z.; Andrews, M.; Bertsatos, I.; Godø, O.; Nero, R.; Jech, J. Critical Population Density Triggers Rapid Formation of Vast Oceanic Fish Shoals. Science 2009, 323, 1734–1737. [Google Scholar] [CrossRef] [PubMed]
- Makris, N.C.; Ratilal, P.; Symonds, D.T.; Jagannathan, S.; Lee, S.; Nero, R.W. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science 2006, 311, 660–663. [Google Scholar] [CrossRef]
- Duane, D.; Godø, O.R.; Makris, N.C. Quantification of Wide-Area Norwegian Spring-Spawning Herring Population Density with Ocean Acoustic Waveguide Remote Sensing (OAWRS). Remote Sens. 2021, 13, 4546. [Google Scholar] [CrossRef]
- Eleftherios, K.; Ratilal, P.; Makris, N.C. Optimal Automatic Wide-Area Discrimination of Fish Shoals from Seafloor Geology with Multi-Spectral Ocean Acoustic Waveguide Remote Sensing in the Gulf of Maine. Remote Sens. 2023, 15, 437. [Google Scholar] [CrossRef]
- Gong, Z.; Andrews, M.; Jagannathan, S.; Patel, R.; Jech, J.M.; Makris, N.C.; Ratilal, P. Low-Frequency Target Strength and Abundance of Shoaling Atlantic Herring (Clupea harengus) in the Gulf of Maine during the Ocean Acoustic Waveguide Remote Sensing 2006 Experiment. J. Acoust. Soc. Am. 2010, 127, 104–123. [Google Scholar] [CrossRef]
- Lee, W.J.; Tang, D.; Stanton, T.K.; Thorsos, E.I. Macroscopic Observations of Diel Fish Movements around a Shallow Water Artificial Reef Using a Mid-Frequency Horizontal-Looking Sonar. J. Acoust. Soc. Am. 2018, 144, 1424–1434. [Google Scholar] [CrossRef]
- Yi, D.H.; Gong, Z.; Jech, J.M.; Ratilal, P.; Makris, N.C. Instantaneous 3D Continental-Shelf Scale Imaging of Oceanic Fish by Multi-Spectral Resonance Sensing Reveals Group Behavior during Spawning Migration. Remote Sens. 2018, 10, 108. [Google Scholar] [CrossRef]
- Yi, D.H.; Makris, N.C. Feasibility of Acoustic Remote Sensing of Large Herring Shoals and Seafloor by Baleen Whales. Remote Sens. 2016, 8, 693. [Google Scholar] [CrossRef]
- Wang, D.; Huang, W.; Garcia, H.; Ratilal, P. Vocalization Source Level Distributions and Pulse Compression Gains of Diverse Baleen Whale Species in the Gulf of Maine. Remote Sens. 2016, 8, 881. [Google Scholar] [CrossRef]
- Preston, J.R.; Akal, T.; Berkson, J. Analysis of Backscattering Data in the Tyrrhenian Sea. J. Acoust. Soc. Am. 1990, 87, 119–134. [Google Scholar] [CrossRef]
- Makris, N.C.; Chia, C.S.; Fialkowski, L.T. The Bi-Azimuthal Scattering Distribution of an Abyssal Hill. J. Acoust. Soc. Am. 1999, 106, 2491–2512. [Google Scholar] [CrossRef]
- Chia, C.S.; Makris, N.C.; Fialkowski, L.T. A Comparison of Bistatic Scattering from Two Geologically Distinct Abyssal Hills. J. Acoust. Soc. Am. 2000, 108, 2053–2070. [Google Scholar] [CrossRef]
- Yang, J.; Tang, D.; Hefner, B.T.; Williams, K.L.; Preston, J.R. Overview of Midfrequency Reverberation Data Acquired During the Target and Reverberation Experiment 2013. IEEE J. Oceanic Eng. 2018, 43, 563–585. [Google Scholar] [CrossRef]
- Jung, Y.; Lee, K. Observation of the Relationship between Ocean Bathymetry and Acoustic Bearing-Time Record Patterns Acquired during a Reverberation Experiment in the Southwestern Continental Margin of the Ulleung Basin, Korea. J. Mar. Sci. Eng. 2021, 9, 1259. [Google Scholar] [CrossRef]
- Ratilal, P.; Lai, Y.; Symonds, D.T.; Ruhlmann, L.A.; Preston, J.R.; Scheer, E.K.; Garr, M.T.; Holland, C.W.; Goff, J.A.; Makris, N.C. Long Range Acoustic Imaging of the Continental Shelf Environment: The Acoustic Clutter Reconnaissance Experiment 2001. J. Acoust. Soc. Am. 2005, 117, 1977–1998. [Google Scholar] [CrossRef]
- Galinde, A.; Donabed, N.; Andrews, M.; Lee, S.; Makris, N.C.; Ratilal, P. Range-Dependent Waveguide Scattering Model Calibrated for Bottom Reverberation in a Continental Shelf Environment. J. Acoust. Soc. Am. 2008, 123, 1270–1281. [Google Scholar] [CrossRef]
- Jagannathan, S.; Küsel, E.T.; Ratilal, P.; Makris, N.C. Scattering from Extended Targets in Range-Dependent Fluctuating Ocean-Waveguides with Clutter from Theory and Experiments. J. Acoust. Soc. Am. 2012, 132, 680–693. [Google Scholar] [CrossRef]
- Preston, J.R.; Ellis, D.D. Extracting Bottom Information from Towed-Array Reverberation Data: Part I: Measurement Methodology. J. Mar. Syst. 2009, 78 (Suppl. C), S359–S371. [Google Scholar] [CrossRef]
- Preston, J.R. Extracting bottom information from towed-array reverberation data. Part II: Extraction procedure and modelling methodology. J. Mar. Syst. 2009, 78 (Suppl. S), S372–S381. [Google Scholar] [CrossRef]
- Ellis, D.D.; Yang, J.; Preston, J.R.; Pecknold, S. A Normal Mode Reverberation and Target Echo Model to Interpret Towed Array Data in the Target and Reverberation Experiments. IEEE J. Ocean. Eng. 2017, 42, 344–361. [Google Scholar] [CrossRef]
- Prior, M.K. A Scatterer Map for the Malta Plateau. IEEE J. Ocean. Eng. 2005, 30, 676–690. [Google Scholar] [CrossRef]
- Preston, J.R.; Abraham, D.A. Statistical Analysis of Multistatic Echoes from a Shipwreck in the Malta Plateau. IEEE J. Ocean. Eng. 2015, 40, 643–656. [Google Scholar] [CrossRef]
- Holland, C. Mapping seabed variability: Rapid surveying of coastal regions. J. Acoust. Soc. Am. 2006, 119, 1373–1387. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, P.; Tan, C.; Ying, W. BP Algorithm for the Multireceiver SAS. IET Radar Sonar Navig. 2019, 13, 830–838. [Google Scholar] [CrossRef]
- Ellis, D.D.; Crowe, D.V. Bistatic reverberation calculations using a three-dimensional scattering function. J. Acoust. Soc. Am. 1991, 89, 2207–2214. [Google Scholar] [CrossRef]
- Wang, L.; Qin, J.; Fu, D.; Li, Z.; Liu, J.; Weng, J. Bottom reverberation for large receiving depth in deep water. Acta Phys. Sin. 2019, 68, 134303. [Google Scholar] [CrossRef]






| The Vertical Transmitting Array | The Horizontal Receiving Array | Frequency of the Signal | ||
|---|---|---|---|---|
| Number of Elements | Element Spacing | Number of Elements | Element Spacing | LFM |
| 10 | 0.42 m | 96 | 0.416 m | 1700 Hz–1900 Hz |
| The Extent of Deviation from the Minimum | |||
|---|---|---|---|
| 1500 m/s | 1000 m | 1000 m | 0.57 × 10−2 |
| The Center of the Source | The Initial Position of the Receiver | Scatterer P1 | Scatterer P2 | Scatterer P3 | Scatterer P4 |
|---|---|---|---|---|---|
| (−4 km, 0, 60 m) | (−5 km, −5 km, 60 m) | (2 km, 4 km, 1100 m) | (2 km, 2 km, 1100 m) | (4 km, 4 km, 1100 m) | (4 km, 2 km, 1100 m) |
| The Coordinates (x, y) of the Scatterer | Ping No.1 | Ping No.10 | Ping No.25 | Ping No.40 | |
|---|---|---|---|---|---|
| P1 (2, 4) | (2.01, 4.00) | (2.01, 4.01) | (2.02, 4.03) | (2.02, 4.02) | |
| (m) | 10 | 14.14 | 36.05 | 28.28 | |
| P2 (2, 2) | (2.03, 2.01) | (2.01, 2.00) | (1.98, 2.06) | (1.99, 2.01) | |
| (m) | 31.62 | 10 | 63.24 | 14.14 | |
| P3 (4, 4) | (4.03, 4.00) | (4.00, 4.40) | (4.02, 4.02) | (3.99, 4.04) | |
| (m) | 30 | 40 | 28.28 | 41.23 | |
| P4 (4, 2) | (4.01, 2.00) | (4.01, 2.01) | (4.00, 2.01) | (4.00, 2.07) | |
| (m) | 10 | 14.14 | 10 | 70.00 | |
| The Coordinates (x, y) of the Scatterer | Ping No.1 | Ping No.10 | Ping No.25 | Ping No.40 | |
|---|---|---|---|---|---|
| P1 (2, 4) | (2.17, 4.15) | (2.12, 4.23) | (2.07, 4.31) | (1.95, 4.35) | |
| (m) | 226.71 | 259.42 | 317.81 | 353.55 | |
| P2 (2, 2) | (2.23, 2.17) | (2.19, 2.23) | (2.08, 2.42) | (1.93, 2.47) | |
| (m) | 286.00 | 298.33 | 427.55 | 475.18 | |
| P3 (4, 4) | (4.36, 4.33) | (4.30, 4.43) | (4.24, 4.53) | (4.04, 4.68) | |
| (m) | 488.36 | 524.31 | 581.81 | 681.17 | |
| P4 (4, 2) | (4.42, 2.31) | (4.41, 2.40) | (4.31, 2.59) | (4.09, 2.87) | |
| (m) | 522.02 | 572.80 | 666.48 | 874.64 | |
| The Number of Data | The Center Coordinates of the Stripes for the MAS-BP Method | The Center Coordinates of the Stripes for the BP Method | The Distance Difference of Stripes (m) |
|---|---|---|---|
| Ping No.1 | (−5.9, 4.2) | (−6.0, 4.3) | 141.42 |
| Ping No.2 | (−5.3, 4.6) | (−5.2,4.8) | 223.61 |
| Ping No.3 | (−5.0, 4.9) | (−5.1, 5.1) | 223.61 |
| Ping No.4 | (−4.1, 5.6) | (−4.2, 5.8) | 223.61 |
| Ping No.5 * | (5.8, 6.0) | (5.9, 6.3) | 316.23 |
| Ping No.6 * | (5.8, 6.3) | (6.3, 6.3) | 500.00 |
| Ping No.7 | (6.1, 6.0) | (6.3, 6.1) | 223.61 |
| Ping No.8 | (6.6, 5.7) | (6.7, 5.8) | 141.42 |
| Ping No.9 | (2.4, 7.7) | (2.7, 8.0) | 424.26 |
| Ping No.10 | (1.8, 7.2) | (2.1, 7.6) | 500.00 |
| Ping No.11 | (1.7, 7.2) | (1.6, 7.4) | 223.61 |
| Ping No.12 | (1.6, 7.3) | (1.5, 7.7) | 412.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z.; Zhuo, J.; Sun, C. Imaging Seafloor Features Using Multipath Arrival Structures. Remote Sens. 2024, 16, 2586. https://doi.org/10.3390/rs16142586
Su Z, Zhuo J, Sun C. Imaging Seafloor Features Using Multipath Arrival Structures. Remote Sensing. 2024; 16(14):2586. https://doi.org/10.3390/rs16142586
Chicago/Turabian StyleSu, Zhaohua, Jie Zhuo, and Chao Sun. 2024. "Imaging Seafloor Features Using Multipath Arrival Structures" Remote Sensing 16, no. 14: 2586. https://doi.org/10.3390/rs16142586
APA StyleSu, Z., Zhuo, J., & Sun, C. (2024). Imaging Seafloor Features Using Multipath Arrival Structures. Remote Sensing, 16(14), 2586. https://doi.org/10.3390/rs16142586





