Spatiotemporal Feature Fusion Transformer for Precipitation Nowcasting via Feature Crossing
Abstract
:1. Introduction
- (1)
- We propose an encoder–forecaster framework for precipitation nowcasting; the encoder explicitly processes the temporal sequence data and the forecaster processes the sequence data in total. The framework efficiently integrates the merits of the models based RNN and FCN.
- (2)
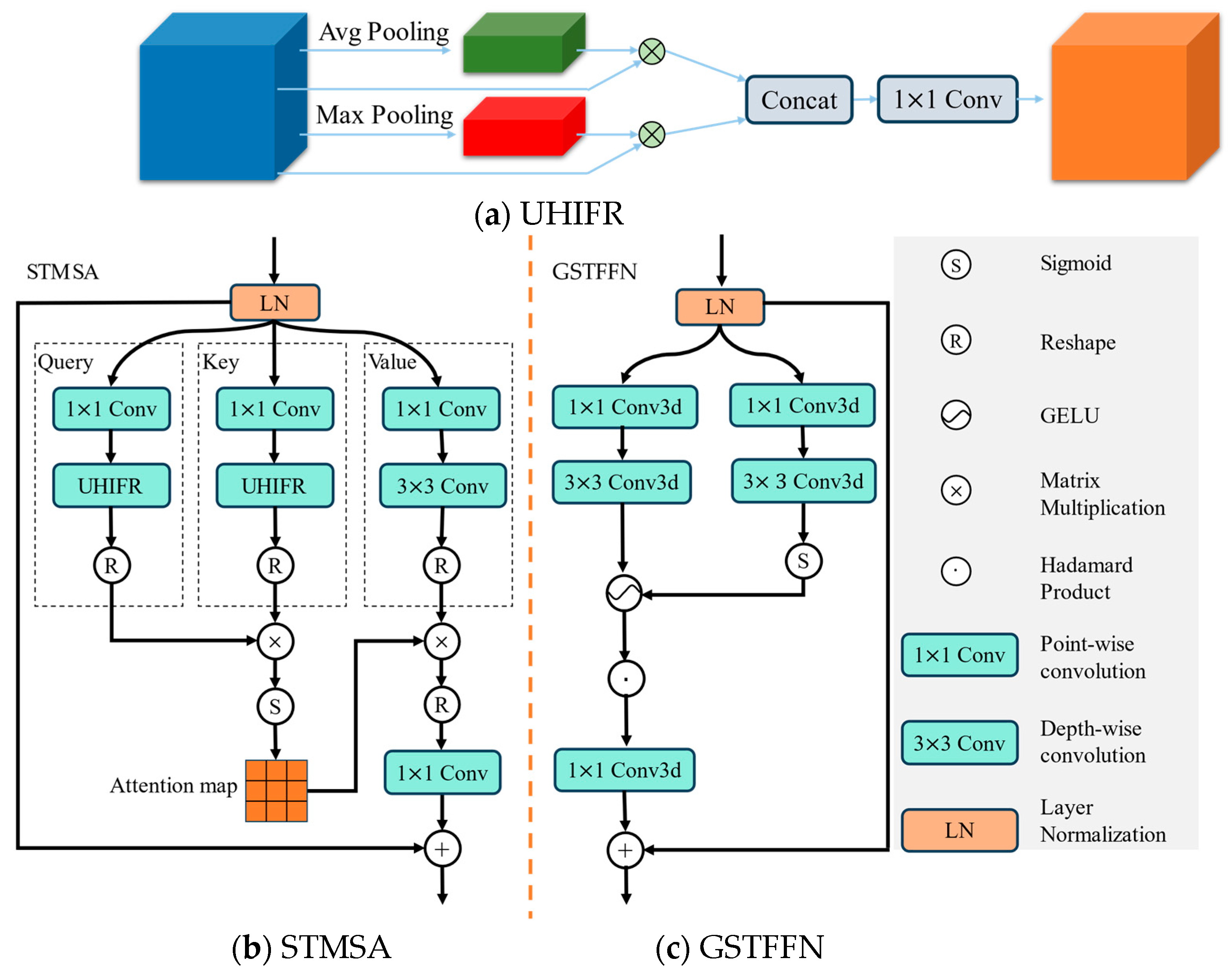
- A component with MaxPool and AvgPool operations [43] is integrated with the attention model which can effectively capture the features of high intensities. At the same time, the GSTFFN strengths the spatial–temporal features. These operations will effectively mitigate the error rates of forecasting higher intensities and longer forecasting times for the proposed model.
- (3)
- Based on the strategy of feature crossing, a cross-channel attention is proposed in the forecaster to effectively simulate the movements of these radar echo sequences.
- (4)
- The forecaster, which is similar to that of the models based on FCN, effectively reduces accumulated errors and improves the forecasting accuracies of longer nowcasting times.
2. Dataset
3. Methods
3.1. Problem Statement
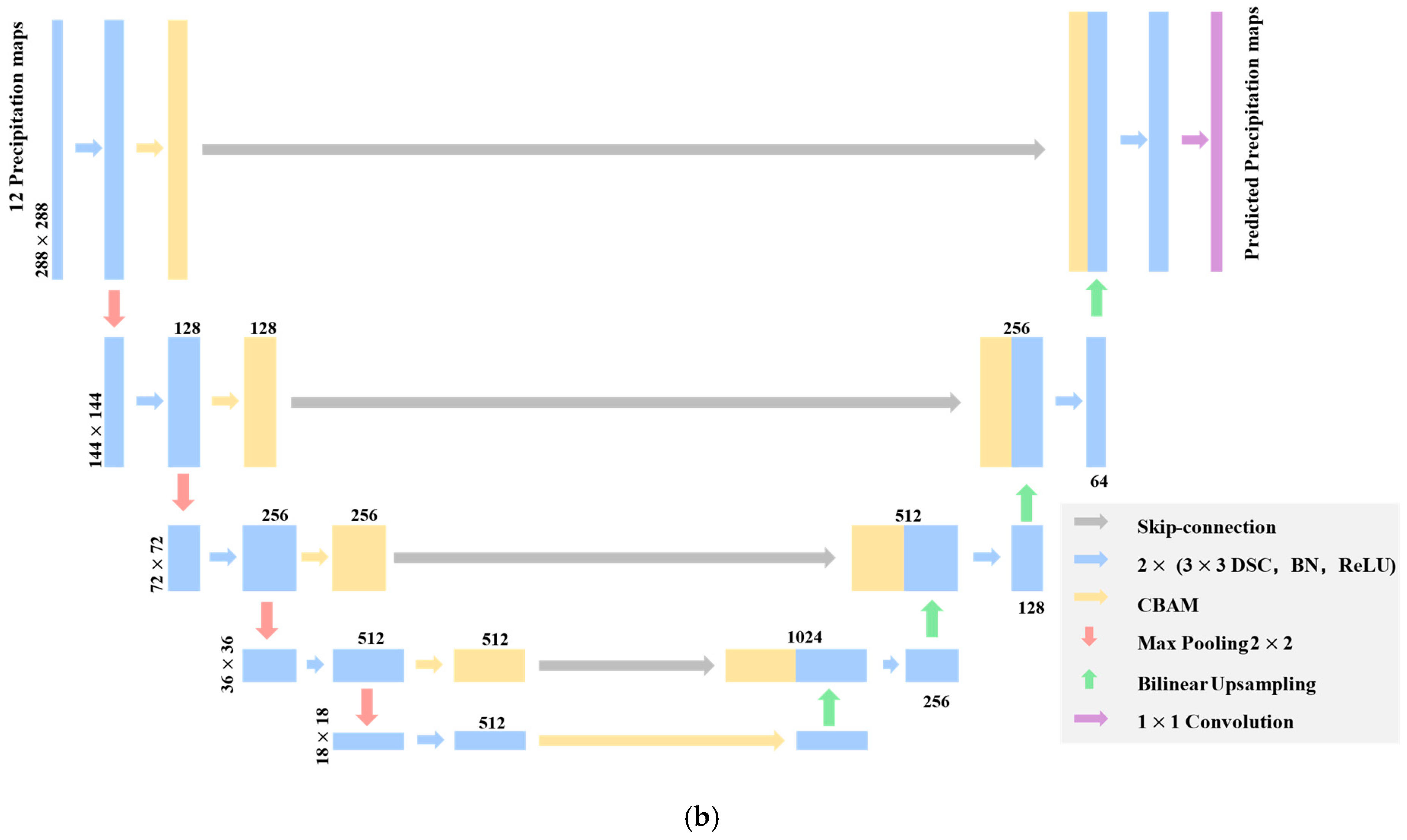
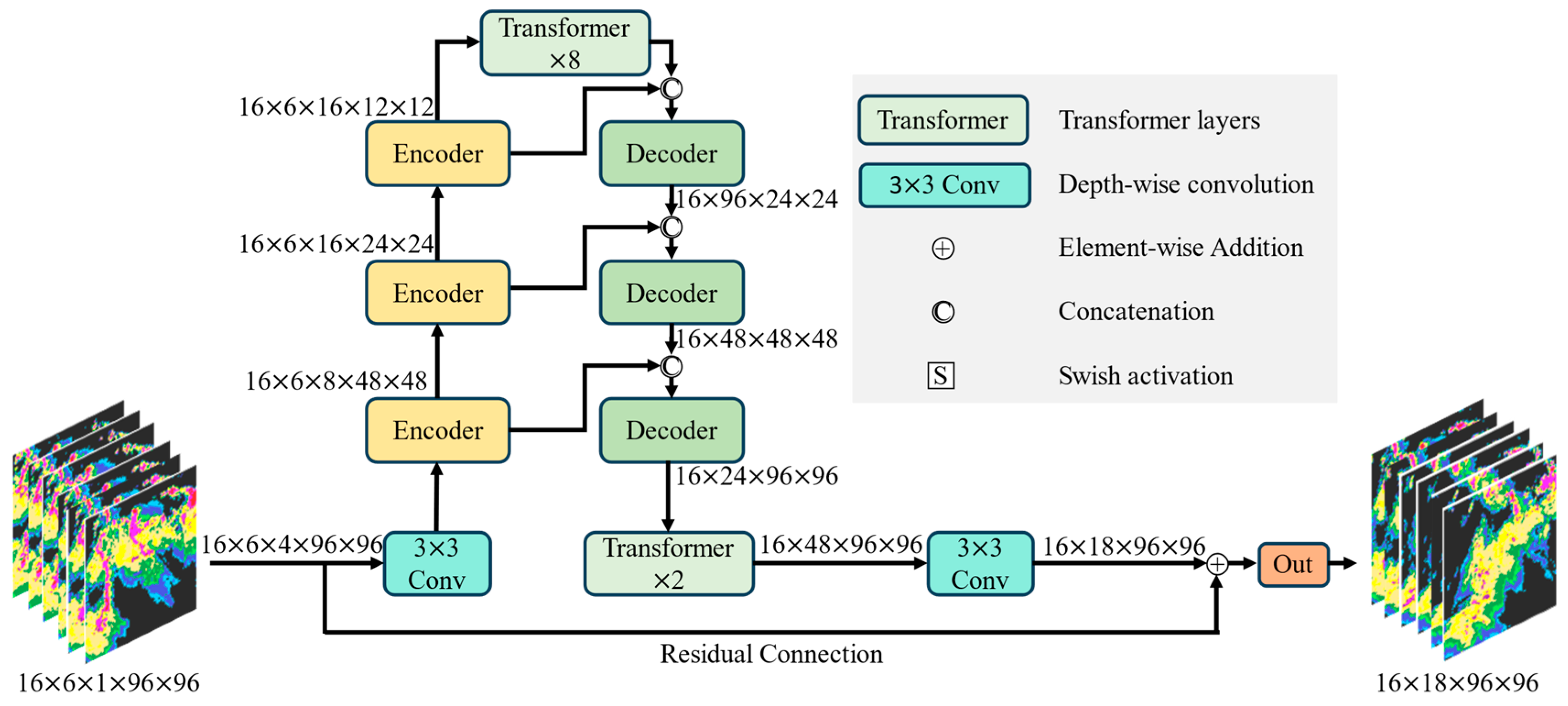
3.2. Network Architecture
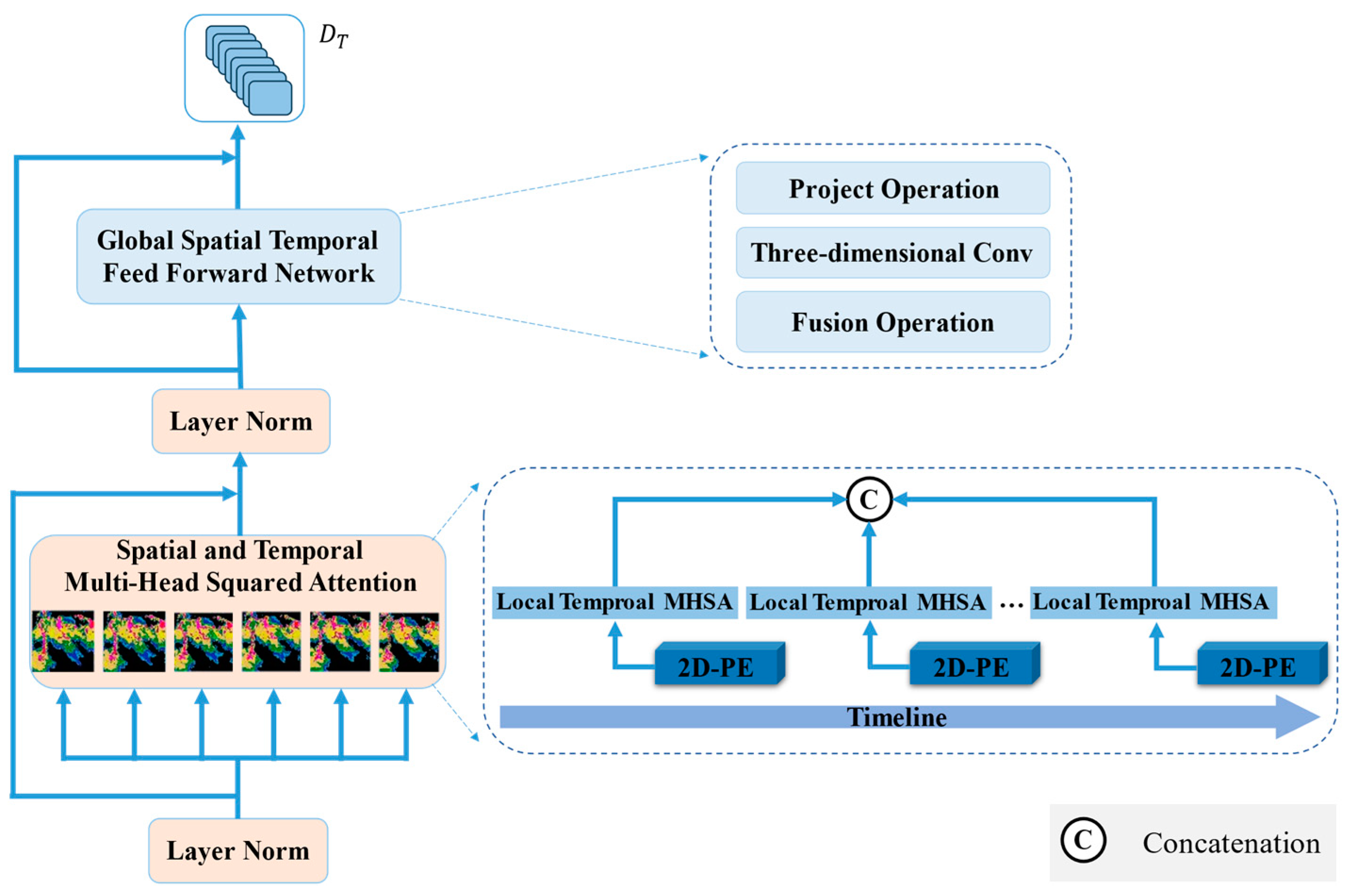
3.3. Spatiotemporal Encoder
3.4. Forecaster
4. Experiment
4.1. Implementation Details
4.2. Evaluation Metrics
4.3. Quantitative Performance
4.4. Visual Performance
5. Summary and Conclusions
- The components of an encoder consisting of STMSA and GSTFFN can effectively capture the global and long-distance spatial–temporal features; furthermore, the UHIFR integrated with STMSA strengthens the ability of model to learn the features of high-intensity pixels.
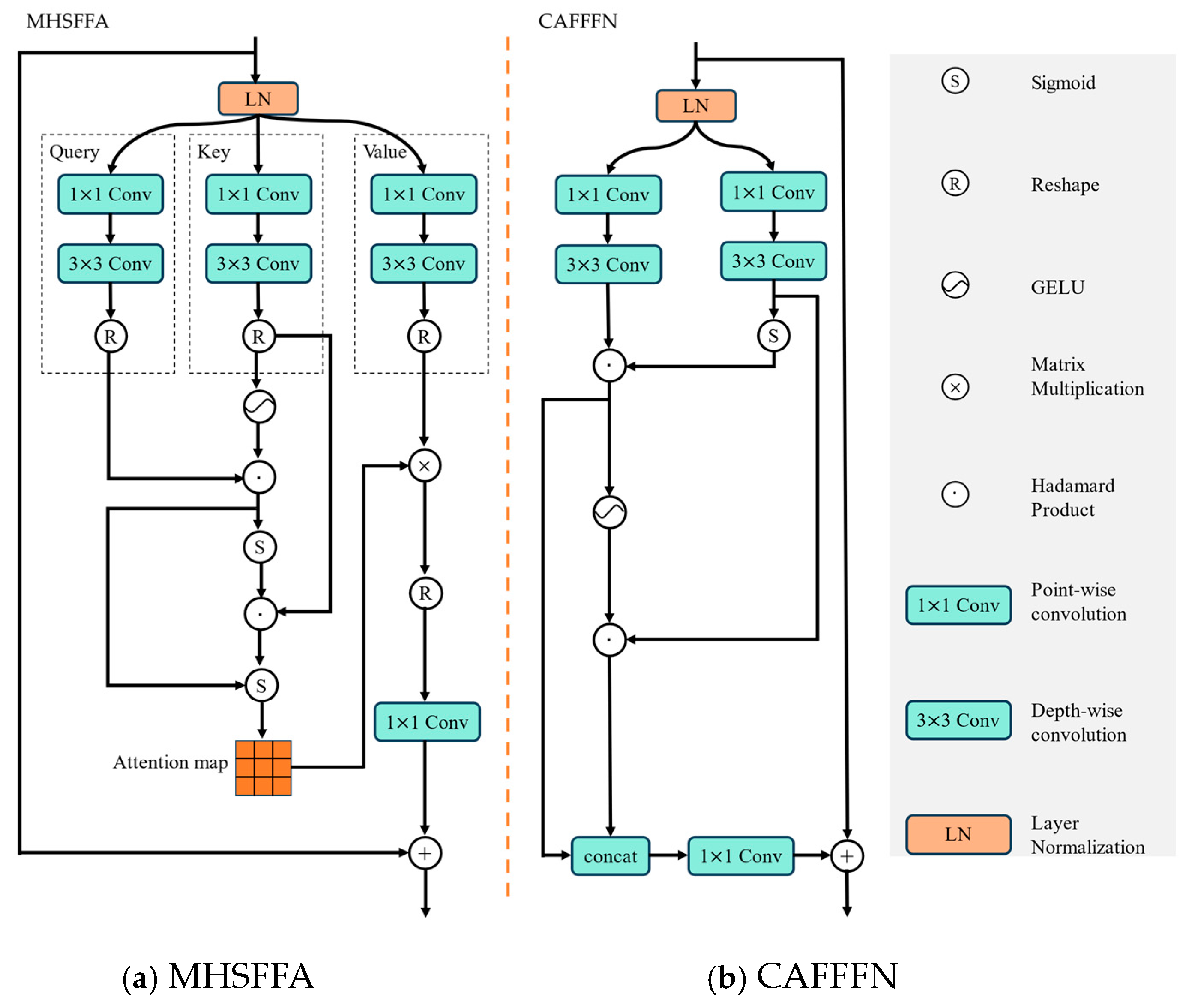
- Based on the cross-feature fusion strategy, the MHSFFA and CAFFFN units in the decoder not only effectively simulate the movements of radar echoes by capturing the interactions of the echo sequences, but also more precisely nowcast the longer time information.
- The quantitative and qualitative experiments demonstrate the effectiveness of the proposed model. In particular, the proposed model obtains better results for higher intensities and longer nowcasting times, which demonstrates that it pays more attention to such intensities and can capture the longer-distance features. The experimental results also demonstrate the superiority of our proposed model in forecasting severe weather and longer times information.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Camporeale, J.E. The challenge of machine learning in space weather: Nowcasting and forecasting. Space Weather 2019, 17, 1166–1207. [Google Scholar] [CrossRef]
- Fang, W.; Shen, L.; Sheng, V.S. VRNet: A Vivid Radar Network for Precipitation Nowcasting. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–11. [Google Scholar] [CrossRef]
- Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.M.; Li, P.W.; Golding, B.; et al. Use of NWP for nowcasting convective precipitation: Recent progress and challenges. Bull. Am. Meteorol. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Reyniers, M. Quantitative Precipitation Forecasts Based on Radar Observations: Principles, Algorithms and Operational Systems; Institut Royal Météorologique de Belgique: Bruxelles, Belgium, 2008. [Google Scholar]
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1987, 273, 287–289. [Google Scholar] [CrossRef]
- Rinehart, R.E. A pattern recognition technique for use with conventional weather radar to determine internal storm motions. Atmos. Technol. 1981, 13, 119–134. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; Volume 39, pp. 770–778. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Deep learning for precipitation nowcasting: A benchmark and a new model. Adv. Neural Inf. Process. Syst. 2017, 30, 5617–5627. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent neural networks for predictive learning using spatiotemporal LSTMs. Adv. Neural Inf. Process. Syst. 2017, 30, 879–888. [Google Scholar]
- Lin, Z.; Li, M.; Zheng, Z.; Cheng, Y.; Yuan, C. Self-attention ConvLSTM for spatiotemporal prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11531–11538. [Google Scholar]
- Xiong, T.; He, J.; Wang, H.; Tang, X.; Shi, Z.; Zeng, Q. Contextual Sa-Attention Convolutional LSTM for Precipitation Nowcasting: A Spatiotemporal Sequence Forecasting View. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12479–12491. [Google Scholar] [CrossRef]
- Tan, C.; Li, S.; Gao, Z.; Guan, W.; Wang, Z.; Liu, Z.; Li, S.Z. OpenSTL: A Comprehensive Benchmark of Spatio-Temporal Predictive Learning. Adv. Neural Inf. Process. Syst. 2023, 36, 69819–69831. [Google Scholar]
- Agrawal, S.; Barrington, L.; Bromberg, C.; Burge, J.; Gazen, C.; Hickey, J. Machine learning for precipitation nowcasting from radar images. arXiv 2019, arXiv:1912.12132. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Toronto, ON, Canada, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Ayzel, G.; Scheffer, T.; Heistermann, M. RainNet v1.0: A convolutional neural network for radar-based precipitation nowcasting. Geosci. Model Dev. 2020, 13, 2631–2644. [Google Scholar] [CrossRef]
- Trebing, K.; Staǹczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Guen, V.L.; Thome, N. Disentangling physical dynamics from unknown factors for unsupervised video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11474–11484. [Google Scholar]
- Li, D.; Deng, K.; Zhang, D.; Liu, Y.; Leng, H.; Yin, F.; Song, J. LPT-QPN: A Lightweight Physics-informed Transformer for Quantitative Precipitation Nowcasting. IEEE Trans. Geosci. Remote Sens. 2023, 61. [Google Scholar] [CrossRef]
- Ritvanen, J.; Harnist, B.; Aldana, M.; Mäkinen, T.; Pulkkinen, S. Advection-free convolutional neural network for convective rainfall nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1654–1667. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, M.; Chen, K.; Xing, L.; Jin, R.; Jordan, M.I.; Wang, J. Skilful nowcasting of extreme precipitation with NowcastNet. Nature 2023, 619, 526–532. [Google Scholar] [CrossRef]
- Tian, L.; Li, X.; Ye, Y.; Xie, P.; Li, Y. A generative adversarial gated recurrent unit model for precipitation nowcasting. IEEE Geosci. Remote Sens. Lett. 2019, 17, 601–605. [Google Scholar] [CrossRef]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Mohamed, S. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef]
- Gong, A.; Li, R.; Pan, B.; Chen, H.; Ni, G.; Chen, M. Enhancing spatial variability representation of radar nowcasting with generative adversarial networks. Remote Sens. 2023, 15, 3306. [Google Scholar] [CrossRef]
- Bai, C.; Sun, F.; Zhang, J.; Song, Y.; Chen, S. Rainformer: Features extraction balanced network for radar-based precipitation nowcasting. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021; p. 11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Dong, X.; Bao, J.; Chen, D.; Zhang, W.; Yu, N.; Yuan, L.; Chen, D.; Guo, B. CSWin Transformer: A General Vision Transformer Backbone with Cross-Shaped Windows. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 12124–12134. [Google Scholar]
- Chen, G.; Jiao, P.; Hu, Q.; Xiao, L.; Ye, Z. SwinSTFM: Remote Sensing Spatiotemporal Fusion Using Swin Transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, L.; Wang, Z.; Li, H. SwinVRNN: A Data-Driven Ensemble Forecasting Model via Learned Distribution Perturbation. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003211. [Google Scholar] [CrossRef]
- Chen, L.; Du, F.; Hu, Y.; Wang, Z.; Wang, F. SwinRDM: Integrate SwinRNN with Diffusion Model towards High-Resolution and High-Quality Weather Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 322–330. [Google Scholar]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhong, X.; Zhang, F.; Cheng, Y.; Xu, Y.; Qi, Y.; Li, H. FuXi: A cascade machine learning forecasting system for 15-day global weather forecast. NPJ Clim. Atmos. Sci. 2023, 6, 190. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, X.; Wang, H.; Zhu, Y.; Wang, Y.B.; Li, M.; Yeung, D.Y. Earthformer: Exploring space-time transformers for earth system forecasting. In Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 25390–25403. [Google Scholar]
- Chen, S.; Shu, T.; Zhao, H.; Zhong, G.; Chen, X. TempEE: Temporal–Spatial Parallel Transformer for Radar Echo Extrapolation Beyond Autoregression. IEEE Trans. Geosci. Remote Sens. 2023, 61. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Y.; Li, Y.; Song, D.; Wei, Z.; Liu, A.A. Hierarchical Transformer with Lightweight Attention for Radar-based Precipitation Nowcasting. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Jin, Q.; Zhang, X.; Xiao, X.; Wang, Y.; Xiang, S.; Pan, C. Preformer: Simple and Efficient Design for Precipitation Nowcasting with Transformers. IEEE Geosci. Remote Sens. Lett. 2023, 21, 1–5. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Veillette, M.S.; Samsi, S.; Mattioli, C.J. SEVIR: AStormEvent Imagery Dataset for Deep Learning Applications in Radar and Satellite Meteorology. Adv. Neural Inf. Process. Syst. 2020, 33, 22009–22019. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. In Proceedings of the 7th International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017; pp. 1–8. [Google Scholar]
- Gao, Z.; Tan, C.; Wu, L.; Li, S.Z. SimVP: Simpler yet Better Video Prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 3160–3170. [Google Scholar]
- Barnes, L.R.; Schultz, D.M.; Gruntfest, E.C.; Hayden, M.H.; Benight, C.C. Corrigendum: False Alarm Rate or False Alarm Ratio? Weather Forecast. 2009, 24, 1452–1454. [Google Scholar] [CrossRef]
- Guo, S.; Sun, N.; Pei, Y.; Li, Q. 3D-UNet-LSTM: A Deep Learning-Based Radar Echo Extrapolation Model for Convective Nowcasting. Remote Sens. 2023, 15, 1529. [Google Scholar] [CrossRef]
- Schaefer, J.T. The Critical Success Index as an Indicator of Warning Skill. Weather Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, H.; Liu, J. MM-RNN: MM-RNN: A Multimodal RNN for Precipitation Nowcasting. IEEE Trans. Geosci. Remote Sens. 2023, 61. [Google Scholar] [CrossRef]
- Gilewski, P. Application of Global Environmental Multiscale (GEM) Numerical Weather Prediction (NWP) Model for Hydrological Modeling in Mountainous Environment. Atmosphere 2022, 13, 1348. [Google Scholar] [CrossRef]
- Yang, S.; Yuan, H. A Customized Multi-Scale Deep Learning Framework for Storm Nowcasting. Geophys. Res. Lett. 2023, 50, e2023GL103979. [Google Scholar] [CrossRef]
- Hu, J.; Yin, B.; Guo, C. METEO-DLNet: Quantitative Precipitation Nowcasting Net Based on Meteorological Features and Deep Learning. Remote Sens. 2024, 16, 1063. [Google Scholar] [CrossRef]



| Items | Training | Validation | Test |
|---|---|---|---|
| Sequences | 35,718 | 9060 | 12,159 |
| Model | Modified Details | Official Configuration | Our Adaptations |
|---|---|---|---|
| SmaAt-UNet | Input length | 12 | 6 |
| Output length | 1 | 18 | |
| ConvLSTM | Loss function | Balanced MSE | MSE |
| Input length | 5 | 6 | |
| Output length | 20 | 18 | |
| SimVP | Input length Output length | 10 | 6 |
| 10 | 18 | ||
| LPT-QPN | Input length | 5 | 6 |
| Output length | 20 | 18 |
| Model | POD | CSI | BIAS | FAR | ||
|---|---|---|---|---|---|---|
| RainNet | 0.3768 | 0.3111 | 0.9050 | 0.6232 | 5.183 | 34.06 |
| SmaAt-UNet | 0.4258 | 0.3432 | 1.1437 | 0.5742 | 5.288 | 34.977 |
| ConvLSTM | 0.3970 | 0.3332 | 0.9357 | 0.6030 | 4.943 | 31.525 |
| LPT-QPN | 0.4257 | 0.3444 | 1.0853 | 0.5743 | 5.111 | 33.56 |
| SimVP | 0.4082 | 0.3452 | 0.9481 | 0.5918 | 4.648 | 30.319 |
| STFFT-WA | 0.4233 | 0.3464 | 1.0378 | 0.5767 | 4.908 | 33.796 |
| STFFT-WM | 0.4181 | 0.3417 | 1.0366 | 0.5819 | 4.889 | 33.796 |
| STFFT | 0.4269 | 0.3522 | 1.0162 | 0.5731 | 4.893 | 32.162 |
| Model | POD-M | POD-16 | POD-74 | POD-133 | POD-160 | POD-181 | POD-219 |
|---|---|---|---|---|---|---|---|
| RainNet | 0.3768 | 0.8953 | 0.7044 | 0.3150 | 0.1731 | 0.1212 | 0.0515 |
| SmaAt-UNet | 0.4258 | 0.8999 | 0.7351 | 0.3881 | 0.2438 | 0.1917 | 0.0964 |
| ConvLSTM | 0.3970 | 0.8800 | 0.7108 | 0.3597 | 0.2128 | 0.1560 | 0.0629 |
| LPT-QPN | 0.4257 | 0.9049 | 0.7489 | 0.4123 | 0.2290 | 0.1684 | 0.0909 |
| SimVP | 0.4082 | 0.8891 | 0.7247 | 0.3705 | 0.2209 | 0.1670 | 0.0771 |
| STFFT-WA | 0.4233 | 0.9087 | 0.7311 | 0.3856 | 0.2257 | 0.1766 | 0.1120 |
| STFFT-WM | 0.4181 | 0.9129 | 0.7404 | 0.3803 | 0.2129 | 0.1638 | 0.0986 |
| STFFT | 0.4269 | 0.9037 | 0.7408 | 0.3817 | 0.2376 | 0.1891 | 0.1085 |
| Model | CSI-M | CSI-16 | CSI-74 | CSI-133 | CSI-160 | CSI-181 | CSI-219 |
|---|---|---|---|---|---|---|---|
| RainNet | 0.3111 | 0.6777 | 0.5984 | 0.2673 | 0.1595 | 0.1145 | 0.0492 |
| SmaAt-UNet | 0.3432 | 0.6891 | 0.6114 | 0.3106 | 0.2068 | 0.1632 | 0.0779 |
| ConvLSTM | 0.3332 | 0.7104 | 0.6131 | 0.2994 | 0.1867 | 0.1371 | 0.0526 |
| LPT-QPN | 0.3444 | 0.6848 | 0.6157 | 0.3227 | 0.2035 | 0.1555 | 0.0844 |
| SimVP | 0.3478 | 0.7109 | 0.6236 | 0.3142 | 0.2038 | 0.1583 | 0.0758 |
| STFFT-WA | 0.3464 | 0.6865 | 0.6173 | 0.3129 | 0.2009 | 0.1611 | 0.0995 |
| STFFT-WM | 0.3417 | 0.6840 | 0.6208 | 0.3108 | 0.1928 | 0.1517 | 0.0904 |
| STFFT | 0.3522 | 0.6957 | 0.6196 | 0.3147 | 0.2121 | 0.1720 | 0.0990 |
| Model | Mean | 5 min | 25 min | 45 min | 65 min | 75 min | 90 min |
|---|---|---|---|---|---|---|---|
| RainNet | 0.4217 | 0.5832 | 0.4621 | 0.4094 | 0.3632 | 0.3311 | 0.3161 |
| SmaAt-UNet | 0.4773 | 0.6321 | 0.5190 | 0.4640 | 0.4145 | 0.3976 | 0.3794 |
| ConvLSTM | 0.4589 | 0.6302 | 0.5105 | 0.4311 | 0.4036 | 0.3911 | 0.3618 |
| LPT-QPN | 0.4867 | 0.6445 | 0.5384 | 0.4774 | 0.4306 | 0.3980 | 0.3659 |
| SimVP | 0.4699 | 0.6370 | 0.5278 | 0.4620 | 0.4010 | 0.3813 | 0.3541 |
| STFFT | 0.5236 | 0.6433 | 0.5563 | 0.5240 | 0.4753 | 0.4571 | 0.4238 |
| Model | Mean | 5 min | 25 min | 45 min | 65 min | 75 min | 90 min |
|---|---|---|---|---|---|---|---|
| RainNet | 0.5108 | 0.6937 | 0.5337 | 0.4905 | 0.4710 | 0.4189 | 0.4040 |
| SmaAt-UNet | 0.5620 | 0.7706 | 0.5841 | 0.5666 | 0.5157 | 0.4840 | 0.4710 |
| ConvLSTM | 0.5378 | 0.7246 | 0.5789 | 0.5248 | 0.5028 | 0.4764 | 0.4272 |
| LPT-QPN | 0.5322 | 0.7529 | 0.5632 | 0.5315 | 0.4830 | 0.4381 | 0.4128 |
| SimVP | 0.5548 | 0.7713 | 0.5659 | 0.5531 | 0.5284 | 0.4995 | 0.4402 |
| STFFT | 0.5783 | 0.7603 | 0.5952 | 0.5630 | 0.5596 | 0.5130 | 0.4918 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, T.; Wang, W.; He, J.; Su, R.; Wang, H.; Hu, J. Spatiotemporal Feature Fusion Transformer for Precipitation Nowcasting via Feature Crossing. Remote Sens. 2024, 16, 2685. https://doi.org/10.3390/rs16142685
Xiong T, Wang W, He J, Su R, Wang H, Hu J. Spatiotemporal Feature Fusion Transformer for Precipitation Nowcasting via Feature Crossing. Remote Sensing. 2024; 16(14):2685. https://doi.org/10.3390/rs16142685
Chicago/Turabian StyleXiong, Taisong, Weiping Wang, Jianxin He, Rui Su, Hao Wang, and Jinrong Hu. 2024. "Spatiotemporal Feature Fusion Transformer for Precipitation Nowcasting via Feature Crossing" Remote Sensing 16, no. 14: 2685. https://doi.org/10.3390/rs16142685
APA StyleXiong, T., Wang, W., He, J., Su, R., Wang, H., & Hu, J. (2024). Spatiotemporal Feature Fusion Transformer for Precipitation Nowcasting via Feature Crossing. Remote Sensing, 16(14), 2685. https://doi.org/10.3390/rs16142685










