Abstract
As an important representative of ancient Chinese cultural heritage, the classification of Terracotta Warriors point cloud data aids in cultural heritage preservation and digital reconstruction. However, these data face challenges such as complex morphological and structural variations, sparsity, and irregularity. This paper proposes a method named Multi-scale Local Geometric Transformer-Mamba (MLGTM) to improve the accuracy and robustness of Terracotta Warriors point cloud classification tasks. To effectively capture the geometric information of point clouds, we introduce local geometric encoding, including local coordinates and feature information, effectively capturing the complex local morphology and structural variations of the Terracotta Warriors and extracting representative local features. Additionally, we propose a multi-scale Transformer-Mamba information aggregation module, which employs a dual-branch Transformer with a Mamba structure and finally aggregates them on multiple scales to effectively handle the sparsity and irregularity of the Terracotta Warriors point cloud data. We conducted experiments on several datasets, including the ModelNet40, ScanObjectNN, ShapeNetPart, ETH, and 3D Terracotta Warriors fragment datasets. The results show that our method significantly improves the classification task of Terracotta Warriors point clouds, demonstrating strong accuracy.
1. Introduction
With the continuous development and popularization of digital technology, 3D point cloud data are increasingly applied in various fields, especially in object recognition [,], scene segmentation [,], pose estimation [,], etc. The Terracotta Warriors, as outstanding representatives of ancient Chinese culture, attract scholars, researchers, and cultural enthusiasts worldwide due to their immense historical and cultural value. With the development of digital technology, the 3D scan data of the Terracotta Warriors are increasing, and how to effectively use these data for classification and analysis has become an urgent problem. Traditional methods for classifying Terracotta Warriors primarily rely on manually designed features and traditional machine learning algorithms, which often require substantial human and time costs and are sensitive to data quality and feature selection, making it difficult to adapt to large-scale and diverse Terracotta Warriors data.
In point cloud classification tasks, traditional methods often use feature extraction and machine learning, implementing classification through manually designed feature extraction operators and classifiers. However, this approach often requires substantial human effort and experience, and it is challenging to fully exploit the features of point cloud data, resulting in low classification accuracy and robustness. Therefore, designing an automated, efficient, and accurate point cloud classification method has become a research hotspot [,,,,].
To address these issues, a series of deep learning methods have emerged in recent years, such as PointNet [], PointNet++ [], DGCNN [], etc. These methods extract features directly from the raw point cloud data through end-to-end learning and use deep neural networks for classification. Although these methods have achieved certain results, they still have problems such as insufficient utilization of local geometric information and inadequate handling of multi-scale information.
With the development of deep learning, the Transformer has become a powerful sequence modeling tool and has achieved significant success in natural language processing. Transformer is capable of extracting global features from the entire point cloud, rather than just local features, which is very helpful for understanding the overall structure of the point cloud. Recently, the Transformer has been successfully applied to images, audio, etc., achieving a series of breakthroughs [,]. However, so far, the application of Transformer in point cloud data processing is still limited and has not fully realized its potential [,,,].
Besides the Transformer, the Mamba model has also been proposed as a powerful sequence modeling tool, achieving certain results in fields such as natural language processing [,,]. The Mamba model can effectively capture long-range dependencies between sequence data and has good sequence modeling capabilities. However, the application of the Mamba model in point cloud data processing is also relatively rare and has not been fully utilized.
To address these issues, this paper proposes a method called Multi-scale Local Geometric Transformer-Mamba (MLGTM) application in the classification task of Terracotta Warriors point clouds. Specifically, we apply the Transformer and Mamba models to the feature extraction and classification process of point cloud data, utilizing their powerful sequence modeling capabilities to achieve global feature modeling and information interaction of point cloud data. At the same time, we combine local geometric encoding methods to fully exploit the local geometric features of point cloud data, improving classification accuracy and robustness.
Local Geometric Encoding:Local geometric encoding includes local coordinate information and local feature information. For each point, we select its surrounding neighboring points as local information and calculate their relative positions with respect to the center point, as well as the attributes of each point and its nearest neighbors. This method effectively captures the complex local morphology and structural variations of the Terracotta Warriors, improving classification accuracy and robustness.
Multi-scale Transformer-Mamba: The multi-scale information interaction module inputs local geometric encoding into a dual-branch Transformer-Mamba network and aggregates multi-scale Transformer and Mamba information to achieve local–local and local–global information interaction. This method effectively improves point cloud classification performance, especially when dealing with the sparsity and irregularity of Terracotta Warriors point cloud data, as well as complex scenes and large-scale data, demonstrating good adaptability and generalization ability.
In the experimental section, we validate our proposed method on several commonly used point cloud datasets, including the ModelNet40, ScanObjectNN, ShapeNetPart, ETH, and 3D Terracotta Warriors fragment datasets. The experimental results show that, compared with traditional classification methods, our method significantly improves classification accuracy and robustness, especially when processing Terracotta Warriors point cloud data.
2. Related Work
Feature Learning-based Methods: Feature learning-based methods aim to use deep learning techniques to learn meaningful feature representations from point cloud data. Traditional point cloud deep learning models, such as those based on PointNet architecture and graph convolutional neural networks, mainly focus on local geometric structures. However, due to the high complexity and unstructured nature of the point cloud data of the Terracotta Warriors, this task is extremely challenging.
To address the issues of time-consuming and labor-intensive traditional, manual-based classification methods application in Terracotta Warriors, which heavily rely on archaeologists’ expertise, Yang et al. [] propose a novel 3D Terracotta Warriors fragment classification framework. At its core is a dual-modal neural network that integrates both geospatial and texture information of the fragments to output their respective categories. Geospatial information is directly extracted from the point cloud, while texture information is extracted using a method based on 3D mesh models and an improved Canny edge detection algorithm.
To address the issue of insufficient accuracy of PointNet++ in point cloud understanding, PointNeXt [] introduces a set of improved training strategies, significantly enhancing the overall accuracy in object classification tasks. Additionally, it incorporates an inverted residual bottleneck design and separable MLPs to achieve efficient and effective model scaling. This algorithm demonstrates superior performance in 3D classification and segmentation tasks.
To address the classification problem of unstructured 3D point clouds, Huang et al. [] proposed a global–local graph attention convolutional neural network method. This method introduces a graph attention convolution module, where the global attention module analyzes spatial relationships between all points, while the local attention module dynamically learns convolution weights of local neighborhood points and reweights the convolution weights based on the density of the local region.
To further improve the robustness of the model, Li et al. [] proposed an innovative point anomaly removal method using the capabilities of downstream classification models. This method draws on tail risk minimization methods in finance, rephrasing the anomaly removal process as an optimization problem.
To better classify the Terracotta Warriors by recognizing facial features, Sheng et al. [] proposed an enhanced SqueezeNet model, replacing the initial convolution kernels and improving the FaceNet backbone feature extraction network. The feature extraction layer of this model is composed of alternating convolution layers, pooling layers, Fire modules, and pooling layers, with the introduction of an exponential function to smooth the shape of the loss function. Finally, Agglomerative Clustering is used for the facial classification of the Terracotta Warriors. This method meets the requirements for facial recognition and classification of the Terracotta Warriors.
Transformer-based Methods: Compared with traditional CNN methods, Transformers can better capture global dependencies among point cloud data, making them suitable for irregular shapes and sparsely distributed point cloud data, which facilitates the handling of the sparse distribution and complex structure of Terracotta Warriors data. Inspired by the success of self-attention networks in natural language processing and image analysis, Zhao et al. [] proposed a self-attention layer for point clouds and used these layers to construct self-attention networks for semantic scene segmentation, object part segmentation, and object classification tasks.
To address the issue of low accuracy in traditional Terracotta Warriors classification, Liu et al. [] propose an attention-based multi-scale neural network named AMS-Net. This network includes a multi-scale set abstraction block (MS-BLOCK) and a fully connected (FC) layer. The MS-BLOCK consists of a local–global layer (LGLayer) and an improved multi-layer perceptron (IMLP). Using a multi-scale strategy, LGLayer can simultaneously extract local and global features from different scales. IMLP concatenates high-level and low-level features for classification tasks. The results demonstrate that this method achieves high accuracy in classifying Terracotta Warriors fragments.
To address the issues of location information leakage and uneven information density in point cloud self-supervised learning, Point-MAE [] proposes a neat masked autoencoding scheme for point cloud self-supervised learning. The specific method involves dividing the input point cloud into irregular point patches and randomly masking them at a high ratio. Then, a standard Transformer-based autoencoder learns high-level latent features from the unmasked point patches, aiming to reconstruct the masked point patches. The results show that this method is efficient during the pre-training phase and generalizes well to various downstream tasks, improving the state-of-the-art accuracy in classification tasks by 1.5%–2.3%.
To address the problem of generalizing the concept of Masked Point Modeling (MPM) to 3D point clouds, Point-BERT [] pre-trains point cloud Transformers by designing an MPM task. Specifically, the method involves dividing the point cloud into local patches, generating discrete point tokens through a discrete Variational AutoEncoder (dVAE), and randomly masking some of the input point cloud patches. These masked patches are then fed into the backbone Transformer with the goal of recovering the original point tokens at the masked locations under the supervision of the tokenizer-generated point tokens. The results show that this pre-training strategy significantly enhances the performance of standard point cloud Transformers, achieving high accuracy on ModelNet40 and ScanObjectNN, demonstrating good transferability and advancements in point cloud classification tasks.
Due to the irregularity and disorder of point clouds, adopting a 3D Transformer to improve point cloud processing brings significant computational and memory costs. To address this issue, Lu et al. [] proposed a hierarchical framework combining convolution and Transformer for point cloud classification. This method combines the powerful local feature learning capabilities of convolution with the excellent global context modeling capabilities of Transformer. The main module of this method operates on downsampled point sets, with each module including a multi-scale local feature aggregation block and a global feature learning block implemented through graph convolution and Transformer, respectively.
Unlike most existing methods focusing on local spatial attention, PointConT [] leverages the locality of points in feature space, clustering sampling points with similar features into the same category and computing self-attention within each category to balance capturing long-range dependencies and computational complexity. Additionally, an Inception feature aggregator for point cloud classification uses a parallel structure to aggregate high-frequency and low-frequency information in each branch.
For the feature learning difficulties caused by the irregularity and disorder of point clouds, Zhou et al. [] proposed a hierarchical local–global framework based on Transformer networks. This method uses two parallel branches in the local feature extraction module: the Transformer branch and the shared multi-layer perceptron branch, designed to learn the related features between any two points and the local high-dimensional semantic features between sampling center points and their neighborhoods. The global feature extraction module consists of a center point contact module and a global point cloud Transformer layer, improving the effectiveness of global feature extraction without increasing parameters and computation.
Mamba-based Methods: Inspired by the success of the Mamba model in achieving fast inference and linear sequence length extension, recent research has extended it to 3D point cloud tasks [,]. The Transformer has become a fundamental architecture in point cloud analysis tasks due to its excellent global modeling capabilities, but its attention mechanism has quadratic complexity, making it challenging to scale to long sequence modeling. To address this issue, Liang et al. [] proposed the PointMamba framework, aiming to improve point cloud analysis tasks through global modeling and linear complexity. This method embeds point patches as input and proposes a reordering strategy to provide a more logical geometric scan order to enhance the global modeling capabilities of the SSM. The reordered point tokens are sent to a series of Mamba modules to gradually capture the point cloud structure.
To more effectively process 3D point cloud data, Zhang et al. [] proposed a consistent traversal serialization method that converts the point cloud into a 1D point sequence while ensuring that neighboring points in the sequence are also adjacent in space. This method generates six variants by arranging the x, y, and z coordinates in different orders. To better handle point sequences with different orders, point hints are introduced to inform the Mamba sequence’s arrangement rules, combined with position encoding based on spatial coordinate mapping, to better inject positional information into the point cloud sequence.
Although SSM performs well in language and image fields with linear complexity and long sequence modeling capabilities, extending it to point cloud fields is not easy due to the unordered and irregular nature of point clouds and the causality requirement of SSM. To build causal dependencies, Liu et al. [] proposed an octree-based sorting strategy, operating on the original irregular points, performing global sorting by z-order while maintaining spatial adjacency.
Inspired by feature learning for irregular, complex spatial structures; the generalization ability of Transformer learning methods for different scenarios; and the success of the Mamba model in achieving fast inference and linear sequence length extension, we propose a Multi-Scale Local Geometric Transformer-Mamba point cloud classification method.
3. Methods
This paper proposes a Multi-Scale Local Geometric Transformer-Mamba (MLGTM) method application in the classification of Terracotta Warriors point clouds. The overall network structure proposed in this paper is shown in Figure 1. The MLGTM mainly includes two innovations: local geometric encoding and multi-scale information interaction module. The MLGTM network structure proposed is shown in Figure 2.
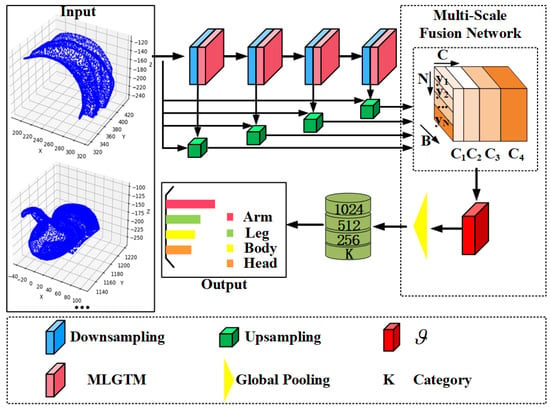
Figure 1.
The overall network structure ( is multi-scale aggregation function).
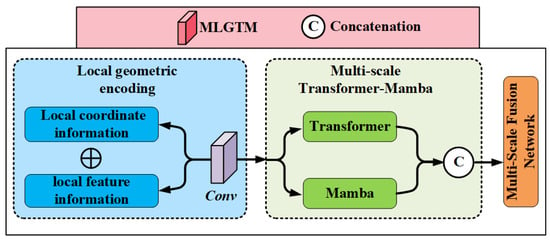
Figure 2.
The MLGTM structure.
3.1. Local Geometric Encoding
Local geometric encoding includes both the local coordinate information and local feature information of the points. Local coordinate information represents the relative position relationship of points concerning their nearest neighbors, while local feature information represents the feature attributes of the points and its nearest neighbors themselves. This method effectively captures the complex local morphology and structural variations of the Terracotta Warriors, improving classification accuracy and robustness. Details of local geometric encoding are shown in Figure 3.
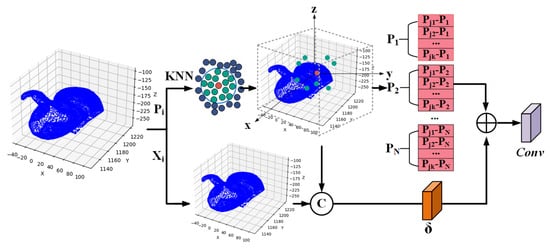
Figure 3.
Details of local geometric encoding ( represents each point in the point cloud; represents the coordinates of each point).
The local feature information are used as the basis for local geometric point cloud feature encoding. The specific function is shown as follows:
where represents the neighboring points of the i-th point in the point cloud, selected using the KNN function. This ensures that we select the k points closest to , forming a local region. is the local geometric feature function, which is a graph convolution function used to encode the coordinate features of a point and its neighboring points.
After processing the local feature information and aggregating them with the local coordinate information, the specific function is shown as follows:
where [;] represents the vector concatenation operation. represents the convolution operation. represents the relative positions of neighboring points with respect to the central point , reflecting the spatial relationships between points.
In a word, the concatenation operation combines the local feature information with the local coordinate information , while the convolution operation further learns features from this concatenated information, capturing the geometric structure of point within its local neighborhood.
3.2. Multi-Scale Information Interaction Module
The multi-scale information interaction module combines Transformer and Mamba to achieve feature fusion of local geometric encoding and global information interaction. Specifically, we first input the local geometric encoding into a dual-branch Transformer-Mamba network, where one branch is the Transformer and the other branch is Mamba. Then, we fuse the outputs of the two branches and finally aggregate the multi-scale Transformer and Mamba information to achieve local–local and local–global information interaction. The details of Mamba are shown in Figure 4.
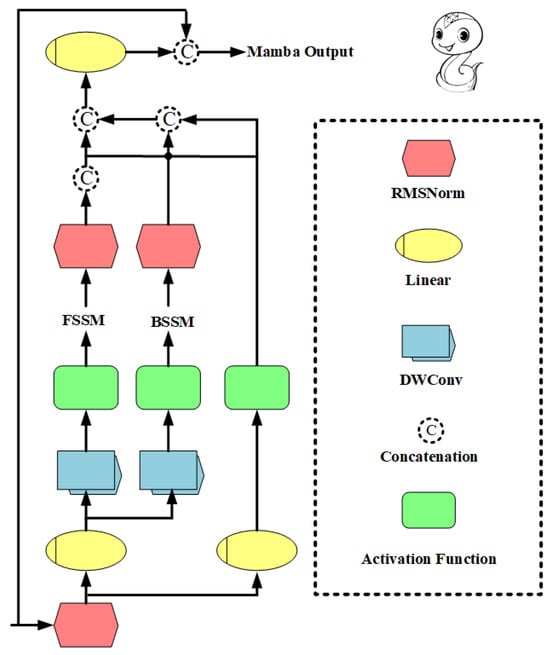
Figure 4.
Details of Mamba (FSSM: Forward State Space Model; BSSM: Backward State Space Model).
Transformer: To handle sparse and irregular point cloud data and promote local and global information interaction, we use Transformer to capture long-range dependencies and global features in the data, independent of the local structure of the data. The expression is as follows:
where ⊙ represents the Hadamard product, used to apply attention weights to features. By using the generated attention weights , the features of neighboring point are weighted and fused, resulting in the updated representation of local features .
Mamba: The Mamba model, after normalization, Semantic Similarity Measure (SSM), and depthwise separable convolution, is expressed as follows:
where represents the concatenation operation and represents the output features of the Mamba module. Merge the forward and backward semantic similarity features and , and perform feature mapping and transformation using a multi-layer perceptron (MLP) to generate the final output feature of the Mamba module. The expression of and are as follows:
where represents root mean square normalization, represents Forward State Space Model, represents Backward State Space Model, represents the activation function, and represents depthwise separable convolution, which extracts and process spatial information from features. represents the features before SSM input and its expression is as follows:
where is the output of local geometric encoding. The SSM is used to process features for extracting global semantic information.
Finally, the outputs of Transformer and Mamba are fused, and the expression is as follows:
where represents the output of Transformer-Mamba information fusion and m represents the number of network layers.
Multi-Scale Fusion Network: To further capture the details and global information of the object, thereby improving the overall performance of the model, we use a multi-scale fusion network to process features of different scales.
where represent features at different scales. is a multi-scale aggregation function that takes features from different scales as inputs and merges them into a unified feature representation. is output of multi-scale fusion network.
Multi-Scale Information Interaction Module effectively addresses the sparsity and irregularity of Terracotta Warriors point cloud data, as well as the challenges posed by complex scenes and large-scale data. It demonstrates good adaptability and generalization ability.
4. Experiments
4.1. Dataset, Implementation Details, and Evaluation Metrics
Dataset: In this section, we evaluated the proposed Multi-Scale Local Geometric Transformer-Mamba (MLGTM) model on multiple datasets to validate its performance and generalization ability. Below is a brief overview of the main datasets used in the experiments:
ModelNet40: ModelNet40 [] is a 3D model classification dataset consisting of CAD models, containing 40 categories of models from common object categories such as chairs, tables, airplanes, etc.
ScanObjectNN: ScanObjectNN [] is a real-world 3D scanning dataset containing 15 object categories, with multiple scan sequences per category, totaling approximately 1500 scan sequences.
ShapeNetPart dataset: ShapeNetPart [] is a dataset for object part segmentation, containing 16 object categories, each with multiple models and corresponding part annotations, totaling approximately 16881 point cloud models.
ETH: The core of the ETH [] dataset consists of 3D laser point clouds, primarily composed of vegetation (trees, gazebo, shrubs, etc.). The only structured element is a small paved path that runs through the forest. The scanner path starts in the forest, continues with approximately 12 scans, and then merges into the path.
Three-Dimensional Terracotta Warriors fragment dataset: The 3D Terracotta Warriors fragment dataset is specifically designed for Terracotta Warriors point cloud processing. The point cloud models of the Terracotta Warriors fragments were obtained using the Artec EVA 3D Scanner handheld 3D scanner. This dataset includes point cloud models from different parts of the Terracotta Warriors, covering various poses and details. In this experiment, we extracted 11,996 point cloud fragments from 40 complete Terracotta Warriors to train the network. For the Terracotta Warriors fragment dataset, there are four categories: Arm, Body, Head, and Leg. Among them, 10,144 fragments are used for training (Arm: 2656, Body: 2720, Head: 2272, Leg: 2496) and the remaining 1852 for testing (test Arm: 476, test Body: 504, test Head: 428, test Leg: 444).
Implementation Details: To ensure fairness in the experiments, we used consistent settings for training, testing, and validation hyperparameters across each dataset. We adopt the Stochastic Gradient Descent (SGD) method, and the SGD optimizer trains for 350 epochs. The initial learning rate of the SGD optimizer is set to 0.01, the weight decay is 0.0002, and the dropout rate is set to 0.5. The batch size for all training models is set to 32. Additionally, we implemented the proposed algorithm using the PyTorch language and deployed it for training on a system with an Nvidia RTX 4090, Intel(R) Core(TM) i7-13700KF CPU @ 3.40 GHz, and 128 GB RAM running Windows 10.
Evaluation Metrics: In the experiments, we used metrics such as mean accuracy within each category (mAcc), overall accuracy (OA), mean class Intersection over Union (mcIoU), mean instance Intersection over Union (mIoU), Parameter, FLOPs, and Throughput to evaluate the effectiveness of the algorithm. The detailed definitions of Parameter, FLOPs, and Throughput are as follows.
Parameter: The Parameter refers to the total number of trainable weights and biases in a model. It determines the model’s complexity and expressive power. Assuming represents all model parameters, and denotes the number of parameters in the i-th layer of the network, Parameter is defined as
FLOPs: FLOPs (Floating Point Operations Per Second) refers to the total number of floating-point operations executed by a model during one forward and backward pass. It reflects the computational complexity of the model. Assuming that represents the number of operations in each layer i, the total FLOPs is defined as
Throughput: Throughput refers to the amount of data processed by a model per unit of time, measured in this study as the number of point cloud fragments processed per second. Throughput reflects the operational efficiency of the model in practice. Assuming the model processes N samples in T seconds, the throughput is defined as
4.2. Classification Based on ModelNet40 Dataset
We evaluated the performance of the proposed model algorithm on the ModelNet40 dataset using the mean accuracy within each category (mAcc) and the overall accuracy (OA) across all categories. Additionally, we compared the proposed algorithm with other state-of-the-art algorithms on the ModelNet40 dataset, such as PointNet [], PointCNN [], PointNet++ [], DGCNN [], PointNeXt [], Point-MAE [], Point-BERT [], OctFormer [], PCM [], and PointMamba []. Figure 5 shows visualizations for the ModelNet40 dataset.

Figure 5.
Classification visualization of ModelNet40 dataset.
From Table 1, it can be seen that the proposed algorithm not only achieves significant improvements in accuracy on the ModelNet40 dataset compared with other outstanding algorithms but also exhibits greater efficiency. Additionally, compared to the PCM, OctFormer, and Point-BERT algorithms, we have increased the overall accuracy by 0.8, 1.1, and 0.7, respectively.

Table 1.
Classification results of ModelNet40 dataset (1K P represents 1024 point cloud).
4.3. Classification Based on ScanObjectNN Dataset
We continue to evaluate the performance of the proposed model algorithm on the ScanObjectNN dataset using mAcc and OA. Additionally, we compare the proposed algorithm with other state-of-the-art algorithms on the ScanObjectNN dataset, such as PointNet, PointCNN, PointNet++, DGCNN, Point-MAE, Point-BERT, TNPC [], and PointMamba.
From Table 2, it can be observed that the proposed algorithm achieves significant improvements in accuracy on the ScanObjectNN dataset compared to other outstanding algorithms. Additionally, compared to the PointMamba, TNPC, and Point-BERT algorithms, we have increased the overall accuracy by 1.3, 4.8, and 3.1, respectively.

Table 2.
Classification results of ScanObjectNN dataset.
4.4. Part Segmentation
We use the mean class Intersection over Union (mcIoU) and mean instance Intersection over Union (mIoU) to evaluate the performance of the proposed model algorithm on the ShapeNetPart dataset. Additionally, we compare the proposed algorithm with other state-of-the-art algorithms on the ShapeNetPart dataset, such as PointNet, PointCNN, PointNet++, DGCNN, PointNeXt, Point-MAE, 3DGTN [], MNAT-Net [], and PointMamba.
From Table 3, it is evident that the proposed algorithm achieves significant improvements in accuracy on the ScanObjectNN dataset compared to other outstanding algorithms. Additionally, compared to the PointMamba, Point-MAE, and PointNeXt algorithms, we have increased the mIoU by 0.9, 0.8, and 0.2, respectively.

Table 3.
Part segmentation results of ShapeNetPart dataset.
4.5. ETH Dataset
To validate the performance of our proposed algorithm in complex scenes such as forests and gazebos, we conducted experiments using the ETH dataset. We evaluated the model algorithm’s performance on the ETH dataset using Overall Accuracy (OA). Additionally, we compared our proposed algorithm with other algorithms on this dataset, such as PointNet and DGCNN. Figure 6 depicts the classification visualization results.

Figure 6.
Classification visualization of ETH dataset.
From Table 4, it can be seen that the proposed algorithm achieves significant improvements in accuracy on the ETH dataset. Additionally, compared to the PointNet and DGCNN algorithms, our overall accuracy improved by 8.08 and 0.67, respectively. Figure 6 depict the classification of gazebos in summer and dynamic settings, as well as tree classification in summer and autumn. It is evident that our proposed algorithm performs well in complex structures and scenes, demonstrating good accuracy.

Table 4.
Classification results of ETH dataset.
4.6. Cultural Heritage Dataset
Unlike the previous datasets, to validate the performance of the model algorithm on cultural heritage data, we conducted experiments using the 3D Terracotta Warriors fragment dataset. We used the overall accuracy (OA) to evaluate the performance of the proposed model algorithm on the Terracotta Warriors fragment dataset. Additionally, we compared the proposed algorithm with other outstanding algorithms on this dataset, such as PointNet, DGCNN [], Yang et al. [], AMS-Net [], and UMA-Net []. Figure 7 shows visualizations for the 3D Terracotta Warriors fragment dataset.
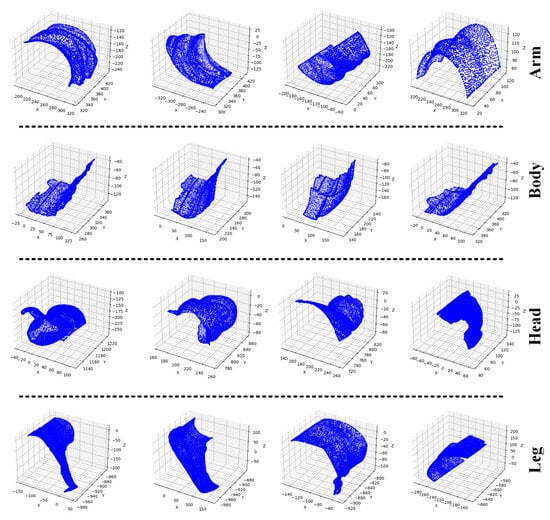
Figure 7.
Classification visualization of 3D Terracotta Warriors fragments dataset.
From Table 5, it can be seen that the proposed algorithm not only achieves significant improvements in accuracy on the 3D Terracotta Warriors fragment dataset compared to other outstanding algorithms but also exhibits greater efficiency. Additionally, compared to UMA-Net, AMS-Net, and PointNet algorithms, we have increased the overall accuracy by 2.03, 0.25, and 7.0, respectively.

Table 5.
Classification results of 3D Terracotta Warriors fragment dataset (“P” represents point cloud; “Supervised” represents whether it is a supervised type).
4.7. Ablation Study
To validate the effectiveness of our proposed method and the contributions of each module, we designed and conducted ablation experiments on the ModelNet40 dataset. By gradually removing key components in the modules, we were able to assess the impact of each part on overall performance. These experiments aim to demonstrate the importance of local geometric encoding, the feature extraction modules (Mamba and Transformer), and the contribution of multi-scale analysis to point cloud classification tasks.
In Table 6, Feature infor. represents feature information only; Coordinate infor. represents coordinate information only; and F+C represents both feature and coordinate information, utilizing the local geometric encoding method. Mamba only represents Mamba operation only; Transformer only represents Transformer operation only; and M+T represents both Transformer and Mamba operations, utilizing the dual-branch Transformer-Mamba network. Multi-scale refers to the Multi-Scale Fusion Network. It can be observed that in the comparison of Local Geometric Encoding, F+C outperforms feature information only or coordinate information only. This indicates that local geometric encoding effectively captures the complex local morphology and structural variations of the Terracotta Warriors, extracting representative local features. In the comparison of Feature decisions, M+T performs better than Mamba only or Transformer only. Regarding multi-scale analysis, the multi-scale model outperforms the non-multi-scale model. This demonstrates that the multi-scale information interaction module exhibits superior performance in handling the sparsity and irregularity of Terracotta Warriors point cloud data, as well as in complex scenes and large-scale data scenarios.

Table 6.
Ablation study of Local Geometric Encoding, Feature decisions, and Multi-Scale Fusion Network (infor.: information, F+C: both feature and coordinate information, M+T: both Transformer and Mamba operations, M-S: Multi-scale fusion network).
Number of Neighbors: For the experiment on the number of nearest neighbors: Under uniform parameter settings, all networks were trained using 1k points as input points. For the ModelNet40 dataset, this paper randomly selected a series of representative numbers of nearest neighbors ranging from 8 to 40 for comparative testing experiments, with results shown in Table 7. For the ScanObjectNN dataset, this paper randomly selected a series of representative numbers of nearest neighbors ranging from 16 to 40 for comparative testing experiments, with results shown in Table 8.

Table 7.
Ablation study of different nearest neighbors k in ModelNet40 dataset.

Table 8.
Ablation study of different nearest neighbors k in ScanObjectNN dataset.
From Table 7 and Table 8, it can be observed that when the number of nearest neighbors k is 24, the model demonstrates better performance. As the number of nearest neighbors decreases within a certain range, the visual perception field is also limited, leading to a decrease in performance. However, when the number of neighbors reaches a certain level, with an increase in the nearest neighbors, adjacent local information also gets incorporated, leading to a decline in performance.
4.8. Robustness Study
In order to evaluate the robustness of the proposed model, we conducted point cloud density and noise test experiments on the ModelNet40 dataset.
For point cloud density and noise experiment, under the premise of unified parameter settings, the neighborhood size is set to k = 24. To test the influence of point cloud density, a series of points were deleted randomly during the test. In this paper, a series of points from 128 to 1024 were selected randomly. The scatter diagram is shown in Figure 8. For noise testing, we introduce additional Gaussian noise based on the standard deviation of the point cloud radius. The point cloud density and noise experiment results are shown in Figure 9.
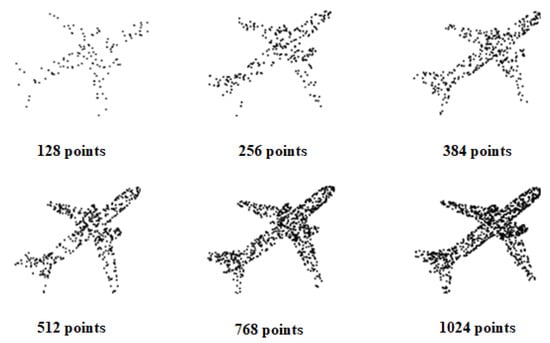
Figure 8.
The point cloud is randomly sampled as a simplified model of 128 points, 256 points, 384 points, 512 points, 768 points, and 1024 points.
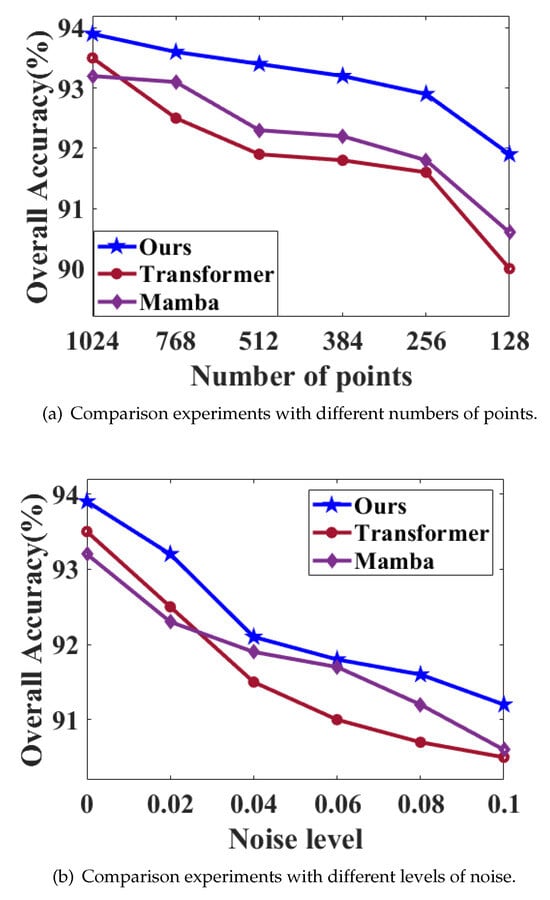
Figure 9.
Robustness test on ModelNet40 for classification.
It can be seen from Figure 9 that, compared with other structural models, the model proposed has better robustness in point cloud experiments.
5. Conclusions
This paper proposes a novel Multi-Scale Local Geometry Transformer-Mamba (MLGTM) model application in the classification task of Terracotta Warriors point clouds. By integrating local geometry encoding, Transformer, and Mamba models, we achieve efficient feature extraction and multi-scale information interaction for point cloud data, thereby improving the accuracy and robustness of the classification task. In terms of local geometry encoding, we introduce a new feature extraction method that captures the local geometry information of point cloud data through the nearest neighbor method and encodes it into two parts: local coordinate information and local feature information. This method not only effectively captures the geometric features of point cloud data but also preserves the local structural information of the point cloud data, particularly adapting well to the complex morphological and structural variations of Terracotta Warriors. Regarding the multi-scale information interaction module, we combine the Transformer and Mamba models, utilizing their powerful sequence modeling capabilities to achieve multi-scale information interaction for point cloud data. The Transformer model realizes global interaction through self-attention mechanisms, while the Mamba model achieves local–global interaction through long-range dependency modeling. Their combination fully explores the feature information of point cloud data, demonstrating strong adaptability and generalization capabilities in handling the sparsity and irregularity of Terracotta Warriors point clouds.
Through the above methods, we conduct experimental verification on multiple public datasets and compare them with existing methods. The experimental results show that our method achieves significant performance improvement in the classification task of Terracotta Warriors point clouds, validating the effectiveness and validity of the method.
Author Contributions
Conceptualization, P.Z., Y.W. and L.A.; methodology, L.A. and Y.W.; resources, L.A. and G.G.; writing—original draft preparation, P.Z. and L.A.; writing—review and editing, G.G. and L.A.; visualization, L.A. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Laboratory Project of the Ministry of Culture and Tourism: 1222000812, crrt2021K01; National Social Science and Art Major Project: 24ZD10; The National Natural Science Foundation of China: 62271393; Xi’an Science and Technology Plan Project: 2024JH-CXSF-0014; Shaanxi Provincial Natural Science Foundation: 2024GX-YBXM-555; and the National key research and development plan: 2020YFC1523301, 2020YFC1523303.
Data Availability Statement
Restrictions apply to the availability of these data. The datasets were accessed on 2 November 2021. They can be found at the following links: http://modelnet.cs.princeton.edu/ (2 November 2021), https://www.shapenet.org/ (2 November 2021), https://projects.asl.ethz.ch/datasets/doku.php?id=laserregistration:laserregistration (2 March 2024), and https://hkust-vgd.github.io/scanobjectnn/ (2 November 2021).
Acknowledgments
The authors want to thank Stanford University for providing the experimental datasets. We also thank Emperor Qinshihuang’s Mausoleum Site Museum for providing the Terracotta Warriors data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lu, B.; Sun, Y.; Yang, Z.; Song, R.; Jiang, H.; Liu, Y. HRNet: 3D object detection network for point cloud with hierarchical refinement. Pattern Recognit. 2024, 149, 110254. [Google Scholar] [CrossRef]
- Dong, J.; Cong, Y.; Sun, G.; Wang, L.; Lyu, L.; Li, J.; Konukoglu, E. Inor-net: Incremental 3-d object recognition network for point cloud representation. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 6955–6967. [Google Scholar] [CrossRef]
- Han, X.; Liu, C.; Zhou, Y.; Tan, K.; Dong, Z.; Yang, B. WHU-Urban3D: An urban scene LiDAR point cloud dataset for semantic instance segmentation. ISPRS J. Photogramm. Remote Sens. 2024, 209, 500–513. [Google Scholar] [CrossRef]
- Xu, Y.; Tang, W.; Zeng, Z.; Wu, W.; Wan, J.; Guo, H.; Xie, Z. NeiEA-NET: Semantic segmentation of large-scale point cloud scene via neighbor enhancement and aggregation. Int. J. Appl. Earth Obs. Geoinf. 2023, 119, 103285. [Google Scholar] [CrossRef]
- Dang, Z.; Wang, L.; Guo, Y.; Salzmann, M. Match normalization: Learning-based point cloud registration for 6d object pose estimation in the real world. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4489–4503. [Google Scholar] [CrossRef]
- Zhuang, C.; Li, S.; Ding, H. Instance segmentation based 6D pose estimation of industrial objects using point clouds for robotic bin-picking. Robot. Comput.-Integr. Manuf. 2023, 82, 102541. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Li, J.; Zhao, Z.; Chen, G.; Liu, A.; Heng, P.A. Pointpatchmix: Point cloud mixing with patch scoring. Proc. AAAI Conf. Artif. Intell. 2024, 38, 5686–5694. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Yu, L.; Tian, S.; Ning, X.; Rodrigues, J. PointGT: A Method for Point-Cloud Classification and Segmentation Based on Local Geometric Transformation. IEEE Trans. Multimed. 2024, 26, 8052–8062. [Google Scholar] [CrossRef]
- Wen, C.; Long, J.; Yu, B.; Tao, D. PointWavelet: Learning in Spectral Domain for 3-D Point Cloud Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2024; early access. [Google Scholar] [CrossRef]
- Xu, J.; Ma, X.; Zhang, L.; Zhang, B.; Chen, T. Push-and-Pull: A General Training Framework with Differential Augmentor for Domain Generalized Point Cloud Classification. IEEE Trans. Circuits Syst. Video Technol. 2024; early access. [Google Scholar] [CrossRef]
- Wang, Z.; Rao, Y.; Yu, X.; Zhou, J.; Lu, J. Point-to-Pixel Prompting for Point Cloud Analysis With Pre-Trained Image Models. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4381–4397. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017. Available online: https://proceedings.neurips.cc/paper/2017/hash/d8bf84be3800d12f74d8b05e9b89836f-Abstract.html (accessed on 6 August 2024).
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. (TOG) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Brehmer, J.; De Haan, P.; Behrends, S.; Cohen, T.S. Geometric Algebra Transformer. Adv. Neural Inf. Process. Syst. 2024. Available online: https://proceedings.neurips.cc/paper_files/paper/2023/hash/6f6dd92b03ff9be7468a6104611c9187-Abstract-Conference.html (accessed on 6 August 2024).
- Hassani, A.; Walton, S.; Li, J.; Li, S.; Shi, H. Neighborhood attention transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 6185–6194. [Google Scholar]
- An, L.; Zhou, P.; Zhou, M.; Wang, Y.; Zhang, Q. PointTr: Low-Overlap Point Cloud Registration With Transformer. IEEE Sens. J. 2024, 24, 12795–12805. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, P.; Geng, G.; An, L.; Li, K.; Li, R. Neighborhood Multi-compound Transformer for point cloud registration. IEEE Trans. Circuits Syst. Video Technol. 2024; early access. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, P.; Geng, G.; An, L.; Liu, Y. CCAG: End-to-End Point Cloud Registration. IEEE Robot. Autom. Lett. 2023, 9, 435–442. [Google Scholar] [CrossRef]
- Sun, J.; Qing, C.; Tan, J.; Xu, X. Superpoint transformer for 3d scene instance segmentation. Proc. AAAI Conf. Artif. Intell. 2023, 37, 2393–2401. [Google Scholar] [CrossRef]
- Lieber, O.; Lenz, B.; Bata, H.; Cohen, G.; Osin, J.; Dalmedigos, I.; Safahi, E.; Meirom, S.; Belinkov, Y.; Shalev-Shwartz, S.; et al. Jamba: A hybrid transformer-mamba language model. arXiv 2024, arXiv:2403.19887. [Google Scholar]
- Xing, Z.; Ye, T.; Yang, Y.; Liu, G.; Zhu, L. Segmamba: Long-range sequential modeling mamba for 3d medical image segmentation. arXiv 2024, arXiv:2401.13560. [Google Scholar]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision mamba: Efficient visual representation learning with bidirectional state space model. arXiv 2024, arXiv:2401.09417. [Google Scholar]
- Yang, K.; Cao, X.; Geng, G.; Li, K.; Zhou, M. Classification of 3D terracotta warriors fragments based on geospatial and texture information. J. Vis. 2021, 24, 251–259. [Google Scholar] [CrossRef]
- Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.; Elhoseiny, M.; Ghanem, B. Pointnext: Revisiting pointnet++ with improved training and scaling strategies. Adv. Neural Inf. Process. Syst. 2022, 35, 23192–23204. [Google Scholar]
- Huang, C.Q.; Jiang, F.; Huang, Q.H.; Wang, X.Z.; Han, Z.M.; Huang, W.Y. Dual-Graph Attention Convolution Network for 3-D Point Cloud Classification. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 4813–4825. [Google Scholar] [CrossRef]
- Li, X.; Lu, J.; Ding, H.; Sun, C.; Zhou, J.T.; Chee, Y.M. PointCVaR: Risk-Optimized Outlier Removal for Robust 3D Point Cloud Classification. Proc. AAAI Conf. Artif. Intell. 2024, 38, 21340–21348. [Google Scholar] [CrossRef]
- Sheng, Y. Facial Recognition and Classification of Terracotta Warriors in the Mausoleum of the First Emperor Using Deep Learning. ISPRS Ann.Photogramm. Remote Sens. Spat. Inf. Sci. 2024, 10, 205–212. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 16259–16268. [Google Scholar]
- Liu, J.; Cao, X.; Zhang, P.; Xu, X.; Liu, Y.; Geng, G.; Zhao, F.; Li, K.; Zhou, M. AMS-Net: An attention-based multi-scale network for classification of 3D terracotta warrior fragments. Remote Sens. 2021, 13, 3713. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, W.; Tay, F.E.; Liu, W.; Tian, Y.; Yuan, L. Masked autoencoders for point cloud self-supervised learning. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2022; pp. 604–621. [Google Scholar]
- Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-bert: Pre-training 3d point cloud transformers with masked point modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 19313–19322. [Google Scholar]
- Lu, D.; Xie, Q.; Gao, K.; Xu, L.; Li, J. 3DCTN: 3D Convolution-Transformer Network for Point Cloud Classification. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24854–24865. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, B.; Lv, Y.; Li, L.; Wang, F.Y. Point cloud classification using content-based transformer via clustering in feature space. IEEE/CAA J. Autom. Sin. 2023, 11, 231–239. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, Y.; Xiao, Y.; Min, X.; Yi, J. TNPC: Transformer-based network for point cloud classification. Expert Syst. Appl. 2024, 239, 122438. [Google Scholar] [CrossRef]
- Li, Y.; Yang, W.; Fei, B. 3DMambaComplete: Exploring Structured State Space Model for Point Cloud Completion. arXiv 2024, arXiv:2404.07106. [Google Scholar]
- Han, X.; Tang, Y.; Wang, Z.; Li, X. Mamba3D: Enhancing Local Features for 3D Point Cloud Analysis via State Space Model. arXiv 2024, arXiv:2404.14966. [Google Scholar]
- Liang, D.; Zhou, X.; Wang, X.; Zhu, X.; Xu, W.; Zou, Z.; Ye, X.; Bai, X. PointMamba: A Simple State Space Model for Point Cloud Analysis. arXiv 2024, arXiv:2402.10739. [Google Scholar]
- Zhang, T.; Li, X.; Yuan, H.; Ji, S.; Yan, S. Point Could Mamba: Point Cloud Learning via State Space Model. arXiv 2024, arXiv:2403.00762. [Google Scholar]
- Liu, J.; Yu, R.; Wang, Y.; Zheng, Y.; Deng, T.; Ye, W.; Wang, H. Point mamba: A novel point cloud backbone based on state space model with octree-based ordering strategy. arXiv 2024, arXiv:2403.06467. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Uy, M.A.; Pham, Q.H.; Hua, B.S.; Nguyen, T.; Yeung, S.K. Revisiting point cloud classification: A new benchmark dataset and classification model on real-world data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1588–1597. [Google Scholar]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.C.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A scalable active framework for region annotation in 3d shape collections. ACM Trans. Graph. (TOG) 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Pomerleau, F.; Liu, M.; Colas, F.; Siegwart, R. Challenging data sets for point cloud registration algorithms. Int. J. Robot. Res. 2012, 31, 1705–1711. [Google Scholar] [CrossRef]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. Adv. Neural Inf. Process. Syst. 2018. Available online: https://proceedings.neurips.cc/paper/2018/hash/f5f8590cd58a54e94377e6ae2eded4d9-Abstract.html (accessed on 6 August 2024).
- Wang, P.S. Octformer: Octree-based transformers for 3d point clouds. ACM Trans. Graph. (TOG) 2023, 42, 1–11. [Google Scholar] [CrossRef]
- Lu, D.; Gao, K.; Xie, Q.; Xu, L.; Li, J. 3DGTN: 3-D Dual-Attention GLocal Transformer Network for Point Cloud Classification and Segmentation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5406912. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, Y. MNAT-Net: Multi-Scale Neighborhood Aggregation Transformer Network for Point Cloud Classification and Segmentation. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9153–9167. [Google Scholar] [CrossRef]
- Liu, J.; Tian, Y.; Geng, G.; Wang, H.; Song, D.; Li, K.; Zhou, M.; Cao, X. UMA-Net: An unsupervised representation learning network for 3D point cloud classification. J. Opt. Soc. Am. A 2022, 39, 1085–1094. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).