Pyramid Cascaded Convolutional Neural Network with Graph Convolution for Hyperspectral Image Classification
Abstract
1. Introduction
2. Related Work
2.1. Convolutional Neural Network
2.2. Graph Convolutional Network
2.3. CNN and GCN for HSI Classifications
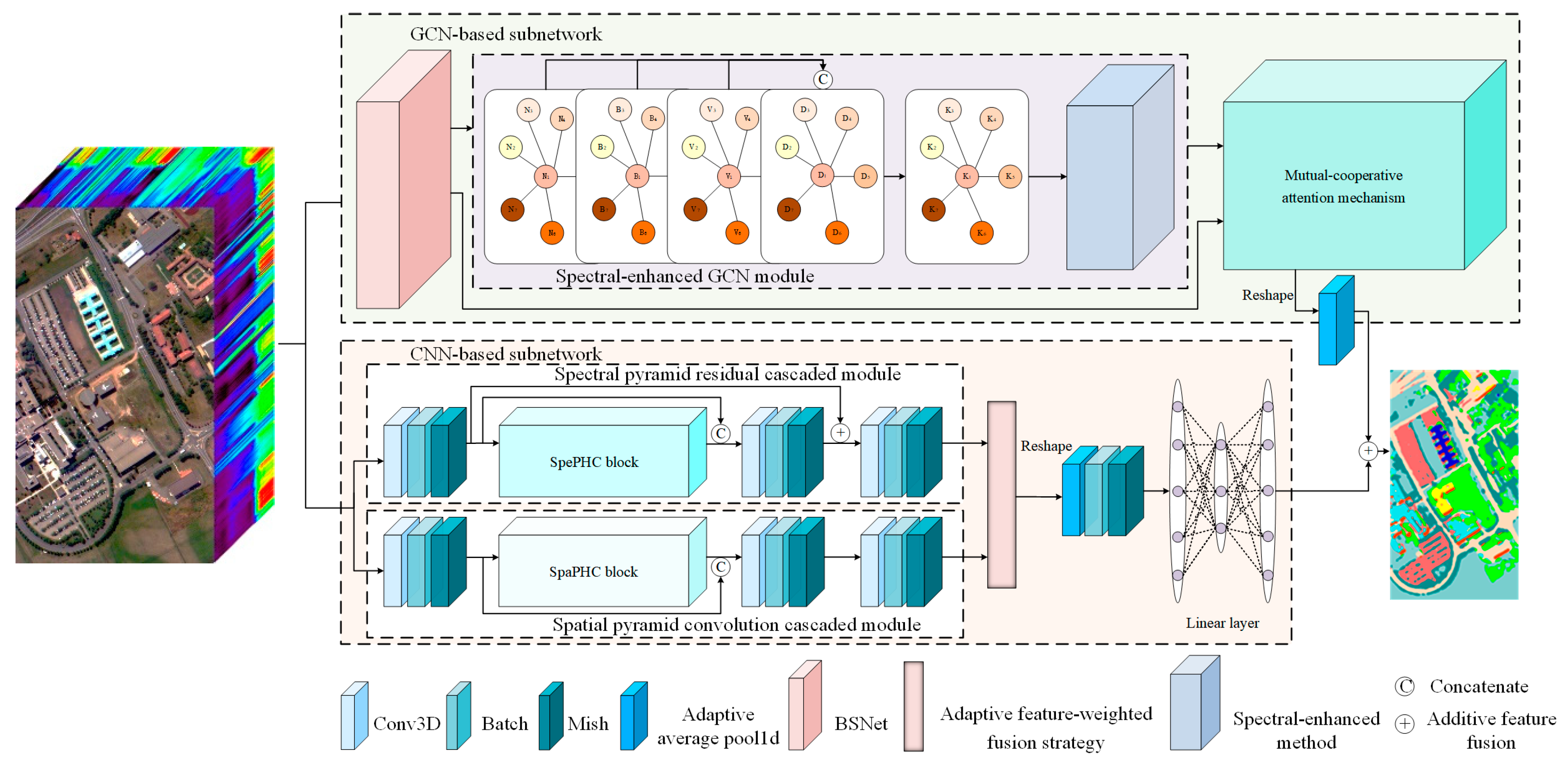
3. Methods
3.1. The Overall Structure of PCCGC
3.2. Adaptive Feature-Weighted Feature Fusion Based SpePRCM and SpaPCCM
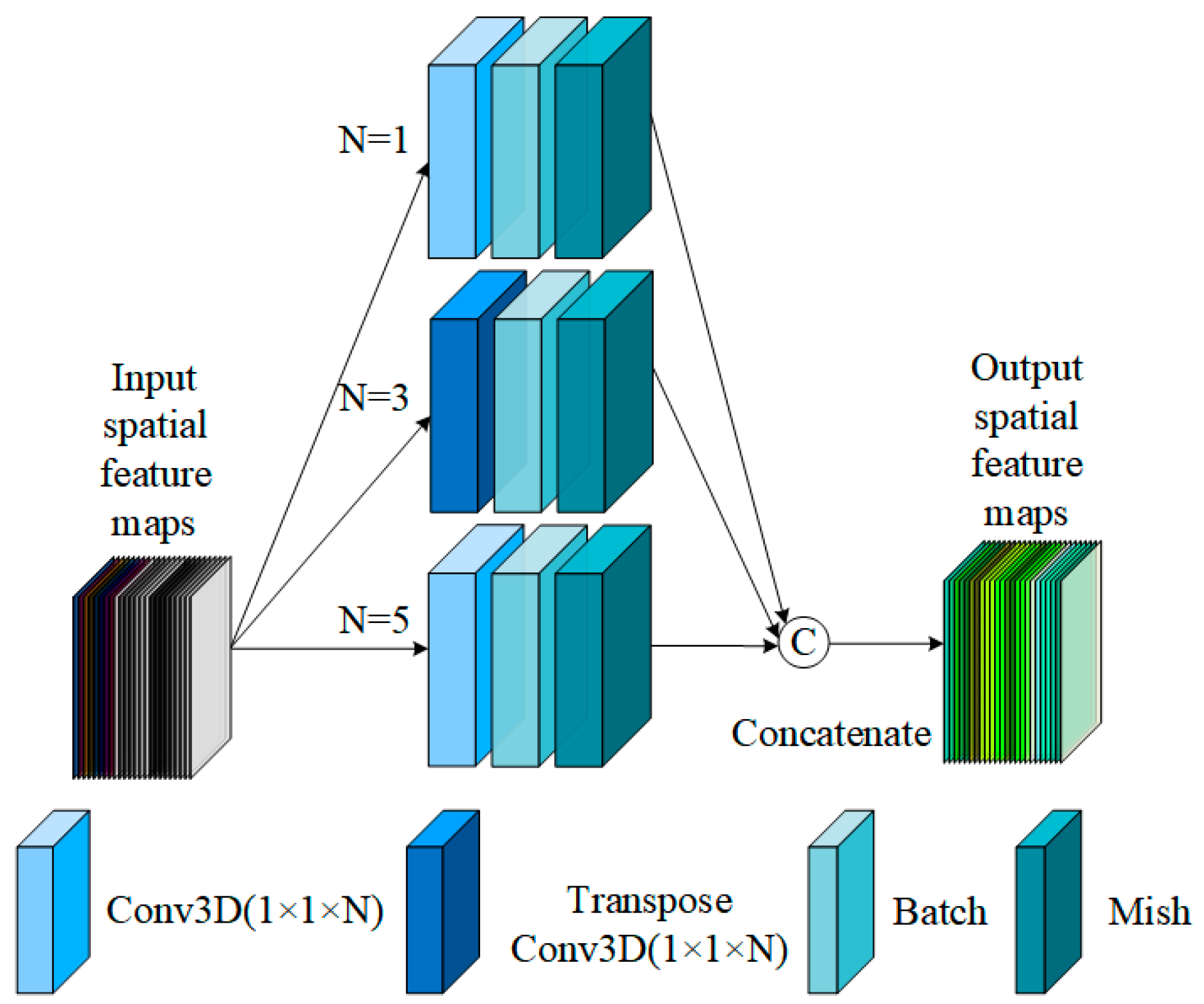
3.2.1. Spectral Pyramid Hybrid Convolution Block
3.2.2. Spatial Pyramid Hybrid Convolution Block
3.2.3. The Multiscale Spectral and Spatial Feature Extraction of SpePRCM and SpaPCCM
3.2.4. The Multiscale Spectral and Spatial Feature Fusion with the Adaptive Feature-Weighted Fusion Strategy
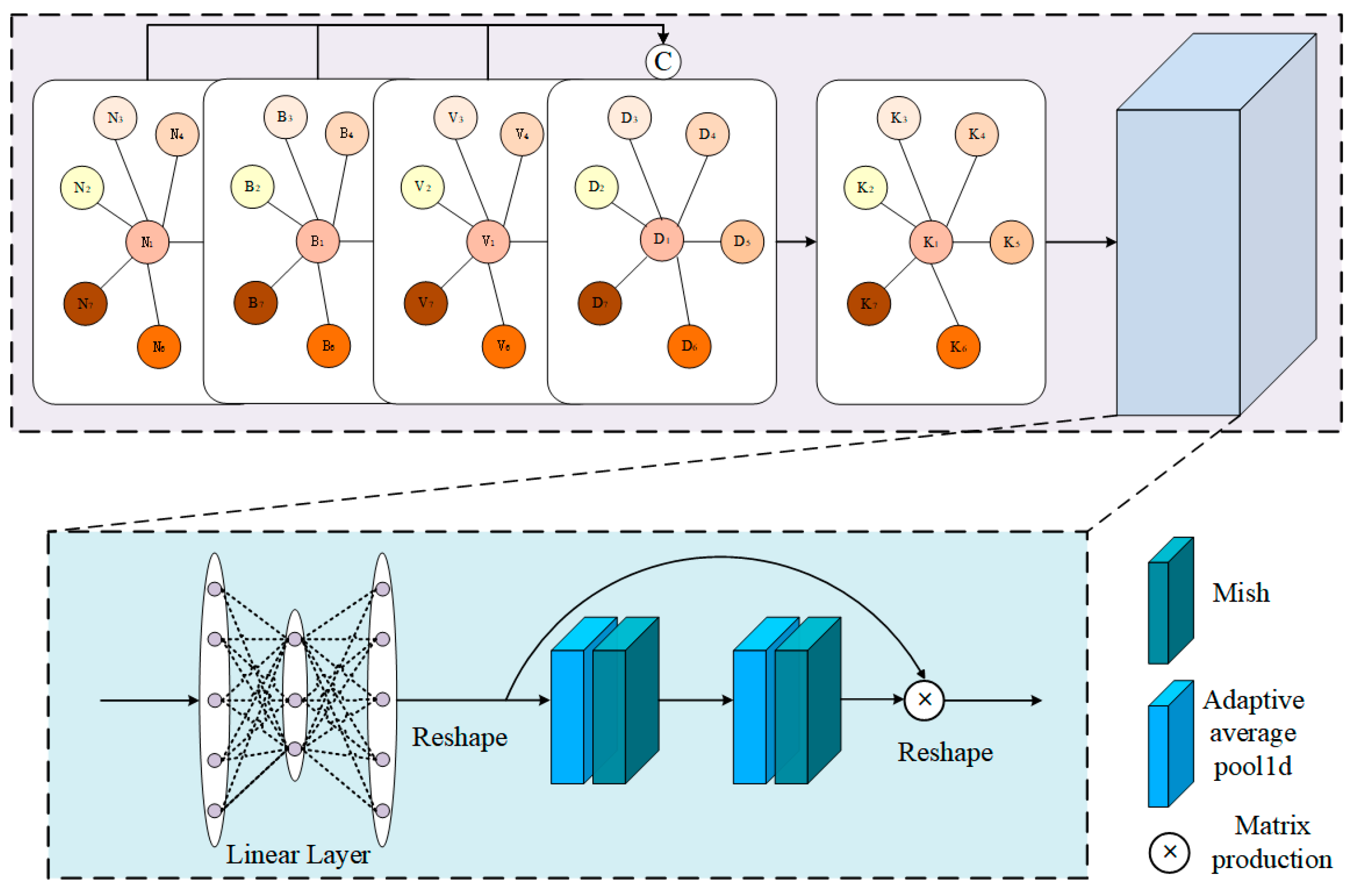
3.3. Spectral-Enhanced GCN Module
3.4. Mutual-Cooperative Attention Mechanism
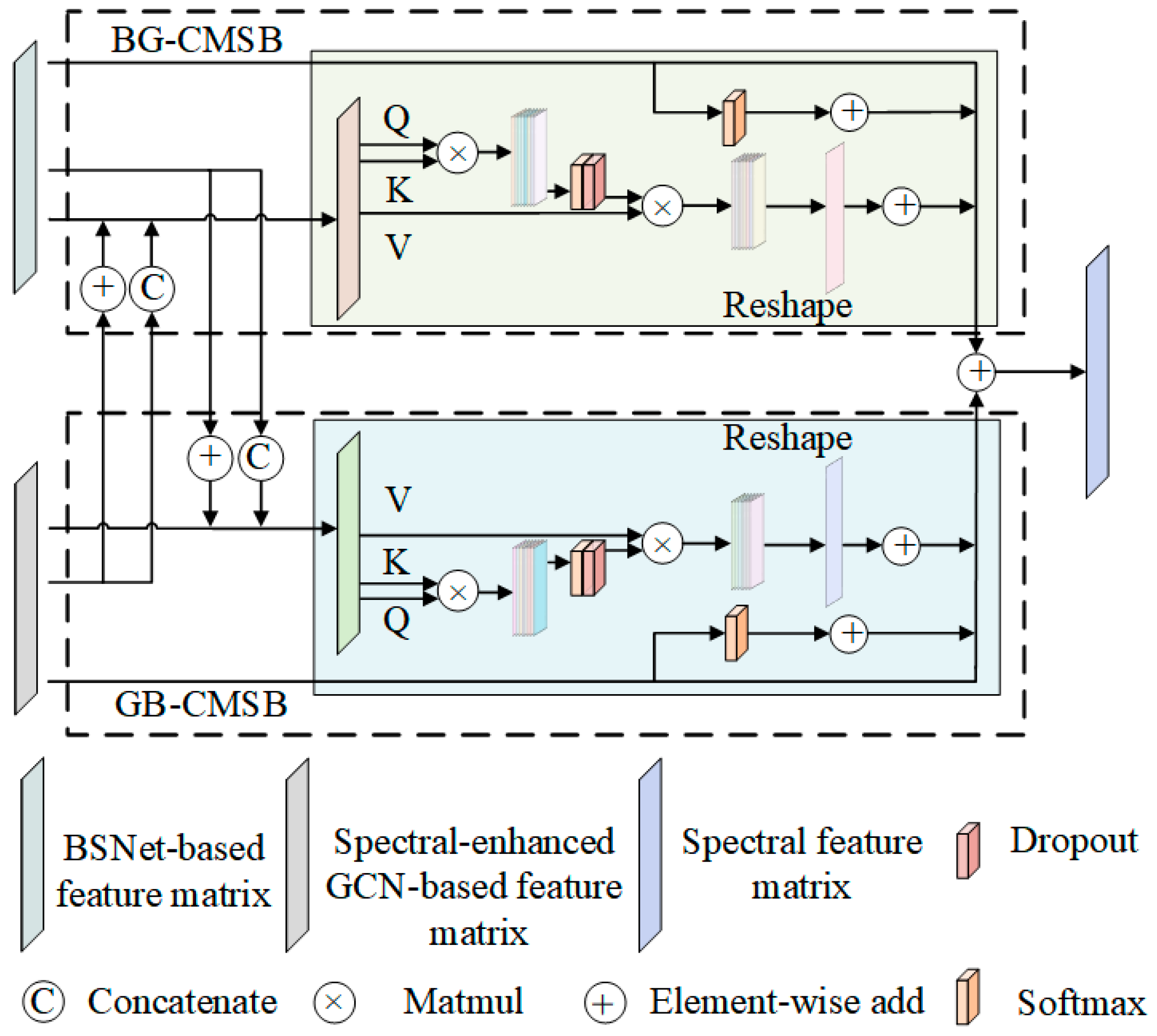
3.4.1. BS-Based Feature Matrix to GCN-Based Feature Matrix Cross Multi-Head Self-Attention Block
3.4.2. GCN-Based Feature Matrix to BS-Based Feature Matrix Cross Multi-Head Self-Attention Block
3.5. Additive Feature Fusion Based on CNN-Based Subnetworks and GCN-Based Subnetworks
4. Experiments
4.1. Experimental Datasets
4.2. Experimental Setting
4.2.1. The Details of Experiment Implementation
4.2.2. The Fourteen State-of-the-Art Comparison Methods
4.3. Experimental Results
5. Discussion
5.1. The Importance of an Adaptive Feature-Weighted Strategy in Feature Fusion
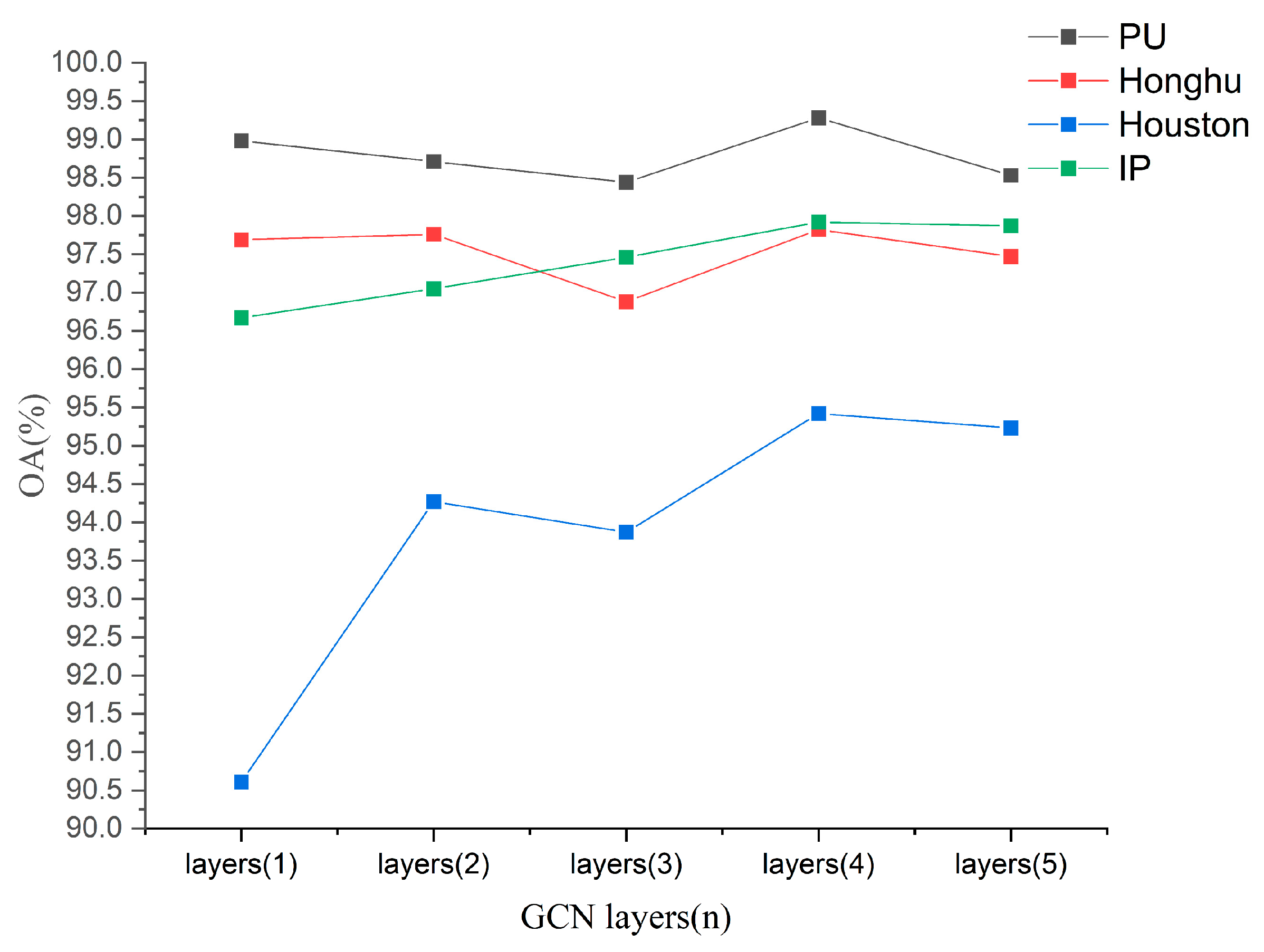
5.2. The Value of n in n-Layer GCN of the Spectral-Enhanced GCN Module
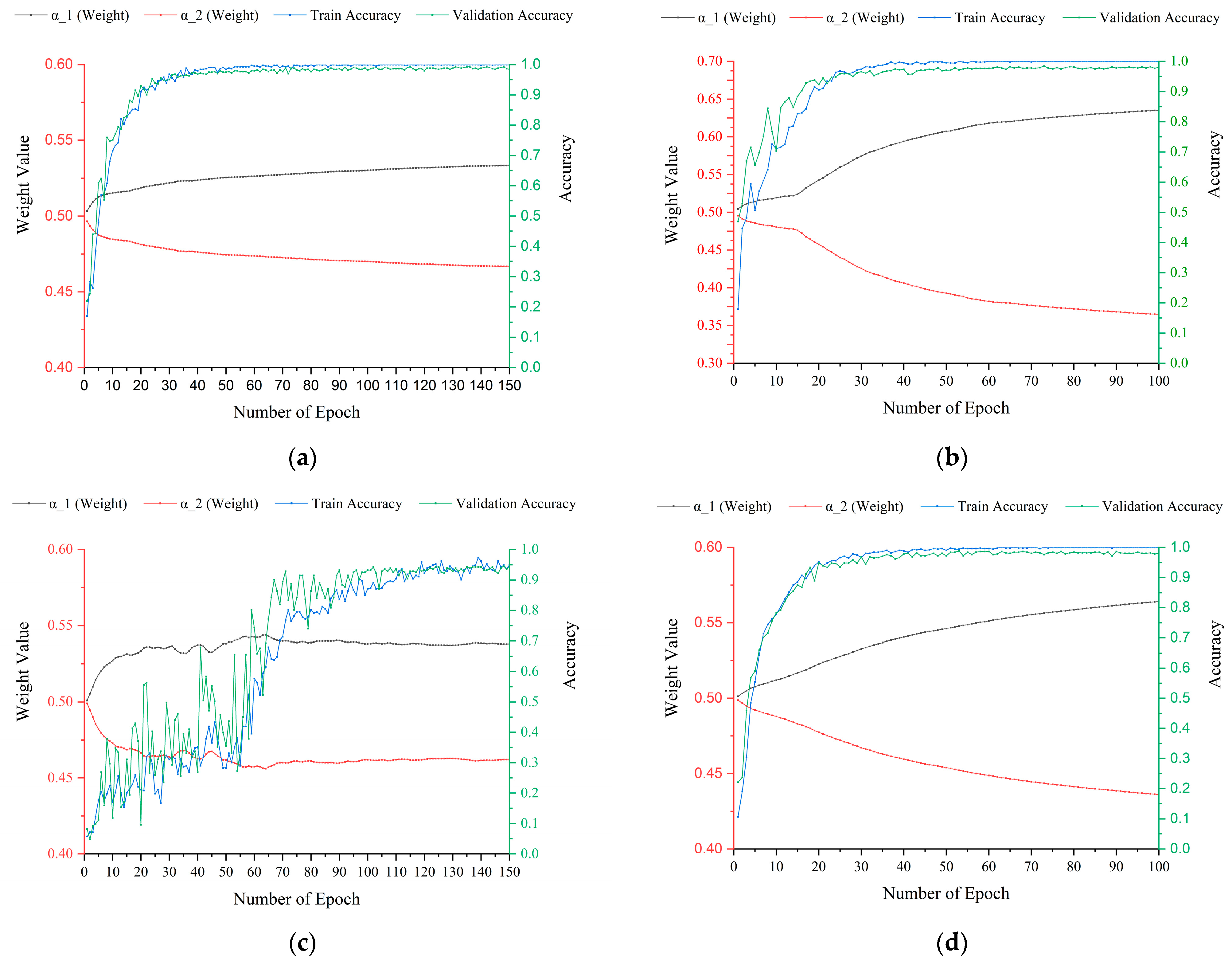
5.3. The Learning Rate under Different Epoch Numbers
5.4. Impact of Different Training Samples on the Classification Result
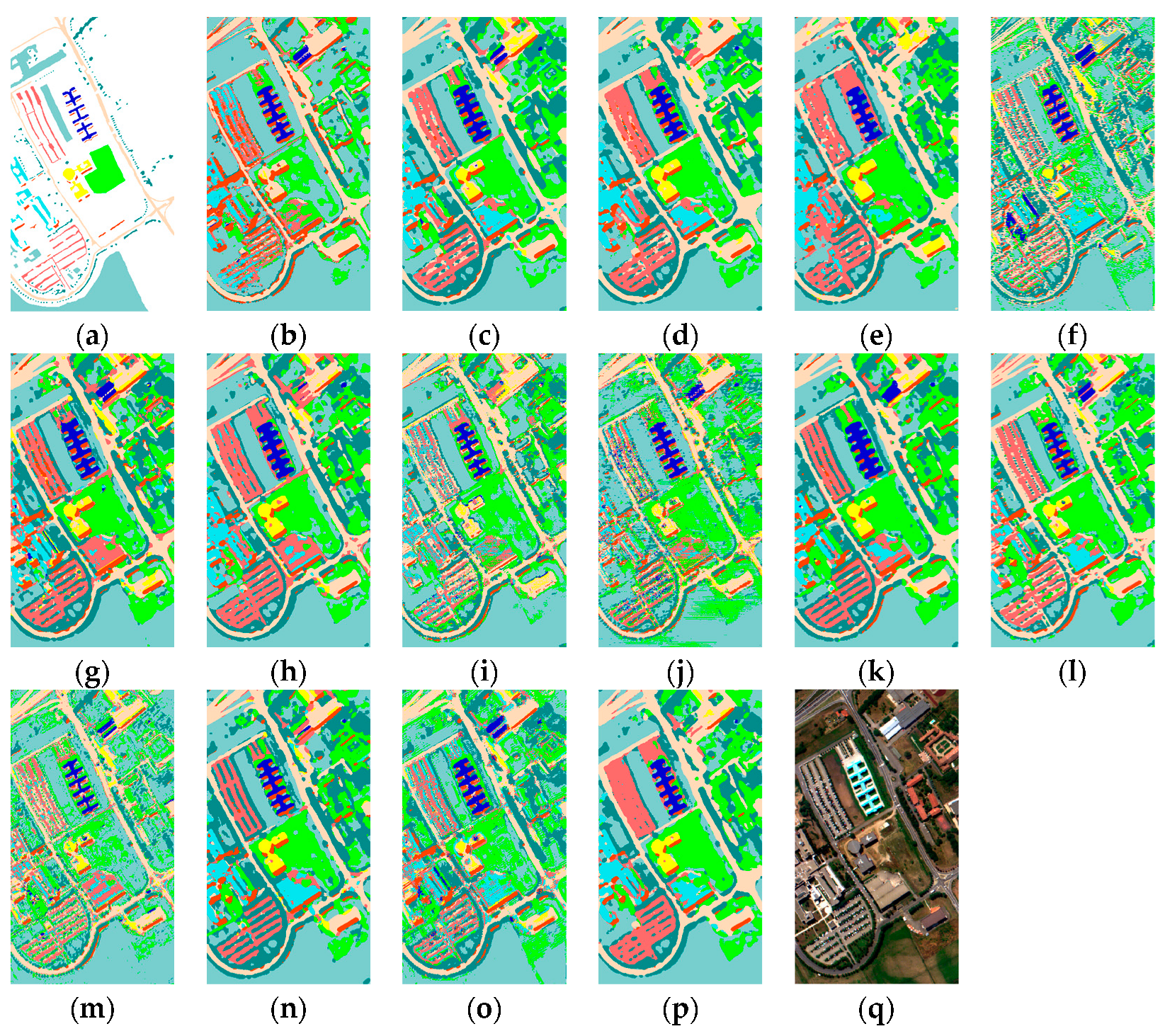
5.5. Visual Results about Different Methods
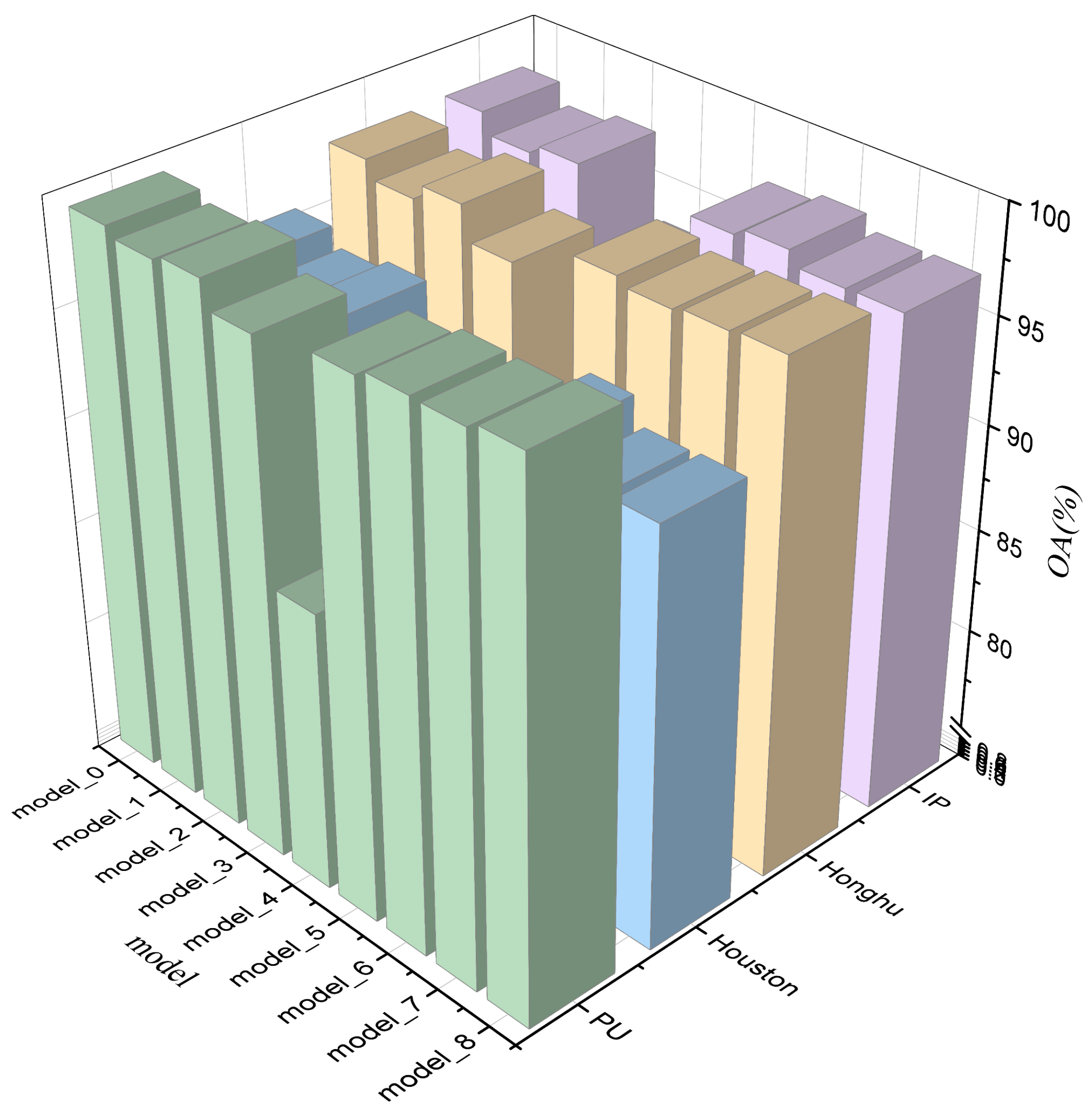
5.6. Ablation Experiment
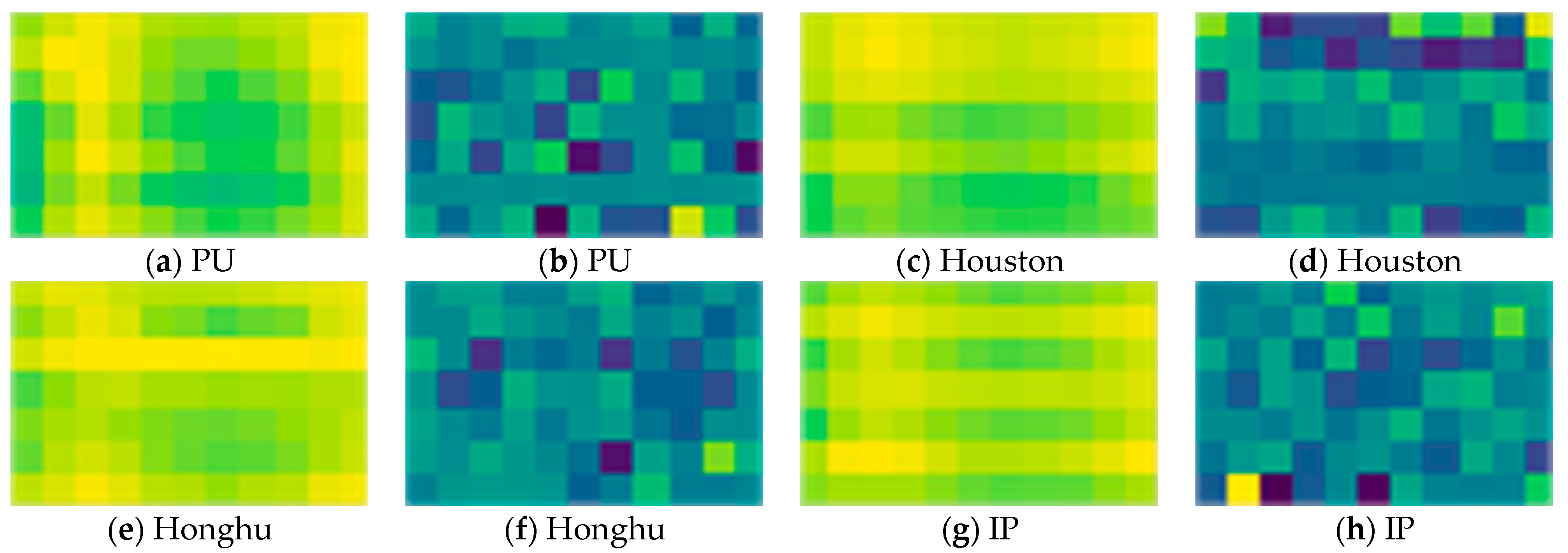
5.7. The Visualization of the Spectral-Enhanced GCN Module
5.8. Training Times
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenz, S.; Salehi, S.; Kirsch, M.; Zimmermann, R.; Unger, G.; Vest Sørensen, E.; Gloaguen, R. Radiometric Correction and 3D Integration of Long-Range Ground-Based Hyperspectral Imagery for Mineral Exploration of Vertical Outcrops. Remote Sens. 2018, 10, 176. [Google Scholar] [CrossRef]
- Rajabi, R.; Zehtabian, A.; Singh, K.D.; Tabatabaeenejad, A.; Ghamisi, P.; Homayouni, S. Editorial: Hyperspectral Imaging in Environmental Monitoring and Analysis. Front. Environ. Sci. 2024, 11, 1353447. [Google Scholar] [CrossRef]
- Kütük, M.; Geneci, İ.; Bilge Özdemir, O.; Koz, A.; Esentürk, O.; Yardımcı Çetin, Y.; Alatan, A.A. Ground-Based Hyperspectral Image Surveillance System for Explosive Detection: Methods, Experiments, and Comparisons. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8747–8763. [Google Scholar] [CrossRef]
- Waczak, J.; Aker, A.; Wijeratne, L.O.H.; Talebi, S.; Fernando, A.; Dewage, P.M.H.; Iqbal, M.; Lary, M.; Schaefer, D.; Lary, D.J. Characterizing Water Composition with an Autonomous Robotic Team Employing Comprehensive In Situ Sensing, Hyperspectral Imaging, Machine Learning, and Conformal Prediction. Remote Sens. 2024, 16, 996. [Google Scholar] [CrossRef]
- Gallacher, C.; Benz, S.; Boehnke, D.; Jehling, M. A Collaborative Approach for the Identification of Thermal Hot-Spots: From Remote Sensing Data to Urban Planning Interventions. AGILE GIScience Ser. 2024, 5, 23. [Google Scholar] [CrossRef]
- Ge, H.; Wang, L.; Liu, M.; Zhao, X.; Zhu, Y.; Pan, H.; Liu, Y. Pyramidal Multiscale Convolutional Network with Polarized Self-Attention for Pixel-Wise Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5504018. [Google Scholar] [CrossRef]
- Jia, X.; Kuo, B.-C.; Crawford, M.M. Feature Mining for Hyperspectral Image Classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Liu, Q.; Xiao, L.; Yang, J.; Wei, Z. CNN-Enhanced Graph Convolutional Network with Pixel- and Superpixel-Level Feature Fusion for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8657–8671. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, Y.; Zhang, Y.; Luo, H. A Fast Dynamic Graph Convolutional Network and CNN Parallel Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5530215. [Google Scholar] [CrossRef]
- Zhao, C.; Wan, X.; Zhao, G.; Cui, B.; Liu, W.; Qi, B. Spectral-Spatial Classification of Hyperspectral Imagery Based on Stacked Sparse Autoencoder and Random Forest. Eur. J. Remote Sens. 2017, 50, 47–63. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, H.; Han, S.; Sun, Y.; Bai, Y. Spectral–Spatial HyperspectralImage Classification With K-Nearest Neighbor and Guided Filter. IEEE Access 2018, 6, 18582–18591. [Google Scholar] [CrossRef]
- Chen, Y.-N.; Thaipisutikul, T.; Han, C.-C.; Liu, T.-J.; Fan, K.-C. Feature Line Embedding Based on Support Vector Machine for Hyperspectral Image Classification. Remote Sens. 2021, 13, 130. [Google Scholar] [CrossRef]
- Sun, W.; Yang, G.; Peng, J.; Du, Q. Lateral-Slice Sparse Tensor Robust Principal Component Analysis for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 107–111. [Google Scholar] [CrossRef]
- Luo, H.; Tang, Y.Y.; Biuk-Aghai, R.P.; Yang, X.; Yang, L.; Wang, Y. Wavelet-Based Extended Morphological Profile and Deep Autoencoder for Hyperspectral Image Classification. Int. J. Wavelets Multiresolution Inf. Process. 2018, 16, 1850016. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral–Spatial Classification of Hyperspectral Images With a Superpixel-Based Discriminative Sparse Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4186–4201. [Google Scholar] [CrossRef]
- Wang, T.; Wang, G.; Tan, K.E.; Tan, D. Spectral Pyramid Graph Attention Network for Hyperspectral Image Classification. arXiv 2020, arXiv:2001.07108. [Google Scholar]
- Zhang, X.; Chen, S.; Zhu, P.; Tang, X.; Feng, J.; Jiao, L. Spatial Pooling Graph Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Liu, M.; Pan, H.; Ge, H.; Wang, L. MS3Net: Multiscale Stratified-Split Symmetric Network with Quadra-View Attention for Hyperspectral Image Classification. Signal Process. 2023, 212, 109153. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar] [CrossRef]
- Yang, A.; Li, M.; Ding, Y.; Hong, D.; Lv, Y.; He, Y. GTFN: GCN and Transformer Fusion Network With Spatial-Spectral Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 6600115. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, B.; Li, C.; Hong, D.; Chanussot, J. Extended Vision Transformer (ExViT) for Land Use and Land Cover Classification: A Multimodal Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5514415. [Google Scholar] [CrossRef]
- Mei, S.; Song, C.; Ma, M.; Xu, F. Hyperspectral Image Classification Using Group-Aware Hierarchical Transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5539014. [Google Scholar] [CrossRef]
- Wu, K.; Fan, J.; Ye, P.; Zhu, M. Hyperspectral Image Classification Using Spectral–Spatial Token Enhanced Transformer With Hash-Based Positional Embedding. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5507016. [Google Scholar] [CrossRef]
- Miftahushudur, T.; Grieve, B.; Yin, H. Permuted KPCA and SMOTE to Guide GAN-Based Oversampling for Imbalanced HSI Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 489–505. [Google Scholar] [CrossRef]
- Xu, M.; Sun, J.; Yao, K.; Cai, Q.; Shen, J.; Tian, Y.; Zhou, X. Developing Deep Learning Based Regression Approaches for Prediction of Firmness and pH in Kyoho Grape Using Vis/NIR Hyperspectral Imaging. Infrared Phys. Technol. 2022, 120, 104003. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.-Q.; Chan, J.C.-W. Learning and Transferring Deep Joint Spectral–Spatial Features for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, X.; Wang, N.; Zhang, M.; Cen, Y. A Spectral-Spatial Cascaded 3D Convolutional Neural Network with a Convolutional Long Short-Term Memory Network for Hyperspectral Image Classification. Remote Sens. 2019, 11, 2363. [Google Scholar] [CrossRef]
- Fu, C.; Du, B.; Zhang, L. ReSC-Net: Hyperspectral Image Classification Based on Attention-Enhanced Residual Module and Spatial-Channel Attention. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5518615. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Tang, D.; Zhou, Z. RDTN: Residual Densely Transformer Network for Hyperspectral Image Classification. Expert Syst. Appl. 2024, 250, 123939. [Google Scholar] [CrossRef]
- Pan, H.; Zhao, X.; Ge, H.; Liu, M.; Shi, C. Hyperspectral Image Classification Based on Multiscale Hybrid Networks and Attention Mechanisms. Remote Sens. 2023, 15, 2720. [Google Scholar] [CrossRef]
- Ding, Y.; Chong, Y.; Pan, S.; Zheng, C.-H. Class-Imbalanced Graph Convolution Smoothing for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5510618. [Google Scholar] [CrossRef]
- Wan, S.; Gong, C.; Zhong, P.; Du, B.; Zhang, L.; Yang, J. Multi-scale Dynamic Graph Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3162–3177. [Google Scholar] [CrossRef]
- Zhang, Y.; Miao, R.; Dong, Y.; Du, B. Multiorder Graph Convolutional Network With Channel Attention for Hyperspec-tral Change Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 1523–1534. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, Q.; Du, B.; Zhang, L. Weighted Feature Fusion of Convolutional Neural Network and Graph Attention Network for Hyperspectral Image Classification. IEEE Trans. Image Process. 2022, 31, 1559–1572. [Google Scholar] [CrossRef]
- Guan, R.; Li, Z.; Tu, W.; Wang, J.; Liu, Y.; Li, X.; Tang, C.; Feng, R. Contrastive Multiview Subspace Clustering of Hyperspectral Images Based on Graph Convolutional Networks. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5510514. [Google Scholar] [CrossRef]
- Zhou, H.; Luo, F.; Zhuang, H.; Weng, Z.; Gong, X.; Lin, Z. Attention Multihop Graph and Multiscale Convolutional Fusion Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5508614. [Google Scholar] [CrossRef]
- Li, W.; Liu, Q.; Fan, S.; Xu, C.; Bai, H. Dual-Stream GNN Fusion Network for Hyperspectral Classification. Appl. Intell. 2023, 53, 26542–26567. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Zhang, S.; Xu, M.; Jia, X. Graph-in-Graph Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 1157–1171. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Gao, H.; Sheng, R.; Chen, Z.; Liu, H.; Xu, S.; Zhang, B. Multiscale Random-Shape Convolution and Adaptive Graph Convolution Fusion Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5516017. [Google Scholar] [CrossRef]
- Zhang, Z.; Cai, Y.; Liu, X.; Zhang, M.; Meng, Y. An Efficient Graph Convolutional RVFL Network for Hyperspectral Image Classification. Remote Sens. 2023, 16, 37. [Google Scholar] [CrossRef]
- Liu, X.; Liu, S.; Chen, W.; Qu, S. HDECGCN: A Heterogeneous Dual Enhanced Network Based on Hybrid CNNs Joint Multiscale Dynamic GCNs for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5515717. [Google Scholar] [CrossRef]
- Shi, C.; Yue, S.; Wu, H.; Zhu, F.; Wang, L. A Multihop Graph Rectify Attention and Spectral Overlap Grouping Convolutional Fusion Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5520517. [Google Scholar] [CrossRef]
- K Ghotekar, R.; Shaw, K.; Rout, M. Deep Feature Segmentation Model Driven by Hybrid Convolution Network for Hyper Spectral Image Classification. Int. J. Comput. Digit. Syst. 2024, 15, 719–738. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Mei, S.; Xu, F.; Ma, M.; Wang, X. Separable Deep Graph Convolutional Network Integrated With CNN and Prototype Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5516216. [Google Scholar] [CrossRef]
- Li, H.; Xiong, X.; Liu, C.; Ma, Y.; Zeng, S.; Li, Y. SFFNet: Staged Feature Fusion Network of Connecting Convolutional Neural Networks and Graph Convolutional Neural Networks for Hyperspectral Image Classification. Appl. Sci. 2024, 14, 2327. [Google Scholar] [CrossRef]
- El Abady, N.F.; Zayed, H.H.; Taha, M. An Efficient Technique for Detecting Document Forgery in Hyperspectral Document Images. Alex. Eng. J. 2023, 85, 207–217. [Google Scholar] [CrossRef]
- Fan, S.; Liu, Q.; Li, W.; Bai, H. A Frequency and Topology Interaction Network for Hyperspectral Image Classification. Eng. Appl. Artif. Intell. 2024, 133, 108234. [Google Scholar] [CrossRef]
- Feng, H.; Wang, Y.; Chen, C.; Xu, D.; Zhao, Z.; Zhao, T. Hyperspectral Image Classification Framework Based on Multichannel Graph Convolutional Networks and Class-Guided Attention Mechanism. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5515115. [Google Scholar] [CrossRef]
- Jiang, M.; Su, Y.; Gao, L.; Plaza, A.; Zhao, X.-L.; Sun, X.; Liu, G. GraphGST: Graph Generative Structure-Aware Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5504016. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2019, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Wan, S.; Li, G.; Yang, J.; Gong, C. Hyperspectral Image Classification with Contrastive Graph Convolutional Network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5503015. [Google Scholar] [CrossRef]
- Shi, C.; Wu, H.; Wang, L. CEGAT: A CNN and Enhanced-GAT Based on Key Sample Selection Strategy for Hyperspectral Image Classification. Neural Netw. 2023, 168, 105–122. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Huang, J.; Meng, Y.; Shen, T. DF2Net: Differential Feature Fusion Network for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 10660–10673. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Shi, Y.; Lai, J.; Tan, X. AM3Net: Adaptive Mutual-Learning-Based Multimodal Data Fusion Network. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 5411–5426. [Google Scholar] [CrossRef]
- Xue, H.; Sun, X.-K.; Sun, W.-X. Multi-Hop Hierarchical Graph Neural Networks. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing (BigComp), Busan, Republic of Korea, 19–22 February 2020; IEEE: Busan, Republic of Korea, 2020; pp. 82–89. [Google Scholar]
- Cai, Y.; Liu, X.; Cai, Z. BS-Nets: An End-to-End Framework for Band Selection of Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1969–1984. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of Hyperspectral Image Based on Double-Branch Dual-Attention Mechanism Network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef]
- Li, Z.; Cui, X.; Wang, L.; Zhang, H.; Zhu, X.; Zhang, Y. Spectral and Spatial Global Context Attention for Hyperspectral Image Classification. Remote Sens. 2021, 13, 771. [Google Scholar] [CrossRef]
- Shi, H.; Cao, G.; Ge, Z.; Zhang, Y.; Fu, P. Double-Branch Network with Pyramidal Convolution and Iterative Attention for Hyperspectral Image Classification. Remote Sens. 2021, 13, 1403. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Chen, Z.; Li, C. A Multiscale Dual-Branch Feature Fusion and Attention Network for Hyperspectral Images Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8180–8192. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, L.; Dong, Y.; Huang, L. Hybrid Dense Network with Dual Attention for Hyperspectral Image Classification. Remote Sens. 2021, 13, 4921. [Google Scholar] [CrossRef]
- Ge, H.; Wang, L.; Liu, M.; Zhu, Y.; Zhao, X.; Pan, H.; Liu, Y. Two-Branch Convolutional Neural Network with Polarized Full Attention for Hyperspectral Image Classification. Remote Sens. 2023, 15, 848. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering; EPFL: Lausanne, Switzerland, 2017. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Zhao, F.; Zhang, J.; Meng, Z.; Liu, H.; Chang, Z.; Fan, J. Multiple Vision Architectures-Based Hybrid Network for Hyperspectral Image Classification. Expert Syst. Appl. 2023, 234, 121032. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, F.; Liu, H.; Yu, J. Data and Knowledge-Driven Deep Multiview Fusion Network Based on Diffusion Model for Hyperspectral Image Classification. Expert Syst. Appl. 2024, 249, 123796. [Google Scholar] [CrossRef]









| Class | Color | Total | Train | Validation | Test |
|---|---|---|---|---|---|
| C1 | 6631 | 66 | 66 | 6499 | |
| C2 | 18,649 | 186 | 186 | 18,277 | |
| C3 | 2099 | 20 | 20 | 2059 | |
| C4 | 3064 | 30 | 30 | 3004 | |
| C5 | 1345 | 13 | 13 | 1319 | |
| C6 | 5029 | 50 | 50 | 4929 | |
| C7 | 1330 | 13 | 13 | 1304 | |
| C8 | 3682 | 36 | 36 | 3610 | |
| C9 | 947 | 9 | 9 | 929 | |
| Total | 42,776 | 423 | 423 | 41,930 |
| Class | Color | Total | Train | Validation | Test |
|---|---|---|---|---|---|
| C1 | 1251 | 25 | 25 | 1201 | |
| C2 | 1254 | 25 | 25 | 1204 | |
| C3 | 697 | 13 | 13 | 671 | |
| C4 | 1244 | 24 | 24 | 1196 | |
| C5 | 1242 | 24 | 24 | 1194 | |
| C6 | 325 | 6 | 6 | 313 | |
| C7 | 1268 | 25 | 25 | 1218 | |
| C8 | 1244 | 24 | 24 | 1196 | |
| C9 | 1252 | 25 | 25 | 1202 | |
| C10 | 1227 | 24 | 24 | 1179 | |
| C11 | 1235 | 24 | 24 | 1187 | |
| C12 | 1233 | 24 | 24 | 1185 | |
| C13 | 469 | 9 | 9 | 451 | |
| C14 | 428 | 8 | 8 | 412 | |
| C15 | 660 | 13 | 13 | 634 | |
| Total | 15,029 | 293 | 293 | 14,443 |
| Class | Color | Total | Train | Validation | Test |
|---|---|---|---|---|---|
| C1 | 3320 | 33 | 33 | 3254 | |
| C2 | 1482 | 14 | 14 | 1454 | |
| C3 | 18,725 | 187 | 187 | 18,351 | |
| C4 | 1792 | 17 | 17 | 1758 | |
| C5 | 14,939 | 149 | 149 | 14,641 | |
| C6 | 5808 | 58 | 58 | 5692 | |
| C7 | 4054 | 40 | 40 | 3974 | |
| C8 | 2375 | 23 | 23 | 2329 | |
| C9 | 939 | 9 | 9 | 921 | |
| C10 | 2584 | 25 | 25 | 2534 | |
| C11 | 3979 | 39 | 39 | 3901 | |
| C12 | 4307 | 43 | 43 | 4221 | |
| C13 | 1002 | 10 | 10 | 982 | |
| C14 | 563 | 5 | 5 | 553 | |
| C15 | 973 | 9 | 9 | 955 | |
| C16 | 2037 | 20 | 20 | 1997 | |
| Total | 68,879 | 681 | 681 | 67,517 |
| Class | Color | Total | Train | Validation | Test |
|---|---|---|---|---|---|
| C1 | 46 | 2 | 2 | 42 | |
| C2 | 1428 | 71 | 71 | 1286 | |
| C3 | 830 | 41 | 41 | 748 | |
| C4 | 237 | 11 | 11 | 215 | |
| C5 | 483 | 24 | 24 | 435 | |
| C6 | 730 | 36 | 36 | 658 | |
| C7 | 28 | 1 | 1 | 26 | |
| C8 | 478 | 23 | 23 | 432 | |
| C9 | 20 | 1 | 1 | 18 | |
| C10 | 972 | 48 | 48 | 876 | |
| C11 | 2455 | 122 | 122 | 2211 | |
| C12 | 593 | 29 | 29 | 535 | |
| C13 | 205 | 10 | 10 | 185 | |
| C14 | 1265 | 63 | 63 | 1139 | |
| C15 | 386 | 19 | 19 | 348 | |
| C16 | 93 | 4 | 4 | 85 | |
| Total | 10,249 | 505 | 505 | 9239 |
| Class | Color | Total | Train | Validation | Test |
|---|---|---|---|---|---|
| C1 | 426,138 | 4261 | 4261 | 417,616 | |
| C2 | 187,425 | 1874 | 1874 | 183,677 | |
| C3 | 124,862 | 1248 | 1248 | 122,366 | |
| C4 | 91,518 | 915 | 915 | 89,688 | |
| C5 | 197,218 | 1972 | 1972 | 193,274 | |
| C6 | 19,663 | 196 | 196 | 19,271 | |
| C7 | 296,538 | 2965 | 2965 | 290,608 | |
| C8 | 276,755 | 2767 | 2767 | 271,221 | |
| C9 | 44,232 | 442 | 442 | 43,348 | |
| C10 | 372,708 | 3727 | 3727 | 365,254 | |
| C11 | 67,210 | 672 | 672 | 65,866 | |
| C12 | 29,763 | 297 | 297 | 29,169 | |
| C13 | 85,547 | 855 | 855 | 83,837 | |
| C14 | 68,885 | 688 | 688 | 67,509 | |
| C15 | 986,139 | 9861 | 9861 | 966,417 | |
| C16 | 7456 | 74 | 74 | 7308 | |
| C17 | 27,178 | 271 | 271 | 26,636 | |
| C18 | 6506 | 65 | 65 | 6376 | |
| C19 | 26,140 | 261 | 261 | 25,618 | |
| Total | 3,341,881 | 33,411 | 33,411 | 3,275,059 |
| Class | SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 84.43 ± 1.35 | 96.21 ± 0.34 | 96.20 ± 1.10 | 98.47 ± 0.31 | 85.75 ± 0.29 | 95.57 ± 0.35 | 99.51 ± 0.20 | 78.60 ± 0.77 | 83.78 ± 1.35 | 98.60 ± 0.12 | 92.69 ± 0.14 | 88.98 ± 0.49 | 98.58 ± 0.54 | 84.90 ± 2.53 | 98.54 ± 0.07 |
| C2 | 88.67 ± 0.90 | 98.54 ± 0.10 | 99.33 ± 0.09 | 99.86 ± 0.12 | 85.74 ± 0.29 | 99.28 ± 0.35 | 98.91 ± 0.10 | 94.58 ± 0.26 | 95.19 ± 0.08 | 99.78 ± 0.13 | 99.07 ± 0.44 | 86.15 ± 0.33 | 98.22 ± 0.84 | 92.03 ± 1.93 | 99.79 ± 0.06 |
| C3 | 53.60 ± 2.47 | 95.66 ± 0.48 | 99.03 ± 0.35 | 94.83 ± 1.13 | 59.23 ± 1.18 | 91.31 ± 1.58 | 96.23 ± 1.16 | 67.15 ± 0.80 | 73.84 ± 1.55 | 99.23 ± 0.11 | 94.47 ± 0.10 | 54.21 ± 1.52 | 96.70 ± 1.52 | 53.67 ± 4.21 | 99.31 ± 0.40 |
| C4 | 100.00 ± 0.00 | 97.46 ± 0.13 | 98.59 ± 0.02 | 99.23 ± 0.33 | 93.43 ± 0.22 | 96.73 ± 0.69 | 99.24 ± 0.14 | 98.51 ± 0.19 | 97.37 ± 0.32 | 98.35 ± 0.11 | 99.73 ± 0.02 | 98.97 ± 0.24 | 93.97 ± 0.58 | 95.27 ± 1.97 | 98.83 ± 0.09 |
| C5 | 99.84 ± 0.14 | 99.58 ± 0.04 | 99.66 ± 0.04 | 96.30 ± 0.92 | 97.49 ± 0.25 | 98.08 ± 0.55 | 95.00 ± 0.20 | 97.50 ± 0.32 | 97.15 ± 0.36 | 92.61 ± 0.18 | 100.00 ± 0.00 | 96.27 ± 0.27 | 99.97 ± 0.04 | 97.48 ± 0.34 | 98.38 ± 0.11 |
| C6 | 98.44 ± 0.61 | 99.09 ± 0.21 | 99.84 ± 0.02 | 99.97 ± 0.03 | 76.62 ± 1.23 | 99.01 ± 2.37 | 99.90 ± 0.03 | 94.70 ± 0.21 | 92.13 ± 0.26 | 99.66 ± 0.05 | 98.12 ± 1.38 | 78.57 ± 2.17 | 99.47 ± 0.04 | 73.36 ± 1.44 | 99.92 ± 0.02 |
| C7 | 99.92 ± 0.20 | 98.84 ± 0.23 | 100.00 ± 0.00 | 98.79 ± 1.36 | 64.78 ± 0.55 | 83.10 ± 0.61 | 94.13 ± 4.53 | 57.20 ± 3.01 | 54.53 ± 4.93 | 99.97 ± 0.05 | 98.36 ± 0.95 | 63.48 ± 3.21 | 93.12 ± 1.87 | 65.58 ± 4.14 | 100.00 ± 0.00 |
| C8 | 81.16 ± 1.93 | 83.32 ± 0.40 | 95.54 ± 0.82 | 87.18 ± 1.18 | 78.63 ± 1.00 | 86.94 ± 1.02 | 90.01 ± 0.61 | 72.23 ± 0.35 | 76.07 ± 0.68 | 95.64 ± 0.34 | 84.89 ± 1.11 | 70.00 ± 3.84 | 92.79 ± 0.52 | 70.45 ± 1.18 | 97.58 ± 1.19 |
| C9 | 74.69 ± 6.55 | 96.18 ± 0.39 | 98.97 ± 0.23 | 97.34 ± 0.47 | 99.35 ± 0.07 | 98.28 ± 0.95 | 100.00 ± 0.00 | 95.95 ± 0.79 | 95.88 ± 0.76 | 96.38 ± 0.20 | 97.73 ± 0.43 | 99.58 ± 0.28 | 98.85 ± 0.35 | 94.38 ± 1.71 | 99.79 ± 0.03 |
| OA | 85.95 ± 0.70 | 96.52 ± 0.05 | 98.52 ± 0.27 | 97.98 ± 0.15 | 83.65 ± 0.12 | 96.39 ± 0.44 | 97.90 ± 0.25 | 88.35 ± 0.33 | 89.40 ± 0.60 | 98.78 ± 0.07 | 96.42 ± 0.09 | 83.70 ± 0.53 | 97.44 ± 0.47 | 84.96 ± 1.15 | 99.28 ± 0.08 |
| AA | 86.75 ± 0.26 | 96.10 ± 0.04 | 98.57 ± 0.20 | 96.89 ± 0.30 | 82.34 ± 0.12 | 94.26 ± 0.23 | 96.99 ± 0.63 | 84.05 ± 0.64 | 85.11 ± 0.67 | 97.80 ± 0.04 | 96.12 ± 0.09 | 81.80 ± 0.47 | 96.85 ± 0.30 | 80.79 ± 0.94 | 99.13 ± 0.10 |
| × 100 | 80.88 ± 1.00 | 95.38 ± 0.07 | 98.04 ± 0.36 | 97.32 ± 0.20 | 77.82 ± 0.17 | 95.22 ± 0.58 | 97.21 ± 0.33 | 84.35 ± 0.45 | 85.84 ± 0.77 | 98.39 ± 0.09 | 95.24 ± 0.11 | 77.87 ± 0.74 | 96.60 ± 0.62 | 79.91 ± 1.72 | 99.05 ± 0.10 |
| Class | SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 88.54 ± 8.24 | 97.98 ± 0.11 | 97.36 ± 0.18 | 95.64 ± 0.69 | 86.00 ± 0.47 | 87.66 ± 0.58 | 92.15 ± 0.39 | 89.93 ± 0.36 | 86.42 ± 1.31 | 85.30 ± 1.05 | 96.52 ± 0.42 | 82.39 ± 1.73 | 98.05 ± 0.20 | 91.32 ± 0.72 | 92.51 ± 0.78 |
| C2 | 95.54 ± 7.93 | 94.21 ± 0.71 | 91.47 ± 0.42 | 95.99 ± 0.16 | 92.30 ± 0.31 | 95.44 ± 0.05 | 100.00 ± 0.00 | 76.75 ± 0.60 | 85.50 ± 1.32 | 94.08 ± 0.80 | 90.86 ± 0.46 | 94.99 ± 1.16 | 86.94 ± 0.62 | 90.32 ± 1.07 | 95.19 ± 0.97 |
| C3 | 99.53 ± 0.27 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.55 ± 0.00 | 100.00 ± 0.00 | 99.97 ± 0.09 | 96.10 ± 0.41 | 95.98 ± 0.91 | 100.00 ± 0.00 | 99.11 ± 0.24 | 91.96 ± 0.64 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| C4 | 61.95 ± 48.01 | 93.14 ± 0.08 | 91.69 ± 0.37 | 94.39 ± 0.13 | 85.90 ± 0.79 | 95.48 ± 0.41 | 96.39 ± 0.16 | 92.61 ± 0.50 | 85.69 ± 1.46 | 96.05 ± 0.28 | 90.65 ± 0.18 | 88.72 ± 0.51 | 94.16 ± 0.19 | 90.92 ± 027 | 98.78 ± 0.34 |
| C5 | 75.29 ± 8.44 | 97.85 ± 0.29 | 89.59 ± 0.34 | 98.51 ± 0.13 | 98.91 ± 0.04 | 99.72 ± 0.08 | 99.83 ± 0.31 | 85.72 ± 0.22 | 88.48 ± 1.90 | 99.24 ± 0.33 | 98.59 ± 0.18 | 91.35 ± 0.19 | 96.14 ± 0.35 | 94.20 ± 1.53 | 99.91 ± 0.03 |
| C6 | 97.70 ± 1.88 | 96.82 ± 0.21 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.23 ± 0.00 | 99.68 ± 0.00 | 100.00 ± 0.00 | 97.83 ± 0.40 | 90.79 ± 1.90 | 97.44 ± 0.85 | 99.28 ± 0.00 | 83.58 ± 1.83 | 100.00 ± 0.00 | 98.88 ± 0.32 | 95.23 ± 1.13 |
| C7 | 61.44 ± 12.39 | 88.84 ± 0.62 | 92.83 ± 0.91 | 96.14 ± 0.51 | 74.51 ± 0.45 | 96.67 ± 0.22 | 94.79 ± 0.90 | 82.64 ± 0.46 | 65.89 ± 0.92 | 92.87 ± 0.22 | 85.87 ± 1.50 | 77.83 ± 3.65 | 95.43 ± 0.24 | 85.81 ± 2.10 | 96.33 ± 0.55 |
| C8 | 45.99 ± 8.92 | 99.98 ± 0.05 | 91.71 ± 0.81 | 99.12 ± 0.24 | 94.20 ± 0.25 | 94.16 ± 0.55 | 97.83 ± 0.38 | 89.00 ± 1.19 | 58.57 ± 2.04 | 97.58 ± 0.35 | 92.61 ± 0.06 | 80.89 ± 0.64 | 100.00 ± 0.00 | 88.48 ± 3.54 | 97.83 ± 0.30 |
| C9 | 95.56 ± 3.75 | 93.04 ± 0.90 | 96.93 ± 0.17 | 91.69 ± 0.42 | 78.02 ± 0.68 | 87.56 ± 0.75 | 89.39 ± 0.74 | 67.54 ± 0.32 | 70.58 ± 2.06 | 96.06 ± 1.20 | 88.20 ± 0.85 | 58.22 ± 1.95 | 91.47 ± 0.48 | 69.44 ± 10.00 | 89.30 ± 0.70 |
| C10 | 87.82 ± 10.21 | 93.50 ± 0.15 | 96.03 ± 1.76 | 81.71 ± 0.11 | 78.84 ± 0.47 | 96.13 ± 1.71 | 84.75 ± 0.93 | 54.53 ± 0.30 | 48.84 ± 1.52 | 91.91 ± 1.30 | 87.83 ± 0.94 | 72.43 ± 2.53 | 80.86 ± 0.37 | 66.28 ± 4.48 | 95.81 ± 0.51 |
| C11 | 99.64 ± 0.95 | 97.17 ± 0.35 | 88.07 ± 5.38 | 97.72 ± 0.27 | 79.86 ± 0.54 | 95.64 ± 2.16 | 91.72 ± 0.62 | 74.35 ± 0.41 | 51.76 ± 0.96 | 96.78 ± 0.42 | 93.19 ± 0.06 | 74.38 ± 2.05 | 92.68 ± 0.17 | 83.28 ± 3.06 | 89.99 ± 0.49 |
| C12 | 82.08 ± 4.49 | 90.85 ± 0.47 | 89.34 ± 0.29 | 88.37 ± 0.57 | 81.50 ± 0.50 | 95.09 ± 0.35 | 96.37 ± 0.42 | 54.03 ± 0.68 | 53.69 ± 0.45 | 83.75 ± 1.60 | 88.68 ± 1.19 | 63.24 ± 0.85 | 89.64 ± 1.23 | 81.07 ± 3.51 | 95.75 ± 0.44 |
| C13 | 100.00 ± 0.00 | 67.17 ± 0.66 | 67.51 ± 6.86 | 90.58 ± 0.89 | 93.29 ± 0.21 | 89.55 ± 0.72 | 92.40 ± 0.35 | 84.42 ± 1.71 | 50.65 ± 3.93 | 96.00 ± 0.61 | 58.10 ± 2.60 | 23.40 ± 2.68 | 84.87 ± 0.18 | 80.37 ± 2.17 | 88.31 ± 0.25 |
| C14 | 88.63 ± 4.61 | 92.38 ± 0.00 | 95.59 ± 0.00 | 99.30 ± 0.07 | 92.99 ± 0.20 | 92.03 ± 0.61 | 89.51 ± 1.43 | 95.18 ± 0.17 | 97.65 ± 0.42 | 95.40 ± 0.59 | 92.38 ± 0.00 | 98.78 ± 0.16 | 95.15 ± 0.00 | 92.11 ± 0.18 | 99.29 ± 1.09 |
| C15 | 88.34 ± 0.62 | 94.63 ± 0.00 | 94.11 ± 0.14 | 99.83 ± 0.05 | 98.66 ± 0.14 | 93.33 ± 0.19 | 96.02 ± 0.53 | 97.82 ± 0.26 | 78.67 ± 3.31 | 98.05 ± 0.52 | 96.52 ± 0.08 | 93.28 ± 1.10 | 98.60 ± 0.00 | 85.64 ± 0.45 | 99.63 ± 0.12 |
| OA | 77.23 ± 2.16 | 93.55 ± 0.10 | 91.69 ± 0.41 | 94.49 ± 0.03 | 86.77 ± 0.10 | 94.36 ± 0.32 | 94.31 ± 0.06 | 77.87 ± 0.10 | 72.02 ± 0.76 | 93.81 ± 0.10 | 90.42 ± 0.33 | 79.46 ± 0.95 | 92.84 ± 0.12 | 84.35 ± 0.62 | 95.42 ± 0.08 |
| AA | 84.53 ± 3.25 | 93.17 ± 0.09 | 92.15 ± 0.07 | 95.27 ± 0.03 | 88.92 ± 0.06 | 94.54 ± 0.29 | 94.74 ± 0.11 | 82.56 ± 0.10 | 73.94 ± 0.58 | 94.70 ± 0.03 | 90.56 ± 0.30 | 78.36 ± 0.74 | 93.60 ± 0.09 | 86.54 ± 0.13 | 95.59 ± 0.13 |
| × 100 | 75.34 ± 2.33 | 93.03 ± 0.11 | 91.03 ± 0.44 | 94.05 ± 0.03 | 85.69 ± 0.10 | 93.90 ± 0.34 | 93.85 ± 0.06 | 76.03 ± 0.11 | 69.74 ± 0.82 | 93.31 ± 0.11 | 89.65 ± 0.36 | 77.75 ± 1.03 | 92.26 ± 0.12 | 83.08 ± 0.68 | 95.04 ± 0.09 |
| Class | SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 60.82 ± 3.50 | 95.24 ± 0.40 | 97.91 ± 0.40 | 98.85 ± 0.12 | 71.95 ± 0.39 | 98.28 ± 0.35 | 96.53 ± 0.52 | 98.07 ± 0.08 | 95.22 ± 1.12 | 96.22 ± 0.05 | 94.47 ± 0.05 | 92.93 ± 0.72 | 93.39 ± 0.17 | 88.86 ± 1.39 | 99.64 ± 0.15 |
| C2 | 93.96 ± 2.01 | 80.88 ± 2.27 | 84.51 ± 1.62 | 87.29 ± 1.16 | 90.40 ± 0.35 | 73.60 ± 5.34 | 95.10 ± 1.54 | 78.06 ± 2.36 | 90.21 ± 1.55 | 80.05 ± 0.39 | 92.11 ± 0.43 | 74.01 ± 0.85 | 86.14 ± 1.20 | 77.75 ± 3.59 | 91.11 ± 0.63 |
| C3 | 95.54 ± 0.90 | 95.85 ± 0.98 | 98.40 ± 0.81 | 98.02 ± 0.18 | 87.87 ± 0.31 | 97.97 ± 0.79 | 95.06 ± 2.31 | 91.54 ± 0.82 | 92.21 ± 0.46 | 98.61 ± 0.10 | 95.48 ± 1.41 | 92.43 ± 1.39 | 97.76 ± 0.36 | 96.12 ± 0.73 | 96.84 ± 0.20 |
| C4 | 40.80 ± 4.22 | 98.55 ± 0.58 | 99.86 ± 0.05 | 98.38 ± 0.11 | 83.39 ± 0.80 | 98.45 ± 1.53 | 99.25 ± 0.51 | 85.24 ± 1.23 | 85.30 ± 3.86 | 97.44 ± 0.15 | 99.80 ± 0.10 | 88.84 ± 0.34 | 97.78 ± 0.20 | 93.86 ± 0.38 | 99.96 ± 0.03 |
| C5 | 92.91 ± 1.93 | 99.21 ± 0.13 | 99.78 ± 0.07 | 99.41 ± 0.04 | 87.51 ± 0.34 | 99.31 ± 0.09 | 97.42 ± 1.93 | 93.39 ± 0.39 | 95.24 ± 0.64 | 99.71 ± 0.00 | 99.61 ± 0.08 | 95.79 ± 0.34 | 99.28 ± 0.13 | 93.65 ± 0.39 | 99.83 ± 0.08 |
| C6 | 83.91 ± 3.23 | 97.05 ± 1.27 | 93.87 ± 1.47 | 97.90 ± 0.18 | 75.01 ± 0.47 | 96.48 ± 0.49 | 94.11 ± 5.31 | 81.05 ± 0.52 | 95.06 ± 0.72 | 97.73 ± 0.20 | 96.76 ± 0.93 | 84.65 ± 0.53 | 97.86 ± 0.24 | 88.15 ± 1.90 | 95.47 ± 0.21 |
| C7 | 99.30 ± 0.46 | 89.84 ± 0.97 | 90.91 ± 2.71 | 88.35 ± 1.15 | 45.58 ± 0.28 | 90.23 ± 1.53 | 92.70 ± 2.49 | 63.99 ± 1.54 | 63.17 ± 1.53 | 92.60 ± 0.35 | 88.33 ± 0.49 | 61.71 ± 1.50 | 87.36 ± 1.31 | 69.02 ± 4.47 | 96.43 ± 0.49 |
| C8 | 100.00 ± 0.00 | 98.42 ± 0.37 | 99.49 ± 0.09 | 99.70 ± 0.09 | 65.29 ± 0.66 | 98.16 ± 0.63 | 99.16 ± 0.73 | 93.27 ± 0.50 | 95.73 ± 0.79 | 99.28 ± 0.08 | 98.61 ± 0.37 | 96.23 ± 0.25 | 99.61 ± 0.07 | 97.50 ± 1.08 | 99.50 ± 0.02 |
| C9 | 0.00 ± 0.00 | 96.80 ± 0.37 | 95.89 ± 1.08 | 88.48 ± 0.16 | 51.10 ± 1.19 | 89.93 ± 1.71 | 93.05 ± 2.58 | 66.94 ± 5.48 | 76.26 ± 2.67 | 97.35 ± 0.61 | 88.49 ± 0.99 | 65.09 ± 6.69 | 91.57 ± 1.17 | 81.28 ± 6.15 | 97.25 ± 0.54 |
| C10 | 98.47 ± 0.74 | 95.58 ± 1.16 | 89.02 ± 1.25 | 94.14 ± 0.38 | 63.10 ± 0.57 | 88.64 ± 5.61 | 93.79 ± 1.21 | 69.90 ± 0.75 | 86.43 ± 1.19 | 93.64 ± 0.60 | 88.95 ± 0.89 | 77.72 ± 1.81 | 96.07 ± 0.18 | 74.03 ± 2.48 | 97.17 ± 0.29 |
| C11 | 76.94 ± 2.25 | 96.54 ± 3.46 | 97.57 ± 1.24 | 93.92 ± 0.61 | 79.23 ± 1.05 | 94.72 ± 3.87 | 99.21 ± 0.42 | 75.94 ± 0.36 | 71.28 ± 3.90 | 99.07 ± 0.16 | 97.89 ± 0.70 | 73.36 ± 2.18 | 97.56 ± 0.97 | 81.47 ± 1.85 | 96.80 ± 0.23 |
| C12 | 68.79 ± 4.20 | 99.66 ± 0.10 | 96.69 ± 5.00 | 99.61 ± 0.03 | 81.52 ± 0.72 | 92.99 ± 0.50 | 99.16 ± 1.40 | 72.69 ± 0.60 | 79.37 ± 0.58 | 99.55 ± 0.23 | 97.41 ± 0.37 | 85.27 ± 1.90 | 98.72 ± 0.48 | 84.78 ± 0.83 | 99.86 ± 0.04 |
| C13 | 34.11 ± 6.88 | 93.04 ± 0.26 | 99.41 ± 0.17 | 98.08 ± 0.12 | 76.92 ± 0.72 | 99.13 ± 0.24 | 98.82 ± 0.88 | 96.91 ± 0.86 | 81.88 ± 6.61 | 99.07 ± 0.09 | 95.26 ± 0.75 | 84.20 ± 2.66 | 96.70 ± 0.28 | 92.54 ± 2.21 | 97.54 ± 0.69 |
| C14 | 90.80 ± 1.04 | 98.65 ± 1.22 | 99.96 ± 0.12 | 98.39 ± 1.68 | 78.85 ± 0.62 | 88.55 ± 4.02 | 100.00 ± 0.00 | 82.92 ± 0.78 | 64.85 ± 1.69 | 95.79 ± 0.51 | 88.31 ± 1.04 | 77.50 ± 2.78 | 98.62 ± 0.09 | 80.27 ± 5.06 | 100.00 ± 0.00 |
| C15 | 89.76 ± 29.92 | 89.61 ± 1.71 | 91.15 ± 3.13 | 97.40 ± 0.70 | 50.53 ± 1.26 | 94.36 ± 1.69 | 99.00 ± 0.71 | 72.71 ± 0.96 | 67.11 ± 3.71 | 96.25 ± 0.94 | 99.19 ± 0.60 | 73.17 ± 1.31 | 99.74 ± 0.18 | 41.04 ± 3.60 | 99.17 ± 0.14 |
| C16 | 0.00 ± 0.00 | 91.89 ± 1.29 | 97.68 ± 0.68 | 96.37 ± 0.11 | 73.70 ± 1.18 | 89.16 ± 1.25 | 97.26 ± 1.88 | 85.56 ± 0.86 | 76.50 ± 1.42 | 95.56 ± 0.45 | 91.10 ± 0.46 | 78.54 ± 1.65 | 97.32 ± 0.52 | 84.91 ± 2.42 | 97.66 ± 0.46 |
| OA | 82.12 ± 1.37 | 96.16 ± 0.74 | 96.87 ± 0.53 | 97.09 ± 0.13 | 80.20 ± 0.10 | 95.66 ± 0.85 | 96.20 ± 1.71 | 86.25 ± 0.09 | 88.21 ± 0.78 | 97.56 ± 0.07 | 95.90 ± 0.33 | 87.09 ± 0.17 | 96.91 ± 0.01 | 88.70 ± 0.32 | 97.82 ± 0.05 |
| AA | 70.38 ± 2.05 | 94.80 ± 0.74 | 95.76 ± 0.20 | 95.89 ± 0.29 | 72.62 ± 0.22 | 93.12 ± 1.02 | 96.85 ± 0.89 | 81.76 ± 0.28 | 82.24 ± 1.28 | 96.12 ± 0.12 | 94.49 ± 0.13 | 81.34 ± 0.54 | 95.96 ± 0.17 | 82.83 ± 0.54 | 97.77 ± 0.07 |
| × 100 | 79.00 ± 1.64 | 95.49 ± 0.87 | 96.34 ± 0.62 | 96.60 ± 0.16 | 76.54 ± 0.12 | 94.92 ± 1.00 | 95.52 ± 2.03 | 83.77 ± 0.10 | 86.11 ± 0.92 | 97.14 ± 0.09 | 95.19 ± 0.40 | 84.84 ± 0.22 | 96.38 ± 0.01 | 86.75 ± 0.37 | 97.44 ± 0.06 |
| Class | SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 97.55 ± 0.82 | 64.44 ± 1.79 | 94.03 ± 1.91 | 100.00 ± 0.00 | 100.00 ± 0.00 | 73.83 ± 4.12 | 96.87 ± 0.52 | 100.00 ± 0.00 | 100.00±0.00 | 97.63 ± 0.03 | 0.00 ± 0.00 | 100.00 ± 0.00 |
| C2 | 89.93 ± 10.42 | 94.41 ± 3.03 | 97.63 ± 1.21 | 98.62 ± 1.70 | 47.25 ± 0.74 | 94.85 ± 0.50 | 98.16 ± 0.51 | 71.35 ± 0.77 | 76.26 ± 0.90 | 97.61 ± 0.26 | 85.29 ± 1.08 | 65.15 ± 1.31 | 97.77 ± 0.44 | 60.57 ± 1.75 | 97.40 ± 0.54 |
| C3 | 84.88 ± 5.88 | 94.66 ± 0.20 | 98.44 ± 0.66 | 97.11 ± 0.31 | 46.46 ± 0.81 | 96.20 ± 0.31 | 92.39 ± 0.57 | 67.13 ± 1.10 | 46.93 ± 4.01 | 96.63 ± 0.18 | 89.36 ± 1.93 | 52.57 ± 1.46 | 96.50 ± 0.44 | 61.54 ± 3.65 | 98.99 ± 0.42 |
| C4 | 60.00 ± 48.98 | 98.42 ± 1.36 | 94.93 ± 2.58 | 99.10 ± 0.33 | 56.10 ± 1.98 | 95.06 ± 1.20 | 99.03 ± 2.29 | 63.51 ± 4.08 | 57.63 ± 4.48 | 99.48 ± 0.14 | 85.04 ± 4.29 | 41.21 ± 3.51 | 100.00 ± 0.00 | 59.34 ± 3.46 | 92.98 ± 0.28 |
| C5 | 71.86 ± 21.30 | 96.05 ± 1.03 | 93.77 ± 1.88 | 94.40 ± 0.64 | 63.99 ± 0.97 | 95.13 ± 0.69 | 97.62 ± 0.50 | 94.35 ± 0.61 | 74.96 ± 1.87 | 99.74 ± 0.00 | 96.64 ± 0.20 | 79.13 ± 2.32 | 99.02 ± 0.66 | 83.44 ± 0.88 | 97.04 ± 0.55 |
| C6 | 80.70 ± 4.30 | 99.18 ± 0.12 | 97.74 ± 0.20 | 96.80 ± 0.15 | 76.59 ± 0.45 | 99.13 ± 0.54 | 96.68 ± 0.69 | 77.77 ± 0.48 | 85.92 ± 1.29 | 98.59 ± 0.07 | 98.14 ± 0.21 | 67.46 ± 0.99 | 99.95 ± 0.07 | 75.49 ± 2.63 | 98.31 ± 0.60 |
| C7 | 0.00 ± 0.00 | 72.61 ± 9.26 | 62.86 ± 22.03 | 69.96 ± 35.02 | 50.92 ± 7.44 | 100.00 ± 0.00 | 90.00 ± 30.00 | 0.00 ± 0.00 | 90.92 ± 14.46 | 63.15 ± 1.59 | 81.23 ± 13.36 | 80.00 ± 28.28 | 43.58 ± 0.35 | 0.00 ± 0.00 | 98.89 ± 2.22 |
| C8 | 96.65 ± 4.01 | 93.57 ± 0.60 | 99.36 ± 1.41 | 99.84 ± 0.41 | 78.48 ± 1.56 | 99.04 ± 0.32 | 96.09 ± 0.33 | 89.18 ± 0.35 | 89.13 ± 0.96 | 96.68 ± 1.27 | 97.60 ± 1.36 | 89.09 ± 0.60 | 99.85 ± 0.11 | 88.17 ± 0.82 | 100.00 ± 0.00 |
| C9 | 0.00 ± 0.00 | 100.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | 24.72 ± 4.38 | 96.32 ± 2.41 | 0.00 ± 0.00 | 0.00 ± 0.00 | 53.33 ± 6.67 | 100.00 ± 0.00 | 92.31 ± 10.88 | 16.67 ± 23.57 | 86.63 ± 0.73 | 0.00 ± 0.00 | 73.85 ± 2.31 |
| C10 | 63.66 ± 4.72 | 94.64 ± 1.36 | 93.50 ± 1.49 | 95.07 ± 0.44 | 44.05 ± 1.09 | 93.06 ± 0.59 | 92.37 ± 4.97 | 85.09 ± 0.60 | 73.67 ± 1.22 | 96.33 ± 0.60 | 94.22 ± 1.70 | 72.67 ± 0.27 | 95.75 ± 0.10 | 53.86 ± 2.15 | 96.79 ± 0.36 |
| C11 | 93.00 ± 2.71 | 96.20 ± 0.25 | 98.50 ± 0.89 | 95.48 ± 0.24 | 60.26 ± 0.41 | 96.20 ± 0.29 | 95.70 ± 0.47 | 68.66 ± 0.68 | 77.30 ± 3.00 | 97.84 ± 0.13 | 90.66 ± 1.56 | 67.85 ± 0.57 | 98.12 ± 0.30 | 71.57 ± 0.68 | 98.97 ± 0.42 |
| C12 | 71.53 ± 12.24 | 96.95 ± 0.18 | 93.14 ± 6.70 | 96.91 ± 0.15 | 40.18 ± 1.31 | 95.00 ± 1.08 | 96.45 ± 0.86 | 47.91 ± 0.49 | 51.25 ± 1.98 | 98.03 ± 0.65 | 84.41 ± 0.83 | 48.40 ± 2.91 | 92.82 ± 0.68 | 54.63 ± 0.49 | 95.85 ± 0.72 |
| C13 | 98.28 ± 2.57 | 99.39 ± 0.17 | 93.98 ± 3.18 | 98.98 ± 0.16 | 66.73 ± 0.66 | 98.35 ± 0.28 | 100.00 ± 0.00 | 93.07 ± 0.43 | 73.91 ± 2.10 | 98.35 ± 0.28 | 99.61 ± 0.27 | 89.17 ± 1.46 | 100.00 ± 0.00 | 97.57 ± 1.23 | 100.00 ± 0.00 |
| C14 | 96.40 ± 3.05 | 97.92 ± 0.23 | 99.75 ± 0.10 | 97.00 ± 0.14 | 77.88 ± 1.29 | 96.53 ± 0.21 | 97.85 ± 0.67 | 86.36 ± 0.69 | 87.83 ± 3.69 | 97.18 ± 0.24 | 97.05 ± 0.48 | 94.41 ± 0.33 | 96.35 ± 0.70 | 87.82 ± 2.09 | 97.78 ± 0.43 |
| C15 | 94.16 ± 7.94 | 96.39 ± 0.58 | 90.55 ± 1.31 | 96.08 ± 0.26 | 70.61 ± 1.03 | 93.91 ± 0.50 | 94.50 ± 1.17 | 82.25 ± 0.75 | 70.41 ± 3.42 | 98.10 ± 0.26 | 94.20 ± 2.01 | 70.71 ± 0.94 | 93.89 ± 0.23 | 83.21 ± 1.36 | 98.70 ± 0.13 |
| C16 | 87.48 ± 9.94 | 97.51 ± 0.03 | 98.74 ± 0.04 | 98.79 ± 0.00 | 59.59 ± 3.10 | 94.22 ± 2.83 | 98.73 ± 0.04 | 96.63 ± 1.15 | 53.61 ± 3.20 | 98.45 ± 0.52 | 97.54 ± 0.98 | 100.00 ± 0.00 | 96.18 ± 0.51 | 91.96 ± 1.35 | 96.03 ± 0.68 |
| OA | 84.12 ± 3.52 | 96.03 ± 0.65 | 96.86 ± 0.97 | 96.74 ± 0.22 | 60.16 ± 0.11 | 95.87 ± 0.14 | 96.02 ± 0.87 | 75.38 ± 0.13 | 74.00 ± 1.78 | 97.48 ± 0.12 | 91.80 ± 0.50 | 70.68 ± 0.38 | 96.94 ± 0.11 | 70.88 ± 0.89 | 97.92 ± 0.12 |
| AA | 68.03 ± 4.54 | 95.49 ± 0.22 | 88.31 ± 2.00 | 89.48 ± 2.26 | 58.02 ± 0.43 | 96.06 ± 0.33 | 90.35 ± 2.47 | 70.20 ± 0.34 | 71.06 ± 1.26 | 95.81 ± 0.25 | 92.71 ± 0.36 | 70.91 ± 2.66 | 93.38 ± 0.10 | 60.58 ± 0.57 | 96.35 ± 0.13 |
| × 100 | 81.82 ± 4.04 | 95.47 ± 0.74 | 96.42 ± 1.11 | 96.27 ± 0.25 | 54.13 ± 0.14 | 95.29 ± 0.16 | 95.45 ± 0.99 | 71.49 ± 0.16 | 70.29 ± 2.10 | 97.12 ± 0.14 | 90.62 ± 0.58 | 66.15 ± 0.44 | 96.51 ± 0.12 | 66.49 ± 1.05 | 97.63 ± 0.13 |
| Class | SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 100.00 ± 0.00 | 99.78 ± 0.19 | 99.96 ± 0.03 | 99.99 ± 0.00 | 99.98 ± 0.01 | 99.97 ± 0.03 | 99.74 ± 0.20 | 98.54 ± 1.08 | 99.63 ± 0.12 | 99.40 ± 0.19 | 99.95 ± 0.02 | 99.83 ± 0.14 | 99.99 ± 0.00 | 99.83 ± 0.04 | 99.99 ± 0.00 |
| C2 | 98.23 ± 2.46 | 99.59 ± 0.10 | 99.90 ± 0.08 | 99.86 ± 0.07 | 99.83 ± 0.09 | 99.94 ± 0.03 | 99.32 ± 0.31 | 96.38 ± 1.61 | 98.77 ± 0.44 | 99.75 ± 0.01 | 99.70 ± 0.09 | 99.53 ± 0.09 | 99.95 ± 0.01 | 99.56 ± 0.07 | 99.85 ± 0.12 |
| C3 | 0.00 ± 0.00 | 99.81 ± 0.06 | 97.85 ± 0.54 | 99.62 ± 0.03 | 99.73 ± 0.03 | 99.40 ± 0.59 | 98.64 ± 0.37 | 93.36 ± 2.38 | 98.79 ± 0.42 | 99.84 ± 0.02 | 99.34 ± 0.22 | 99.05 ± 0.36 | 99.91 ± 0.03 | 99.49 ± 0.10 | 99.63 ± 0.03 |
| C4 | 0.00 ± 0.00 | 90.32 ± 1.66 | 90.51 ± 4.25 | 91.70 ± 0.73 | 94.56 ± 0.29 | 84.12 ± 15.56 | 82.52 ± 6.36 | 69.78 ± 2.19 | 86.06 ± 0.71 | 93.58 ± 1.52 | 96.09 ± 0.26 | 90.54 ± 2.97 | 94.86 ± 0.96 | 91.83 ± 1.77 | 96.91 ± 0.18 |
| C5 | 32.23 ± 9.18 | 92.43 ± 5.12 | 88.48 ± 3.61 | 93.13 ± 0.23 | 98.12 ± 0.49 | 94.51 ± 6.08 | 92.22 ± 2.16 | 75.28 ± 7.74 | 91.31 ± 0.75 | 98.30 ± 0.32 | 97.93 ± 0.49 | 93.76 ± 0.40 | 98.15 ± 0.32 | 96.03 ± 0.57 | 98.46 ± 0.22 |
| C6 | 0.00 ± 0.00 | 88.32 ± 1.40 | 98.55 ± 0.30 | 90.20 ± 0.87 | 94.88 ± 0.45 | 96.32 ± 0.69 | 97.04 ± 1.44 | 63.51 ± 16.50 | 75.40 ± 4.80 | 93.89 ± 0.96 | 96.48 ± 0.51 | 87.09 ± 5.12 | 96.37 ± 1.18 | 91.04 ± 1.37 | 96.19 ± 1.09 |
| C7 | 80.50 ± 6.06 | 92.18 ± 1.25 | 84.66 ± 7.52 | 88.95 ± 2.25 | 95.23 ± 0.86 | 90.00 ± 8.54 | 82.93 ± 1.88 | 69.82 ± 3.18 | 86.47 ± 0.90 | 95.34 ± 0.80 | 95.16 ± 2.06 | 90.43 ± 0.31 | 94.98 ± 0.29 | 92.43 ± 1.18 | 96.56 ± 0.29 |
| C8 | 51.68 ± 40.89 | 88.89 ± 1.98 | 93.28 ± 4.18 | 84.64 ± 0.88 | 93.49 ± 0.56 | 93.20 ± 3.32 | 78.54 ± 3.23 | 70.64 ± 4.37 | 83.63 ± 1.34 | 93.60 ± 0.67 | 95.79 ± 0.46 | 90.15 ± 1.37 | 92.33 ± 0.74 | 91.14 ± 0.54 | 94.55 ± 0.21 |
| C9 | 0.00 ± 0.00 | 94.33 ± 2.15 | 86.48 ± 3.62 | 95.76 ± 0.41 | 90.91 ± 0.35 | 96.31 ± 2.77 | 99.56 ± 0.18 | 85.51 ± 3.69 | 91.52 ± 0.48 | 95.14 ± 0.27 | 88.31 ± 0.59 | 88.79 ± 1.25 | 93.08 ± 0.77 | 87.02 ± 3.78 | 95.90 ± 0.58 |
| C10 | 63.74 ± 14.91 | 90.53 ± 3.95 | 97.67 ± 1.24 | 89.41 ± 1.68 | 96.34 ± 0.19 | 94.98 ± 2.19 | 93.51 ± 1.49 | 63.64 ± 5.56 | 88.00 ± 0.60 | 96.67 ± 0.46 | 97.93 ± 0.27 | 92.58 ± 1.31 | 95.81 ± 0.79 | 94.37 ± 0.35 | 98.19 ± 0.34 |
| C11 | 0.00 ± 0.00 | 97.30 ± 0.92 | 96.21 ± 1.36 | 96.78 ± 0.20 | 96.33 ± 0.73 | 96.99 ± 0.78 | 98.00 ± 1.10 | 83.84 ± 9.08 | 93.78 ± 1.40 | 96.71 ± 0.26 | 98.00 ± 0.79 | 91.32 ± 2.73 | 97.49 ± 0.25 | 94.13 ± 0.54 | 98.10 ± 0.71 |
| C12 | 0.00 ± 0.00 | 80.38 ± 1.64 | 58.62 ± 7.80 | 87.68 ± 2.58 | 82.00 ± 2.42 | 80.46 ± 10.32 | 78.03 ± 4.57 | 39.88 ± 15.45 | 79.10 ± 2.46 | 85.88 ± 1.32 | 88.53 ± 1.33 | 71.02 ± 2.00 | 84.82 ± 0.63 | 77.96 ± 1.56 | 93.03 ± 1.00 |
| C13 | 64.70 ± 45.79 | 80.04 ± 5.37 | 73.53 ± 1.02 | 84.17 ± 1.86 | 86.61 ± 1.58 | 76.37 ± 16.98 | 89.34 ± 1.49 | 76.51 ± 1.55 | 79.02 ± 1.02 | 83.06 ± 0.58 | 89.18 ± 0.12 | 78.95 ± 1.65 | 83.35 ± 0.35 | 81.30 ± 1.87 | 88.43 ± 1.09 |
| C14 | 66.42 ± 46.97 | 85.55 ± 2.96 | 66.59 ± 3.75 | 82.75 ± 2.29 | 90.89 ± 0.63 | 90.00 ± 4.76 | 91.32 ± 4.87 | 63.62 ± 1.93 | 72.84 ± 2.67 | 92.93 ± 0.47 | 92.14 ± 0.89 | 86.26 ± 0.33 | 89.46 ± 0.99 | 85.11 ± 1.61 | 94.24 ± 1.09 |
| C15 | 58.84 ± 3.72 | 93.69 ± 0.95 | 84.31 ± 5.34 | 92.99 ± 1.31 | 95.74 ± 0.55 | 94.86 ± 3.08 | 87.22 ± 2.55 | 74.14 ± 3.30 | 88.88 ± 0.40 | 97.67 ± 0.27 | 93.26 ± 1.13 | 93.15 ± 0.08 | 96.01 ± 0.20 | 94.51 ± 0.37 | 97.63 ± 0.54 |
| C16 | 0.00 ± 0.00 | 88.50 ± 1.46 | 78.74 ± 7.44 | 95.92 ± 1.45 | 84.86 ± 1.69 | 88.46 ± 20.3 | 95.69 ± 0.58 | 74.06 ± 8.96 | 71.91 ± 3.61 | 84.28 ± 1.52 | 88.12 ± 2.40 | 77.68 ± 2.72 | 93.04 ± 0.59 | 85.89 ± 1.22 | 88.42 ± 0.83 |
| C17 | 0.00 ± 0.00 | 93.56 ± 1.38 | 84.63 ± 9.40 | 95.75 ± 1.84 | 96.16 ± 0.45 | 98.27 ± 0.31 | 98.47 ± 0.56 | 0.00 ± 0.00 | 86.94 ± 4.19 | 98.31 ± 0.19 | 98.03 ± 0.14 | 94.76 ± 3.07 | 96.41 ± 0.31 | 96.41 ± 0.34 | 98.82 ± 0.23 |
| C18 | 0.00 ± 0.00 | 76.80 ± 10.70 | 33.16 ± 46.90 | 95.55 ± 2.38 | 85.99 ± 3.50 | 73.69 ± 22.98 | 73.94 ± 9.50 | 0.00 ± 0.00 | 71.11 ± 3.12 | 89.63 ± 1.04 | 93.83 ± 0.34 | 74.54 ± 1.31 | 90.70 ± 1.33 | 86.79 ± 2.12 | 92.54 ± 1.17 |
| C19 | 100.00 ± 0.00 | 98.88 ± 0.58 | 99.27 ± 0.47 | 98.53 ± 0.18 | 98.83 ± 0.32 | 99.05 ± 0.69 | 96.02 ± 2.76 | 0.00 ± 0.00 | 96.92 ± 1.04 | 98.93 ± 0.28 | 99.86 ± 0.03 | 96.57 ± 2.24 | 98.67 ± 0.09 | 97.88 ± 0.83 | 98.78 ± 0.47 |
| OA | 62.40 ± 2.47 | 93.38 ± 1.47 | 89.00 ± 2.59 | 92.65 ± 0.39 | 96.09 ± 0.06 | 94.04 ± 4.22 | 89.81 ± 1.19 | 77.14 ± 2.75 | 89.90 ± 0.29 | 96.66 ± 0.11 | 95.89 ± 0.54 | 93.14 ± 0.39 | 96.02 ± 0.11 | 94.39 ± 0.20 | 97.49 ± 0.15 |
| AA | 37.70 ± 5.49 | 91.10 ± 1.56 | 84.86 ± 3.50 | 92.81 ± 0.24 | 93.71 ± 0.43 | 91.94 ± 4.87 | 91.16 ± 1.02 | 63.08 ± 3.14 | 86.32 ± 0.91 | 94.36 ± 0.18 | 95.14 ± 0.08 | 89.26 ± 1.19 | 94.49 ± 0.09 | 91.72 ± 0.07 | 96.12 ± 0.24 |
| × 100 | 54.16 ± 2.56 | 92.28 ± 1.73 | 87.04 ± 3.13 | 91.42 ± 0.47 | 95.44 ± 0.08 | 93.07 ± 4.90 | 88.02 ± 1.43 | 72.89 ± 3.39 | 88.20 ± 0.34 | 96.11 ± 0.13 | 95.19 ± 0.64 | 92.00 ± 0.45 | 95.37 ± 0.12 | 93.47 ± 0.24 | 97.07 ± 0.18 |
| SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train Time (s) | 23.79 | 42.37 | 31.39 | 26.77 | 51.72 | 211.94 | 50.55 | 12.86 | 13.25 | 48.39 | 92.50 | 69.94 | 84.06 | 23.00 | 50.12 |
| Test Time (s) | 3.88 | 7.20 | 4.19 | 5.42 | 12.50 | 21.42 | 7.93 | 2.30 | 2.32 | 8.16 | 28.28 | 9.67 | 12.09 | 18.78 | 7.15 |
| SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train Time (s) | 177.35 | 10.30 | 10.00 | 10.15 | 14.80 | 22.77 | 11.42 | 4.14 | 3.81 | 16.33 | 46.42 | 78.58 | 53.41 | 23.46 | 17.79 |
| Test Time (s) | 0.64 | 0.84 | 0.87 | 1.10 | 1.51 | 2.36 | 1.03 | 0.46 | 0.44 | 1.51 | 8.23 | 3.51 | 3.17 | 5.84 | 1.56 |
| SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train Time (s) | 793.08 | 206.92 | 194.94 | 215.90 | 252.04 | 1026.96 | 190.63 | 7.90 | 10.25 | 51.13 | 110.74 | 102.42 | 156.44 | 61.60 | 362.80 |
| Test Time (s) | 14.94 | 20.98 | 17.51 | 24.08 | 66.60 | 86.48 | 21.48 | 3.16 | 3.26 | 13.76 | 51.80 | 16.97 | 30.97 | 31.92 | 44.05 |
| SSRN | DBDA | SSGCA | PCIA | MDBNet | HDDA | DBPFA | ChebNet | GCN | MVAHN | DGFNet | FTINet | DKDMN | MRCAG | Ours | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train Time (s) | 798.44 | 152.24 | 86.51 | 111.95 | 127.58 | 442.71 | 81.32 | 14.04 | 10.91 | 51.09 | 86.10 | 98.10 | 90.18 | 34.22 | 114.91 |
| Test Time (s) | 1.64 | 3.18 | 1.88 | 2.27 | 5.64 | 8.87 | 2.40 | 1.08 | 0.69 | 4.71 | 6.41 | 2.36 | 2.46 | 4.26 | 3.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Yan, H.; Ge, H.; Wang, L.; Shi, C. Pyramid Cascaded Convolutional Neural Network with Graph Convolution for Hyperspectral Image Classification. Remote Sens. 2024, 16, 2942. https://doi.org/10.3390/rs16162942
Pan H, Yan H, Ge H, Wang L, Shi C. Pyramid Cascaded Convolutional Neural Network with Graph Convolution for Hyperspectral Image Classification. Remote Sensing. 2024; 16(16):2942. https://doi.org/10.3390/rs16162942
Chicago/Turabian StylePan, Haizhu, Hui Yan, Haimiao Ge, Liguo Wang, and Cuiping Shi. 2024. "Pyramid Cascaded Convolutional Neural Network with Graph Convolution for Hyperspectral Image Classification" Remote Sensing 16, no. 16: 2942. https://doi.org/10.3390/rs16162942
APA StylePan, H., Yan, H., Ge, H., Wang, L., & Shi, C. (2024). Pyramid Cascaded Convolutional Neural Network with Graph Convolution for Hyperspectral Image Classification. Remote Sensing, 16(16), 2942. https://doi.org/10.3390/rs16162942









