Assessment of Hygroscopic Behavior of Arctic Aerosol by Contemporary Lidar and Radiosonde Observations
Abstract
1. Introduction
2. Instruments, Methods and Data
2.1. The Koldewey Aerosol Raman Lidar and Measurement Site
2.2. Dataset and Cloud Mask
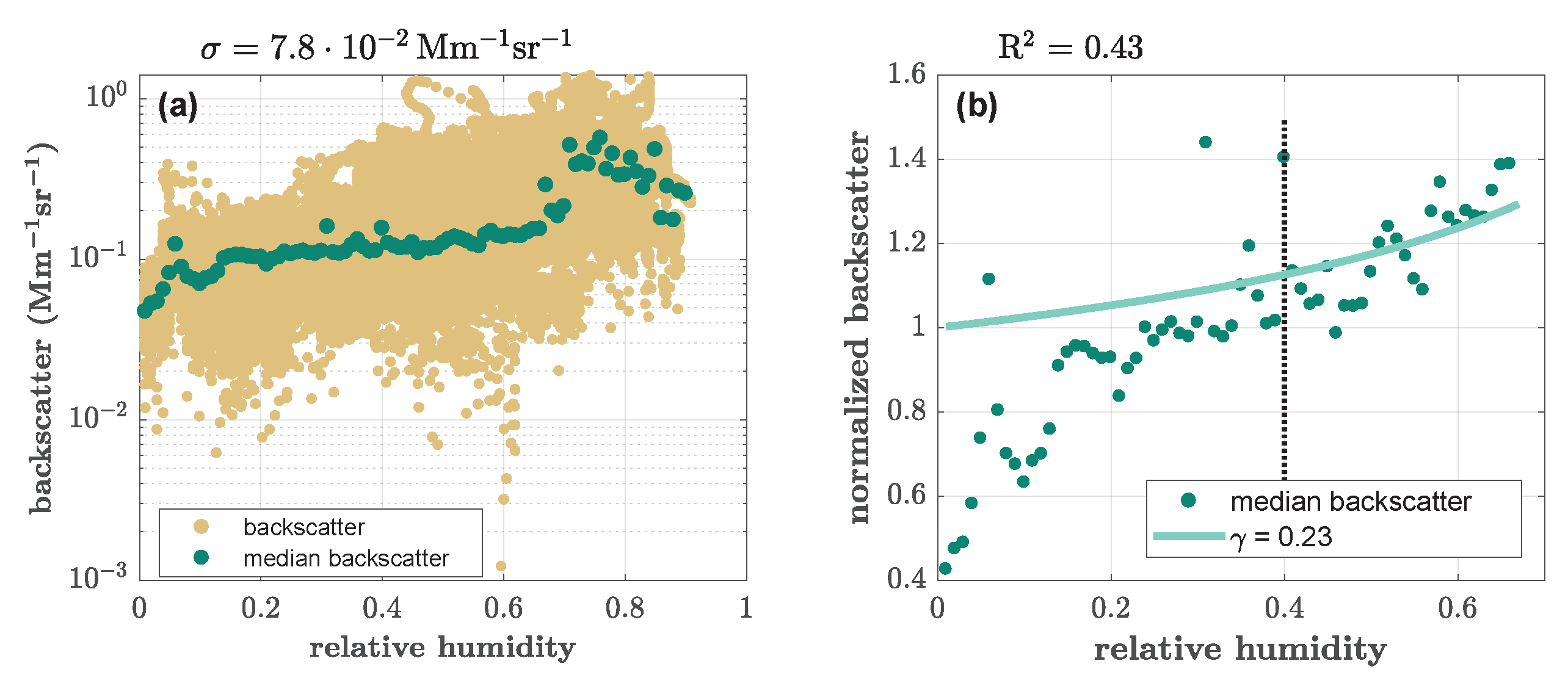
2.3. Hygroscopic Growth and the Growth Curve Model
3. Aerosol Properties in Spring and Summer 2021
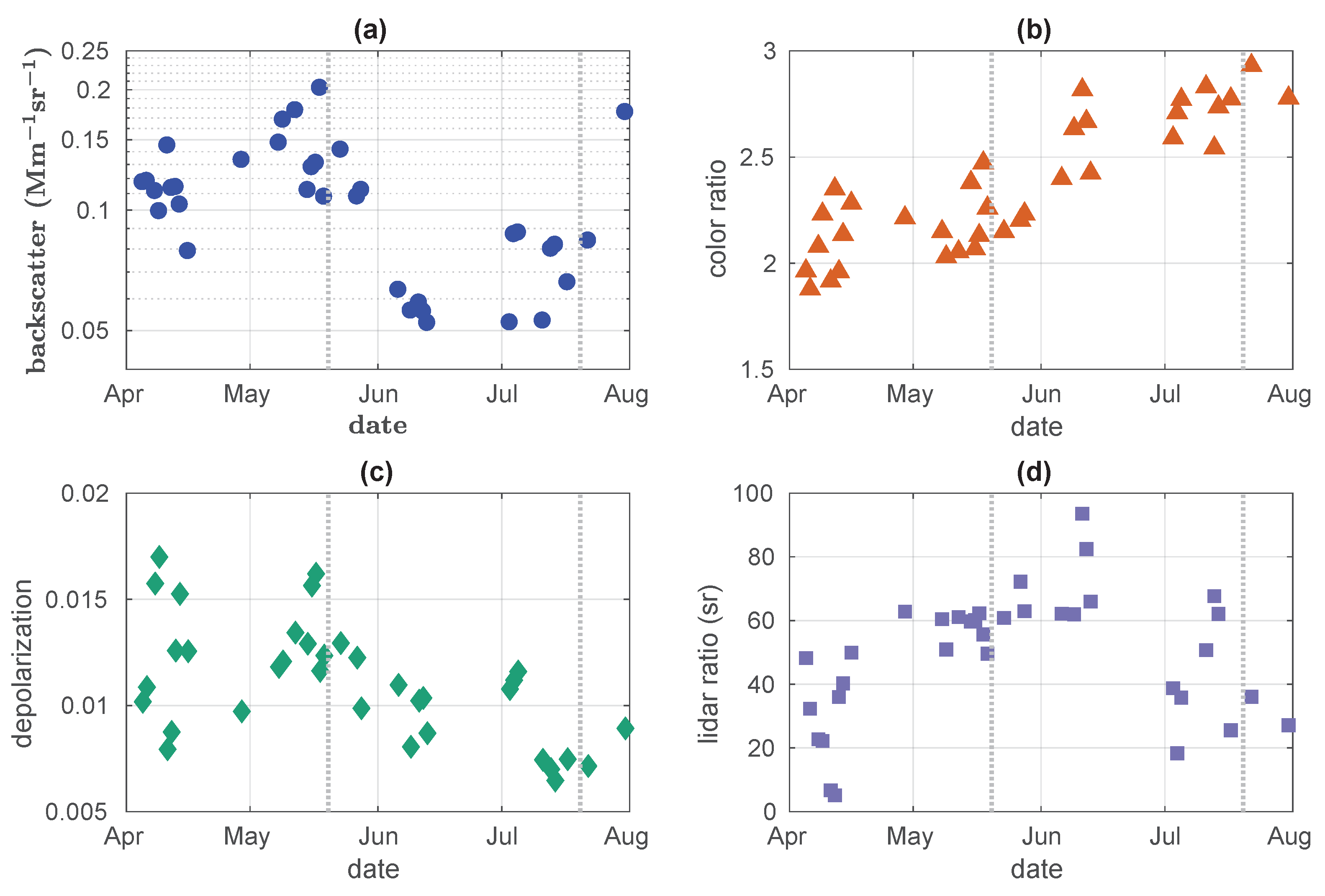
3.1. The Seasonal Aerosol Cycle from Spring to Summer 2021
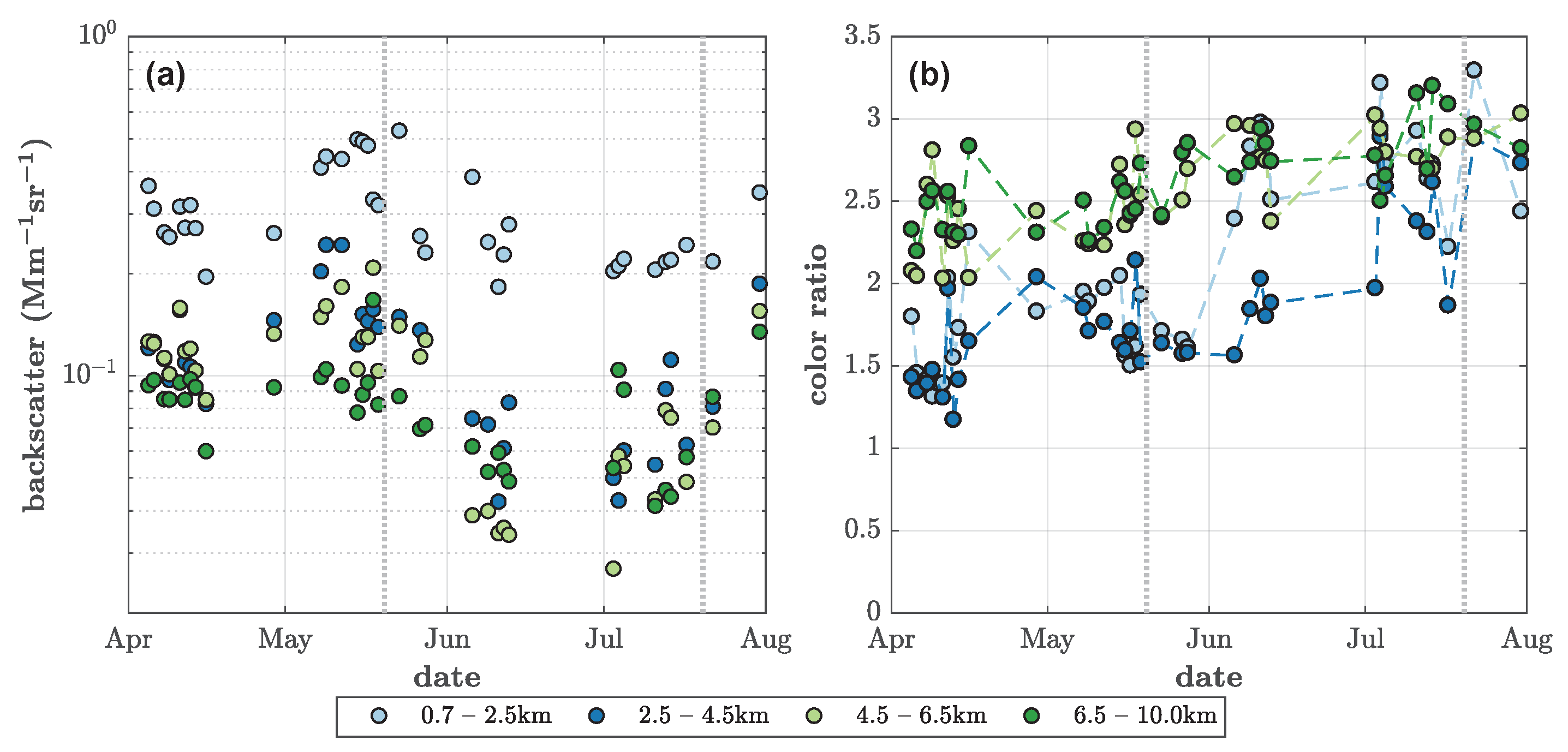
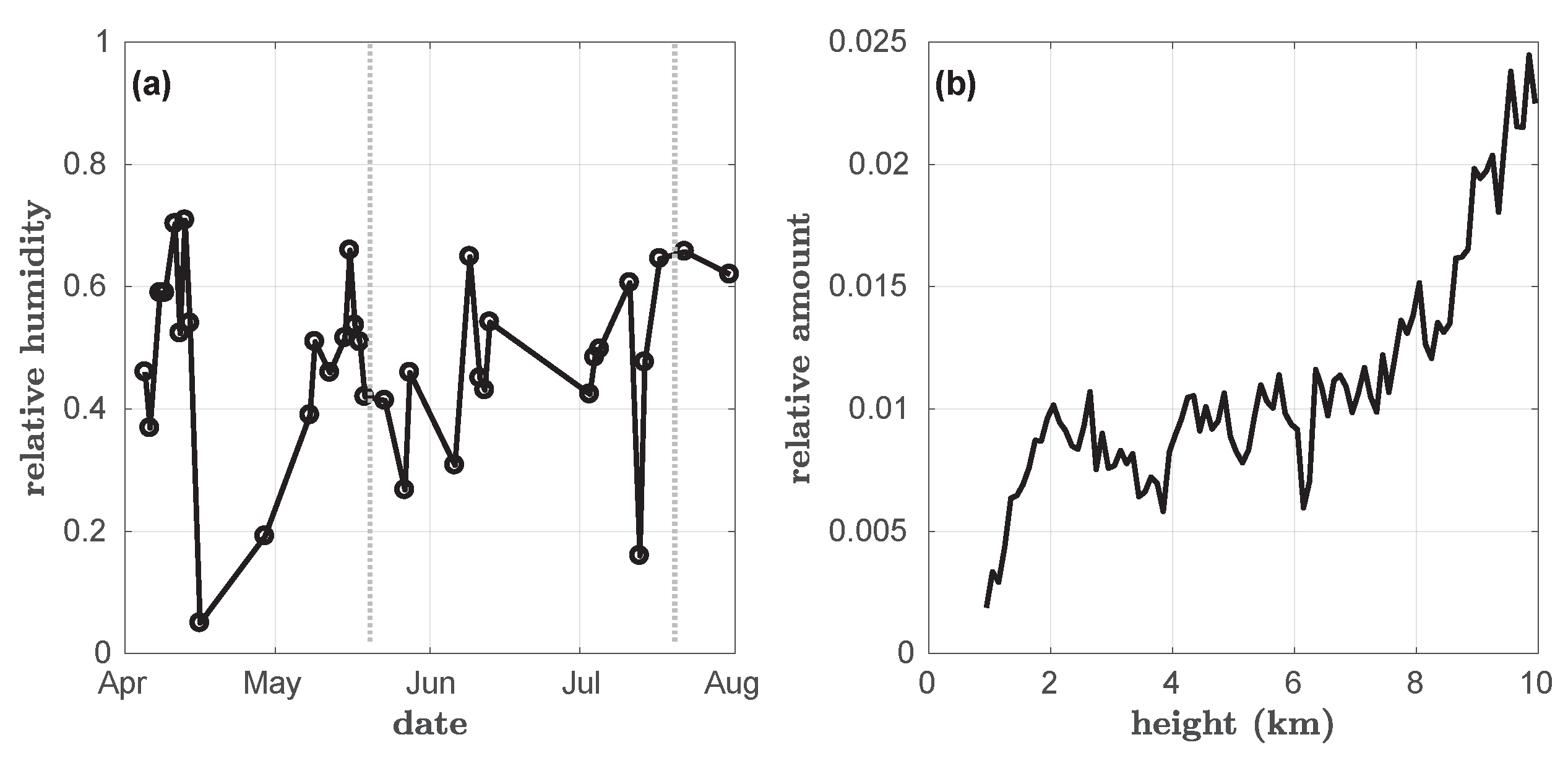
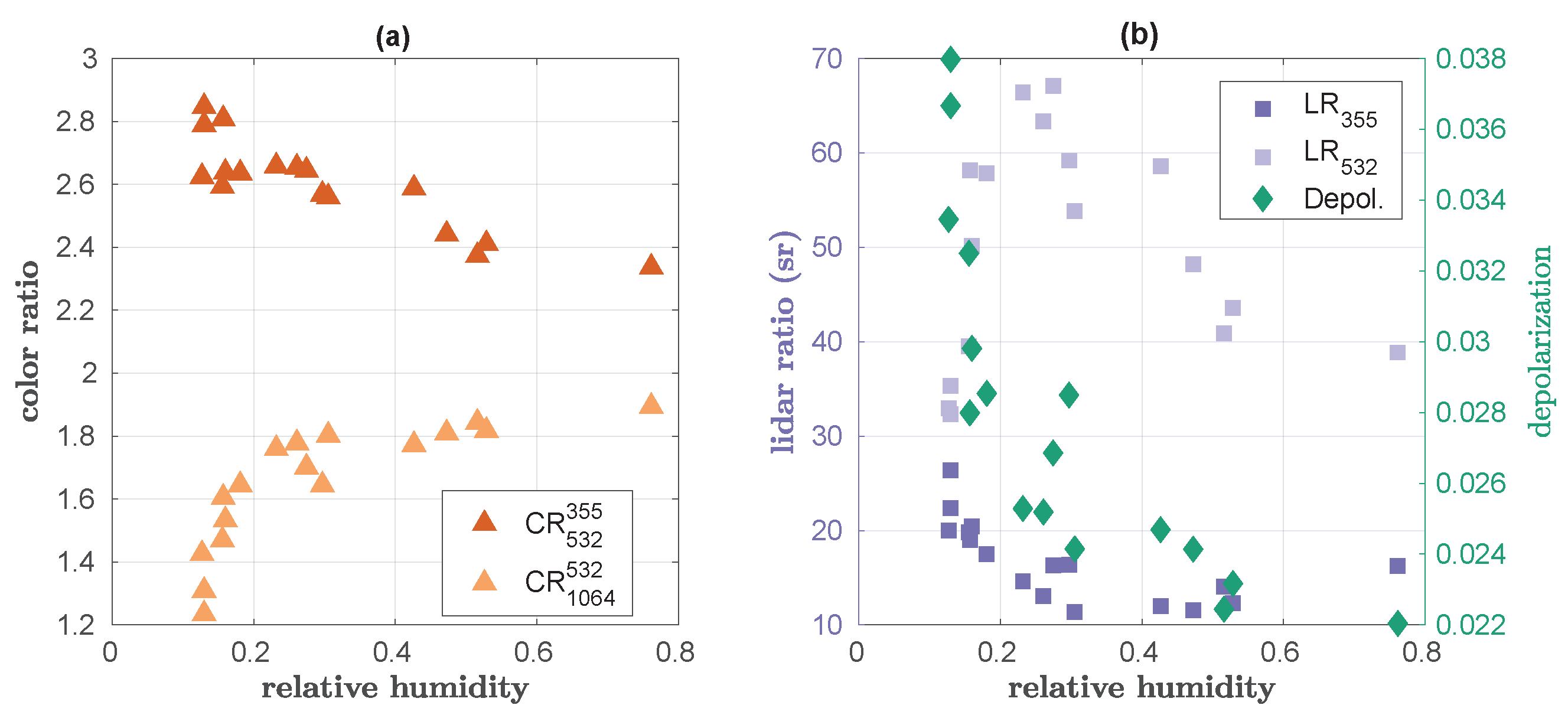
3.2. Vertical Trends in Backscatter and Color Ratio, and the Relative Humidity over Water of the Season
4. Hygroscopic Properties
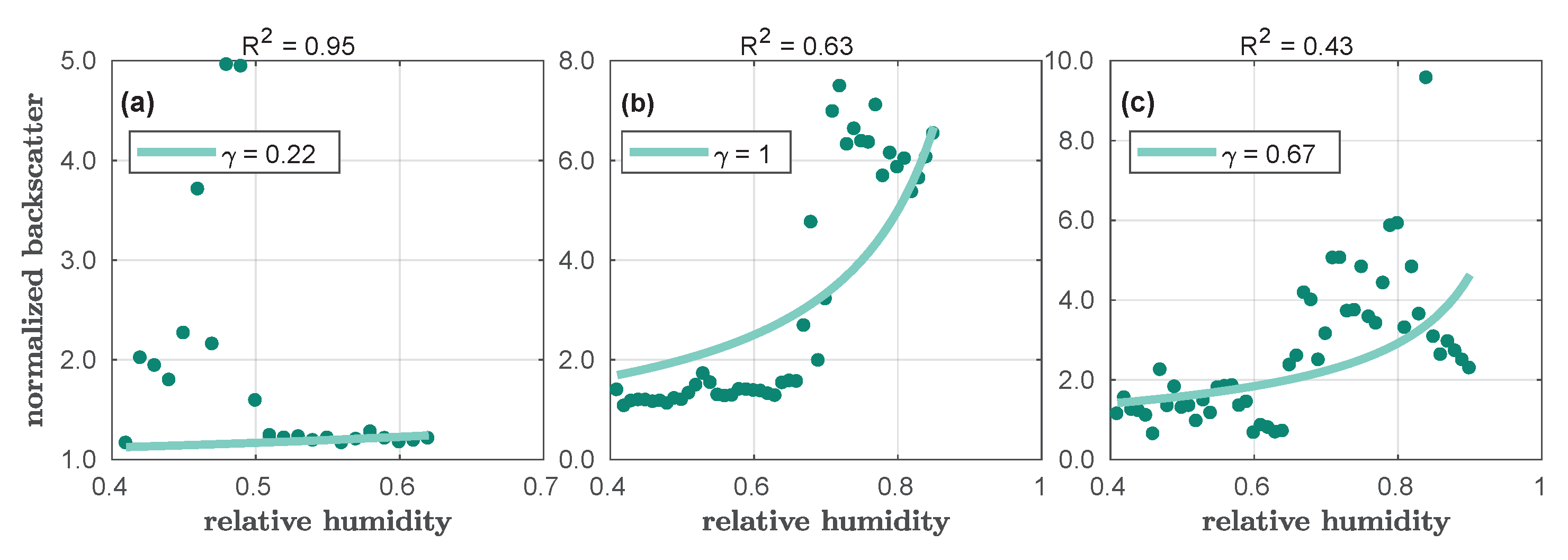
4.1. Hygroscopic Growth Analysis, Dependent on Aerosol Diameter
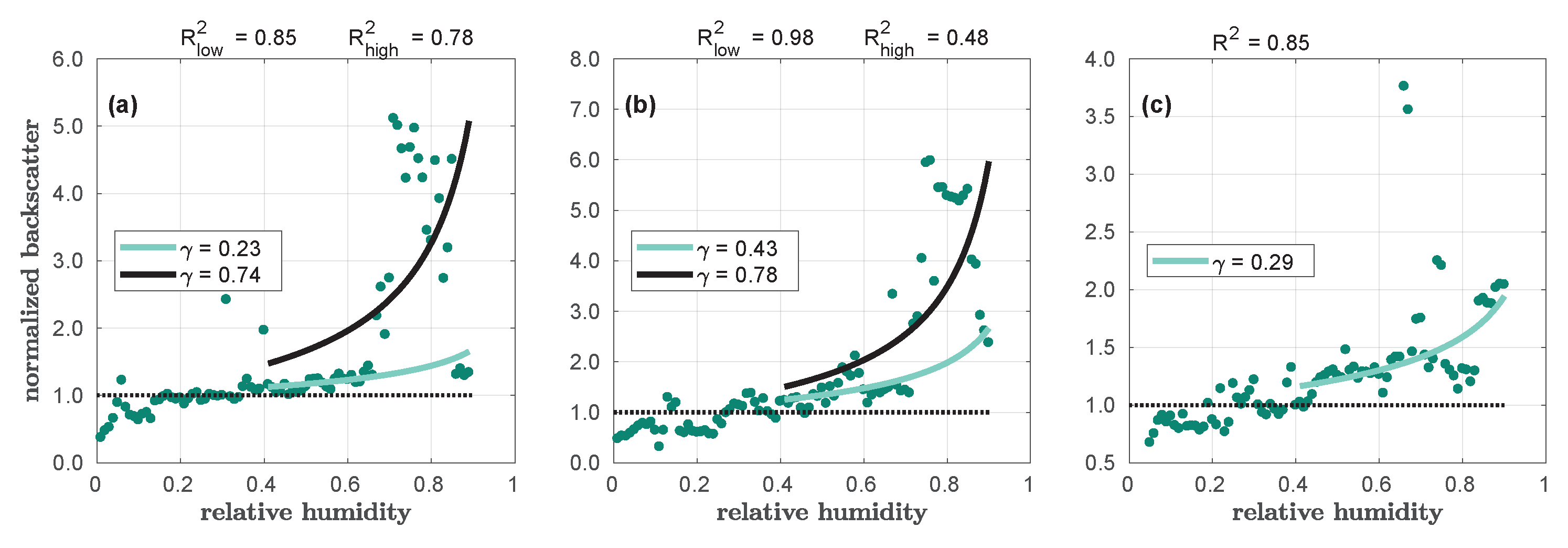
4.2. Hygroscopic Growth Analysis, Dependent on the Season
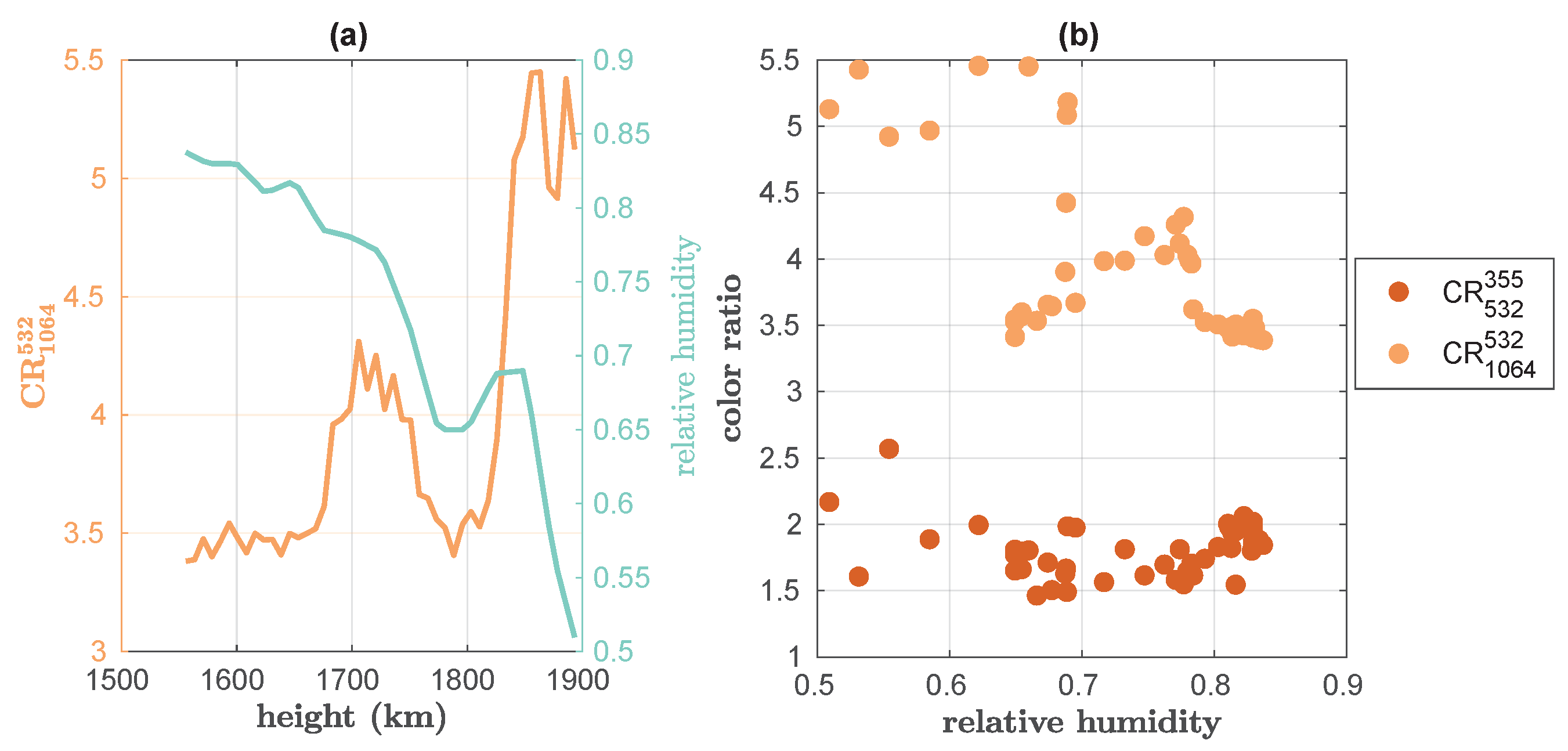
4.3. Hygroscopic Growth Analysis, Dependent on Altitude
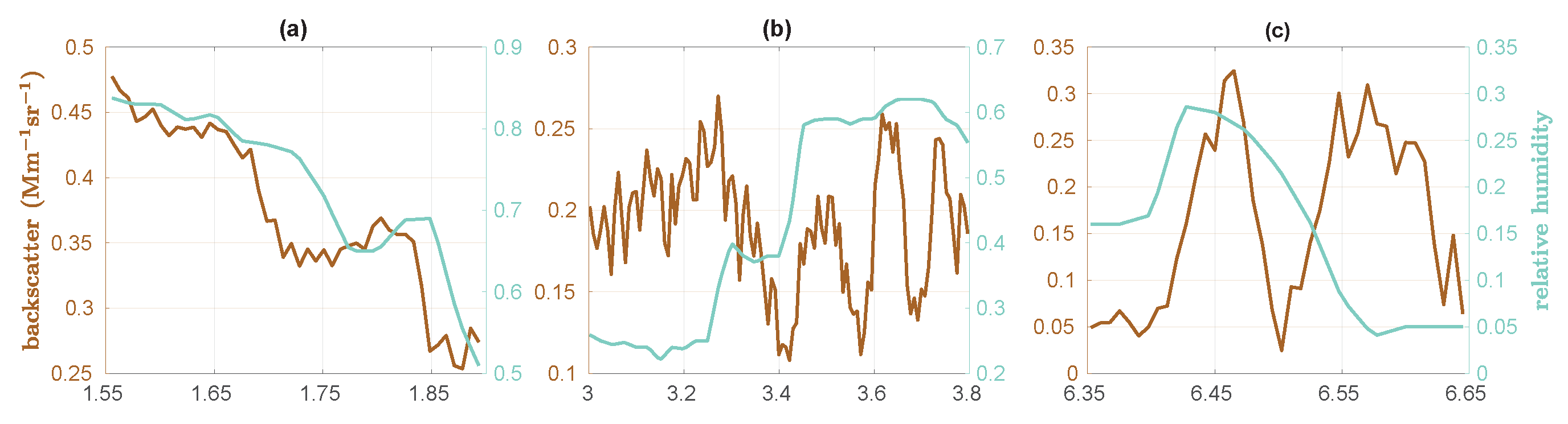
4.4. Case Study: 23 May 2021
4.5. Case Study: 29 April 2021
5. Discussion
5.1. Estimation of the Effective Aerosol Radius—According to Mie Theory
5.2. The Seasonal Cycle of Arctic Aerosol in 2021
5.3. Dependence of Hygroscopicity on Particle Size, Season and Altitude
- Particle Diameter Trends
- Seasonal Trends
- Vertical Trends
6. Conclusions
- A subdivision of the dataset according to the aerosols’ color ratio, season and altitude. The application of the growth curve model then estimated the hygroscopicity of the subdataset.
- An illustration of the often complex interpretation of the lidar data, and in particular, the color ratio. A Mie calculation was performed to obtain the relation between the color ratio and the effective aerosol radius. We showed that by three backscatter coefficients (two color ratios, no extinction coefficient) the hygroscopic growth for a large, relevant size interval could be captured with only mild assumptions on the refractive index.
- No clear trend in the hygroscopic growth with regard to the aerosol diameter could be observed. This probably resulted from its strong dependence on the aerosols’ geographical location and altitude, or even the development of backscatter with the particle radius itself (according to Mie theory). The hygroscopic growth of larger particles surely happens in the atmosphere, but it is hard to see from the inspection of the color ratio alone. Here, a full inversion of the lidar data seems necessary.
- Generally, we found two modes in hygroscopicity in different seasons: one of stronger (, only missing during the forest fire season) and one of weaker () hygroscopicity. During summer only, this weakly hygroscopic mode had a higher value. Since this hygroscopicity parameter in the present work was based on the aerosol backscatter coefficient, this number may not be directly comparable to the existing literature. However, in the atmospheric column, the aerosol may, on average, be less hygroscopic than previously derived by ground-based measurements.
- An interplay of processes causes the vertical trend in hygroscopicity to be complex. We found higher hygroscopicity and high relative humidity in the lowest altitude but could not say whether this was due to a different chemical composition or due to orographic effects. In the middle troposphere, the hygroscopicity was reduced, maybe because the probability of having aerosols that never encountered moist conditions is the highest. Finally, in the upper free troposphere, highly hygroscopic aerosols were found. These particles must have been lifted up, hence the surrounding air had apparently cooled to saturation level prior to its advection towards the Arctic. Case studies enabled this further detangling of the complex vertical trend.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Sensitivity Study: Amplifying Noise in the Extinction Coefficient with Altitude
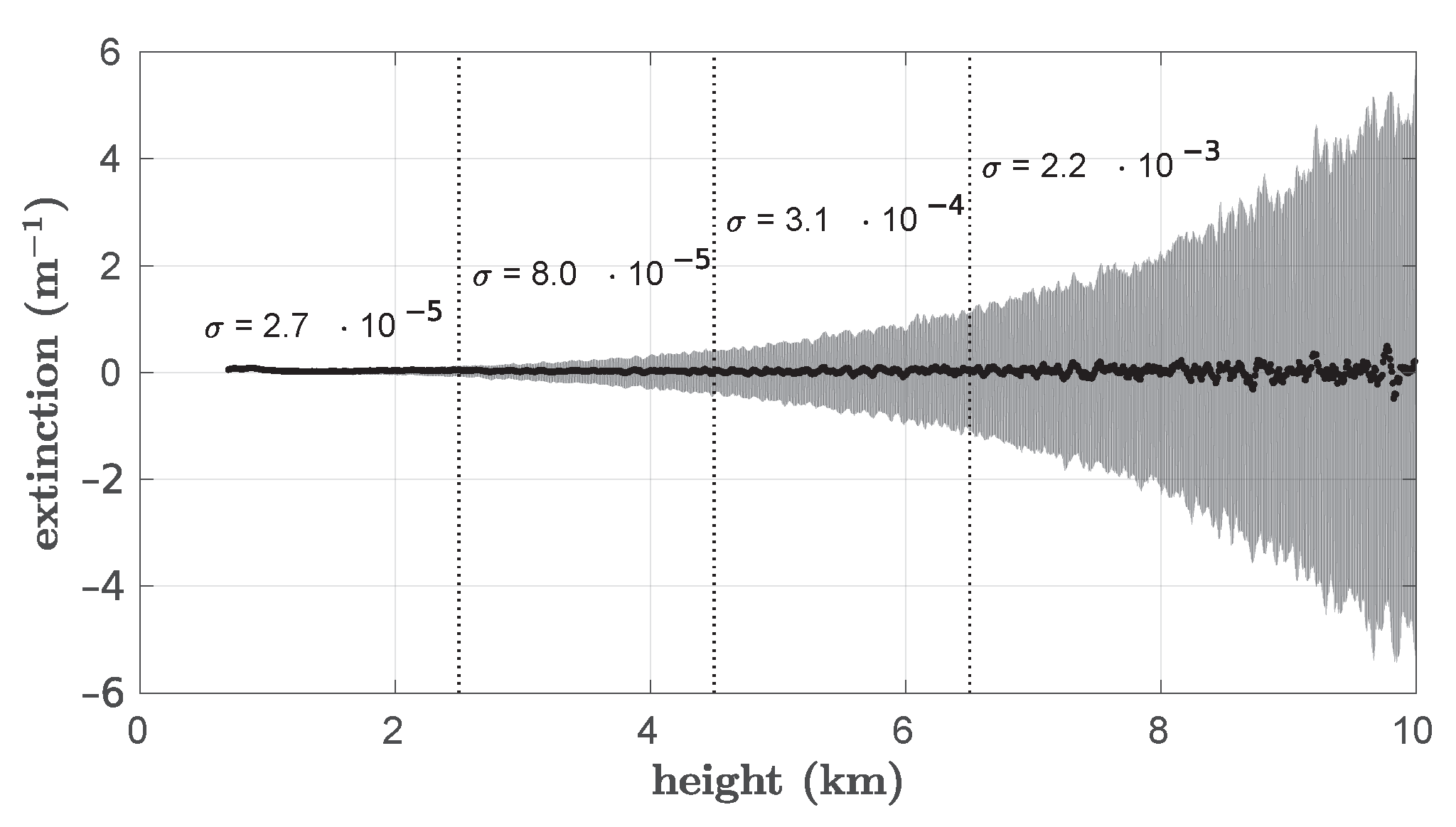
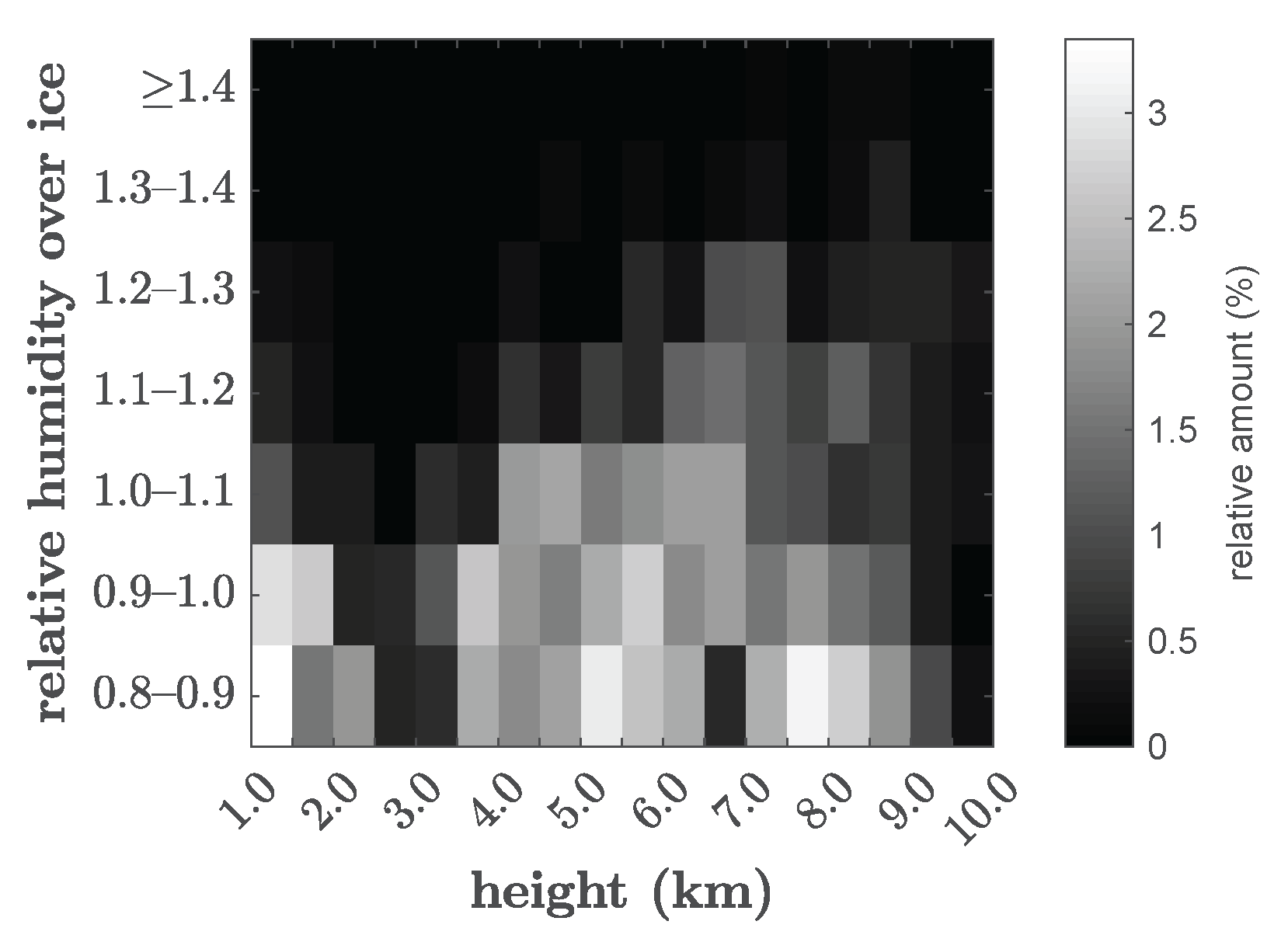
Appendix A.2. Discussion on the Importance of Relative Humidity over Ice in This Work
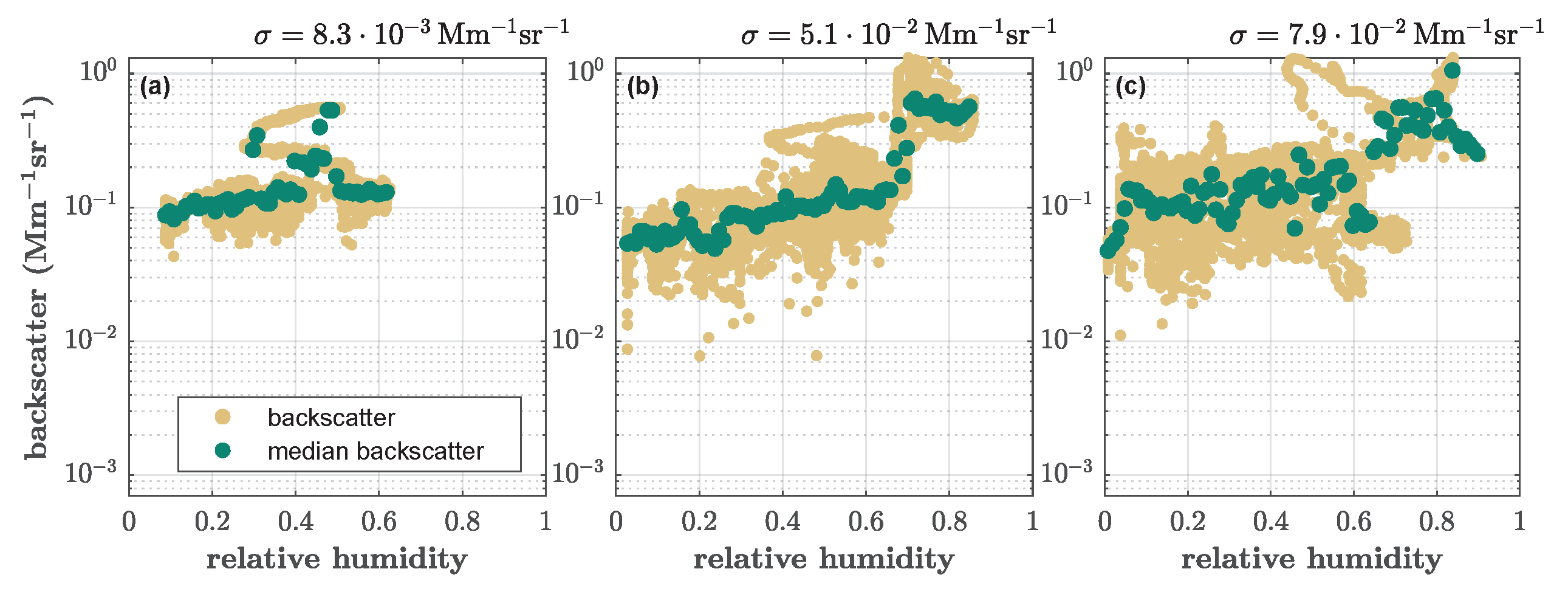
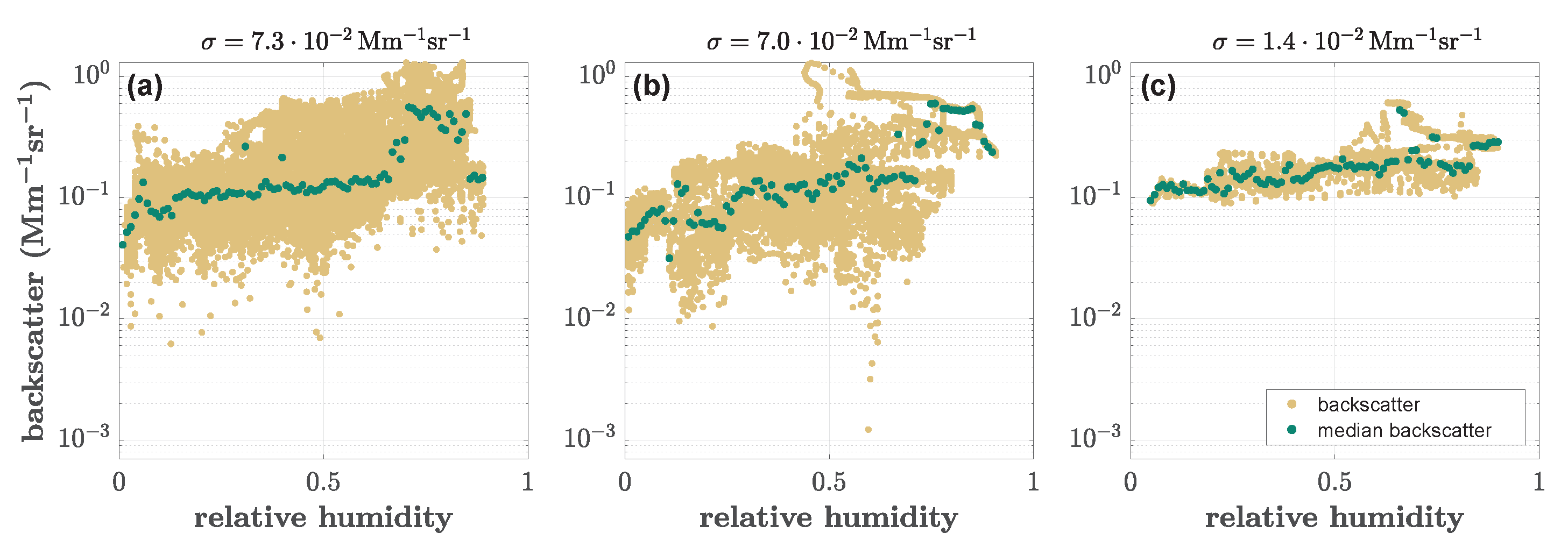
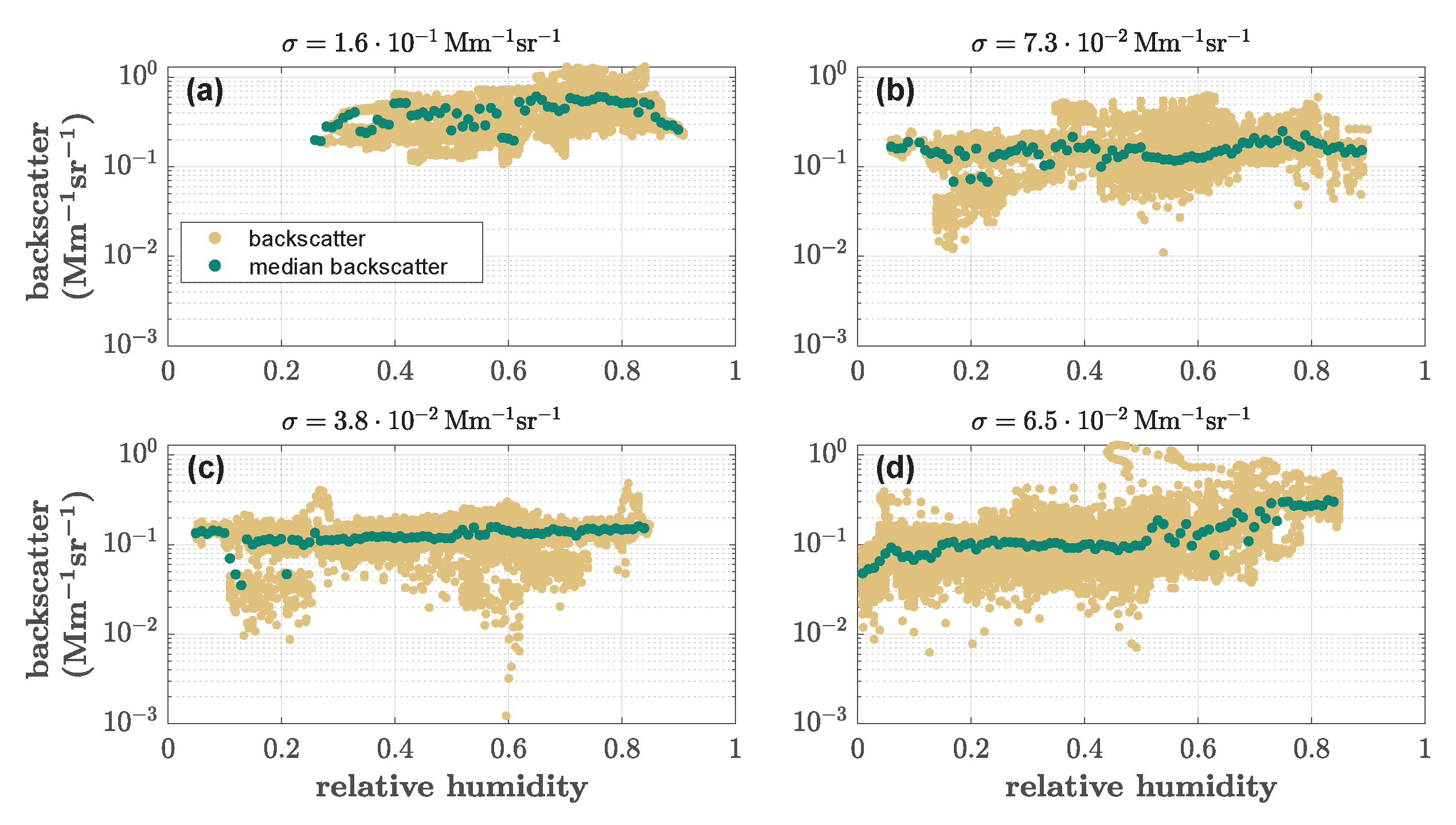
Appendix A.3. Backscatter Development with Relative Humidity for the Subdivided Datasets
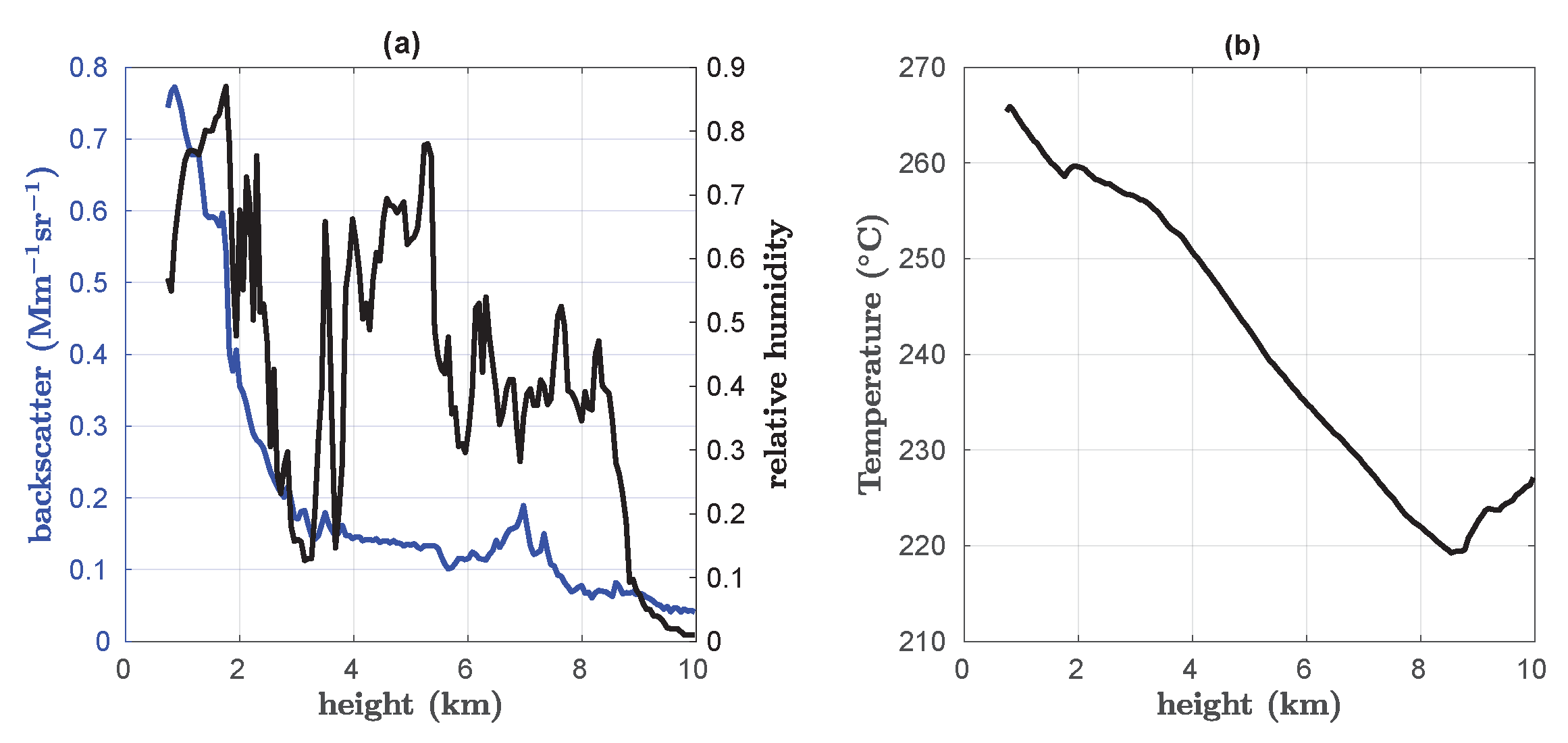
Appendix A.4. Backscatter, Relative Humidity and Temperature Profiles on 23 May 2021
References
- Maturilli, M.; Herber, A.; König-Langlo, G. Surface radiation climatology for Ny-Ålesund, Svalbard (78.9 N), basic observations for trend detection. Theor. Appl. Climatol. 2015, 120, 331–339. [Google Scholar]
- Wendisch, M.; Brückner, M.; Crewell, S.; Ehrlich, A.; Notholt, J.; Lüpkes, C.; Macke, A.; Burrows, J.; Rinke, A.; Quaas, J.; et al. Atmospheric and surface processes, and feedback mechanisms determining Arctic amplification: A review of first results and prospects of the (AC) 3 project. Bull. Am. Meteorol. Soc. 2023, 104, E208–E242. [Google Scholar]
- Serreze, M.C.; Barry, R.G. Processes and impacts of Arctic amplification: A research synthesis. Glob. Planet. Chang. 2011, 77, 85–96. [Google Scholar] [CrossRef]
- Previdi, M.; Smith, K.L.; Polvani, L.M. Arctic amplification of climate change: A review of underlying mechanisms. Environ. Res. Lett. 2021, 16, 093003. [Google Scholar] [CrossRef]
- Stjern, C.W.; Lund, M.T.; Samset, B.H.; Myhre, G.; Forster, P.M.; Andrews, T.; Boucher, O.; Faluvegi, G.; Fläschner, D.; Iversen, T.; et al. Arctic Amplification Response to Individual Climate Drivers. J. Geophys. Res. Atmos. 2019, 124, 6698–6717. [Google Scholar] [CrossRef]
- Schmale, J.; Zieger, P. Aerosols in current and future Arctic climate. Nat. Clim. Chang. 2021, 11, 95–105. [Google Scholar] [CrossRef]
- Creamean, J.M.; Barry, K.; Hill, T.C.J.; Hume, C.; DeMott, P.J.; Shupe, M.D.; Dahlke, S.; Willmes, S.; Schmale, J.; Beck, I.; et al. Annual cycle observations of aerosols capable of ice formation in central Arctic clouds. Nat. Commun. 2022, 13, 3537. [Google Scholar] [CrossRef]
- Li, J.; Carlson, B.E.; Yung, Y.L.; Lv, D.; Hansen, J.; Penner, J.E.; Liao, H.; Ramaswamy, V.; Kahn, R.A.; Zhang, P.; et al. Scattering and absorbing aerosols in the climate system. Nat. Rev. Earth Environ. 2022, 3, 363–379. [Google Scholar] [CrossRef]
- Quinn, P.K.; Shaw, G.; Andrews, E.; Dutton, E.; Ruoho-Airola, T.; Gong, S. Arctic haze: Current trends and knowledge gaps. Tellus B Chem. Phys. Meteorol. 2007, 59, 99–114. [Google Scholar]
- Stohl, A. Characteristics of atmospheric transport into the Arctic troposphere. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Zielinski, T.; Bolzacchini, E.; Cataldi, M.; Ferrero, L.; Graßl, S.; Hansen, G.; Mateos, D.; Mazzola, M.; Neuber, R.; Pakszys, P.; et al. Study of chemical and optical properties of biomass burning aerosols during long-range transport events toward the arctic in summer 2017. Atmosphere 2020, 11, 84. [Google Scholar] [CrossRef]
- Udisti, R.; Bazzano, A.; Becagli, S.; Bolzacchini, E.; Caiazzo, L.; Cappelletti, D.; Ferrero, L.; Frosini, D.; Giardi, F.; Grotti, M.; et al. Sulfate source apportionment in the Ny-Ålesund (Svalbard Islands) Arctic aerosol. Rend. Lincei 2016, 27, 85–94. [Google Scholar]
- Tunved, P.; Ström, J.; Krejci, R. Arctic aerosol life cycle: Linking aerosol size distributions observed between 2000 and 2010 with air mass transport and precipitation at Zeppelin station, Ny-Ålesund, Svalbard. Atmos. Chem. Phys. 2013, 13, 3643–3660. [Google Scholar] [CrossRef]
- Ritter, C.; Neuber, R.; Schulz, A.; Markowicz, K.; Stachlewska, I.; Lisok, J.; Makuch, P.; Pakszys, P.; Markuszewski, P.; Rozwadowska, A.; et al. 2014 iAREA campaign on aerosol in Spitsbergen–Part 2: Optical properties from Raman-lidar and in-situ observations at Ny-Ålesund. Atmos. Environ. 2016, 141, 1–19. [Google Scholar]
- Platt, S.M.; Hov, Ø.; Berg, T.; Breivik, K.; Eckhardt, S.; Eleftheriadis, K.; Evangeliou, N.; Fiebig, M.; Fisher, R.; Hansen, G.; et al. Atmospheric composition in the European Arctic and 30 years of the Zeppelin Observatory, Ny-Ålesund. Atmos. Chem. Phys. Discuss. 2021, 22, 3321–3369. [Google Scholar]
- Graßl, S.; Ritter, C. Properties of arctic aerosol based on sun photometer long-term measurements in Ny-Ålesund, Svalbard. Remote Sens. 2019, 11, 1362. [Google Scholar] [CrossRef]
- Ferrero, L.; Ritter, C.; Cappelletti, D.; Moroni, B.; Močnik, G.; Mazzola, M.; Lupi, A.; Becagli, S.; Traversi, R.; Cataldi, M.; et al. Aerosol optical properties in the Arctic: The role of aerosol chemistry and dust composition in a closure experiment between Lidar and tethered balloon vertical profiles. Sci. Total. Environ. 2019, 686, 452–467. [Google Scholar] [PubMed]
- Schmale, J.; Baccarini, A. Progress in Unraveling Atmospheric New Particle Formation and Growth Across the Arctic. Geophys. Res. Lett. 2021, 48, e2021GL094198. [Google Scholar] [CrossRef]
- Nakoudi, K.; Ritter, C.; Böckmann, C.; Kunkel, D.; Eppers, O.; Rozanov, V.; Mei, L.; Pefanis, V.; Jäkel, E.; Herber, A.; et al. Does the Intra-Arctic Modification of Long-Range Transported Aerosol Affect the Local Radiative Budget? (A Case Study). Remote Sens. 2020, 12, 2112. [Google Scholar] [CrossRef]
- Johnson, J.S.; Regayre, L.A.; Yoshioka, M.; Pringle, K.J.; Turnock, S.T.; Browse, J.; Sexton, D.M.H.; Rostron, J.W.; Schutgens, N.A.J.; Partridge, D.G.; et al. Robust observational constraint of uncertain aerosol processes and emissions in a climate model and the effect on aerosol radiative forcing. Atmos. Chem. Phys. 2020, 20, 9491–9524. [Google Scholar] [CrossRef]
- Tang, I.N. Chemical and size effects of hygroscopic aerosols on light scattering coefficients. J. Geophys. Res. Atmos. 1996, 101, 19245–19250. [Google Scholar] [CrossRef]
- Gassó, S.; Hegg, D.A.; Covert, D.S.; Collins, D.; Noone, K.J.; Öström, E.; Schmid, B.; Russell, P.B.; Livingston, J.M.; Durkee, P.A.; et al. Influence of humidity on the aerosol scattering coefficient and its effect on the upwelling radiance during ACE-2. Tellus B Chem. Phys. Meteorol. 2000, 52, 546–567. [Google Scholar] [CrossRef]
- Vu, T.V.; Shi, Z.; Harrison, R.M. Estimation of hygroscopic growth properties of source-related sub-micrometre particle types in a mixed urban aerosol. npj Clim. Atmos. Sci. 2021, 4, 21. [Google Scholar] [CrossRef]
- Zieger, P.; Fierz-Schmidhauser, R.; Weingartner, E.; Baltensperger, U. Effects of relative humidity on aerosol light scattering: Results from different European sites. Atmos. Chem. Phys. 2013, 13, 10609–10631. [Google Scholar] [CrossRef]
- Zieger, P.; Fierz-Schmidhauser, R.; Gysel, M.; Ström, J.; Henne, S.; Yttri, K.E.; Baltensperger, U.; Weingartner, E. Effects of relative humidity on aerosol light scattering in the Arctic. Atmos. Chem. Phys. 2010, 10, 3875–3890. [Google Scholar] [CrossRef]
- Rastak, N.; Silvergren, S.; Zieger, P.; Wideqvist, U.; Ström, J.; Svenningsson, B.; Maturilli, M.; Tesche, M.; Ekman, A.M.L.; Tunved, P.; et al. Seasonal variation of aerosol water uptake and its impact on the direct radiative effect at Ny-Ålesund, Svalbard. Atmos. Chem. Phys. 2014, 14, 7445–7460. [Google Scholar] [CrossRef]
- Dawson, K.; Ferrare, R.; Moore, R.; Clayton, M.; Thorsen, T.; Eloranta, E. Ambient aerosol hygroscopic growth from combined Raman lidar and HSRL. J. Geophys. Res. Atmos. 2020, 125, e2019JD031708. [Google Scholar]
- Zhao, Y.; Wang, X.; Cai, Y.; Pan, J.; Yue, W.; Xu, H.; Wang, J. Measurements of atmospheric aerosol hygroscopic growth based on multi-channel Raman-Mie lidar. Atmos. Environ. 2021, 246, 118076. [Google Scholar]
- Wang, Q.; Mao, J.; Zhang, Y. Effect of aerosol hygroscopic growth on radiative forcing based on a Raman lidar. Air Qual. Atmos. Health 2023, 16, 1489–1499. [Google Scholar]
- Hoffmann, A. Comparative Aerosol Studies Based on Multi-Wavelength Raman LIDAR at Ny-Ålesund, Spitsbergen. Ph.D. Thesis, Universität Potsdam, Potsdam, Germany, 2011. [Google Scholar]
- Maturilli, M.; Kayser, M. Arctic warming, moisture increase and circulation changes observed in the Ny-Ålesund homogenized radiosonde record. Theor. Appl. Climatol. 2017, 130, 1–17. [Google Scholar]
- Ansmann, A.; Wandinger, U.; Riebesell, M.; Weitkamp, C.; Michaelis, W. Independent measurement of extinction and backscatter profiles in cirrus clouds by using a combined Raman elastic-backscatter lidar. Appl. Opt. 1992, 31, 7113–7131. [Google Scholar] [CrossRef] [PubMed]
- Klett, J.D. Lidar inversion with variable backscatter/extinction ratios. Appl. Opt. 1985, 24, 1638–1643. [Google Scholar] [CrossRef] [PubMed]
- Shibata, T.; Shiraishi, K.; Shiobara, M.; Iwasaki, S.; Takano, T. Seasonal Variations in High Arctic Free Tropospheric Aerosols Over Ny-Ålesund, Svalbard, Observed by Ground-Based Lidar. J. Geophys. Res. Atmos. 2018, 123, 12353–12367. [Google Scholar] [CrossRef]
- Nakoudi, K.; Stachlewska, I.S.; Ritter, C. An extended lidar-based cirrus cloud retrieval scheme: First application over an Arctic site. Opt. Express 2021, 29, 8553–8580. [Google Scholar] [CrossRef] [PubMed]
- Vu, T.V.; Delgado-Saborit, J.M.; Harrison, R.M. A review of hygroscopic growth factors of submicron aerosols from different sources and its implication for calculation of lung deposition efficiency of ambient aerosols. Air Qual. Atmos. Health 2015, 8, 429–440. [Google Scholar] [CrossRef]
- Swietlicki, E.; Hansson, H.C.; Hämeri, K.; Svenningsson, B.; Massling, A.; Mcfiggans, G.; Mcmurry, P.H.; Petäjä, T.; Tunved, P.; Gysel, M.; et al. Hygroscopic properties of submicrometer atmospheric aerosol particles measured with H-TDMA instruments in various environments—A review. Tellus B Chem. Phys. Meteorol. 2008, 60, 432–469. [Google Scholar] [CrossRef]
- Dube, J.; Böckmann, C.; Ritter, C. Lidar-Derived Aerosol Properties from Ny-Ålesund, Svalbard during the MOSAiC Spring 2020. Remote Sens. 2022, 14, 2578. [Google Scholar] [CrossRef]
- Foken, T. Springer Handbook of Atmospheric Measurements, 1st ed.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Khattatov, V.; Tyabotov, A.; Alekseev, A. An aircraft lidar method of studying aerosol in the free troposphere over Siberia. Atmos. Res. 1997, 44, 89–98. [Google Scholar]
- Ferrare, R.A.; Melfi, S.H.; Whiteman, D.N.; Evans, K.D.; Poellot, M.; Kaufman, Y.J. Raman lidar measurements of aerosol extinction and backscattering: 2. Derivation of aerosol real refractive index, single-scattering albedo, and humidification factor using Raman lidar and aircraft size distribution measurements. J. Geophys. Res. Atmos. 1998, 103, 19673–19689. [Google Scholar] [CrossRef]
- Böckmann, C.; Ritter, C.; Graßl, S. Improvement of Aerosol Coarse-Mode Detection through Additional Use of Infrared Wavelengths in the Inversion of Arctic Lidar Data. Remote Sens. 2024, 16, 1576. [Google Scholar] [CrossRef]
- Böckmann, C. Hybrid regularization method for the ill-posed inversion of multiwavelength lidar data in the retrieval of aerosol size distributions. Appl. Opt. 2001, 40, 1329–1342. [Google Scholar]
- Sassen, K. Polarization in Lidar. In Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Weitkamp, C., Ed.; Springer: New York, NY, USA, 2005; pp. 19–42. [Google Scholar] [CrossRef]
- Herber, A.; Thomason, L.W.; Gernandt, H.; Leiterer, U.; Nagel, D.; Schulz, K.H.; Kaptur, J.; Albrecht, T.; Notholt, J. Continuous day and night aerosol optical depth observations in the Arctic between 1991 and 1999. J. Geophys. Res. Atmos. 2002, 107, AAC 6-1–AAC 6-13. [Google Scholar]
- Schmeisser, L.; Backman, J.; Ogren, J.A.; Andrews, E.; Asmi, E.; Starkweather, S.; Uttal, T.; Fiebig, M.; Sharma, S.; Eleftheriadis, K.; et al. Seasonality of aerosol optical properties in the Arctic. Atmos. Chem. Phys. 2018, 18, 11599–11622. [Google Scholar] [CrossRef]
- Koffi, B.; Schulz, M.; Bréon, F.M.; Dentener, F.; Steensen, B.M.; Griesfeller, J.; Winker, D.; Balkanski, Y.; Bauer, S.E.; Bellouin, N.; et al. Evaluation of the aerosol vertical distribution in global aerosol models through comparison against CALIOP measurements: AeroCom phase II results. J. Geophys. Res. Atmos. 2016, 121, 7254–7283. [Google Scholar] [CrossRef]
- Tomasi, C.; Kokhanovsky, A.A.; Lupi, A.; Ritter, C.; Smirnov, A.; O’Neill, N.T.; Stone, R.S.; Holben, B.N.; Nyeki, S.; Wehrli, C.; et al. Aerosol remote sensing in polar regions. Earth-Sci. Rev. 2015, 140, 108–157. [Google Scholar] [CrossRef]
- Rader, F.; Traversi, R.; Severi, M.; Becagli, S.; Müller, K.J.; Nakoudi, K.; Ritter, C. Overview of Aerosol Properties in the European Arctic in Spring 2019 Based on In Situ Measurements and Lidar Data. Atmosphere 2021, 12, 271. [Google Scholar] [CrossRef]
- Dall’Osto, M.; Beddows, D.C.; Tunved, P.; Harrison, R.M.; Lupi, A.; Vitale, V.; Becagli, S.; Traversi, R.; Park, K.T.; Yoon, Y.J.; et al. Simultaneous measurements of aerosol size distributions at three sites in the European high Arctic. Atmos. Chem. Phys. 2019, 19, 7377–7395. [Google Scholar]
- Navas-Guzmán, F.; Martucci, G.; Collaud Coen, M.; Granados-Muñoz, M.J.; Hervo, M.; Sicard, M.; Haefele, A. Characterization of aerosol hygroscopicity using Raman lidar measurements at the EARLINET station of Payerne. Atmos. Chem. Phys. 2019, 19, 11651–11668. [Google Scholar] [CrossRef]
- Lv, M.; Liu, D.; Li, Z.; Mao, J.; Sun, Y.; Wang, Z.; Wang, Y.; Xie, C. Hygroscopic growth of atmospheric aerosol particles based on lidar, radiosonde, and in situ measurements: Case studies from the Xinzhou field campaign. J. Quant. Spectrosc. Radiat. Transf. 2017, 188, 60–70. [Google Scholar] [CrossRef]
- Rissler, J.; Vestin, A.; Swietlicki, E.; Fisch, G.; Zhou, J.; Artaxo, P.; Andreae, M.O. Size distribution and hygroscopic properties of aerosol particles from dry-season biomass burning in Amazonia. Atmos. Chem. Phys. 2006, 6, 471–491. [Google Scholar] [CrossRef]
- Lathem, T.L.; Beyersdorf, A.J.; Thornhill, K.L.; Winstead, E.L.; Cubison, M.J.; Hecobian, A.; Jimenez, J.L.; Weber, R.J.; Anderson, B.E.; Nenes, A. Analysis of CCN activity of Arctic aerosol and Canadian biomass burning during summer 2008. Atmos. Chem. Phys. 2013, 13, 2735–2756. [Google Scholar] [CrossRef]
- Hara, K.; Yamagata, S.; Yamanouchi, T.; Sato, K.; Herber, A.; Iwasaka, Y.; Nagatani, M.; Nakata, H. Mixing states of individual aerosol particles in spring Arctic troposphere during ASTAR 2000 campaign. J. Geophys. Res. Atmos. 2003, 108, 4209. [Google Scholar] [CrossRef]
- Schacht, J.; Heinold, B.; Quaas, J.; Backman, J.; Cherian, R.; Ehrlich, A.; Herber, A.; Huang, W.T.K.; Kondo, Y.; Massling, A.; et al. The importance of the representation of air pollution emissions for the modeled distribution and radiative effects of black carbon in the Arctic. Atmos. Chem. Phys. 2019, 19, 11159–11183. [Google Scholar] [CrossRef]
- Schrod, J.; Thomson, E.S.; Weber, D.; Kossmann, J.; Pöhlker, C.; Saturno, J.; Ditas, F.; Artaxo, P.; Clouard, V.; Saurel, J.M.; et al. Long-term INP measurements from four stations across the globe. Atmos. Chem. Phys. Discuss. 2020, 20, 15983–16006. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eggers, N.; Graßl, S.; Ritter, C. Assessment of Hygroscopic Behavior of Arctic Aerosol by Contemporary Lidar and Radiosonde Observations. Remote Sens. 2024, 16, 3087. https://doi.org/10.3390/rs16163087
Eggers N, Graßl S, Ritter C. Assessment of Hygroscopic Behavior of Arctic Aerosol by Contemporary Lidar and Radiosonde Observations. Remote Sensing. 2024; 16(16):3087. https://doi.org/10.3390/rs16163087
Chicago/Turabian StyleEggers, Nele, Sandra Graßl, and Christoph Ritter. 2024. "Assessment of Hygroscopic Behavior of Arctic Aerosol by Contemporary Lidar and Radiosonde Observations" Remote Sensing 16, no. 16: 3087. https://doi.org/10.3390/rs16163087
APA StyleEggers, N., Graßl, S., & Ritter, C. (2024). Assessment of Hygroscopic Behavior of Arctic Aerosol by Contemporary Lidar and Radiosonde Observations. Remote Sensing, 16(16), 3087. https://doi.org/10.3390/rs16163087






