Incoherent Detection Performance Analysis of the Distributed Multiple-Input Multiple-Output Radar for Rice Fluctuating Targets
Abstract
:1. Introduction
- A new closed-form expression of the sum of independent and weighted squares of Rice variables is proposed in terms of the infinite series involving the confluent Lauricella function.
- For the the independent identically distributed (i.i.d.) Rice case, the proposed PDF expression is reduced to the infinite series involving the confluent hypergeometric function.
- The uniform convergence of this closed-form expression is also analyzed.
- The proposed expression is exploited to evaluate the detection probability of MIMO radar for the Rice fluctuating targets.
2. System Model
3. PDF of the Variable Y
4. Detection Performance Prediction
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Wang, H.; Xu, L.; Yan, Z.; Gulliver, T.A. Low-complexity MIMO-FBMC sparse channel parameter estimation for industrial big data communications. IEEE Trans. Ind. Inform. 2021, 17, 3422–3430. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Lin, Y.; Cui, G.; Yuen, C.; Sari, H. Joint DOD and DOA estimation for NLOS target using IRS-aided bistatic MIMO radar. IEEE Trans. Veh. Technol. 2024. [Google Scholar] [CrossRef]
- Xu, Z.; Fan, C.; Huang, X. MIMO radar waveform design for multipath exploitation. IEEE Trans. Signal Process. 2021, 69, 5359–5371. [Google Scholar] [CrossRef]
- Ma, Y.; Miao, C.; Long, W.; Zhang, R.; Chen, Q.; Zhang, J.; Wu, W. Time-modulated arrays in scanning mode using wideband signals for range-doppler estimation with time-frequency filtering and fusion. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 980–990. [Google Scholar] [CrossRef]
- Haimovich, A.M.; Blum, R.S.; Cimini, L.J. MIMO radar with widely separated antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Kalkan, Y. 20 years of MIMO radar. IEEE Aerosp. Electron. Syst. Mag. 2024, 39, 28–35. [Google Scholar] [CrossRef]
- Sun, S.; Hu, Y.; Mishra, K.V.; Petropulu, A.P. Widely separated MIMO radar using matrix completion. IEEE Trans. Radar Syst. 2024, 2, 180–196. [Google Scholar] [CrossRef]
- Luo, D.; Wen, G.; Liang, Y.; Zhu, L.; Song, H. Beam scheduling for early warning with distributed MIMO radars. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6044–6058. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.; Cimini, R.; Chizhik, D.; Valenzuela, R. Spatial diversity in radars–Models and detection perofrmance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Liang, Y.; Wen, G.; Zhu, L.; Luo, D.; Song, H.; Kuai, Y. Target measurement performance of distributed MIMO radar systems under nonideal conditions. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1006–1022. [Google Scholar] [CrossRef]
- Liang, Y.; Wen, G.; Zhu, L.; Luo, D.; Kuai, Y.; Li, B. Target detection performance of distributed MIMO radar systems under nonideal conditions. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1951–1969. [Google Scholar] [CrossRef]
- Wang, B.; Cui, G.; Yi, W.; Kong, L.; Yang, Y. Performance prediction of noncoherent detector for independent and nonidentically distributed NCG fluctuating targets. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2184–2192. [Google Scholar] [CrossRef]
- Wang, J.; Ye, J.; Hua, G. The optimal detector of distributed MIMO radar under Swerling-Chi scattering models. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1129–1133. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, F.; Li, H.; Govoni, M.A. Target detection for distributed MIMO radar with nonorthogonal waveforms in cluttered environments. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5448–5459. [Google Scholar]
- Zhang, R.; Cheng, L.; Wang, S.; Lou, Y.; Gao, Y.; Wu, W.; Ng, D.W.K. Integrated sensing and communication with massive MIMO: A unified tensor approach for channel and target parameter estimation. IEEE Trans. Wirel. Commun. 2024, 23, 8571–8587. [Google Scholar] [CrossRef]
- Zhao, X.; Li, J.; Guo, Q. Robust target localization in distributed MIMO radar with nonconvex ℓp minimization and iterative reweighting. IEEE Commun. Lett. 2023, 27, 3230–3234. [Google Scholar] [CrossRef]
- Ni, L.; Zhang, D.; Sun, Y.; Liu, N.; Liang, J.; Wan, Q. Detection and localization of one-bit signal in multiple distributed subarray systems. IEEE Trans. Signal Process. 2023, 71, 2776–2791. [Google Scholar] [CrossRef]
- Song, H.; Wen, G.; Liang, Y.; Zhu, L.; Luo, D. Target localization and clock refinement in distributed MIMO radar systems with time synchronization errors. IEEE Trans. Signal Process. 2021, 69, 3088–3103. [Google Scholar] [CrossRef]
- Dontamsetti, S.G.; Kumar, R.V.R. A distributed MIMO radar with joint optimal transmit and receive signal combining. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 623–635. [Google Scholar] [CrossRef]
- Aittomaki, T.; Koivunen, V. Performance of MIMO radar with angular diversity under Swerling scattering models. IEEE J. Sel. Top. Signal Process. 2010, 4, 101–114. [Google Scholar]
- Moya, M.D.; Amores, M.J.; Zurera, R.M.; Borge, J.C.N.; Ferreras, F.L. Combining MLPs and RBFNNs to detect signals with unknown parameters. IEEE Trans. Instrum. Meas. 2009, 58, 2989–2995. [Google Scholar] [CrossRef]
- He, Q.; Blum, R.S.; Haimovich, A.M. Noncoherent MIMO radar for location and velocity estimation: More antennas means better performance. IEEE Trans. Signal Process. 2010, 58, 3661–3680. [Google Scholar] [CrossRef]
- Yang, H.; Chun, J. An improved algebraic solution for moving target localization in noncoherent MIMO radar systems. IEEE Trans. Signal Process. 2016, 64, 258–270. [Google Scholar] [CrossRef]
- Yi, W.; Zhou, T.; Ai, Y.; Blum, R.S. Suboptimal low complexity joint multi-target detection and localization for non-coherent MIMO radar with widely separated antennas. IEEE Trans. Signal Process. 2020, 68, 901–916. [Google Scholar] [CrossRef]
- Yang, Y.; Yi, W.; Zhang, T.; Cui, G.; Kong, L.; Yang, X.; Yang, J. Fast optimal antenna placement for distributed MIMO radar with surveillance performance. IEEE Signal Process. Lett. 2015, 22, 1955–1959. [Google Scholar] [CrossRef]
- Cui, G.; DeMaio, A.; Piezzo, M. Performance prediction of the incoherent radar detector for correlated generalized Swerling-chi fluctuating targets. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 356–368. [Google Scholar] [CrossRef]
- Papanicolopoulos, C.D.; Blair, W.D.; Sherman, D.L.; BrandtPearce, M. Use of a Rician distribution for modeling aspect-dependent RCS amplitude and scintillation. In Proceedings of the IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 218–223. [Google Scholar]
- Song, X.; Blair, W.D.; Willett, P.; Zhou, S. Dominant-plus-Rayleigh models for RCS: Swerling III/IV versus Rician. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 54–60. [Google Scholar] [CrossRef]
- Richards, M.A.; Scheer, J.A.; Holm, W.A. Principles of Modern Radar: Basic Principles; SciTech Publishing: Raleigh, NC, USA, 2010. [Google Scholar]
- Cui, G.; DeMaio, A.; Carotenuto, V.; Pallotta, L. Performance prediction of the incoherent detector for a Weibull fluctuating target. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2176–2184. [Google Scholar] [CrossRef]
- Jacobs, L.; Alexandropoulos, G.; Moeneclaey, M.; Bruneel, H.; Mathiopoulos, P. Analysis and efficient evaluation of the BER of OSTBCs with imperfect channel estimation in arbitrarily correlated fading channels. IEEE Trans. Signal Process. 2011, 59, 2720–2733. [Google Scholar] [CrossRef]
- Simon, M.K.; Alouini, M.S. Digital Communication over Fading Channels, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Kaur, M.; Yadav, R.K. Performance analysis of Beaulieu-Xie fading channel with MRC diversity reception. Trans. Emerg. Telecommun. Technol. 2020, 31, 1–13. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Karlsson, P.W. Multiple Gaussian Hypergeometric Series; Wiley: Hoboken, NJ, USA, 1985. [Google Scholar]
- Paris, J.F. Statistical characterization of κ–μ shadowed fading. IEEE Trans. Veh. Technol. 2014, 63, 518–526. [Google Scholar] [CrossRef]
- Al-Hmood, H.; Al-Raweshidy, H.S. On the sum and the maximum of nonidentically distributed composite η–μ/gamma variates using a mixture gamma distribution with applications to diversity receivers. IEEE Trans. Veh. Technol. 2016, 65, 10048–10052. [Google Scholar] [CrossRef]
- Clemente, M.C.; Paris, J.F. Closed-form statistics for sum of squared rician shadowed variates and its application. Electron. Lett. 2014, 50, 120–121. [Google Scholar] [CrossRef]
- Martos-Naya, E.; Romero-Jerez, J.M.; Lopez-Martinez, F.J.; Paris, J.F. A MATLAB Program for the Computation of the Confluent Hypergeometric Function Φ2; Tech. Rep. 10630/12068; Repositorio Institucional Universidad de Málaga: Málaga, Spain, 2016. [Google Scholar]
- Arfken, G. Mathematical Methods for Physicists, 3rd ed.; Academic Press: Orlando, FL, USA, 1985; pp. 301–303. [Google Scholar]
- András, S.; Baricz, Á.; Sun, Y. The generalized Marcum Q-function: An orthogonal polynomial approach. Acta Univ. Sapientiae Math. 2011, 3, 60–76. [Google Scholar]
- Kalyani, S.; Karthik, R.M. The asymptotic distribution of maxima of independent and identically distributed sums of correlated or non-identical gamma random variables and its applications. IEEE Trans. Commun. 2012, 60, 2747–2758. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge Univ. Press: New York, NY, USA, 2010. [Google Scholar]
- Aalo, V.A.; Piboongungon, T.; Efthymoglou, G.P. Another look at the performance of MRC schemes in Nakagami-m fading channels with arbitrary parameters. IEEE Trans. Commun. 2005, 53, 2002–2005. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 9th ed.; Dover: New York, NY, USA, 1972. [Google Scholar]
- Liu, J.; Liu, W.; Chen, B.; Liu, H.; Li, H. Detection probability of a CFAR matched filter with signal steering vector errors. IEEE Signal Process. Lett. 2015, 22, 2474–2478. [Google Scholar] [CrossRef]
- Tao, T. An Introduction to Measure Theory; AMS: Providence, RI, USA, 2011; Volume 126. [Google Scholar]
- Kumar, S. Approximate outage probability and capacity for κ − μ shadowed fading. IEEE Commun. Lett. 2015, 4, 301–304. [Google Scholar] [CrossRef]
- Mordell, L.J.; Bromwich, T.J. An Introduction to the Theory of Infinite Series. Math. Gaz. 1908, 13, 453. [Google Scholar]
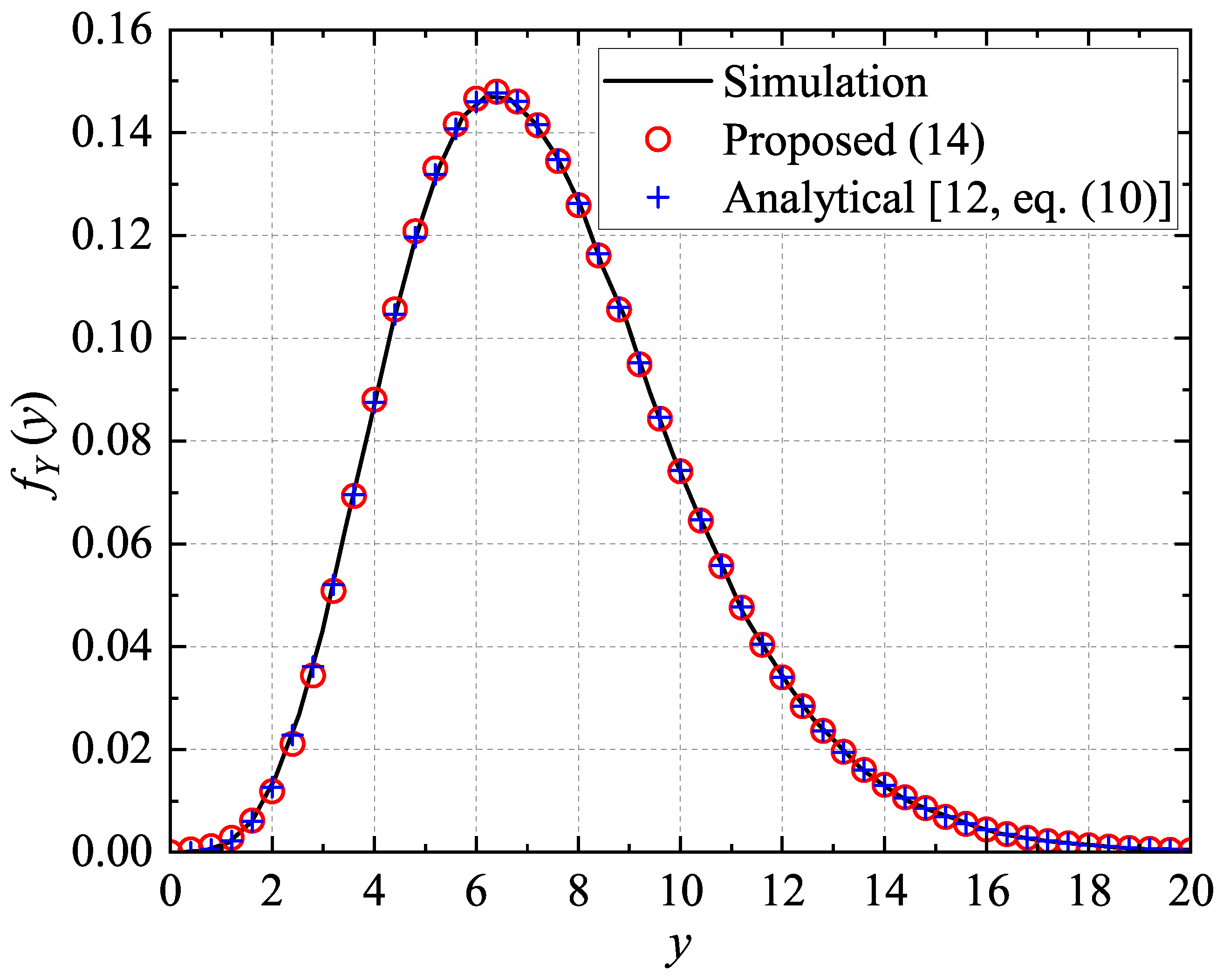
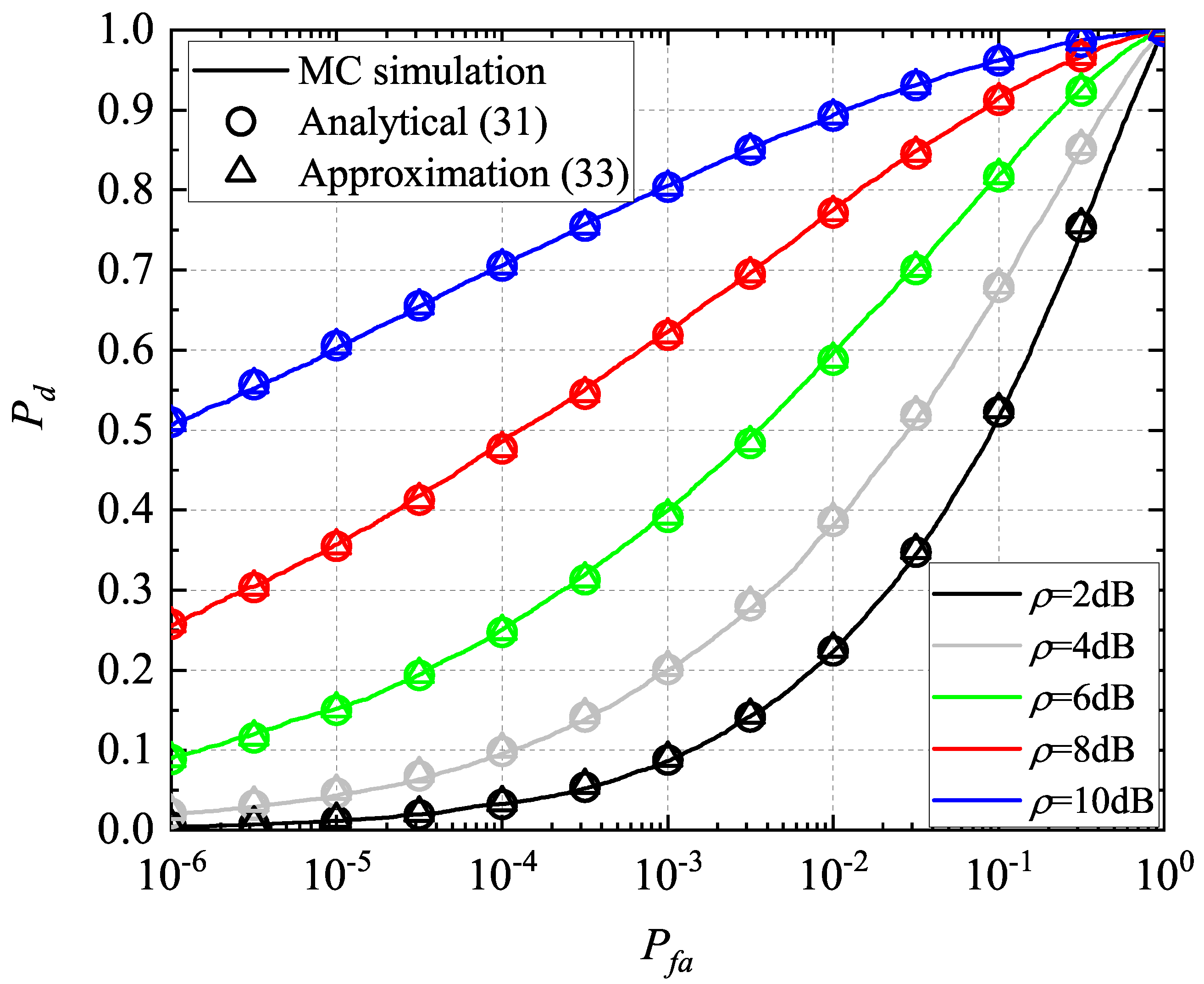


| Symbol | Definition |
|---|---|
| P | The total transmitted power |
| M | The number of transmitters |
| N | The number of receivers |
| The target scattering coefficient between the ith transmitter, the target, and the jth receiver | |
| The target scattering coefficient amplitude between the ith transmitter, the target, and the jth receiver | |
| The target scattering coefficient phase between the ith transmitter, the target, and the jth receiver | |
| The shape parameter of the Rice variable | |
| The scale parameter of the Rice variable | |
| The noise variance | |
| The probability of false alarm | |
| The probability of detection | |
| The threshold |
| Variable | Proposed (14) | Analytical ([12], Equation (10)) |
|---|---|---|
| 0.088019 | 0.087541 | |
| 0.125869 | 0.126226 | |
| 0.034027 | 0.034013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Z.-W.; Wang, J. Incoherent Detection Performance Analysis of the Distributed Multiple-Input Multiple-Output Radar for Rice Fluctuating Targets. Remote Sens. 2024, 16, 3240. https://doi.org/10.3390/rs16173240
Miao Z-W, Wang J. Incoherent Detection Performance Analysis of the Distributed Multiple-Input Multiple-Output Radar for Rice Fluctuating Targets. Remote Sensing. 2024; 16(17):3240. https://doi.org/10.3390/rs16173240
Chicago/Turabian StyleMiao, Zhuo-Wei, and Jianbo Wang. 2024. "Incoherent Detection Performance Analysis of the Distributed Multiple-Input Multiple-Output Radar for Rice Fluctuating Targets" Remote Sensing 16, no. 17: 3240. https://doi.org/10.3390/rs16173240






