Stripe Noise Elimination with a Novel Trend Repair Method for Push-Broom Thermal Images
Abstract
:1. Introduction
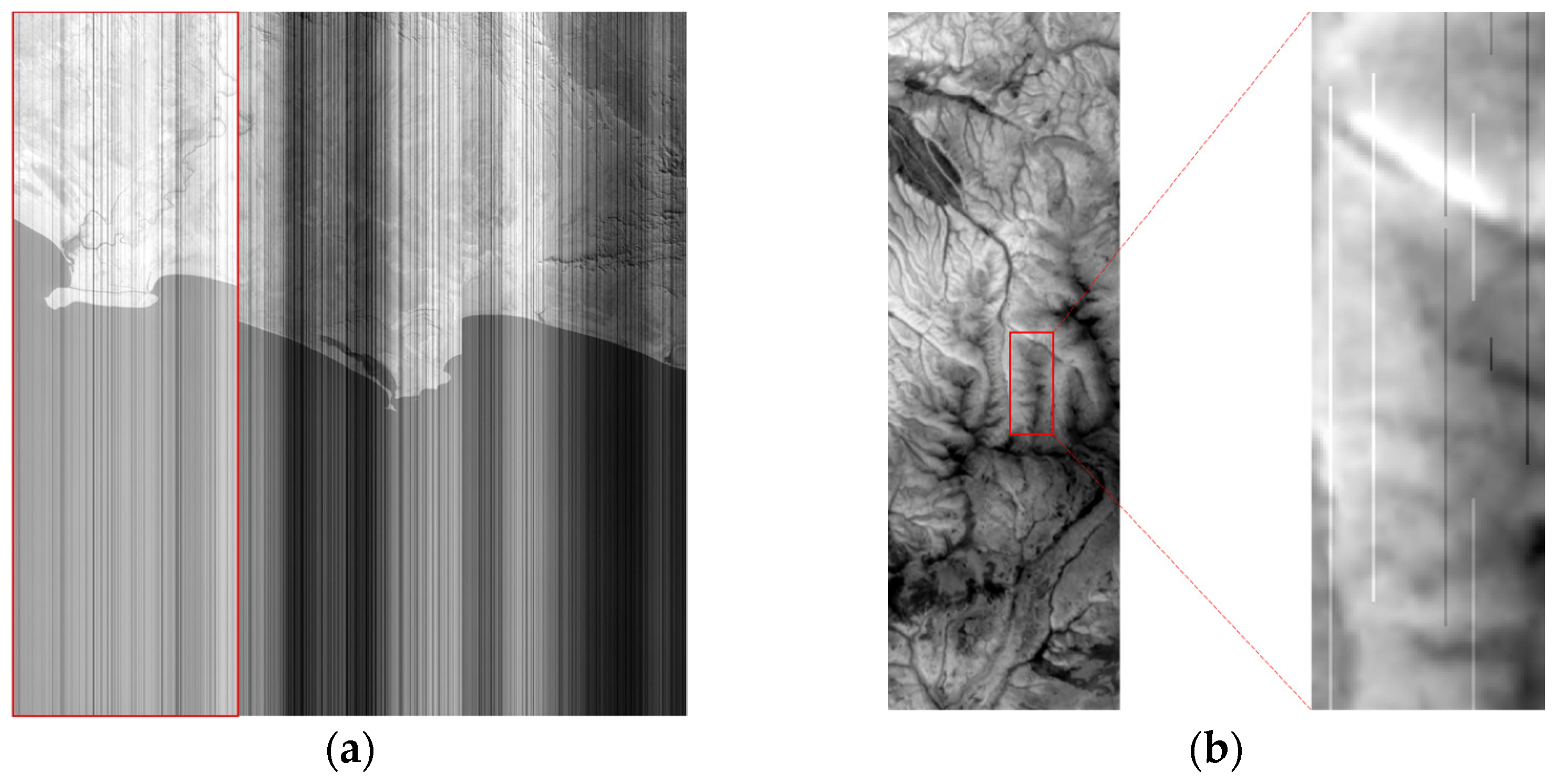
2. Experimental Data
2.1. GF5-02 VIMI Data
2.2. Landsat 8 TIRS Data
3. Methodology
3.1. Histogram Matching Method
- (1)
- Calculate the probability density function (PDF) of each column and the entire image:
- (2)
- Calculate the CPDF of each PDF histogram:
- (3)
- Match each column CPDF curve to the entire image CPDF curve to obtain a lookup table:
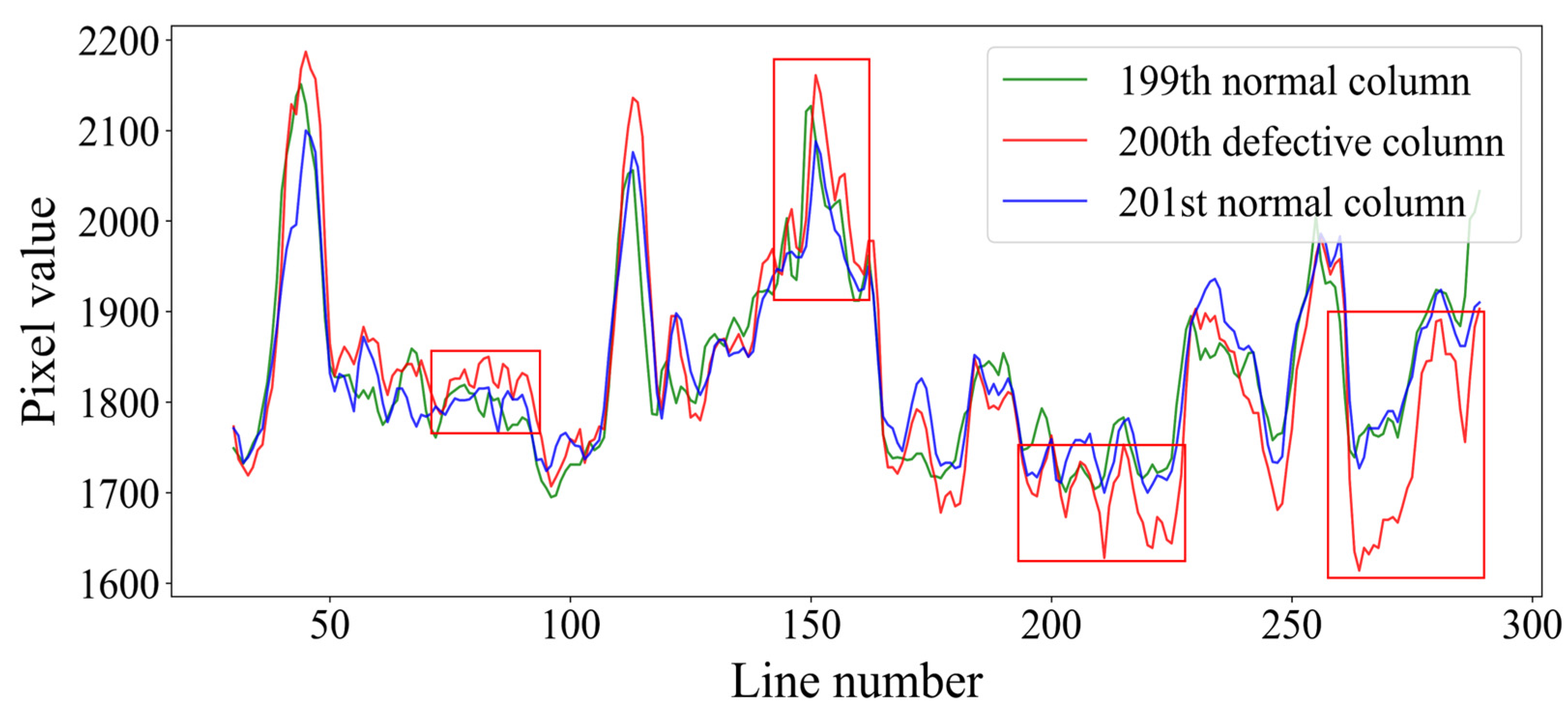
3.2. Trend Repair Method
- (1)
- Find two nearest adjacent normal columns: find two adjacent normal columns located on both sides of the defective column; record the distances (dis1 and dis2) to the defective column separately.
- (2)
- Calculate the mean and standard deviation columns: combine one of two adjacent normal columns with the defective column and define a 2 × 2 window. Slide the window and calculate its mean and standard deviation iteratively. The mean column (MC) and standard deviation column (SC) are obtained at the end of the ergodic.
- (3)
- Classify within two columns: contrast the first mean value in the mean column with the subsequent mean values and compare each pair of contiguous standard deviation values in the standard deviation column acquired from previous steps in sequence. If the difference values are less than the preset thresholds TMC and TSC (these two thresholds are automatically determined according to the mean and standard deviation columns; for the calculation method, refer to Formulas (6) and (7)) simultaneously, then label the corresponding 2 × 2 pixels in the same class; otherwise, two pixels at the end of the current window are labeled as the beginning of another class. Then, the comparison steps are repeated until the final pixel is reached. Ultimately, the two combined columns are partitioned into several distinct segments, and corresponding segments which represent class in defective column (CDC) and class in normal column (CNC) exhibit similar structural characteristics.where and are thresholds to subsection. and are the mth values in mean and standard deviation columns acquired in step (2), respectively. is the mean value of the mean column, and is the length of the standard deviation column.
- (4)
- Calculate mean value: calculate mean values of the different classes in the defective column and corresponding normal column to reach classified mean columns.where and denote the mth class mean at the location of the defective column and the normal column separately. and denote the pixel value at the location in the mth class of the defective column and the normal column, respectively. and denote the number of pixels in the mth class of the defective column and the normal column.
- (5)
- Repeat the steps: for the other adjacent normal column, repeat steps (2) to (4).
- (6)
- Correct preliminarily: traverse every pixel in the original defective column, subtract the mean of the class to which the pixel belongs in the classified defective mean column from its initial value. Then, add the difference value to its corresponding class mean in the classified normal mean column to obtain its preliminary correction value:where denotes the preliminary correction columns combined with the left and right normal columns. represents the DN value at the ith line and jth column on the image. , and denote the mean value at location , and of the defective column and its left and right normal column, respectively.
- (7)
- Weight the preliminary corrected values: considering the influence of the geospatial structure of adjacent pixels on the contaminated value, calculate the final corrected value by preliminary correction values of both side pixels using the inverse distance weighting method:where is the corrected value at the ith line and the jth column on the image. dis1 and dis2 indicate the distance from the normal column to the left and right defective column, respectively. denotes the preliminary correction value obtained from step (6).
- (8)
- Traverse the defective column: traverse and correct each pixel in the defective columns to reach the new corrected image.
3.3. Index of Assessment
3.3.1. Streaking Metrics
3.3.2. Structural Similarity
3.3.3. Peak Signal-to-Noise Ratio
3.3.4. Improvement Factor
4. Results
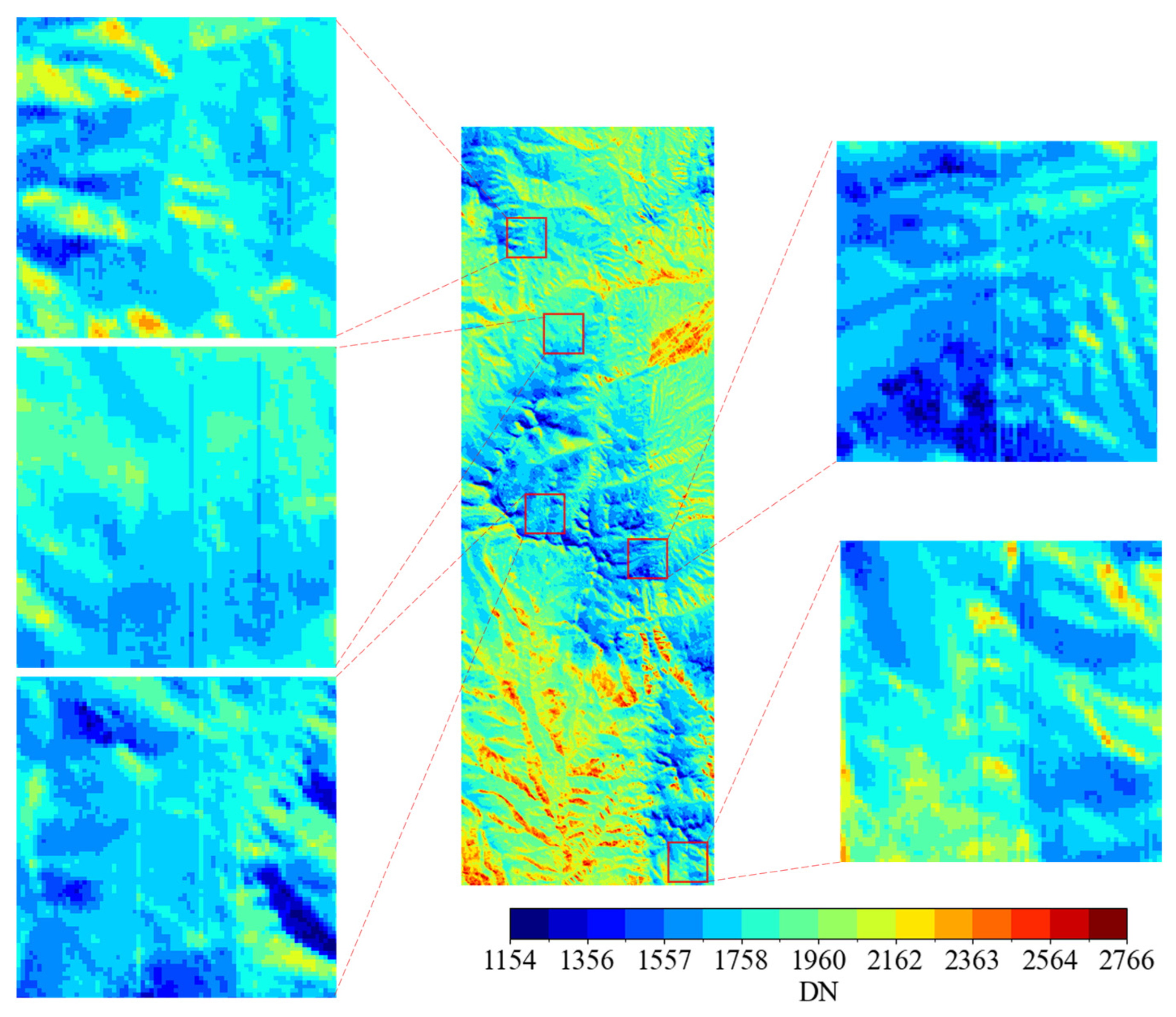
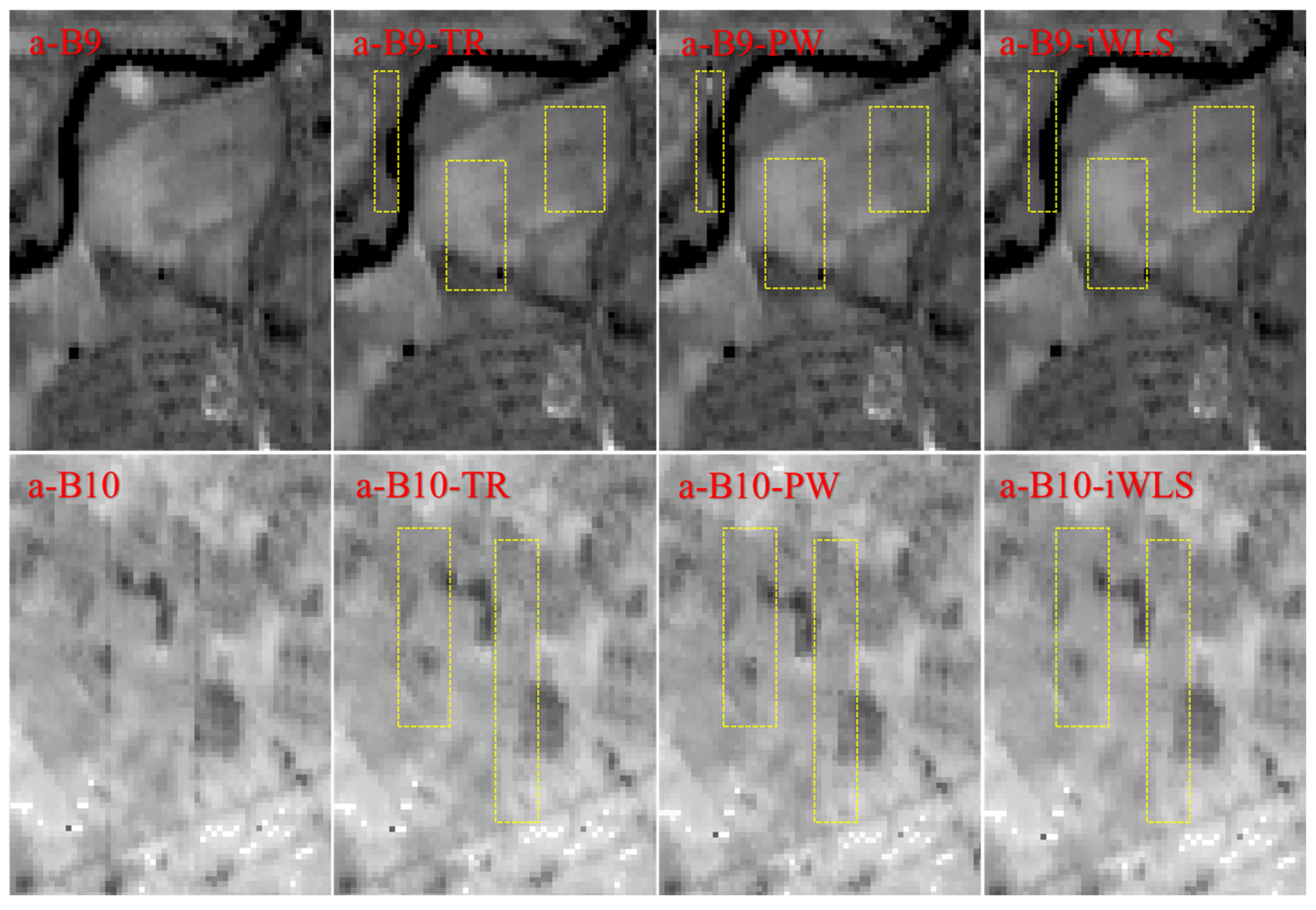
4.1. Visual Analysis
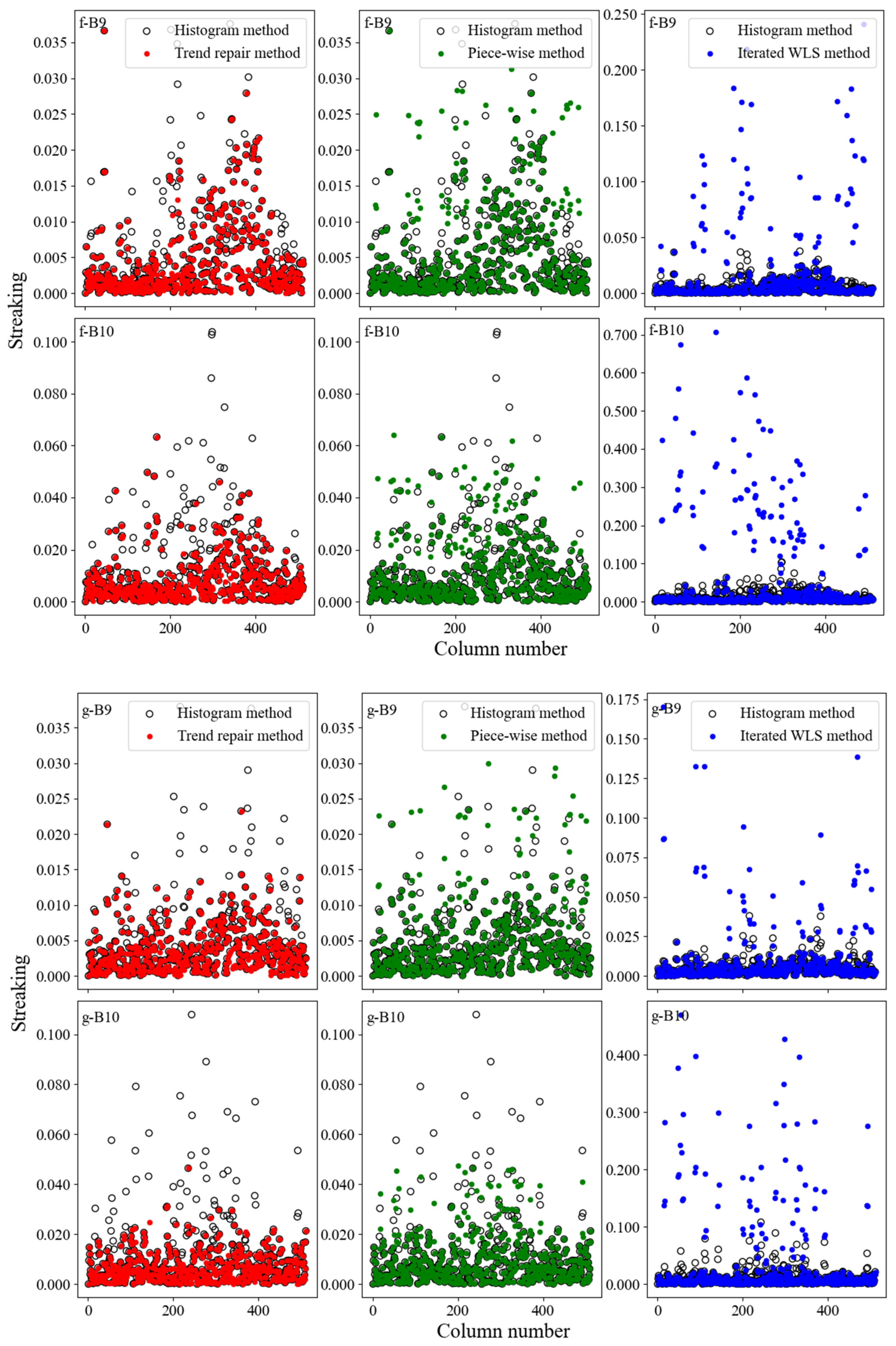
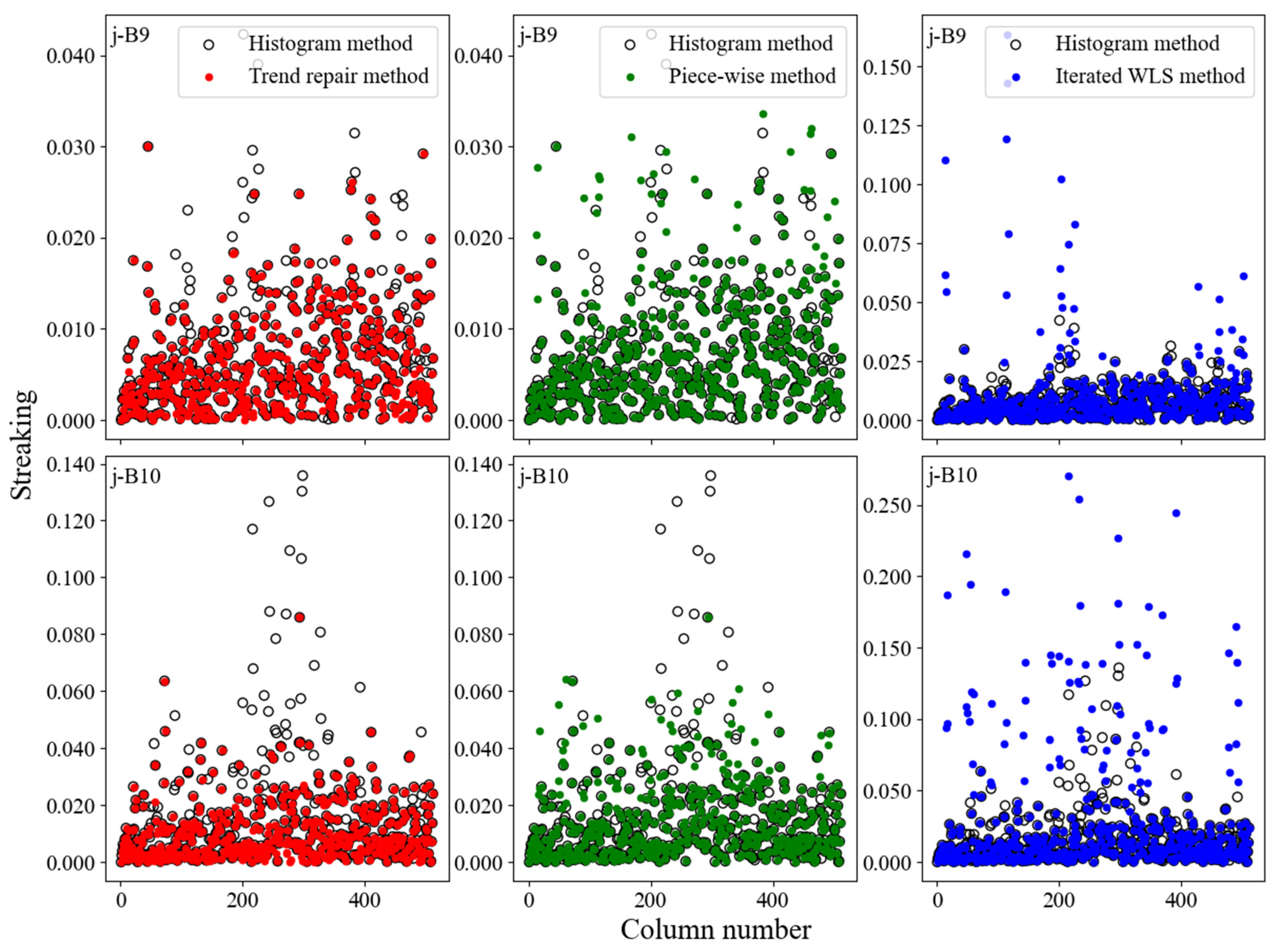
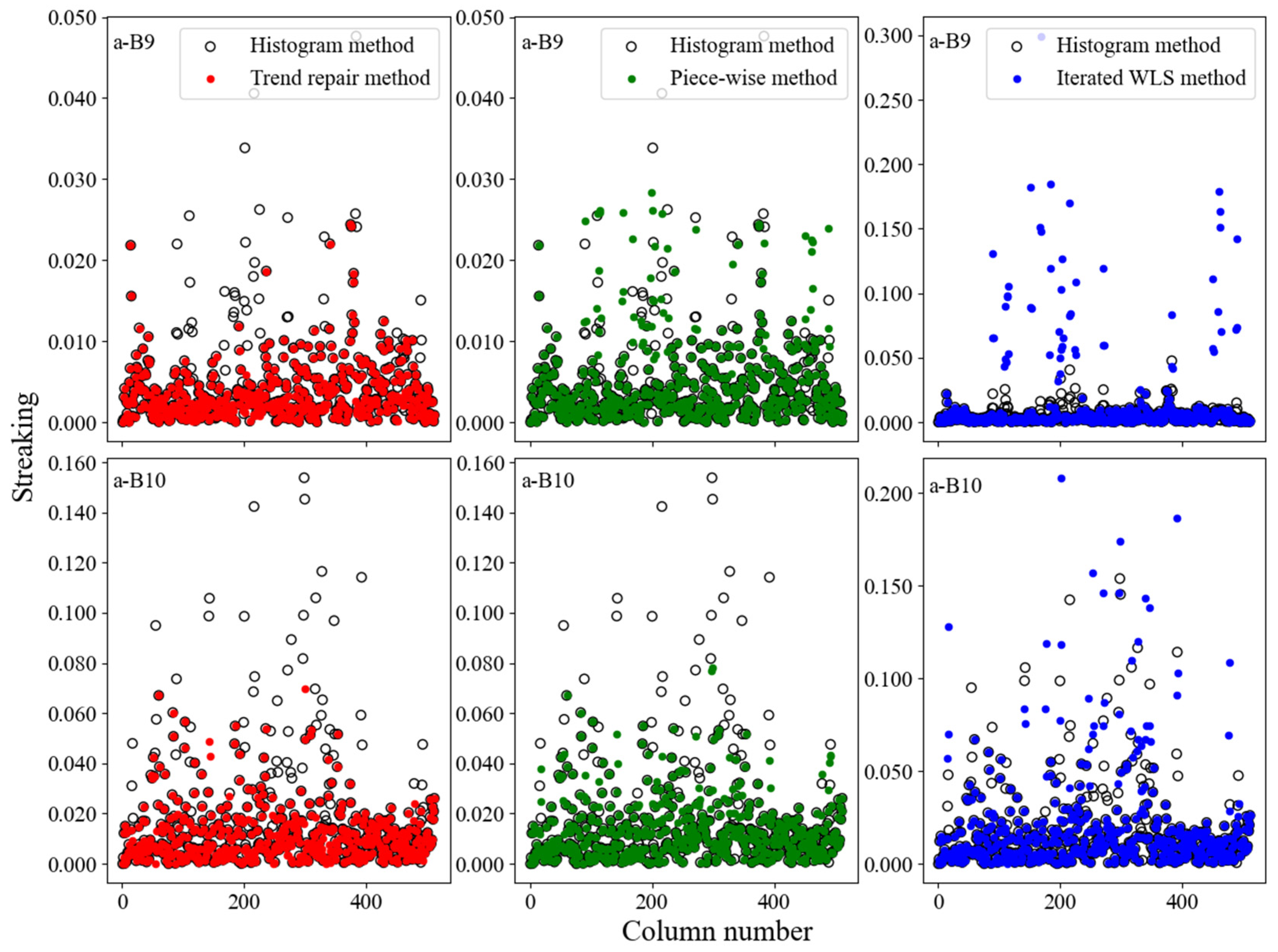
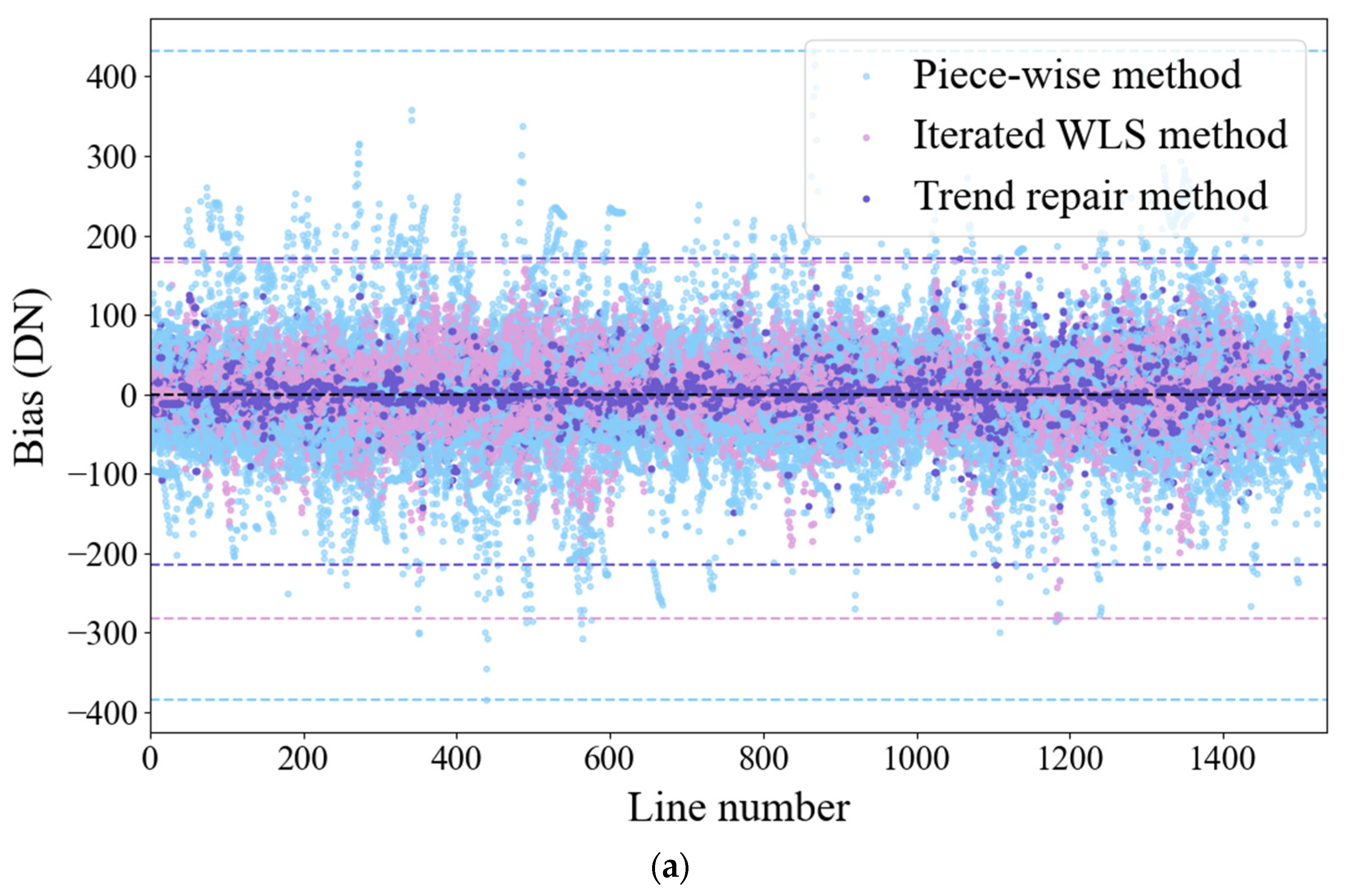
4.2. Results of the Assessment Index
4.3. Accuracy
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
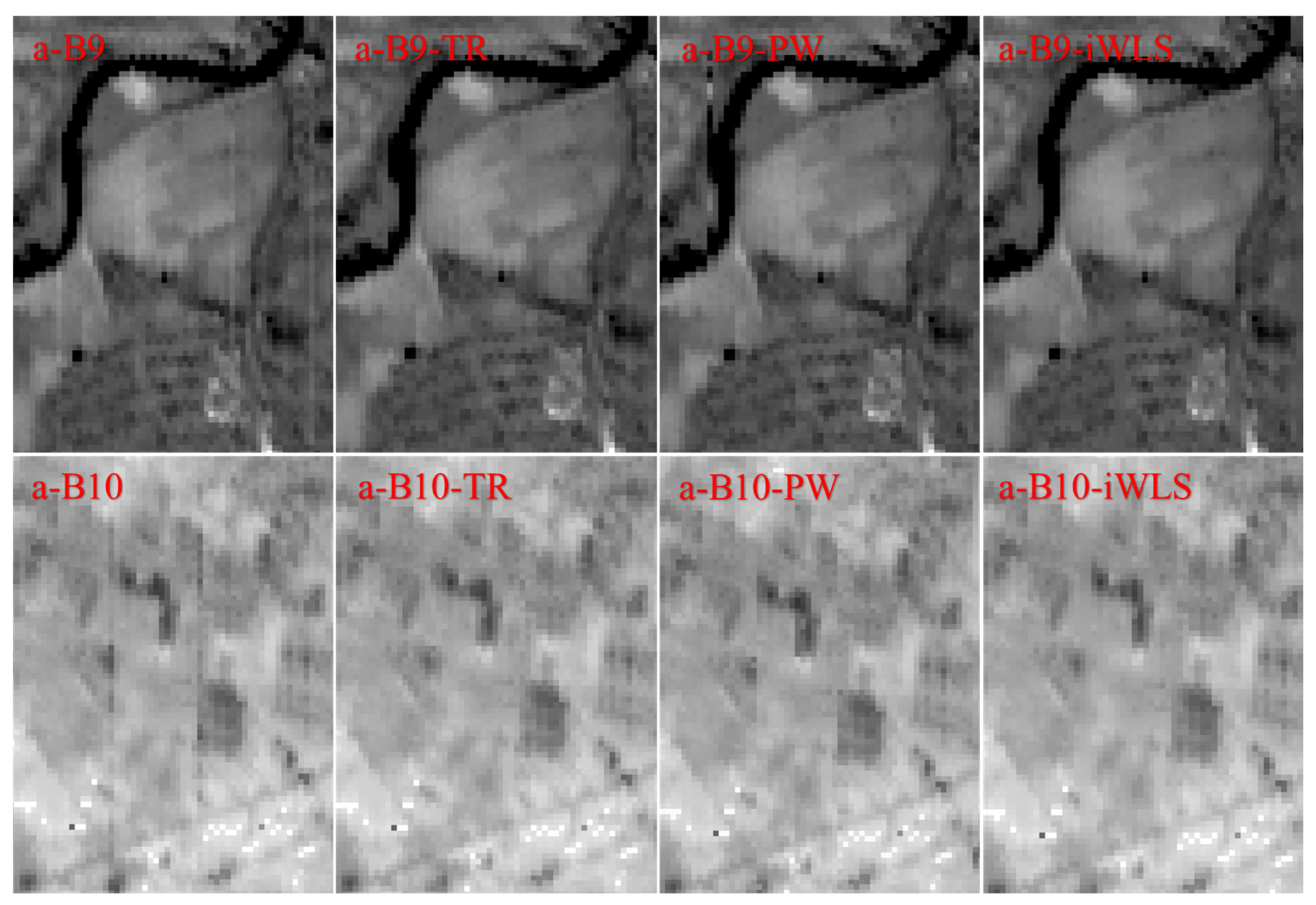
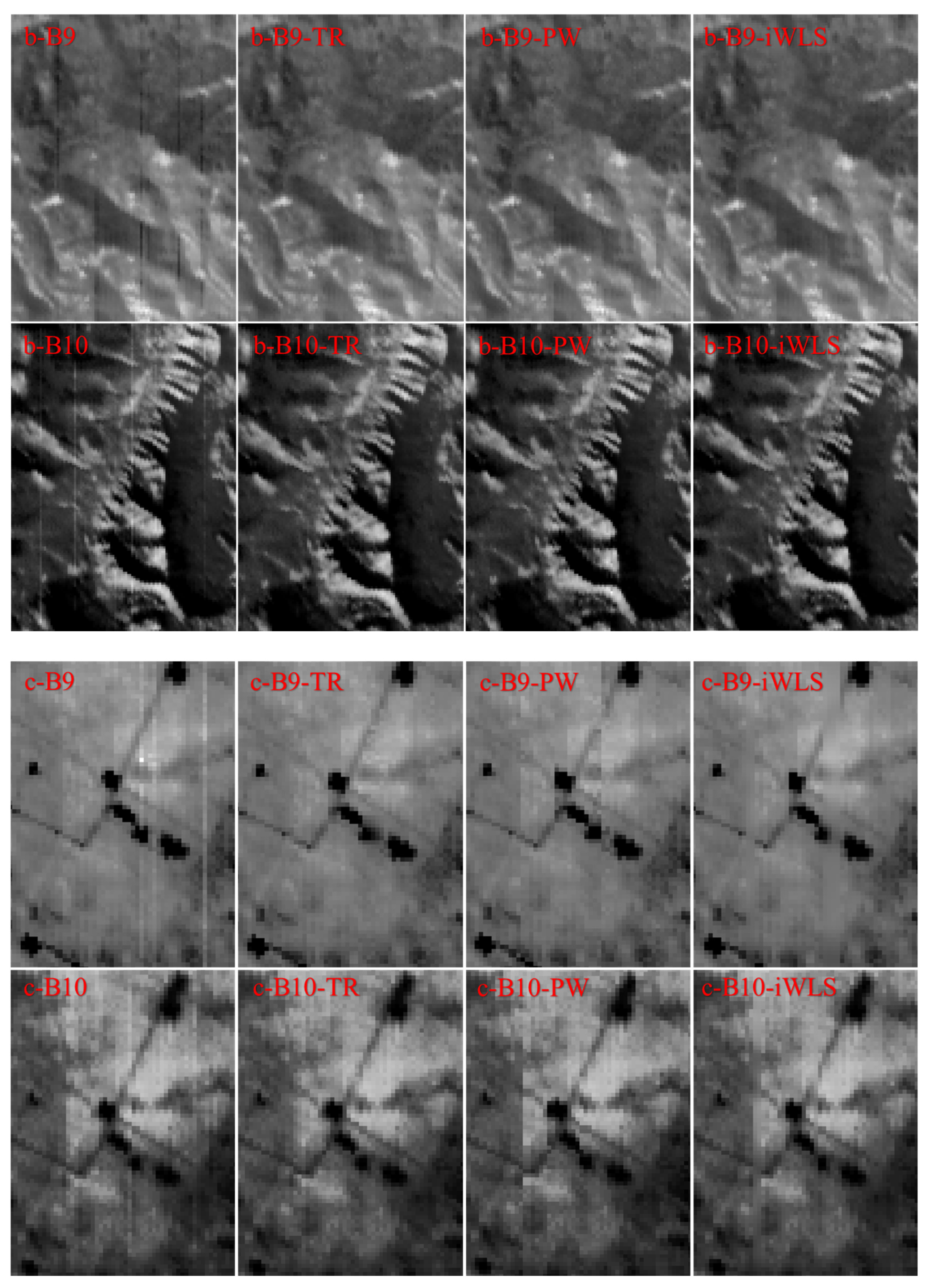




Appendix B
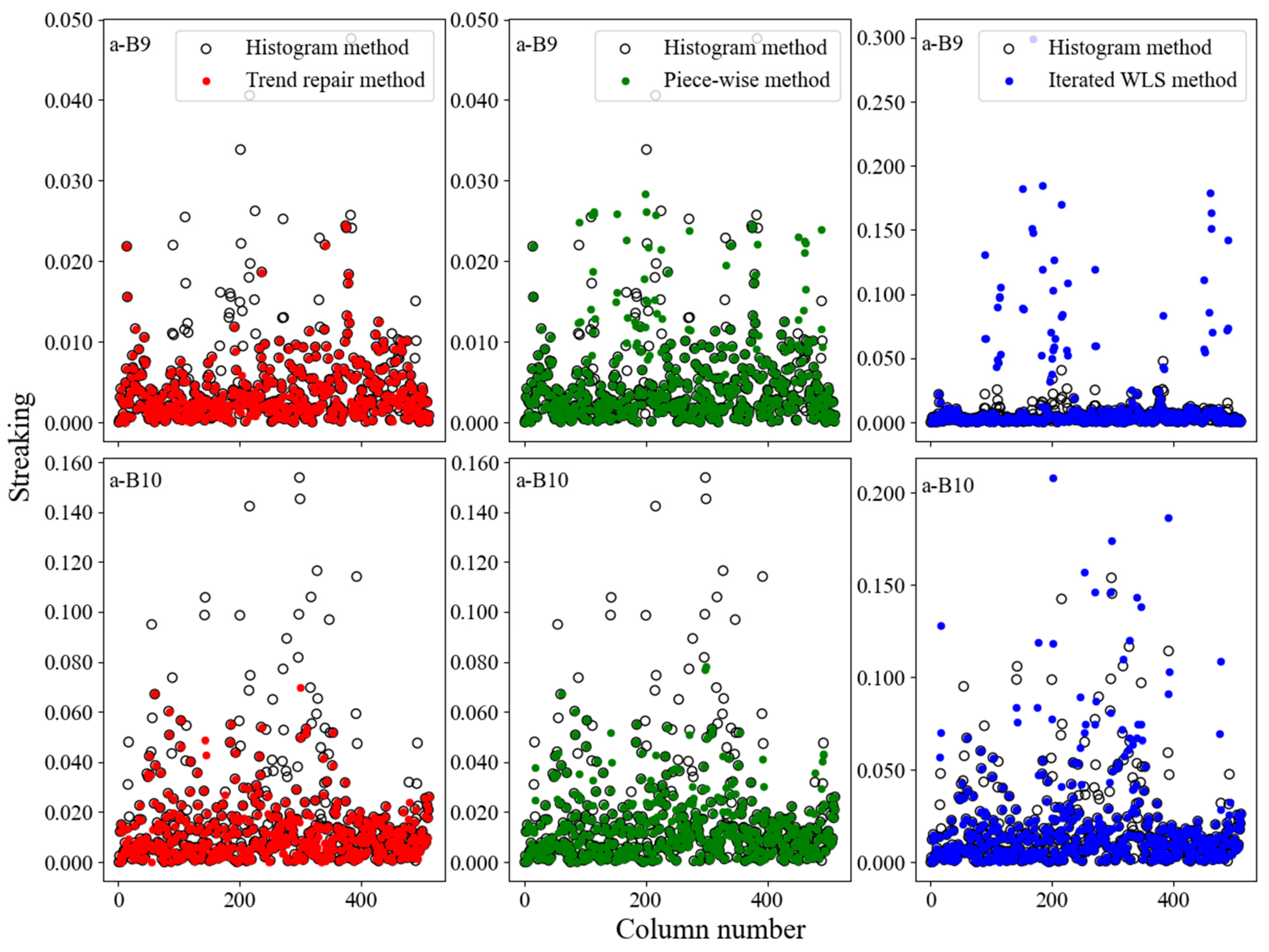
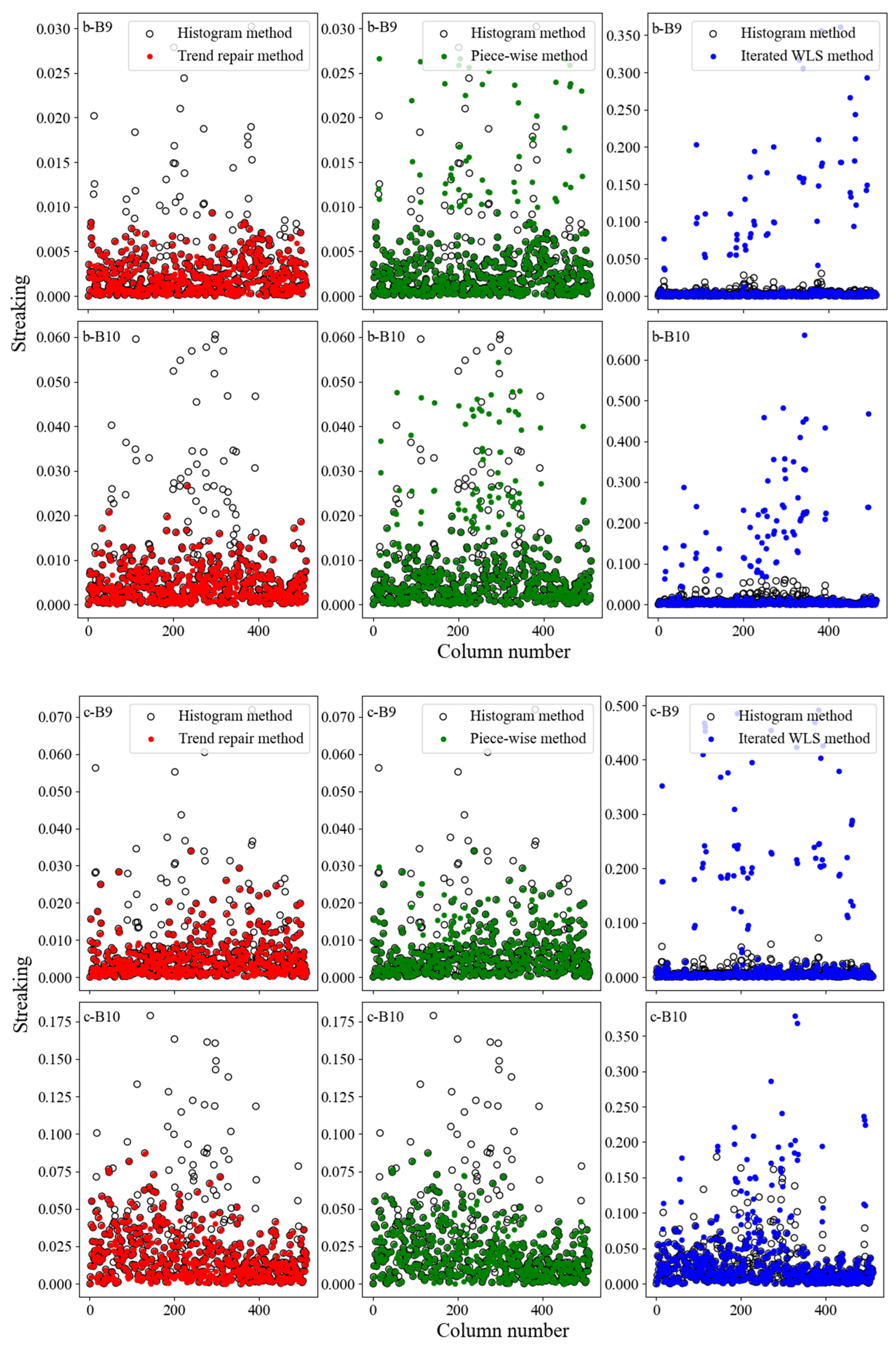
References
- Liu, J.G. Remote Sensing | Passive Sensors. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2013; p. 9780124095489029560. ISBN 978-0-12-409548-9. [Google Scholar]
- Yan, F.; Wu, S.; Zhang, Q.; Liu, Y.; Sun, H. Destriping of Remote Sensing Images by an Optimized Variational Model. Sensors 2023, 23, 7529. [Google Scholar] [CrossRef] [PubMed]
- Cao, B.; Du, Y.; Xu, D.; Li, H.; Liu, Q. An Improved Histogram Matching Algorithm for the Removal of Striping Noise in Optical Remote Sensing Imagery. Optik 2015, 126, 4723–4730. [Google Scholar] [CrossRef]
- Chen, B.; Liu, L.; Zou, Z.; Shi, Z. Target Detection in Hyperspectral Remote Sensing Image: Current Status and Challenges. Remote Sens. 2023, 15, 3223. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Hu, T.; Bian, Z.; Liu, F.; Cao, B.; Du, Y.; Sun, L.; Liu, Q. Land Surface Temperature Retrieval From Sentinel-3A SLSTR Data: Comparison Among Split-Window, Dual-Window, Three-Channel, and Dual-Angle Algorithms. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5003114. [Google Scholar] [CrossRef]
- Li, H.; Li, R.; Yang, Y.; Cao, B.; Bian, Z.; Hu, T.; Du, Y.; Sun, L.; Liu, Q. Temperature-Based and Radiance-Based Validation of the Collection 6 MYD11 and MYD21 Land Surface Temperature Products Over Barren Surfaces in Northwestern China. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1794–1807. [Google Scholar] [CrossRef]
- Bian, Z.; Roujean, J.L.; Fan, T.; Dong, Y.; Hu, T.; Cao, B.; Li, H.; Du, Y.; Xiao, Q.; Liu, Q. An Angular Normalization Method for Temperature Vegetation Dryness Index (TVDI) in Monitoring Agricultural Drought. Remote Sens. Environ. 2023, 284, 113330. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Bioucas-Dias, J.M.; Gottsche, F.-M. Quantifying the Uncertainty of Land Surface Temperature Retrievals From SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2010, 48, 523–534. [Google Scholar] [CrossRef]
- Zhao, X.; Li, M.; Nie, T.; Han, C.; Huang, L. An Innovative Approach for Removing Stripe Noise in Infrared Images. Sensors 2023, 23, 6786. [Google Scholar] [CrossRef]
- Srinivasan, R.; Cannon, M.; White, J. Landsat Data Destriping Using Power Spectral Filtering. Opt. Eng. 1988, 27, 939–943. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A Transformation for Ordering Multispectral Data in Terms of Image Quality with Implications for Noise Removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Donoho, D.L. De-Noising by Soft-Thresholding. IEEE Trans. Inform. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Chang, S.G.; Yu, B.; Vetterli, M. Adaptive Wavelet Thresholding for Image Denoising and Compression. IEEE Trans. Image Process. 2000, 9, 1532–1546. [Google Scholar] [CrossRef]
- Pande-Chhetri, R.; Abd-Elrahman, A. De-Striping Hyperspectral Imagery Using Wavelet Transform and Adaptive Frequency Domain Filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Alaeiyan, H.; Mosavi, M.R.; Ayatollahi, A. Hybrid Noise Removal to Improve the Accuracy of Inertial Sensors Using Lifting Wavelet Transform Optimized by Genetic Algorithm. Alex. Eng. J. 2023, 80, 326–341. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Woodham, R.J. Destriping LANDSAT MSS Images by Histogram Modification. Comput. Graph. Image Process. 1979, 10, 69–83. [Google Scholar] [CrossRef]
- Fischel, D. Validation of the Thematic Mapper Radiometric and Geometric Correction Algorithms. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 237–242. [Google Scholar] [CrossRef]
- Gadallah, F.L.; Csillag, F.; Smith, E.J.M. Destriping Multisensor Imagery with Moment Matching. Int. J. Remote Sens. 2000, 21, 2505–2511. [Google Scholar] [CrossRef]
- Li, M.; Nong, S.; Nie, T.; Han, C.; Huang, L.; Qu, L. A Novel Stripe Noise Removal Model for Infrared Images. Sensors 2022, 22, 2971. [Google Scholar] [CrossRef] [PubMed]
- Kuang, X.; Sui, X.; Chen, Q.; Gu, G. Single Infrared Image Stripe Noise Removal Using Deep Convolutional Networks. IEEE Photonics J. 2017, 9, 3900913. [Google Scholar] [CrossRef]
- Xiao, P.; Guo, Y.; Zhuang, P. Removing Stripe Noise from Infrared Cloud Images via Deep Convolutional Networks. IEEE Photonics J. 2018, 10, 7801114. [Google Scholar] [CrossRef]
- Weinreb, M.P.; Xie, R.; Lienesch, J.H.; Crosby, D.S. Destriping GOES Images by Matching Empirical Distribution Functions. Remote Sens. Environ. 1989, 29, 185–195. [Google Scholar] [CrossRef]
- Su, J.; Zhou, C.; Li, Y.; Zhang, K. Relative Radiometric Correction of OHS Remote Sensing Images Based on Improved Moment Matching. Geomat. Spat. Inf. Technol. 2021, 44, 98–101. [Google Scholar]
- Wang, H.; Yu, J.; Li, Z. Analysis of Relative Calibration Algorithm of Space-Borne Infrared Camera. Spacecr. Recovery Remote Sens. 2009, 30, 44–49. [Google Scholar]
- Pesta, F.; Bhatta, S.; Helder, D.; Mishra, N. Radiometric Non-Uniformity Characterization and Correction of Landsat 8 OLI Using Earth Imagery-Based Techniques. Remote Sens. 2015, 7, 430–446. [Google Scholar] [CrossRef]
- Li, L.; Zhang, G.; Jiang, Y.; Shen, X. An Improved On-Orbit Relative Radiometric Calibration Method for Agile High-Resolution Optical Remote-Sensing Satellites with Sensor Geometric Distortion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Wegener, M. Destriping Multiple Sensor Imagery by Improved Histogram Matching. Int. J. Remote Sens. 1990, 11, 859–875. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Stripe Noise Reduction in MODIS Data by Combining Histogram Matching with Facet Filter. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1844–1856. [Google Scholar] [CrossRef]
- Shen, H.; Jiang, W.; Zhang, H.; Zhang, L. A Piece-Wise Approach to Removing the Nonlinear and Irregular Stripes in MODIS Data. Int. J. Remote Sens. 2014, 35, 44–53. [Google Scholar] [CrossRef]
- Zhao, Y.; Dai, L.; Bai, S.; Liu, J.; Peng, H.; Wang, H. Design and Implementation of Full-spectrum Spectral Imager System. Spacecr. Recovery Remote Sens. 2018, 39, 38–50. [Google Scholar]
- Zhang, M.; Wen, Y.; Sun, L.; Li, Y. Overview and Application of GaoFen 5-02 Satellite. Aerosp. China 2022, 12, 9–15. [Google Scholar] [CrossRef]
- Tian, X.; Benkrid, K. Mersenne Twister Random Number Generation on FPGA, CPU and GPU. In Proceedings of the 2009 NASA/ESA Conference on Adaptive Hardware and Systems, San Francisco, CA, USA, 29 July–1 August 2009; pp. 460–464. [Google Scholar]
- Pan, Z.; Gu, X.; Liu, G.; Yan, X. Relative Radiometric Correction of CBERS-01 CCD Data Based on Detector Histogram Matching. Editor. Board Geomat. Inf. Sci. Wuhan Univ. 2005, 30, 925–927. [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Krause, K.S. Relative Radiometric Characterization and Performance of the QuickBird High-Resolution Commercial Imaging Satellite. In Proceedings of the SPIE 49th Annual Meeting Optical Science and Technology, Denver, CO, USA, 26 October 2004; Barnes, W.L., Butler, J.J., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; p. 35. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. Mean Squared Error: Lot It or Leave It? A New Look at Signal Fidelity Measures. Signal Process. Mag. IEEE 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Corsini, G.; Diani, M.; Walzel, T. Striping Removal in MOS-B Data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1439–1446. [Google Scholar] [CrossRef]
- Landsat 8 (L8) Data Users Handbook; Department of the Interior U.S. Geological Survey: Sioux Falls, SD, USA, 2019.



| Number | Date | Surface Type |
|---|---|---|
| a | 28 October 2021 | Cropland Building |
| b | 28 October 2021 | Mountain |
| c | 30 October 2021 | Building |
| d | 1 November 2021 | Cloud Desert |
| e | 9 November 2021 | Water Soil |
| f | 2 November 2021 | Desert Mountain |
| g | 7 November 2021 | Cloud Mountain |
| h | 7 November 2021 | Desert |
| i | 7 November 2021 | Water Building Soil |
| j | 9 November 2021 | Cloud Vegetation |
| Number | Method | Piece-Wise Method | Iterated WLS Facet Method | Trend Repair Method | |||
|---|---|---|---|---|---|---|---|
| Index | B9 | B10 | B9 | B10 | B9 | B10 | |
| a | SSIM | 0.9376 | 0.9538 | 0.9544 | 0.9679 | 0.9616 | 0.9712 |
| PSNR | 62.53 | 60.98 | 64.26 | 62.70 | 64.77 | 63.13 | |
| IF | 6.19 | 11.43 | −6.64 | 2.44 | 22.84 | 28.26 | |
| b | SSIM | 0.9609 | 0.9654 | 0.9703 | 0.9737 | 0.9746 | 0.9764 |
| PSNR | 61.20 | 61.87 | 62.60 | 63.18 | 63.16 | 63.60 | |
| IF | 4.75 | 5.33 | −2.73 | −3.63 | 16.77 | 21.00 | |
| c | SSIM | 0.8615 | 0.9362 | 0.8870 | 0.9487 | 0.9119 | 0.9592 |
| PSNR | 56.70 | 58.13 | 58.39 | 59.31 | 58.97 | 60.18 | |
| IF | 10.90 | 14.60 | −2.83 | −4.84 | 26.65 | 27.06 | |
| d | SSIM | 0.9508 | 0.9119 | 0.9602 | 0.9273 | 0.9592 | 0.9256 |
| PSNR | 60.13 | 57.57 | 61.15 | 58.57 | 60.95 | 58.35 | |
| IF | 4.51 | 10.21 | −1.94 | −1.93 | 22.72 | 32.11 | |
| e | SSIM | 0.9039 | 0.9365 | 0.9257 | 0.9436 | 0.9294 | 0.9605 |
| PSNR | 55.53 | 57.39 | 56.92 | 58.08 | 56.93 | 59.49 | |
| IF | 12.59 | 12.34 | −1.32 | 9.38 | 29.14 | 21.89 | |
| f | SSIM | 0.9443 | 0.8996 | 0.9469 | 0.8935 | 0.9637 | 0.9215 |
| PSNR | 56.09 | 56.56 | 56.39 | 56.45 | 57.99 | 57.69 | |
| IF | 3.81 | 6.35 | −2.29 | −2.49 | 20.91 | 23.30 | |
| g | SSIM | 0.9558 | 0.9538 | 0.9600 | 0.9555 | 0.9742 | 0.9688 |
| PSNR | 61.18 | 60.01 | 61.77 | 60.31 | 63.55 | 61.77 | |
| IF | 4.23 | 8.01 | −2.32 | −2.39 | 20.04 | 27.59 | |
| h | SSIM | 0.9299 | 0.9160 | 0.9216 | 0.9024 | 0.9500 | 0.9327 |
| PSNR | 59.83 | 59.43 | 59.52 | 59.03 | 61.29 | 60.49 | |
| IF | 5.13 | 9.76 | 1.45 | 3.56 | 20.76 | 27.68 | |
| i | SSIM | 0.7782 | 0.8055 | 0.7943 | 0.8040 | 0.8505 | 0.8747 |
| PSNR | 56.29 | 54.29 | 57.20 | 54.74 | 58.16 | 56.35 | |
| IF | 4.86 | 12.82 | −3.22 | 5.63 | 19.37 | 29.75 | |
| j | SSIM | 0.9474 | 0.9344 | 0.9497 | 0.9330 | 0.9591 | 0.9489 |
| PSNR | 58.95 | 58.93 | 59.25 | 58.97 | 60.05 | 60.04 | |
| IF | 3.42 | 8.29 | −1.44 | 1.28 | 17.12 | 23.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Li, H.; Du, Y.; Chen, Y.; Zhao, G.; Bian, Z.; Cao, B.; Xiao, Q.; Liu, Q. Stripe Noise Elimination with a Novel Trend Repair Method for Push-Broom Thermal Images. Remote Sens. 2024, 16, 3299. https://doi.org/10.3390/rs16173299
Zhang Z, Li H, Du Y, Chen Y, Zhao G, Bian Z, Cao B, Xiao Q, Liu Q. Stripe Noise Elimination with a Novel Trend Repair Method for Push-Broom Thermal Images. Remote Sensing. 2024; 16(17):3299. https://doi.org/10.3390/rs16173299
Chicago/Turabian StyleZhang, Zelin, Hua Li, Yongming Du, Yao Chen, Guoxiang Zhao, Zunjian Bian, Biao Cao, Qing Xiao, and Qinhuo Liu. 2024. "Stripe Noise Elimination with a Novel Trend Repair Method for Push-Broom Thermal Images" Remote Sensing 16, no. 17: 3299. https://doi.org/10.3390/rs16173299
APA StyleZhang, Z., Li, H., Du, Y., Chen, Y., Zhao, G., Bian, Z., Cao, B., Xiao, Q., & Liu, Q. (2024). Stripe Noise Elimination with a Novel Trend Repair Method for Push-Broom Thermal Images. Remote Sensing, 16(17), 3299. https://doi.org/10.3390/rs16173299







