Contrastive Transformer Network for Track Segment Association with Two-Stage Online Method
Abstract
:1. Introduction
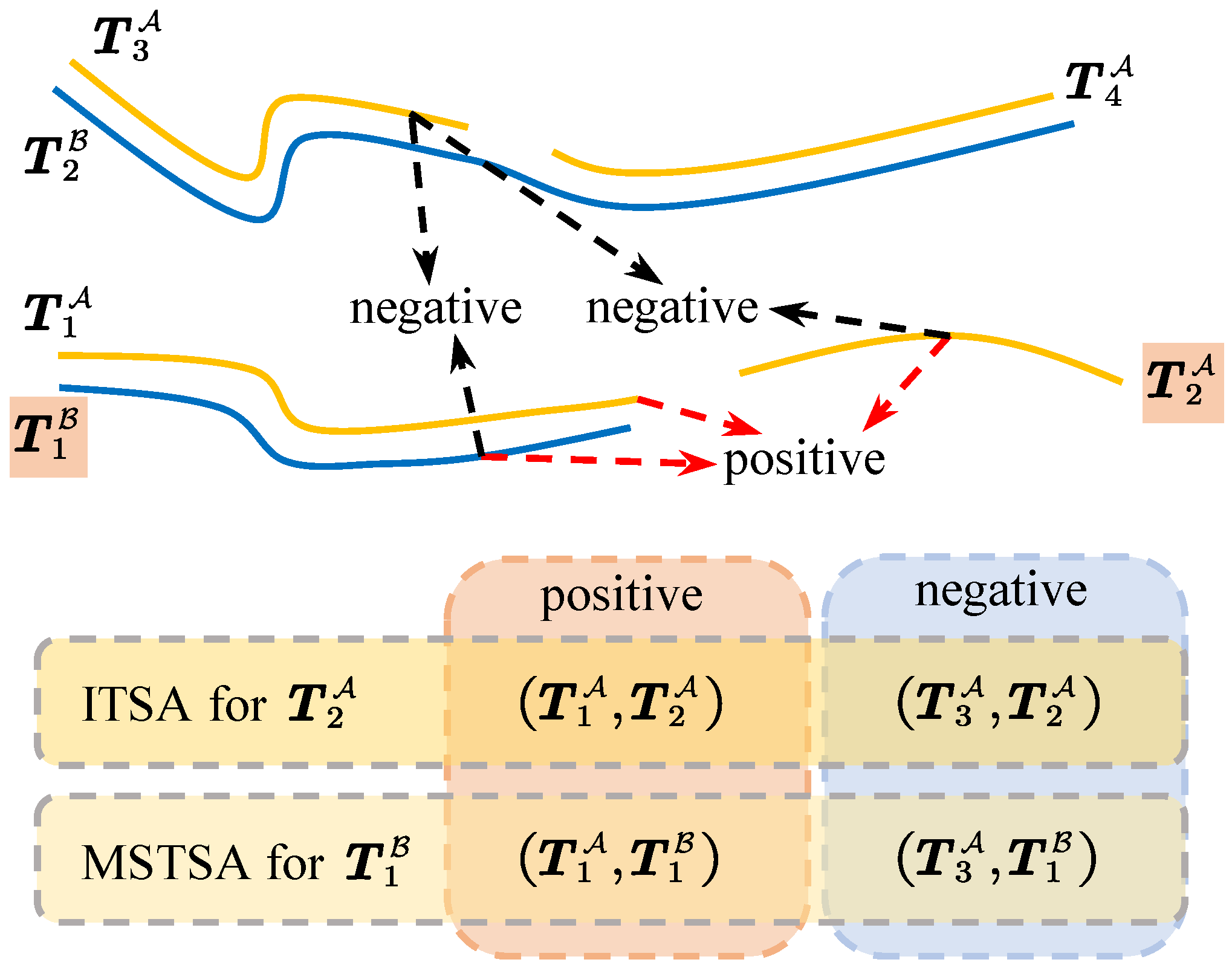
- From the perspective of trajectory similarity measurement, we unify the problems of interrupted track segment association and multi-source track segment association under a unified framework.
- To tackle these challenges, we introduce a network called TSA-cTFER, which combines contrastive learning with the Transformer Encoder to produce high-dimensional feature representations of trajectories. This network effectively transforms the task of trajectory similarity calculation into a distance measurement problem in a high-dimensional vector space.
- Furthermore, in dynamic scenarios where targets may appear or disappear unpredictably, we present a two-stage online association algorithm. This algorithm adapts different association strategies based on the difficulty levels of association pairs, enhancing association accuracy and reducing error rates.
2. Problem
3. Proposed Method
3.1. Overall Framework
3.2. Input Embedding Module
3.3. Transformer Encoder Module
3.3.1. Multi-Head Self-Attention
3.3.2. Feed-Forward Network
3.3.3. Block Connecting and Layer Stacking
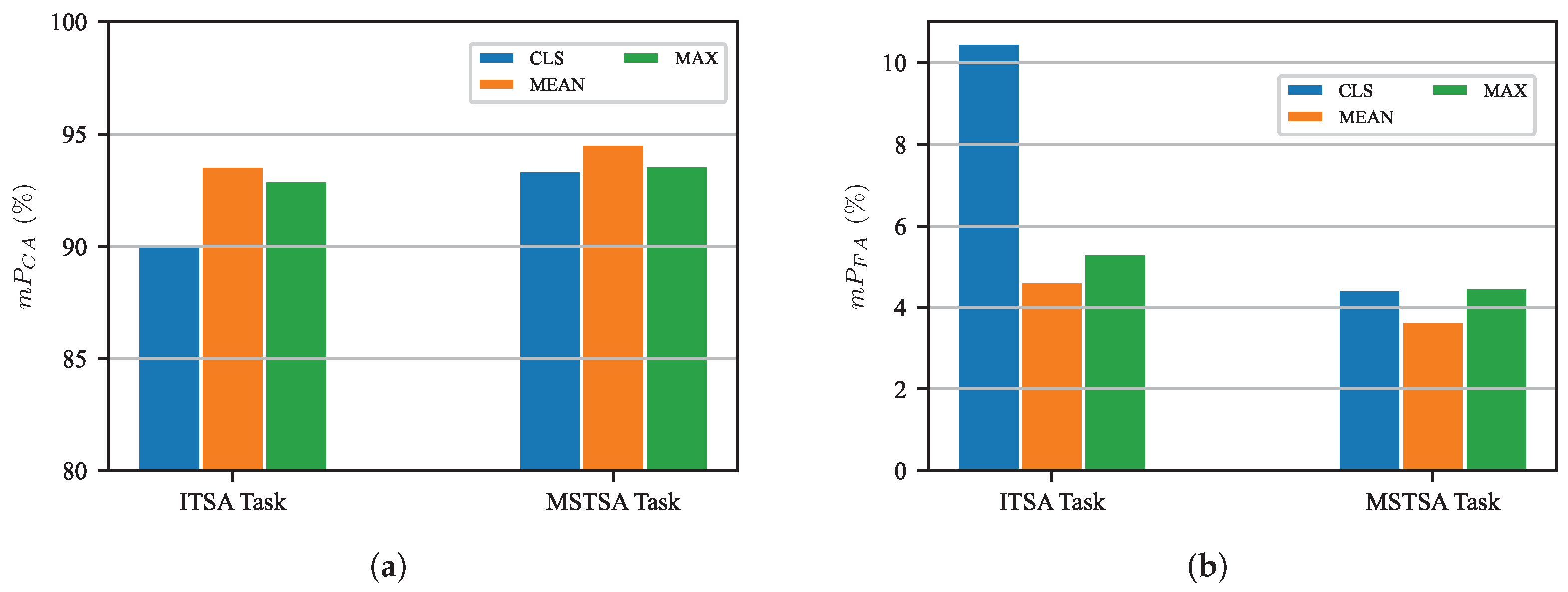
3.4. Output Pooling Module
- •
- CLS-strategyLike class-token described in previous works such as ViT [18] and BERT [20], we introduce a trainable embedding at the beginning of the embedded sequence. The state of this embedding at the output of the Transformer Encoder serves as a representation of the entire trajectory.Here, corresponds to the input class-token and is located at the beginning of the output state.
- •
- MEAN-strategyMEAN-strategy computes the mean-over-time of the context matrix . It calculates the average value of each column in and returns a D-dim vector .Here, indicates that the mean operation is performed on each column of the matrix and is a masked matrix similar to , where the D column vectors are identical, and the first elements in each of the N rows are active.
- •
- MAX-strategySimilar to the MEAN-strategy, MAX-strategy computes the max-over-time of the context matrix as follows
3.5. Contrastive Loss Function
4. Two-Stage Online Association Algorithm
4.1. Track State Update
| Algorithm 1: Track State Update. |
 |
4.2. Two-Stage Association Method
| Algorithm 2: Two-Stage Association. |
 |
| Algorithm 3: Select Easy/Hard Association Pairs. |
 |
5. Experimental Results
5.1. Datasets
5.2. Metrics
- The tracks originate from the same target.
- In the case of ITSA, the time interval between interruptions in the two tracks is required to be less than 20 min, and each track must have a duration longer than 2 min.
- For the MSTSA problem, the intersection time of the two-track segments needs to exceed 2 min.
5.3. Baselines
5.3.1. Traditional Methods
- •
- Multiple Hypothesis TSA: The Multiple Hypothesis TSA algorithm (MH TSA) [5] starts by constructing multiple potential models of target motion and performing trajectory prediction. Next, based on position and velocity information, a fuzzy correlation function is utilized to depict the relationship between predicted old tracks and new tracks. Finally, the Multiple Hypothesis TSA algorithm constructs a fuzzy similarity matrix between the old and young tracks and then employs the two-dimensional assignment principle to determine the association between targets.
- •
- Multi-Frame 2-D TSA: The Multi-Frame 2-D TSA algorithm (MF 2-D TSA) [1] assumes that the target motion follows the constant velocity model before and after interruption. Additionally, it incorporates a constant turn with a turning rate of w throughout the breakage period. By exploring various turning rates, if the distance between the predicted state of the old track and the state of the young track meets specific criteria, this correlation is deemed successful.
- •
- Distance-Based TSA: The Euclidean distance (ED) is the most commonly used distance metric for track correlation as used in [23]. However, it assumes that trajectories are the same length. Here, we also utilize Dynamic Time Warping (DTW) [25,26,27] as a criterion to measure the similarity of multi-source tracks. Similar to ED, DTW is also a measure designed for time series and can be applied to trajectory data. However, unlike ED, DTW can align a point of one trajectory with one or more consecutive points of another trajectory. This flexibility makes DTW suitable for cases where track lengths vary or where there are temporal variations in the data.
5.3.2. Deep Learning Based Methods
- •
- TSADCNN: TSADCNN [10] uses a temporal and spatial information extraction module to extract track information. The temporal module, composed of LSTM, is responsible for capturing temporal information, while the spatial module, consisting of multi-scale CNN, extracts spatial information. Initially, the track information undergoes processing through the LSTM module to capture temporal dependencies. Then, it is fed to the CNN module to extract spatial features. By mapping the track data onto a high-dimensional space, TSADCNN determines whether the trajectories belong to the same target based on the similarity of high-dimensional vectors.
- •
- TGRA: Similar to TSADCNN, TGRA [12] utilizes a graph network to extract track information. It employs the Graph Isomorphism Network (GIN) [28] and Graph Convolutional Network (GCN) [29] to obtain node-level local representations of track points. Subsequently, the Graph Attention Network (GAT) [30] is employed to acquire representations at the graph level. In this way, This approach enables the extraction of high-dimensional representations that encompass both the spatial and temporal information of the entire trajectory.
5.4. Implementation Details
5.4.1. Data Preparation
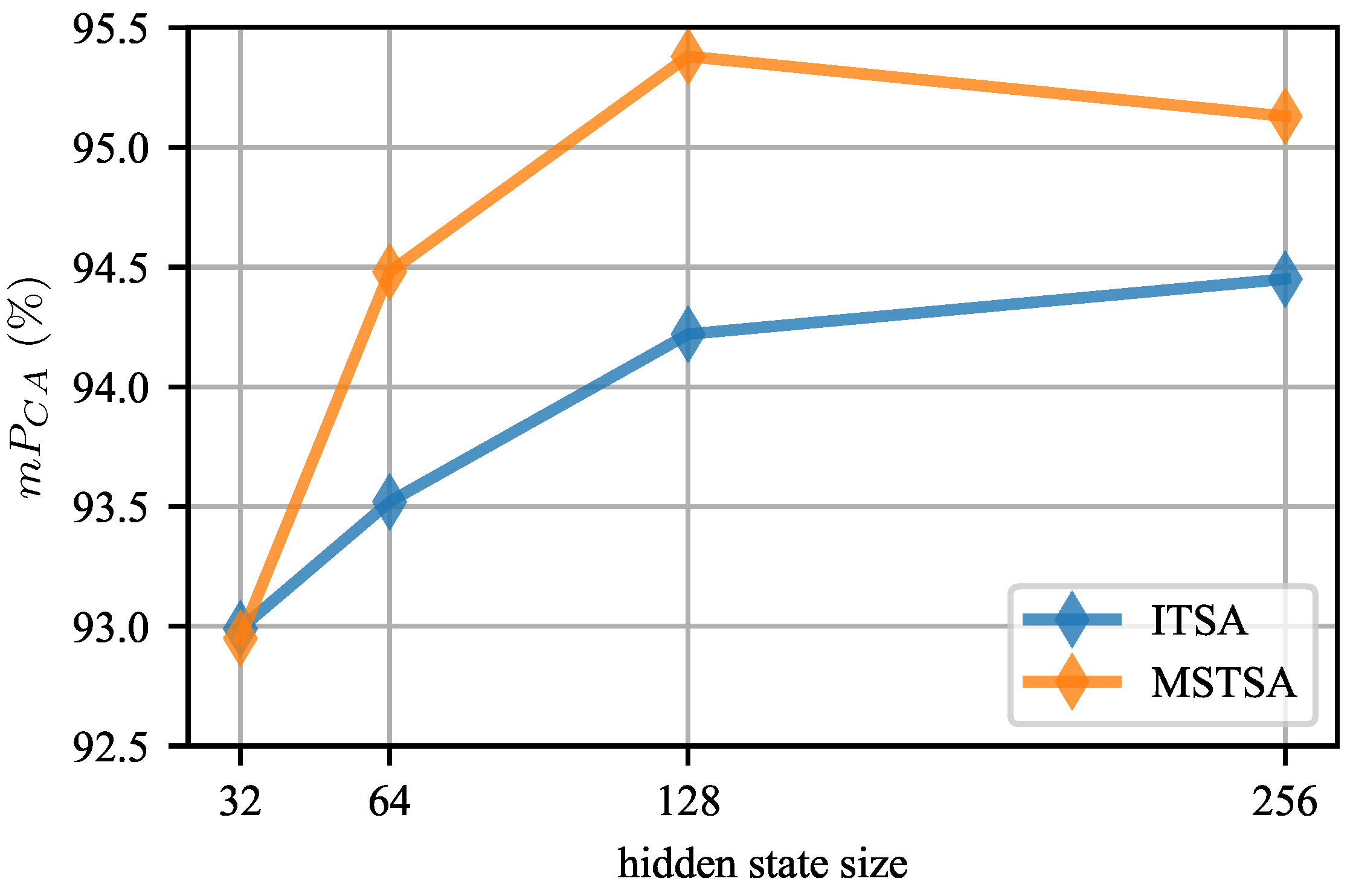
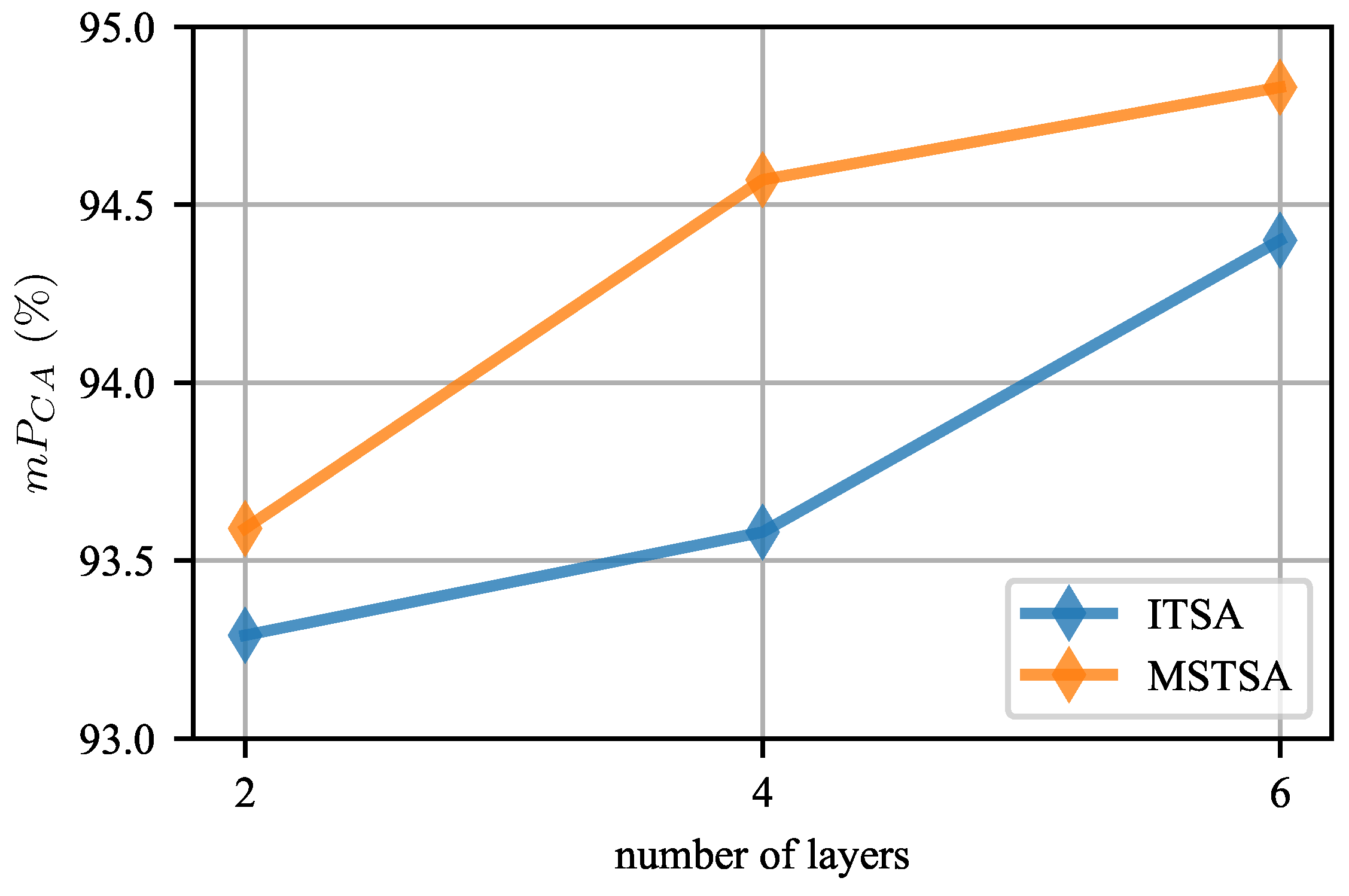
5.4.2. Model Settings
5.4.3. Training Details
5.5. Performance Analysis
5.5.1. ITSA Task
5.5.2. MSTSA Task
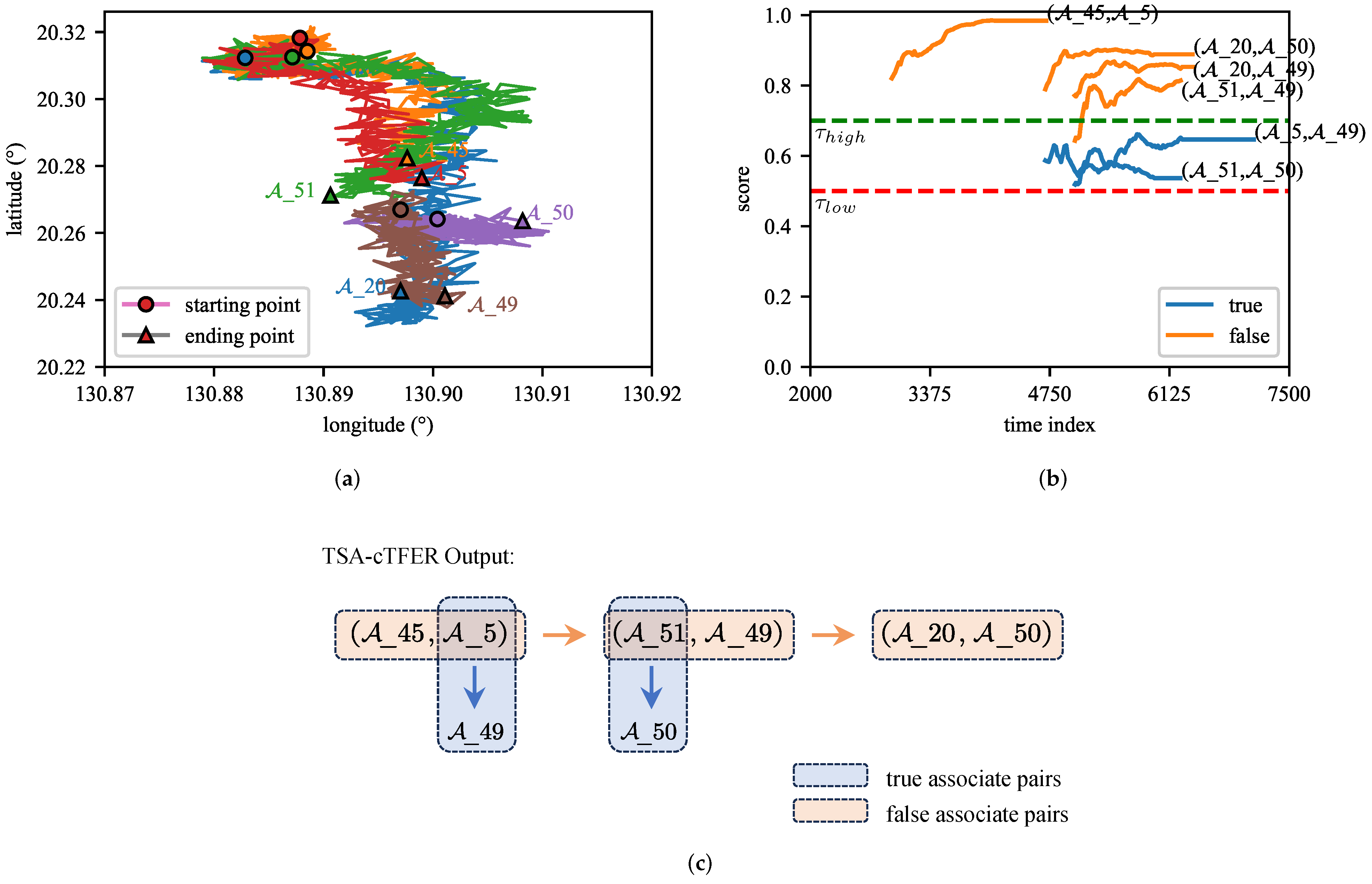
5.5.3. Analysis of a Typical Scenario
5.6. Ablation Study
6. Discussion
6.1. Analysis of a Failure Scenario
6.2. Limitations and Future Work
- •
- Data Features and Augumentation: As highlighted in the failure scenarios above, recalculating speed and heading angle based on smoothed latitude and longitude and incorporating these features into the input embedding module of TSA-cTFER could improve the model’s ability to assess trajectory similarity. In addition, as noted in Section 5.4.3, this work has only used random cropping for data augmentation. Exploration of other techniques, such as random masking, may further improve the robustness of the model to meet practical application requirements.
- •
- Training Process: Building upon our data preparation strategy described in Section 5.4.1, we mixed the data from all scenarios and then randomly sampled a batch for training. Although this data sampling method proved effective in the early stages of training, it may not provide sufficient meaningful information for the model to learn effectively in the later stages, especially in failure scenarios where multiple similar trajectories exist. Thus, further fine-tuning of the network based on the specific scenarios may be necessary to optimize performance.
- •
- End-to-End Association: To achieve online track segment association, we propose a heuristic two-stage online association algorithm that heavily relies on TSA-cTFER’s assessment of trajectory similarity. However, this heuristic algorithm depends on manually defined rules and parameters, limiting its adaptability to different scenarios. Therefore, developing an end-to-end network that integrates trajectory information from the entire scenario and optimizes the association process through deep learning could effectively address these limitations, thereby improving accuracy and significantly reducing the time required for track association.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIS | Automatic Identification System |
| CV | Constant Velocity model |
| CA | Constant Acceleration model |
| CT | Coordinated Turn model |
| CNN | Convolutional Neural Network |
| DTW | Dynamic Time Warping |
| ED | Euclidean Distance |
| ITSA | Interrupted Track Segment Association |
| LSTM | Long Short-Term Memory |
| MTAD | Multi-source Track Association Dataset |
| MH TSA | Multiple Hypothesis Track segment association |
| MF 2-D TSA | Multi-Frame 2-D Track segment association |
| MSTSA | Multi-Source Track Segment Association |
| TSA | Track Segment Association |
| TSADCNN | TSA with Dual Contrast Neural Network |
| TGRA | Track Graph Representation Association |
| TSA-cTFER | TSA-contrastive TransFormer Encoder Representation Network |
References
- Raghu, J.; Srihari, P.; Tharmarasa, R.; Kirubarajan, T. Comprehensive Track Segment Association for Improved Track Continuity. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2463–2480. [Google Scholar] [CrossRef]
- Wei, X.; Pingliang, X.; Yaqi, C. Unsupervised and interpretable track-to-track association based on homography estimation of radar bias. IET Radar Sonar Nav. 2024, 18, 294–307. [Google Scholar] [CrossRef]
- Yeom, S.W.; Kirubarajan, T.; Bar-Shalom, Y. Track segment association, fine-step IMM and initialization with Doppler for improved track performance. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 293–309. [Google Scholar] [CrossRef]
- Zhang, S.; Bar-Shalom, Y. Track Segment Association for GMTI Tracks of Evasive Move-Stop-Move Maneuvering Targets. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1899–1914. [Google Scholar] [CrossRef]
- Lin, Q.; Hai-peng, W.; Wei, X.; Kai, D. Track segment association algorithm based on multiple hypothesis models with priori information. J. Syst. Eng. Electron. 2015, 37, 732–739. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Tian, W.; Wang, Y.; Shan, X.; Yang, J. Track-to-Track Association for Biased Data Based on the Reference Topology Feature. IEEE Signal Process. Lett. 2014, 21, 449–453. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, W.; Wang, C. Robust track-to-track association in the presence of sensor biases and missed detections. Inform. Fusion 2016, 27, 33–40. [Google Scholar] [CrossRef]
- Zhao, H.; Sha, Z.; Wu, J. An improved fuzzy track association algorithm based on weight function. In Proceedings of the IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 1125–1128. [Google Scholar] [CrossRef]
- Wei, X.; Xu, P.; Cui, Y.; Xiong, Z.; Lv, Y.; Gu, X. Track Segment Association with Dual Contrast Neural Network. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 247–261. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Wei, X.; Xu, P.; Cui, Y.; Xiong, Z.; Gu, X.; Lv, Y. Track Segment Association via track graph representation learning. IET Radar Sonar Nav. 2021, 15, 1458–1471. [Google Scholar] [CrossRef]
- Jin, B.; Tang, Y.; Zhang, Z.; Lian, Z.; Wang, B. Radar and AIS Track Association Integrated Track and Scene Features Through Deep Learning. IEEE Sens. J. 2023, 23, 8001–8009. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Proc. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceedings of the 9th International Conference on Learning Representations (ICLR), Virtual, Austria, 3–7 May 2021. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units. arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the NAACL HLT—Conference of the North American Chapter of the Association for Computational Linguistics, Minneapolis, MN, USA, 2–7 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- Oord, A.v.d.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Yaqi, C.; Pingliang, X.; Cheng, G.; Zhouchuan, Y.; Jianting, Z.; Hongbo, Y.; Kai, D. Multisource Track Association Dataset Based on the Global AIS. J. Electron. Inf. Techn. 2023, 45, 746–756. [Google Scholar] [CrossRef]
- Multi-Source Track Association Dataset. Available online: https://jeit.ac.cn/web/data/getData?dataType=Dataset (accessed on 23 April 2024).
- Agrawal, R.; Faloutsos, C.; Swami, A. Efficient similarity search in sequence databases. In Proceedings of the International Conference on Foundations of Data Organization and Algorithms, Chicago, IL, USA, 13–15 October 1993; pp. 69–84. [Google Scholar]
- Zheng, Y. Trajectory data mining: An overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–41. [Google Scholar] [CrossRef]
- Hu, D.; Chen, L.; Fang, H.; Fang, Z.; Li, T.; Gao, Y. Spatio-Temporal Trajectory Similarity Measures: A Comprehensive Survey and Quantitative Study. arXiv 2023, arXiv:2303.05012. [Google Scholar] [CrossRef]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2016. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 8024–8035. [Google Scholar]
- Reimers, N.; Gurevych, I. Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks. In Proceedings of the EMNLP-IJCNLP—Conference on Empirical Methods in Natural Language Processing and 9th International Joint Conference on Natural Language Processing, Hong Kong, China, 3–7 November 2019; pp. 3982–3992. [Google Scholar]







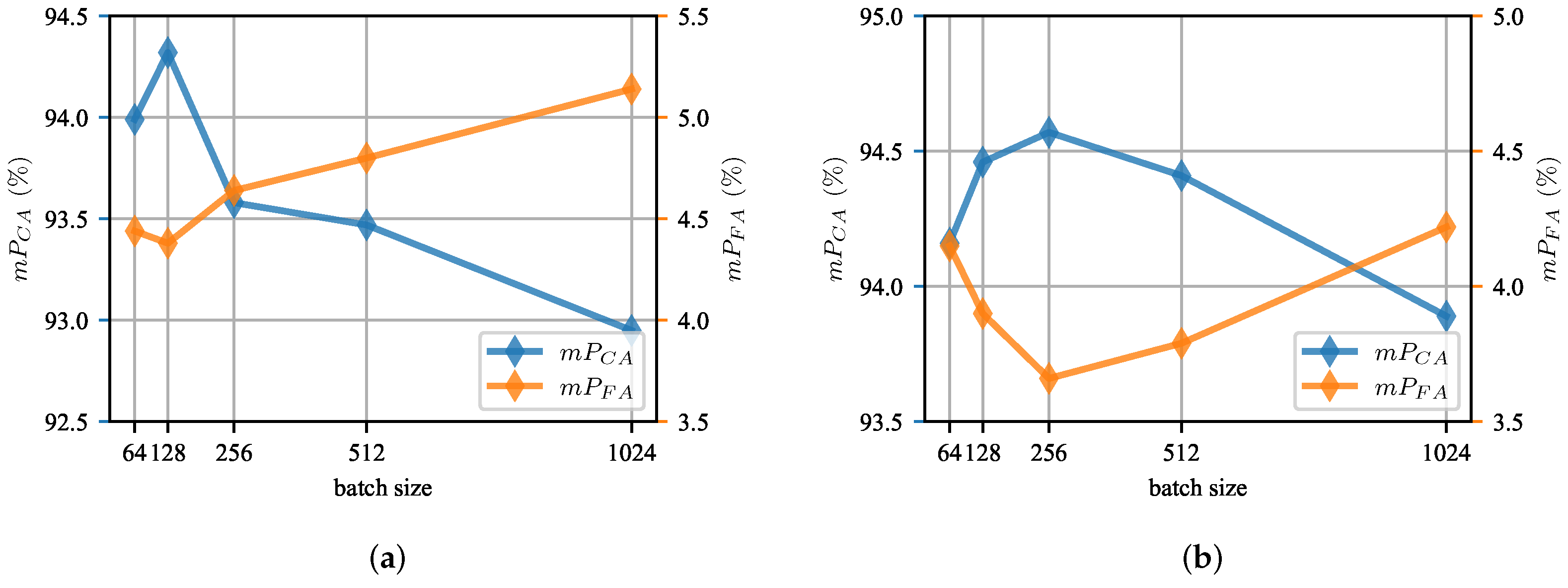
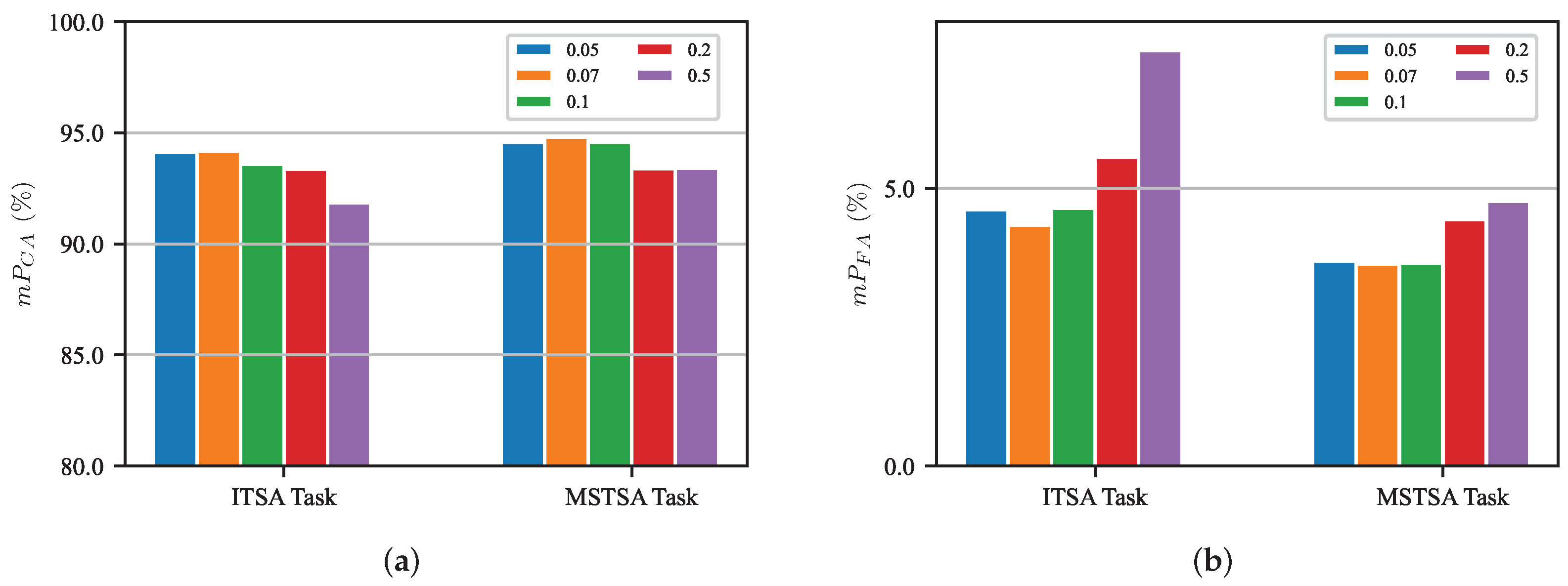
| #params. (M) | (%) | (%) | (s) | (%) | (%) | (s) | |
|---|---|---|---|---|---|---|---|
| ED-based TSA | - | 48.87 | 55.59 | 86.92 | 27.98 | 75.05 | 79.44 |
| MH TSA [5] | - | 93.79 | 6.35 | 49.34 | 90.87 | 11.99 | 43.42 |
| MF 2-D TSA [1] | - | 80.54 | 5.30 | 156.82 | 75.73 | 9.92 | 132.59 |
| TSADCNN (Sep.) [10] | 0.908 | 79.41 ± 3.03 | 6.61 ± 0.59 | 227.27 ± 23.24 | 76.70 ± 2.66 | 12.14 ± 0.74 | 212.43 ± 15.62 |
| TSADCNN [10] | 1.301 | 83.86 ± 0.13 | 5.52 ± 0.24 | 201.01 ± 13.63 | 80.82 ± 0.15 | 10.85 ± 0.05 | 189.51 ± 2.17 |
| TGRA (Sep.) [12] | 0.534 | 85.64 ± 0.72 | 8.63 ± 0.27 | 152.71 ± 8.68 | 79.55 ± 0.62 | 16.16 ± 0.23 | 153.70 ± 1.26 |
| TGRA [12] | 0.534 | 85.02 ± 0.29 | 9.02 ± 0.07 | 160.85 ± 10.76 | 79.55 ± 0.18 | 16.17 ± 0.11 | 150.42 ± 1.00 |
| TSA-cTFER (Sep.) | 0.670 | 94.21 ± 0.05 | 3.46 ± 0.06 | 130.91 ± 1.13 | 90.77 ± 0.09 | 7.39 ± 0.07 | 139.19 ± 0.96 |
| TSA-cTFER | 0.674 | 94.59 ± 0.04 | 3.49 ± 0.08 | 131.00 ± 9.49 | 91.29 ± 0.13 | 7.34 ± 0.15 | 136.13 ± 2.97 |
| #params. (M) | (%) | (%) | (s) | (%) | (%) | (s) | |
|---|---|---|---|---|---|---|---|
| ED-based TSA | - | 50.99 | 25.85 | 464.38 | 39.30 | 39.86 | 247.04 |
| DTW-based TSA | - | 54.24 | 41.77 | 505.52 | 35.27 | 60.56 | 638.35 |
| TSADCNN (Sep.) [10] | 0.908 | 94.68 ± 0.51 | 2.73 ± 0.40 | 235.85 ± 6.74 | 91.80 ± 0.94 | 5.13 ± 0.70 | 269.29 ± 11.55 |
| TSADCNN [10] | 1.301 | 92.85 ± 0.22 | 4.22 ± 0.22 | 259.49 ± 2.13 | 85.36 ± 0.30 | 8.05 ± 0.27 | 311.86 ± 3.01 |
| TGRA (Sep.) [12] | 0.534 | 93.81 ± 0.13 | 3.41 ± 0.11 | 252.84 ± 1.52 | 90.03 ± 0.42 | 6.47 ± 0.38 | 303.85 ± 3.13 |
| TGRA [12] | 0.534 | 91.61 ± 0.13 | 5.32 ± 0.11 | 271.25 ± 2.26 | 85.60 ± 0.31 | 10.59 ± 0.27 | 334.80 ± 2.54 |
| TSA-cTFER (Sep.) | 0.670 | 94.83 ± 0.38 | 2.61 ± 0.34 | 234.65 ± 1.10 | 92.20 ± 0.52 | 4.79 ± 0.47 | 269.79 ± 2.01 |
| TSA-cTFER | 0.674 | 94.25 ± 0.09 | 3.06 ± 0.11 | 246.95 ± 0.78 | 91.00 ± 0.12 | 5.75 ± 0.11 | 290.20 ± 1.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Liu, B.; Yang, J.; Tan, K.; Dai, Z.; Lu, X.; Gu, H. Contrastive Transformer Network for Track Segment Association with Two-Stage Online Method. Remote Sens. 2024, 16, 3380. https://doi.org/10.3390/rs16183380
Cao Z, Liu B, Yang J, Tan K, Dai Z, Lu X, Gu H. Contrastive Transformer Network for Track Segment Association with Two-Stage Online Method. Remote Sensing. 2024; 16(18):3380. https://doi.org/10.3390/rs16183380
Chicago/Turabian StyleCao, Zongqing, Bing Liu, Jianchao Yang, Ke Tan, Zheng Dai, Xingyu Lu, and Hong Gu. 2024. "Contrastive Transformer Network for Track Segment Association with Two-Stage Online Method" Remote Sensing 16, no. 18: 3380. https://doi.org/10.3390/rs16183380
APA StyleCao, Z., Liu, B., Yang, J., Tan, K., Dai, Z., Lu, X., & Gu, H. (2024). Contrastive Transformer Network for Track Segment Association with Two-Stage Online Method. Remote Sensing, 16(18), 3380. https://doi.org/10.3390/rs16183380








