Westward Migration of the Chenghai–Jinsha Drainage Divide and Its Implication for the Initiation of the Chenghai Fault
Abstract
:1. Introduction

2. Background
3. Methods
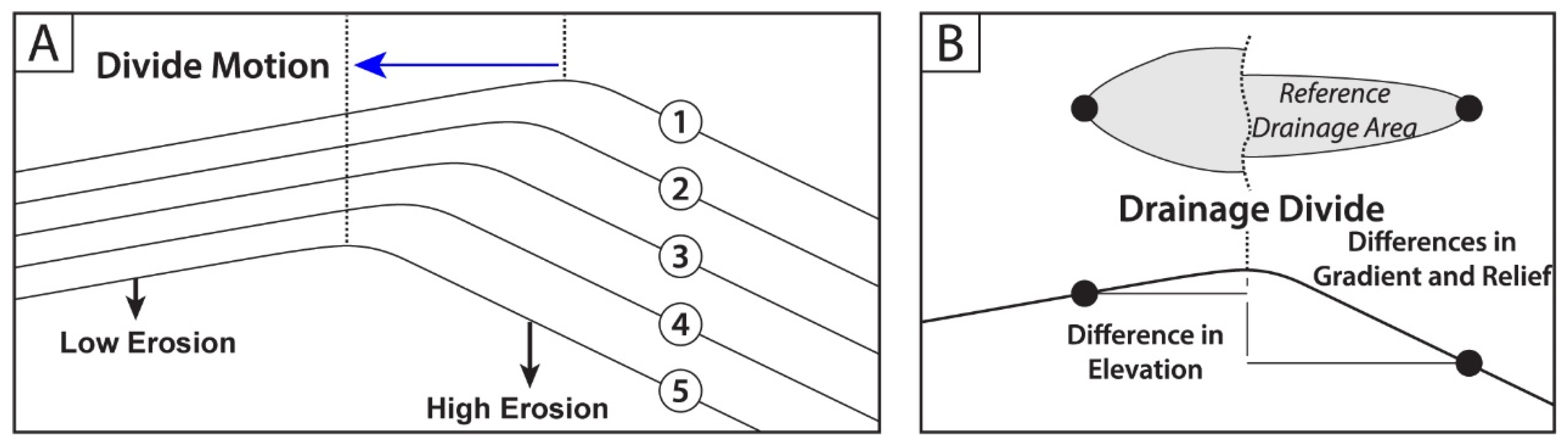
3.1. Measuring Drainage Divide Stability
3.2. Estimation of the Stable Location of Drainage Divides
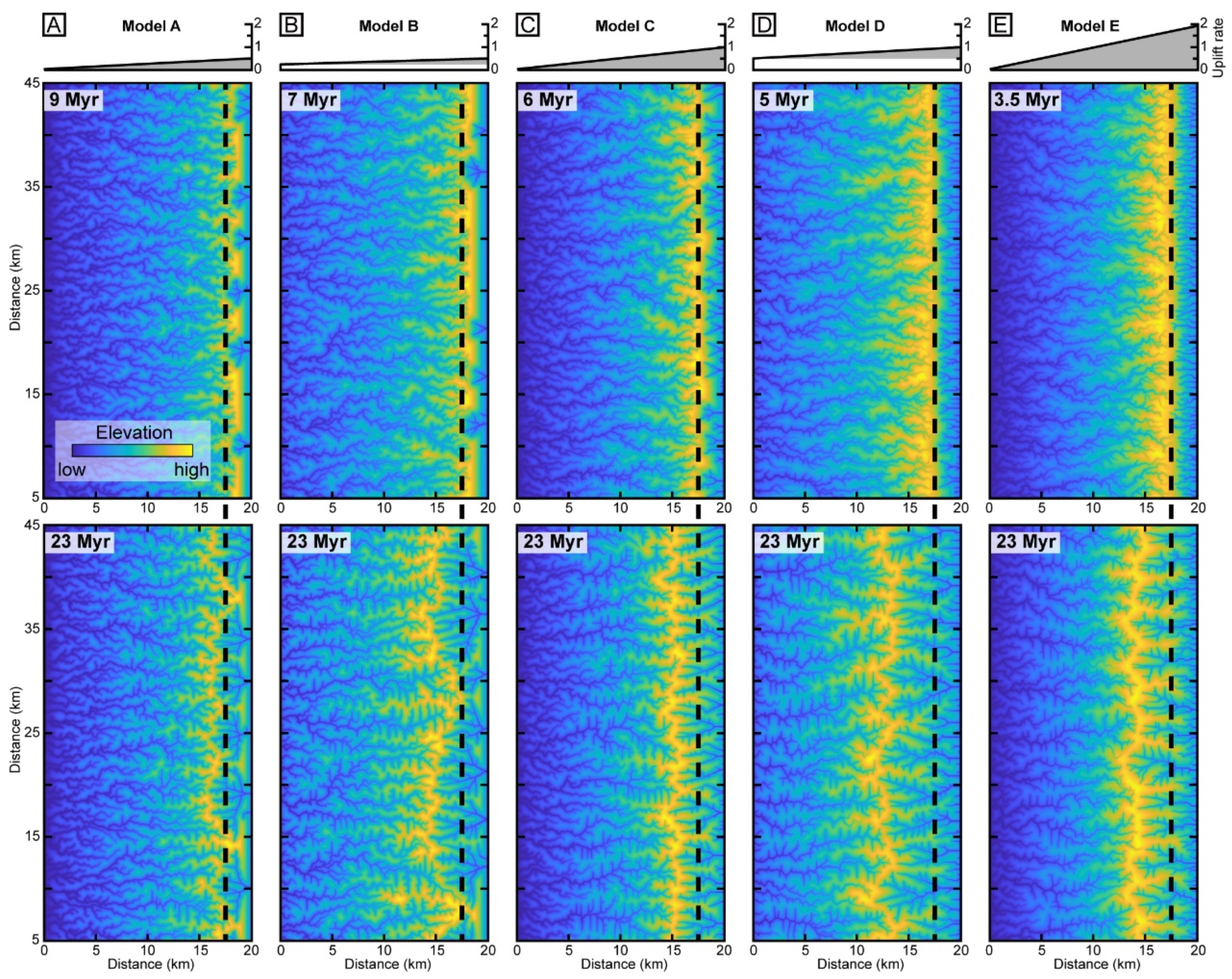
3.3. Numerical Modeling of Landscape Evolution
4. Results
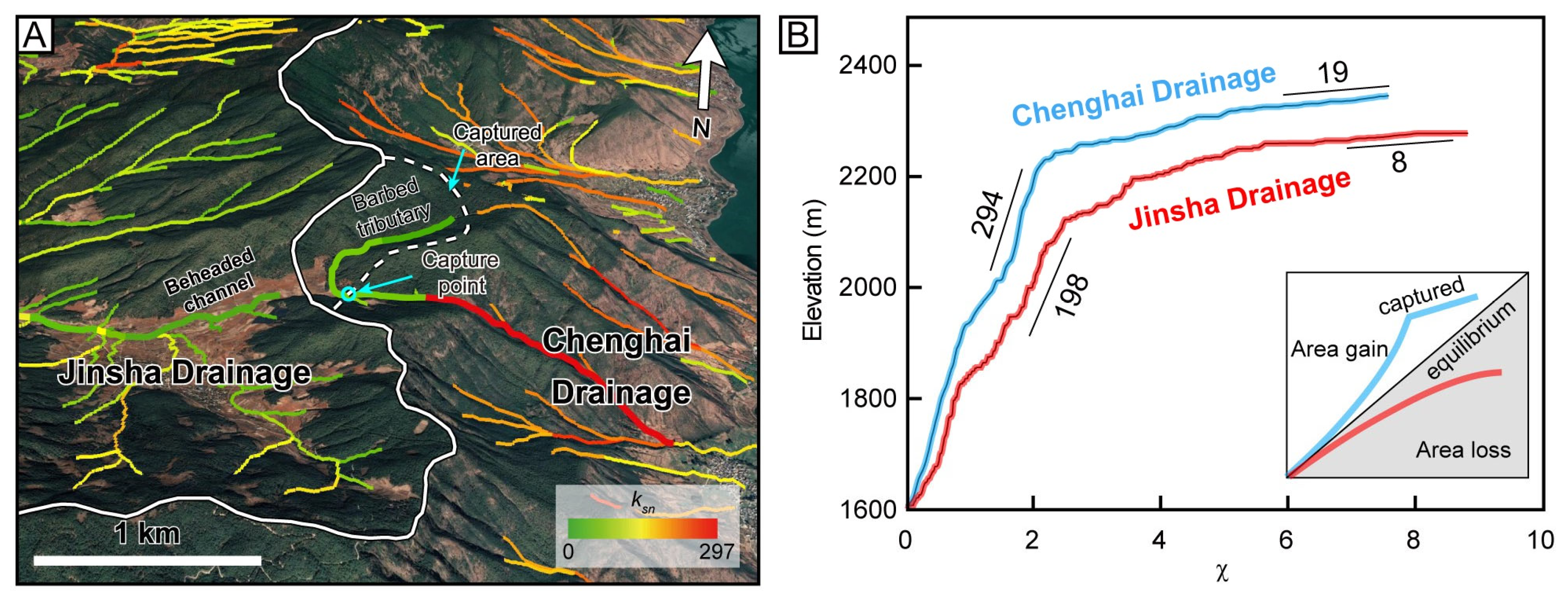
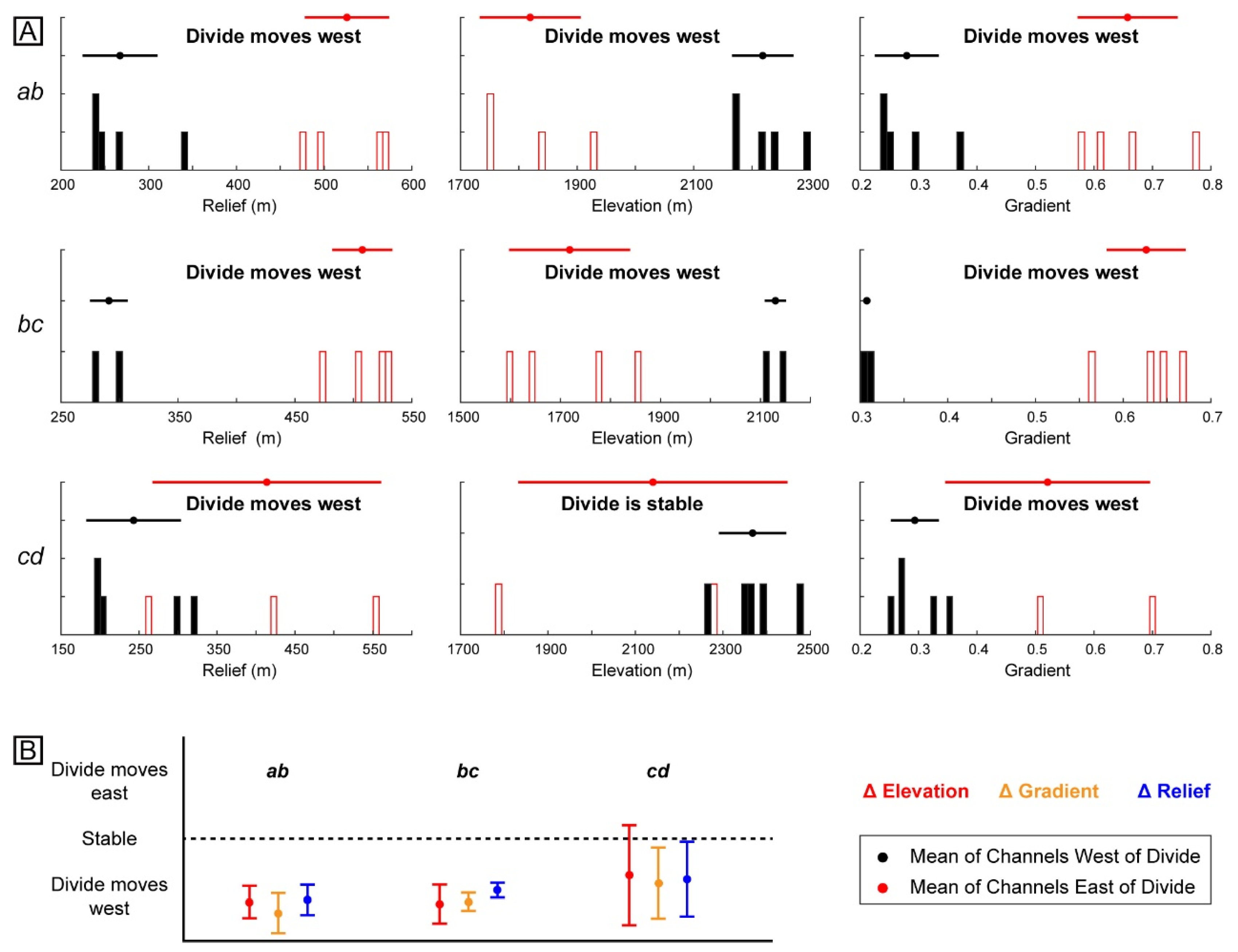
4.1. Stability of the Chenghai–Jinsha Drainage Divide
4.2. Future Stable Location of the Chenghai–Jinsha Drainage Divide
4.3. Numerical Modeling on Landscape Evolution
5. Discussion
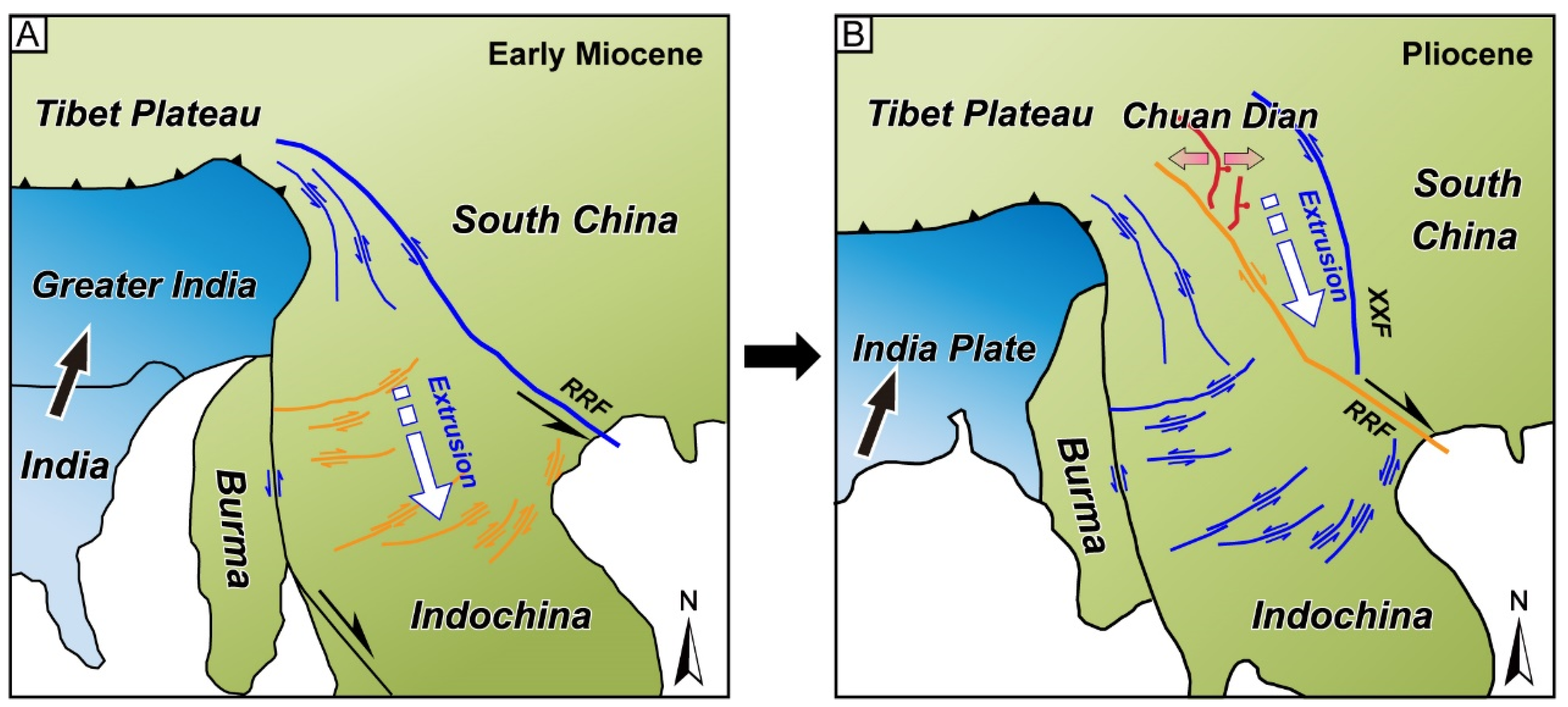
5.1. Drainage Reorganization around the Chenghai Fault
5.2. Implications for the Initiation of the Chenghai Fault
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Molnar, P.; Tapponnier, P. Cenozoic Tectonics of Asia: Effects of a Continental Collision: Features of recent continental tectonics in Asia can be interpreted as results of the India-Eurasia collision. Science 1975, 189, 419–426. [Google Scholar] [CrossRef] [PubMed]
- Tapponnier, P.; Molnar, P. Active faulting and tectonics in China. J. Geophys. Res. 1977, 82, 2905–2930. [Google Scholar] [CrossRef]
- Yin, A.; Harrison, T.M. Geologic evolution of the Himalayan-Tibetan orogen. Annu. Rev. Earth Planet. Sci. 2000, 28, 211–280. [Google Scholar] [CrossRef]
- Tapponnier, P.; Xu, Z.Q.; Roger, F.; Meyer, B.; Arnaud, N.; Wittlinger, G.; Yang, J.S. Oblique stepwise rise and growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef]
- Tapponnier, P.; Peltzer, G.; Le Dain, A.Y.; Armijo, R.; Cobbold, P. Propagating extrusion tectonics in Asia: New insights from simple experiments with plasticine. Geology 1982, 10, 611–616. [Google Scholar] [CrossRef]
- Molnar, P.; England, P.; Martinod, J. Mantle dynamics, uplift of the Tibetan Plateau, and the Indian monsoon. Rev. Geophys. 1993, 31, 357–396. [Google Scholar] [CrossRef]
- Royden, L.H.; Burchfiel, B.C.; van der Hilst, R.D. The geological evolution of the Tibetan Plateau. Science 2008, 321, 1054–1058. [Google Scholar] [CrossRef]
- Royden, L.H.; Burchfiel, B.C.; King, R.W.; Wang, E.; Chen, Z.; Shen, F.; Liu, Y. Surface deformation and lower crustal flow in eastern Tibet. Science 1997, 276, 788–790. [Google Scholar] [CrossRef]
- Wang, E.; Burchfiel, B.C.; Royden, L.H.; Chen, L.Z.; Chen, J.S.; Li, W.X.; Chen, Z.L. Late Cenozoic Xianshuihe-Xiaojiang, Red River, and Dali Fault Systems of Southwestern Sichuan and Central Yunnan, China; Geological Society of America Special Paper; Geological Society of America: Boulder, CO, USA, 1998; Volume 327. [Google Scholar]
- Leloup, P.H.; Arnaud, N.; Lacassin, R.; Kienast, J.R.; Harrison, T.M.; Trong, T.P.; Replumaz, A.; Tapponnier, P. New constraints on the structure, thermochronology, and timing of the Ailao Shan-Red River shear zone, SE Asia. J. Geophys. Res. Solid Earth 2001, 106, 6683–6732. [Google Scholar] [CrossRef]
- Xu, X.W.; Cheng, G.L.; Yu, G.H.; Song, F.M.; Xiang, H.F.; Zhang, L.F.; Ron, H.; Wang, Y.L.; Wen, X.Z. Tectonic and paleomagnetic evidence for the clockwise rotation of the Sichuan-Yunnan rhombic block. Seismol. Geol. 2003, 25, 61–70, (In Chinese with English abstract). [Google Scholar]
- Li, S.H.; Advokaat, E.L.; van Hinsbergen, D.J.; Koymans, M.; Deng, C.; Zhu, R. Paleomagnetic constraints on the Mesozoic-Cenozoic paleolatitudinal and rotational history of Indochina and South China: Review and updated kinematic reconstruction. Earth-Sci. Rev. 2017, 171, 58–77. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.J.; Zhang, P.Z.; Zhang, J.J.; Zhang, B.; Jing, L.-Z.; Zhou, R.J.; Wang, W.T.; Zhang, H.P.; Li, Z.J. Cenozoic tectonic evolution of regional fault systems in the SE Tibetan Plateau. Sci. China Earth Sci. 2022, 65, 601–623. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Schoenbohm, L.M.; Zhang, P.; Zhang, B.; Sobel, E.R.; Zhou, R.J.; Shi, X.H.; Zhang, J.J.; Stockli, D.F.; et al. Cenozoic exhumation of the Ailaoshan-Red River shear zone: New insights from low-temperature thermochronology. Tectonics 2020, 39, e2020TC006151. [Google Scholar] [CrossRef]
- Leloup, P.H.; Harrison, T.M.; Ryerson, F.J.; Cheng, W.J.; Li, Q.; Tapponnier, P.; Lacassin, R. Structural, petrological and thermal evolution of a Tertiary ductile strike-slip shear zone, Diancang Shan, Yunnan. J. Geophys. Res. Solid Earth 1993, 98, 6715–6743. [Google Scholar] [CrossRef]
- Cao, S.Y.; Neubauer, F.; Liu, J.L.; Genser, J.; Leiss, B. Exhumation of the Diancang Shan metamorphic complex along the Ailao Shan-Red River belt, southwestern Yunnan, China: Evidence from 40Ar/39Ar thermochronology. J. Asian Earth Sci. 2011, 42, 525–550. [Google Scholar] [CrossRef]
- Li, S.H.; Deng, C.L.; Yao, H.T.; Huang, S.; Liu, C.Y.; He, H.Y.; Pan, Y.X.; Zhu, R.X. Magnetostratigraphy of the Dali Basin in Yunnan and implications for late Neogene rotation of the southeast margin of the Tibetan Plateau. J. Geophys. Res. Solid Earth 2013, 118, 791–807. [Google Scholar] [CrossRef]
- England, P.; Molnar, P. Surface uplift, uplift of rocks, and exhumation of rocks. Geology 1990, 18, 1173–1177. [Google Scholar] [CrossRef]
- Copley, A. Kinematics and dynamics of the southeastern margin of the Tibetan Plateau. Geophys. J. Int. 2008, 174, 1081–1100. [Google Scholar] [CrossRef]
- Department of Earthquake Disaster Prevention, China Earthquake Administration (DEDP). Catalogue of Strong Earthquakes in Chinese History: 23rd Century BC–1911 AD; Seismological Press: Beijing, China, 1995. [Google Scholar]
- Wang, B.; Wu, G.; Su, Y.; Wang, B.; Ge, H.; Jin, M. Site construction of the Binchuan transmitting seismic stations and preliminary observational data. J. Seismol. Res. 2015, 38, 1–6. [Google Scholar]
- Zhou, Q.; Guo, S.; Xiang, H. Principle and method of delineation of potential seismic sources in northeastern Yunnan province. Seismol. Geol. 2004, 26, 761–771. [Google Scholar]
- Ji, H.; Ren, Z.; Zhu, X.; Bai, M.; Bao, G.; Liu, J.; Ha, G.; He, Z. Slip distribution along the Chenghai fault from airborne LiDAR and tectonic implications for the 1515 Yongsheng earthquake, China. Tectonics 2024, 43, e2024TC008285. [Google Scholar] [CrossRef]
- U.S. Geological Survey, Earthquake Hazards Program (USGSEHP). Advanced National Seismic System (ANSS) Comprehensive Catalog of Earthquake Events and Products: Various; U.S. Geological Survey: Reston, VA, USA, 2017. [CrossRef]
- Guo, L.; He, Z.; Li, L. Responses of Stream Geomorphic Indices to Piedmont Fault Activity in the Northern Segment of the Red River Fault Zone. Remote Sens. 2023, 15, 988. [Google Scholar] [CrossRef]
- Gao, M.; Hao, M.; Zeilinger, G.; Xu, X. Recent Uplift Characteristics of the Southeast Tibetan Plateau, an Analysis Based on Fluvial Indices. Remote Sens. 2023, 15, 433. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, S.; Yu, H.; Zhang, W.; Guo, F.; Chen, X.; Guo, J. Quantitative Analysis of Tectonic Geomorphology Research Based on Web of Science from 1981 to 2021. Remote Sens. 2022, 14, 5227. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, P.; Oguchi, T.; He, Z. Remote Sensing Perspectives on Geomorphology and Tectonic Processes. Remote Sens. 2023, 15, 2327. [Google Scholar] [CrossRef]
- Shen, K.; Dong, S.; Wang, Y. Active Tectonics Assessment Using Geomorphic and Drainage Indices in the Sertengshan, Hetao Basin, China. Remote Sens. 2023, 15, 3230. [Google Scholar] [CrossRef]
- Sakashita, A.; Endo, N. Mobility and Location of Drainage Divides Affected by Tilting Uplift in Sado Island, Japan. Remote Sens. 2023, 15, 729. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Y.; Zhang, J.; Wang, W.; Lu, R. Channel Profiles Reveal Fault Activity along the Longmen Shan, Eastern Tibetan Plateau. Remote Sens. 2023, 15, 4721. [Google Scholar] [CrossRef]
- Willett, S.D.; McCoy, S.W.; Perron, J.T.; Goren, L.; Chen, C.Y. Dynamic reorganization of river basins. Science 2014, 343, 1248765. [Google Scholar] [CrossRef]
- Forte, A.M.; Whipple, K.X. Criteria and tools for determining drainage divide stability. Earth Planet. Sci. Lett. 2018, 493, 102–117. [Google Scholar] [CrossRef]
- He, C.Q.; Yang, C.J.; Turowski, J.M.; Rao, G.; Roda-Boluda, D.C.; Yuan, X.P. Constraining tectonic uplift and advection from the main drainage divide of a mountain belt. Nat. Commun. 2021, 12, 544. [Google Scholar] [CrossRef] [PubMed]
- Shi, F.; Tan, X.; Zhou, C.; Liu, Y. Impact of asymmetric uplift on mountain asymmetry: Analytical solution, numerical modeling, and natural examples. Geomorphology 2021, 389, 107862. [Google Scholar] [CrossRef]
- Zhou, C.; Tan, X.; Liu, Y.; Shi, F. A cross-divide contrast index (C) for assessing controls on the main drainage divide stability of a mountain belt. Geomorphology 2022, 398, 108071. [Google Scholar] [CrossRef]
- Buscher, J.T.; Ascione, A.; Valente, E. Decoding the role of tectonics, incision and lithology on drainage divide migration in the Mt. Alpi region, southern Apennines, Italy. Geomorphology 2017, 276, 37–50. [Google Scholar] [CrossRef]
- He, C.; Rao, G.; Yang, R.; Hu, J.; Yao, Q.; Yang, C.J. Divide migration in response to asymmetric uplift: Insights from the Wula Shan horst, North China. Geomorphology 2019, 339, 44–57. [Google Scholar] [CrossRef]
- Yang, R.; Suhail, H.A.; Gourbet, L.; Willett, S.D.; Fellin, M.G.; Lin, X.B.; Gong, J.F.; Wei, X.C.; Maden, C.; Jiao, R.H.; et al. Early Pleistocene drainage pattern changes in Eastern Tibet: Constraints from provenance analysis, thermochronometry, and numerical modeling. Earth Planet. Sci. Lett. 2020, 531, 115955. [Google Scholar] [CrossRef]
- Chen, C.; Willett, S.D.; Christl, M.; Shyu, J.B.H. Drainage basin dynamics during the transition from early to mature orogeny in Southern Taiwan. Earth Planet. Sci. Lett. 2021, 562, 116874. [Google Scholar] [CrossRef]
- Ye, Y.J.; Tan, X.B.; Zhou, C. Initial topography matters in drainage divide migration analysis: Insights from numerical simulations and natural examples. Geomorphology 2022, 409, 108266. [Google Scholar] [CrossRef]
- Bian, S.; Tan, X.; Liu, Y.; Fan, S.; Gong, J.; Zhou, C.; Shi, F.; Murphy, M.A. Orographic rainfall drives the Himalaya drainage divide to move north. Geomorphology 2024, 444, 108952. [Google Scholar] [CrossRef]
- Ye, Y.J.; Tan, X.B.; Liu, Y.D.; Bian, S.; Zhou, C.; Zeng, X.; Shi, F.; Gao, M.X. Drainage reorganization and divide migration driven by basin subsidence: An example from the Micang Shan, outskirts of eastern Tibet and its implications for Cenozoic evolution of the Yangtze River. Basin Res. 2024, 36, e12875. [Google Scholar] [CrossRef]
- Taylor, M.; Yin, A. Active structures of the Himalayan-Tibetan orogen and their relationships to earthquake distribution, contemporary strain field, and Cenozoic volcanism. Geosphere 2009, 5, 199–214. [Google Scholar] [CrossRef]
- Tapponnier, P.; Lacassin, R.; Leloup, P.H.; Schärer, U.; Zhong, D.L.; Wu, H.W.; Liu, X.H.; Ji, S.C.; Zhang, L.S.; Zhong, J.Y. The Ailao Shan/Red River metamorphic belt: Tertiary left-lateral shear between Indochina and South China. Nature 1990, 343, 431–437. [Google Scholar] [CrossRef]
- Clark, M.; Schoenbohm, L.M.; Royden, L.H.; Whipple, K.X.; Burchfiel, B.C.; Zhang, X.; Tang, W.; Wang, E.; Chen, L. Surface uplift, tectonics, and erosion of eastern Tibet from large-scale drainage patterns. Tectonics 2004, 23, TC1006. [Google Scholar] [CrossRef]
- Yang, R.; Willett, S.D.; Goren, L. In situ low-relief landscape formation as a result of river network disruption. Nature 2015, 520, 526–529. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Wang, G.; Wang, S.F.; Wang, E. Structural interpretation of extensional deformation along the Dali fault system, southeastern margin of the Tibetan Plateau. Int. Geol. Rev. 2006, 48, 287–310. [Google Scholar] [CrossRef]
- Luo, R.; Wu, Z.; Huang, X.; Huang, X.; Zhou, C.; Tian, T. The main active faults and the active tectonic system of Binchuan area, northwestern Yunnan. Geol. Bull. China 2015, 34, 155–170. [Google Scholar]
- Li, G.R.; Jin, D.S. Neoid Activity on the Chenghai Fracture. Yunnan Geol. 1990, 9, 1–24, (In Chinese with English abstract). [Google Scholar]
- Huang, X.J.; Wu, Z.H.; Huang, X.L.; Luo, R.J. Tectonic Geomorphology Constrains on the Quaternary Activity and Segmentation along Chenghai-Binchuan Fault Zone in Northwest Yunnan, China. Earth Sci. 2018, 43, 4651–4670, (In Chinese with English abstract). [Google Scholar]
- Huang, X.L.; Wu, Z.H.; Liu, F.; Tian, T.T.; Huang, X.J.; Zhang, D. Tectonic interpretation of the main paleoseismic landslides and their distribution characteristics in the Chenghai fault zone, Northwest Yunnan. Earth Sci. Front. 2021, 28, 125–139, (In Chinese with English abstract). [Google Scholar]
- Howard, A.D.; Kerby, G. Channel changes in badlands. Geol. Soc. Am. Bull. 1983, 94, 739–752. [Google Scholar] [CrossRef]
- Kirby, E.; Whipple, K.X. Quantifying differential rock-uplift rates via stream profile analysis. Geology 2001, 29, 415–418. [Google Scholar] [CrossRef]
- Kirby, E.; Whipple, K.X. Expression of active tectonics in erosional landscapes. J. Struct. Geol. 2012, 44, 54–75. [Google Scholar] [CrossRef]
- Whipple, K.X.; Tucker, G.E. Dynamics of the stream-power river incision model: Implications for height limits of mountain ranges, landscape response timescales, and research needs. J. Geophys. Res. Solid Earth 1999, 104, 17661–17674. [Google Scholar] [CrossRef]
- Perron, J.T.; Royden, L. An integral approach to bedrock river profile analysis. Earth Surf. Process. Landf. 2013, 38, 570–576. [Google Scholar] [CrossRef]
- Zhou, C.; Tan, X.; Liu, Y.; Lu, R.; Murphy, M.A.; He, H.; Han, Z.; Xu, X. Ongoing westward migration of drainage divides in eastern Tibet, quantified from topographic analysis. Geomorphology 2022, 402, 108123. [Google Scholar] [CrossRef]
- Ye, Y.J.; Tan, X.B.; Zhou, C.; Bian, S.; Liu, Y.D.; Shi, F. Cross-divide difference of steady-state channel-head elevation controls drainage-divide migration. Earth Surf. Process. Landf. 2024, 1–12. [Google Scholar] [CrossRef]
- Zhou, C.; Tan, X.; Liu, Y.; Shi, F. Quantifying the migration rate of drainage divides from high-resolution topographic data. Earth Surf. Dyn. 2024, 12, 433–448. [Google Scholar] [CrossRef]
- Gilbert, G.K. Geology of the Henry Mountains; USGS Report; Government Printing Office: Washington, DC, USA, 1877.
- Forte, A.M.; Whipple, K.X. Short communication: The Topographic Analysis Kit (TAK) for TopoToolbox. Earth Surf. Dyn. 2019, 7, 87–95. [Google Scholar] [CrossRef]
- Schwanghart, W.; Scherler, D. TopoToolbox 2–MATLAB-based software for topographic analysis and modeling in Earth surface sciences. Earth Surf. Dyn. 2014, 2, 1–7. [Google Scholar] [CrossRef]
- Campforts, B.; Schwanghart, W.; Govers, G. Accurate simulation of transient landscape evolution by eliminating numerical diffusion: The TTLEM 1.0 model. Earth Surf. Dyn. 2017, 5, 47–66. [Google Scholar] [CrossRef]
- Sassolas-Serrayet, T.; Cattin, R.; Ferry, M.; Godard, V.; Simoes, M. Estimating the disequilibrium in denudation rates due to divide migration at the scale of river basins. Earth Surf. Dyn. 2019, 7, 1041–1057. [Google Scholar] [CrossRef]
- Bishop, P. Drainage rearrangement by river capture, beheading and diversion. Prog. Phys. Geogr. 1995, 19, 449–473. [Google Scholar] [CrossRef]
- Harel, E.; Goren, L.; Shelef, E.; Ginat, H. Drainage reversal toward cliffs induced by lateral lithologic differences. Geology 2019, 47, 928–932. [Google Scholar] [CrossRef]
- Shelef, E.; Goren, L. The rate and extent of wind-gap migration regulated by tributary confluences and avulsions. Earth Surf. Dyn. 2021, 9, 687–700. [Google Scholar] [CrossRef]
- Hack, J.T. Studies of Longitudinal Stream Profiles in Virginia and Maryland; U.S. Geological Survey Professional Paper; U.S. Government Printing Office: Washington, DC, USA, 1957; pp. 45–97.
- Whipple, K.X. Fluvial landscape response time: How plausible is steady-state denudation? Am. J. Sci. 2001, 301, 313–325. [Google Scholar] [CrossRef]
- Authemayou, C.; Brocard, G.; Delcaillau, B.; Molliex, S.; Pedoja, K.; Husson, L.; Aribowo, S.; Cahyarini, S.Y. Unraveling the roles of asymmetric uplift, normal faulting and groundwater flow to drainage rearrangement in an emerging karstic landscape. Earth Surf. Process. Landf. 2018, 43, 1885–1898. [Google Scholar] [CrossRef]
- Su, Q.; Wang, X.; Lu, H.; Xie, H. Dynamic divide migration as a response to asymmetric uplift: An example from the Zhongtiao Shan, North China. Remote Sens. 2020, 12, 4188. [Google Scholar] [CrossRef]
- Whipple, K.X.; DiBiase, R.A.; Ouimet, W.B.; Forte, A.M. Preservation or piracy: Diagnosing low-relief, high-elevation surface formation mechanisms. Geology 2017, 45, 91–94. [Google Scholar] [CrossRef]
- Zeng, X.; Tan, X.B. Drainage divide migration in response to strike-slip faulting: An example from northern Longmen Shan, eastern Tibet. Tectonophysics 2023, 848, 229720. [Google Scholar] [CrossRef]
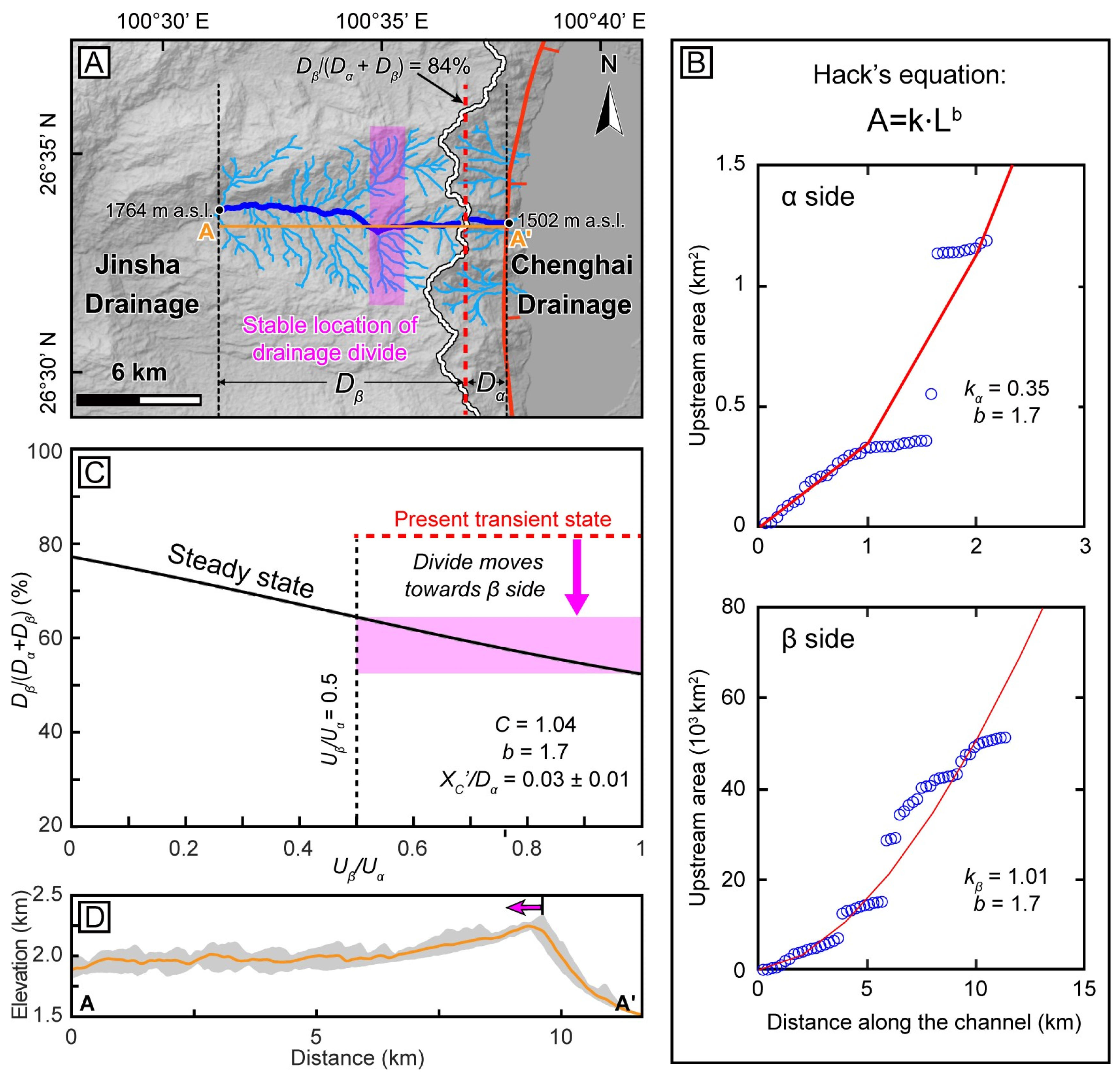
| Hα (m) | Hβ (m) | xα (m) | xβ (m) | Tα | Tβ | kα | kβ | b | C | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 708 | 474 | 2145 | 11,537 | 2045 | 9367 | 1.05 | 1.23 | 0.35 | 1.01 | 1.7 | 1.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, S.; Tan, X.; Liu, Y.; Shi, F.; Gong, J. Westward Migration of the Chenghai–Jinsha Drainage Divide and Its Implication for the Initiation of the Chenghai Fault. Remote Sens. 2024, 16, 3471. https://doi.org/10.3390/rs16183471
Bian S, Tan X, Liu Y, Shi F, Gong J. Westward Migration of the Chenghai–Jinsha Drainage Divide and Its Implication for the Initiation of the Chenghai Fault. Remote Sensing. 2024; 16(18):3471. https://doi.org/10.3390/rs16183471
Chicago/Turabian StyleBian, Shuang, Xibin Tan, Yiduo Liu, Feng Shi, and Junfeng Gong. 2024. "Westward Migration of the Chenghai–Jinsha Drainage Divide and Its Implication for the Initiation of the Chenghai Fault" Remote Sensing 16, no. 18: 3471. https://doi.org/10.3390/rs16183471
APA StyleBian, S., Tan, X., Liu, Y., Shi, F., & Gong, J. (2024). Westward Migration of the Chenghai–Jinsha Drainage Divide and Its Implication for the Initiation of the Chenghai Fault. Remote Sensing, 16(18), 3471. https://doi.org/10.3390/rs16183471






