A Robust Translational Motion Compensation Method for Moving Target ISAR Imaging Based on Phase Difference-Lv’s Distribution and Auto-Cross-Correlation Algorithm
Abstract
1. Introduction
2. Materials and Methods
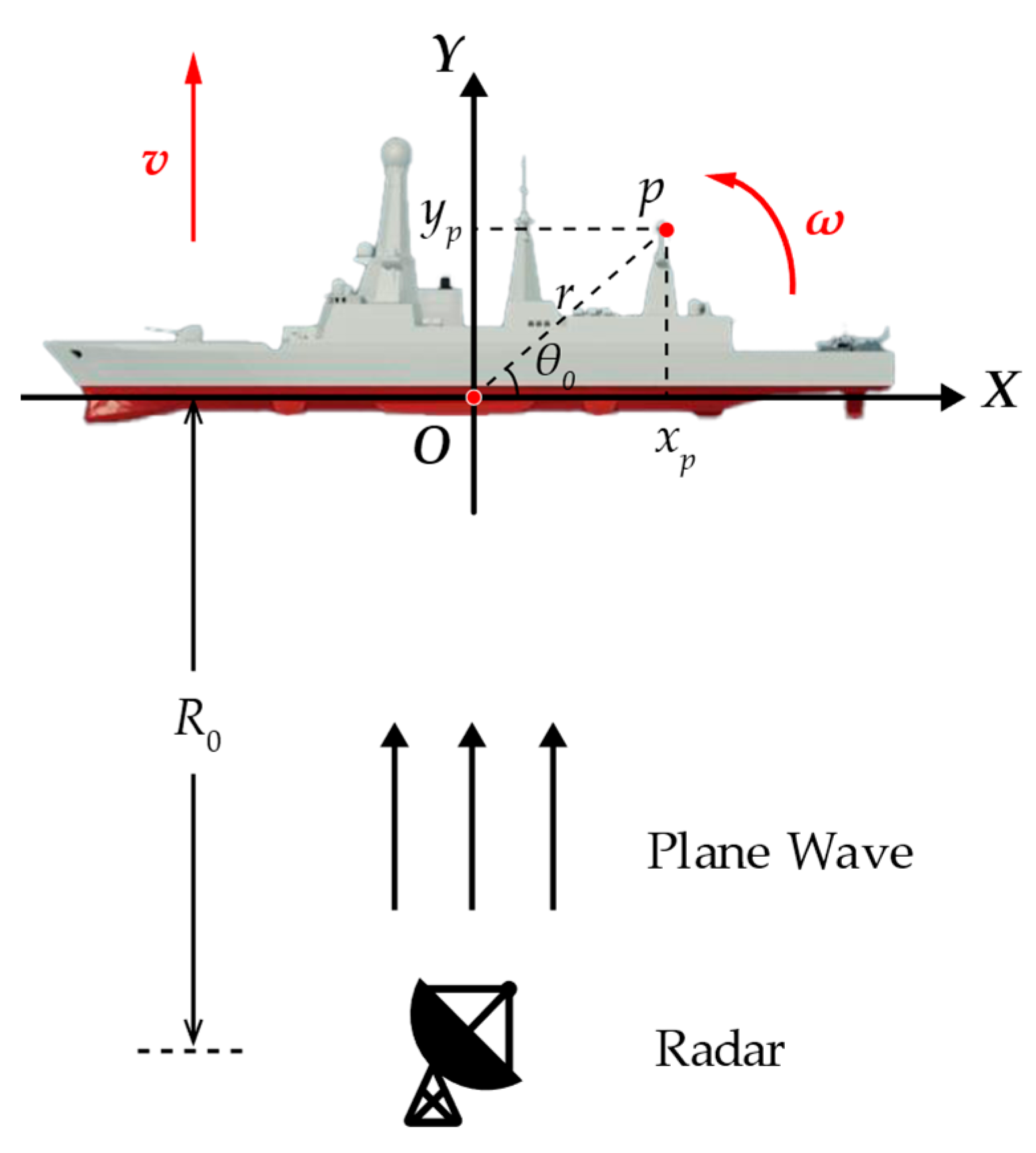
2.1. ISAR Imaging Geometry and Cubic Phase Signal Model
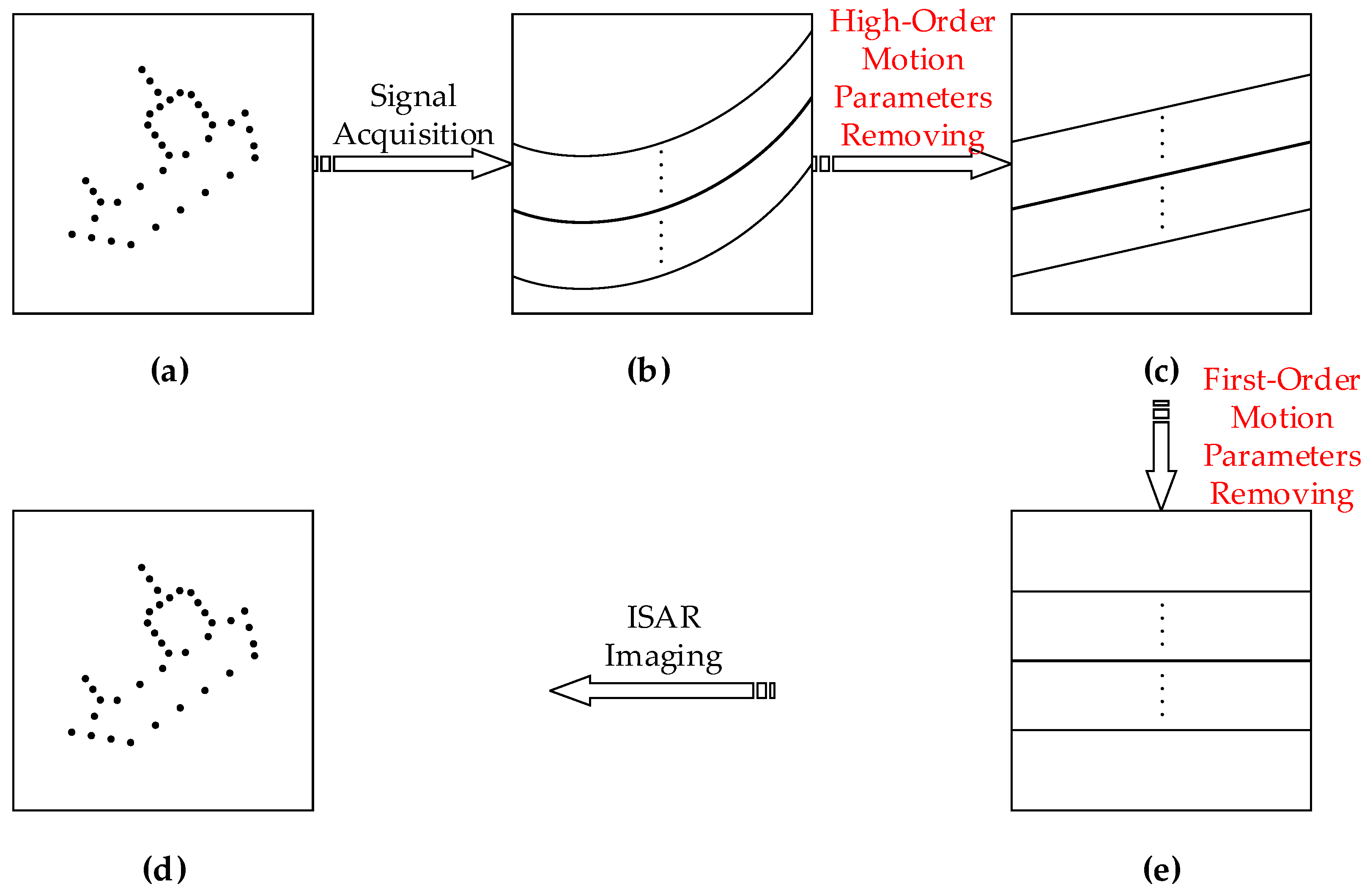
2.2. Proposed Translational Motion Compensation Method
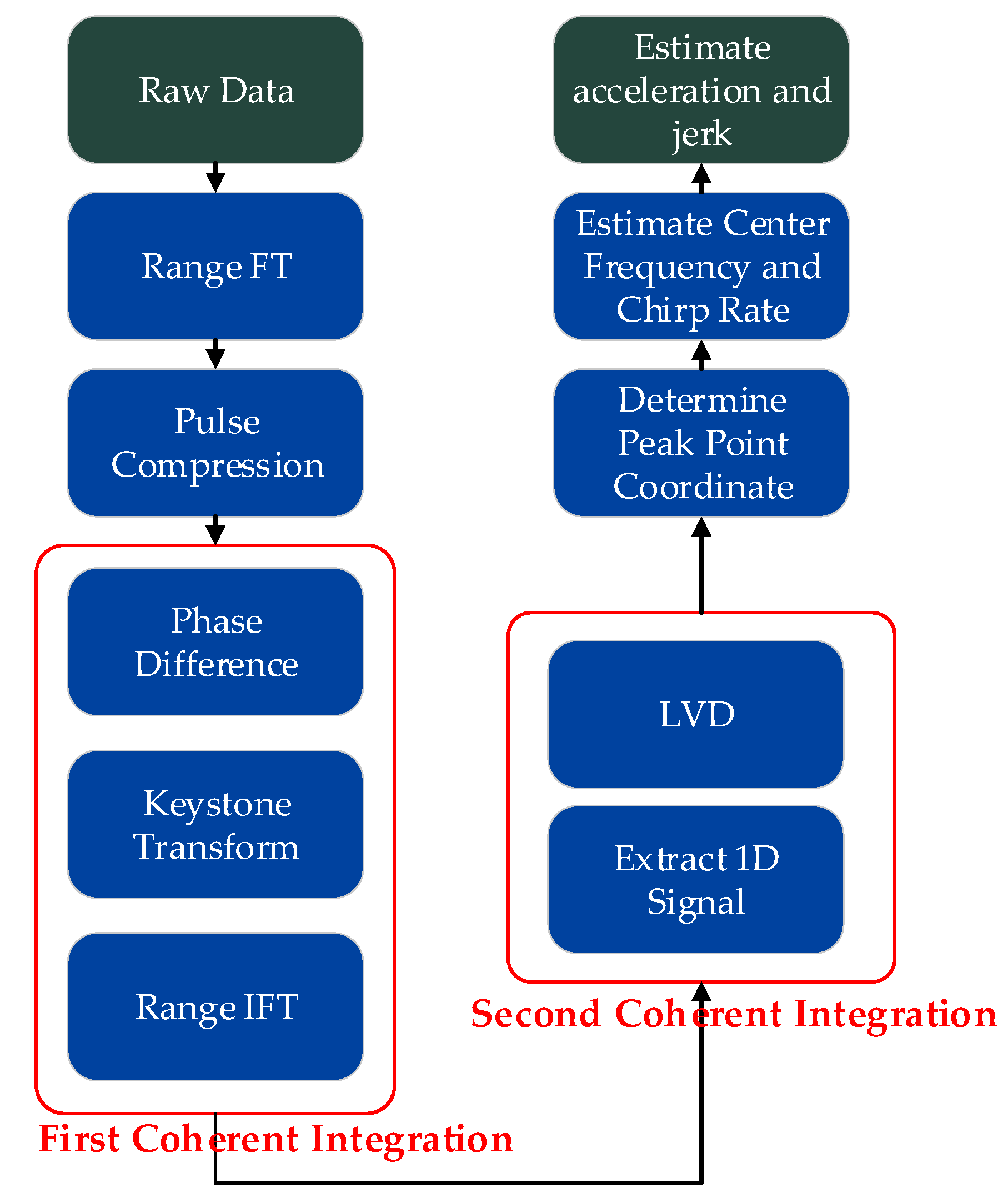
2.2.1. High-Order Polynomial Coefficient Estimation Based on PD-LVD
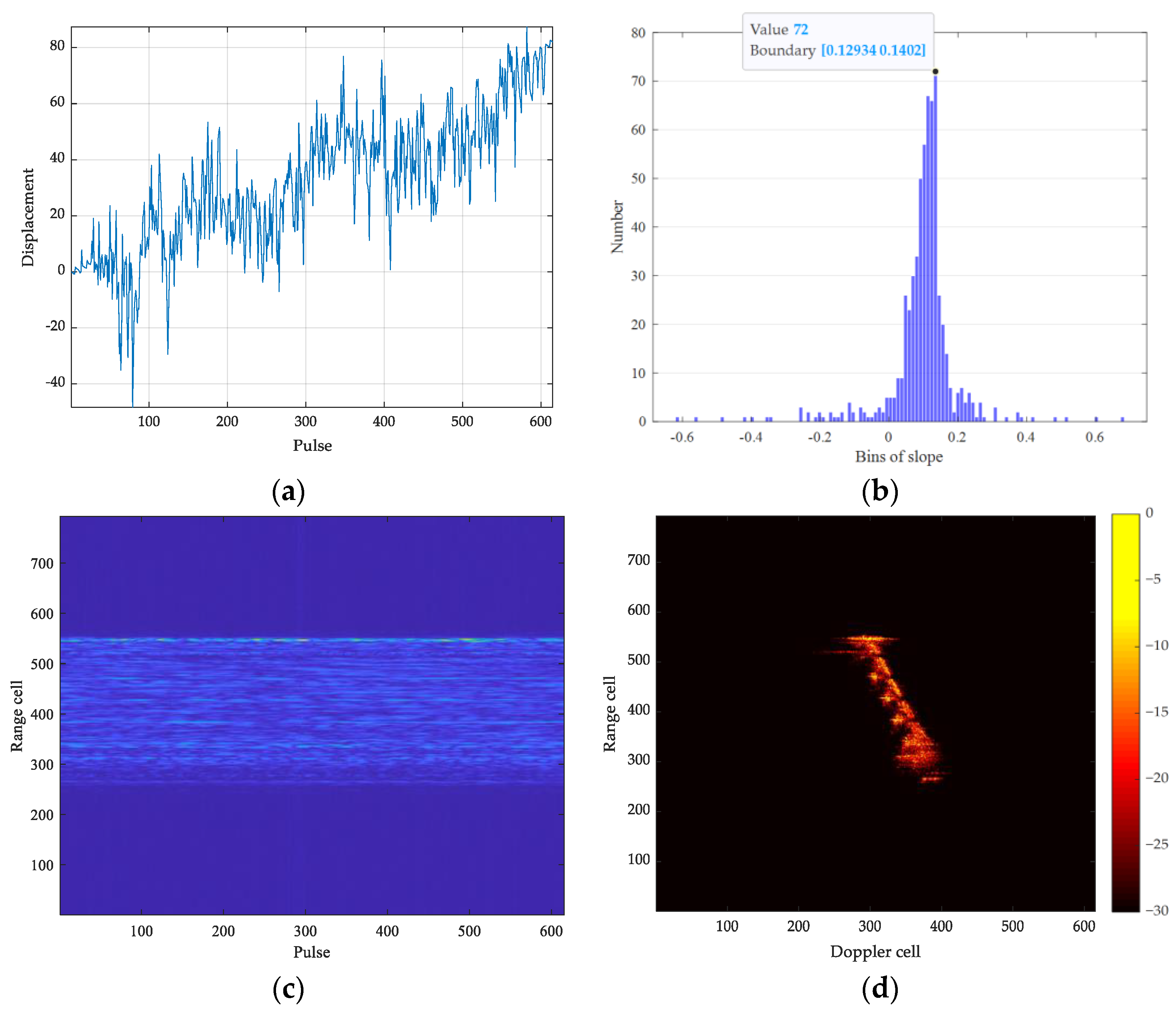
2.2.2. First-Order Polynomial Coefficient Estimation Based on ACCA
| Algorithm 1: Auto-Cross-Correlation Algorithm (ACCA) |
| Input: The discrete range profiles: . Output: The estimation of the first-order translational motion parameter: . 1: Use DFT to transform the signal to frequency domain. ; 2: For Iterate over the slow time indexes ; 3: Calculate the CCF ; 4: Calculate the ACCF ; 5: Select Q data points in the middle of ACCF to construct , ; 6: Compute the phase vector ; 7: Construct vector ; 8: Estimate the displacement ; 9: End For 10: Construct the displacement vector ; 11: Construct the slow time vector ; 12: Calculate the slope vector ; 13: Establish the slope histogram ; 14: Detect the bin with the most points and save the picked indexes ; 15: Estimate the first-order translational motion parameter ; |
2.2.3. Translational Motion Compensation and ISAR Imaging Based on the Proposed Method
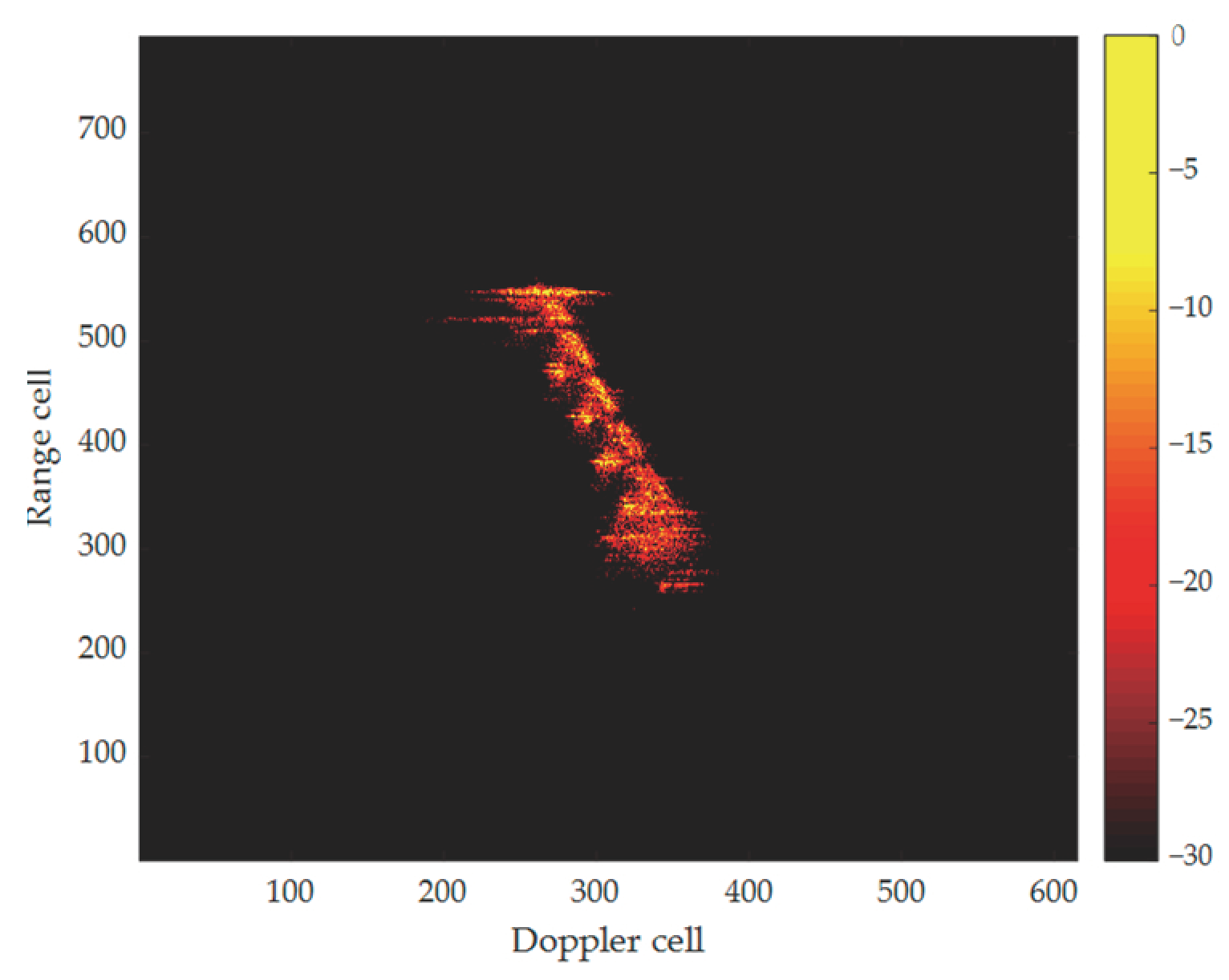
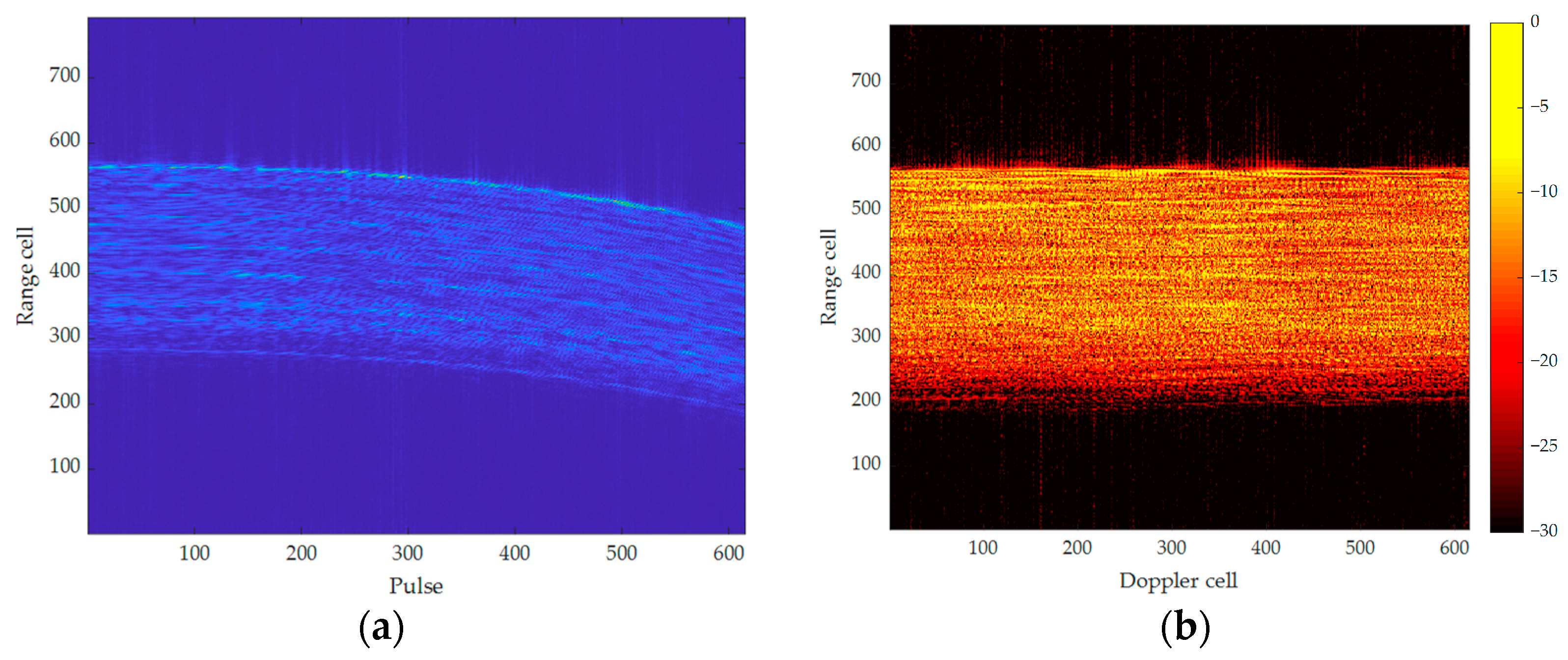
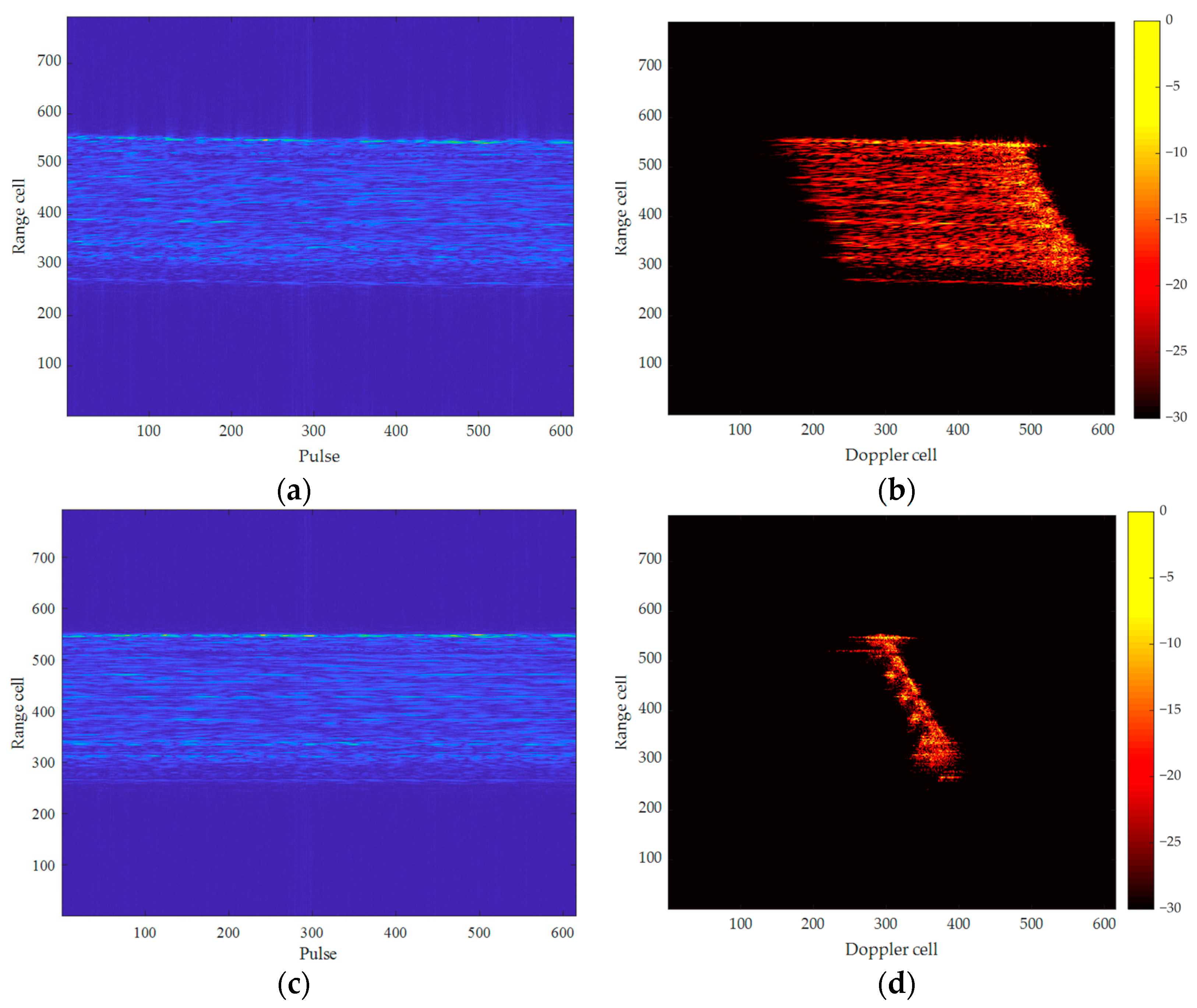
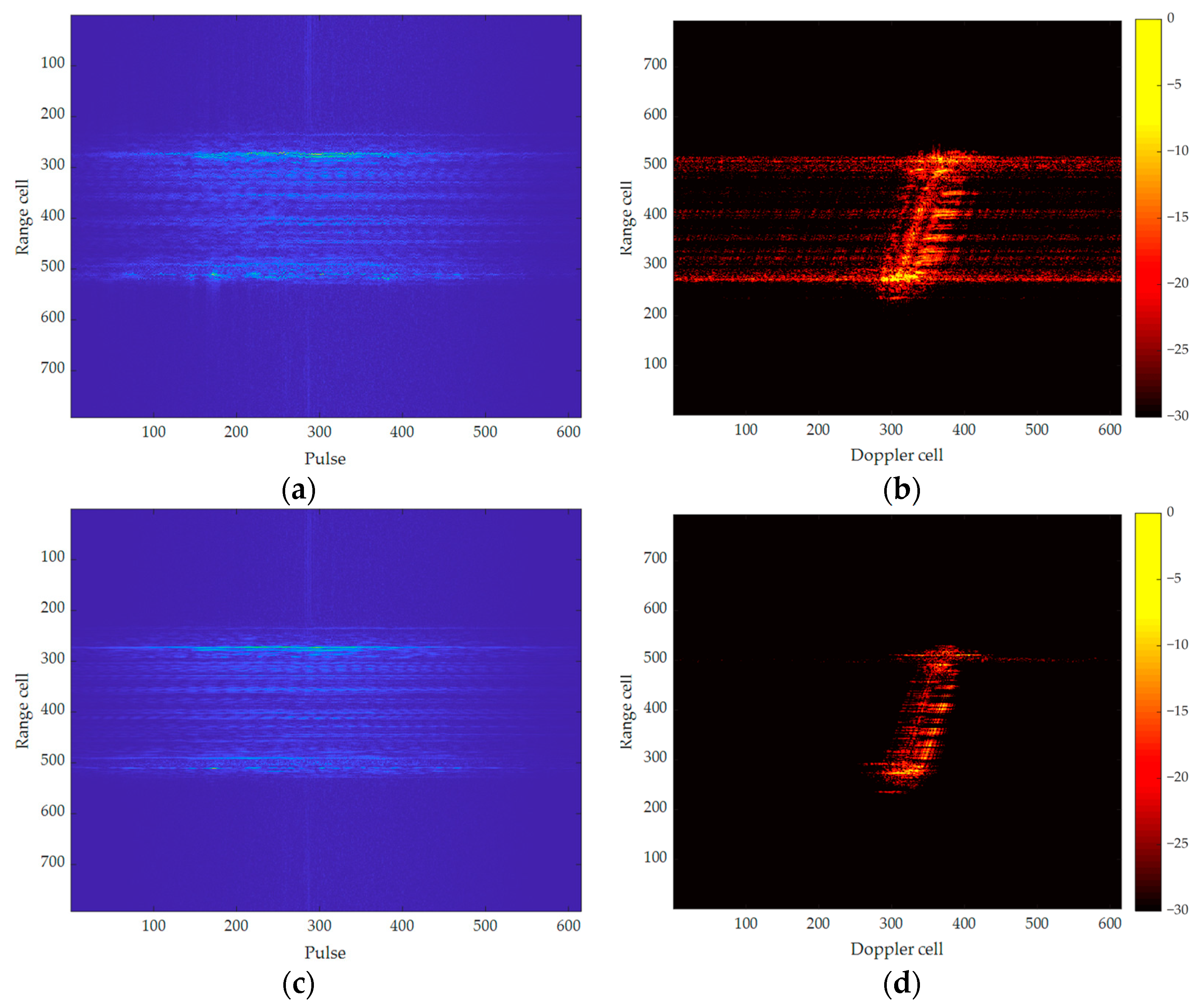
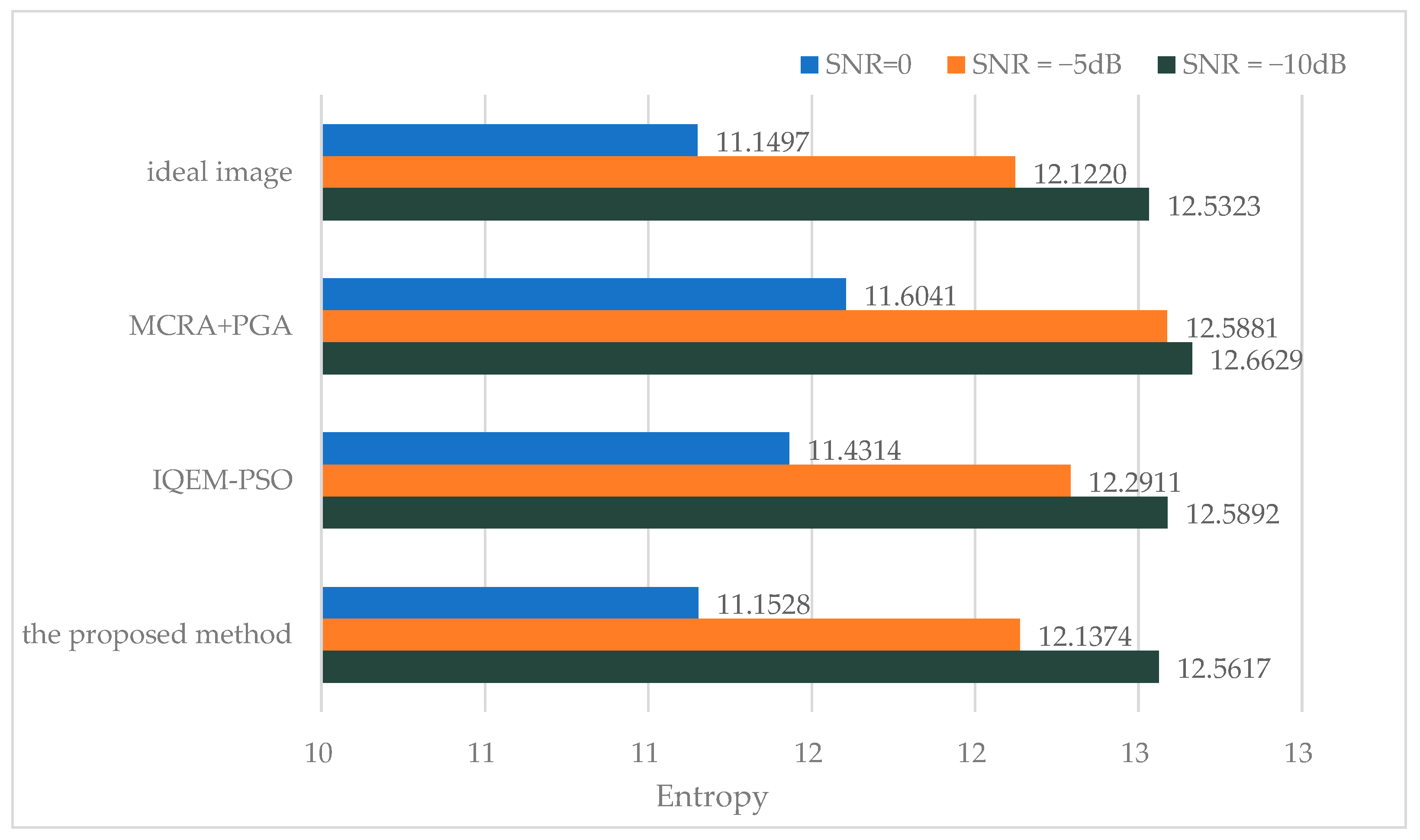
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Ozdemir, C. Inverse Synthetic Aperture Radar Imaging with MATLAB Algorithms, 2nd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2021. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data Algorithms and Implementation; Artech House Publishers: Norwood, MA, USA, 2005. [Google Scholar]
- Liu, C.; Luo, Y.; Yu, Z.; Feng, J. ISAR Imaging of Non-Stationary Moving Target Based on Parameter Estimation and Sparse Decomposition. Remote Sens. 2023, 15, 22. [Google Scholar] [CrossRef]
- Xiong, S.; Li, K.; Wang, H.; Zhao, S.; Luo, Y.; Zhang, Q. Sparse Aperture High-Resolution RID ISAR Imaging of Maneuvering Target Based on Parametric Efficient Sparse Bayesian Learning. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5. [Google Scholar] [CrossRef]
- Liu, W.; Wang, H.; Yang, Q.; Deng, B.; Fan, L.; Yi, J. High Precision Motion Compensation THz-ISAR Imaging Algorithm Based on KT and ME-MN. Remote Sens. 2023, 15, 22. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Liu, H.; Liao, Y.; Liao, G. A Robust Translational Motion Compensation Method for ISAR Imaging Based on Keystone Transform and Fractional Fourier Transform under Low SNR Environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2140–2156. [Google Scholar] [CrossRef]
- Jack, L.W. Range-Doppler Imaging of Rotating Objects. IEEE Trans. Aerosp. Electron. Syst. 1980, 1, 23–52. [Google Scholar]
- Zhang, Z.; Zhang, L.; Wu, J.; Guo, W. Optical and Synthetic Aperture Radar Image Fusion for Ship Detection and Recognition: Current state, challenges, and future prospects. IEEE Geosci. Remote Sens. Mag. 2024, 2–38. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Y.; Gao, X.; Dai, W.; Zeng, X.; Diao, W.; Sun, X. DPFF-Net: Dual-Polarization Image Feature Fusion Network for SAR Ship Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5216514. [Google Scholar] [CrossRef]
- Wang, C.; Pei, J.; Luo, S.; Huo, W.; Huang, Y.; Zhang, Y.; Yang, J. SAR Ship Target Recognition via Multiscale Feature Attention and Adaptive-Weighed Classifier. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4003905. [Google Scholar] [CrossRef]
- Sun, Z.; Leng, X.; Zhang, X.; Xiong, B.; Ji, K.; Kuang, G. Ship Recognition for Complex SAR Images via Dual-Branch Transformer Fusion Network. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4009905. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, Y. New approach for ISAR imaging of ship target with 3D rotation. Multidimens. Syst. Signal Process. 2010, 21, 18. [Google Scholar] [CrossRef]
- Chen, C.; Xu, Z.; Tian, S. An Efficient Sparse Aperture ISAR Imaging Framework for Maneuvering Targets. IEEE Trans. Antennas Propag. 2024, 72, 14. [Google Scholar] [CrossRef]
- Yang, S.; Li, S.; Jia, X.; Cai, Y.; Liu, Y. An Efficient Translational Motion Compensation Approach for ISAR Imaging of Rapidly Spinning Targets. Remote Sens. 2022, 14, 21. [Google Scholar] [CrossRef]
- Yang, S.; Li, S.; Fan, H.; Liu, Y. High-Resolution ISAR Imaging of Maneuvering Targets Based on Azimuth Adaptive Partitioning and Compensation Function Estimation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 15. [Google Scholar] [CrossRef]
- Yang, S.; Li, S.; Fan, H.; Li, H. An Effective Translational Motion Compensation Approach for High-Resolution ISAR Imaging with Time-Varying Amplitude. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4007805. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, G.; Zhang, T.; Gao, Y.; Zhu, K.; Li, L.; Wei, Y. An Improved Parametric Translational Motion Compensation Algorithm for Targets with Complex Motion under Low Signal-to-Noise Ratios. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5237514. [Google Scholar] [CrossRef]
- Wang, X.; Dai, Y.; Song, S.; Jin, T.; Huang, X. Deep Learning-Based Enhanced ISAR-RID Imaging Method. Remote Sens. 2023, 15, 24. [Google Scholar] [CrossRef]
- Cherif, A.A.; Wang, Y. Imaging of target with complicated motion using ISAR system based on IPHAF-TVA. Chin. J. Aeronaut. 2021, 34, 252–264. [Google Scholar] [CrossRef]
- Chen, C.C.; Andrews, H.C. Target-motion-induced radar imaging. IEEE Trans. Aerosp. Electron. Syst. 1980, 16, 2–14. [Google Scholar] [CrossRef]
- Wang, J.F.; Kasilingam, D. Global range alignment for ISAR. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 351–357. [Google Scholar] [CrossRef]
- Wang, J.F.; Liu, X.Z. Improvement of ISAR global range alignment. In Proceedings of the IEEE International Conference on Image Processing, Genova, Italy, 14 September 2005; Volume 1–5, pp. 1369–1372. [Google Scholar]
- Wang, J.; Li, Y.; Song, M.; Huang, P.; Xing, M. Noise Robust High-Speed Motion Compensation for ISAR Imaging Based on Parametric Minimum Entropy Optimization. Remote Sens. 2022, 14, 26. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, L.; Yu, Y.; Tao, Q.; Zhu, Z. Robust ISAR Range Alignment via Minimizing the Entropy of the Average Range Profile. IEEE Geosci. Remote Sens. Lett. 2009, 6, 204–208. [Google Scholar]
- Liu, Y.; Wang, L.; Bi, G.; Liu, H.; Bi, H. Novel ISAR Range Alignment via Minimizing the Entropy of the Sum Range Profile. In Proceedings of the 2020 21st International Radar Symposium (Irs 2020), Warsaw, Poland, 5–8 October 2020; pp. 135–138. [Google Scholar]
- Ye, W.; Yeo, T.S.; Bao, Z. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2487–2494. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Huang, D.R.; Feng, C.Q.; Tong, N.N.; Guo, Y.D. 2D spatial-variant phase errors compensation for ISAR imagery based on contrast maximisation. Electron. Lett. 2016, 52, 1480–1481. [Google Scholar]
- Huang, D.; Guo, X.; Zhang, Z.; Yu, W.; Truong, T. Full-Aperture Azimuth Spatial-Variant Autofocus Based on Contrast Maximization for Highly Squinted Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 330–347. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Du, L.; Yang, D.; Chen, B. Noise-Robust Motion Compensation for Aerial Maneuvering Target ISAR Imaging by Parametric Minimum Entropy Optimization. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4202–4217. [Google Scholar] [CrossRef]
- Martorella, M.; Berizzi, F.; Haywood, B. Contrast maximisation based technique for 2-D ISAR autofocusing. IEE Proc.-Radar Sonar Navig. 2005, 152, 253–262. [Google Scholar] [CrossRef]
- Zhang, L.; Sheng, J.; Duan, J.; Xing, M.; Qiao, Z.; Bao, Z. Translational motion compensation for ISAR imaging under low SNR by minimum entropy. Eurasip J. Adv. Signal Process. 2013, 2013, 33. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, F.; Tao, M.; Sun, P.; Zhang, Z. Adaptive Translational Motion Compensation Method for ISAR Imaging under Low SNR Based on Particle Swarm Optimization. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 5146–5157. [Google Scholar] [CrossRef]
- Lv, X.; Bi, G.; Wan, C.; Xing, M. Lv’s Distribution: Principle, Implementation, Properties, and Performance. IEEE Trans. Signal Process. 2011, 59, 3576–3591. [Google Scholar] [CrossRef]
- Luo, S.; Xu, Q.; Wu, T. An introduction to Lv’s distirbution: Definition and performance for time-frequency analysis. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications, Chengdu, China, 13–16 December 2017. [Google Scholar]
- Liu, L.; Qi, M.; Zhou, F. A Novel Non-Uniform Rotational Motion Estimation and Compensation Method for Maneuvering Targets ISAR Imaging Utilizing Particle Swarm Optimization. IEEE Sens. J. 2018, 18, 299–309. [Google Scholar] [CrossRef]
- Mai, Y.; Zhang, S.; Jiang, W.; Zhang, C.; Huo, K.; Liu, Y. ISAR Imaging of Precession Target Based on Joint Constraints of Low Rank and Sparsity of Tensor. IEEE Trans. Geosci. Remote Sens. 2023, 61, 13. [Google Scholar] [CrossRef]
- Vehmas, R.; Jylha, J.; Vaila, M.; Vihonen, J.; Visa, A. Data-Driven Motion Compensation Techniques for Noncooperative ISAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 295–314. [Google Scholar] [CrossRef]
- Zheng, J.; Su, T.; Zhu, W.; Liu, Q.H. ISAR Imaging of Targets with Complex Motions Based on the Keystone Time-Chirp Rate Distribution. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1275–1279. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A Keystone Transform without Interpolation for SAR Ground Moving-Target Imaging. IEEE Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Liu, C.; Luo, Y.; Sun, H.; Xu, Y.; Yu, Z. Application of LV’s distribution on the parameter estimation of multicomponent radar emitter signals. In Proceedings of the International Conference on Radar Systems (RADAR 2022), Edinburgh, UK, 24 October 2022. [Google Scholar]
- Zhu, L.; Geng, X. A New Translation Matching Method Based on Autocorrelated Normalized Cross-Power Spectrum. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6956–6968. [Google Scholar] [CrossRef]




| Parameters | Values |
|---|---|
| Carrier frequency | 9.6 GHz |
| Signal bandwidth | 500 MHz |
| Pulse repetition frequency | 125 Hz |
| Rang samples | 792 |
| Azimuth samples | 615 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Luo, Y.; Yu, Z. A Robust Translational Motion Compensation Method for Moving Target ISAR Imaging Based on Phase Difference-Lv’s Distribution and Auto-Cross-Correlation Algorithm. Remote Sens. 2024, 16, 3554. https://doi.org/10.3390/rs16193554
Liu C, Luo Y, Yu Z. A Robust Translational Motion Compensation Method for Moving Target ISAR Imaging Based on Phase Difference-Lv’s Distribution and Auto-Cross-Correlation Algorithm. Remote Sensing. 2024; 16(19):3554. https://doi.org/10.3390/rs16193554
Chicago/Turabian StyleLiu, Can, Yunhua Luo, and Zhongjun Yu. 2024. "A Robust Translational Motion Compensation Method for Moving Target ISAR Imaging Based on Phase Difference-Lv’s Distribution and Auto-Cross-Correlation Algorithm" Remote Sensing 16, no. 19: 3554. https://doi.org/10.3390/rs16193554
APA StyleLiu, C., Luo, Y., & Yu, Z. (2024). A Robust Translational Motion Compensation Method for Moving Target ISAR Imaging Based on Phase Difference-Lv’s Distribution and Auto-Cross-Correlation Algorithm. Remote Sensing, 16(19), 3554. https://doi.org/10.3390/rs16193554








