On the Relationships between Clear-Sky Indices in Photosynthetically Active Radiation and Broadband Ranges in Overcast and Broken-Cloud Conditions
Abstract
1. Introduction
2. Problem Statement
3. Data Used
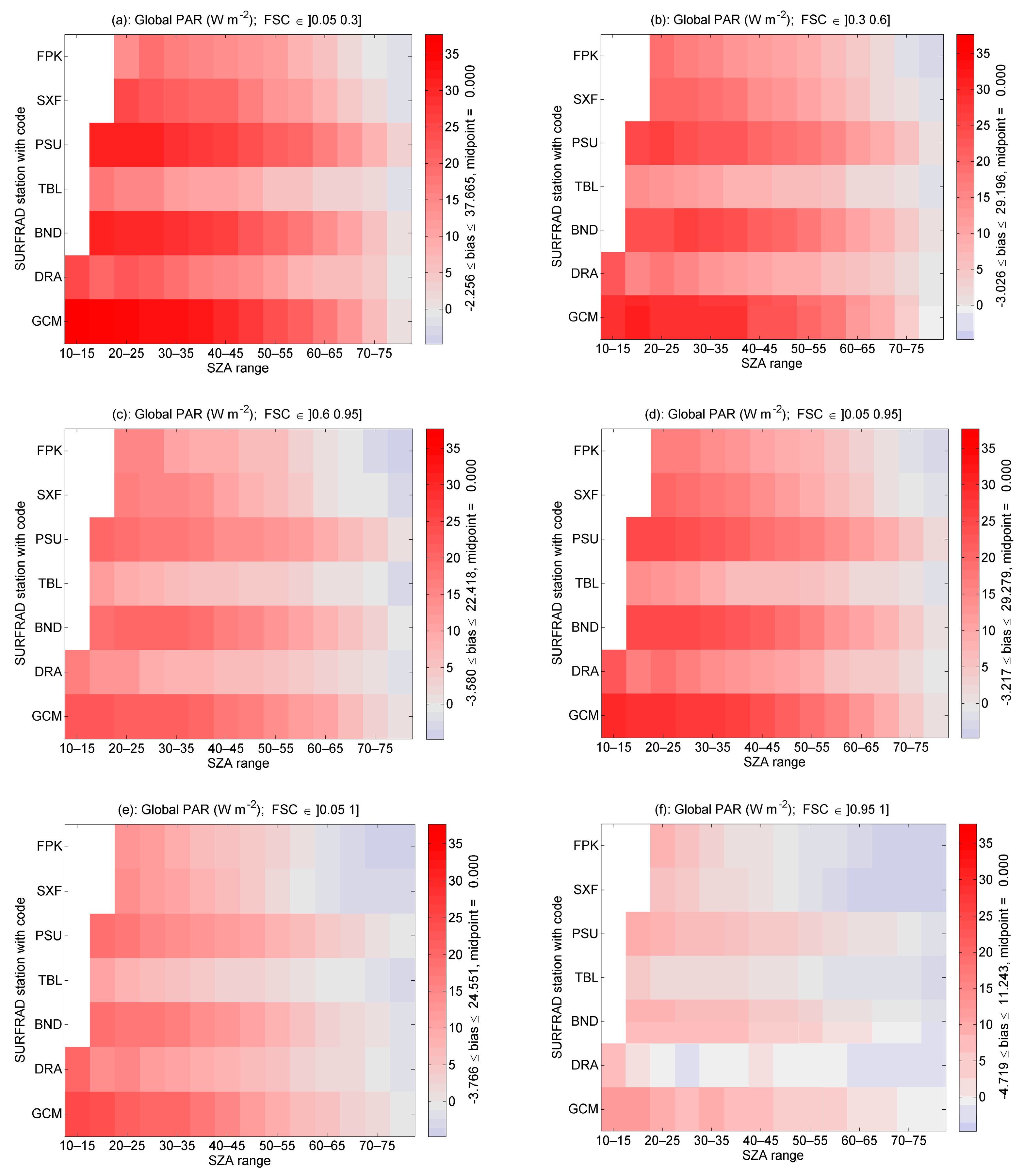
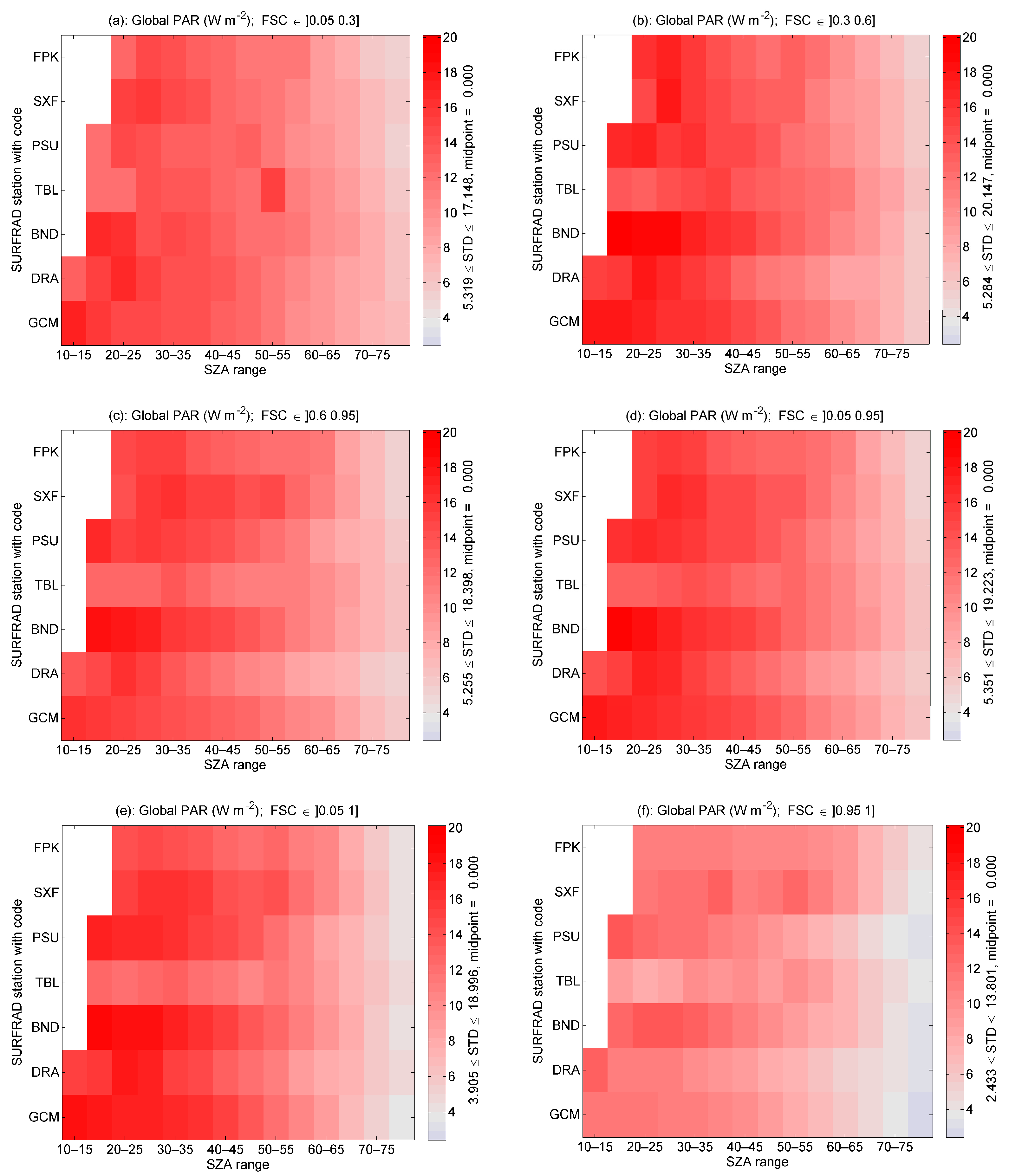
4. Analysis of the Relationships between and for Different Cloudy Situations
- Class C1: 0.05 < FSC ≤ 0.30;
- Class C2: 0.30 < FSC ≤ 0.60;
- Class C3: 0.60 < FSC < 0.95;
- Class “any broken-cloud situation”: 0.05 < FSC < 0.95;
- Class “any cloudy situation” that comprises any cloudy situation whether overcast or broken: 0.05 < FSC ≤ 1.00.
5. Testing the Accuracy of the WN2024 Model in Broken-Cloud Situations
6. Accuracy of the Combination of a Clear-Sky Model and the WN2024 Model in Any Cloudy Situation at SURFRAD Stations
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McCree, K.J. Test of current definitions of photosynthetically active radiation against leaf photosynthesis data. Agric. For. Meteorol. 1972, 10, 443–453. [Google Scholar] [CrossRef]
- Akitsu, T.; Kume, A.; Hirose, Y.; Ijima, O.; Nasahara, K.N. On the stability of radiometric ratios of photosynthetically active radiation to global solar radiation in Tsukuba, Japan. Agric. For. Meteorol. 2015, 209–210, 59–68. [Google Scholar] [CrossRef]
- Nwokolo, S. A global review of empirical models for estimating photosynthetically active radiation. Trends Renew. Energy 2018, 4, 236–327. [Google Scholar] [CrossRef]
- Musleh, Y.J.K.; Rahman, T. Predictive models for photosynthetic active radiation irradiance in temperate climates. Renew. Sustain. Energy Rev. 2024, 200, 114599. [Google Scholar] [CrossRef]
- LI-190R Quantum Sensor. Available online: https://www.licor.com/env/products/light/quantum.html (accessed on 15 March 2024).
- Pinker, R.T.; Laszlo, I. Global distribution of photosynthetically active radiation as observed from satellites. J. Clim. 1992, 5, 56–65. Available online: www.jstor.org/stable/26197041 (accessed on 20 June 2024). [CrossRef]
- Frouin, R.; Pinker, R.T. Estimating photosynthetically active radiation (PAR) at the Earth’s surface from satellite observations. Remote Sens. Environ. 1995, 51, 98–107. [Google Scholar] [CrossRef]
- Frouin, R.; Murakami, H. Estimating photosynthetically available radiation at the ocean surface from ADEOS-II global imager data. J. Oceanogr. 2007, 63, 493–503. [Google Scholar] [CrossRef]
- Su, W.; Charlock, T.P.; Rose, F.G.; Rutan, D. Photosynthetically active radiation from Clouds and the Earth’s Radiant Energy System (CERES) products. J. Geophys. Res. Biogeosci. 2007, 112, G02022. [Google Scholar] [CrossRef]
- Müller, R.; Behrendt, T.; Hammer, A.; Kemper, A. A new algorithm for the satellite-based retrieval of solar surface irradiance in spectral bands. Remote Sens. 2012, 4, 622–647. [Google Scholar] [CrossRef]
- Vindel, J.M.; Valenzuela, R.X.; Navarro, A.A.; Zarzalejo, L.F.; Paz-Gallardo, A.; Souto, J.A.; Méndez-Gómez, R.; Cartelle, D.; Casares, J.J. Modeling photosynthetically active radiation from satellite-derived estimations over mainland Spain. Remote Sens. 2018, 10, 849. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, X.; Xi, B.; Xin, X.; Liu, Q.; He, H.; Xie, X.; Li, L.; Yu, S. Retrieving high-resolution surface photosynthetically active radiation from the MODIS and GOES-16 ABI data. Remote Sens. Environ. 2021, 260, 112436. [Google Scholar] [CrossRef]
- Tang, W.; Qin, J.; Yang, K.; Jiang, Y.; Pan, W. Mapping long-term and high-resolution global gridded photosynthetically active radiation using the ISCCP H-series cloud product and reanalysis data. Earth Syst. Sci. Data 2022, 14, 2007–2019. [Google Scholar] [CrossRef]
- Nwokolo, S.C.; Ogbulezie, J.C.; Obiwulu, A.U. Impacts of climate change and meteo-solar parameters on Photosynthetically Active Radiation prediction using hybrid machine learning with physics-based models. Adv. Space Res. 2022, 70, 3614–3637. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Kothe, S.; Müller, R.; Trentmann, J.; Hollmann, R.; Fuchs, P.; Werscheck, M. Surface Radiation Data Set—Heliosat (SARAH)—Edition 2. Satellite Application Facility on Climate Monitoring: Darmstadt, Germany, 2017. [Google Scholar] [CrossRef]
- Qu, Z.; Oumbe, A.; Blanc, P.; Espinar, B.; Gesell, G.; Gschwind, B.; Klüser, L.; Lefèvre, M.; Saboret, L.; Schroedter-Homscheidt, M.; et al. Fast radiative transfer parameterisation for assessing the surface solar irradiance: The Heliosat-4 method. Meteorol. Z. 2017, 26, 33–57. [Google Scholar] [CrossRef]
- Müller, R.; Pfeifroth, U. Remote sensing of solar surface radiation—A reflection of concepts, applications and input data based on experience with the effective cloud albedo. Atmos. Meas. Tech. 2022, 15, 1537–1561. [Google Scholar] [CrossRef]
- Chen, S.; Li, C.; Xie, Y.; Li, M. Global and direct solar irradiance estimation using deep learning and selected spectral satellite images. Appl. Energy 2023, 352, 121979. [Google Scholar] [CrossRef]
- Aradpour, S.; Deng, Z. Remote sensing algorithm for retrieving global-scale sea surface solar irradiance. Environ. Monit. Assess. 2023, 195, 1355. [Google Scholar] [CrossRef]
- Huang, C.; Shi, H.; Yang, D.; Gao, L.; Zhang, P.; Fu, D.; Xia, X.; Chen, Q.; Yuan, Y.; Liu, M.; et al. Retrieval of sub-kilometer resolution solar irradiance from Fengyun-4A satellite using a region-adapted Heliosat-2 method. Sol. Energy 2023, 264, 112038. [Google Scholar] [CrossRef]
- Verbois, H.; Saint-Drenan, Y.-M.; Becquet, V.; Gschwind, B.; Blanc, P. Retrieval of surface solar irradiance from satellite imagery using machine learning: Pitfalls and perspectives. Atmos. Meas. Tech. 2023, 16, 4165–4181. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Drücke, J.; Kothe, S.; Trentmann, J.; Schröder, M.; Hollmann, R. SARAH-3—Satellite-based climate data records of surface solar radiation. Earth Syst. Sci. Data Discuss. 2024, 1–28. [Google Scholar] [CrossRef]
- Boilley, A.; Wald, L. Comparison between meteorological re-analyses from ERA-Interim and MERRA and measurements of daily solar irradiation at surface. Renew. Energy 2015, 75, 135–143. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Hersbach, H.; Dee, D. ERA5 reanalysis is in production. ECMWF Newsl. 2016, 147, 7. [Google Scholar]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Liu, C.; Allan, R.P.; Mayer, M.; Hyder, P.; Loeb, N.G.; Roberts, C.D.; Valdivieso, M.; Edwards, J.M.; Vidale, P.-L. Evaluation of satellite and reanalysis based global net surface energy flux and uncertainty estimates. J. Geophys. Res. Atmos. 2017, 122, 6250–6272. [Google Scholar] [CrossRef]
- Trolliet, M.; Walawender, J.P.; Bourlès, B.; Boilley, A.; Trentmann, J.; Blanc, P.; Lefèvre, M.; Wald, L. Estimating downwelling solar irradiance at the surface of the tropical Atlantic Ocean: A comparison of PIRATA measurements against several re-analyses and satellite-derived data sets. Ocean. Sci. 2018, 14, 1021–1056. [Google Scholar] [CrossRef]
- Yang, D.; Bright, J.M. Worldwide validation of 8 satellite-derived and reanalysis solar radiation products: A preliminary evaluation and overall metrics for hourly data over 27 years. Sol. Energy 2020, 210, 3–19. [Google Scholar] [CrossRef]
- Thomas, C.; Dorling, S.; Wandji Nyamsi, W.; Wald, L.; Rubino, S.; Saboret, L.; Trolliet, M.; Wey, E. Assessment of five different methods for the estimation of surface photosynthetically active radiation from satellite imagery at three sites—Application to the monitoring of indoor soft fruit crops in southern UK. Adv. Sci. Res. 2019, 16, 229–240. [Google Scholar] [CrossRef]
- de Blas, M.; García-Rodríguez, A.; García, I.; Torres, J.L. Validation and calibration of models to estimate photosynthetically active radiation considering different time scales and sky conditions. Adv. Space Res. 2022, 70, 1737–1760. [Google Scholar] [CrossRef]
- Thomas, C.; Wandji Nyamsi, W.; Arola, A.; Pfeifroth, U.; Trentmann, J.; Dorling, S.; Laguarda, A.; Fischer, M.; Aculinin, A. Smart approaches for evaluating photosynthetically active radiation at various stations based on MSG prime satellite imagery. Atmosphere 2023, 14, 1259. [Google Scholar] [CrossRef]
- Ferrera-Cobos, F.; Vindel, J.M.; Valenzuela, R.X.; González, J.A. Models for estimating daily photosynthetically active radiation in oceanic and Mediterranean climates and their improvement by site adaptation techniques. Adv. Space Res. 2020, 65, 1894–1909. [Google Scholar] [CrossRef]
- García-Rodríguez, A.; García-Rodríguez, S.; Granados-López, D.; Díez-Mediavilla, M.; Alonso-Tristán, C. Extension of PAR models under local all-sky conditions to different climatic zones. Appl. Sci. 2022, 12, 2372. [Google Scholar] [CrossRef]
- Bosch, J.L.; López, G.; Batlles, F.J. Global and direct photosynthetically active radiation parameterizations for clear-sky conditions. Agric. For. Meteorol. 2009, 149, 146–158. [Google Scholar] [CrossRef]
- Wang, L.; Gong, W.; Feng, L.; Lin, A.; Hu, B.; Zhou, M. Estimation of hourly and daily photosynthetically active radiation in Inner Mongolia, China, from 1990 to 2012. Int. J. Climatol. 2015, 35, 3120–3131. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Espinar, B.; Blanc, P.; Wald, L. Estimating the photosynthetically active radiation under clear skies by means of a new approach. Adv. Sci. Res. 2015, 12, 5–10. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Blanc, P.; Augustine, J.A.; Arola, A.; Wald, L. A new clear-sky method for assessing photosynthetically active radiation at the surface level. Atmosphere 2019, 10, 219. [Google Scholar] [CrossRef]
- Oumbe, A.; Qu, Z.; Blanc, P.; Lefèvre, M.; Wald, L.; Cros, S. Decoupling the effects of clear atmosphere and clouds to simplify calculations of the broadband solar irradiance at ground level. Geosci. Model Dev. 2014, 7, 1661–1669. [Google Scholar] [CrossRef]
- Calbó, J.; Pages, D.; González, J.A. Empirical studies of cloud effects on UV radiation: A review. Rev. Geophys. 2005, 43, RG2002. [Google Scholar] [CrossRef]
- Sabburg, J.; Calbó, J. Five years of cloud enhanced surface UV radiation measurements at two sites (in the Northern and Southern Hemispheres). Atmos. Res. 2009, 93, 902–912. [Google Scholar] [CrossRef]
- Piedehierro, A.A.; Antón, M.; Cazorla, A.; Alados-Arboledas, L.; Olmo, F.J. Evaluation of enhancement events of total solar irradiance during cloudy conditions at Granada (Southeastern Spain). Atmos. Res. 2014, 135, 1–7. [Google Scholar] [CrossRef]
- Pecenak, Z.K.; Mejia, F.A.; Kurtz, B.; Evan, A.; Kleissl, J. Simulating irradiance enhancement dependence on cloud optical depth and solar zenith angle. Sol. Energy 2016, 136, 675–681. [Google Scholar] [CrossRef]
- Gueymard, C.A. Cloud and albedo enhancement impacts on solar irradiance using high frequency measurements from thermopile and photodiode radiometers. Part 1: Impacts on global horizontal irradiance. Sol. Energy 2017, 153, 755–765. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Moore, K.; Kmiecik, M.; Chain, C.; George, R.; Vignola, F. A new operational model for satellite-derived irradiances: Description and validation. Sol. Energy 2002, 73, 307–317. [Google Scholar] [CrossRef]
- Hammer, A.; Heinemann, D.; Hoyer, C.; Kuhlemann, R.; Lorenz, E.; Müller, R.; Beyer, H.G. Solar energy assessment using remote sensing technologies. Remote Sens. Environ. 2003, 86, 423–432. [Google Scholar] [CrossRef]
- Rigollier, C.; Lefèvre, M.; Wald, L. The method Heliosat-2 for deriving shortwave solar radiation from satellite images. Sol. Energy 2004, 77, 159–169. [Google Scholar] [CrossRef]
- Krotkov, N.A.; Herman, J.R.; Bhartia, P.K.; Fioletov, V.; Ahmad, Z. Satellite estimation of spectral surface UV irradiance: 2. Effects of homogeneous clouds and snow. J. Geophys. Res. Atmos. 2001, 106, 11743–11759. [Google Scholar] [CrossRef]
- den Outer, P.N.; Slaper, H.; Kaurola, J.; Lindfors, A.; Kazantzidis, A.; Bais, A.F.; Feister, U.; Junk, J.; Janouch, M.; Josefsson, W. Reconstructing of erythemal ultraviolet radiation levels in Europe for the past 4 decades. J. Geophys. Res. Atmos. 2010, 115, D10102. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Saint-Drenan, Y.-M.; Agustine, J.A.; Arola, A.; Wald, L. Evidence of linear relationships between clear-sky indices in photosynthetically active radiation and broadband ranges. Meteorol. Z. 2024, 33, 117–129. [Google Scholar] [CrossRef]
- Ma, J.; Wu, H.; Wang, C.; Zhang, X.; Li, Z.; Wang, X. Multiyear satellite and surface observations of cloud fraction over China. J. Geophys. Res. Atmos. 2014, 119, 7655–7666. [Google Scholar] [CrossRef]
- Bojanowski, J.S.; Stöckli, R.; Duguay-Tetzlaff, A.; Finkensieper, S.; Hollmann, R. Performance assessment of the COMET Cloud Fractional Cover Climatology across Meteosat generations. Remote Sens. 2018, 10, 804. [Google Scholar] [CrossRef]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. SURFRAD—A national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc. 2000, 81, 2341–2357. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- SURFRAD FTP Server. Available online: https://gml.noaa.gov/aftp/data/radiation/surfrad/ (accessed on 17 March 2024).
- Table of Uncertainties. Available online: https://gml.noaa.gov/aftp/data/radiation/surfrad/RadFlux/RadFlux_Uncert_Table.pdf (accessed on 17 March 2024).
- Michalsky, J.; Dutton, E.G.; Nelson, D.; Wendell, J.; Wilcox, S.; Andreas, A.; Gotseff, P.; Myers, D.; Reda, I.; Stoffel, T.; et al. An extensive comparison of commercial pyrheliometers under a wide range of routine observing conditions. J. Atmos. Ocean. Technol. 2011, 28, 752–766. [Google Scholar] [CrossRef][Green Version]
- Long, C.N.; Ackerman, T.P.; Gaustad, K.L.; Cole, J.N.S. Estimation of fractional sky cover from broadband short-wave radiometer measurements. J. Geophys. Res. 2006, 111, D11204. [Google Scholar] [CrossRef]
- Long, C.N.; Ackerman, T.P. Identification of clear skies from broadband pyranometer measurements and calculation of downwelling shortwave cloud effects. J. Geophys. Res. Atmos. 2000, 105, 15609–15626. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Saint-Drenan, Y.-M.; Arola, A.; Wald, L. Further validation of the estimates of the downwelling solar radiation at ground level in cloud-free conditions provided by the McClear service: The case of Sub-Saharan Africa and the Maldives Archipelago. Atmos. Meas. Tech. 2023, 16, 2001–2036. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Lindfors, A. Detecting clear-sky periods from photovoltaic power measurements. Meteorol. Appl. 2024, 31, e2201. [Google Scholar] [CrossRef]
- Blanc, P.; Wald, L. The SG2 algorithm for a fast and accurate computation of the position of the Sun. Sol. Energy 2012, 86, 3072–3083. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. The libRadtran software package for radiative transfer calculations-description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- International Astronomical Union General Assembly, 2015: Resolution B3 on Recommended Nominal Conversion Constants for Selected Solar and Planetary Properties. Available online: https://www.iau.org/static/resolutions/IAU2015_English.pdf (accessed on 27 August 2024).
- Kato, S.; Ackerman, T.; Mather, J.; Clothiaux, E. The k-distribution method and correlated-k approximation for shortwave radiative transfer model. J. Quant. Spectrosc. Radiat. Transf. 1999, 62, 109–121. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Arola, A.; Blanc, P.; Lindfors, A.V.; Cesnulyte, V.; Pitkänen, M.R.A.; Wald, L. Technical Note: A novel parameterization of the transmissivity due to ozone absorption in the k-distribution method and correlated-k approximation of Kato et al. (1999) over the UV band. Atmos. Chem. Phys. 2015, 15, 7449–7456. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Espinar, B.; Blanc, P.; Wald, L. How close to detailed spectral calculations is the k distribution method and correlated k approximation of Kato et al. (1999) in each spectral interval? Meteorol. Z. 2014, 23, 547–556. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Pitkänen, M.R.A.; Aoun, Y.; Blanc, P.; Heikkilä, A.; Lakkala, K.; Bernhard, G.; Koskela, T.; Lindfors, A.V.; Arola, A.; et al. A new method for estimating UV fluxes at ground level in cloud-free conditions. Atmos. Meas. Tech. 2017, 10, 4965–4978. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Blanc, P.; Dumortier, D.; Mouangue, R.; Arola, A.; Wald, L. Using Copernicus Atmosphere Monitoring Service (CAMS) products to assess illuminances at ground level under cloudless conditions. Atmosphere 2021, 12, 643. [Google Scholar] [CrossRef]
- Gschwind, B.; Ménard, L.; Albuisson, M.; Wald, L. Converting a successful research project into a sustainable service: The case of the SoDa Web service. Environ. Model. Softw. 2006, 21, 1555–1561. [Google Scholar] [CrossRef]
- Blanc, P.; Gschwind, B.; Lefèvre, M.; Wald, L. Twelve monthly maps of ground albedo parameters derived from MODIS data sets. In Proceedings of the IGARSS 2014, Quebec, QC, Canada, 13–18 July 2014; pp. 3270–3272. [Google Scholar] [CrossRef]


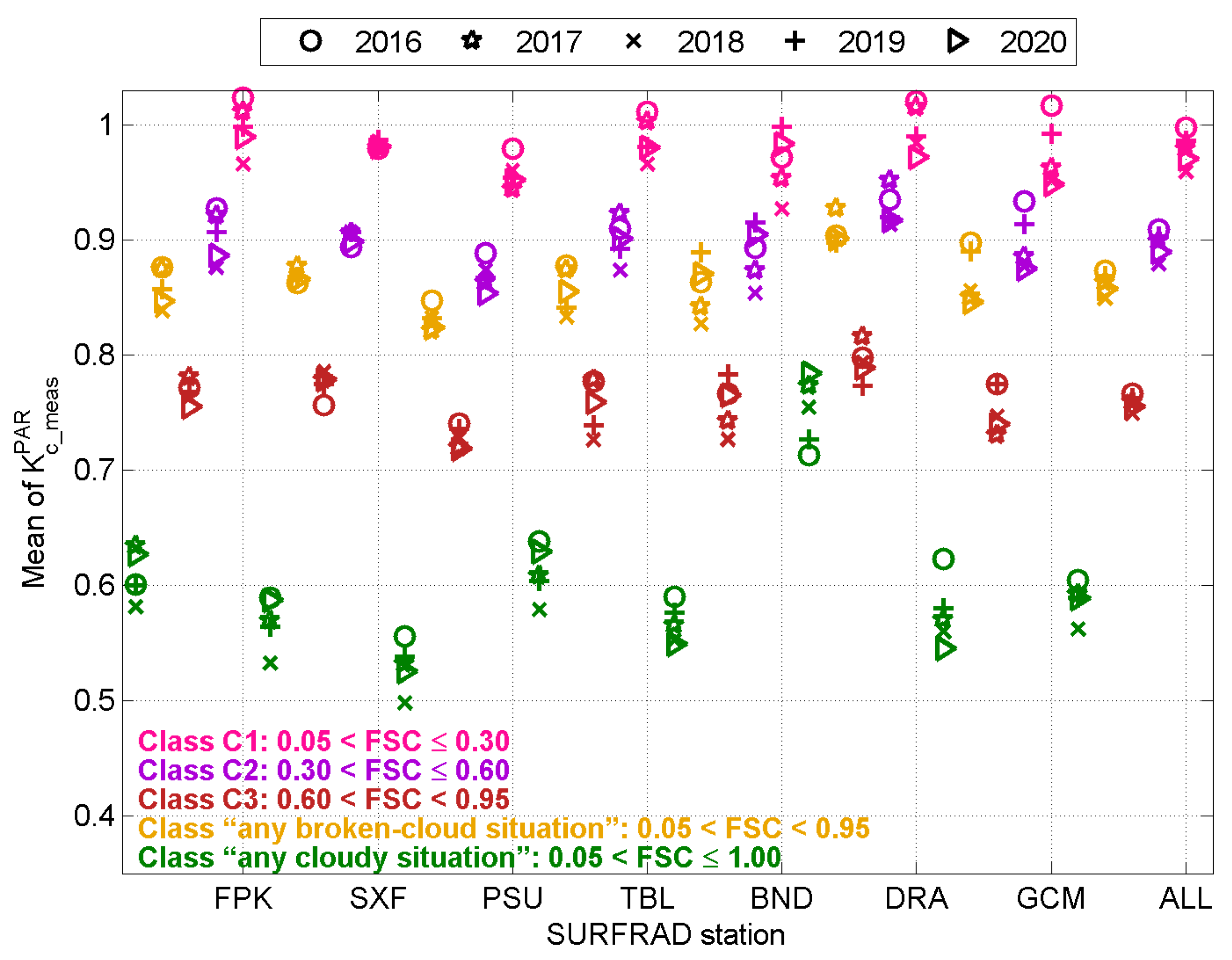
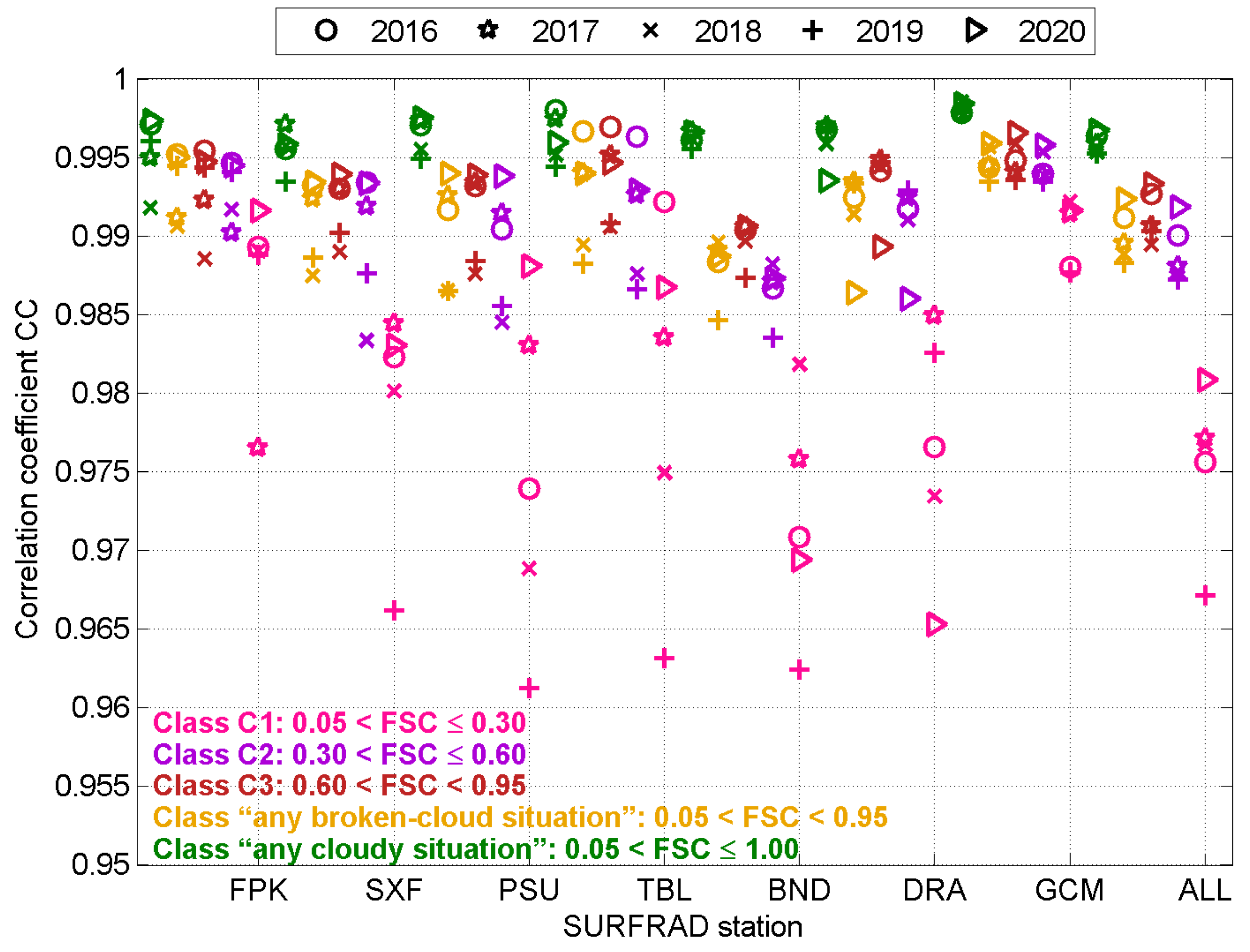

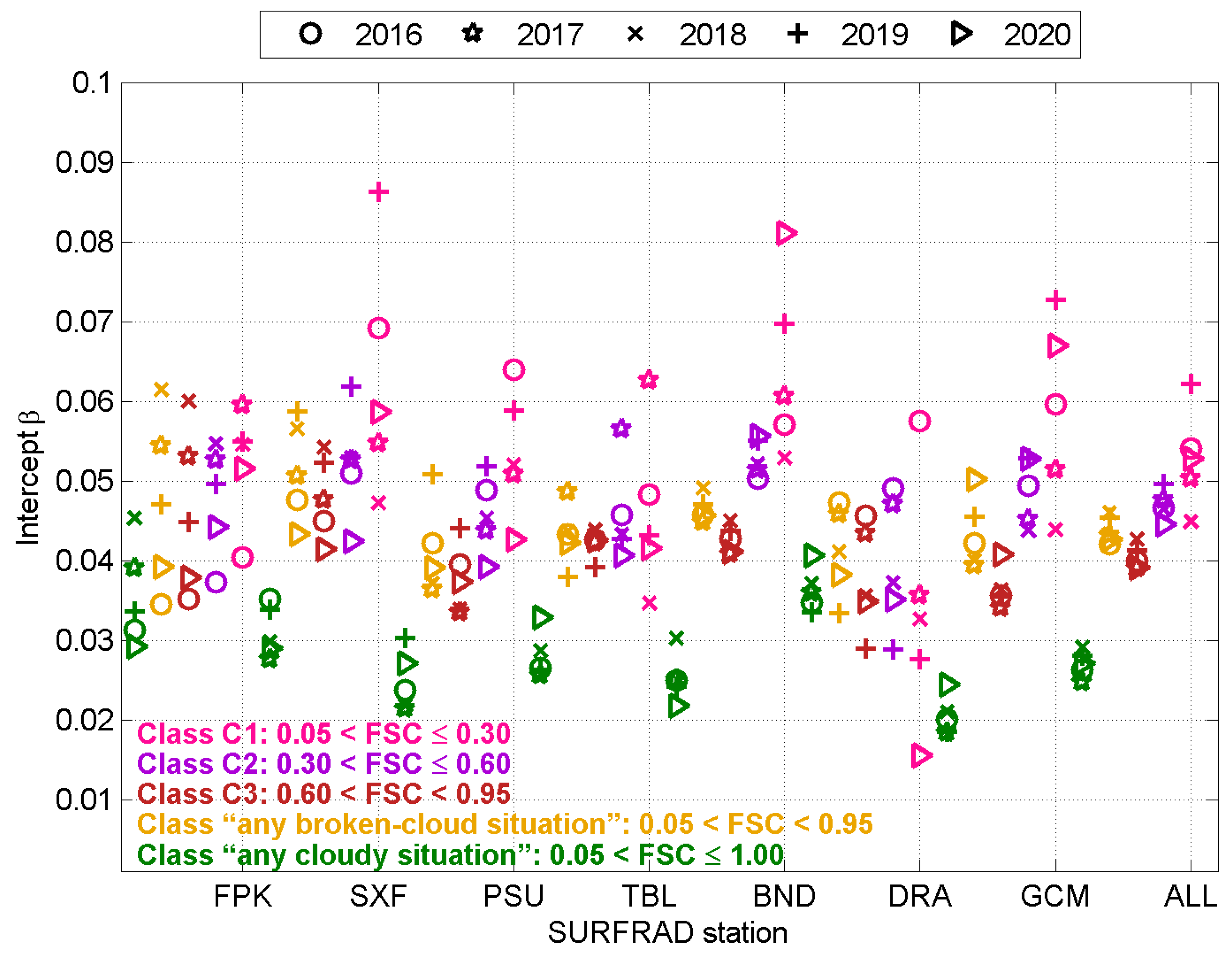

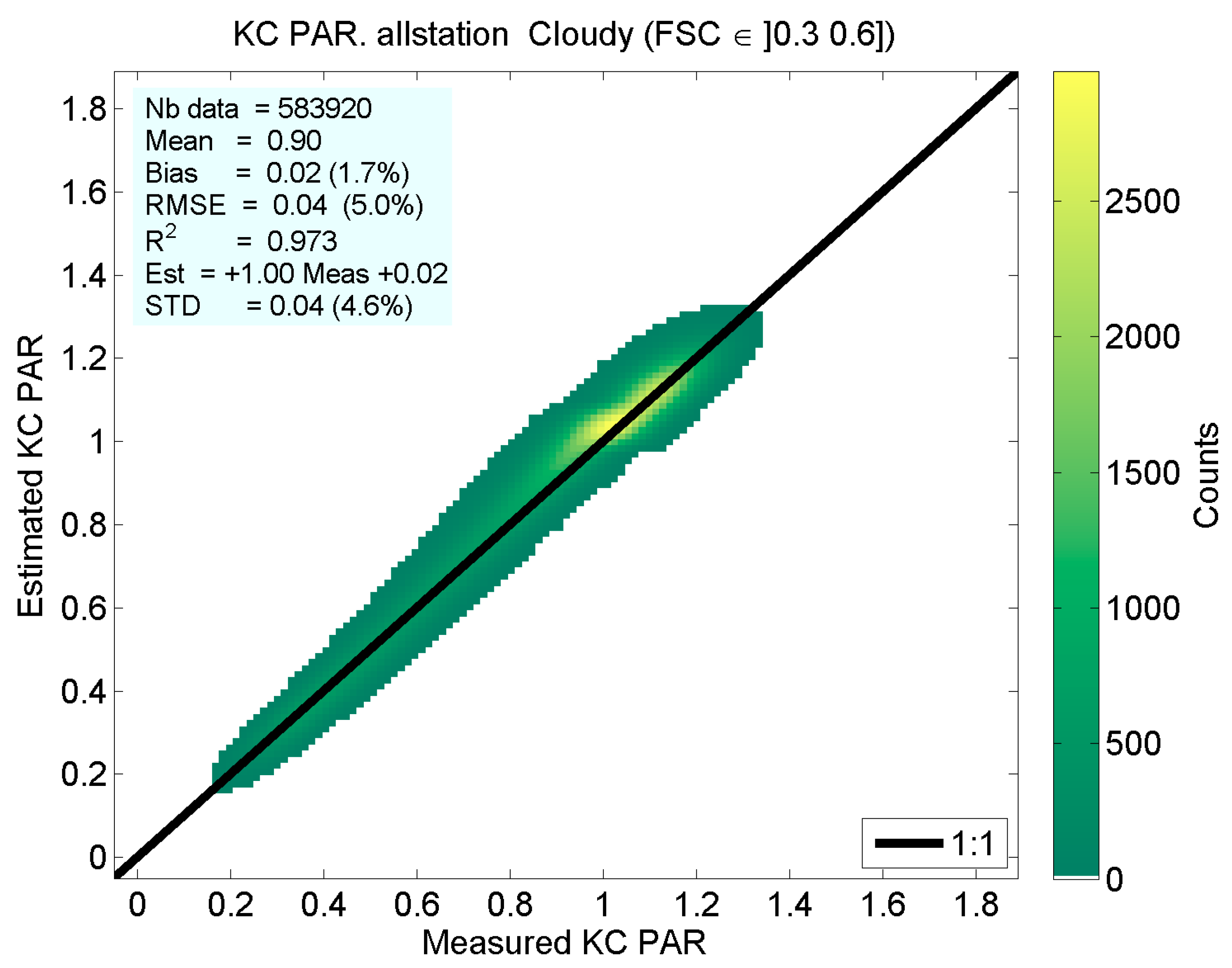
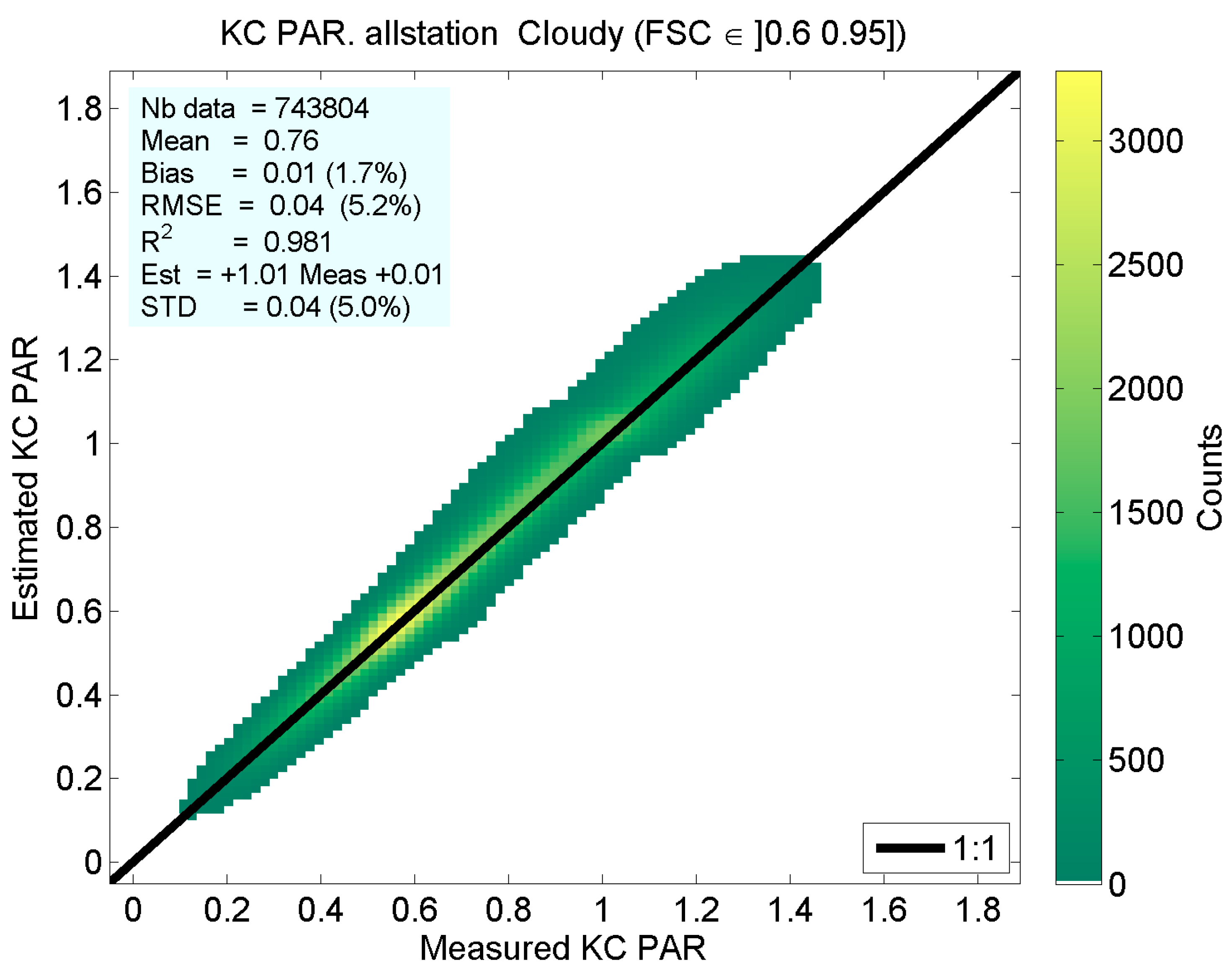


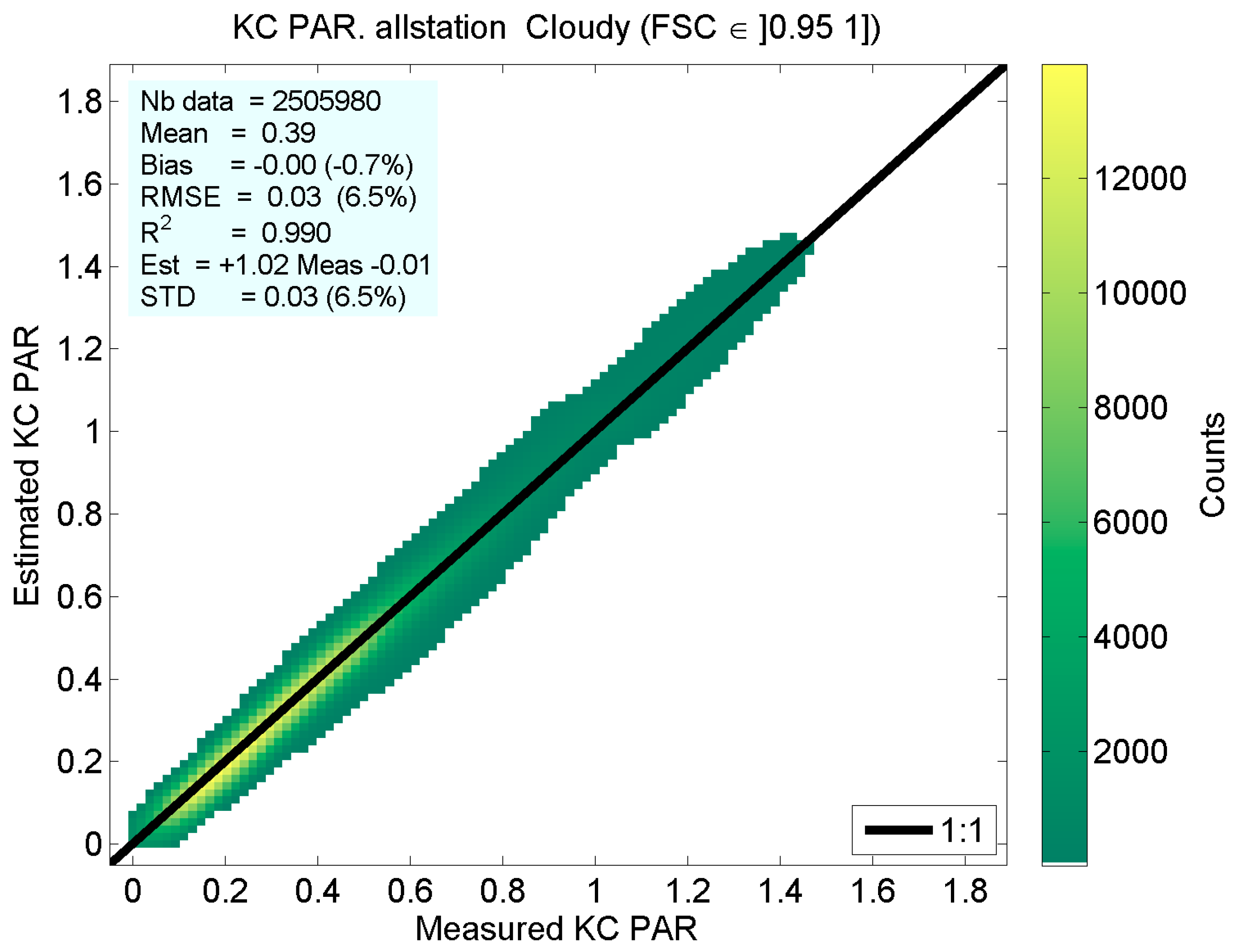
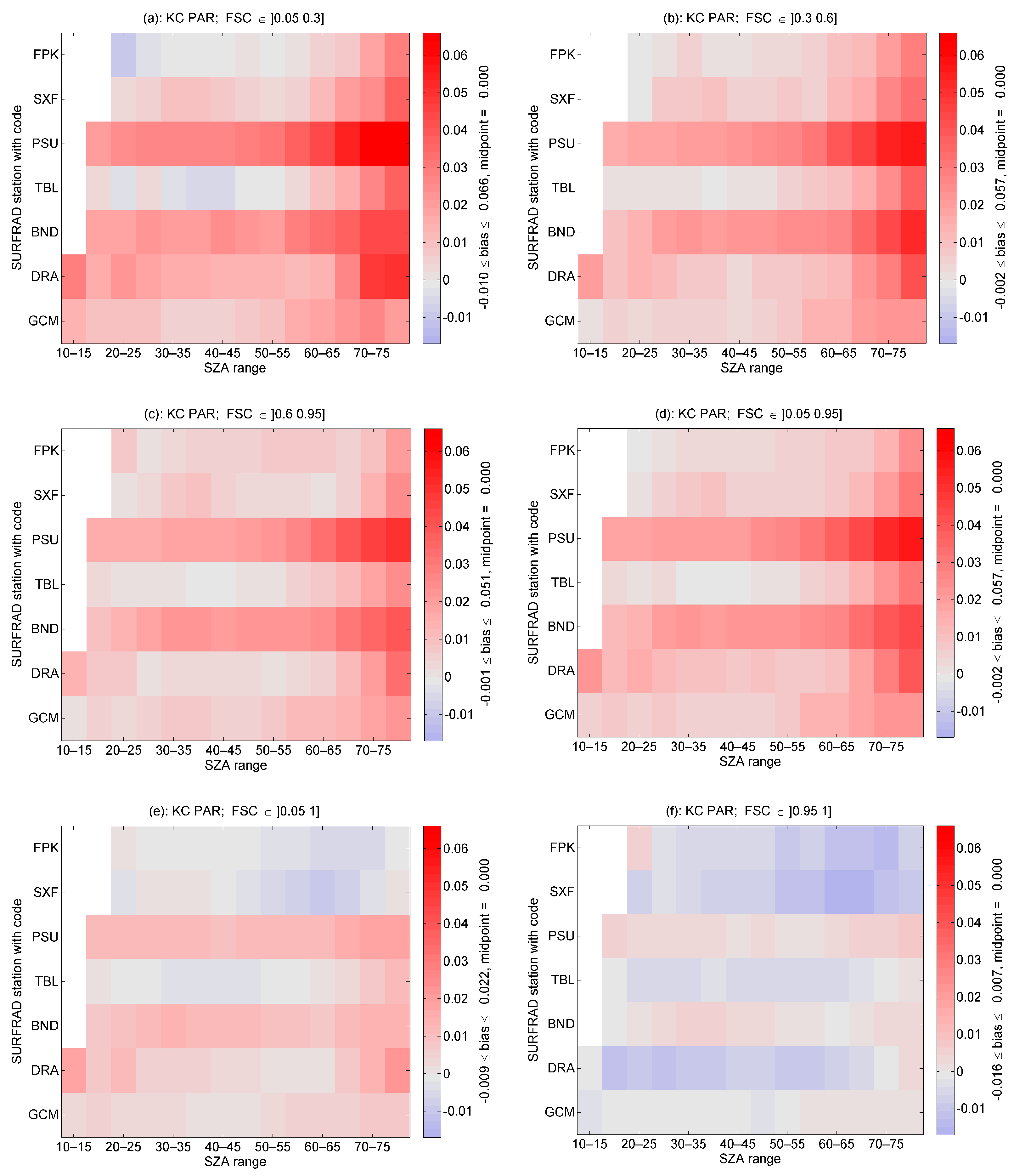
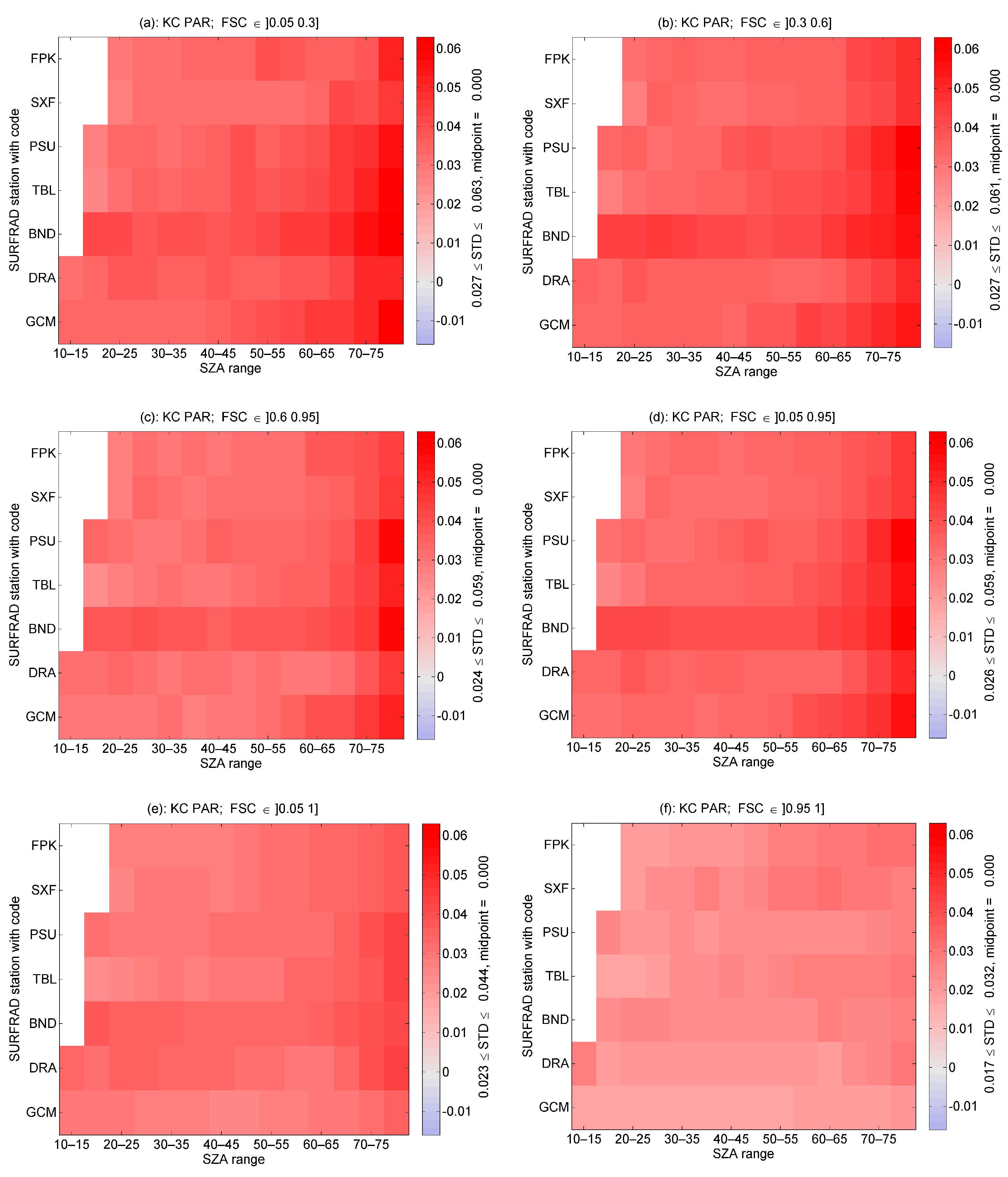



| Station | Fort Peck | Sioux Falls | Penn. State Univ. | Table Mountain | Bondville | Desert Rock | Goodwin Creek |
|---|---|---|---|---|---|---|---|
| Code | FPK | SXF | PSU | TBL | BND | DRA | GCM |
| Latitude (°) | 48.31 | 43.73 | 40.72 | 40.12 | 40.05 | 36.62 | 34.25 |
| Longitude (°) | −105.10 | −96.62 | −77.93 | −105.24 | −88.37 | −116.02 | −89.87 |
| Elevation * (m) | 634 | 473 | 376 | 1689 | 230 | 1007 | 98 |
| Köppen–Geiger classifications [54] | BSk (arid steppe cold) climate | Dfa climate (cold with hot summer without dry season) | Dfa climate | BSk climate | Dfa climate | BWk climate | Cfa climate |
| Measurement | Instrument | Wavelength Range (nm) | Estimated 95% Uncertainty | References |
|---|---|---|---|---|
| Broadband diffuse component | Eppley 8-48 “black and white” pyranometer | 280 to 3000 | 3% or 4 W m−2 | [56] |
| Broadband direct component | Kipp and Zonen, model CHP1 | 280 to 3000 | 2% or [5, 7] W m−2 | [57] |
| Broadband global irradiance | Spectrolab SR-75 pyranometer | 280 to 3000 | 6% or 10 W m−2 | [56] |
| PAR global irradiance | LI-COR Quantum Sensor | 400 to 700 | Total error approx. between 5% and 8% | [5,53] |
| C1 | C2 | C3 | Any Broken-Cloud | Any Cloudy | Overcast | |
|---|---|---|---|---|---|---|
| FSC | ]0.05, 0.30] | ]0.30, 0.60] | ]0.60, 0.95] | ]0.05, 0.95] | ]0.05, 1.00] | ]0.95, 1.00] |
| Mean value | 0.98 | 0.90 | 0.76 | 0.86 | 0.59 | 0.39 |
| Correl. coeff. | 0.966 | 0.986 | 0.990 | 0.988 | 0.995 | 0.995 |
| Bias | 0.02 | 0.02 | 0.01 | 0.01 | 0.00 | 0.00 |
| Slope | 0.96 | 1.00 | 1.01 | 1.00 | 1.02 | 1.02 |
| Intercept | 0.06 | 0.02 | 0.01 | 0.01 | −0.01 | −0.01 |
| Standard dev. | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 | 0.03 |
| RMSE | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 | 0.03 |
| C1 | C2 | C3 | Any Broken-Cloud | Any Cloudy | Overcast | |
|---|---|---|---|---|---|---|
| FSC | ]0.05, 0.30] | ]0.30, 0.60] | ]0.60, 0.95] | ]0.05, 0.95] | ]0.05, 1.00] | ]0.95, 1.00] |
| Mean value | 0.94 | 0.87 | 0.74 | 0.83 | 0.58 | 0.39 |
| Correl. Coeff. | 0.944 | 0.977 | 0.980 | 0.978 | 0.990 | 0.987 |
| Bias | 0.06 | 0.04 | 0.03 | 0.04 | 0.02 | 0.00 |
| Slope | 0.99 | 1.03 | 1.02 | 1.03 | 1.05 | 1.01 |
| Intercept | 0.07 | 0.02 | 0.02 | 0.01 | −0.02 | −0.01 |
| Standard dev. | 0.05 | 0.06 | 0.05 | 0.06 | 0.05 | 0.04 |
| RMSE | 0.08 | 0.07 | 0.06 | 0.06 | 0.05 | 0.04 |
| C1 | C2 | C3 | Any Broken-Cloud | Any Cloudy | Overcast | |
|---|---|---|---|---|---|---|
| FSC | ]0.05, 0.30] | ]0.30, 0.60] | ]0.60, 0.95] | ]0.05, 0.95] | ]0.05, 1.00] | ]0.95, 1.00] |
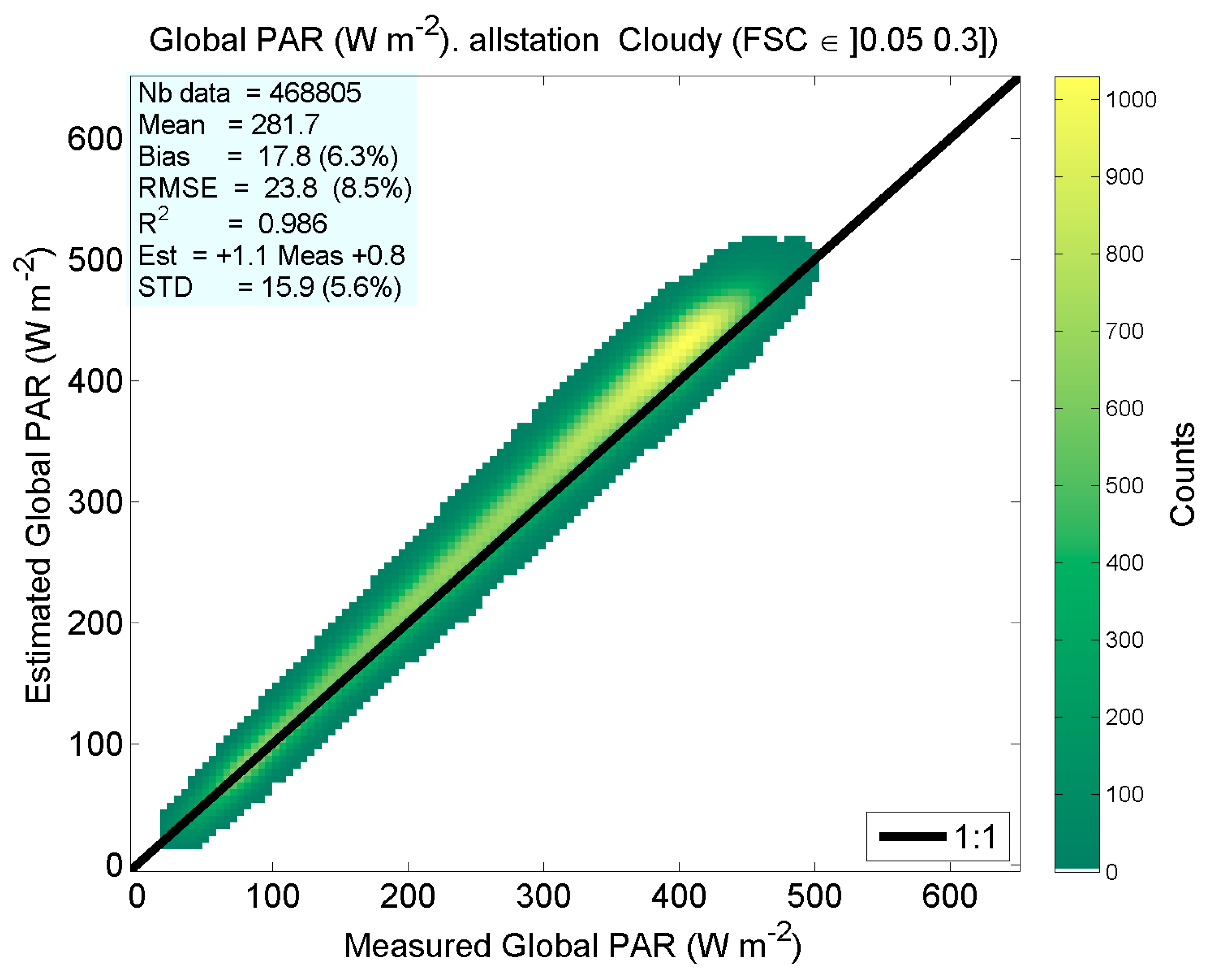
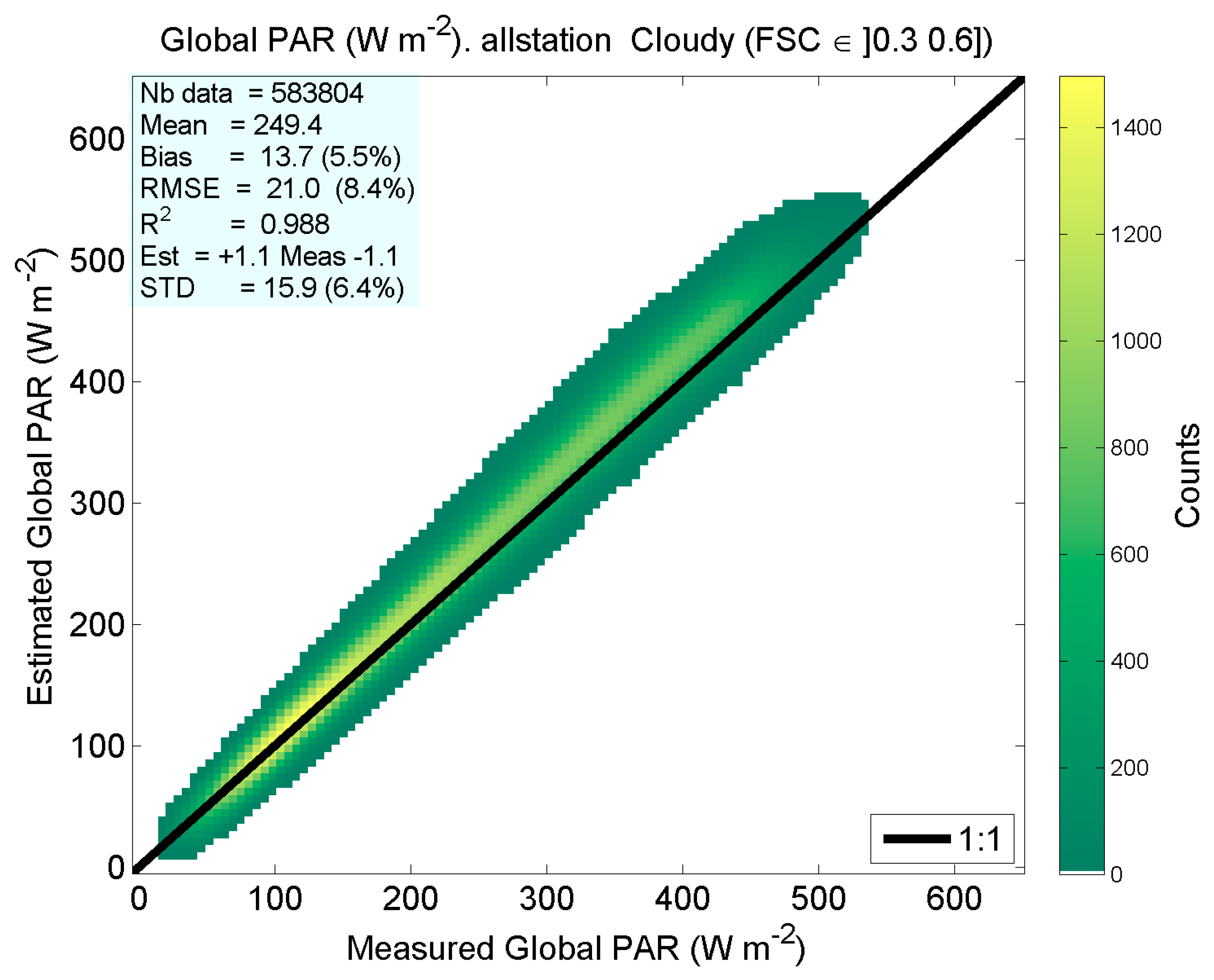
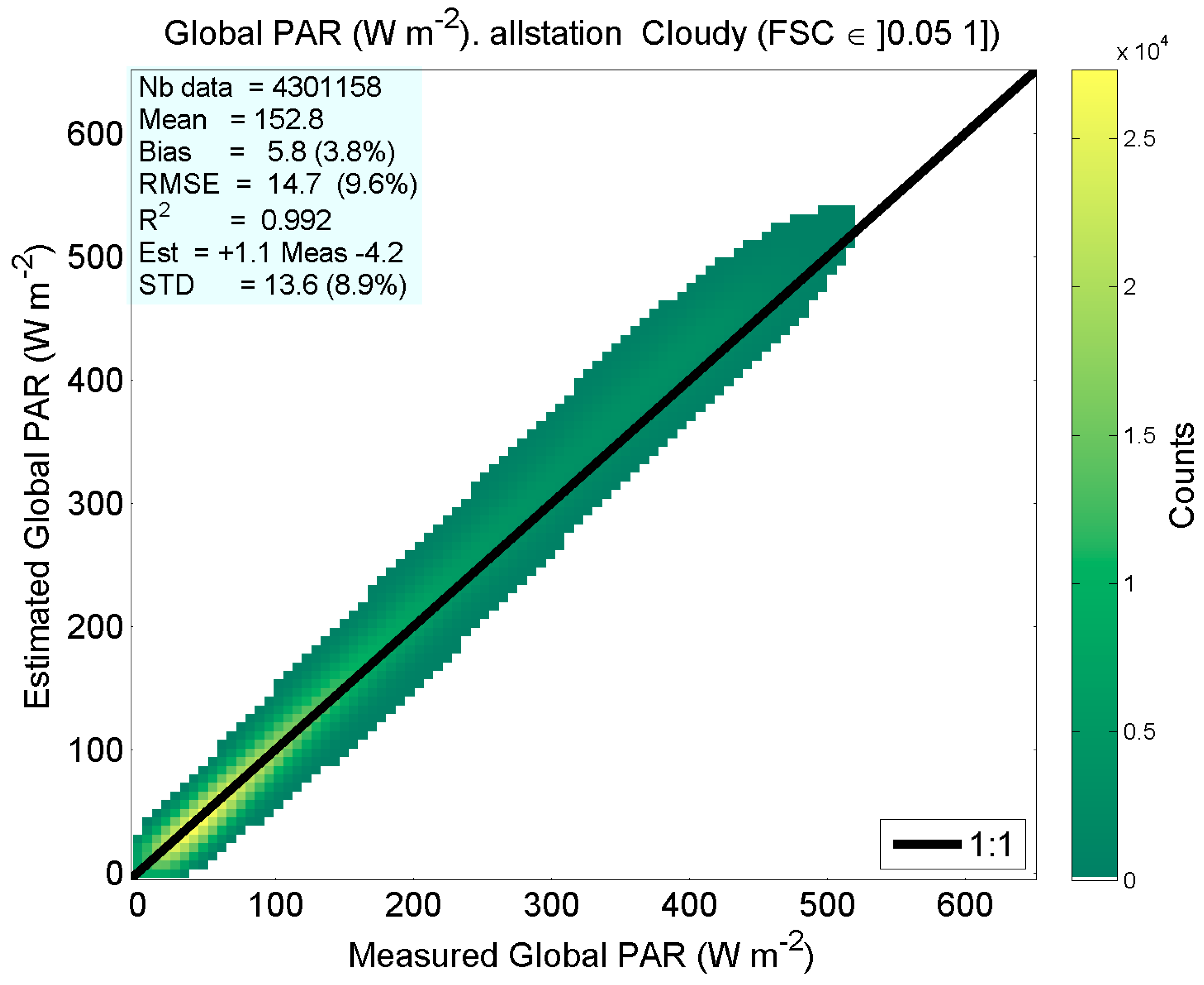
| Mean value | 281.7 | 249.4 | 198.2 | 236.6 | 152.8 | 92.7 |
| Correl. Coeff. | 0.993 | 0.994 | 0.993 | 0.994 | 0.996 | 0.994 |
| Bias | 17.8 | 13.7 | 8.9 | 12.8 | 5.8 | 0.8 |
| Slope | 1.1 | 1.1 | 1.1 | 1.1 | 1.1 | 1.0 |
| Intercept | 0.8 | −1.1 | −1.7 | −1.8 | −4.2 | −3.3 |
| Standard dev. | 15.9 | 15.9 | 13.9 | 15.5 | 13.6 | 9.1 |
| RMSE | 23.8 | 21.0 | 16.5 | 20.1 | 14.7 | 9.1 |
| C1 | C2 | C3 | Any Broken-Cloud | Any Cloudy | Overcast | |
|---|---|---|---|---|---|---|
| FSC | ]0.05, 0.30] | ]0.30, 0.60] | ]0.60, 0.95] | ]0.05, 0.95] | ]0.05, 1.00] | ]0.95, 1.00] |
| Mean value | 0.79 | 0.72 | 0.61 | 0.69 | 0.47 | 0.32 |
| Correl. Coeff. | 0.963 | 0.982 | 0.984 | 0.982 | 0.992 | 0.989 |
| Bias | 0.05 | 0.04 | 0.02 | 0.03 | 0.01 | 0.00 |
| Slope | 1.03 | 1.05 | 1.04 | 1.05 | 1.06 | 1.03 |
| Intercept | 0.03 | 0.00 | 0.00 | −0.00 | −0.02 | −0.01 |
| Standard dev. | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 |
| RMSE | 0.06 | 0.06 | 0.05 | 0.06 | 0.04 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wandji Nyamsi, W.; Saint-Drenan, Y.-M.; Augustine, J.A.; Arola, A.; Wald, L. On the Relationships between Clear-Sky Indices in Photosynthetically Active Radiation and Broadband Ranges in Overcast and Broken-Cloud Conditions. Remote Sens. 2024, 16, 3718. https://doi.org/10.3390/rs16193718
Wandji Nyamsi W, Saint-Drenan Y-M, Augustine JA, Arola A, Wald L. On the Relationships between Clear-Sky Indices in Photosynthetically Active Radiation and Broadband Ranges in Overcast and Broken-Cloud Conditions. Remote Sensing. 2024; 16(19):3718. https://doi.org/10.3390/rs16193718
Chicago/Turabian StyleWandji Nyamsi, William, Yves-Marie Saint-Drenan, John A. Augustine, Antti Arola, and Lucien Wald. 2024. "On the Relationships between Clear-Sky Indices in Photosynthetically Active Radiation and Broadband Ranges in Overcast and Broken-Cloud Conditions" Remote Sensing 16, no. 19: 3718. https://doi.org/10.3390/rs16193718
APA StyleWandji Nyamsi, W., Saint-Drenan, Y.-M., Augustine, J. A., Arola, A., & Wald, L. (2024). On the Relationships between Clear-Sky Indices in Photosynthetically Active Radiation and Broadband Ranges in Overcast and Broken-Cloud Conditions. Remote Sensing, 16(19), 3718. https://doi.org/10.3390/rs16193718






