Evaluating and Correcting Temperature and Precipitation Grid Products in the Arid Region of Altay, China
Abstract
1. Introduction
2. Materials and Methods
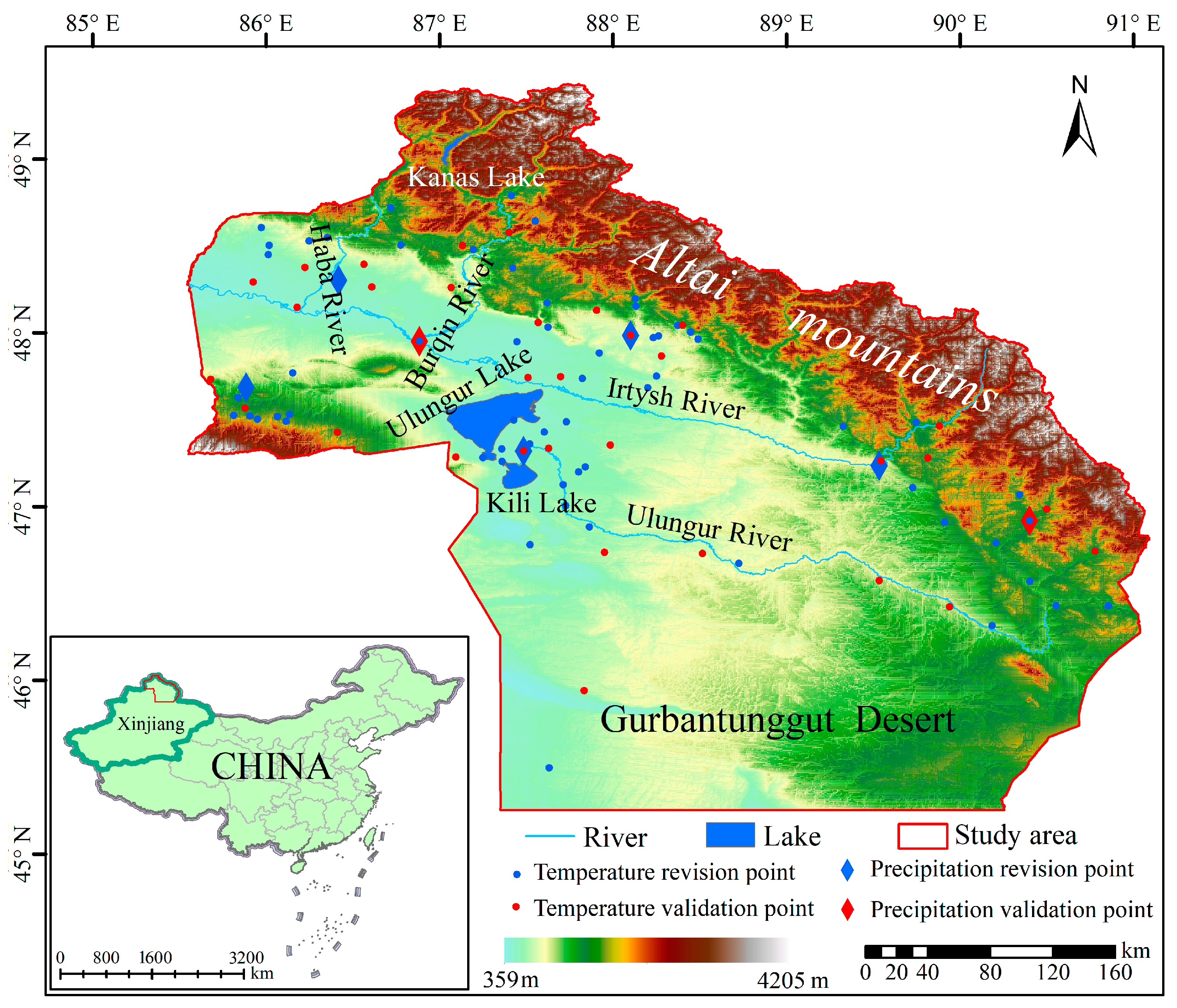
2.1. Study Area
2.2. Dataset
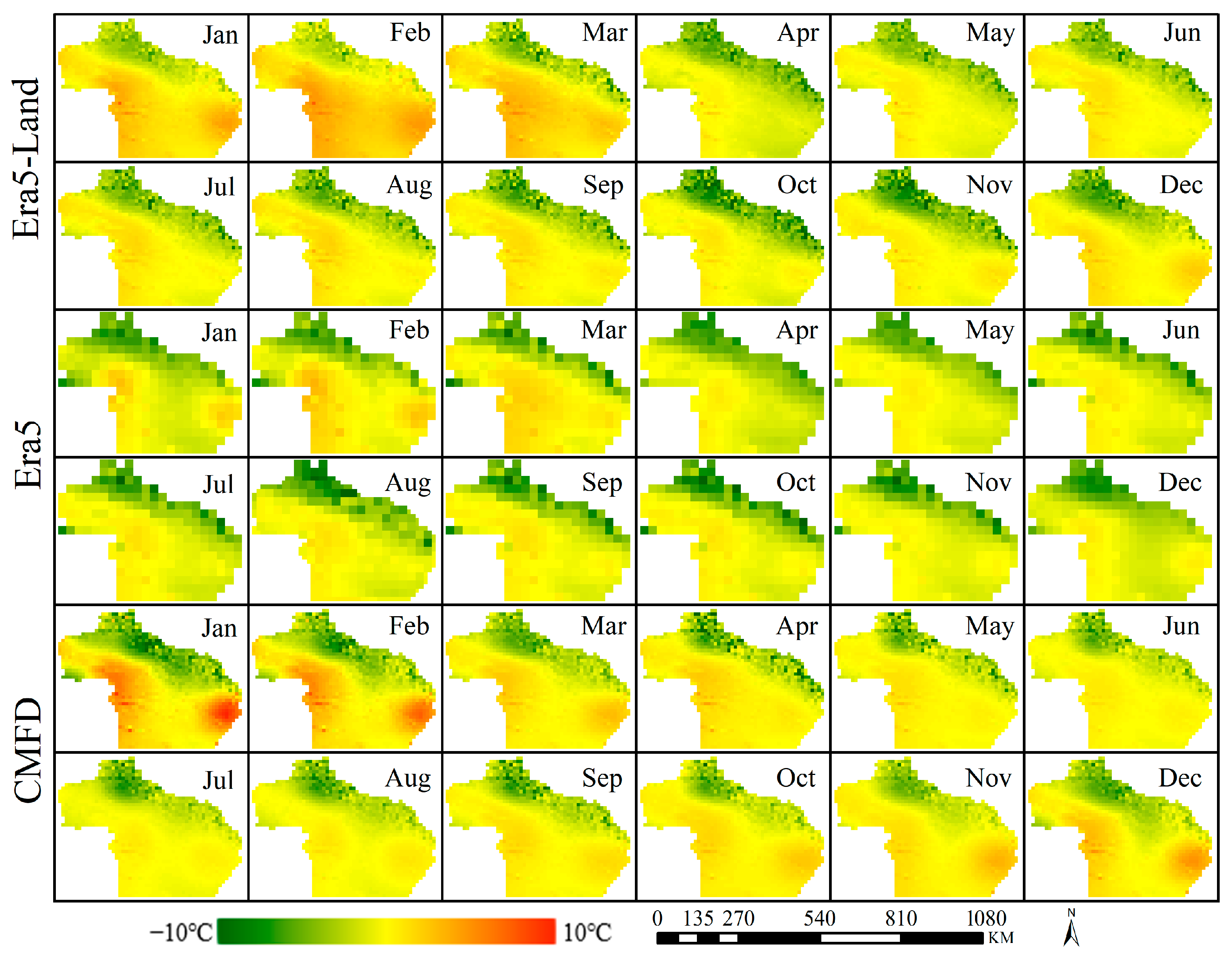
2.2.1. ERA5 and ERA5-Land Temperature and Precipitation Data
2.2.2. CMFD Temperature and Precipitation Data
2.2.3. TRMM Satellite Precipitation Data
2.2.4. Temperature and Precipitation Observation Data at Meteorological Stations
2.3. Methods
2.3.1. Residual Revision Method
2.3.2. Coefficient Revision Method
2.3.3. Accuracy Assessment
3. Results
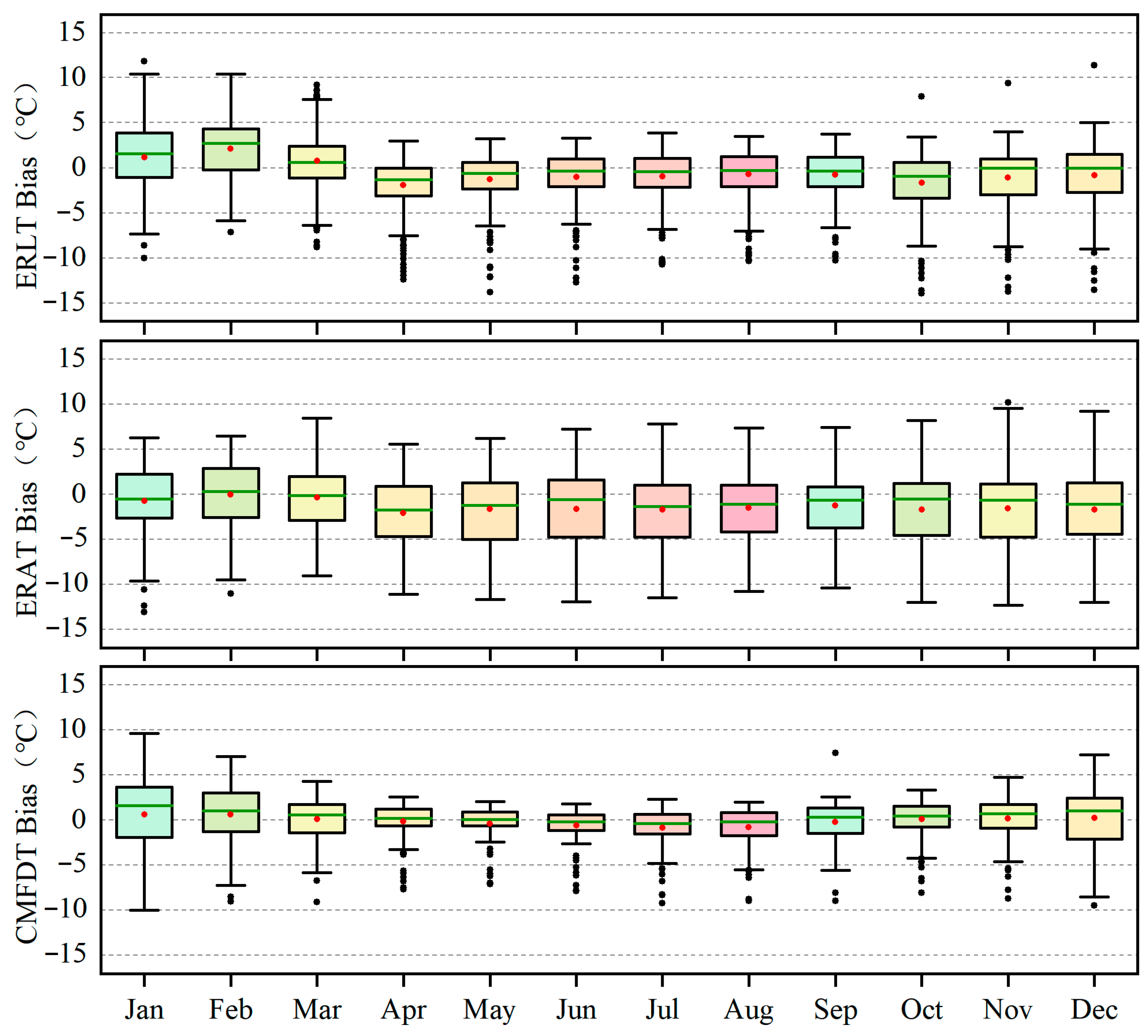
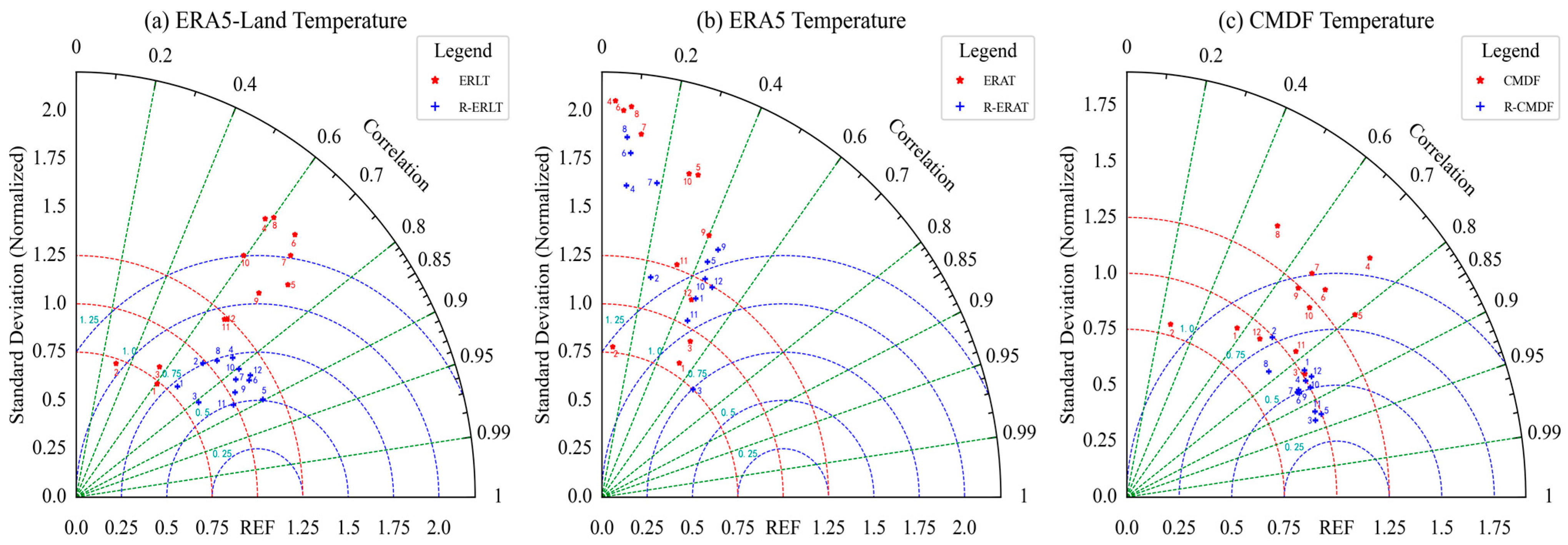
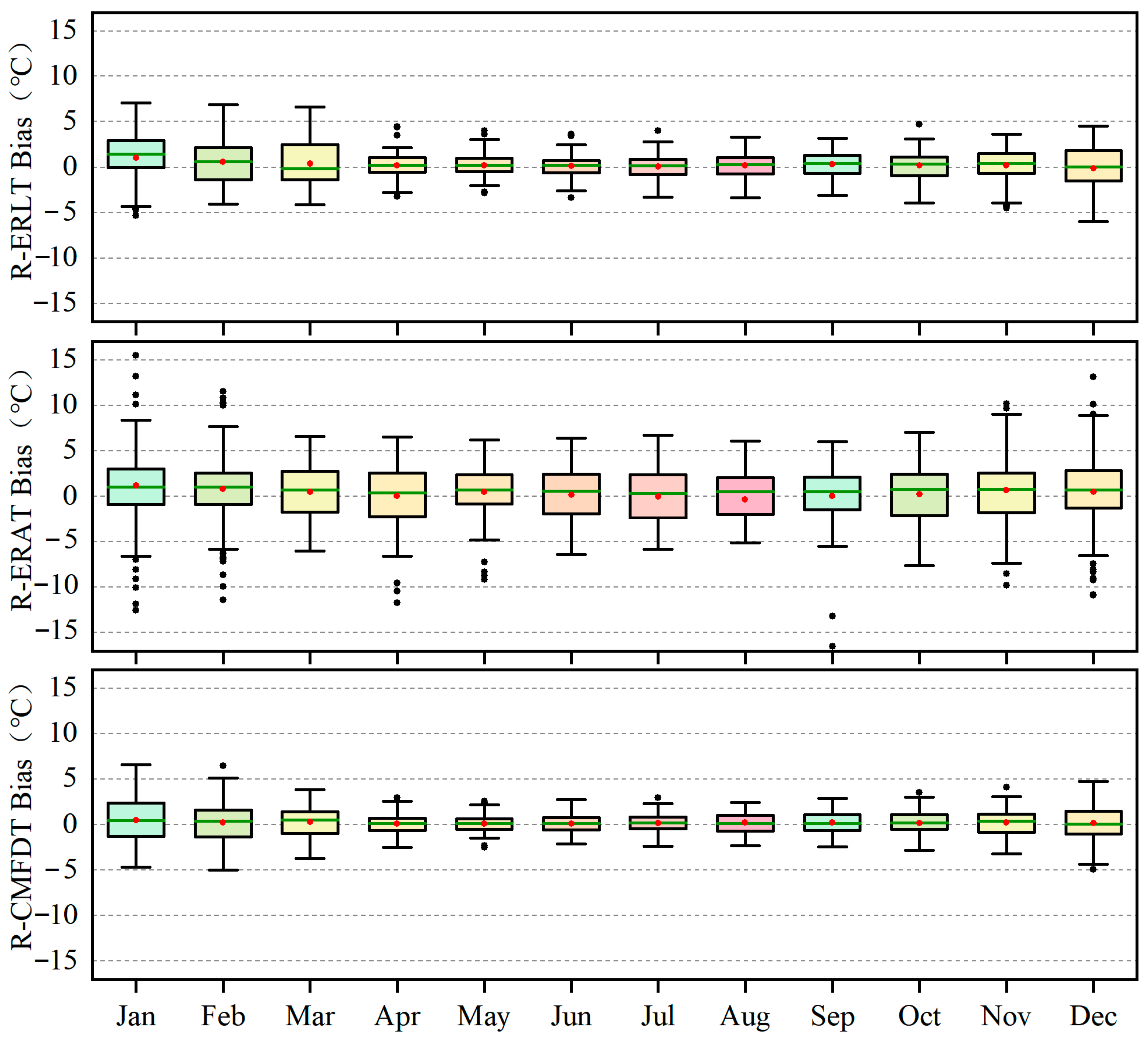
3.1. Accuracy Assessment for the ERA5-Land, ERA5 and CMFD Monthly Temperature Data
3.2. Accuracy Assessment for the ERA5-LandPR, ERA5PR, and CMFDPR Monthly Temperature Data
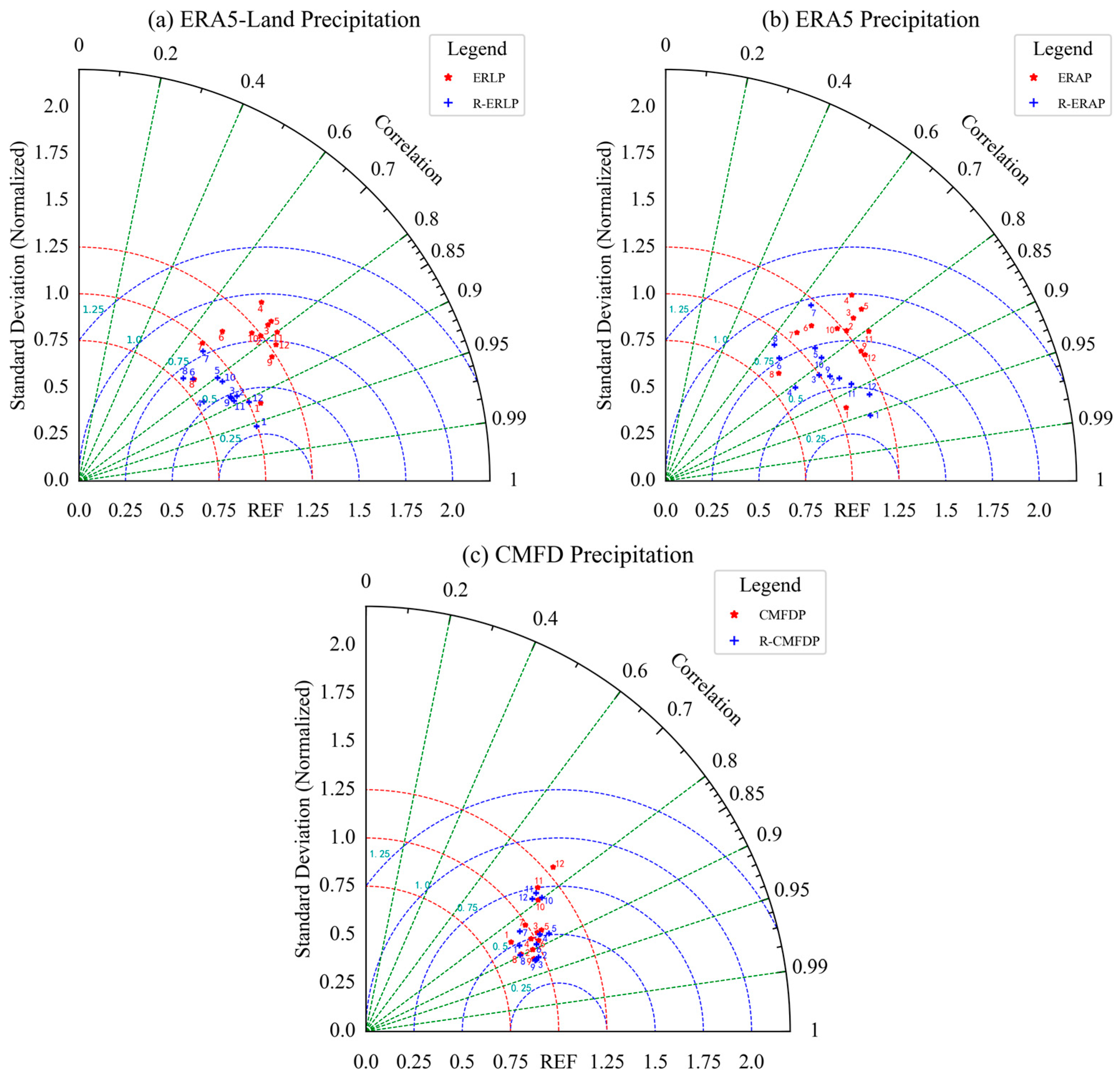
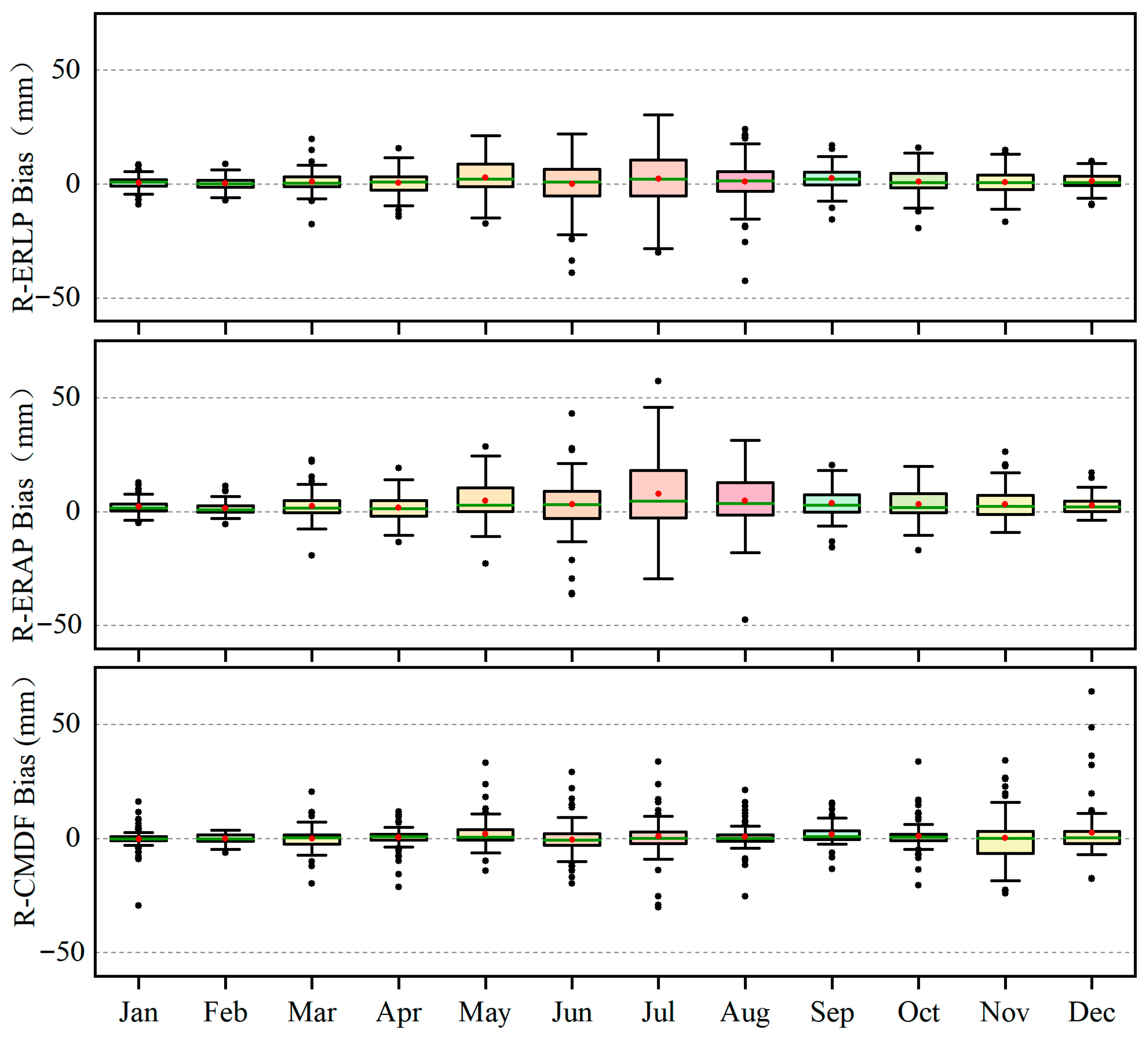
3.3. Accuracy Assessment for the ERA5-Land, ERA5, and CMFD Monthly Precipitation Data
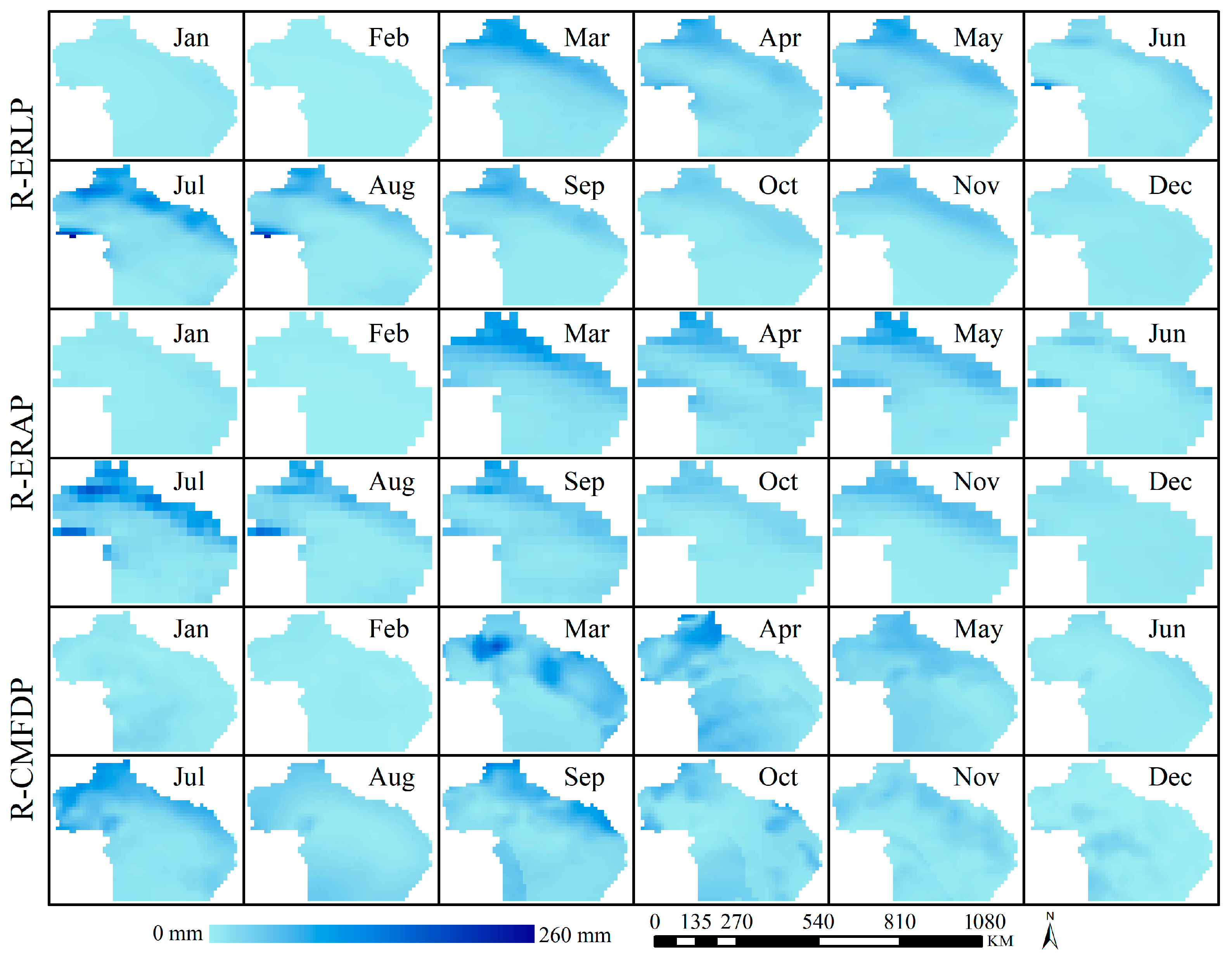
3.4. Accuracy Assessment for the ERA5-LandPR, ERA5PR, and CMFDPR Monthly Precipitation
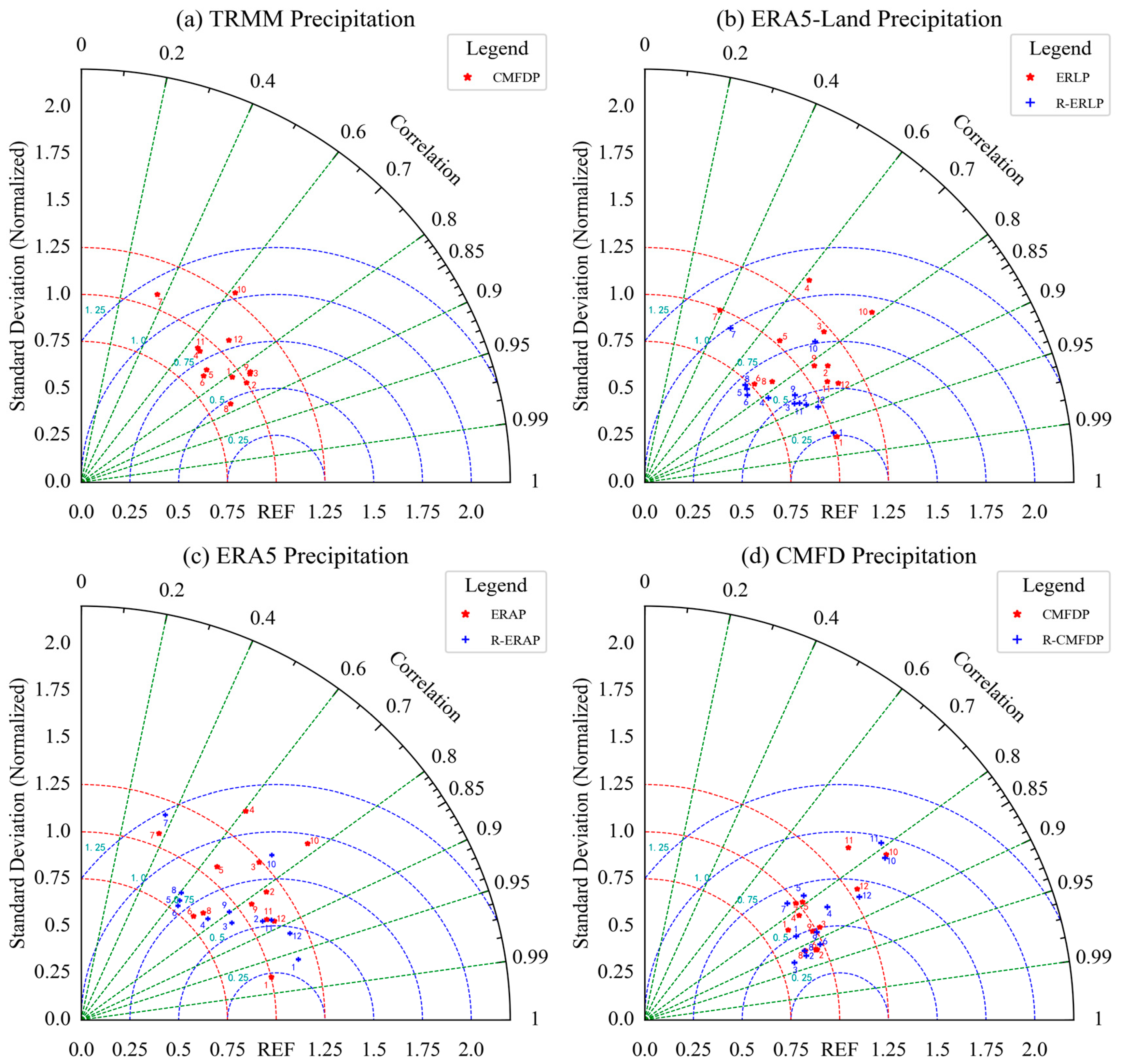
3.5. Comparison Analysis between TRMM Satellite Precipitation Data and Pre- and Post-Correction ERA5-Land, ERA5, and CMFD Precipitation Data
4. Discussion
5. Conclusions
- (1)
- ERA5-Land, ERA5, and CMFD exhibit significant differences in their ability to capture temperature and precipitation in the Altay region. In general, ERA5-Land, ERA5, and CMFD temperature and precipitation data underperformed in the Altay region and required error correction before scientific research could be conducted, especially for ERA5-Land and ERA5 temperature and precipitation data.
- (2)
- Residual and coefficient revision method significantly improved the ability of ERA5-Land, ERA5, and CMFD to capture temperature and precipitation. With the exception of ERA5PR temperature data, all other datasets meet the accuracy requirements for temperature and precipitation in the Altay region and can provide reliable data support for studying climate and ecological change in arid and semi-arid areas.
- (3)
- There are differences in the ability of ERA5-LandPR, ERA5PR, and CMFDPR to capture temperature and precipitation. Overall, CMFDPR demonstrates better temperature capture capabilities than both ERA5-LandPR and ERA5PR. Additionally, all three datasets exhibit weaker temperature capture abilities in mountainous regions compared to plains. Furthermore, ERA5-LandPR, ERA5PR, and CMFDPR exhibit weaker precipitation capture abilities during months with high precipitation compared to months with lower precipitation. CMFDPR and ERA5-LandPR exhibit varying abilities in capturing precipitation in different months, but both outperform ERA5PR.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Year | Month | ERALP | ERAP | CMFDP |
|---|---|---|---|---|
| 1979 | 1 | 0.47 | 0.53 | 1.49 |
| 1979 | 2 | 0.47 | 0.53 | 1.37 |
| 1979 | 3 | 0.41 | 0.42 | 1.22 |
| 1979 | 4 | 0.54 | 0.62 | 0.97 |
| 1979 | 5 | 0.67 | 0.64 | 0.98 |
| 1979 | 6 | 0.81 | 0.96 | 0.95 |
| 1979 | 7 | 0.68 | 1.33 | 0.98 |
| 1979 | 8 | 0.26 | 0.39 | 0.85 |
| 1979 | 9 | 0.73 | 0.98 | 0.99 |
| 1979 | 10 | 0.44 | 0.45 | 0.95 |
| 1979 | 11 | 0.70 | 0.78 | 0.98 |
| 1979 | 12 | 0.59 | 0.71 | 1.69 |
| 1980 | 1 | 0.62 | 0.69 | 0.97 |
| 1980 | 2 | 0.41 | 0.73 | 1.21 |
| 1980 | 3 | 0.46 | 0.56 | 1.13 |
| 1980 | 4 | 0.44 | 0.45 | 0.98 |
| 1980 | 5 | 0.98 | 1.02 | 0.94 |
| 1980 | 6 | 0.60 | 0.75 | 0.97 |
| 1980 | 7 | 1.07 | 1.18 | 0.97 |
| 1980 | 8 | 0.80 | 1.00 | 0.95 |
| 1980 | 9 | 0.89 | 0.90 | 0.97 |
| 1980 | 10 | 0.51 | 0.74 | 0.91 |
| 1980 | 11 | 0.55 | 0.57 | 0.97 |
| 1980 | 12 | 0.54 | 0.54 | 1.11 |
| 1981 | 1 | 0.88 | 0.93 | 1.15 |
| 1981 | 2 | 0.34 | 0.54 | 1.07 |
| 1981 | 3 | 0.56 | 0.66 | 0.93 |
| 1981 | 4 | 0.65 | 0.67 | 1.02 |
| 1981 | 5 | 0.60 | 0.62 | 1.00 |
| 1981 | 6 | 0.59 | 0.58 | 0.90 |
| 1981 | 7 | 0.78 | 0.70 | 1.00 |
| 1981 | 8 | 0.73 | 0.92 | 0.88 |
| 1981 | 9 | 0.93 | 0.97 | 0.99 |
| 1981 | 10 | 0.52 | 0.68 | 0.99 |
| 1981 | 11 | 0.49 | 0.51 | 0.97 |
| 1981 | 12 | 0.50 | 0.46 | 1.41 |
| 1982 | 1 | 0.32 | 0.48 | 1.07 |
| 1982 | 2 | 0.27 | 0.40 | 1.14 |
| 1982 | 3 | 0.46 | 0.59 | 0.92 |
| 1982 | 4 | 0.33 | 0.39 | 0.57 |
| 1982 | 5 | 0.94 | 1.09 | 0.95 |
| 1982 | 6 | 0.43 | 0.55 | 0.98 |
| 1982 | 7 | 1.14 | 0.73 | 0.88 |
| 1982 | 8 | 0.63 | 1.14 | 0.95 |
| 1982 | 9 | 0.69 | 0.51 | 0.90 |
| 1982 | 10 | 0.48 | 0.46 | 0.88 |
| 1982 | 11 | 0.42 | 0.52 | 0.89 |
| 1982 | 12 | 0.58 | 0.63 | 1.51 |
| 1983 | 1 | 0.55 | 0.62 | 0.90 |
| 1983 | 2 | 0.34 | 0.37 | 1.36 |
| 1983 | 3 | 0.50 | 0.76 | 0.92 |
| 1983 | 4 | 0.35 | 0.65 | 0.78 |
| 1983 | 5 | 0.67 | 0.80 | 0.99 |
| 1983 | 6 | 0.88 | 1.01 | 1.01 |
| 1983 | 7 | 0.82 | 0.86 | 0.97 |
| 1983 | 8 | 1.58 | 1.73 | 0.99 |
| 1983 | 9 | 0.59 | 0.57 | 0.98 |
| 1983 | 10 | 0.55 | 0.47 | 0.96 |
| 1983 | 11 | 0.36 | 0.33 | 0.93 |
| 1983 | 12 | 0.86 | 0.91 | 1.65 |
| 1984 | 1 | 0.63 | 0.57 | 1.27 |
| 1984 | 2 | 0.43 | 0.56 | 1.04 |
| 1984 | 3 | 0.61 | 0.84 | 1.02 |
| 1984 | 4 | 0.50 | 0.46 | 0.90 |
| 1984 | 5 | 0.54 | 0.64 | 0.99 |
| 1984 | 6 | 0.66 | 0.62 | 0.99 |
| 1984 | 7 | 1.05 | 1.22 | 0.99 |
| 1984 | 8 | 0.60 | 0.58 | 0.88 |
| 1984 | 9 | 0.73 | 0.70 | 1.00 |
| 1984 | 10 | 0.45 | 0.58 | 0.92 |
| 1984 | 11 | 0.56 | 0.58 | 1.25 |
| 1984 | 12 | 1.14 | 1.28 | 1.87 |
| 1985 | 1 | 0.60 | 0.63 | 0.88 |
| 1985 | 2 | 0.39 | 0.39 | 1.18 |
| 1985 | 3 | 0.35 | 0.41 | 2.04 |
| 1985 | 4 | 0.44 | 0.43 | 0.88 |
| 1985 | 5 | 0.41 | 0.40 | 0.97 |
| 1985 | 6 | 1.05 | 1.13 | 0.98 |
| 1985 | 7 | 0.62 | 0.80 | 0.96 |
| 1985 | 8 | 0.64 | 0.73 | 0.97 |
| 1985 | 9 | 0.81 | 0.67 | 1.00 |
| 1985 | 10 | 0.45 | 0.47 | 0.97 |
| 1985 | 11 | 0.55 | 0.63 | 1.13 |
| 1985 | 12 | 0.67 | 0.78 | 1.29 |
| 1986 | 1 | 0.40 | 0.37 | 0.91 |
| 1986 | 2 | 0.48 | 0.49 | 1.00 |
| 1986 | 3 | 0.32 | 0.31 | 1.41 |
| 1986 | 4 | 0.65 | 0.67 | 0.99 |
| 1986 | 5 | 0.60 | 0.49 | 0.96 |
| 1986 | 6 | 0.39 | 0.43 | 0.94 |
| 1986 | 7 | 0.62 | 0.95 | 0.98 |
| 1986 | 8 | 0.80 | 0.74 | 0.97 |
| 1986 | 9 | 0.70 | 0.74 | 0.96 |
| 1986 | 10 | 0.54 | 0.45 | 1.03 |
| 1986 | 11 | 0.99 | 1.08 | 1.00 |
| 1986 | 12 | 0.59 | 0.78 | 1.48 |
| 1987 | 1 | 0.68 | 0.77 | 1.50 |
| 1987 | 2 | 0.44 | 0.45 | 1.65 |
| 1987 | 3 | 0.61 | 0.60 | 1.33 |
| 1987 | 4 | 0.49 | 0.60 | 0.95 |
| 1987 | 5 | 0.67 | 0.72 | 1.01 |
| 1987 | 6 | 0.56 | 0.66 | 0.99 |
| 1987 | 7 | 0.66 | 0.69 | 0.98 |
| 1987 | 8 | 0.96 | 1.10 | 0.96 |
| 1987 | 9 | 0.49 | 0.48 | 1.00 |
| 1987 | 10 | 0.66 | 0.82 | 0.99 |
| 1987 | 11 | 0.43 | 0.51 | 1.16 |
| 1987 | 12 | 0.59 | 0.66 | 1.52 |
| 1988 | 1 | 0.48 | 0.57 | 0.96 |
| 1988 | 2 | 0.71 | 0.79 | 0.95 |
| 1988 | 3 | 0.44 | 0.57 | 1.12 |
| 1988 | 4 | 0.61 | 0.68 | 0.96 |
| 1988 | 5 | 0.76 | 0.79 | 1.00 |
| 1988 | 6 | 0.62 | 0.74 | 0.96 |
| 1988 | 7 | 0.94 | 1.09 | 0.98 |
| 1988 | 8 | 0.52 | 0.43 | 0.97 |
| 1988 | 9 | 0.55 | 0.55 | 0.95 |
| 1988 | 10 | 0.62 | 0.69 | 0.97 |
| 1988 | 11 | 0.78 | 0.90 | 0.94 |
| 1988 | 12 | 0.51 | 0.47 | 0.93 |
| 1989 | 1 | 0.57 | 0.65 | 0.95 |
| 1989 | 2 | 0.29 | 0.40 | 1.12 |
| 1989 | 3 | 0.64 | 1.23 | 0.78 |
| 1989 | 4 | 0.31 | 0.47 | 0.92 |
| 1989 | 5 | 0.24 | 0.32 | 0.59 |
| 1989 | 6 | 0.50 | 0.58 | 0.95 |
| 1989 | 7 | 0.87 | 0.82 | 0.98 |
| 1989 | 8 | 0.62 | 0.73 | 0.85 |
| 1989 | 9 | 0.69 | 0.77 | 0.97 |
| 1989 | 10 | 0.55 | 0.65 | 0.98 |
| 1989 | 11 | 0.68 | 0.80 | 1.54 |
| 1989 | 12 | 0.38 | 0.48 | 1.01 |
| 1990 | 1 | 0.67 | 0.72 | 1.06 |
| 1990 | 2 | 0.35 | 0.41 | 1.42 |
| 1990 | 3 | 0.72 | 0.86 | 1.02 |
| 1990 | 4 | 0.63 | 0.66 | 0.97 |
| 1990 | 5 | 0.38 | 0.42 | 0.95 |
| 1990 | 6 | 1.08 | 0.73 | 0.91 |
| 1990 | 7 | 1.06 | 1.22 | 1.00 |
| 1990 | 8 | 0.53 | 0.55 | 0.96 |
| 1990 | 9 | 1.34 | 1.76 | 0.86 |
| 1990 | 10 | 0.50 | 0.53 | 1.01 |
| 1990 | 11 | 0.63 | 0.69 | 1.03 |
| 1990 | 12 | 0.54 | 0.53 | 1.10 |
| 1991 | 1 | 0.56 | 0.74 | 0.92 |
| 1991 | 2 | 0.48 | 0.59 | 1.15 |
| 1991 | 3 | 0.44 | 0.54 | 1.02 |
| 1991 | 4 | 0.68 | 0.96 | 0.44 |
| 1991 | 5 | 0.76 | 0.88 | 0.97 |
| 1991 | 6 | 1.04 | 1.14 | 0.94 |
| 1991 | 7 | 0.72 | 0.78 | 0.97 |
| 1991 | 8 | 0.94 | 0.78 | 0.93 |
| 1991 | 9 | 0.70 | 0.86 | 0.96 |
| 1991 | 10 | 0.74 | 0.80 | 0.94 |
| 1991 | 11 | 0.52 | 0.60 | 1.16 |
| 1991 | 12 | 0.75 | 0.82 | 1.24 |
| 1992 | 1 | 0.53 | 0.73 | 1.10 |
| 1992 | 2 | 0.47 | 0.51 | 1.08 |
| 1992 | 3 | 0.63 | 0.63 | 1.28 |
| 1992 | 4 | 0.64 | 0.74 | 0.99 |
| 1992 | 5 | 0.73 | 0.63 | 0.95 |
| 1992 | 6 | 1.50 | 1.93 | 0.96 |
| 1992 | 7 | 0.93 | 0.90 | 0.97 |
| 1992 | 8 | 1.01 | 1.26 | 0.99 |
| 1992 | 9 | 0.74 | 0.83 | 0.99 |
| 1992 | 10 | 0.59 | 0.56 | 0.93 |
| 1992 | 11 | 0.70 | 0.64 | 1.01 |
| 1992 | 12 | 0.64 | 0.77 | 1.75 |
| 1993 | 1 | 0.75 | 0.82 | 0.92 |
| 1993 | 2 | 0.54 | 0.61 | 1.42 |
| 1993 | 3 | 0.45 | 0.49 | 1.01 |
| 1993 | 4 | 0.57 | 0.60 | 0.94 |
| 1993 | 5 | 1.01 | 1.00 | 0.95 |
| 1993 | 6 | 0.60 | 0.68 | 0.97 |
| 1993 | 7 | 0.88 | 1.26 | 0.99 |
| 1993 | 8 | 0.83 | 0.89 | 1.01 |
| 1993 | 9 | 0.73 | 0.64 | 1.00 |
| 1993 | 10 | 0.40 | 0.42 | 0.87 |
| 1993 | 11 | 0.95 | 1.02 | 0.98 |
| 1993 | 12 | 0.73 | 0.77 | 0.90 |
| 1994 | 1 | 0.72 | 0.84 | 0.97 |
| 1994 | 2 | 0.45 | 0.59 | 0.97 |
| 1994 | 3 | 0.48 | 0.55 | 1.40 |
| 1994 | 4 | 0.53 | 0.59 | 0.98 |
| 1994 | 5 | 0.46 | 0.51 | 0.96 |
| 1994 | 6 | 0.41 | 0.77 | 0.82 |
| 1994 | 7 | 0.88 | 1.11 | 1.00 |
| 1994 | 8 | 1.01 | 0.88 | 0.98 |
| 1994 | 9 | 0.69 | 0.64 | 0.91 |
| 1994 | 10 | 0.45 | 0.49 | 0.91 |
| 1994 | 11 | 0.59 | 0.59 | 0.98 |
| 1994 | 12 | 0.45 | 0.64 | 1.56 |
| 1995 | 1 | 0.54 | 0.67 | 1.00 |
| 1995 | 2 | 0.48 | 0.49 | 1.27 |
| 1995 | 3 | 0.31 | 0.44 | 0.87 |
| 1995 | 4 | 0.28 | 0.41 | 0.84 |
| 1995 | 5 | 0.65 | 0.64 | 0.98 |
| 1995 | 6 | 0.56 | 0.68 | 0.98 |
| 1995 | 7 | 0.71 | 0.93 | 0.98 |
| 1995 | 8 | 0.68 | 0.85 | 0.97 |
| 1995 | 9 | 0.66 | 0.68 | 1.00 |
| 1995 | 10 | 0.61 | 0.72 | 0.98 |
| 1995 | 11 | 0.68 | 0.58 | 0.93 |
| 1995 | 12 | 0.52 | 0.54 | 0.95 |
| 1996 | 1 | 0.52 | 0.59 | 0.93 |
| 1996 | 2 | 0.42 | 0.80 | 0.88 |
| 1996 | 3 | 0.48 | 0.46 | 0.98 |
| 1996 | 4 | 0.56 | 0.69 | 0.83 |
| 1996 | 5 | 0.83 | 0.78 | 0.84 |
| 1996 | 6 | 0.72 | 1.17 | 0.91 |
| 1996 | 7 | 0.85 | 1.26 | 0.89 |
| 1996 | 8 | 0.83 | 0.99 | 0.82 |
| 1996 | 9 | 0.49 | 0.54 | 0.92 |
| 1996 | 10 | 0.87 | 0.92 | 0.93 |
| 1996 | 11 | 0.81 | 0.90 | 0.93 |
| 1996 | 12 | 0.56 | 0.63 | 0.92 |
| 1997 | 1 | 0.77 | 0.84 | 0.96 |
| 1997 | 2 | 0.49 | 0.54 | 1.27 |
| 1997 | 3 | 0.29 | 0.41 | 0.89 |
| 1997 | 4 | 0.36 | 0.30 | 0.83 |
| 1997 | 5 | 0.51 | 0.28 | 0.63 |
| 1997 | 6 | 0.49 | 0.47 | 0.94 |
| 1997 | 7 | 1.13 | 0.62 | 0.88 |
| 1997 | 8 | 0.47 | 1.69 | 0.89 |
| 1997 | 9 | 0.86 | 0.85 | 0.85 |
| 1997 | 10 | 2.06 | 1.54 | 0.49 |
| 1997 | 11 | 0.96 | 1.00 | 1.65 |
| 1997 | 12 | 0.73 | 0.86 | 0.93 |
| 1998 | 1 | 0.71 | 0.75 | 1.03 |
| 1998 | 2 | 0.51 | 0.54 | 1.48 |
| 1998 | 3 | 0.59 | 0.63 | 1.12 |
| 1998 | 4 | 0.43 | 0.47 | 0.98 |
| 1998 | 5 | 0.68 | 0.66 | 0.95 |
| 1998 | 6 | 1.06 | 1.23 | 0.98 |
| 1998 | 7 | 0.69 | 1.17 | 0.98 |
| 1998 | 8 | 0.98 | 1.77 | 0.97 |
| 1998 | 9 | 0.73 | 0.59 | 1.01 |
| 1998 | 10 | 0.23 | 0.22 | 0.65 |
| 1998 | 11 | 0.79 | 0.95 | 0.98 |
| 1998 | 12 | 0.65 | 0.73 | 0.95 |
| 1999 | 1 | 0.77 | 0.95 | 1.02 |
| 1999 | 2 | 0.47 | 0.64 | 1.47 |
| 1999 | 3 | 0.60 | 0.82 | 1.55 |
| 1999 | 4 | 0.49 | 0.51 | 0.97 |
| 1999 | 5 | 0.45 | 0.44 | 0.96 |
| 1999 | 6 | 0.50 | 0.45 | 0.99 |
| 1999 | 7 | 0.60 | 0.70 | 1.02 |
| 1999 | 8 | 0.53 | 0.60 | 0.99 |
| 1999 | 9 | 0.48 | 0.50 | 0.97 |
| 1999 | 10 | 0.68 | 0.84 | 1.01 |
| 1999 | 11 | 0.62 | 0.72 | 0.96 |
| 1999 | 12 | 1.03 | 1.15 | 1.41 |
| 2000 | 1 | 0.75 | 0.86 | 0.99 |
| 2000 | 2 | 0.29 | 0.35 | 0.89 |
| 2000 | 3 | 0.39 | 0.59 | 0.97 |
| 2000 | 4 | 0.32 | 0.34 | 0.97 |
| 2000 | 5 | 0.74 | 0.87 | 1.21 |
| 2000 | 6 | 0.81 | 0.87 | 1.17 |
| 2000 | 7 | 0.77 | 0.95 | 0.99 |
| 2000 | 8 | 0.46 | 0.31 | 1.04 |
| 2000 | 9 | 0.51 | 0.51 | 1.16 |
| 2000 | 10 | 0.67 | 0.82 | 1.30 |
| 2000 | 11 | 0.83 | 0.97 | 1.25 |
| 2000 | 12 | 0.91 | 1.14 | 1.01 |
| 2001 | 1 | 0.74 | 0.92 | 1.27 |
| 2001 | 2 | 0.50 | 0.61 | 0.87 |
| 2001 | 3 | 0.72 | 0.63 | 1.05 |
| 2001 | 4 | 0.42 | 0.48 | 1.34 |
| 2001 | 5 | 0.72 | 0.83 | 1.05 |
| 2001 | 6 | 0.66 | 0.92 | 1.03 |
| 2001 | 7 | 0.64 | 0.74 | 1.01 |
| 2001 | 8 | 1.19 | 1.34 | 1.02 |
| 2001 | 9 | 0.57 | 0.62 | 1.00 |
| 2001 | 10 | 0.58 | 0.64 | 0.87 |
| 2001 | 11 | 0.64 | 0.66 | 1.24 |
| 2001 | 12 | 1.53 | 1.60 | 1.02 |
| 2002 | 1 | 0.81 | 1.00 | 0.94 |
| 2002 | 2 | 0.98 | 1.00 | 0.88 |
| 2002 | 3 | 0.46 | 0.52 | 1.04 |
| 2002 | 4 | 0.48 | 0.51 | 0.98 |
| 2002 | 5 | 0.77 | 0.79 | 1.03 |
| 2002 | 6 | 0.90 | 0.95 | 0.98 |
| 2002 | 7 | 0.67 | 0.64 | 0.97 |
| 2002 | 8 | 0.53 | 0.51 | 1.06 |
| 2002 | 9 | 0.49 | 0.44 | 0.94 |
| 2002 | 10 | 0.83 | 0.98 | 0.99 |
| 2002 | 11 | 0.81 | 0.85 | 1.27 |
| 2002 | 12 | 0.67 | 0.70 | 1.00 |
| 2003 | 1 | 0.81 | 0.90 | 0.94 |
| 2003 | 2 | 0.54 | 0.68 | 0.92 |
| 2003 | 3 | 0.33 | 0.38 | 0.94 |
| 2003 | 4 | 0.57 | 0.66 | 1.05 |
| 2003 | 5 | 0.92 | 0.77 | 0.89 |
| 2003 | 6 | 0.61 | 0.51 | 1.01 |
| 2003 | 7 | 0.82 | 0.91 | 1.01 |
| 2003 | 8 | 0.95 | 1.09 | 1.03 |
| 2003 | 9 | 0.73 | 0.71 | 0.99 |
| 2003 | 10 | 0.44 | 0.47 | 1.03 |
| 2003 | 11 | 0.85 | 1.07 | 0.92 |
| 2003 | 12 | 1.00 | 1.01 | 0.91 |
| 2004 | 1 | 0.71 | 0.94 | 1.01 |
| 2004 | 2 | 0.74 | 0.88 | 0.90 |
| 2004 | 3 | 0.61 | 0.67 | 1.26 |
| 2004 | 4 | 0.55 | 0.43 | 0.90 |
| 2004 | 5 | 0.80 | 0.91 | 1.08 |
| 2004 | 6 | 0.60 | 1.31 | 1.13 |
| 2004 | 7 | 0.58 | 0.56 | 1.00 |
| 2004 | 8 | 1.01 | 0.91 | 0.99 |
| 2004 | 9 | 0.86 | 0.92 | 0.96 |
| 2004 | 10 | 0.26 | 0.27 | 0.82 |
| 2004 | 11 | 0.77 | 0.86 | 1.21 |
| 2004 | 12 | 1.02 | 1.15 | 0.98 |
| 2005 | 1 | 1.28 | 1.31 | 0.95 |
| 2005 | 2 | 0.93 | 1.32 | 0.90 |
| 2005 | 3 | 0.32 | 0.32 | 0.87 |
| 2005 | 4 | 0.53 | 0.56 | 1.10 |
| 2005 | 5 | 0.86 | 0.84 | 0.94 |
| 2005 | 6 | 1.08 | 1.09 | 0.98 |
| 2005 | 7 | 0.47 | 0.42 | 0.89 |
| 2005 | 8 | 0.71 | 0.67 | 0.99 |
| 2005 | 9 | 0.71 | 0.84 | 0.86 |
| 2005 | 10 | 0.46 | 0.58 | 0.90 |
| 2005 | 11 | 0.90 | 1.10 | 1.00 |
| 2005 | 12 | 0.65 | 0.74 | 0.85 |
| 2006 | 1 | 0.87 | 1.30 | 0.91 |
| 2006 | 2 | 0.82 | 0.95 | 0.95 |
| 2006 | 3 | 0.72 | 0.78 | 1.14 |
| 2006 | 4 | 0.70 | 0.71 | 1.22 |
| 2006 | 5 | 0.63 | 0.73 | 0.93 |
| 2006 | 6 | 1.06 | 1.56 | 1.01 |
| 2006 | 7 | 0.73 | 0.93 | 0.93 |
| 2006 | 8 | 1.08 | 1.15 | 0.99 |
| 2006 | 9 | 0.34 | 0.50 | 0.73 |
| 2006 | 10 | 0.58 | 0.60 | 0.90 |
| 2006 | 11 | 0.84 | 0.92 | 0.84 |
| 2006 | 12 | 0.66 | 0.78 | 0.96 |
| 2007 | 1 | 0.77 | 0.80 | 0.90 |
| 2007 | 2 | 0.65 | 0.74 | 0.97 |
| 2007 | 3 | 0.75 | 0.79 | 1.24 |
| 2007 | 4 | 1.30 | 1.00 | 0.93 |
| 2007 | 5 | 0.54 | 0.56 | 0.87 |
| 2007 | 6 | 1.25 | 1.13 | 0.96 |
| 2007 | 7 | 1.12 | 1.13 | 0.97 |
| 2007 | 8 | 1.85 | 1.83 | 0.94 |
| 2007 | 9 | 0.81 | 0.70 | 0.91 |
| 2007 | 10 | 1.13 | 1.33 | 1.06 |
| 2007 | 11 | 0.84 | 0.87 | 1.10 |
| 2007 | 12 | 0.55 | 0.51 | 0.91 |
| 2008 | 1 | 0.86 | 0.88 | 1.02 |
| 2008 | 2 | 0.51 | 0.56 | 0.89 |
| 2008 | 3 | 0.53 | 0.68 | 0.97 |
| 2008 | 4 | 0.68 | 0.66 | 0.98 |
| 2008 | 5 | 0.31 | 0.25 | 0.82 |
| 2008 | 6 | 0.97 | 2.24 | 0.95 |
| 2008 | 7 | 1.36 | 1.41 | 0.97 |
| 2008 | 8 | 0.72 | 0.90 | 0.97 |
| 2008 | 9 | 0.81 | 0.79 | 0.97 |
| 2008 | 10 | 0.52 | 0.70 | 1.30 |
| 2008 | 11 | 0.68 | 0.79 | 0.90 |
| 2008 | 12 | 0.91 | 1.23 | 1.05 |
| 2009 | 1 | 0.89 | 1.01 | 0.90 |
| 2009 | 2 | 0.64 | 0.77 | 1.09 |
| 2009 | 3 | 0.63 | 0.64 | 0.86 |
| 2009 | 4 | 0.52 | 0.47 | 1.01 |
| 2009 | 5 | 0.83 | 0.84 | 0.94 |
| 2009 | 6 | 0.50 | 0.43 | 1.00 |
| 2009 | 7 | 0.71 | 0.60 | 0.96 |
| 2009 | 8 | 1.02 | 0.89 | 0.87 |
| 2009 | 9 | 0.89 | 1.03 | 1.00 |
| 2009 | 10 | 0.69 | 0.72 | 0.98 |
| 2009 | 11 | 0.73 | 0.84 | 0.80 |
| 2009 | 12 | 0.85 | 0.98 | 1.04 |
| 2010 | 1 | 1.03 | 1.19 | 1.02 |
| 2010 | 2 | 0.80 | 0.85 | 0.89 |
| 2010 | 3 | 0.93 | 0.91 | 0.89 |
| 2010 | 4 | 0.71 | 0.69 | 0.90 |
| 2010 | 5 | 0.69 | 0.75 | 0.96 |
| 2010 | 6 | 1.22 | 1.04 | 0.97 |
| 2010 | 7 | 1.90 | 2.21 | 0.88 |
| 2010 | 8 | 0.78 | 1.02 | 0.99 |
| 2010 | 9 | 0.60 | 0.55 | 0.95 |
| 2010 | 10 | 1.08 | 1.13 | 1.02 |
| 2010 | 11 | 0.75 | 0.90 | 0.93 |
| 2010 | 12 | 0.76 | 0.97 | 0.97 |
| 2011 | 1 | 1.01 | 1.20 | 1.04 |
| 2011 | 2 | 1.05 | 1.04 | 0.91 |
| 2011 | 3 | 1.06 | 1.15 | 1.31 |
| 2011 | 4 | 0.68 | 0.87 | 1.02 |
| 2011 | 5 | 1.03 | 1.11 | 0.96 |
| 2011 | 6 | 1.13 | 0.69 | 0.90 |
| 2011 | 7 | 1.22 | 1.46 | 0.92 |
| 2011 | 8 | 1.20 | 1.38 | 1.04 |
| 2011 | 9 | 0.94 | 1.04 | 0.85 |
| 2011 | 10 | 0.56 | 0.70 | 1.01 |
| 2011 | 11 | 0.90 | 1.08 | 1.06 |
| 2011 | 12 | 0.91 | 1.13 | 0.94 |
| 2012 | 1 | 1.14 | 1.48 | 0.90 |
| 2012 | 2 | 1.02 | 0.68 | 1.01 |
| 2012 | 3 | 0.41 | 0.36 | 0.88 |
| 2012 | 4 | 0.72 | 0.82 | 1.05 |
| 2012 | 5 | 0.56 | 0.63 | 1.06 |
| 2012 | 6 | 1.17 | 1.79 | 1.04 |
| 2012 | 7 | 1.12 | 1.17 | 0.97 |
| 2012 | 8 | 0.97 | 1.33 | 0.96 |
| 2012 | 9 | 1.16 | 1.28 | 0.91 |
| 2012 | 10 | 0.74 | 0.82 | 1.01 |
| 2012 | 11 | 0.69 | 0.86 | 0.97 |
| 2012 | 12 | 0.94 | 1.05 | 0.94 |
| 2013 | 1 | 0.63 | 0.64 | 0.77 |
| 2013 | 2 | 0.73 | 0.84 | 0.98 |
| 2013 | 3 | 0.49 | 0.56 | 1.39 |
| 2013 | 4 | 0.46 | 0.69 | 0.89 |
| 2013 | 5 | 0.93 | 1.18 | 0.98 |
| 2013 | 6 | 0.97 | 0.87 | 1.04 |
| 2013 | 7 | 1.16 | 1.28 | 1.00 |
| 2013 | 8 | 1.07 | 0.95 | 0.91 |
| 2013 | 9 | 1.08 | 1.27 | 0.99 |
| 2013 | 10 | 0.74 | 0.86 | 0.96 |
| 2013 | 11 | 0.58 | 0.62 | 1.01 |
| 2013 | 12 | 1.10 | 1.17 | 1.13 |
| 2014 | 1 | 0.91 | 1.08 | 0.99 |
| 2014 | 2 | 0.79 | 1.05 | 1.00 |
| 2014 | 3 | 0.64 | 0.78 | 1.06 |
| 2014 | 4 | 0.52 | 0.52 | 0.96 |
| 2014 | 5 | 0.77 | 0.85 | 1.04 |
| 2014 | 6 | 0.68 | 0.40 | 0.76 |
| 2014 | 7 | 1.61 | 1.27 | 1.22 |
| 2014 | 8 | 0.45 | 0.47 | 0.83 |
| 2014 | 9 | 0.89 | 1.06 | 1.11 |
| 2014 | 10 | 0.74 | 0.96 | 0.88 |
| 2014 | 11 | 0.79 | 0.90 | 0.98 |
| 2014 | 12 | 0.62 | 0.62 | 0.97 |
| 2015 | 1 | 0.83 | 1.23 | 1.00 |
| 2015 | 2 | 0.60 | 0.80 | 1.01 |
| 2015 | 3 | 0.50 | 0.53 | 1.00 |
| 2015 | 4 | 0.68 | 0.51 | 0.72 |
| 2015 | 5 | 0.80 | 1.00 | 1.09 |
| 2015 | 6 | 0.67 | 0.56 | 1.00 |
| 2015 | 7 | 1.49 | 1.06 | 0.94 |
| 2015 | 8 | 0.92 | 0.88 | 0.90 |
| 2015 | 9 | 0.66 | 0.69 | 1.06 |
| 2015 | 10 | 0.55 | 0.71 | 1.00 |
| 2015 | 11 | 0.67 | 0.75 | 1.15 |
| 2015 | 12 | 0.78 | 0.85 | 0.95 |
| 2016 | 1 | 1.14 | 1.12 | 0.99 |
| 2016 | 2 | 0.41 | 0.48 | 0.92 |
| 2016 | 3 | 0.54 | 0.60 | 1.37 |
| 2016 | 4 | 0.82 | 0.78 | 1.00 |
| 2016 | 5 | 0.61 | 0.77 | 1.35 |
| 2016 | 6 | 0.99 | 0.94 | 1.00 |
| 2016 | 7 | 0.71 | 0.78 | 0.97 |
| 2016 | 8 | 1.00 | 1.20 | 1.22 |
| 2016 | 9 | 0.93 | 1.41 | 0.95 |
| 2016 | 10 | 0.71 | 0.82 | 1.33 |
| 2016 | 11 | 0.77 | 0.93 | 0.98 |
| 2016 | 12 | 0.85 | 0.93 | 1.32 |
| 2017 | 1 | 0.63 | 0.75 | 1.02 |
| 2017 | 2 | 1.10 | 1.18 | 0.90 |
| 2017 | 3 | 0.71 | 0.74 | 0.91 |
| 2017 | 4 | 0.48 | 0.59 | 0.94 |
| 2017 | 5 | 1.02 | 1.07 | 1.15 |
| 2017 | 6 | 0.92 | 1.02 | 1.07 |
| 2017 | 7 | 1.29 | 1.52 | 1.21 |
| 2017 | 8 | 0.80 | 1.77 | 1.06 |
| 2017 | 9 | 1.04 | 1.11 | 1.02 |
| 2017 | 10 | 0.65 | 0.78 | 1.02 |
| 2017 | 11 | 0.58 | 0.71 | 1.35 |
| 2017 | 12 | 0.70 | 0.89 | 0.93 |
| 2018 | 1 | 1.13 | 1.28 | 0.94 |
| 2018 | 2 | 0.16 | 0.20 | 0.79 |
| 2018 | 3 | 0.53 | 0.59 | 1.33 |
| 2018 | 4 | 0.91 | 0.92 | 1.25 |
| 2018 | 5 | 0.67 | 0.70 | 1.12 |
| 2018 | 6 | 0.71 | 0.64 | 0.99 |
| 2018 | 7 | 0.89 | 0.99 | 0.95 |
| 2018 | 8 | 0.90 | 0.87 | 0.91 |
| 2018 | 9 | 1.06 | 0.96 | 1.03 |
| 2018 | 10 | 0.41 | 0.45 | 0.85 |
| 2018 | 11 | 0.44 | 0.49 | 0.76 |
| 2018 | 12 | 0.98 | 1.08 | 0.71 |
References
- Xu, J.T.; Zhu, S.Y.; Ma, Z.Q.; Liu, H.; Shangguan, Y.L.; Yang, Y.J. Calibrating GPM IMERG Late-Run product using ground-based CPC daily precipitation data: A case study in the Beijing-Tianjin-Hebei urban agglomeration. Remote Sens. Lett. 2021, 12, 848–858. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. Climate Change 2021: The Physical Science Basis; Contribution of Working Group to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar]
- Min, S.K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Rodrigues, D.T.; Gonçalves, W.A.; Spyrides, M.H.C.; Santos e Silva, C.M.; Souza, D.O. Spatial distribution of the level of return of extreme precipitation events in Northeast Brazil. Int. J. Climatol. 2020, 40, 5098–5113. [Google Scholar] [CrossRef]
- Dong, S.Y.; Sun, Y.; Li, C.; Zhang, X.B.; Min, S.K.; Kim, Y.H. Attribution of Extreme Precipitation with Updated Observations and CMIP6 Simulations. J. Clim. 2021, 34, 871–881. [Google Scholar] [CrossRef]
- Lang, T.; Pan, L.; Liu, B.; Guo, T.; Hou, X. Vegetation Characteristics and Response to the Soil Properties of Three Medicinal Plant Communities in Altay Prefecture, China. Sustainability 2020, 12, 10306. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; He, Q.; Yi, L. Study on Climate Change in Altay Prefecture since Recent 40 Years. Arid Zone Res. 2006, 23, 637–643. [Google Scholar]
- Gulzat, H.; Zhao, J. Analysis on Climate Change in Recent 50 Years in Altay Prefecture, Xinjiang. Arid Zone Res. 2011, 28, 268–274. [Google Scholar]
- Gulzat, H.; Jingbo, Z. Changes of extreme temperature and precipitation in Altay Region, Xinjiang in recent 50 years. J. Arid Land Resour. Environ. 2011, 25, 112–116. [Google Scholar]
- He, Y.; Xiong, J.; Abhayatihali, A.; Chen, W.; Ye, C.; He, W.; Yong, Z.; Tian, J. Spatiotemporal Pattern and Driving Force Analysis of Vegetation Variation in Altay Prefecture based on Google Earth Engine. J. Resour. Ecol. 2021, 12, 729–742. [Google Scholar]
- Gao, L.; Wei, J.H.; Wang, L.X.; Bernhardt, M.; Schulz, K.; Chen, X.W. A high-resolution air temperature data set for the Chinese Tian Shan in 1979–2016. Earth Syst. Sci. Data 2018, 10, 2097–2114. [Google Scholar] [CrossRef]
- Zhang, C.; Mou, N.X.; Niu, J.Q.; Zhang, L.X.; Liu, F. Spatio-Temporal Variation Characteristics of Snow Depth and Snow Cover Days over the Tibetan Plateau. Water 2021, 13, 307. [Google Scholar] [CrossRef]
- Bağçaci, S.Ç.; Yucel, I.; Duzenli, E.; Yilmaz, M.T. Intercomparison of the expected change in the temperature and the precipitation retrieved from CMIP6 and CMIP5 climate projections: A Mediterranean hot spot case, Turkey. Atmos. Res. 2021, 256, 105576. [Google Scholar] [CrossRef]
- Yu, T.; Jiapaer, G.; Bao, A.; Zhang, J.; Tu, H.; Chen, B.; De Maeyer, P.; Van de Voorde, T. Evaluating surface soil moisture characteristics and the performance of remote sensing and analytical products in Central Asia. J. Hydrol. 2023, 617, 128921. [Google Scholar] [CrossRef]
- Jiao, D.; Xu, N.; Yang, F.; Xu, K. Evaluation of spatial-temporal variation performance of ERA5 precipitation data in China. Sci. Rep. 2021, 11, 17956. [Google Scholar] [CrossRef]
- Li, Y.; Qin, X.; Liu, Y.; Jin, Z.; Liu, J.; Wang, L.; Chen, J. Evaluation of Long-Term and High-Resolution Gridded Precipitation and Temperature Products in the Qilian Mountains, Qinghai–Tibet Plateau. Front. Environ. Sci. 2022, 10, 906821. [Google Scholar] [CrossRef]
- Araujo, C.S.P.; Silva, I.; Ippolito, M.; Almeida, C. Evaluation of air temperature estimated by ERA5-Land reanalysis using surface data in Pernambuco, Brazil. Environ. Monit. Assess. 2022, 194, 381. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; He, Z. A First Evaluation of ERA5-Land Reanalysis Temperature Product Over the Chinese Qilian Mountains. Front. Earth Sci. 2022, 10, 907730. [Google Scholar] [CrossRef]
- Ma, M.; Chen, Y.; Kang, G.; Zhao, Z.; Huang, W.; Tan, C.; Ding, F. Deviation analysis of reanalysis data in boundary layer in summer over Tibetan Plateau and its simulation correction. J. Arid Meteorol. 2022, 40, 95–107. [Google Scholar]
- Wang, X.; Shi, G.; Zhou, Z.; Zhen, Y. Revision of solar radiation product ERA5 based on random forest algorithm. Remote Sens. Nat. Resour. 2022, 34, 105–111. [Google Scholar]
- Fu, Q.; Li, B.; Hou, Y.; Bi, X.; Zhang, X.S. Effects of land use and climate change on ecosystem services in Central Asia’s arid regions: A case study in Altay Prefecture, China. Sci. Total Environ. 2017, 607, 633–646. [Google Scholar] [CrossRef]
- Zhao, J.; Zhuang, X.; Zhang, Y. Spatial and temporal distribution characteristics of short-term heavy rainfall in Altay area of Xinjiang in summer. Meteorol. Disaster Reduct. Res. 2022, 45, 31–37. [Google Scholar]
- Hanchu, L.; Jie, F.; Baoyin, L.; Li, W.; Qin, Q. Practical Exploration of Ecological Restoration and Management of the Mountains-Rivers-Forests-Farmlands-Lakes-Grasslands System in the Irtysh River Basin in Altay, Xinjiang. J. Resour. Ecol. 2021, 12, 766–776. [Google Scholar] [CrossRef]
- Lavers, D.A.; Simmons, A.; Vamborg, F.; Rodwell, M.J. An evaluation of ERA5 precipitation for climate monitoring. Q. J. R. Meteorol. Soc. 2022, 148, 3152–3165. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Mihalevich, B.A.; Neilson, B.T.; Buahin, C.A. Evaluation of the ERA5-Land Reanalysis Data Set for Process-Based River Temperature Modeling Over Data Sparse and Topographically Complex Regions. Water Resour. Res. 2022, 58, e2021WR031294. [Google Scholar] [CrossRef]
- Pelosi, A.; Chirico, G.B. Regional assessment of daily reference evapotranspiration: Can ground observations be replaced by blending ERA5-Land meteorological reanalysis and CM-SAF satellite-based radiation data? Agric. Water Manag. 2021, 258, 107169. [Google Scholar] [CrossRef]
- Xin, Y.; Yang, Y.; Chen, X.; Yue, X.; Liu, Y.; Yin, C. Evaluation of IMERG and ERA5 precipitation products over the Mongolian Plateau. Sci. Rep. 2022, 12, 21776. [Google Scholar] [CrossRef] [PubMed]
- Ou, T.H.; Chen, D.L.; Tang, J.P.; Lin, C.G.; Wang, X.J.; Kukulies, J.; Lai, H.W. Wet bias of summer precipitation in the northwestern Tibetan Plateau in ERA5 is linked to overestimated lower-level southerly wind over the plateau. Clim. Dyn. 2023, 61, 2139–2153. [Google Scholar] [CrossRef]
- Song, L.L.; Xu, C.C.; Long, Y.X.; Lei, X.N.; Suo, N.J.; Cao, L.L. Performance of Seven Gridded Precipitation Products over Arid Central Asia and Subregions. Remote Sens. 2022, 14, 6039. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, L.; Shen, Y.; Zhang, Y.; Zhang, B. Evaluation of applicability of ERA-Interim and CMFD meteorological forcing data in the Irtysh River basin, Xinjiang. J. Glaciol. Geocryol. 2022, 44, 179–187. [Google Scholar]
- He, J.; Yang, K.; Tang, W.J.; Lu, H.; Qin, J.; Chen, Y.Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Wang, D.G.; Zhu, J.X.; Lin, Z.Q.; Zhong, Y.X. Intercomparison of multiple high-resolution precipitation products over China: Climatology and extremes. Atmos. Res. 2022, 278, 106342. [Google Scholar] [CrossRef]
- Chen, C.; Zheng, J.; Liu, Y.; Xu, Z. The response of glacial lakes in the Altay Mountains of China to climate change during 1992–2013. Geogr. Res. 2015, 34, 270–284. [Google Scholar]
- Michot, V.; Vila, D.; Arvor, D.; Corpetti, T.; Ronchail, J.; Funatsu, B.M.; Dubreuil, V. Performance of TRMM TMPA 3B42 V7 in Replicating Daily Rainfall and Regional Rainfall Regimes in the Amazon Basin (1998–2013). Remote Sens. 2018, 10, 1879. [Google Scholar] [CrossRef]
- Kumar, D.; Pandey, A.; Sharma, N.; Flugel, W.A. Evaluation of TRMM-Precipitation with Rain-Gauge Observation Using Hydrological Model J2000. J. Hydrol. Eng. 2017, 22, E5015007. [Google Scholar] [CrossRef]
- Cao, Y.Q.; Zhang, W.; Wang, W.J. Evaluation of TRMM 3B43 data over the Yangtze River Delta of China. Sci. Rep. 2018, 8, 5290. [Google Scholar] [CrossRef] [PubMed]
- Shi, W. Assessment of Multi-Source Precipitation Products and Characterization of Daily Changes in Extreme Precipitation in Central Asia. Master’s Thesis, Nanjing University of Information Engineering, Nanjing, China, 2021. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res.-Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Janssen, P.H.M.; Heuberger, P.S.C. Calibration of process-oriented models. Ecol. Model. 1995, 83, 55–66. [Google Scholar] [CrossRef]
- Wang, S.J.; Zhang, M.J.; Sun, M.P.; Wang, B.L.; Huang, X.Y.; Wang, Q.; Feng, F. Comparison of surface air temperature derived from NCEP/DOE R2, ERA-Interim, and observations in the arid northwestern China: A consideration of altitude errors. Theor. Appl. Climatol. 2015, 119, 99–111. [Google Scholar] [CrossRef]
- Zou, J.; Lu, N.; Jiang, H.; Qin, J.; Yao, L.; Xin, Y.; Su, F. Performance of air temperature from ERA5-Land reanalysis in coastal urban agglomeration of Southeast China. Sci Total Env. 2022, 828, 154459. [Google Scholar] [CrossRef]
- Hou, C.; Huang, D.; Xu, H.; Xu, Z. Evaluation of ERA5 reanalysis over the deserts in northern China. Theor. Appl. Climatol. 2022, 151, 801–816. [Google Scholar] [CrossRef]
- Yan, W.; Zhao, J.; Yang, Y. Comparative evaluation of the ability of GHCN-CAMS and CMFD reanalysis data to reflect regional temperature in Ningxia. Prog. Geogr. 2021, 40, 2061–2072. [Google Scholar] [CrossRef]
- Chen, Y.; Sharma, S.; Zhou, X.; Yang, K.; Li, X.; Niu, X.; Hu, X.; Khadka, N. Spatial performance of multiple reanalysis precipitation datasets on the southern slope of central Himalaya. Atmos. Res. 2021, 250, 105365. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Yan, S.; Peng, J. Do ERA5 and ERA5-land precipitation estimates outperform satellite-based precipitation products? A comprehensive comparison between state-of-the-art model-based and satellite-based precipitation products over mainland China. J. Hydrol. 2022, 605, 127353. [Google Scholar] [CrossRef]
- Izadi, N.; Karakani, E.G.; Saadatabadi, A.R.; Shamsipour, A.; Fattahi, E.; Habibi, M. Evaluation of ERA5 Precipitation Accuracy Based on Various Time Scales over Iran during 2000–2018. Water 2021, 13, 2538. [Google Scholar] [CrossRef]
- Tang, G.Q.; Behrangi, A.; Long, D.; Li, C.M.; Hong, Y. Accounting for spatiotemporal errors of gauges: A critical step to evaluate gridded precipitation products. J. Hydrol. 2018, 559, 294–306. [Google Scholar] [CrossRef]
- Wang, X.J.; Pang, G.J.; Yang, M.X.; Zhao, G.H. Evaluation of climate on the Tibetan Plateau using ERA-Interim reanalysis and gridded observations during the period 1979–2012. Quat. Int. 2017, 444, 76–86. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Dahri, Z.H.; Moors, E.; Ludwig, F.; Ahmad, S.; Khan, A.; Ali, I.; Kabat, P. Adjustment of measurement errors to reconcile precipitation distribution in the high-altitude Indus basin. Int. J. Climatol. 2018, 38, 3842–3860. [Google Scholar] [CrossRef]
- Song, Y.; Broxton, P.D.; Ehsani, M.R.; Behrangi, A. Assessment of Snowfall Accumulation from Satellite and Reanalysis Products Using SNOTEL Observations in Alaska. Remote Sens. 2021, 13, 2922. [Google Scholar] [CrossRef]
- Schleiss, M.; Olsson, J.; Berg, P.; Niemi, T.; Kokkonen, T.; Thorndahl, S.; Nielsen, R.; Ellerbæk Nielsen, J.; Bozhinova, D.; Pulkkinen, S. The accuracy of weather radar in heavy rain: A comparative study for Denmark, the Netherlands, Finland and Sweden. Hydrol. Earth Syst. Sci. 2020, 24, 3157–3188. [Google Scholar] [CrossRef]
- Zhao, P.; Gao, L.; Wei, J.; Ma, M.; Deng, H.; Gao, J.; Chen, X. Evaluation of ERA-Interim Air Temperature Data over the Qilian Mountains of China. Adv. Meteorol. 2020, 2020, 7353482. [Google Scholar] [CrossRef]




| Station No. | CMFD/°C | ERA5-Land/°C | ERA5/°C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2016 | 2017 | 2018 | 2016 | 2017 | 2018 | 2016 | 2017 | 2018 | |
| 51058 | 0.51 | 0.75 | 0.89 | 1.13 | 1.77 | 1.62 | 3.04 | 3.17 | 3.08 |
| 51068 | 0.85 | 0.61 | 1.20 | 1.28 | 1.45 | 1.62 | −0.82 | −0.89 | −0.13 |
| 51076 | −0.16 | −0.15 | 0.00 | −1.65 | −0.70 | −1.94 | 1.50 | 1.67 | 1.64 |
| 51084 | −1.71 | −2.62 | −1.93 | −4.97 | −4.47 | −4.89 | 5.88 | 5.60 | 6.20 |
| 51166 | 0.80 | 0.09 | 0.37 | 1.23 | 1.00 | 1.46 | 1.72 | 1.20 | 1.79 |
| 51187 | −0.25 | −0.64 | 0.01 | −0.31 | −0.65 | −0.50 | −3.75 | −3.81 | −3.03 |
| 51189 | 1.32 | 1.63 | 1.57 | −1.06 | −0.48 | −0.52 | −2.64 | −1.97 | −2.16 |
| Y5303 | 0.40 | 0.57 | 0.93 | 0.54 | 1.01 | 1.19 | −6.30 | −5.66 | −4.84 |
| Y5304 | −1.34 | −1.49 | −1.14 | −1.22 | −1.36 | −1.54 | −8.88 | −8.65 | −8.55 |
| Y5307 | 0.97 | 0.05 | 0.41 | 1.30 | 1.06 | 2.03 | 0.46 | 0.27 | 0.37 |
| Y5308 | 1.09 | 0.51 | 1.08 | −0.54 | 0.04 | 0.03 | 7.22 | 7.18 | 7.03 |
| Y5329 | −1.12 | −1.73 | −1.17 | −3.29 | −3.09 | −3.74 | −3.91 | −4.66 | −5.11 |
| Y5334 | −0.54 | −1.08 | −0.73 | −0.64 | −0.64 | −1.11 | −4.78 | −4.68 | −4.55 |
| Y5335 | −7.80 | −7.88 | −7.25 | −7.03 | −7.52 | −7.82 | −2.12 | −2.65 | −2.98 |
| Y5339 | 0.19 | 0.44 | 0.37 | 1.43 | 2.18 | 1.99 | −1.69 | −1.61 | −1.31 |
| Y5341 | 0.19 | −0.46 | 0.32 | 0.10 | 0.40 | 1.01 | 1.72 | 1.64 | 1.64 |
| Y5342 | −1.06 | −1.44 | −1.22 | −4.33 | −3.57 | −3.90 | 1.96 | 2.34 | 1.54 |
| Y5346 | −1.11 | −1.18 | −1.17 | −3.28 | −2.50 | −2.90 | 1.16 | 1.93 | 0.52 |
| Y5349 | −0.01 | −0.61 | −0.29 | −0.35 | −0.10 | −0.38 | −11.12 | −10.56 | −11.87 |
| Y5365 | −3.95 | −4.47 | −4.24 | −5.21 | −5.15 | −5.67 | −5.67 | −6.02 | −6.50 |
| Y5372 | 0.12 | 0.28 | 0.89 | 0.73 | 1.26 | 1.50 | −7.25 | −6.55 | −6.88 |
| Y5376 | −0.77 | −0.77 | −0.29 | 1.09 | 1.11 | 1.35 | 1.06 | 0.98 | 1.11 |
| Y5379 | −0.41 | −0.66 | −0.34 | −0.58 | −0.39 | −0.43 | −4.52 | −4.73 | −4.58 |
| Y5386 | 0.29 | 0.15 | −0.65 | −0.37 | −0.20 | −0.73 | 1.29 | 1.01 | 0.91 |
| Y6701 | −1.40 | −1.70 | −1.33 | −0.81 | −0.86 | −1.02 | 1.60 | 0.87 | 0.66 |
| Y6712 | −0.26 | −0.76 | −0.43 | −3.23 | −2.57 | −3.64 | 1.04 | 0.31 | −0.32 |
| Y6714 | 0.10 | 0.05 | 0.88 | −1.31 | −1.02 | −1.46 | −2.48 | −2.69 | −2.99 |
| Y6715 | 1.23 | 1.09 | 1.68 | 1.14 | 1.45 | 1.35 | −4.92 | −4.93 | −4.98 |
| Y6718 | 0.95 | 0.91 | 1.44 | 0.85 | 1.36 | 1.08 | −10.25 | −9.52 | −11.04 |
| Y6721 | 1.77 | 1.33 | 1.36 | 1.83 | 1.65 | 1.81 | −0.06 | 0.05 | −0.27 |
| Y6723 | −0.47 | −0.83 | −2.08 | −2.10 | −2.07 | −2.49 | 3.09 | 2.82 | 3.35 |
| Y6724 | −6.12 | −5.81 | −5.26 | −7.71 | −7.05 | −7.64 | −2.04 | −1.37 | −1.88 |
| RMSE/°C | RMSE Improvement Rate/% | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ERLT | ERAT | CMFDT | R-ERLT | R-ERAT | R-CMFDT | ERLT | ERAT | CMFDT | |
| January | 3.77 | 4.03 | 3.97 | 3.14 | 3.30 | 2.66 | 16.75 | 17.97 | 32.94 |
| February | 3.87 | 3.67 | 3.34 | 2.43 | 3.27 | 2.14 | 37.06 | 10.86 | 36.08 |
| March | 3.50 | 3.98 | 2.46 | 2.51 | 3.17 | 1.42 | 28.31 | 20.39 | 42.10 |
| April | 3.34 | 4.53 | 2.21 | 1.32 | 3.36 | 1.01 | 60.46 | 25.79 | 54.31 |
| May | 3.07 | 4.48 | 2.00 | 1.30 | 3.25 | 0.95 | 57.59 | 27.57 | 52.43 |
| June | 2.97 | 4.67 | 2.08 | 1.21 | 3.59 | 0.97 | 59.24 | 23.20 | 53.15 |
| July | 2.86 | 4.62 | 2.42 | 1.23 | 3.72 | 1.08 | 56.81 | 19.45 | 55.34 |
| August | 2.82 | 4.32 | 2.48 | 1.38 | 4.22 | 1.12 | 51.28 | 2.24 | 54.62 |
| September | 2.74 | 4.01 | 2.56 | 1.38 | 3.63 | 1.31 | 49.55 | 9.49 | 48.68 |
| October | 3.53 | 4.57 | 2.21 | 1.54 | 3.06 | 1.25 | 56.48 | 33.01 | 43.20 |
| November | 3.32 | 4.90 | 2.53 | 1.80 | 3.52 | 1.37 | 46.00 | 28.09 | 45.83 |
| December | 3.58 | 4.78 | 3.15 | 2.47 | 4.39 | 2.04 | 31.07 | 8.19 | 35.25 |
| RMSE/mm | RMSE Improvement Rate/% | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ERLP | ERAP | CMFDP | R-ERLP | R-ERAP | R-CMFD | ERLP | ERAP | CMFDP | |
| January | 5.92 | 5.62 | 5.30 | 3.10 | 4.28 | 4.97 | 47.69 | 23.86 | 6.26 |
| February | 6.69 | 6.67 | 2.37 | 2.60 | 3.26 | 2.04 | 61.10 | 51.14 | 13.69 |
| March | 11.84 | 12.06 | 4.97 | 4.82 | 6.12 | 3.81 | 59.33 | 49.24 | 23.20 |
| April | 14.66 | 15.26 | 5.13 | 5.43 | 6.14 | 5.04 | 62.96 | 59.78 | 1.76 |
| May | 15.12 | 16.34 | 6.79 | 7.94 | 10.18 | 6.63 | 47.45 | 37.69 | 2.38 |
| June | 15.15 | 16.22 | 7.80 | 10.83 | 12.79 | 7.53 | 28.51 | 21.13 | 3.53 |
| July | 15.13 | 16.57 | 9.75 | 13.55 | 18.52 | 9.78 | 10.48 | −11.76 | −0.34 |
| August | 10.79 | 11.64 | 6.72 | 10.57 | 13.28 | 6.63 | 2.01 | −14.10 | 1.35 |
| September | 10.85 | 11.24 | 5.00 | 6.04 | 7.42 | 4.79 | 44.35 | 34.04 | 4.10 |
| October | 13.01 | 13.15 | 6.84 | 5.71 | 7.22 | 6.30 | 56.08 | 45.09 | 7.84 |
| November | 14.45 | 14.20 | 5.79 | 5.87 | 7.23 | 5.92 | 59.41 | 49.06 | −2.35 |
| December | 8.84 | 8.34 | 5.82 | 3.94 | 4.97 | 5.70 | 55.38 | 40.44 | 2.17 |
| RMSE/mm | |||||||
|---|---|---|---|---|---|---|---|
| ERLP | ERAP | CMFDP | TRMM | R-ERLP | R-ERAP | R-CMFD | |
| January | 3.98 | 3.72 | 6.94 | 4.28 | 3.46 | 5.15 | 6.34 |
| February | 5.75 | 5.90 | 2.52 | 5.43 | 2.84 | 3.70 | 2.13 |
| March | 13.11 | 13.41 | 5.96 | 7.86 | 5.77 | 7.04 | 4.59 |
| April | 16.18 | 16.87 | 6.46 | 8.59 | 6.16 | 6.97 | 6.30 |
| May | 13.09 | 14.12 | 7.94 | 8.03 | 8.09 | 10.12 | 7.55 |
| June | 13.52 | 14.29 | 7.91 | 13.30 | 12.63 | 12.26 | 7.47 |
| July | 15.80 | 17.07 | 9.51 | 15.18 | 13.92 | 18.14 | 9.62 |
| August | 11.73 | 12.62 | 7.09 | 9.55 | 12.23 | 12.06 | 7.02 |
| September | 8.43 | 8.55 | 4.90 | 6.85 | 5.35 | 6.70 | 4.77 |
| October | 12.64 | 12.81 | 8.51 | 9.06 | 6.18 | 8.17 | 8.21 |
| November | 10.77 | 10.42 | 5.77 | 8.78 | 6.70 | 8.45 | 5.94 |
| December | 6.56 | 6.33 | 5.96 | 6.53 | 4.39 | 5.55 | 5.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Jiapaer, G.; Yu, T.; Umuhoza, J.; Tu, H.; Chen, B.; Liang, H.; Lin, K.; Ju, T.; De Maeyer, P.; et al. Evaluating and Correcting Temperature and Precipitation Grid Products in the Arid Region of Altay, China. Remote Sens. 2024, 16, 283. https://doi.org/10.3390/rs16020283
Zhang L, Jiapaer G, Yu T, Umuhoza J, Tu H, Chen B, Liang H, Lin K, Ju T, De Maeyer P, et al. Evaluating and Correcting Temperature and Precipitation Grid Products in the Arid Region of Altay, China. Remote Sensing. 2024; 16(2):283. https://doi.org/10.3390/rs16020283
Chicago/Turabian StyleZhang, Liancheng, Guli Jiapaer, Tao Yu, Jeanine Umuhoza, Haiyang Tu, Bojian Chen, Hongwu Liang, Kaixiong Lin, Tongwei Ju, Philippe De Maeyer, and et al. 2024. "Evaluating and Correcting Temperature and Precipitation Grid Products in the Arid Region of Altay, China" Remote Sensing 16, no. 2: 283. https://doi.org/10.3390/rs16020283
APA StyleZhang, L., Jiapaer, G., Yu, T., Umuhoza, J., Tu, H., Chen, B., Liang, H., Lin, K., Ju, T., De Maeyer, P., & Van de Voorde, T. (2024). Evaluating and Correcting Temperature and Precipitation Grid Products in the Arid Region of Altay, China. Remote Sensing, 16(2), 283. https://doi.org/10.3390/rs16020283








