A New Waveform Design Method for Multi-Target Inverse Synthetic Aperture Radar Imaging Based on Orthogonal Frequency Division Multiplexing Chirp
Abstract
1. Introduction
- (i)
- Radar should form multiple beams, ensuring that each target can be illuminated simultaneously.
- (ii)
- The signals arriving at different targets should share the same bandwidth, avoiding a decrease in range resolution.
- (iii)
- The signals arriving at different targets should be approximately orthogonal, ensuring the separability of target echoes.
- (iv)
- The time cost of generating the transmit waveform should be minimized to satisfy the real-time request for ISAR imaging.
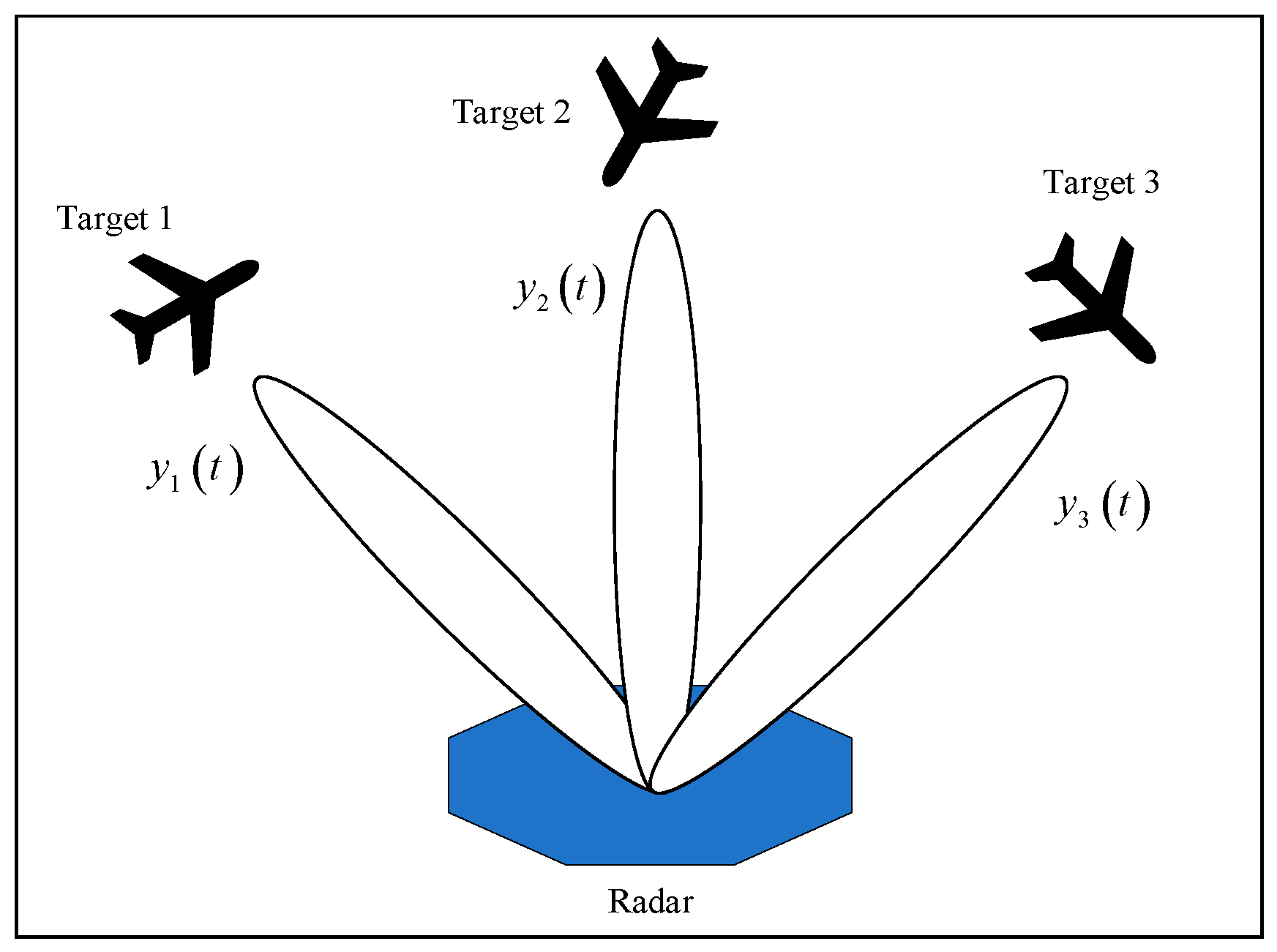
2. Problem Formulation
3. Multi-Target ISAR Imaging with 2D Orthogonal Waveform
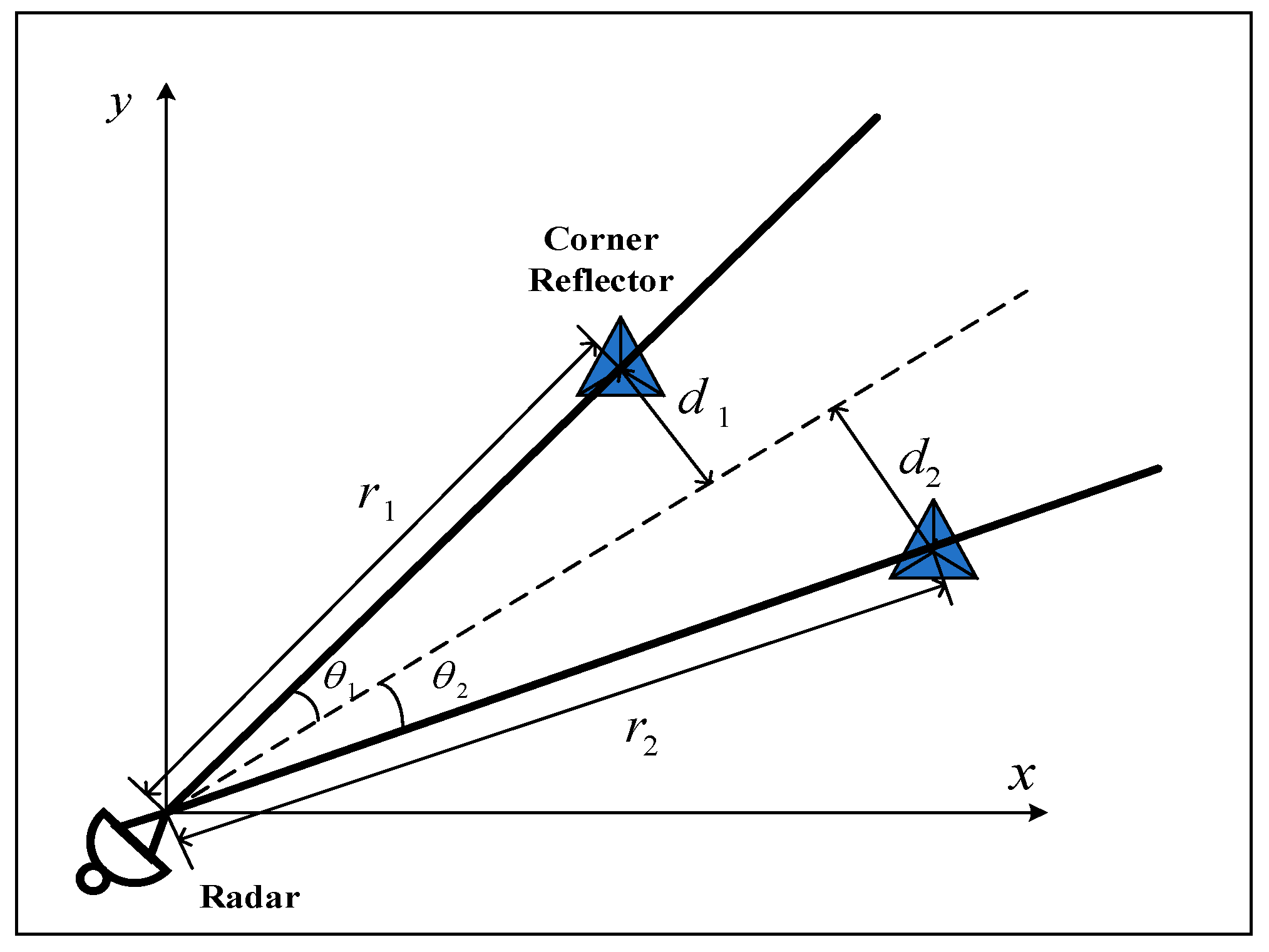
3.1. Principle of Waveform Design for Multi-Target ISAR Imaging
3.2. Waveform Design for Multi-Target Imaging with Non-Convex Optimization Algorithm
4. Fast Waveform Design Method for Multi-Target Imaging
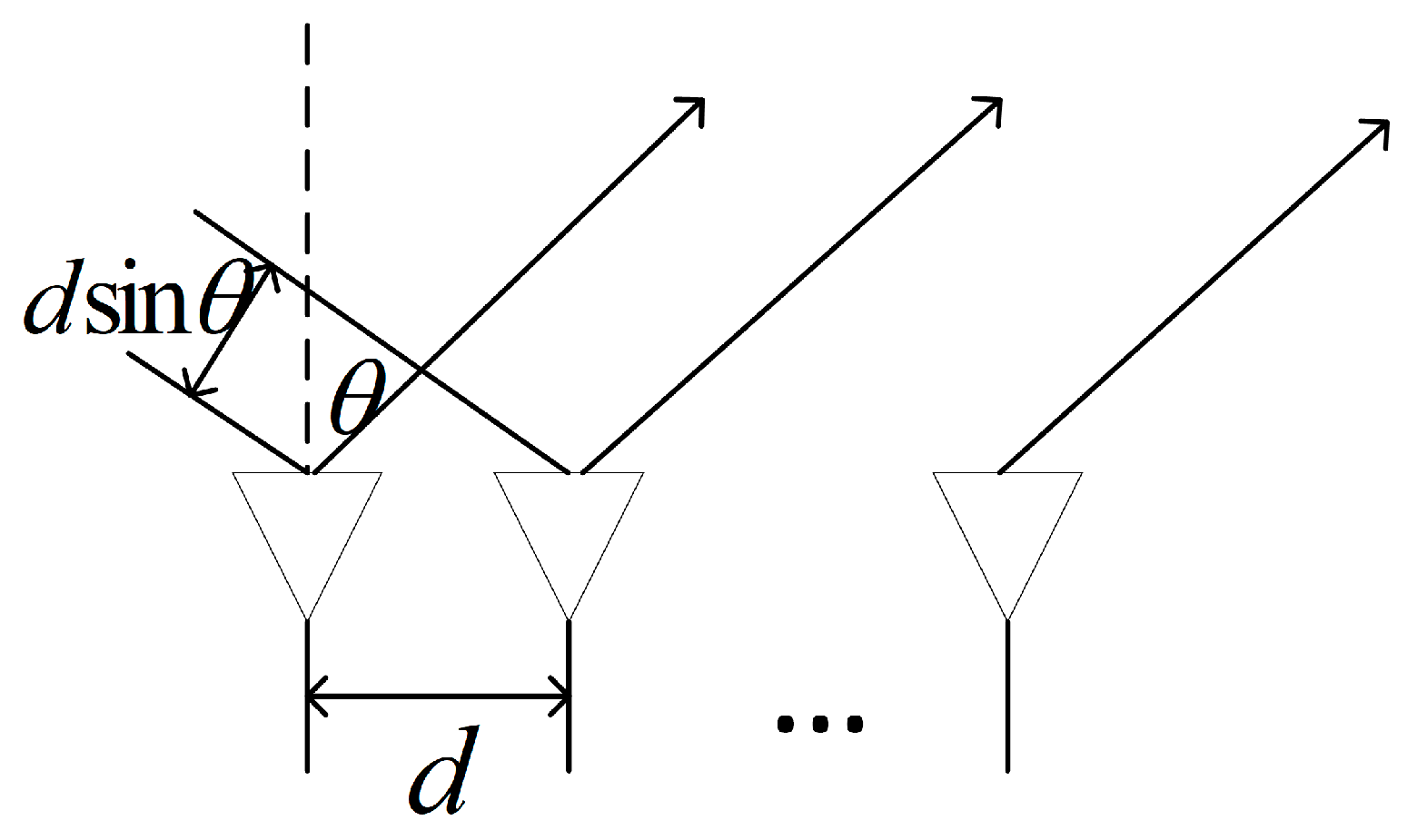
4.1. Multi-Beam Forming with Time-Variant Weighting
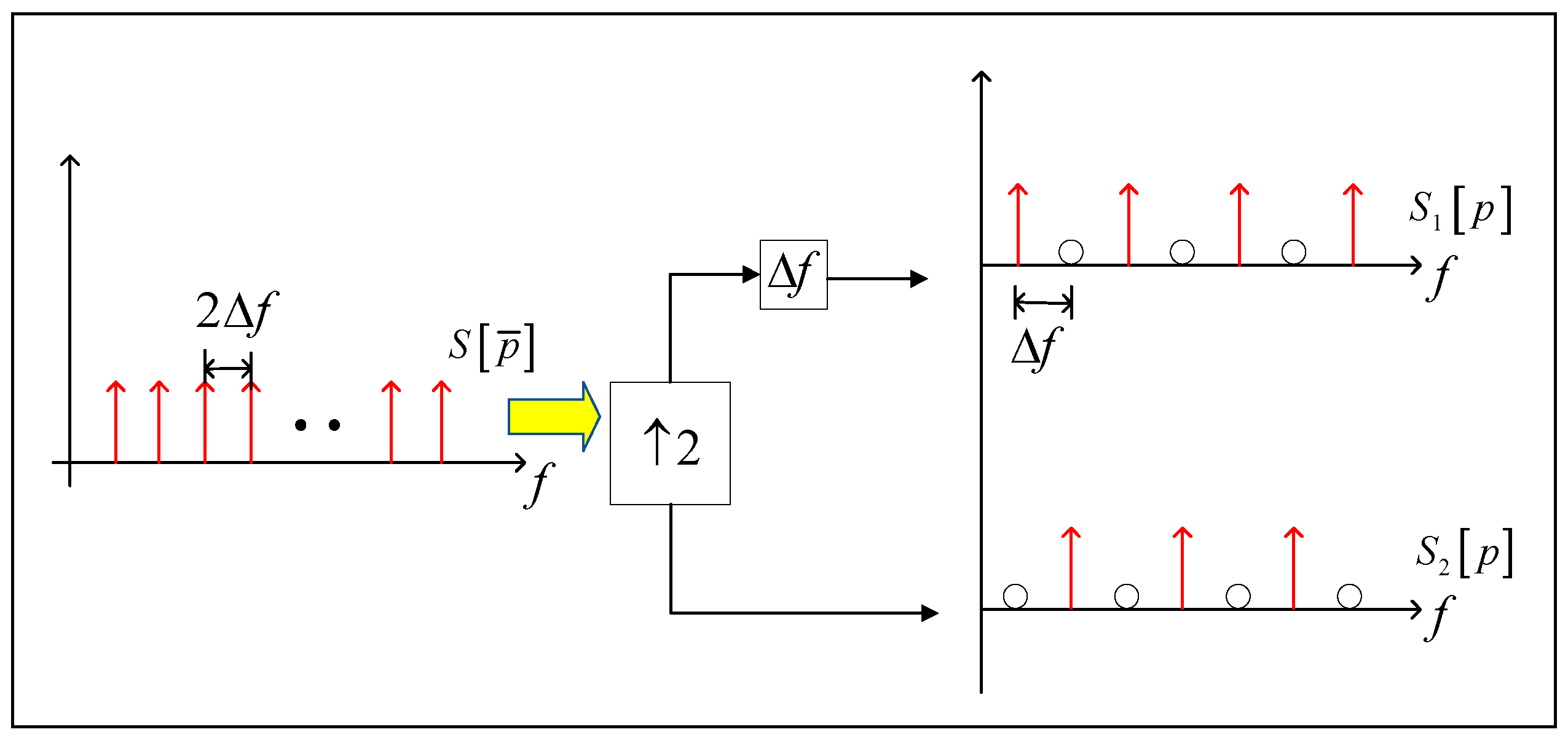
4.2. Orthogonal Waveform Generation with OFDM Modulation Based on Single DAR

4.3. Analysis of the Proposed Method for Multi-Target Imaging
- Time Complexity
- B.
- Constraints of the Proposed Method
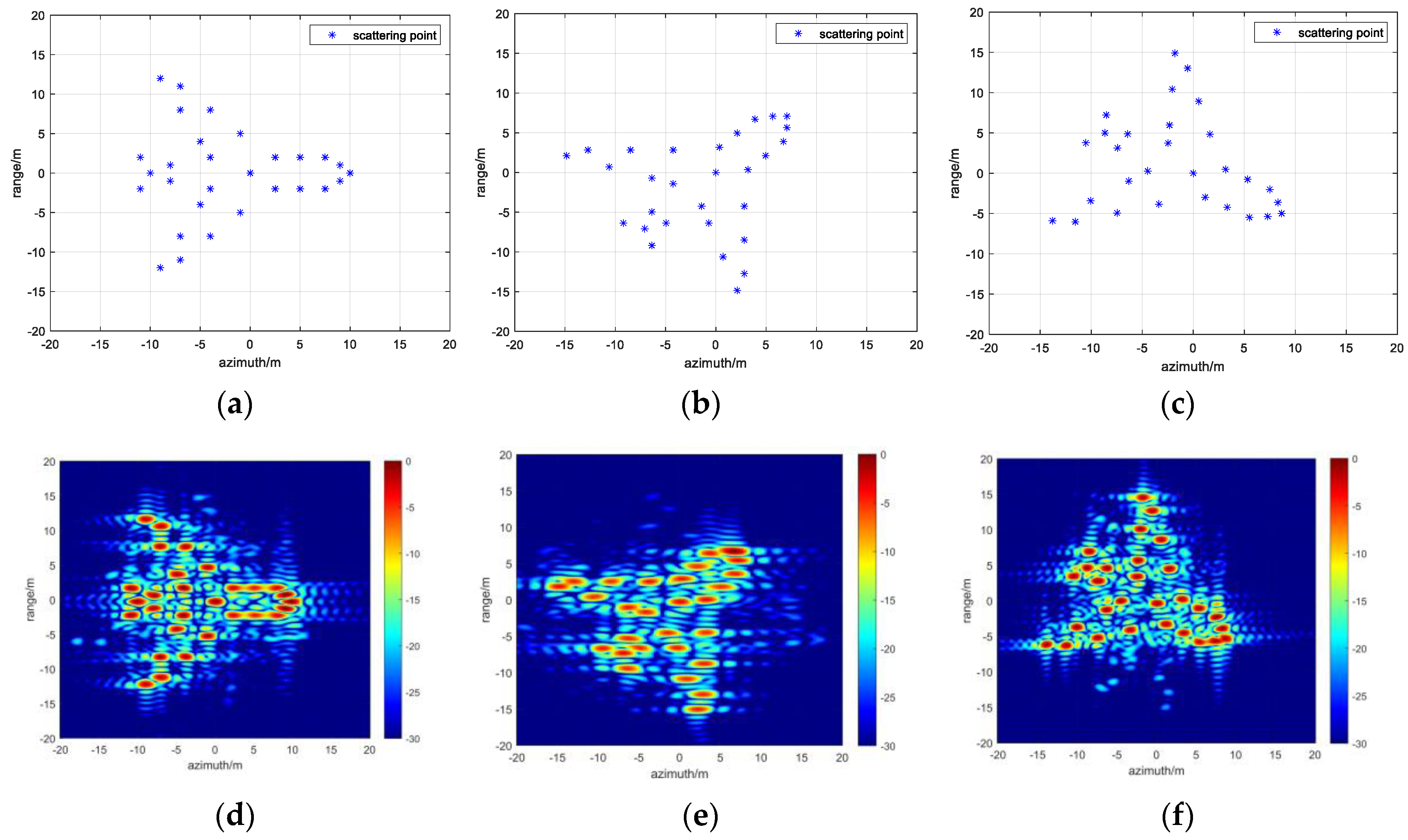
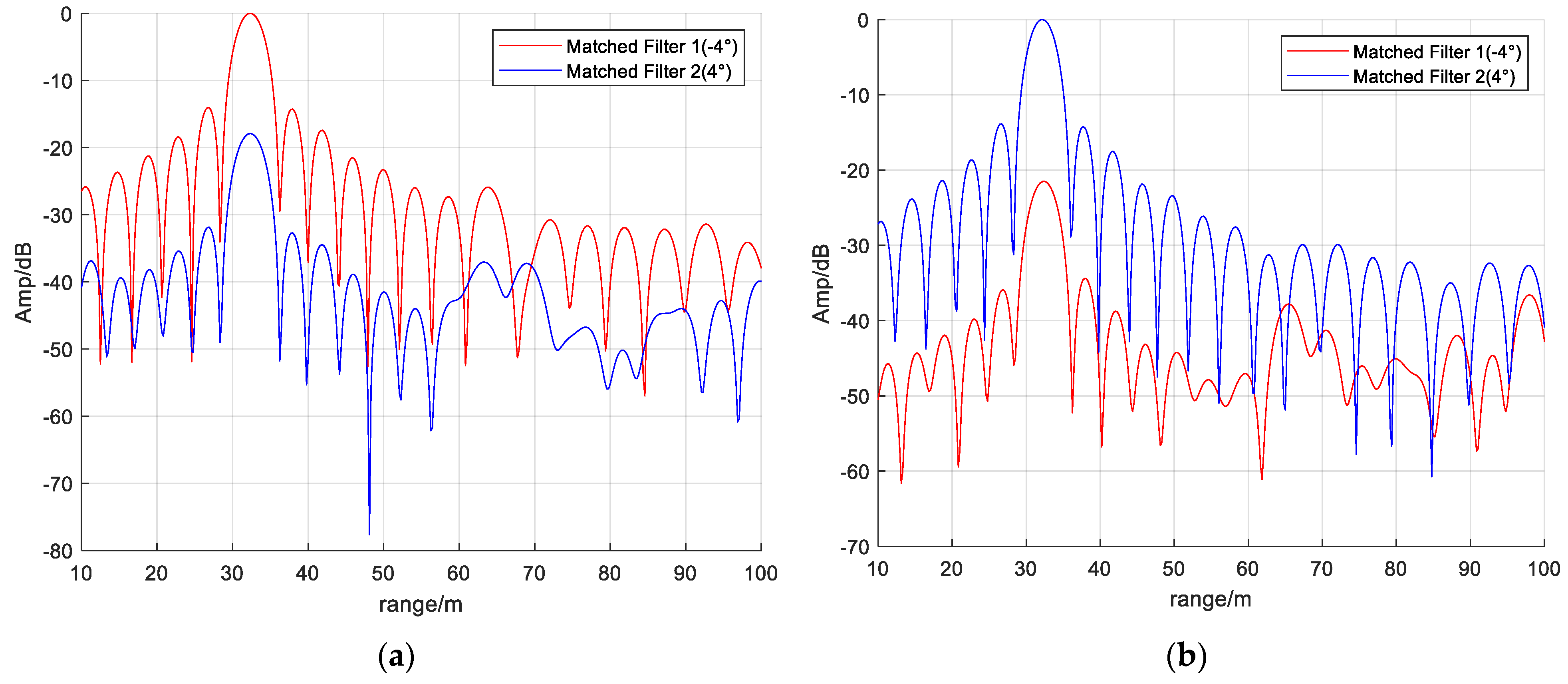
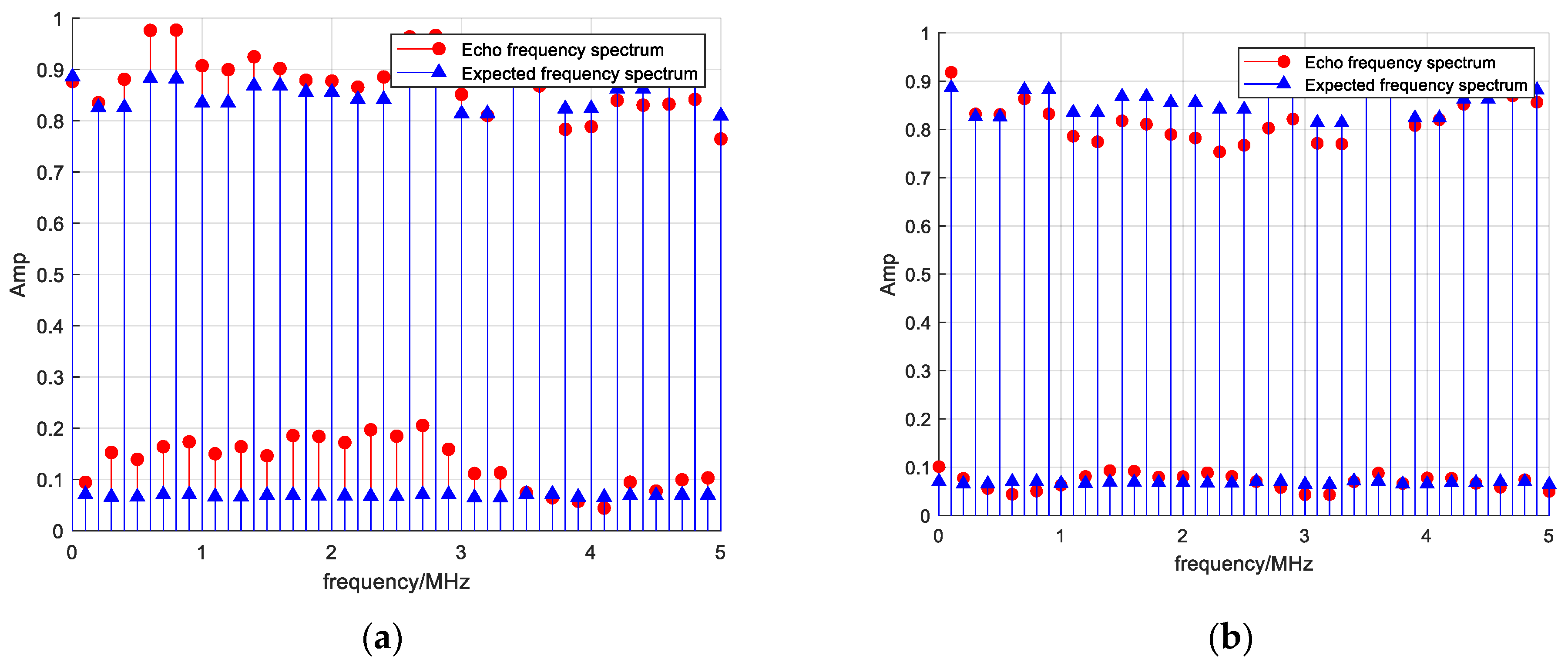
5. Experiments and Results
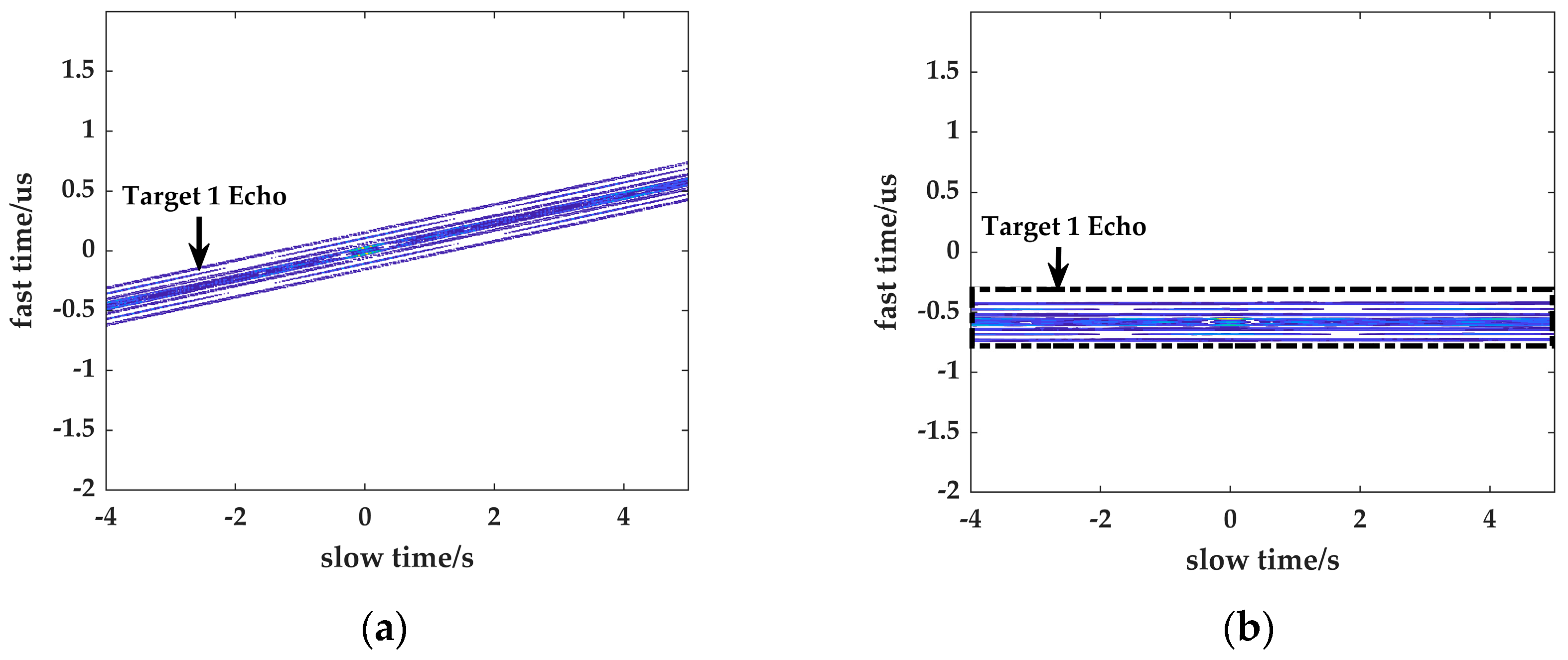
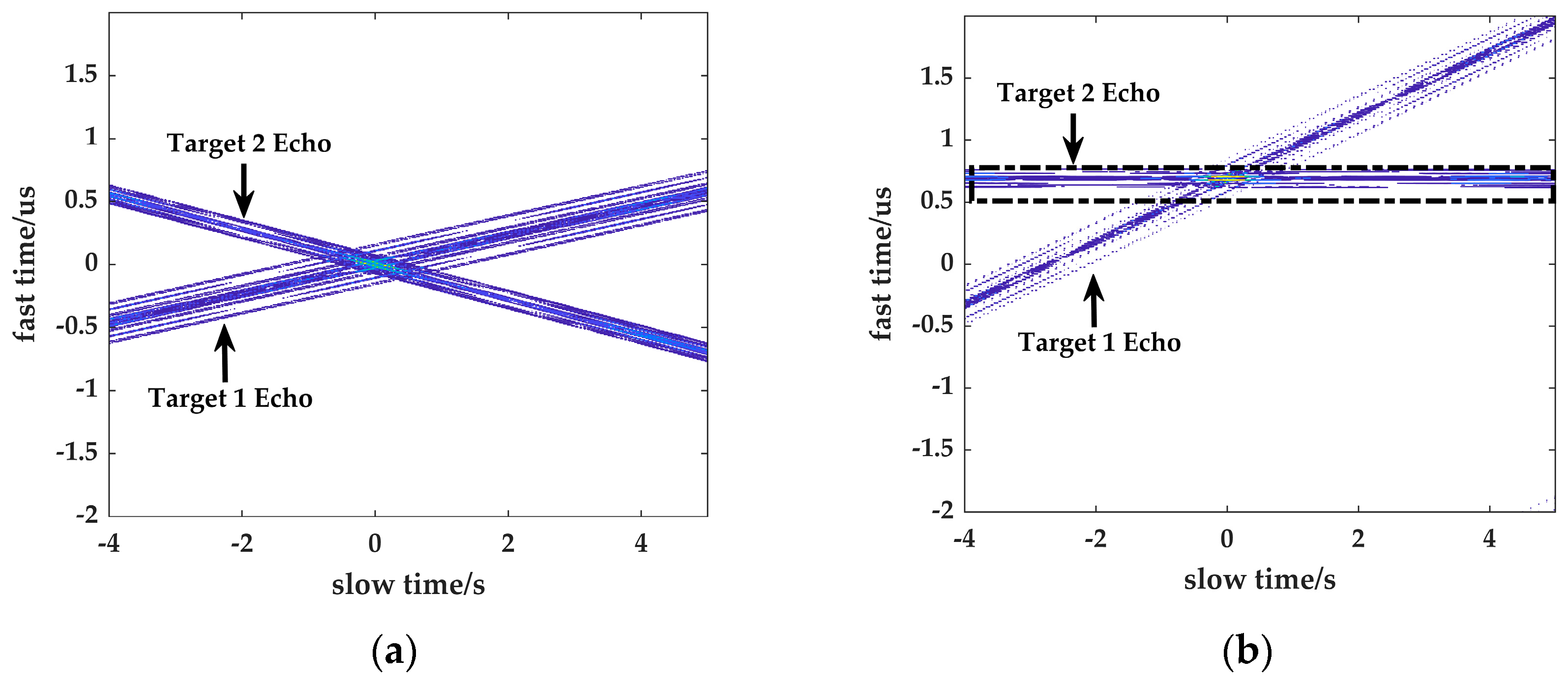
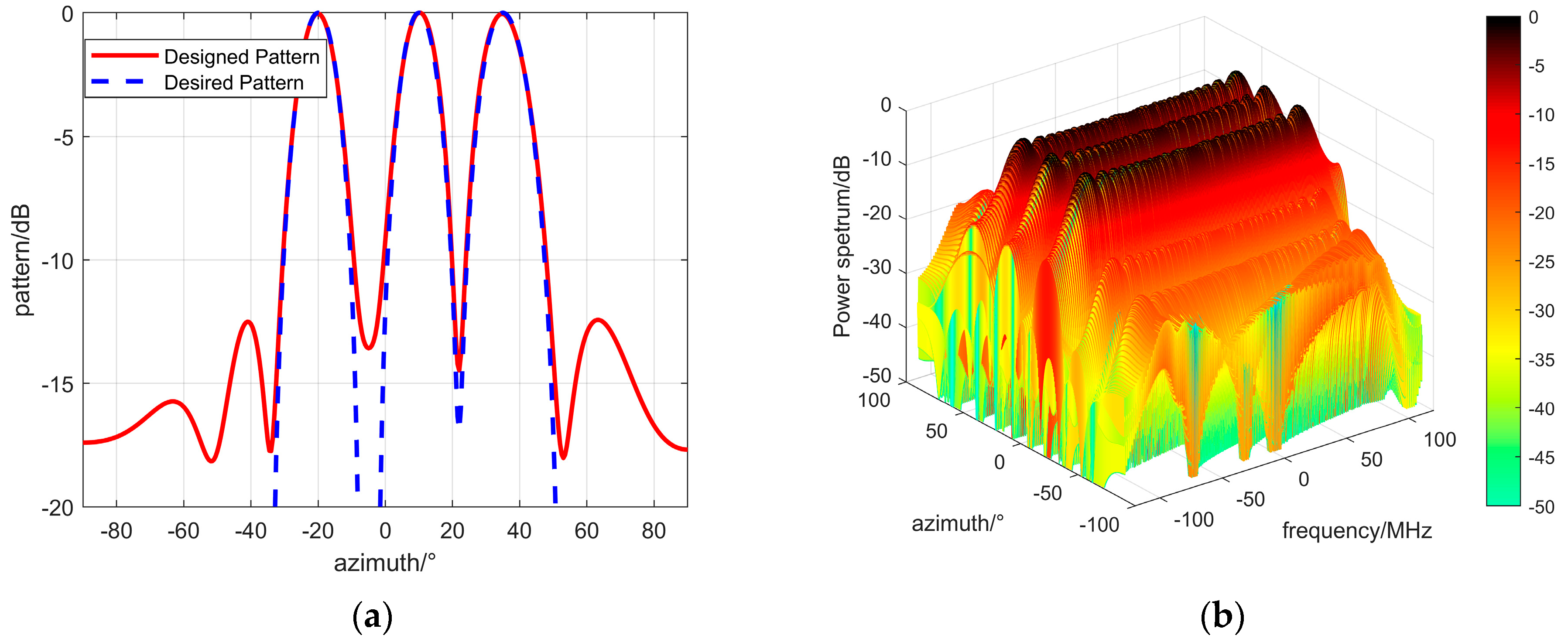
5.1. Validation of Transmit Waveform for Multi-Target Imaging
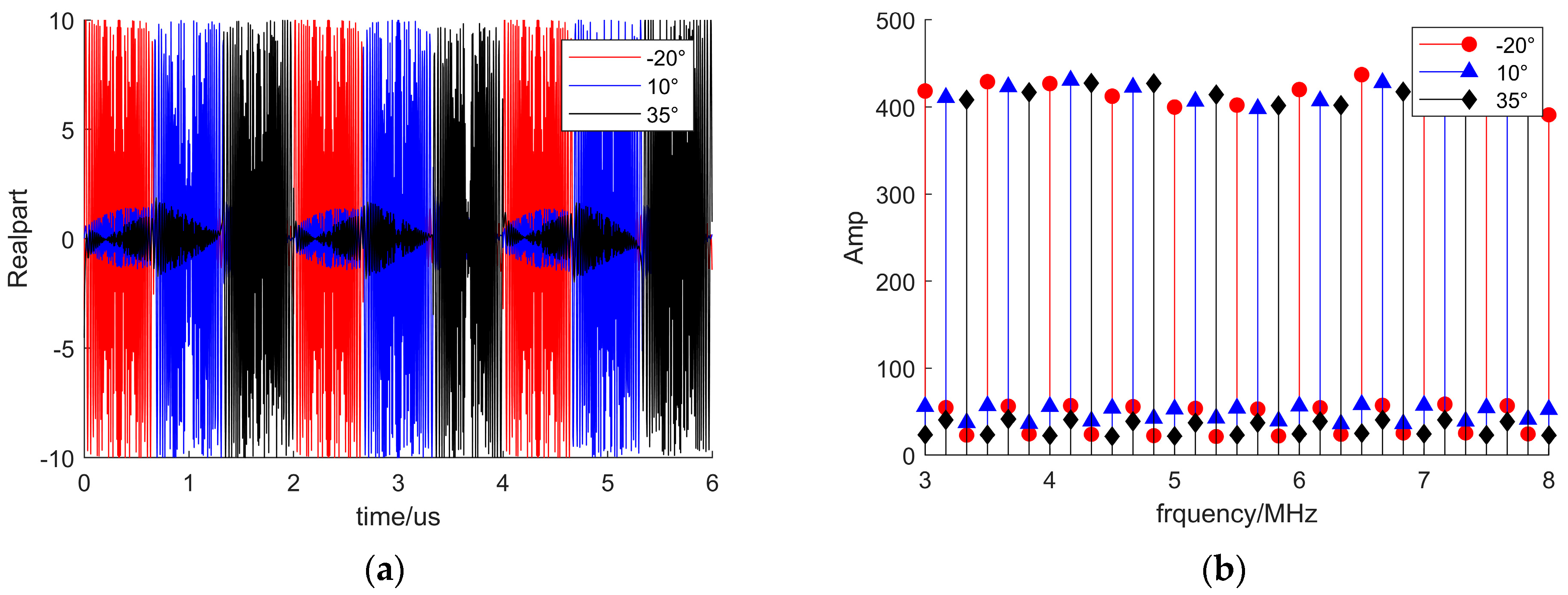
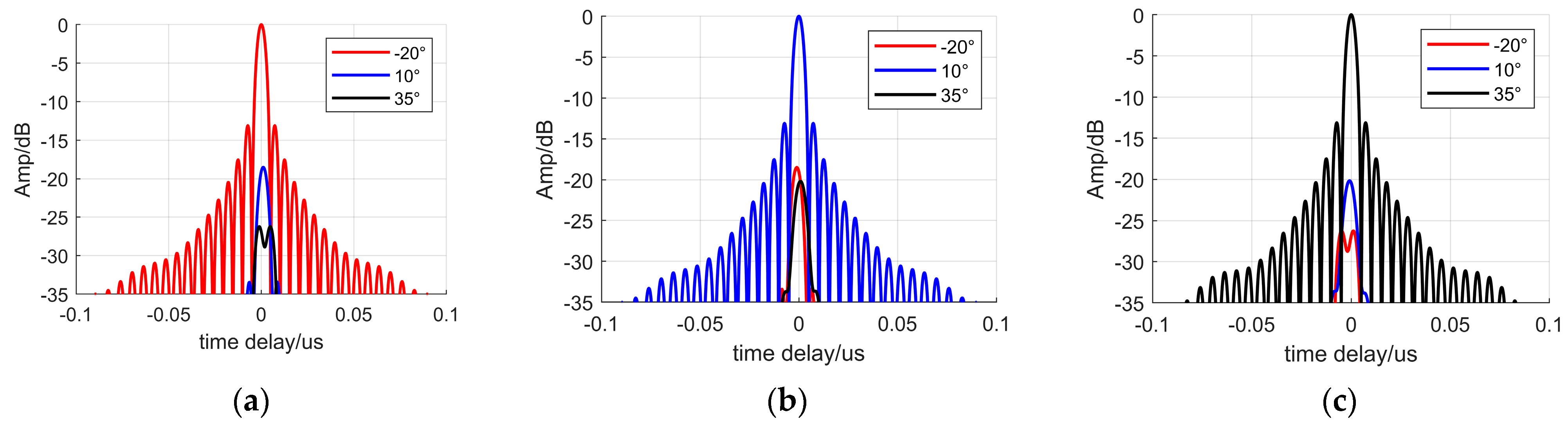
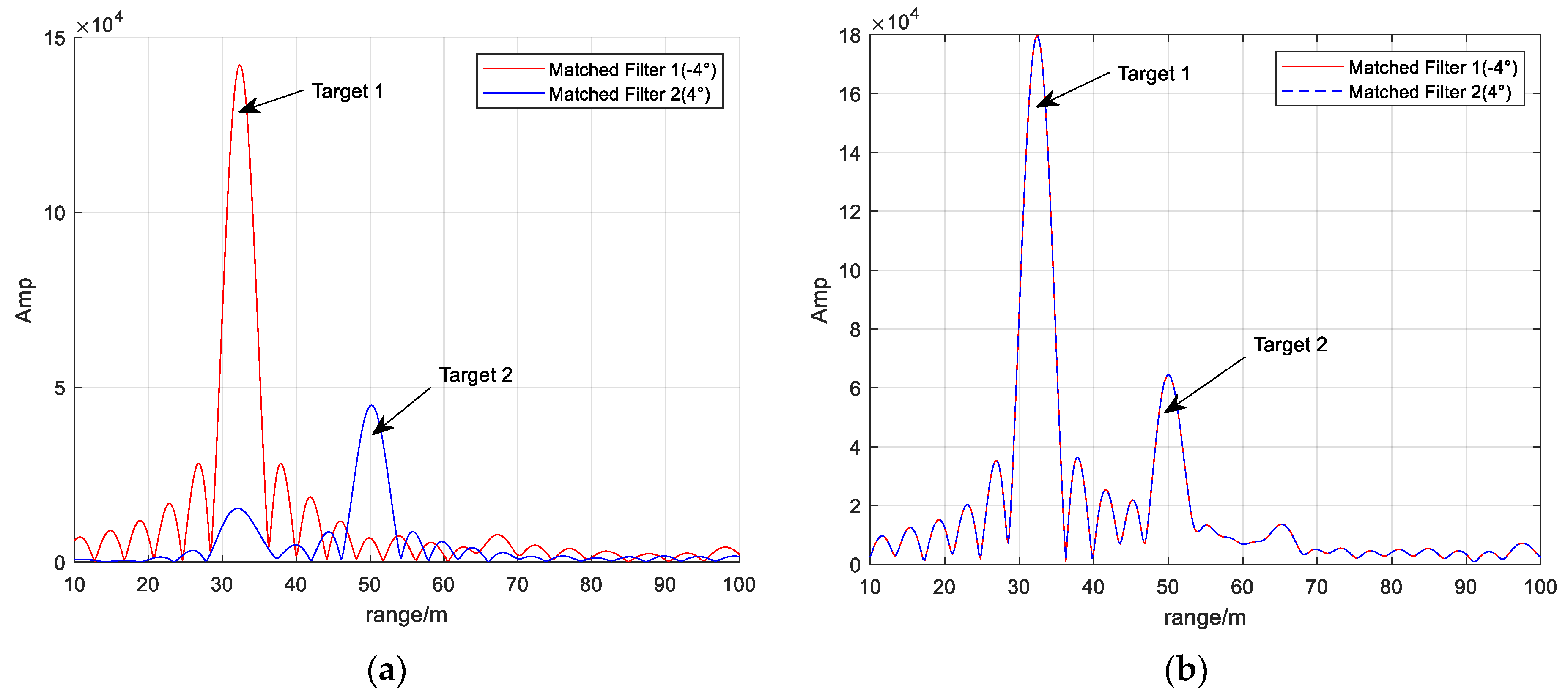
5.2. Experimental Verification of the Proposed Algorithm
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, H.-S.; Shin, B.-S.; Thomasson, J.A.; Wang, T.; Zhang, Z.; Han, X. Development of Multiple UAV Collaborative Driving Systems for Improving Field Phenotyping. Sensors 2022, 22, 1423. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, S.; Gong, F.; Wang, W.; Tian, H. Imaging of Moving Target for Cooperative Sar Between High-Orbit and Low-Orbit Satellites. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 597–600. [Google Scholar] [CrossRef]
- Zheng, H.; Jiu, B.; Liu, H. Waveform Design Based ECCM Scheme Against Interrupted Sampling Repeater Jamming for Wideband MIMO Radar in Multiple Targets Scenario. IEEE Sens. J. 2022, 22, 1652–1669. [Google Scholar] [CrossRef]
- Zhu, J.; Song, Y.; Jiang, N.; Xie, Z.; Fan, C.; Huang, X. Enhanced Doppler Resolution and Sidelobe Suppression Performance for Golay Complementary Waveforms. Remote Sens. 2023, 15, 2452. [Google Scholar] [CrossRef]
- Raei, E.; Alaee-Kerahroodi, M.; Babu, P.; Bhavani Shankar, M.R. Generalized waveform design for sidelobe reduction in MIMO radar systems. Signal Process. 2023, 206, 108914. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, H.; Song, Z.; Fan, H. Simultaneous ISAR imaging of group targets flying in formation. Chin. J. Aeronaut. 2014, 27, 1554–1561. [Google Scholar] [CrossRef]
- Chen, V.C.; Qian, S. Joint time-frequency transform for radar range-Doppler imaging. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 486. [Google Scholar] [CrossRef]
- Kong, L.; Zhang, W.; Zhang, S.; Zhou, B. Radon transform and the modified envelope correlation method for ISAR imaging of multi-target. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010; pp. 637–641. [Google Scholar]
- Xueru, B.; Feng, Z.; Mengdao, X.; Zheng, B. A Novel Method for Imaging of Group Targets Moving in a Formation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 221–231. [Google Scholar] [CrossRef]
- Xiao, D.; Su, F.; Wu, J. Multi-target ISAR imaging based on image segmentation and Short-time Fourier Transform. In Proceedings of the 2012 5th International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012; pp. 1832–1836. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, F.; Tao, M.; Zhang, Z. A Novel Method for Multi-Targets ISAR Imaging Based on Particle Swarm Optimization and Modified CLEAN Technique. IEEE Sens. J. 2016, 16, 97–108. [Google Scholar] [CrossRef]
- Li, H.; Su, F. A Multi-Target ISAR Imaging Method Based on Zhang-Suen Thinning and Radon Transform. In Proceedings of the 2022 15th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Beijing, China, 5–7 November 2022; pp. 1–5. [Google Scholar]
- Zhang, Y.; Xu, N.; Li, N.; Guo, Z. A Multi-Domain Joint Novel Method for ISAR Imaging of Multi-Ship Targets. Remote Sens. 2023, 15, 4878. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Liu, R.; Ding, J.; Zhang, P.; Xing, M. Joint Translational Motion Compensation for Multitarget ISAR Imaging Based on Integrated Kalman Filter. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5108716. [Google Scholar] [CrossRef]
- Li, G.; Hou, Q.; Xu, S.; Chen, Z. Multi-target simultaneous ISAR imaging based on compressed sensing. EURASIP J. Adv. Signal Process. 2016, 2016, 27. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Q.; Yuan, N.; Luo, Y.; Lou, H. An Adaptive ISAR-Imaging-Considered Task Scheduling Algorithm for Multi-Function Phased Array Radars. IEEE Trans. Signal Process. 2015, 63, 5096–5110. [Google Scholar] [CrossRef]
- Stoica, P.; Jian, L.; Yao, X. On Probing Signal Design for MIMO Radar. IEEE Trans. Signal Process. 2007, 55, 4151–4161. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J.; Zhu, X. Waveform Synthesis for Diversity-Based Transmit Beampattern Design. IEEE Trans. Signal Process. 2008, 56, 2593–2598. [Google Scholar] [CrossRef]
- Zheng, H.; Jiu, B.; Li, K.; Liu, H. Joint Design of the Transmit Beampattern and Angular Waveform for Colocated MIMO Radar under a Constant Modulus Constraint. Remote Sens. 2021, 13, 3392. [Google Scholar] [CrossRef]
- He, H.; Stoica, P.; Li, J. Wideband MIMO Systems: Signal Design for Transmit Beampattern Synthesis. IEEE Trans. Signal Process. 2011, 59, 618–628. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Jiu, B.; Yan, J.; Wu, M.; Bao, Z. Wideband MIMO Radar Waveform Design for Multiple Target Imaging. IEEE Sens. J. 2016, 16, 8545–8556. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Yang, J.; Kong, L. Wideband MIMO radar beampattern shaping with space-frequency nulling. Signal Process. 2019, 160, 80–87. [Google Scholar] [CrossRef]
- Zou, X.; Jin, G.; He, F.; Zhang, Y. A Novel MIMO Radar Waveform Design Method for Multi-Target ISAR Imaging. In Proceedings of the 2023 6th International Conference on Electronics Technology (ICET), Chengdu, China, 12–15 May 2023; pp. 1371–1375. [Google Scholar] [CrossRef]
- Chu, C.; Chen, Y.; Luo, Y.; Zhang, Q. Wideband MIMO Radar Waveform Design Under Multiple Criteria. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3298098. [Google Scholar] [CrossRef]
- Chen, Y.J.; Zhang, Q.; Luo, Y.; Li, K.M. Multi-Target Radar Imaging Based on Phased-MIMO Technique—Part II: Adaptive Resource Allocation. IEEE Sens. J. 2017, 17, 6198–6209. [Google Scholar] [CrossRef]
- Zhang, M.; Liao, G.; Xu, J.; Lan, L.; Deng, K. ISAR Imaging of Multiple Targets with Time-Delay Receive Array. IEEE Access 2020, 8, 199759–199767. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Luo, Y.; Li, K.M.; Liu, X.W. Task Scheduling for Multi-Target ISAR Imaging in Radar Network. IEEE Access 2020, 8, 46092–46101. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Luo, Y.; Liu, X.; Ni, J.; Su, L. Joint Optimization of Time and Aperture Resource Allocation Strategy for Multi-Target ISAR Imaging in Radar Sensor Network. IEEE Sens. J. 2021, 21, 19570–19581. [Google Scholar] [CrossRef]
- Liu, X.W.; Zhang, Q.; Luo, Y.; Chen, Y.J.; Lu, X. ISAR Imaging Task Allocation for Multi-Target in Radar Network Based on Potential Game. IEEE Sens. J. 2019, 19, 11192–11204. [Google Scholar] [CrossRef]
- Kim, J.H.; Younis, M.; Moreira, A.; Wiesbeck, W. A Novel OFDM Chirp Waveform Scheme for Use of Multiple Transmitters in SAR. IEEE Geosci. Remote Sens. Lett. 2013, 10, 568–572. [Google Scholar] [CrossRef]





| Algorithms | Time Complexity |
|---|---|
| This paper | |
| CG algorithm in paper [21] | |
| IOA algorithm in paper [22] | |
| IOA algorithm in paper [23] |
| Parameters | Value |
|---|---|
| Number of antennas | 10 |
| Carrier frequency | 1 GHz |
| Signal bandwidth | 200 MHz |
| Sampling frequency | 240 MHz |
| Pulse Duration | 6 μs |
| Discrete azimuth number | 361 |
| Target number | 3 |
| Target azimuth | [−20°, 10°, 35°] |
| Mixed Echo | Separation in This Paper (dB) | Separation in Paper [23] (dB) | Separation in Spatial Filtering (dB) |
|---|---|---|---|
| −20° and 10° | −18.5 | −18.4 | −17.6 |
| 10° and 35° | −20.2 | −20.8 | −19.9 |
| −20° and 35° | −26.7 | −26.9 | −25.9 |
| Signal Length (μs) | Time Overhead in Paper [23] (s) | Time Overhead in This Paper (s) |
|---|---|---|
| 4 | 0.721 | 0.0167 |
| 8 | 4.108 | 0.0175 |
| 12 | 13.141 | 0.0178 |
| 16 | 43.209 | 0.0186 |
| Parameters | Value |
|---|---|
| Number of antennas | 4 |
| Carrier frequency | 17 GHz |
| Signal bandwidth | 40 MHz |
| Signal duration | 10 μs |
| Sampling frequency | 80 MHz |
| Element spacing | 60 mm |
| Pulse repetition frequency (PRF) | 1000 Hz |
| Target azimuth | [−4°, 4°] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, X.; Jin, G.; He, F.; Zhang, Y. A New Waveform Design Method for Multi-Target Inverse Synthetic Aperture Radar Imaging Based on Orthogonal Frequency Division Multiplexing Chirp. Remote Sens. 2024, 16, 308. https://doi.org/10.3390/rs16020308
Zou X, Jin G, He F, Zhang Y. A New Waveform Design Method for Multi-Target Inverse Synthetic Aperture Radar Imaging Based on Orthogonal Frequency Division Multiplexing Chirp. Remote Sensing. 2024; 16(2):308. https://doi.org/10.3390/rs16020308
Chicago/Turabian StyleZou, Xuebo, Guanghu Jin, Feng He, and Yongsheng Zhang. 2024. "A New Waveform Design Method for Multi-Target Inverse Synthetic Aperture Radar Imaging Based on Orthogonal Frequency Division Multiplexing Chirp" Remote Sensing 16, no. 2: 308. https://doi.org/10.3390/rs16020308
APA StyleZou, X., Jin, G., He, F., & Zhang, Y. (2024). A New Waveform Design Method for Multi-Target Inverse Synthetic Aperture Radar Imaging Based on Orthogonal Frequency Division Multiplexing Chirp. Remote Sensing, 16(2), 308. https://doi.org/10.3390/rs16020308






