Downlink Analysis of a Low-Earth Orbit Satellite Considering an Airborne Interference Source Moving on Various Trajectory
Abstract
:1. Introduction
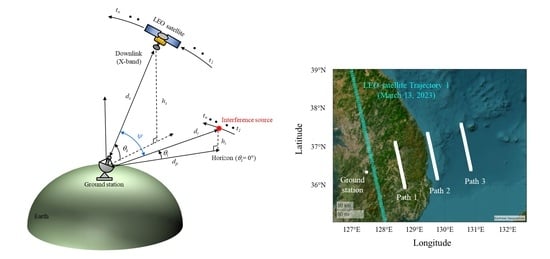
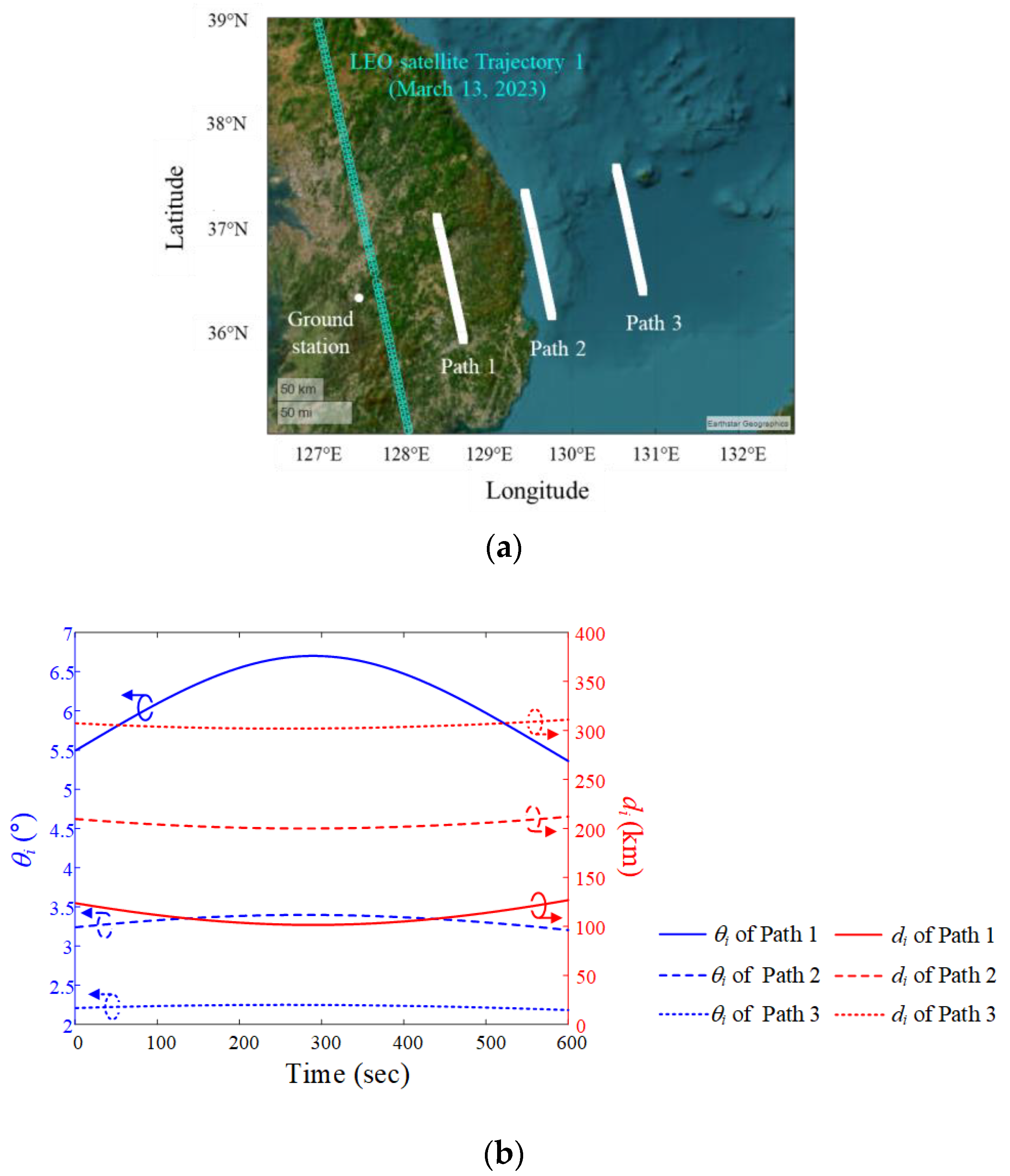
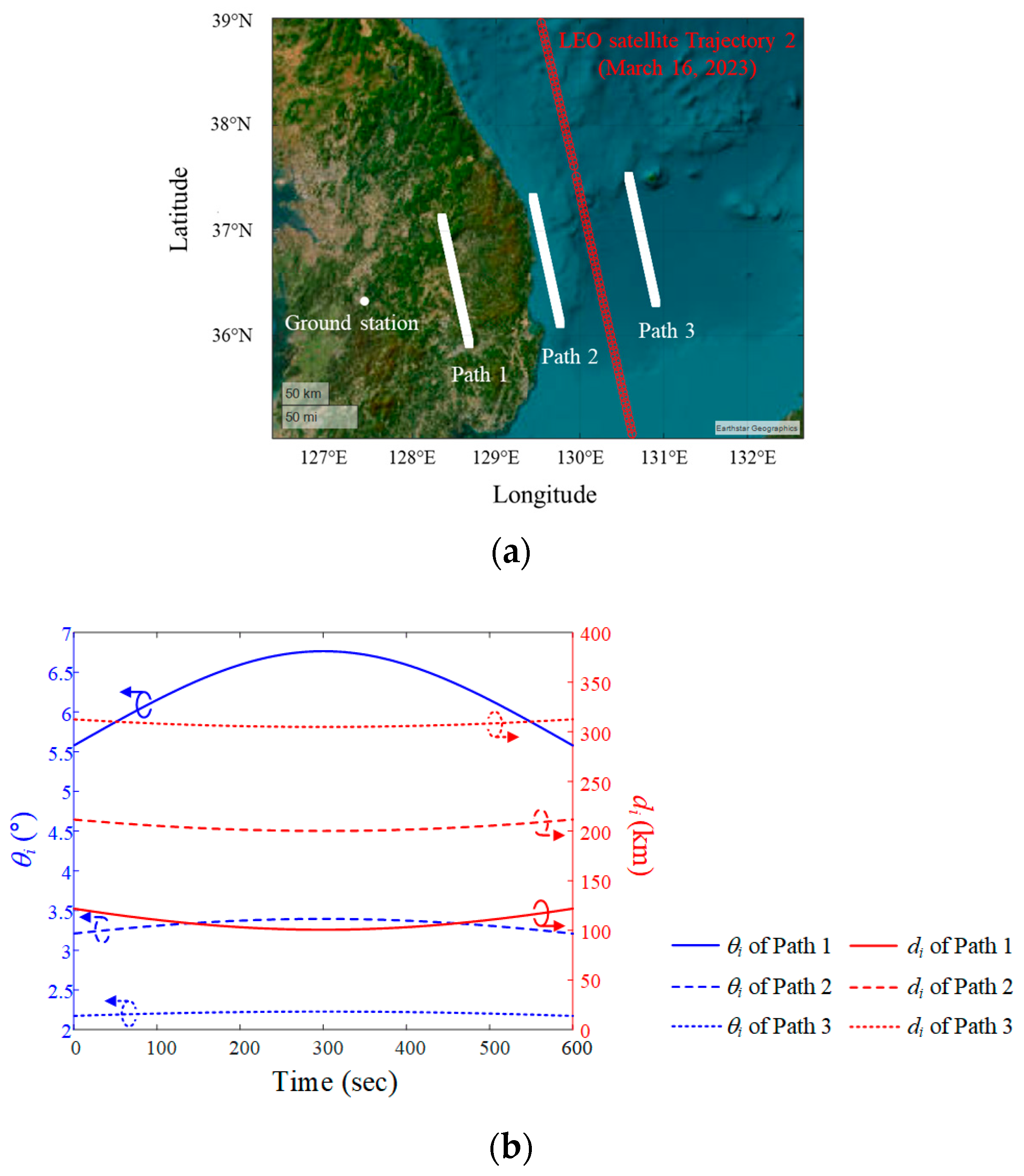
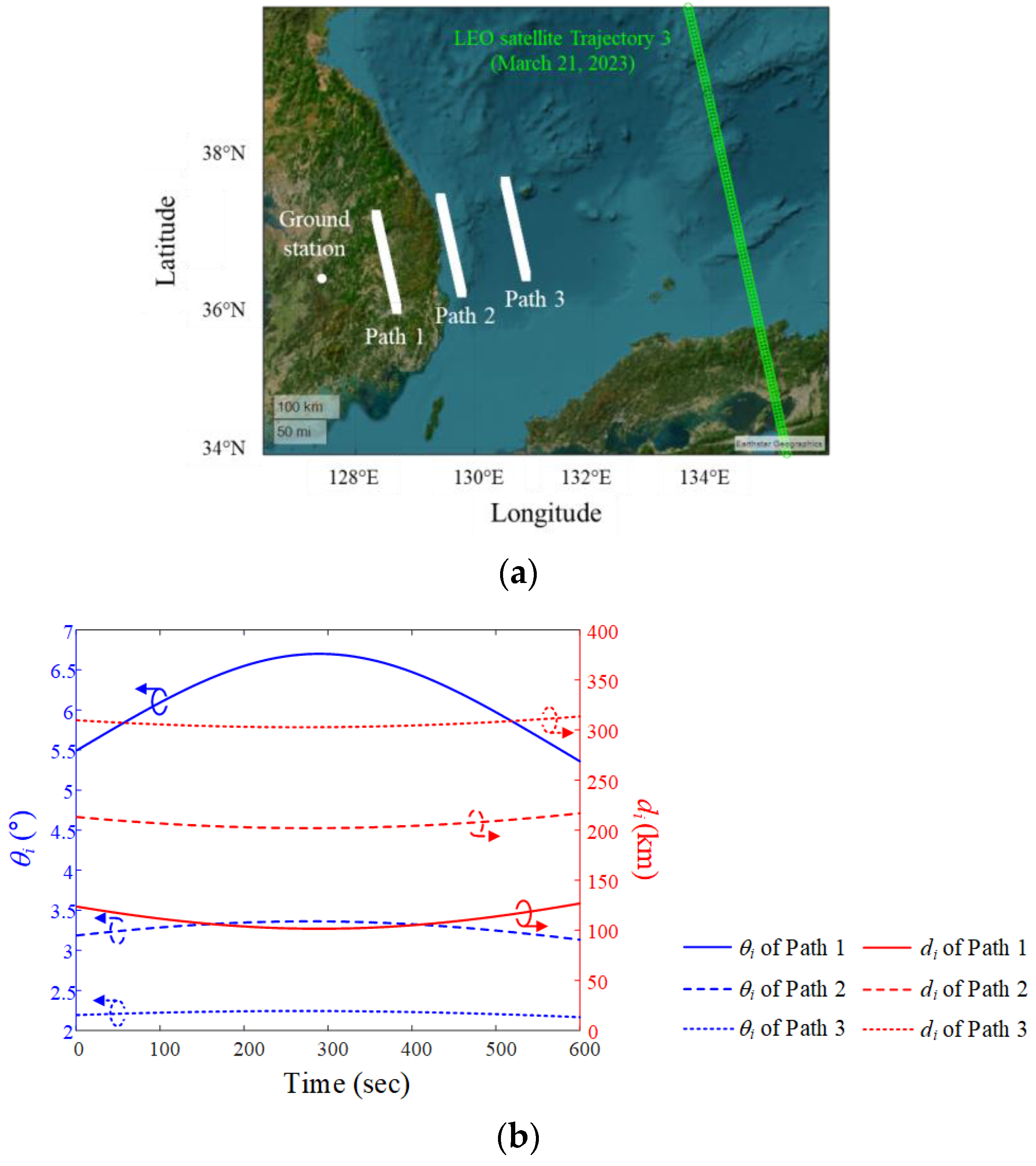
2. Scenario of Interference Source Moving along the Satellite Trajectory
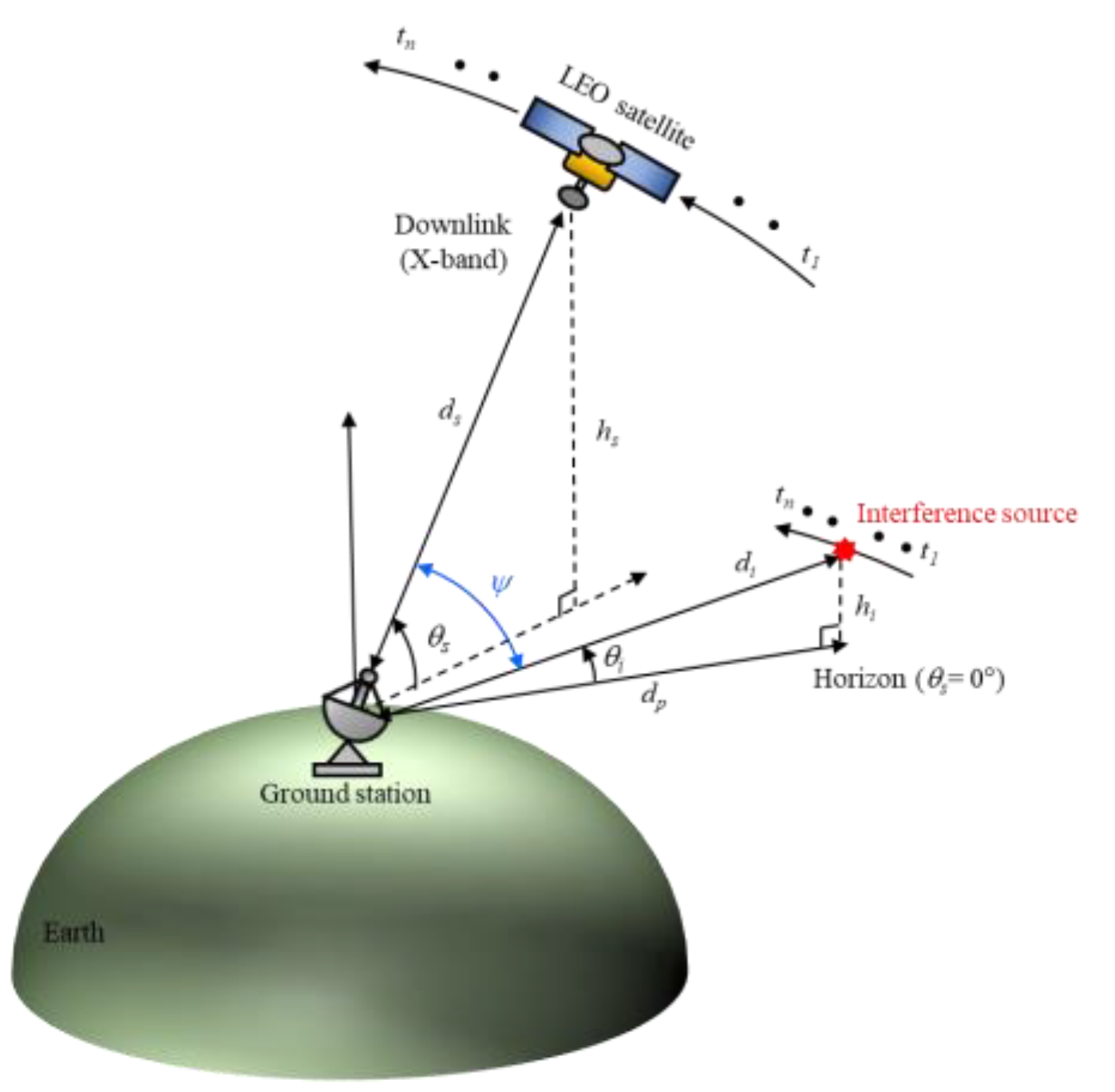
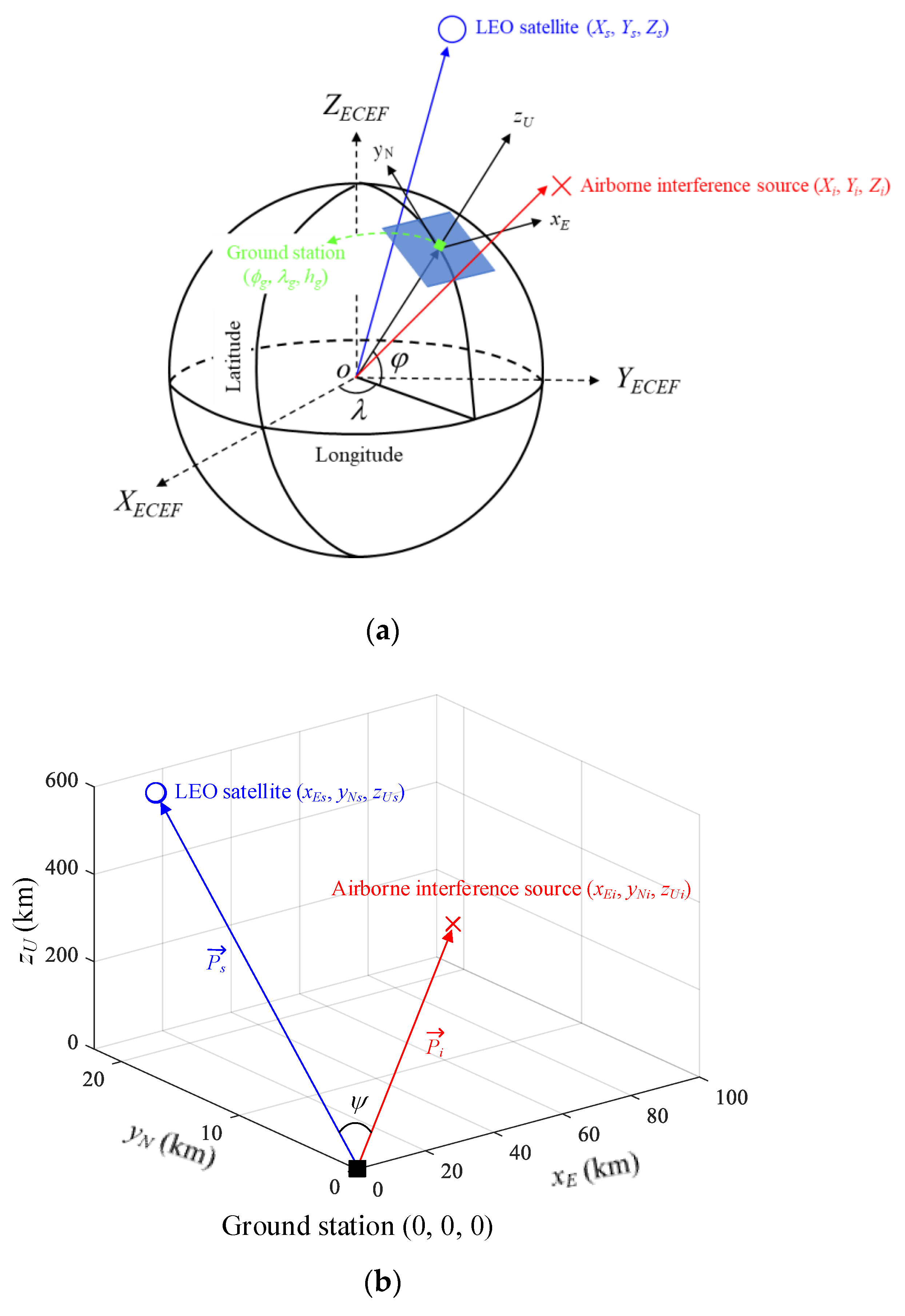
2.1. LEO Satellite Downlink Scenario and J/S Ratio Calculation
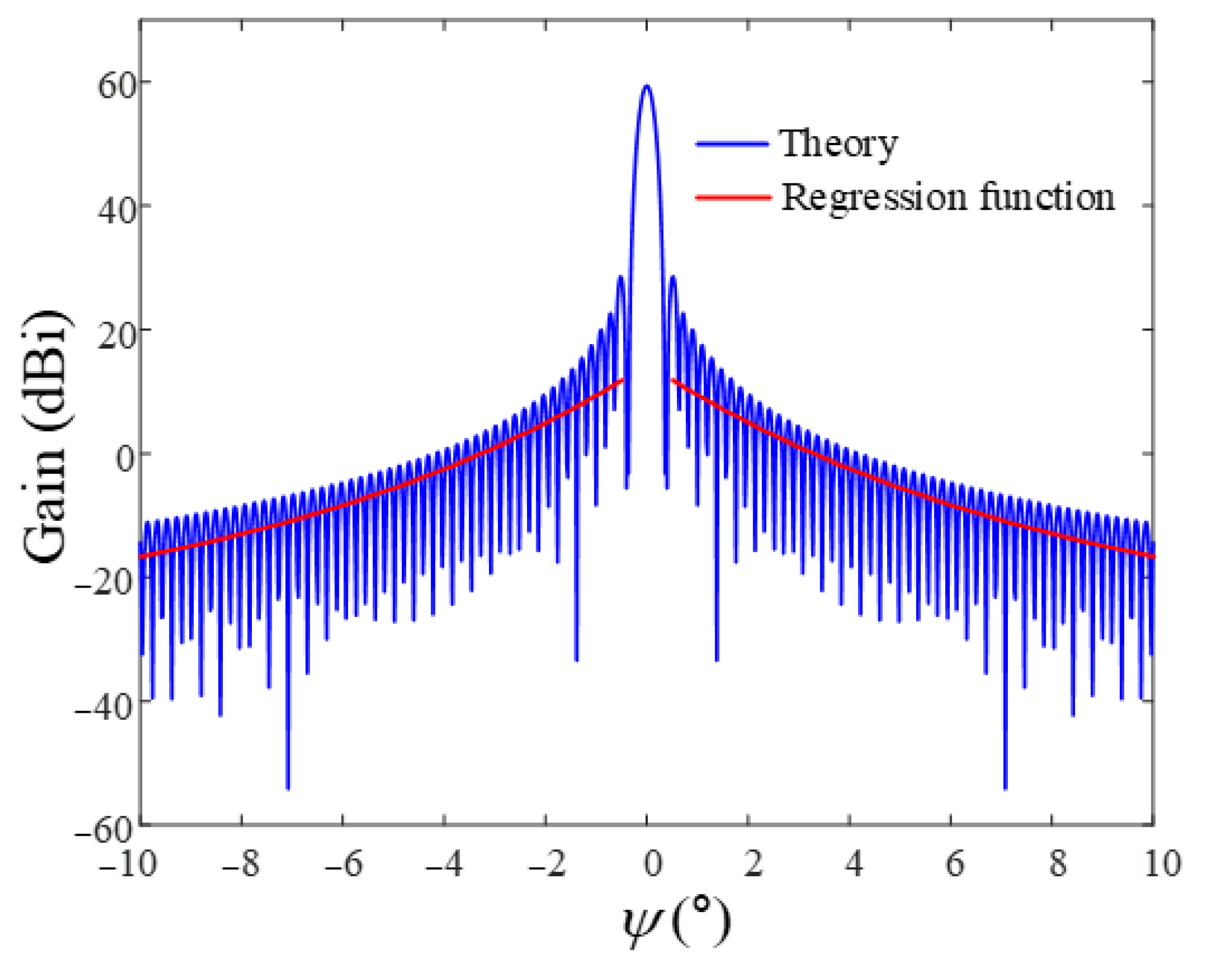
2.2. Derivation of Relative Angle Difference ψ with Sidelobe Gain
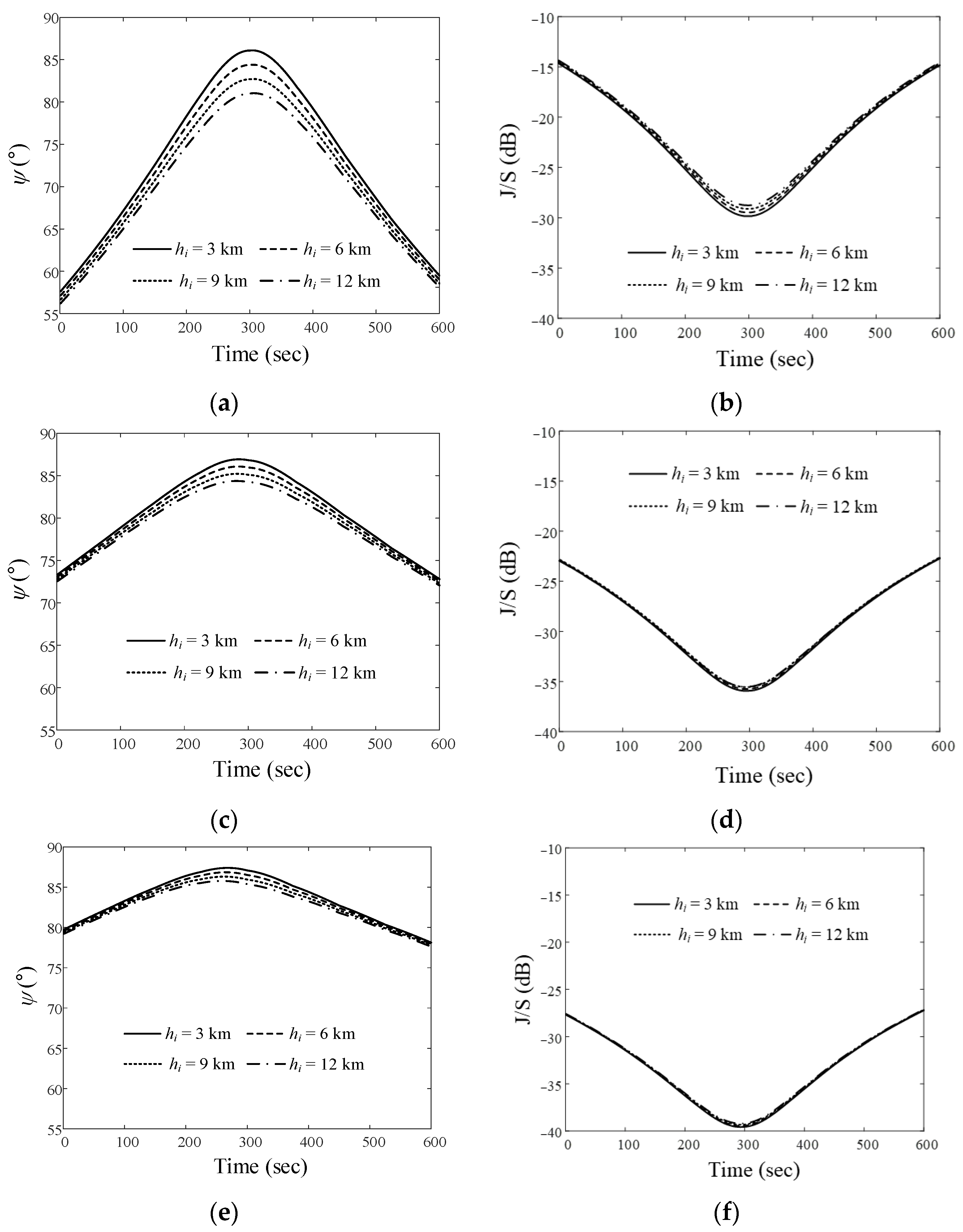
3. Analysis of the LEO Satellite Downlinks in Interference Situations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, M.J.; Lim, S.; Shin, D.C. Analysis method for determining optimal synthetic aperture time using estimated range and doppler cone angle at the center of synthetic aperture length. J. Electromagn. Eng. Sci. 2023, 23, 205–211. [Google Scholar] [CrossRef]
- Kang, Y.G.; Kim, C.K.; Park, S.O. Ocean image formation algorithm using altimeter data for next generation satellite SAR. J. Electromagn. Eng. Sci. 2022, 22, 85–94. [Google Scholar] [CrossRef]
- Lewark, U.J.; Antes, J.; Walheim, J.; Timmermann, J.; Zwick, T.; Kallfass, I. Link budget analysis for future E-band gigabit satellite communication links (71–76 and 81–84 Ghz). CEAS Space J. 2013, 4, 41–46. [Google Scholar] [CrossRef]
- Cakaj, S.; Malarić, K. Rigorous analysis on performance of LEO satellite ground station in urban environment. Int. J. Satell. Commun. Netw. 2007, 25, 619–643. [Google Scholar] [CrossRef]
- Li, S.Y.; Liu, C.H. Modeling the effects of ionospheric scintillations on LEO satellite communications. Int. J. Satell. Commun. Netw. 2004, 8, 147–149. [Google Scholar] [CrossRef]
- Kilcoyne, D.K.; Rowe, S.A.; Headley, W.C.; Mortensen, D.J.; McGwier, R.W.; Leffke, Z.J.; Reinhart, R.C. Link adaptation for mitigating earth-to-space propagation effects on the NASA scan testbed. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016. [Google Scholar]
- Barbarić, D.; Vuković, J.; Babic, D. Link budget analysis for a proposed Cubesat Earth observation mission. In Proceedings of the 2018 41st International Convention on Information and Communication Technology, Opatija, Croatia, 21–25 May 2018; pp. 133–138. [Google Scholar]
- Reiten, K.; Schlanbusch, R.; Kristiansen, R.; Vedal, F.; Nicklasson, P.J.; Berntsen, P.C. Link and doppler analysis for space-based AIS reception. In Proceedings of the 2007 3rd International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 14–16 June 2007; pp. 556–561. [Google Scholar]
- Xu, H.; Zhang, J.; Sun, Z.; Yang, H. Event-based wireless tracking control for a wheeled mobile robot against reactive jamming Attacks. IEEE Trans. Control Netw. Syst. 2023, 10, 1925–1936. [Google Scholar] [CrossRef]
- Lineswala, P.L.; Shah, S.N.; Shah, R. Different categorization for jammer: The enemy of satellite navigation. In Proceedings of the 2017 2nd International Conference for Convergence in Technology (I2CT), Mumbai, India, 7–9 April 2017; pp. 282–287. [Google Scholar]
- Sathaye, H.; Noubir, G.; Ranganathan, A. On the implications of spoofing and jamming aviation datalink applications. In Proceedings of the 38th Annual Computer Security Applications Conference, Austin, TX, USA, 5–9 December 2022; pp. 548–560. [Google Scholar]
- Senapati, M.; Anand, B.; Barsaiyan, V.; Rajalakshmi, P. Geo-referencing system for locating objects globally in LiDAR point cloud. In Proceedings of the 2020 IEEE 6th World Forum on Internet of Things (WF-IoT), New Orleans, LA, USA, 2–16 June 2020; pp. 1–5. [Google Scholar]
- Wang, Y.; Huynh, G.; Williamson, C. Integration of Google Maps/Earth with microscale meteorology models and data visualization. Comput. Geosci. 2013, 61, 23–31. [Google Scholar] [CrossRef]
- Merabtine, N.; Boualleg, A.; Benslama, M. Analysis of radiation patterns and feed illumination of the reflector antenna using the physical and geometrical optics. Semicond. Phys. Quant. 2006, 9, 53–57. [Google Scholar] [CrossRef]
- Piu, H.; Rahmat Samii, Y. Analysis and characterization of multilayered reflector antennas: Rain/snow accumulation and deployable membrane. IEEE Trans. Antennas Propagat. 1998, 46, 1593–1605. [Google Scholar]
- Hung, C.; Mittra, R. Secondary pattern and focal region distribution of reflector antennas under wide-angle scaning. IEEE Trans. Antennas Propagat. 1983, 31, 756–763. [Google Scholar] [CrossRef]
- Rusch, W. The current state of the reflector antenna art. IEEE Trans. Antennas Propagat. 1984, 32, 313–329. [Google Scholar] [CrossRef]
- Moreira, F.J.; Prata, A. Generalized classical axially symmetric dual-reflector antennas. IEEE Trans. Antennas Propagat. 2001, 49, 547–554. [Google Scholar] [CrossRef]
- Duan, D.W.; Rahmat-Samii, Y. A generalized diffraction synthesis technique for high performance reflector antennas. IEEE Trans. Antennas Propagat. 1995, 43, 27–40. [Google Scholar] [CrossRef]
- Hoferer, R.A.; Rahmat-Samii, Y. Subreflector shaping for antenna distortion compensation: An efficient Fourier-Jacobi expansion with GO/PO analysis. IEEE Trans. Antennas Propagat. 2002, 50, 1676–1687. [Google Scholar] [CrossRef]



| Parameters | Values | |
|---|---|---|
| Frequency | 8 GHz | |
| Ground station | Bore-sight gain (ξ = 0°) | 59 dBi |
| Sidelobe gain (ξ = ψ°) | ||
| LEO satellite | Satellite altitude | 550 km |
| Transmission power | 30 dBm | |
| Bore-sight gain | 4.4 dBi | |
| Free-space path loss | ||
| Airborne interference source | Transmission power | 70 dBm |
| Bore-sight gain | 30 dBi | |
| Velocity | 850 km/h | |
| Interference source altitude hi | 3 km, 6 km, 9 km, and 12 km | |
| Free-space path loss |
| Trajectory | Altitude hi (km) | Path 1 | Path 2 | Path 3 | |||
|---|---|---|---|---|---|---|---|
| ψave (°) | Jave/Save Ratio (dB) | ψave (°) | Jave/Save Ratio (dB) | ψave (°) | Jave/Save Ratio (dB) | ||
| 1 | 3 | 73.2 | −22.3 | 80.8 | −29.5 | 83.6 | −33.6 |
| 6 | 72.2 | −22.1 | 80.3 | −29.4 | 83.3 | −33.5 | |
| 9 | 71.1 | −21.9 | 79.8 | −29.2 | 82.9 | −33.4 | |
| 12 | 70.2 | −21.7 | 79.3 | −29.1 | 82.6 | −33.4 | |
| 2 | 3 | 59.4 | −18.7 | 67.1 | −26.0 | 70.0 | −30.3 |
| 6 | 58.4 | −18.4 | 66.6 | −25.9 | 69.7 | −30.2 | |
| 9 | 57.3 | −18.2 | 66.0 | −25.8 | 69.3 | −30.1 | |
| 12 | 56.3 | −17.9 | 65.5 | −25.7 | 68.9 | −30.1 | |
| 3 | 3 | 40.7 | −12.2 | 48.4 | −20.1 | 51.3 | −24.2 |
| 6 | 39.6 | −11.9 | 47.8 | −19.9 | 50.9 | −24.1 | |
| 9 | 38.5 | −11.5 | 47.3 | −19.7 | 50.6 | −24.0 | |
| 12 | 37.5 | −11.1 | 46.8 | −19.6 | 50.2 | −23.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, E.; Park, Y.; Kim, J.; Choo, H. Downlink Analysis of a Low-Earth Orbit Satellite Considering an Airborne Interference Source Moving on Various Trajectory. Remote Sens. 2024, 16, 321. https://doi.org/10.3390/rs16020321
Kang E, Park Y, Kim J, Choo H. Downlink Analysis of a Low-Earth Orbit Satellite Considering an Airborne Interference Source Moving on Various Trajectory. Remote Sensing. 2024; 16(2):321. https://doi.org/10.3390/rs16020321
Chicago/Turabian StyleKang, Eunjung, YoungJu Park, JungHoon Kim, and Hosung Choo. 2024. "Downlink Analysis of a Low-Earth Orbit Satellite Considering an Airborne Interference Source Moving on Various Trajectory" Remote Sensing 16, no. 2: 321. https://doi.org/10.3390/rs16020321
APA StyleKang, E., Park, Y., Kim, J., & Choo, H. (2024). Downlink Analysis of a Low-Earth Orbit Satellite Considering an Airborne Interference Source Moving on Various Trajectory. Remote Sensing, 16(2), 321. https://doi.org/10.3390/rs16020321