A Spatial–Spectral Transformer for Hyperspectral Image Classification Based on Global Dependencies of Multi-Scale Features

Abstract

Vision transformers (ViTs) are increasingly utilized for HSI classification due to their outstanding performance. However, ViTs encounter challenges in capturing global dependencies among objects of varying sizes, and fail to effectively exploit the spatial–spectral information inherent in HSI. In response to this limitation, we propose a novel solution: the multi-scale spatial–spectral transformer (MSST). Within the MSST framework, we introduce a spatial–spectral token generator (SSTG) and a token fusion self-attention (TFSA) module. Serving as the feature extractor for the MSST, the SSTG incorporates a dual-branch multi-dimensional convolutional structure, enabling the extraction of semantic characteristics that encompass spatial–spectral information from HSI and subsequently tokenizing them. TFSA is a multi-head attention module with the ability to encode attention to features across various scales. We integrated TFSA with cross-covariance attention (CCA) to construct the transformer encoder (TE) for the MSST. Utilizing this TE to perform attention modeling on tokens derived from the SSTG, the network effectively simulates global dependencies among multi-scale features in the data, concurrently making optimal use of spatial–spectral information in HSI. Finally, the output of the TE is fed into a linear mapping layer to obtain the classification results. Experiments conducted on three popular public datasets demonstrate that the MSST method achieved higher classification accuracy compared to state-of-the-art (SOTA) methods.

1. Introduction

Hyperspectral imagery (HSI) consists of numerous spectral bands that reflect the spatial and spectral characteristics of objects, revealing their chemical and physical information [1,2]. This technology has many applications in geological research, environmental protection, plant disease monitoring, fine agriculture, food detection, and military reconnaissance [3,4,5]. Pixel-wise HSI classification is crucial for the effective utilization of HSI data. Researchers have devoted considerable attention to this area. However, the increasing resolution and number of bands pose challenges to HSI classification, including high spectral redundancy, increased spectral variability within similar features, and difficulties in fully exploiting spatial–spectral data [6].

Early HSI classification was based on classification features designed by experts, which were simple and easy to use; however, they were shallow features, and the classification accuracy was inadequate [7,8,9,10]. Later, machine learning methods were adopted by researchers, with representative studies including principal component analysis (PCA) [11], random forests (RFs) [12], support vector machines (SVMs) [13], sparse representation (SR) [14], morphological profiles (MPs) [15,16,17], and extreme learning machine (ELM) [18,19]. However, the majority of machine learning methods primarily focus on the spectral information of HSI, neglecting the spatial dimension. This limitation can lead to inaccurate classification, especially when dealing with targets that have spectrally similar but spatially distinct objects.

In recent years, deep learning has been widely used in image processing tasks due to its powerful feature extraction capabilities [20,21,22], attracting many researchers to introduce deep learning methods into HSI classification tasks [23,24,25,26,27]. The most studied among these is the convolutional neural network (CNN) [28,29,30]. CNN-based methods typically extract patches from HSI and feed them into the network, which is used to learn characteristics of the patches, and finally predict the category of the query pixel within each patch. Roy et al. [31] proposed a spatial–spectral hybrid network consisting of 2DCNN and 3DCNN to extract the spatial–spectral joint features from stacked spectra. To obtain more discriminative features, Zhong et al. [32] utilized two successive residual modules to learn spatial and spectral representations. Liu et al. [33] enhanced informative features that proved beneficial for classification and suppressing irrelevant information by constructing an interaction attention module. GAF-NAU [34] departs from the conventional practice of classifying patches, and instead represents one-dimensional spectral features as two-dimensional feature maps using the Gramian angular field (GAF). Subsequently, these GAF representations are embedded into a deep network to generate classification results. Such CNN-based hyperspectral classification networks have greatly improved classification accuracy. However, research in the past few years has shown that such methods are consistently limited by fixed convolutional kernel sizes, leading to unreliability in classifying multi-scale targets [35]. Furthermore, the monotonous sliding window mechanism prevents these networks from modeling the global dependencies among different image elements [36,37].

BERT [38] and GPT [39], among other NLP models, have demonstrated the powerful learning capabilities of transformer, which has also attracted researchers to explore the application of transformer in computer vision tasks. The emergence of vision transformers has effectively contested the supremacy of CNNs in computer vision, opening up new possibilities for HSI classification [40,41]. He et al. [42] proposed a method to use a convolutional network to extract spatial features fromHSI, and constructed a dense transformer to capture the spectral correlations within the HSI. Finally, they employed a multilayer perceptron for classification. Roy et al. [43] introduced a morphological block before computing multi-head attention, enhancing the information interaction performance of HSI tokens and class tokens through the utilization of dilation and erosion operators. Also, Roy [44] proposed a multimodal fusion transformer in another paper, where multiple sources of remote sensing data such as LiDAR and SAR were used to generate class tokens for better model generalization. Mei et al. [45] constructed grouped pixel embedding to complement the over-separated features extracted by MHSA, which controls the attention in the local–global range and effectively solves the feature dispersion problem of MHSA. Ouyang et al. [37] proposed a transformer encoder with spatial–spectral attention mechanism to capture global dependencies between different tokens, enabling the model to focus on more differentiated channels and spatial locations.

These transformer-based HSI classification methods can capture high-level semantic features that incorporate global dependencies, effectively improving classification performance. However, since the tokens used for attention modeling in the transformer are derived from patches with fixed scales, this framework largely ignores the multi-scale nature of the targets in the images. This lack of multi-scale features can lead to distortions in the classification of objects of different sizes in the images [46,47]. Additionally, the transformer network cannot directly exploit the rich spatial and spectral information in HSI, which also constrains its classification accuracy.

In this paper, we propose a multi-scale spatial–spectral transformer (MSST) specifically designed for HSI classification tasks. The goal is to enhance the transformer’s ability to model global dependencies across multiple scales while fully leveraging the spatial–spectral features of HSI. The MSST is a non-hierarchical network structure primarily consisting of a spatial–spectral token generator (SSTG), a transformer encoder (TE), and a classifier. The SSTG is a novel multi-dimensional convolutional feature extractor. Departing from the conventional token generator, SSTG extracts spatial–spectral information from patches, while also incorporating an additional branch to retrieve spectral features from query pixels. This extra branch supplements damaged spectral features during the convolution process. The semantic features extracted by SSTG are transformed into tokens and fed into a TE, which is composed of a cross-covariance attention (CCA) module [48] and a token fusion self-attention (TFSA) module for attention modeling. CCA is employed to capture correlations among spectral sequences. TFSA is a novel attention mechanism that aggregates tokens to varying extents before feeding them into different attention heads within the same attention layer. Through these distinct attention heads, attention encoding is performed on features of different scales, allowing the encoder to globally model the dependencies of multi-scale features in HSI. Finally, the output of the encoder is directed to a classifier to obtain the ultimate result.

The main contributions of this research are listed below.

1.

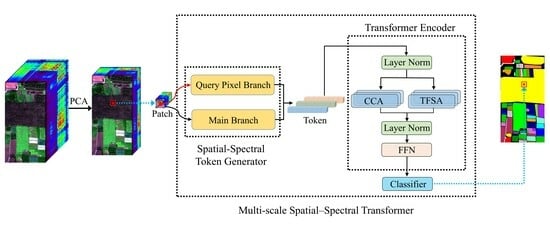
To tackle the challenge of the transformer inadequately leveraging spatial–spectral features, we redesigned the feature extractor—SSTG. SSTG incorporates a dense multi-dimensional convolutional structure, adeptly extracting HSI spatial–spectral features. Additionally, it introduces a branch to extract spectral features of query pixels, compensating for damaged spectral features during the convolution process. Attention encoding on features from SSTG enables the expression of spatial–spectral semantic characteristics of HSI during classification.

2.

To simulate global dependencies among multi-scale features during attention modeling, we innovatively introduce TFSA. This module, after subsampling tokens to varying extents, generates keys and values of different sizes. Subsequently, different attention heads compute attention outputs by operating on the corresponding-sized keys, values, and queries. This novel attention mechanism effectively simulates global dependencies among multi-scale features, demonstrating enhanced capabilities in classifying multi-scale targets.

3.

We employed SSTG and TFSA, introducing CCA to construct the MSST HSI classification network. This hybrid network effectively integrates both global and local modeling capabilities, enabling the consideration of multi-scale characteristics of targets in HSI and the effective utilization of spatial–spectral features.

2. Related Research

2.1. Applying Spatial–Spectral Information to Transformer

To leverage the spatial–spectral information of HSI in transformer architecture, researchers often construct hybrid networks combining CNN and transformers, such as HybridFormer [37], HiT [49], and FusionNet [50]. In these approaches, spatial–spectral features are extracted using CNN, and then embedded into transformers for attention modeling. This strategy effectively expresses the spatial–spectral characteristics of HSI within the transformer framework. In the SSTFF proposed by Sun et al. [51], a feature extraction module was designed using both two-dimensional and three-dimensional convolutions to extract spatial–spectral features. These features are subsequently input into the transformer for representation and learning. However, current methods apply multi-dimensional convolution directly to HSI patches. This can distort the spectral characteristics of the query pixel, which plays a crucial role in determining land cover categories. Such distortion is highly detrimental for HSI classification.

2.2. Multi-Scale Attention Modeling in Transformer

To address the single-scale problem in transformers, Swin transformer [47], 3D Swin transformer [52], and PVT [53] have been developed. In these approaches, researchers extract multi-scale features through a hierarchical network structure with gradual contraction. Ren et al. [54] proposed shunted self-attention, which unifies multi-scale feature extraction within a self-attention layer through multi-scale token aggregation, and then adopts a hierarchical structure to model the attention of multi-scale features. While these studies have, to some extent, enhanced the transformer’s ability to capture global dependencies across multi-scale features, the introduction of such multi-level structures inevitably leads to an increase in network complexity. Additionally, certain methods such as Swin transformer impose limitations on the network’s globality. This elevated complexity poses challenges, particularly for intricate HSI data, and may even result in a decrease rather than an increase in classification accuracy. Consequently, it becomes imperative to develop multi-scale ViT networks specifically tailored for HSI data.

3. Methods

3.1. Proposed MSST Architecture

Figure 1 illustrates the overall structure and operational flow of the proposed MSST architecture, which forsakes complex cascaded structures for a lightweight single-stage mode. Initially, dimensionality reduction is performed on HSI using PCA. Subsequently, a patch of query pixels is segmented from the HSI and input into the SSTG module, generating tokens with deep spatial–spectral features. Then, these tokens are fed into the transformer encoder, which contains a TFSA branch, a CCA branch, and a feedforward network; the TFSA module is used to learn the dependencies between features of different sizes, while the CCA branch can capture correlations between spectral sequences, and the feedforward network can enhance local information through convolutional structures. Ultimately, the network output utilizes the highest probability value from the linear mapping result.

3.2. Spatial–Spectral Token Generator

For transformer-based HSI classification tasks, researchers often employ convolutional networks to extract spatial–spectral semantic features from HSI patches, which are then mapped to tokens and fed into the transformer encoder. We have observed that the convolutional operation on the patches distorts the spectral characteristics of the query pixels, which are crucial for inferring the corresponding land cover class. Therefore, this paper presents a redesigned token generator called SSTG, as illustrated in Figure 2. The generator initially extracts the spatial–spectral representation from HSI data, using a 3DCNN. Subsequently, a multi-branch 2DCNN refines the semantic features. Additionally, an independent 1DCNN branch is used to extract spectral features from the query pixels, compensating for the loss of information during the patch convolution process.

As shown in Figure 1, we initially process an HSI patch of size w × h × c using a 3DCNN composed of eight convolutional kernels, each of size 3 × 3 × 3. The computational procedure is defined as follows:

$${\mathrm{X}}^{3\mathrm{D}}{=\mathrm{ReLU}\left(\mathrm{BN}\right(3\mathrm{DConv}(X}_{patch}^{in}\left)\right))$$

(1)

where 3DConv is the 3D convolution, BN stands for batch normalization, and ReLU is the rectified linear activation function. BN is used to normalize the output of 3DConv, an operation that effectively prevents gradient explosion and gradient disappearance, and speeds up the network convergence. Moreover, the activation function increases the nonlinearity of the network. 3DCNN outputs X^3D ∈ R^{(w−2) × (h−2) × (c−2) × 8}, a high-dimensional feature block containing the spatial–spectral information extracted from the patch.

We reshape the dimensionality of X^3D ∈ R^{(w−2) × (h−2) × (c−2) × 8} to $X_{reshape}^{3D}$ ∈ R^{(w−2) × (h−2) × ((c−2) × 8)} as the input to 2DCNN. The 2DCNN comprises multiple branches, each equipped with convolutional kernels of different sizes to extract features that encompass richer contextual information. The computational process is as follows:

$${\mathrm{X}}^{2\mathrm{D} }{=\mathrm{ReLU}\left(\mathrm{BN}\right(2\mathrm{DConv}(X}_{reshape}^{3D}\left)\right))$$

(2)

In the network, we adjust the receptive field of the 2DCNN by adjusting the size of the convolutional kernel. The output channel of each branch is configured to n. The output dimension can be expressed as $X^{2D}$ ∈ R^{si × si × n}, where si varies depending on the convolutional kernel. Subsequently, in terms of dimensions, we flatten $X^{2D}$ to $X_{flatten}^{2D}$ ∈ R^{(si * si) × n} and map it to the same $X_{weighted}^{2D}$ ∈ R^{(s * s) × n} through weighted mapping, further refining the shallow spatial–spectral features. Finally, we sum up the $X_{weighted}^{2D}$ of multiple branches to obtain $X^{out1}$ as the output.

We constructed a 1DCNN for the query pixel, a branch designed to supplement the distortions caused by the spectral features of the query pixel during the convolution of the patch. We extract the query pixels and process them as follows:

$${\mathrm{X}}^{\mathrm{out}2}{=\mathrm{ReLU}\left(\mathrm{BN}\right(1\mathrm{DConv}(X}_{pixel}^{in}\left)\right))$$

(3)

where $X_{pixel}^{in}$ refers to the query pixel of the patch.

We concatenate the resulting $X^{out1}$ with $X^{out2}$ to obtain the final output. This dense convolutional network with additional query pixel spectral branches allows us to obtain a more robust and discriminative spatial–spectral feature output, significantly enhancing the exploitation of spatial–spectral information from HSI data.

3.3. Token Fusion Self-Attention

In the modeling process of the classical self-attention module, the input token is initially projected through three learnable weight matrices as query, key, and value. Subsequently, a weight distribution is computed using the query, key, and SoftMax functions. Finally, the obtained weights are applied to the value, resulting in the attention output as follows:

$$\mathrm{SA}=\mathrm{Attention}(Q, K, V)=\mathrm{SoftMax}(\frac{{QK}^T}{\sqrt{d_k}})V$$

(4)

where Q, K, and V denote query, key, and value, respectively. The computation flow is shown in Figure 3a. In practice, to enable models to jointly attend to information from different subspaces, h attention heads are used to divide Q, K, and V into h groups for parallel computation of outputs. This process is illustrated in the following equation:

$${\mathrm{MSA}=\mathrm{Concat}(SA}_i{)W}^o (i=1, 2, \cdots , h)$$

(5)

where W^O represents the parameter matrix of size ${hd}_V{ \times n}_{token}$ ($n_{token}$ denotes the number of tokens). ${SA}_i$ represents the i-th group of attention output.

In previous attentional modeling, Q, K, and V were obtained by direct linear mapping of tokens, and thus at a single scale. This limitation inevitably restricted the receptive field of the attention layer, resulting in the inability of the attention layer to model the global dependencies of multi-scale features. However, for HSI, which exhibits diverse object scales, this mechanism is highly unfavorable for HSI classification. To address this issue, we proposed a TFSA module that captures global dependencies among multi-scale features and more effectively simulates targets of different sizes. Unlike conventional self-attention mechanisms, TFSA first fuses tokens to different scales, and then maps them to different scale keys and values using weight matrices. Subsequently, different attention heads in the attention layer are used to model the attention of features at different scales.

Figure 3b presents a concise illustration of the computational process of TFSA. For acquiring features at various scales, our algorithm first performs token fusion to varying scales in the quantity dimension. After the integration at a larger scale, we obtain tokens with feature information at a larger scale, corresponding to a reduced quantity. Similarly, after integration at a smaller scale, tokens retain more detailed features, corresponding to a relatively larger quantity. Through the fusion of multiple scales, we obtain tokens with diverse scales, enhancing their ability to represent the true state of the object. In practice, we achieve token fusion through learnable convolutional layers. Then, the fused tokens are mapped to generate keys and values of different sizes, as illustrated in the following formula:

$$\begin{array}{c}{Q}_i{=X W}_i^Q\\ K_i{=\mathrm{Conv}\left(\mathrm{reshape}\right(X), f}_i{, s}_i{) W}_i^K\\ V_i{=\mathrm{Conv}\left(\mathrm{reshape}\right(X), f}_i{, s}_i{) W}_i^V\end{array}$$

(6)

where i represents the i-th attention head group. Q_i, K_i, and V_i represent the query, key, and value of the i-th attention head group, respectively. The term “reshape” signifies the reshaping of the dimensions. F_i represents the size of the convolutional kernel, and s_i represents the strides. Different attention head groups feature different convolutional kernel sizes and strides. ${W }_i^Q$, ${W }_i^K$, and ${W }_i^V$ represent the weight matrices. The attention calculation can be represented as follows:

$$\begin{array}{c}{\mathrm{TFSA}=MSA+\mathrm{Concat}(head}_i) (i=1, 2,\cdots , h)\\ {\mathrm{where} head}_i=\mathrm{SoftMax}\left(\frac{Q_i{K}_i^T}{\sqrt{d_k}}\right)V_i\end{array}$$

(7)

where i represents the i-th type of token fusion, which also corresponds to the number of attention head groups. MSA represents the output of the attention coding without token fusion.

By leveraging multi-dimensional keys and values, our TFSA module can pay more attention to the multi-scale characteristics of HSI data during the coding process. This capability allows the classification network to effectively simulate objects with various scales.

3.4. Transformer Encoder

To further improve the exploitation of spectral information by the network, we added a cross-covariance attention mechanism [48] in parallel with the TFSA module when building the transformer encoder. CCA is a ‘transposed’ version of self-attention that operates across feature channels rather than tokens, where the interactions are based on the cross-covariance matrix between keys and queries. The complexity of this attention computation mechanism is linearly proportional to the number of tokens, and allows for efficient processing of high-resolution images. The transposed attention mechanism effectively captures features across the channel dimension in images. In this research, we introduced it to the HSI classification task to enhance the interaction efficiency among spectral features. The calculation formula for CCA is as follows:

$$\begin{array}{c}\mathrm{CCA}(Q, K, V)=V\ast \mathrm{CM}(K,Q)\\ \mathrm{where} \mathrm{CM}(K, Q)=\mathrm{SoftMax}(\frac{K^{T}Q}{\sqrt{h}})\end{array}$$

(8)

where CM refers to the context vector of the transpose attention, while Q, K, and V are derived from the mapping of tokens.

The complete transformer encoder is shown in Figure 4. The CCA mechanism is connected in parallel with the TFSA module, and the output of both is fed into the feedforward network (FFN) after summation. The FFN consists of two fully connected layers designed to enhance the model’s discriminative power and remove low discriminative feature combinations. The calculation process is as follows:

$$X_1=X+\mathrm{TFSA}\left(\mathrm{Norm}\right(X\left)\right)+\mathrm{CCA}\left(\mathrm{Norm}\right(X\left)\right)$$

(9)

$${\mathrm{TE}\left(X\right)=\left[\right(\mathrm{ReLU}(X}_1{W}_1{+b}_1{\left)\right)W}_2{+b}_2{]+X}_1$$

(10)

Here, TFSA(-) is the output of token fusion self-attention, CCA(-) is the output of cross-covariance attention, Norm signifies the layer normalization, ReLU denotes the rectified linear activation function, and W₁, W₂, b₁, and b₂ denote the weights and biases of the first and second convolutional layers in the FFN, respectively.

4. Experiment and Results

We compared our network against the current SOTA methods on three commonly used public datasets to evaluate classification performance.

4.1. Data Descriptions and Experimental Settings

4.1.1. Data Detail

The Trento dataset was collected with the AISA Eagle sensor in a rural area south of Trento, Italy. It consists of 63 spectral bands (0.42–0.99 µm), and has a size of 600 × 166 pixels. The image was divided into six land cover types; Figure 5a,b display the false color map and the ground truth map, respectively. The numbers of training and test samples are shown in

Table 1. Details of classes in the Trento dataset and the numbers of samples used for training and testing.

Class No.	Color		Class Name	Test	Train
1		MidnightBlue	Apple trees	3994	40
2		Blue	Buildings	2874	29
3		LawnGreen	Ground	474	5
4		Yellow	Woods	9032	91
5		Red	Vineyard	10,396	105
6		FireBrick	Roads	3142	32

.

The Pavia University dataset was acquired using the ROSIS-3 sensor over the University of Pavia, Italy. The sensor continuously images 115 bands in the wavelength range 0.43–0.86 μm, with an image size of 610 × 340 pixels. Figure 6 presents the false color map in (a) and the ground truth map in (b). The numbers of training and test samples are shown in

Table 2. Details of classes in the Pavia University dataset and the numbers of samples used for training and testing.

Class No.	Color		Class Name	Test	Train
1		Blue	Asphalt	1249	13
2		Green	Meadows	201	3
3		Cyan	Gravel	607	7
4		ForestGreen	Trees	148	2
5		Magenta	Painted metal sheets	1750	18
6		SaddleBrown	Bare Soil	357	4
7		Purple	Bitumen	4984	51
8		Red	Self-Blocking Bricks	6310	64
9		Yellow	Shadows	394	4

.

Houston2013 was collected using the ITERS CASI-1500 sensor in Houston, USA, and its surrounding rural areas, at a spatial resolution of 2.5 m. The image consists of 349 × 1905 pixels and 144 spectral bands with wavelengths ranging from 364–1046 nm. The study region encompasses 15 distinct land cover types, as depicted in Figure 7a,b, illustrating the false color and ground truth maps, respectively. The numbers of training and test samples are shown in

Table 3. Details of classes in the Houston dataset and the numbers of samples used for training and testing.

Class No.	Color		Class Name	Test	Train
1		SaddleBrown	Healthy Grass	13,901	140
2		Blue	Stressed Grass	3477	35
3		Orange	Synthetic Grass	21,603	218
4		Green	Trees	161,653	1632
5		Orchid	Soil	6156	62
6		SkyBlue	Water	44,111	446
7		MintGreen	Residential	23,862	241
8		CoolGray	Commercial	4013	41
9		Yellow	Road	10,711	108
10		BananaYellow	Highway	12,270	124
11		Magenta	Railway	10,905	110
12		BlueViolet	Parking Lot 1	8864	90
13		DodgerBlue	Parking Lot 2	22,282	225
14		Linen	Tennis Court	7282	74
15		Red	Running Track	4000	40

.

4.1.2. Experimental Settings

All of the experiments in this study were conducted on a 15 vCPU AMD EPYC 7543 32-core processor equipped with 80 GB of RAM, and an A40 48 GB GPU. PyTorch 1.11.0 served as the development framework; the learning rate was set to 0.001, the number of training epochs was set to 100, the batch size was set to 64, and Adam was chosen as the optimizer. Each experiment was conducted 10 times, and the results were then averaged. To precisely depict the classification accuracy of the model, the overall accuracy (OA), average accuracy (AA), and kappa coefficient (k) were used as evaluation metrics to assess the algorithm’s performance. A higher value for each metric indicates better classification performance.

4.2. Comparison and Analyses of Methods

To validate the effectiveness of the proposed network in this study, we conducted comparative experiments with nine mainstream HSI classification methods, which were classified into three categories of machine learning, convolutional networks, and transformer networks, including SVM, RF, 3DCNN [55], G2C-3DCNN [56], HybridSN [31], SSRN [32], ViT [42], SpectralFormer [57], and SSFTT [51]. For the setting of parameters and network structure of these methods, we followed the corresponding references. We reduced the number of spectral bands in HSI to 30 using PCA, set the patch size to 15 × 15, and randomly partitioned the training and test sample sets for each experiment.

4.2.1. Quantitative Results and Analysis

Table 4. Classification performance obtained by different methods for the Pavia University dataset (best results are bolded).

Class	SVM	RF	3D-CNN	G2C-3DCNN	HybridSN	SSRN	ViT	SpecFormer	SSFFT	Ours
1	89.00	92.92	96.92	96.73	94.01	98.08	93.12	96.98	97.36	96.38
2	94.41	97.39	99.76	99.81	99.49	99.63	99.80	99.98	99.88	99.90
3	49.47	23.00	56.59	82.44	75.31	84.46	60.73	71.90	90.18	90.42
4	83.02	79.95	84.37	89.02	87.90	88.33	92.71	84.31	92.05	93.68
5	98.80	99.77	99.62	99.85	100.00	98.87	99.55	99.77	99.10	99.22
6	62.88	27.70	85.46	98.57	93.63	100.00	94.92	97.33	99.84	100.00
7	27.79	33.64	68.03	97.27	90.51	94.76	79.57	90.05	100.00	100.00
8	68.20	80.43	85.87	91.08	82.28	97.06	88.34	88.29	92.37	95.35
9	73.32	71.78	37.99	99.68	94.34	84.20	91.14	75.88	90.50	91.21
OA (%)	82.19 ± 0.47	80.04 ± 0.65	90.86 ± 0.41	96.73 ± 0.24	94.08 ± 0.40	97.14 ± 0.23	93.95 ± 0.54	94.85 ± 0.10	97.57 ± 0.08	97.85 ± 0.24
AA (%)	71.88 ± 0.66	67.40 ± 0.74	79.40 ± 0.26	94.94 ± 0.21	90.83 ± 0.32	93.93 ± 0.18	88.88 ± 0.61	89.39 ± 0.25	95.70 ± 0.20	96.24 ± 0.05
K × 100	75.94 ± 0.42	72.50 ± 0.50	87.70 ± 0.14	95.65 ± 0.15	92.11 ± 0.18	96.21 ± 0.06	91.93 ± 0.51	93.12 ± 0.28	96.78 ± 0.33	97.16 ± 0.37

,

Table 5. Classification performance obtained by different methods for the Trento dataset (best results are bolded).

Class	SVM	RF	3D-CNN	G2C-3DCNN	HybridSN	SSRN	ViT	SpecFormer	SSFFT	Ours
1	78.14	68.70	97.65	98.87	99.70	99.17	96.52	98.97	99.67	99.65
2	59.19	64.65	66.74	82.67	85.32	88.45	84.06	90.22	94.33	95.72
3	31.01	36.71	49.16	83.33	81.86	46.62	36.50	22.36	57.38	81.22
4	95.26	94.39	99.09	99.92	99.03	100.00	99.75	100.00	99.98	99.98
5	85.58	90.22	99.89	100.00	99.72	100.00	99.99	99.95	99.97	100.00
6	66.65	77.94	79.28	90.07	85.55	88.77	84.28	83.96	97.45	96.12
OA (%)	82.12 ± 1.02	84.01 ± 0.74	93.20 ± 0.37	96.92 ± 0.17	96.35 ± 0.38	96.75 ± 0.10	95.27 ± 0.41	95.99 ± 0.24	98.45 ± 0.08	98.83 ± 0.38
AA (%)	69.30 ± 0.84	72.10 ± 0.58	81.97 ± 0.32	92.58 ± 0.34	91.86 ± 0.15	87.17 ± 0.07	83.52 ± 0.55	82.58 ± 0.10	91.46 ± 0.15	95.45 ± 0.20
K × 100	76.00 ± 0.80	78.43 ± 0.66	90.86 ± 0.24	95.88 ± 0.20	95.13 ± 0.26	95.66 ± 0.07	93.66 ± 0.34	94.64 ± 0.14	97.93 ± 0.18	98.44 ± 0.18

and

Table 6. Classification performance obtained by different methods for the Houston 2013 dataset (best results are bolded).

Class	SVM	RF	3D-CNN	G2C-3DCNN	HybridSN	SSRN	ViT	SpecFormer	SSFFT	Ours
1	96.40	96.32	89.01	86.62	98.01	86.03	84.49	87.87	86.47	89.12
2	87.57	96.04	82.37	91.67	95.63	90.28	95.63	93.16	95.90	92.85
3	99.62	99.75	97.78	97.97	94.54	97.20	95.55	94.16	95.93	95.43
4	90.57	90.25	88.49	89.05	89.69	93.76	83.21	89.49	81.14	91.13
5	97.59	99.46	99.77	100.00	99.30	100.00	99.46	99.77	100.00	100.00
6	45.24	61.01	83.63	83.33	84.82	86.31	83.33	61.76	86.31	86.31
7	81.66	81.66	63.72	67.28	74.81	79.95	75.63	67.45	74.06	72.35
8	76.57	68.43	67.31	72.46	65.75	70.00	80.97	77.54	78.06	76.87
9	68.88	79.27	64.72	77.26	77.52	88.43	79.53	76.16	80.25	79.40
10	78.23	79.50	94.90	99.08	96.95	100.00	99.72	98.98	100.00	99.57
11	79.94	87.87	76.68	87.29	74.39	88.00	64.45	83.39	95.48	98.06
12	69.89	68.90	90.04	94.49	75.76	91.95	94.70	93.71	98.16	98.09
13	23.80	12.78	50.32	65.50	68.05	81.63	31.79	39.54	73.00	80.35
14	86.61	96.46	90.16	99.61	100.00	99.02	68.31	70.97	100.00	100.00
15	96.08	97.09	99.69	99.37	100.00	99.37	84.05	84.69	100.00	100.00
OA (%)	81.02 ± 0.34	83.14 ± 0.27	82.03 ± 0.21	87.02 ± 0.48	85.51 ± 0.16	89.59 ± 0.41	83.32 ± 0.58	84.07 ± 0.15	89.48 ± 0.10	90.29 ± 0.12
AA (%)	78.58 ± 0.62	80.99 ± 0.29	82.57 ± 0.18	87.40 ± 0.30	86.35 ± 0.29	90.10 ± 0.64	81.39 ± 0.60	81.24 ± 0.08	89.65 ± 0.07	90.63 ± 0.08
K × 100	79.45 ± 0.33	81.74 ± 0.53	80.56 ± 0.15	85.96 ± 0.23	84.34 ± 0.08	88.75 ± 0.28	81.94 ± 0.52	82.74 ± 0.22	88.62 ± 0.28	89.50 ± 0.27

display the classification accuracies achieved by MSST and the other nine methods on the Pavia University, Trento, and Houston 2013 datasets. The accuracy metrics include OA, AA, and κ, and the precision for each category. The best results for each metric are indicated in bold. The results of the three experiments consistently demonstrate that the MSST method outperforms other methods in classification performance. This is evidenced by the fact that MSST achieved the highest OA, AA, and κ across all three experiments.

The Pavia University and Houston 2013 datasets are high-resolution images of complex urban areas with discrete samples, complex contextual information, and a variety of target scales. Conventional CNN and transformer networks exhibit limitations in handling such data. Despite SSRN and SSFTT demonstrating relatively promising results, SSRN, as a CNN-based approach, still struggles to capture global information, while SSFTT fails to account for the multi-scale nature of HSI data. The use of TFSA allows MSST to learn global dependencies among objects at different scales, resulting in superior accuracy compared to a series of convolutional and transformer networks.

As evidenced by experiments conducted at the University of Pavia, our proposed MSST method demonstrates a distinct advantage over the other methods in classifying targets with spatially similar features, such as meadows, gravel, bare soil, and bitumen; despite GAHT [45] displaying comparable overall classification accuracy, our approach outperforms it specifically for these targets, achieving higher classification accuracies by 0.31%, 2.27%, 2.04%, and 8.0%, respectively. This superiority is attributed to the utilization of SSTG within our method, which enables more effective exploitation of spectral features. In the Trento experiment, the imbalance between inter-class samples resulted in poor performance for transformer networks such as ViT, SpecFormer, and SSFTT on imbalanced classes (e.g., ground). However, the results obtained by MSST were not only the most accurate overall, but were also more uniform for each class, demonstrating to some extent that this mechanism of joint spatial–spectral features plus global multi-scale self-attention has advantages over other methods when faced with imbalanced datasets.

4.2.2. Qualitative Results and Analysis

Figure 8, Figure 9 and Figure 10 show the classification results of the different methods on the three datasets. Overall, our proposed method achieves results that closely align with the ground truth map, surpassing other methods. The classification results of the SVM and RF models demonstrate considerable noise in their classification of large area classes like trees and vineyards in Trento, due to the limitations of machine learning algorithms to effectively use spatial information. However, our proposed MSST method successfully resolves the confusion between bare soil and meadows in the Pavia dataset, and reduces “speckles” produced by other methods. Similarly, the Houston 2013 classification results obtained by the MSST model demonstrate superior accuracy compared to the other methods.

4.2.3. Time Complexity Comparison

Table 7. Training times and test times for the contrasting methods and the proposed method on the three datasets.

Methods	Train(S)			Test(S)
	Trento	PU	Houston 2013	Trento	PU	Houston 2013
3DCNN	127.99	174.96	103.97	2.65	3.12	1.53
G2C-3DCNN	122.41	192.26	101.98	2.51	4.37	1.34
HybridSN	124.03	163.80	95.05	2.22	3.84	1.58
SSRN	165.22	200.15	122.02	3.37	4.54	2.23
ViT	188.06	236.09	145.92	4.56	6.12	3.40
SpecFormer	187.24	227.10	142.248	4.01	5.71	2.90
SSFTT	145.59	183.85	116.71	3.22	3.79	2.17
MSST	185.72	222.32	123.47	4.12	5.44	2.94

in this study records the training and testing times for the reference methods and the proposed MSST on the three datasets. The results clearly demonstrate that the transformer-based methods require more time for both training and testing compared to the CNN-based methods, which is an unavoidable cost of using the self-attention mechanism. Our MSST approach has a higher time cost compared to conventional CNN methods, yet this cost is notably lower than ViT and SpectralFormer. In terms of computational complexity, the MSST method is positioned in the medium-to-high range, mainly due to the inclusion of the SSTG module and CCA. Although MSST does not outperform the other methods in terms of efficiency, the manageable time cost is deemed acceptable, considering its superiority in accuracy.

5. Discussion

5.1. Parameter Sensitivity Analysis

To determine the optimal network configuration, we experimentally analyzed several parameters that could impact the classification performance and training process. These parameters included the size of the input patch, the number of tokens generated by SSTG (n), the token fusion patterns in TFSA, and the number of attention heads in transformer.

5.1.1. The Impact of Patch Size and Number of Tokens

Based on existing research, this research set the patch sizes to (11, 13, 15, 17, 19), while the numbers of tokens were chosen from the set (49, 64, 81, 100, 121). Figure 11 shows how classification accuracy is affected by patch size and the number of tokens in the three experimental sets.

As depicted in Figure 11, for the Pavia University and Trento data, the overall accuracy shows a convex functional trend of increasing and then decreasing as the patch size went from 11 to 19, with an optimum value attained at a patch size of 15. Similarly, in the experiments conducted on the Pavia University and Trento datasets, configuring the number of tokens to 64 yielded significantly better results than other values. For the Houston 2013 dataset, on the other hand, the best overall accuracy was achieved when the patch size was set to 11 × 11 and the number of tokens to 49.

5.1.2. The Impact of the Number of Attentional Heads

To ascertain the optimal number of attention heads, we examined the impact of varying their quantity on classification accuracy in our experiments. This exploration was conducted with the patch size and the number of tokens fixed at 15 × 15 and 64, respectively. The results of these experiments are presented in Figure 12. Taking all three datasets into consideration, we ultimately selected 8 as the number of attention heads.

5.1.3. The Impact of Token Fusion Patterns in TFSA

To identify the optimal token fusion mode for TFSA, we proposed five different schemes. The different schemes correspond to different fusion parameters R. Detailed configurations are shown in

Table 8. Details of the settings for the five fusion modes of TFSA.

Pattern1	Pattern2	Pattern3	Pattern4	Pattern5
$R_1\left\{\begin{array}{c}4 i=\frac{head}{2}\\ 2 i=\frac{head}{2}\\ 1 i=head\end{array}\right.$	$R_2\left\{\begin{array}{c}8 i=\frac{head}{2}\\ 2 i=\frac{head}{2}\\ 1 i=head\end{array}\right.$	$R_3\left\{\begin{array}{c}8 i=\frac{head}{2}\\ 4 i=\frac{head}{2}\\ 1 i=head\end{array}\right.$	$R_4\left\{\begin{array}{c}7 i=\frac{head}{2}\\ 3 i=\frac{head}{2}\\ 1 i=head\end{array}\right.$	$R_5\left\{\begin{array}{c}7 i=\frac{head}{2}\\ 3 i=\frac{head}{2}\\ 1 i=head\end{array}\right.$

. For example, in Pattern1, the tokens are fused using three downsampling methods; specifically, the downsampling scale parameters (convolution kernel size and strides) were set to 4, 2, and 1. Through this downsampling at different scales, different degrees of token fusion are performed, and thus multi-scale information is obtained. Here, i signifies tokens with i heads performing this type of downsampling.

The five configuration schemes in Table 8 were compared across three datasets, with the patch size, number of tokens, and number of attention heads fixed at 15 × 15, 64, and 8, respectively. The results are shown in Figure 13. As can be seen from the figures, the fusion pattern has an effect on the classification accuracy, but it is not significant. In the case of the Trento and PU datasets, the Pattern1 schemes yield the highest accuracies. Conversely, for the Houston 2013 dataset, the most suitable configuration scheme is Pattern5.

5.2. Ablation Study

5.2.1. Ablation Study on the Main Modules

We conducted an analysis of the contributions of the three modules used by MSST to classify performance through ablation experiments. Specifically, we divided the main work of this paper into SSTG, TFSA, and CCA, and tested the impact of each module and its different groups on the overall accuracy. As shown in

Table 9. Ablation study results of the main components on three datasets (best results are bolded).

Case	Components			Dataset
	SSTG	TFSA	CCA	Houston 2013	Trento	PU
1	×	×	×	83.49	95.45	93.15
2	√	×	×	88.85	97.05	96.22
3	×	√	×	89.65	97.49	95.57
4	√	√	×	90.01	98.68	97.80
5	×	√	√	89.46	97.62	96.85
6	√	√	√	90.29	98.83	97.85

, six cases were tested on each dataset. In Table 9, a checkmark (√) in the component column indicates the usage of the corresponding module, while a cross (×) indicates the non-utilization of the corresponding module.

From Table 9, it is evident that the first case (baseline transformer) achieved the lowest classification accuracy. With the adoption of SSTG as the tokenization method, there was a significant improvement in classification accuracy, with overall accuracy improvements of 5.36%, 1.6%, and 3.07% on the three datasets. Both case 3 and case 5 with the TFSA module had higher overall accuracies than the non-use case. Case 5, which additionally incorporated the CCA module, exhibited a slight improvement in classification accuracy compared to case 3, although the impact of CCA on accuracy was not as significant as that for TFSA and SSTG. Case 6, which represents the implementation of all three modules, yielded the best results. These results demonstrate the effectiveness of the methodology proposed in this study.

5.2.2. Ablation Study on the TFSA Module

More specifically, we performed ablation experiments on SSTG to demonstrate the effectiveness of the query pixel feature extraction branch. We divided the SSTG into two parts, the backbone branch and the query pixel branch (query pixel spectral features only), and tested the effect of both on classification accuracy under the identical experimental conditions. In

Table 10. Ablation study results of the detailed elements of the SSTG on three datasets (best results are bolded).

Case	Components		Dataset
	Main Branch	Query Pixel Branch	Houston 2013	Trento	PU
1	√	×	89.67	98.81	97.44
2	×	√	84.18	93.73	94.62
3	√	√	90.29	98.83	97.85

, a checkmark (√) signifies that the corresponding branch is utilized, while an (×) denotes it being unused. From the experimental results, it becomes evident that the most optimal classification outcomes were obtained in the third scenario, suggesting that the model with the backbone branch in parallel with the query pixel branch is able to make better use of the spatial-spectral features of HSI.

5.3. Impact of Training Data Size on Method Performance

To evaluate the stability of our proposed method, we conducted comparative experiments using different amounts of training samples, as detailed in Figure 14. In the experiments, we selected 1%, 2%, 4%, and 8% of the data as training sets to investigate the impact of different training sample sizes on the classification accuracy of each method. In all three sets of experiments, the OA achieved by the MSST approach consistently increased as the number of training samples expanded. This demonstrates the feasibility and stability of our MSST.

In each subplot, the MSST method is represented by the red dashed line at the top, as shown in Figure 14. This indicates that our method consistently achieved better classification accuracy, regardless of the number of training samples. The only exception is in the Pavia University experiment, where the best classification accuracy was achieved by SSRN when 4% of the data volume was used as the training set. However, this does not mean that it is better than MSST, as both MSST and SSRN approach 100% OA at this juncture.

5.4. Semantic Feature Analysis

The input images, after being encoded by the proposed MSST method, are transformed into high-dimensional semantic features. Using the t-SNE method, the features extracted by the MSST method can be visualized as 2D graphical plots in Figure 15a–c for the Trento, Pavia University, and Houston 2013 datasets, respectively. Notably, samples from the same category are successfully clustered together, signifying that the network learns feature information for each type. The aggregation of the feature visualization plots is evident for the Trento and Pavia University datasets, while Houston 2013’s is more dispersed. These results correspond to the fact that the Houston 2013 dataset is more complex compared to the other two.

6. Conclusions

In this study, we proposed a multi-scale spatial–spectral transformer, which is based on spatial–spectral token generator, token fusion self-attention module, and cross-covariance attention. The redesigned token generator is capable of extracting spatial–spectral features from patches while concurrently employing a separate feature extraction branch to repair the damaged spectral characteristics of query pixels. Additionally, CCA is employed to capture dependencies among spectral sequences during attention encoding. Furthermore, TFSA is used to enhance the network’s ability to model attention across mixed scales, enabling our network to learn global dependencies among objects of varying sizes. The experiments on the three HSI datasets demonstrated that MSST has the highest accuracy compared to the SOTA methods. MSST exhibits pronounced advantages in handling data characterized by dispersed samples and multi-scale targets. In our future research, we intend to delve deeper into HSI classification tasks from perspectives such as model light weighting, unsupervised learning, self-supervised learning, and multi-source data fusion.