Modeling of Biologically Effective Daily Radiant Exposures over Europe from Space Using SEVIRI Measurements and MERRA-2 Reanalysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ground-Based Measurements of UV Radiation
2.2. Ancillary Data
2.3. Model Description
2.3.1. Biologically Weighted Radiant Exposures
2.3.2. Clear-Sky Radiation
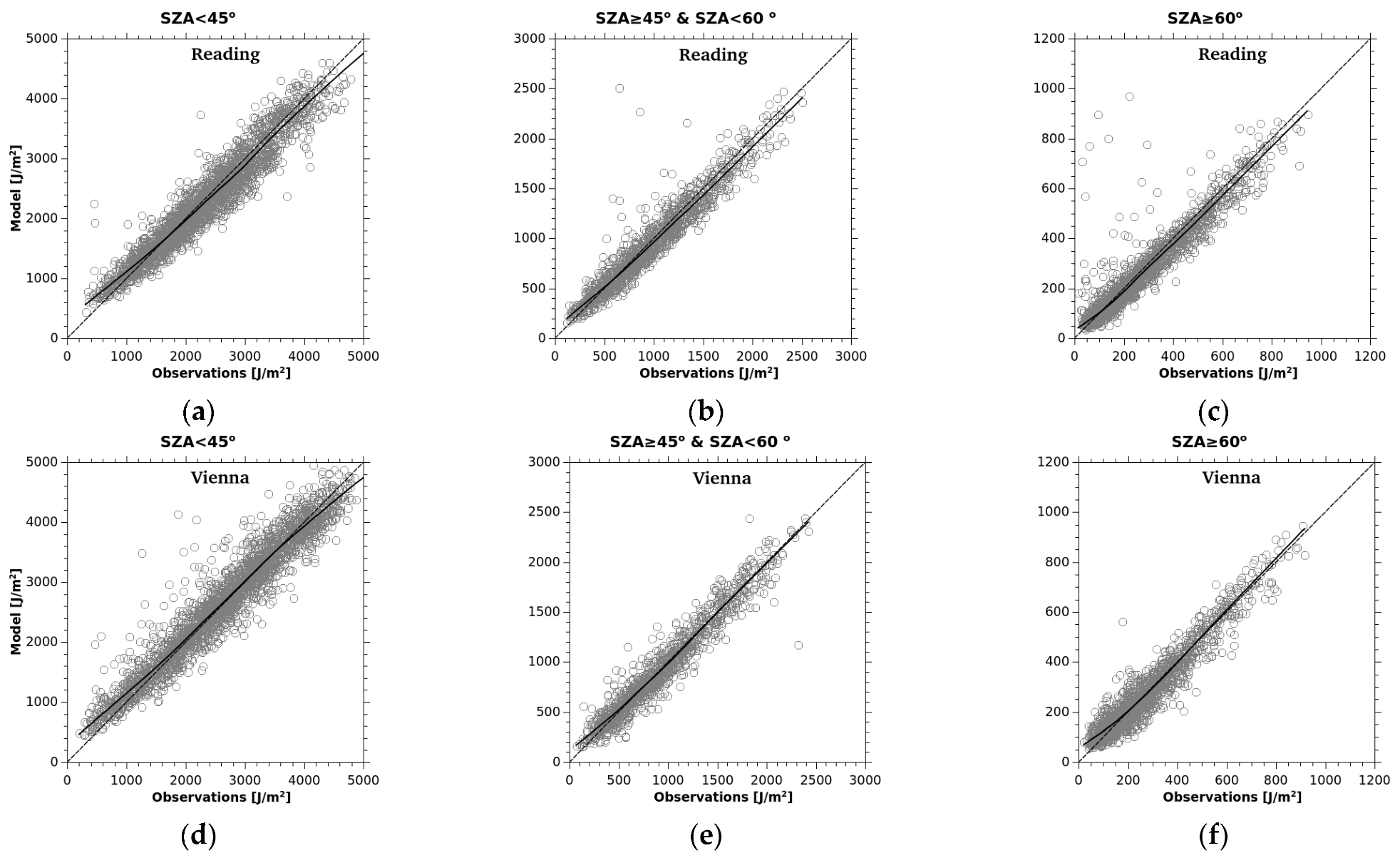
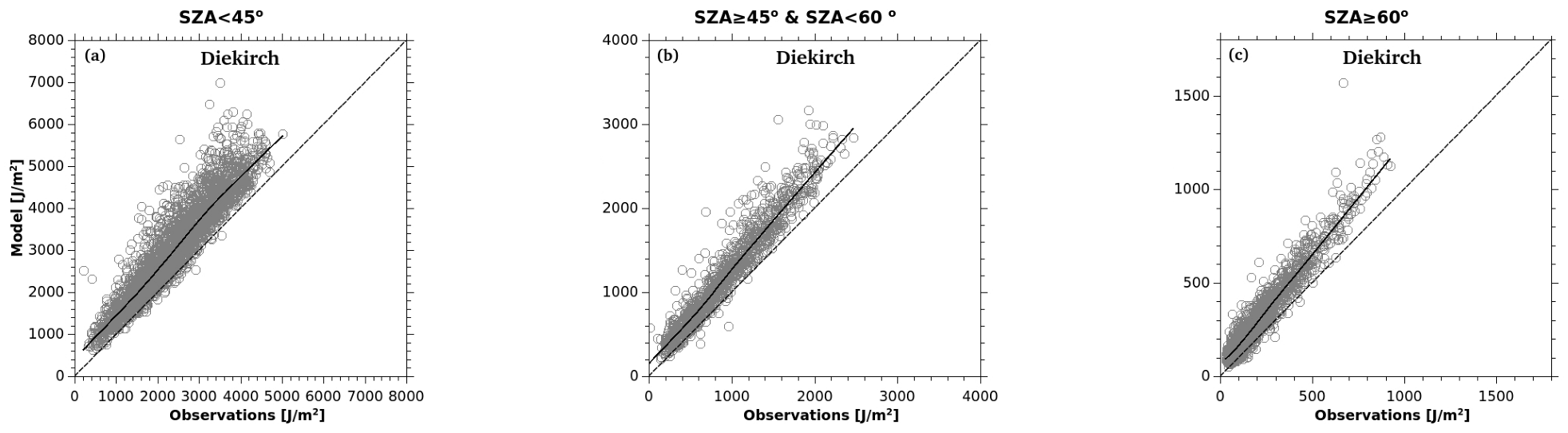
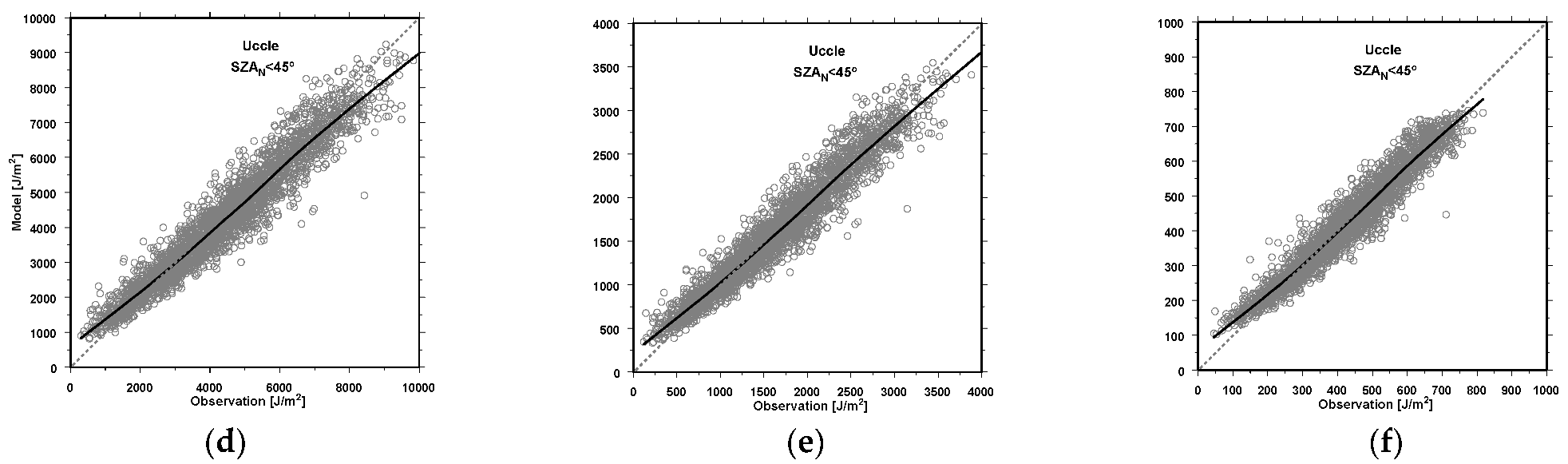
2.4. Model Validation
3. Results
3.1. Erythema Appearance
3.2. Other (Non-Erythemal) Biological Effects
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Station | SZAN < 45° | SZAN ≥ 45° and SZAN < 60° | SZAN ≥ 60° |
|---|---|---|---|
| Belsk (Poland) | 8 April–5 September | 28 February–7 April 6 September–14 October | 1 January–27 February 15 October–31 December |
| Reading (UK) | 6 April–6 September | 27 February–5 April 7 September–15 October | 1 January–26 February 16 October–31 December |
| Uccle (Belgium) | 4 April–7 September | 25 February–3 April 8 September–17 October | 1 January–24 February 18 October–31 December |
| Vienna (Austria) | 29 March–14 September | 18 February–28 March 15 September–23 October | 1 January–17 February 24 October–31 December |
| Diekirch (Luxembourg) | 2 April–10 September | 23 February–1 April 11 September–19 October | 1 January–22 February 20 October–31 December |
| Davos (Switzerland) | 26 March–18 September | 14 February–25 March 19 September–28 October | 1 January–13 February 29 October–1 December |
| Chisinau (Moldavia) | 26 March–17 September | 15 February–25 March 18 September–27 October | 1 January–14 February 28 October–31 December |
| Statistics [%] | Belsk | Uccle | Reading | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SZAN <45° | SZAN [45°, 60°] | SZAN >60° | SZAN <45° | SZAN [45°, 60°] | SZAN >60° | SZAN <45° | SZAN [45°, 60°] | SZAN >60° | |
| MRE | −17.15 | −6.49 | −6.63 | −13.67 | −6.74 | −1.68 | −17.18 | −9.14 | −2.17 |
| MAE | 18.17 | 15.42 | 18.06 | 15.03 | 11.91 | 15.71 | 18.52 | 13.02 | 14.38 |
| RMSE | 24.84 | 22.83 | 24.96 | 21.68 | 18.08 | 21.68 | 25.04 | 18.97 | 20.08 |
| SD | 17.98 | 21.94 | 24.10 | 16.83 | 16.79 | 21.62 | 18.23 | 16.63 | 19.97 |


References
- Berger, D.S.; Urbach, F. A climatology of sunburning ultraviolet radiation. Photochem. Photobiol. 1982, 35, 187–192. [Google Scholar] [CrossRef] [PubMed]
- Holick, M.F.; Chen, T.C. Vitamin D deficiency: A worldwide problem with health consequences. Am. J. Clin. Nutr. 2008, 87, 1080S–1086S. [Google Scholar] [CrossRef] [PubMed]
- Sivamani, R.K.; Crane, L.A.; Dellavalle, R.P. The benefits and risks of ultraviolet tanning and its alternatives: The role of prudent sun exposure. Dermatol. Clin. 2009, 27, 149–154. [Google Scholar] [CrossRef] [PubMed]
- Krzyścin, J.W.; Guzikowski, J.; Rajewska-Więch, B. Optimal vitamin D3 daily intake of 2000IU inferred from modeled solar exposure of ancestral humans in Northern Tanzania. J. Photochem. Photobiol. B Biol. 2016, 159, 101–105. [Google Scholar] [CrossRef] [PubMed]
- Young, A.R. Acute effects of UVR on human eyes and skin. Prog. Biophys. Mol. Biol. 2006, 92, 80–85. [Google Scholar] [CrossRef]
- Krzyścin, J.W.; Narbutt, J.; Lesiak, A.; Jarosławski, J.; Sobolewski, P.S.; Rajewska-Wiȩch, B.; Szkop, A.; Wink, J.; Czerwińska, A. Perspectives of the antipsoriatic heliotherapy in Poland. J. Photochem. Photobiol. B Biol. 2014, 140, 111–119. [Google Scholar] [CrossRef]
- Liu, D.; Fernandez, B.O.; Hamilton, A.; Lang, N.N.; Gallagher, J.M.; Newby, D.E.; Feelisch, M.; Weller, R.B. UVA irradiation of human skin vasodilates arterial vasculature and lowers blood pressure independently of nitric oxide synthase. J. Investig. Dermatol. 2014, 134, 1839–1846. [Google Scholar] [CrossRef]
- Bernhard, G.H.; Madronich, S.; Lucas, R.M.; Byrne, S.N.; Schikowski, T.; Neale, R.E. Linkages between COVID-19, solar UV radiation, and the Montreal protocol. Photochem. Photobiol. Sci. 2023, 22, 991–1009. [Google Scholar] [CrossRef]
- Biasin, M.; Strizzi, S.; Bianco, A.; Macchi, A.; Utyro, O.; Pareschi, G.; Loffreda, A.; Cavalleri, A.; Lualdi, M.; Trabattoni, D.; et al. UV and violet light can neutralize SARS-CoV-2 infectivity. J. Photochem. Photobiol. 2022, 10, 100107. [Google Scholar] [CrossRef]
- Lucas, R.M.; Yazar, S.; Young, A.R.; Norval, M.; de Gruijl, F.R.; Takizawa, Y.; Rhodes, L.E.; Sinclair, C.A.; Neale, R.E. Human health in relation to exposure to solar ultraviolet radiation under changing stratospheric ozone and climate. Photochem. Photobiol. Sci. 2019, 18, 641–680. [Google Scholar] [CrossRef]
- Berger, D.S. The sunburning ultraviolet meter: Design and performance. Photochem. Photobiol. 1976, 24, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Słomka, J.; Słomka, K. Biologically active solar UV radiation at Belsk in years 1976–1992. Inst. Geophys. Pol. Acad. Sci. 1993, D-40, 71–81. [Google Scholar]
- Josefsson, W. UV-radiation 1983−2003 measured at Norrköping, Sweden. Theor. Appl. Climatol. 2006, 83, 59–76. [Google Scholar] [CrossRef]
- Hülsen, G.; Gröbner, J. Characterization and calibration of ultraviolet broadband radiometers measuring erythemally weighted irradiance. Appl. Opt. 2007, 46, 5877–5886. [Google Scholar] [CrossRef] [PubMed]
- Schmalwieser, A.W.; Gröbner, J.; Blumthaler, M.; Klotz, B.; De Backer, H.; Bolsée, D.; Werner, R.; Tomsic, D.; Metelka, L.; Eriksen, P.; et al. UV index monitoring in Europe. Photochem. Photobiol. Sci. 2017, 16, 1349–1370. [Google Scholar] [CrossRef]
- Tanskanen, A.; Lindfors, A.; Määttä, A.; Krotkov, N.; Herman, J.; Kaurola, J.; Koskela, T.; Lakkala, K.; Fioletov, V.; Bernhard, G.; et al. Validation of daily erythemal doses from Ozone Monitoring Instrument with ground-based UV measurement data. J. Geophys. Res. 2007, 112, D24S44. [Google Scholar] [CrossRef]
- Zempila, M.-M.; van Geffen, J.H.; Taylor, M.; Fountoulakis, I.; Koukouli, M.-E.; van Weele, M.; van der A, R.J.; Bais, A.; Meleti, C.; Balis, D. TEMIS UV product validation using NILU-UV ground-based measurements in Thessaloniki. Atmos. Chem. Phys. 2017, 17, 7157–7174. [Google Scholar] [CrossRef]
- Dave, J.V. Meaning of successive iteration of the auxiliary equation in the theory of radiative transfer. Astrophys. J. 1964, 140, 1292–1303. [Google Scholar] [CrossRef]
- Allaart, M.; van Weele, M.; Fortuin, P.; Kelder, H. An empirical model to predict the UV-index based on solar zenith angles and total ozone. Meteorol. Appl. 2004, 11, 59–65. [Google Scholar] [CrossRef]
- Czerwińska, A.; Krzyścin, J. Measurements of biologically effective solar radiation using erythemal weighted broadband meters. Photochem. Photobiol. Sci. 2024, 23, 479–492. [Google Scholar] [CrossRef]
- Madronich, S. The atmosphere and UV-B radiation at ground level. In Environmental UV Photobiology; Björn, L.O., Young, A.R., Eds.; Springer: Boston, MA, USA, 1993; pp. 1–39. [Google Scholar]
- Slaper, H.; Reinen, H.; Blumthaler, M.; Huber, M.; Kuik, F. Comparing ground level spectrally resolved UV measurements from various instruments: A technique resolving effects of wavelength shifts and slit width. Geophys. Res. Lett. 1995, 22, 2721–2724. [Google Scholar] [CrossRef]
- ISO/CIE 17166:2019(E); Erythema Reference Action Spectrum and Standard Erythema Dose. CIE: Vienna, Austria, 2019; pp. 1–5.
- Collow, A.; Bosilovich, M.; Dezfuli, A.; Lucchesi, R. File Specification for MERRA-2 Climate Statistics Products; GMAO Office Note No. 19 (Version 1.0); 2020; 15p. Available online: https://gmao.gsfc.nasa.gov/pubs/docs/Collow1253.pdf (accessed on 9 October 2024).
- Wargan, K.; Labow, G.; Frith, S.; Pawson, S.; Livesey, N.; Partyka, G. Evaluation of the Ozone Fields in NASA’s MERRA-2 Reanalysis. J. Clim. 2017, 30, 2961–2988. [Google Scholar] [CrossRef] [PubMed]
- Coldewey-Egbers, M.; Loyola, D.G.; Labow, G.; Frith, S.M. Comparison of GTO-ECV and adjusted MERRA-2 total ozone columns from the last 2 decades and assessment of interannual variability. Atmos. Meas. Tech. 2020, 13, 1633–1654. [Google Scholar] [CrossRef]
- Gupta, P.; Payra, S.; Bhatla, R.; Verma, S. An evaluation of long-term gridded datasets of total columnar ozone retrieved from MERRA-2 and AIRS over the Indian region. Environ. Sci. Pollut. Res. 2023, 30, 43586–43603. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.Y.H.; Jordan, R.C. The Interrelationship and Characteristic Distribution of Direct, Diffuse, and Total Solar Radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- CAMS Solar Radiation Time-Series. Available online: https://ads.atmosphere.copernicus.eu/datasets/cams-solar-radiation-timeseries?tab=overview (accessed on 26 August 2024).
- Giovanni: The Bridge between Data and Science v. 4.40. Available online: https://giovanni.gsfc.nasa.gov/giovanni/ (accessed on 26 August 2024).
- OMI/Aura Surface UVB Irradiance and Erythemal Dose Daily L3 Global Gridded 1.0 Degree x 1.0 Degree V3. NASA Goddard Space Flight Center, Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: https://catalog.data.gov/dataset/omi-aura-surface-uvb-irradiance-and-erythemal-dose-daily-l3-global-gridded-1-0-degree-x-1- (accessed on 26 August 2024).
- Yesterday’s UV Dose and Archives. Available online: https://www.temis.nl/uvradiation/UVdose.php (accessed on 26 August 2024).
- UV Station Data Based on Operational TEMIS Satellite Ozone Data. Available online: https://www.temis.nl/uvradiation/UVarchive/stations_uv.php (accessed on 28 August 2024).
- CIE 174:2006; Action Spectrum for the Production of Previtamin D3 in Human Skin. CIE: Vienna, Austria, 2006; pp. 1–16.
- Krzyścin, J.W.; Jarosławski, J.; Rajewska-Więch, B.; Sobolewski, P.S.; Narbutt, J.; Lesiak, A.; Pawlaczyk, M. Effectiveness of heliotherapy for psoriasis clearance in low and mid-latitudinal regions: A theoretical approach. J. Photochem. Photobiol. B Biol. 2012, 115, 35–41. [Google Scholar] [CrossRef]
- Vanicek, K.; Frei, T.; Litynska, Z.; Schmalwieser, A. UV-Index for the Public; COST-713 Action; Publication of the European Communities: Brussels, Belgium, 2000; pp. 1–27. [Google Scholar]
- Engelsen, O.; Kylling, A. Fast simulation tool for ultraviolet radiation at the earth’s surface. Opt. Eng. 2005, 44, 041012. [Google Scholar] [CrossRef]
- Majewski, G.; Rogula-Kozłowska, W.; Czechowski, P.O.; Badyda, A.; Brandyk, A. The impact of selected parameters on visibility: First results from a long-term campaign in Warsaw, Poland. Atmosphere 2015, 6, 1154–1174. [Google Scholar] [CrossRef]
- Singh, A.; Bloss, W.J.; Pope, F.D. 60 years of UK visibility measurements: Impact of meteorology and atmospheric pollutants on visibility. Atmos. Chem. Phys. 2017, 17, 2085–2101. [Google Scholar] [CrossRef]
- Horvath, H. On the applicability of the Koschmieder visibility formula. Atmos. Environ. 1971, 5, 177–184. [Google Scholar] [CrossRef]
- Aeronet Aerosol Optical Depth. Available online: https://aeronet.gsfc.nasa.gov/new_web/climo_menu_new_v3.html (accessed on 26 August 2024).
- Schmalwieser, A.W.; Eschenbacher, S.; Schreder, J. UV-Biometer—The usage of erythemal weighted broadband meters for other biological effects. J. Photochem. Photobiol. B Biol. 2022, 230, 112442. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; Schmalwieser, A.W.; Raptis, P.I.; Papachristopoulou, K.; Fountoulakis, I.; Masoom, A.; Bais, A.F.; Bilbao, J.; Blumthaler, M.; et al. Real-time UV index retrieval in Europe using Earth observation-based techniques: System description and quality assessment. Atmos. Meas. Tech. 2021, 14, 5657–5699. [Google Scholar] [CrossRef]
- den Outer, P.N.; Slaper, H.; Kaurola, J.; Lindfors, A.; Kazantzidis, A.; Bais, A.F.; Feister, U.; Junk, J.; Janouch, M.; Josefsson, W. Reconstructing of erythemal ultraviolet radiation levels in Europe for the past 4 decades. J. Geophys. Res. 2010, 115, D10102. [Google Scholar] [CrossRef]
- Kato, S.; Marshak, A. Solar zenith and viewing geometry-dependent errors in satellite retrieved cloud optical thickness: Marine stratocumulus case. J. Geophys. Res. 2009, 114, D01202. [Google Scholar] [CrossRef]



| Station | Location | Altitude [m a.s.l.] | Instrument | Data Period | Data Source |
|---|---|---|---|---|---|
| Belsk Poland | 51.85°N, 20.79°E | 180 | SL Biometer, 501A Kipp&Zonen UV-S-E-T Brewer MK II | 2004–2012 2013–2023 2011–2023 | Upon request |
| Reading UK | 51.44°N, 0.94°W | 66 | Bentham DM150 | 2004–2023 | WOUDC No. 353 |
| Uccle Belgium | 50.80°N, 4.36°E | 100 | Brewer MK III | 2004–2023 | WOUDCNo. 053 |
| Diekirch Luxembourg | 49.87°N, 6.17°E | 218 | SL Biometer, 501A | 2004–2023 | WOUDC No. 412 |
| Vienna Austria | 48.26°N, 16.43°E | 160 | SL Biometer, 501A | 2004–2022 | WOUDC No. 167 |
| Chisinau Moldavia | 47.00°N, 28.82°E | 205 | Kipp&Zonen UV-S-B-C | 2004–2023 | WOUDC No. 455 |
| Davos Switzerland | 46.82°N, 9.85°E | 1590 | Kipp&Zonen UV-S-E-T | 2007–2023 | WOUDC No. 501 |
| Site | Regression Constants | |||||
|---|---|---|---|---|---|---|
| SZAN < 45° | SZAN ≥ 45° and < 60° | SZAN ≥ 60° | ||||
| Belsk | 0.954 | 0.817 | 0.928 | 0.755 | 0.952 | 0.649 |
| Reading | 1.012 | 0.822 | 1.018 | 0.778 | 1.031 | 0.727 |
| Vienna | 0.951 | 0.850 | 0.917 | 0.743 | 0.946 | 0.799 |
| Average | 0.973 | 0.830 | 0.954 | 0.758 | 0.977 | 0.725 |
| Metric | Belsk | Reading | Vienna | ||||||
|---|---|---|---|---|---|---|---|---|---|
| [%] | SZAN <45° | SZAN [45°, 60°] | SZAN >60° | SZAN <45° | SZAN [45°, 60°] | SZAN > 60° | SZAN <45° | SZAN [45°, 60°] | SZAN >60° |
| UBE model | |||||||||
| MRE | 0.49 | 3.88 | 4.26 | −3.66 | −3.39 | −0.70 | −3.01 | 1.03 | 0.11 |
| MAE | 9.45 | 12.97 | 20.22 | 9.48 | 10.66 | 12.49 | 9.99 | 12.19 | 15.55 |
| RMSE | 14.18 | 18.62 | 27.35 | 13.79 | 15.51 | 18.72 | 15.96 | 17.09 | 21.20 |
| SD | 14.18 | 18.22 | 27.03 | 13.30 | 15.52 | 18.71 | 15.68 | 17.07 | 21.22 |
| TEMIS_UV | |||||||||
| MRE | −13.36 | −8.45 | −17.33 | −20.14 | −11.34 | −2.63 | −15.24 | −8.67 | −9.16 |
| MAE | 14.58 | 15.23 | 27.15 | 20.68 | 13.70 | 12.39 | 16.49 | 15.59 | 19.64 |
| RMSE | 22.36 | 25.06 | 44.10 | 26.39 | 19.64 | 18.66 | 24.35 | 23.42 | 27.15 |
| SD | 17.94 | 23.61 | 40.57 | 17.07 | 16.04 | 18.48 | 18.99 | 21.77 | 25.57 |
| OMI_UV | |||||||||
| MRE | 1.53 | −7.27 | −27.01 | −18.95 | −24.75 | −25.39 | −1.72 | −8.76 | −13.37 |
| MAE | 13.19 | 18.50 | 39.24 | 21.23 | 26.31 | 28.19 | 12.99 | 17.86 | 24.56 |
| RMSE | 19.56 | 27.20 | 54.72 | 27.07 | 32.53 | 34.60 | 19.57 | 25.32 | 32.75 |
| SD | 19.51 | 26.23 | 47.56 | 19.34 | 21.12 | 23.51 | 19.50 | 23.79 | 29.92 |
| Metrics | UBE | OMI_UV | Temis_UV (Overpass) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| [%] | SZAN <45° | SZAN [45°, 60°] | SZAN >60° | SZAN <45° | SZAN [45°, 60°] | SZAN >60° | SZAN <45° | SZAN [45°, 60°] | SZAN >60° |
| Diekirch | |||||||||
| MRE | −5.38 | −8.07 | −18.77 | −16.33 | −30.36 | −50.27 | Not Available | ||
| MAE | 9.06 | 11.40 | 23.04 | 19.61 | 33.35 | 50.75 | |||
| RMSE | 13.85 | 16.83 | 30.37 | 25.94 | 39.22 | 56.37 | |||
| SD | 12.77 | 14.77 | 23.06 | 20.16 | 24.83 | 25.51 | |||
| Uccle | |||||||||
| MRE | −4.10 | −6.53 | −9.19 | −17.56 | −28.74 | −37.67 | −20.45 | −14.30 | −12.60 |
| MAE | 9.86 | 11.03 | 15.59 | 20.12 | 29.62 | 38.86 | 20.75 | 15.17 | 16.52 |
| RMSE | 14.61 | 16.83 | 23.19 | 26.36 | 35.73 | 45.00 | 26.52 | 21.23 | 24.29 |
| SD | 14.02 | 15.51 | 25.97 | 19.66 | 21.23 | 24.62 | 16.88 | 15.70 | 20.77 |
| Davos | |||||||||
| MRE | 10.28 | 20.86 | 23.05 | 1.86 | 16.73 | 18.88 | −2.35 | 22.52 | 35.09 |
| MAE | 16.67 | 23.54 | 25.24 | 20.75 | 24.54 | 26.60 | 15.92 | 27.04 | 39.60 |
| RMSE | 20.91 | 27.73 | 29.02 | 27.38 | 28.97 | 30.58 | 21.96 | 32.35 | 45.60 |
| SD | 18.21 | 18.29 | 17.64 | 27.33 | 23.67 | 24.07 | 21.84 | 23.23 | 29.14 |
| Chisinau | |||||||||
| MRE | 37.44 | 47.97 | 56.97 | 32.24 | 34.58 | 44.46 | 29.47 | 36.22 | 43.51 |
| MAE | 37.81 | 48.31 | 57.34 | 33.86 | 36.93 | 46.41 | 30.42 | 39.91 | 45.43 |
| RMSE | 38.86 | 49.91 | 58.90 | 35.57 | 40.41 | 50.49 | 31.84 | 42.34 | 48.55 |
| SD | 10.42 | 13.79 | 14.96 | 15.03 | 20.93 | 23.93 | 12.06 | 21.95 | 21.55 |
| Metric | No-Snow in Davos | Snow in Davos | ||||
|---|---|---|---|---|---|---|
| UBE | OMI_UV | Temis_UV | UBE | OMI_UV | Temis_UV | |
| MRE [%] | −0.47 | −14.26 | −7.27 | 26.13 | 25.17 | 40.60 |
| MAE [%] | 11.71 | 20.25 | 13.04 | 27.66 | 29.80 | 44.06 |
| RMSE [%] | 16.50 | 30.65 | 18.78 | 30.36 | 33.29 | 48.76 |
| SD [%] | 16.52 | 27.18 | 17.35 | 15.46 | 21.80 | 27.02 |
| Site | Regression Constants | |||||
|---|---|---|---|---|---|---|
| SZAN < 45° | SZAN ≥ [45°, 60°] | SZAN > 60° | ||||
| previtamin D3 synthesis | ||||||
| Belsk | 0.968 | 0.828 | 0.967 | 0.714 | 1.074 | 0.605 |
| Reading | 1.013 | 0.847 | 1.039 | 0.783 | 1.106 | 0.732 |
| Uccle | 1.063 | 0.867 | 1.044 | 0.776 | 1.140 | 0.765 |
| Average | 1.015 | 0.847 | 1.017 | 0.758 | 1.107 | 0.700 |
| psoriasis clearance | ||||||
| Belsk | 0.961 | 0.829 | 0.939 | 0.722 | 0.950 | 0.617 |
| Reading | 1.014 | 0.850 | 1.033 | 0.792 | 1.060 | 0.745 |
| Uccle | 1.045 | 0.867 | 1.014 | 0.778 | 1.058 | 0.770 |
| Average | 1.007 | 0.849 | 0.995 | 0.764 | 1.023 | 0.710 |
| SARS-CoV-2 virions inactivation | ||||||
| Belsk | 0.935 | 0.787 | 0.883 | 0.710 | 0.865 | 0.616 |
| Reading | 1.041 | 0.819 | 1.043 | 0.787 | 1.067 | 0.756 |
| Uccle | 1.003 | 0.820 | 0.970 | 0.757 | 1.009 | 0.764 |
| Average | 0.993 | 0.809 | 0.965 | 0.751 | 0.980 | 0.711 |
| Erythema Appearance (from Table 2) | ||||||
| Average | 0.973 | 0.830 | 0.954 | 0.758 | 0.977 | 0.725 |
| Statistics [%] | Belsk | Uccle | Reading | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SZAN <45° | SZA [45°, 60°] | SZAN >60° | SZAN <45° | SZA [45°, 60°] | SZAN >60° | SZAN <45° | SZA [45°, 60°] | SZAN >60° | |
| previtamin D3 synthesis | |||||||||
| MRE | −10.59 | −3.46 | 1.53 | −6.02 | −8.04 | −8.83 | −8.50 | −8.94 | −9.11 |
| MAE | 12.86 | 14.07 | 18.32 | 10.89 | 12.84 | 16.64 | 12.35 | 13.21 | 15.60 |
| RMSE | 19.24 | 20.45 | 24.41 | 15.64 | 19.38 | 24.45 | 17.90 | 19.22 | 22.23 |
| SD | 16.09 | 20.20 | 24.40 | 14.44 | 17.65 | 22.81 | 15.75 | 17.03 | 20.29 |
| psoriasis clearance | |||||||||
| MRE | −9.75 | −1.65 | 3.80 | −6.38 | −7.74 | −7.08 | −7.57 | −7.21 | −5.66 |
| MAE | 12.25 | 13.30 | 17.37 | 10.89 | 12.07 | 14.88 | 11.61 | 11.82 | 13.30 |
| RMSE | 18.66 | 19.30 | 22.93 | 15.93 | 18.22 | 22.61 | 16.82 | 17.33 | 20.13 |
| SD | 15.93 | 19.27 | 22.64 | 14.60 | 16.50 | 21.48 | 15.03 | 15.77 | 19.34 |
| SARS-CoV-2 virions inactivation | |||||||||
| MRE | −6.51 | −0.26 | 3.96 | −6.04 | −7.41 | −6.40 | −2.53 | −2.31 | −1.31 |
| MAE | 9.47 | 12.19 | 17.11 | 9.01 | 10.82 | 14.07 | 8.12 | 9.03 | 12.32 |
| RMSE | 15.61 | 18.31 | 22.55 | 13.33 | 16.64 | 21.45 | 12.08 | 13.05 | 18.61 |
| SD | 14.21 | 18.35 | 22.23 | 11.88 | 14.91 | 20.48 | 11.81 | 12.85 | 18.56 |
| Statistics [%] | Belsk | Uccle | Reading | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SZAN <45° | SZA [45°, 60°] | SZAN >60° | SZAN <45° | SZA [45°, 60°] | SZAN >60° | SZAN <45° | SZAN [45°, 60°] | SZAN >60° | |
| previtamin D3 synthesis | |||||||||
| MRE | −3.38 | 0.89 | 12.33 | 1.26 | 1.98 | 6.65 | −1.97 | 0.83 | 6.32 |
| MAE | 10.09 | 12.14 | 21.75 | 10.46 | 11.59 | 17.05 | 10.62 | 11.97 | 15.32 |
| RMSE | 15.92 | 18.14 | 27.55 | 14.54 | 16.10 | 21.85 | 15.34 | 16.50 | 19.98 |
| SD | 15.56 | 18.13 | 24.64 | 14.49 | 15.98 | 20.82 | 15.22 | 16.49 | 18.96 |
| psoriasis clearance | |||||||||
| MRE | −3.91 | −1.55 | 2.91 | −0.16 | −0.41 | 0.17 | −1.95 | −0.02 | 1.82 |
| MAE | 9.93 | 11.52 | 18.48 | 10.08 | 10.52 | 14.28 | 10.30 | 11.30 | 13.30 |
| RMSE | 15.68 | 17.75 | 24.96 | 14.52 | 15.36 | 20.27 | 14.83 | 15.83 | 18.75 |
| SD | 15.19 | 17.69 | 24.80 | 14.52 | 15.36 | 20.27 | 14.71 | 15.84 | 18.66 |
| SARS-CoV-2 virions inactivation | |||||||||
| MRE | −3.47 | −5.78 | −4.40 | −0.41 | −2.86 | −3.65 | 3.11 | 2.02 | 1.93 |
| MAE | 8.26 | 12.02 | 19.47 | 7.83 | 9.01 | 13.56 | 8.72 | 10.00 | 12.93 |
| RMSE | 12.99 | 18.01 | 25.92 | 11.78 | 13.93 | 20.37 | 11.79 | 13.58 | 18.28 |
| SD | 12.52 | 17.06 | 25.56 | 11.77 | 13.64 | 20.04 | 11.38 | 13.43 | 18.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czerwińska, A.; Krzyścin, J. Modeling of Biologically Effective Daily Radiant Exposures over Europe from Space Using SEVIRI Measurements and MERRA-2 Reanalysis. Remote Sens. 2024, 16, 3797. https://doi.org/10.3390/rs16203797
Czerwińska A, Krzyścin J. Modeling of Biologically Effective Daily Radiant Exposures over Europe from Space Using SEVIRI Measurements and MERRA-2 Reanalysis. Remote Sensing. 2024; 16(20):3797. https://doi.org/10.3390/rs16203797
Chicago/Turabian StyleCzerwińska, Agnieszka, and Janusz Krzyścin. 2024. "Modeling of Biologically Effective Daily Radiant Exposures over Europe from Space Using SEVIRI Measurements and MERRA-2 Reanalysis" Remote Sensing 16, no. 20: 3797. https://doi.org/10.3390/rs16203797
APA StyleCzerwińska, A., & Krzyścin, J. (2024). Modeling of Biologically Effective Daily Radiant Exposures over Europe from Space Using SEVIRI Measurements and MERRA-2 Reanalysis. Remote Sensing, 16(20), 3797. https://doi.org/10.3390/rs16203797






