An Improved Adaptive Grid-Based Progressive Triangulated Irregular Network Densification Algorithm for Filtering Airborne LiDAR Data
Abstract
:1. Introduction
2. Datasets
3. Methodology
3.1. Outlier Removal
3.1.1. Radius Outlier Removal Algorithm
3.1.2. Kd-Tree Outlier Removal Algorithm
3.2. Seed Point Selection
3.2.1. Primary Grid Division
3.2.2. Secondary Grid Division
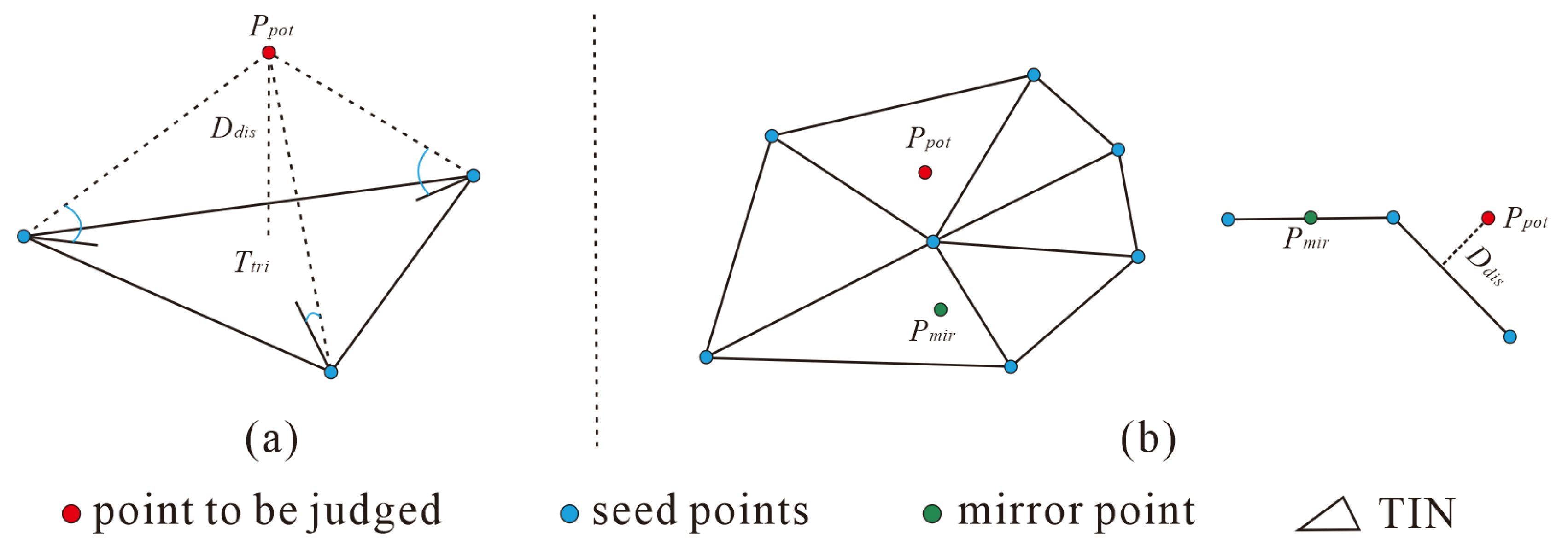
3.3. Iterative Densification
3.4. Evaluation Strategy
4. Results
4.1. Outlier Removal
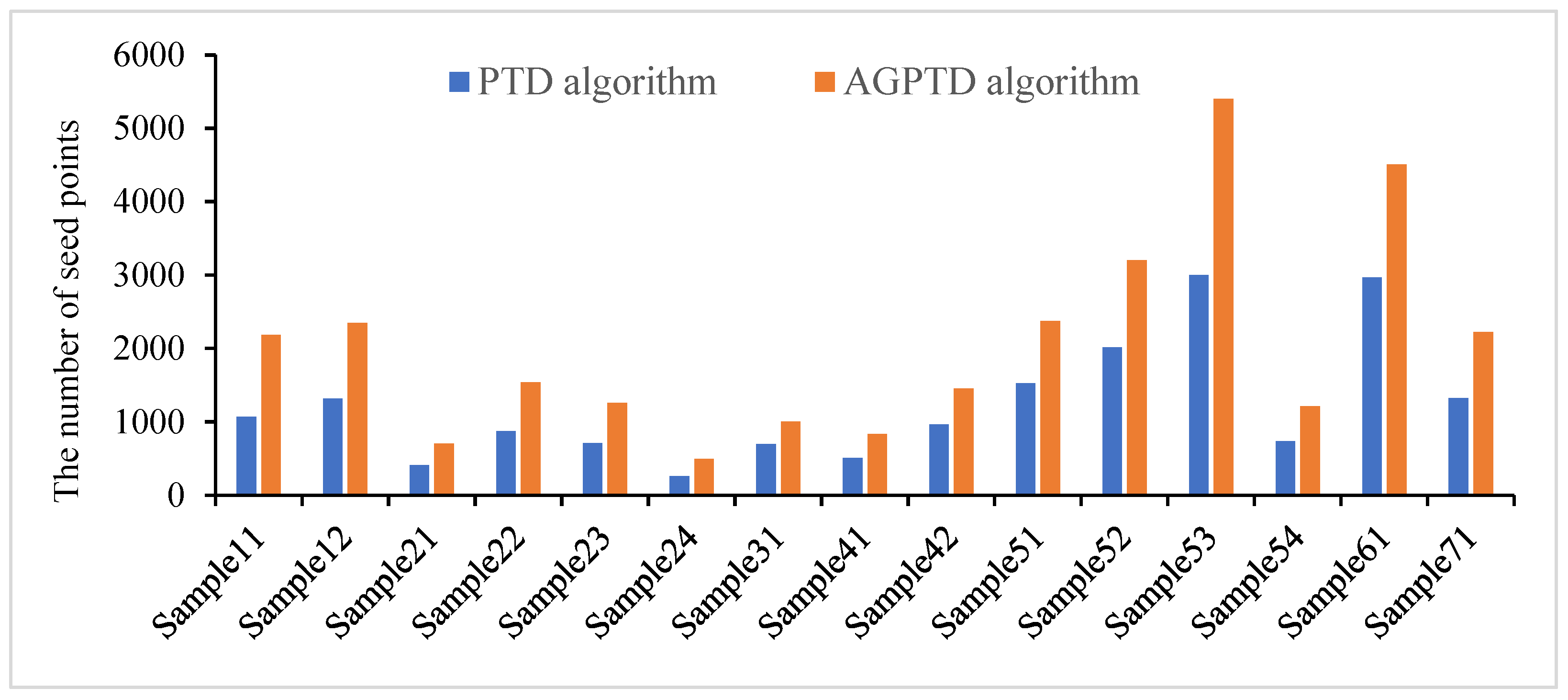
4.2. Seed Point Selection
4.3. Filtering Performance
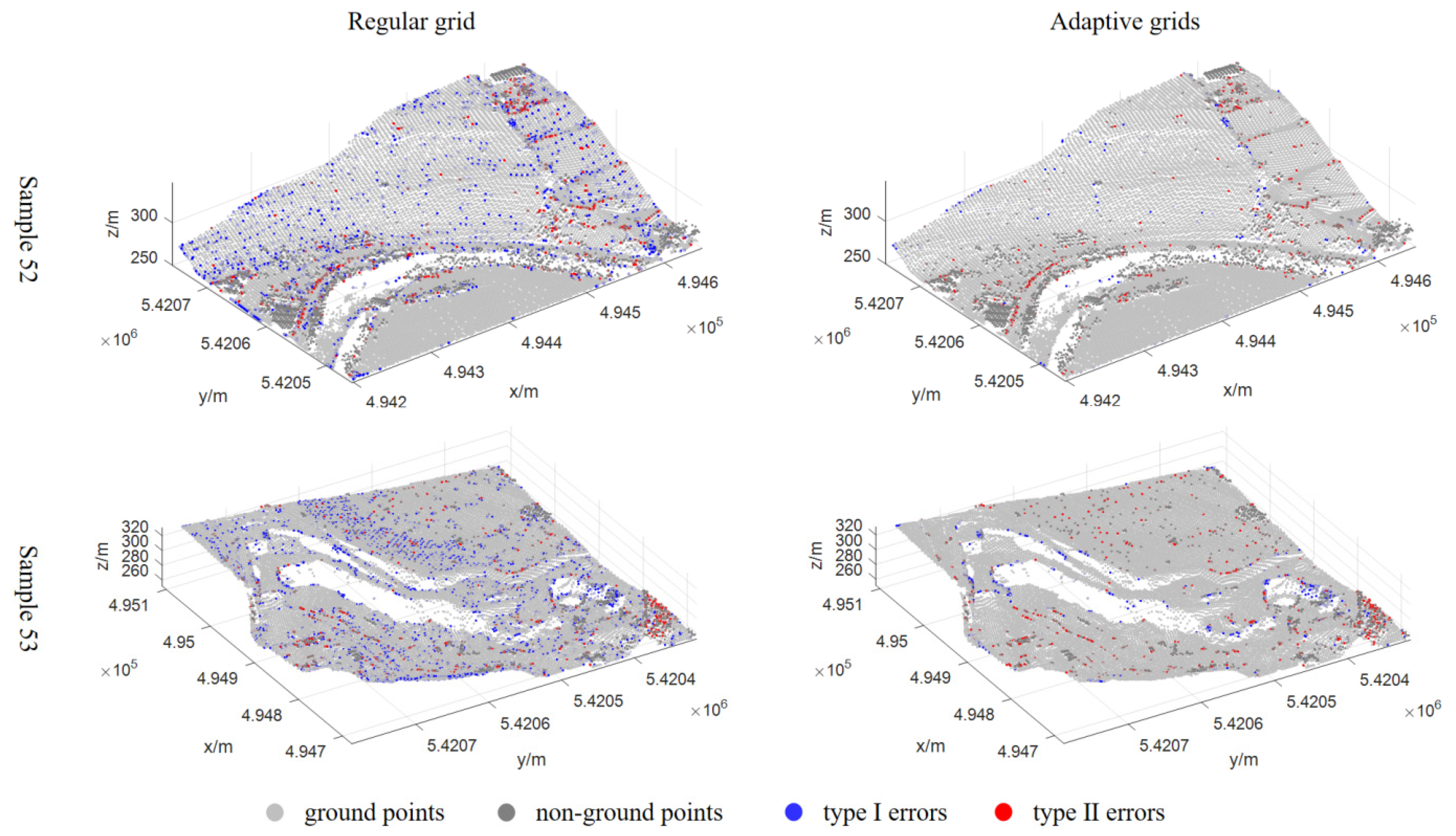
4.3.1. Qualitative Analysis
4.3.2. Quantitative Analysis
5. Discussion
5.1. Comparison with Publicized Improved PTD Algorithm
5.2. Comparison with Other Filtering Methods
5.3. Limitations and Prospects
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, M.E.N.O.; Taha, L.G.E.-D.; Mohamed, M.H.A.; Mandouh, A.A. Generation of Digital Terrain Model from Multispectral LiDar Using Different Ground Filtering Techniques. Egypt. J. Remote Sens. Space Sci. 2021, 24, 181–189. [Google Scholar] [CrossRef]
- Chen, C.; Wu, H.; Yang, Z.; Li, Y. Adaptive Coarse-to-Fine Clustering and Terrain Feature-Aware-Based Method for Reducing LiDAR Terrain Point Clouds. ISPRS J. Photogramm. Remote Sens. 2023, 200, 89–105. [Google Scholar] [CrossRef]
- Shao, J.; Yao, W.; Wan, P.; Luo, L.; Wang, P.; Yang, L.; Lyu, J.; Zhang, W. Efficient Co-Registration of UAV and Ground LiDAR Forest Point Clouds Based on Canopy Shapes. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103067. [Google Scholar] [CrossRef]
- Guo, L.; Wu, Y.; Deng, L.; Hou, P.; Zhai, J.; Chen, Y. A Feature-Level Point Cloud Fusion Method for Timber Volume of Forest Stands Estimation. Remote Sens. 2023, 15, 2995. [Google Scholar] [CrossRef]
- Gao, J.; Chen, Y.; Junior, J.; Wang, C.; Li, J. Rapid Extraction of Urban Road Guardrails From Mobile LiDAR Point Clouds. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1572–1577. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Li, J.; Tian, M.; Dai, W.; Zhong, R. Automated Reconstruction of Building LoDs from Airborne LiDAR Point Clouds Using an Improved Morphological Scale Space. Remote Sens. 2017, 9, 14. [Google Scholar] [CrossRef]
- Almeida, D.R.A.; Broadbent, E.N.; Zambrano, A.M.A.; Wilkinson, B.E.; Ferreira, M.E.; Chazdon, R.; Meli, P.; Gorgens, E.B.; Silva, C.A.; Stark, S.C.; et al. Monitoring the Structure of Forest Restoration Plantations with a Drone-Lidar System. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 192–198. [Google Scholar] [CrossRef]
- Morsy, S.; Shaker, A.; El-Rabbany, A. Classification of Multispectral Airborne LiDAR Data Using Geometric and Radiometric Information. Geomatics 2022, 2, 370–389. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Tian, S.; Lu, B.; Zhang, L.; Ning, X.; Bai, X. Deep Learning-Based 3D Point Cloud Classification: A Systematic Survey and Outlook. Displays 2023, 79, 102456. [Google Scholar] [CrossRef]
- Pan, Y.; Han, Y.; Wang, L.; Chen, J.; Meng, H.; Wang, G.; Zhang, Z.; Wang, S. 3D Reconstruction of Ground Crops Based on Airborne LiDAR Technology. IFAC-Pap. 2019, 52, 35–40. [Google Scholar] [CrossRef]
- Coiffier, G.; Basselin, J.; Ray, N.; Sokolov, D. Parametric Surface Fitting on Airborne Lidar Point Clouds for Building Reconstruction. Comput.-Aided Des. 2021, 140, 103090. [Google Scholar] [CrossRef]
- Bizjak, M.; Mongus, D.; Žalik, B.; Lukač, N. Novel Half-Spaces Based 3D Building Reconstruction Using Airborne LiDAR Data. Remote Sens. 2023, 15, 1269. [Google Scholar] [CrossRef]
- Qin, N.; Tan, W.; Guan, H.; Wang, L.; Ma, L.; Tao, P.; Fatholahi, S.; Hu, X.; Li, J. Towards Intelligent Ground Filtering of Large-Scale Topographic Point Clouds: A Comprehensive Survey. Int. J. Appl. Earth Obs. Geoinf. 2023, 125, 103566. [Google Scholar] [CrossRef]
- Qi, C.; Wang, X.; Su, D.; Guo, Y.; Yang, F. Comparison and Analysis of Ground Seed Detectors and Interpolation Methods in Airborne LiDAR Filtering. Egypt. J. Remote Sens. Space Sci. 2023, 26, 1009–1019. [Google Scholar] [CrossRef]
- Vosselman, G. Slope Based Filtering of Laser Altimetry Data. Int. Soc. Photogramm. Remote Sens. 2000, 33 Pt B3, 935–942. [Google Scholar]
- Susaki, J. Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation. Remote Sens. 2012, 4, 1804–1819. [Google Scholar] [CrossRef]
- Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering Airborne Laser Scanning Data with Morphological Methods. Photogramm. Eng. Remote Sens. 2007, 73, 175–185. [Google Scholar] [CrossRef]
- Li, Y.; Yong, B.; Van Oosterom, P.; Lemmens, M.; Wu, H.; Ren, L.; Zheng, M.; Zhou, J. Airborne LiDAR Data Filtering Based on Geodesic Transformations of Mathematical Morphology. Remote Sens. 2017, 9, 1104. [Google Scholar] [CrossRef]
- Meng, X.; Lin, Y.; Yan, L.; Gao, X.; Yao, Y.; Wang, C.; Luo, S. Airborne LiDAR Point Cloud Filtering by a Multilevel Adaptive Filter Based on Morphological Reconstruction and Thin Plate Spline Interpolation. Electronics 2019, 8, 1153. [Google Scholar] [CrossRef]
- Filin, S. Surface Clustering from Airborne Laser Scanning Data. Remote Sens. Spat. Inf. Sci. 2002, 34, 119–124. [Google Scholar]
- Ni, H.; Lin, X.; Zhang, J.; Chen, D.; Peethambaran, J. Joint Clusters and Iterative Graph Cuts for ALS Point Cloud Filtering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 990–1004. [Google Scholar] [CrossRef]
- Liu, H.; Dong, P.; Wu, C.; Wang, P.; Fang, M. Individual Tree Identification Using a New Cluster-Based Approach with Discrete-Return Airborne LiDAR Data. Remote Sens. Environ. 2021, 258, 112382. [Google Scholar] [CrossRef]
- Axelsson, P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2000, 33, 111–118. [Google Scholar]
- Zhang, J.; Lin, X. Filtering Airborne LiDAR Data by Embedding Smoothness-Constrained Segmentation in Progressive TIN Densification. ISPRS J. Photogramm. Remote Sens. 2013, 81, 44–59. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, J. Segmentation-Based Filtering of Airborne LiDAR Point Clouds by Progressive Densification of Terrain Segments. Remote Sens. 2014, 6, 1294–1326. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Dong, P.; Xi, X.; Luo, S.; Qin, H. A Revised Progressive TIN Densification for Filtering Airborne LiDAR Data. Measurement 2017, 104, 70–77. [Google Scholar] [CrossRef]
- Cai, S.; Zhang, W.; Liang, X.; Wan, P.; Qi, J.; Yu, S.; Yan, G.; Shao, J. Filtering Airborne LiDAR Data Through Complementary Cloth Simulation and Progressive TIN Densification Filters. Remote Sens. 2019, 11, 1037. [Google Scholar] [CrossRef]
- Hu, X.; An, X.; Li, L. Easy Synthesis of Highly Fluorescent Carbon Dots from Albumin and Their Photoluminescent Mechanism and Biological Imaging Applications. Mater. Sci. Eng. C 2016, 58, 730–736. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Zhao, X.; Hu, T.; Guo, Q. A Point-Based Fully Convolutional Neural Network for Airborne LiDAR Ground Point Filtering in Forested Environments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3958–3974. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Teferle, F.; Li, J.; Lindenbergh, R.; Hunegnaw, A. An Efficient Deep Learning Approach for Ground Point Filtering in Aerial Laser Scanning Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2021, 43, 31–38. [Google Scholar] [CrossRef]
- Qin, N.; Tan, W.; Ma, L.; Zhang, D.; Guan, H.; Li, J. Deep Learning for Filtering the Ground from ALS Point Clouds: A Dataset, Evaluations and Issues. ISPRS J. Photogramm. Remote Sens. 2023, 202, 246–261. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. Parameter-Free Ground Filtering of LiDAR Data for Automatic DTM Generation. ISPRS J. Photogramm. Remote Sens. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Dong, Z.; Zang, Y.; Li, J. Two-Step Adaptive Extraction Method for Ground Points and Breaklines from Lidar Point Clouds. ISPRS J. Photogramm. Remote Sens. 2016, 119, 373–389. [Google Scholar] [CrossRef]
- Pingel, T.J.; Clarke, K.C.; McBride, W.A. An Improved Simple Morphological Filter for the Terrain Classification of Airborne LIDAR Data. ISPRS J. Photogramm. Remote Sens. 2013, 77, 21–30. [Google Scholar] [CrossRef]
- Gu, Y.; Zhou, D.; An, Y.; Wang, R.; Wu, K.; Diao, X. Ground Point Extraction Using Self-Adaptive-Grid and Point to Surface Comparison. Measurement 2022, 204, 112057. [Google Scholar] [CrossRef]
- Chen, N.; Wang, N.; He, Y.; Ding, X.; Kong, J. An Improved Progressive Triangular Irregular Network Densification Filtering Algorithm for Airborne LiDAR Data. Front. Earth Sci. 2023, 10, 1015153. [Google Scholar] [CrossRef]
- Dong, Y.; Cui, X.; Zhang, L.; Ai, H. An Improved Progressive TIN Densification Filtering Method Considering the Density and Standard Variance of Point Clouds. ISPRS Int. J. Geo-Inf. 2018, 7, 409. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved Progressive TIN Densification Filtering Algorithm for Airborne LiDAR Data in Forested Areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Li, W.; Dai, H. A Multiresolution Hierarchical Classification Algorithm for Filtering Airborne LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2013, 82, 1–9. [Google Scholar] [CrossRef]
- Hu, H.; Ding, Y.; Zhu, Q.; Wu, B.; Lin, H.; Du, Z.; Zhang, Y.; Zhang, Y. An Adaptive Surface Filter for Airborne Laser Scanning Point Clouds by Means of Regularization and Bending Energy. ISPRS J. Photogramm. Remote Sens. 2014, 92, 98–111. [Google Scholar] [CrossRef]
- Mongus, D.; Zalik, B. Computationally Efficient Method for the Generation of a Digital Terrain Model From Airborne LiDAR Data Using Connected Operators. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 340–351. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Zhao, N.; Guo, J.; Liu, G. A Fast and Robust Interpolation Filter for Airborne Lidar Point Clouds. PLoS ONE 2017, 12, e0176954. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.; Li, Y. Aerial Lidar Point Cloud Voxelization with Its 3D Ground Filtering Application. Photogramm. Eng. Remote Sens. 2017, 83, 95–107. [Google Scholar] [CrossRef]
- Bayram, E.; Frossard, P.; Vural, E.; Alatan, A. Analysis of Airborne LiDAR Point Clouds With Spectral Graph Filtering. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1284–1288. [Google Scholar] [CrossRef]
- Buján, S.; Cordero, M.; Miranda, D. Hybrid Overlap Filter for LiDAR Point Clouds Using Free Software. Remote Sens. 2020, 12, 1051. [Google Scholar] [CrossRef]
- Chen, C.; Chang, B.; Li, Y.; Shi, B. Filtering Airborne LiDAR Point Clouds Based on a Scale-Irrelevant and Terrain-Adaptive Approach. Measurement 2021, 171, 108756. [Google Scholar] [CrossRef]
- Roggero, M. Airborne Laser Scanning-Clustering in Raw Data. ISPRS Arch. 2001, XXXIV, 227–232. [Google Scholar]
- Kraus, K.; Pfeifer, N. Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Wack, R.; Wimmer, A. Digital Terrain Models from Airborne Laser Scanner Data—A Grid Based Approach. ISPRS Arch. 2002, 34, 293–296. [Google Scholar]
- Sithole, G. Filtering of Laser Altimetry Data Using a Slope Adaptive Filter. ISPRS Arch. 2001, XXXIV-3/W4, 22–24. [Google Scholar]
- Brovelli, M.; Cannata, M.; Longoni, U. Managing and Processing LIDAR Data within GRASS; University of Trento: Trento, Italy, 2002. [Google Scholar]
- Elmqvist, M.; Jungert, E.; Lantz, F.; Persson, Å.; Söderman, U. Terrain Modelling and Analysis Using Laser Scanner Data. ISPRS Arch. 2001, 34, 219–226. [Google Scholar]
- Sohn, G.; Dowman, I. Terrain Surface Reconstruction by the Use of Tetrahedron Model with the MDL Criterion. ISPRS Arch. 2002, 34, 336–344. [Google Scholar]








| Sample | 11 | 12 | 21 | 22 | 23 | 24 | 31 | 41 | 42 | 51 | 52 | 53 | 54 | 61 | 71 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter setting | k | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| s (m) | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 14 | 14 | 14 | 14 | 14 | 14 | |
| θ (°) | 39 | 34 | 45 | 35 | 34 | 39 | 34 | 45 | 37 | 26 | 28 | 29 | 15 | 28 | 35 | |
| d (m) | 0.8 | 0.6 | 0.4 | 1.0 | 1.2 | 0.7 | 0.5 | 1.4 | 0.5 | 0.5 | 1.2 | 1.4 | 0.6 | 1.0 | 0.9 | |
| Filtered | Metrics of Quantitative Evaluations | Additional Metrics | ||||
|---|---|---|---|---|---|---|
| Ground | Non-ground | T.I = b/(a + b) | Po = (a + d)/e | accuracy = (a + d)/e | ||
| Reference | Ground | a | b | T.II = c/(c + d) | Pc = ((a + b) × (a + c) + (c + d) × (b + d))/e2 | precision = a/(a + c) |
| Non-ground | c | d | T.E. = (b + c)/e | kp = (Po − Pc)/(1 − Pc) | recall = a/(a + b) | |
| Sample | Number of Points | Number of Outliers | Precision (%) | Filtration Proportion (%) | ||||
|---|---|---|---|---|---|---|---|---|
| T | GP | NGP | T | GP | NGP | |||
| 11 | 38,010 | 21,786 | 16,224 | 14,103 | 28 | 14,075 | 99.80% | 86.75% |
| 12 | 52,119 | 26,691 | 25,428 | 23,893 | 32 | 23,861 | 99.87% | 93.84% |
| 21 | 12,960 | 10,085 | 2875 | 2581 | 8 | 2573 | 99.69% | 89.50% |
| 22 | 32,706 | 22,504 | 10,202 | 9428 | 52 | 9376 | 99.45% | 91.90% |
| 23 | 25,095 | 13,223 | 11,872 | 11,077 | 14 | 11,063 | 99.87% | 93.19% |
| 24 | 7492 | 5434 | 2058 | 1730 | 3 | 1727 | 99.83% | 83.92% |
| 31 | 28,862 | 15,556 | 13,306 | 12,632 | 21 | 12,611 | 99.83% | 94.78% |
| 41 | 11,231 | 5602 | 5629 | 5504 | 7 | 5497 | 99.87% | 97.66% |
| 42 | 42,470 | 12,443 | 30,027 | 29,381 | 8 | 29,373 | 99.97% | 97.82% |
| 51 | 17,845 | 13,950 | 3895 | 2497 | 7 | 2490 | 99.72% | 63.93% |
| 52 | 22,474 | 20,112 | 2362 | 1533 | 14 | 1519 | 99.09% | 64.31% |
| 53 | 34,378 | 32,989 | 1389 | 490 | 14 | 476 | 97.14% | 34.27% |
| 54 | 8608 | 3983 | 4625 | 3897 | 1 | 3896 | 99.97% | 84.24% |
| 61 | 35,060 | 33,854 | 1206 | 629 | 8 | 621 | 98.73% | 51.49% |
| 71 | 15,645 | 13,875 | 1770 | 1244 | 4 | 1240 | 99.68% | 70.06% |
| Sample | NSP for Classical PTD | NSP for AGPTD | Difference | Precision of Seed Point Selection by AGPTD (%) | |||
|---|---|---|---|---|---|---|---|
| PG | SG | TSP | NSP | Rates | |||
| 11 | 1071 | 1071 | 1934 | 2179 | 1108 | 103.45% | 98.72% |
| 12 | 1318 | 1318 | 1497 | 2345 | 1027 | 77.92% | 98.93% |
| 21 | 408 | 408 | 401 | 702 | 294 | 72.06% | 99.43% |
| 22 | 876 | 876 | 956 | 1542 | 666 | 76.03% | 99.61% |
| 23 | 710 | 710 | 836 | 1257 | 547 | 77.04% | 98.65% |
| 24 | 258 | 258 | 349 | 497 | 239 | 92.64% | 98.99% |
| 31 | 697 | 697 | 429 | 1001 | 304 | 43.62% | 98.70% |
| 41 | 508 | 508 | 470 | 833 | 325 | 63.98% | 99.64% |
| 42 | 962 | 962 | 716 | 1451 | 489 | 50.83% | 97.17% |
| 51 | 1528 | 1528 | 1423 | 2373 | 845 | 55.30% | 98.65% |
| 52 | 2013 | 2013 | 2292 | 3198 | 1185 | 58.87% | 99.19% |
| 53 | 2998 | 2998 | 4020 | 5399 | 2401 | 80.09% | 99.83% |
| 54 | 734 | 734 | 734 | 1210 | 476 | 64.85% | 96.69% |
| 61 | 2967 | 2967 | 2408 | 4502 | 1535 | 51.74% | 99.80% |
| 71 | 1325 | 1325 | 1358 | 2222 | 897 | 67.70% | 99.59% |
| Sample | 11 | 12 | 21 | 22 | 23 | 24 | 31 | 41 | 42 | 51 | 52 | 53 | 54 | 61 | 71 | Avg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| accuracy | 95.37 | 97.84 | 98.98 | 97.48 | 96.83 | 95.78 | 98.69 | 98.39 | 99.26 | 98.16 | 97.40 | 97.21 | 96.79 | 98.88 | 98.34 | 97.69 |
| precision | 94.53 | 97.34 | 99.23 | 97.12 | 95.19 | 96.58 | 98.34 | 97.92 | 98.26 | 98.49 | 97.90 | 98.32 | 95.40 | 99.41 | 98.77 | 97.52 |
| recall | 97.63 | 98.57 | 99.52 | 99.32 | 99.03 | 97.75 | 99.31 | 99.11 | 99.31 | 99.17 | 99.22 | 98.78 | 97.79 | 99.43 | 99.37 | 98.89 |
| Sample | Classical PTD Algorithm | AGPTD Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|
| T.I (%) | T.II (%) | T.E. (%) | kp (%) | T.I (%) | T.II (%) | T.E. (%) | kp (%) | |
| 11 | 15.96 | 3.65 | 10.76 | 78.48 | 2.37 | 7.58 | 4.60 | 90.50 |
| 12 | 4.89 | 1.48 | 3.25 | 93.51 | 1.43 | 2.83 | 2.11 | 95.69 |
| 21 | 0.46 | 18.53 | 4.25 | 86.34 | 0.48 | 2.71 | 0.97 | 97.05 |
| 22 | 2.68 | 5.87 | 3.63 | 91.33 | 0.68 | 6.49 | 2.49 | 94.05 |
| 23 | 3.69 | 4.34 | 4.00 | 91.97 | 0.97 | 5.58 | 3.15 | 93.63 |
| 24 | 3.38 | 7.45 | 4.42 | 88.50 | 2.25 | 9.14 | 4.14 | 89.34 |
| 31 | 7.91 | 1.03 | 4.78 | 90.43 | 0.69 | 1.95 | 1.27 | 97.36 |
| 41 | 25.81 | 1.89 | 13.91 | 72.21 | 0.89 | 2.10 | 1.50 | 96.78 |
| 42 | 4.68 | 0.26 | 1.62 | 96.15 | 0.69 | 0.73 | 0.72 | 98.22 |
| 51 | 0.13 | 12.00 | 2.72 | 91.68 | 0.83 | 5.44 | 1.84 | 94.57 |
| 52 | 1.78 | 14.21 | 3.07 | 83.63 | 0.78 | 18.16 | 2.60 | 85.42 |
| 53 | 8.58 | 16.76 | 8.91 | 39.13 | 1.22 | 40.17 | 2.79 | 61.94 |
| 54 | 1.25 | 4.93 | 3.23 | 93.52 | 2.21 | 4.06 | 3.21 | 93.56 |
| 61 | 1.94 | 6.23 | 2.08 | 74.52 | 0.57 | 16.50 | 1.12 | 83.16 |
| 71 | 0.14 | 13.25 | 1.63 | 91.44 | 0.63 | 9.72 | 1.66 | 91.57 |
| Avg | 5.55 | 7.46 | 4.82 | 84.19 | 1.11 | 8.88 | 2.28 | 90.86 |
| Std | 6.98 | 6.00 | 3.56 | 14.39 | 0.65 | 10.04 | 1.15 | 9.10 |
| Sample | Zhang (2013) [24] | Lin (2014) [25] | Nie (2017) [26] | Cai (2019) [27] | Chen (2023) [36] | AGPTD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T.I | T.II | T.I | T.II | T.I | T.II | T.I | T.II | T.I | T.II | T.I | T.II | |
| 11 | 25.67 | 8.84 | 26.28 | 10.40 | 37.24 | 1.35 | 7.51 | 27.98 | 29.87 | 7.59 | 2.37 | 7.58 |
| 12 | 8.13 | 3.61 | 6.56 | 3.31 | 11.86 | 1.05 | 4.68 | 13.21 | 15.00 | 7.21 | 1.43 | 2.83 |
| 21 | 1.17 | 18.23 | 0.85 | 24.45 | 6.20 | 4.49 | 16.27 | 6.87 | 5.07 | 9.18 | 0.48 | 2.71 |
| 22 | 19.05 | 3.44 | 6.43 | 15.44 | 20.82 | 3.60 | 2.22 | 8.73 | 17.57 | 9.43 | 0.68 | 6.49 |
| 23 | 19.25 | 4.05 | 23.21 | 4.64 | 35.63 | 1.60 | 3.48 | 14.13 | 24.45 | 8.75 | 0.97 | 5.58 |
| 24 | 22.86 | 13.41 | 3.99 | 8.70 | 32.58 | 15.42 | 3.13 | 48.49 | 17.59 | 12.05 | 2.25 | 9.14 |
| 31 | 2.10 | 2.59 | 0.54 | 2.59 | 2.02 | 2.41 | 12.74 | 0.91 | 15.79 | 6.31 | 0.69 | 1.95 |
| 41 | 39.54 | 1.44 | 62.22 | 1.92 | 52.03 | 0.32 | 25.56 | 0.35 | 41.24 | 3.00 | 0.89 | 2.10 |
| 42 | 9.72 | 1.55 | 19.02 | 0.54 | 6.69 | 1.26 | 9.71 | 2.71 | 4.31 | 2.97 | 0.69 | 0.73 |
| 51 | 2.05 | 16.97 | 2.22 | 10.81 | 2.90 | 2.77 | 0.07 | 15.81 | 0.68 | 11.27 | 0.83 | 5.44 |
| 52 | 12.53 | 16.77 | 6.46 | 16.89 | 16.14 | 2.96 | 0.98 | 35.90 | 22.42 | 6.22 | 0.78 | 18.16 |
| 53 | 4.25 | 37.22 | 9.62 | 16.41 | 20.22 | 0.72 | 2.72 | 33.05 | 10.35 | 3.96 | 1.22 | 40.17 |
| 54 | 3.59 | 8.82 | 3.16 | 17.23 | 6.76 | 1.78 | 1.16 | 3.81 | 8.44 | 2.53 | 2.21 | 4.06 |
| 61 | 16.62 | 2.49 | 6.26 | 6.55 | 8.17 | 2.07 | 0.39 | 13.93 | 2.58 | 2.24 | 0.57 | 16.50 |
| 71 | 10.07 | 13.39 | 2.62 | 25.65 | 5.24 | 0.79 | 0.28 | 15.71 | 4.57 | 8.76 | 0.63 | 9.72 |
| Avg | 13.11 | 10.19 | 11.96 | 11.04 | 17.63 | 2.84 | 6.06 | 16.11 | 14.66 | 6.76 | 1.11 | 8.88 |
| Std | 10.82 | 9.65 | 16.06 | 8.04 | 15.21 | 3.66 | 7.26 | 14.23 | 11.38 | 3.22 | 0.65 | 10.04 |
| Sample | 11 | 12 | 21 | 22 | 23 | 24 | 31 | 41 | 42 | 51 | 52 | 53 | 54 | 61 | 71 | Avg | Std | Akp |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mongus (2012) [32] | 11.01 | 5.17 | 1.98 | 6.56 | 5.83 | 7.98 | 3.34 | 3.71 | 5.72 | 2.59 | 7.11 | 8.52 | 6.73 | 4.85 | 3.14 | 5.62 | 2.47 | 81.74 |
| Chen (2013) [39] | 13.01 | 3.38 | 1.34 | 4.67 | 5.24 | 6.29 | 1.11 | 5.58 | 1.72 | 1.64 | 4.18 | 7.29 | 3.09 | 1.81 | 1.33 | 4.11 | 3.17 | 86.27 |
| Pingel (2013) [34] | 8.28 | 2.92 | 1.10 | 3.35 | 4.61 | 3.52 | 0.91 | 5.91 | 1.48 | 1.43 | 3.82 | 2.43 | 2.27 | 0.86 | 1.65 | 2.97 | 2.07 | 90.02 |
| Zhang (2013) [24] | 18.49 | 5.92 | 4.95 | 14.18 | 12.06 | 20.26 | 2.32 | 20.44 | 3.94 | 5.31 | 12.98 | 5.58 | 6.40 | 16.13 | 10.44 | 10.63 | 6.22 | 68.93 |
| Hu (2014) [40] | 8.31 | 2.58 | 0.95 | 3.23 | 4.42 | 3.80 | 0.90 | 5.91 | 0.73 | 2.04 | 2.52 | 2.74 | 2.35 | 0.84 | 1.50 | 2.85 | 2.10 | 90.32 |
| Lin (2014) [25] | 19.50 | 4.78 | 6.08 | 9.24 | 14.43 | 5.28 | 1.61 | 32.00 | 5.95 | 4.09 | 7.56 | 9.90 | 10.72 | 6.27 | 5.22 | 9.51 | 7.66 | 71.80 |
| Mongus (2014) [41] | 10.18 | 3.32 | 1.37 | 4.25 | 6.18 | 4.50 | 3.52 | 4.07 | 2.82 | 6.11 | 4.48 | 4.10 | 4.58 | 3.49 | 3.17 | 4.41 | 2.00 | 83.83 |
| Yang (2016) [33] | 10.52 | 2.68 | 2.76 | 4.65 | 4.48 | 3.40 | 1.58 | 2.49 | 1.26 | 3.49 | 2.92 | 3.11 | 3.13 | 1.23 | 4.90 | 3.51 | 2.24 | 87.40 |
| Zhang (2016) [42] | 12.01 | 2.97 | 3.42 | 8.94 | 4.79 | 2.87 | 1.61 | 5.14 | 1.58 | 3.08 | 3.93 | 5.20 | 3.18 | 1.49 | 5.71 | 4.39 | 2.86 | 83.86 |
| Chen (2017) [43] | 9.50 | 2.85 | 1.11 | 3.80 | 4.47 | 3.63 | 1.29 | 3.81 | 0.85 | 1.87 | 3.13 | 3.42 | 2.76 | 0.95 | 2.06 | 3.03 | 2.14 | 89.44 |
| Nie (2017) [26] | 18.79 | 6.62 | 5.60 | 14.89 | 18.08 | 24.57 | 2.14 | 27.13 | 2.43 | 2.85 | 14.43 | 19.37 | 4.00 | 6.89 | 3.68 | 11.43 | 8.60 | 67.88 |
| Wang (2017) [44] | 19.49 | 4.02 | 2.05 | 4.97 | 5.91 | 6.34 | 1.58 | 2.17 | 1.07 | 8.09 | 4.90 | 3.46 | 5.62 | 1.93 | 5.42 | 5.13 | 4.46 | 80.94 |
| Bayram (2018) [45] | 13.56 | 4.35 | 0.89 | 6.65 | 11.21 | 7.27 | 2.63 | 8.49 | 2.13 | 2.00 | 5.42 | 5.23 | 3.31 | 0.99 | 1.90 | 5.07 | 3.79 | 84.16 |
| Cai (2019) [27] | 16.24 | 8.85 | 14.18 | 4.25 | 8.52 | 15.59 | 7.28 | 13.04 | 4.75 | 3.51 | 4.65 | 3.95 | 2.58 | 0.86 | 2.03 | 7.35 | 5.16 | 78.49 |
| Meng (2019) [19] | 10.20 | 2.97 | 1.35 | 3.82 | 5.03 | 5.22 | 2.13 | 6.40 | 0.66 | 1.71 | 3.39 | 6.58 | 2.93 | 2.10 | 1.34 | 3.72 | 2.57 | 87.16 |
| Buján (2020) [46] | 10.64 | 2.49 | 1.00 | 5.06 | 5.67 | 4.51 | 1.22 | 1.67 | 0.81 | 1.77 | 3.40 | 3.60 | 2.39 | 1.00 | 1.34 | 3.10 | 2.61 | 89.38 |
| Chen (2021) [47] | 8.72 | 2.56 | 0.96 | 3.78 | 4.13 | 4.14 | 0.78 | 3.11 | 1.53 | 1.43 | 2.25 | 2.30 | 2.58 | 0.97 | 1.23 | 2.70 | 2.02 | 90.84 |
| Chen (2023) [36] | 20.36 | 11.20 | 5.98 | 15.03 | 17.02 | 16.07 | 11.42 | 22.07 | 3.36 | 2.99 | 20.72 | 10.09 | 5.26 | 2.57 | 5.04 | 11.28 | 6.92 | 70.08 |
| AGPTD | 4.60 | 2.11 | 0.97 | 2.49 | 3.15 | 4.14 | 1.27 | 1.50 | 0.72 | 1.84 | 2.60 | 2.79 | 3.21 | 1.12 | 1.66 | 2.28 | 1.15 | 90.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Xiang, M.; Zhang, T.; Zhou, J. An Improved Adaptive Grid-Based Progressive Triangulated Irregular Network Densification Algorithm for Filtering Airborne LiDAR Data. Remote Sens. 2024, 16, 3846. https://doi.org/10.3390/rs16203846
Zheng J, Xiang M, Zhang T, Zhou J. An Improved Adaptive Grid-Based Progressive Triangulated Irregular Network Densification Algorithm for Filtering Airborne LiDAR Data. Remote Sensing. 2024; 16(20):3846. https://doi.org/10.3390/rs16203846
Chicago/Turabian StyleZheng, Jinjun, Man Xiang, Tao Zhang, and Ji Zhou. 2024. "An Improved Adaptive Grid-Based Progressive Triangulated Irregular Network Densification Algorithm for Filtering Airborne LiDAR Data" Remote Sensing 16, no. 20: 3846. https://doi.org/10.3390/rs16203846
APA StyleZheng, J., Xiang, M., Zhang, T., & Zhou, J. (2024). An Improved Adaptive Grid-Based Progressive Triangulated Irregular Network Densification Algorithm for Filtering Airborne LiDAR Data. Remote Sensing, 16(20), 3846. https://doi.org/10.3390/rs16203846







